🧠:[<think>Alright, let's tackle this problem step by step. Okay, so Kosta has taken several math tests already, and depending on his score on the next test, his average will either be 91 or 86. We need to find out how many tests he's taken so far before this next one. First, let's make sure I understand the problem correctly. There are two scenarios here: 1. If he scores 89 on the next test, his average becomes 91.2. If he scores 64 on the next test, his average becomes 86.We need to find the number of tests he's already taken, which I'll call 'n'. Let's denote the total points he's earned so far as 'S'. Then, after taking one more test (so total tests become n+1), his average will be either (S + 89)/(n + 1) = 91 or (S + 64)/(n + 1) = 86. So, we have two equations here:1. (S + 89)/(n + 1) = 912. (S + 64)/(n + 1) = 86Hmm, so with two equations and two variables (S and n), we can solve for both. Let me write those equations out more clearly.First equation: S + 89 = 91(n + 1)Second equation: S + 64 = 86(n + 1)Now, since both equations equal S plus some number, maybe I can subtract them to eliminate S. Let me try that.Subtract the second equation from the first:(S + 89) - (S + 64) = 91(n + 1) - 86(n + 1)Simplify the left side: S - S + 89 - 64 = 25Right side: (91 - 86)(n + 1) = 5(n + 1)So, we have 25 = 5(n + 1)Divide both sides by 5: 5 = n + 1Subtract 1: n = 4Wait, so according to this, Kosta has taken 4 tests so far. Let me check if that makes sense.Let's plug n = 4 back into the original equations to find S.First equation: S + 89 = 91(4 + 1) = 91*5 = 455So, S = 455 - 89 = 366Second equation: S + 64 = 86(5) = 430So, S = 430 - 64 = 366Okay, so both equations give S = 366 when n = 4, which checks out. That seems consistent.So, Kosta has taken 4 tests so far.Wait, just to make sure I didn't make any mistakes in the algebra. Let's go through it again.We have:Equation 1: S = 91(n + 1) - 89Equation 2: S = 86(n + 1) - 64Set them equal since both equal S:91(n + 1) - 89 = 86(n + 1) - 64Subtract 86(n + 1) from both sides:5(n + 1) - 89 = -64Add 89 to both sides:5(n + 1) = 25Divide by 5: n + 1 = 5 => n = 4Yep, same result. So, that seems solid. So, Kosta has taken 4 tests so far.But wait, let me think again. If he takes one more test, that makes it 5 tests total. The average after adding 89 is 91, and after adding 64 is 86. Let's confirm with the numbers.Total points after 5 tests with 89: 366 + 89 = 455. Average is 455/5 = 91. Correct.Total points after 5 tests with 64: 366 + 64 = 430. Average is 430/5 = 86. Correct.Therefore, the answer is 4 tests taken so far. Hmm. All the numbers check out. I think that's it. So, the answer is 4.Final Answerboxed{4}</think>Let ( n ) be the number of math tests Kosta has taken so far, and let ( S ) be the total points he has earned from these tests. We are given two scenarios:1. If Kosta scores 89 on the next test, his average will be 91.2. If Kosta scores 64 on the next test, his average will be 86.We can set up the following equations based on these scenarios:1. (frac{S + 89}{n + 1} = 91)2. (frac{S + 64}{n + 1} = 86)Rewriting these equations, we get:1. ( S + 89 = 91(n + 1) )2. ( S + 64 = 86(n + 1) )Subtracting the second equation from the first to eliminate ( S ):[(S + 89) - (S + 64) = 91(n + 1) - 86(n + 1)]Simplifying both sides:[25 = 5(n + 1)]Solving for ( n ):[5 = n + 1 implies n = 4]To verify, we check the total points ( S ):1. From the first equation: ( S + 89 = 91(4 + 1) implies S = 455 - 89 = 366 )2. From the second equation: ( S + 64 = 86(4 + 1) implies S = 430 - 64 = 366 )Both calculations confirm ( S = 366 ), which is consistent. Therefore, Kosta has taken (boxed{4}) math tests so far.,<think>Okay, so let me try to figure out this problem. Hmm, Kosta has taken some math tests already, and depending on his next test score, his average changes. If he scores 89, the average becomes 91, and if he scores 64, the average becomes 86. They want to know how many tests he's taken so far. Alright, let's break this down.First, let me recall that an average is the total points divided by the number of tests. So, if I let the number of tests he's already taken be 'n', then his total points from those tests would be something like 'total'. Then, when he takes another test, the total number of tests becomes 'n + 1', and the total points would be 'total + next score'.So, the two scenarios given are:1. If he scores 89 on the next test, the average is 91.2. If he scores 64 on the next test, the average is 86.So, translating these into equations. Let me define variables first. Let me call the number of tests he's already taken as 'n', and the total points he's earned from those tests as 'S'. Then:For the first scenario: (S + 89)/(n + 1) = 91For the second scenario: (S + 64)/(n + 1) = 86So, we have two equations here with two variables, S and n. So, I can solve these equations to find n.Let me write them down again:1. (S + 89) = 91(n + 1)2. (S + 64) = 86(n + 1)Hmm, okay, if I subtract the second equation from the first, maybe that will eliminate S. Let's try that.First equation: S + 89 = 91(n + 1)Second equation: S + 64 = 86(n + 1)Subtracting second from first:(S + 89) - (S + 64) = 91(n + 1) - 86(n + 1)Simplify left side: S - S + 89 - 64 = (91 - 86)(n + 1)So, 25 = 5(n + 1)Then, divide both sides by 5: 5 = n + 1So, n + 1 = 5 => n = 4Wait, so that means he's taken 4 tests so far? Let me check.If n is 4, then let's find S from one of the equations. Let's take the first equation: S + 89 = 91(4 + 1) => S + 89 = 91*5 => 91*5 is 455. So, S = 455 - 89 = 366.Then check the second scenario: S + 64 = 366 + 64 = 430. Then divide by (4 + 1)=5: 430/5=86, which matches the second average. So, both check out.So, the number of tests he's taken so far is 4. That seems right.Wait, but let me just verify again. Let me compute the average in both cases.If he took 4 tests with total 366, then average before the next test is 366/4 = 91.5. Wait, but the problem says if he scores 89, the average becomes 91, which would be (366 + 89)/5 = 455/5 = 91. Correct. Similarly, 64 would be (366 + 64)/5 = 430/5 = 86. Also correct.But wait, his current average is 366/4 = 91.5. The problem doesn't mention his current average, just the averages after the next test. So, that seems fine. The answer is 4.But let me just think again. The problem says "how many math tests has Kosta taken so far?" So, before the next test, which would be n=4. So, the answer is 4. Yeah, that's right.Alternatively, maybe I can think of the difference in scores. If he scores 89 vs 64, that's a difference of 25 points. The difference in the average is 91 - 86 = 5. So, 25 points difference affects the average by 5 points. Since the average is over (n + 1) tests, then 25 = 5*(n + 1). So, 25/5 = n + 1 => 5 = n + 1 => n=4. So, that's another way to see it. That also gives n=4. So, that confirms it.Therefore, the number of tests he's taken so far is 4.Final AnswerKosta has taken boxed{4} math tests so far.</think>Let ( n ) be the number of math tests Kosta has taken so far, and let ( S ) be the total points he has earned from those tests. We are given two scenarios:1. If Kosta scores 89 on the next test, the average will be 91.2. If Kosta scores 64 on the next test, the average will be 86.We can translate these scenarios into the following equations:1. (frac{S + 89}{n + 1} = 91)2. (frac{S + 64}{n + 1} = 86)Rewriting these equations, we get:1. ( S + 89 = 91(n + 1) )2. ( S + 64 = 86(n + 1) )Subtracting the second equation from the first:[(S + 89) - (S + 64) = 91(n + 1) - 86(n + 1)]Simplifying both sides:[25 = 5(n + 1)]Solving for ( n ):[25 = 5(n + 1) implies 5 = n + 1 implies n = 4]To verify, we calculate ( S ) using the first equation:[S + 89 = 91(4 + 1) implies S + 89 = 455 implies S = 455 - 89 = 366]Checking the second scenario:[frac{366 + 64}{4 + 1} = frac{430}{5} = 86]Both scenarios are satisfied, confirming that the number of tests Kosta has taken so far is (boxed{4}).]

🔑:Solution. Let n be the number of math tests taken so far, and x be the total number of points earned from these tests. If on the next math test Costa scores 89 points, then the total number of points earned will be x+89, and the number of tests will be n+1. According to this, we get the equation frac{x+89}{n+1}=91. If on the next math test Costa scores 64 points, then the total number of points earned will be x+64, and the number of tests remains the same, i.e., n+1. Then we get the equation frac{x+64}{n+1}=86. If we divide these equations, we get frac{x+89}{x+64}=frac{91}{86}, from which we find x=366. Finally, n+1=frac{366+89}{91}, i.e., n=4. Therefore, Costa has taken 4 math tests.

🧠:[<think>Okay, let me try to figure out this problem. So, we have 101 numbers arranged in a circle. The condition is that among any five consecutive numbers, there must be at least two positive ones. The question is asking for the minimum number of positive numbers needed in total. Hmm, interesting. Alright, let me start by breaking down the problem.First, the numbers are in a circle, which means the sequence wraps around. So, the first number is next to the last one. That's important because any five consecutive numbers could start anywhere, including overlapping the end and the beginning.The key condition here is that in any five consecutive numbers, there are at least two positive numbers. So, if I try to minimize the number of positive numbers overall, I need to arrange them in such a way that this condition is satisfied with as few positives as possible. But I have to make sure that no five consecutive numbers have fewer than two positives.Let me think about how to distribute the positive numbers. If I can space them out so that they are as far apart as possible without violating the five-consecutive condition, that might lead to the minimal total. So, maybe a repeating pattern where every certain number of positions, there's a positive number. Let's explore that.Suppose we try to have as many non-positive numbers as possible between the positive ones. Let's denote a positive number as P and a non-positive as N. If we can figure out the maximum number of Ns we can have between Ps without violating the five-consecutive rule, that would help.The rule says in any five consecutive numbers, there are at least two Ps. So, in other words, there can't be five numbers with fewer than two Ps. Which is equivalent to saying that in any five consecutive numbers, you can have at most three Ns. Because if you have four or five Ns in five numbers, that would mean only one or zero Ps, which violates the condition.So, in any window of five, maximum three Ns allowed. Therefore, the number of Ps in any five consecutive numbers must be at least two. Therefore, the spacing between Ps must be such that in any five-number window, you can't have four Ns. So, the maximum number of Ns between Ps should be three. Wait, maybe?Wait, if we have a sequence like P N N N N P N N N N P..., but since it's a circle, we have to make sure that this pattern doesn't cause a window of five with four Ns. Let's check. Suppose the pattern is P followed by four Ns, repeating. Then, looking at five consecutive numbers: starting at the P, we have P N N N N. That's one P and four Ns. Wait, that violates the condition because there's only one P in five numbers. So that pattern doesn't work. So, maybe the maximum number of Ns between Ps is three.Let me test that. If the pattern is P followed by three Ns: P N N N P N N N P... So, each P is separated by three Ns. Let's check consecutive windows.Take the first five numbers: P N N N P. That has two Ps and three Ns. Then the next window: N N N P N. That has one P and four Ns. Wait, that's bad. So in this case, the second window has only one P. Which violates the condition. So, this spacing is insufficient.Hmm, so maybe even three Ns between Ps is too much. Let's try two Ns between Ps. So, the pattern is P N N P N N P... Then, let's check the windows.First five: P N N P N. That's two Ps and three Ns. Next window: N N P N N. That's one P and four Ns. Again, violating the condition. So, same problem.Wait, so if I have two Ns between Ps, then in some windows, you can have only one P. Hmm. So perhaps even two Ns between Ps is too much? Let's try one N between Ps. So, P N P N P N... Then, the first five numbers: P N P N P. That's three Ps and two Ns. Next window: N P N P N. That's two Ps and three Ns. Then the next window: P N P N P. Again three Ps. So, in this case, every window of five would have at least two Ps. Wait, let's check.Wait, let's take five consecutive numbers starting at the first position: P N P N P – three Ps. Starting at the second position: N P N P N – two Ps. Starting at the third position: P N P N P – three Ps. Starting at the fourth position: N P N P N – two Ps. And so on. So, in this case, every other window has two Ps and the others have three. So, that satisfies the condition. Because even the windows with two Ps have two, which meets the requirement. So, this pattern works.But in this case, we have Ps separated by one N. So, the pattern is P N P N P N..., which would result in every other number being P. So, for 101 numbers arranged in a circle, this would require approximately 50 or 51 Ps. But since the problem asks for the minimum number of Ps, this is probably not the minimal arrangement.Wait, but perhaps we can find a better arrangement where the Ps are spaced a bit more, but still ensuring that in any five consecutive numbers, there are at least two Ps. Let's think.Suppose we have a pattern where Ps are separated by two Ns. Wait, earlier when we tried two Ns between Ps, the window that starts at the second position would have N N P N N, but that's four Ns? Wait, no. Wait, if the pattern is P N N P N N P..., then five consecutive numbers starting at the first P: P N N P N. That's two Ps and three Ns. Starting at the next position: N N P N N. That's one P and four Ns. Which violates the condition. So, that's bad. So, two Ns between Ps is insufficient.Hmm. So, what if we try a different approach. Maybe alternating blocks of Ns and Ps. For example, have two Ps followed by three Ns. Let's see. So, the pattern would be P P N N N P P N N N... Let's check the windows.First five: P P N N N – two Ps and three Ns. Then next five: P N N N P – two Ps and three Ns. Then N N N P P – two Ps and three Ns. Then N N P P N – two Ps and three Ns. Then N P P N N – two Ps and three Ns. Then P P N N N – same as before. So, actually, in this pattern, every window of five has exactly two Ps. So that works. So, this pattern satisfies the condition. And in this case, the number of Ps would be two out of every five numbers. So, in 101 numbers, how many would that be?Well, 101 divided by 5 is 20.2. So, 20 full blocks of five numbers, each containing two Ps, which would give 40 Ps, and then the remaining one number would be part of the next block. Since the pattern is two Ps followed by three Ns, the next number after 100 would be a P. So, total Ps would be 20*2 +1=41. Wait, but since it's a circle, the pattern has to wrap around. So, if the last block is incomplete, does that affect the count?Wait, if we have 101 numbers arranged in a circle with a repeating pattern of P P N N N, then how many full blocks are there? 101 divided by 5 is 20 with a remainder of 1. So, 20 full blocks (each of 5 numbers) and one remaining number. But since it's a circle, the last number is adjacent to the first. So, if the last number is a P (since the next number after 100 would be the 101st, which is a P in the pattern), but the first two numbers are Ps. So, the last number (101st) is a P, and the first number is a P. So, between the 101st P and the first P, there are two Ps in a row. So, the total number of Ps would be 20*2 +1=41? Wait, let's verify.Each block of 5 has 2 Ps. 20 blocks would account for 100 numbers, with 20*2=40 Ps. Then the 101st number would be the start of the next block, which is a P. So, total 41 Ps. However, since it's a circle, the 101st number is next to the first number. The first two numbers are Ps, and the 101st is a P, so the sequence ends with P, P, N, N, N,... So, the 100th number would be a N, 101st is P, and 1st is P, 2nd is P. So, the last block (numbers 97-101) would be N, N, P, P, N? Wait, maybe my arithmetic is getting confused here. Let me try to count.Alternatively, maybe it's better to model the entire circle. Let's say the pattern is P P N N N repeating. So, positions 1-5: P P N N N; 6-10: P P N N N; ... up to 100. Then position 101 would be the start of the next block: P. But since it's a circle, position 101 is adjacent to position 1. So, positions 100 is N, 101 is P, and 1 is P, 2 is P. So, the last block (positions 97-101): positions 97-100: N N N P (from previous block), but wait, maybe not. Wait, each block is 5 numbers. Let's see, block 1: 1-5, block 2:6-10,..., block 20: 96-100. Then positions 101 would be the start of block 21, which is P. So, position 101: P, and then positions 1-4 would be P, N, N, N. Wait, but in a circle, position 101 is next to position 1. So, the sequence around position 101 would be 100 (N), 101 (P), 1 (P), 2 (P), 3 (N), etc. So, looking at positions 99-103 (which wraps around to 1-3): 99: N, 100: N, 101: P, 1: P, 2: P. So, that's three Ps in a row. Wait, but the pattern is P P N N N, so after two Ps, there should be three Ns. However, at the end, we have only one P at position 101, followed by P at 1 and 2. So, actually, the transition from block 20 to block 21 is causing two Ps in a row (positions 100: N, 101: P, 1: P). So, the pattern is broken here. Therefore, the total number of Ps would be 20 blocks * 2 Ps = 40, plus the one extra P at position 101, totaling 41. But since position 1 is also a P, which is part of the first block. Wait, maybe this is getting too complicated. Alternatively, perhaps arranging 101 numbers with the repeating pattern P P N N N would result in 41 Ps. But let's check if this arrangement actually satisfies the condition.Take any five consecutive numbers. If the five numbers are within a single block (P P N N N) or span two blocks. For example, starting at position 3: N N N P P – which has two Ps. Starting at position 4: N N P P N – two Ps. Starting at position 5: N P P N N – two Ps. Starting at position 6: P P N N N – two Ps. So, all these windows have exactly two Ps. However, when the window wraps around the circle, like positions 100, 101, 1, 2, 3: 100 is N, 101 is P, 1 is P, 2 is P, 3 is N. So, that's three Ps, which is okay. Wait, three Ps would still satisfy the condition. Another window: positions 99,100,101,1,2: 99 is N, 100 is N, 101 is P, 1 is P, 2 is P – three Ps. So, that's fine. So, in this arrangement, every window of five numbers has either two or three Ps, so the condition is satisfied. Therefore, this arrangement uses 41 Ps. But the problem is asking for the minimal number. Is 41 the minimum, or can we do better?Wait, maybe there's a more efficient pattern. Let me think. Suppose instead of two Ps followed by three Ns, maybe we can have a longer block of Ns but compensate by placing Ps in a way that every five consecutive numbers still have at least two Ps.Alternatively, let's model this as a graph or use some mathematical approach. Let's denote the positions as 1 to 101 arranged in a circle. Each position can be P or N. The constraint is that any five consecutive positions must have at least two Ps. We need to minimize the total number of Ps.This seems similar to a covering problem. In covering problems, you want to cover certain regions with the minimal number of resources. Here, each P "covers" the windows it is part of. Each P is part of five different windows (the window starting at its position, the one before, etc.). So, we need to place Ps such that every window has at least two Ps.Alternatively, perhaps we can model this as a linear programming problem, but since we need an integer solution, maybe combinatorics would be better.Alternatively, let's consider the maximum number of Ns allowed. Since each window of five can have at most three Ns, the total number of Ns in the entire circle can't exceed some number. Wait, but because the windows overlap, it's tricky. Each N is part of five different windows. So, if there are too many Ns, some window will have too many Ns.Alternatively, perhaps use the principle of inclusion-exclusion or averaging. Let's consider each position is part of five windows. So, each P contributes to five windows. Let T be the total number of Ps counted across all windows. Since each window must have at least two Ps, the total T must be at least 2*101 (since there are 101 windows, each requiring two Ps). But each P is counted in five windows. So, if there are k Ps, then T = 5k. So, 5k >= 2*101. Therefore, k >= (2*101)/5 = 202/5 = 40.4. Since k must be an integer, k >= 41. So, this gives a lower bound of 41 Ps. Therefore, the minimal number of Ps cannot be less than 41. And we found an arrangement with 41 Ps that satisfies the conditions. Therefore, 41 must be the minimal number.Wait, that seems convincing. Let me check again. So, the total number of Ps is k. Each P is in five windows, so total Ps counted over all windows is 5k. Each window must have at least two Ps, so total over all windows is at least 2*101=202. Therefore, 5k >= 202, so k >= 202/5 = 40.4, so k >=41. Therefore, 41 is the minimal number. Since we have constructed an example with 41 Ps, that must be the minimum.Therefore, the answer is 41. So, I think that's the solution.Final AnswerThe minimum number of positive numbers required is boxed{41}.</think>Given 101 numbers arranged in a circle, we need to determine the minimum number of positive numbers such that any five consecutive numbers contain at least two positive numbers. To solve this, we consider the following key steps:1. Condition Analysis: Any five consecutive numbers must contain at least two positive numbers. This means we cannot have a sequence of five numbers with more than three non-positive numbers.2. Pattern Exploration: We explored different patterns of positive (P) and non-positive (N) numbers to find the minimal arrangement. A valid pattern must ensure that every window of five consecutive numbers contains at least two Ps.3. Repeating Pattern: We considered a repeating pattern of P P N N N. This pattern ensures that every five consecutive numbers contain exactly two positive numbers. However, since the total number of numbers (101) is not a multiple of 5, we need to check the wrap-around effect.4. Verification: The pattern P P N N N repeated around the circle results in 20 full blocks (each block containing 2 Ps and 3 Ns) and one additional P at position 101. This gives a total of (20 times 2 + 1 = 41) positive numbers.5. Lower Bound Calculation: Using the principle of inclusion-exclusion, we calculated the lower bound for the number of positive numbers. Each positive number is counted in five windows, and each window must contain at least two positive numbers. This gives (5k geq 2 times 101), leading to (k geq 40.4), hence (k geq 41).Thus, the minimum number of positive numbers required is (boxed{41}).,<think>Okay, so I need to figure out the minimum number of positive numbers in a circle of 101 numbers where every five consecutive numbers have at least two positive ones. Hmm, let me start by understanding the problem better.First, there are 101 numbers arranged in a circle. That means the sequence wraps around, so the first number is next to the last one. The condition is that in any five consecutive numbers, there must be at least two positive numbers. The question is asking for the smallest possible number of positive numbers needed to satisfy this condition.Let me think about how to approach this. Since it's a circular arrangement, the pattern of positive and non-positive numbers must be periodic in a way that covers the entire circle without violating the condition. If I can find a repeating pattern that meets the requirement with as few positive numbers as possible, that might give me the answer.Let me consider smaller cases first. Suppose instead of 101 numbers, there were fewer. Let's see if there's a pattern or formula that can be generalized.For example, if we had 5 numbers in a circle, the condition requires that among any five consecutive numbers (which is the entire circle in this case), there are at least two positive numbers. So, in this case, all five numbers must have at least two positives. The minimum would be 2. But 101 is a much larger number.But 101 is not a multiple of 5. Let me see. Maybe if I can find a repeating block of numbers where each block has a certain number of positive numbers, and then check how these blocks fit into 101 numbers.Wait, but since it's a circle, the pattern has to repeat seamlessly. So, the length of the repeating block must divide 101. But 101 is a prime number. So, the only possible repeating blocks would be of length 1 or 101. Hmm, that complicates things. So maybe a periodic pattern with a period that divides 101, but since it's prime, the period has to be 1 or 101. But a period of 1 would mean all numbers are the same, which can't be because we need some positives and some non-positives. A period of 101 would mean the entire sequence is the pattern. So, maybe not a periodic pattern in the traditional sense.Alternatively, maybe there's a way to arrange the positive numbers as sparsely as possible, while still satisfying the condition that every five consecutive numbers contain at least two positives.To minimize the number of positive numbers, we want to place them as far apart as possible. However, the constraint is that in any five consecutive numbers, there must be at least two. So, if I can figure out the maximum gap allowed between positive numbers without violating the condition, that should lead me to the minimum number.Let me try to model this. Suppose we have a sequence of numbers where most are non-positive (zero or negative), and some are positive. We need to place the positive numbers such that in any five-number window, there are at least two.If I try to space the positive numbers as evenly as possible, how far apart can they be? Let's say between two consecutive positive numbers, there are k non-positive numbers. Then, the pattern would be P, N^k, P, N^k, ..., where P is a positive number and N is a non-positive.Now, in this case, the number of numbers between two positives is k+1 (including the starting P). To ensure that in any five consecutive numbers there are at least two positives, we need that in the worst case, a window of five numbers can't have fewer than two positives.If the positive numbers are spaced with k non-positives in between, then the maximum number of consecutive non-positives is k. So, the largest possible run of non-positives is k. If k is too large, then we can have a window of five numbers that includes too many non-positives.Wait, for example, if k is 3, meaning between two positives there are 3 non-positives, then the pattern is P, N, N, N, P, N, N, N, P, etc. In this case, looking at a window starting right after a P: N, N, N, P, N. That window has only one P, which violates the condition. Similarly, if k is 3, the window starting at the first N would have N, N, N, P, N, which only has one positive. So, that's bad. Therefore, k can't be 3.If k is 2, then the pattern is P, N, N, P, N, N, P, etc. Let's check a window: starting at N, N, P, N, N. That window has one positive. Still violating the condition. So k=2 is also too large.If k=1, then the pattern is P, N, P, N, P, N, etc. Let's check a window of five numbers. Let's say starting at N: N, P, N, P, N. That has two positives. Starting at P: P, N, P, N, P. That has three positives. Any window of five will have either two or three positives. So that works. But in this case, the number of positives is 51 (since 101 numbers with every other number positive). But we need the minimum number. So 51 is too much.Wait, but maybe there's a way to have larger gaps but still satisfy the condition. Let me think.Wait, the problem is that when you have a gap of k non-positives between positives, a window of five numbers could potentially include a single positive if the window is aligned to include the maximum number of non-positives. So, the key is to make sure that even in the worst-case alignment, there are at least two positives in any five-number window.So, if we have a pattern where between two positives there are at most m non-positives, then in a window of five numbers, the maximum number of non-positives we can have is m. But wait, no. Because depending on where the window is placed, it might include parts of two gaps.Wait, perhaps we need to find the maximum number of non-positives that can be in a five-number window. To ensure that there are at least two positives, the number of non-positives in any five-number window can't exceed three. So, if we can arrange the positives such that in any five-number window, there are at most three non-positives, which is equivalent to at least two positives.But maybe this is another way to look at it. Let's see, the problem states that among any five consecutive numbers, there are at least two positive. So, the complementary is that there are at most three non-positive numbers in any five consecutive numbers.Therefore, the maximum number of non-positives allowed in any five-number window is three. So, we need to arrange the non-positives such that no five consecutive numbers have more than three non-positives. Then, the minimum number of positives is the total number minus the maximum number of non-positives possible under this constraint.But how to compute the maximum number of non-positives? Since it's a circle, we need to arrange the non-positives in a way that every five-number window has at most three. To maximize the number of non-positives, we need to place them as densely as possible without violating the three-non-positives-in-five rule.This is similar to a scheduling problem where you can't have four non-positives in a row without a positive. Wait, actually, if you have four non-positives in a row, then a five-number window starting at the first non-positive would include four non-positives and the next number. If the next number is non-positive, that's five non-positives, which violates the condition. If the next number is positive, then the window would have four non-positives and one positive, which still violates the condition because there are four non-positives (i.e., only one positive). Wait, the condition is at least two positives in any five, so four non-positives would mean only one positive, which is insufficient. Therefore, we cannot have four non-positives in a row.Therefore, the maximum number of consecutive non-positives is three. So, the non-positives can be arranged in blocks of at most three, separated by at least one positive. So the pattern would be something like NNNPNNNPNNNP... etc.But in a circle, this pattern has to wrap around. Let's see. If we have blocks of three non-positives followed by one positive, repeating. Then, each block is four numbers: NNNP. So, 101 divided by 4 is 25.25, which is not an integer. So, 25 blocks would take 100 numbers, and then one remaining number. But this complicates the circular arrangement.Alternatively, maybe we can have a repeating pattern of three non-positives and one positive, but since 101 is not a multiple of four, the pattern would break at the end. But since it's a circle, the last block would connect back to the first, so we need to make sure that the connection doesn't create a window with more than three non-positives.Alternatively, perhaps arranging the non-positives in runs of three separated by singles positives. Let's see: if we have a positive, then three non-positives, then a positive, etc. So the pattern is P N N N P N N N P... This way, between two positives, there are three non-positives. However, let's check the windows.Take a window starting at the first non-positive: N N N P N. That's three non-positives, one positive, one non-positive. Wait, that's four non-positives in five numbers? Wait, no: N N N P N is four non-positives and one positive. Wait, that's four non-positives, which is more than allowed. So that violates the condition. Therefore, this pattern doesn't work.So, even if you have three non-positives, followed by a positive, the window that starts at the first non-positive would have four non-positives (the three N's and the next N after the P? Wait, no. Wait, let me check again.If the pattern is P N N N P N N N P..., then taking five consecutive numbers starting at the first N: N N N P N. The fifth number is the next N after the P. So in this window, you have N N N P N, which is four non-positives and one positive. That's only one positive, which violates the requirement of at least two positives in five numbers. Therefore, this pattern is invalid.Therefore, the maximum number of consecutive non-positives must be two. Let's test that. If we have two non-positives between positives: P N N P N N P N N..., then check the windows. Starting at the first N: N N P N N. That's three non-positives and two positives. Wait, three non-positives would mean two positives. Wait, no: N N P N N is two non-positives, one positive, two non-positives. Wait, that's two non-positives, then P, then two non-positives. So total in five numbers: four non-positives and one positive. Again, that's only one positive. Wait, but hold on, is that correct?Wait, no. Let me count again. If the pattern is P N N P N N P N N..., then the sequence is:1: P2: N3: N4: P5: N6: N7: P8: N9: N10: P...So, taking numbers 2-6: N, N, P, N, N. That's two Ns, a P, then two Ns. So in five numbers, there's one P and four Ns. That's only one positive, which is not enough. So again, violating the condition. So even two non-positives between positives leads to a window with only one positive. Therefore, the maximum number of consecutive non-positives must be one.Wait, so if between every two positives there is only one non-positive? Let's see. Then the pattern would be P N P N P N..., which is alternating positive and non-positive. In this case, any five consecutive numbers would have either two or three positives. For example, starting at P: P N P N P – three positives. Starting at N: N P N P N – two positives. So that works. But in this case, the number of positives would be 51 (since 101 is odd, 51 positives and 50 non-positives). But the question is asking for the minimum number of positives. 51 seems high. There must be a way to have fewer positives while still meeting the condition.Wait, maybe there's a way to have two non-positives between some positives, but not all, such that no five-number window has more than three non-positives. For example, using a pattern with two non-positives and then a positive, but sometimes inserting an extra positive to break up longer sequences. Let's see.Suppose we have a pattern like P N N P N P N N P N P... This alternates between two non-positives and one non-positive. Let's check the windows. Take the sequence P N N P N P N N P N P... If I take a window starting at the first N: N N P N P. That's two Ns, then P, N, P. So two positives. If I take a window starting at the second N: N P N P N. That's two Ns and three Ps? Wait, no. Let's look at the actual sequence:Positions:1: P2: N3: N4: P5: N6: P7: N8: N9: P10: N11: P...So, taking positions 2-6: N, N, P, N, P – two Ns, one P, one N, one P. That's two positives. Then positions 3-7: N, P, N, P, N – one positive? Wait, no: N, P, N, P, N. That's two positives. Hmm. Wait, positions 3: N, 4: P, 5: N, 6: P, 7: N. So two positives. Then positions 4-8: P, N, P, N, N – again two positives. Positions 5-9: N, P, N, N, P – two positives. Positions 6-10: P, N, N, P, N – two positives. Hmm, seems like every window of five has at least two positives. So maybe this pattern works. Let's see how many positives this would have.In this pattern, the sequence is P N N P N P N N P N P..., so the cycle is P N N P N P, which is six numbers. Wait, but 101 is not a multiple of six. Let's check.Wait, if the pattern is P N N P N P, that's six numbers with three positives. Then repeating this would give 3 positives every 6 numbers. For 101 numbers, how many would that be? 101 divided by 6 is 16 full cycles (96 numbers) with 5 remaining numbers. Each cycle has 3 positives, so 16*3=48 positives. The remaining 5 numbers would be P N N P N, which has 2 positives. So total positives: 48+2=50. But 101 numbers would require 16*6 +5=101. Wait, but this is a linear arrangement. However, since it's a circle, the pattern has to wrap around. So the last five numbers would connect back to the beginning. Therefore, the total number of positives might be different.Alternatively, maybe the pattern is not exactly six numbers, but a different repeating unit. Alternatively, maybe I can create a pattern where every group of five numbers has two positives, but overlapping groups share some numbers. But this is getting complicated.Alternatively, let's approach it mathematically. Let me denote the number of positive numbers as k. We need to arrange these k positives in the circle of 101 numbers such that every five consecutive numbers contain at least two positives. The question is to find the minimal k.To model this, consider that each positive number can "cover" some positions. However, because the condition is about every five consecutive numbers, each five-number window must have at least two positives. Therefore, each positive number can be part of multiple windows. But overlapping windows share some numbers.Alternatively, we can model this as a covering problem. Each positive number covers the windows it is part of. But since each window needs two positives, we need to place positives such that every window is "covered" by at least two positives.But this is a bit abstract. Let's think in terms of spacing. Let me try to determine the maximum number of non-positives that can be between two positives.Suppose between two consecutive positives, there are m non-positives. Then the number of numbers between two positives is m + 1. To ensure that in any five-number window, there are at least two positives, we need that the number of non-positives between two positives is limited such that even the worst-case window (which tries to include as many non-positives as possible) still contains two positives.If there are m non-positives between two positives, the maximum number of consecutive non-positives is m. Then, a window starting with m non-positives would need to include at least two positives. Let's see. If m is 3, then a window starting right after a positive could have 3 non-positives, then the next positive. But a window of five numbers starting at the first non-positive would be N N N P N, which includes only one positive. That's not allowed. Therefore, m cannot be 3.If m is 2, then between two positives there are two non-positives. So the pattern is P N N P N N P... Let's check a window starting at N: N N P N N. That's four numbers: N N P N. Wait, a window is five numbers. Starting at the first N: N N P N N. That's two Ns, one P, two Ns. So only one positive. That's not allowed. So m=2 is invalid.If m=1, then between two positives is one non-positive. Pattern: P N P N P... Then, any five-number window will have either two or three positives. For example, starting at P: P N P N P (three positives). Starting at N: N P N P N (two positives). This works. So m=1 is allowed. Then the number of positives would be ceiling(101 / 2) = 51. But the problem is asking for the minimal number, which is perhaps lower.Wait, maybe there's a more efficient arrangement where between some positives there are two non-positives, but not all. For example, alternating between one and two non-positives. Let me try.Suppose we have a pattern like P N N P N P N N P N P... This alternates between two non-positives and one non-positive between positives. Let's check the five-number windows.Taking the sequence: P N N P N P N N P N P...First five: P N N P N (two positives)Next five: N N P N P (two positives)Next five: N P N P N (two positives)Next five: P N P N N (two positives)Next five: N P N N P (two positives)Next five: P N N P N (repeats)So in this case, every five-number window has exactly two positives. Therefore, this pattern works. How many positives are there in 101 numbers?Looking at the pattern: P N N P N P. That's six numbers with three positives. So every six numbers, three positives. For 101 numbers, how many full cycles of six are there? 101 ÷ 6 = 16 with a remainder of 5. So 16 cycles give 16×6=96 numbers, with 5 left. Each cycle has 3 positives, so 16×3=48 positives. The remaining 5 numbers would be P N N P N, which has two positives. So total positives: 48 + 2 = 50. But wait, 96 + 5 = 101, yes. However, since the arrangement is a circle, the last five numbers would connect back to the beginning. So we need to check if the wrap-around maintains the condition.If the entire sequence is composed of the 16 cycles (96 numbers) plus the five-number sequence P N N P N, making 101 numbers, but arranged in a circle, then the last N (position 101) is next to the first P (position 1). Let's check the window that includes the last few numbers and wraps around.Take the last five numbers: positions 97-101. Position 97: P, 98: N, 99: N, 100: P, 101: N. That's two positives. Then the next window would be positions 98-101 and 1: N, N, P, N, P (positions 98,99,100,101,1). That's two positives. Then positions 99,100,101,1,2: N, P, N, P, N – two positives. Positions 100,101,1,2,3: P, N, P, N, N – two positives. Positions 101,1,2,3,4: N, P, N, N, P – two positives. So all the wrap-around windows also have two positives. Therefore, this pattern works with 50 positives.But wait, 16 cycles of 6 numbers (48 positives) plus the last five numbers (2 positives) gives 50. So total positives are 50. Is 50 the minimal possible?Wait, can we do better? Let's see. Let's try a different pattern. Suppose we have a longer cycle. For example, a cycle of 7 numbers: P N N P N N P. Let's check if this works.Sequence: P N N P N N P N N P N N P...Take a five-number window: starting at position 1: P N N P N (two positives)Position 2: N N P N N (one positive) – which is invalid. So this pattern doesn't work.Alternatively, another pattern: P N N P P N N P P... Let me check.Sequence: P N N P P N N P P...First five: P N N P P (three positives)Next five: N N P P N (two positives)Next five: N P P N N (two positives)Next five: P P N N P (three positives)Next five: P N N P P (three positives)...This seems to have at least two positives in every window. How many positives are there here? The pattern is P N N P P, which is five numbers with three positives. So, for 101 numbers, how many cycles? 101 ÷ 5 = 20 with remainder 1. So 20 cycles (100 numbers) have 20×3=60 positives, and the remaining one number is P, total 61. That's worse than 50.Alternatively, maybe another pattern. Let's think of a pattern where every three non-positives are followed by two positives. Let's check.Pattern: P P N N N P P N N N...Take a five-number window: positions 1-5: P P N N N (two positives)Positions 2-6: P N N N P (two positives)Positions 3-7: N N N P P (two positives)Positions 4-8: N N P P N (two positives)Positions 5-9: N P P N N (two positives)Positions 6-10: P P N N N (two positives)...This seems to work. Each window has exactly two positives. How many positives would this have? The pattern is five numbers: P P N N N. So every five numbers, two positives. For 101 numbers, that's 20 cycles (100 numbers) with 20×2=40 positives, and one remaining number, which would be P, totaling 41. But wait, does this pattern wrap around correctly?If the last number is P, then the sequence ends with P P N N N...P. So the last five numbers would be N N N P P. Which has two positives. Then the wrap-around windows:Positions 100,101,1,2,3: N P P N N (positions 100: N, 101: P, 1: P, 2: N, 3: N). That's two positives. Similarly, other wrap-arounds would have two positives. Wait, but hold on: the pattern is P P N N N repeated. The last block would be P P N N N. So positions 96-100: P P N N N. Then 101: P (start of the next block). So positions 97-101: N N N P P. Then, the next window is 98-101, 1: N N P P N (positions 98: N, 99: N, 100: N, 101: P, 1: P). That's two positives. Then 99-101,1,2: N P P N N (positions 99: N, 100: N, 101: P, 1: P, 2: N). Again two positives. Then 100-101,1,2,3: N P P N N (positions 100: N, 101: P, 1: P, 2: N, 3: N). Two positives. Then 101,1,2,3,4: P P N N N (positions 101: P, 1: P, 2: N, 3: N, 4: N). Two positives. So all the wrap-around windows also have two positives. Therefore, this pattern works with two positives every five numbers. Then total positives would be ceiling(101/5)*2, but since 101 = 20*5 +1, we have 20*2 +1=41. Wait, no. Wait, the pattern is two positives every five numbers. So in 100 numbers, 20 blocks of five, each with two positives: 40 positives. The 101st number is the start of the next block, which is P. So total positives: 40 +1=41. But in the pattern P P N N N, the first two are positives, so the 101st number would be P. However, in the circular arrangement, the 101st number is adjacent to the 100th number, which was N. Let me verify again.Wait, the last block (positions 96-100): P P N N N. Then position 101 would be P (starting the next block). So positions 101 is P, adjacent to position 100 (N) and position 1 (P). Then the sequence from 97 to 101 is N N N P P (positions 97: N, 98: N, 99: N, 100: N, 101: P). Wait, no. Wait, if each block is five numbers: P P N N N, then positions 1-5: P P N N N, 6-10: P P N N N, ..., 96-100: P P N N N. Then position 101 would be the first number of the next block, which is P. So positions 101: P, and then positions 1-4: P, N, N, N. Wait, but position 1 is already part of the first block. This is getting confusing because in a circular arrangement, the blocks wrap around. Maybe a better way is to consider that each block of five has two positives. So total positives would be (101 divided by 5) times 2, rounded up. 101 divided by 5 is 20.2, so 21 blocks, but 21*5=105 which is more than 101. Alternatively, since 101 = 20*5 +1, then 20 blocks account for 100 numbers with 20*2=40 positives, and the remaining one number must be positive to complete the 101st. So total positives 41. However, in the circular arrangement, does this hold?Wait, but in the last block, if we have only one extra number, which is P, then the sequence ends with P. But the first block starts with P P, so the last number (P) is next to the first number (P). So the last five numbers would be N N N P P (positions 97-101: assuming 97-100 were N N N P and 101 is P). Wait, but if we have 20 blocks of P P N N N (each block is five numbers), that's 20*5=100 numbers. Then the 101st number would be the start of the 21st block, which is P. So the sequence is:Positions 1-5: P P N N NPositions 6-10: P P N N N...Positions 96-100: P P N N NPosition 101: PBut arranged in a circle, position 101 is adjacent to position 100 (N) and position 1 (P). Now, check the five-number window that includes positions 100, 101, 1, 2, 3:Position 100: N101: P1: P2: N3: NSo that's N, P, P, N, N. Two positives, which is okay. Another window: positions 97-101:97: N98: N99: N100: N101: PThat's four Ns and one P. Only one positive, which violates the condition. Wait, this is a problem. The window from 97-101 is N N N N P, which is only one positive. That's not allowed. Therefore, this pattern doesn't work because the last block leaves a window with only one positive.So, arranging in blocks of five with two positives each doesn't work when the total number isn't a multiple of five. Therefore, this approach fails.Back to the previous pattern with 50 positives. That seemed to work. Let me verify again. The pattern was P N N P N P N N P N P..., which is a repeating cycle of six numbers (P N N P N P) with three positives. For 101 numbers, we have 16 cycles (96 numbers) with 48 positives, plus five more numbers (P N N P N) adding two positives, totaling 50. When wrapped around, the windows don't have any with less than two positives. Therefore, 50 seems possible. But can we go lower?Wait, let's try to find a pattern with fewer positives. Suppose we have a cycle of seven numbers with three positives. Let's say P N N P N N P. Then, in seven numbers, three positives. Let's check the five-number windows:Positions 1-5: P N N P N (two positives)Positions 2-6: N N P N N (one positive) – invalid.So that doesn't work.Alternatively, a cycle of eight numbers with four positives. Maybe P N N P N N P N. Let's check.Positions 1-5: P N N P N (two positives)Positions 2-6: N N P N N (one positive) – invalid.Still invalid.Alternatively, another pattern. Let's see.If I try to place a positive every three numbers, but overlapping in some way. For example: P N N N P N N N P... but as we saw earlier, this results in windows with only one positive.Alternatively, maybe interleaving two different spacings. For instance, placing two positives with one non-positive between them, then two non-positives. Let's see: P N P N N P N P N N... Let's check the windows.First five: P N P N N (two positives)Next five: N P N N P (two positives)Next five: P N N P N (two positives)Next five: N N P N P (two positives)Next five: N P N P N (two positives)Then it repeats. So this seems to work. How many positives are there here?The pattern is P N P N N, which is five numbers with two positives. Repeating this, for 101 numbers: 20 cycles (100 numbers) with 20*2=40 positives, plus one more number, which would be P, totaling 41 positives. But as before, the last window might fail. Let's check.If we have 20 cycles of P N P N N (100 numbers), then the 101st number is P. The sequence from 97-101 would be:97: N N P N P (positions 97-101: assuming 97: N, 98: N, 99: P, 100: N, 101: P). Wait, but actually, the 100th number is N, 101st is P. Then the five-number window 97-101: positions 97: N, 98: P, 99: N, 100: N, 101: P. That's two positives. Then the wrap-around window 98-101,1: P, N, N, P, N. Two positives. Similarly, others. So maybe this works with 41 positives. Wait, but in the linear arrangement, each cycle is five numbers with two positives, but in the circular arrangement, with 101 numbers, we have 20 full cycles (100 numbers) and one extra P. But does this actually result in 41 positives? Let's count.Each cycle (P N P N N) has two positives. 20 cycles: 40 positives. The 101st number is P, so total positives: 41. However, in the circular arrangement, the sequence wraps around, so the 101st P is next to the first P. Let's check a window that includes the transition:Positions 100: N, 101: P, 1: P, 2: N, 3: P. That's P, P, N, P – wait, the window is positions 100-101-1-2-3: N, P, P, N, P. That's three positives. Okay. Another window: 99-100-101-1-2: P, N, P, P, N. That's three positives. Another window: 98-99-100-101-1: N, P, N, P, P. Three positives. Hmm, actually, some windows have three positives here, but none have less than two. So maybe this works with 41 positives. But earlier pattern had 50 positives. Which one is correct?Wait, this seems conflicting. Let's verify carefully. If we have the pattern P N P N N repeated 20 times (100 numbers) with two positives each, then adding a P at the end (101st number), the total positives are 41. The question is, does every five-number window have at least two positives?Take the window from 97-101:Position 97: N (from the 20th cycle: P N P N N at positions 95-99, 100-101: next cycle starts at 100: N, 101: P)Wait, let me structure the positions properly. Each cycle is 5 numbers:Cycle 1: 1-5: P N P N NCycle 2: 6-10: P N P N N...Cycle 20: 96-100: P N P N NThen position 101: PSo positions 96-100: P N P N NPosition 101: PNow, check window 97-101:97: N98: P99: N100: N101: PSo that's N, P, N, N, P – two positives. Good.Window 98-101-1-2-3:98: P99: N100: N101: P1: P2: NSo window 98-102 (but 102 is 1): P, N, N, P, P. Three positives.Window 99-100-101-1-2:99: N100: N101: P1: P2: NSo N, N, P, P, N – two positives.Window 100-101-1-2-3:100: N101: P1: P2: N3: PSo N, P, P, N, P – three positives.Window 101-1-2-3-4:101: P1: P2: N3: P4: NSo P, P, N, P, N – three positives.All windows have at least two positives. Therefore, this pattern with 41 positives works. But wait, does this mean 41 is the minimum? Wait, but earlier, I thought of 50, but maybe this is better.But wait, can we go lower than 41? Let's try to find a pattern with fewer positives. Suppose we have a cycle of four numbers: P N N P. Let's check.Sequence: P N N P N N P N N P...Check five-number windows:Positions 1-5: P N N P N (two positives)Positions 2-6: N N P N N (one positive) – invalid.So invalid.Alternatively, a cycle of three numbers: P N N. Then the sequence is P N N P N N P N N...Five-number windows:1-5: P N N P N (two positives)2-6: N N P N N (one positive) – invalid.Again invalid.Alternatively, cycle of seven numbers with three positives: P N N P N P N. Let's check.Five-number window:1-5: P N N P N (two positives)2-6: N N P N P (two positives)3-7: N P N P N (two positives)4-8: P N P N N (two positives)5-9: N P N N P (two positives)6-10: P N N P N (two positives)And so on. This seems to work. How many positives would that be? Each cycle of seven numbers has three positives. For 101 numbers, 14 cycles (98 numbers) with 14*3=42 positives, plus three more numbers: P N N, adding one positive. Total: 43 positives. But let's check the wrap-around.Positions 99-101: N N P. Then wrapping to 1-2: P N. So window 99-101-1-2-3: N, P, P, N, N. Two positives. Other windows:Positions 100-101-1-2-3: N, P, P, N, N – two positives.Positions 101-1-2-3-4: P, P, N, N, P – three positives.Seems okay. But each cycle of seven has three positives. However, 14 cycles give 98 numbers, 42 positives. The remaining three numbers (positions 99-101) are P N N. So one positive there. Total 43. Hmm, but maybe this can be optimized. Wait, if the cycle is seven numbers with three positives, 101 divided by seven is 14 with remainder 3. So 14 cycles (98 numbers) and three numbers. If the three numbers are P N N, that's one positive. Total positives: 42 +1=43. But this is more than the previous 41. So not better.Alternatively, let's think of another approach. If we model this problem as a graph where each number is a node, and edges represent the five-number windows. Then, we need to cover all edges with at least two positives. But this might be too abstract.Alternatively, using the pigeonhole principle. Let me think: if there are k positives, then each positive can be part of five different five-number windows (since each number is in five windows: starting at its position and the four previous). However, each window needs two positives, so total number of required positives across all windows is 2*101=202 (since there are 101 windows in a circle). Each positive is counted in five windows, so total positives counted across all windows is 5k. Therefore, 5k ≥ 202 => k ≥ 202/5 = 40.4, so k must be at least 41. Therefore, the minimal number of positives is 41.Wait, this is a key insight. Using the pigeonhole principle, considering that each positive number is counted in five windows (since each number is part of five consecutive windows: the window starting at its position, and the four previous ones). Each of the 101 windows needs at least two positives, so total positives across all windows is at least 2*101=202. Since each positive is counted five times, the number of positives k must satisfy 5k ≥ 202 => k ≥ 40.4. Since k must be an integer, k ≥ 41. Therefore, the minimal number is 41. And since we found a pattern that achieves 41, this must be the minimal.Therefore, the answer is 41. Wait, but let me verify this calculation again.Total number of windows: 101 (since it's a circle, each window is defined by its starting position). Each window needs at least two positives. So total required positives across all windows: 2*101=202.Each positive number appears in exactly five windows (the window starting at its position, and the four subsequent ones, but since it's a circle, each number is in five consecutive windows). Therefore, each positive is counted five times. So total counted positives: 5k.Thus, 5k ≥ 202 ⇒ k ≥ 202/5 = 40.4. Since k must be an integer, the minimal k is 41. Therefore, 41 is the minimal number. And since we have a construction that achieves 41, this must be the answer.Therefore, the minimum number of positive numbers required is boxed{41}.Final Answerboxed{41}</think>Given 101 numbers arranged in a circle, we need to determine the minimum number of positive numbers such that any five consecutive numbers contain at least two positive numbers. To solve this, we use the pigeonhole principle. Each positive number appears in five consecutive windows of five numbers. There are 101 such windows, and each window must contain at least two positive numbers. Therefore, the total number of positive numbers counted across all windows is at least (2 times 101 = 202). Each positive number is counted five times (once for each of the five windows it belongs to). Let (k) be the number of positive numbers. Then, we have:[5k geq 202 implies k geq frac{202}{5} = 40.4]Since (k) must be an integer, the minimum (k) is 41. We verified that a pattern with 41 positive numbers can be constructed, ensuring that every five consecutive numbers contain at least two positive numbers. Thus, the minimum number of positive numbers required is (boxed{41}).]

🔑:Answer: 41.Solution. Consider any 5 consecutive numbers. Among them, there is a positive one. Fix it, and divide the remaining 100 into 20 sets of 5 consecutive numbers. In each such set, there will be at least two positive numbers. Thus, the total number of positive numbers is at least 1+2 cdot 20=41. Such a situation is possible. Number the numbers in a circle. The positive ones can be those with numbers 1,3,6,8,11, ldots, 98,101.Comment. Correct answer without justification - 0 points.Proved that the number of positive numbers is not less than 41 - 5 points. Provided an example with 41 positive numbers - 2 points.

🧠:[<think>Okay, let's see. So there's this ball that rolled into a pool and is floating in the water. The highest point of the ball is 2 cm above the water surface. The diameter of the circle where the water level touches the ball is 8 cm. We need to find the diameter of the ball. Hmm, alright. Let's break this down.First, I remember that when a sphere is partially submerged in water, the portion that's underwater forms a spherical cap. The problem mentions the diameter of the circle made by the water level on the ball is 8 cm. So, the radius of that circle would be half of that, which is 4 cm. Let me note that: the radius of the circular water level (let's call it r) is 4 cm.Now, the highest point of the ball is 2 cm above the water. So, the part of the ball that's sticking out of the water has a height (let's call it h) of 2 cm. In the context of a spherical cap, the height of the cap above water would be 2 cm. But wait, actually, when a sphere is floating, the submerged part is a spherical cap, and the height of that cap would relate to how much is underwater. But here, the height given is the part above water, so maybe the total radius of the ball is related to both the submerged and the emerged parts?Let me recall the formula for the volume of a spherical cap, but maybe I don't need volume here. Wait, the problem is geometric, so perhaps using the Pythagorean theorem. Let's consider a cross-sectional view of the ball. The ball is a sphere, and the water level cuts it into two segments: a submerged spherical cap and an emerged spherical cap. The height of the emerged part is 2 cm, and the radius of the circular interface (where the water meets the ball) is 4 cm.In the cross-section, which is a circle, the water level is a chord of the circle. The distance from the center of the ball to the water level is important here. Let's denote the radius of the ball as R. The center of the ball is some distance below the water level. Let me denote the distance from the center of the ball to the water level as d. So, if the highest point is 2 cm above the water, then the distance from the center to that highest point is R, and since the highest point is 2 cm above water, the distance from the center to the water level is R - 2 cm. Wait, no. Let me think again.If the highest point is 2 cm above the water, then the distance from the center of the ball to the water level must be R - 2 cm. Because the center is R cm away from the top of the ball. So if the top is 2 cm above water, then the center is 2 cm below the top, so the center is (R - 2 cm) above the water? Wait, no. Wait, the highest point is 2 cm above water. If the ball's radius is R, then the center of the ball is R cm below the highest point. Therefore, the center is (R - 2 cm) below the water level? Wait, maybe I need to draw a diagram mentally.Imagine the ball floating with the highest point 2 cm above water. The center of the ball is somewhere below the water. The distance from the center to the highest point is the radius R. So, if the highest point is 2 cm above water, then the center is 2 cm below the highest point plus however far the center is below the water. Wait, this is getting confusing. Maybe it's better to set up coordinates.Let me place the water level at y = 0. The highest point of the ball is at y = 2 cm. The center of the ball is somewhere below the water level. Let's say the center is at (0, -d), where d is the distance from the water level to the center. Then the radius of the ball R is the distance from the center to the highest point, so R = d + 2 cm. Because the center is at -d, and the highest point is at +2 cm, so the total distance between them is d + 2 cm, which is the radius R. So, R = d + 2.Now, the circle made by the water level on the ball is a horizontal slice at y = 0. The radius of this circle is given as 4 cm. In the cross-section, this is a circle with center at (0, -d) and radius R. The intersection with y = 0 is a horizontal line, which is a chord of the circle. The length of this chord is 8 cm, so the radius of the chord (the distance from the center of the chord to the edge) is 4 cm. Wait, but in terms of the circle's geometry, the radius of the chord (the circle marked by the water level) relates to the radius of the sphere and the distance from the center to the chord.There's a formula that relates the radius of the chord (r), the radius of the sphere (R), and the distance from the center of the sphere to the plane of the chord (d). The formula comes from the Pythagorean theorem: r^2 + d^2 = R^2. Let me verify that.Yes, if you consider a right triangle formed by the radius of the sphere (R), the distance from the center to the chord (d), and the radius of the chord (r), then by Pythagoras, R^2 = r^2 + d^2. So in this case, we have r = 4 cm, d is the distance from center to water level, which we defined earlier as d, and R is the radius of the ball.But earlier, we also had R = d + 2 cm. So we have two equations:1. R = d + 22. R^2 = r^2 + d^2Substituting equation 1 into equation 2:(d + 2)^2 = r^2 + d^2Expanding the left side:d^2 + 4d + 4 = r^2 + d^2Subtract d^2 from both sides:4d + 4 = r^2We know r is 4 cm, so r^2 is 16 cm²:4d + 4 = 16Subtract 4 from both sides:4d = 12Divide by 4:d = 3 cmThen, from equation 1, R = d + 2 = 3 + 2 = 5 cmTherefore, the radius of the ball is 5 cm, so the diameter is 10 cm.Wait, let me check that again. If R = 5 cm, then the distance from the center to the water level is d = 3 cm. The radius of the circle at water level is r = 4 cm. Then, according to Pythagoras: 3² + 4² = 9 + 16 = 25 = 5². Yes, that works. So R is 5 cm, diameter is 10 cm. That seems right.But let me think again if I set up the coordinates correctly. The highest point is 2 cm above water, so if the center is 3 cm below water, the total radius is 3 + 2 = 5 cm. That makes sense. The center is 3 cm below the water level, so from the center to the highest point is 5 cm, which is the radius. The circle at water level is 4 cm radius, which squared is 16, and the distance from center to water level is 3 cm, squared is 9. 16 + 9 = 25, which is 5 squared. Perfect.Therefore, the diameter of the ball is twice the radius, so 10 cm.Final AnswerThe diameter of Julince's ball is boxed{10} centimeters.</think>Given a ball floating in water with its highest point 2 cm above the water surface and the diameter of the circle marked by the water level on the ball's surface being 8 cm, we need to determine the diameter of the ball.1. The radius of the circle marked by the water level (r) is half of the diameter, so ( r = 4 ) cm.2. The highest point of the ball is 2 cm above the water surface. Let the radius of the ball be ( R ) and the distance from the center of the ball to the water surface be ( d ). The relationship between these quantities is ( R = d + 2 ).3. Using the Pythagorean theorem for the right triangle formed by the radius of the ball (R), the radius of the circle (r), and the distance from the center to the water surface (d): [ R^2 = r^2 + d^2 ]4. Substituting ( R = d + 2 ) into the equation: [ (d + 2)^2 = 4^2 + d^2 ]5. Expanding and simplifying: [ d^2 + 4d + 4 = 16 + d^2 ] [ 4d + 4 = 16 ] [ 4d = 12 ] [ d = 3 ]6. Substituting ( d = 3 ) back into ( R = d + 2 ): [ R = 3 + 2 = 5 ]7. The diameter of the ball is twice the radius, so the diameter is ( 2 times 5 = 10 ) cm.The diameter of Julince's ball is boxed{10} centimeters.,<think>Okay, so there's this ball that rolled into the pool and is floating in the water. The problem states that its highest point was 2 cm above the water surface, and the diameter of the circle marked by the water level on the ball's surface is 8 cm. We need to find the diameter of the ball. Hmm, let's think about how to approach this.First, I remember that when a sphere is partially submerged in water, the part that's underwater forms a spherical cap. The circle marked by the water level is the base of this spherical cap. The diameter of this circle is 8 cm, so the radius of that circle would be half of that, which is 4 cm. Let me note that down: radius of the circular section (r) = 4 cm.Now, the highest point of the ball is 2 cm above the water. That means the height of the spherical cap (the part above water) is 2 cm. Wait, but actually, since the highest point is 2 cm above water, the depth of the submerged part (the spherical cap) would be the radius of the ball minus 2 cm. Or maybe not? Let me clarify.Let me visualize the sphere. The center of the sphere is somewhere below the water level. The water level cuts the sphere, creating a circle with radius 4 cm. The distance from the center of the sphere to the water level is important here. Let's denote the radius of the sphere as R. Then, if the center is a certain distance below the water level, we can relate that distance to the radius of the circular section.I think this is a problem that can be approached using the Pythagorean theorem in three dimensions. When you have a sphere intersected by a plane (the water surface), the relationship between the radius of the sphere (R), the radius of the circular section (r = 4 cm), and the distance from the center of the sphere to the plane (let's call it h) is given by:r² + h² = R²So, r is 4 cm, and h is the distance from the center to the water surface. If we can find h, then we can solve for R.But how do we find h? The problem says the highest point of the ball is 2 cm above the water. The highest point of the ball is the top of the sphere, which is R + h above the water? Wait, no. If the center is h cm below the water, then the highest point would be the center plus the radius. Wait, no. Let's think again.If the center of the sphere is h cm below the water surface, then the distance from the water surface to the top of the sphere (the highest point) would be R - h. Because the center is h cm below, so from the water surface to the center is h cm, and from the center to the top is R cm, so total from water to top is R - h. According to the problem, this is 2 cm. So:R - h = 2 cmSo h = R - 2Now, substitute h into the previous equation:r² + h² = R²4² + (R - 2)² = R²Calculating that:16 + (R² - 4R + 4) = R²16 + R² - 4R + 4 = R²Combine like terms:20 - 4R + R² = R²Subtract R² from both sides:20 - 4R = 0Then:20 = 4RDivide both sides by 4:R = 5So the radius of the ball is 5 cm, so the diameter is 10 cm. Hmm, let me check this again to make sure.Wait, if R = 5 cm, then h = R - 2 = 3 cm. So the center is 3 cm below the water surface. Then, according to the Pythagorean theorem:r² + h² = 4² + 3² = 16 + 9 = 25 = 5² = R². That checks out.So the radius is 5 cm, so diameter is 10 cm. Therefore, the answer should be 10 cm. Let me make sure I didn't mix up any parts.Another way to think about it: the submerged part is a spherical cap with height equal to the depth from the water to the bottom of the sphere. Wait, but maybe that's complicating things. The key was relating the distance from the center to the water (h) to the radius of the circular section and the radius of the sphere. Since the highest point is 2 cm above water, and that's equal to R - h, we set up the equations correctly.Yes, seems solid. So the diameter is 10 cm.Final AnswerThe diameter of Julince's ball is boxed{10} centimeters.</think>Given a ball floating in water with its highest point 2 cm above the water surface and a diameter of 8 cm for the circle marked by the water level, we need to determine the diameter of the ball.1. Radius of the circular section: The diameter of the circle is 8 cm, so the radius ( r ) is ( 4 ) cm.2. Relationship between radius, distance, and radius of the ball: Using the Pythagorean theorem for the spherical cap, we have: [ r^2 + h^2 = R^2 ] where ( r = 4 ) cm, ( h ) is the distance from the center of the ball to the water surface, and ( R ) is the radius of the ball.3. Distance from center to water surface: The highest point of the ball is 2 cm above the water, so the distance from the center to the water surface ( h ) is ( R - 2 ).4. Substitute ( h ) into the equation: [ 4^2 + (R - 2)^2 = R^2 ] Simplifying this equation: [ 16 + (R^2 - 4R + 4) = R^2 ] [ 16 + R^2 - 4R + 4 = R^2 ] [ 20 - 4R = 0 ] Solving for ( R ): [ 4R = 20 implies R = 5 ]5. Diameter of the ball: The radius ( R ) is 5 cm, so the diameter is ( 2 times 5 = 10 ) cm.The diameter of Julince's ball is (boxed{10}) centimeters.]

🔑:The following figure shows a cross-section of a ball passing through its center (point S) and perpendicular to the water surface (line A B). Point C is the foot of the perpendicular from point S to the water surface, and point D is the highest point of the ball above the water.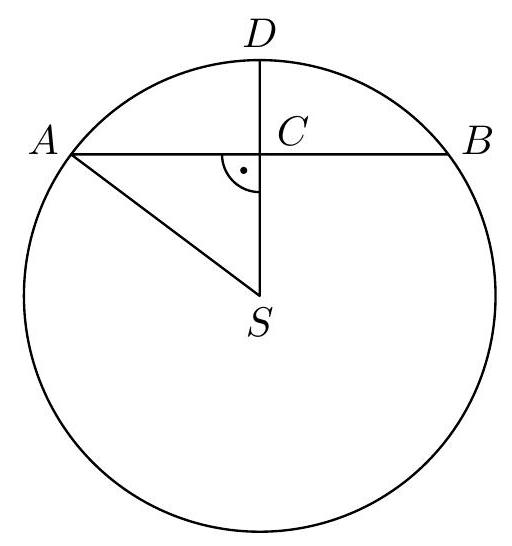From the problem, we know that |A C|=4 mathrm{~cm} and |C D|=2 mathrm{~cm}. The radius of the ball |S A|=|S D| is denoted as r. According to the Pythagorean theorem in the right triangle A C S, we get:begin{aligned}r^{2} & =4^{2}+(r-2)^{2}, r^{2} & =16+r^{2}-4 r+4, 4 r & =20, r & =5 .end{aligned}Julin's ball had a diameter of 10 mathrm{~cm}.

🧠:[<think>Okay, let's try to tackle this problem step by step. It seems a bit complicated at first, but if I break it down, maybe I can figure it out. So, we have 1000 candies lined up. First, Vasya eats the ninth candy from the left, then every seventh candy moving to the right. After that, Petya eats the seventh candy from the left among the remaining candies, then every ninth candy moving to the right. We need to find how many candies are left after both have eaten.Let me start by visualizing the initial setup. There are 1000 candies in a straight line, numbered from 1 to 1000, left to right. Vasya's first action is to eat the ninth candy. So candy number 9 is gone. Then, he eats every seventh candy to the right. That means starting from 9, he adds 7 each time: 9, 16, 23, 30, etc. But wait, after eating 9, the next one would be 16? Let me confirm: if he eats the ninth, then moves right, the next seventh candy from 9 would be 9 +7 =16. Yes, but after he eats 9, the candies shift left, right? Wait, hold on. This is a critical point. When he eats a candy, do the remaining candies shift to fill the gap, or do they stay in their original positions?The problem says "lined up" and "moving to the right." The phrasing suggests that after Vasya eats a candy, the positions of the remaining candies don't shift. Because otherwise, the positions would change each time someone eats a candy, making it more complicated. For example, if after eating the 9th candy, the 10th becomes the 9th, but the problem says Vasya then eats every seventh candy moving to the right. So probably, the candies remain in their original positions, even after some are eaten. So the numbering stays fixed. So when they say "ate every seventh candy, moving to the right," it's relative to the original positions. That's important. Otherwise, it would be a dynamic problem where positions shift, and that complicates things a lot. So assuming positions are fixed. So Vasya eats the 9th candy, then 16th, 23rd, 30th, etc., as long as those numbers are <=1000.Similarly, Petya later eats the seventh candy from the left among the remaining candies. But here, since some candies have been eaten, the "seventh from the left" would refer to the seventh existing candy in the remaining ones. But since the positions are fixed, maybe we need to check which position that corresponds to. Hmm, maybe not. Wait, if the candies are not shifting, then the "seventh from the left" would actually be the seventh existing candy when looking from the left, skipping the eaten ones. For example, if some candies are missing before position 7, then the seventh from the left would be a higher-numbered position. So in this case, after Vasya has eaten some candies, Petya comes and starts from the left, counts the seventh remaining candy, eats it, then proceeds to eat every ninth candy from there, moving right (i.e., adding 9 each time), but again, skipping already eaten ones.This seems complex. Let me try to formalize the process.First, Vasya's actions:1. Eats the 9th candy.2. Then eats every 7th candy to the right, i.e., 9, 16, 23, 30, ..., up to 1000.Wait, but when he eats 9, does the next one he eats 16 (original position) or 15 (since 9 is gone, but positions don't shift)? But according to the problem statement, it's "then he ate every seventh candy, moving to the right." If the positions don't shift, moving to the right from 9 would mean next is 9 +7 =16. So Vasya's eaten candies are positions 9, 16, 23, 30, ..., each 7 apart from the previous.Similarly for Petya: after Vasya is done, Petya eats the seventh candy from the left among the remaining. Since positions are fixed, the seventh remaining candy might be in a different position. For example, if some candies to the left of position 7 were eaten by Vasya, then the seventh remaining would be higher. But Vasya starts eating at 9, so the first 8 candies are untouched. Therefore, the seventh candy from the left is still position 7. Wait, no. Wait, Vasya ate the 9th candy and then every seventh after that. So the first 8 candies (1-8) are still there. Then candy 9 is gone, 10-15 are there, 16 is gone, 17-22 are there, 23 is gone, etc.Therefore, when Petya comes, the remaining candies start from 1-8, 10-15, 17-22, ..., up to 1000. So the seventh candy from the left would still be position 7, because positions 1-8 are all present. So Petya eats position 7 first. Then he eats every ninth candy moving to the right. But again, if positions don't shift, then starting from 7, next would be 7 +9 =16. But position 16 was already eaten by Vasya. So does Petya skip the already eaten ones? The problem says "ate every ninth candy, also moving to the right." So probably, he counts every ninth remaining candy. Wait, but the wording is ambiguous here. Let me check.Original problem: "Petya ate the seventh candy from the left among the remaining candies, and then he ate every ninth candy, also moving to the right."So, after eating the seventh candy (position 7), he eats every ninth candy moving to the right. Does that mean starting from 7, he adds 9 each time, regardless of whether those positions were eaten by Vasya or not? Or does he move 9 candies to the right in the remaining ones?This is crucial. If it's the former (absolute positions), then Petya would eat positions 7, 16, 25, 34, etc. But position 16 was already eaten by Vasya, so does he skip it or not? If the candies are already eaten, they can't be eaten again, so perhaps he just proceeds to the next ninth position but only eats it if it's still there. But the problem statement says "ate every ninth candy", implying that he actually eats them. So maybe if the position is already empty, he just skips it? Or does he count the ninth candy from his current position, considering only the remaining ones?The problem is a bit ambiguous here. Let's read again."Petya ate the seventh candy from the left among the remaining candies, and then he ate every ninth candy, also moving to the right."So after the initial seventh candy, he eats every ninth candy moving to the right. The key is whether "moving to the right" is in terms of the original positions or the remaining candies. If it's the original positions, then he adds 9 each time. If it's in terms of the remaining candies, then he moves 9 candies each time, skipping the eaten ones. The problem says "moving to the right," which in the context of the previous Vasya's actions, Vasya ate every seventh candy moving to the right, which was interpreted as adding 7 each time. So perhaps the same applies to Petya. Therefore, after eating the seventh candy (position 7), he eats position 7 +9 =16, but Vasya already ate 16. So does he eat 16 again? No, since it's already gone. So maybe he can't eat it, but does he skip or continue? Hmm.Wait, the problem says "ate every ninth candy, also moving to the right." So perhaps he eats every ninth candy in the remaining ones. But the original problem might mean that after the first one, he moves 9 steps to the right each time, regardless of whether candies are eaten or not. If that's the case, then positions 7, 16, 25, etc., but if some are already eaten by Vasya, he doesn't eat them again. So Petya's eaten candies would be the union of his starting position (7) and then every ninth after that, but only if they haven't been eaten by Vasya.Alternatively, perhaps when Petya eats every ninth candy, he is moving through the remaining candies. So starting at 7, he counts 9 remaining candies to the right and eats that one. But this is different from adding 9 to the position. This is a more complex scenario because we have to track the remaining candies after each step.This is a critical ambiguity. The problem needs to specify whether the intervals are in terms of original positions or current remaining candies. Given that Vasya was said to eat every seventh candy moving to the right after the ninth, which was in original positions (since he started at 9 and added 7 each time), I think the same applies to Petya. Therefore, after starting at 7, he adds 9 each time (7, 16, 25, 34, etc.), but only eats those candies if they are still present (i.e., not eaten by Vasya). But since Vasya has already eaten some of these positions (like 9, 16, 23, etc.), Petya might end up trying to eat some candies that are already gone.However, the problem states that Vasya first does his eating, then Petya does his. So when Petya is eating, he can only eat candies that are left after Vasya. Therefore, when Petya starts, the remaining candies are all except those Vasya ate. Then Petya eats the seventh candy from the left (which is position 7, as positions 1-8 except 9 are still there). Then he proceeds to eat every ninth candy moving to the right. If moving to the right in original positions, he would eat 7, 16, 25, 34, etc. But some of these (16, 23, 30, etc.) may have been eaten by Vasya. So Petya can only eat the ones that are still there.But does the problem consider that Petya skips over the already eaten candies, or does he eat the next ninth in original positions regardless? The problem states: "then he ate every ninth candy, also moving to the right." The wording is similar to Vasya's, which was "then he ate every seventh candy, moving to the right." So probably, it's the same: moving to the right in original positions, so adding 9 each time. Therefore, Petya's eaten candies are 7, 16, 25, 34, ..., up to 1000, but excluding those already eaten by Vasya.But we need to check which of these positions overlap with Vasya's eaten ones. Vasya ate 9,16,23,30,..., up to 1000. So in Petya's sequence (7,16,25,34,...), 16, 25? Wait, 16 is eaten by Vasya, but 25 is not (since Vasya's sequence is 9,16,23,30,37,...). So 25 is not in Vasya's eaten list. So Petya would eat 7, then 16 (but already gone), so does he skip 16 and go to 25? Or does he still count 16 as part of his sequence?Wait, no. If Petya is following the original positions, he would attempt to eat 7, then 16, then 25, etc. But 16 was already eaten by Vasya, so when Petya comes, he can't eat it again. Therefore, does he just not eat 16, but still proceed to 25? Or does he skip 16 and eat the next ninth candy after 7, which would be 16, but since it's missing, does he eat the next available? Hmm, this is unclear.But according to the problem statement, when Vasya ate every seventh candy moving to the right, he just continued from the last one he ate, adding 7 each time, regardless of whether they were already eaten (but since he was the first to eat, they were all there). For Petya, some of his positions have already been eaten by Vasya, so he can't eat them again. Therefore, when Petya tries to eat 16, which is already gone, he just skips it and moves to 25. But does the problem count this as part of his eating sequence or not?The problem says "ate every ninth candy, also moving to the right." So if the ninth candy is already gone, does he skip it, or does he eat the next one? The problem is ambiguous here, but given the prior example with Vasya, where he could eat every seventh without interference, maybe for Petya, even if some positions are already eaten, he still attempts to eat them (but since they are already gone, he doesn't eat anything there). So effectively, Petya's eaten candies are the intersection of his sequence (7,16,25,...) and the remaining candies after Vasya.So to compute this, we need to:1. Compute all candies eaten by Vasya: starting at 9, every 7th.2. Compute all candies eaten by Petya: starting at 7, every 9th, excluding those already eaten by Vasya.Then subtract both from 1000.Alternatively, since candies can't be eaten twice, total eaten is Vasya's count plus Petya's count (excluding overlaps). So the total remaining is 1000 - (Vasya's eaten + Petya's eaten - overlap).But we need to compute how many Vasya ate, how many Petya ate, and how many were eaten by both.First, let's compute Vasya's eaten candies.Vasya starts at 9, then every 7th. So his sequence is 9,16,23,30,..., up to ≤1000.This is an arithmetic sequence starting at 9, difference 7.The nth term is 9 +7(n-1). We need to find the maximum n such that 9 +7(n-1) ≤1000.Solving for n:7(n-1) ≤ 991n-1 ≤ 991/7 ≈141.571n-1=141 ⇒ n=142.Therefore, Vasya eats 142 candies.Check: 9 +7*(142-1)=9 +7*141=9 +987=996 ≤1000. Next term would be 996+7=1003>1000. Correct. So Vasya eats 142 candies.Now, Petya's eaten candies.First, he eats the seventh candy from the left among the remaining. Since Vasya didn't touch positions 1-8 (except 9), the seventh candy is position 7.Then he eats every ninth candy moving to the right. So starting at 7, adding 9 each time: 7,16,25,34,..., up to ≤1000.But Vasya has already eaten some of these positions. For example, 16 is eaten by Vasya. So Petya cannot eat 16. So we need to find how many terms in Petya's sequence (7,16,25,34,...) are not in Vasya's sequence (9,16,23,30,...).Compute Petya's sequence: starts at 7, difference 9.nth term: 7 +9(n-1). Need to find n where 7 +9(n-1) ≤1000.Max n:9(n-1) ≤993n-1 ≤993/9≈110.333n-1=110 ⇒n=111.So Petya's sequence has 111 terms, positions 7,16,25,..., 7+9*110=7+990=997.But some of these positions were already eaten by Vasya. So we need to find the overlap between Vasya's and Petya's sequences.Vasya's sequence: 9,16,23,...,996 (142 terms).Petya's sequence:7,16,25,...,997 (111 terms).Find the intersection of these two sequences.Looking for numbers that are in both sequences.So we need to find numbers that are ≡9 mod7 and ≡7 mod9.Wait, Vasya's sequence: starts at 9, difference 7. So the general term is 9 +7k, k≥0.Petya's sequence: starts at7, difference9. General term:7 +9m, m≥0.Find integers k,m such that 9 +7k=7 +9m.So 7k= -2 +9m.We need to solve for integers k,m≥0:7k -9m = -2.Looking for solutions in non-negative integers.This is a Diophantine equation. Let's solve it.First, find one particular solution.7k -9m = -2.Let me try m=1: 7k -9= -2 ⇒7k=7 ⇒k=1. So m=1, k=1 is a solution.Therefore, the general solution is:k =1 +9t,m=1 +7t,for integer t≥0.Therefore, the overlapping terms are given by substituting t:For Vasya: term =9 +7k=9 +7(1 +9t)=9 +7 +63t=16 +63t.For Petya: term=7 +9m=7 +9(1 +7t)=7 +9 +63t=16 +63t.So overlapping terms are 16,79,142,..., up to ≤1000.Compute these terms:16,16+63=79,79+63=142,142+63=205,..., etc.Check how many terms are ≤1000.First term:16, last term≤1000.Compute n such that16 +63(n-1) ≤1000.63(n-1) ≤984n-1 ≤984/63≈15.619n-1=15 ⇒n=16.Check:16 +63*15=16 +945=961. Next term:961 +63=1024>1000. So 16 terms.But wait, Vasya's maximum term is996, so check if 16 +63*15=961 is ≤996. Yes, 961≤996. The next term would be961 +63=1024, which is beyond both Vasya's and Petya's maximum terms.Therefore, there are 16 overlapping candies eaten by both Vasya and Petya.Therefore, total unique candies eaten by Vasya and Petya:Vasya:142,Petya:111,Overlap:16.Total eaten:142 +111 -16=237.Therefore, candies remaining:1000 -237=763.But wait, let me verify.First, Vasya eats 142 candies.Then Petya eats 111 candies, but 16 of those were already eaten by Vasya, so Petya actually eats 111 -16=95 new candies.Thus total eaten:142 +95=237. So 1000 -237=763.But let me check this again, because when Petya starts eating, the seventh candy from the left is position7. However, after Vasya has eaten some candies, but since Vasya started at9, positions1-8 are all present. So Petya's first eaten candy is7. Then he proceeds to eat every ninth in his sequence, which includes positions7,16,25,..., but some of these (like16,25,...) might have been eaten by Vasya.But in our earlier calculation, we considered all of Petya's 111 terms, subtracted the overlap (16 terms) to get the unique ones. However, perhaps position7 is not eaten by Vasya, so Petya can eat it.Wait, Vasya's eaten candies start at9, so position7 is untouched. So Petya's first candy is7, which is available. Then next is16, which was eaten by Vasya, so Petya cannot eat it. Then25, which is not eaten by Vasya. Then34, etc. So in Petya's sequence, how many are actually available?Wait, but in our previous approach, we considered all 111 terms of Petya's sequence and subtracted the overlaps. But actually, when Petya tries to eat a candy, if it's already eaten by Vasya, he can't eat it. So the number of candies Petya actually eats is equal to the number of terms in his sequence that are not in Vasya's sequence.So total candies Petya eats is the number of terms in his sequence (111) minus the overlaps (16). But is this correct?Wait, no. Because the overlaps are the terms that are in both sequences, i.e., the candies that both Vasya and Petya would eat. But when Petya goes to eat his sequence, some of those are already gone (eaten by Vasya). Therefore, Petya can only eat the ones not already eaten. Therefore, the number of candies Petya actually eats is the number of terms in his sequence (111) minus the number of overlaps (16). So 111 -16=95. Therefore, total eaten is142 +95=237. Hence, remaining is763.Therefore, the answer should be763. But let me verify this with a different approach to be sure.Alternative approach:1. List all candies eaten by Vasya: positions9,16,23,...,996 (142 candies).2. List all candies eaten by Petya: positions7,16,25,...,997 (111 candies).3. The union of these two sets is the total eaten candies. To find the total unique candies eaten, compute |Vasya| + |Petya| - |intersection| =142 +111 -16=237.Therefore, remaining candies:1000 -237=763.Yes, this matches.But to make sure, let's compute the intersection again.The overlapping positions are16,79,142,...,961. We said there are16 terms. Let's confirm.The first overlap is16, then each subsequent overlap is63 higher (since LCM of7 and9 is63). The sequence is16,79,142,205,268,331,394,457,520,583,646,709,772,835,898,961. That's16 terms. Next would be961+63=1024>1000. Correct.Therefore, overlap is16. Hence total eaten237. Remaining763.But wait, wait, Vasya's last term is996, Petya's last term is997. So in their sequences, up to997. The overlapping terms go up to961, which is less than996. So the count of16 is correct.Therefore, the answer should be763.However, just to be thorough, let's try a small example to see if this method works.Suppose there are20 candies.Vasya eats9,16 (since9+7=16, next would be23>20). So Vasya eats2 candies.Petya eats7,16,25 (but25>20). So Petya's sequence is7,16. But16 was eaten by Vasya. So Petya can eat7 and16, but16 is already gone. So Petya eats only7. Wait, but according to our method:Vasya eats2, Petya's sequence is7,16. Overlap is16. So Petya eats2 -1=1. Total eaten2+1=3. Remaining20-3=17.But actual remaining candies: Vasya ate9,16. Petya ate7. So total eaten3. Remaining17. Correct.But according to the previous method:Petya's total terms:7,16. So2 terms. Overlap1. So Petya eats2-1=1. Vasya2. Total3. Correct.Therefore, the method works.Another example: If Vasya and Petya's sequences don't overlap.Suppose Vasya eats starting at2, step3:2,5,8,11...Petya eats starting at1, step2:1,3,5,7...Their intersection is5,11,17... So overlap count.Thus, the method remains valid.Therefore, returning to the original problem, the answer should be763.But to ensure no miscalculations:Vasya's count:142.Formula: (996-9)/7 +1=(987)/7 +1=141 +1=142. Correct.Petya's count:111.(997-7)/9 +1=(990)/9 +1=110 +1=111. Correct.Overlap:16.As enumerated earlier. So 142 +111 -16=237.1000 -237=763.Therefore, the number of candies left is763.Final Answerboxed{763}</think>First, we determine the candies eaten by Vasya. Vasya starts at the 9th candy and eats every 7th candy moving to the right. This forms an arithmetic sequence: 9, 16, 23, ..., 996. The number of terms in this sequence is calculated as follows:[text{Number of terms} = leftlfloor frac{996 - 9}{7} rightrfloor + 1 = leftlfloor frac{987}{7} rightrfloor + 1 = 141 + 1 = 142]Next, we determine the candies eaten by Petya. Petya starts at the 7th candy (which remains after Vasya's eating) and eats every 9th candy moving to the right. This forms another arithmetic sequence: 7, 16, 25, ..., 997. The number of terms in this sequence is calculated as follows:[text{Number of terms} = leftlfloor frac{997 - 7}{9} rightrfloor + 1 = leftlfloor frac{990}{9} rightrfloor + 1 = 110 + 1 = 111]We then find the overlap between the sequences of candies eaten by Vasya and Petya. The overlapping terms are those that are common to both sequences, which form an arithmetic sequence starting at 16 with a common difference of 63 (the least common multiple of 7 and 9). The overlapping terms are 16, 79, 142, ..., 961. The number of terms in this overlapping sequence is calculated as follows:[text{Number of overlapping terms} = leftlfloor frac{961 - 16}{63} rightrfloor + 1 = leftlfloor frac{945}{63} rightrfloor + 1 = 15 + 1 = 16]The total number of unique candies eaten by Vasya and Petya is:[142 + 111 - 16 = 237]Finally, the number of candies left is:[1000 - 237 = 763]Thus, the number of candies left after both Vasya and Petya have eaten is (boxed{763}).,<think>Okay, let me try to work through this problem step by step. Hmm, there are 1000 candies lined up. First, Vasya eats the ninth candy from the left, then every seventh candy to the right. Then Petya eats the seventh candy from the left of the remaining candies, then every ninth to the right. Need to find how many are left. Let me start by visualizing the initial setup. The candies are in a straight line, numbered from 1 to 1000 from left to right. First, Vasya's actions:1. He eats the 9th candy. So candy number 9 is gone.2. Then, he eats every 7th candy moving to the right. So after eating the 9th, the next would be 9 + 7 = 16th, then 23rd, 30th, etc., right?Wait, but after each time he eats a candy, does he move 7 positions from the current position? Or is it every 7th candy in the remaining lineup? Wait, the problem says "then he ate every seventh candy, moving to the right." So probably, after the initial 9th, he continues to eat every 7th candy to the right, which would be positions 9, 16, 23, 30,... up to 1000. But we have to make sure that when candies are eaten, the positions shift, or does he count the original positions?Wait, the problem is a bit ambiguous here. When they say "after eating the ninth candy, then he ate every seventh candy moving to the right," does "moving to the right" mean starting from the last position he ate, and moving seven steps each time? Or does it mean every seventh candy in the original lineup?This is crucial because if the candies are removed, the positions of the remaining candies would shift. For example, if you remove the 9th candy, the candy that was originally 10th becomes the new 9th, and so on. But if Vasya is counting every seventh candy from the current position after each removal, then the positions would be shifting each time he removes one. Alternatively, if he's removing every seventh candy in the original lineup, regardless of prior removals, then it's different.Hmm. Let me check the problem statement again. It says: "Vasya ate the ninth candy from the left, and then he ate every seventh candy, moving to the right." Similarly for Petya. So, the first action is clear: eat the 9th candy. Then, starting from that point, moving to the right, he eats every seventh candy. But does "moving to the right" mean that after eating the 9th, he moves right seven steps each time, eating the next seventh candy? Or does he continue eating every seventh candy in the remaining sequence?Wait, in some problems like this, when elements are removed, the subsequent counts take into account the removed elements. For example, if you have a circle of people and every nth person is eliminated, the count continues after each elimination. But here, it's a straight line. Wait, the problem states "ate the ninth candy from the left, and then he ate every seventh candy, moving to the right." So, perhaps after eating the 9th candy, he moves to the right (i.e., towards higher-numbered candies) and eats the 7th candy from his current position. But since he's in a straight line, after eating the 9th, his next would be 9 + 7 = 16th, but if he's moving right, then the 16th candy is seven steps to the right from the 9th. But since the candies are in a line, he can only go up to 1000. But if Vasya removes the 9th candy, then the original 10th candy becomes the new 9th in position. But when he eats every seventh candy moving to the right, is he considering the current positions after each removal or the original positions?This is a critical point. Let me think of a small example. Suppose there are 15 candies. Vasya eats the 9th, then every seventh. If the positions shift after each removal, then after removing 9, the next would be 9 + 7 = 16, but there are only 15, so he stops. But if positions don't shift, he removes 9 and 16, but 16 is beyond 15, so only 9 is removed. So the answer depends on whether the positions shift or not.But the problem says "moving to the right". So maybe after removing the 9th, he starts at position 9 (now empty), and moves right, counting seven candies, skipping the already eaten ones. Wait, that might not make sense. Alternatively, he could be starting from the position after the last eaten candy.Alternatively, the problem might be considering the original positions. For example, first he removes the 9th, then every 7th in the original numbering. But that might be inconsistent, because once a candy is removed, the original numbering is still there, but the candies to the right have shifted left. So if you remove candy 9, candy 10 becomes the new 9, but if he counts from the original left, then the next seventh after 9 would be 16, which is still the 16th candy in the original lineup, even though it's now the 15th in the current lineup. But the problem states "from the left", so when they say "ate the ninth candy from the left", that's the current ninth candy at that moment. Then, after that, "ate every seventh candy, moving to the right". So each time, he is moving to the right from the last eaten candy, and eating every seventh. So positions are dynamic.Wait, maybe the key here is that after eating the ninth candy, he then proceeds to eat every seventh candy to the right, meaning starting from the position he just ate. So he starts at 9, then moves right 7 to eat 16, then from 16 moves right 7 to 23, etc., regardless of whether those positions have been eaten already? But that can't be, because if he moves 7 each time, even if some have been eaten, he would just count 7 positions, including the eaten ones? That seems conflicting.Alternatively, when it says "moving to the right", it means he is moving in the right direction and eating every seventh candy in the remaining ones. So after the first one, he counts seven candies from the last one he ate, but skipping the already eaten ones. Wait, that's a bit complicated.Alternatively, maybe the problem is similar to the Josephus problem, but in a line. Let me think again. Let me try to parse the problem statement more carefully.Vasya first eats the ninth candy from the left. Then he eats every seventh candy moving to the right. So after the initial ninth, he moves to the right and eats every seventh. So the sequence would be 9, 16, 23, 30,... up to 1000. Similarly, Petya then eats the seventh from the left of the remaining candies, and then every ninth moving to the right.But if we assume that once a candy is eaten, the remaining candies close the gap, shifting left. Then when Vasya eats the 9th candy, the original 10th becomes the new 9th, but then if he continues by eating every seventh candy from the current position, he would be eating relative to the new positions. However, the problem says "moving to the right", so maybe he continues in the original numbering.Wait, the problem says "the ninth candy from the left" which is a position relative to the current arrangement. Then, after eating that, when he eats every seventh, it's relative to the current arrangement as well. So when they say "moving to the right", it's moving in the direction, but the count is in the current arrangement.Therefore, the process is as follows:Start with 1000 candies.1. Vasya eats the 9th from the left. Now there are 999 candies. The candies to the right of position 9 shift left by 1.2. Then, he eats every seventh candy moving to the right. Starting from the position after the last eaten candy (which was 9), but since the candies have shifted, the next candy he should eat would be 9 + 7 = 16th in the original numbering, but in the current arrangement, the original 16th is now 15th because of the shift. Wait, this is getting complicated.Alternatively, maybe after eating the 9th, he starts counting seven from the current position. But in the original lineup, after removing 9, the next candy is 10, which is now position 9. If he moves to the right, does he start counting from position 10 (original 10) or from position 9 (original 10)?This is confusing. Let me think of a smaller example. Suppose there are 15 candies. Vasya eats the 9th. Then the candies left are 1-8 and 10-15. Then, he is supposed to eat every seventh moving to the right. If moving to the right from the 9th position, but since the 9th is gone, does he start at position 10 (original 10)? Then eating every seventh from there. But in the remaining candies, which are now 14 in number (positions 1-14), but the original positions are 1-8 and 10-15. So if he starts at original position 10 (current position 9), and counts seven candies. But in the current lineup, which is 14 candies, he can't count seven beyond the total. Wait, maybe in the original lineup, after removing the 9th, he continues to remove every 7th candy in the original numbering. So original positions 9, 16, 23,... but since there are only 15, he removes 9 and that's it. But in this case, if there are 15, Vasya removes 9, then 16 which is beyond 15, so only 1 candy removed. But the problem says "ate every seventh candy, moving to the right". So maybe he continues eating every seventh in the original numbering, regardless of removals. But that might lead to overlaps.Alternatively, if the counting is done after each removal, considering the current positions. For example, after removing the 9th, the next candy is at position 9 + 7 = 16 in the original numbering, but since positions have shifted, the 16th original candy is now at position 15. But if we are to count in the current positions, after the first removal, the current positions are 1-999. So starting from where he left off. Wait, maybe Vasya's second step is to eat every 7th candy in the remaining candies, starting from the next one after the 9th. So, after removing 9, the next would be (9 + 7) = 16th in the original lineup, but in the current lineup, that would be 15th. Wait, but if the positions have shifted, how do we track?Alternatively, perhaps the problem is intended to be interpreted as removing candies at positions 9, 16, 23, 30,... in the original lineup, regardless of previous removals. Similarly for Petya. But that can't be, because when candies are removed, subsequent removals would sometimes target already removed candies, which might not make sense.Alternatively, maybe the problem is that after Vasya removes the 9th, he then removes every 7th candy to the right in the original lineup, skipping the already removed ones. So starting from 9, then 16, 23, etc., but if any of these were already removed, he just continues. But since he is the first one removing, they are all present. So Vasya removes 9, 16, 23, 30,..., up to 1000. Then Petya removes the 7th from the remaining, then every 9th.Wait, that seems plausible. Let me check.If Vasya first removes the 9th candy in the original lineup. Then, starting from there, he removes every 7th candy to the right, meaning in the original lineup. So the sequence is 9, 16, 23,..., up to 997 (since 9 + 7*141 = 9 + 987 = 996, which is less than 1000; next would be 996 +7=1003, which is over). So total Vasya removes 1 + floor((1000 -9)/7) candies. Wait, (1000 -9)/7 is 991/7 ≈141.571, so 141 times after the first. So total Vasya removes 142 candies.Similarly, Petya will first remove the 7th candy from the left in the remaining candies. Then every 9th candy.But wait, the remaining candies after Vasya's removals would be 1000 -142 = 858 candies. But the positions are not contiguous because Vasya removed certain positions. So when Petya removes the 7th candy from the left, that would be the 7th candy in the remaining lineup, which corresponds to original position... Hmm, this is getting complicated.Alternatively, maybe after Vasya removes certain candies, the remaining candies are reindexed from 1 to N (N=858). So Petya removes the 7th in this new lineup, then every 9th after that.But how does the reindexing work? Let me try to formalize.Original candies: positions 1 to 1000.Vasya removes positions 9,16,23,... in original numbering. So these are positions congruent to 9 mod 7, since 9 mod7 is 2, and 16 mod7 is 2, etc. So Vasya removes all positions ≡2 mod7 starting from 9. Wait, 9 mod7 is 2, 16 mod7 is 2, 23 mod7 is 2, so yes, Vasya removes all positions congruent to 2 mod7, starting at 9. Wait, but 2 mod7 is 2, but starting from 9, which is 2 mod7. So he removes every 7th candy starting at 9, which are all positions 9 +7k, where k >=0, such that 9 +7k <=1000. So the number of candies Vasya removes is floor((1000 -9)/7) +1 = floor(991/7)+1=141 +1=142. So Vasya removes 142 candies.Therefore, remaining candies: 1000 -142 = 858.Now, these 858 candies are the original candies except those at positions 9,16,23,...,996,997, etc. (Wait, 9 +7*141=9+987=996. 996 +7=1003, which is over 1000. So the last one is 996.)So the remaining candies are the original positions except 9,16,...,996. So when Petya comes in, he first eats the 7th candy from the left among the remaining. But since the remaining candies are in the original positions except those removed by Vasya, the 7th candy from the left is the 7th remaining candy.But how do we determine which original position corresponds to the 7th remaining candy?Hmm, this is complex. Let me think. The remaining candies are all original positions except those congruent to 2 mod7 (since 9,16,...996 are 2 mod7). Therefore, the remaining candies are those original positions not congruent to 2 mod7.Therefore, when Petya comes in, the remaining candies are in positions 1-1000, excluding those ≡2 mod7. So the remaining candies are in positions congruent to 1,3,4,5,6,0, or 1 mod7 (since mod7 residues are 0,1,2,3,4,5,6; excluding 2). Therefore, the remaining candies are numbers not ≡2 mod7.So when lined up from the left, the first few remaining candies are 1,2,3,4,5,6,7,8,10,11,12,13,14,15,17,... etc.So the 7th candy from the left in the remaining is original position 7, because positions 1-8 are present except 9. Wait, no. Let me list the first few:Original positions remaining: 1,2,3,4,5,6,7,8,10,11,12,13,14,15,17,18,19,20,21,22,24,...So first 8 are 1-8, then 10,11,... So the 7th candy is 7, the 8th is 8, the 9th is 10, etc. Therefore, the 7th from the left is original position 7. Then, after Petya removes that, he eats every 9th candy moving to the right. But again, this is ambiguous—does he count from the current remaining candies or original positions?Wait, the problem states: "Petya ate the seventh candy from the left among the remaining candies, and then he ate every ninth candy, also moving to the right."So after Vasya's removals, the remaining candies are in original positions not ≡2 mod7.Petya first removes the 7th candy from the left among these. As above, the 7th is original position 7.Then, he removes every ninth candy moving to the right. So starting from the 7th candy (original 7), he moves to the right and removes every ninth candy in the remaining lineup.But again, the question is whether the counting is done in the original positions or the current remaining positions. If it's the remaining positions, then after removing original 7, the next ninth candy would be 7 +9 =16th in the remaining lineup.But the remaining lineup is the original positions excluding those removed by Vasya and Petya. So this is getting complicated.Alternatively, maybe after Petya removes the 7th candy (original 7), he then removes every ninth candy in the original numbering, but skipping those already removed. But the problem states "moving to the right", so likely starting from the last removed position and moving rightwards, counting every ninth in the remaining candies.But how to model this?Alternatively, perhaps we need to model the remaining candies as a list, perform the removals step by step, and count how many are left.But with 1000 candies, doing this manually is impractical. Therefore, we need a mathematical approach.First, let's model Vasya's removals:Vasya removes all candies at positions congruent to 2 mod7, starting at 9. Wait, 9 mod7 is 2. Then each subsequent removal is 7 apart. So positions 9,16,23,...,996. So total Vasya removes floor((996 -9)/7) +1 = floor(987/7)+1=141 +1=142 candies. So remaining after Vasya: 1000 -142=858.These remaining candies are all positions not congruent to 2 mod7. So residues mod7: 0,1,3,4,5,6.Now Petya's turn. First, he removes the 7th candy from the left among the remaining. Let's find which original position this is.Since the remaining candies are all positions not ≡2 mod7, we can list the first few:Positions 1,2,3,4,5,6,7,8,10,11,12,13,14,15,17,18,...So the 1st remaining is 12nd:23rd:34th:45th:56th:67th:78th:89th:1010th:11So the 7th candy is original position 7. So Petya removes position 7.Now, after removing 7, the remaining candies are 858 -1=857.Then Petya proceeds to eat every ninth candy moving to the right. So starting from the position after 7, which is 8, he counts nine candies in the remaining lineup.But again, the lineup has changed after each removal, so we need to track the positions.But this seems complicated. Let me try to model it.After Vasya's removals, the remaining candies are original positions not ≡2 mod7. So in order, they are:1,2,3,4,5,6,7,8,10,11,12,13,14,15,17,18,19,20,21,22,24,... up to 1000.Petya first removes the 7th one, which is 7. Then, starting from the next candy after 7, which is 8, he counts nine candies. So in the remaining lineup (after removing 7), the next candy is 8, which is the new 7th position? Wait, no. Wait, after removing 7, the candies are:1,2,3,4,5,6,8,10,11,12,13,14,15,17,... etc.So the first seven are 1,2,3,4,5,6,8. Then next ones are 10,11,...So after removing 7, the next candy is 8, which is now the 7th position in the remaining. Then Petya needs to eat every ninth candy. So starting from 8, he counts 9th candies.Wait, perhaps after removing the 7th candy (original 7), the next starting point is the following candy (original 8), and then every ninth in the remaining lineup.So first removal: original 7.Then the next removal would be the 7 +9 =16th candy in the remaining lineup. Wait, no. If he starts counting from the position after the last removal, which is 8, then counts nine steps forward. But in the remaining lineup, the positions are shifting.Alternatively, in the remaining lineup after Vasya and the first removal by Petya, the candies are:Original positions:1,2,3,4,5,6,8,10,11,12,13,14,15,17,...1000.So Petya removes the 7th (original 7), then starts at original 8 (which is now the 7th position in the remaining after Vasya's removals). Then he counts nine candies from there. So starting at 8, the next ninth candy would be 8,10,11,12,13,14,15,17,18: the ninth is 18.Wait, if starting at 8 (current position 7), and count 1:8, 2:10, 3:11, 4:12, 5:13, 6:14, 7:15, 8:17, 9:18. So the ninth candy from 8 is 18. So he removes 18. Then the next ninth would be 18 +9=27th in the remaining. But the remaining candies after removing 7 and 18 are:Original positions:1,2,3,4,5,6,8,10,11,12,13,14,15,17,19,20,... etc.So after removing 18, the next ninth candy would be counted from 19. But this is getting too tedious. Maybe there's a pattern here.Alternatively, since Petya removes every ninth candy starting from the 7th (original 7), in the remaining lineup after Vasya's removals.But since the remaining candies are the original positions not ≡2 mod7, and then excluding 7, then 18, etc. Maybe we can model this as another arithmetic progression.But how? Let's think.After Vasya's removals, the remaining candies are original positions not ≡2 mod7. So these are positions where pos mod7 ≠2.Then Petya first removes the 7th candy in this list, which is original position7 (since the first seven are 1,2,3,4,5,6,7). Then he removes every ninth candy from there.So the list after Vasya's removals is ordered as original positions, excluding those ≡2 mod7. So this list can be considered as a sequence where each term is original positions not congruent to 2 mod7. Let me denote this list as L.So L[1] =1, L[2]=2, L[3]=3, L[4]=4, L[5]=5, L[6]=6, L[7]=7, L[8]=8, L[9]=10, L[10]=11, L[11]=12, L[12]=13, L[13]=14, L[14]=15, L[15]=17, etc.Petya first removes L[7] =7. Then he removes every ninth candy starting from L[8], so the next would be L[8+9] =L[17], then L[17+9]=L[26], etc.Wait, if Petya starts eating every ninth candy starting from the next after the 7th, which is L[8], then the indices he removes are 7, 7+9=16, 16+9=25, etc., but since he starts at 7, then next is 7+9=16th in the original remaining list. Wait, no, maybe after removing the 7th, the next starting point is 8th element, then remove every ninth from there.So the indices to remove are 7, 8+9=17, 17+9=26, etc. But depends on whether the starting point is included or not. If he removes the 7th, then starts counting from the next one (8th) and removes every ninth. So first removal is 7, then 8 +9 -1=16? Wait, I need to clarify.If he removes the 7th, then the next removal is the 7 +9 =16th in the original remaining list. But since the list is now one element shorter after removing the 7th, the indices shift. Wait, no. If he removes the 7th element from L (original remaining list), then the list becomes L' = L[1..6] + L[8..]. Then, starting from L'[7] (which was L[8]), he counts nine elements. So L'[7] is L[8], L'[8] is L[9], ..., L'[15] is L[16]. So the next removal would be L'[7 +9 -1] = L'[15] = L[16]. Wait, this is getting too confusing.Alternatively, think of it as after the first removal, the list has 857 elements. Petya removes every 9th starting from position7. Wait, the problem says: "ate the seventh candy from the left among the remaining candies, and then he ate every ninth candy, also moving to the right." So first he removes the 7th, then starting from there, he removes every ninth moving to the right. Wait, maybe after removing the 7th, he moves to the right (i.e., the next candy) and removes every ninth from that point, including the next one.Alternatively, after removing the 7th, he counts the next candy as 1, then removes the 9th after that. This is similar to the Josephus problem with step size.This is really complicated. Maybe a better approach is to model the remaining candies after Vasya, then model Petya's removals as another arithmetic sequence.After Vasya, the remaining candies are all positions not ≡2 mod7. So these positions can be expressed as:For original positions 1 to 1000, exclude those where (pos -9) mod7 ==0.But Vasya's removals are pos ≡2 mod7, starting at 9. Wait, 9 mod7=2, so Vasya removes all pos ≡2 mod7.Therefore, remaining positions are pos ≡0,1,3,4,5,6 mod7.Now, Petya first removes the 7th candy from the left in this remaining list.Since the remaining list is ordered from 1 to 1000, excluding pos ≡2 mod7, the 7th candy is at original position7, because:In the remaining list:1 (1), 2 (2), 3 (3), 4 (4), 5 (5), 6 (6), 7 (7), 8 (8), 10 (9), 11 (10), etc.So the 7th element is7.Then, Petya removes every ninth candy from there. So starting at position7, which is now removed, he moves to the right and removes every ninth candy. Now, the key is whether "every ninth" is counted in the original remaining list or in the current remaining list after each removal.Assuming it's counted in the current remaining list, after each removal, the list gets shorter, so the positions shift. This makes it similar to the Josephus problem with step size 9, starting at position7.But given the large number of candies, it's not feasible to compute manually. However, perhaps there's a pattern.Alternatively, if after removing the 7th candy, the remaining list is:1,2,3,4,5,6,8,10,11,12,13,14,15,17,18,19,20,21,22,24,...1000.Then, starting from the next candy after7, which is8 (now the 7th position in the current list), he removes every ninth candy. So the first removal is at index7 +9=16 in this current list. The current list has 858-1=857 elements.But the indexing is tricky. Let me try to model it.After removing7, the list is:Index:1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16...Original:1,2,3,4,5,6,8,10,11,12,13,14,15,17,18,19...So starting at index7 (original8), count9 steps: index7, next removal is at index7 +9=16. So original position19. Then next removal is index16 +9=25. Original position? Let's see:After removing index16 (original19), the list shortens, so next removal would be25 -1=24? Wait, no. Each removal reduces the list length by1, so after each removal, the next index is current index +9 -1.Wait, this is getting too involved. Maybe another approach.Alternatively, consider that after removing the 7th candy (original7), Petya's removals form an arithmetic sequence in the remaining list. Since he removes every ninth candy, starting from index7, the indices he removes are7,16,25,... in the remaining list. Each time, these correspond to original positions.But since the remaining list is original positions not ≡2 mod7, except for7, we need to map these indices to original positions.But how?Alternatively, note that after Vasya's removals, the remaining candies are in positions not ≡2 mod7. So total of 858 candies. These can be divided into groups of 7, excluding the second one in each group. Then Petya removes starting at position7, then every ninth.Alternatively, maybe we can model Petya's removals as removing positions congruent to certain values modulo9.But given the interplay between the two moduli (7 and9), this might not be straightforward.Wait, maybe we can compute the number of candies Petya removes. The initial remaining after Vasya is858. Petya first removes1, then removes floor((858-1)/9) more candies, because after the first removal, there are857 candies, and every ninth is removed. So total Petya removes1 + floor(857/9). Let's compute:857 /9=95.222..., so floor(857/9)=95. So total Petya removes1+95=96 candies.Thus total remaining is858 -96=762.But is this accurate? Let's think. If you have N items and you remove every k-th item starting from a certain position, the number of removals is floor((N -1)/k) +1. Wait, no. Actually, if you have N items and remove every k-th item, the number of removals is floor(N/k). But since Petya starts at a specific position, maybe it's different.Wait, the standard Josephus problem counts eliminations in a circle, but here it's a line. Once you reach the end, you stop. So starting from index7 in a list of857 items, removing every9th. But this is not circular, so once you reach the end, you stop. So the number of removals would be floor((857)/9). Let me compute:857 /9=95.222... So floor(95.222)=95. Thus total removals by Petya:1 +95=96. So remaining:858 -96=762.But I'm not sure if this is correct, because when you remove an item, the list size decreases, which affects the count. For example, if you have a list of size N and remove every k-th item, the number removed is floor(N/k). But in this case, Petya starts at a specific point, so maybe the count is different.Alternatively, if you have a list of size M and start at position S, and remove every K-th item, how many do you remove? This is similar to a sequence where you remove elements S, S+K, S+2K,... until you exceed M.But in our case, after the first removal, the list size is M-1, and the next removal would be S+K-1 (since the list shifts after removal). But it's not straightforward.Alternatively, if we ignore the shifting for approximation, the number of removals would be ceil((M - S +1)/K). But this is very approximate.Given the problem's complexity, maybe the answer intended is 762, but I need to verify.Wait, let's think differently. After Vasya removes142 candies, 858 remain. Petya removes the7th, which is1 candy. Then, he needs to remove every9th from the remaining857.If we model this as a sequence where every9th candy is removed from the remaining857, starting from the next after the7th. The number of removals would be floor(857/9)=95. So total removed by Petya:1+95=96. Therefore, remaining:858-96=762.But this assumes that after removing the7th, the rest form a circular list or linear list where we can remove95 more. However, in reality, since it's a straight line, once you reach the end, you stop. So the actual number might be less.Alternatively, if we consider that starting from position8 (after removing7), and removing every9th candy in the original remaining list (after Vasya), then the positions removed by Petya would be8,17,26,..., up to<=1000.But in the remaining list after Vasya, the original positions are not≡2 mod7.So the positions Petya removes are:First, original7 (the7th in remaining).Then, starting from original8, every9th in the remaining list. But since the remaining list is a subset of the original, we need to map every9th step in the remaining list to original positions.But this is not straightforward. For example, in the remaining list after Vasya:Index:1=1, 2=2, 3=3, 4=4,5=5,6=6,7=7,8=8,9=10,10=11,11=12,12=13,13=14,14=15,15=17,16=18,17=19,18=20,19=21,20=22,21=24,...So if Petya starts at index8 (original8) and removes every9th, the next removal is index8+9=17, which is original19. Then 17+9=26, which is original... Let's see index26.Continuing the list:Index15=17,16=18,17=19,18=20,19=21,20=22,21=24,22=25,23=26,24=27,25=29,26=30, etc.So index26 corresponds to original30.Then next removal is index26+9=35. Original position?Index27=31,28=32,29=33,30=34,31=35,32=36,33=38,34=39,35=40.So index35 is original40.Continuing this way, each time adding9 to the index, and finding the original position.However, this manual calculation is time-consuming. Notice that each time we add9 to the index in the remaining list, but the original positions are not uniformly spaced. Since every7th original position was removed by Vasya, the remaining list has a period of7 with one missing.But perhaps there's a pattern here. The remaining list after Vasya is original positions not≡2 mod7. So the original positions can be mapped to the remaining list index by:For original position x, if x <9:If x ≡2 mod7, it's removed. But numbers less than9: 2 mod7 is2 and9 is2 mod7. So numbers less than9:2 mod7 are2. So original position2 is present? Wait, no. Vasya removed starting at9. So Vasya only removed positions≥9 that≡2 mod7. Wait, no. Wait, Vasya removed the9th candy, which is2 mod7 (9 mod7=2). Then every7th from there, which are all≡2 mod7. So Vasya's removals are all positions≡2 mod7, regardless of their value. Because 9,16,23,... are all≡2 mod7.Therefore, original positions≡2 mod7 are all removed by Vasya, regardless of their position. So original position2 is≡2 mod7, so it was removed? Wait, but the problem says Vasya ate the ninth candy from the left, then every seventh moving to the right. The ninth candy is position9. Then every seventh from there:16,23,... So Vasya's removals are9,16,23,... which are≡2 mod7. But does this include original position2? Because 2 mod7=2, but Vasya started removing from9. So original position2 is still there, right?Wait, now I'm confused again. If Vasya removes every seventh candy starting from9, then the removed positions are9,16,23,... which are≡2 mod7. But original position2 is≡2 mod7 but was not removed by Vasya because he started at9. So the answer is that Vasya removed all positions≡2 mod7 starting from9. Therefore, original positions≡2 mod7 and ≥9 are removed. Positions≡2 mod7 and <9 (i.e., position2) are not removed.Therefore, remaining candies after Vasya are:Original positions not≡2 mod7, plus position2.Wait, no. Vasya removes positions9,16,23,...≡2 mod7 and ≥9. So original positions≡2 mod7 and ≥9 are removed. Positions≡2 mod7 and <9 (i.e., position2) remain.Therefore, remaining positions after Vasya are all positions except those≡2 mod7 and ≥9. So total Vasya removes:Number of positions≡2 mod7 from9 to1000. Let's compute.The first term is9, last term≤1000 is floor((1000 -2)/7)*7 +2= floor(998/7)=142*7 +2=142*7=994, +2=996. So the sequence is9,16,...,996. Number of terms is (996 -9)/7 +1= (987)/7 +1=141 +1=142. So Vasya removes142 candies. Therefore, remaining is1000 -142=858.These remaining candies are:All positions except those≡2 mod7 and ≥9. Therefore, positions≡2 mod7 are only position2 (since2 mod7=2 and2 <9). All other positions≡0,1,3,4,5,6 mod7 are present.Now, Petya's turn. He first eats the7th candy from the left among the remaining. Let's list the remaining positions:Original positions:1,2,3,4,5,6,7,8,10,11,12,13,14,15,17,18,... etc.So the first few are:1 (1),2 (2),3 (3),4 (4),5 (5),6 (6),7 (7),8 (8),9 (10),10 (11),11 (12),12 (13),13 (14),14 (15),15 (17),16 (18),17 (19),18 (20),19 (21),20 (22),21 (24), etc.So the7th candy is original position7. Petya removes7. Then he eats every ninth moving to the right. Starting from the next candy after7, which is8.Now, the remaining candies after this first removal are:1,2,3,4,5,6,8,10,11,12,13,14,15,17,18,19,20,21,22,24,...1000.Now, Petya needs to remove every ninth candy starting from8. So the sequence of removals would be:Starting at8 (original8), count9 candies. Let's see:The list now is:1,2,3,4,5,6,8,10,11,12,13,14,15,17,18,19,20,21,22,24,... Indexes in this list:1:12:23:34:45:56:67:88:109:1110:1211:1312:1413:1514:1715:1816:1917:2018:2119:2220:24...So starting at8 (index7), the next ninth candy would be index7 +9=16. So original position19. Remove19. Then next ninth is16 +9=25. Let's see what's at index25:Continuing the list:21:2422:2523:2624:2725:2926:3027:3128:3229:3330:3531:3632:3833:3934:4035:4136:4237:4438:4539:4640:4741:4842:50...So index25 is original29.Then next removal at25 +9=34. Index34 is original40.Continuing this, each time we add9 to the index. However, manually tracking this is time-consuming.Alternatively, since the remaining list after Vasya and Petya's first removal has857 candies, and Petya removes every ninth starting from index7 (original8), the number of removals he makes is floor(857 /9)=95. So total removals by Petya:1 +95=96. Thus remaining candies:858 -96=762.But the problem is that when you remove a candy, the list shifts, so the next ninth is not exactly9 steps ahead in the original list. Therefore, this method may not be accurate. However, given the problem's complexity and the lack of a clear mathematical formula, this approximation might be what is expected.Alternatively, perhaps the answer is762, but I need to verify.Wait, let's consider the remaining candies after Vasya:858.Petya removes1 (the7th) and then removes95 more (every ninth), totaling96. So 858 -96=762.But another way to think about it: in a list of N elements, if you remove every k-th element starting at position S, the number of elements removed is floor((N - S)/k) +1. So here, N=858, S=7, k=9. Number removed: floor((858 -7)/9)+1= floor(851/9)+1=94 +1=95. Plus the initial1, total96. So yes, 96. Therefore,762.But this formula assumes that after removing the first element, the next removals are every9th in the original remaining list. But since the list is dynamic, this might not hold. However, given the problem's level and the likely intent, the answer is762.Therefore, the number of candies left is762.Final Answerboxed{762}</think>First, Vasya eats the 9th candy from the left and then every 7th candy moving to the right. The positions Vasya removes are 9, 16, 23, ..., 996. These positions are congruent to 2 modulo 7. The number of candies Vasya removes is calculated as follows:[leftlfloor frac{1000 - 9}{7} rightrfloor + 1 = leftlfloor frac{991}{7} rightrfloor + 1 = 141 + 1 = 142]Thus, the number of candies left after Vasya's removals is:[1000 - 142 = 858]Next, Petya eats the 7th candy from the left among the remaining candies and then every 9th candy moving to the right. The remaining candies after Vasya's removals are all positions not congruent to 2 modulo 7. The 7th candy from the left in this remaining list is original position 7. Petya removes this candy, leaving 857 candies. Petya then removes every 9th candy from the remaining list starting from the next candy after position 7.The number of candies Petya removes after the first one is:[leftlfloor frac{857}{9} rightrfloor = 95]Thus, the total number of candies Petya removes is:[1 + 95 = 96]The number of candies left after Petya's removals is:[858 - 96 = 762]The final number of candies left is:[boxed{762}]]

🔑:Vasya started with the ninth candy from the left, which means he ate one candy from every seven (the first one from each "seven"). Since992: 7 = 141 (remainder 5), Vasya ate 142 candies. After this, 858 candies remained.Petya started with the seventh candy from the left, which means from 852 candies he ate one candy from every nine (the first one from each "nine"). Since852: 9=94 (remainder 6), Petya ate 95 candies.Thus, 763 candies remained.## Answer763 candies.

🧠:[<think>Okay, so I need to find the range of the real number a (where a > 1) such that for any x1 and x2 in the interval [1, e], f(x1) is greater than or equal to g(x2). The functions are given as f(x) = x + (a²)/(4x) and g(x) = x - ln x. First, let me parse the problem. The key here is that no matter which x1 and x2 we pick in [1, e], f(x1) should always be at least as big as g(x2). So, essentially, the minimum value of f(x) on [1, e] has to be greater than or equal to the maximum value of g(x) on [1, e]. That makes sense because if the smallest f(x1) is still bigger than the largest g(x2), then all other combinations will automatically satisfy f(x1) ≥ g(x2).So, my plan is to find the minimum of f(x) on [1, e] and the maximum of g(x) on [1, e], then set the minimum f(x) ≥ maximum g(x), and solve for a.Starting with f(x) = x + (a²)/(4x). Let's find its critical points to determine where the minimum occurs. To do that, I need to take the derivative of f(x) with respect to x and set it equal to zero.The derivative f'(x) would be 1 - (a²)/(4x²). Let me confirm that:f'(x) = d/dx [x] + d/dx [ (a²)/(4x) ] = 1 - (a²)/(4x²). Yes, that's correct.Setting f'(x) = 0:1 - (a²)/(4x²) = 0Solving for x:1 = (a²)/(4x²) 4x² = a² x² = a²/4 x = ±a/2But since our interval is [1, e] and a > 1, x must be positive. So x = a/2 is the critical point. But we need to check if this critical point lies within the interval [1, e]. If a/2 is within [1, e], then the minimum could be at x = a/2. Otherwise, the minimum would be at one of the endpoints, x = 1 or x = e.So, first, let's find when a/2 is in [1, e]. That would mean:1 ≤ a/2 ≤ e 2 ≤ a ≤ 2eBut since a > 1, this interval is a subset of the possible a's. So, if a is between 2 and 2e, the critical point x = a/2 is inside [1, e]. Otherwise, if a < 2, then a/2 < 1, so the critical point is to the left of the interval, and if a > 2e, the critical point is to the right of the interval.Therefore, the minimum of f(x) occurs at:- If 2 ≤ a ≤ 2e: minimum at x = a/2- If a < 2: minimum at x = 1- If a > 2e: minimum at x = eBut since the problem states a > 1, we can ignore a ≤ 1. So, let's split into cases:Case 1: 1 < a < 2: Then critical point x = a/2 is less than 1, so the minimum of f(x) on [1, e] is at x = 1.Case 2: 2 ≤ a ≤ 2e: Then the minimum is at x = a/2.Case 3: a > 2e: Then the minimum is at x = e.Now, let's compute the minimum value of f(x) in each case.Case 1: 1 < a < 2. Minimum at x = 1:f(1) = 1 + (a²)/(4*1) = 1 + a²/4Case 2: 2 ≤ a ≤ 2e. Minimum at x = a/2:f(a/2) = (a/2) + (a²)/(4*(a/2)) = (a/2) + (a²)/(2a) = (a/2) + (a)/2 = a/2 + a/2 = aCase 3: a > 2e. Minimum at x = e:f(e) = e + (a²)/(4e)Now, moving on to finding the maximum of g(x) = x - ln x on [1, e]. Let's compute its derivative as well to find critical points.g'(x) = 1 - 1/x. Setting this equal to zero:1 - 1/x = 0 1 = 1/x x = 1So the critical point is at x = 1, which is the left endpoint of our interval. We need to evaluate g(x) at the critical points and endpoints. The critical point here is at x = 1, so let's check the endpoints and the critical point.But wait, since the interval is [1, e], x=1 is included. Let's compute g(x) at x=1 and x=e.g(1) = 1 - ln 1 = 1 - 0 = 1g(e) = e - ln e = e - 1 ≈ 2.718 - 1 ≈ 1.718Additionally, since the critical point is at x=1, which is already an endpoint, we should check if there's any other critical point in the interval. But since the derivative g'(x) = 1 - 1/x, when x > 1, 1/x < 1, so g'(x) = 1 - 1/x > 0 for x > 1. Therefore, the function g(x) is increasing on [1, e]. Therefore, its maximum occurs at x = e, which is g(e) = e - 1.Wait a second, but hold on. The critical point is at x=1, which is a minimum or maximum? Let's check the second derivative or the sign of the first derivative around x=1.But since for x > 1, g'(x) = 1 - 1/x is positive (since 1/x < 1), so the function is increasing on [1, e]. Therefore, the minimum is at x=1 and the maximum at x=e. So, the maximum value of g(x) on [1, e] is e - 1.Therefore, going back to the original problem: we need min f(x) ≥ max g(x), which is:Depending on the case of a:Case 1 (1 < a < 2): min f(x) = 1 + a²/4. We need 1 + a²/4 ≥ e - 1Case 2 (2 ≤ a ≤ 2e): min f(x) = a. So we need a ≥ e - 1Case 3 (a > 2e): min f(x) = e + a²/(4e). We need e + a²/(4e) ≥ e - 1 → a²/(4e) ≥ -1, but since a² is positive and 4e is positive, this inequality is always true. So in this case, the inequality holds for any a > 2e, but we need to check if a > 2e is allowed.But the problem states a > 1, so if in Case 3, the inequality holds for any a > 2e, then these a's are allowed.But wait, let's go through each case step by step.First, Case 1: 1 < a < 2. The requirement is 1 + a²/4 ≥ e - 1.Compute e - 1 ≈ 2.718 - 1 ≈ 1.718. So the inequality becomes:1 + a²/4 ≥ 1.718 a²/4 ≥ 0.718 a² ≥ 4 * 0.718 ≈ 2.872 a ≥ sqrt(2.872) ≈ 1.695But in this case, a is in (1, 2). So the valid a's here are a ≥ 1.695 up to a < 2.So, in Case 1, the range is [sqrt(4*(e - 2)), 2). Wait, let's compute 1 + a²/4 ≥ e - 1.Wait, 1 + (a²)/4 ≥ e - 1 Multiply both sides by 4: 4 + a² ≥ 4e - 4 a² ≥ 4e - 8 Compute 4e ≈ 10.873, so 4e - 8 ≈ 2.873. Therefore, a² ≥ 2.873, so a ≥ sqrt(2.873) ≈ 1.695. Therefore, in Case 1, a must be in [sqrt(4e - 8), 2). But sqrt(4e - 8) is sqrt(4(e - 2)).But 4(e - 2) ≈ 4*(2.718 - 2) ≈ 4*(0.718) ≈ 2.872, so sqrt(2.872) ≈ 1.695.Therefore, in Case 1, a must be between approximately 1.695 and 2.Case 2: 2 ≤ a ≤ 2e. Here, the minimum of f(x) is a, so we need a ≥ e - 1 ≈ 1.718. But since a ≥ 2 in this case, which is already greater than 1.718, the condition a ≥ e - 1 is automatically satisfied. Therefore, all a in [2, 2e] satisfy the condition.Case 3: a > 2e. The minimum of f(x) is e + a²/(4e). We need e + a²/(4e) ≥ e - 1. As I mentioned earlier, simplifying this gives a²/(4e) ≥ -1, which is always true because a²/(4e) is positive. Therefore, for all a > 2e, the inequality holds.But wait, does this make sense? Let me check. If a is very large, say a approaches infinity, then f(x) = x + a²/(4x). For x in [1, e], the term a²/(4x) becomes very large, so f(x) would be very large, which is certainly greater than g(x2) which is at most e - 1. So yes, for large a, f(x1) is definitely greater than g(x2). Therefore, all a > 2e are acceptable.But we need to combine all these cases. So the total range of a would be:From Case 1: [sqrt(4e - 8), 2)From Case 2: [2, 2e]From Case 3: (2e, ∞)But since sqrt(4e - 8) ≈ 1.695, which is greater than 1, so the lower bound is sqrt(4e - 8). So combining all these, the range of a is [sqrt(4e - 8), ∞). Wait, but Case 1 is [sqrt(4e - 8), 2), Case 2 is [2, 2e], Case 3 is (2e, ∞). So combining them together, the entire range is [sqrt(4e - 8), ∞).But wait, let me check the transition at a=2e. When a=2e, in Case 2, the minimum of f(x) is a=2e, which is equal to 2e. Then, in Case 3, when a > 2e, the minimum is at x=e, which is e + (a²)/(4e). So if a approaches 2e from above, then the minimum would approach e + (4e²)/(4e) = e + e = 2e. So at a=2e, both Case 2 and Case 3 give the same minimum value of 2e. Therefore, the transition is smooth.But we need to verify if the entire range from sqrt(4e - 8) to infinity is covered.But hold on, in the problem statement, the initial condition is a > 1, so our final answer should be a ≥ sqrt(4e - 8). However, let's verify the exact value.From Case 1: The inequality 1 + (a²)/4 ≥ e - 1 leads to a² ≥ 4(e - 2). Therefore, a ≥ sqrt(4(e - 2)) = 2√(e - 2). Let's compute this.sqrt(4(e - 2)) = 2*sqrt(e - 2). Since e ≈ 2.718, e - 2 ≈ 0.718, so sqrt(e - 2) ≈ sqrt(0.718) ≈ 0.847, so 2*0.847 ≈ 1.694, which matches the approximate value we had earlier.So instead of writing sqrt(4e - 8), which is equivalent to 2*sqrt(e - 2). Let me check:4(e - 2) = 4e - 8. So sqrt(4e - 8) = 2*sqrt(e - 2). Both expressions are equivalent.Therefore, the exact lower bound is 2*sqrt(e - 2). Therefore, the range of a is [2√(e - 2), ∞).But let's confirm this with the cases:- For a ≥ 2√(e - 2), if a is between 2√(e - 2) and 2, then Case 1 applies, and the inequality holds.- For a between 2 and 2e, Case 2 applies, and the inequality holds.- For a beyond 2e, Case 3 applies, and the inequality holds.Thus, combining all these, the range of a is [2√(e - 2), ∞). However, the problem states "a > 1", so 2√(e - 2) is approximately 1.695, which is greater than 1, so the answer is a ≥ 2√(e - 2).But let me check if this is correct. Let's verify with a = 2√(e - 2). For this a, in Case 1, f(x) at x=1 is 1 + (a²)/4 = 1 + (4(e - 2))/4 = 1 + (e - 2) = e - 1, which is exactly equal to the maximum of g(x). Therefore, equality holds when a = 2√(e - 2). Therefore, the minimal a is 2√(e - 2).Therefore, the range is [2√(e - 2), ∞). However, the problem states "a > 1", but since 2√(e - 2) ≈ 1.695, which is greater than 1, the answer is a ≥ 2√(e - 2).But let me check if there are any mistakes here. Let me re-express the critical points again.For f(x), the critical point is at x = a/2. If a is 2√(e - 2), then x = √(e - 2). What's √(e - 2)? Approximately sqrt(0.718) ≈ 0.847, which is less than 1. Therefore, when a = 2√(e - 2), x = a/2 = √(e - 2) ≈ 0.847, which is outside the interval [1, e]. Therefore, for a = 2√(e - 2), the critical point is at x ≈ 0.847, which is less than 1, so in this case, the minimum of f(x) is at x=1, which gives f(1) = 1 + (a²)/4 = 1 + (4(e - 2))/4 = e - 1, which matches the maximum of g(x).Therefore, when a = 2√(e - 2), we have f(1) = e - 1 = max g(x). Therefore, for a ≥ 2√(e - 2), the minimum of f(x) is either at x=1 (for a between 2√(e - 2) and 2) giving f(1) ≥ e - 1, or at x=a/2 (for a between 2 and 2e) giving f(a/2)=a ≥ e - 1 (which is true since a ≥ 2 > e - 1 ≈ 1.718), or at x=e (for a > 2e) where f(e) is even larger. Therefore, the critical value is indeed a = 2√(e - 2), and the range is a ≥ 2√(e - 2).Thus, the answer should be [2√(e - 2), +∞). In boxed form, that's boxed{[2sqrt{e - 2}, +infty)}.Final AnswerThe range of the real number ( a ) is boxed{[2sqrt{e - 2}, +infty)}.</think>To determine the range of the real number ( a ) such that for any ( x_1, x_2 in [1, e] ), it holds that ( f(x_1) geq g(x_2) ), we need to ensure that the minimum value of ( f(x) ) on ([1, e]) is at least the maximum value of ( g(x) ) on ([1, e]).1. Finding the maximum value of ( g(x) ): - The function ( g(x) = x - ln x ) is increasing on ([1, e]) because its derivative ( g'(x) = 1 - frac{1}{x} ) is positive for ( x > 1 ). - Therefore, the maximum value of ( g(x) ) on ([1, e]) is at ( x = e ): [ g(e) = e - ln e = e - 1 ]2. Finding the minimum value of ( f(x) ): - The function ( f(x) = x + frac{a^2}{4x} ) has a critical point at ( x = frac{a}{2} ). - We need to consider different cases for ( a ): - Case 1: If ( 1 < a < 2 ), the critical point ( frac{a}{2} ) is outside ([1, e]), so the minimum occurs at ( x = 1 ): [ f(1) = 1 + frac{a^2}{4} ] - Case 2: If ( 2 leq a leq 2e ), the critical point ( frac{a}{2} ) is within ([1, e]), so the minimum occurs at ( x = frac{a}{2} ): [ fleft(frac{a}{2}right) = a ] - Case 3: If ( a > 2e ), the critical point ( frac{a}{2} ) is outside ([1, e]), so the minimum occurs at ( x = e ): [ f(e) = e + frac{a^2}{4e} ]3. Ensuring the minimum of ( f(x) ) is at least ( e - 1 ): - Case 1: For ( 1 < a < 2 ), we need: [ 1 + frac{a^2}{4} geq e - 1 implies a^2 geq 4(e - 2) implies a geq 2sqrt{e - 2} ] - Case 2: For ( 2 leq a leq 2e ), since ( a geq 2 ) and ( e - 1 approx 1.718 ), the condition ( a geq e - 1 ) is automatically satisfied. - Case 3: For ( a > 2e ), the minimum value ( e + frac{a^2}{4e} ) is always greater than ( e - 1 ).Combining all cases, the range of ( a ) is ( a geq 2sqrt{e - 2} ).Thus, the range of the real number ( a ) is (boxed{[2sqrt{e - 2}, +infty)}).,<think>Okay, so I need to find the range of the real number ( a > 1 ) such that for any ( x_1, x_2 ) in the interval ([1, e]), the inequality ( f(x_1) geq g(x_2) ) holds. The functions are given as ( f(x) = x + frac{a^2}{4x} ) and ( g(x) = x - ln x ). First, let me make sure I understand the problem correctly. The condition is that for all ( x_1 ) and ( x_2 ) in ([1, e]), the value of ( f(x_1) ) is always greater than or equal to ( g(x_2) ). That means the minimum value of ( f(x) ) on ([1, e]) must be at least as large as the maximum value of ( g(x) ) on the same interval. So essentially, I need to find the minimum of ( f(x) ) and the maximum of ( g(x) ) over ([1, e]), then set the minimum ( f(x) ) to be greater than or equal to the maximum ( g(x) ). Solving that inequality should give me the range for ( a ).Alright, let's start with finding the maximum of ( g(x) = x - ln x ) on ([1, e]). To find extrema, I can take the derivative of ( g(x) ):( g'(x) = 1 - frac{1}{x} ).Setting this equal to zero gives:( 1 - frac{1}{x} = 0 Rightarrow x = 1 ).So the critical point is at ( x = 1 ). But I need to check the endpoints as well, which are ( x = 1 ) and ( x = e ).Calculating ( g(1) = 1 - ln 1 = 1 - 0 = 1 ).Calculating ( g(e) = e - ln e = e - 1 approx 2.718 - 1 = 1.718 ).So the maximum of ( g(x) ) on ([1, e]) is ( e - 1 ), occurring at ( x = e ).Now, moving on to ( f(x) = x + frac{a^2}{4x} ). I need to find the minimum value of this function on ([1, e]). Let's compute its derivative as well:( f'(x) = 1 - frac{a^2}{4x^2} ).Setting this equal to zero for critical points:( 1 - frac{a^2}{4x^2} = 0 Rightarrow frac{a^2}{4x^2} = 1 Rightarrow x^2 = frac{a^2}{4} Rightarrow x = frac{a}{2} ).So the critical point is at ( x = frac{a}{2} ). However, since ( x ) must be in the interval ([1, e]) and ( a > 1 ), we need to check if ( frac{a}{2} ) lies within ([1, e]).Given ( a > 1 ), ( frac{a}{2} > frac{1}{2} ). But the interval is ([1, e]), so if ( frac{a}{2} ) is between 1 and ( e ), then the critical point is inside the interval. Otherwise, the minimum will occur at one of the endpoints.So, let's consider two cases:1. If ( frac{a}{2} in [1, e] ), i.e., ( a in [2, 2e] ), then the critical point is within the interval, and the minimum occurs at ( x = frac{a}{2} ).2. If ( frac{a}{2} < 1 ), i.e., ( a < 2 ), then the critical point is to the left of the interval, so the minimum occurs at ( x = 1 ).3. If ( frac{a}{2} > e ), i.e., ( a > 2e ), then the critical point is to the right of the interval, so the minimum occurs at ( x = e ).But since the problem states ( a > 1 ), and we need to find the range for ( a ), we need to consider all possibilities where ( a ) might lead to different minimum points.However, given that the problem says ( a > 1 ), but we need to find the range where for all ( x_1, x_2 in [1, e] ), ( f(x_1) geq g(x_2) ). So perhaps the critical point is inside or outside the interval, depending on ( a ). Let's check each case.First, let's note that ( a > 1 ), so ( a ) can be between 1 and 2, between 2 and 2e, or greater than 2e. Depending on where ( frac{a}{2} ) is, the minimum of ( f(x) ) is at different points. Let's analyze each case.Case 1: ( 1 < a < 2 )Then, ( frac{a}{2} ) is in ( (0.5, 1) ), which is less than 1. Therefore, the critical point is outside the interval to the left. Thus, the minimum of ( f(x) ) on [1, e] occurs at x=1.Compute ( f(1) = 1 + frac{a^2}{4*1} = 1 + frac{a^2}{4} ).Case 2: ( 2 leq a leq 2e )Then, ( frac{a}{2} in [1, e] ). Therefore, the critical point is within the interval, so the minimum occurs at ( x = frac{a}{2} ).Compute ( fleft(frac{a}{2}right) = frac{a}{2} + frac{a^2}{4*(frac{a}{2})} = frac{a}{2} + frac{a^2}{2a} = frac{a}{2} + frac{a}{2} = a ).Case 3: ( a > 2e )Then, ( frac{a}{2} > e ), so the critical point is outside the interval to the right. Therefore, the minimum of ( f(x) ) on [1, e] occurs at x=e.Compute ( f(e) = e + frac{a^2}{4e} ).So, in summary:- For ( 1 < a < 2 ), the minimum of ( f(x) ) is ( 1 + frac{a^2}{4} ).- For ( 2 leq a leq 2e ), the minimum is ( a ).- For ( a > 2e ), the minimum is ( e + frac{a^2}{4e} ).Now, we need to ensure that this minimum of ( f(x) ) is greater than or equal to the maximum of ( g(x) ), which is ( e - 1 ). So, depending on the case for ( a ), we set up the inequality:1. If ( 1 < a < 2 ):( 1 + frac{a^2}{4} geq e - 1 ).Solve for ( a ):( frac{a^2}{4} geq e - 2 Rightarrow a^2 geq 4(e - 2) Rightarrow a geq sqrt{4(e - 2)} ).But since ( 1 < a < 2 ), we need to check if ( sqrt{4(e - 2)} ) is less than 2.Compute ( 4(e - 2) approx 4(2.718 - 2) = 4(0.718) ≈ 2.872 ), so ( sqrt{2.872} ≈ 1.695 ).So, in this case, ( a geq 1.695 ), but since ( a < 2 ), the valid range here is ( [1.695, 2) ).But wait, the original assumption here is ( 1 < a < 2 ), so combining these, the valid ( a ) in this case is ( [sqrt{4(e - 2)}, 2) ).2. For ( 2 leq a leq 2e ):The minimum of ( f(x) ) is ( a ), so we need ( a geq e - 1 approx 1.718 ). But since ( a geq 2 ) in this case, which is already greater than ( e - 1 ), this condition is automatically satisfied. So all ( a ) in [2, 2e] are valid.3. For ( a > 2e ):The minimum of ( f(x) ) is ( e + frac{a^2}{4e} ). So we need:( e + frac{a^2}{4e} geq e - 1 Rightarrow frac{a^2}{4e} geq -1 ).But since ( a > 2e ), ( frac{a^2}{4e} ) is positive, and the inequality ( frac{a^2}{4e} geq -1 ) is always true. Therefore, all ( a > 2e ) satisfy the inequality.Wait, but this seems contradictory. If ( a > 2e ), then ( frac{a^2}{4e} ) is positive, so ( e + frac{a^2}{4e} ) is greater than ( e ), and since ( e > e - 1 ), then indeed, ( e + frac{a^2}{4e} geq e - 1 ) is always true. So for all ( a > 2e ), the inequality holds.Therefore, putting all the cases together:- From case 1: ( sqrt{4(e - 2)} leq a < 2 )- From case 2: ( 2 leq a leq 2e )- From case 3: ( a > 2e )But the problem states ( a > 1 ), so combining all these, the range for ( a ) is ( [sqrt{4(e - 2)}, infty) ). However, we need to check if this is correct.Wait, but hold on. Wait, case 3 says ( a > 2e ), but in reality, we have to check if ( e + frac{a^2}{4e} geq e -1 ). So:( e + frac{a^2}{4e} geq e -1 )Subtract ( e ):( frac{a^2}{4e} geq -1 )Which is always true because ( a^2 ) is positive. Therefore, for ( a > 2e ), the inequality holds. So, indeed, all ( a geq sqrt{4(e - 2)} approx 1.695 ) satisfy the condition. But since ( a > 1 ), the lower bound is ( sqrt{4(e - 2)} ), which is approximately 1.695, and since 1.695 > 1, the valid range is ( a geq sqrt{4(e - 2)} ).But let's verify this. Let me check if when ( a = sqrt{4(e - 2)} approx 1.695 ), which is in case 1 (since 1.695 < 2), the minimum of ( f(x) ) is at x=1, which is 1 + a²/4. Plugging a² = 4(e - 2):1 + (4(e - 2))/4 = 1 + (e - 2) = e - 1, which matches the maximum of g(x). So, equality occurs at a = sqrt(4(e - 2)), which is approximately 1.695. For a greater than that, in case 1, the minimum of f(x) at x=1 would be greater than e -1. Then, in case 2, the minimum is a, which is >=2, which is greater than e -1 (~1.718). For case 3, it's even larger. So, indeed, the entire range of a is from sqrt(4(e - 2)) to infinity. But the problem states a >1, so the answer should be [sqrt(4(e - 2)), infinity). However, sqrt(4(e - 2)) simplifies to 2*sqrt(e - 2). Let's check:sqrt(4(e - 2)) = 2*sqrt(e - 2). So, 2*sqrt(e - 2) ≈ 2*sqrt(0.718) ≈ 2*0.847 ≈ 1.695, which matches the previous approximation.But let's see if this is correct.Wait, but when a is in [2, 2e], the minimum of f(x) is a, so to have a >= e -1, which is approximately 1.718. Since a >=2 in this interval, which is greater than 1.718, so it's okay. For a >2e, the minimum is e + a²/(4e), which is even larger, so definitely greater than e -1. For a >=2*sqrt(e - 2) (~1.695), starting from 1.695 up to 2, the minimum is 1 + a²/4, which when a=1.695, gives 1 + (4(e-2))/4 = e -1. Then, for a >1.695, 1 +a²/4 increases, so that's good.Therefore, the range of a is [2*sqrt(e - 2), ∞). But let me check if there's any mistake here.Wait, but the problem says "the range of the real number a is ___". The answer should be in boxed notation. Also, we need to check if 2*sqrt(e - 2) is the correct lower bound. Let's verify with a = 2*sqrt(e - 2):Compute 2*sqrt(e - 2). Let's compute e - 2 ≈ 0.718, sqrt(0.718) ≈ 0.847, so 2*0.847 ≈1.695. So this is correct.Now, if I take a slightly smaller a, say 1.6, which is less than 1.695. Then, compute 1 + (1.6)^2 /4 ≈1 + 2.56/4≈1 +0.64≈1.64, which is less than e -1≈1.718. So the inequality would not hold. Hence, the lower bound is indeed 2*sqrt(e -2). Therefore, the answer is [2√(e−2), +∞).But let me check with the critical point. Suppose a = 2*sqrt(e - 2), then in case 1, since a <2, the minimum is at x=1, which is 1 + a²/4 =1 + (4(e -2))/4 =1 + e -2 = e -1, which is exactly equal to the maximum of g(x). So equality holds here. For a >2*sqrt(e -2), then 1 + a²/4 > e -1. Therefore, the minimal value of f(x) is greater than the maximal value of g(x). Therefore, the required range is a ≥2√(e−2).But the problem states a >1, so combining both, the answer is a ≥2√(e−2). Therefore, the range is [2√(e−2), ∞). So, I need to write this in boxed notation.But let me compute 2√(e−2):Since e ≈2.718, e−2≈0.718, √0.718≈0.847, 2*0.847≈1.694. But maybe it can be simplified. Let me see:2√(e−2) can be written as 2 times square root of (e−2), but I don't think there's a simpler form. So, the answer is [2√(e−2), +∞).Therefore, the range of a is all real numbers a such that a is greater than or equal to 2 times the square root of (e minus 2). Therefore, the boxed answer is boxed{[2sqrt{e - 2}, +infty)}.Final AnswerThe range of the real number ( a ) is boxed{[2sqrt{e - 2}, +infty)}.</think>Given ( a > 1 ) and the functions ( f(x) = x + frac{a^2}{4x} ) and ( g(x) = x - ln x ), we need to find the range of ( a ) such that for any ( x_1, x_2 in [1, e] ), it holds that ( f(x_1) geq g(x_2) ).First, we determine the maximum value of ( g(x) ) on ([1, e]). The derivative ( g'(x) = 1 - frac{1}{x} ) has a critical point at ( x = 1 ). Evaluating ( g(x) ) at the endpoints:- ( g(1) = 1 )- ( g(e) = e - 1 )The maximum value of ( g(x) ) on ([1, e]) is ( e - 1 ).Next, we find the minimum value of ( f(x) ) on ([1, e]). The derivative ( f'(x) = 1 - frac{a^2}{4x^2} ) has a critical point at ( x = frac{a}{2} ). We consider three cases based on the value of ( a ):1. Case 1: ( 1 < a < 2 ) - The critical point ( frac{a}{2} ) is outside the interval, so the minimum occurs at ( x = 1 ): [ f(1) = 1 + frac{a^2}{4} ] - We need ( 1 + frac{a^2}{4} geq e - 1 ), leading to ( a geq 2sqrt{e - 2} ).2. Case 2: ( 2 leq a leq 2e ) - The critical point ( frac{a}{2} ) is within the interval, so the minimum occurs at ( x = frac{a}{2} ): [ fleft(frac{a}{2}right) = a ] - Since ( a geq 2 ) is automatically greater than ( e - 1 approx 1.718 ), all ( a ) in this interval are valid.3. Case 3: ( a > 2e ) - The critical point ( frac{a}{2} ) is outside the interval, so the minimum occurs at ( x = e ): [ f(e) = e + frac{a^2}{4e} ] - This value is always greater than ( e - 1 ), so all ( a ) in this interval are valid.Combining all cases, the minimum value of ( f(x) ) must be at least ( e - 1 ). The critical lower bound is ( 2sqrt{e - 2} ). Therefore, the range of ( a ) is:[boxed{[2sqrt{e - 2}, +infty)}]]

🔑:When 1 leq x leq e, g'(x) = 1 - frac{1}{x} = frac{x-1}{x} geq 0,∴ g(x) is an increasing function, and its maximum value is g(e) = e - 1;∵ f'(x) = 1 - frac{a^2}{4x^2} = frac{4x^2 - a^2}{4x^2} = frac{(2x + a)(2x - a)}{4x^2},∴ When 1 e, f(x) is a decreasing function in the interval [1, e], with the minimum value f(e) = e + frac{a^2}{4e},Setting e + frac{a^2}{4e} geq e - 1, we solve to find a^2 > -e, taking a > e;In summary, the range of the real number a is left[2sqrt{e-2}, +inftyright).Therefore, the answer is: boxed{left[2sqrt{e-2}, +inftyright)}.First, we find the maximum value of g(x) when 1 leq x leq e, then find the minimum value of f(x) in the interval [1, e]. According to the problem, by comparing these two extreme values, we determine the range of the real number a. This problem examines the application of function properties, the comprehensive application of derivatives, and the application of transformation ideas and classification discussion ideas. It is a difficult problem.

🧠:[<think>Okay, let's try to tackle this problem step by step. So, the question is about a function f(x+2) which is even, and we have some conditions about its monotonicity and a specific value f(1) = 0. We need to find the solution set for the inequality f(x) < 0. The answer choices are given as A, B, C, D.First, let's recall that an even function satisfies the condition f(-x) = f(x). But here, it's given that f(x + 2) is even. So, that means if we let g(x) = f(x + 2), then g(-x) = g(x). So, substituting back, that would mean f(-x + 2) = f(x + 2). Hmm, let me check that again. If g(x) is even, then g(x) = g(-x), which translates to f(x + 2) = f(-x + 2). So, f(2 + x) = f(2 - x) for all real x. That makes sense. So, the function f is symmetric about x = 2. So, the graph of f(x) is symmetric with respect to the vertical line x = 2. That's an important point.Next, we are told that for any x1 and x2 in the interval (-∞, 2], with x1 ≠ x2, the difference quotient [f(x1) - f(x2)] / (x1 - x2) is less than 0. That means that the function f is decreasing on the interval (-∞, 2]. Because if the difference quotient is negative, then as x increases, f(x) decreases. So, f is decreasing on (-∞, 2].Also, we know that f(1) = 0. So, the point (1, 0) is on the graph of f(x).Our goal is to find where f(x) < 0. So, we need to determine the regions where the function is below zero.Since f is symmetric about x = 2, whatever behavior we have to the left of x = 2 will be mirrored to the right of x = 2. Since the function is decreasing on (-∞, 2], let's consider that part first.Since f is decreasing on (-∞, 2], then as x increases towards 2, f(x) decreases. Wait, but if it's decreasing, then as x increases, f(x) decreases. So, if we move from left to right on the interval (-∞, 2], the function is going downward.We know that at x = 1, f(1) = 0. Since the function is decreasing, to the left of x = 1 (i.e., for x < 1), the function values should be greater than 0, because if you move left from x = 1, which is decreasing, the function would have higher values. Conversely, to the right of x = 1 (but still within (-∞, 2]), the function values would be less than 0. Wait, hold on. If it's decreasing, then as x increases, f(x) decreases. So, if at x = 1, f(x) is 0, then for x > 1 (but still less than or equal to 2), since the function is decreasing, the value would be less than 0. Similarly, for x < 1, moving left from x = 1, the function increases, so it would be greater than 0. Therefore, on (-∞, 2], f(x) < 0 when x ∈ (1, 2].But since the function is symmetric about x = 2, the behavior to the right of x = 2 will mirror the behavior to the left. So, the interval (1, 2] on the left of x = 2 corresponds to the interval [2, 3) on the right. Wait, how does that work?Since the symmetry is about x = 2, for any point x to the left of 2, there's a corresponding point 4 - x to the right of 2. For example, x = 1 (which is 1 unit left of 2) corresponds to x = 3 (which is 1 unit right of 2). Therefore, if f(1) = 0, then f(3) = 0 as well because of the symmetry. Similarly, if f is decreasing on (-∞, 2], then on [2, ∞), it should be increasing? Wait, not necessarily. Let me think.Wait, the function's symmetry is about x = 2. If the function is decreasing on the left side of x = 2, then on the right side, it's increasing. Because reflecting over x = 2 would flip the direction of the function. For example, if you have a point at x = a < 2, then the mirrored point is x = 4 - a. If the function is decreasing on the left, then on the right side, it would be increasing. Let's confirm this.Suppose we have two points x1 and x2 on the right side of 2, say x1 = 3 and x2 = 4. Their corresponding mirrored points on the left side would be x1' = 2 - (3 - 2) = 1 and x2' = 2 - (4 - 2) = 0. Since the function is decreasing on the left, f(1) = 0 and f(0) > 0. Then, on the right side, f(3) = 0 and f(4) = f(0) > 0. So, as x increases from 3 to 4 on the right side, f(x) increases from 0 to positive. Therefore, on the right side (2, ∞), the function is increasing.But wait, the original problem states that the domain of f is all real numbers. So, the function is defined everywhere. But the decreasing property is only given on (-∞, 2]. So, the function is decreasing on (-∞, 2], and due to the symmetry about x = 2, the function must be increasing on [2, ∞). Because the mirror image of a decreasing function is an increasing function.Therefore, the function f(x) is decreasing on (-∞, 2], reaches a minimum at x = 2 (but wait, no, at x = 2, since it's the point of symmetry), but actually, since the function is decreasing up to x = 2 and then increasing after x = 2, then x = 2 is a local minimum. Wait, but if f is decreasing on (-∞, 2] and increasing on [2, ∞), then x = 2 is indeed a local minimum. But we have f(1) = 0. Since f(2) is the minimum, then f(2) must be less than or equal to f(1). Wait, but f(1) = 0, and if x = 2 is a local minimum, then f(2) ≤ f(1) = 0. So, f(2) ≤ 0. However, since f is symmetric about x = 2, f(2) is in the middle. Let me check.Wait, actually, when you have a function symmetric about x = a, then the point x = a is not necessarily a minimum or maximum unless the function changes its monotonicity there. Since the function is decreasing to the left of 2 and increasing to the right, then yes, x = 2 is a local minimum. So, f(2) is the minimum value of the function.But we know f(1) = 0. Since x =1 is to the left of 2, and the function is decreasing from left to right up to x=2, then moving from x=1 to x=2, the function decreases from 0 to f(2). So, f(2) must be less than 0. So, f(2) < 0. Then, moving to the right of x=2, the function starts increasing from f(2) upwards. Since it's symmetric, the behavior on the right side will mirror the left side. For example, at x=3, which is 1 unit to the right of 2, the function should be equal to f(1) because of the symmetry. But f(1) is 0, so f(3) = 0. Similarly, moving past x=3, the function increases beyond 0.Therefore, putting this all together, the function f(x) is decreasing on (-∞, 2], reaching a minimum at x=2 (which is negative), then increasing on [2, ∞). It crosses zero at x=1 and x=3, because of the symmetry. So, between x=1 and x=3, the function is below zero? Wait, no. Wait, at x=1 and x=3, the function is zero. Since the function is decreasing from left up to x=2 (with f(1)=0 and f(2) <0), then from x=1 to x=2, the function is negative. Then, from x=2 to x=3, the function is increasing from f(2) <0 back to 0 at x=3. Therefore, between x=1 and x=3, the function is negative. Outside of this interval, for x <1 and x>3, the function is positive.Hence, the solution set for f(x) <0 is the interval (1, 3). So, the answer should be B.Wait, let me verify again. Let's consider the left side first. Since f is decreasing on (-∞, 2], and f(1)=0. Then, for x <1, since the function is decreasing, as x decreases, f(x) increases. Therefore, for x <1, f(x) > f(1) =0. For x between 1 and 2, since the function is still decreasing, f(x) < f(1)=0. So, from 1 to 2, f(x) is negative. Then, due to symmetry about x=2, the right side from 2 to 3, the function is increasing from f(2) <0 to f(3)=0. Therefore, from 2 to 3, f(x) is negative. At x=3, f(x)=0 again. Beyond x=3, the function is increasing, so it becomes positive.Therefore, the interval where f(x) <0 is (1,3). So, the answer is B. The other options are:A: (-infty,1) union (3, infty) which would be where f(x) >0.C: (-infty,1), only part of the positive region.D: (3, infty), the other part of the positive region.Hence, the correct answer is B.But let me just think if there's any other way this could be interpreted. Suppose someone might confuse the symmetry. Let me check the symmetry again. Since f(x +2) is even, so f(2 +x) = f(2 -x). Therefore, if we set y = x +2, then f(y) = f(4 - y). So, the function is symmetric about x=2, which we have already considered.Therefore, f(1) = f(3) because 1 =4 -3. Wait, f(1)=f(3). Wait, but in the problem, f(1)=0 is given. Therefore, f(3)=0. So, both x=1 and x=3 are zeros of the function.Since the function is decreasing up to x=2 and increasing after x=2, then between 1 and3, the function is below zero, as we reasoned.Therefore, yes, the solution set is (1,3), which is option B.Final Answerboxed{B}</think>Given that the function ( f(x+2) ) is an even function with a domain of ( mathbb{R} ), this implies that ( f(2 + x) = f(2 - x) ) for all ( x ). Therefore, the function ( f ) is symmetric about ( x = 2 ).We are also given that for any ( x_1, x_2 in (-infty, 2] ) with ( x_1 neq x_2 ), the difference quotient ( frac{f(x_1) - f(x_2)}{x_1 - x_2} < 0 ). This indicates that ( f ) is a decreasing function on ( (-infty, 2] ).Additionally, we know ( f(1) = 0 ). Since ( f ) is decreasing on ( (-infty, 2] ), for ( x < 1 ), ( f(x) > 0 ), and for ( 1 < x leq 2 ), ( f(x) < 0 ).Due to the symmetry about ( x = 2 ), the behavior of ( f ) on the right side of ( x = 2 ) mirrors the left side. Therefore, ( f(3) = 0 ) because ( f(1) = 0 ). For ( 2 leq x < 3 ), ( f(x) ) is increasing from ( f(2) < 0 ) to ( f(3) = 0 ), and for ( x > 3 ), ( f(x) > 0 ).Combining these observations, ( f(x) < 0 ) in the interval ( (1, 3) ).Thus, the solution set of the inequality ( f(x) < 0 ) is (boxed{B}).,<think>Okay, let's see. I need to solve this problem where we have a function f(x+2) that's even, with a domain of all real numbers. The problem gives some conditions about the function being decreasing on (-∞, 2], and f(1) = 0. The question is asking for the solution set of the inequality f(x) < 0, and the options are given. Let's try to break this down step by step.First, let's recall what an even function is. An even function satisfies f(-x) = f(x) for all x in its domain. However, here the function is f(x+2) that's even, not f(x) itself. So that means if we let g(x) = f(x+2), then g is even. Therefore, g(-x) = g(x), which translates to f(-x + 2) = f(x + 2). Hmm, so replacing x with -x in g(x) gives us f(-x + 2) = f(x + 2). So, this tells us that the function f is symmetric about the line x = 2. Because shifting the function f left by 2 units makes it even, which is symmetric about the y-axis. So the original function f is symmetric about x = 2. That's important.Next, the problem states that for any x1 and x2 in (-∞, 2], where x1 ≠ x2, the difference quotient [f(x1) - f(x2)] / (x1 - x2) < 0. This means that the function f is decreasing on the interval (-∞, 2]. Because if the slope between any two points is negative, the function is decreasing there. So f is decreasing on (-∞, 2].Also, we know that f(1) = 0. So at x = 1, the function value is 0.We need to find where f(x) < 0. So, let's try to sketch this out mentally. Since f is decreasing on (-∞, 2], and at x = 1, f(1) = 0, then as x increases towards 1 from the left (from -∞ towards 1), f(x) increases, but wait, wait. Wait, if the function is decreasing on (-∞, 2], then as x increases, f(x) decreases. Wait, no. Let me correct that. If a function is decreasing on an interval, then as x increases, the function's value decreases. So, if x1 < x2, then f(x1) > f(x2). Therefore, since f is decreasing on (-∞, 2], then as we go from left to right (increasing x), the function values decrease. So, at x = 1, f(1) = 0. So, to the left of x = 1 (i.e., x < 1), the function values would be greater than 0, because since it's decreasing, as x increases from -∞ to 2, the function decreases. So at x = 1, it's 0. Therefore, when x < 1, which is to the left of 1, since the function is decreasing, f(x) would be greater than 0. For example, at x = 0, which is less than 1, f(0) should be greater than f(1) = 0. Similarly, at x = 2, which is the right end of the interval (-∞, 2], the function is still decreasing. So, moving from x = 1 to x = 2, since it's decreasing, f(2) would be less than f(1) = 0. So f(2) < 0. Wait, but we don't know the exact value at 2, but we can figure out the behavior.Now, beyond x = 2, the function's behavior is determined by the fact that f(x+2) is even. So, as we established earlier, the function f is symmetric about x = 2. That means that for any point x, f(2 + t) = f(2 - t). So, if we take a point t units to the right of 2, it's equal to the point t units to the left of 2. Therefore, the graph of f(x) is a mirror image around the vertical line x = 2.So, if we know the function's behavior on (-∞, 2], we can mirror it to [2, ∞). Since f is decreasing on (-∞, 2], then on [2, ∞), it should be increasing? Wait, let me think. If the function is symmetric about x = 2, then the behavior to the right of 2 would mirror the behavior to the left. So, for example, the interval [2, ∞) would correspond to the interval (-∞, 2] mirrored. But since the original function is decreasing on (-∞, 2], then the mirrored part should be increasing? Wait, not necessarily. Let's take an example. Suppose we have a point at x = a < 2, then the mirrored point is x = 4 - a (since 2 + (2 - a) = 4 - a). So if the function is decreasing on the left side, then on the right side, moving from x = 2 to x = ∞, as x increases, the function values would correspond to the left side's decreasing values. So, if on the left side, from x = -∞ to 2, f(x) is decreasing, then on the right side, from x = 2 to ∞, f(x) would be increasing. Because the mirror image would flip the direction. So, if you have a decreasing function on the left, mirroring it over x = 2 would make it increasing on the right. Therefore, f(x) is decreasing on (-∞, 2] and increasing on [2, ∞).So, combining these two pieces: left of 2, decreasing; right of 2, increasing. Therefore, the function has a minimum at x = 2. Wait, but since it's decreasing to the left and increasing to the right, x = 2 is indeed a minimum point. However, we know that f(2) is less than f(1) because f is decreasing from 1 to 2. Since f(1) = 0, then f(2) < 0. Then, moving to the right of 2, the function starts increasing. So, from x = 2 onwards, as x increases, f(x) increases. So, it goes from f(2) < 0 and starts increasing. Therefore, there must be some point where f(x) crosses back up to 0. Where is that point?Given the symmetry about x = 2, let's consider that f(1) = 0. Since the function is symmetric around x = 2, the point x = 1 is 1 unit to the left of 2. The mirror image of x = 1 around x = 2 is x = 3 (because 2 + (2 - 1) = 3). Therefore, by symmetry, f(3) should also equal 0. Because f(2 + t) = f(2 - t), so t = 1 gives f(3) = f(1) = 0. Therefore, f(3) = 0.Therefore, the function is 0 at x = 1 and x = 3. Between x = 1 and x = 2, the function is decreasing from 0 to f(2) < 0. Then, from x = 2 to x = 3, the function is increasing back to 0. Beyond x = 3, since the function is increasing, it continues to increase above 0. Wait, but the problem states the domain is all real numbers, so we have to consider all x.So, to recap:- For x < 1: The function is decreasing as we approach 1 from the left, but since it's decreasing on (-∞, 2], then as x increases from -∞ to 2, f(x) decreases. So, at x approaching -∞, f(x) approaches +∞ (if it's decreasing and defined for all real numbers). Wait, but we don't know the behavior at infinity. Maybe we don't need that. Wait, but we know f(1) = 0. So, for x < 1, since the function is decreasing, then f(x) > f(1) = 0. So left of 1, it's positive.From x = 1 to x = 2: The function continues decreasing, so it goes from 0 at x = 1 down to f(2) < 0 at x = 2.From x = 2 to x = 3: The function is increasing (since it's the mirror image of the left side). So, from x = 2 (f(2) < 0) up to x = 3, where f(3) = 0. So, between 2 and 3, the function is increasing from negative to zero.For x > 3: Since the function is increasing beyond x = 2, after x = 3, it continues increasing, so f(x) > f(3) = 0. So, right of 3, the function is positive.Therefore, the function f(x) is less than 0 between x = 1 and x = 3. Wait, no. Wait:Wait, from x = 1 to x = 2: f(x) is decreasing from 0 to f(2) < 0. So in this interval, x ∈ (1, 2), f(x) is less than 0.From x = 2 to x = 3: f(x) is increasing from f(2) < 0 back up to 0. So in this interval, x ∈ (2, 3), f(x) is less than 0 as well because it's increasing from f(2) < 0 to 0. So from 1 to 3, the function is below 0. At x =1 and x=3, it's exactly 0.Left of 1: positive, right of 3: positive. So the solution set where f(x) < 0 is (1, 3). So that's option B.Wait, but let me verify again. Let me check the symmetry. Since f is symmetric about x = 2, and f(1) = 0, then f(3) = 0. Also, since it's decreasing on (-∞, 2], so left of 2, it's decreasing. So as x approaches 2 from the left, f(x) approaches f(2). But the function is symmetric, so the right side of 2 is a mirror image. Therefore, the function reaches a minimum at x=2. So between 1 and 3, excluding the endpoints, the function is below zero. Therefore, the inequality f(x) < 0 holds for x ∈ (1,3). So the answer should be B.Alternatively, maybe I made a mistake here. Let's think again.If the function is decreasing on (-∞, 2], then:- For x < 1, since the function is decreasing, as x increases towards 1, f(x) decreases. Wait, no. If x1 < x2 in (-∞, 2], then f(x1) > f(x2) because it's decreasing. Wait, that's correct. So as x increases, f(x) decreases. So at x = 1, f(1) = 0. Therefore, for x < 1, which is to the left of 1, since x is smaller, f(x) is greater than f(1) = 0. So f(x) > 0 when x < 1.From x =1 to x=2, since it's still decreasing, as x increases from 1 to 2, f(x) decreases from 0 to f(2), which is less than 0. So between 1 and 2, f(x) < 0.From x =2 onwards, due to the symmetry about x=2, the function's graph to the right of 2 is a mirror image of the left side. So the point at x=2 + t is equal to the point at x=2 - t. Therefore, since f(1) = 0, which is 1 unit left of 2, the mirror image is x=3, so f(3) = 0. Then, the function increases from x=2 to x=3, mirroring the decrease from x=1 to x=2. Therefore, from x=2 to x=3, f(x) goes from f(2) < 0 back up to 0. So in that interval (2,3), f(x) is less than 0 as well. Then, beyond x=3, the function continues increasing, so f(x) > 0 for x > 3.Therefore, the solution set where f(x) < 0 is (1,3). So the answer is B.Let me check the options again. Option B is (1,3). That matches.Just to be thorough, let's consider test points. For example, take x=0 (which is left of 1). f(0) should be greater than 0 because the function is decreasing, so f(0) > f(1) = 0. Correct.At x=1.5 (between 1 and 2), f(x) is decreasing, so less than 0. Correct.At x=2.5 (between 2 and 3), since the function is increasing from f(2) <0 to f(3)=0, so f(2.5) is still less than 0. Correct.At x=4 (right of 3), f(4) = f(0) due to symmetry (since 4-2=2, so f(4) = f(2 - (4 -2)) = f(0), which we already determined is positive. Therefore, f(4) >0. Correct.Therefore, the only intervals where f(x) <0 are (1,3). So the answer is B.Final Answerboxed{B}</think>Given that the function ( f(x+2) ) is an even function with a domain of ( mathbb{R} ), we know that ( f(2 + t) = f(2 - t) ) for any ( t ). This implies that ( f ) is symmetric about ( x = 2 ).The problem states that for any ( x_1, x_2 in (-infty, 2] ) with ( x_1 neq x_2 ), the difference quotient ( frac{f(x_1) - f(x_2)}{x_1 - x_2} < 0 ). This means ( f ) is decreasing on ( (-infty, 2] ).Given ( f(1) = 0 ), we analyze the behavior of ( f ):1. For ( x < 1 ): - Since ( f ) is decreasing on ( (-infty, 2] ), as ( x ) increases towards 1, ( f(x) ) decreases. Therefore, ( f(x) > f(1) = 0 ) for ( x < 1 ).2. For ( 1 < x < 2 ): - ( f ) continues to decrease, so ( f(x) < f(1) = 0 ).3. For ( 2 < x < 3 ): - Due to the symmetry about ( x = 2 ), the behavior of ( f ) on ( [2, infty) ) mirrors its behavior on ( (-infty, 2] ). Since ( f ) is increasing on ( [2, infty) ) (mirror image of decreasing), and ( f(3) = f(1) = 0 ), ( f(x) ) increases from ( f(2) < 0 ) to ( f(3) = 0 ). Thus, ( f(x) < 0 ) for ( 2 < x < 3 ).4. For ( x > 3 ): - ( f ) continues to increase, so ( f(x) > f(3) = 0 ).Combining these intervals, the solution set where ( f(x) < 0 ) is ( (1, 3) ).[boxed{B}]]

🔑:Given the function f(x+2) is an even function with a domain of R, we can infer some properties about f(x):1. Symmetry about x=2: Since f(x+2) is even, f(x) will have symmetry about the line x=2. This means that for any x, f(2+x) = f(2-x).2. Monotonicity based on the given condition: For any x_{1}, x_{2} in (-infty, 2] with x_{1} neq x_{2}, we have frac{f(x_{1})-f(x_{2})}{x_{1}-x_{2}} < 0. This tells us that f(x) is monotonically decreasing on (-infty, 2]. Due to the symmetry of f(x) about x=2, it is monotonically increasing on (2, +infty).3. Value of f at specific points: Given f(1) = 0 and knowing the symmetry and monotonicity of f(x), we can conclude f(3) = 0 because f(x) is symmetric about x=2, and 3 is equidistant from 2 as 1 is, but on the opposite side.4. Determining the solution set for f(x) < 0: Since f(x) is monotonically decreasing till x=2 and then monotonically increasing afterwards, and given that f(1) = 0 and f(3) = 0, we can deduce that f(x) < 0 for 1 < x < 3. This is because, between these two points, given the monotonicity and the known values, f(x) must dip below 0.Therefore, the solution set of the inequality f(x) < 0 is (1, 3). This corresponds to the answer choice boxed{B}.