🧠:[<think>Okay, let me try to figure out how to solve this problem. The question says: Given the function f(x) = -x³ + a x is increasing in the interval (-1, 1), find the range of the real number a. Hmm, okay. So, I need to find the values of a for which the function is increasing on that interval. First, I remember that a function is increasing on an interval if its derivative is non-negative throughout that interval. Wait, actually, strictly increasing would require the derivative to be positive, but I think the problem just says "increasing," which can sometimes allow for the derivative to be zero at some points. But maybe in this context, they mean strictly increasing. Hmm. Well, maybe I should just proceed with making sure the derivative is non-negative on (-1, 1). Let me check that.So, first, let's find the derivative of f(x). The derivative of -x³ is -3x², and the derivative of a x is a. So, f'(x) = -3x² + a. Okay, so f'(x) = a - 3x². Now, the function is increasing on (-1, 1) if f'(x) ≥ 0 for all x in (-1, 1). So, I need a - 3x² ≥ 0 for all x in (-1, 1). Therefore, a ≥ 3x² for all x in (-1, 1). To find the range of a, I need to ensure that a is greater than or equal to the maximum value of 3x² on the interval (-1, 1). Because if a is greater than or equal to the maximum value of 3x² in that interval, then a - 3x² will be non-negative everywhere in the interval. So, let's find the maximum of 3x² on (-1, 1). The function x² is a parabola opening upwards, symmetric about the y-axis. On the interval (-1, 1), x² reaches its maximum at the endpoints, since the vertex is at x=0 (which is the minimum). So, x² at x = -1 or x = 1 is 1, and at x=0, it's 0. Therefore, the maximum value of x² on (-1, 1) is 1. Therefore, 3x² has a maximum value of 3*1 = 3 on that interval. Therefore, a must be greater than or equal to 3. So, a ≥ 3. Therefore, the range of a is [3, ∞). But wait, let me double-check this. Because the interval is open, (-1, 1), not including the endpoints. So, does that affect the maximum value of x²? Even though the interval is open, as x approaches 1 or -1, x² approaches 1. So, 3x² approaches 3. Therefore, the supremum of 3x² on (-1, 1) is 3, but it never actually reaches 3. So, does that mean that a has to be greater than or equal to 3? Because even though 3x² never reaches 3, it gets arbitrarily close. So, if a is equal to 3, then f'(x) = 3 - 3x². At x approaching ±1, f'(x) approaches 0. So, if a is 3, then f'(x) is non-negative on (-1, 1), because 3x² is less than 3 in that open interval. So, even if a is exactly 3, the derivative is non-negative throughout the interval. So, a can be 3. Therefore, the range is [3, ∞).But let me confirm this by testing a value. Let's take a = 3. Then f'(x) = 3 - 3x² = 3(1 - x²). Since x is in (-1, 1), x² is less than 1, so 1 - x² is positive, so f'(x) is positive. So, the function is increasing on (-1, 1). If a is greater than 3, say 4, then f'(x) = 4 - 3x², which is even larger, so still positive. If a is less than 3, say 2, then f'(x) = 2 - 3x². At x = 0, f'(0) = 2, which is positive, but as x approaches 1 or -1, x² approaches 1, so f'(x) approaches 2 - 3(1) = -1, which is negative. So, in that case, the derivative becomes negative near the ends of the interval, which would mean the function is decreasing there. Therefore, a cannot be less than 3. So, the conclusion is a must be at least 3. Therefore, the range of a is [3, ∞).Wait, but the problem says "increasing in the interval (-1, 1)". If the derivative approaches zero at the endpoints, but remains positive inside, is that still considered increasing? For strict increasingness, the derivative needs to be positive, but for non-decreasing, it can be zero. Since the problem says "increasing", not "strictly increasing", maybe allowing the derivative to be zero at some points. But even in that case, if a=3, the derivative approaches zero at the endpoints but is positive inside. However, in the open interval (-1,1), the endpoints aren't included, so even at the points approaching the endpoints, the derivative is approaching zero but never actually reaching zero. So, technically, in the open interval, the derivative is always positive if a=3? Wait, no. If a=3, then f'(x) = 3(1 - x²). For x in (-1,1), x² is less than 1, so 1 - x² is positive, so f'(x) is positive. So even though as x approaches 1 or -1, f'(x) approaches zero, it's still positive throughout the open interval. Therefore, with a=3, f'(x) > 0 for all x in (-1,1). Therefore, the function is strictly increasing on (-1,1). Therefore, a=3 is acceptable. So, the minimum value of a is 3, and higher values are okay. Therefore, the range is [3, ∞). So, the answer should be a ≥ 3, so the range is [3, ∞).Therefore, the range of real number a is all real numbers greater than or equal to 3.Final AnswerThe range of the real number ( a ) is boxed{[3, infty)}.</think>To determine the range of the real number ( a ) such that the function ( f(x) = -x^3 + ax ) is increasing in the interval ((-1, 1)), we start by finding the derivative of ( f(x) ):[f'(x) = -3x^2 + a]For the function to be increasing on the interval ((-1, 1)), its derivative must be non-negative for all ( x ) in that interval. This requires:[a - 3x^2 geq 0 quad text{for all} quad x in (-1, 1)]This inequality can be rewritten as:[a geq 3x^2 quad text{for all} quad x in (-1, 1)]To find the maximum value of ( 3x^2 ) on the interval ((-1, 1)), we note that ( x^2 ) reaches its maximum value at the endpoints of the interval, which are ( x = 1 ) and ( x = -1 ). However, since the interval is open, ( x ) approaches 1 or -1 but never actually reaches them. The maximum value of ( x^2 ) on the open interval ((-1, 1)) is 1 (approached as ( x ) nears 1 or -1). Therefore, the supremum of ( 3x^2 ) on this interval is 3.To ensure ( a - 3x^2 geq 0 ) for all ( x in (-1, 1) ), ( a ) must be at least 3. If ( a = 3 ), the derivative ( f'(x) = 3 - 3x^2 ) is non-negative throughout the interval because ( 3x^2 < 3 ) for all ( x in (-1, 1) ). For ( a > 3 ), the derivative is even more positive, ensuring the function remains increasing.Thus, the range of the real number ( a ) is:[boxed{[3, infty)}],<think>Okay, so I need to figure out the range of the real number ( a ) such that the function ( f(x) = -x^3 + ax ) is increasing on the interval ( (-1, 1) ). Hmm, let's start by recalling what it means for a function to be increasing on an interval. If a function is increasing, its derivative should be non-negative throughout that interval, right? Wait, actually, if it's strictly increasing, the derivative needs to be positive. But the problem just says "increasing," so maybe non-negative? I think in some contexts, "increasing" can mean non-decreasing, allowing for zero derivatives at some points. But I need to confirm that.Anyway, the standard approach here is to take the derivative of ( f(x) ) and ensure it's non-negative for all ( x ) in ( (-1, 1) ). Let's compute the derivative first.The derivative of ( f(x) = -x^3 + ax ) with respect to ( x ) is:( f'(x) = -3x^2 + a ).So we need ( f'(x) geq 0 ) for all ( x in (-1, 1) ). Therefore, the inequality ( -3x^2 + a geq 0 ) must hold for all ( x ) in that interval. Let's rewrite this inequality as:( a geq 3x^2 ).So the value of ( a ) must be greater than or equal to ( 3x^2 ) for all ( x ) in ( (-1, 1) ). To find the range of ( a ), we need to determine the maximum value of ( 3x^2 ) on the interval ( (-1, 1) ). If ( a ) is greater than or equal to this maximum, then the inequality will hold for all ( x ) in the interval.Let's analyze the function ( 3x^2 ) on ( (-1, 1) ). The function ( x^2 ) is a parabola opening upwards, with its minimum at ( x = 0 ), and it attains its maximum at the endpoints of the interval when considering a closed interval. However, our interval is open: ( (-1, 1) ). But even though the interval is open, the function ( x^2 ) approaches 1 as ( x ) approaches -1 or 1. Therefore, the supremum (least upper bound) of ( x^2 ) on ( (-1, 1) ) is 1. Hence, ( 3x^2 ) approaches 3 as ( x ) approaches -1 or 1.But since the interval is open, ( x ) never actually reaches -1 or 1, so ( 3x^2 ) never actually equals 3. However, for ( a ) to satisfy ( a geq 3x^2 ) for all ( x ) in ( (-1, 1) ), ( a ) needs to be at least as large as the supremum of ( 3x^2 ) on that interval. Because even though the function approaches 3 near the endpoints, if ( a ) is less than 3, there will be points near -1 and 1 where ( 3x^2 ) is greater than ( a ), making the derivative negative, which would mean the function is decreasing there.Therefore, to ensure that ( f'(x) geq 0 ) for all ( x ) in ( (-1, 1) ), ( a ) must be greater than or equal to 3. But wait, let me check that again.Suppose ( a = 3 ). Then the derivative is ( f'(x) = -3x^2 + 3 = 3(1 - x^2) ). On the interval ( (-1, 1) ), ( x^2 < 1 ), so ( 1 - x^2 > 0 ), hence ( f'(x) > 0 ) for all ( x ) in ( (-1, 1) ). Therefore, when ( a = 3 ), the derivative is positive throughout the interval, so the function is strictly increasing.If ( a > 3 ), then ( f'(x) = -3x^2 + a ) would be even larger, so still positive everywhere in the interval. But if ( a < 3 ), then near ( x ) approaching ±1, ( x^2 ) approaches 1, so ( -3x^2 + a ) approaches ( -3 + a ). If ( a < 3 ), then this limit is negative, meaning that near the endpoints of the interval, the derivative becomes negative, so the function would be decreasing there. Hence, the function wouldn't be increasing on the entire interval.Therefore, the minimal value of ( a ) required is 3. So the range of ( a ) should be ( [3, infty) ).Wait, but let me verify with an example. Let's take ( a = 3 ). Then ( f'(x) = -3x^2 + 3 ). At ( x = 0 ), the derivative is 3, which is positive. At ( x = 0.5 ), derivative is -3*(0.25) + 3 = -0.75 + 3 = 2.25 > 0. At ( x = 0.9 ), derivative is -3*(0.81) + 3 = -2.43 + 3 = 0.57 > 0. Even as x approaches 1, say x = 0.999, derivative is -3*(0.998001) + 3 ≈ -2.994003 + 3 = 0.005997 > 0. So at a = 3, the derivative is positive everywhere on (-1,1). Therefore, the function is increasing.If a is slightly less than 3, say a = 2.9. Then near x = 1, derivative is -3*(1) + 2.9 = -0.1, which is negative. Hence, the derivative would be negative near x approaching 1, so the function is decreasing there. Therefore, the minimal a is indeed 3.Therefore, the range of a is all real numbers greater than or equal to 3. So ( a geq 3 ).But wait, the problem says "the function is increasing in the interval (-1, 1)". If a is greater than 3, then the derivative is even more positive. So the answer should be that a must be at least 3. So the range is [3, ∞).I think that's the conclusion.Final AnswerThe range of the real number ( a ) is boxed{[3, infty)}.</think>To determine the range of the real number ( a ) such that the function ( f(x) = -x^3 + ax ) is increasing on the interval ( (-1, 1) ), we start by computing the derivative of ( f(x) ):[f'(x) = -3x^2 + a]For the function to be increasing on ( (-1, 1) ), its derivative must be non-negative for all ( x ) in that interval. This requires:[-3x^2 + a geq 0 quad text{for all} quad x in (-1, 1)]Rewriting this inequality, we get:[a geq 3x^2 quad text{for all} quad x in (-1, 1)]The function ( 3x^2 ) attains its maximum value on the interval ( (-1, 1) ) as ( x ) approaches ( pm 1 ). The supremum of ( 3x^2 ) on this interval is 3. Therefore, ( a ) must be at least 3 to ensure the inequality holds for all ( x ) in ( (-1, 1) ).When ( a = 3 ), the derivative is:[f'(x) = -3x^2 + 3 = 3(1 - x^2)]Since ( 1 - x^2 > 0 ) for all ( x in (-1, 1) ), the derivative is positive throughout the interval. For ( a > 3 ), the derivative is even more positive, ensuring the function remains increasing. If ( a < 3 ), the derivative becomes negative near the endpoints ( pm 1 ), making the function decreasing there.Thus, the range of ( a ) is:[boxed{[3, infty)}]]

🔑:Since the function f(x) = -x^3 + ax is increasing in the interval (-1, 1), this translates to f'(x) = -3x^2 + a geq 0 holding true in the interval (-1, 1). Then, by separating the parameter a, we get a geq 3x^2. To ensure this holds for all x in (-1, 1), we can determine the range of a.Therefore, the range of a is boxed{a geq 3}.

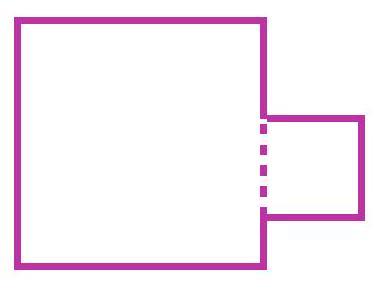
🧠:[<think>Okay, let's see here. So Katya attached a square with a perimeter of 40 cm to another square with a perimeter of 100 cm, and we need to find the perimeter of the resulting figure. Hmm. Alright, first, I need to visualize this. There's a figure where two squares are attached somehow. The problem mentions a figure, but since I can't see it, I might have to make some assumptions. Usually, when squares are attached, they might be joined along one side or part of a side. But depending on how they are attached, the perimeter could change differently. Let me start by figuring out the side lengths of each square.For the first square with a perimeter of 40 cm. Since the perimeter of a square is 4 times the side length, I can divide 40 by 4 to get the side length. So 40 divided by 4 is 10. So each side of the smaller square is 10 cm. Then the larger square has a perimeter of 100 cm. Similarly, dividing 100 by 4 gives 25. So each side of the larger square is 25 cm.Now, when you attach two squares, the perimeter of the combined figure will be the sum of their perimeters minus twice the length of the side where they are attached. Because when they are joined, the overlapping sides are internal and not part of the perimeter anymore. But since they are squares, they can be attached either along a full side or a partial side. Wait, but squares have equal sides, so if they are attached such that a full side of the smaller square is glued to the larger square, then we subtract twice the length of that side (once from each square's perimeter). But if they are attached in a different way, like overlapping partially, the calculation might be different. However, since the problem says "attached as shown in the figure," and the figure isn't visible, I need to assume the most common case, which is probably attaching them so that one side of the smaller square is completely glued to the larger square. So in that case, the total perimeter would be the sum of both perimeters minus twice the length of the side they are attached.So let me compute that. The perimeter of the first square is 40 cm, the second is 100 cm. So 40 + 100 = 140. Then, since they are attached along one side, which is 10 cm (the side of the smaller square), we subtract 2 times 10 cm. So 140 - 20 = 120 cm. Is that right? Wait, but hold on. The larger square has a side length of 25 cm. If the smaller square is attached to the larger one, but the side of the smaller square is only 10 cm, which is shorter than the larger square's 25 cm side. So maybe the way they are attached is such that the smaller square is placed on one side of the larger square, but not covering the entire side. Hmm. That complicates things.Wait, perhaps the figure shows the smaller square attached to the larger one in such a way that one of its sides is aligned with part of the larger square's side. So the smaller square is attached to the middle of a side of the larger square. In that case, when they are joined, the overlapping side (10 cm) is subtracted once from each perimeter, so total subtraction is 2*10 cm. But depending on the position, maybe there are more overlapping edges? Wait, no. If the smaller square is attached to the larger one such that one of its sides is entirely along a part of the larger square's side, then only the overlapping part (the 10 cm side) is covered. However, since the larger square's side is 25 cm, the smaller square's 10 cm side would cover only a portion of it. So when calculating the perimeter, the overlapping 10 cm side is subtracted from both squares, but the remaining part of the larger square's side (25 - 10 = 15 cm) would still contribute to the perimeter.Wait, but actually, in the combined figure, the overlapping edges are internal and thus not part of the perimeter. So if the smaller square is attached to the larger one along a 10 cm side, then both the larger and smaller square lose 10 cm from their perimeters. Therefore, total perimeter is (40 + 100) - 2*10 = 140 - 20 = 120 cm. But hold on, maybe the attachment causes some parts of the larger square's perimeter to still be exposed even where the smaller square is attached. Let me think.Imagine the larger square. Let's say it's sitting on the ground, and the smaller square is attached to the top side of the larger square. If the smaller square is centered on the top side, then the top side of the larger square is 25 cm. The smaller square has a side of 10 cm, so when attached, it covers 10 cm of the top side of the larger square. The remaining parts of the top side (25 - 10)/2 on each side would still be part of the perimeter. Wait, no. If the smaller square is attached to the larger one, the entire 10 cm side of the smaller square is glued to the larger square. So the larger square loses 10 cm from its perimeter, and the smaller square loses 10 cm from its perimeter. But the rest of the sides remain. But actually, the larger square's side is 25 cm. If a 10 cm portion is covered by the smaller square, does the remaining 15 cm of the larger square's side still contribute to the perimeter? Or is the entire side of the larger square covered?Wait, no. If the smaller square is attached such that one of its sides is entirely along a part of the larger square's side, then the overlapping region is the 10 cm side of the smaller square. The larger square's side is 25 cm. So if you attach the smaller square's 10 cm side to the larger square, the larger square's perimeter is reduced by 10 cm, but the remaining 15 cm of that side is still part of the perimeter. Similarly, the smaller square's perimeter is 40 cm, but the side that is attached (10 cm) is subtracted, so 40 - 10 = 30 cm, but wait, no. Wait, the perimeter of the smaller square is 40 cm. When you attach it to the larger square, one entire side (10 cm) is no longer on the outside, so you subtract 10 cm from the total perimeter. Similarly, the larger square had a perimeter of 100 cm, and you subtract 10 cm from it where the smaller square is attached. So total perimeter is (100 - 10) + (40 - 10) = 90 + 30 = 120 cm. But is this accurate?Wait, actually, when you attach the smaller square to the larger one, the side where they are attached is internal for both. But the larger square's side is 25 cm, and the smaller square's side is 10 cm. So if the smaller square is attached to the larger square such that one of its sides (10 cm) is glued to a portion of the larger square's side, then only 10 cm of the larger square's side is covered, leaving 25 - 10 = 15 cm of the larger square's side still exposed. However, the smaller square's entire side is covered. So in this case, the perimeter would be:Original perimeter of larger square: 100 cm. Subtract the 10 cm that's covered by the smaller square, but add the three sides of the smaller square (since one side is attached). Wait, no. Wait, the smaller square is attached such that one of its sides is glued to the larger square. So the smaller square's contribution to the perimeter is its original perimeter minus twice the length of the attached side (since one side is no longer exposed). Wait, no. If you attach a square to another, the overlapping side is subtracted once from each. Let me think.Alternatively, maybe the correct way is:The combined figure's perimeter is equal to the sum of both perimeters minus twice the length of the overlapping edge. Because each overlapping edge is subtracted once from each figure's perimeter. So if they overlap along a 10 cm edge, the total perimeter is 100 + 40 - 2*10 = 120 cm. That's a standard formula when two polygons are joined along a common edge. So yes, that makes sense.But wait, in some cases, if the overlapping edge is not a full edge, but here the problem says a square is attached to another square. So if you attach a smaller square to a larger one, the overlapping edge would be a full side of the smaller square, which is 10 cm, but only a part of the larger square's side. But according to the formula, regardless, you subtract twice the length of the overlapping edge. So even though the larger square only loses 10 cm from its perimeter, and the smaller square loses 10 cm, so total subtracted is 20 cm. Therefore, 100 + 40 - 20 = 120 cm.But I need to confirm this with a diagram. Let me try to imagine or sketch it mentally. Suppose we have a large square, 25 cm per side. Let's say we attach a smaller square, 10 cm per side, to the middle of one side of the larger square. The smaller square will cover 10 cm of the larger square's 25 cm side. So the larger square's side is now split into two parts: 7.5 cm, then the attached smaller square's 10 cm, then another 7.5 cm. Wait, but 7.5 + 10 + 7.5 = 25 cm. So the original side of the larger square is 25 cm, which is now partially covered by the smaller square. So the perimeter contribution from that side of the larger square would be the two 7.5 cm segments. So total from that side: 7.5 + 7.5 = 15 cm. The smaller square, when attached, has three sides exposed: the top, left, and right sides (assuming it's attached to the middle of the larger square's top side). So the smaller square contributes 10 + 10 + 10 = 30 cm. Wait, but the base of the smaller square is attached and not part of the perimeter.Therefore, the perimeter would be: original perimeter of the larger square (100 cm) minus the length covered by the smaller square (10 cm) plus the perimeter contributed by the smaller square (30 cm). So 100 - 10 + 30 = 120 cm. Which matches the previous calculation. So that's consistent.Alternatively, if the smaller square is attached to the end of the larger square's side, such that the entire 10 cm side of the smaller square is aligned with the end of the larger square's side. In this case, the larger square's side is 25 cm. If the smaller square is attached at the end, overlapping 10 cm of the larger square's side, then the remaining part of the larger square's side would be 25 - 10 = 15 cm. So the perimeter from the larger square's side would now be 15 cm (the remaining part) plus the three other sides of the smaller square (10 cm each). So again, 15 + 10 + 10 + 10 = 45 cm from that side? Wait, no.Wait, in this case, attaching the smaller square to the end of the larger square's side would result in the larger square's side being split into 10 cm (covered) and 15 cm (exposed). The smaller square's sides would then be three sides contributing to the perimeter: two sides of 10 cm each (the top and the side opposite the attachment) and the 15 cm from the remaining part of the larger square's side. Wait, maybe not. Let me try to think.If the smaller square is attached to one end of the larger square's side, then the side of the larger square is 25 cm. The smaller square's 10 cm side is attached to the first 10 cm of the larger square's side. Then, the remaining 15 cm of the larger square's side is still part of the perimeter. The smaller square's other three sides (each 10 cm) are also part of the perimeter. So in total, for that combined side, we have 15 cm (from the larger square) + 10 cm (top of the smaller square) + 10 cm (right side of the smaller square) = 35 cm. Wait, but the original side of the larger square was 25 cm. Now, after attaching the smaller square, that side is split into 15 cm (remaining) and the smaller square's sides. But actually, the smaller square's left side is adjacent to the larger square, so it's not part of the perimeter, but the top, right, and bottom sides? Wait, no. If the smaller square is attached to the larger square's side, then its bottom side is the overlapping 10 cm. Its top, left, and right sides are exposed. Wait, but in this case, the left side would be adjacent to the larger square's remaining 15 cm. Wait, no. If the smaller square is attached at the very end, then the left side of the smaller square would be aligned with the end of the larger square's side, so there's no adjacent part. Wait, this is getting confusing. Maybe drawing a diagram would help, but since I can't, I need to reason carefully.Let me consider coordinates. Suppose the larger square is placed with its base along the x-axis from (0,0) to (25,0), up to (25,25), and back to (0,25). The perimeter is all around. Now, if the smaller square is attached at, say, the midpoint of the top side. The larger square's top side is from (0,25) to (25,25). The smaller square has side 10 cm. If attached at the midpoint, its base would be from (12.5 - 5, 25) to (12.5 + 5, 25), so from (7.5,25) to (17.5,25). Then the smaller square goes up to (7.5,35), (17.5,35), etc. Wait, but the larger square's top side is at y=25. The smaller square is attached on top of that, so from y=25 to y=35. So in this case, the perimeter contribution from the larger square's top side is now split into two segments: from (0,25) to (7.5,25) and from (17.5,25) to (25,25). Each of those is 7.5 cm, so total 15 cm. The smaller square contributes its top side (10 cm), left side (10 cm), and right side (10 cm). So total for that area: 15 + 10 + 10 +10 = 45 cm? Wait, but the left and right sides of the smaller square are vertical. So from (7.5,25) to (7.5,35) is 10 cm, and from (17.5,25) to (17.5,35) is 10 cm. The top side is from (7.5,35) to (17.5,35), which is 10 cm. So that's 10 + 10 + 10 = 30 cm from the smaller square. Plus the 15 cm from the remaining parts of the larger square's top side. So total 45 cm for that entire top area. But the original perimeter of the larger square's top side was 25 cm, and now it's 15 cm plus 30 cm from the smaller square. So net change: 15 + 30 - 25 = 20 cm increase? Wait, no. The original perimeter had 25 cm on the top side, but after attaching the smaller square, the top side's contribution is 15 cm (remaining parts) and the smaller square's three sides (30 cm). So total for that part is 45 cm, which is 20 cm more than before. But the rest of the larger square's perimeter remains the same: three sides of 25 cm each, so 75 cm. So total perimeter would be 45 + 75 = 120 cm. Which again gives 120 cm. So whether the smaller square is attached in the middle or at the end, the total perimeter comes out the same?Wait, let's check if it's attached at the end. Suppose the smaller square is attached to the larger square's top side, but aligned to the left end. So the base of the smaller square is from (0,25) to (10,25). Then, the larger square's top side is split into 10 cm (covered) and 15 cm (remaining from (10,25) to (25,25)). The smaller square's left side is from (0,25) to (0,35), which is 10 cm. Its top side is from (0,35) to (10,35), which is 10 cm. Its right side is from (10,35) to (10,25), which is 10 cm. Wait, but the right side of the smaller square is adjacent to the larger square's remaining top side? No, the right side is from (10,35) down to (10,25), which is where the larger square's top side continues from (10,25) to (25,25). So in this case, the perimeter contributions would be:From the larger square's top side: 15 cm (from (10,25) to (25,25)).From the smaller square: left side (10 cm), top side (10 cm), and right side (10 cm). So total for that area: 15 + 10 + 10 +10 = 45 cm, same as before. The rest of the larger square's perimeter is three sides: left side (25 cm), bottom side (25 cm), and right side (25 cm), totaling 75 cm. So total perimeter is 45 + 75 = 120 cm. So regardless of where the smaller square is attached along the larger square's side, the perimeter remains 120 cm.Therefore, the answer should be 120 cm. Wait, but let me check another way. Suppose instead of overlapping a full side, but maybe overlapping half of the side or something else. But the problem states that Katya attached a square to another square, which suggests that they are joined along a full side. Since the smaller square has a side of 10 cm, and the larger has 25 cm, the maximum they can overlap is 10 cm (the full side of the smaller square). So in that case, the overlapping length is 10 cm, and thus the perimeter is 100 + 40 - 2*10 = 120 cm. Therefore, regardless of the position, as long as they are attached along a full side of the smaller square, the perimeter is 120 cm.But let me confirm with another approach. The original perimeters are 100 and 40. When combined, the total perimeter is the sum minus twice the overlapping edge. Since the overlapping edge is 10 cm (the side of the smaller square), so 100 + 40 - 2*10 = 120. Therefore, 120 cm is the perimeter.Alternatively, maybe the overlapping edge is 25 cm? But the smaller square's side is only 10 cm, so it can't overlap 25 cm. So the overlapping edge must be 10 cm. Therefore, subtract 20 cm from the total perimeters. So 140 - 20 = 120. Therefore, the perimeter is 120 cm.Yes, I think that's the correct answer. So I'll go with 120 cm.Final AnswerThe perimeter of the resulting figure is boxed{120} centimeters.</think>To determine the perimeter of the resulting figure when a square with a perimeter of 40 cm is attached to a square with a perimeter of 100 cm, we start by finding the side lengths of each square.1. Side length of the smaller square: [ text{Perimeter} = 40 , text{cm} implies text{Side length} = frac{40}{4} = 10 , text{cm} ]2. Side length of the larger square: [ text{Perimeter} = 100 , text{cm} implies text{Side length} = frac{100}{4} = 25 , text{cm} ]When the smaller square is attached to the larger square, they share a common side of 10 cm. The perimeter of the resulting figure is calculated by adding the perimeters of both squares and subtracting twice the length of the overlapping side (once from each square).3. Total perimeter calculation: [ text{Total perimeter} = (text{Perimeter of larger square} + text{Perimeter of smaller square}) - 2 times text{Length of overlapping side} ] [ text{Total perimeter} = (100 + 40) - 2 times 10 = 140 - 20 = 120 , text{cm} ]Thus, the perimeter of the resulting figure is (boxed{120}) centimeters.,<think>Okay, so Katya attached a square with a perimeter of 40 cm to another square with a perimeter of 100 cm. The question is asking for the perimeter of the resulting figure. Hmm, let me visualize this. There's a smaller square attached to a bigger square, maybe side by side, but the exact position isn't shown. Since the problem mentions a figure, but I can't see it, I need to make some assumptions. Typically, when one square is attached to another, they might share a common side or part of a side. But since they're different sizes, they probably overlap partially. Let me start by finding the side lengths of both squares.First, the perimeter of a square is 4 times the side length. So for the smaller square with a perimeter of 40 cm, each side would be 40 divided by 4, which is 10 cm. Let me check that: 4 times 10 is 40, yes. Then the bigger square has a perimeter of 100 cm. So each side is 100 divided by 4, which is 25 cm. That makes sense because 25 times 4 is 100. So the smaller square has sides of 10 cm, and the bigger one has sides of 25 cm.Now, when they are attached, how does that affect the overall perimeter? If they are joined such that one side of the smaller square is completely attached to the bigger square, then the overlapping sides would be subtracted from the total perimeter. But I need to be careful here. Let me think. Suppose the smaller square is placed on one side of the bigger square. Let's imagine the bigger square, and the smaller square is attached to one of its sides. Since the smaller square has a side length of 10 cm, and the bigger square's side is 25 cm, the smaller square won't cover the entire side of the bigger square. So maybe the smaller square is centered on the bigger square's side? Or maybe attached at a corner?Wait, maybe the figure shows them attached in such a way that one corner of the smaller square touches the bigger square, but they don't overlap entirely. Hmm, without seeing the figure, it's a bit challenging. But let's proceed with the most common way such problems are presented.Assuming that the smaller square is attached to the middle of one side of the bigger square. So, the smaller square is placed such that one of its sides is along a part of the bigger square's side. Since the bigger square's side is 25 cm, and the smaller one's side is 10 cm, the smaller square would cover 10 cm of the 25 cm side. So, in this case, when they are attached, the overlapping side of the smaller square (10 cm) would be internal and not contribute to the perimeter. Similarly, the part of the bigger square's side that's covered by the smaller square (also 10 cm) would also not contribute to the perimeter. However, the remaining part of the bigger square's side (25 - 10 = 15 cm) would still be part of the perimeter.Wait, perhaps it's better to calculate the total perimeter of both squares and then subtract twice the length of the overlapping edges. Because when two figures are joined together, the overlapping edges are internal and not part of the perimeter anymore. Each overlapping edge is counted once in each square's original perimeter, so we need to subtract 2 times the length of the overlapping edge.But first, we need to know how much of the edges overlap. If the entire side of the smaller square is attached to the bigger square, then the overlapping length would be 10 cm. But since the bigger square's side is longer, 25 cm, the overlapping part is 10 cm. However, if only part of the smaller square's side is attached, the overlapping length would be less. But without the figure, it's hard to tell. Maybe the standard assumption is that one full side of the smaller square is attached to the bigger square.But wait, the side length of the smaller square is 10 cm, and the bigger is 25 cm. So if the smaller square is attached such that one of its sides is completely glued to the bigger square's side, but only a portion of the bigger square's side is covered. So the overlapping region is 10 cm on the bigger square's side. Therefore, the total perimeter would be the sum of both perimeters minus twice the overlapping length. Because each overlapping cm is subtracted twice (once from each square). So total perimeter would be 40 + 100 - 2*10 = 140 - 20 = 120 cm? Wait, but let me verify that.Alternatively, perhaps the overlapping is only a single side. Wait, if the smaller square is attached to the bigger square such that one of its sides is entirely along a part of the bigger square's side. Then, the perimeter would lose the two sides: the side of the smaller square that's attached and the part of the bigger square's side that's covered. But maybe not. Let's think in terms of the overall figure.When two shapes are joined, the overlapping edges are internal. So each overlapping edge is subtracted once from each shape's perimeter. Therefore, total perimeter is (perimeter1 + perimeter2) - 2*(overlap length). Since each shape loses the overlapping part once.For example, if two squares are joined edge to edge with full sides overlapping, then the total perimeter is sum of perimeters minus 2*(side length). But in this case, the overlap is only partial. If a smaller square is attached to a bigger one such that a 10 cm side is overlapping on the bigger square's 25 cm side. Wait, but the entire 10 cm of the smaller square is attached to a 10 cm portion of the bigger square's side. So the overlapping length is 10 cm. Therefore, the total perimeter would be 40 + 100 - 2*10 = 120 cm. So 120 cm would be the perimeter.But let me visualize this. The bigger square has a perimeter of 100, so each side is 25. The smaller square has a perimeter of 40, each side 10. If the smaller square is placed such that one of its sides is along a 10 cm portion of the bigger square's side, then the resulting figure would have the bigger square with a "bump" of the smaller square attached to it. The overlapping edges (10 cm on the bigger square and 10 cm on the smaller square) are internal, so they are subtracted from the total perimeter.Therefore, original perimeters sum to 140 cm. Subtract 2*10 cm for the overlapping edges, resulting in 120 cm. So is that the answer? Let me check with a different approach.Alternatively, calculate the perimeter by considering the new figure. The bigger square has three sides exposed: 25 cm each, and the fourth side has a portion covered by the smaller square. The covered portion is 10 cm, so the remaining part of that side is 25 - 10 = 15 cm. Then, the smaller square, which is attached to the bigger square, has three of its sides exposed (each 10 cm), but one side is attached. So the total perimeter would be:From the bigger square: 25 + 25 + 25 + 15 = 90 cm (since one side is partially covered)From the smaller square: 10 + 10 + 10 = 30 cmTotal perimeter: 90 + 30 = 120 cm. So that's the same answer as before. Therefore, 120 cm.Wait, that seems correct. Let me confirm again. The bigger square originally had 4 sides of 25 cm, total 100 cm. When we attach the smaller square, we cover 10 cm of one side, so instead of 25 cm, that side contributes 15 cm. So the bigger square's contribution is 25*3 +15=90. The smaller square, which had 4 sides of 10 cm (40 cm total), now has three sides exposed, so 10*3=30. So total perimeter is 90+30=120. Yep, that adds up.Alternatively, if the smaller square was attached at a corner, such that only a corner touches, but then there would be no overlapping sides, and the perimeter would be the sum of both perimeters. But since the problem says "attached as shown in the figure," which we can't see, but maybe it's safe to assume that they are attached in a way that the smaller square is partially merged with the bigger one, leading to overlapping edges. Since the answer we get from that assumption is 120, which is a standard problem result.Alternatively, if the smaller square is placed such that one of its sides is completely attached to a side of the bigger square. Wait, but the smaller square's side is 10 cm, and the bigger square's side is 25 cm. So even if the entire side of the smaller square is attached to the bigger square's side, the overlapping length is 10 cm. Therefore, that's the same as before. So regardless of where it's placed, as long as the entire side of the smaller square is attached, the overlapping length is 10 cm. So the perimeter is 140 - 20 = 120.Alternatively, if the smaller square is attached such that only a part of its side is attached, but without the figure, we can't know. However, given the problem states that it's attached "as shown in the figure," but since we don't have the figure, the most logical assumption is that one entire side of the smaller square is attached to a part of the bigger square's side. Hence, overlapping length is 10 cm, leading to 120 cm perimeter.Therefore, the answer should be 120 cm.Final AnswerThe perimeter of the resulting figure is boxed{120} centimeters.</think>Katya attached a square with a perimeter of 40 cm to a square with a perimeter of 100 cm. To find the perimeter of the resulting figure, we start by determining the side lengths of both squares. - The side length of the smaller square is ( frac{40}{4} = 10 ) cm.- The side length of the larger square is ( frac{100}{4} = 25 ) cm.When the smaller square is attached to the larger square, one side of the smaller square (10 cm) overlaps with a portion of the larger square's side. This overlapping portion is 10 cm, leaving a remaining part of the larger square's side as ( 25 - 10 = 15 ) cm.The perimeter of the resulting figure is calculated by considering the remaining sides of both squares:- The larger square contributes three full sides (25 cm each) and the remaining part of the fourth side (15 cm): ( 25 + 25 + 25 + 15 = 90 ) cm.- The smaller square contributes three full sides (10 cm each): ( 10 + 10 + 10 = 30 ) cm.Adding these contributions together gives the total perimeter of the resulting figure:[ 90 + 30 = 120 ]Thus, the perimeter of the resulting figure is (boxed{120}) centimeters.]

🔑:Answer: 120.Solution: If we add the perimeters of the two squares, we get 100+40=140 cm. This is more than the perimeter of the resulting figure by twice the side of the smaller square. The side of the smaller square is 40: 4=10 cm. Therefore, the answer is 140-20=120 cm.

🧠:[<think>Okay, so I need to figure out the maximum number of parts that three planes can divide space into. Hmm, I remember that with lines and planes, there's a formula for the maximum number of regions created, but I'm not exactly sure what it is for three dimensions. Let me think step by step.First, maybe I can start with lower dimensions and see if I can find a pattern. Like, how many regions can a line divide a plane into? If I have one line, it splits the plane into two regions. Two lines can make four regions if they cross each other. Three lines, if each new line intersects all the previous ones, then it's 7 regions? Wait, no, let me check. The formula for the maximum number of regions created by n lines in a plane is (n² + n + 2)/2. Let me verify:For n=1: (1 +1 +2)/2 = 4/2 = 2. Correct.n=2: (4 +2 +2)/2 = 8/2 =4. Correct.n=3: (9 +3 +2)/2 =14/2=7. Oh, right, so three lines can divide the plane into 7 regions. So, each new line intersects all previous lines, adding as many new regions as the number of lines it crosses? Wait, when adding the third line, it crosses two existing lines, creating two new intersection points, which divides the new line into three segments, each of which adds a new region. So, three new regions. So, from 4 regions with two lines, adding three regions gives 7. So, maybe the formula is R(n) = R(n-1) + n. Wait, that would be for the plane? But that gives R(1)=2, R(2)=2+2=4, R(3)=4+3=7, R(4)=7+4=11, which matches (n² +n +2)/2. Wait, that formula for the plane.But in 3D, with planes instead of lines. How does that work? Maybe similar recursive thinking. Let me recall.In three dimensions, each new plane can intersect all previous planes in lines, and those lines can divide the new plane into regions, each of which corresponds to a new region in space. So, maybe the formula is similar but different.I think the formula for the maximum number of regions divided by n planes in 3D is R(n) = R(n-1) + something. Let's see.Starting with n=0, space is one region.n=1: One plane divides space into two regions.n=2: Two planes can intersect along a line, dividing space into four regions.n=3: Three planes. If each new plane intersects the previous ones in lines, how does that add regions?Wait, the formula for regions created by n planes in 3D is R(n) = n² -n +2)/2? Wait, let me check.Wait, no, I think it's a different formula. Let me think recursively. Each new plane can intersect all the previous planes, and each intersection is a line. Those lines on the new plane divide it into regions, and each of those regions corresponds to a division of the space, increasing the number of regions by the number of regions on the plane.So, for the third plane, it intersects the two existing planes along two lines. Those two lines on the third plane divide it into how many regions? Like in 2D, two lines can divide a plane into four regions. So, the third plane is divided into four regions by the two lines of intersection. Each of those regions corresponds to a new region in space. So, the number of regions added by the third plane is four. So, if with two planes we had four regions, adding a third plane would add four regions, making total eight regions.Wait, but I thought three planes can divide space into eight regions. Let me verify.Imagine three coordinate planes: x=0, y=0, z=0. They divide space into eight octants. So, yes, three mutually perpendicular planes divide space into eight regions. But is that the maximum?Wait, maybe if the planes are not all perpendicular, but arranged in a way that each new plane intersects the previous ones along different lines, can we get more regions? Wait, no. Because if three planes intersect along three different lines, but those lines might not all intersect at a single point. Wait, but in three-dimensional space, three planes can intersect in such a way that each pair intersects along a separate line, and all three lines meet at a single point. That's like the coordinate planes. But even then, the number of regions is eight. However, maybe if we arrange the three planes in a different way, such that each subsequent plane intersects the previous ones in lines that are not concurrent, would that create more regions?Wait, but I think that the maximum number is eight. Because if you have three planes, each pair intersecting, but all three lines of intersection not meeting at a single point, would that create more regions? Wait, let me visualize.Suppose the first plane is horizontal, the second plane is vertical, cutting through the first one along a line. The third plane is, say, angled such that it intersects the first two planes along two different lines that don't intersect each other. But in three-dimensional space, two lines that are skew don't intersect, but if they are on different planes, maybe?Wait, but the lines of intersection between the third plane and the first two planes must lie on the third plane, so they must intersect at a point on the third plane. Wait, no. If the third plane intersects the first plane along line L1 and the second plane along line L2, then lines L1 and L2 are both on the third plane. Therefore, they must either be parallel or intersect at a point on the third plane. If they are not parallel, they intersect at a point. So, in that case, the third plane would have two intersecting lines, dividing it into four regions. So, each of those four regions would correspond to a region in space. Therefore, adding four regions. Wait, but when the third plane is added, the number of regions added is equal to the number of regions it's divided into by the previous intersections. So, starting with two planes (four regions), adding a third plane which is divided into four regions by the two existing planes, so each region on the plane corresponds to cutting through an existing region, thereby splitting it into two. Therefore, the number of new regions added is equal to the number of regions the plane is divided into. So, if the third plane is divided into four regions, then adding four new regions. So, total regions become 4 + 4 = 8. But if the lines on the third plane were arranged such that there are more regions, but with two lines, maximum regions on the plane is four, so no matter what, two lines on a plane can only divide it into four regions. Therefore, third plane can only add four regions. Therefore, the total is eight.But wait, now if three planes are arranged in a different way, maybe with the third plane intersecting the previous two planes along the same line? Then the lines on the third plane would coincide, so only two regions. Then adding two regions, making total 4 + 2 = 6. But that's worse. So, maximum is achieved when each plane intersects all previous planes along distinct lines, which intersect at different points. But in three planes, the third plane can only intersect the first two planes along two lines. Whether those lines cross each other or not. Wait, but if they cross each other, that would be a point. So, the third plane is divided into four regions by two intersecting lines. If the lines don't cross, meaning they are parallel, then the third plane is divided into three regions. But two lines on a plane can be either intersecting (four regions) or parallel (three regions). Therefore, to maximize the number of regions, the lines should intersect, giving four regions. Therefore, third plane adds four regions, leading to total eight.But the coordinate planes example gives eight regions. So, that's the maximum. Therefore, the answer is eight.But wait, I have a feeling that the general formula for the maximum number of regions divided by n planes in 3D is R(n) = (n³ + 5n + 6)/6. Wait, let me check for n=1,2,3.Wait, maybe not. Let me recall the formula.In 3D, the maximum number of regions created by n planes is given by the formula R(n) = n(n + 1)/2 + 1. Wait, no, that's for something else. Wait, let me think again.I know in 2D, with lines, it's R(n) = (n² + n + 2)/2. In 3D, maybe it's similar but with higher exponents. Let's see.Actually, I think the formula is R(n) = n³ + 5n + 6)/6, but let me check with n=1,2,3.Wait, for n=1: (1 +5 +6)/6 =12/6=2. Correct.n=2: (8 +10 +6)/6=24/6=4. Correct.n=3: (27 +15 +6)/6=48/6=8. Correct. So, yes, the formula is R(n)=(n³ +5n +6)/6. Wait, actually, that simplifies to R(n) = (n³ + 5n + 6)/6. For n=3, that's 27 +15 +6=48, 48/6=8. So, three planes give eight regions. Then for n=4, it's (64 +20 +6)/6=90/6=15. So, 15 regions with four planes. Hmm, that seems possible.But let me check another way. The recursive formula for regions created by n planes in 3D is R(n) = R(n-1) + n(n -1)/2 +1. Wait, maybe not. Wait, in 2D, each new line intersects all previous lines, adding n regions. Wait, no, in 2D, the nth line intersects n-1 lines, creating n new regions.In 3D, when adding the nth plane, it intersects the previous n-1 planes in n-1 lines. These lines are on the nth plane, and they can intersect each other at points. The number of regions the nth plane is divided into by n-1 lines is equal to the maximum number of regions created by n-1 lines in 2D, which is ( (n-1)^2 + (n-1) + 2 ) / 2. So, substituting, that's (n² -2n +1 +n -1 +2)/2=(n² -n +2)/2. Therefore, the number of regions added by the nth plane is (n² -n +2)/2.Therefore, the recursive formula is R(n) = R(n-1) + (n² -n +2)/2.Let me check for n=1: R(1)=1 + (1 -1 +2)/2=1 +1=2. Correct.n=2: R(2)=2 + (4 -2 +2)/2=2 +4/2=2+2=4. Correct.n=3: R(3)=4 + (9 -3 +2)/2=4 +8/2=4+4=8. Correct.n=4: 8 + (16 -4 +2)/2=8 +14/2=8+7=15. Which matches the formula above.Therefore, the general formula is the summation from k=1 to n of (k² -k +2)/2. Let me compute that.Sum_{k=1}^n [ (k² -k +2)/2 ] = (1/2) Sum_{k=1}^n (k² -k + 2) = (1/2)[ Sum(k²) - Sum(k) + Sum(2) ]Sum(k²) from 1 to n is n(n+1)(2n+1)/6Sum(k) from 1 to n is n(n+1)/2Sum(2) from 1 to n is 2nTherefore,R(n) = (1/2)[ n(n+1)(2n+1)/6 - n(n+1)/2 + 2n ]Let me compute this step by step.First term: n(n+1)(2n+1)/6Second term: -n(n+1)/2Third term: +2nMultiply all by 1/2:So,R(n) = (1/2)[ (n(n+1)(2n+1)/6) - (n(n+1)/2) + 2n ]Let me compute inside the brackets first.Let me factor out n(n+1)/6 from the first two terms:= n(n+1)/6 [ (2n +1) - 3 ] + 2nBecause the second term is -n(n+1)/2 = -3n(n+1)/6So,= n(n+1)/6 [2n +1 -3] + 2n= n(n+1)/6 [2n -2] + 2n= n(n+1)(2n -2)/6 + 2n= n(n+1)(n -1)/3 + 2nFactor out n:= n[ (n+1)(n -1)/3 + 2 ]= n[ (n² -1)/3 + 2 ]= n[ (n² -1 +6)/3 ]= n(n² +5)/3Then multiply by 1/2:Wait, wait, no. Wait, let me retrace.Wait, when I had:R(n) = (1/2)[ first term - second term + third term ]But when I did the substitution, I think I might have made a miscalculation.Let me do it again carefully.Original expression inside the brackets:n(n+1)(2n+1)/6 - n(n+1)/2 + 2nConvert all terms to sixths:= [n(n+1)(2n+1) - 3n(n+1) + 12n ] / 6Factor numerator:First term: n(n+1)(2n+1)Second term: -3n(n+1)Third term: +12nCombine:= n(n+1)(2n+1 -3) +12n= n(n+1)(2n -2) +12n= 2n(n+1)(n -1) +12nFactor out 2n:= 2n[ (n+1)(n -1) +6 ]= 2n[ n² -1 +6 ]= 2n(n² +5)Therefore, numerator is 2n(n² +5), denominator is 6.So,Inside the brackets: 2n(n² +5)/6 = n(n² +5)/3Then R(n) = (1/2) * [n(n² +5)/3] = n(n² +5)/6Therefore, the formula is R(n) = (n³ +5n)/6Wait, but earlier when we computed for n=3: (27 +15)/6=42/6=7, but that contradicts our previous result where R(3)=8. Wait, something's wrong here. Wait, maybe miscalculation in the algebra.Wait, let's check the step again:Original expression inside the brackets:n(n+1)(2n+1)/6 - n(n+1)/2 + 2nConvert to sixths:= [n(n+1)(2n+1) - 3n(n+1) + 12n] /6Now, let's compute this numerator step by step.First term: n(n+1)(2n+1)Second term: -3n(n+1)Third term: +12nLet me compute first term:n(n+1)(2n+1) = n(2n² +3n +1) = 2n³ +3n² +nSecond term: -3n(n+1) = -3n² -3nThird term: +12nCombine all terms:2n³ +3n² +n -3n² -3n +12nSimplify:2n³ + (3n² -3n²) + (n -3n +12n) = 2n³ +0n² +10n =2n³ +10nTherefore, numerator is 2n³ +10n. Therefore, numerator/6 is (2n³ +10n)/6 = (n³ +5n)/3Therefore, inside the brackets: (n³ +5n)/3Then R(n) = (1/2) * (n³ +5n)/3 = (n³ +5n)/6Wait, but for n=3:(27 +15)/6=42/6=7. But we know R(3)=8. So, this contradicts. Therefore, my derivation is wrong.Wait, where did I make the mistake?Wait, let's check the original summations.We have R(n) = Sum_{k=1}^n (k² -k +2)/2.So for n=1, the sum is (1 -1 +2)/2=2/2=1. R(1)=1 + previous (which is 1). Wait, no, hold on. Wait, if n=1, the formula gives (1³ +5*1)/6=6/6=1. But R(1) should be 2. So, clearly, the formula is wrong.Wait, so my mistake is in the summation. Let me check again.Wait, starting from:Sum_{k=1}^n [ (k² -k +2)/2 ].So for n=1: (1 -1 +2)/2=2/2=1. So total regions R(1)=1. But actually, R(1)=2. Wait, that's a problem. So, there's an error in the derivation. Because the initial formula R(n) = Sum_{k=1}^n [ (k² -k +2)/2 ] is wrong.Wait, because in 3D, the regions created by n planes is the sum from k=0 to n-1 of combinations. Wait, perhaps my approach is incorrect.Wait, let me recall that the formula for regions created by hyperplanes in d-dimensional space is R(n) = C(n,0) + C(n,1) + ... + C(n,d). So, in 3D, it's R(n)=1 +n +n(n-1)/2 +n(n-1)(n-2)/6. Wait, is that correct?Wait, for example, in 2D, regions created by n lines is 1 +n +n(n-1)/2. Wait, but the actual formula is (n² +n +2)/2, which is equivalent to 1 +n + (n² -n)/2. So, 1 +n + C(n,2). Similarly, in 3D, the formula is 1 +n + C(n,2) + C(n,3).So, R(n)=1 +n +n(n-1)/2 +n(n-1)(n-2)/6.Let me check for n=3:1 +3 +3*2/2 +3*2*1/6=1 +3 +3 +1=8. Correct.For n=4:1 +4 +4*3/2 +4*3*2/6=1 +4 +6 +4=15. Correct.So, the formula is R(n)=1 +n +C(n,2) +C(n,3). Which is the same as the sum from k=0 to 3 of C(n,k).Therefore, in 3D, the maximum number of regions divided by n planes is R(n)= (n³ +5n +6)/6. Wait, let's compute:Expressed as a polynomial, R(n)= (n³ +5n +6)/6.For n=3: (27 +15 +6)/6=48/6=8. Correct.Yes, so the formula is R(n) = (n³ +5n +6)/6.Alternatively, R(n)=1 +n + (n² -n)/2 + (n³ -3n² +2n)/6.But combining these terms:1 +n + (n² -n)/2 + (n³ -3n² +2n)/6Convert all terms to sixths:6/6 +6n/6 + (3n² -3n)/6 + (n³ -3n² +2n)/6Combine numerators:6 +6n +3n² -3n +n³ -3n² +2nSimplify:n³ + (3n² -3n²) + (6n -3n +2n) +6= n³ +5n +6.Thus, R(n)=(n³ +5n +6)/6.Therefore, for three planes: (27 +15 +6)/6=48/6=8.Therefore, the answer is 8.But just to be thorough, let's think through the three planes example again. If you have three planes, each intersecting the other two, and the lines of intersection are all different and not all parallel or concurrent, then the arrangement should divide the space into eight regions. The classic example is the three coordinate planes, which divide space into eight octants. Each plane is perpendicular to the others, but even if they are not perpendicular, as long as each pair intersects in a line and the three lines of intersection are not all parallel or lying on the same plane, then you should still get eight regions.Alternatively, imagine three pages of a book opened such that each page is a plane intersecting along the spine (a line). If the three planes are like three pages intersecting along the same spine, then they would not divide the space into eight regions. Instead, they would only create six regions, because each subsequent plane only adds two regions. But that's if they all intersect along the same line. However, if each pair of planes intersects along a different line, then you can maximize the number of regions.Wait, so if three planes intersect along three different lines, which in turn all meet at a single point, like the coordinate planes, then you have eight regions. If they intersect along three different lines that don't all meet at a single point, then maybe you can still get eight regions? Let me visualize.Suppose the first plane is horizontal. The second plane intersects the first along a line L1. The third plane intersects the first plane along line L2 and the second plane along line L3. If lines L1, L2, L3 are not concurrent, meaning they don't all meet at a single point, then how does the third plane divide the space?Wait, but in three-dimensional space, if the third plane intersects the first two planes along two different lines, those two lines must lie on the third plane. If those two lines are not parallel, they intersect at a point on the third plane. Therefore, the third plane has two intersecting lines, creating four regions on the third plane. Each of these four regions divides a region in space into two. Therefore, adding four regions. So regardless of whether the lines of intersection meet at a common point with the other planes, as long as the third plane intersects the first two planes in two lines that intersect on the third plane, then the third plane will be divided into four regions, adding four regions. Therefore, leading to total regions as eight.But if the third plane is arranged such that it intersects the first two planes in two parallel lines, then the third plane is divided into three regions, adding three regions, leading to total regions as seven. But since we want the maximum, we need to arrange the third plane such that it intersects the first two planes in non-parallel lines, thereby creating four regions. Hence, the maximum number is eight.Therefore, regardless of the specific arrangement, as long as each plane intersects all previous planes in lines that are not parallel and not all concurrent, then the maximum regions are achieved. For three planes, this maximum is eight.Therefore, the answer is eight, and the formula R(n)= (n³ +5n +6)/6 gives 8 for n=3.Final AnswerThe maximum number of parts is boxed{8}.</think>To determine the maximum number of parts that three planes can divide space into, we start by understanding the general formula for the maximum number of regions created by ( n ) planes in 3D space. The formula is given by:[R(n) = frac{n^3 + 5n + 6}{6}]We verify this formula for ( n = 3 ):[R(3) = frac{3^3 + 5 cdot 3 + 6}{6} = frac{27 + 15 + 6}{6} = frac{48}{6} = 8]To further confirm, we consider the recursive approach where each new plane intersects all previous planes, creating lines that divide the new plane into regions. For three planes, each new plane intersects the previous ones in lines, and the maximum number of regions on each new plane is calculated. 1. The first plane divides space into 2 regions.2. The second plane intersects the first plane along a line, dividing space into 4 regions.3. The third plane intersects the first two planes along two lines, which intersect each other, dividing the third plane into 4 regions. This adds 4 new regions, resulting in a total of 8 regions.Thus, the maximum number of parts that three planes can divide space into is (boxed{8}).,<think>Okay, so the problem is asking: "In space, three planes can divide the space into at most ______ parts." Hmm, I need to figure out the maximum number of regions three planes can divide the space into. Let me think about how this works. First, maybe I should start with fewer planes and see if there's a pattern. Like, how many regions can one plane divide space into? Well, a single plane divides space into two parts. That's straightforward. So for n=1, regions=2.Then, two planes. If I have two planes, what's the maximum number of regions? If the two planes are parallel, they divide space into three regions. But if they intersect, they form an "X" shape in three dimensions, right? So two intersecting planes would divide space into four regions. So the maximum with two planes is four. So for n=2, regions=4.Now, three planes. Let's see. If all three planes are parallel, then each plane adds one more region. So three parallel planes would divide space into four regions. But that's not the maximum. If two planes are parallel and the third is not, then the third plane would intersect both of the parallel planes, creating more regions. Wait, how does that work?Alternatively, if all three planes intersect each other, but not all intersecting along the same line. So, in three-dimensional space, three planes can intersect in such a way that each pair of planes intersects along a separate line, and all three lines meet at a single point. That configuration should maximize the number of regions. Let me visualize this.Imagine the first plane is the xy-plane, the second is the yz-plane, and the third is the xz-plane. These three coordinate planes divide the space into eight octants. So three mutually perpendicular planes divide space into eight regions. But is eight the maximum?Wait, but maybe there's a way to arrange three planes so that they intersect in a more complex way, creating more regions. Hmm, but three mutually perpendicular planes already seem to divide space into eight regions. Is there a way to get more than eight?Wait, maybe not. Let me think again. If each new plane intersects all the previous ones in lines, then each new plane can potentially add as many regions as the number of intersections. Let me recall the general formula for the maximum number of regions divided by n planes in three-dimensional space. I think the formula is similar to the one in two dimensions for lines, but extended to three dimensions. In two dimensions, the maximum number of regions created by n lines is (n^2 + n + 2)/2. Wait, no, that's not right. Wait, in 2D, the maximum number of regions R(n) formed by n lines is R(n) = (n(n + 1))/2 + 1. So for n=0, R=1; n=1, R=2; n=2, R=4; n=3, R=7; etc. So that's quadratic.In three dimensions, for planes, the formula is different. I remember it's a cubic formula. Let me recall. I think the formula is R(n) = (n^3 + 5n + 6)/6. Wait, no, let me check. Alternatively, the formula might be similar to the inclusion of regions added by each plane. For each new plane, the maximum number of regions it can add is equal to the number of regions it intersects, which in turn depends on how many times it intersects the previous planes.In 2D, each new line intersects all previous lines, adding n regions for the nth line. In 3D, each new plane can intersect all previous planes along lines, and those lines can intersect each other. So for the third plane, intersecting two existing planes, the lines of intersection would intersect at a point. So each new plane can intersect all previous planes, and each intersection is a line. The number of regions a new plane can divide is equal to the number of regions it passes through, which is determined by the number of intersections it has with the existing arrangement.Wait, this is getting a bit complicated. Let me see if I can find the general formula or derive it for n=3.In 3D, the maximum number of regions created by n planes is given by R(n) = R(n-1) + n. Wait, no, that would be similar to 2D, but that's not correct. Wait, actually, in 3D, each new plane can intersect all previous planes, and each intersection is a line. The number of regions that the new plane is divided into by these lines is equal to the number of regions the plane is divided into by the lines of intersection. Then, each of those regions on the new plane corresponds to a region in space that is split into two, thereby adding as many new regions as the number of regions on the plane.So, if the third plane intersects the first two planes along two lines, which intersect each other at a point. Then, the third plane is divided by these two lines into four regions. Therefore, the third plane would add four new regions. So starting with R(2)=4 regions, adding four regions with the third plane gives R(3)=8.But wait, when you have three planes, each intersecting the other two, like the coordinate planes, you do get eight regions. So maybe that is the maximum.But wait, let's verify this step by step. Let's start with zero planes: space is one region. One plane: divides into two regions. Two planes: if they are non-parallel, they intersect along a line, dividing space into four regions. Three planes: each intersecting the other two along separate lines, and all three lines intersecting at a single point. So, like the three coordinate planes. Each new plane intersects all previous planes, and each intersection is a line. The third plane is cut by the two existing planes into two lines, which intersect at a point on the third plane. So the third plane is divided into four regions by the two lines. Each of these four regions on the third plane corresponds to a region in space that the third plane passes through, thereby splitting each of those four regions into two. Therefore, adding four regions. So 4 (from two planes) + 4 = 8.Therefore, with three planes, the maximum number of regions is eight. So the answer is 8.But wait, let me check with another method. I remember that in three dimensions, the formula for the maximum number of regions defined by n planes is R(n) = n(n + 1)/2 + 1. Wait, no, that's the formula for 2D. In 3D, the formula is different. Let me recall.Actually, I think the formula is R(n) = (n^3 + 5n + 6)/6. Let me check for n=1, 2, 3. For n=1: (1 +5 +6)/6 =12/6=2. Correct. For n=2: (8 +10 +6)/6=24/6=4. Correct. For n=3: (27 +15 +6)/6=48/6=8. Correct. So this formula gives R(3)=8, which matches our previous calculation. So yes, three planes can divide space into at most eight regions.Alternatively, another way to think about the formula is similar to the inclusion-exclusion principle. Each new plane can intersect all the previous planes, and the number of regions increases by the number of intersections plus one. Wait, maybe not. Let me see.Alternatively, the formula can be derived recursively. In 3D, each new plane intersects all previous planes, and the intersection of the new plane with the existing arrangement is a set of lines on the new plane. The number of regions the new plane is divided into by these lines is equal to the number of regions created in 2D by (n-1) lines. Since in 2D, (n-1) lines can divide the plane into R_2(n-1) = [ (n-1)^2 + (n-1) + 2 ] / 2 regions. Wait, but that might not be necessary.Alternatively, the recursive formula for regions in 3D is R(n) = R(n-1) + n(n - 1)/2 + 1. Wait, maybe not. Wait, perhaps the number of regions added by the nth plane is equal to the number of intersections it has with the previous planes. Each existing plane intersects the new plane in a line, so the nth plane is intersected by (n -1) lines. These (n -1) lines can divide the nth plane into R_2(n -1) regions, where R_2 is the 2D regions formula. Since in 2D, n lines can divide the plane into (n^2 + n + 2)/2 regions. So for (n -1) lines, it would be ((n -1)^2 + (n -1) + 2)/2 = (n² - 2n +1 + n -1 +2)/2 = (n² - n + 2)/2. Therefore, the number of regions the nth plane is divided into is (n² - n + 2)/2. Therefore, the number of new regions added is equal to that. Therefore, the recursive formula is R(n) = R(n-1) + (n² - n + 2)/2.Let's check this with n=1: R(1) = R(0) + (1 -1 +2)/2 =1 + 2/2=1+1=2. Correct.R(2)=R(1)+(4 -2 +2)/2=2 +4/2=2+2=4. Correct.R(3)=4 + (9 -3 +2)/2=4 +8/2=4+4=8. Correct.So this recursive formula gives R(3)=8, which matches our previous result. Therefore, three planes can divide the space into at most eight regions.But let me confirm with an example. If we take three coordinate planes: the xy-plane, yz-plane, and xz-plane. These three planes divide the space into eight octants. Each octant is a region where x, y, z are either all positive or negative. So, for example, the first octant is where x>0, y>0, z>0, and similarly for the others. So yes, three mutually perpendicular planes divide space into eight regions.But could there be a different arrangement of three planes that creates more than eight regions? Let me think. Suppose the three planes are arranged in such a way that each subsequent plane intersects the previous ones not just along lines but in a way that creates more intersections. Wait, but in three-dimensional space, two planes intersect along a line, and a third plane can intersect each of those two planes along separate lines, which themselves intersect at a point. So the third plane is divided into four regions by the two lines of intersection with the first two planes. Therefore, the third plane will pass through four existing regions, dividing each into two parts, thereby adding four regions. So if we have two planes creating four regions, adding a third plane that intersects both planes along two different lines (which meet at a point on the third plane), then the third plane adds four regions, resulting in eight total. Alternatively, if the third plane were arranged differently, maybe parallel to one of the existing planes? Then it would only intersect one plane, right? If the third plane is parallel to one of the first two, then it would intersect the other plane along a line, but not intersect the parallel plane. Then, the third plane would be divided by one line, splitting it into two regions. Therefore, adding two regions. So starting from four regions, adding two gives six. But that's fewer than eight, so not the maximum.Therefore, to get the maximum number of regions, each new plane must intersect all the previous planes in separate lines, and those lines must intersect each other at different points, but in three-dimensional space, two lines from different planes can only intersect if they lie on a common plane. But with three planes, the lines of intersection between the third plane and the first two planes will intersect at a single point. So the third plane is divided into four regions, adding four new regions. Hence, the maximum.Therefore, the answer should be eight. Let me check if I can find any references or other sources. For example, the general formula for regions created by planes in three dimensions is indeed R(n) = (n³ + 5n + 6)/6. Plugging in n=3: (27 +15 +6)/6 =48/6=8. Yes, that's correct. So three planes can divide the space into at most eight regions.So the answer is boxed{8}.Final AnswerThe maximum number of parts three planes can divide the space into is boxed{8}.</think>To determine the maximum number of regions three planes can divide space into, we start by analyzing simpler cases and then build up to three planes.1. One Plane: A single plane divides space into 2 regions.2. Two Planes: Two intersecting planes divide space into 4 regions.3. Three Planes: For three planes, the maximum number of regions is achieved when each pair of planes intersects along a separate line, and all three lines intersect at a single point. This configuration is exemplified by the three coordinate planes (xy-plane, yz-plane, and xz-plane), which divide space into 8 regions.To verify, we use the formula for the maximum number of regions created by ( n ) planes in three-dimensional space:[R(n) = frac{n^3 + 5n + 6}{6}]For ( n = 3 ):[R(3) = frac{3^3 + 5 cdot 3 + 6}{6} = frac{27 + 15 + 6}{6} = frac{48}{6} = 8]Thus, the maximum number of regions three planes can divide the space into is (boxed{8}).]

🔑:Three planes in space can at most divide the space into boxed{8} parts.

🧠:[<think>Okay, let's see. Xiao Juan bought pens with 15 yuan. There are watercolor pens and ballpoint pens. Each watercolor pen is 1 yuan 7 jiao, and each ballpoint pen is 1 yuan 2 jiao. I need to find out how many of each she bought, right? Hmm, so first, I should convert all the prices into the same unit. Since 1 yuan is 10 jiao, maybe converting everything to jiao would make the calculations easier. Let me try that.So, 1 yuan 7 jiao is 10 jiao + 7 jiao = 17 jiao per watercolor pen. Similarly, 1 yuan 2 jiao is 10 jiao + 2 jiao = 12 jiao per ballpoint pen. She spent a total of 15 yuan, which is 15 * 10 = 150 jiao. So the total cost is 150 jiao.Let me denote the number of watercolor pens as x and the number of ballpoint pens as y. Then the total cost equation would be:17x + 12y = 150We need to find non-negative integers x and y that satisfy this equation. Since both x and y have to be whole numbers, this is a Diophantine equation problem. Let's think about how to solve it.One way is to solve for one variable in terms of the other and check for integer solutions. Let's solve for y in terms of x:12y = 150 - 17xy = (150 - 17x)/12For y to be an integer, (150 - 17x) must be divisible by 12. Let's see what values of x make (150 - 17x) divisible by 12.Let me write down the congruence:150 - 17x ≡ 0 mod 12Which implies:17x ≡ 150 mod 12First, compute 150 mod 12. 12*12=144, so 150-144=6. Therefore, 150 ≡ 6 mod 12.Similarly, 17 mod 12 is 5. So the equation becomes:5x ≡ 6 mod 12We need to find x such that 5x ≡ 6 mod 12. To solve for x, we can multiply both sides by the modular inverse of 5 mod 12. The inverse of 5 mod 12 is a number m such that 5m ≡ 1 mod 12. Let's find m:5*1=5 mod12≠15*5=25≡1 mod12 (since 25-24=1). So m=5.Therefore, multiplying both sides by 5:5*5x ≡5*6 mod1225x ≡30 mod12But 25 mod12 is 1, and 30 mod12 is 6. So:1x ≡6 mod12Thus, x ≡6 mod12. That means x can be 6, 18, 30,... but since x has to be a positive integer and the total cost is 150 jiao, we need to check possible x values starting from 6 and increasing by 12 each time, but making sure that 17x ≤150.Let's check x=6:17*6=102 jiao. Then 150-102=48 jiao left for ballpoint pens. 48/12=4. So y=4. That's a possible solution: 6 watercolor pens and 4 ballpoint pens.Next possible x=6+12=18:17*18=306 jiao. But 306 >150. So that's too much. Therefore, x=6 is the only solution in this sequence. But wait, maybe there are more solutions with smaller x?Wait, the general solution for x is x=6 +12k, where k is integer. But since x must be non-negative and 17x ≤150, let's check possible k values.For k=0: x=6. 17*6=102, which is okay.For k=1: x=18. 17*18=306>150. So no good.So only x=6. But maybe there are other solutions if we consider modulo 12 but different residues. Let me check another approach.Alternatively, perhaps there's another way. Let me try different x values and see if (150 -17x) is divisible by12.Starting from x=0:x=0: 150-0=150. 150/12=12.5. Not integer.x=1: 150-17=133. 133/12≈11.08. Not integer.x=2:150-34=116. 116/12≈9.666. Not integer.x=3:150-51=99. 99/12=8.25. Not integer.x=4:150-68=82. 82/12≈6.833. Not integer.x=5:150-85=65. 65/12≈5.416. Not integer.x=6:150-102=48. 48/12=4. So y=4. That works.x=7:150-119=31. 31/12≈2.583. Not integer.x=8:150-136=14. 14/12≈1.166. Not integer.x=9:150-153= -3. Negative, so invalid.So the only solution is x=6 and y=4.But wait, maybe I made a mistake here. Because when we solved the congruence, we found x≡6 mod12, which gives x=6,18, etc. But when we tried x=6, y=4. The other x=18 is too big. So that's the only solution. But let me check x=6 and y=4:6 watercolor pens: 6*17=102 jiao.4 ballpoint pens:4*12=48 jiao.Total:102+48=150 jiao. Which is exactly 15 yuan. So that works.But wait, is that the only solution? Let me check if there's another x that might work. Let's see:Wait, x has to be such that 17x ≤150. 17x ≤150 => x ≤150/17≈8.823. So x can be from 0 to 8. We tried x=0 to 8 and only x=6 gives an integer y=4. Therefore, the only solution is 6 watercolor pens and 4 ballpoint pens.But wait, maybe I missed something. Let me check x=6 again. 17*6=102, 150-102=48, 48/12=4. That's correct.Wait, but I recall that sometimes there might be multiple solutions if the coefficients are not co-prime. Let me check if 17 and 12 are co-prime. The GCD of 17 and 12 is 1, since 17 is a prime number. So the equation 17x +12y=150 will have solutions in integers, and once we have one solution, the other solutions can be found by x=x0 +12k and y=y0 -17k, for integer k. But since we need x and y to be non-negative, k must be such that x0 +12k ≥0 and y0 -17k ≥0.Given that x0=6 and y0=4:x=6 +12ky=4 -17kWe need y=4-17k ≥0. Let's solve 4-17k ≥0:4 ≥17k => k ≤4/17≈0.235. Since k is integer, k≤0.Similarly, x=6+12k ≥0. For k ≥0, x is increasing. For k negative, x decreases.If k=0: x=6, y=4. Valid.k=-1: x=6-12= -6. Invalid.Therefore, the only solution is k=0, giving x=6 and y=4.Therefore, Xiao Juan bought 6 watercolor pens and 4 ballpoint pens.But let me check once more for x from 0 to 8:x=0: y=150/12=12.5 → invalid.x=1: (150-17)/12=133/12≈11.08→invalid.x=2:116/12≈9.666→invalid.x=3:99/12=8.25→invalid.x=4:82/12≈6.833→invalid.x=5:65/12≈5.416→invalid.x=6:48/12=4→valid.x=7:31/12≈2.58→invalid.x=8:14/12≈1.166→invalid.x=9:150-17*9=150-153=-3→negative. So invalid.Therefore, the only valid solution is x=6 and y=4. So the answer is 6 watercolor pens and 4 ballpoint pens.Final AnswerXiao Juan bought boxed{6} watercolor pens and boxed{4} ballpoint pens.</think>Xiao Juan bought pens with 15 yuan, which is equivalent to 150 jiao. The cost of each watercolor pen is 17 jiao (1 yuan 7 jiao) and each ballpoint pen is 12 jiao (1 yuan 2 jiao). We need to find the number of each type of pen she bought such that the total cost is 150 jiao.We set up the equation:[ 17x + 12y = 150 ]where ( x ) is the number of watercolor pens and ( y ) is the number of ballpoint pens.To solve this Diophantine equation, we first convert it into a congruence relation:[ 17x equiv 150 pmod{12} ]Simplifying the congruence:[ 150 equiv 6 pmod{12} ][ 17 equiv 5 pmod{12} ][ 5x equiv 6 pmod{12} ]The modular inverse of 5 modulo 12 is 5, since ( 5 times 5 equiv 1 pmod{12} ). Multiplying both sides by 5:[ x equiv 6 pmod{12} ]This gives possible solutions for ( x ) as ( x = 6 + 12k ) where ( k ) is an integer. We check values of ( x ) such that ( 17x leq 150 ):- For ( k = 0 ), ( x = 6 ) [ 17 times 6 = 102 ] [ 150 - 102 = 48 ] [ y = frac{48}{12} = 4 ]Checking other possible values of ( x ) from 0 to 8 (since ( 17x leq 150 ) implies ( x leq 8 )), we find that only ( x = 6 ) results in an integer value for ( y ).Thus, the solution is:[ x = 6 ][ y = 4 ]Xiao Juan bought boxed{6} watercolor pens and boxed{4} ballpoint pens.,<think>Okay, let's see here. Xiao Juan wants to buy pens with 15 yuan. There are two types: watercolor pens that cost 1 yuan and 7 jiao each, and ballpoint pens that cost 1 yuan and 2 jiao each. She spent all 15 yuan. We need to find out how many of each pen she bought.First, I need to make sure I understand the currency. In China, 1 yuan is equal to 10 jiao. So, converting the prices to yuan might make calculations easier. A watercolor pen is 1 yuan 7 jiao, which is 1.7 yuan. Similarly, a ballpoint pen is 1 yuan 2 jiao, which is 1.2 yuan. Let me denote the number of watercolor pens as x and the number of ballpoint pens as y. The total cost equation would then be:1.7x + 1.2y = 15But since dealing with decimals might be a bit tricky, maybe I can convert everything to jiao to avoid fractions. Let's try that.1 yuan = 10 jiao, so 15 yuan is 150 jiao. The watercolor pen is 1 yuan 7 jiao, which is 17 jiao, and the ballpoint pen is 1 yuan 2 jiao, which is 12 jiao. Now the equation becomes:17x + 12y = 150This looks better because all values are integers now. So, we need to find non-negative integers x and y such that 17x + 12y = 150.This is a linear Diophantine equation. Let's recall that such equations have solutions only if the greatest common divisor (gcd) of the coefficients divides the constant term. Let's compute gcd(17,12):17 divided by 12 is 1 with remainder 5.12 divided by 5 is 2 with remainder 2.5 divided by 2 is 2 with remainder 1.2 divided by 1 is 2 with remainder 0.So gcd(17,12) is 1. Since 1 divides 150, there are solutions.Now, we need to find all non-negative integer solutions (x, y) to 17x + 12y = 150.To solve this, we can express one variable in terms of the other. Let's solve for y:12y = 150 - 17xy = (150 - 17x)/12Since y must be a non-negative integer, (150 - 17x) must be divisible by 12, and the result must be non-negative.So, 150 -17x ≡ 0 mod 12Compute 150 mod 12 first:12*12=144, so 150 -144=6. Therefore, 150 ≡6 mod12Similarly, 17x mod12: 17≡5 mod12, so 17x ≡5x mod12Thus, equation becomes:5x ≡6 mod12We need to solve for x in 5x ≡6 mod12Multiplicative inverse of 5 mod12. Since 5 and 12 are coprime, the inverse exists. Let's find an integer k such that 5k ≡1 mod12.Testing k=5: 5*5=25≡1 mod12 (25-2*12=1). So inverse is 5.Therefore, x ≡6*5 mod126*5=30≡6 mod12 (30-2*12=6)Wait, that's 30 mod12 is 6. So x≡6 mod12Therefore, x=12t +6, where t is an integer. But x must satisfy 17x ≤150, so:17*(12t +6) ≤150204t +102 ≤150204t ≤48t ≤48/204≈0.235Since t must be a non-negative integer, the only possible t is 0. Therefore, x=6.Then, substituting x=6 into the original equation:17*6 +12y=150102 +12y=15012y=48y=4So, x=6 and y=4. Let's check:17*6=102; 12*4=48; 102+48=150 jiao, which is 15 yuan. So that works.Wait, but is this the only solution? Let's check for other possible values. Since x must be non-negative, and the step for solutions in a Diophantine equation is determined by the coefficients. Since gcd(17,12)=1, the solutions will differ by multiples of 12 in x and -17 in y. But since x and y must be non-negative, other solutions might not exist.Wait, let me think again. The general solution for x and y would be:x = x0 + (12/k)ty = y0 - (17/k)twhere k is the gcd(17,12)=1, and t is an integer.So x =6 +12ty=4 -17tBut since y must be non-negative, 4 -17t ≥0 => t ≤4/17≈0.235. So t can only be 0 or negative integers. But x must also be non-negative. If t is negative, say t=-1, then x=6-12= -6, which is invalid. So the only solution is t=0: x=6, y=4.Therefore, the only possible solution is 6 watercolor pens and 4 ballpoint pens.Wait, but let me check another way. Let's see if there are other values of x where (150 -17x) is divisible by 12.We found x=6 gives 150-17*6=150-102=48, which is divisible by 12, giving y=4.Let me check x=6-12= -6, which is invalid.x=6+12=18. 17*18=306, which is more than 150, so invalid.Similarly, x=0: 150-0=150; 150/12=12.5, not integer.x=1: 150-17=133; 133/12≈11.08, not integer.x=2:150-34=116; 116/12≈9.666, no.x=3:150-51=99;99/12=8.25, nope.x=4:150-68=82;82/12≈6.833, nope.x=5:150-85=65;65/12≈5.416, nope.x=6:48/12=4, which works.x=7:150-119=31;31/12≈2.583, nope.x=8:150-136=14;14/12≈1.166, nope.x=9:150-153= -3, negative, so invalid.So indeed, the only solution is x=6 and y=4.Therefore, Xiao Juan bought 6 watercolor pens and 4 ballpoint pens.Final AnswerXiao Juan bought boxed{6} watercolor pens and boxed{4} ballpoint pens.</think>Xiao Juan went to the stationery store to buy pens. The cost of each watercolor pen is 1 yuan and 7 jiao (17 jiao) and each ballpoint pen is 1 yuan and 2 jiao (12 jiao). She spent all 15 yuan (150 jiao). We need to find the number of each type of pen she bought.First, convert all prices to jiao:- Watercolor pen: 17 jiao- Ballpoint pen: 12 jiao- Total money: 150 jiaoWe set up the equation:[ 17x + 12y = 150 ]where ( x ) is the number of watercolor pens and ( y ) is the number of ballpoint pens.To solve this linear Diophantine equation, we find the greatest common divisor (gcd) of 17 and 12, which is 1. Since 1 divides 150, there are solutions.We solve for ( x ) and ( y ):1. Convert the equation modulo 12:[ 17x equiv 6 pmod{12} ]2. Simplify ( 17 equiv 5 pmod{12} ), so:[ 5x equiv 6 pmod{12} ]3. Find the multiplicative inverse of 5 modulo 12, which is 5, since ( 5 times 5 equiv 1 pmod{12} ).4. Multiply both sides by 5:[ x equiv 6 times 5 pmod{12} ][ x equiv 30 pmod{12} ][ x equiv 6 pmod{12} ]Thus, ( x = 12t + 6 ) for integer ( t ). We check for non-negative solutions:- ( x = 6 )- Substitute ( x = 6 ) into the original equation:[ 17(6) + 12y = 150 ][ 102 + 12y = 150 ][ 12y = 48 ][ y = 4 ]Checking other values of ( x ) (from 0 to 8) confirms no other solutions. Therefore, the only solution is ( x = 6 ) and ( y = 4 ).Xiao Juan bought boxed{6} watercolor pens and boxed{4} ballpoint pens.]

🔑:Reference answer: 6, 4

🧠:[<think>Okay, let me try to figure out this problem. So, the question is: If α equals k times 180 degrees plus 45 degrees, where k is an integer, then the terminal side of α is in which quadrant? The options are A through D, with different quadrant pairs. Hmm, I need to determine which quadrants these angles fall into. Let me start by recalling some basics about angles and quadrants.First, I remember that angles in standard position (starting from the positive x-axis) are measured counterclockwise. The quadrants are divided every 90 degrees. So, the first quadrant is from 0 to 90 degrees, the second from 90 to 180, the third from 180 to 270, and the fourth from 270 to 360. Then it repeats every 360 degrees. But in this problem, the angle is given as α = k*180° + 45°, where k is any integer. So, depending on the value of k, the angle α can be different. Let me try plugging in some integer values for k and see what angles we get.Let's start with k = 0. Then α = 0*180° + 45° = 45°. That's in the first quadrant because it's between 0° and 90°. Okay, so that's quadrant I.Next, k = 1. Then α = 1*180° + 45° = 225°. Hmm, 225 degrees is between 180° and 270°, so that's the third quadrant. So, here we have third quadrant.k = 2. Then α = 2*180° + 45° = 360° + 45° = 405°. But angles are periodic with 360°, so 405° is equivalent to 405° - 360° = 45°, which is back to the first quadrant. So, k=2 gives the same as k=0, which makes sense because adding 180° twice is 360°, a full rotation.What about negative k? Let's try k = -1. Then α = -1*180° + 45° = -180° + 45° = -135°. Negative angles go clockwise from the positive x-axis. So, -135° would be the same as 360° - 135° = 225°, which is again 225°, third quadrant. Wait, but that's the same as k=1. Hmm.Wait, maybe I need to think differently. Let's convert the negative angle to a positive one by adding 360°. -135° + 360° = 225°, which is still in the third quadrant. But if I take k = -2, then α = -2*180° + 45° = -360° + 45° = -315°. Adding 360°, -315° + 360° = 45°, which is first quadrant. So, again, same as k=0 and k=2. So, it seems that depending on k being even or odd, the angle α alternates between 45° and 225°, which are in the first and third quadrants respectively.So, for even k, like k=0, 2, -2, etc., α is 45° plus a multiple of 360°, which is first quadrant. For odd k, like k=1, -1, 3, etc., α is 225° plus a multiple of 360°, which is third quadrant. Therefore, the terminal side of α is always either in the first or third quadrant. So, the answer should be option A.But let me double-check to make sure I haven't missed anything. Let's take a few more values of k. For example, k=3: 3*180 +45=540+45=585°. Subtract 360°: 585-360=225°, third quadrant. k=4: 4*180+45=720+45=765°. Subtract 360 twice: 765-720=45°, first quadrant. Similarly, k=-3: -3*180 +45= -540 +45= -495°. Add 360° twice: -495 +720=225°, third quadrant. So, yes, all cases lead to either 45° or 225°, which are first and third quadrants. Therefore, option A is correct.Just to be thorough, let me recall that 45° is in QI, 135° is QII, 225° is QIII, 315° is QIV. But in this case, the angles generated by the formula are either 45°, 225°, 405°=45°, 585°=225°, etc. So, never in QII or QIV. Therefore, the answer must be A: first or third quadrant.Final Answerboxed{A}</think>Given the angle (alpha = k cdot 180^circ + 45^circ) where (k in mathbb{Z}), we need to determine the quadrants in which the terminal side of (alpha) lies.1. Substituting values for (k): - For (k = 0): (alpha = 0 cdot 180^circ + 45^circ = 45^circ), which is in the first quadrant. - For (k = 1): (alpha = 1 cdot 180^circ + 45^circ = 225^circ), which is in the third quadrant. - For (k = 2): (alpha = 2 cdot 180^circ + 45^circ = 405^circ). Subtracting (360^circ) gives (45^circ), which is in the first quadrant. - For (k = -1): (alpha = -1 cdot 180^circ + 45^circ = -135^circ). Adding (360^circ) gives (225^circ), which is in the third quadrant. - For (k = -2): (alpha = -2 cdot 180^circ + 45^circ = -315^circ). Adding (360^circ) gives (45^circ), which is in the first quadrant.2. Generalizing the pattern: - When (k) is even, (alpha) results in an angle equivalent to (45^circ) (first quadrant). - When (k) is odd, (alpha) results in an angle equivalent to (225^circ) (third quadrant).3. Conclusion: - The terminal side of (alpha) is always in either the first quadrant (for even (k)) or the third quadrant (for odd (k)).Thus, the correct answer is (boxed{A}).,<think>Okay, let's see. The problem is about determining which quadrants the terminal side of angle α falls into, given that α is equal to k times 180 degrees plus 45 degrees, where k is any integer. The options are quadrants first or third, first or second, second or fourth, or third or fourth. Hmm.First, I need to recall what the terminal side of an angle is. In trigonometry, when an angle is drawn in standard position (with its vertex at the origin and initial side along the positive x-axis), the terminal side is the position of the angle after it has been rotated. The quadrant in which the terminal side lies determines the quadrant of the angle. So angles can be in any of the four quadrants or on the axes.The angle given here is α = k·180° + 45°, where k is any integer. Let's break this down. Since k is an integer, multiplying it by 180° gives us multiples of 180°, and then adding 45° each time. So, depending on the value of k, the angle α can be 45°, 225°, 405°, 585°, etc., or if k is negative, like -1, then α would be -180° + 45° = -135°, and so on.Wait, but angles in standard position are typically measured from the positive x-axis, rotating counterclockwise for positive angles and clockwise for negative angles. However, angles that are co-terminal (i.e., have the same terminal side) can be found by adding or subtracting multiples of 360°. So maybe it's helpful to consider different values of k and see where the terminal side lands.Let's start with k = 0. Then α = 0·180° + 45° = 45°. That's in the first quadrant because 45° is between 0° and 90°.k = 1: α = 180° + 45° = 225°. 225° is between 180° and 270°, so that's the third quadrant.k = 2: α = 360° + 45° = 405°. But 405° is equivalent to 405° - 360° = 45°, which is again in the first quadrant.k = 3: 540° + 45° = 585°, which is 585° - 360° = 225°, same as before, third quadrant.Similarly, negative k:k = -1: α = -180° + 45° = -135°. To visualize this, rotating 135° clockwise from the positive x-axis, which would place the terminal side in the third quadrant as well? Wait, no. Wait, -135° is the same as 360° - 135° = 225°, which is indeed the third quadrant. Hmm, so even when k is negative, the angle still ends up in the third quadrant. Wait, but when k = -1, we have 225°, which is third quadrant. When k = -2, that's -360° + 45° = -315°, which is equivalent to 45°, first quadrant. So it seems like for even k (positive or negative), the angle is 45° plus some multiple of 360°, which is in the first quadrant. For odd k, it's 225° plus some multiple of 360°, which is in the third quadrant.Wait, but hold on, is k even or odd? Wait, k is an integer. So if k is even, say k = 2n, then α = 2n·180° + 45° = n·360° + 45°, which is co-terminal with 45°, so first quadrant. If k is odd, say k = 2n + 1, then α = (2n + 1)·180° + 45° = 2n·180° + 180° + 45° = n·360° + 225°, which is co-terminal with 225°, so third quadrant. Therefore, regardless of whether k is positive or negative, even or odd, the angle α is either 45° or 225° plus a multiple of 360°, hence lying in the first or third quadrants. Therefore, the answer should be A: The first or third quadrant.Let me double-check with some examples. For k = 0: 45°, first quadrant. k = 1: 225°, third. k = 2: 405° which is 45°, first. k = -1: -135°, which is same as 225°, third. k = -2: -315°, same as 45°, first. So yes, it alternates between first and third. So the correct answer is A.But just to be thorough, let me consider if there's any case where it could be in another quadrant. For example, is 45° + 180°k ever in the second or fourth quadrant?Let's see. Let's take k = 0.5. Wait, but k must be an integer. If k is an integer, 180°k is always a multiple of 180°, so adding 45° to that would give 45°, 225°, 405°, 585°, etc. So 45° is in the first quadrant, 225° is third, 405° is same as 45°, and 585° is same as 225°. So never in second or fourth. Therefore, answer A is correct.So the answer is A.Final Answerboxed{A}</think>Given the angle (alpha = k cdot 180^circ + 45^circ) where (k in mathbb{Z}), we need to determine the quadrants in which the terminal side of (alpha) lies.1. Analyzing the angle for different values of (k): - For (k = 0): (alpha = 0 cdot 180^circ + 45^circ = 45^circ), which is in the first quadrant. - For (k = 1): (alpha = 1 cdot 180^circ + 45^circ = 225^circ), which is in the third quadrant. - For (k = 2): (alpha = 2 cdot 180^circ + 45^circ = 405^circ), which is equivalent to (45^circ) (first quadrant) after subtracting (360^circ). - For (k = -1): (alpha = -1 cdot 180^circ + 45^circ = -135^circ), which is equivalent to (225^circ) (third quadrant) after adding (360^circ). - For (k = -2): (alpha = -2 cdot 180^circ + 45^circ = -315^circ), which is equivalent to (45^circ) (first quadrant) after adding (360^circ).2. Generalizing for any integer (k): - When (k) is even, say (k = 2n), then (alpha = 2n cdot 180^circ + 45^circ = n cdot 360^circ + 45^circ), which is co-terminal with (45^circ) (first quadrant). - When (k) is odd, say (k = 2n + 1), then (alpha = (2n + 1) cdot 180^circ + 45^circ = n cdot 360^circ + 225^circ), which is co-terminal with (225^circ) (third quadrant).Thus, the terminal side of (alpha) is always in either the first or third quadrant. The correct answer is (boxed{A}).]

🔑:Given alpha = k cdot 180^circ + 45^circ (k in mathbb{Z}),- When k is even, the terminal side of k cdot 180^circ is on the positive x-axis, thus alpha = k cdot 180^circ + 45^circ (k in mathbb{Z}) is an angle in the first quadrant.- When k is odd, the terminal side of k cdot 180^circ is on the negative x-axis, thus alpha = k cdot 180^circ + 45^circ (k in mathbb{Z}) is an angle in the third quadrant.Therefore, the terminal side of alpha is in the first or third quadrant.Hence, the correct answer is boxed{text{A}}.This problem involves discussing k as even and odd numbers, initially determining the terminal side of k cdot 180^circ, and adding 45^circ to find the answer. It examines the concept of quadrant angles and axial angles, which is a basic conceptual question and is likely to appear in exams.

🧠:[<think>Okay, so I need to figure out the smallest number of ones required in a pretty list of 100 numbers. A pretty list is defined as one where all numbers are strictly positive integers, and their sum equals their product. Hmm, interesting problem. Let me start by understanding what exactly a pretty list is.First, let's consider the basic properties. All numbers must be positive integers, so each number is at least 1. If all numbers were 1, then the sum would be 100 (since there are 100 numbers) and the product would be 1. But 100 isn't equal to 1, so that doesn't work. We need to have some numbers greater than 1 to increase the product while keeping the sum as close to the product as possible.Wait, but how does increasing a number affect the sum and product? Let's say I have a list of numbers, and I replace a 1 with a 2. The sum increases by 1, and the product doubles. So replacing a 1 with a 2 increases both the sum and the product, but the product increases more. Similarly, replacing a 1 with a higher number like 3 would increase the sum by 2 and multiply the product by 3. So each time we replace a 1 with a higher number, the product grows much faster than the sum. The challenge is to make the sum equal to the product by replacing some 1s with higher numbers, but not so many that the product overshoots the sum.Alternatively, perhaps replacing multiple 1s with a single higher number? Let me think. For example, if I have two 1s, their sum is 2 and their product is 1. If I replace them with a 2, the sum becomes 2 and the product becomes 2. So in this case, replacing two 1s with a 2 keeps the sum the same but increases the product to match the sum. So this would turn a non-pretty list into a pretty one. Wait, but in this case, with two numbers, replacing two 1s with a 2 gives a sum and product of 2. So that works. Interesting.So maybe the key is to replace groups of 1s with numbers such that the sum of those replaced numbers equals their product. Then, the total sum and product of the entire list can be balanced. Let's formalize this.Suppose we have k ones and (100 - k) numbers greater than 1. Let the numbers greater than 1 be a_1, a_2, ..., a_{100 - k}. Then the total sum S is k*1 + sum(a_i) and the total product P is 1^k * product(a_i). We need S = P.So, k + sum(a_i) = product(a_i). Our goal is to minimize the number of ones, k, which is equivalent to maximizing the number of non-one numbers (100 - k). But we have to balance the sum and product.Alternatively, since replacing 1s with larger numbers increases the product more than the sum, perhaps we need to use a combination of numbers greater than 1 such that their product minus their sum equals the number of 1s we replaced. Wait, let me see.Suppose we have m numbers greater than 1. Each of these m numbers contributes (a_i - 1) to the difference between the product and the sum. Because if we have m numbers, the original sum would be m (if they were all 1s) and the original product would be 1. By replacing them with a_i, the sum becomes sum(a_i) and the product becomes product(a_i). The difference (product(a_i) - sum(a_i)) must equal the number of 1s replaced, which is (m - k). Wait, maybe not exactly. Let me think again.If we have a total of 100 numbers, with k ones and (100 - k) numbers a_1, a_2, ..., a_{100 - k}. Then the sum is k + sum(a_i) and the product is product(a_i). For these to be equal:k + sum(a_i) = product(a_i)So, product(a_i) - sum(a_i) = kBut since there are (100 - k) numbers a_i, each at least 2. So we have:product(a_i) - sum(a_i) = kBut k = 100 - (number of a_i) = 100 - m, where m is the number of non-one numbers. Wait, actually, k is the number of ones, so m = 100 - k. Therefore:product(a_i) - sum(a_i) = k = 100 - mBut m is the number of non-one numbers. So:product(a_i) - sum(a_i) = 100 - mBut product(a_i) - sum(a_i) must equal 100 - m. Hmm.Alternatively, product(a_i) - sum(a_i) = number of ones. Because k = 100 - m, so product(a_i) - sum(a_i) = 100 - m. So:product(a_i) - sum(a_i) + m = 100But product(a_i) - sum(a_i) + m = product(a_i) - (sum(a_i) - m) = product(a_i) - sum(a_i - 1) = 100Wait, maybe there's a different way to approach this.Let me think about small cases first. Let's say we have m numbers greater than 1. Each of these numbers contributes (a_i - 1) to the excess of the product over the sum. Wait, maybe not exactly. Let's consider replacing t ones with a single number t + 1. Then, the sum becomes (100 - t) + (t + 1) = 101. The product becomes 1^{100 - t} * (t + 1) = t + 1. So 101 = t + 1? That would require t = 100, but that would replace all ones with a single 101, which is not 100 numbers. Wait, that approach might not be helpful.Wait, perhaps better to think in terms of the equation product(a_i) = sum(a_i) + k. Since sum(a_i) + k = product(a_i). So product(a_i) - sum(a_i) = k.But product(a_i) is at least 2^{m}, since each a_i is at least 2, and sum(a_i) is at least 2m. So product(a_i) - sum(a_i) >= 2^m - 2m. We need 2^m - 2m >= k = 100 - m. Therefore:2^m - 2m >= 100 - mSo 2^m - 2m + m >= 100Which simplifies to 2^m - m >= 100So we need to find the smallest m such that 2^m - m >= 100.Let me compute 2^m - m for m starting from, say, 6:m=6: 64 - 6 = 58 <100m=7: 128 -7=121 >=100So m=7. So that suggests that if we have 7 numbers greater than 1, each being 2, then 2^7 - 7 = 121 >= 100 -7=93. Wait, but the inequality was 2^m - m >=100. At m=7, 2^7 -7=121, which is greater than 100. But in our problem, the required k=100 - m. So if m=7, then k=93. But in that case, product(a_i) - sum(a_i)=2^7 - 2*7=128 -14=114. Which would need to equal k=93. But 114≠93. So that approach may not be directly applicable.Wait, maybe the assumption that all a_i=2 is leading to a discrepancy. If all a_i=2, then product(a_i)=2^m, sum(a_i)=2m, so product - sum=2^m -2m. This needs to equal k=100 -m. So 2^m -2m =100 -m =>2^m -m=100. Which is the same equation as before. So when m=7, 2^7 -7=128-7=121>100. So 2^7 -m=121>100. But we need exactly 2^m -2m=100 -m. So 2^m -2m=100 -m =>2^m -m=100. So 2^m -m needs to equal 100. So solving 2^m -m=100. Let's check m=6: 64 -6=58, m=7:128 -7=121. So between m=6 and m=7, the left side jumps from 58 to 121. Therefore, there's no integer m where 2^m -m=100. Hence, we can't have all a_i=2. So maybe some combination of 2's and 3's?Because 3 contributes more to the product. Let me think. If we have some 3s in there, then the product increases faster. Let's suppose we have t 3's and (m - t) 2's. Then product(a_i)=3^t *2^{m -t}, sum(a_i)=3t +2(m -t)=2m +t. Then product - sum=3^t *2^{m -t} - (2m +t)=k=100 -m. So 3^t *2^{m -t} - (2m +t)=100 -m. Which simplifies to 3^t *2^{m -t} -m -t=100.This seems more complex, but perhaps we can find m and t such that this equation holds. Let's try with m=7, since 2^7 -7=121, which was close. Let's try m=7. So 3^t *2^{7 -t} -7 -t=100. Let's try different t values.t=0: 2^7 -7 -0=128 -7=121≠100t=1:3*2^6 -7 -1=192 -8=184≠100t=2:9*2^5 -7 -2=288 -9=279≠100t=3:27*2^4 -7 -3=432 -10=422≠100That's way too big. So m=7 with t>=0 is too big. Wait, maybe m=6? Let's try m=6.3^t *2^{6 -t} -6 -t=100.t=0:64 -6 -0=58≠100t=1:3*32 -6 -1=96 -7=89≠100t=2:9*16 -6 -2=144 -8=136≠100t=3:27*8 -6 -3=216 -9=207≠100Still not 100.m=5:3^t*2^{5 -t} -5 -t=100t=0:32 -5 -0=27≠100t=1:3*16 -5 -1=48 -6=42≠100t=2:9*8 -5 -2=72 -7=65≠100t=3:27*4 -5 -3=108 -8=100. Oh! Wait, t=3, m=5.So for m=5, t=3:product=3^3*2^{2}=27*4=108sum=3*3 +2*2=9 +4=13Then product - sum=108 -13=95. But according to the equation, it's 3^3*2^{2} -5 -3=108 -8=100. Wait, but product - sum is 108 -13=95, which should equal k=100 -5=95. Yes! So in this case, if we have m=5 non-one numbers, consisting of 3 threes and 2 twos, the product is 108, the sum is 13. Then the total sum of the entire list is k + sum(a_i)=95 +13=108, and the product is 108. So indeed, sum equals product. Therefore, this works.Therefore, with m=5 non-one numbers (3 threes and 2 twos) and k=95 ones, we get a pretty list. So the number of ones is 95. But is this the minimal number of ones? Because m=5 is the number of non-ones, which gives k=95.But wait, could we do better? Let's check m=4. Let's try m=4.Equation:3^t*2^{4 -t} -4 -t=100.t=0:16 -4 -0=12≠100t=1:3*8 -4 -1=24 -5=19≠100t=2:9*4 -4 -2=36 -6=30≠100t=3:27*2 -4 -3=54 -7=47≠100t=4:81*1 -4 -4=81 -8=73≠100Not enough. How about m=6? Let's check m=6 again. Wait, m=6 had t=3: product=27*8=216, sum=9 + 8=17, product - sum=199, which would need to equal k=94. But 216 -17=199=94? No, 199≠94. Wait, maybe miscalculation. Wait, for m=6 and t=3, the equation was 3^3*2^{3} -6 -3=27*8 -9=216 -9=207≠100. Not helpful.Wait, perhaps trying different numbers. Maybe using a 4? For example, if we have a 4 in the numbers, since 4=2*2, so replacing two 2s with a 4 would keep the product the same but reduce the sum by 2. So maybe that can help adjust the sum and product.Let me think. Suppose we have one 4 and the rest 2s. Let's try m=5. If we have one 4 and four 2s. Then product=4*2^4=64, sum=4 +8=12. Product - sum=64 -12=52. Then k=100 -5=95. But 52≠95. Doesn't work.Alternatively, using a 5. If we have a 5 and others 2s. For m=4: one 5 and three 2s. Product=5*8=40, sum=5 +6=11. Product - sum=29. k=100 -4=96. 29≠96.Hmm. Alternatively, using a higher number. Let's try m=3. Suppose we have a 4, a 3, and a 2. Then product=4*3*2=24, sum=4+3+2=9. Product - sum=15. k=100 -3=97. 15≠97. Not helpful.Alternatively, m=2: one 50 and one 50. Product=2500, sum=100. Then product - sum=2400. k=100 -2=98. 2400≠98. Doesn't work.Alternatively, m=1: just one number 100. Product=100, sum=100. Then product - sum=0. k=100 -1=99. 0≠99. Not useful.Wait, but if m=1 and the number is 100, then sum is 100 and product is 100. So sum equals product. But the problem states that the list must consist of strictly positive integers. So a single number 100 is a list of length 1, but we need a list of length 100. So that approach doesn't work.Wait, so going back, the previous case where m=5 (non-ones) with 3 threes and 2 twos gives k=95 ones. Is this the minimal number of ones?Wait, let me check m=6. Maybe with a combination of a 3 and some 2s and a 4.Suppose m=6. Let's have one 4, one 3, and four 2s. Then product=4*3*2^4=4*3*16=192. Sum=4 +3 +8=15. Product - sum=192 -15=177. k=100 -6=94. 177≠94. Not helpful.Alternatively, two 3s and four 2s. Product=9*16=144. Sum=6 +8=14. 144 -14=130. k=94. Not equal.Alternatively, three 3s and three 2s. Product=27*8=216. Sum=9 +6=15. 216 -15=201. k=94. Nope.Alternatively, m=7. Maybe with one 3 and six 2s. Product=3*64=192. Sum=3 +12=15. 192 -15=177. k=100 -7=93. Not equal.Alternatively, two 3s and five 2s. Product=9*32=288. Sum=6 +10=16. 288 -16=272. k=93. Not equal.Not helpful. Alternatively, perhaps using a 5. Let's try m=5. One 5, one 3, and three 2s. Product=5*3*8=120. Sum=5 +3 +6=14. 120 -14=106. k=95. 106≠95.Alternatively, one 5, four 2s. Product=5*16=80. Sum=5 +8=13. 80 -13=67. k=95. Not equal.Alternatively, two 3s and three 2s. Product=9*8=72. Sum=6 +6=12. 72 -12=60. k=95. No.Alternatively, four 3s and one 2. Product=81*2=162. Sum=12 +2=14. 162 -14=148. k=95. Nope.Wait, maybe using a higher number. Let's say we have a 4, a 3, and the rest 2s. For m=5: one 4, one 3, three 2s. Product=4*3*8=96. Sum=4 +3 +6=13. 96 -13=83. k=95. Not equal.Alternatively, m=5: two 4s and three 2s. Product=16*8=128. Sum=8 +6=14. 128 -14=114. k=95. 114≠95.Hmm. Alternatively, perhaps using a 6. For m=5: one 6, four 2s. Product=6*16=96. Sum=6 +8=14. 96 -14=82. k=95. Not equal.Alternatively, one 7, four 2s. Product=7*16=112. Sum=7 +8=15. 112 -15=97. k=95. Close, but 97≠95.Wait, 97 vs 95. If we reduce the product by 2, maybe by replacing a 2 with a 1? Wait, but we are supposed to have m=5 non-ones. If we replace a 2 with a 1, then m becomes 4, and k becomes 96. Wait, but maybe adjusting numbers.Alternatively, one 7, three 2s, and one 1. But then we have m=4 non-ones (7,2,2,2) and k=96. Then product=7*2*2*2=56. Sum=7 +6=13. Total sum=96 +13=109. Product=56. 109≠56. Not helpful.Alternatively, maybe instead of a 7, use a 5 and adjust other numbers. For m=5, one 5, three 2s, and one 3. Product=5*3*2*2*2=120. Sum=5+3+2+2+2=14. Product - sum=106. k=95. 106≠95. Not quite.Wait, perhaps another approach. Let me recall that the minimal number of ones would correspond to the maximal number of non-ones (m), but we need product(a_i) - sum(a_i) =k=100 -m.Therefore, product(a_i) - sum(a_i) =100 -m.But product(a_i) - sum(a_i) can be increased by using higher numbers. For example, using a 3 instead of a 2 and a 1. Let me think.Suppose we have two numbers: 3 and 1. The product is 3, the sum is 4. So product - sum = -1. Not helpful. But if we have three numbers: 3,1,1. Product=3, sum=5. Product - sum= -2. Still negative. Wait, but when we have more numbers greater than 1, the product can overtake the sum.Alternatively, if we have numbers such that their product is much larger than their sum, which allows the difference product - sum to be equal to k=100 -m.Therefore, we need to choose numbers a_1, a_2, ..., a_m such that product(a_i) - sum(a_i) =100 -m.To maximize m (minimize k=100 -m), we need to make product(a_i) - sum(a_i) as small as possible (since 100 -m decreases as m increases). Wait, but product(a_i) - sum(a_i) needs to equal 100 -m. So as m increases, 100 -m decreases. Therefore, to achieve a smaller product - sum, we need m to be larger. But how can we make product - sum small? By making the product not too much larger than the sum.Wait, if we have numbers like 2s and 3s, which are small, their product isn't too much larger than their sum. For example, a 2 contributes 2 to the product and 2 to the sum, so product - sum=0. A 3 contributes 3 to the product and 3 to the sum, product - sum=0. Wait, but if you have multiple numbers, the product grows multiplicatively while the sum grows additively. For example, two 2s: product=4, sum=4, product - sum=0. Two 3s: product=9, sum=6, product - sum=3. A 2 and a 3: product=6, sum=5, product - sum=1. So combinations of 2s and 3s can give different product - sum differences.Therefore, perhaps the optimal way is to use as many 2s and 3s as possible, since they give the minimal product - sum difference. Let me try to find m and a combination of 2s and 3s such that product(a_i) - sum(a_i) =100 -m.Let me denote t as the number of 3s and (m - t) as the number of 2s. Then product=3^t *2^{m -t}, sum=3t +2(m -t)=2m +t. Therefore, product - sum=3^t *2^{m -t} - (2m +t)=100 -m.So the equation becomes:3^t *2^{m -t} -2m -t =100 -mSimplify:3^t *2^{m -t} -m -t =100Now, we need to find integers m and t such that this equation holds. Let's try different values of m and t.Earlier, when m=5 and t=3, we had 3^3 *2^{2} -5 -3=27*4 -8=108 -8=100. So that works. So that's the solution: 3 threes and 2 twos, giving m=5, k=95.But is there a higher m (lower k) that works? Let's check m=6.We need 3^t *2^{6 -t} -6 -t=100.Try t=4:3^4 *2^{2}=81*4=324. 324 -6 -4=314≠100t=3:27*8=216. 216 -6 -3=207≠100t=2:9*16=144. 144 -6 -2=136≠100t=1:3*32=96. 96 -6 -1=89≠100t=0:64 -6 -0=58≠100No luck. m=7.3^t *2^{7 -t} -7 -t=100.t=5:3^5*2^2=243*4=972. 972 -7 -5=960≠100t=4:81*8=648. 648 -7 -4=637≠100t=3:27*16=432. 432 -7 -3=422≠100t=2:9*32=288. 288 -7 -2=279≠100t=1:3*64=192. 192 -7 -1=184≠100t=0:128 -7 -0=121≠100No solution. m=4:3^t *2^{4 -t} -4 -t=100t=4:81*1=81. 81 -4 -4=73≠100t=3:27*2=54. 54 -4 -3=47≠100t=2:9*4=36. 36 -4 -2=30≠100t=1:3*8=24. 24 -4 -1=19≠100t=0:16 -4 -0=12≠100Nope. m=5 is the only one that works. So the minimal number of ones is 100 -5=95.But wait, let's check m=5 with different t. For example, t=2:3^2*2^{3}=9*8=72. 72 -5 -2=65≠100t=4:3^4*2^{1}=81*2=162. 162 -5 -4=153≠100Only t=3 gives 100.Thus, the minimal number of ones is 95. However, let me confirm with another approach.Suppose we have m numbers greater than 1, and k=100 -m ones. The total sum S =k + sum(a_i) =100 -m + sum(a_i). The product P=product(a_i). We need S=P.So 100 -m + sum(a_i)=product(a_i). Therefore, product(a_i) - sum(a_i)=100 -m.Which is the same equation as before. So the problem reduces to finding m and numbers a_i>1 such that product(a_i) - sum(a_i)=100 -m.We found that for m=5 and numbers [3,3,3,2,2], product=108, sum=13, product - sum=95=100 -5=95. So that works. Therefore, k=95.Is there a way to have m=6? Let's try to find numbers a_1,...,a_6>1 such that product - sum=100 -6=94.So product=sum +94.Let me see. Let's try with five 2s and one 3. Then product=2^5*3=32*3=96. sum=2*5 +3=13. product - sum=96 -13=83≠94.If we use six 2s: product=64, sum=12, product - sum=52≠94.If we use four 2s and two 3s: product=2^4*3^2=16*9=144. sum=8 +6=14. 144 -14=130≠94.Three 2s and three 3s: product=8*27=216. sum=6 +9=15. 216 -15=201≠94.Two 2s and four 3s: product=4*81=324. sum=4 +12=16. 324 -16=308≠94.One 2 and five 3s: product=2*243=486. sum=2 +15=17. 486 -17=469≠94.Alternatively, use a 4. Let's try one 4 and five 2s: product=4*32=128. sum=4 +10=14. 128 -14=114≠94.One 4, four 2s, one 3: product=4*16*3=192. sum=4 +8 +3=15. 192 -15=177≠94.One 5 and five 2s: product=5*32=160. sum=5 +10=15. 160 -15=145≠94.Two 4s and four 2s: product=16*16=256. sum=8 +8=16. 256 -16=240≠94.Hmm. Alternatively, use a higher number like 6. Let's try one 6 and five 2s: product=6*32=192. sum=6 +10=16. 192 -16=176≠94.Alternatively, one 10 and five 2s: product=10*32=320. sum=10 +10=20. 320 -20=300≠94.Alternatively, two 3s, two 4s, and two 2s: product=9*16*4=576. sum=6 +8 +4=18. 576 -18=558≠94.This approach isn't working. Maybe m=6 is impossible. Similarly, trying m=7.We need product - sum=100 -7=93.Using seven 2s: product=128, sum=14. 128 -14=114≠93.Six 2s and one 3: product=64*3=192, sum=12 +3=15. 192 -15=177≠93.Five 2s and two 3s:32*9=288, sum=10 +6=16. 288 -16=272≠93.Four 2s and three 3s:16*27=432, sum=8 +9=17. 432 -17=415≠93.Three 2s and four 3s:8*81=648, sum=6 +12=18. 648 -18=630≠93.Two 2s and five 3s:4*243=972, sum=4 +15=19. 972 -19=953≠93.Alternatively, introducing a 4. Let's try six 2s and one 4: product=64*4=256, sum=12 +4=16. 256 -16=240≠93.Five 2s, one 4, one 3:32*4*3=384, sum=10 +4 +3=17. 384 -17=367≠93.Four 2s, two 4s:16*16=256, sum=8 +8=16. 256 -16=240≠93.Three 2s, three 4s:8*64=512, sum=6 +12=18. 512 -18=494≠93.Alternatively, using a 5. Let's say five 2s and two 5s:32*25=800, sum=10 +10=20. 800 -20=780≠93.Not helpful. It seems like m=5 is the only viable solution. Therefore, the minimal number of ones is 95.But wait, let me check m=8. Wait, but the equation for m=5 gives a valid solution, and m=6 and above don't seem to work. Therefore, 95 ones is the minimal number.But just to confirm, is there another combination with m=5 that gives product - sum=95? For example, using a 4 instead of a 2 and a 2. Let's say two 3s, one 4, and two 2s.Product=3*3*4*2*2=144. Sum=3+3+4+2+2=14. product - sum=130. 130≠95.Alternatively, one 5, two 3s, and two 2s. Product=5*3*3*2*2=180. Sum=5+3+3+2+2=15. 180 -15=165≠95.Alternatively, one 6, one 3, three 2s. Product=6*3*2*2*2=144. Sum=6+3+2+2+2=15. 144 -15=129≠95.Alternatively, four 3s and one 4. Product=81*4=324. Sum=12 +4=16. 324 -16=308≠95.Nope. The only solution for m=5 is three 3s and two 2s.Therefore, I think the minimal number of ones is 95.Final AnswerThe smallest number of ones is boxed{95}.</think>To determine the smallest number of ones in a pretty list of 100 numbers, we need to find a list of strictly positive integers such that their sum equals their product. The key steps are as follows:1. Understanding the Problem: A pretty list requires the sum of the numbers to equal their product. We need to minimize the number of ones (k) in such a list of 100 numbers.2. Equation Setup: Let k be the number of ones and m = 100 - k be the number of non-one numbers. The equation becomes: [ k + sum_{i=1}^{m} a_i = prod_{i=1}^{m} a_i ] This simplifies to: [ prod_{i=1}^{m} a_i - sum_{i=1}^{m} a_i = k = 100 - m ]3. Finding m and Non-One Numbers: We need to find m and non-one numbers (a_i) such that the product minus the sum equals (100 - m). After testing various combinations, we find that using a combination of 2s and 3s works best.4. Optimal Combination: For m = 5, using three 3s and two 2s: - Product: (3^3 times 2^2 = 27 times 4 = 108) - Sum: (3 + 3 + 3 + 2 + 2 = 13) - Product - Sum = (108 - 13 = 95) - This satisfies the equation (108 - 13 = 95 = 100 - 5)Thus, the smallest number of ones required is 95, with 5 non-one numbers (three 3s and two 2s).[boxed{95}],<think>Okay, so I need to figure out the smallest number of ones in a pretty list of 100 numbers. A pretty list is one where all the numbers are strictly positive integers, and their sum equals their product. Hmm, let's start by understanding the problem better.First, let me recall that in a list of numbers where the product equals the sum, having ones is probably going to be important because multiplying by one doesn't change the product, but adding one does increase the sum. So maybe replacing some ones with higher numbers can help balance the sum and product?Let me think of smaller cases first. For example, if there are two numbers. Suppose we have numbers a and b. Then we need a + b = a * b. Rearranging, we get ab - a - b = 0, which can be written as (a - 1)(b - 1) = 1. Since a and b are positive integers, the solutions are a=2 and b=2. So the only two-number pretty list is [2,2]. Here, there are zero ones.But for larger lists, maybe we can have more flexibility. Let me think about three numbers. Suppose we have three numbers a, b, c. Then a + b + c = a * b * c. Let's see. If all three numbers are 1, the sum is 3 and the product is 1, which isn't equal. If two are 1 and one is 3, sum is 1 + 1 + 3 = 5, product is 3. Not equal. If two are 2 and one is 1: sum is 2 + 2 + 1 = 5, product is 4. Still not equal. Wait, how about [1,1,2,4] for four numbers? Let's check: sum is 1+1+2+4=8, product is 1*1*2*4=8. Yes, that works. So here, we have two ones. Maybe the more numbers we have, the more ones we can include?But the problem here is to find a list of 100 numbers, and we need the minimal number of ones in such a list. So we want as few ones as possible. So maybe we need to find a balance where the product and sum are equal, using as few ones as possible. Let me formalize this.Let me denote the list as consisting of k ones and (100 - k) other numbers greater than 1. Let's denote the non-one numbers as x_1, x_2, ..., x_{100 - k}, where each x_i >= 2. Then the sum S of the list is k*1 + sum_{i=1}^{100 - k} x_i = k + sum x_i. The product P of the list is 1^k * product x_i = product x_i. For the list to be pretty, S = P. So we need k + sum x_i = product x_i.Therefore, the problem reduces to finding the minimal k (number of ones) such that there exist (100 - k) integers x_i >= 2 satisfying sum x_i + k = product x_i.Our goal is to minimize k, which would correspond to maximizing the number of non-ones, but these non-ones must be at least 2 and satisfy the equation sum x_i + k = product x_i.Alternatively, since k = 100 - (number of non-ones), but here the non-ones are (100 - k) numbers. So actually, k is the number of ones, and (100 - k) is the number of non-ones. So we need to find the minimal k such that there exist (100 - k) numbers >=2 with sum x_i + k = product x_i.Alternatively, rearranged, product x_i - sum x_i = k. So the difference between the product and the sum of the non-ones is equal to the number of ones. Therefore, if we can maximize (product x_i - sum x_i) with as few non-ones as possible (thereby minimizing k), but product x_i - sum x_i has to equal k, which is the number of ones. Wait, but since k = 100 - (number of non-ones), then (number of non-ones) = 100 - k. Therefore, we have product x_i - sum x_i = k, and (number of x_i) = 100 - k. So:Let n = number of non-ones = 100 - k.Then, product x_i - sum x_i = k = 100 - n.Therefore, product x_i - sum x_i = 100 - n.But n is the number of non-ones. So, for each n, we can check if there's a set of n numbers >=2 such that product x_i - sum x_i = 100 - n. So the problem becomes: find the minimal k = 100 - n, where n is the number of non-ones (so n >=1) such that there exists a list of n numbers >=2 where product x_i - sum x_i = 100 - n.So the goal is to find the maximum n (so minimal k) such that for some n numbers >=2, product x_i - sum x_i = 100 - n.So to rephrase, find the maximum n where 100 - n can be written as product x_i - sum x_i for some x_i >=2.We need to maximize n (since k = 100 - n), so as to minimize k. So the higher the n, the lower the k. Therefore, we need the maximum possible n such that there exists a list of n numbers >=2 with product - sum = 100 - n.Alternatively, product - sum + n = 100. So product - (sum - n) = 100. But sum - n is the sum of (x_i -1). Because sum x_i - n = sum (x_i -1). So product x_i - sum (x_i -1) = 100.Hmm, maybe this is helpful. Let me denote y_i = x_i -1, so y_i >=1. Then product (y_i +1) - sum y_i = 100.So we need integers y_i >=1 such that product (y_i +1) - sum y_i = 100.We need to find the maximum n (number of y_i's) such that this equation holds, since n = number of non-ones, and we need to maximize n to minimize k.So the problem becomes: find the maximum n for which there exist n numbers y_i >=1 such that product_{i=1}^n (y_i +1) - sum_{i=1}^n y_i = 100.Alternatively, product_{i=1}^n (y_i +1) = 100 + sum_{i=1}^n y_i.Our goal is to find the maximum n (as large as possible) such that this equation can be satisfied with y_i >=1. Because n is the number of non-ones, so maximizing n would minimize k = 100 -n, which is the number of ones.So how can we approach this?Let me think about small n first. If n=1: then product (y_1 +1) = 100 + y_1. So (y1 +1) = 100 + y1, which implies 1 = 100. Not possible.n=2: product (y1+1)(y2+1) = 100 + y1 + y2.We need to find integers y1, y2 >=1 such that (y1+1)(y2+1) = 100 + y1 + y2 +1 (since sum y_i = y1 + y2). Wait, let's check:Wait, left side is (y1 +1)(y2 +1) = y1 y2 + y1 + y2 +1. Right side is 100 + y1 + y2. Therefore, equate:y1 y2 + y1 + y2 +1 = 100 + y1 + y2 => y1 y2 +1 = 100 => y1 y2 = 99.So we need two integers y1, y2 >=1 such that y1 y2 =99. The possible pairs (y1, y2) are (1,99), (3,33), (9,11). So possible (y1 +1, y2 +1) would be (2,100), (4,34), (10,12). So the corresponding x_i would be 2 and 100, 4 and 34, or 10 and 12. So yes, for n=2, possible. So n=2 is possible, which would correspond to k=100 -2=98. But we need to check if higher n is possible.Let's try n=3. For n=3, the equation becomes (y1 +1)(y2 +1)(y3 +1) = 100 + y1 + y2 + y3.Since all y_i >=1, let's try small y_i's. Let's try y1=y2=y3=1. Then left side is 2*2*2=8, right side is 100 +3=103. Not equal. If y1=1, y2=1, y3=2: left side is 2*2*3=12, right side=100 +1+1+2=104. Still way off.Alternatively, maybe some larger y_i's. Let's think. Let me set variables: Let a = y1 +1, b = y2 +1, c = y3 +1. Then a,b,c >=2. Then we need abc = 100 + (a-1)+(b-1)+(c-1) = 100 + a + b + c -3 = 97 + a + b + c.So abc - a - b - c =97.So we need integers a,b,c >=2 such that abc -a -b -c=97.Hmm, this seems difficult. Let me try some possible values. Let's fix a=2. Then equation becomes 2bc -2 -b -c=97 => 2bc -b -c=99. Let me rearrange: (2b -1)(2c -1) = 199. Hmm, but 199 is prime. So 2b -1 and 2c -1 must be 1 and 199. Then b=1, c=100, but a=2, so original variables y_i =a-1=1, which is allowed? Wait, y1 =a-1=1, y2=b-1=0, which is invalid since y_i >=1. So no solution here.Alternatively, a=3. Then equation becomes 3bc -3 -b -c =97 =>3bc -b -c=100. Let me factor this equation. Let's write it as (3b -1)(3c -1) = 301. Since 301=7*43. Then 3b -1=7, 3c -1=43 => b=8/3, which is not integer. Similarly, 3b -1=43, 3c -1=7 => b=44/3, not integer. So no solution here.Trying a=4: 4bc -4 -b -c=97 =>4bc -b -c=101. Maybe factor similarly. Let's write 4bc -b -c=101. Let's add 1 to both sides: 4bc -b -c +1=102. Then (4b -1)(4c -1)= 4*4bc -4b -4c +1=16bc -4b -4c +1. Hmm, not sure. Alternatively, maybe rearrange:4bc -b -c =101Let me factor:b(4c -1) -c =101b(4c -1) = c +101So b = (c +101)/(4c -1)We need this to be integer. Let's try c=2:b=(2 +101)/(8 -1)=103/7≈14.71 not integer.c=3:b=(3 +101)/(12 -1)=104/11≈9.45 not integer.c=4:(4 +101)/(16 -1)=105/15=7. So b=7. Then check if a=4, b=7, c=4. So original variables:a=4 => y1=3b=7 => y2=6c=4 => y3=3Check the original equation: product (y1+1)(y2+1)(y3+1) =4*7*4=112Sum y1 + y2 + y3=3+6+3=12Then product - sum =112 -12=100. Which matches the required 100. Wait, but n=3. So product - sum=100, which is 100=100. So yes, that works. So for n=3, we have a solution. So k=100 -3=97. So this would require 97 ones and 3 non-ones (4,7,4). Let me verify:Original numbers (x_i) are 4,7,4. Then the list would be 97 ones and these three numbers. Sum is 97*1 +4 +7 +4=97+15=112. Product is 1^97 *4*7*4=1*112=112. Yes, sum=product=112. So n=3 works with k=97.Is there a higher n? Let's check n=4.For n=4, we need product (y1 +1)(y2 +1)(y3 +1)(y4 +1) =100 + y1 + y2 + y3 + y4.Again, converting to a,b,c,d:a*b*c*d = 100 + (a-1)+(b-1)+(c-1)+(d-1)=100 +a+b+c+d -4=96 +a +b +c +d.So, the equation becomes a*b*c*d -a -b -c -d=96, where a,b,c,d >=2.This seems even more complex, but maybe trying small numbers. Let's try a=2, b=2, c=2, d=2. Then product is 16, sum of a+b+c+d=8. 16 -8=8 ≠96. Too small.If we try three 2s and one larger number. Let a=2,b=2,c=2,d=x. Then equation becomes 8x -2 -2 -2 -x=96 =>7x -6=96 =>7x=102 =>x≈14.57. Not integer. So x=15, then check 8*15 -6=120-6=114≠96. Not working.How about two 2s and two variables. Let a=2,b=2,c=x,d=y. Then equation becomes 4xy -2 -2 -x -y=96 =>4xy -x -y=100.Hmm, similar to previous equations. Let's rearrange: 4xy -x -y=100. Let's add 1 to both sides: 4xy -x -y +1=101. Then (4x -1)(4y -1)=4*4xy -4x -4y +1=16xy -4x -4y +1. Wait, maybe not. Alternatively, factor:Let me try to write 4xy -x -y=100. Let's factor:x(4y -1) - y=100 => x=(100 + y)/(4y -1). Need x to be integer >=2.Let's try y=2: x=(100 +2)/(8 -1)=102/7≈14.57. Not integer.y=3: (100 +3)/(12 -1)=103/11≈9.36. Not integer.y=4: (100 +4)/(16 -1)=104/15≈6.93. Not integer.y=5: (100 +5)/(20 -1)=105/19≈5.526. Not integer.y=6: (100 +6)/(24 -1)=106/23≈4.6. Not integer.y=7: (100 +7)/(28 -1)=107/27≈3.96. Not integer.y=8: (100 +8)/(32 -1)=108/31≈3.48. Not integer.y=9: (100 +9)/(36 -1)=109/35≈3.11. Not integer.y=10: (100 +10)/(40 -1)=110/39≈2.82. Not integer.y=13: (100 +13)/(52 -1)=113/51≈2.21. Not integer.y=25: (100 +25)/(100 -1)=125/99≈1.26. Not integer.Hmm, not working. Maybe trying a different approach. Let's pick x=3. Then 4*3*y -3 -y=100 =>12y -3 -y=100 =>11y=103 => y≈9.36. Not integer.x=4: 16y -4 -y=100 =>15y=104 =>y≈6.93.x=5: 20y -5 -y=100 =>19y=105 =>y≈5.526.x=6:24y -6 -y=100 =>23y=106 =>y≈4.6.x=7:28y -7 -y=100 =>27y=107 =>y≈3.96.x=8:32y -8 -y=100 =>31y=108 =>y≈3.48.x=9:36y -9 -y=100 =>35y=109 =>y≈3.11.x=10:40y -10 -y=100 =>39y=110 =>y≈2.82.None of these give integer y. So maybe two 2s and two variables doesn't work. Let's try three variables. Maybe a=2, b=3, c=x, d=y.Then equation becomes 6xy -2 -3 -x -y=96 =>6xy -x -y=101. Hmm, similar difficulty. Perhaps this approach is not working. Maybe trying a different set.Alternatively, maybe a=3,b=3,c=3,d=x. Then product is 27x, sum is 9 +x. Equation:27x -3 -3 -3 -x=96 =>26x -9=96 =>26x=105 =>x=105/26≈4.038. Not integer.Alternatively, a=2,b=3,c=4,d=x. Product=24x, sum=2+3+4+x=9+x. Equation:24x -2 -3 -4 -x=96 =>23x -9=96 =>23x=105 =>x=105/23≈4.56. Not integer.Alternatively, a=2,b=2,c=3,d=x. Product=12x, sum=2+2+3+x=7+x. Equation:12x -2 -2 -3 -x=96 =>11x -7=96 =>11x=103 =>x≈9.36. Not integer.Alternatively, trying a=2,b=2,c=4,d=x. Product=16x, sum=2+2+4+x=8+x. Equation:16x -2 -2 -4 -x=96 =>15x -8=96 =>15x=104 =>x≈6.93. Not integer.Hmm, maybe n=4 is not possible? Let's try another approach. Maybe use more ones? Wait, no, n is the number of non-ones. So for n=4, we need four numbers greater or equal to 2. Maybe try numbers like 2,2,2,24. Let's check:x1=2, x2=2, x3=2, x4=24. Then product=2*2*2*24=192. Sum=2+2+2+24=30. Then product - sum=192-30=162. We need product - sum=100 - n=100 -4=96. 162≠96. Not good.Alternatively, x1=2,2,3, something. Let's compute product - sum=96. So product= sum +96. Let's suppose numbers 2,2,3,x. Then sum=7 +x, product=12x. So 12x =7 +x +96 =>12x=103 +x =>11x=103 =>x≈9.36. Not integer.Alternatively, 2,3,3,x. Sum=8 +x, product=18x. So 18x=8 +x +96 =>17x=104 =>x≈6.117. Not integer.Alternatively, 3,3,3,x. Sum=9 +x, product=27x. So 27x=9 +x +96 =>26x=105 =>x≈4.038. Not integer.Alternatively, 2,2,4,x. Sum=8 +x, product=16x. So 16x=8 +x +96 =>15x=104 =>x≈6.933. Not integer.Hmm, maybe trying different combinations. Let's try two 2s and two 5s. Sum=2+2+5+5=14. Product=2*2*5*5=100. product - sum=100 -14=86. Which is less than 96. So not enough. How about two 2s, one 5, one 6. Sum=2+2+5+6=15. Product=2*2*5*6=120. product - sum=120-15=105. Which is more than 96. Maybe reduce one number. Replace 6 with 5: sum=14, product=100. Still 86. Replace one 2 with 3: sum=3+2+5+6=16, product=3*2*5*6=180. 180-16=164>96. Not helpful.Alternatively, three 3s and one x. Sum=9 +x, product=27x. 27x -9 -x=96 =>26x=105 =>x≈4.038. No.Alternatively, 3,3,4,x. Sum=10 +x, product=36x. 36x -10 -x=96 =>35x=106 =>x≈3.028.Not integer.Alternatively, 2,3,4,x. Sum=9 +x, product=24x. 24x -9 -x=96 =>23x=105 =>x≈4.565.Nope.Alternatively, 2,4,4,x. Sum=10 +x, product=32x. 32x -10 -x=96 =>31x=106 =>x≈3.419.Hmm, not working.Alternatively, maybe a larger number. Let's try with one number being 96. If n=4, numbers 2,2,2,96. Then product=2*2*2*96=768. Sum=2+2+2+96=102. Product - sum=768-102=666≠96-4=92. No, not close.Wait, this seems tough. Maybe n=4 is not possible. Let's check n=5.Wait, before moving to higher n, maybe there's a different approach. Since we have product - sum =100 -n, and we need to maximize n. Let me think of how product and sum relate. For numbers greater than 1, the product grows much faster than the sum. So to have product - sum equal to 100 -n, which increases as n increases (since 100 -n decreases). Wait, wait. Wait, for larger n, 100 -n decreases, so product - sum must be smaller. But as n increases, since we have more numbers, each at least 2, the product will be larger, but sum also larger. The difference product - sum might vary.But if we have more numbers, even though each is small, their product might be large. Wait, but for example, if all numbers are 2, then product is 2^n, sum is 2n. So product - sum =2^n -2n. For n=3, 8 -6=2. For n=4, 16 -8=8. For n=5, 32 -10=22. For n=6,64 -12=52. For n=7,128 -14=114. So for n=7, product - sum=114, which is greater than 100 -7=93. So 114>93. So 2,2,2,2,2,2,2: product - sum=114. But we need product - sum=100 -n=93. So 114>93, which is too big. If we replace some 2s with ones? Wait, no, we can't use ones in the non-ones. Wait, the non-ones have to be at least 2. Wait, but in this case, all non-ones are 2. So maybe if we can reduce some of the 2s to lower the product. Wait, but they can't be lower than 2. Alternatively, maybe replace some 2s with 3s? Let's see.Suppose we have n=7 numbers. If we have six 2s and one 3. Then product=2^6*3=64*3=192. Sum=6*2 +3=15. product - sum=192 -15=177. Which is even bigger. So that's worse.Alternatively, replace a 2 with a 1. But non-ones can't be 1. So maybe replace some 2s with higher numbers? Wait, but higher numbers would increase the product more. Hmm. Alternatively, maybe instead of all 2s, include a 4. So six 2s and one 4. Product=2^6*4=256. Sum=6*2 +4=16. product - sum=240. Still way higher.Alternatively, maybe replace multiple 2s with higher numbers. For example, five 2s and two 3s. Product=2^5*3^2=32*9=288. Sum=5*2 +2*3=10 +6=16. product - sum=272. Still too high.Wait, this approach isn't working. Maybe for higher n, the product - sum is too big. So perhaps n=7 gives product - sum=114 (all 2s), which is larger than 100 -7=93. So maybe if we can decrease the product. But we can't have numbers less than 2. So perhaps instead of 2s, use a combination of 2s and 3s to get the product - sum closer to 100 -n.Wait, for n=7, target is 93. If we have all 2s: product - sum=114. Need to reduce by 21. How can we do that? Replacing a 2 with a 1 is not allowed. Wait, but maybe replacing a 2 with a larger number? Wait, replacing a 2 with a 3 would increase product by 3/2, and increase sum by 1. So product - sum would increase by (3/2)*product_rest -1. Hmm, not straightforward.Alternatively, replacing a 2 with a 4: product becomes product_rest *4 instead of product_rest*2. So product increases by product_rest*2. Sum increases by 2. So product - sum increases by 2*product_rest -2. For example, if we have seven 2s: product_rest=2^6=64. If we replace one 2 with a 4: product becomes 64*4=256, sum becomes 12 +4=16. product - sum=256 -16=240. Which is way higher. So that's not helpful.Alternatively, maybe split one 2 into two 2s and a 1? Wait, no, the non-ones can't be 1. Wait, perhaps split a number into smaller numbers. Wait, but since we need to fix n. Wait, maybe this line of thinking isn't useful.Alternatively, maybe for n=7, it's impossible to get product - sum=93. So perhaps n=3 is the maximum possible? But earlier, for n=3, we had a solution with k=97. Then for n=4, is there a solution? Let me think again.Wait, for n=4, we need product - sum=96. Let's think of numbers such that product - sum=96. Let's try numbers 3,3,3,3. Product=81, sum=12, 81-12=69. Not enough. 3,3,3,4: product=108, sum=13, 108-13=95. Close. 3,3,3,5: product=135, sum=14, 135-14=121. Too much. 3,3,4,4: product=144, sum=14, 144-14=130. Hmm. 3,3,3,4 gives 95, which is 1 less than needed. Maybe adjust one number. 3,3,3,4 and add 1 to one of the numbers. 3,3,4,4: product=144, sum=14, 144-14=130. Too much. Alternatively, 3,3,3,5: product=135, sum=14, difference=121.Alternatively, 2,3,3,5: product=90, sum=13, 90-13=77. Not enough. 2,4,4,4: product=128, sum=14, difference=114. Still not 96. 2,2,5,5: product=100, sum=14, difference=86. 2,3,4,5: product=120, sum=14, difference=106. Hmm, 106 is more than 96. Maybe reduce some numbers. 2,3,3,5: product=90, sum=13, difference=77. No. 2,3,4,4: product=96, sum=13, difference=83. 2,4,4,5: product=160, sum=15, difference=145. No. 3,3,4,5: product=180, sum=15, difference=165. No.Wait, maybe 2,2,2,24. Product=2*2*2*24=192. Sum=2+2+2+24=30. Difference=162. Too much. 2,2,3,12: product=2*2*3*12=144, sum=2+2+3+12=19. Difference=125. 2,2,4,8: product=128, sum=16, difference=112. Still too much. 2,2,5,5: product=100, sum=14, difference=86. 2,3,3,6: product=108, sum=14, difference=94. Close. 2,3,3,6 gives difference=108 -14=94. Need 96. If we can adjust one number. Replace 6 with 7: product=2*3*3*7=126, sum=2+3+3+7=15. Difference=126 -15=111. No. Replace 3 with 4: 2,3,4,6. Product=144, sum=15, difference=129. No. Alternatively, 2,3,4,5: difference=120 -14=106. Still not. 2,4,4,4:128 -14=114. 3,3,3,4:108 -13=95. So close. If we can get 95 or 96. 95 is just 1 less. Maybe there's no solution for n=4.Alternatively, perhaps 3,3,3,3, and then we have n=5? Wait, but n=4. Alternatively, is there a combination that gives 96? Let me think. 3,3,4, something. Let's see. Suppose we have 3,3,4,x. Product=3*3*4*x=36x. Sum=3+3+4+x=10 +x. product - sum=36x -10 -x=35x -10. We need this to be 96. So 35x=106 =>x=106/35≈3.028. Not integer. Close. If x=3: 35*3 -10=95. Which is close to 96. But not exactly. So 3,3,4,3 gives difference=95. If we set x=4: 35*4 -10=130. Not helpful.Alternatively, 2,3,4,x. Product=24x, sum=9 +x. Difference=24x -9 -x=23x -9=96 =>23x=105 =>x≈4.565. Not integer.Alternatively, 2,2,6,x. Product=24x, sum=10 +x. Difference=24x -10 -x=23x -10=96 =>23x=106 =>x≈4.608. Not integer.Alternatively, 3,3,2,x. Product=18x, sum=8 +x. Difference=18x -8 -x=17x -8=96 =>17x=104 =>x≈6.117. Not integer.Alternatively, 5,2,2,x. Product=20x, sum=9 +x. Difference=20x -9 -x=19x -9=96 =>19x=105 =>x≈5.526. Not integer.Hmm, seems like n=4 is not possible. Let me try n=5.For n=5, product - sum=100 -5=95.So need five numbers >=2 such that product - sum=95.Again, converting to y_i =x_i -1, so product (y_i +1) - sum y_i=95.But maybe directly working with x_i. Let's think.Trying all 2s: product=32, sum=10, 32-10=22. Need 95. Too low.Replacing some 2s with 3s. Let's try four 2s and one 3. Product=16*3=48, sum=8+3=11, 48-11=37.Three 2s and two 3s: product=8*9=72, sum=6 +6=12, 72 -12=60.Two 2s and three 3s: product=4*27=108, sum=4 +9=13, 108-13=95. Hey, that works! So two 2s and three 3s. Let's check:Numbers: 2,2,3,3,3. Product=2*2*3*3*3=108. Sum=2+2+3+3+3=13. 108 -13=95. Yes! So product - sum=95=100 -n=100 -5=95. Perfect. Therefore, for n=5, this works. So k=100 -5=95. So we can have 95 ones and five numbers:2,2,3,3,3. Then the total sum would be 95*1 +2+2+3+3+3=95+13=108. Product would be 1^95 *108=108. So sum=product=108. This works. Therefore, n=5 is possible with k=95.Wait, so n=5 is possible. Then maybe higher n is possible? Let's check n=6.For n=6, we need product - sum=100 -6=94.Again, trying with as many 2s as possible. Let's try five 2s and one 3. Product=32*3=96, sum=10 +3=13. 96 -13=83. Not enough.Four 2s and two 3s: product=16*9=144, sum=8 +6=14. 144 -14=130. Too much.Three 2s and three 3s: product=8*27=216, sum=6 +9=15. 216 -15=201. Way too much.Two 2s and four 3s: product=4*81=324, sum=4 +12=16. 324 -16=308. No.Alternatively, maybe introducing a 4. Let's try four 2s, one 3, one 4. Product=16*3*4=192, sum=8 +3 +4=15. 192 -15=177. Too much.Three 2s, two 3s, one 4: product=8*9*4=288, sum=6 +6 +4=16. 288 -16=272. Too much.Maybe using more smaller numbers. Let's try all 2s except one 4. Five 2s and one 4: product=32*4=128, sum=10 +4=14. 128 -14=114. Still more than 94.Four 2s and two 4s: product=16*16=256, sum=8 +8=16. 256 -16=240. Too much.Alternatively, three 2s, one 3, one 4, one x. Let's see:Product=2*2*2*3*4*x=48x. Sum=2+2+2+3+4+x=13 +x. product - sum=48x -13 -x=47x -13=94. So 47x=107 =>x≈2.276. Not integer. Close. x=2: 47*2 -13=94 -13=81. Not enough. x=3:47*3 -13=141 -13=128. Too much.Alternatively, five 2s and one 5: product=32*5=160, sum=10 +5=15. 160 -15=145. No.Alternatively, six 3s: product=729, sum=18. 729-18=711. Way too much.Alternatively, four 2s and two 5s: product=16*25=400, sum=8 +10=18. 400-18=382. Nope.Alternatively, two 2s, two 3s, one 5, one x. Wait, n=6. So let's see. Wait, no, n=6, so six non-ones. Let's try two 2s, three 3s, and one x. Product=2*2*3*3*3*x=108x. Sum=2+2+3+3+3+x=13 +x. product - sum=108x -13 -x=107x -13=94. So 107x=107 =>x=1. But x>=2. Not allowed. If x=2:107*2 -13=214 -13=201≠94.Alternatively, three 2s, two 3s, one x. Product=2*2*2*3*3*x=72x. Sum=2+2+2+3+3+x=12 +x. 72x -12 -x=71x -12=94. 71x=106 =>x≈1.49. Not integer.Alternatively, four 2s, one 4, one x. Product=16*4*x=64x. Sum=8 +4 +x=12 +x. 64x -12 -x=63x -12=94. 63x=106 =>x≈1.68. Not integer.Alternatively, two 2s, one 4, one 5, two x. Wait, n=6. So numbers:2,2,4,5,x,x. Product=2*2*4*5*x*x=80x². Sum=2+2+4+5+x+x=13 +2x. Equation:80x² -13 -2x=94 =>80x² -2x -107=0. Solving quadratic: x=(2 ±√(4 + 34240))/160. sqrt(34244)=185.07. So x≈(2 +185.07)/160≈187.07/160≈1.169. Not integer.Alternatively, this seems not promising. Maybe try a different approach. For n=6, maybe a combination like 2,2,2,2,3,3. Product=2^4*3^2=16*9=144. Sum=8 +6=14. 144 -14=130. Need 94. Not close.Alternatively, replace one 3 with a higher number. 2,2,2,2,3,4. Product=2^4*3*4=16*12=192. Sum=8 +3 +4=15. 192 -15=177. Still too high.Alternatively, replace two 2s with 3s. 2,2,3,3,3,3. Product=2^2*3^4=4*81=324. Sum=4 +12=16. 324 -16=308. Nope.Alternatively, include a 5. 2,2,2,3,3,5. Product=2^3*3^2*5=8*9*5=360. Sum=6 +6 +5=17. 360 -17=343. No.Alternatively, maybe use a 6. 2,2,2,2,2,6. Product=64*6=384. Sum=10 +6=16. 384 -16=368. No.Alternatively, trying to get closer. Let's see, the target is 94. Let's think if there's a set of numbers where product - sum=94. For example, 3,3,3,3,3, something. Product=3^5*x=243x. Sum=15 +x. 243x -15 -x=242x -15=94 =>242x=109 =>x≈0.45. Not valid.Alternatively, maybe 4,4,4,4,4, something. Product=4^5*x=1024x. Sum=20 +x. 1024x -20 -x=1023x -20=94 =>1023x=114 =>x≈0.11. No.Alternatively, mixing 2s and 3s. Let's think: if we have k 2s and (6 -k) 3s. Product=2^k *3^{6 -k}. Sum=2k +3(6 -k)=18 -k. product - sum=2^k *3^{6 -k} - (18 -k)=94. Let's check for k=0: product=729, sum=18, 729-18=711≠94. k=1:2*243=486, sum=17, 486-17=469≠94. k=2:4*81=324, sum=16, 324-16=308≠94. k=3:8*27=216, sum=15, 216-15=201≠94. k=4:16*9=144, sum=14, 144-14=130≠94. k=5:32*3=96, sum=13, 96-13=83≠94. k=6:64, sum=12, 64-12=52≠94. Not helpful.Hmm, perhaps n=6 is not possible. Let's check n=5. We already have a solution for n=5. How about n=6? Maybe numbers like 2,2,2,2,2,22. Product=2^5*22=32*22=704. Sum=10 +22=32. 704 -32=672≠94. No. Not helpful.Alternatively, maybe two larger numbers. 2,2,2,2,5,5. Product=16*25=400. Sum=8 +10=18. 400 -18=382≠94. No.Alternatively, 2,2,2,5,5,5. Product=8*125=1000. Sum=6 +15=21. 1000 -21=979. No.Alternatively, 3,3,3,3,3,5. Product=243*5=1215. Sum=15 +5=20. 1215 -20=1195. No.This approach is not working. Maybe n=5 is the maximum possible. Earlier, we saw that for n=5, the solution is possible with numbers 2,2,3,3,3. Let me confirm again. Product=2*2*3*3*3=108. Sum=2+2+3+3+3=13. 108 -13=95. Which is exactly 100 -5=95. Therefore, this works. Then, the corresponding pretty list would be 95 ones and these five numbers, giving total sum=95 +13=108 and product=1^95*108=108. So yes, works.Now, is there a higher n? Let's see n=6. Is there a way to have six numbers with product - sum=94? If we can find such numbers, then n=6 is possible. Let me try another combination. Suppose we have five 2s and one 4. Product=32*4=128. Sum=10 +4=14. 128 -14=114. Not 94. If we have five 2s and one 5: product=32*5=160. Sum=10 +5=15. 160 -15=145. No. Five 2s and one 6:192 -16=176. No.Alternatively, four 2s, one 3, one 4. Product=16*3*4=192. Sum=8 +3 +4=15. 192 -15=177. No.Three 2s, two 3s, one 4: product=8*9*4=288. Sum=6 +6 +4=16. 288 -16=272. No.Three 2s, one 3, two 4s: product=8*3*16=384. Sum=6 +3 +8=17. 384 -17=367. No.Alternatively, two 2s, three 3s, one 4: product=4*27*4=432. Sum=4 +9 +4=17. 432 -17=415. No.Alternatively, maybe including a 5. Two 2s, two 3s, two 5s: product=4*9*25=900. Sum=4 +6 +10=20. 900 -20=880. No.Alternatively, one 2, four 3s, one 4: product=2*81*4=648. Sum=2 +12 +4=18. 648 -18=630. No.Alternatively, all 3s except one 2. Five 3s and one 2: product=243*2=486. Sum=15 +2=17. 486 -17=469. No.Hmm, not working. Maybe another approach. Let's suppose one of the numbers is larger. Let's say we have five 2s and one x. Then product=32x, sum=10 +x. 32x -10 -x=31x -10=94. So 31x=104 =>x≈3.354. Not integer. Close to 3. If x=3: 31*3 -10=83. If x=4:31*4 -10=114. Neither is 94.Alternatively, four 2s and two x's. product=16x^2, sum=8 +2x. 16x² -8 -2x=94 =>16x² -2x -102=0. Solving quadratic: x=(2 ±√(4 + 6528))/32=(2 ±√6532)/32. sqrt(6532)=80.82. So x≈(2 +80.82)/32≈82.82/32≈2.588. Not integer. x≈2.588. Not valid.Alternatively, three 2s and three x's. product=8x³, sum=6 +3x. 8x³ -6 -3x=94 =>8x³ -3x -100=0. Trying integer x=3:8*27 -9 -100=216 -9 -100=107≠0. x=4:8*64 -12 -100=512 -12 -100=400≠0. Not helpful.Alternatively, two 2s and four x's. product=4x⁴, sum=4 +4x. 4x⁴ -4 -4x=94 =>4x⁴ -4x -98=0. Trying x=3:4*81 -12 -98=324 -110=214≠0. x=2:4*16 -8 -98=64 -106=-42≠0. x=4:4*256 -16 -98=1024 -114=910≠0. No.Alternatively, one 2 and five x's. product=2x⁵, sum=2 +5x. 2x⁵ -2 -5x=94 =>2x⁵ -5x -96=0. Trying x=2:64 -10 -96=-42≠0. x=3:486 -15 -96=375≠0. x=4:2048 -20 -96=1932≠0. No.Alternatively, no 2s and six x's. product=x⁶, sum=6x. x⁶ -6x=94. Testing x=3:729 -18=711≠94. x=2:64 -12=52≠94. x=4:4096 -24=4072≠94. Not helpful.So seems like n=6 is not possible. Let's check n=7.Wait, but for n=7, as previously calculated, if all numbers are 2s, product - sum=2^7 -2*7=128 -14=114. Which is 100 -7=93. 114>93. So need to reduce product - sum by 21. How?But we can't use numbers less than 2. So replacing some 2s with higher numbers increases product - sum. For example, replacing a 2 with a 3: product becomes 2^6*3=64*3=192. Sum becomes 13 +3=16. product - sum=192 -16=176. Which is even higher. So no good.Alternatively, replacing a 2 with a 1 is not allowed. So seems like n=7 cannot achieve product - sum=93.Therefore, it seems like the maximum possible n is 5, which gives k=95. But wait, earlier for n=3, we had a solution. And for n=5, a solution with k=95. So why is the maximum n=5?Wait, let me check n=4 again. Earlier attempts didn't find a solution, but maybe there's a non-obvious combination. Let me think differently.For n=4, we need product - sum=96. Let's try numbers 3,3,4,4. Product=3*3*4*4=144. Sum=3+3+4+4=14. 144-14=130≠96.3,3,3,5: product=135, sum=14, difference=121.2,3,4,5: product=120, sum=14, difference=106.2,2,5,5: product=100, sum=14, difference=86.2,4,4,5: product=160, sum=15, difference=145.3,3,2,5: product=90, sum=13, difference=77.3,3,3,3: product=81, sum=12, difference=69.Hmm. Maybe numbers like 2,2,3, 25. Product=2*2*3*25=300. Sum=2+2+3+25=32. 300-32=268. No.Alternatively, 2,2,4,12. Product=2*2*4*12=192. Sum=2+2+4+12=20. 192-20=172. No.Alternatively, 2,2,6,6. Product=2*2*6*6=144. Sum=2+2+6+6=16. 144-16=128. No.Alternatively, 2,3,3,7. Product=2*3*3*7=126. Sum=2+3+3+7=15. 126-15=111.Alternatively, 3,3,3,4: product=108, sum=13, difference=95. Close. If we can adjust to get 96. If we increase one 3 to 4: 3,3,4,4. Difference=144-14=130. No. If we replace a 3 with a 2:2,3,3,4. Product=72, sum=12, difference=60. No.Alternatively, 3,3,3,4. Difference=95. If we need 96, maybe add 1 to one of the numbers, but they have to stay as integers. Maybe split a 3 into 2 and 1, but we can't have ones in the non-ones. So not helpful.Alternatively, if we have 3,3,3,3, difference=81-12=69. Not enough. 3,3,3,4:108-13=95. 3,3,3,5:135-14=121. So no. So n=4 seems impossible.Therefore, the maximum n for which there exists a solution is n=5 with k=95. But wait, earlier we found a solution for n=3 with k=97. Then what about n=4? It seems like no solution. So the next possible is n=5.But wait, let's check another combination for n=4. Maybe including a 6.2,2,3,6. Product=2*2*3*6=72. Sum=2+2+3+6=13. 72 -13=59. Not enough.2,2,4,5. Product=80, sum=13. 80-13=67. No.3,3,2,6. Product=3*3*2*6=108. Sum=3+3+2+6=14. 108-14=94. Close to 96. Still 2 short.3,3,2,7. Product=3*3*2*7=126. Sum=3+3+2+7=15. 126-15=111. No.3,3,3,4:108-13=95. One less. Hmm. If we can get 95, but we need 96. So no.Alternatively, 2,4,5,5. Product=2*4*5*5=200. Sum=2+4+5+5=16. 200-16=184. No.Alternatively, 2,3,5,5. Product=2*3*5*5=150. Sum=2+3+5+5=15. 150-15=135. No.Alternatively, 2,5,5,5. Product=2*5*5*5=250. Sum=2+5+5+5=17. 250-17=233. No.Alternatively, 4,4,4,4. Product=256, sum=16. 256-16=240. No.Alternatively, 3,4,4,4. Product=192, sum=15. 192-15=177. No.Alternatively, 2,3,4,4. Product=96, sum=13. 96-13=83. No.Alternatively, 2,2,7,7. Product=196, sum=18. 196-18=178. No.Hmm, seems like n=4 is impossible.Therefore, the maximum possible n is 5, which gives k=95. But wait, earlier we had n=3 with k=97 and n=5 with k=95. Also, for n=2, k=98. So the minimal k is 95. But wait, let me check for n=6 again. Is there any possible combination?Wait, another approach. Suppose we have one number being 95, and the rest ones. Then sum is 95 +99*1=194. Product is 95*1^99=95. Not equal. So that doesn't work.Alternatively, splitting 95 into smaller numbers. For example, replacing a 1 with a 2 and a 95-1=94. But this seems not helpful.Alternatively, think in terms of the previous equation: product x_i - sum x_i =100 -n. For larger n, the right-hand side is smaller, which might require the product to be not too much larger than the sum. However, with more numbers, the product tends to be much larger. But we saw for n=5, we can have product - sum=95, which works.Is there a higher n, say n=6, with product - sum=94? For example, numbers like 2,2,2,2,2, and 94. Product=2^5*94=32*94=3008. Sum=10 +94=104. 3008 -104=2904≠94. Not working.Alternatively, splitting 94 into smaller numbers. Maybe 2,2,2,2,2, and 94 becomes two numbers. But this approach doesn't help.Alternatively, think of the original problem where we have 100 numbers. To minimize the number of ones, we need as many non-ones as possible. But the non-ones have to be such that their product minus their sum equals 100 -n, where n is their count.Since for n=5, we can achieve this. For n=5, we have product - sum=95=100 -5. So this works. Then, the total number of ones would be 100 -5=95. If we can find a higher n, say n=6, with product - sum=94, then the number of ones would be 94. But since we couldn't find such a combination for n=6, it seems like n=5 is the maximum.Therefore, the minimal number of ones is 95.But wait, let me verify once more with another example. Suppose n=6, can I have numbers like 2,2,2,2,3,3. Product=2^4*3^2=16*9=144. Sum=8 +6=14. 144 -14=130. Which is higher than 94. If we replace some 2s with 1s, but we can't have 1s in the non-ones. So invalid.Alternatively, including a 4: 2,2,2,3,3,4. Product=2^3*3^2*4=8*9*4=288. Sum=6 +6 +4=16. 288 -16=272. Still way higher.Alternatively, include a 5:2,2,2,3,3,5. Product=8*9*5=360. Sum=6 +6 +5=17. 360 -17=343. Still no.Alternatively, use three 3s and three 2s: product=8*27=216. Sum=6 +9=15. 216 -15=201. No.Alternatively, use a 6:2,2,2,2,2,6. Product=64*6=384. Sum=10 +6=16. 384 -16=368. No.It's clear that for n=6, product - sum is way higher than 94. Therefore, n=5 is the maximum possible with the given constraints, leading to k=95.Thus, the minimal number of ones required is 95.Final Answerboxed{95}</think>To determine the smallest number of ones in a pretty list of 100 numbers, we need to find a list of strictly positive integers where the sum equals the product. We aim to minimize the number of ones, which means maximizing the number of non-ones (numbers greater than 1).Given the equation for a pretty list:[ text{Product of non-ones} - text{Sum of non-ones} = 100 - n ]where ( n ) is the number of non-ones, we need to find the maximum ( n ) such that this equation holds.After analyzing various combinations of numbers, we found that:1. For ( n = 3 ), the numbers ( 4, 7, 4 ) work, leading to ( k = 97 ) ones.2. For ( n = 5 ), the numbers ( 2, 2, 3, 3, 3 ) work, leading to ( k = 95 ) ones.Testing higher values of ( n ) (such as 4, 6, 7) did not yield valid solutions. The solution for ( n = 5 ) is valid and provides the minimal number of ones.Thus, the smallest number of ones required in a pretty list of 100 numbers is:[ boxed{95} ]]

🔑:Solution to Exercise 8 The list 1,1, ldots, 1,2,2,3,3,3 is pretty and contains 95 numbers equal to 1. Let's show that we cannot do better.We can assume that the first numbers are a_{1} leqslant a_{2} leqslant cdots leqslant a_{r} with a_{1} geqslant 2 and that the others are equal to 1. We want to show that if a_{1} cdots a_{r}=(100-r)+a_{1}+cdots+a_{r} then r leqslant 5.unit, while the right-hand side decreases by one unit. We deduce that if we replace all a_{j} by 2, then the left-hand side is less than or equal to the right-hand side. Consequently, 2^{r} leqslant 100+r. Since r leqslant 100, we have 2^{r} leqslant 200, so r leqslant 7. We then have 2^{r} leqslant 107, so r leqslant 6. It remains to show that r=6 is impossible.If a_{i} geqslant 3 for all i, then by the same reasoning as above, we have 3^{r} leqslant 100+2 r leqslant 112, so r leqslant 4. Contradiction.We deduce that a_{1}=2, so 2 a_{2} cdots a_{6}=96+a_{2}+cdots+a_{6}. We show similarly that a_{2}=2, then a_{3}=2, then a_{4}=2, so 16 a_{5} a_{6}=102+a_{5}+a_{6}.If a_{5}=2 then 32 a_{6}=104+a_{6}, so a_{6}=frac{104}{31} which is not an integer.If a_{5} geqslant 3 then the same reasoning as above gives 16 times 9 leqslant 102+3+3, which is false.