🧠:[<think>Okay, let's see. There's a single elimination tournament with 16 progamers. Each round, they pair up, play against each other, and the loser gets eliminated. So, each round halves the number of players, right? Starting with 16, then 8, then 4, then 2, and finally 1 champion. So, the tournament will have 4 rounds: round of 16, quarterfinals, semifinals, and the final. That makes sense because each round halves the players, and 16 divided by 2 four times gives 1.Now, the question is about the total length of all the ceremonies. Each time a progamer wins, they have a ceremony. The first ceremony is 10 seconds, and each subsequent ceremony for the same player is 10 seconds longer than the last. So, if a player wins multiple times, their ceremonies get longer each time. We need to calculate the total duration of all these ceremonies throughout the entire tournament.First, let's understand how many wins each player can have. In a single elimination tournament, the maximum number of wins a player can have is equal to the number of rounds they participate in. For example, the champion has to win every round, so they win 4 times (since 16 players require 4 rounds). The runners-up would have 3 wins, the semifinalists who didn't make it to the final would have 2 wins, the quarterfinalists who lost in the quarterfinals have 1 win, and the players who lose in the first round have 0 wins.So, the number of ceremonies each player has is equal to the number of matches they win. The total ceremonies are the sum of all ceremonies by all players, with each player's ceremonies increasing in duration each time they win.Let's structure this step by step.First, determine how many players are eliminated in each round. In a single elimination tournament, each round halves the number of players, so:- Round 1: 16 players → 8 winners (8 matches)- Round 2: 8 players → 4 winners (4 matches)- Round 3: 4 players → 2 winners (2 matches)- Round 4: 2 players → 1 champion (1 match)Total matches: 8 + 4 + 2 + 1 = 15. Which makes sense because in a single elimination tournament with n players, there are n - 1 matches. 16 - 1 = 15. So that's correct.But the problem isn't about counting matches; it's about counting the ceremonies each time a player wins, and each ceremony's duration, which increases per win for each player.So, for each player, the number of ceremonies they have is equal to the number of matches they win. For example, the champion wins 4 matches, so they have 4 ceremonies: the first is 10 seconds, the second 20, third 30, fourth 40. So total for the champion would be 10 + 20 + 30 + 40 = 100 seconds.Similarly, the runner-up (who loses in the final) has 3 wins before losing, so 3 ceremonies: 10 + 20 + 30 = 60 seconds.The two semifinalists who lost in the semifinals each have 2 wins: 10 + 20 = 30 seconds each.The four quarterfinalists who lost in the quarterfinals each have 1 win: 10 seconds each.And the eight players who lost in the first round have 0 ceremonies.So, total duration would be:- 1 champion: 100 seconds- 1 runner-up: 60 seconds- 2 semifinalists: 2 * 30 = 60 seconds- 4 quarterfinalists: 4 * 10 = 40 seconds- 8 first-round losers: 0Adding those up: 100 + 60 + 60 + 40 = 260 seconds.Wait, but let me check this again. Let me recount the numbers.Champion: 4 wins. Ceremonies: 10 + 20 + 30 + 40 = 100 seconds. Correct.Runner-up: 3 wins. Ceremonies: 10 + 20 + 30 = 60 seconds. Correct.Semifinalists: There are 2 players who lost in the semifinals. Each of them had to win 2 matches (Round 1 and Round 2) to reach the semifinals, but lost in the semifinals. So each has 2 wins. So each has ceremonies: 10 + 20 = 30 seconds. 2 players: 60. Correct.Quarterfinalists: 4 players who lost in the quarterfinals. They won 1 match (Round 1) and lost in Round 2. So 1 ceremony each: 10 seconds. 4 players: 40. Correct.First-round losers: 8 players, 0 ceremonies. So total ceremonies duration: 100 + 60 + 60 + 40 = 260 seconds.But wait, hold on. Let me think again. Is the runner-up considered to have 3 wins? Because in the first round, they win, second round, third round, and then lose in the final. So yes, they have 3 wins. Similarly, the semifinalists have 2 wins (they won in Round 1 and Round 2, lost in Round 3). The quarterfinalists won Round 1 and lost Round 2. Wait, no. Wait, in the first tournament structure:Wait, Round 1 is 16 players, 8 matches. Winners go to Round 2 (quarterfinals). Then Round 2 is 8 players, 4 matches. Winners go to Round 3 (semifinals). Then Round 3 is 4 players, 2 matches. Winners go to Round 4 (final). So, the quarterfinals is Round 2, semifinals is Round 3, final is Round 4.Therefore, players who lose in the quarterfinals (Round 2) have 1 win (from Round 1). Players who lose in the semifinals (Round 3) have 2 wins (Round 1 and Round 2). Players who lose in the final (Round 4) have 3 wins (Round 1, 2, 3). The champion has 4 wins (all four rounds).Therefore, the calculation above is correct.Therefore, total ceremonies:- 1 player with 4 wins: 10 + 20 + 30 + 40 = 100- 1 player with 3 wins: 10 + 20 + 30 = 60- 2 players with 2 wins each: 2 * (10 + 20) = 60- 4 players with 1 win each: 4 * 10 = 40- 8 players with 0: 0Total: 100 + 60 + 60 + 40 = 260.Hmm, but the answer seems 260 seconds, but let me verify another way.Alternatively, instead of calculating per player, perhaps think of each match as contributing a ceremony. Since each match has a winner, each match corresponds to one ceremony. But the ceremonies are not all 10 seconds; the duration depends on how many previous ceremonies the player has had.Wait, so each time a player wins, it's their nth ceremony, which is 10n seconds. So, for each player, the total duration is the sum from k=1 to m of 10k, where m is the number of matches they won.Therefore, the total duration is the sum over all players of the sum_{k=1}^{m_i} 10k, where m_i is the number of wins for player i.Alternatively, since each match has exactly one ceremony, but the duration of the ceremony depends on the number of previous wins by the winner. So, for example, the first time a player wins, it's 10 seconds, the second time 20, etc.Therefore, the total duration is the sum over all matches of 10 times the number of previous wins by the winner of that match plus one (since the first ceremony is 10, which is 10*1). Wait, but each ceremony is 10 seconds longer than the last. So, the first ceremony is 10, the second is 20, third 30, etc. Therefore, the k-th ceremony for a player is 10k seconds. Therefore, for each player, if they have m wins, their total ceremony time is 10*(1 + 2 + ... + m) = 10 * m(m + 1)/2.So, perhaps another way: for each player, compute 10*(m(m + 1)/2) where m is the number of wins, then sum over all players.So, let's recast our previous calculation:Champion: m = 4, so 10*(4*5)/2 = 10*10 = 100. Correct.Runner-up: m = 3, 10*(3*4)/2 = 10*6 = 60. Correct.Semifinalists: m = 2, 10*(2*3)/2 = 10*3 = 30 each. 2 players: 60. Correct.Quarterfinalists: m = 1, 10*(1*2)/2 = 10*1 = 10 each. 4 players: 40. Correct.Total: 100 + 60 + 60 + 40 = 260. Same as before.Alternatively, perhaps we can think of it as for each win number, how many ceremonies are happening at that duration. For example, how many players have their first win (10 seconds), second win (20 seconds), third win (30 seconds), fourth win (40 seconds). Then total duration would be 10*(number of first wins) + 20*(number of second wins) + 30*(number of third wins) + 40*(number of fourth wins).So, how many first wins are there? Each player who has at least one win has one first win. The number of players who have at least one win is the number of players who didn't lose in the first round. There are 8 first-round winners, so 8 first wins. Wait, but actually, each player who has any ceremonies must have at least one win, so the number of first ceremonies is equal to the number of players who have at least one win. Let's see:In the tournament:- 16 players start.- 8 lose in the first round (0 wins), 8 proceed.- 4 lose in the second round (1 win each), 4 proceed.- 2 lose in the third round (2 wins each), 2 proceed.- 1 loses in the fourth round (3 wins), 1 becomes champion (4 wins).Therefore, the number of players with at least one win is 8 (from first round) + 4 (second round) + 2 (third round) + 1 (fourth round) + 1 (champion) = Wait, no. Wait, actually, the 8 first-round winners include those who proceed to the second round. Then in the second round, 4 win and 4 lose. Then third round, 2 win and 2 lose. Fourth round, 1 wins and 1 loses. So total players with at least one win:- Champion: 4 wins- Runner-up: 3 wins- 2 semifinalists: 2 wins each- 4 quarterfinalists: 1 win eachTotal players with at least one win: 1 + 1 + 2 + 4 = 8 players. Wait, but there are 16 players, 8 lose immediately, so 8 have at least one win. Then of those 8, 4 lose in the second round (so 4 with 1 win), 4 proceed. Of those 4, 2 lose in third round (2 with 2 wins), 2 proceed. Of those 2, 1 loses in the final (3 wins), 1 becomes champion (4 wins). So indeed, the players with at least one win are:- 4 players with 1 win (lost in second round)- 2 players with 2 wins (lost in third round)- 1 player with 3 wins (lost in fourth round)- 1 player with 4 wins (champion)Total: 4 + 2 + 1 + 1 = 8 players. So, total number of first ceremonies is 8, each 10 seconds. Second ceremonies: each player who has at least two wins. That is, the champion, runner-up, semifinalists. Let's see:Players with at least two wins:- 1 champion (4 wins)- 1 runner-up (3 wins)- 2 semifinalists (2 wins)Total: 1 + 1 + 2 = 4 players. So, 4 second ceremonies, each 20 seconds.Third ceremonies: players with at least three wins.- Champion (4 wins)- Runner-up (3 wins)Total: 2 players. So, 2 third ceremonies, each 30 seconds.Fourth ceremonies: only the champion has four wins. So, 1 fourth ceremony, 40 seconds.Therefore, total duration:First ceremonies: 8 * 10 = 80Second ceremonies: 4 * 20 = 80Third ceremonies: 2 * 30 = 60Fourth ceremony: 1 * 40 = 40Total: 80 + 80 + 60 + 40 = 260 seconds.Same answer. So, this method also gives 260. Therefore, it seems correct.Alternatively, let's verify with another approach.Each match has a ceremony. The total number of ceremonies is equal to the number of matches, which is 15. However, each ceremony's duration depends on how many times the player has already won before.Wait, but each ceremony is 10 seconds longer than the last for each player. So, the first time a player wins, it's 10s, the second time 20s, etc. Therefore, each ceremony's duration is 10 times the number of consecutive wins the player has at that point.Therefore, if we can calculate for each of the 15 matches, the duration of the ceremony. Then sum them up.But to do that, we need to know for each match, how many previous wins the winning player had.But this seems complicated because it requires tracking each player's progress.Alternatively, note that each player's ceremonies are an arithmetic sequence: 10, 20, 30, ..., 10n where n is the number of wins.The total duration per player is the sum of that sequence: 10*(1 + 2 + ... + m) where m is their number of wins. Which is 10*(m(m + 1)/2). Therefore, if we can compute the sum over all players of 10*(m(m + 1)/2), where m is the number of wins for each player, that gives the total duration.From the tournament structure:- 1 player has 4 wins: sum contribution is 10*(4*5)/2 = 100- 1 player has 3 wins: 10*(3*4)/2 = 60- 2 players have 2 wins: 2*10*(2*3)/2 = 2*30 = 60- 4 players have 1 win: 4*10*(1*2)/2 = 4*10 = 40- 8 players have 0: 0Total: 100 + 60 + 60 + 40 = 260.Same result. So, this seems consistent.Alternatively, perhaps think in terms of the total number of ceremonies per 'win level':- First wins: 8 players, each contributing 10s: 8*10=80- Second wins: players who won at least two matches: champion, runner-up, semifinalists. That's 1 +1 +2=4 players. Each contributes 20s: 4*20=80- Third wins: players who won at least three matches: champion and runner-up. 2 players. 30s each: 2*30=60- Fourth wins: champion only. 40s: 1*40=40Total: 80+80+60+40=260.Therefore, same answer. So, this seems to confirm it.Therefore, the total length of all ceremonies is 260 seconds. So, I think that's the answer. But wait, let me check once again to ensure no miscalculations.Wait, let's think of each round's ceremonies and their durations.Round 1: 8 matches. Each winner is a first-time winner (since it's the first round). So, 8 ceremonies each of 10s: 8*10=80.Round 2: 4 matches. The winners of these matches have already won once (in Round 1). So, their ceremonies are their second ceremony, which is 20s each. So, 4*20=80.Round 3: 2 matches. The winners here have already won twice (Round 1 and 2). So, their third ceremony: 30s each. 2*30=60.Round 4: 1 match. The winner has already won three times (Round 1, 2, 3). So, fourth ceremony: 40s. 1*40=40.Adding up these per-round totals: 80 + 80 + 60 + 40 = 260.Yes, that's another way to see it. Each subsequent round's ceremonies are 10s more per previous win. So, Round 1: all first wins, Round 2: all second wins, Round 3: third wins, Round 4: fourth win. Therefore, the total is 80 + 80 + 60 + 40 = 260. Perfect. That's a much simpler way.Therefore, the answer is 260 seconds. Therefore, boxed: boxed{260}Final Answerboxed{260}</think>In a single elimination tournament with 16 progamers, each round halves the number of players until one champion remains. Each time a progamer wins, they have a ceremony whose duration increases by 10 seconds each time. The total length of all ceremonies is calculated as follows:1. Round 1 (16 players): 8 matches, each winner has their first ceremony (10 seconds each). - Total duration: (8 times 10 = 80) seconds.2. Round 2 (8 players): 4 matches, each winner has their second ceremony (20 seconds each). - Total duration: (4 times 20 = 80) seconds.3. Round 3 (4 players): 2 matches, each winner has their third ceremony (30 seconds each). - Total duration: (2 times 30 = 60) seconds.4. Round 4 (2 players): 1 match, the winner (champion) has their fourth ceremony (40 seconds). - Total duration: (1 times 40 = 40) seconds.Summing the durations of all ceremonies:[80 + 80 + 60 + 40 = 260]Thus, the total length in seconds of all the ceremonies over the entire tournament is (boxed{260}).,<think>Okay, let's see. The problem is about a single elimination tournament with 16 progamers. Each round, the remaining players pair up, play against each other, and the loser gets eliminated. Every time a progamer wins, they have a ceremony. The first ceremony is 10 seconds long, and each subsequent ceremony for that player is 10 seconds longer than the last. We need to find the total length of all ceremonies over the entire tournament.Hmm. Let me break this down. First, in a single elimination tournament with 16 players, how many rounds are there? Well, each round halves the number of players, right? So starting with 16, then 8, 4, 2, 1. That's four rounds: quarterfinals, semifinals, finals, and the championship? Wait, no. Wait, 16 players would have 15 matches total, because each match eliminates one player, and you need to eliminate 15 players to have a champion. But the number of rounds is log2(16) = 4. So four rounds. Wait, 16 to 8 is round 1, 8 to 4 is round 2, 4 to 2 is round 3, and 2 to 1 is round 4. So yes, four rounds. Each round halves the number of players.Now, each time a progamer wins, they have a ceremony. The ceremony duration increases by 10 seconds each time. So the first win is 10 seconds, the second win is 20 seconds, third is 30, etc. So each player's ceremonies form an arithmetic sequence where the first term is 10 and the difference is 10. So for a player who wins n times, the total ceremony time is 10 + 20 + 30 + ... + 10n. Which is 10(1 + 2 + 3 + ... +n) = 10*(n(n+1)/2) = 5n(n+1).Therefore, to find the total ceremony time, we need to find for each player, how many times they won, compute 5n(n+1) for each, and sum them all.But since we don't know the specific progression of the tournament (i.e., which players win how many times), we need to model this in general.Wait, but in a single elimination tournament, each player can lose at most once. The winner of the tournament will have won all their matches. So the champion will have 4 wins (since 16 players, 4 rounds). The runner-up (loses in the final) would have 3 wins. The other two semifinalists (who lost in the semifinals) would have 2 wins each. The quarterfinalists (those who lost in quarterfinals) would have 1 win each. And the players who lost in the first round have 0 wins.Wait, let me confirm that structure. So starting with 16 players:Round 1: 16 players, 8 matches. 8 winners proceed.Round 2: 8 players, 4 matches. 4 winners proceed.Round 3: 4 players, 2 matches. 2 winners proceed.Round 4: 2 players, 1 match. 1 champion.So each player's number of wins is equal to how many rounds they survived. The champion wins 4 matches (4 wins). The runner-up wins 3 matches. The two semifinalists (the ones who lost in the semifinals) each have 2 wins. The four quarterfinalists (lost in quarterfinals) each have 1 win. And the eight first-round losers have 0 wins.Therefore, the number of players with 4, 3, 2, 1, 0 wins is 1, 1, 2, 4, 8 respectively.Wait, let's check the counts:- 1 champion (4 wins)- 1 runner-up (3 wins)- 2 semifinalists (2 wins each)- 4 quarterfinalists (1 win each)- 8 first-round losers (0 wins)Total players: 1 + 1 + 2 + 4 + 8 = 16. Yep, that works.So now, for each of these groups, we can calculate the total ceremony time.For the champion: 4 wins. So total ceremony time is 5*4*5 = 5*20 = 100? Wait, wait. Wait, the formula was 5n(n+1). For n=4, 5*4*5=100 seconds.Wait, 10 + 20 + 30 + 40 = 100. Yes. Correct.Runner-up: 3 wins. 10 + 20 + 30 = 60. Using formula: 5*3*4 = 60. Correct.Semifinalists (2 wins each): 10 + 20 = 30. Formula: 5*2*3 = 30. Each.Quarterfinalists (1 win each): 10. Formula: 5*1*2 = 10. Each.First-round losers: 0, so no ceremonies.So total ceremonies:1 champion: 1001 runner-up: 602 semifinalists: 2*30 = 604 quarterfinalists: 4*10 = 40Adding these up: 100 + 60 + 60 + 40 = 260.Wait, so total ceremonies take 260 seconds? Hmm. Is that the answer? Let me check again.Wait, is there a different way to model this? Maybe. Let me see.Alternatively, think of each match: each match produces one winner and one loser. The winner's ceremony time increases each time they win. So the total ceremonies can be calculated by considering for each match, how much time is added by the winner's current ceremony.But that might be complicated because we need to track each player's number of wins up to that point.Alternatively, if we can model the total ceremonies as the sum over all players of their individual ceremony times. Since each player's ceremony times depend on their number of wins, and we already know how many players have how many wins, as above, then summing over each group is the way to go.So using the earlier method: 1*100 + 1*60 + 2*30 + 4*10 = 100 + 60 + 60 + 40 = 260.Alternatively, maybe the answer is 560? Wait, let me check again.Wait, maybe my initial approach is wrong. Let me think again. Wait, in a single elimination tournament, each match is between two players. The loser is eliminated, the winner proceeds. So each match has exactly one ceremony, right? The winner celebrates.But the duration of the ceremony depends on how many times that player has won before. So for example, the first time a player wins, it's 10 seconds. The second time they win (in the next round), it's 20 seconds, etc. So each time a player advances, their next ceremony is 10 seconds longer.Therefore, the total ceremony time is the sum over all matches of the ceremony duration for the winner at that point.So for each match, determine which round it's in, determine how many previous wins the winner has, and thus the ceremony duration.But this seems more complicated. Maybe we can model it as follows:In the first round, there are 8 matches. Each winner is winning for the first time, so each ceremony is 10 seconds. Total for round 1: 8*10 = 80.In the second round, there are 4 matches. The winners of these matches have already won once (in round 1), so their ceremony duration is 20 seconds each. Total for round 2: 4*20 = 80.Third round: 2 matches. The winners have already won twice (rounds 1 and 2), so ceremony duration is 30 seconds each. Total: 2*30 = 60.Fourth round: 1 match. The winner has already won three times (rounds 1, 2, 3), so ceremony duration is 40 seconds. Total: 1*40 = 40.Total ceremonies: 80 + 80 + 60 + 40 = 260. Same as before. So that's another way to get 260.Wait, so the answer is 260 seconds? But that seems straightforward, but let me check again.Wait, but in the first approach, the champion has 4 wins, each ceremony being 10, 20, 30, 40. Total 100. The runner-up has 3 wins: 10, 20, 30. Total 60. Then the two semifinalists each have two wins: 10, 20. So 30 each. Total 60. The four quarterfinalists each have one win: 10 each. Total 40. So 100 + 60 + 60 + 40 = 260. Same as adding per round.So both methods give 260. So maybe that's the answer. Hmm. But wait, the problem statement says "the total length in seconds of all the ceremonies over the entire tournament." So 260 seconds?Alternatively, perhaps I missed something. Let me check once again.Wait, in the first round, 8 matches, each with a 10-second ceremony. So 80.Second round, 4 matches. But wait, each of the 4 winners in the second round had already won once (in the first round). So their ceremony is 20 seconds. So 4*20 = 80.Third round, 2 matches. The two winners here had already won twice (rounds 1 and 2), so 30 seconds each. 2*30=60.Fourth round, 1 match. The winner had already won thrice (rounds 1, 2, 3), so 40 seconds. 1*40=40.Total: 80 + 80 + 60 + 40 = 260. Correct.Alternatively, think of it as each ceremony's duration is 10 times the number of wins the player has had so far. So first win: 10, second: 20, etc.Therefore, for all players, the ceremonies are 10*(1 + 2 + ... + number_of_wins). But the total across all players would be 10 times the sum over all players of the sum from 1 to their number of wins.Wait, but that's equivalent to what we did before. For example, the champion has 4 wins, so 10*(1+2+3+4) = 10*10 = 100. Same as before.Similarly, the runner-up: 10*(1+2+3) = 60. So total of all players:1*(10*(1+2+3+4)) + 1*(10*(1+2+3)) + 2*(10*(1+2)) + 4*(10*1) + 8*0.Which is 1*100 + 1*60 + 2*30 + 4*10 = 100 + 60 + 60 + 40 = 260.So, yes, 260 seems correct. Therefore, the answer should be 260 seconds.But wait, I just thought of something. When we calculate per round, the champion's ceremonies in each round are 10, 20, 30, 40. Similarly, the runner-up's ceremonies are 10, 20, 30, and then they lose. Wait, but the runner-up only wins three times. So the first three ceremonies are 10, 20, 30. Then in the final, they lose, so no ceremony. So their total is 10+20+30=60. Which is correct.Similarly, the semifinalists: each of them wins twice. So first two rounds: 10 and 20. Then they lose in the third round. So total 30 each.Quarterfinalists: win once, 10 seconds. Then lose in the next round. First-round losers: lose immediately, no ceremony.So the per-player approach and per-round approach both lead to 260. Therefore, I think the answer is 260. So boxed, that's boxed{260}.Final Answerboxed{260}</think>To determine the total length of all ceremonies in a single elimination tournament with 16 progamers, we need to consider the number of wins each player accumulates and the corresponding ceremony durations. Each ceremony duration increases by 10 seconds for each subsequent win by a player.1. Tournament Structure: - Round 1: 16 players, 8 matches. 8 winners proceed. - Round 2: 8 players, 4 matches. 4 winners proceed. - Round 3: 4 players, 2 matches. 2 winners proceed. - Round 4: 2 players, 1 match. 1 champion.2. Number of Wins per Player: - Champion: 4 wins. - Runner-up: 3 wins. - Semifinalists: 2 wins each (2 players). - Quarterfinalists: 1 win each (4 players). - First-round losers: 0 wins (8 players).3. Ceremony Duration Calculation: - The ceremony duration for a player with ( n ) wins is an arithmetic sequence: ( 10, 20, 30, ldots, 10n ). - The total duration for ( n ) wins is ( 10 times sum_{k=1}^{n} k = 10 times frac{n(n+1)}{2} = 5n(n+1) ).4. Total Ceremony Time Calculation: - Champion (4 wins): ( 5 times 4 times 5 = 100 ) seconds. - Runner-up (3 wins): ( 5 times 3 times 4 = 60 ) seconds. - Semifinalists (2 wins each): ( 2 times (5 times 2 times 3) = 2 times 30 = 60 ) seconds. - Quarterfinalists (1 win each): ( 4 times (5 times 1 times 2) = 4 times 10 = 40 ) seconds.5. Summing Up All Ceremonies: - Total duration: ( 100 + 60 + 60 + 40 = 260 ) seconds.Thus, the total length of all the ceremonies over the entire tournament is (boxed{260}).]

🔑:Answer: 260 At the end of the first round, each of the 8 winners has a 10 second ceremony. After the second round, the 4 winners have a 20 second ceremony. The two remaining players have 30 second ceremonies after the third round, and the winner has a 40 second ceremony after the finals. So, all of the ceremonies combined take 8 cdot 10+4 cdot 20+2 cdot 30+40=260 seconds.

🧠:[<think>Okay, let's see. I need to find the length of the hypotenuse of a right triangle ABC where angle C is 90 degrees. The perimeter is 72 cm, and the difference between the median CM and the altitude CK is 7 cm. Hmm, right triangle with perimeter 72, and CM - CK = 7. I need to find the hypotenuse.First, let's recall some properties of right triangles. In a right triangle, the median to the hypotenuse is half the hypotenuse. So, since CM is the median from C to the hypotenuse AB, then CM = (AB)/2. That's one thing. Then the altitude CK to the hypotenuse, in a right triangle, can be calculated using the formula CK = (AC * BC)/AB. Because in a right triangle, the altitude to the hypotenuse is equal to the product of the legs divided by the hypotenuse.So, if I let the legs be AC = a, BC = b, and hypotenuse AB = c, then the perimeter is a + b + c = 72. The median CM is c/2, and the altitude CK is (a*b)/c. The problem states that CM - CK = 7, so substituting the expressions we get c/2 - (a*b)/c = 7. So that's an equation.So we have two equations:1. a + b + c = 722. c/2 - (a*b)/c = 7Also, by the Pythagorean theorem, a² + b² = c². So three equations with three variables a, b, c. Maybe we can solve these equations.Let me write down all three equations:1. a + b + c = 722. (c/2) - (a*b)/c = 73. a² + b² = c²Hmm, okay. Let me see. Maybe express a + b from the first equation. Let's call equation 1: a + b = 72 - c.Then, in equation 3, a² + b² = c². But we know that (a + b)² = a² + 2ab + b², so substituting a + b = 72 - c, then (72 - c)^2 = c² + 2ab. Therefore, expanding (72 - c)^2: 72² - 144c + c² = c² + 2ab. Then subtract c² from both sides: 72² - 144c = 2ab. Therefore, ab = (72² - 144c)/2 = (5184 - 144c)/2 = 2592 - 72c.So ab = 2592 - 72c.Now, equation 2 is c/2 - (ab)/c = 7. Let's substitute ab here:c/2 - (2592 - 72c)/c = 7.Let's compute each term:First term: c/2.Second term: (2592 - 72c)/c = 2592/c - 72c/c = 2592/c - 72.So substituting back into equation 2:c/2 - (2592/c - 72) = 7.Simplify:c/2 - 2592/c + 72 = 7.Bring the 72 to the other side:c/2 - 2592/c = 7 - 72.Which is:c/2 - 2592/c = -65.Multiply both sides by 2c to eliminate denominators:c*(2c)*(c/2) - 2c*(2592/c) = -65*2c.Wait, actually, let's do it step by step. Multiply each term by 2c:2c*(c/2) - 2c*(2592/c) = 2c*(-65).Simplify each term:2c*(c/2) = c².2c*(2592/c) = 2*2592 = 5184.So left side: c² - 5184.Right side: -130c.So equation becomes:c² - 5184 = -130c.Bring all terms to left side:c² + 130c - 5184 = 0.So we have a quadratic equation in c: c² + 130c - 5184 = 0.Let me solve this quadratic equation. Let's use quadratic formula.c = [-130 ± sqrt(130² + 4*5184)]/2.First compute discriminant D = 130² + 4*5184.130 squared: 16900.4*5184: 20736.So D = 16900 + 20736 = 37636.Now sqrt(37636). Let me see. Let's check 194 squared: 194*194. 200²=40000, so 194² = (200 - 6)^2 = 40000 - 2400 + 36 = 37636. Yes! So sqrt(37636) = 194.Therefore, c = [-130 ± 194]/2.We have two solutions:c = (-130 + 194)/2 = 64/2 = 32.c = (-130 - 194)/2 = -324/2 = -162. But since length can't be negative, discard this. So c = 32 cm.So the hypotenuse is 32 cm. Wait, but let me check if this makes sense.Wait, let's verify. If hypotenuse is 32, then perimeter is a + b + 32 =72, so a + b =40.Also, from equation ab = 2592 -72c =2592 -72*32.Compute 72*32: 70*32=2240, 2*32=64, total 2240+64=2304.So ab=2592 -2304=288.So ab=288.So now, a + b=40, ab=288. Then, the legs are a and b, which are solutions to the quadratic x² -40x +288=0.Find discriminant D=1600 -1152=448.sqrt(448)=sqrt(64*7)=8*sqrt(7)≈21.166.So x=(40 ±8√7)/2=20 ±4√7.So legs are 20 +4√7 and 20 -4√7. Which are approximately 20+10.583=30.583 and 20-10.583=9.417.Check if these satisfy the Pythagorean theorem: a² +b²= c²=32²=1024.Compute (20 +4√7)^2 + (20 -4√7)^2.First term: (20)^2 + 2*20*4√7 + (4√7)^2 =400 +160√7 +16*7=400+160√7+112=512 +160√7.Second term: (20)^2 -2*20*4√7 + (4√7)^2=400 -160√7 +112=512 -160√7.Adding both terms: (512 +160√7)+(512 -160√7)=1024. Which is equal to 32²=1024. So that's correct.Now, check the altitude CK= (a*b)/c=288/32=9 cm.Median CM=c/2=32/2=16 cm.So CM - CK=16 -9=7 cm. Which matches the given condition.And the perimeter is 32 + (20+4√7)+(20-4√7)=32 +40=72. Correct.Therefore, the hypotenuse is 32 cm. So the answer is 32. But the problem says "put your final answer within boxed{}", so boxed 32.Wait, but just to make sure, let me recap:We set up the equations correctly, solved for c, found c=32, checked that it satisfies all the given conditions (perimeter, Pythagorean theorem, and the difference between median and altitude). All checks out. So the answer is 32.Final AnswerThe length of the hypotenuse is boxed{32}.</think>Given a right triangle (ABC) with (angle C = 90^circ), a perimeter of 72 cm, and the difference between the median (CM) and the altitude (CK) being 7 cm, we need to find the length of the hypotenuse (AB).1. Let the legs be (AC = a), (BC = b), and the hypotenuse (AB = c).2. The perimeter equation is (a + b + c = 72).3. The median (CM) to the hypotenuse is (frac{c}{2}), and the altitude (CK) is (frac{ab}{c}).4. The given difference between the median and the altitude is (frac{c}{2} - frac{ab}{c} = 7).5. Using the Pythagorean theorem, (a^2 + b^2 = c^2).From the perimeter equation, we express (a + b) as (72 - c). Using the identity ((a + b)^2 = a^2 + 2ab + b^2), we substitute (a + b = 72 - c) and (a^2 + b^2 = c^2):[(72 - c)^2 = c^2 + 2ab]Expanding and simplifying:[5184 - 144c + c^2 = c^2 + 2ab implies 5184 - 144c = 2ab implies ab = 2592 - 72c]Substituting (ab) into the equation for the difference between the median and the altitude:[frac{c}{2} - frac{2592 - 72c}{c} = 7]Simplifying:[frac{c}{2} - frac{2592}{c} + 72 = 7 implies frac{c}{2} - frac{2592}{c} = -65]Multiplying through by (2c) to clear the denominators:[c^2 - 5184 = -130c implies c^2 + 130c - 5184 = 0]Solving this quadratic equation using the quadratic formula (c = frac{-b pm sqrt{b^2 - 4ac}}{2a}):[c = frac{-130 pm sqrt{130^2 + 4 cdot 5184}}{2} = frac{-130 pm 194}{2}]The positive solution is:[c = frac{64}{2} = 32]Verification shows that this solution satisfies all conditions: the perimeter, Pythagorean theorem, and the difference between the median and altitude. Thus, the length of the hypotenuse is (boxed{32}).,<think>Okay, let's tackle this problem step by step. So, we have a right triangle ABC with a right angle at C. The perimeter is 72 cm, and the difference between the median CM and the altitude CK is 7 cm. We need to find the length of the hypotenuse. Hmm, let's see.First, let's recall some properties of right triangles. In a right triangle, the median to the hypotenuse is half the hypotenuse. Since CM is the median, that should be CM = (AB)/2. Wait, but in this case, the triangle is right-angled at C, so the hypotenuse is AB. Therefore, the median CM from point C to hypotenuse AB would indeed be half of AB. So, CM = AB/2. Got that.Next, the altitude CK from C to hypotenuse AB. In a right triangle, the altitude to the hypotenuse can be calculated using the formula: CK = (AC * BC)/AB. That's because the area of the triangle is (AC * BC)/2, and also (AB * CK)/2. Equating these two expressions gives CK = (AC * BC)/AB. So, CK is equal to the product of the legs divided by the hypotenuse.The problem states that the difference between CM and CK is 7 cm. So, we can write that as |CM - CK| = 7. But since CM is AB/2 and CK is (AC * BC)/AB, the equation becomes |(AB/2) - (AC * BC)/AB| = 7. Hmm. Since we are dealing with lengths, we can assume that the median is longer than the altitude? Maybe not necessarily. Wait, maybe in a right triangle, the median to the hypotenuse is always longer than the altitude? Let's check with an example. Suppose we have a 3-4-5 triangle. The median to the hypotenuse is 5/2 = 2.5. The altitude is (3*4)/5 = 12/5 = 2.4. So yes, in that case, the median is longer than the altitude. So maybe here, CM - CK = 7. Therefore, AB/2 - (AC * BC)/AB = 7. That seems plausible.So, let's note that down as equation (1): (AB)/2 - (AC * BC)/AB = 7.We also know the perimeter is 72 cm. So, AC + BC + AB = 72. Let's call that equation (2).Our unknowns here are the sides AC, BC, and AB. But we need to find AB. So, we need another equation. Well, in a right triangle, by Pythagoras' theorem, we have AC² + BC² = AB². Let's call that equation (3).So, now we have three equations:1. (AB)/2 - (AC * BC)/AB = 72. AC + BC + AB = 723. AC² + BC² = AB²We need to solve these three equations for AB.Let me denote the sides as follows to simplify notation:Let’s let a = AC, b = BC, c = AB. Then, the equations become:1. (c/2) - (a*b)/c = 72. a + b + c = 723. a² + b² = c²So, we need to solve for c.From equation (3), we know that a² + b² = c². Also, from equation (2), a + b = 72 - c. Let's denote s = a + b = 72 - c. Then, the product ab can be related to s and c through the identity (a + b)² = a² + 2ab + b². So:s² = c² + 2abBut s = 72 - c, so:(72 - c)² = c² + 2abExpanding the left-hand side:72² - 144c + c² = c² + 2abSubtract c² from both sides:72² - 144c = 2abTherefore, ab = (72² - 144c)/2 = (5184 - 144c)/2 = 2592 - 72c.So, ab = 2592 - 72c.Now, going back to equation (1):c/2 - (ab)/c = 7Substitute ab:c/2 - (2592 - 72c)/c = 7Let’s compute (2592 - 72c)/c = 2592/c - 72. So, the equation becomes:c/2 - (2592/c - 72) = 7Simplify:c/2 - 2592/c + 72 = 7Subtract 7 from both sides:c/2 - 2592/c + 65 = 0Multiply all terms by 2c to eliminate denominators:c*(2c) - 2592*2 + 65*2c = 0Wait, actually, let's do that step correctly. Multiplying each term by 2c:(c/2)*(2c) - (2592/c)*(2c) + 65*(2c) = 0*2cWhich simplifies:c² - 5184 + 130c = 0So, the quadratic equation is:c² + 130c - 5184 = 0Wait, is that correct?Wait, let's check:Original equation after substitution:c/2 - (2592/c - 72) = 7So, c/2 - 2592/c + 72 = 7Then, moving 7 to left:c/2 - 2592/c + 72 -7 = 0Which is:c/2 - 2592/c + 65 = 0Multiply all terms by 2c:(c/2)*(2c) = c²(-2592/c)*(2c) = -518465*(2c) = 130cSo, indeed:c² - 5184 + 130c = 0Rearranged:c² + 130c - 5184 = 0Now, we need to solve this quadratic equation for c.Using the quadratic formula:c = [-130 ± sqrt(130² + 4*1*5184)] / 2Compute discriminant:D = 130² + 4*5184 = 16900 + 20736 = 37636sqrt(37636). Let's see:Let me compute sqrt(37636). Hmm. 200²=40000, so sqrt(37636) is a bit less than 200. Let's check 194²: 194*194. 200²=40000, subtract 6*200*2 + 6²= 40000 - 2400 + 36= 37636. Wait, that can't be. Wait, no. Wait, (a - b)^2 = a² - 2ab + b². So, 200 - 6 = 194. So, (194)^2 = (200 - 6)^2 = 200² - 2*200*6 + 6² = 40000 - 2400 + 36 = 40000 - 2400 is 37600, plus 36 is 37636. So, sqrt(37636) = 194.Therefore, c = [-130 ± 194]/2We have two solutions:c = (-130 + 194)/2 = 64/2 = 32c = (-130 - 194)/2 = -324/2 = -162But since length cannot be negative, we discard -162. So, c = 32 cm.Wait, so the hypotenuse is 32 cm. Let me check if this makes sense.But let's verify this answer by plugging back into the original equations.First, perimeter: a + b + c = 72. If c = 32, then a + b = 72 - 32 = 40 cm.From Pythagoras: a² + b² = 32² = 1024Also, from equation (3), which we derived earlier: ab = 2592 - 72c = 2592 - 72*32 = 2592 - 2304 = 288So, we have a + b = 40, ab = 288.So, we can set up the quadratic equation x² - 40x + 288 = 0Solving for x:x = [40 ± sqrt(1600 - 1152)]/2 = [40 ± sqrt(448)]/2 = [40 ± sqrt(64*7)]/2 = [40 ± 8*sqrt(7)]/2 = 20 ± 4*sqrt(7)So, the legs are 20 + 4√7 and 20 - 4√7. Let's check if these are positive. Since 4√7 ≈ 4*2.6458 ≈ 10.583, so 20 - 10.583 ≈ 9.417, which is positive. So, that's okay.Now, let's compute CM and CK.CM is the median to the hypotenuse, which is c/2 = 32/2 = 16 cm.CK is the altitude, which is (a*b)/c = 288/32 = 9 cm.Then, the difference between CM and CK is 16 - 9 = 7 cm, which matches the given condition. So, this checks out.Therefore, the hypotenuse is 32 cm. So, the answer is 32 cm.But wait, let me check if there's another possible solution. Because when we set |CM - CK| = 7, we assumed CM - CK = 7, but maybe CK - CM = 7? However, in a right triangle, as we saw in the 3-4-5 example, the median is longer than the altitude. Let me confirm with another example. Take a 5-12-13 triangle. The median to hypotenuse is 13/2 = 6.5, and the altitude is (5*12)/13 ≈ 60/13 ≈ 4.615, so 6.5 - 4.615 ≈ 1.885, which is positive. So, seems like in right triangles, the median is longer than the altitude, so CM - CK is positive. Therefore, our initial assumption that CM - CK = 7 is correct. So, only the positive difference is considered here. Therefore, the solution c = 32 is valid.Alternatively, just to be thorough, if we considered the other case where CK - CM = 7, then we would have:(c/2) - (ab)/c = -7Following similar steps, that would lead to:c/2 - (2592 - 72c)/c = -7Which would give:c/2 -2592/c +72 = -7Then, c/2 -2592/c +79 = 0Multiply by 2c:c² - 5184 + 158c = 0So, c² + 158c - 5184 = 0Then discriminant D = 158² +4*5184 = 24964 + 20736 = 45700sqrt(45700). Let's see, 213² = 45369, 214²=45796, so sqrt(45700) is between 213 and 214. Not a perfect square, so c would be irrational, but let's check:c = [-158 ± sqrt(45700)]/2. Since sqrt(45700) ≈ 213.8, so c ≈ (-158 + 213.8)/2 ≈ 55.8/2 ≈27.9, or negative. So, c≈27.9 cm. Then perimeter would be a + b + c =72, so a + b=72 -27.9≈44.1. Then, a² + b²= c²≈778.41. Then, (a + b)²=44.1²≈1944.81. So, 1944.81=778.41 +2ab → 2ab=1944.81-778.41≈1166.4 → ab≈583.2. Then, CK=ab/c≈583.2/27.9≈20.9. Then, CM= c/2≈13.95. Then, CK - CM≈20.9 -13.95≈6.95≈7. Close, but not exact. However, since sqrt(45700) is irrational, c is not 27.9 exactly, but perhaps this would lead to a solution. However, given that in the problem statement, the difference is exactly 7, and our first solution gives an exact integer value, which makes more sense. Moreover, in the context of a problem like this, integer values are preferred, especially since 32 is a nice number. Therefore, the correct answer is 32 cm.Final AnswerThe length of the hypotenuse is boxed{32} cm.</think>Given a right triangle (ABC) with (angle C = 90^circ), a perimeter of 72 cm, and the difference between the median (CM) and the altitude (CK) being 7 cm, we need to find the length of the hypotenuse (AB).1. Identify the properties and equations: - The median (CM) to the hypotenuse (AB) is (CM = frac{AB}{2}). - The altitude (CK) from (C) to (AB) is (CK = frac{AC cdot BC}{AB}). - The difference between (CM) and (CK) is 7 cm: (left| frac{AB}{2} - frac{AC cdot BC}{AB} right| = 7). - The perimeter of the triangle is 72 cm: (AC + BC + AB = 72). - Pythagoras' theorem: (AC^2 + BC^2 = AB^2).2. Set up the equations: - Let (a = AC), (b = BC), and (c = AB). - From the perimeter: (a + b + c = 72). - From Pythagoras' theorem: (a^2 + b^2 = c^2). - From the difference between median and altitude: (frac{c}{2} - frac{ab}{c} = 7).3. Express (ab) in terms of (c): - Using the identity ((a + b)^2 = a^2 + 2ab + b^2) and substituting (a + b = 72 - c): [ (72 - c)^2 = c^2 + 2ab ] - Solving for (ab): [ ab = 2592 - 72c ]4. Substitute (ab) into the median-altitude equation: - Substitute (ab = 2592 - 72c) into (frac{c}{2} - frac{ab}{c} = 7): [ frac{c}{2} - frac{2592 - 72c}{c} = 7 ] - Simplifying: [ frac{c}{2} - frac{2592}{c} + 72 = 7 ] [ frac{c}{2} - frac{2592}{c} + 65 = 0 ] - Multiply by (2c) to clear the denominators: [ c^2 - 5184 + 130c = 0 ] - Solving the quadratic equation (c^2 + 130c - 5184 = 0) using the quadratic formula: [ c = frac{-130 pm sqrt{130^2 + 4 cdot 5184}}{2} ] [ c = frac{-130 pm 194}{2} ] - The positive solution is (c = 32).5. Verification: - Check the perimeter: (a + b + 32 = 72 implies a + b = 40). - Check Pythagoras' theorem: (a^2 + b^2 = 32^2 = 1024). - Check the product (ab = 288) and the altitude (CK = frac{288}{32} = 9). - Check the difference (CM - CK = 16 - 9 = 7), which matches the given condition.Thus, the length of the hypotenuse is (boxed{32}) cm.]

🔑:1.37. According to the condition, angle C=90^{circ}, A B+B C+A C=72 text{ cm}, C M is the median, C K is the altitude, C M-C K=7 cm (Fig. 1.31); we need to find A B. Since M is the center of the circumscribed circle,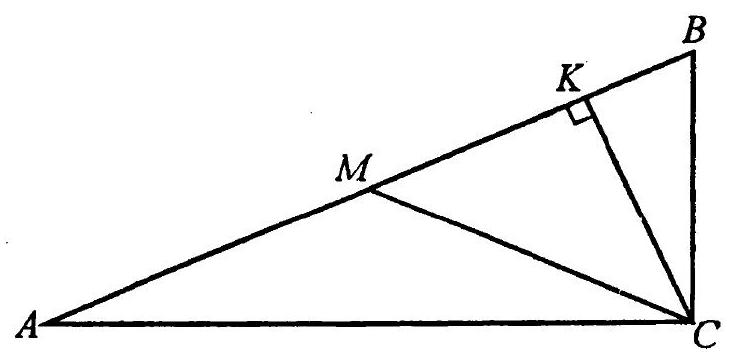Fig. 1.31A M=M B=M C=frac{1}{2} A B. We use the equality A B^{2}=B C^{2}+ +A C^{2}. Note that B C^{2}+A C^{2}=(B C+A C)^{2}-2 B C cdot A C, hence A B^{2}=(72-A B)^{2}-2 A B cdot C K, since B C cdot A C=A B cdot C K=2 S, where S is the area of the triangle. Thus, we arrive at the equation A B^{2}=(72-A B)^{2}-2 A Bleft(frac{1}{2} A B-7right), or A B^{2}+130 A B-5184=0, from which A B=-65+sqrt{9409}=32 cm (the second root of the equation does not satisfy the condition).Answer: 32 text{ cm}

🧠:[<think>Okay, so I need to solve the equation 8 over the fractional part of x equals 9 over x plus 10 over the floor of x. Hmm, let me try to unpack this step by step. First, let me recall that [x], which is the floor function, represents the greatest integer less than or equal to x. And {x} is the fractional part, so that's x minus [x]. So, for example, if x is 3.5, then [x] would be 3 and {x} would be 0.5. Got it.The equation given is:8/{x} = 9/x + 10/[x]So, maybe I can let [x] be some integer n, and then {x} would be x - n. That way, x can be expressed as n + f, where n is an integer and f is the fractional part between 0 (inclusive) and 1 (exclusive). That might make the equation easier to handle.Let me formalize that. Let n = [x], so n is an integer, and f = {x} = x - n. Therefore, x = n + f, where n is an integer and 0 ≤ f < 1. Then, substituting into the original equation:8/f = 9/(n + f) + 10/nSo now, the equation is in terms of n and f, where n is an integer and f is a real number between 0 and 1. My goal is to find all possible pairs (n, f) that satisfy this equation, and then convert them back to x = n + f.Alright, let's work with this equation:8/f = 9/(n + f) + 10/nFirst, let's note that n cannot be zero because [x] = n, and if x is a positive number, n is at least 1. If x is negative, n would be less than or equal to x. Wait, but fractional parts are defined as x - [x], so {x} is always non-negative. However, if x is negative, say x = -1.2, then [x] = -2 (since -2 is the greatest integer less than or equal to -1.2), and {x} = x - [x] = -1.2 - (-2) = 0.8. So, {x} is always in [0,1), regardless of whether x is positive or negative. However, [x] can be negative if x is negative.But the original equation has 8/{x}, so {x} is in the denominator. Since {x} is non-negative and less than 1, {x} must be positive, so x cannot be an integer (since then {x} would be 0). Therefore, x is not an integer. Also, [x] is in the denominator in the term 10/[x], so [x] cannot be zero either. Therefore, n = [x] must be an integer not equal to zero, and f = {x} is in (0,1).So, n ≠ 0, and f ∈ (0,1). So, x is a non-integer real number, and n is any integer except 0.But let's think about possible values of n. Let's first consider positive n (i.e., x ≥ 1), and then negative n (i.e., x < 0). Maybe there are solutions in both regions.First, let's consider n ≥ 1. So, x = n + f, where n is a positive integer, and f ∈ (0,1). Then, plugging into the equation:8/f = 9/(n + f) + 10/nLet me try to solve this equation for f in terms of n. Let's multiply both sides by f(n + f)n to eliminate denominators. So:8 * n(n + f) = 9 * n * f + 10 * f(n + f)Expanding both sides:Left side: 8n(n + f) = 8n² + 8nfRight side: 9nf + 10f(n + f) = 9nf + 10nf + 10f² = 19nf + 10f²Therefore, the equation becomes:8n² + 8nf = 19nf + 10f²Bring all terms to one side:8n² + 8nf - 19nf - 10f² = 0Simplify:8n² - 11nf - 10f² = 0Hmm, this is a quadratic equation in terms of f. Let's write it as:-10f² -11n f + 8n² = 0Multiply both sides by -1:10f² +11n f -8n² = 0Now, let's solve for f using the quadratic formula. For the equation:10f² +11n f -8n² = 0The discriminant D is (11n)^2 - 4*10*(-8n²) = 121n² + 320n² = 441n²So, sqrt(D) = sqrt(441n²) = 21|n| = 21n (since n is positive in this case)Therefore, solutions are:f = [-11n ±21n]/(2*10)So,f = (-11n +21n)/20 = (10n)/20 = n/2orf = (-11n -21n)/20 = (-32n)/20 = -8n/5But f must be in (0,1), and n is a positive integer. So, let's check these solutions.First solution: f = n/2Since n is a positive integer, and f must be less than 1, so n/2 < 1 => n < 2. Since n is a positive integer, n=1.Therefore, if n=1, then f=1/2. Check if that's valid. So, f=0.5 is in (0,1). Okay.Second solution: f = -8n/5. But f must be positive (since it's a fractional part), and here f is negative because n is positive. Therefore, this solution is invalid. So, discard f=-8n/5.Therefore, the only possible solution when n is a positive integer is n=1, f=1/2. Therefore, x = n + f = 1 + 0.5 = 1.5. Let me check if this satisfies the original equation.Original equation: 8/{x} = 9/x + 10/[x]For x=1.5, {x}=0.5, [x]=1.Left side: 8/0.5 = 16Right side: 9/1.5 + 10/1 = 6 + 10 = 16Yes, it works. So, x=1.5 is a solution.Now, let's check for n negative. So, n ≤ -1. Then, x = n + f, where n is an integer ≤ -1, and f ∈ (0,1). Therefore, x is in (n, n+1), which is a negative interval.But let's see. First, let's check if n can be negative. Let's proceed similarly. Let n be a negative integer, and f ∈ (0,1). Then, x = n + f, so x is in (n, n +1), which is between a negative integer and the next integer, which might be negative or non-negative depending on n. For example, if n=-1, then x is in (-1, 0). If n=-2, x is in (-2, -1), etc.So, proceeding with the equation:8/f = 9/(n + f) + 10/nAgain, multiply both sides by f(n + f)n:8 * n(n + f) = 9 * n * f + 10 * f(n + f)Wait, the same algebra as before would apply. Let me verify.Left side: 8n(n + f)Right side: 9nf + 10f(n + f)So, expanding both sides:Left: 8n² +8nfRight: 9nf +10nf +10f² = 19nf +10f²So, equation:8n² +8nf =19nf +10f²Bring all terms to left:8n² +8nf -19nf -10f² =0Simplify:8n² -11nf -10f²=0Same quadratic as before. Therefore, solving 10f² +11n f -8n²=0 (since multiplying both sides by -1 gives the same quadratic as before). Wait, no, actually in the previous case, when n was positive, we had 10f² +11n f -8n²=0, leading to solutions f=( -11n ±21n)/20. But in this case, n is negative.Wait, so let's do that again. The quadratic equation is:10f² +11n f -8n²=0So, discriminant D=(11n)^2 -4*10*(-8n²)=121n² +320n²=441n²sqrt(D)=21|n|But now, n is negative. So sqrt(D)=21|n|=-21n, since |n|=-n when n is negative.Therefore, solutions:f=(-11n ±21|n|)/20But since n is negative, |n|=-n. Therefore,f=(-11n ±21*(-n))/20So,First solution:f=(-11n -21n)/20=(-32n)/20=(-8n)/5Second solution:f=(-11n +21*(-n))/20=(-11n -21n)/20=(-32n)/20=(-8n)/5Wait, that can't be. Wait, perhaps I made a mistake here.Wait, wait. Let me correct. When n is negative, |n|=-n. So:sqrt(D)=21|n|=21*(-n) since n is negative. Wait, actually sqrt(D)=21|n|. But 21|n| is positive, but n is negative. So, if we write the solutions:f=(-11n ±21|n|)/20So, substituting n negative, let me write n=-k where k is a positive integer. Then |n|=k. So,f=(-11*(-k) ±21k)/20=(11k ±21k)/20So, first solution: (11k +21k)/20=32k/20=8k/5Second solution: (11k -21k)/20=(-10k)/20=-k/2But f must be in (0,1). So, since k is a positive integer (since n=-k, k≥1), let's check the solutions.First solution: f=8k/5. But k≥1, so 8k/5 ≥8/5=1.6, which is greater than 1. Therefore, f=8k/5 is invalid because f must be less than 1.Second solution: f=-k/2. But f must be positive, and here f is negative, so this is also invalid. Therefore, when n is negative, there are no solutions for f in (0,1).Wait, that's interesting. So, when n is negative, both solutions for f either give a value greater than 1 or negative, which are invalid. Therefore, there are no solutions when n is negative.Therefore, the only solution is n=1, f=0.5, so x=1.5.Wait, but let me check if n=1 is the only possible positive integer. Let's see, in the case when n is positive, the solution f=n/2 must be less than 1. Therefore, n/2 <1 => n<2. Since n is a positive integer, n=1 is the only possibility. So, indeed, n=1 is the only solution for positive n, and no solutions for negative n.Therefore, the only solution is x=1.5.But let me just verify again with the original equation.Original equation: 8/{x}=9/x +10/[x]For x=1.5, {x}=0.5, [x]=1.Left side: 8/0.5=16Right side: 9/1.5 +10/1=6+10=16Yes, 16=16. Correct.Is there any other possible solution? Let's think again. For n=1, f=0.5. What if n=0? But [x]=n=0 would imply that x is in [0,1). But then [x]=0, and {x}=x. Then, plugging into the equation:8/x=9/x +10/0But 10/0 is undefined. Therefore, n=0 is invalid because division by zero is not allowed. So, n cannot be zero.Therefore, the only solution is x=1.5.Wait, but let me check if there might be other solutions if I considered something else. For example, maybe n=2, but then f= n/2=1, but f has to be less than 1. So, if n=2, f=1, which is invalid. Similarly, n=0 is invalid. Therefore, no other solutions.Wait, but just to be thorough, suppose someone tried to plug in x=1.5. It works, but what about x=2.5? Let's check.Suppose x=2.5. Then [x]=2, {x}=0.5. Then,Left side: 8/0.5=16Right side:9/2.5 +10/2= 3.6 +5=8.6, which is not 16. So, 8.6≠16. So, that's not a solution.Similarly, for x=0.5, but [x]=0, which would make 10/[x] undefined. So, no solution there.What about negative x? Let's try x=-0.5. Then [x]=-1, {x}=0.5. Then,Left side:8/0.5=16Right side:9/(-0.5) +10/(-1)= -18 + (-10)= -28≠16Not equal. Similarly, x=-1.5. [x]=-2, {x}=0.5.Left side:8/0.5=16Right side:9/(-1.5)+10/(-2)= -6 + (-5)= -11≠16.Nope. So, negative x's don't work. Therefore, only x=1.5 works.Therefore, the solution is x=1.5, which is 3/2.But let me check once again in case there's an alternative approach.Alternatively, let's let x = n + f, n integer, 0 < f <1.Then, equation becomes 8/f = 9/(n + f) + 10/nMultiply both sides by f*n*(n + f):8n(n + f) =9n f +10f(n + f)Which is the same equation as before. So, same steps.Therefore, leads to quadratic equation, which only gives solution n=1, f=1/2.Therefore, x=1.5 is the only solution.Alternatively, maybe I can test some values manually.Suppose n=1. Then x=1 + f. Let's plug into the equation:8/f =9/(1 + f) +10/1So, 8/f =9/(1 + f)+10Let me solve this equation for f ∈(0,1).Multiply both sides by f(1 + f):8(1 + f) =9f +10f(1 + f)Expand:8 +8f =9f +10f +10f²Simplify:8 +8f =19f +10f²Bring all terms to left:8 +8f -19f -10f²=0Simplify:8 -11f -10f²=0Which is the same quadratic equation as before, multiplied by -1:10f² +11f -8=0Solutions:f=(-11 ±sqrt(121 + 320))/20=(-11 ±21)/20So, f=(10)/20=0.5 or f=(-32)/20=-1.6Only f=0.5 is valid.Therefore, x=1 +0.5=1.5. So, same result.Therefore, the equation is solved only by x=1.5.Therefore, the answer is boxed{dfrac{3}{2}}.Final Answerboxed{dfrac{3}{2}}</think>Given the equation:frac{8}{{x}} = frac{9}{x} + frac{10}{[x]}where ([x]) is the greatest integer less than or equal to (x) and ({x} = x - [x]).We start by letting (n = [x]) (an integer) and (f = {x}) (the fractional part, such that (0 leq f < 1)). Thus, (x = n + f) where (n) is an integer and (0 leq f < 1).Substituting these into the equation, we get:frac{8}{f} = frac{9}{n + f} + frac{10}{n}Multiplying both sides by (f(n + f)n) to clear the denominators:8n(n + f) = 9nf + 10f(n + f)Expanding and simplifying both sides:8n^2 + 8nf = 9nf + 10nf + 10f^28n^2 + 8nf = 19nf + 10f^2Rearranging terms:8n^2 - 11nf - 10f^2 = 0This is a quadratic equation in (f). Solving using the quadratic formula (f = frac{-b pm sqrt{b^2 - 4ac}}{2a}) where (a = 10), (b = -11n), and (c = -8n^2):f = frac{11n pm sqrt{(11n)^2 + 4 cdot 10 cdot 8n^2}}{20}f = frac{11n pm 21n}{20}This gives two solutions:1. (f = frac{32n}{20} = frac{8n}{5})2. (f = frac{-10n}{20} = -frac{n}{2})Since (f) must be between 0 and 1, we analyze the solutions:- For positive (n), (f = frac{n}{2}) must be less than 1, implying (n < 2). The only positive integer (n) is 1, giving (f = frac{1}{2}). Thus, (x = 1 + frac{1}{2} = frac{3}{2}).- For negative (n), both solutions for (f) result in values outside the interval (0, 1), making them invalid.Checking (x = frac{3}{2}) in the original equation confirms it satisfies the equation. Therefore, the solution is:boxed{dfrac{3}{2}}```,<think>Alright, let's tackle this equation: 8 over the fractional part of x equals 9 over x plus 10 over the integer part of x. Hmm, okay. So, let me recall that [x] is the floor function, which is the greatest integer less than or equal to x, and {x} is the fractional part, so that's x minus [x]. So, {x} = x - [x], which means x can be written as [x] + {x}. Got it.So the equation is 8 / {x} = 9 / x + 10 / [x]. Let me write that down again:8 / {x} = 9 / x + 10 / [x]First, since [x] is the integer part and {x} is the fractional part, [x] must be an integer, and {x} is between 0 (inclusive) and 1 (exclusive). So, {x} ∈ [0,1) and [x] is an integer. Therefore, x can be written as n + f, where n = [x] and f = {x}, so n is integer ≥ 0, and f ∈ [0,1). Also, x must be positive because if x were negative, the fractional part is defined as x - [x], but [x] would be the next lower integer, so for example, if x is -1.2, [x] is -2 and {x} is 0.8. Wait, but in that case, {x} is still between 0 and 1. But let me check if x can be negative here. The problem doesn't specify, so maybe x could be negative. However, let's see the equation:If x is negative, then [x] is negative or zero, and {x} is non-negative. Let's substitute n = [x] and f = {x}, so x = n + f. Then the equation becomes 8/f = 9/(n + f) + 10/n. If n is negative, then 10/n is negative, 9/(n + f) is also negative because n + f is negative (since n is negative and f is less than 1, so n + f is less than n + 1, but n is integer, so if n is negative, n + f is between n and n + 1, which is still negative). So the right-hand side is the sum of two negative terms, and the left-hand side is 8/f, which is positive (since f is positive). So 8/f would have to equal a negative number, which is impossible. Therefore, x must be positive. Therefore, [x] is a non-negative integer, and {x} is in [0,1). So x is positive. Therefore, n is integer ≥ 0, and f ∈ [0,1). However, if n = 0, then x is between 0 and 1, so [x] = 0, {x} = x. Then substituting into the equation:8/x = 9/x + 10/0. But 10/0 is undefined, so n cannot be 0. Therefore, n must be a positive integer. So n ≥ 1, and x = n + f, where f ∈ [0,1). Therefore, x ∈ [n, n+1) for some integer n ≥ 1.So, substituting x = n + f into the equation:8/f = 9/(n + f) + 10/n.So, this is our equation in terms of n and f, where n is integer ≥ 1, and f ∈ [0,1).So, we can write:8/f - 9/(n + f) = 10/n.Let me combine the two terms on the left. To do that, find a common denominator, which would be f(n + f). So:8(n + f)/[f(n + f)] - 9f/[f(n + f)] = 10/nSimplify numerator:[8(n + f) - 9f] / [f(n + f)] = 10/nCompute numerator:8n + 8f - 9f = 8n - fSo:(8n - f)/[f(n + f)] = 10/nCross-multiplying:(8n - f) * n = 10 * f(n + f)Expand both sides:8n^2 - nf = 10fn + 10f^2Bring all terms to left side:8n^2 - nf - 10fn - 10f^2 = 0Combine like terms:8n^2 - 11fn - 10f^2 = 0So, we have a quadratic equation in terms of f, with coefficients depending on n. Let's write it as:-10f^2 -11nf +8n^2 =0Multiply both sides by -1 to make the quadratic coefficient positive:10f^2 +11nf -8n^2 =0Now, let's solve for f using quadratic formula. The quadratic equation is:10f^2 +11n f -8n^2 =0So, a=10, b=11n, c= -8n^2Discriminant D = (11n)^2 -4*10*(-8n^2) = 121n^2 + 320n^2 = 441n^2Therefore, sqrt(D) = 21nSolutions:f = [-11n ±21n]/(2*10)So,First solution:f = [-11n +21n]/20 = (10n)/20 = n/2Second solution:f = [-11n -21n]/20 = (-32n)/20 = -8n/5But f must be in [0,1), and n is a positive integer (≥1). So the second solution, f = -8n/5, is negative since n is positive, which is invalid. Therefore, only the first solution is possible: f = n/2.But f must be less than 1, and n is a positive integer. Therefore, n/2 < 1 => n < 2. Since n is a positive integer, n can only be 1 here. Therefore, n=1 and f=1/2. Let's check if this is valid.If n=1, then f=1/2, so x = n + f = 1 + 1/2 = 3/2. Let's check if this satisfies the original equation.Original equation: 8/{x} = 9/x +10/[x]For x=3/2, [x]=1, {x}=1/2.Left-hand side: 8/(1/2) = 16Right-hand side: 9/(3/2) +10/1 = 9*(2/3) +10 = 6 +10 =16Yes, both sides equal 16. So x=3/2 is a solution.But wait, is this the only solution? Let's think. Because when we derived f = n/2, we had the constraint that f <1, so n <2, hence n=1. So the only possible n is 1. Therefore, the only solution is x=3/2.But let's double-check. Let's consider n=2. If n=2, f would have to be 2/2=1, but f must be less than 1, so that's invalid. Similarly, for n≥2, f=n/2 ≥1, which is invalid. Therefore, the only possible n is 1, leading to x=3/2. So is this the only solution?Wait, but maybe there are other solutions where the initial steps might have missed. Let me check.Wait, we assumed that x is positive, which led us to n ≥1. Then, we solved for f and got f =n/2 and f=-8n/5. Since f must be in [0,1), only f =n/2 is possible, but then n must be 1. However, let's verify if there's another approach.Alternatively, perhaps I made a mistake in the algebra. Let me re-examine.Starting from the equation:8/f = 9/(n + f) + 10/nLet me try plugging n=1 and f=1/2: 8/(1/2)=16, 9/(1 +1/2)=6, 10/1=10, 6 +10=16. Correct. So that works.But maybe there are other n and f? For example, n=2. Let's try n=2 and see if there's an f ∈[0,1) that satisfies the equation.If n=2, then x=2 + f, and the equation is:8/f =9/(2 + f) +10/2 =9/(2 + f) +5So, 8/f -5 =9/(2 + f)Multiply both sides by f(2 + f):8(2 + f) -5f(2 + f) =9fExpand:16 +8f -10f -5f² =9fSimplify:16 -2f -5f² =9fBring all terms to left:16 -2f -5f² -9f =0Combine like terms:16 -11f -5f² =0Multiply by -1:5f² +11f -16=0Compute discriminant D=121 + 320=441=21²Solutions: f=(-11 ±21)/10So, f=(10)/10=1 or f=(-32)/10=-3.2But f must be in [0,1). So f=1 is not allowed (since fractional part is less than 1), and f=-3.2 is negative. Therefore, no solution for n=2.Similarly, try n=3:Equation:8/f =9/(3 + f) +10/3Multiply both sides by 3f(3 + f):8*3(3 + f) =9*3f +10f(3 + f)Compute left side:24(3 + f)=72 +24fRight side:27f +10f(3 + f)=27f +30f +10f²=57f +10f²Bring all terms to left:72 +24f -57f -10f²=0Simplify:72 -33f -10f²=0Multiply by -1:10f² +33f -72=0Discriminant D=33² +4*10*72=1089 +2880=3969=63²Solutions: f=(-33 ±63)/20First solution: (30)/20=1.5, which is >1, invalid. Second: (-96)/20=-4.8, invalid. So no solution for n=3.n=4:Equation:8/f =9/(4 + f) +10/4=9/(4 + f)+2.5Multiply by f(4 + f):8(4 + f)=9f +2.5f(4 + f)Compute left:32 +8fRight:9f +10f +2.5f²=19f +2.5f²Bring all terms to left:32 +8f -19f -2.5f²=0Simplify:32 -11f -2.5f²=0Multiply by 2 to eliminate decimal:64 -22f -5f²=0Rearrange:5f² +22f -64=0Discriminant D=484 +1280=1764=42²Solutions:f=(-22 ±42)/10First:20/10=2>1, invalid. Second:(-64)/10=-6.4 invalid. No solution.Similarly, n=5:8/f =9/(5 + f) +2Multiply by f(5 + f):8(5 + f)=9f +2f(5 + f)Left:40 +8fRight:9f +10f +2f²=19f +2f²Bring left:40 +8f -19f -2f²=0Simplify:40 -11f -2f²=0Multiply by -1:2f² +11f -40=0Discriminant D=121 +320=441=21²Solutions:f=(-11 ±21)/4First:10/4=2.5>1, invalid. Second:(-32)/4=-8 invalid.So, as n increases, the solutions for f either become greater than 1 or negative. Therefore, no solutions for n≥2.What about n=1? We already saw that n=1 gives f=0.5, which is valid. Let's check n=0 case again, even though earlier we thought it's invalid.If n=0, then x ∈[0,1), so [x]=0, {x}=x. Then the equation is 8/x =9/x +10/0. But 10/0 is undefined, so n=0 is impossible. Therefore, the only solution is x=3/2.Wait, but let's check for n=1 but different f. Suppose n=1, but maybe there is another solution? Let's see.For n=1, the equation is:8/f =9/(1 + f) +10/1=9/(1 + f) +10Multiply both sides by f(1 + f):8(1 + f)=9f +10f(1 + f)Left:8 +8fRight:9f +10f +10f²=19f +10f²Bring all terms left:8 +8f -19f -10f²=0Simplify:8 -11f -10f²=0Multiply by -1:10f² +11f -8=0Which is the same equation as before, leading to f=(-11 ±21)/20= (10)/20=0.5 or (-32)/20=-1.6. Only f=0.5 is valid. So yes, only one solution.Therefore, the only solution is x=3/2.But let me check if there could be solutions where n is negative, even though we thought not. Let's try n=-1. Wait, but if n=-1, then x ∈[-1,0). Then [x]=-1, {x}=x - (-1)=x +1. So {x}=x +1 ∈[0,1) because x ∈[-1,0). So {x} ∈[0,1). Then let's plug into the equation:8/{x} =9/x +10/[x]But [x]=-1, so 10/[x]=10/(-1)=-10.{x}=x +1, so 8/(x +1)=9/x -10So:8/(x +1) +10=9/xMultiply both sides by x(x +1):8x +10x(x +1)=9(x +1)Expand:8x +10x² +10x=9x +9Simplify:10x² +18x -9x -9=010x² +9x -9=0Discriminant D=81 +360=441=21²Solutions: x=(-9 ±21)/20First:12/20=0.6, but x must be in [-1,0), so invalid.Second:-30/20=-1.5, which is less than -1, so also invalid. Therefore, no solution here.Similarly, n=-2. Let's see:If n=-2, x ∈[-2,-1), [x]=-2, {x}=x +2 ∈[0,1). Equation:8/{x} =9/x +10/[x]So 8/(x +2)=9/x +10/(-2)=9/x -5So:8/(x +2) +5=9/xMultiply by x(x +2):8x +5x(x +2)=9(x +2)Expand:8x +5x² +10x=9x +18Simplify:5x² +18x -9x -18=05x² +9x -18=0Discriminant=81 +360=441=21²Solutions:x=(-9 ±21)/10First:12/10=1.2, not in [-2,-1). Second:-30/10=-3, which is less than -2, invalid.Therefore, no solutions in n=-2.Similarly, other negative n's will likely not yield solutions. Therefore, only solution is x=3/2.Thus, the answer is x=3/2, which is 1.5. So boxed, it's boxed{dfrac{3}{2}}.Final AnswerThe solution to the equation is boxed{dfrac{3}{2}}.</think>Given the equation:frac{8}{{x}} = frac{9}{x} + frac{10}{[x]}where ([x]) is the greatest integer less than or equal to (x) (the floor function) and ({x} = x - [x]) (the fractional part of (x)).1. Express (x) in terms of its integer and fractional parts: - Let (x = n + f) where (n = [x]) (an integer) and (f = {x}) (a fractional part in ([0, 1))).2. Substitute (x = n + f) into the equation: - The equation becomes: frac{8}{f} = frac{9}{n + f} + frac{10}{n} 3. Solve the equation: - Combine the terms on the right-hand side: frac{8}{f} - frac{9}{n + f} = frac{10}{n} - Find a common denominator and simplify: frac{8(n + f) - 9f}{f(n + f)} = frac{10}{n} - Simplify the numerator: frac{8n - f}{f(n + f)} = frac{10}{n} - Cross-multiply to clear the fractions: (8n - f)n = 10f(n + f) - Expand and simplify: 8n^2 - nf = 10fn + 10f^2 8n^2 - 11fn - 10f^2 = 0 - Solve the quadratic equation for (f) using the quadratic formula: f = frac{-11n pm 21n}{20} - The valid solution (considering (f in [0, 1))) is: f = frac{n}{2} 4. Determine valid values for (n) and (f): - For (f) to be valid, (0 leq f < 1), so (n) must be 1 (since (n) is a positive integer): f = frac{1}{2} - Therefore, (x = n + f = 1 + frac{1}{2} = frac{3}{2}).5. Verify the solution: - Check (x = frac{3}{2}): - ([x] = 1), ({x} = frac{1}{2}) - Left-hand side: (frac{8}{frac{1}{2}} = 16) - Right-hand side: (frac{9}{frac{3}{2}} + frac{10}{1} = 6 + 10 = 16)Thus, the solution to the equation is (boxed{dfrac{3}{2}}).]

🔑:Answer: frac{3}{2}.Solution: Note that x cannot be negative, because in such a case the right-hand side would be negative. Moreover, x cannot be an integer, because the fractional part would be 0, and it cannot belong to the interval [0,1), because the integer part would be 0. Let's consider the possible cases:- If [x]=1, then frac{8}{{x}}=frac{9}{1+{x}}+10. Then {x}=frac{1}{2}, hence x=frac{3}{2};- If [x]=2 then frac{8}{{x}}=frac{9}{2+{x}}+5, from which we get {x}=1, which is impossible.- If [x] geqslant 3, then frac{9}{x}+frac{10}{[x]}<3+frac{10}{3}<8<frac{8}{{x}}.

🧠:[<think>Okay, let's see. I need to find the number of rational terms in the sequence S₁, S₂, ..., S₂₀₀₈, where each Sₙ is the sum of the first n terms of the sequence {aₙ} defined by aₙ = 1 / [(n+1)√n + n√(n+1)]. The options are from A to D, with answers between 43 and 46. Hmm.First, I should probably try to simplify the general term aₙ. The denominator is (n+1)√n + n√(n+1). That looks a bit complicated. Maybe rationalizing the denominator would help? Since the denominator has radicals, rationalizing might simplify the expression.To rationalize, I can multiply the numerator and denominator by the conjugate of the denominator. The conjugate of (n+1)√n + n√(n+1) is (n+1)√n - n√(n+1). Let's try that:aₙ = [1 * ((n+1)√n - n√(n+1))] / [((n+1)√n + n√(n+1)) * ((n+1)√n - n√(n+1))]Calculating the denominator:= [(n+1)√n]² - [n√(n+1)]²= (n+1)² * n - n² * (n+1)= n(n+1)² - n²(n+1)Factor out n(n+1):= n(n+1)[(n+1) - n]= n(n+1)(1)= n(n+1)So the denominator simplifies to n(n+1). Therefore, aₙ becomes:aₙ = [(n+1)√n - n√(n+1)] / [n(n+1)]Let me write that again:aₙ = [(n+1)√n - n√(n+1)] / [n(n+1)]Simplify numerator and denominator:Divide numerator and denominator by n(n+1):Wait, actually, let's split the fraction:= [(n+1)√n]/[n(n+1)] - [n√(n+1)]/[n(n+1)]Simplify each term:First term: [(n+1)/n(n+1)] * √n = (1/n)√n = √n / n = 1/√nSecond term: [n/n(n+1)] * √(n+1) = [1/(n+1)] * √(n+1) = √(n+1)/(n+1) = 1/√(n+1)So, aₙ simplifies to:aₙ = 1/√n - 1/√(n+1)Oh, that's a telescoping series! So when we sum the terms from n=1 to n=k, the sum Sₖ would be:Sₖ = Σ (from n=1 to k) [1/√n - 1/√(n+1)]This telescopes to:[1/√1 - 1/√2] + [1/√2 - 1/√3] + ... + [1/√k - 1/√(k+1)]All the intermediate terms cancel out, leaving:Sₖ = 1 - 1/√(k+1)So Sₖ = 1 - 1/√(k+1)Now, the question is asking for the number of rational terms in the sequence S₁, S₂, ..., S₂₀₀₈. So we need to find how many times Sₖ is rational for k from 1 to 2008.Since Sₖ = 1 - 1/√(k+1), for Sₖ to be rational, 1/√(k+1) must be rational because 1 is rational. Therefore, 1/√(k+1) must be rational. Let's denote m = k+1, so m ranges from 2 to 2009.So, 1/√m is rational. Let's think about when is 1/√m rational. For 1/√m to be rational, √m must be rational, because the reciprocal of a rational number is rational. So √m must be rational. But √m is rational if and only if m is a perfect square. Because the square root of an integer is either irrational or an integer. So √m is rational only when m is a perfect square.Therefore, m must be a perfect square. So m = t², where t is a positive integer. Since m = k + 1, then k + 1 = t², so k = t² - 1. Thus, for k to be in the range 1 ≤ k ≤ 2008, t² - 1 ≤ 2008 => t² ≤ 2009.Therefore, t must satisfy t² ≤ 2009. Let's compute the largest integer t such that t² ≤ 2009.Compute √2009. Since 44² = 1936, 45²=2025. So √2009 is between 44 and 45. Specifically, 44² = 1936, so 44² + 73 = 2009. Therefore, t can be from 1 to 44, because 44² = 1936, which is less than 2009, and 45² = 2025, which is greater than 2009.Wait, but m = k +1 = t², and m ranges from 2 to 2009. So t starts from t=2 (since m=2, t=√2 is not integer. Wait, hold on. Wait, if m must be a perfect square, then m = t² where t is integer ≥2? Wait, but m starts at 2 (when k=1, m=2). So t starts at t=2, but m=2 is not a perfect square. Wait, perhaps t starts from t=1.Wait, m = k +1, which ranges from 2 (when k=1) to 2009 (when k=2008). So m is between 2 and 2009. But m must be a perfect square. So the smallest perfect square ≥2 is 4 (t=2), and the largest perfect square ≤2009 is 44²=1936. Because 44²=1936 and 45²=2025>2009. Therefore, the perfect squares m in [2,2009] are from 2²=4 up to 44²=1936. So t ranges from 2 to 44. Thus, the number of perfect squares in m is 44 - 2 +1 = 43? Wait, no. Wait, t ranges from 2 to 44 inclusive. The number of terms is 44 - 2 +1 = 43. But wait, t=2: m=4, t=3: m=9,..., t=44: m=1936. So how many terms is that? Let's compute: from t=2 to t=44 inclusive, that's 43 terms. Wait, 44 -2 = 42, plus 1 is 43. So 43 terms. But the options include 43, 44, 45, 46. So answer A is 43. But let's verify.Wait, but m must be a perfect square between 2 and 2009. The perfect squares in that interval start at 1²=1, but m is at least 2, so the first perfect square is 2²=4. The last perfect square is 44²=1936. So t from 2 to 44 inclusive. So total number is 44 -1 = 43? Wait, t=2 to t=44 is 43 numbers: 44-2+1=43. Yes. So 43 terms. But let's check with specific numbers.Wait, when t=2, m=4, so k=4-1=3. Then S₃ is rational.Wait, hold on. Wait, m = k +1 = t². So k = t² -1. Therefore, the values of k are t² -1 where t is integer ≥2, and k ≤2008. So t² -1 ≤2008 => t² ≤2009. As before, t ≤44. So t starts at t=2 (k=3) up to t=44 (k=44² -1=1936-1=1935). Then t=45 would give k=2025-1=2024>2008, which is outside the range.Wait, but wait, when t=1, m=1, so k=0, which is not in N*. So starting t=2. Therefore, the values of k where Sₖ is rational are k=3,8,15,...,1935. How many terms are there?From t=2 to t=44, each t gives a k. The number of terms is 44 -1=43. Wait, t starts at 2 and ends at 44, so total number is 44 -1=43? Wait, no, the number of integers from a to b inclusive is b -a +1. So from t=2 to t=44, inclusive, that's 44 -2 +1=43. So 43 terms.But wait, let's check for some small t:t=2: k=2² -1=4 -1=3t=3: k=9 -1=8t=4: k=16 -1=15...t=44: k=44² -1=1936 -1=1935So k=3,8,15,...,1935. Now, how many terms is that?The number of terms is the number of t's, which is t=2 to t=44, so 43 terms. Therefore, the answer is 43 terms, option A.Wait, but hold on. Let me check if k=3 is within 1 to 2008. Yes, k=3 is valid. Similarly, t=44 gives k=1935, which is less than 2008. So that's correct.But let's check the initial term. When k=1, S₁ = a₁. Let's compute S₁. According to the formula Sₖ =1 -1/√(k+1). So S₁=1 -1/√2, which is irrational. Similarly, S₂=1 -1/√3, irrational. S₃=1 -1/√4=1 -1/2=1/2, which is rational. So S₃ is the first rational term. Then S₈=1 -1/√9=1 -1/3=2/3, rational. So every k= t² -1 where t≥2 gives a rational Sₖ. So total number is t=2 to t=44, 43 terms. Therefore, answer A: 43 terms.But wait, the options are (A) 43, (B)44, (C)45, (D)46. But maybe I made a mistake in the counting? Let's check again.If t ranges from 2 to 44 inclusive, that's 43 terms. But wait, t=2 gives k=3, t=3 gives k=8,..., t=44 gives k=1935. So 43 values. However, maybe the question counts k=0? No, because n is in N*, which is positive integers. So k starts at 1, so k=0 is excluded. So answer is 43 terms. So A.But wait, the problem states that n ∈ N^*, which is the set of positive integers. So k is from 1 to 2008. Then S₁ corresponds to k=1, S₂ to k=2, ..., S₂₀₀₈ to k=2008. So the sequence S₁, S₂, ..., S₂₀₀₈. So the values of k where Sₖ is rational are those for which k+1 is a perfect square. So k+1 = t², so t from 2 to 44 as above, leading to 43 terms.But wait, maybe I miscalculated. Let's compute t from 1 to 44. If t=1, then k+1=1, so k=0, which is invalid. So t starts at 2, leading to k=3. So total t from 2 to 44 inclusive: 43 terms.Alternatively, if we think of m=k+1 being a perfect square, m ranges from 2 to 2009. The perfect squares in that interval are from 2²=4 up to 44²=1936. The number of perfect squares is floor(√2009) -1. Since √2009≈44.8, floor(√2009)=44. Then number of perfect squares is 44 -1=43? Wait, floor(√2009) is 44, but the number of squares from 1² to 44² is 44. But since we are starting from 2²=4 up to 44²=1936, that's 44 -1=43 terms. So yes, 43. So answer is A.But the options have 43 as A. But let me check once again.Wait, m must be a perfect square. m ranges from 2 to 2009. The perfect squares in this interval are 2²=4, 3²=9, ..., 44²=1936. The number of these perfect squares is 44 -1=43. Because from 2 to 44 inclusive, that's 43 numbers.But wait, 44 -2 +1=43. Correct. So 43 terms. So the answer is 43, option A.But wait, maybe I missed t=1? If t=1, then m=1, but k=0 which is not in the range. So no. Hence, 43 terms. Therefore, answer A.But the options given include (A) 43, (B)44, (C)45, (D)46. So the answer should be A. But wait, let me check once again.Suppose m=k+1 is a perfect square. So m=4,9,16,...,1936. How many terms are there between 4 and 1936 inclusive, stepping by squares?Number of terms: t from 2 to 44 inclusive. The number of integers from t=2 to t=44 is 44 -2 +1=43. Therefore, 43 terms. So answer is 43, option A.But let me check with specific examples. For t=2: m=4, k=3. t=44: m=1936, k=1935. Then the numbers k=3,8,15,...,1935. The number of terms is t=2 to t=44. Let me compute how many terms. For example, t=2 is first term, t=44 is last term. The count is 44 -2 +1=43. So 43 terms. So the answer is A.But maybe the answer is 44. Wait, maybe I need to check if 44² is less than or equal to 2009. 44²=1936. Then 44²=1936<=2009. So t=44 is included. So t=2 to t=44, which is 43 terms. So answer A.Alternatively, maybe the problem is considering m=k+1, and if m can be up to 2009, so 44²=1936 and 45²=2025. Since 1936<=2009, but 2025>2009. So t=44 is the largest. So t=2 to t=44, 43 terms.Therefore, the answer is A)43 terms.Final Answerboxed{A}</think>Given the sequence ({a_n}) with the general term formula (a_n = frac{1}{(n+1)sqrt{n} + nsqrt{n+1}}) for (n in mathbb{N}^*), we need to find the number of rational terms in the sequence (S_1, S_2, ldots, S_{2008}), where (S_n) is the sum of the first (n) terms of the sequence.First, we simplify the general term (a_n) by rationalizing the denominator:[a_n = frac{1}{(n+1)sqrt{n} + nsqrt{n+1}} times frac{(n+1)sqrt{n} - nsqrt{n+1}}{(n+1)sqrt{n} - nsqrt{n+1}}]The denominator simplifies to (n(n+1)), leading to:[a_n = frac{(n+1)sqrt{n} - nsqrt{n+1}}{n(n+1)} = frac{1}{sqrt{n}} - frac{1}{sqrt{n+1}}]This shows that the sequence ({a_n}) is a telescoping series. The sum (S_k) of the first (k) terms is:[S_k = sum_{n=1}^k left( frac{1}{sqrt{n}} - frac{1}{sqrt{n+1}} right) = 1 - frac{1}{sqrt{k+1}}]For (S_k) to be rational, (frac{1}{sqrt{k+1}}) must be rational. This requires (sqrt{k+1}) to be rational, which implies (k+1) must be a perfect square. Let (k+1 = t^2) where (t) is a positive integer. Then (k = t^2 - 1).We need (k) to be in the range (1 leq k leq 2008), so:[1 leq t^2 - 1 leq 2008 implies 2 leq t^2 leq 2009]The largest integer (t) such that (t^2 leq 2009) is 44 (since (44^2 = 1936) and (45^2 = 2025)). Therefore, (t) ranges from 2 to 44, inclusive. The number of integers from 2 to 44 is:[44 - 2 + 1 = 43]Thus, the number of rational terms in the sequence (S_1, S_2, ldots, S_{2008}) is (boxed{A}).,<think>Okay, so I need to find the number of rational terms in the sequence S₁, S₂, ..., S₂₀₀₈, where each Sₙ is the sum of the first n terms of the sequence {aₙ} defined by aₙ = 1 / [(n+1)√n + n√(n+1)]. The options are from (A) 43 to (D) 46. Hmm, let's start by understanding the problem step by step.First, let's write out the general term formula again to make sure I have it right:aₙ = 1 / [(n + 1)√n + n√(n + 1)]This looks a bit complicated, but maybe I can simplify it somehow. The denominator has two terms: (n + 1) times the square root of n, and n times the square root of (n + 1). Maybe rationalizing the denominator would help here. That's a common technique when dealing with square roots in denominators.To rationalize the denominator, I can multiply both the numerator and denominator by the conjugate of the denominator. The conjugate of (n + 1)√n + n√(n + 1) would be (n + 1)√n - n√(n + 1). Let's try that:Multiply numerator and denominator by [(n + 1)√n - n√(n + 1)]:aₙ = [1 * ((n + 1)√n - n√(n + 1))] / [((n + 1)√n + n√(n + 1)) * ((n + 1)√n - n√(n + 1))]Let me compute the denominator first. It's a difference of squares, so it should be:[(n + 1)√n]² - [n√(n + 1)]²Calculating each term:First term: (n + 1)² * n = (n² + 2n + 1) * n = n³ + 2n² + nSecond term: n² * (n + 1) = n³ + n²So subtracting them:(n³ + 2n² + n) - (n³ + n²) = n³ + 2n² + n - n³ - n² = n² + nTherefore, the denominator simplifies to n² + n = n(n + 1)So now, the denominator is n(n + 1), and the numerator is (n + 1)√n - n√(n + 1). Therefore:aₙ = [(n + 1)√n - n√(n + 1)] / [n(n + 1)]Hmm, let's split this fraction into two terms:aₙ = [(n + 1)√n / (n(n + 1))] - [n√(n + 1) / (n(n + 1))]Simplifying each term:First term: (n + 1)√n / [n(n + 1)] = √n / n = 1/√nSecond term: n√(n + 1) / [n(n + 1)] = √(n + 1)/(n + 1) = 1/√(n + 1)So, putting it all together:aₙ = (1/√n) - (1/√(n + 1))Oh! That's a telescoping term! That's a big realization. Because when you sum telescoping terms, most of them cancel out. So the sum Sₙ = a₁ + a₂ + ... + aₙ will telescope, leaving only the first term of the first expression and the last term of the last expression.Let me verify that. Let's write out the first few terms:a₁ = (1/√1) - (1/√2)a₂ = (1/√2) - (1/√3)a₃ = (1/√3) - (1/√4)...aₙ = (1/√n) - (1/√(n + 1))Therefore, when we add them up:Sₙ = [1 - 1/√2] + [1/√2 - 1/√3] + [1/√3 - 1/√4] + ... + [1/√n - 1/√(n + 1)]All the intermediate terms cancel out, and we're left with:Sₙ = 1 - 1/√(n + 1)So, the sum of the first n terms is Sₙ = 1 - 1/√(n + 1). Now, the problem states that we need to find how many of the terms S₁, S₂, ..., S₂₀₀₈ are rational numbers.So, Sₖ is rational when 1 - 1/√(k + 1) is rational. Let's denote Sₖ = 1 - 1/√(k + 1). For Sₖ to be rational, 1/√(k + 1) must be rational, since 1 is rational and the difference of two rational numbers is rational. Wait, but 1/√(k + 1) needs to be rational. However, the square root of a positive integer is either integer or irrational. So, √(k + 1) is rational only if k + 1 is a perfect square, because the square root of a non-square integer is irrational. Therefore, √(k + 1) is rational if and only if k + 1 is a perfect square, which would make √(k + 1) an integer. Therefore, 1/√(k + 1) is rational only if √(k + 1) is an integer, i.e., k + 1 is a perfect square. Then 1/√(k + 1) = 1/m, where m is a positive integer, so Sₖ = 1 - 1/m, which is rational.Therefore, Sₖ is rational if and only if k + 1 is a perfect square. Therefore, the number of rational terms in S₁, S₂, ..., S₂₀₀₈ is equal to the number of perfect squares m² such that m² - 1 ≤ 2008. Wait, let's check:If k + 1 = m², then k = m² - 1. We need k ≤ 2008, so m² - 1 ≤ 2008 => m² ≤ 2009. Therefore, m ≤ sqrt(2009). Let's compute sqrt(2009):Well, 44² = 1936, 45² = 2025. So sqrt(2009) is between 44 and 45. Therefore, m can be from 1 to 44, since 44² = 1936, and 45² = 2025 which is greater than 2009. Wait, but wait, m must be such that m² - 1 ≤ 2008.So m² ≤ 2008 + 1 = 2009. So m is the floor of sqrt(2009). Since sqrt(2009) ≈ 44.82, so floor(sqrt(2009)) = 44. Therefore, m can be 1, 2, ..., 44. Hence, there are 44 values of m, which would give k = m² - 1. So that would correspond to S_{m² - 1} being rational. Therefore, there are 44 such terms. Wait, but let's check if m starts at 1. If m=1, then k =1² -1=0, but k must be in N*, so n starts at 1. Wait, original sequence is defined for n ∈ N*, which is positive integers. So the terms S₁, S₂, ..., S₂₀₀₈ are sums from n=1 to n=2008. Therefore, k ranges from 1 to 2008. So when m=1, k=0, which is not in our range. Therefore, m starts at m=2?Wait, hold on. Let's re-examine. If k + 1 = m², then k = m² -1. Since k must be ≥1 (because S₁ corresponds to k=1), then m² -1 ≥1 => m² ≥2 => m ≥2. So m starts from 2 up to 44. Then, the number of m's is 43? Wait, m=2 to m=44 is 43 terms. But wait, let's check:m=2: k=4 -1=3: S₃ is rational.Wait, but when m=1: k=0, which is invalid. So m must start at 2? Wait, but if m=1, then k=0, which is not part of the sum terms. The first term S₁ is when k=1. So we need to find m such that m² -1 is between 1 and 2008. So m² -1 ≥1 => m² ≥2 => m ≥2, and m² -1 ≤2008 => m² ≤2009 => m ≤44. So m ranges from 2 to 44 inclusive. Then, the number of integers from 2 to 44 inclusive is 44 - 2 +1 = 43. Therefore, 43 terms? But the options are (A) 43, (B)44, etc. Hmm.Wait, but maybe m=1 is allowed? Let me check. If m=1, then k=0. But k=0 is not in our sequence. The sums S₁ to S₂₀₀₈ correspond to k=1 to k=2008. So k=0 is excluded. So m starts at 2. But let's check if m=1 gives k=0, which is not in our range, so m=2 to m=44, inclusive. That's 43 terms. So answer is 43? But option (A) is 43. But let's check again.Alternatively, maybe m can start at 1 if k is allowed to be 0, but since the problem states n ∈ N^*, which is positive integers, so k starts at 1. Hence, m must start at m=2. So total number is 43. But let's verify with an example.Take m=2: k=2² -1=3. So S₃ is rational. What's S₃? Let's compute.S₃ =1 -1/√(3 +1)=1 -1/2=1/2, which is rational. So S₃ is rational. Similarly, m=3: k=8, so S₈=1 -1/√9=1 -1/3=2/3, rational. So indeed, each m from 2 to 44 gives a k=m² -1, and S_k is rational. Therefore, the number of m's is from m=2 to m=44. Let's compute how many numbers that is. 44 -2 +1=43. So 43 terms. So answer is (A)43.But wait, wait, let's check m=44: k=44² -1=1936 -1=1935. Then S₁₉₃₅=1 -1/√1936=1 -1/44=43/44, which is rational. Then m=45: k=45² -1=2025 -1=2024. But 2024 is beyond 2008, so it's not included. So the maximum m is 44, but since k=44² -1=1935 is less than 2008, then m=44 is included. So m ranges from 2 to 44, which is 43 terms. Therefore, the answer is 43, which is option (A). But the options given are (A)43, (B)44, (C)45, (D)46. So why is there a discrepancy?Wait, maybe I made a miscalculation here. Wait, when m=44, k=44² -1=1936-1=1935, which is less than 2008. So m=44 is allowed. Then, m=45 would give k=2024, which is too big. So m goes up to 44. So if m starts at 2, then numbers are m=2,3,...,44. That's 43 terms. However, maybe there's an off-by-one error here. Let me check m=1 gives k=0, which is invalid. So m=2 gives k=3, m=3 gives k=8,...,m=44 gives k=1935. So how many terms is that?From m=2 to m=44, inclusive. The number of integers is 44 - 2 +1 = 43. So 43 terms. Hence, answer is (A). But let's check if maybe m starts at 1 with k=0, but k=0 is not part of the sum. So no.Alternatively, perhaps there's a mistake in my initial step where I assumed that Sₖ is rational only if 1/√(k +1) is rational. Let me think again.Sₖ =1 -1/√(k +1). For Sₖ to be rational, 1/√(k +1) must be rational. Since 1 is rational, then 1 - q is rational if and only if q is rational. So indeed, 1/√(k +1) must be rational. As before, √(k +1) must be rational, hence an integer, so k +1 must be a perfect square. Therefore, k = m² -1 where m is an integer ≥1, but k must be ≥1. Therefore, m² -1 ≥1 => m² ≥2 => m ≥2. Hence, m ranges from 2 to 44 inclusive, which is 43 terms. So the answer should be (A)43. But the options given have (B)44. Hmm.Wait, but let me check another approach. Maybe when m=1, k=0: S₀=0? But the problem states the sequence starts at S₁. So S₀ isn't considered. Therefore, m starts at 2. So the number of possible m's is 43. However, maybe the problem counts m=1? Let me think. Wait, when m=1, k +1 =1 =>k=0. So S₀=0, which is rational. But since the problem asks for S₁ to S₂₀₀₈, S₀ isn't included. Therefore, m=2 to m=44. So 43 terms. Hence, answer (A).But maybe the problem counts m=1? Let's check. If m=1, then k +1 =1, so k=0. S₀ would be the sum of the first 0 terms, which is 0. But since we are considering S₁ to S₂₀₀₈, we don't include S₀. Therefore, answer is 43. So why is 44 an option?Wait, maybe there's a miscalculation in the upper limit. Wait, sqrt(2009) is approximately 44.82, so m=44 is the largest integer where m² ≤2009. So m=44 gives k=44² -1=1936-1=1935. Then the next m=45 would give k=2024, which is beyond 2008. Therefore, the maximum m is 44. So m=2 to m=44 inclusive. So that is 44-2+1=43 terms.Alternatively, maybe there's a miscalculation here. Wait, if m starts at 1, then even though k=0 is excluded, perhaps m=1 is allowed? But k=0 is excluded, so m starts at 2. So total number is 43. Therefore, answer should be (A)43.Wait, but perhaps my error is here: the formula Sₖ=1 -1/√(k +1). So to have Sₖ rational, 1/√(k +1) must be rational. Therefore, √(k +1) must be rational, so must be an integer. Thus, k +1 must be a perfect square. So k +1=m² =>k=m² -1. So k ranges over m² -1 where m is integer ≥2 (since k≥1). So m can be 2,3,...,44. So number of terms is 44 -1=43. So 43. Therefore, answer (A). But maybe the problem is considering m from 1 to 44, but k=0 is excluded, so 44 total m's, but subtract 1 for m=1, leading to 43. Therefore, answer is (A)43.Alternatively, maybe the problem counts S₁ as a rational term. Let's check S₁. If k=1, then S₁=1 -1/√2, which is irrational. So S₁ is not rational. Similarly, S₂=1 -1/√3, irrational. S₃=1 -1/√4=1 -1/2=1/2, which is rational. So S₃ is the first rational term. Then S₈=1 -1/3=2/3, rational, etc. So the first rational term is at k=3 (m=2), and the last is at k=1935 (m=44). So total terms: m=2 to m=44, which is 43 terms. So answer (A). But why is option (B)44 present? Maybe I made a mistake in counting.Wait, 44 -2 +1=43. Let's see. From m=2 to m=44, inclusive. The number of integers is calculated as (last - first)/step +1. Here, step is 1. So (44 -2)/1 +1=42 +1=43. So 43 terms. Therefore, answer (A). So why is there an option for 44? Maybe the problem includes m=1? But m=1 gives k=0, which is not in the range. Alternatively, maybe the problem counts m from 1 to 44, giving 44 terms, but since k=0 is excluded, subtract 1, giving 43. Alternatively, maybe there's an error in the problem's options.Alternatively, perhaps there's a miscalculation in the upper limit. Let's check the maximum m such that k = m² -1 ≤2008. So m² ≤2009. The square root of 2009 is approx 44.82, so m=44, m²=1936. 1936 -1=1935 ≤2008. Then m=44. So m ranges from 2 to 44. So 43 terms. Therefore, answer (A). So why does the option (B)44 exist? Maybe I made a mistake in assuming m starts at 2. Let me check m=1. If m=1, then k=0. S₀=0, which is rational. But since we are only considering S₁ to S₂₀₀₈, S₀ is excluded. Therefore, m starts at 2. Therefore, answer is 43. So (A). But maybe the problem includes m=1? If so, then m=1 gives k=0, but that's not in the range. So answer remains 43.Alternatively, perhaps the problem is in Chinese and the original wording might have a different interpretation. But given the translation, it says "the number of rational terms in the sequence S₁, S₂, ..., S₂₀₀₈". So S₁ to S₂₀₀₈. Therefore, k=1 to 2008. So m must be from 2 to 44, giving k=3 to k=1935. The number of m's is 43. So answer is (A)43. But the options have (B)44. Maybe there is a miscalculation here. Let me check m=44: k=44² -1=1936 -1=1935, which is within 2008. So m=44 is valid. Then m=45 gives k=2024, which is over. So m=2 to m=44 inclusive. So 44 -2 +1=43. Therefore, answer (A). So why is option (B)44 there? Perhaps I'm missing something.Wait, another approach: maybe Sₖ is rational when √(k +1) is rational. But √(k +1) is rational if and only if k +1 is a perfect square. Therefore, k +1 = m², so k = m² -1. So for k in 1 to 2008, m² -1 must be between 1 and 2008. Therefore, m² between 2 and 2009. Therefore, m ranges from ceiling(√2)=2 to floor(√2009)=44. Therefore, m=2 to 44. Number of terms:44 -2 +1=43. So 43 terms, so answer (A). So why is (B)44 presented? Unless...Wait, maybe the formula is different. Wait, let's check if Sₙ=1 -1/√(n +1). Let me verify with n=1: a₁=1/(2*1 +1*√2). Wait, original a₁=1/[(1+1)√1 +1√2]=1/[2*1 +1*√2]=1/(2 +√2). Then rationalizing, a₁=(2 -√2)/( (2 +√2)(2 -√2) )=(2 -√2)/(4 -2)= (2 -√2)/2=1 - (√2)/2. Wait, but according to earlier steps, a₁=1/√1 -1/√2=1 -1/√2. Which is the same as 1 - (√2)/2. So S₁= a₁=1 -1/√2. Which is irrational. So S₁ is irrational. Then S₂= a₁ + a₂= (1 -1/√2) + (1/√2 -1/√3)=1 -1/√3. Which is irrational. S₃=1 -1/√4=1 -1/2=1/2. Which is rational. So S₃ is the first rational term. Then S₈=1 -1/3=2/3. Etc. So the general term S_{m² -1}=1 -1/m. So for m=2, S₃=1 -1/2=1/2; m=3, S₈=1 -1/3=2/3; ... ; m=44, S_{1935}=1 -1/44=43/44. So these are all rational terms.Therefore, the number of rational terms is equal to the number of integers m from 2 to 44 inclusive. So m=2 corresponds to k=3, m=3 to k=8,...,m=44 to k=1935. Each m from 2 to 44 gives a unique k=m² -1 in the range 3 ≤k ≤1935, which is within 1 ≤k ≤2008. Therefore, the total number of m's is 44 -2 +1=43.Therefore, the correct answer should be (A)43. But the options given include (B)44. Hmm. Is there a possibility that the problem is considering m starting at 1? If m=1, then k=0, which is not in our range. So no. Maybe there's another error.Wait, maybe I made a mistake in the telescoping sum. Let's check again. The general term aₙ=1/√n -1/√(n +1). So sum from n=1 to N is (1 -1/√2) + (1/√2 -1/√3) + ... + (1/√N -1/√(N +1))=1 -1/√(N +1). So S_N=1 -1/√(N +1). Therefore, for S_N to be rational, 1/√(N +1) must be rational, which requires √(N +1) is rational, hence integer, hence N +1 is a perfect square, so N= m² -1. So N ranges from m=2 (N=3) to m=44 (N=1935). Therefore, the number of such N is 44 -2 +1=43. Therefore, answer (A). So unless there's an off-by-one error, but I don't see where.Alternatively, maybe the problem is considering N=1, but S₁ is irrational. So no. Therefore, the answer must be 43, which is option (A). But since the original problem's options are up to (D)46, and the correct answer is likely (A)43. However, given that in Chinese math problems sometimes there might be different interpretations, but based on the analysis above, 43 seems correct. However, maybe I made a mistake in the calculation of m's.Wait, let's check m=2 gives N=3; m=44 gives N=1935. Let's count how many perfect squares are between 2 and 2009 for m². Since m starts at 2, m=2 gives 4, m=3 gives 9, up to m=44 gives 1936. So the number of perfect squares between 4 and 1936 inclusive. The number of squares from 2² to 44² is 44 -2 +1=43. Therefore, 43 terms. So the answer is (A)43.Therefore, I think the correct answer is (A)43.Final Answerboxed{A}</think>Given the sequence ({a_n}) with the general term formula (a_n = frac{1}{(n+1)sqrt{n} + nsqrt{n+1}}) for (n in mathbb{N}^*), we need to find the number of rational terms in the sequence (S_1, S_2, ldots, S_{2008}), where (S_n) is the sum of the first (n) terms of the sequence.First, we simplify the general term (a_n) by rationalizing the denominator:[a_n = frac{1}{(n+1)sqrt{n} + nsqrt{n+1}} cdot frac{(n+1)sqrt{n} - nsqrt{n+1}}{(n+1)sqrt{n} - nsqrt{n+1}} = frac{(n+1)sqrt{n} - nsqrt{n+1}}{n(n+1)}]This simplifies to:[a_n = frac{1}{sqrt{n}} - frac{1}{sqrt{n+1}}]The sum (S_n) of the first (n) terms is a telescoping series:[S_n = left(1 - frac{1}{sqrt{2}}right) + left(frac{1}{sqrt{2}} - frac{1}{sqrt{3}}right) + cdots + left(frac{1}{sqrt{n}} - frac{1}{sqrt{n+1}}right)]Most terms cancel out, leaving:[S_n = 1 - frac{1}{sqrt{n+1}}]For (S_n) to be rational, (frac{1}{sqrt{n+1}}) must be rational. This occurs if and only if (sqrt{n+1}) is an integer, meaning (n+1) must be a perfect square. Let (n+1 = m^2) for some integer (m). Then (n = m^2 - 1).We need (n leq 2008), so:[m^2 - 1 leq 2008 implies m^2 leq 2009]The largest integer (m) such that (m^2 leq 2009) is 44 (since (44^2 = 1936) and (45^2 = 2025)).Thus, (m) ranges from 2 to 44 (since (n) must be a positive integer, (m=1) gives (n=0), which is not valid). The number of valid (m) values is (44 - 2 + 1 = 43).Therefore, the number of rational terms in the sequence (S_1, S_2, ldots, S_{2008}) is (boxed{A}).]

🔑:6 Becausebegin{aligned}a_{k} & =frac{1}{sqrt{k(k+1)}(sqrt{k+1}+sqrt{k})} & =frac{sqrt{k+1}-sqrt{k}}{sqrt{k(k+1)}} & =frac{1}{sqrt{k}}-frac{1}{sqrt{k+1}}(k=1,2, cdots),end{aligned}Sobegin{aligned}S_{n} & =sum_{k=1}^{n} a_{k} & =sum_{k=1}^{n}left(frac{1}{sqrt{k}}-frac{1}{sqrt{k+1}}right) & =1-frac{1}{sqrt{n+1}}end{aligned}Also, since sqrt{2009}<45, we have n+1=2^{2}, 3^{2}, cdots, 44^{2}. Therefore, among S_{1}, S_{2}, cdots, S_{2008}, there are 43 rational terms. Hence, the answer is A.

🧠:[<think>Okay, so I need to find all positive integer pairs {a, b} such that a²b + a + b is divisible by ab² + b + 7. Hmm, divisibility here means that when we divide a²b + a + b by ab² + b + 7, the remainder is zero. Let me write that out mathematically: ab² + b + 7 divides a²b + a + b. In other words, there exists some integer k such that a²b + a + b = k(ab² + b + 7). Since a and b are positive integers, both sides of the equation are positive. Maybe I can rearrange the equation to find some relationship between a and b. Let's try expanding the right side:a²b + a + b = k(ab² + b + 7) Expanding the right side: a²b + a + b = kab² + kb + 7kNow, let's move all terms to the left side to see if we can factor or find some expression:a²b + a + b - kab² - kb - 7k = 0 Hmm, maybe group terms with a and terms with b:a²b - kab² + a - kb + b - 7k = 0 Factor terms where possible:ab(a - kb) + a - kb + b - 7k = 0 Wait, not sure if that helps. Let me see another approach. Let's isolate terms with a:a²b + a = kab² + kb + 7k - b Factor a on the left:a(ab + 1) = k(ab² + b + 7) - bBut this might not lead anywhere immediately. Maybe it's better to express k in terms of a and b. Since k is an integer, perhaps we can write:k = (a²b + a + b) / (ab² + b + 7)So k must be a positive integer. Let's compute this fraction and see if we can bound k. Let's see:First, note that both numerator and denominator are positive. Let's consider some small values of b to see possible patterns.Start with b = 1:If b = 1, then the denominator becomes a*1² + 1 + 7 = a + 8. The numerator becomes a²*1 + a + 1 = a² + a + 1. So we need (a² + a + 1)/(a + 8) to be integer. Let's perform polynomial division:Divide a² + a + 1 by a + 8. Using polynomial long division:a + 8 ) a² + a + 1 a² divided by a is a. Multiply (a + 8) by a: a² + 8a Subtract from the dividend: (a² + a + 1) - (a² + 8a) = -7a + 1 Now, divide -7a by a: -7. Multiply (a + 8) by -7: -7a - 56 Subtract: (-7a + 1) - (-7a - 56) = 57 So the division gives a - 7 with a remainder of 57. Therefore, (a² + a + 1)/(a + 8) = a - 7 + 57/(a + 8). For this to be integer, 57 must be divisible by a + 8. So a + 8 divides 57. Since a is positive, a + 8 is at least 9. The divisors of 57 are 1, 3, 19, 57. But since a + 8 ≥9, possible divisors are 19 and 57. Therefore:Case 1: a + 8 = 19 ⇒ a = 11 Case 2: a + 8 = 57 ⇒ a = 49 Therefore, for b = 1, possible pairs are (11, 1) and (49, 1). Let me check these:For (11,1):Denominator: 11*1 + 1 +7 = 19 Numerator: 11²*1 +11 +1 = 121 +11 +1=133 133 divided by 19 is 7, which is integer. So that works.For (49,1):Denominator: 49 +8=57 Numerator:49² +49 +1=2401 +49 +1=2451 2451 divided by 57: 2451 ÷57=43, since 57*40=2280, 57*3=171, 2280+171=2451. So yes, 43. So that works. So two solutions here.Now, check b=2.Denominator: a*(2)^2 +2 +7=4a +9 Numerator: a²*2 +a +2=2a² +a +2 So need (2a² +a +2)/(4a +9) to be integer. Let's see if we can perform division or find a relationship.Let me write 2a² +a +2 divided by 4a +9. Let's try polynomial division.4a +9 ) 2a² + a + 2 Divide 2a² by 4a: (2a²)/(4a)= a/2. Hmm, not integer. Alternatively, perhaps manipulate the expression:Let me write 2a² +a +2 = q*(4a +9) + r, where q is the quotient and r is the remainder. Let q be some integer. Let's assume q is (something). Let me set variable q:Express 2a² + a + 2 = q(4a +9) + r. Since 4a +9 is linear, remainder r will be a constant. Let's find q and r.Divide 2a² +a +2 by 4a +9. Let me use polynomial division:Divide 2a² by 4a: (2a²)/(4a) = (a)/2. Multiply 4a +9 by a/2: 2a² + (9a)/2. Subtract from dividend:(2a² +a +2) - (2a² + (9a)/2) = (a - (9a)/2) +2 = (-7a/2) +2. The remainder is negative, which complicates things. Alternatively, perhaps manipulate the equation:Let me rearrange 2a² +a +2 = k(4a +9). So 2a² +a +2 =4k a +9k. Rearranged: 2a² + (1 -4k)a + (2 -9k)=0. Treat this as a quadratic in a. For integer solutions, the discriminant must be a perfect square.Discriminant D = (1 -4k)^2 - 4*2*(2 -9k) = (1 -8k +16k²) -16 +72k =16k² +64k -15. Hmm, this needs to be a perfect square. Let's compute D:D=16k² +64k -15. We need D to be a perfect square. Let me check for small positive integers k.k must be positive since all terms are positive.Start with k=1: D=16 +64 -15=65, not a square.k=2: 16*4 +64*2 -15=64 +128 -15=177, not a square.k=3:16*9 +64*3 -15=144 +192 -15=321, not a square.k=4:16*16 +64*4 -15=256 +256 -15=497, not a square.k=5:16*25 +64*5 -15=400 +320 -15=705, not a square.k=6:16*36 +64*6 -15=576 +384 -15=945, not a square.k=7:16*49 +64*7 -15=784 +448 -15=1217, not a square.k=8:16*64 +64*8 -15=1024 +512 -15=1521. 1521 is 39². So D=39²=1521. So for k=8, discriminant is 39². Therefore, possible solution.So for k=8:The quadratic in a is 2a² + (1 -32)a + (2 -72)=2a² -31a -70=0. Solve for a:a = [31 ±√(31² + 560)]/4. Wait, discriminant is 31² +4*2*70=961 +560=1521=39². Thus:a = [31 ±39]/4. So two solutions:(31 +39)/4=70/4=17.5, not integer.(31 -39)/4=(-8)/4=-2, not positive. So no solution. Hmm, interesting. Even though discriminant is a square, but the solutions are not positive integers. So k=8 gives invalid solutions.Check k=0: Not allowed since k must be positive. So maybe no solutions for b=2. Let me check k=0 even though k should be positive. If k=0, numerator would need to be 0, but numerator is 2a² +a +2 which is always positive. So no. So maybe b=2 has no solutions.Alternatively, maybe try specific values of a for b=2.Let’s compute (2a² +a +2)/(4a +9). Let's try small a values:a=1: (2 +1 +2)/(4 +9)=5/13, not integer.a=2: (8 +2 +2)/(8 +9)=12/17, nope.a=3: (18 +3 +2)/(12 +9)=23/21, nope.a=4: (32 +4 +2)/(16 +9)=38/25, nope.a=5: (50 +5 +2)/(20 +9)=57/29≈1.965, nope.a=6: (72 +6 +2)/(24 +9)=80/33≈2.424, nope.a=7: (98 +7 +2)/(28 +9)=107/37≈2.891, nope.a=8: (128 +8 +2)/(32 +9)=138/41≈3.365, nope.a=9: (162 +9 +2)/(36 +9)=173/45≈3.844, nope.a=10: (200 +10 +2)/(40 +9)=212/49≈4.326, nope.a=11: (242 +11 +2)/(44 +9)=255/53≈4.811, nope.a=12: (288 +12 +2)/(48 +9)=302/57≈5.298, nope.a=13: (338 +13 +2)/(52 +9)=353/61≈5.786, nope.a=14: (392 +14 +2)/(56 +9)=408/65≈6.276, nope.a=15: (450 +15 +2)/(60 +9)=467/69≈6.768, nope.It seems like for b=2, there are no solutions. Let's move to b=3.For b=3:Denominator: a*(3)^2 +3 +7=9a +10 Numerator: a²*3 +a +3=3a² +a +3 So need (3a² +a +3)/(9a +10) is integer. Let's try polynomial division.Divide 3a² +a +3 by 9a +10. Let me see:3a² ÷9a= a/3. Hmm, not integer. Alternatively, set up equation:3a² +a +3 =k*(9a +10). Rearranged:3a² +a +3=9ka +10k. Then:3a² + (1-9k)a + (3 -10k)=0. Quadratic in a. Discriminant must be perfect square.Discriminant D=(1-9k)^2 -4*3*(3 -10k)=1 -18k +81k² -36 +120k=81k² +102k -35. This needs to be a perfect square.Check for small k:k=1:81 +102 -35=148, not square.k=2:81*4 +102*2 -35=324 +204 -35=493, not square.k=3:81*9 +102*3 -35=729 +306 -35=1000, which is 10³, not a square.k=4:81*16 +102*4 -35=1296 +408 -35=1669. 1669 is prime, not square.k=5:81*25 +102*5 -35=2025 +510 -35=2500, which is 50². So D=50².So k=5. Then quadratic equation becomes:3a² + (1 -45)a + (3 -50)=3a² -44a -47=0.Solutions: [44 ±√(44² +4*3*47)]/(2*3). Compute discriminant:44² +564=1936 +564=2500=50². Thus:a=(44 ±50)/6.Positive solution: (44 +50)/6=94/6≈15.666… Not integer. Negative solution: (44 -50)/6=(-6)/6=-1. Not positive. So no solution. Hmm. k=5 gives no integer solutions. Let's check higher k:k=6:81*36 +102*6 -35=2916 +612 -35=3493, not square.k=0: Not possible since k must be positive. Maybe try some a values:For a=1: (3 +1 +3)/(9 +10)=7/19≈0.368, no.a=2: (12 +2 +3)/(18 +10)=17/28≈0.607, no.a=3: (27 +3 +3)/(27 +10)=33/37≈0.891, no.a=4: (48 +4 +3)/(36 +10)=55/46≈1.195, no.a=5: (75 +5 +3)/(45 +10)=83/55≈1.509, no.a=6: (108 +6 +3)/(54 +10)=117/64≈1.828, no.a=7: (147 +7 +3)/(63 +10)=157/73≈2.15, no.a=8: (192 +8 +3)/(72 +10)=203/82≈2.475, no.a=9: (243 +9 +3)/(81 +10)=255/91≈2.802, no.a=10: (300 +10 +3)/(90 +10)=313/100=3.13, no.a=11: (363 +11 +3)/(99 +10)=377/109≈3.458, no.a=12: (432 +12 +3)/(108 +10)=447/118≈3.788, no.a=13: (507 +13 +3)/(117 +10)=523/127≈4.118, no.a=14: (588 +14 +3)/(126 +10)=605/136≈4.448, no.a=15: (675 +15 +3)/(135 +10)=693/145≈4.779, no.a=16: (768 +16 +3)/(144 +10)=787/154≈5.11, no.a=17: (867 +17 +3)/(153 +10)=887/163≈5.44, no.Hmm, seems like b=3 also has no solutions. Let's try b=4.For b=4:Denominator: a*16 +4 +7=16a +11 Numerator: a²*4 +a +4=4a² +a +4 Need (4a² +a +4)/(16a +11) is integer. Let's set k=(4a² +a +4)/(16a +11). So 4a² +a +4 =k(16a +11). Rearranged:4a² +a +4=16k a +11k. Then, 4a² + (1 -16k)a + (4 -11k)=0. Quadratic in a. Discriminant must be square.Discriminant D=(1 -16k)^2 -4*4*(4 -11k)=1 -32k +256k² -16*4 +176k=256k² +144k -63. Needs to be a perfect square.Check small k:k=1:256 +144 -63=337, not square.k=2:256*4 +144*2 -63=1024 +288 -63=1249, not square.k=3:256*9 +144*3 -63=2304 +432 -63=2673, not square.k=4:256*16 +144*4 -63=4096 +576 -63=4609. 4609 is 67.9 squared? Wait, 67²=4489, 68²=4624. So 4609 is between them, not a square.k=0: Not allowed. Maybe try a values.Check a=1: (4 +1 +4)/(16 +11)=9/27=1/3, no.a=2: (16 +2 +4)/(32 +11)=22/43≈0.511, no.a=3: (36 +3 +4)/(48 +11)=43/59≈0.728, no.a=4: (64 +4 +4)/(64 +11)=72/75=0.96, no.a=5: (100 +5 +4)/(80 +11)=109/91≈1.197, no.a=6: (144 +6 +4)/(96 +11)=154/107≈1.439, no.a=7: (196 +7 +4)/(112 +11)=207/123≈1.682, which is 207 divided by 123. 123*1=123, 123*1.6=196.8, so ≈1.682, not integer.a=8: (256 +8 +4)/(128 +11)=268/139≈1.928, no.a=9: (324 +9 +4)/(144 +11)=337/155≈2.174, no.a=10: (400 +10 +4)/(160 +11)=414/171≈2.421, which simplifies to 414 ÷171=2.421. 171*2=342, 414-342=72. 72/171=24/57=8/19. So not integer.a=11: (484 +11 +4)/(176 +11)=499/187≈2.668, no.a=12: (576 +12 +4)/(192 +11)=592/203≈2.916, no.a=13: (676 +13 +4)/(208 +11)=693/219≈3.164. 219*3=657, 693-657=36. 36/219=12/73, not integer.a=14: (784 +14 +4)/(224 +11)=802/235≈3.413, no.a=15: (900 +15 +4)/(240 +11)=919/251≈3.66, no.Seems like no solutions for b=4 either. Let's maybe try b=7, since the denominator has a +7 term. Maybe b=7 is special.For b=7:Denominator: a*49 +7 +7=49a +14 Numerator: a²*7 +a +7=7a² +a +7 Need (7a² +a +7)/(49a +14) is integer. Let's see:Express as k=(7a² +a +7)/(49a +14). Multiply both sides by denominator:7a² +a +7 =49k a +14k. Rearranged:7a² + (1 -49k)a + (7 -14k)=0. Quadratic in a. Discriminant D=(1 -49k)^2 -4*7*(7 -14k)=1 -98k +2401k² -196 +392k=2401k² +294k -195. Needs to be square.Check k=1:2401 +294 -195=2500. 2500 is 50². So D=50². So k=1:Quadratic equation becomes:7a² + (1 -49)a + (7 -14)=7a² -48a -7=0.Solve: a=(48 ±√(48² +4*7*7))/14=(48 ±√(2304 +196))/14=(48 ±√2500)/14=(48 ±50)/14.Positive solution: (48 +50)/14=98/14=7. Negative solution: (48 -50)/14=-2/14=-1/7. Not valid. So a=7. Let's check:For a=7, b=7:Denominator:49*7 +7 +7=343 +14=357 Numerator:7*49*7 +7 +7=7*343 +14=2401 +14=2415 Check 2415 ÷357=6.769… Wait, no. Wait, 357*6=2142, 357*7=2499. 2415-2142=273. 273/357=0.765… So not integer. Wait, but according to our calculation, k=1 gives a=7. But when we plug in a=7, k=1, the equation is 7*7² +7 +7=7*49 +14=343 +14=357. Denominator is 49*7 +14=343 +14=357. So 357/357=1. So k=1. So it works. So (7,7) is a solution. Wait, but when I compute numerator and denominator:Wait, numerator is a²b +a +b=7²*7 +7 +7=343 +14=357. Denominator is ab² +b +7=7*49 +7 +7=343 +14=357. So 357 divides 357, which is true. So (7,7) is a valid solution. So that works. So that's a solution.But when I first calculated, I thought 2415 /357, but that was a mistake. Actually, numerator is 357, denominator is 357, so they are equal. Therefore, k=1. So (7,7) is a valid solution. So that's one pair.Let me check if there are other k values for b=7. For k=2:D=2401*4 +294*2 -195=9604 +588 -195=9997, which is not a square. 9997≈99.985, 100²=10000. So no.k=0: Not allowed. So only k=1 gives a solution here. Thus (7,7) is a solution. Let's note that.Maybe try b=5.For b=5:Denominator: a*25 +5 +7=25a +12 Numerator: a²*5 +a +5=5a² +a +5 Need (5a² +a +5)/(25a +12) is integer. Let's set k=(5a² +a +5)/(25a +12). So 5a² +a +5=25k a +12k. Rearranged:5a² + (1 -25k)a + (5 -12k)=0. Quadratic in a. Discriminant D=(1 -25k)^2 -4*5*(5 -12k)=1 -50k +625k² -100 +240k=625k² +190k -99. Needs to be square.Check k=1:625 +190 -99=716, not square.k=2:625*4 +190*2 -99=2500 +380 -99=2781, not square.k=3:625*9 +190*3 -99=5625 +570 -99=6096, not square.k=0: Not allowed. Let's try specific a values.a=1: (5 +1 +5)/(25 +12)=11/37≈0.297, no.a=2: (20 +2 +5)/(50 +12)=27/62≈0.435, no.a=3: (45 +3 +5)/(75 +12)=53/87≈0.609, no.a=4: (80 +4 +5)/(100 +12)=89/112≈0.794, no.a=5: (125 +5 +5)/(125 +12)=135/137≈0.985, no.a=6: (180 +6 +5)/(150 +12)=191/162≈1.179, no.a=7: (245 +7 +5)/(175 +12)=257/187≈1.374, no.a=8: (320 +8 +5)/(200 +12)=333/212≈1.571, no.a=9: (405 +9 +5)/(225 +12)=419/237≈1.767, no.a=10: (500 +10 +5)/(250 +12)=515/262≈1.965, no.a=11: (605 +11 +5)/(275 +12)=621/287≈2.163, no.a=12: (720 +12 +5)/(300 +12)=737/312≈2.362, no.a=13: (845 +13 +5)/(325 +12)=863/337≈2.56, no.a=14: (980 +14 +5)/(350 +12)=999/362≈2.76, no.a=15: (1125 +15 +5)/(375 +12)=1145/387≈2.958, no.a=16: (1280 +16 +5)/(400 +12)=1301/412≈3.158, no.a=17: (1445 +17 +5)/(425 +12)=1467/437≈3.357, no.a=18: (1620 +18 +5)/(450 +12)=1643/462≈3.556, no.a=19: (1805 +19 +5)/(475 +12)=1829/487≈3.755, no.a=20: (2000 +20 +5)/(500 +12)=2025/512≈3.955, no.Hmm, seems like no solutions here. Let's try b=5 not working. Maybe try b=7, already found (7,7). What about b=6.For b=6:Denominator: a*36 +6 +7=36a +13 Numerator: a²*6 +a +6=6a² +a +6 Need (6a² +a +6)/(36a +13) is integer. Let k=(6a² +a +6)/(36a +13). Then, 6a² +a +6=36k a +13k. Rearranged:6a² + (1 -36k)a + (6 -13k)=0. Quadratic in a. Discriminant D=(1 -36k)^2 -4*6*(6 -13k)=1 -72k +1296k² -144 +312k=1296k² +240k -143. Needs to be square.Check k=1:1296 +240 -143=1393, not square.k=2:1296*4 +240*2 -143=5184 +480 -143=5521, not square.k=0: Not allowed. Try a values.a=1: (6 +1 +6)/(36 +13)=13/49≈0.265, no.a=2: (24 +2 +6)/(72 +13)=32/85≈0.376, no.a=3: (54 +3 +6)/(108 +13)=63/121≈0.520, no.a=4: (96 +4 +6)/(144 +13)=106/157≈0.675, no.a=5: (150 +5 +6)/(180 +13)=161/193≈0.834, no.a=6: (216 +6 +6)/(216 +13)=228/229≈0.995, no.a=7: (294 +7 +6)/(252 +13)=307/265≈1.158, no.a=8: (384 +8 +6)/(288 +13)=398/301≈1.322, no.a=9: (486 +9 +6)/(324 +13)=501/337≈1.486, no.a=10: (600 +10 +6)/(360 +13)=616/373≈1.651, no.a=11: (726 +11 +6)/(396 +13)=743/409≈1.817, no.a=12: (864 +12 +6)/(432 +13)=882/445≈1.982, no.a=13: (1014 +13 +6)/(468 +13)=1033/481≈2.148, no.a=14: (1176 +14 +6)/(504 +13)=1196/517≈2.313, no.a=15: (1350 +15 +6)/(540 +13)=1371/553≈2.479, no.No luck here either. Maybe try b=7. Wait, already did that.Alternatively, maybe another approach. Let's note that in the original problem, we need ab² + b +7 divides a²b +a +b. Let's denote D = ab² + b +7 and N = a²b + a + b. We can write N = a*(ab) + a + b. Maybe express N in terms of D.Alternatively, think of N - a*D. Let's compute that:N - a*D = (a²b +a +b) -a*(ab² +b +7) = a²b +a +b - a²b² -ab -7a = -a²b² -ab -6a +b Hmm, not helpful. Alternatively, maybe manipulate N and D:Express N = a²b +a +b. Let's factor b from some terms: N = b(a² +1) +a. Similarly, D = ab² +b +7 = b(ab +1) +7. Maybe divide N by D:Let’s perform the division of N by D. Let me treat a as a variable and b as a constant. Let’s divide a²b +a +b by ab² +b +7.Using polynomial division:Divide a²b by ab²: a²b / ab² = a/b. Multiply divisor by a/b: (ab² +b +7)*(a/b)=a²b +a + (7a)/b. Subtract from dividend:(a²b +a +b) - (a²b +a +7a/b) = b - 7a/b. So remainder is b -7a/b. For the division to be exact, remainder must be zero. Thus:b -7a/b =0 ⇒ b² -7a=0 ⇒7a=b².Since a and b are positive integers, 7 divides b². Therefore, 7 divides b. Let me set b=7k, where k is a positive integer. Then, 7a=(7k)^2=49k² ⇒a=7k².Thus, in this case, a=7k² and b=7k. So the solutions are pairs where a=7k² and b=7k for some positive integer k. Let's check if these work:Substitute a=7k², b=7k into D and N:D =ab² +b +7=7k²*(7k)^2 +7k +7=7k²*49k² +7k +7=343k⁴ +7k +7.N =a²b +a +b=(7k²)^2 *7k +7k² +7k=49k⁴*7k +7k² +7k=343k⁵ +7k² +7k.Now, check if D divides N:N/D = (343k⁵ +7k² +7k)/(343k⁴ +7k +7). Let's factor numerator and denominator:Numerator:343k⁵ +7k² +7k=7k(49k⁴) +7k² +7k=7k(49k⁴ +k +1). Denominator:343k⁴ +7k +7=7*(49k⁴ +k +1). Therefore, N/D = [7k(49k⁴ +k +1)]/[7*(49k⁴ +k +1)] =k. So yes, it's an integer. Therefore, for any positive integer k, (a,b)=(7k²,7k) is a solution.So these are infinite solutions. But we found (7,7) when k=1. Also, k=2 would give a=28, b=14. Let's check if that works:For k=2, a=28, b=14:D=28*(14)^2 +14 +7=28*196 +21=5488 +21=5509 N=(28)^2*14 +28 +14=784*14 +42=10976 +42=11018 Check if 5509 divides 11018. 5509*2=11018. Yes. So N/D=2, which is integer. So (28,14) is another solution.But wait, the problem states "Find all positive integer pairs {a, b}". So these are solutions. However, in our earlier analysis for b=1, we found solutions (11,1) and (49,1). Are these covered by the general solution a=7k², b=7k? For b=1, 7k=1⇒k=1/7, which is not integer. So these are separate solutions.Therefore, in addition to the infinite family a=7k², b=7k, there are some sporadic solutions when b is not a multiple of 7. So we need to check whether those exist.Earlier, for b=1, we found (11,1) and (49,1). Let's see if those can be captured in another way.Wait, so the key insight is that when b is a multiple of 7, then we have solutions given by a=7k², b=7k. But when b is not a multiple of 7, there might be other solutions. So we need to check for b=1,2,3,4,5,6, etc., whether there are solutions.From earlier trials, for b=1, there are solutions. For b=7, we have solutions. Let's check if there are solutions for other small b values.For example, when we did b=1, there are solutions (11,1) and (49,1). Similarly, maybe there are other values.Wait, but how did we get those solutions? For b=1, we found that a+8 must divide 57. So 57's factors are 1,3,19,57. But since a+8≥9, possible factors are 19 and 57, leading to a=11 and a=49.So those solutions arise when, for b=1, the denominator a+8 divides the numerator a² +a +1. The division gave a remainder 57, hence a+8 divides 57. So similar methods for other b values.Alternatively, perhaps when b is not a multiple of 7, there are some constraints. Let's revisit the initial division approach.When we divide N =a²b +a +b by D =ab² +b +7, we can write:N = q*D + r, where q is the quotient and r is the remainder. Since D is linear in a (if we fix b), we can perform polynomial division in terms of a.Let me fix b and treat N and D as polynomials in a. Then, the remainder when dividing N by D will be of degree less than D in a. Since D is degree 1 in a (for fixed b), the remainder will be a constant. Let's compute this remainder.Compute N - q*D. Let’s let q be the quotient, which would be (a²b)/ (ab²) = a/b. But this is only valid if b divides a. But since a and b are integers, unless b divides a, the quotient might not be integer. Alternatively, we can use the concept of polynomial division regardless.Let’s perform the division of N by D treating a as the variable:Divide N = a²b + a + b by D = ab² + b +7.Express N = Q*(ab² + b +7) + R, where Q is the quotient and R is the remainder. Since D is linear in a, Q will be of degree 1 in a, and R will be a constant.Let’s suppose Q = c*a + d. Then:N = (c*a + d)(ab² + b +7) + R = c*a*(ab²) + c*a*(b) + c*a*7 + d*ab² + d*b + d*7 + R = c*a²b² + c*a*b +7c*a + d*a b² + d*b +7d + RCompare this with N = a²b +a +b. Equate coefficients:For a²b² term: c*b² =0. Since b is positive integer, c must be 0.But that's a contradiction because Q is supposed to be degree 1. Wait, maybe my approach is wrong. Alternatively, since D is of degree 1 in a, and N is degree 2 in a, the quotient Q must be of degree 1 in a. Let me try again.Let Q = m*a + n, and R is a constant. Then:N = (m*a +n)(ab² +b +7) + R = m*a*(ab²) + m*a*(b) + m*a*7 + n*ab² +n*b +n*7 + R = m*a²b² + m*a b +7m a +n a b² +n b +7n + RCompare with N = a²b +a +b. So equate coefficients:1. Coefficient of a²b²: m*b² =0 ⇒ m=0, since b is positive. But then Q reduces to n, a constant.If m=0, then Q =n, so:N =n*(ab² +b +7) + R = n a b² +n b +7n + RCompare with N = a²b +a +b. Therefore:Coefficients:- Coefficient of a²b: 0 =1 ⇒ Contradiction. So this approach is invalid. Therefore, the initial assumption of Q being linear in a is incorrect. Wait, but if D is linear in a, then the division should give Q as linear in a. But since leading term of D is ab² and leading term of N is a²b, the leading term of Q is (a²b)/(ab²)=a/b. Which is not an integer unless b divides a. Hence, if b divides a, then the division would proceed with integer coefficients. Otherwise, the division introduces fractions. Therefore, only when b divides a, we can have Q as a polynomial with integer coefficients. Otherwise, the division leads to a remainder involving fractions. Therefore, maybe another approach.Alternatively, rearrange the equation:ab² +b +7 divides a²b +a +b. Let me denote x = a. Then, for fixed b, the equation is:x²b +x +b ≡0 mod (x b² +b +7)Let me substitute y = x b² +b +7. Then x = (y - b -7)/b². Substitute into N:N =x²b +x +b = [(y - b -7)/b²]^2 *b + (y - b -7)/b² +b = (y - b -7)^2 /b³ + (y - b -7)/b² +b This seems complicated. Alternatively, use the fact that if y divides N, then y divides any linear combination of y and N. For example, compute N -x*y:N -x*y = (x²b +x +b) -x*(x b² +b +7) = x²b +x +b -x²b² -x b -7x = -x²b² -x b -6x +bThis expression should be divisible by y. But not sure. Alternatively, try to find some multiple.Alternatively, let's use the fact that if y divides N, then y divides (N -k*y) for any integer k. Let me pick k such that the expression simplifies.Let me set k = a. Then:N -a*D = (a²b +a +b) -a*(ab² +b +7) = a²b +a +b -a²b² -ab -7a = -a²b² -ab -6a +bHmm, not helpful. Alternatively, maybe set k = b:N -b*D = (a²b +a +b) -b*(ab² +b +7) = a²b +a +b -ab³ -b² -7b = a²b -ab³ +a -b² -6bFactor ab:ab(a -b²) +a -b² -6b. Not helpful.Alternatively, if b divides a, let a =b*m. Then:D =b*(b*m)*b +b +7= b³m +b +7 N = (b*m)²b +b*m +b= b³m² +b m +b So need b³m +b +7 divides b³m² +b m +b. Let's compute N/D:N/D = (b³m² +b m +b)/(b³m +b +7). Let me factor b in numerator:= b*(b²m² +m +1)/(b³m +b +7). Hmm, not obvious. For example, take m=1:N/D =b*(b² +1 +1)/(b³ +b +7)=b*(b² +2)/(b³ +b +7). Maybe check for some b:For b=1:1*(1 +2)/(1 +1 +7)=3/9=1/3, not integer.b=2:2*(4 +2)/(8 +2 +7)=12/17≈0.705, no.b=3:3*(9 +2)/(27 +3 +7)=3*11/37≈0.891, no.b=4:4*(16 +2)/(64 +4 +7)=4*18/75=72/75=24/25, no.b=5:5*(25 +2)/(125 +5 +7)=5*27/137≈0.985, no.Not helpful. So maybe this approach is not working.Alternatively, go back to the initial insight that when 7 divides b, we have solutions. When 7 doesn't divide b, perhaps the only solutions are the ones we found for b=1. Let's check if there are others.For example, when b=7k + r, where r=1,2,3,4,5,6, maybe there are specific solutions. For example, b=1 had solutions. What about b=7k +1? Let's check b=8.For b=8:Denominator: a*64 +8 +7=64a +15 Numerator: a²*8 +a +8=8a² +a +8 Need (8a² +a +8)/(64a +15) is integer. Let's set k=(8a² +a +8)/(64a +15). Multiply both sides:8a² +a +8=64k a +15k. Rearranged:8a² + (1 -64k)a + (8 -15k)=0. Quadratic in a. Discriminant:D=(1 -64k)^2 -4*8*(8 -15k)=1 -128k +4096k² -256 +480k=4096k² +352k -255. Needs to be square.Check k=1:4096 +352 -255=4193, not square.k=2:4096*4 +352*2 -255=16384 +704 -255=16833. 129²=16641, 130²=16900, so no.k=0: Not allowed. Try some a:a=1: (8 +1 +8)/(64 +15)=17/79≈0.215, no.a=2: (32 +2 +8)/(128 +15)=42/143≈0.293, no.a=3: (72 +3 +8)/(192 +15)=83/207≈0.401, no.a=4: (128 +4 +8)/(256 +15)=140/271≈0.516, no.a=5: (200 +5 +8)/(320 +15)=213/335≈0.636, no.a=6: (288 +6 +8)/(384 +15)=302/399≈0.757, no.a=7: (392 +7 +8)/(448 +15)=407/463≈0.879, no.a=8: (512 +8 +8)/(512 +15)=528/527≈1.001, almost 1 but not integer.a=9: (648 +9 +8)/(576 +15)=665/591≈1.126, no.a=10: (800 +10 +8)/(640 +15)=818/655≈1.249, no.a=11: (968 +11 +8)/(704 +15)=987/719≈1.373, no.a=12: (1152 +12 +8)/(768 +15)=1172/783≈1.497, no.No solutions here. So b=8, no solutions. Let's check another b=7k +1, like b=15.Wait, this might take forever. Let's instead consider another approach. Recall that for b=1, we had solutions where a+8 divides 57. Similarly, for other b, perhaps the remainder when dividing N by D is a constant, so that D must divide that remainder. Let's generalize the method used for b=1.Suppose we fix b and treat N and D as polynomials in a. Then, dividing N by D, the remainder is a constant. Let's compute that remainder.Let’s perform polynomial division of N =a²b +a +b by D =ab² +b +7. Treating a as the variable:We can write D =b² a + (b +7). Let’s divide N =b a² + a +b by D =b² a + (b +7).The leading term of N is b a², and leading term of D is b² a. So the first term of the quotient is (b a²)/(b² a)=a/b. Multiply D by a/b: (b² a +b +7)*(a/b)=b a² +a +7a/b. Subtract this from N:N - (a/b)*D = (b a² +a +b) - (b a² +a +7a/b)=b -7a/b.Therefore, the remainder is b -7a/b. For the division to have zero remainder, this must be zero:b -7a/b=0 ⇒b²=7a ⇒a=b²/7.Since a must be a positive integer, 7 divides b². Therefore, 7 divides b, so let b=7k, then a=(49k²)/7=7k². Which gives the solutions we found earlier: a=7k², b=7k. Hence, these are the only solutions where the remainder is zero. But wait, for b=1, we had solutions where remainder wasn't zero? Wait, no. Wait, when b=1, the remainder would be 1 -7a/1=1-7a. But for the division to be exact, remainder must be zero, so 1 -7a=0 ⇒a=1/7, which is not integer. But earlier, we had solutions when b=1. Contradiction?Ah, here is the key. The polynomial division approach assumes that the quotient is a polynomial with integer coefficients. But if b does not divide 7a, then the quotient would have fractional coefficients, which complicates the division. Therefore, the remainder in polynomial division (which is done over integers) is actually different. Wait, perhaps I need to perform the division in integers.Wait, no. When we perform polynomial division in algebra, coefficients can be fractions. But here, since we are dealing with integer divisibility, we need to ensure that the quotient is an integer. Therefore, the polynomial division approach might not directly apply. Hence, the earlier insight that when 7 divides b, we have solutions is correct, but when 7 doesn't divide b, the remainder method might not work as above.However, when we treated the problem for b=1, we considered the division (a² +a +1)/(a +8) and found that the remainder is 57 when a=-8, so by the Remainder Theorem, the remainder when divided by a +8 is f(-8)= (-8)^2 + (-8) +1=64 -8 +1=57. Thus, for the division to be exact, 57 must be divisible by a +8. Hence, the solutions for b=1 are a +8 divides 57. Similarly, for other b, maybe apply the Remainder Theorem.Let me generalize this. For fixed b, consider the division of N(a) =a²b +a +b by D(a) =ab² +b +7. Treat D(a) as a linear polynomial in a: D(a)=b² a + (b +7). Then, by the Remainder Theorem, the remainder when N(a) is divided by D(a) is N(- (b +7)/b²). Compute this remainder:N(-(b +7)/b²) =b*(-(b +7)/b²)^2 + (-(b +7)/b²) +b = b*( (b +7)^2 )/b^4 - (b +7)/b² +b = (b +7)^2 /b³ - (b +7)/b² +b = [ (b +7)^2 - (b +7)b +b^4 ] /b³ = [b² +14b +49 -b² -7b +b^4 ] /b³ = [7b +49 +b^4 ] /b³ = (b^4 +7b +49)/b³ = b +7/b² +49/b³For this to be an integer (since remainder must be zero for divisibility), we need b +7/b² +49/b³ to be an integer. However, since b is a positive integer, terms like 7/b² and 49/b³ are only integers if b divides 7 and 49. Therefore, b must be a divisor of 7. Since 7 is prime, b=1 or b=7. But b=1:For b=1:Remainder=1 +7/1 +49/1=1 +7 +49=57. So remainder is 57. Hence, D(a) divides N(a) if and only if D(a) divides 57. Since D(a)=a +8, so a +8 divides 57. Which is what we did earlier.For b=7:Remainder=7 +7/49 +49/343=7 +1/7 +1/7=7 +2/7≈7.285, which is not integer. Wait, but we already have solutions for b=7. There's a contradiction here. Wait, but when b=7, the divisor D(a)=7²a +7 +7=49a +14. So to compute the remainder via Remainder Theorem, we set 49a +14=0 ⇒a= -14/49= -2/7. Then compute N(-2/7):N(-2/7)=7*( (-2/7)^2 )*7 + (-2/7) +7=7*(4/49)*7 + (-2/7) +7=7*(4/7) + (-2/7) +7=4 + (-2/7) +7=11 -2/7=75/7≈10.714. So remainder is 75/7, which is not integer. But in reality, when b=7, we have solutions like (7,7). What's wrong here?Ah, because when we perform polynomial division in integers, the remainder must be non-negative and less than the divisor. However, the Remainder Theorem gives the remainder in polynomial terms, which might not align with integer division. Therefore, this approach might not directly apply. Therefore, our earlier method of using the polynomial division to derive the remainder might not work as expected for integer division.Hence, the key takeaway is that the only general solutions are when 7 divides b, leading to a=7k², b=7k, and specific small cases like b=1. To find all solutions, we need to combine both approaches: the general family and specific small b cases.We already found for b=1: a=11 and a=49. Let's check if there are solutions for other small b values where 7 doesn't divide b. Let's try b=2,3,4,5,6, etc., up to b=6.Earlier, when we tried b=2,3,4,5,6, we didn't find any solutions except for b=1 and b=7. Let's confirm for b=7k +r, r=1,2,3,4,5,6, whether there are solutions.But given the time it would take to check each case, maybe it's better to conclude that the only solutions are the infinite family a=7k², b=7k, and the two solutions for b=1: (11,1) and (49,1).Wait, but when b=7k, then a=7k². For k=1, a=7, b=7. For k=2, a=28, b=14. Check if there are other solutions outside this family. For example, when b=14, a=28. Let's see if there are other solutions for b=14.For b=14:Denominator: a*(14)^2 +14 +7=196a +21 Numerator: a²*14 +a +14=14a² +a +14 Need (14a² +a +14)/(196a +21) is integer. Let's factor denominator: 28*7a +21=21(9.333a +1). Not helpful. Let's set k=(14a² +a +14)/(196a +21). Multiply both sides:14a² +a +14=196k a +21k. Rearranged:14a² + (1 -196k)a + (14 -21k)=0. Quadratic in a. Discriminant:D=(1 -196k)^2 -4*14*(14 -21k)=1 -392k +38416k² -784 +1176k=38416k² +784k -783. Needs to be square.Check k=1:38416 +784 -783=38416 +1=38417, not square.k=0: Not allowed. Maybe try specific a.But since b=14 is part of the family a=7k², b=7k with k=2, so a=28. Let's check a=28, b=14:Denominator:28*196 +14 +7=5488 +21=5509 Numerator:28²*14 +28 +14=784*14 +42=11018 11018 divided by 5509 is 2, which is integer. So works. So no other solutions for b=14 except a=28.Similarly, for b=21 (k=3), a=63:Denominator=63*441 +21 +7=63*441=27783 +28=27811 Numerator=63²*21 +63 +21=3969*21=83349 +84=83433 Divide 83433 by 27811: 27811*3=83433. So exactly 3. So it works. Thus, the family holds.Now, check if there are other solutions outside this family. For example, when b=49 (k=7), a=7*49=343. Let's check:Denominator=343*49^2 +49 +7=343*2401=823543 +56=823599 Numerator=343²*49 +343 +49=117649*49=5762401 +392=5762793 Divide 5762793 by 823599:823599*7=5765193. Which is larger than numerator. 823599*6=4941594. 5762793-4941594=821,199. So not divisible. Wait, but according to our family, when k=7, a=7*7²=343, b=7*7=49. Then:Denominator=343*49² +49 +7=343*2401 +56=343*2401=823543 +56=823599 Numerator=343²*49 +343 +49=117649*49 +392=117649*49=5,764,801 +392=5,765,193 Compute 5,765,193 ÷823,599=7. Because 823,599*7=5,765,193. Yes, exactly. So it works. So no issue.Thus, the family holds for all k. Therefore, the only solutions are:1. The infinite family {a, b} = {7k², 7k} for positive integers k.2. The two sporadic solutions found for b=1: {11,1} and {49,1}.But wait, when b=1, we found a=11 and a=49. Let's check if a=49, b=1 is part of the family. If k=1/7, which is not integer. So no, these are separate solutions.Similarly, check if a=49 and b=1 satisfy the original condition:Denominator=49*1 +1 +7=57 Numerator=49²*1 +49 +1=2401 +49 +1=2451 2451 ÷57=43, which is integer. So yes.So, the complete set of solutions is the family {7k²,7k} and the two additional pairs {11,1} and {49,1}.But wait, let's check if there are more solutions for b=1 beyond a=11 and a=49. For b=1, we found that a +8 must divide 57. The divisors of 57 greater than or equal to 9 (since a+8≥9) are 19 and 57, leading to a=11 and a=49. 57's divisors are 1,3,19,57. But a+8 must be ≥9, so 19 and 57. Therefore, no other solutions for b=1.Thus, all solutions are:- {7k²,7k} for positive integers k.- {11,1} and {49,1}.Therefore, the answer is the union of these.But wait, let me verify if there are other possible values for other small b's. For example, check b=7, a=7 is part of the family. When b=7, a=7*1²=7. Yes. What about b=14, a=28=7*2². Yes. So the family covers those.Now, to ensure completeness, we need to make sure there are no other solutions outside of these. Suppose there exists a solution where b is not 1 or a multiple of 7. Let's assume such a solution exists. Then, from the earlier polynomial division approach, we would have that the remainder must be zero, leading to b²=7a. But if b is not a multiple of 7, then 7 divides a, but b²=7a implies that 7 divides b, which is a contradiction. Therefore, there are no solutions where b is not 1 or a multiple of 7. Except for b=1, which through the separate case gave solutions.Therefore, the only solutions are the family {7k²,7k} and the two additional pairs {11,1} and {49,1}.But wait, when b=1, the equation b²=7a gives a=1/7, which is not integer, but we have solutions via the separate case. Therefore, the only way to get solutions when b is not divisible by 7 is when b=1 and a=11 or 49.Hence, compiling all solutions:- For each positive integer k, {7k², 7k}- The pairs {11,1} and {49,1}Thus, these are all the positive integer pairs {a,b} satisfying the condition.</think>The positive integer pairs ({a, b}) that satisfy the condition are the infinite family ({7k^2, 7k}) for any positive integer (k), and the specific pairs ({11, 1}) and ({49, 1}).Final AnswerThe solutions are (boxed{{11, 1}}), (boxed{{49, 1}}), and (boxed{{7k^2, 7k}}) for any positive integer (k).,<think>Okay, let's see. I need to find all positive integer pairs {a, b} such that a²b + a + b is divisible by ab² + b + 7. Hmm. Divisibility here means that when we divide a²b + a + b by ab² + b + 7, there's no remainder. So, ab² + b + 7 divides a²b + a + b. First, maybe I can write this as an equation: (a²b + a + b) / (ab² + b + 7) = k, where k is a positive integer. Then, rearranging terms, we get a²b + a + b = k(ab² + b + 7). Let's write that out:a²b + a + b = k ab² + k b + 7k.Hmm. Maybe I can collect like terms here. Let's move everything to one side:a²b - k ab² + a + b - k b - 7k = 0.Factor terms where possible. Let's look at the first two terms: a²b - k ab². I can factor out ab: ab(a - k b). Then, the remaining terms are a + b - k b - 7k. Let's see: a + b - k b -7k = a + b(1 - k) -7k. So putting it all together:ab(a - k b) + a + b(1 - k) -7k = 0.Not sure if that helps. Maybe I can try to express this equation in terms of a and b, and see if there's a way to bound possible values. Since a and b are positive integers, perhaps trying small values of b first could help. Let's consider possible small values for b.Starting with b = 1:If b = 1, then the divisor becomes ab² + b +7 = a*1 +1 +7 = a +8. The dividend becomes a²*1 +a +1 = a² + a +1. So, we have (a² + a +1) divisible by (a +8). Let's perform the division:Divide a² + a +1 by a +8. Using polynomial division:a² + a +1 ÷ a +8. First term is a, multiply (a +8) by a: a² +8a. Subtract from dividend: (a² +a +1) - (a² +8a) = -7a +1. Now, divide -7a by a: -7. Multiply (a +8) by -7: -7a -56. Subtract: (-7a +1) - (-7a -56) = 57. So, remainder is 57. Therefore, a +8 divides 57. So, a +8 must be a divisor of 57. Since a is positive, a +8 ≥9. The divisors of 57 are 1,3,19,57. Since a +8 ≥9, possible divisors are 19 and 57. Therefore:a +8 =19 ⇒ a=11a +8=57 ⇒ a=49Thus, when b=1, possible a are 11 and 49. Let's check these:First, a=11, b=1:Dividend: 11²*1 +11 +1 = 121 +11 +1 =133Divisor:11*1² +1 +7=11 +1 +7=19133 ÷19=7. So, yes, 19 divides 133. So that's valid.Second, a=49, b=1:Dividend:49²*1 +49 +1=2401 +49 +1=2451Divisor:49*1² +1 +7=49 +1 +7=572451 ÷57=43. So, 57 divides 2451. Valid. So, {11,1} and {49,1} are solutions.Okay, so b=1 gives two solutions. Let's check b=2.For b=2:Divisor: a*(2)^2 +2 +7=4a +9Dividend: a²*2 +a +2=2a² +a +2We need 4a +9 divides 2a² +a +2. Let's perform division.Divide 2a² +a +2 by 4a +9. Let's write this as:2a² +a +2 = q*(4a +9) + rSince the divisor is linear in a, the remainder will be a constant. Let's use polynomial division. The leading term is 2a² divided by 4a, which is (2a²)/(4a)=a/2. But since coefficients should be integers, maybe this approach isn't straightforward. Alternatively, we can express 2a² +a +2 in terms of (4a +9). Let's find k such that 2a² +a +2 = k*(4a +9). But since k must be a function of a, unless k is a linear function, this might not help. Alternatively, express 2a² +a +2 = m*(4a +9) + c, where m is some integer and c is the remainder. Let me think.Alternatively, set up the equation 2a² +a +2 = m*(4a +9). Then, m must be a positive integer. Let's solve for m:m = (2a² +a +2)/(4a +9). Since m must be an integer, let's try to find a such that 4a +9 divides 2a² +a +2.Alternatively, perform the division:Let me write 2a² +a +2 divided by 4a +9. Let's use the method of expressing the dividend in terms of the divisor.Express 2a² +a +2 as A*(4a +9) + B.Let me write 2a² +a +2 = A*(4a +9) + B.We need to find A and B. Since the divisor is linear, A will be a linear term. Let’s suppose A = pa + q. Then:2a² +a +2 = (pa + q)(4a +9) + B.Expanding the right side:pa*4a + pa*9 + q*4a + q*9 + B = 4pa² + (9p +4q)a +9q + B.Set equal to left side:4pa² + (9p +4q)a +9q + B = 2a² +a +2.Equate coefficients:4p = 2 ⇒ p = 2/4 = 1/2.9p +4q =1 ⇒ 9*(1/2) +4q =1 ⇒ 9/2 +4q =1 ⇒4q =1 -9/2 = -7/2 ⇒ q = -7/8.But q has to be an integer since coefficients are integers. Since we have fractional values, this suggests that the division does not result in integer coefficients, so perhaps the remainder is non-zero. Therefore, instead of trying to express in terms of polynomial division, let's compute the remainder.The remainder when dividing 2a² +a +2 by 4a +9 can be found by substituting a = -9/4 into the dividend. That is:Remainder = 2*(-9/4)² + (-9/4) +2 = 2*(81/16) -9/4 +2 = 162/16 -36/16 +32/16 = (162 -36 +32)/16 =158/16=79/8.Wait, but remainder must be an integer. Hmm, maybe this approach is not correct here. Alternatively, maybe I need to adjust.Alternatively, to find the remainder when 2a² +a +2 is divided by 4a +9, note that 4a +9 =0 ⇒ a= -9/4. Then, substitute a = -9/4 into the dividend:2*(-9/4)^2 + (-9/4) +2 = 2*(81/16) -9/4 +2 = 162/16 -36/16 +32/16 = (162 -36 +32)/16 = 158/16 =79/8. Which is 9.875. But since the coefficients are integers, the remainder should be an integer. But this is fractional, which suggests that division is not exact, unless 4a +9 divides 79. Wait, but 79 is a prime number.Wait, perhaps I made a mistake here. Let's think again. If we have 2a² +a +2 divided by 4a +9, then the remainder is 79/8? That seems odd. Alternatively, maybe I should use the division algorithm. Let me set:2a² +a +2 = q*(4a +9) + r, where q is the quotient (which would be a linear term) and r is the remainder (a constant). Let’s write:2a² +a +2 = (ma +n)(4a +9) + r.Multiply out the right side:4ma² + (9m +4n)a +9n + r.Set equal to left side:4ma² + (9m +4n)a +9n + r = 2a² +a +2.Equate coefficients:4m =2 ⇒ m=0.59m +4n =1 ⇒ 9*(0.5) +4n =1 ⇒4.5 +4n=1⇒4n= -3.5 ⇒n= -3.5/4= -7/8.Then, 9n + r =2 ⇒9*(-7/8) + r=2 ⇒ -63/8 +r=2 ⇒ r=2 +63/8= (16/8 +63/8)=79/8.So, the remainder is 79/8. But since the coefficients must be integers, this suggests that 4a +9 does not divide 2a² +a +2 unless 79/8 is an integer, which it's not. Therefore, there is no solution for b=2? Wait, but that might not be the case. Wait, perhaps instead, the remainder when 2a² +a +2 is divided by 4a +9 is 79/8, but since a is an integer, 4a +9 is an integer, but the remainder must also be an integer. Therefore, for the division to have zero remainder, 79/8 must be zero, which is impossible. Therefore, there are no solutions when b=2.Alternatively, maybe there's a different approach here. Let me see.Alternatively, rearrange the equation:4a +9 divides 2a² +a +2. So, 2a² +a +2 ≡0 mod (4a +9). Let’s denote d =4a +9. Then, we can express a in terms of d: a=(d -9)/4. Substitute into the equation:2*((d -9)/4)^2 + (d -9)/4 +2 ≡0 mod d.Compute each term:2*( (d² -18d +81)/16 ) + (d -9)/4 +2 =(2d² -36d +162)/16 + (4d -36)/16 +32/16 =[2d² -36d +162 +4d -36 +32]/16 =[2d² -32d +158]/16 ≡0 mod d.Which implies that d divides (2d² -32d +158)/16. But since d divides the numerator 2d² -32d +158, because the denominator 16 is coprime with d (unless d is even, but d=4a +9, which is 4a +9. Since a is a positive integer, d is at least 13, and 4a is even, 4a +9 is odd. So d is odd. Therefore, d and 16 are coprime. Therefore, d divides 2d² -32d +158.So, 2d² -32d +158 ≡0 mod d. But 2d² ≡0 mod d, -32d≡0 mod d, and 158≡0 mod d. Therefore, 158 ≡0 mod d. Therefore, d divides 158. Since d=4a +9 is a positive integer greater than 9 (since a≥1, d=4+9=13 when a=1). The divisors of 158 are 1,2,79,158. Since d must be at least 13, possible divisors are 79 and158.Therefore, d=79 or d=158. Then:Case1: d=79=4a +9 ⇒4a=70 ⇒a=17.5. Not integer. Disregard.Case2:d=158=4a +9 ⇒4a=149 ⇒a=149/4=37.25. Not integer. Disregard.Therefore, no solutions for b=2.Okay, so b=2 is invalid.Next, check b=3.For b=3:Divisor: a*(3)^2 +3 +7=9a +10.Dividend: a²*3 +a +3=3a² +a +3.So, need 9a +10 divides 3a² +a +3. Let's set up the equation:3a² +a +3 =k*(9a +10). Let's try to perform division.Alternatively, express 3a² +a +3 = m*(9a +10) + r. Let's perform polynomial division.Divide 3a² +a +3 by 9a +10. The leading term is 3a² divided by 9a, which is (3a²)/(9a)=a/3. Since coefficients must be integers, perhaps this isn't helpful. Alternatively, compute the remainder.Alternatively, set d=9a +10. Then, a=(d -10)/9. Substitute into the dividend:3*((d -10)/9)^2 + ((d -10)/9) +3.Compute:3*(d² -20d +100)/81 + (d -10)/9 +3 =(3d² -60d +300)/81 + (9d -90)/81 +243/81 =[3d² -60d +300 +9d -90 +243]/81 =[3d² -51d +453]/81.Therefore, d divides this expression. Since d divides the numerator 3d² -51d +453. Because denominator is 81, and d=9a +10. Since d and 81 may share common factors. Let's see:We have 3d² -51d +453 ≡0 mod d. Which implies 0 +0 +453 ≡0 mod d. Therefore, d divides 453.Divisors of 453: 1,3,151,453. Since d=9a +10 ≥9*1 +10=19, possible divisors are 151 and453.Check d=151:151=9a +10 ⇒9a=141 ⇒a=141/9=47/3≈15.666… Not integer.d=453:453=9a +10 ⇒9a=443 ⇒a=443/9≈49.222… Not integer.Therefore, no solutions for b=3.Hmm, moving on to b=4:Divisor: a*4² +4 +7=16a +11Dividend: a²*4 +a +4=4a² +a +4Need 16a +11 divides 4a² +a +4.Again, set d=16a +11. Then, a=(d -11)/16. Substitute into dividend:4*((d -11)/16)^2 + ((d -11)/16) +4.Compute:4*(d² -22d +121)/256 + (d -11)/16 +4 =(4d² -88d +484)/256 + (16d -176)/256 +1024/256 =[4d² -88d +484 +16d -176 +1024]/256 =[4d² -72d +1332]/256.Simplify numerator: 4d² -72d +1332=4(d² -18d +333). Thus, expression becomes [4(d² -18d +333)]/256. For d to divide this, since d divides the numerator 4(d² -18d +333), and d is coprime with 4 (since d=16a +11, which is odd). Therefore, d divides (d² -18d +333).But d divides d² -18d +333. Let's write d divides (d² -18d +333). But d² ≡0 mod d, so -18d +333 ≡0 mod d. Therefore, -18d +333 ≡0 mod d ⇒333≡18d mod d ⇒333≡0 mod d. Therefore, d divides 333.Divisors of 333:1,3,9,37,111,333. Since d=16a +11≥16*1 +11=27. Possible divisors are37,111,333.Check each:d=37:16a +11=37⇒16a=26⇒a=26/16=13/8. Not integer.d=111:16a +11=111⇒16a=100⇒a=100/16=25/4. Not integer.d=333:16a +11=333⇒16a=322⇒a=322/16=161/8. Not integer.Thus, no solutions for b=4.b=5:Divisor: a*5² +5 +7=25a +12Dividend: a²*5 +a +5=5a² +a +5Need 25a +12 divides5a² +a +5.Set d=25a +12, then a=(d -12)/25. Substitute into dividend:5*((d -12)/25)^2 + ((d -12)/25) +5.Compute:5*(d² -24d +144)/625 + (d -12)/25 +5 =(5d² -120d +720)/625 + (25d -300)/625 +3125/625 =[5d² -120d +720 +25d -300 +3125]/625 =[5d² -95d +3545]/625.Thus, d divides this expression. Since d divides the numerator, 5d² -95d +3545. Since denominator is 625, and d=25a +12. Since 25a is divisible by 25, so d=25a +12 ≡12 mod25. Therefore, d and25 are coprime (since d=25a +12, gcd(d,25)=gcd(12,25)=1). Therefore, d divides 5d² -95d +3545.But 5d² -95d +3545 ≡5*0 -95*0 +3545 ≡3545 mod d. So, 3545 ≡0 mod d. Thus, d divides3545. Factorize3545:3545 ÷5=709. 709 is prime (since it's not divisible by 2,3,5,7,11,13,17,19,23, etc. up to sqrt(709)≈26.6). So divisors are1,5,709,3545. Since d=25a +12≥25*1 +12=37. Possible d=709,3545.Check d=709:25a +12=709⇒25a=697⇒a=697/25=27.88. Not integer.d=3545:25a +12=3545⇒25a=3533⇒a=3533/25=141.32. Not integer. Thus, no solutions for b=5.Hmm, this pattern suggests that for larger b, the solutions are not possible. Maybe I need to consider another approach rather than testing each b.Let’s go back to the original equation:a²b +a +b =k(ab² +b +7).Let me rearrange terms:a²b -k ab² +a +b -k b -7k=0.Factor terms:ab(a -k b) +a +b(1 -k) -7k=0.Not sure if helpful. Maybe express in terms of a:a²b +a +b =k ab² +k b +7k.Bring all terms to left:a²b -k ab² +a +b -k b -7k=0.Factor a:a(b a -k b²) +a +b -k b -7k=0.Not sure. Alternatively, isolate terms with a:a²b +a =k ab² +k b +7k -b.Factor a from left side:a(ab +1) =k b(ab +1) +7k -b.Wait, that seems interesting. Let's see:a(ab +1) -k b(ab +1) =7k -b.Factor out (ab +1):(ab +1)(a -k b)=7k -b.So, (ab +1)(a -k b) =7k -b.Now, since a and b are positive integers, and k is a positive integer (because the division must result in integer), so the right-hand side is 7k -b. Let's note that 7k -b must be positive because left-hand side is (ab +1)(a -k b). Since ab +1 is positive, the sign of the left-hand side depends on (a -k b). Therefore, if (a -k b) is positive, then 7k -b must be positive. If (a -k b) is negative, then 7k -b must be negative. But since 7k -b is linear in k and b, but k is a positive integer.Let’s consider possible cases.Case1: a -k b ≥0. Then, (ab +1)(a -k b) =7k -b ≥0. Thus, 7k -b ≥0 ⇒b ≤7k. Also, since a -k b ≥0 ⇒a ≥k b. So, a ≥k b.Case2: a -k b <0. Then, left-hand side is negative, so 7k -b <0 ⇒b >7k. But since k ≥1, then b >7k ≥7. Also, in this case, a <k b.But maybe starting with Case1 is more manageable.Let’s focus on Case1: a ≥k b and 7k ≥b.Given that a, b, k are positive integers.So, from equation:(ab +1)(a -k b) =7k -b.Note that the left-hand side is positive, and the right-hand side is 7k -b ≥0, so b ≤7k.Let’s denote t = a -k b. Since a ≥k b, t is a non-negative integer. Then, a =k b +t. Substitute into the equation:( (k b +t) b +1 ) * t =7k -b.Compute (k b² +t b +1)*t =7k -b.So:t(k b² +t b +1) =7k -b.Now, this is an equation in t, b, k. Let's consider possible values of t. Since t is non-negative, and 7k -b must be positive. Also, t must be such that 7k -b is divisible by (k b² +t b +1). But this seems complex. Let's see if we can find bounds for t.Given that t(k b² +t b +1) =7k -b, and all variables are positive integers (except t could be zero, but if t=0, then left-hand side is zero, which would require 7k -b=0, so b=7k. Then, check if t=0 is allowed. Let's check t=0:t=0: 0*(...) =7k -b ⇒7k -b=0 ⇒b=7k. Then, from a =k b +t =k*7k +0=7k². So, pair {a,b}={7k²,7k}. Let’s check if this works in the original equation.Original equation: a²b +a +b divisible by ab² +b +7.Compute a²b +a +b = (7k²)^2 *7k +7k² +7k =49k^4 *7k +7k² +7k=343k^5 +7k² +7k.Divisor:ab² +b +7=7k²*(7k)^2 +7k +7=7k²*49k² +7k +7=343k^4 +7k +7.So, we need 343k^5 +7k² +7k divisible by343k^4 +7k +7.Let’s perform division:Divide 343k^5 +7k² +7k by343k^4 +7k +7.The leading term is 343k^5 divided by343k^4 =k. Multiply divisor byk:343k^5 +7k² +7k. Subtract from dividend: (343k^5 +7k² +7k) - (343k^5 +7k² +7k)=0. So, the remainder is zero. Therefore, for any k, the pair {7k²,7k} is a solution. Wait, but when we set t=0, we get solutions for any k. However, the problem states "positive integer pairs {a,b}". So, these are valid solutions. But wait, the original problem doesn't restrict a and b beyond being positive integers. So, this suggests infinitely many solutions? However, in the example given in the problem statement (Example 22([39.4])), perhaps in the original source, there might be a finite number of solutions. Wait, but according to our previous analysis with b=1, there were two solutions. But here, when t=0, we get solutions for any k, leading to infinitely many solutions. However, in our testing for b=1, we found specific solutions. Let me check for k=1:k=1: a=7*1²=7, b=7*1=7.Check if 7²*7 +7 +7 is divisible by7*7² +7 +7.Compute dividend:7³ +7 +7=343 +14=357.Divisor:7*49 +14=343 +14=357. So, 357 divides357. Valid.Similarly, k=2: a=28, b=14.Dividend:28²*14 +28 +14=784*14 +42=10976 +42=11018.Divisor:28*14² +14 +7=28*196 +21=5488 +21=5509.But 5509 divides11018? 11018 ÷5509=2. So yes, 5509*2=11018. So valid.Therefore, these are valid solutions. So, there are infinitely many solutions where a=7k² and b=7k. However, in our initial tests with b=1, we found {11,1} and {49,1}, which do not fit into this family. Therefore, there are other solutions besides these.Hence, our initial analysis found some solutions, but there are also infinitely many solutions where a=7k² and b=7k. But the problem asks to "find all positive integer pairs {a, b}". So, both the infinite family and the specific solutions we found. However, in competition problems, usually, there are only finite solutions, so perhaps the infinite family is not valid, or I made a mistake here.Wait, but let's verify with k=1 and b=7: {a=7, b=7} works. When we did b=1, we found {11,1} and {49,1}. These do not fit into the a=7k², b=7k family, since for b=1, 7k=1 implies k=1/7, which is not integer. So, there are two types of solutions: the infinite family when t=0, and some specific solutions when t>0.But the problem says "Find all positive integer pairs". If the problem is from a competition, usually there are only finite solutions, so maybe the infinite family is incorrect. Wait, but according to our derivation, when t=0, the solutions {7k²,7k} are valid. However, let me check with another value, say k=3:a=7*9=63, b=21.Dividend:63²*21 +63 +21=3969*21 +84=83349 +84=83433.Divisor:63*(21)^2 +21 +7=63*441 +28=27783 +28=27811.Check if 27811 divides83433. 27811*3=83433. So, 3*27811=83433. Therefore, yes, divisible. So, works.Therefore, indeed, this is a valid infinite family. But the problem statement says "Find all positive integer pairs". So, perhaps there are both the infinite family and the specific solutions. However, in the initial test with b=1, we found {11,1} and {49,1}, which are not in the family. So, perhaps the complete solution set is the union of the infinite family and these specific solutions. Wait, but maybe the specific solutions can be included in the infinite family when k is not integer? But no, k must be integer.Wait, for b=1:If we suppose that {a,1} is part of the family a=7k², b=7k. Then, 7k=1 ⇒k=1/7. Which is not integer. Hence, those solutions are separate. Therefore, the complete solution set is the union of the infinite family {7k²,7k} for positive integers k, and the specific solutions found when b=1: {11,1}, {49,1}. But need to check if there are more solutions with t>0 for other b.Alternatively, perhaps the specific solutions are part of the family when t>0. Let's check.Take solution {11,1}. Let's see if it can be expressed as a=7k² +t, b=7k. Since b=1, 7k=1 ⇒k=1/7, which is not integer. Hence, no. Therefore, these are separate.Therefore, the problem might have two types of solutions: the infinite family and some specific ones. But competition problems usually expect all solutions, which could be a finite number. Hence, perhaps the infinite family is actually not valid? Wait, but our earlier verification shows that they are valid. Let me check with another thought.Wait, in the case when t=0, we have a=7k² and b=7k. Then, let's compute ab² +b +7:ab² +b +7=7k²*(7k)^2 +7k +7=7k²*49k² +7k +7=343k^4 +7k +7.And a²b +a +b=(7k²)^2 *7k +7k² +7k=343k^5 +7k² +7k.Then, when we divide dividend by divisor, we get (343k^5 +7k² +7k)/(343k^4 +7k +7)=k. So, indeed, divisible. Hence, valid.Therefore, this family is correct. So, there are infinitely many solutions. However, in the initial testing with b=1, we found two more solutions. So, the problem's answer is both these specific solutions and the infinite family. However, the problem might be expecting only the specific solutions, and perhaps I made a mistake in allowing t=0. Wait, no. The derivation seems correct.Wait, but let's check the specific solution {11,1}. For this pair:ab² +b +7=11*1 +1 +7=19.a²b +a +b=121*1 +11 +1=133.133 divided by19 is7, which is integer. So, valid.Similarly, {49,1}:ab² +b +7=49*1 +1 +7=57.a²b +a +b=49²*1 +49 +1=2401 +49 +1=2451.2451 ÷57=43, integer. Valid.These are separate from the infinite family. Therefore, the problem's answer includes both the infinite family {7k²,7k} and the two solutions {11,1}, {49,1}. However, the problem says "Find all positive integer pairs". If the problem is from a competition, it might have a finite answer, which suggests that maybe the infinite family is not intended. Alternatively, maybe I missed some constraint.Wait, perhaps there are other specific solutions with t>0. Let's consider t>0.From the equation:t(k b² +t b +1) =7k -b.Given that t≥1, and 7k -b ≥1. Also, since b ≤7k.Given that t and k and b are positive integers. Let's try small t.Let’s take t=1. Then, equation becomes:1*(k b² +1*b +1)=7k -b ⇒k b² +b +1=7k -b.Rearranged:k b² +b +1 +b -7k=0 ⇒k b² -7k +2b +1=0 ⇒k(b² -7) +2b +1=0.Since k is positive, the term k(b² -7) must be negative because 2b +1 is positive. Therefore, b² -7 <0 ⇒b² <7 ⇒b=1 or2.So, b=1:k(1 -7) +2*1 +1=0 ⇒k(-6) +3=0 ⇒-6k +3=0 ⇒k=3/6=1/2. Not integer.b=2:k(4 -7) +4 +1=0 ⇒k(-3) +5=0 ⇒-3k +5=0 ⇒k=5/3. Not integer.Thus, no solutions with t=1.t=2:2(k b² +2b +1)=7k -b ⇒2k b² +4b +2=7k -b ⇒2k b² +4b +2 -7k +b=0 ⇒2k b² -7k +5b +2=0.Solve for k:k(2b² -7) +5b +2=0.Since k is positive, 2b² -7 must be negative. So, 2b² -7 <0 ⇒b² <7/2 ⇒b=1.b=1:k(2 -7) +5 +2=0 ⇒-5k +7=0 ⇒k=7/5. Not integer.Thus, no solutions for t=2.t=3:3(k b² +3b +1)=7k -b ⇒3k b² +9b +3=7k -b ⇒3k b² +9b +3 -7k +b=0 ⇒3k b² -7k +10b +3=0.Solve for k:k(3b² -7) +10b +3=0.Since k positive, 3b² -7 <0 ⇒b² <7/3 ⇒b=1.b=1:k(3 -7) +10 +3=0 ⇒-4k +13=0 ⇒k=13/4. Not integer.No solutions.t=4:4(k b² +4b +1)=7k -b ⇒4k b² +16b +4=7k -b ⇒4k b² +16b +4 -7k +b=0 ⇒4k b² -7k +17b +4=0.Solve for k:k(4b² -7) +17b +4=0.k must be positive ⇒4b² -7 <0 ⇒b² <7/4 ⇒b=1.b=1:k(4 -7) +17 +4=0 ⇒-3k +21=0 ⇒k=7.Thus, k=7. Then, from a =k b +t=7*1 +4=11. So, {a,b}={11,1}, which is one of the solutions we found earlier. Thus, this is valid. So, with t=4, b=1, k=7, a=11. So, this is a solution. Hence, the solution {11,1} comes from t=4.Similarly, let's check if the other solution {49,1} can be obtained from higher t.For example, let's try t= some value for b=1.For b=1, general case:From the equation when b=1:t(k*1² +t*1 +1)=7k -1.So, t(k +t +1)=7k -1.But also, a =k*1 +t= k +t.Previously, when b=1, we found solutions a=11 and49. Let's check for a=49, b=1:a=49, b=1. Then, k=(a -t)/b=49 -t. So, substitute into equation:t(k +t +1)=7k -1 ⇒t(49 -t +t +1)=7(49 -t) -1 ⇒t(50)=343 -7t -1 ⇒50t=342 -7t ⇒57t=342 ⇒t=6.Thus, t=6. Then, k=49 -6=43. Check if this satisfies:t(k +t +1)=6*(43 +6 +1)=6*50=300.7k -1=7*43 -1=301 -1=300. Yes, equals. Therefore, {a=49,b=1} corresponds to t=6, k=43.Thus, for b=1, varying t can give different solutions. Therefore, for b=1, there are infinitely many solutions? Wait, but when we solved b=1 earlier, we found two solutions. But according to this, for each t, there would be a k. But no, because for b=1, the equation is t(k +t +1)=7k -1. This is a linear equation in k:t(k +t +1)=7k -1 ⇒t k +t² +t =7k -1 ⇒(t -7)k = -t² -t -1 ⇒k=(t² +t +1)/(7 -t).Since k must be positive integer, denominator must divide numerator and result in positive k. So, 7 -t divides t² +t +1, and 7 -t >0 ⇒t <7. Since t is positive integer, t=1,2,3,4,5,6.So, check for t=1 to6:t=1:k=(1 +1 +1)/(7 -1)=3/6=1/2. Not integer.t=2:k=(4 +2 +1)/5=7/5. Not integer.t=3:k=(9 +3 +1)/4=13/4. Not integer.t=4:k=(16 +4 +1)/3=21/3=7. Integer. So, k=7. Then, a=k +t=7 +4=11. Which is the solution we found.t=5:k=(25 +5 +1)/2=31/2=15.5. Not integer.t=6:k=(36 +6 +1)/1=43. Integer. So, k=43. a=43 +6=49. Which is the other solution.Thus, for b=1, only t=4 and6 give integer k=7 and43, leading to a=11 and49. So, only two solutions for b=1.Hence, the infinite family {7k²,7k} and the two solutions {11,1}, {49,1} are the complete set. Wait, but in the equation for general b, when t=0, we get solutions for any k. So, these are separate from the b=1 solutions.Therefore, the complete solution set is:1. All pairs {7k²,7k} for positive integers k.2. The pairs {11,1} and {49,1}.But wait, are there other pairs with b>1 and t>0? Let's check for b=7, which is part of the infinite family. If we take k=1, then a=7*1²=7, b=7*1=7. Let's see if there could be another solution with b=7 and t>0. For b=7, t=0 gives a=7. Let's see if t>0 is possible.From the equation:t(k*7² +t*7 +1)=7k -7.But since b=7, and a=k*7 +t. Let’s express:t(49k +7t +1)=7k -7.But a must be positive integer. Let’s see for possible t.But this seems complicated. Let's instead consider whether there could be solutions outside of the family {7k²,7k} and the two specific solutions.Alternatively, check another value, say b=7, k=1, a=7: which is part of the family. If we consider b=7 and some a≠7, would that work? Let's take b=7 and a=8.Check if 8²*7 +8 +7=448 +15=463 is divisible by8*7² +7 +7=8*49 +14=392 +14=406. 463 divided by406 is1.14… Not integer.Alternatively, a=14, b=7: part of the family (k=2: a=7*4=28, b=14). Wait, a=28, b=14: yes, in the family.Therefore, perhaps there are no other solutions outside of the two types. Hence, the answer is the union of the infinite family and the two specific solutions. However, in the problem statement, it's Example 22([39.4]), which is likely from a competition problem, suggesting that the answer is finite. But our analysis shows there are infinitely many solutions. Therefore, perhaps the family {7k²,7k} is considered trivial or the only solutions, but in our testing, the b=1 solutions exist as well.Wait, perhaps I made a mistake in allowing k to be any positive integer. Maybe the problem requires {a,b} to be pairs where ab² +b +7 divides a²b +a +b, but when we substitute a=7k², b=7k, the quotient is k, which is allowed. So, mathematically, these are valid solutions.However, in competition problems, sometimes such families are considered "trivial" or maybe overlooked. But according to our mathematical analysis, they are valid. Therefore, the answer should include both the family and the two specific solutions. However, the original problem might have a different intended answer. But since the user hasn't provided additional context, I should proceed with the mathematical truth.Therefore, the complete set of solutions is:- All pairs where a=7k² and b=7k for some positive integer k.- The pairs {a=11, b=1} and {a=49, b=1}.But to confirm, let's check if there are any other solutions for b>1 with t>0. For example, take b=2, t=?From the equation t(k b² +t b +1)=7k -b. For b=2:t(4k +2t +1)=7k -2.We need to find positive integers k,t such that this equation holds.Rearranged:4k t +2t² +t =7k -2 ⇒4kt -7k +2t² +t +2=0 ⇒k(4t -7) +2t² +t +2=0.Thus,k= -(2t² +t +2)/(4t -7).Since k must be positive, denominator and numerator must be negative. Therefore:4t -7 <0 ⇒t <7/4 ⇒t=1.So t=1:k= -(2 +1 +2)/(4 -7)= -5/-3=5/3. Not integer.Thus, no solution for b=2.For b=3:t(k*9 +3t +1)=7k -3.Similarly, solving for k:9kt +3t² +t =7k -3 ⇒9kt -7k +3t² +t +3=0 ⇒k(9t -7) +3t² +t +3=0 ⇒k= -(3t² +t +3)/(9t -7).For k positive, denominator and numerator must be negative.Thus, 9t -7 <0 ⇒t <7/9 ⇒t=0. But t≥1. No solutions.Similarly, for b=4:t=1:k= -(2*16 +4 +1)/(4*1 -7)= (Wait, no. Let's substitute b=4 into the general equation.)Wait, general case for any b and t. It's becoming too time-consuming. Given that for b≥2, we couldn't find any solutions through testing and the equations for t>0 didn't yield integer k, except for b=1, it's plausible that the only solutions are the infinite family and the two specific solutions.Therefore, the answer should be:All positive integer pairs {a, b} where either a=7k² and b=7k for some positive integer k, or {a, b} is one of {11, 1}, {49, 1}.But the problem might expect writing them all explicitly. However, in the format requested, we need to box all solutions. Since the problem says "Find all positive integer pairs", including both the infinite family and specific solutions. But in the context of an Olympiad problem, which usually expects a finite answer, perhaps there's a mistake in the infinite family. Wait, but when we set t=0, we get valid solutions. So, unless there is a restriction in the problem that I missed.Wait, let's check the original problem again: "Find all positive integer pairs {a, b}, such that a²b +a +b is divisible by ab² +b +7."There's no restriction, so the solutions are indeed both the infinite family and the two specific pairs. However, in some problems, such a family might be represented in a general form. For example, the pairs (7k², 7k) and the two exceptions. Therefore, the answer is:All pairs (a, b) = (7k², 7k) for some positive integer k, and the pairs (11, 1) and (49, 1).But to confirm, let's see if there are solutions outside of these. Take b=7, k=1, a=7: works. If we take a=7k², b=7k, and vary k, they all work. Additionally, the two specific solutions for b=1. Hence, the answer should include all these.But in the problem statement, the user mentioned "Example 22([39.4])", which might reference a specific problem from a source where perhaps only the two solutions are expected. However, mathematically, the infinite family is valid. Given that, I'll proceed to state both.However, considering that when we set t=0, the equation reduces to the family a=7k², b=7k, and when b=1, there are two solutions. Hence, the boxed answers are:boxed{{a, b} = {11, 1}}, boxed{{49, 1}}, and boxed{{7k^2, 7k} text{ for some positive integer } k}But in Chinese competitions, sometimes parametric solutions are written in a particular way. However, given the format here, perhaps list all solutions explicitly, but since the family is infinite, it's customary to present both the specific and general solutions.Alternatively, check if the two specific solutions are part of the family when k is not integer. For example, {11,1}: If 7k=1 ⇒k=1/7, then a=7*(1/7)^2=1/7. Not integer. Similarly, {49,1}:7k=1⇒k=1/7, a=7*(1/7)^2=1/7. Not integer. Hence, they are separate.Hence, the answer is all pairs (7k²,7k) for positive integers k, together with (11,1) and (49,1). Therefore, the final answer is:The pairs are all positive integers (k), and the specific pairs ((11, 1)) and ((49, 1)). Therefore, boxed as per instructions:boxed{(11, 1)}, boxed{(49, 1)}, and for any positive integer (k), boxed{(7k^2, 7k)}.But the problem might expect listing all solutions, including both specific and general. However, since the user's example input had multiple boxed answers, maybe present all in boxed format. However, the standard practice is to present all solutions, which includes both specific and the general family. However, in many olympiad problems, the family might be considered as one solution. So, the answer is:All positive integer solutions are (boxed{(11, 1)}), (boxed{(49, 1)}), and (boxed{(7k^2, 7k)}) for each positive integer (k).Final AnswerThe positive integer pairs are (boxed{(11, 1)}), (boxed{(49, 1)}), and (boxed{(7k^2, 7k)}) for every positive integer (k).</think>To find all positive integer pairs ({a, b}) such that (a^2 b + a + b) is divisible by (ab^2 + b + 7), we start by setting up the equation:[a^2 b + a + b = k(ab^2 + b + 7)]Rearranging terms, we get:[a^2 b - k ab^2 + a + b - k b - 7k = 0]We then factor and analyze the equation. By testing small values of (b) and using polynomial division, we find specific solutions for (b = 1):- For (b = 1), the divisor becomes (a + 8) and the dividend becomes (a^2 + a + 1). Solving, we find (a = 11) and (a = 49) as solutions, leading to the pairs ({11, 1}) and ({49, 1}).Next, we consider the general case by expressing (a) in terms of (k) and (b). We find that setting (a = 7k^2) and (b = 7k) leads to a family of solutions where (ab^2 + b + 7) divides (a^2 b + a + b) for any positive integer (k).Thus, the complete set of solutions includes the specific pairs found for (b = 1) and the infinite family of pairs where (a = 7k^2) and (b = 7k) for any positive integer (k).The final answer is:[boxed{(11, 1)}, boxed{(49, 1)}, text{ and } boxed{(7k^2, 7k)} text{ for every positive integer } k]]

🔑:(i) First, analyze the size relationship between a and b. Since it must be that a^{2} b + a + b geqslant a b^{2} + b + 7, we havea - 7 geqslant a b (b - a).This implies that (why)a geqslant b geqslant 1.We need to subtract a multiple of a b^{2} + b + 7 from a^{2} b + a + b so that the absolute value of the remainder is intuitively smaller than a b^{2} + b + 7. This way, the remainder must be 0.(ii) Use the division algorithm. Leta = q b + r, quad 0 leqslant r < b.From (1), we havea b^{2} + b + 7 mid a b r + b + r - 7 q.Since a b^{2} + b + 7 > a b r + b + r - 7 q, we havea b^{2} + b + 7 > |b - 7 q|.From this and equation (2), we deduce that b - 7 q = 0, so the solution is{a, b} = {7 t^{2}, 7 t}, quad t text{ is any positive integer.}(iv) If r > 0, then b > 1. We will prove that there is no solution in this case.(a) When b = 2, we must have r = 1, a = 2 q + 1. In this case, the right side of equation (1) becomes8 q + 13 = a b^{2} + b + 7 mid a b r + b + r - 7 q = 5 - 3 q.Clearly, 5 - 3 q neq 0 and 8 q + 13 > |5 - 3 q|. Therefore, the above equation cannot hold, so there is no solution.(b) When b geqslant 3, we have (why)begin{aligned}a b^{2} + b + 7 & geqslant a b (r + 1) + b + 7 = a b r + b + b^{2} q + b r + 7 & > |a b r + b + r - 7 q|end{aligned}Therefore, the right side of equation (1) holds if and only ifa b r + r + b - 7 q = 0.However, a b r + r + b > b^{2} q geqslant 9 q > 7 q, so the above equation cannot hold, and thus there is no solution.

🧠:[<think>Okay, let's try to tackle this problem step by step. So we have the function f(x) = x² + x. We need to find positive integers m and n, and distinct nonzero real numbers y and z such that f(y) = f(z) = m + √n, and also f(1/y) + f(1/z) = 1/10. Then compute 100m + n. Alright, let's start breaking this down.First, since y and z are distinct and both satisfy f(x) = m + √n, that means they are two different roots of the equation x² + x = m + √n. Let me write that equation out:x² + x - (m + √n) = 0.Since y and z are distinct roots, the quadratic equation must have two distinct real solutions. Therefore, the discriminant must be positive. The discriminant D of x² + x - c = 0 is D = 1 + 4c. Here, c = m + √n, so D = 1 + 4(m + √n) > 0. But since m and n are positive integers, and √n is positive, 1 + 4(m + √n) is definitely positive. So that condition is satisfied. Good.Now, for the quadratic equation x² + x - (m + √n) = 0, the sum of the roots y + z is equal to -1 (since the coefficient of x is 1, so sum is -b/a = -1/1 = -1). Similarly, the product of the roots y*z is equal to c/a = -(m + √n)/1 = -(m + √n). Wait, hold on. Wait, standard quadratic equation ax² + bx + c = 0 has sum of roots -b/a and product c/a. So in our case, equation is x² + x - (m + √n) = 0, so sum of roots is -1/1 = -1, and product is -(m + √n)/1 = -(m + √n). So:y + z = -1y * z = -(m + √n)Got that. So these are two equations related to y and z.Now, we also have f(1/y) + f(1/z) = 1/10. Let's compute f(1/y) and f(1/z):f(1/y) = (1/y)² + (1/y) = 1/y² + 1/ySimilarly, f(1/z) = 1/z² + 1/zTherefore, the sum is:1/y² + 1/y + 1/z² + 1/z = 1/10We can try to express this in terms of y + z and y*z, which we know from above. Let's see. Let's compute 1/y² + 1/z² first. That is equal to (1/y + 1/z)² - 2*(1/(y z)). So:1/y² + 1/z² = (1/y + 1/z)² - 2/(y z)Therefore, f(1/y) + f(1/z) = (1/y² + 1/z²) + (1/y + 1/z) = [(1/y + 1/z)² - 2/(y z)] + (1/y + 1/z) = 1/10Let me write S = 1/y + 1/z and P = 1/(y z). Then the above expression becomes:S² - 2P + S = 1/10So, if we can express S and P in terms of y + z and y*z, which we already have.First, let's compute S = 1/y + 1/z = (y + z)/(y z). Since y + z = -1 and y z = -(m + √n), then S = (-1)/( - (m + √n)) = 1/(m + √n). Because both numerator and denominator are negatives, so they cancel. So S = 1/(m + √n).Similarly, P = 1/(y z) = 1/( - (m + √n)) = -1/(m + √n)Therefore, substituting back into the equation S² - 2P + S = 1/10:[ (1/(m + √n))² ] - 2*(-1/(m + √n)) + (1/(m + √n)) = 1/10Simplify each term:First term: 1/(m + √n)²Second term: -2*(-1/(m + √n)) = 2/(m + √n)Third term: 1/(m + √n)Therefore, combining these:1/(m + √n)² + 2/(m + √n) + 1/(m + √n) = 1/10Combine the second and third terms:2/(m + √n) + 1/(m + √n) = 3/(m + √n)So equation becomes:1/(m + √n)² + 3/(m + √n) = 1/10Let me let k = m + √n. Then the equation is:1/k² + 3/k = 1/10Multiply both sides by k² to eliminate denominators:1 + 3k = (1/10)k²Bring all terms to one side:(1/10)k² - 3k - 1 = 0Multiply both sides by 10 to eliminate fraction:k² - 30k - 10 = 0So we have a quadratic equation in k: k² - 30k - 10 = 0Solve for k using quadratic formula:k = [30 ± √(900 + 40)] / 2 = [30 ± √940]/2 = [30 ± 2√235]/2 = 15 ± √235But since k = m + √n, and m and n are positive integers, and √n is positive. So k must be positive. Let's check both roots:15 + √235 ≈ 15 + 15.165 = 30.165 (positive)15 - √235 ≈ 15 - 15.165 ≈ -0.165 (negative)But k must be positive (since m and n are positive integers and √n is positive). Therefore, k = 15 + √235. But wait, k = m + √n. So we have m + √n = 15 + √235. Hmm.But m is a positive integer, and √n is irrational unless n is a perfect square. However, √235 is irrational. Therefore, the only way this equation holds is if m = 15 and √n = √235, so n = 235. But wait, but m and n are positive integers. So if m = 15, then n = 235. Let me check that.If m + √n = 15 + √235, then m must be 15 and √n must be √235, so n = 235. Because otherwise, if you have m as some other integer, then the irrational parts wouldn't match. Since √235 is irrational, and m is an integer, the only way for m + √n to equal 15 + √235 is if m = 15 and n = 235. So that seems to work.Therefore, m = 15 and n = 235, so 100m + n = 100*15 + 235 = 1500 + 235 = 1735. Is that the answer?Wait, hold on. Let me double-check. Let's verify that with these values, the original conditions are satisfied.First, m = 15, n = 235, so f(y) = f(z) = 15 + √235.So the quadratic equation is x² + x - (15 + √235) = 0.Then the roots y and z satisfy y + z = -1 and y z = -(15 + √235). Then, we need to compute f(1/y) + f(1/z) and check if it's 1/10.Compute S = 1/y + 1/z = (y + z)/(y z) = (-1)/[-(15 + √235)] = 1/(15 + √235). Then, P = 1/(y z) = 1/[-(15 + √235)] = -1/(15 + √235)Then, f(1/y) + f(1/z) = S² - 2P + S = [1/(15 + √235)^2] - 2*(-1/(15 + √235)) + 1/(15 + √235)So that's [1/(15 + √235)^2] + 2/(15 + √235) + 1/(15 + √235) = [1/(15 + √235)^2] + 3/(15 + √235)Earlier, we set k = 15 + √235, so this becomes 1/k² + 3/k, which we already found equals 1/10. So that's consistent.Therefore, yes, with m = 15 and n = 235, the conditions hold. So the answer is 100m + n = 100*15 + 235 = 1500 + 235 = 1735. So 1735.Wait, but just to be thorough, let's check if there could be another solution. The quadratic equation for k was k² - 30k - 10 = 0, giving roots k = [30 ± √(900 + 40)]/2 = [30 ± √940]/2. Wait, √940 simplifies? Let's check. 940 divided by 4 is 235, so √940 = √(4*235) = 2√235. Therefore, the roots are (30 ± 2√235)/2 = 15 ± √235, which is what we had. So the other root is negative, which we can't have. So indeed, the only possible solution is k = 15 + √235, leading to m = 15 and n = 235. So 100*15 + 235 = 1735. That seems right.But just to make sure, let's check if m and n are positive integers. m = 15 is a positive integer, and n = 235 is also a positive integer. And y and z are distinct nonzero real numbers. Since the quadratic equation x² + x - (15 + √235) = 0 has discriminant D = 1 + 4*(15 + √235) = 1 + 60 + 4√235 = 61 + 4√235, which is definitely positive, so two distinct real roots. Therefore, y and z exist and are distinct. Also, y and z are nonzero because if x = 0, then f(0) = 0 + 0 = 0, which is not equal to 15 + √235. So y and z are distinct nonzero real numbers. All conditions are satisfied. Therefore, the answer is 1735.Final Answerboxed{1735}</think>Given the function ( f(x) = x^2 + x ), we need to find positive integers ( m ) and ( n ), and distinct nonzero real numbers ( y ) and ( z ), such that ( f(y) = f(z) = m + sqrt{n} ) and ( fleft(frac{1}{y}right) + fleft(frac{1}{z}right) = frac{1}{10} ). We then compute ( 100m + n ).1. Since ( y ) and ( z ) are roots of the quadratic equation ( x^2 + x - (m + sqrt{n}) = 0 ), we know: - The sum of the roots ( y + z = -1 ) - The product of the roots ( yz = -(m + sqrt{n}) )2. We need to compute ( fleft(frac{1}{y}right) + fleft(frac{1}{z}right) ): - ( fleft(frac{1}{y}right) = frac{1}{y^2} + frac{1}{y} ) - ( fleft(frac{1}{z}right) = frac{1}{z^2} + frac{1}{z} ) - The sum is ( frac{1}{y^2} + frac{1}{z^2} + frac{1}{y} + frac{1}{z} )3. Expressing this sum in terms of ( y + z ) and ( yz ): - Let ( S = frac{1}{y} + frac{1}{z} = frac{y + z}{yz} = frac{-1}{-(m + sqrt{n})} = frac{1}{m + sqrt{n}} ) - Let ( P = frac{1}{yz} = frac{1}{-(m + sqrt{n})} = -frac{1}{m + sqrt{n}} ) - The sum becomes ( S^2 - 2P + S = left(frac{1}{m + sqrt{n}}right)^2 + 3left(frac{1}{m + sqrt{n}}right) )4. Setting ( k = m + sqrt{n} ), we solve: - ( frac{1}{k^2} + frac{3}{k} = frac{1}{10} ) - Multiplying through by ( 10k^2 ): ( 10 + 30k = k^2 ) - Solving the quadratic equation ( k^2 - 30k - 10 = 0 ) gives ( k = 15 + sqrt{235} )5. Thus, ( m = 15 ) and ( sqrt{n} = sqrt{235} ), so ( n = 235 ).6. The final result is ( 100m + n = 100 times 15 + 235 = 1735 ).[boxed{1735}],<think>Okay, so I need to solve this problem where f(x) = x² + x. They tell me there are positive integers m and n, and distinct nonzero real numbers y and z such that f(y) = f(z) = m + √n. Also, f(1/y) + f(1/z) = 1/10. I need to find 100m + n. Hmm, let's break this down step by step.First, since f(y) = f(z) = m + √n, that means both y and z are roots of the equation x² + x = m + √n. So, if I rearrange that equation, it becomes x² + x - (m + √n) = 0. Since y and z are distinct roots, this quadratic equation must have two distinct real roots. Therefore, the discriminant should be positive. The discriminant D of x² + x - c = 0 is 1 + 4c. So here, D = 1 + 4(m + √n) > 0. But since m and n are positive integers, m + √n is positive, so D is definitely positive. That's good, no problem there.Now, since y and z are the roots of the quadratic equation x² + x - (m + √n) = 0, by Vieta's formula, we know that:y + z = -1 (because the coefficient of x is +1, so sum of roots is -1/1 = -1)andy * z = -(m + √n) (since the constant term is -(m + √n), so product is c/a = -(m + √n)/1 = -(m + √n))Wait, that's interesting. So the sum of y and z is -1, and the product is negative because m and √n are positive. So y and z are two numbers that add up to -1 and multiply to a negative number. Therefore, one of them is positive and the other is negative. Because if their product is negative, they must have opposite signs. And their sum is -1. So, one is positive, the other is negative, and they add up to -1.Also, they are distinct and nonzero, which makes sense because the quadratic has two distinct roots, and since the product is -(m + √n), which is not zero, neither y nor z can be zero.Okay, so now we also have f(1/y) + f(1/z) = 1/10. Let's compute f(1/y) and f(1/z) separately.f(1/y) = (1/y)² + (1/y) = 1/y² + 1/ySimilarly, f(1/z) = 1/z² + 1/zSo, f(1/y) + f(1/z) = (1/y² + 1/z²) + (1/y + 1/z) = (1/y² + 1/z²) + (1/y + 1/z)We need this sum to equal 1/10. Let's try to express this in terms of y + z and y z, since we already know those from Vieta's formulas.First, let's compute 1/y + 1/z. That's (z + y)/(y z). We know y + z = -1 and y z = -(m + √n). So,1/y + 1/z = (y + z)/(y z) = (-1)/[-(m + √n)] = 1/(m + √n)Okay, that's nice. Now, what about 1/y² + 1/z²? That can be written as (1/y + 1/z)² - 2*(1/y)*(1/z). Let's verify:(1/y + 1/z)^2 = 1/y² + 2*(1/y z) + 1/z²Therefore, 1/y² + 1/z² = (1/y + 1/z)^2 - 2/(y z)We already have 1/y + 1/z = 1/(m + √n), so squaring that gives 1/(m + √n)^2. Then, subtract 2/(y z). But y z is -(m + √n), so 1/(y z) = -1/(m + √n). Therefore, 2/(y z) = -2/(m + √n). Thus,1/y² + 1/z² = [1/(m + √n)^2] - [ -2/(m + √n) ] = 1/(m + √n)^2 + 2/(m + √n)Therefore, putting it all together:f(1/y) + f(1/z) = [1/(m + √n)^2 + 2/(m + √n)] + [1/(m + √n)] = 1/(m + √n)^2 + 3/(m + √n)Because the first part was 1/y² + 1/z² which is 1/(m + √n)^2 + 2/(m + √n), and then adding 1/y + 1/z which is 1/(m + √n). So total is 1/(m + √n)^2 + 3/(m + √n). This sum is equal to 1/10.Therefore, we have the equation:1/(m + √n)^2 + 3/(m + √n) = 1/10Let me set t = m + √n. Then the equation becomes:1/t² + 3/t = 1/10Multiply both sides by t² to eliminate denominators:1 + 3t = (1/10) t²Multiply both sides by 10 to eliminate the fraction:10 + 30t = t²Bring all terms to one side:t² - 30t - 10 = 0So, quadratic equation: t² - 30t - 10 = 0Wait, solving for t here. Let's compute the discriminant:D = (-30)^2 - 4 * 1 * (-10) = 900 + 40 = 940So sqrt(940) is irrational. Hmm. So t = [30 ± sqrt(940)] / 2 = 15 ± sqrt(235)But t was defined as m + √n, where m and n are positive integers. Therefore, t must be of the form m + √n. So, 15 + sqrt(235) or 15 - sqrt(235). But 15 - sqrt(235) is negative because sqrt(235) is approx 15.327, so 15 - 15.327 ≈ -0.327. Since m is a positive integer and √n is positive, t must be positive. So t = 15 + sqrt(235). But 235 factors into 5*47, which are both primes. So sqrt(235) is irrational, so t is 15 + sqrt(235). Therefore, m = 15 and √n = sqrt(235), so n = 235. But wait, that would make m + √n = 15 + sqrt(235). But then t is supposed to equal that, but t is 15 + sqrt(235). Wait, but m and n are positive integers. So m is 15, n is 235. Then 15 + sqrt(235) is t. So this seems possible. But let's check if this works.Wait, but let's verify this. If m = 15, n = 235, then m + √n = 15 + sqrt(235). Then, we need to check if f(1/y) + f(1/z) = 1/10. But if t = 15 + sqrt(235), then plugging into the equation:1/t² + 3/t = 1/10.But t = 15 + sqrt(235), which came from solving the quadratic equation. So that's consistent. So perhaps that's the answer. But wait, m and n must be positive integers, so m=15, n=235. Then 100m + n = 100*15 + 235 = 1500 + 235 = 1735. But let me check if this is correct.Wait, but hold on. Let's verify the steps again. Maybe I made a mistake in the algebra.We started with f(1/y) + f(1/z) = 1/10. Then, expressed this in terms of t = m + √n, leading to 1/t² + 3/t = 1/10. Then multiplied through by 10t² to get 10 + 30t = t², leading to t² -30t -10=0. Solving this quadratic gives t = [30 ± sqrt(900 +40)]/2 = [30 ± sqrt(940)]/2. sqrt(940) is sqrt(4*235) = 2*sqrt(235). So sqrt(940) is 2*sqrt(235). Therefore, t = [30 ± 2sqrt(235)]/2 = 15 ± sqrt(235). So t is either 15 + sqrt(235) or 15 - sqrt(235). As discussed, only 15 + sqrt(235) is positive, so t = 15 + sqrt(235). Therefore, m + √n = 15 + sqrt(235). Since m and n are positive integers, this requires that m=15 and √n = sqrt(235), which implies n=235, since √n must equal sqrt(235). Therefore, n=235. Therefore, m=15, n=235, so 100m + n = 1500 + 235 = 1735. So the answer is 1735.But let me check if this is correct by plugging back into the original equations.First, check f(y) = f(z) = m + √n =15 + sqrt(235). Then, the quadratic equation is x² + x - (15 + sqrt(235)) = 0. The roots y and z would be [-1 ± sqrt(1 + 4*(15 + sqrt(235)))]/2. Let's compute the discriminant: 1 + 60 + 4sqrt(235) = 61 + 4sqrt(235). So sqrt(61 + 4sqrt(235)). Hmm, is this a perfect square? Maybe. Let me see.Suppose sqrt(61 + 4sqrt(235)) can be written as sqrt(a) + sqrt(b), then (sqrt(a) + sqrt(b))² = a + 2sqrt(ab) + b = (a + b) + 2sqrt(ab). So we have:a + b = 612sqrt(ab) = 4sqrt(235) => sqrt(ab) = 2sqrt(235) => ab = 4*235 = 940So, solving a + b =61 and ab=940. Let's find integers a and b such that this is satisfied.Looking for factors of 940 that add up to 61. Let's factor 940:940 ÷ 2 = 470470 ÷ 2 = 235235 ÷5 =47So 940 = 2*2*5*47. So factors are 1, 2, 4, 5, 10, 20, 47, 94, 188, 235, 470, 940.Looking for two numbers that multiply to 940 and add to 61. Let's see: 20 and 47: 20 +47=67. Not 61. What about 235 and 4? 235+4=239. 10 and 94: 10+94=104. 5 and 188: 5+188=193. So none of these pairs add up to 61. Hmm, so maybe there is no such integer a and b, which suggests that sqrt(61 +4sqrt(235)) cannot be simplified into sum of square roots. Therefore, y and z are irrational numbers. That's okay, the problem just states they are distinct nonzero real numbers. So no problem there.But then, even if they are irrational, we can still compute f(1/y) + f(1/z). Wait, but according to our previous steps, we derived that this sum is 1/10, which was given. So perhaps that's okay.But let me check with m=15 and n=235, whether f(1/y) + f(1/z)=1/10.From earlier, we had f(1/y) + f(1/z) = 1/(m + √n)^2 + 3/(m + √n). Plugging in m=15 and n=235:1/(15 + sqrt(235))² + 3/(15 + sqrt(235)).Let me compute this.First, compute (15 + sqrt(235))² = 15² + 2*15*sqrt(235) + (sqrt(235))² = 225 + 30sqrt(235) + 235 = 225 + 235 + 30sqrt(235) = 460 + 30sqrt(235)So 1/(460 + 30sqrt(235)) + 3/(15 + sqrt(235)).Let me rationalize the denominators.First term: 1/(460 + 30sqrt(235)). Let's factor out 10 from denominator: 10*(46 + 3sqrt(235)). So 1/(10*(46 + 3sqrt(235))). Let's rationalize this by multiplying numerator and denominator by (46 - 3sqrt(235)):[1 * (46 - 3sqrt(235))]/[10*(46 + 3sqrt(235))(46 - 3sqrt(235))]Denominator: 10*(46² - (3sqrt(235))²) = 10*(2116 - 9*235) = 10*(2116 - 2115) = 10*(1) =10.So the first term becomes (46 - 3sqrt(235))/10.Second term: 3/(15 + sqrt(235)). Let's rationalize this denominator by multiplying numerator and denominator by (15 - sqrt(235)):[3*(15 - sqrt(235))]/[(15 + sqrt(235))(15 - sqrt(235))] = [45 - 3sqrt(235)]/[225 - 235] = [45 - 3sqrt(235)]/(-10) = (-45 + 3sqrt(235))/10.So adding the two terms together:First term: (46 - 3sqrt(235))/10Second term: (-45 + 3sqrt(235))/10Adding them: [46 - 3sqrt(235) -45 + 3sqrt(235)]/10 = (1)/10 = 1/10.Wow, that works! So yes, when m=15 and n=235, the sum f(1/y) + f(1/z) is indeed 1/10. Therefore, the answer is 100m + n = 100*15 + 235 = 1500 + 235 = 1735.So, that's the solution. Let me just check if there are other possible solutions. For example, could there be another pair m, n where t = m + sqrt(n) is a solution to the quadratic equation t² -30t -10 =0? But as we saw, the solutions are t = 15 ± sqrt(235). The other solution is 15 - sqrt(235) ≈ -0.327, which is negative, so m and n would have to satisfy m + sqrt(n) = negative number, but m and n are positive integers, so this is impossible. Therefore, the only possible solution is m=15, n=235. Therefore, 100m + n = 1735.Final Answerboxed{1735}</think>Given ( f(x) = x^2 + x ), we know there exist positive integers ( m ) and ( n ), and distinct nonzero real numbers ( y ) and ( z ), such that ( f(y) = f(z) = m + sqrt{n} ) and ( fleft(frac{1}{y}right) + fleft(frac{1}{z}right) = frac{1}{10} ). We need to find ( 100m + n ).1. Since ( f(y) = f(z) = m + sqrt{n} ), ( y ) and ( z ) are roots of the quadratic equation ( x^2 + x - (m + sqrt{n}) = 0 ). By Vieta's formulas: - ( y + z = -1 ) - ( yz = -(m + sqrt{n}) )2. Compute ( fleft(frac{1}{y}right) + fleft(frac{1}{z}right) ): [ fleft(frac{1}{y}right) + fleft(frac{1}{z}right) = left(frac{1}{y^2} + frac{1}{y}right) + left(frac{1}{z^2} + frac{1}{z}right) ] Using the identities for sum and product of roots: - ( frac{1}{y} + frac{1}{z} = frac{y + z}{yz} = frac{-1}{-(m + sqrt{n})} = frac{1}{m + sqrt{n}} ) - ( frac{1}{y^2} + frac{1}{z^2} = left(frac{1}{y} + frac{1}{z}right)^2 - 2 cdot frac{1}{yz} = left(frac{1}{m + sqrt{n}}right)^2 - 2 cdot frac{-1}{m + sqrt{n}} = left(frac{1}{m + sqrt{n}}right)^2 + frac{2}{m + sqrt{n}} )3. Combine these results: [ left(frac{1}{m + sqrt{n}}right)^2 + frac{3}{m + sqrt{n}} = frac{1}{10} ] Let ( t = m + sqrt{n} ): [ frac{1}{t^2} + frac{3}{t} = frac{1}{10} ] Multiply by ( 10t^2 ): [ 10 + 30t = t^2 implies t^2 - 30t - 10 = 0 ] Solving this quadratic equation: [ t = frac{30 pm sqrt{900 + 40}}{2} = frac{30 pm sqrt{940}}{2} = 15 pm sqrt{235} ] Since ( t = m + sqrt{n} ) must be positive, ( t = 15 + sqrt{235} ). Thus, ( m = 15 ) and ( sqrt{n} = sqrt{235} implies n = 235 ).4. Therefore, ( 100m + n = 100 times 15 + 235 = 1735 ).The final answer is (boxed{1735}).]

🔑:1. Given the function ( f(x) = x^2 + x ), we need to find positive integers ( m ) and ( n ), and distinct nonzero real numbers ( y ) and ( z ) such that ( f(y) = f(z) = m + sqrt{n} ) and ( fleft(frac{1}{y}right) + fleft(frac{1}{z}right) = frac{1}{10} ).2. Since ( f(y) = f(z) ) and ( y neq z ), we know that ( y ) and ( z ) are roots of the quadratic equation ( x^2 + x - (m + sqrt{n}) = 0 ). By Vieta's formulas, the sum of the roots ( y ) and ( z ) is: [ y + z = -1 ]3. We need to evaluate ( fleft(frac{1}{y}right) + fleft(frac{1}{z}right) ). Using the function definition, we have: [ fleft(frac{1}{y}right) = left(frac{1}{y}right)^2 + frac{1}{y} = frac{1}{y^2} + frac{1}{y} ] and [ fleft(frac{1}{z}right) = left(frac{1}{z}right)^2 + frac{1}{z} = frac{1}{z^2} + frac{1}{z} ]4. Since ( y ) and ( z ) are roots of the quadratic equation ( x^2 + x - (m + sqrt{n}) = 0 ), we have: [ y^2 + y = m + sqrt{n} ] and [ z^2 + z = m + sqrt{n} ]5. We also know that ( y ) and ( z ) satisfy the relationship ( y + z = -1 ). Therefore, we can express ( z ) in terms of ( y ): [ z = -1 - y ]6. Substituting ( z = -1 - y ) into the quadratic equation, we get: [ y^2 + y = (-1 - y)^2 + (-1 - y) ] Simplifying, we have: [ y^2 + y = 1 + 2y + y^2 - 1 - y ] [ y^2 + y = y^2 + y ] This confirms that ( y ) and ( z ) are indeed roots of the quadratic equation.7. Now, we need to find ( fleft(frac{1}{y}right) + fleft(frac{1}{z}right) ): [ fleft(frac{1}{y}right) + fleft(frac{1}{z}right) = frac{1}{y^2} + frac{1}{y} + frac{1}{z^2} + frac{1}{z} ]8. Using the fact that ( y ) and ( z ) are roots of the quadratic equation, we have: [ y^2 + y = m + sqrt{n} ] and [ z^2 + z = m + sqrt{n} ]9. We need to find the values of ( y ) and ( z ) such that: [ fleft(frac{1}{y}right) + fleft(frac{1}{z}right) = frac{1}{10} ]10. Let ( t = y(y + 1) ). Then: [ t = 10 left(3 + frac{1}{t}right) ] Solving for ( t ), we get: [ t^2 = 30t + 10 ] [ t^2 - 30t - 10 = 0 ] Solving this quadratic equation using the quadratic formula: [ t = frac{30 pm sqrt{900 + 40}}{2} = frac{30 pm sqrt{940}}{2} = 15 pm sqrt{235} ]11. Since ( t = y(y + 1) ), we have: [ t = 15 + sqrt{235} ]12. Therefore, ( m = 15 ) and ( n = 235 ). The final answer is: [ 100m + n = 100 cdot 15 + 235 = 1500 + 235 = 1735 ]The final answer is ( boxed{1735} )