🧠:[<think>Okay, so I have this problem here where set A is defined as all real numbers x such that -3 is less than or equal to x, which is less than or equal to 2. So, A is the interval [-3, 2]. Then set B is given as all real numbers x where x is less than k, and k is a real number. So, B is the interval (-∞, k). The question is asking for the range of real numbers k such that the union of A and B is equal to B. Hmm, let me parse that.First, let me recall what a union of two sets means. The union of A and B, denoted A ∪ B, is the set of all elements that are in A, in B, or in both. So, if A ∪ B = B, that means every element in A is already in B. Because if you take the union and it's still just B, then A must be a subset of B. Because if there were elements in A not in B, then the union would be bigger than B. So, the condition A ∪ B = B is equivalent to saying that A is a subset of B. That makes sense. So, for all x in A, x must also be in B.Given that A is [-3, 2] and B is (-∞, k), we need to find all real numbers k such that every x in [-3, 2] is also in (-∞, k). So, in other words, every x in A must satisfy x < k. Therefore, the upper bound of A, which is 2, must be less than k. Because if even the largest element in A is less than k, then all the other elements in A, which are smaller than 2, will definitely be less than k. Wait, but A includes 2, so for 2 to be in B, which is x < k, 2 must be less than k. But hold on, if k is equal to 2, then B is (-∞, 2), which does not include 2. So, since A includes 2, but B would not include 2 if k is 2. Therefore, k must be greater than 2 so that 2 is less than k, hence 2 is included in B? Wait, no. If B is x < k, then even if k is greater than 2, 2 is still in B because 2 < k. So, if k > 2, then 2 is in B, so A is entirely contained in B. However, if k is equal to 2, then B is (-∞, 2), which does not include 2, but A does include 2. Therefore, A would not be a subset of B if k is 2. Therefore, k must be greater than 2. So, the range of k is (2, ∞). Is that right?Let me check again. So, set A is from -3 to 2, including both endpoints. Set B is all real numbers less than k. So, to have A ∪ B = B, A must be a subset of B. So, every element of A is in B. Since A includes -3, which is definitely in B because B is everything up to k, and k is a real number. Since -3 is less than any real number k (unless k is less than -3, but in that case, B would be (-∞, k) where k is less than -3, but then A's lower bound is -3, so if k is less than -3, then A would not be a subset of B. Wait, hold on. Wait, no. Wait, if k is less than -3, then B is (-∞, k), which is all numbers less than k. But since A starts at -3, if k is less than -3, then the elements in A from -3 up to 2 would not be in B, because B stops at k, which is less than -3. So, in that case, A is not a subset of B. Therefore, to ensure that A is a subset of B, we need that all elements of A are in B. The leftmost element of A is -3. So, in order for -3 to be in B, B must include numbers up to at least -3, but since B is x < k, as long as k is greater than -3, then -3 is in B. Wait, but if k is greater than -3, then B includes (-∞, k). So, -3 is in B if -3 < k. But actually, no. Wait, if k is greater than -3, then since B is x < k, then -3 is in B only if -3 < k. But wait, if k is, say, -2, then B is (-∞, -2), which doesn't include -3. Wait, hold on. Let's think. If k is -2, then B is all real numbers less than -2. But -3 is less than -2, so -3 is in B. Wait, actually, yes. If k is -2, then x < -2. But -3 is less than -2, so -3 is in B. But -2 is not in B. But A starts at -3. So, if k is -2, then A is from -3 to 2. The elements from -3 up to -2 would be in B (since B is up to -2, but not including -2). Then from -2 to 2, those elements are not in B. So, in that case, A is not a subset of B. Therefore, even though -3 is in B, the rest of A from -3 to 2 would not be entirely in B unless k is greater than or equal to 2. Wait, this is getting a bit confusing. Let me approach this step by step.First, the condition is A ∪ B = B, which implies A is a subset of B. So, all elements of A must be in B. Set A is [-3, 2], and set B is (-∞, k). So, for all x in [-3, 2], x must be in (-∞, k). Which means x < k for all x in [-3, 2]. Therefore, the maximum element in A is 2, so to have 2 < k. Because if 2 is in A, and A is a subset of B, then 2 must be in B. But B is x < k, so 2 < k. Therefore, k must be greater than 2. If k is equal to 2, then 2 is not in B, so A is not a subset of B. If k is greater than 2, then all elements of A, including 2, are less than k, so they are in B. So, the answer is k > 2, which is (2, ∞). But wait, let me check if there are any other considerations.Suppose k is 3. Then B is (-∞, 3), which includes all of A since A is up to 2. So, A ∪ B would be (-∞, 3), which is B. So, that works. If k is 2.5, same thing. If k is 2, B is (-∞, 2), so A ∪ B would be [-3, 2], which is not equal to B. Because B is (-∞, 2), and A is [-3, 2], so the union is [-3, 2], which is not equal to B. So, k cannot be 2. If k is less than 2, say 1, then B is (-∞, 1), and A is [-3, 2], so their union is [-3, 2], which is not equal to B. So, again, A ∪ B is not equal to B unless A is entirely contained in B. Therefore, the key is that the maximum element of A must be less than k. Since the maximum element of A is 2, k must be greater than 2. Therefore, the range of k is all real numbers greater than 2.But wait, let me think again. What if k is less than -3? Let's say k is -4. Then B is (-∞, -4). Then A is [-3, 2], so the union of A and B would be (-∞, -4) ∪ [-3, 2]. Which is not equal to B. So, definitely, k cannot be less than -3. What if k is between -3 and 2? For example, k is 0. Then B is (-∞, 0). The union of A and B would be (-∞, 0) ∪ [-3, 2]. But since [-3, 2] includes numbers from -3 to 2, and (-∞, 0) includes everything up to 0. So the union would be (-∞, 2]. Which is not equal to B, which is (-∞, 0). So that's not equal either. Therefore, in order for A ∪ B to be equal to B, all elements of A must be in B. Therefore, the entire interval [-3, 2] must be inside (-∞, k). Which only happens if 2 < k. So, k must be greater than 2. Therefore, the range is k > 2. So, the answer should be k is in (2, ∞). Therefore, the range of real number k is all real numbers greater than 2.But just to verify once more. Suppose k is exactly 2. Then B is (-∞, 2). The union of A and B would be (-∞, 2] ∪ [-3, 2] which is (-∞, 2]. But B is (-∞, 2). So, the union would include 2, which is not in B. Therefore, A ∪ B would not equal B. So, k must be greater than 2. If k is greater than 2, then B is (-∞, k) which includes all of A because A's maximum is 2, which is less than k. Therefore, A ∪ B = B. So yes, that's correct. Therefore, the range of k is (2, ∞).Final AnswerThe range of real number ( k ) is boxed{(2, infty)}.</think>Given set ( A = {x mid -3 leq x leq 2} ) and set ( B = {x mid x < k, k in mathbb{R}} ), we need to find the range of real number ( k ) such that ( A cup B = B ).To solve this, we recognize that ( A cup B = B ) implies that ( A ) is a subset of ( B ). This means every element in ( A ) must also be in ( B ).Set ( A ) is the interval ([-3, 2]) and set ( B ) is the interval ((-∞, k)). For ( A ) to be a subset of ( B ), all elements of ( A ) must be less than ( k ). The maximum element in ( A ) is 2, so we need ( 2 < k ). If ( k ) were equal to 2, ( B ) would be ((-∞, 2)), which does not include 2, contradicting the requirement since ( A ) includes 2. Therefore, ( k ) must be greater than 2.Thus, the range of real number ( k ) is (boxed{(2, infty)}).,<think>Alright, let's tackle this problem step by step. So, we have two sets, A and B. Set A is defined as all real numbers x such that -3 is less than or equal to x, which is less than or equal to 2. In other words, A is the closed interval from -3 to 2. Then, set B is all real numbers x such that x is less than k, where k is a real number. So, B is an open interval that goes up to k but doesn't include k itself.The problem states that the union of A and B is equal to B itself. So, A union B = B. We need to find the range of the real number k for which this is true. First, let me recall what the union of two sets means. The union of A and B, denoted as A ∪ B, is the set of all elements that are in A, in B, or in both. So, if A ∪ B = B, that means every element of A must already be in B. Because if there was an element in A that wasn't in B, then the union would have that extra element, making it not equal to B. Therefore, for the union to be exactly B, set A must be a subset of set B. So, the key here is that A is a subset of B. That is, every x in A must also be in B. Let's write that out formally. For all x in A, x must satisfy the condition of B, which is x < k. So, the maximum value in A is 2, right? Because A is from -3 to 2, inclusive. So, the highest x can be in A is 2. Therefore, if all elements of A are in B, even the largest element of A, which is 2, must be in B. But B is defined as x < k. So, 2 must be less than k? Wait, but B is x < k. So, 2 has to be less than k for 2 to be in B. However, B is x < k, so 2 would have to be less than k. But if k is equal to 2, then B would be x < 2, which doesn't include 2. But A includes 2. Therefore, if k is 2, then 2 isn't in B, so A isn't a subset of B because 2 is in A but not in B. Therefore, k must be greater than 2 to include all elements of A in B. Wait, let me check that again. If k is greater than 2, then the set B includes all real numbers less than k. Since A goes up to 2, which is less than k, then every element in A, from -3 up to 2, is less than k. Therefore, all elements of A are in B, so A ∪ B would just be B, because adding elements less than k (which are already in B) doesn't change the set. But what if k is equal to 2? Then B would be all real numbers less than 2. But A includes numbers up to and including 2. So, the number 2 is in A but not in B. Therefore, A ∪ B would include all numbers less than 2 from B and also the number 2 from A. Therefore, A ∪ B would be all numbers less than or equal to 2, which is different from B (since B was strictly less than 2). Therefore, if k is equal to 2, A ∪ B is not equal to B. Similarly, if k is less than 2, then even more elements of A are not included in B. For example, if k is 1, then B is all numbers less than 1. But A includes numbers from -3 up to 2, so numbers between 1 and 2 would be in A but not in B. Hence, the union would include numbers up to 2, so again, A ∪ B would not equal B. Therefore, k must be greater than 2. Wait, but is that the only condition? Let me think. If k is greater than 2, then all elements of A are in B, so their union is B. If k is 2 or less, the union is larger than B. Therefore, the range of k should be all real numbers greater than 2, that is, k > 2. But let me verify this with an example. Let's take k = 3. Then B is all numbers less than 3. A is from -3 to 2. Since 2 < 3, all elements of A are in B. So A ∪ B = B. If k = 2.5, same thing; all elements of A up to 2 are less than 2.5, so they're in B. If k = 2.1, same logic. However, if k = 2, as before, the union is not B. Therefore, the conclusion is that k must be greater than 2. But let me check if there's another perspective. Maybe the problem is expecting a different answer? Let's rephrase the question. When they say A ∪ B = B, this is equivalent to saying that A is a subset of B. So, for A to be a subset of B, every element of A must be in B. Given that A is the interval [-3, 2], and B is the interval (-∞, k). So, for [-3, 2] to be a subset of (-∞, k), the upper bound of A, which is 2, must be less than k. Because if k is greater than 2, then 2 is less than k, and all elements of A, which are up to 2, are in B. If k is equal to 2, then B is (-∞, 2), which does not include 2, but A does include 2, so A is not a subset. Therefore, k must be greater than 2. Therefore, the range of real number k is all real numbers greater than 2. So, in interval notation, that would be (2, ∞). Wait, but the problem says "the range of real number k". So, probably, the answer is k > 2, or in other words, k is greater than 2. So, written as an interval, (2, ∞). I think that's it. Let me just check once more. Suppose k is 2. Then B is up to but not including 2. A includes 2, so the union would be up to 2, but including 2. So, A ∪ B would be [-3, 2], which is not equal to B. If k is greater than 2, say 3, then B is up to 3, and A is included in B, so their union is B. If k is less than 2, like 1, then B is up to 1, and A ∪ B would be [-3, 2], which is not B. Therefore, yes, k must be greater than 2. Therefore, the range of k is all real numbers greater than 2.Final AnswerThe range of real number ( k ) is boxed{(2, infty)}.</think>Given set ( A = {x mid -3 leq x leq 2} ) and set ( B = {x mid x < k, k in mathbb{R}} ), we need to determine the range of ( k ) such that ( A cup B = B ).1. Understanding the Union Condition: - The union ( A cup B = B ) implies that every element of ( A ) must be in ( B ). This means ( A ) is a subset of ( B ).2. Interval Analysis: - Set ( A ) is the closed interval ([-3, 2]). - Set ( B ) is the open interval ((-infty, k)).3. Subset Requirement: - For ( A ) to be a subset of ( B ), all elements of ( A ) must be in ( B ). The maximum element in ( A ) is 2. Therefore, 2 must be in ( B ).4. Condition on ( k ): - Since ( B ) is defined as ( x < k ), the value 2 must be less than ( k ). If ( k leq 2 ), then 2 would not be in ( B ), making ( A cup B neq B ).5. Conclusion: - Therefore, ( k ) must be greater than 2 to ensure all elements of ( A ) are included in ( B ).The range of the real number ( k ) is (boxed{(2, infty)}).]

🔑:Since Acup B=B, it follows that Asubset B. Given A={x|-3leq xleq 2} and B={x|x2. Therefore, the range of the real number k is (2, +infty). Hence, the answer is boxed{(2, +infty)}.

🧠:[<think>Okay, so I have this equation here: the sum from some starting point up to 2018 times 2019 of x divided by (n times (n+1)) equals 2017. The question is asking for the value of x that satisfies this equation. Hmm, let me try to parse this.First, the equation is written as:x/(2×3) + x/(3×4) + x/(4×5) + ... + x/(2018×2019) = 2017So, the denominators are consecutive integers multiplied together, starting from 2×3 up to 2018×2019. Each term in the sum is x divided by one of these products. The variable here is x, and we need to solve for it.Since x is a common factor in all the terms, maybe I can factor that out first. So, factoring x out, the left-hand side becomes x multiplied by the sum of 1/(n(n+1)) where n starts at 2 and goes up to 2018. That seems right. So, the equation simplifies to:x * [1/(2×3) + 1/(3×4) + ... + 1/(2018×2019)] = 2017Therefore, to solve for x, I need to compute that sum inside the brackets and then divide 2017 by it. The key here is figuring out the value of that sum.I remember that fractions like 1/(n(n+1)) can be broken down using partial fractions. Let me recall how that works. For a general term 1/(n(n+1)), we can express it as A/n + B/(n+1). To find A and B, let's set up the equation:1/(n(n+1)) = A/n + B/(n+1)Multiply both sides by n(n+1) to eliminate denominators:1 = A(n+1) + BnExpanding the right-hand side:1 = An + A + BnCombine like terms:1 = (A + B)n + AFor this to hold for all n, the coefficients of the corresponding powers of n on both sides must be equal. On the left side, the coefficient of n is 0, and the constant term is 1. On the right side, the coefficient of n is (A + B) and the constant term is A. Therefore, we can set up the following system of equations:A + B = 0 (coefficient of n)A = 1 (constant term)Solving this, we get A = 1 and then B = -1. Therefore,1/(n(n+1)) = 1/n - 1/(n+1)Ah, that's a telescoping series! So, each term in the sum can be written as the difference of two reciprocals. That means when we add them up, most terms will cancel out.So, let's apply this to the sum in our equation. The sum is from n = 2 to n = 2018 of 1/(n(n+1)) which telescopes to:Sum from n=2 to 2018 of [1/n - 1/(n+1)]Let's write out the first few terms to see the pattern:For n=2: 1/2 - 1/3For n=3: 1/3 - 1/4For n=4: 1/4 - 1/5...For n=2018: 1/2018 - 1/2019When we add all these up, the -1/3 from the first term cancels with the +1/3 from the second term, the -1/4 from the second term cancels with the +1/4 from the third term, and so on. This cancellation continues all the way to the end. The only terms that don't get canceled are the very first term of the first expression, which is 1/2, and the very last term of the last expression, which is -1/2019. Therefore, the entire sum simplifies to:1/2 - 1/2019Therefore, the sum inside the brackets is (1/2 - 1/2019). Let me compute that value.First, find a common denominator for 1/2 and 1/2019. The common denominator is 2×2019=4038.So, 1/2 = 2019/4038 and 1/2019 = 2/4038.Therefore, 1/2 - 1/2019 = 2019/4038 - 2/4038 = (2019 - 2)/4038 = 2017/4038So, the sum is 2017/4038.Therefore, going back to the original equation:x * (2017/4038) = 2017To solve for x, divide both sides by (2017/4038):x = 2017 / (2017/4038) = 2017 * (4038/2017) = 4038Wait, so x equals 4038? Let me verify that.If the sum of the series is 2017/4038, then multiplying by x gives (x * 2017)/4038 = 2017. Then, multiplying both sides by 4038 gives x * 2017 = 2017 * 4038, so dividing both sides by 2017 gives x = 4038. Yes, that seems correct.Just to make sure I didn't make a mistake in the telescoping part. Let's confirm with a smaller example. Suppose instead of going up to 2018×2019, let's take a smaller case, like up to 3×4.So, if the sum is 1/(2×3) + 1/(3×4), which is (1/2 - 1/3) + (1/3 - 1/4) = 1/2 - 1/4 = 1/4. Then, according to the formula, n starts at 2 and ends at 3, so the sum should be 1/2 - 1/(3+1) = 1/2 - 1/4 = 1/4. That checks out. Similarly, if I take up to n=4, sum from 2 to 4: (1/2 -1/3) + (1/3 -1/4) + (1/4 -1/5) = 1/2 -1/5 = 3/10. According to the formula, 1/2 -1/(4+1)=1/2 -1/5=3/10. Correct.Therefore, the telescoping works as expected, and the sum from n=k to n=m of 1/(n(n+1)) is 1/k - 1/(m+1). In our problem, k=2 and m=2018, so the sum is 1/2 - 1/(2018+1) = 1/2 -1/2019 = 2017/4038. Therefore, the value of x is 4038.So, I think that's the answer. Let me just check if there was any miscalculation with the denominators. The common denominator between 2 and 2019 is indeed 4038. Then, 2019 - 2 is 2017. So, 2017/4038. Then, solving for x gives 4038. Yeah, that seems right.Final Answerboxed{4038}</think>The given equation is:[frac{x}{2 times 3} + frac{x}{3 times 4} + frac{x}{4 times 5} + ldots + frac{x}{2018 times 2019} = 2017]We factor out ( x ) from the left-hand side:[x left( frac{1}{2 times 3} + frac{1}{3 times 4} + frac{1}{4 times 5} + ldots + frac{1}{2018 times 2019} right) = 2017]Each term (frac{1}{n(n+1)}) can be decomposed using partial fractions:[frac{1}{n(n+1)} = frac{1}{n} - frac{1}{n+1}]This transforms the sum into a telescoping series:[sum_{n=2}^{2018} left( frac{1}{n} - frac{1}{n+1} right)]Writing out the terms, we see most terms cancel out:[left( frac{1}{2} - frac{1}{3} right) + left( frac{1}{3} - frac{1}{4} right) + ldots + left( frac{1}{2018} - frac{1}{2019} right)]The remaining terms are the first and the last:[frac{1}{2} - frac{1}{2019}]Calculating the sum:[frac{1}{2} - frac{1}{2019} = frac{2019}{4038} - frac{2}{4038} = frac{2017}{4038}]Substituting this back into the equation:[x left( frac{2017}{4038} right) = 2017]Solving for ( x ):[x = 2017 times frac{4038}{2017} = 4038]Thus, the value of ( x ) is:[boxed{4038}],<think>Okay, so I need to solve this equation: [frac{x}{2 times 3} + frac{x}{3 times 4} + frac{x}{4 times 5} + ldots + frac{x}{2018 times 2019} = 2017]Hmm, let me see. First, I notice that each term in the sum has a similar structure. The denominators are products of consecutive integers starting from 2×3 up to 2018×2019. And each numerator is just x. So maybe I can factor out the x and then deal with the sum of reciprocals of these products. Let me write the equation as:[x left( frac{1}{2 times 3} + frac{1}{3 times 4} + frac{1}{4 times 5} + ldots + frac{1}{2018 times 2019} right) = 2017]So if I can compute that sum inside the parentheses, then I can just divide 2017 by that sum to get x. Now, the sum is:[S = sum_{k=2}^{2018} frac{1}{k(k+1)}]Wait, let me check the indices. The first term is 2×3, which is k=2, and the last term is 2018×2019, so k=2018. So yeah, the summation would be from k=2 to k=2018 of 1/(k(k+1)). I remember that there's a telescoping series formula for terms like 1/(k(k+1)). Let me recall: using partial fractions, 1/(k(k+1)) can be written as A/k + B/(k+1). Let me compute A and B.So,[frac{1}{k(k+1)} = frac{A}{k} + frac{B}{k+1}]Multiply both sides by k(k+1):[1 = A(k+1) + Bk]Let me solve for A and B. Expanding the right side:[1 = Ak + A + Bk = (A + B)k + A]For this to hold for all k, the coefficients of like terms must be equal. So:Coefficient of k: A + B = 0Constant term: A = 1So solving these equations:From the constant term, A = 1. Then from A + B = 0, we get B = -1.Therefore,[frac{1}{k(k+1)} = frac{1}{k} - frac{1}{k+1}]Right, so each term in the sum S can be written as the difference of reciprocals. That should telescope when we sum them up.So let's substitute that into the sum S:[S = sum_{k=2}^{2018} left( frac{1}{k} - frac{1}{k+1} right )]If I write out the terms, maybe it becomes clearer:For k=2: 1/2 - 1/3For k=3: 1/3 - 1/4For k=4: 1/4 - 1/5...For k=2018: 1/2018 - 1/2019So when we add all these up, the -1/3 from the first term cancels with the +1/3 from the second term. Similarly, the -1/4 cancels with the +1/4, and so on, all the way up to -1/2018 cancels with the next term, but since the last term is 1/2018 -1/2019, only the first term of the first fraction and the last term of the last fraction remain.So the sum S simplifies to:[left( frac{1}{2} - frac{1}{3} right ) + left( frac{1}{3} - frac{1}{4} right ) + ldots + left( frac{1}{2018} - frac{1}{2019} right ) = frac{1}{2} - frac{1}{2019}]Because all the middle terms cancel out. Therefore,[S = frac{1}{2} - frac{1}{2019}]Now, compute that value:First, find a common denominator for 1/2 and 1/2019. The denominators are 2 and 2019, so the common denominator is 2*2019 = 4038.So,[frac{1}{2} = frac{2019}{4038}]and[frac{1}{2019} = frac{2}{4038}]Therefore,[S = frac{2019}{4038} - frac{2}{4038} = frac{2017}{4038}]So S = 2017/4038.Now, going back to the original equation:[x times frac{2017}{4038} = 2017]To solve for x, divide both sides by (2017/4038):[x = 2017 div frac{2017}{4038} = 2017 times frac{4038}{2017} = 4038]So the value of x is 4038.Wait, let me verify that again. If S is 2017/4038, then multiplying by x gives x*(2017/4038)=2017. So x is 2017 divided by (2017/4038) which is 2017*(4038/2017) = 4038. Yep, that cancels out the 2017. So x=4038.Therefore, the root of the equation is x=4038.Final AnswerThe root of the equation is boxed{4038}.</think>The given equation is:[frac{x}{2 times 3} + frac{x}{3 times 4} + frac{x}{4 times 5} + ldots + frac{x}{2018 times 2019} = 2017]We factor out ( x ) and rewrite the equation as:[x left( sum_{k=2}^{2018} frac{1}{k(k+1)} right) = 2017]Using partial fractions, each term (frac{1}{k(k+1)}) can be decomposed as:[frac{1}{k(k+1)} = frac{1}{k} - frac{1}{k+1}]This transforms the sum into a telescoping series:[sum_{k=2}^{2018} left( frac{1}{k} - frac{1}{k+1} right)]Writing out the terms, we see that most terms cancel out, leaving:[left( frac{1}{2} - frac{1}{2019} right)]Simplifying this sum:[frac{1}{2} - frac{1}{2019} = frac{2019}{4038} - frac{2}{4038} = frac{2017}{4038}]Substituting this back into the equation, we get:[x times frac{2017}{4038} = 2017]Solving for ( x ):[x = 2017 div frac{2017}{4038} = 2017 times frac{4038}{2017} = 4038]Thus, the root of the equation is (boxed{4038}).]

🔑:4038

🧠:[<think>Okay, so I need to figure out the largest subset of the set { y | 0 ≤ y ≤ π } such that the inequality sin(x + y) ≤ sin x + sin y holds for all x in [0, π]. The options are given, and I need to determine which one is correct. Let me try to break this down step by step.First, let's recall the trigonometric identity for sin(x + y). The sine of a sum is sin x cos y + cos x sin y. So, substituting that into the inequality:sin(x + y) = sin x cos y + cos x sin y ≤ sin x + sin y.So, we can rearrange the inequality:sin x cos y + cos x sin y ≤ sin x + sin y.Let me subtract sin x cos y + cos x sin y from both sides to see if that helps, but actually, maybe it's better to bring all terms to one side:sin x cos y + cos x sin y - sin x - sin y ≤ 0.Factor terms with sin x and sin y:sin x (cos y - 1) + sin y (cos x - 1) ≤ 0.Hmm, interesting. So, we have sin x (cos y - 1) + sin y (cos x - 1) ≤ 0.Now, note that for all real numbers θ, cos θ - 1 ≤ 0, because the maximum value of cos θ is 1. So, cos y - 1 ≤ 0 and cos x - 1 ≤ 0. Also, sin x and sin y are non-negative in [0, π], since x and y are between 0 and π. So, sin x ≥ 0 and sin y ≥ 0.Therefore, each term in the sum sin x (cos y - 1) and sin y (cos x - 1) is non-positive because they are products of non-negative and non-positive terms. Therefore, the entire left-hand side is the sum of two non-positive terms, which is non-positive. Therefore, the inequality sin(x + y) ≤ sin x + sin y holds for all x, y in [0, π]? Wait, but that can't be right, because if we take specific values, maybe the inequality is strict?Wait, hold on. Let me test some specific values to see if the inequality actually holds.Take x = 0. Then sin(0 + y) = sin y. On the right-hand side, sin 0 + sin y = 0 + sin y = sin y. So, sin y ≤ sin y, which is equality. That's fine.Take x = π/2. Then sin(π/2 + y) = sin(π/2 + y) = cos y (since sin(π/2 + y) = cos y). On the right-hand side, sin(π/2) + sin y = 1 + sin y. So, the inequality becomes cos y ≤ 1 + sin y. Since cos y - sin y ≤ 1 for all y? Let's check y = π/2. cos(π/2) - sin(π/2) = 0 - 1 = -1 ≤ 1. True. At y = 0: cos 0 - sin 0 = 1 - 0 = 1 ≤ 1. Equality. At y = π: cos π - sin π = -1 - 0 = -1 ≤ 1. So, indeed, cos y ≤ 1 + sin y is always true. So, in this case, equality holds when y = 0, but it's true for all y. Wait, but this seems like the inequality holds for all x and y in [0, π]. But then the answer would be (E) 0 ≤ y ≤ π. But the options include (E), so maybe that's the answer? But let me check another case.Wait, let's take x = π. Then sin(π + y) = -sin y. On the right-hand side, sin π + sin y = 0 + sin y = sin y. So, the inequality becomes -sin y ≤ sin y, which simplifies to 0 ≤ 2 sin y. Since sin y is non-negative in [0, π], this is true. So, again, holds for all y.Wait, so does this inequality hold for all x and y in [0, π]? Let me check a case where maybe it doesn't. Suppose x = 3π/4 and y = 3π/4. Then x + y = 3π/4 + 3π/4 = 3π/2. sin(3π/2) = -1. On the right-hand side, sin(3π/4) + sin(3π/4) = √2/2 + √2/2 = √2 ≈ 1.414. So, -1 ≤ √2, which is true.Wait, another one. Suppose y = π/2, x = π/2. Then sin(π) = 0. Right-hand side: sin(π/2) + sin(π/2) = 1 + 1 = 2. So, 0 ≤ 2. True.Wait, maybe it does hold for all x and y in [0, π]? But let's think again. When is sin(x + y) ≤ sin x + sin y?We can also approach this by rearranging the inequality. Let's subtract sin(x + y) from both sides:0 ≤ sin x + sin y - sin(x + y).So, the inequality is equivalent to sin x + sin y - sin(x + y) ≥ 0.Is this always true? Let's express sin x + sin y - sin(x + y). Using the identity sin x + sin y = 2 sin( (x + y)/2 ) cos( (x - y)/2 ). But maybe another approach. Let's compute sin x + sin y - sin(x + y):sin x + sin y - [sin x cos y + cos x sin y] = sin x (1 - cos y) + sin y (1 - cos x).Since 1 - cos y and 1 - cos x are both non-negative (because cos θ ≤ 1 for all θ), and sin x and sin y are non-negative in [0, π]. Therefore, sin x (1 - cos y) + sin y (1 - cos x) ≥ 0.Therefore, the inequality holds for all x, y ∈ [0, π]. So, this suggests that the largest subset is the entire interval [0, π], which is option (E). But let me verify once again with an example where maybe the inequality fails.Take y = π. Then the inequality becomes sin(x + π) ≤ sin x + sin π. Since sin(x + π) = -sin x, and sin π = 0. So, -sin x ≤ sin x. Which simplifies to 0 ≤ 2 sin x. Since sin x is non-negative in [0, π], this is true. Similarly, for y = π/2, x arbitrary. Let's take x = π/4. Then sin(π/4 + π/2) = sin(3π/4) = √2/2. Right-hand side: sin(π/4) + sin(π/2) = √2/2 + 1 ≈ 1.707. So, √2/2 ≈ 0.707 ≤ 1.707. True.Wait, so maybe the answer is indeed (E). But why are the other options given? Maybe the question is different? Wait, let me check the problem statement again.It says: "the largest subset of the set { y | 0 ≤ y ≤ π } satisfies sin(x + y) ≤ sin x + sin y for all x ∈ [0, π]." So, we need to find the largest subset of y values in [0, π] such that for all x in [0, π], the inequality holds. Wait, but our previous analysis suggests that for all y in [0, π], the inequality holds for all x in [0, π]. Therefore, the largest subset would be the entire interval [0, π], which is option (E). However, I might be missing something here.Wait, let's consider a specific case where y is in [0, π] but the inequality could fail. Suppose y = 3π/4, and x = 3π/4. Then sin(x + y) = sin(3π/2) = -1. The right-hand side is sin(3π/4) + sin(3π/4) = √2/2 + √2/2 = √2 ≈ 1.414. So, -1 ≤ √2, which is true.Another case: y = π, x = π/2. Then sin(π/2 + π) = sin(3π/2) = -1. RHS: sin(π/2) + sin(π) = 1 + 0 = 1. So, -1 ≤ 1. True.Wait, maybe there's no case where the inequality fails? Let's try x = π - y. Then sin(x + y) = sin(π) = 0. RHS: sin(π - y) + sin y = sin y + sin y = 2 sin y. Since sin y ≥ 0, 0 ≤ 2 sin y, which is always true.Alternatively, take x such that x + y > π. For example, x = 2π/3, y = 2π/3. Then x + y = 4π/3. sin(4π/3) = -√3/2. RHS: sin(2π/3) + sin(2π/3) = √3/2 + √3/2 = √3 ≈ 1.732. So, -√3/2 ≈ -0.866 ≤ 1.732. True.Another angle: Let's take y = π/2, x = π. Then sin(π + π/2) = sin(3π/2) = -1. RHS: sin π + sin π/2 = 0 + 1 = 1. So, -1 ≤ 1. True.Wait, so in all these test cases, the inequality holds. Therefore, perhaps the inequality sin(x + y) ≤ sin x + sin y is always true for x, y ∈ [0, π]. Therefore, the largest subset is the entire interval [0, π], which is option (E). But the options given include (E), so that should be the answer.But wait, the original problem says "the largest subset of the set { y | 0 ≤ y ≤ π } satisfies sin(x + y) ≤ sin x + sin y (x ∈ [0, π])", so all y in [0, π] work, so the answer is (E).However, maybe I made a mistake in the initial analysis. Let's check again.Suppose we rearrange the inequality:sin(x + y) - sin x - sin y ≤ 0.Using the identity sin(x + y) = sin x cos y + cos x sin y.So, sin x cos y + cos x sin y - sin x - sin y ≤ 0.Factor:sin x (cos y - 1) + sin y (cos x - 1) ≤ 0.As both terms (cos y - 1) and (cos x - 1) are non-positive (since cos θ ≤ 1), and sin x, sin y are non-negative in [0, π], each term in the sum is non-positive. Therefore, their sum is non-positive. Therefore, the inequality holds for all x, y ∈ [0, π]. Therefore, the largest subset is indeed [0, π], so option (E).But wait, the problem might have a trick. For example, maybe when x + y exceeds π, but since x and y are both in [0, π], x + y can be up to 2π, but sin is periodic. However, in the range [0, 2π], sin is positive in [0, π] and negative in [π, 2π]. But even so, when x + y is in [π, 2π], sin(x + y) is non-positive, while sin x + sin y is non-negative (as both sin x and sin y are non-negative in [0, π]). Therefore, a non-positive number is certainly less than or equal to a non-negative number. Wait, but sin x + sin y is non-negative, and sin(x + y) is ≤ sin x + sin y. But if sin(x + y) is negative, then since the right-hand side is non-negative, the inequality would hold. Therefore, in cases where sin(x + y) is positive, we need to check if it's still less than or equal to sin x + sin y.Wait, for x + y in [0, π], sin(x + y) is positive. So, in that case, we need sin(x + y) ≤ sin x + sin y. Let's verify that. Take x and y such that x + y is in [0, π]. For example, x = y = π/4. Then sin(π/2) = 1, and sin(π/4) + sin(π/4) = √2/2 + √2/2 = √2 ≈ 1.414. So, 1 ≤ 1.414, which is true.Another example: x = π/3, y = π/6. Then x + y = π/2. sin(π/2) = 1. RHS: sin(π/3) + sin(π/6) = (√3/2) + (1/2) ≈ 0.866 + 0.5 = 1.366. So, 1 ≤ 1.366. True.Another example: x = π/2, y = π/2. Then x + y = π. sin π = 0. RHS: sin(π/2) + sin(π/2) = 1 + 1 = 2. 0 ≤ 2. True.Wait, so even when x + y is in [0, π], the inequality holds. For angles where x + y is in [0, π], sin(x + y) ≤ sin x + sin y because of the concavity of sine in [0, π]. Since sine is concave in [0, π], we have sin(a + b) ≤ sin a + sin b for a, b, a + b in [0, π]. But even when a + b exceeds π, as we saw earlier, sin(a + b) becomes negative, making the inequality hold as well.Therefore, in all cases, the inequality holds. Therefore, the largest possible subset is the entire interval [0, π], so the answer is (E).But wait, the options don't include (E) as a possible answer? Wait, no, checking the original problem statement: (E) is 0 ≤ y ≤ π. So yes, (E) is an option. So, maybe the answer is (E).But why are other options presented? Maybe there's a misunderstanding in the problem. Let me check again.Wait, the problem says "the largest subset of the set { y | 0 ≤ y ≤ π } satisfies sin(x + y) ≤ sin x + sin y (x ∈[0, π])". So, the set { y | 0 ≤ y ≤ π } is the entire interval [0, π]. We need to find the largest subset of this set (so a subset of [0, π]) such that for all x in [0, π], the inequality holds. But as we showed, the inequality holds for all y in [0, π], so the largest subset is the entire set itself, which is [0, π], option (E). Therefore, the answer should be (E).But maybe the problem is translated incorrectly or there's a typo. Let me check once again with another approach.Alternative approach: Let's fix y and check for which y the inequality sin(x + y) ≤ sin x + sin y holds for all x ∈ [0, π].We need to ensure that for a fixed y, the inequality is true for all x ∈ [0, π].Let's rearrange the inequality:sin(x + y) - sin x ≤ sin y.Using the identity sin(x + y) - sin x = 2 cos(x + y/2) sin(y/2).Wait, let's use the identity:sin A - sin B = 2 cos((A + B)/2) sin((A - B)/2).So, sin(x + y) - sin x = 2 cos((x + y + x)/2) sin((x + y - x)/2) = 2 cos((2x + y)/2) sin(y/2).Therefore, the inequality becomes:2 cos((2x + y)/2) sin(y/2) ≤ sin y.But sin y = 2 sin(y/2) cos(y/2). Therefore, substituting:2 cos((2x + y)/2) sin(y/2) ≤ 2 sin(y/2) cos(y/2).Divide both sides by 2 sin(y/2) (assuming sin(y/2) ≠ 0, i.e., y ≠ 0):cos((2x + y)/2) ≤ cos(y/2).Therefore, the inequality reduces to:cos(x + y/2) ≤ cos(y/2).So, for y ≠ 0, the inequality is equivalent to cos(x + y/2) ≤ cos(y/2).Now, cos is a decreasing function on [0, π], so if x + y/2 ≥ y/2, which it is since x ≥ 0. So, since x ∈ [0, π], then x + y/2 can range from y/2 to π + y/2. However, since y ∈ [0, π], π + y/2 can be up to 3π/2. But cos is decreasing from 0 to π, and increasing from π to 2π, but since our angles here might exceed π, we have to be careful.But let's consider that we need cos(x + y/2) ≤ cos(y/2) for all x ∈ [0, π]. Let's analyze when this is true.Case 1: If x + y/2 ≤ π. Then since cos is decreasing on [0, π], the maximum value of cos(x + y/2) occurs at the minimum x, which is x = 0. So, cos(y/2) ≤ cos(y/2), which is equality. Then as x increases, cos(x + y/2) decreases, so cos(x + y/2) ≤ cos(y/2) holds for all x in [0, π] such that x + y/2 ≤ π. But when x + y/2 exceeds π, cos(x + y/2) becomes cos of an angle greater than π but less than 3π/2 (since y ≤ π). In that interval, cos is negative, so cos(x + y/2) ≤ cos(y/2) is still true because cos(y/2) is non-negative (since y/2 ∈ [0, π/2], so cos(y/2) ≥ 0) and the left side is non-positive.Therefore, when x + y/2 exceeds π, cos(x + y/2) is negative, and cos(y/2) is non-negative, so the inequality holds. Therefore, for all x ∈ [0, π], cos(x + y/2) ≤ cos(y/2). Therefore, the inequality holds for any y ∈ [0, π]. Hence, the largest subset is [0, π], which is option (E).Therefore, after multiple approaches and checks, it seems that the inequality holds for all y ∈ [0, π], making option (E) the correct answer.Final Answerboxed{E}</think>To determine the largest subset of the set ({ y mid 0 leqslant y leqslant pi }) that satisfies (sin(x + y) leqslant sin x + sin y) for all (x in [0, pi]), we start by using the trigonometric identity for (sin(x + y)):[sin(x + y) = sin x cos y + cos x sin y]Substituting this into the inequality, we get:[sin x cos y + cos x sin y leqslant sin x + sin y]Rearranging terms, we have:[sin x (cos y - 1) + sin y (cos x - 1) leqslant 0]Since (cos theta - 1 leqslant 0) for all (theta) and (sin x, sin y geqslant 0) for (x, y in [0, pi]), each term in the sum is non-positive. Therefore, the entire expression is non-positive, implying the inequality holds for all (x, y in [0, pi]).To verify, we consider specific values and general cases:- For (x = 0), (sin y leqslant sin y).- For (x = pi/2), (cos y leqslant 1 + sin y), which is always true.- For (x = pi), (-sin y leqslant sin y), which holds as (sin y geqslant 0).Additionally, using the identity (sin(x + y) - sin x - sin y = sin x (1 - cos y) + sin y (1 - cos x)), we see it is non-negative, confirming the inequality.Thus, the inequality holds for all (y in [0, pi]), making the largest subset the entire interval ([0, pi]).[boxed{E}],<think>Okay, let's see. The problem is asking for the largest subset of the set { y | 0 ≤ y ≤ π } such that the inequality sin(x + y) ≤ sin x + sin y holds for all x in [0, π]. The options are given from (A) to (E), with (E) being the entire interval. So I need to figure out which of these intervals is the largest possible where the inequality holds for every x between 0 and π.First, let me recall some trigonometric identities. The sine of a sum formula: sin(x + y) = sin x cos y + cos x sin y. So substituting that into the inequality:sin x cos y + cos x sin y ≤ sin x + sin y.Let me rearrange the terms:sin x cos y - sin x + cos x sin y - sin y ≤ 0Factor out sin x and sin y:sin x (cos y - 1) + sin y (cos x - 1) ≤ 0Hmm, that might be helpful. Alternatively, maybe I can subtract sin x and sin y from both sides:sin(x + y) - sin x - sin y ≤ 0Which would be:sin x cos y + cos x sin y - sin x - sin y ≤ 0Which simplifies to:sin x (cos y - 1) + sin y (cos x - 1) ≤ 0Same as before. So, we have two terms here: sin x (cos y - 1) and sin y (cos x - 1). Let me note that (cos y - 1) and (cos x - 1) are both non-positive because cosine is at most 1. So cos y - 1 ≤ 0 and cos x - 1 ≤ 0 for all x and y in [0, π]. Also, sin x and sin y are non-negative in [0, π] because sine is non-negative in this interval.Therefore, both terms sin x (cos y - 1) and sin y (cos x - 1) are non-positive. So their sum is also non-positive. Wait, but that would mean that the entire left-hand side is always ≤ 0, which would imply that the inequality holds for all x and y in [0, π]. But that's option (E). However, the answer options don't have (E) as correct? Wait, the problem says "the largest subset of the set { y | 0 ≤ y ≤ π }" so maybe my reasoning is flawed.Wait, perhaps I made a mistake here. Let me check with specific values. Let me pick y = π. Then sin(x + π) = sin x cos π + cos x sin π = -sin x. So sin(x + π) = -sin x. Then the inequality becomes -sin x ≤ sin x + sin π, which is -sin x ≤ sin x + 0. So -sin x ≤ sin x. Since sin x ≥ 0 in [0, π], this becomes -sin x ≤ sin x ⇒ 0 ≤ 2 sin x, which is always true. So for y = π, the inequality holds. Wait, but maybe there's a problem when x = 0? Let me check x = 0. Then sin(0 + y) ≤ sin 0 + sin y. So sin y ≤ 0 + sin y, which is equality. So that's okay. How about x = π? sin(π + y) ≤ sin π + sin y. sin(π + y) = -sin y ≤ 0 + sin y. So -sin y ≤ sin y. Since sin y ≥ 0, this is equivalent to 0 ≤ 2 sin y, which is always true. So even for y = π, the inequality holds for all x in [0, π]. Hmm, so maybe (E) is the correct answer? But the options are given, and (E) is indeed 0 ≤ y ≤ π. But let me check with another example.Suppose y = π/2. Then sin(x + π/2) = cos x. The inequality becomes cos x ≤ sin x + sin(π/2) = sin x + 1. Since cos x ≤ 1 and sin x ≥ 0, cos x ≤ 1 ≤ sin x + 1 (since sin x ≥ 0). So this holds. Wait, cos x ≤ 1, and sin x + 1 ≥ 1, so indeed cos x ≤ sin x + 1. So that holds. What about y = 3π/4. Let's pick y = 3π/4. Then sin(x + 3π/4) = sin x cos(3π/4) + cos x sin(3π/4) = sin x (-√2/2) + cos x (√2/2). The inequality is:-sin x (√2/2) + cos x (√2/2) ≤ sin x + sin(3π/4).Simplify both sides. Left side: (√2/2)(cos x - sin x). Right side: sin x + √2/2.So the inequality becomes (√2/2)(cos x - sin x) ≤ sin x + √2/2.Multiply both sides by 2/√2 to simplify:(cos x - sin x) ≤ (2/√2) sin x + 1Simplify 2/√2 to √2:cos x - sin x ≤ √2 sin x + 1Bring all terms to left:cos x - sin x - √2 sin x - 1 ≤ 0cos x - (1 + √2) sin x - 1 ≤ 0Hmm, is this always true for x in [0, π]? Let's check at x = 0: cos 0 - (1 + √2) sin 0 - 1 = 1 - 0 - 1 = 0 ≤ 0. So equality holds. At x = π/2: cos π/2 - (1 + √2) sin π/2 -1 = 0 - (1 + √2)(1) -1 = -1 - √2 -1 = -2 - √2 ≤ 0. True. At x = π: cos π - (1 + √2) sin π -1 = -1 - 0 -1 = -2 ≤0. True. What about x = π/4? cos π/4 - (1 + √2) sin π/4 -1 = (√2/2) - (1 + √2)(√2/2) -1.Compute:√2/2 - [√2/2 + (√2)(√2)/2] -1 = √2/2 - [√2/2 + 2/2] -1 = √2/2 - √2/2 -1 -1 = -2 ≤0. True.Hmm, seems like even for y =3π/4, the inequality holds. Wait, but maybe there's a value of x where it might not hold? Let me check x somewhere else. Maybe x = π/3.For x = π/3 (60 degrees):cos π/3 - (1 + √2) sin π/3 -1 = 0.5 - (1 + √2)(√3/2) -1 ≈ 0.5 - (1 + 1.414)(0.866) -1 ≈ 0.5 - (2.414)(0.866) -1 ≈ 0.5 - 2.090 -1 ≈ -2.590 ≤0. True.So even for y = 3π/4, the inequality holds. Then maybe the answer is (E). But why are the options including smaller intervals? Maybe I made a mistake in my initial reasoning.Wait, let me check the original problem again. It says "the largest subset of the set { y | 0 ≤ y ≤ π } satisfies sin(x + y) ≤ sin x + sin y for all x ∈ [0, π]". So if for all y in [0, π], the inequality holds for all x in [0, π], then the largest subset is the entire interval. But maybe my examples are not sufficient. Let me check with y = π and x = π/2.Wait, y = π, x = π/2: sin(π/2 + π) = sin(3π/2) = -1. The right-hand side is sin(π/2) + sin(π) = 1 + 0 = 1. So -1 ≤1, which is true. Another example: y = π, x = π/4. sin(π/4 + π) = sin(5π/4) = -√2/2. Right-hand side: sin(π/4) + sin π = √2/2 + 0 = √2/2. So -√2/2 ≤ √2/2, which is true. How about y = π, x = 3π/4: sin(3π/4 + π) = sin(7π/4) = -√2/2. RHS: sin(3π/4) + sin π = √2/2 +0 = √2/2. So again, -√2/2 ≤ √2/2, which is true.Wait, but maybe there's a y where the inequality fails? Let's check y = π/2 and x = π. Then sin(π + π/2) = sin(3π/2) = -1. RHS: sin π + sin(π/2) = 0 +1 =1. So -1 ≤1, which holds. How about y = π/2 and x = 0. sin(0 + π/2)=1. RHS: sin0 + sin(π/2)=0 +1=1. So equality holds.Wait, perhaps the inequality holds for all y in [0, π]. If that's the case, then the answer is (E). But why is this the case? Let's go back to the transformed inequality:sin x (cos y -1) + sin y (cos x -1) ≤ 0.Since cos y -1 ≤0 and cos x -1 ≤0 for all x, y in [0, π], and sin x and sin y are non-negative, both terms are non-positive. Therefore, their sum is non-positive. Therefore, the inequality holds for all x, y in [0, π]. Therefore, the largest subset is the entire interval [0, π]. So answer is (E). But wait, the original problem is from an exam, so maybe there is a trick here. Let me check with the expansion again.Alternatively, maybe there is a mistake in assuming that both terms are non-positive. For example, if cos y -1 is negative (which it always is except when y=0) and sin x is non-negative, so sin x (cos y -1) is ≤0. Similarly, sin y (cos x -1) is ≤0. Therefore, their sum is ≤0. Therefore, the inequality holds for all x, y in [0, π]. Therefore, the answer is (E).But maybe I need to verify with more examples. Let's take y = π/3 and x = 2π/3. Then sin(2π/3 + π/3)=sin(π)=0. RHS: sin(2π/3) + sin(π/3)= (√3/2) + (√3/2)=√3 ≈1.732. So 0 ≤1.732, which holds. Another case: y = π/4, x = 3π/4. sin(3π/4 + π/4)=sin(π)=0. RHS: sin(3π/4) + sin(π/4)= (√2/2)+(√2/2)=√2≈1.414. So 0 ≤1.414, true.Alternatively, take x and y such that x + y > π. For example, x = 3π/4, y = 3π/4. Then x + y = 3π/2. sin(3π/2) = -1. RHS: sin(3π/4) + sin(3π/4)=√2/2 +√2/2=√2≈1.414. So -1 ≤1.414, which is true. So even when x + y exceeds π, the inequality holds because sin(x + y) can be negative, but the right-hand side is the sum of two non-negative terms. So sin(x + y) being negative will always be less than or equal to the sum of two non-negative terms. Therefore, the inequality holds for all x, y in [0, π].Wait, but if y is in [0, π], then x + y can be in [0, 2π]. But since x is in [0, π], and y is in [0, π], x + y is in [0, 2π]. The sine function is non-negative in [0, π] and non-positive in [π, 2π]. So if x + y is in [0, π], then sin(x + y) is non-negative, and we have sin(x + y) ≤ sin x + sin y. If x + y is in [π, 2π], then sin(x + y) is non-positive, and since sin x + sin y is non-negative (as x and y are in [0, π]), the inequality sin(x + y) ≤ sin x + sin y holds as well. Therefore, in all cases, the inequality holds. Therefore, the largest subset is the entire interval [0, π], which is option (E).But wait, the problem is from a test, so maybe the answer is not (E). Wait, maybe I made a mistake. Let me check with specific values where sin(x + y) could be greater than sin x + sin y. For example, if x and y are such that x + y is in [0, π], then sin(x + y) = sin x cos y + cos x sin y. So sin(x + y) ≤ sin x + sin y is equivalent to sin x cos y + cos x sin y ≤ sin x + sin y. Which can be written as sin x (cos y - 1) + sin y (cos x - 1) ≤ 0. Since cos y -1 ≤0 and cos x -1 ≤0, as before, then yes, each term is non-positive. Therefore, the sum is non-positive, so the inequality holds. If x + y is in [π, 2π], then sin(x + y) is negative, and sin x + sin y is non-negative, so the inequality holds. So in all cases, the inequality holds. Therefore, the answer is (E). But the problem is presented as a multiple-choice question, and (E) is an option, so maybe that's correct.But let me check again the options:(A) y=0(B) 0≤y≤π/4(C) 0≤y≤π/2(D) 0≤y≤3π/4(E) 0≤y≤πSince according to the reasoning, (E) is correct. So why would the problem be here? Maybe I missed something. Let me think again.Alternatively, maybe there are cases where sin(x + y) > sin x + sin y. Let me see. Suppose x and y are both π/2. Then sin(π/2 + π/2)=sin π=0. RHS: sin π/2 + sin π/2=1+1=2. 0 ≤2, which holds.Another example: x = y = π/4. Then sin(π/4 + π/4)=sin(π/2)=1. RHS: sin π/4 + sin π/4=√2/2 +√2/2=√2≈1.414. So 1 ≤1.414, which holds.Wait, how about x = 0, y = π/2. Then sin(0 + π/2)=1. RHS: sin0 + sin π/2=0 +1=1. Equality holds.Another case: x = π/6, y = π/6. Then sin(π/3)=√3/2≈0.866. RHS: sin π/6 + sin π/6=0.5 +0.5=1. So √3/2 ≤1, which holds.Another example: x = π/3, y = π/6. Then sin(π/3 + π/6)=sin(π/2)=1. RHS: sin π/3 + sin π/6= (√3/2) +0.5≈0.866 +0.5=1.366. So 1 ≤1.366, holds.How about x = y = π. Then sin(2π)=0. RHS: sin π + sin π=0+0=0. Equality.Wait, so in all these examples, the inequality holds. Therefore, maybe the answer is indeed (E). But let me check a case where x + y is in [0, π], say x = π/3, y = π/6 as before. We saw that holds. But maybe when x + y is in [0, π], and y is such that sin(x + y) is maximized? For example, if x + y = π/2, which is the maximum of sine. But sin(π/2)=1, and sin x + sin y would be sin x + sin(π/2 -x). For example, if x + y = π/2, then y = π/2 -x. Then sin x + sin y = sin x + sin(π/2 -x) = sin x + cos x. The maximum of sin x + cos x is √2 at x = π/4. So sin x + sin y = √2 ≈1.414, which is larger than sin(x + y)=1. So here, 1 ≤1.414, holds.Alternatively, if x + y = something else. Wait, but according to our transformed inequality, it's always true. So perhaps the answer is (E). Then why is the problem here? Maybe the original problem was in Chinese and the translation is slightly different? Wait, no, the problem is given in English here.Wait, maybe I made a mistake in the initial steps. Let's re-examine the inequality:sin(x + y) ≤ sin x + sin y.Using the identity sin(x + y) = sin x cos y + cos x sin y.So the inequality becomes:sin x cos y + cos x sin y ≤ sin x + sin y.Rearranged:sin x (cos y - 1) + sin y (cos x - 1) ≤ 0.As we said before, since cos y - 1 ≤0 and cos x -1 ≤0, and sin x, sin y ≥0, then each term is non-positive, so the sum is non-positive. Therefore, the inequality holds for all x, y ∈ [0, π]. Therefore, the largest subset is the entire interval, so answer is (E).Therefore, the answer is boxed{E}Final Answerboxed{E}</think>To determine the largest subset of ({ y mid 0 leqslant y leqslant pi }) that satisfies (sin(x + y) leqslant sin x + sin y) for all (x in [0, pi]), we start by using the trigonometric identity for the sine of a sum:[sin(x + y) = sin x cos y + cos x sin y]Substituting this into the inequality, we get:[sin x cos y + cos x sin y leqslant sin x + sin y]Rearranging terms, we have:[sin x (cos y - 1) + sin y (cos x - 1) leqslant 0]We note that (cos y - 1 leqslant 0) and (cos x - 1 leqslant 0) for all (x, y in [0, pi]). Additionally, (sin x) and (sin y) are non-negative in ([0, pi]). Therefore, each term (sin x (cos y - 1)) and (sin y (cos x - 1)) is non-positive. The sum of two non-positive terms is also non-positive, hence the inequality holds for all (x, y in [0, pi]).To verify, consider specific values of (x) and (y):- For (y = pi), (sin(x + pi) = -sin x), which is always less than or equal to (sin x).- For (y = frac{pi}{2}), (sin(x + frac{pi}{2}) = cos x), which is always less than or equal to (sin x + 1).In all cases, whether (x + y) is in ([0, pi]) or ([pi, 2pi]), the inequality (sin(x + y) leqslant sin x + sin y) holds. Therefore, the largest subset is the entire interval ([0, pi]).The answer is (boxed{E}).]

🔑:9. E.Since x in [0, pi], cos x in [0, 1], therefore,begin{array}{l}sin (x+y) = sin x cdot cos y + cos x cdot sin y leqslant sin x + sin y.end{array}Thus, 0 leqslant y leqslant pi.

🧠:[<think>Alright, let's tackle this problem step by step. So, the problem says: "The ratio of the perimeter of a rhombus to the sum of its diagonals is k. Find the angles of the rhombus and the permissible values of k." Hmm, okay. Let's start by recalling some properties of a rhombus.First off, a rhombus is a quadrilateral with all sides equal in length. Also, the diagonals of a rhombus bisect each other at right angles. That means the diagonals cut each other exactly in half and form four right triangles inside the rhombus. The perimeter of a rhombus would just be 4 times the length of one side, right? So if the side length is 'a', then the perimeter is 4a.Now, the problem mentions the ratio of the perimeter to the sum of the diagonals being k. Let's denote the diagonals as d1 and d2. So, according to the problem, k = (4a) / (d1 + d2). Our goal is to find the angles of the rhombus and the permissible values of k.Okay, so we need to relate the diagonals to the angles of the rhombus. I remember that in a rhombus, the diagonals are related to the angles. Specifically, the diagonals split the angles into two equal parts. Since the diagonals intersect at right angles, each of the four triangles formed is a right-angled triangle. The legs of these triangles are half of the diagonals, so (d1/2) and (d2/2), and the hypotenuse is the side length 'a' of the rhombus.Therefore, by the Pythagorean theorem, we have:(a)^2 = (d1/2)^2 + (d2/2)^2Which simplifies to:4a^2 = d1^2 + d2^2Hmm, that's one equation relating the diagonals to the side length. But we need another relation to connect them with the angles. Let's think about trigonometry. In a rhombus, the diagonals can also be expressed in terms of the angles. For a rhombus with angles θ and 180° - θ (since consecutive angles are supplementary), the lengths of the diagonals can be found using the sine and cosine of half those angles.Specifically, the diagonals split the angles into two equal parts. So, each half-angle is θ/2. In the right triangles formed by the diagonals, we can use trigonometric ratios. For example, the length of half of diagonal d1 (which is d1/2) can be expressed as a * sin(θ/2), and half of diagonal d2 (d2/2) can be expressed as a * cos(θ/2). Wait, is that right?Wait, actually, let me verify. Let's consider one of the angles of the rhombus, say θ. When the diagonal splits this angle into two equal parts, each part is θ/2. In the right triangle, the legs are (d1/2) and (d2/2). Depending on which diagonal we are considering, the trigonometric relations might differ. Let me think.Suppose we take angle θ. The diagonals bisect θ and 180° - θ. Let's denote the diagonals as d1 and d2. Let me recall the formula for the diagonals in terms of the sides and angles. The diagonals of a rhombus can be calculated using:d1 = 2a * sin(θ/2)d2 = 2a * cos(θ/2)Wait, is that correct? Let's check. If we consider the right triangle formed by half of each diagonal and the side, then:sin(θ/2) = (d1/2) / a => d1 = 2a * sin(θ/2)Similarly, cos(θ/2) = (d2/2) / a => d2 = 2a * cos(θ/2)But wait, if θ is one of the angles, then the other angle is 180° - θ. So when we take half of that angle, it's (90° - θ/2). Therefore, the other diagonal would involve sin(90° - θ/2) = cos(θ/2). So yes, that formula seems correct. So, diagonals can be written as d1 = 2a sin(θ/2) and d2 = 2a cos(θ/2). Let me verify with a square. If the rhombus is a square, then θ = 90°, so sin(45°) = √2/2, so d1 = 2a*(√2/2) = a√2, which is correct for the diagonal of a square. Similarly, the other diagonal would be the same since cos(45°) is also √2/2. So, yes, that seems correct. Wait, but in a square, both diagonals are equal, which makes sense because θ is 90°, so sin(θ/2) = cos(θ/2). So, that checks out.But in a general rhombus, θ is not 90°, so the diagonals are of different lengths. So, the longer diagonal corresponds to the angle with the larger sine value. So, if θ is acute, then θ/2 is less than 45°, so sin(θ/2) < cos(θ/2). Therefore, d1 = 2a sin(θ/2) would be the shorter diagonal, and d2 = 2a cos(θ/2) would be the longer diagonal.But since θ can be either acute or obtuse, but in a rhombus, the angles are either θ or 180° - θ. So, if θ is acute, the other angle is obtuse, and vice versa. However, when we split θ, which is acute, into two parts, each is θ/2, which is acute, and splitting the obtuse angle, which is 180° - θ, gives (180° - θ)/2 = 90° - θ/2, which is still acute if θ is acute. So, either way, the half-angles are acute, so the sine and cosine would be positive and less than 1.But let's make sure. If θ is the acute angle, then d1 (the shorter diagonal) is 2a sin(θ/2), and d2 (the longer diagonal) is 2a cos(θ/2). Alternatively, if θ is the obtuse angle, then θ = 180° - α, where α is acute. Then, the diagonals would be:d1 = 2a sin((180° - α)/2) = 2a sin(90° - α/2) = 2a cos(α/2)d2 = 2a cos((180° - α)/2) = 2a cos(90° - α/2) = 2a sin(α/2)So, in that case, the labels of d1 and d2 switch. So, regardless of whether we take θ as acute or obtuse, the diagonals can be expressed in terms of sine and cosine of θ/2, but we need to be careful about which is which. However, since the problem is asking for the angles of the rhombus, we can assume θ is the acute angle, and the other angle is 180° - θ. But maybe we need to consider both cases.Alternatively, perhaps we can just take θ as one of the angles (could be acute or obtuse), but given that the diagonals are determined by the angles, maybe the ratio k depends on θ, and we can express θ in terms of k, then find permissible k values.So, let's proceed. Let's denote θ as one of the angles of the rhombus (say, the acute angle). Then, the diagonals are d1 = 2a sin(θ/2) and d2 = 2a cos(θ/2). Therefore, the sum of the diagonals is d1 + d2 = 2a [sin(θ/2) + cos(θ/2)].The perimeter is 4a. Therefore, the ratio k is:k = 4a / (d1 + d2) = 4a / [2a (sin(θ/2) + cos(θ/2))] = 2 / [sin(θ/2) + cos(θ/2)]So, k = 2 / [sin(θ/2) + cos(θ/2)]Therefore, we can write this as:k = 2 / [sin(θ/2) + cos(θ/2)]Our goal is to find θ in terms of k and then find permissible values of k.Alternatively, since θ is an angle of the rhombus, θ can be between 0° and 180°, excluding 0° and 180°, because otherwise, it would collapse into a line. But in reality, θ is between greater than 0° and less than 180°, with θ ≠ 90°, unless it's a square. Wait, a square is a special case of a rhombus with all angles 90°, but in a square, the diagonals are equal. But in our case, we can have θ as 90°, which would make the rhombus a square.But in the problem statement, they just say a rhombus, so it can be a square. So permissible angles are θ ∈ (0°, 180°), but in actuality, in a rhombus, the angles come in pairs: θ and 180° - θ, so they are supplementary.But let's think about the possible values of k. Since θ is between 0° and 180°, θ/2 is between 0° and 90°, so sin(θ/2) + cos(θ/2) is between... Let's analyze sin(x) + cos(x) where x is between 0° and 90°. The function sin(x) + cos(x) has a maximum and minimum in this interval. Let's recall that sin(x) + cos(x) = √2 sin(x + 45°). Therefore, the maximum value is √2 when x + 45° = 90°, so x = 45°, and the minimum value is when x is 0° or 90°, which is sin(0°) + cos(0°) = 0 + 1 = 1, and sin(90°) + cos(90°) = 1 + 0 = 1. Wait, so actually, sin(x) + cos(x) reaches a maximum of √2 at x = 45°, and a minimum of 1 at x = 0° and x = 90°. Wait, but x here is θ/2, which ranges from 0° to 90°, so θ ranges from 0° to 180°, as we said.Therefore, sin(θ/2) + cos(θ/2) ∈ [1, √2]. Therefore, since k = 2 / [sin(θ/2) + cos(θ/2)], then k ∈ [2/√2, 2/1] = [√2, 2].Therefore, permissible values of k are between √2 and 2. But we need to check if these bounds are achievable. When θ/2 approaches 0°, sin(θ/2) approaches 0, cos(θ/2) approaches 1, so sin(θ/2) + cos(θ/2) approaches 1, so k approaches 2. Similarly, when θ/2 approaches 90°, sin(θ/2) approaches 1, cos(θ/2) approaches 0, so again sin(θ/2) + cos(θ/2) approaches 1, and k approaches 2. But when θ/2 is 45°, sin(45°) + cos(45°) = √2/2 + √2/2 = √2, so k = 2 / √2 = √2. Therefore, k can range from √2 to 2, with √2 achieved when θ/2 = 45°, which means θ = 90°, so the rhombus is a square. Wait, but θ is the angle of the rhombus. If θ is 90°, then the rhombus is a square, and indeed, in that case, both diagonals are equal, and the ratio k is √2. For other angles, k is between √2 and 2. But wait, hold on: when θ approaches 0°, the rhombus becomes very "flat", with one pair of angles approaching 0° and the other approaching 180°, so the diagonals become very unequal: one diagonal becomes very long (approaching 2a) and the other becomes very short (approaching 0). Therefore, the sum of the diagonals approaches 2a, so the ratio k = 4a / (2a) = 2. Similarly, when θ approaches 180°, same thing. So that's why k approaches 2. When θ is 90°, it's a square, sum of diagonals is 2*(a√2 + a√2) = 4a√2? Wait, no. Wait, in a square, each diagonal is a√2, so sum is 2a√2. Therefore, k = 4a / (2a√2) = 2 / √2 = √2. Right, so that's consistent.So permissible values of k are from √2 to 2. So, k ∈ [√2, 2]. Now, we need to find the angles of the rhombus in terms of k. Since k = 2 / [sin(θ/2) + cos(θ/2)], let's denote S = sin(θ/2) + cos(θ/2) = √2 sin(θ/2 + 45°). But maybe we can solve for θ in terms of k.Starting with:k = 2 / [sin(θ/2) + cos(θ/2)]Let's denote x = θ/2, so x ∈ (0°, 90°). Then:k = 2 / [sin x + cos x]We can write sin x + cos x = 2 / kWe need to solve for x in terms of k. Let's square both sides to use the Pythagorean identity:(sin x + cos x)^2 = (2 / k)^2sin²x + 2 sinx cosx + cos²x = 4 / k²But sin²x + cos²x = 1, so:1 + 2 sinx cosx = 4 / k²Also, 2 sinx cosx = sin 2x, so:1 + sin 2x = 4 / k²Therefore:sin 2x = 4 / k² - 1But 2x = θ, since x = θ/2. Wait, no: if x = θ/2, then 2x = θ. So θ = 2x. Therefore:sin θ = 4 / k² - 1Therefore, θ = arcsin(4/k² - 1)But we need to make sure that 4/k² - 1 is within the domain of arcsin, which is [-1, 1]. Since θ is an angle of the rhombus between 0° and 180°, and θ = 2x, x ∈ (0°, 90°), so θ ∈ (0°, 180°). Therefore, θ must be in (0°, 180°), and sin θ must equal 4/k² - 1. Let's check the possible values.Given that k ∈ [√2, 2], then k² ∈ [2, 4], so 4/k² ∈ [1, 2], so 4/k² - 1 ∈ [0, 1]. Therefore, sin θ ∈ [0, 1]. But θ ∈ (0°, 180°), so sin θ is non-negative. Therefore, θ can be in (0°, 180°), but sin θ = 4/k² - 1. So, θ = arcsin(4/k² - 1) or θ = 180° - arcsin(4/k² - 1). Wait, because arcsin returns values between -90° and 90°, but since 4/k² - 1 is between 0 and 1, arcsin(4/k² - 1) is between 0° and 90°, so θ can be either that value or 180° minus that value. However, in the context of a rhombus, the angles come in pairs: θ and 180° - θ. So, depending on whether θ is acute or obtuse, we have two possible angles. But since we derived that sin θ = 4/k² - 1, and 4/k² - 1 ∈ [0,1], θ can be either arcsin(4/k² - 1) or 180° - arcsin(4/k² - 1). Therefore, the two angles of the rhombus are θ = arcsin(4/k² - 1) and 180° - θ.But wait, let's check with k = √2. Then, 4/k² - 1 = 4/2 -1 = 2 -1 = 1. So sin θ = 1, which implies θ = 90°, which is the square case. Then, the other angle is 90°, which makes sense. For k = 2, 4/k² -1 = 4/4 -1 = 1 -1 = 0, so sin θ = 0, which would imply θ = 0° or 180°, but those are degenerate cases. However, as k approaches 2 from above, θ approaches 0°, which corresponds to a very "flat" rhombus. But since θ must be strictly between 0° and 180°, the permissible values of k are (√2, 2), excluding the endpoints? Wait, but earlier we said k ∈ [√2, 2]. Wait, when k = √2, θ = 90°, which is valid (a square). When k approaches 2, θ approaches 0°, which is a degenerate rhombus. But in reality, θ can be arbitrarily close to 0°, making k approach 2, but not including 2. Similarly, θ can't actually be 0°, so perhaps k ∈ (√2, 2). Wait, but in the problem statement, it says "permissible values of k". If the rhombus is non-degenerate, then θ must be in (0°, 180°), so k ∈ (√2, 2). However, if we allow degenerate rhombuses (which are essentially line segments), then k can be √2 and 2. But generally, in geometry problems, we consider non-degenerate cases. Therefore, permissible values of k are √2 < k < 2.But wait, when θ = 90°, which is a valid non-degenerate rhombus (a square), k = √2, so √2 should be included. Similarly, as θ approaches 0°, k approaches 2, but doesn't reach 2. Therefore, permissible values of k are [√2, 2). Hmm, need to be careful here.Wait, when θ = 90°, we have a square, which is a valid rhombus, so k = √2 is permissible. When θ approaches 0°, the rhombus becomes a line segment, which is degenerate, so k approaches 2 but doesn't reach it. Therefore, permissible values of k are √2 ≤ k < 2. So k can be equal to √2 but not 2.But in the problem statement, it's not specified whether degenerate rhombuses are allowed. Typically, in math problems, unless stated otherwise, we consider non-degenerate figures. Therefore, θ is in (0°, 180°), so k is in (√2, 2). However, the case θ = 90° is allowed (a square), which gives k = √2, so √2 is permissible. So maybe the permissible values are √2 ≤ k < 2. So including √2 but not including 2.Hence, the angles would be θ = arcsin(4/k² - 1) and 180° - θ, where k ∈ [√2, 2). Wait, but when k = 2, θ would be 0°, which is degenerate, so k ∈ [√2, 2). Hmm. But perhaps the problem allows k = 2 if we consider the limit. However, strictly speaking, a rhombus with θ = 0° is not a rhombus anymore. So, the answer is that the permissible values of k are √2 ≤ k < 2, and the angles are θ and 180° - θ, where θ = arcsin(4/k² - 1).Alternatively, since we can write sin θ = 4/k² - 1, and θ is the angle of the rhombus, perhaps we can express the angles in terms of k as:θ = arcsin(4/k² - 1) and 180° - arcsin(4/k² - 1)But let's check with an example. Take k = √2. Then, sin θ = 4/( (√2)^2 ) -1 = 4/2 -1 = 1. So θ = 90°, which is correct. For another value, say k = 2. Then, sin θ = 4/4 -1 = 0. So θ = 0°, which is degenerate. For k = √2 + ε, where ε is a small positive number, θ would be slightly less than 90°, so the rhombus is "opening up" from a square. For k approaching 2, θ approaches 0°, as expected.Alternatively, we can write the angles in terms of inverse trigonometric functions. Let me see.Given that θ = arcsin(4/k² - 1), but since 4/k² -1 = sin θ, we can also express θ as:θ = 2 arcsin( [sqrt( (4/k² -1)/2 + 1/2 ) ] )Wait, maybe not. Alternatively, since we had earlier:From sin θ = 4/k² - 1, but θ = 2x, where x is such that sin x + cos x = 2/k.Alternatively, maybe we can express θ in terms of the original equation. Let's go back.We have k = 2 / [sin(θ/2) + cos(θ/2)]Let’s denote sin(θ/2) + cos(θ/2) = 2/kLet’s square both sides:[sin(θ/2) + cos(θ/2)]^2 = 4/k²sin²(θ/2) + 2 sin(θ/2)cos(θ/2) + cos²(θ/2) = 4/k²Again, sin² + cos² = 1, so:1 + sin θ = 4/k²Therefore, sin θ = 4/k² -1Thus, θ = arcsin(4/k² -1) or θ = 180° - arcsin(4/k² -1)But since θ is an angle of a rhombus, which is either acute or obtuse, depending on the value. So, if 4/k² -1 is positive, θ is acute; if 4/k² -1 is 1, θ is 90°, which is right angle. Wait, but 4/k² -1 is between 0 and 1, as k is between √2 and 2. Therefore, arcsin(4/k² -1) is between 0° and 90°, so θ is between 0° and 180°, but since θ is equal to that arcsine value or 180° minus it. Wait, no. Wait, θ = arcsin(4/k² -1) gives θ between 0° and 90°, and 180° - θ would be the obtuse angle. Wait, but hold on: from the equation sin θ = 4/k² -1, θ can be in the first or second quadrant. So θ can be either arcsin(4/k² -1) or 180° - arcsin(4/k² -1). But in a rhombus, the angles are θ and 180° - θ. Therefore, the two angles are θ = arcsin(4/k² -1) and 180° - arcsin(4/k² -1). However, since arcsin(4/k² -1) is between 0° and 90° (because 4/k² -1 is between 0 and 1), then 180° - arcsin(4/k² -1) is between 90° and 180°, which makes sense. Therefore, the angles of the rhombus are arcsin(4/k² -1) and 180° - arcsin(4/k² -1), and permissible k values are √2 ≤ k < 2.But let me confirm this with another example. Let's take k = 2. Then, sin θ = 4/4 -1 = 0, so θ = 0° or 180°, which are degenerate. For k = √2, sin θ = 1, so θ = 90°, which is valid. For a value in between, say k = √3. Then, sin θ = 4/(3) -1 = 1/3 ≈ 0.333. So θ ≈ arcsin(1/3) ≈ 19.47°, and the other angle is 180° - 19.47° ≈ 160.53°. That seems reasonable. So, the angles are θ ≈ 19.47° and ≈160.53°, and k = √3 ≈1.732, which is between √2 ≈1.414 and 2. So that checks out.Therefore, putting it all together, the angles of the rhombus are arcsin(4/k² -1) and 180° - arcsin(4/k² -1), and permissible values of k are √2 ≤ k < 2. However, in the problem statement, it says "permissible values of k". If we consider non-degenerate rhombuses, then k must be greater than √2 and less than 2. But when k = √2, the rhombus is a square, which is a valid case. So, depending on whether the problem considers squares as permissible, which they usually are, then k can be equal to √2. But k cannot be equal to 2 because that corresponds to a degenerate rhombus. Therefore, permissible k values are √2 ≤ k < 2.But let's see another way. Since when θ approaches 0°, the rhombus becomes very "flat", with one diagonal approaching 2a (the longer diagonal) and the other approaching 0. Therefore, the sum of diagonals d1 + d2 approaches 2a, so k = 4a / (d1 + d2) approaches 4a / 2a = 2. So k can get arbitrarily close to 2, but never actually reaches 2. Therefore, permissible values of k are [√2, 2). So including √2 but not including 2.Hence, the answer is:Angles of the rhombus are θ = arcsin(4/k² - 1) and 180° - θ, and permissible values of k are √2 ≤ k < 2.But we need to express the angles in terms of k. Since arcsin(4/k² -1) can be written as inverse sine function. Alternatively, we can write θ = 2 arcsin(t) or something, but perhaps it's better to leave it as arcsin(4/k² -1). However, let's see if there's a way to express it more neatly.Wait, from the equation:sin θ = 4/k² -1We can also recall that in the rhombus, the diagonals are related to the angles. Let me check another approach. Let's denote the diagonals d1 and d2. Then, in a rhombus, the area is (d1*d2)/2. Also, the area can be expressed as a^2 sin θ. Therefore:a^2 sin θ = (d1*d2)/2But we also know from the Pythagorean theorem that (d1/2)^2 + (d2/2)^2 = a^2, so d1^2 + d2^2 = 4a^2.But perhaps this isn't necessary here. Since we've already derived the relationship in terms of k and θ, maybe we can proceed.Alternatively, going back to the original expression:k = 2 / [sin(θ/2) + cos(θ/2)]Let’s rationalize the denominator. Multiply numerator and denominator by [sin(θ/2) + cos(θ/2)]:Wait, that would just give 2[sin(θ/2) + cos(θ/2)] / [sin²(θ/2) + 2 sin(θ/2)cos(θ/2) + cos²(θ/2)] = 2[sin(θ/2) + cos(θ/2)] / (1 + sinθ), which might not help.Alternatively, write sin(θ/2) + cos(θ/2) as √2 sin(θ/2 + 45°). Then:k = 2 / [√2 sin(θ/2 + 45°)] = √2 / sin(θ/2 + 45°)Therefore, sin(θ/2 + 45°) = √2 / kSo, θ/2 + 45° = arcsin(√2 / k)Therefore, θ/2 = arcsin(√2 / k) - 45°Multiply both sides by 2:θ = 2 arcsin(√2 / k) - 90°But θ must be positive, so 2 arcsin(√2 / k) - 90° > 0°, so arcsin(√2 /k) > 45°, which implies that √2 /k > sin45° = √2/2, so √2/k > √2/2 => 1/k > 1/2 => k < 2, which is consistent with our previous result.Alternatively, θ = 2 arcsin(√2 / k) - 90°, but this might not be the most straightforward expression. Let's verify with k = √2. Then, √2 /k = 1, so arcsin(1) = 90°, so θ = 2*90° -90° = 90°, which is correct. For k approaching 2, √2/k approaches √2/2 ≈ 0.707, so arcsin(0.707) ≈ 45°, so θ ≈ 2*45° -90° = 0°, which matches our previous analysis.But this seems more complicated. Maybe it's better to stick with θ = arcsin(4/k² -1). Let's see:Given that θ = arcsin(4/k² -1), and 4/k² -1 = sin θ, so for a given k, θ is determined. So, the angles are θ and 180° - θ where θ = arcsin(4/k² -1).Therefore, summarizing:The angles of the rhombus are arcsin(4/k² - 1) and 180° - arcsin(4/k² - 1), and permissible values of k are √2 ≤ k < 2.But to present this neatly, we can write:The angles are θ = sin⁻¹(4/k² − 1) and 180° − θ, and the permissible values of k are √2 ≤ k < 2.Alternatively, if we want to write θ in a different form, but I think this is acceptable.Therefore, the final answer is:The angles of the rhombus are boxed{arcsinleft(frac{4}{k^2} - 1right)} and boxed{180^circ - arcsinleft(frac{4}{k^2} - 1right)}, and the permissible values of k are boxed{sqrt{2} leq k < 2}.Wait, but in the problem statement, it says "Find the angles of the rhombus and the permissible values of k". So, they might expect specific expressions or a range. Let me check once again.Alternatively, perhaps using the relationship with θ, and since sin θ = 4/k² -1, we can express θ in terms of k as θ = 2 arctan(t), but that might complicate things. Alternatively, since we know that θ is related to k, and permissible k is between √2 and 2, and angles are θ and 180° - θ.Alternatively, maybe using half-angle formulas. Let's recall that:sin(θ/2) = √[(1 - cosθ)/2]cos(θ/2) = √[(1 + cosθ)/2]But I don't know if that helps here.Wait, in our earlier equation, we have:k = 2 / [sin(θ/2) + cos(θ/2)]Let’s denote S = sin(θ/2) + cos(θ/2) = √2 sin(θ/2 + 45°)Then, k = 2/S => S = 2/kTherefore, √2 sin(θ/2 + 45°) = 2/kSo, sin(θ/2 + 45°) = √2 /kTherefore, θ/2 + 45° = arcsin(√2 /k) or θ/2 + 45° = 180° - arcsin(√2 /k)Therefore, θ/2 = arcsin(√2 /k) -45° or θ/2 = 135° - arcsin(√2 /k)Therefore, θ = 2 arcsin(√2 /k) -90° or θ = 270° - 2 arcsin(√2 /k)But θ must be between 0° and 180°, so let's check the first solution:θ = 2 arcsin(√2 /k) -90°. For k = √2, arcsin(1) =90°, so θ = 2*90° -90°=90°, which is correct. For k approaching 2, arcsin(√2 /2)= arcsin(1/√2)=45°, so θ= 2*45° -90°=0°, which is the degenerate case. For the second solution, θ=270° -2 arcsin(√2/k). Let's take k=√2, arcsin(1)=90°, so θ=270° -180°=90°, which is the same as before. For k approaching 2, arcsin(√2/2)=45°, so θ=270° -90°=180°, which is the other degenerate case. Therefore, both solutions give θ and 180° -θ, which makes sense.But since θ is between 0° and 180°, the two solutions correspond to θ and 180° -θ. Therefore, the angles of the rhombus can be expressed as:θ = 2 arcsin(√2 /k) -90° and 180° - (2 arcsin(√2 /k) -90°) = 270° -2 arcsin(√2 /k)But this seems more complicated. Alternatively, stick with θ = arcsin(4/k² -1) and 180° -θ. However, both expressions are equivalent.Alternatively, since sin θ = 4/k² -1, perhaps we can write θ in terms of cosine. Let me see:From sin θ = 4/k² -1, then cos θ = √(1 - sin²θ) = √[1 - (4/k² -1)^2]But expanding that:1 - (16/k⁴ - 8/k² +1) = 1 -16/k⁴ +8/k² -1 = 8/k² -16/k⁴ = 8/k²(1 - 2/k²)But not sure if this helps.Alternatively, we can relate θ to k through tan(θ/2). Let's recall that:From the diagonals, d1 = 2a sin(θ/2), d2 = 2a cos(θ/2)Therefore, the ratio of diagonals is d1/d2 = tan(θ/2)But the sum of diagonals is d1 + d2 = 2a [sin(θ/2) + cos(θ/2)]And the perimeter is 4a, so k = 4a / [2a (sin(θ/2) + cos(θ/2)) ] = 2 / [sin(θ/2) + cos(θ/2)] as before.Alternatively, we can write tan(θ/2) = d1/d2. But unless we have more information, this might not help.Alternatively, let's consider expressing θ in terms of k using trigonometric identities. For example, we can write:sin(θ/2) + cos(θ/2) = √2 sin(θ/2 + 45°) = 2/kTherefore, sin(θ/2 + 45°) = √2 /kTherefore, θ/2 +45° = arcsin(√2 /k)Therefore, θ = 2 [arcsin(√2 /k) -45° ]Alternatively, converting to radians if necessary, but the problem doesn't specify, so we can keep it in degrees.This gives θ = 2 arcsin(√2 /k) -90°, which is the same as earlier.But in terms of presenting the answer, maybe expressing θ as arcsin(4/k² -1) is simpler, even if it's derived from the double-angle formula.In any case, the key result is that the angles are θ and 180° - θ where θ = arcsin(4/k² -1), and k is between √2 and 2.So, after carefully going through the trigonometric relationships and ensuring that all steps are valid, we can conclude that the angles of the rhombus are arcsin(4/k² -1) and its supplement, and permissible k values are from √2 up to but not including 2.Final AnswerThe angles of the rhombus are boxed{arcsinleft(frac{4}{k^2} - 1right)} and boxed{180^circ - arcsinleft(frac{4}{k^2} - 1right)}, and the permissible values of k are boxed{sqrt{2} leq k < 2}.</think>Given a rhombus with side length (a), perimeter (4a), and diagonals (d_1) and (d_2), we need to find the angles of the rhombus and the permissible values of (k) where (k) is the ratio of the perimeter to the sum of the diagonals.1. Relating Diagonals to Angles: - The diagonals of a rhombus bisect the angles at right angles. - Using trigonometric relationships, the diagonals can be expressed as: [ d_1 = 2a sinleft(frac{theta}{2}right) quad text{and} quad d_2 = 2a cosleft(frac{theta}{2}right) ] - Here, (theta) is one of the angles of the rhombus.2. Sum of Diagonals: - The sum of the diagonals is: [ d_1 + d_2 = 2a left(sinleft(frac{theta}{2}right) + cosleft(frac{theta}{2}right)right) ]3. Ratio (k): - The ratio (k) is given by: [ k = frac{4a}{d_1 + d_2} = frac{4a}{2a left(sinleft(frac{theta}{2}right) + cosleft(frac{theta}{2}right)right)} = frac{2}{sinleft(frac{theta}{2}right) + cosleft(frac{theta}{2}right)} ]4. Simplifying the Ratio: - Using the identity (sin x + cos x = sqrt{2} sinleft(x + 45^circright)), we get: [ k = frac{2}{sqrt{2} sinleft(frac{theta}{2} + 45^circright)} = sqrt{2} cscleft(frac{theta}{2} + 45^circright) ]5. Permissible Values of (k): - The function (sinleft(frac{theta}{2}right) + cosleft(frac{theta}{2}right)) ranges from 1 to (sqrt{2}) as (theta) varies from (0^circ) to (180^circ). - Therefore, (k) ranges from (sqrt{2}) to 2. However, (k = 2) corresponds to a degenerate rhombus, so the permissible values are (sqrt{2} leq k < 2).6. Finding the Angles: - From the equation (k = frac{2}{sinleft(frac{theta}{2}right) + cosleft(frac{theta}{2}right)}), we solve for (theta): [ sinleft(frac{theta}{2}right) + cosleft(frac{theta}{2}right) = frac{2}{k} ] - Squaring both sides and using trigonometric identities, we find: [ sin theta = frac{4}{k^2} - 1 ] - The angles of the rhombus are (theta = arcsinleft(frac{4}{k^2} - 1right)) and (180^circ - arcsinleft(frac{4}{k^2} - 1right)). Final AnswerThe angles of the rhombus are (boxed{arcsinleft(frac{4}{k^2} - 1right)}) and (boxed{180^circ - arcsinleft(frac{4}{k^2} - 1right)}), and the permissible values of (k) are (boxed{sqrt{2} leq k < 2}).,<think>Okay, so I need to find the angles of a rhombus and the permissible values of k, where k is the ratio of the perimeter of the rhombus to the sum of its diagonals. Let me start by recalling some properties of a rhombus. First, all sides of a rhombus are equal in length. Let's denote the side length as 'a'. Therefore, the perimeter of the rhombus is 4a. The problem states that the ratio of the perimeter (4a) to the sum of its diagonals (let's call the diagonals d1 and d2) is k. So, mathematically, that would be:k = 4a / (d1 + d2)Our goal is to find the angles of the rhombus and the possible values of k. Since a rhombus has opposite angles equal and adjacent angles supplementary, we can denote the angles as θ and 180° - θ, where θ is one of the angles. So, essentially, we need to find θ in terms of k, or vice versa, and determine the permissible k values.I remember that in a rhombus, the diagonals are related to the angles. The diagonals of a rhombus bisect the angles and each other at right angles. So, each diagonal divides the rhombus into two congruent triangles. Also, the diagonals can be expressed in terms of the side length and the angles. Let me recall the formulas for the diagonals. If θ is one of the angles of the rhombus, then the lengths of the diagonals d1 and d2 can be found using the relationships:d1 = 2a sin(θ/2)d2 = 2a cos(θ/2)Wait, is that right? Let me think. If we split the rhombus along its diagonals, we get four right-angled triangles. Each right triangle has legs of length d1/2 and d2/2, and hypotenuse of length a. The angle between the side of the rhombus and the diagonal would be θ/2, since the diagonals bisect the angles. So, in one of those right triangles, the legs are (d1/2) and (d2/2). The angle θ/2 is adjacent to d1/2 and opposite to d2/2. Therefore:sin(θ/2) = (d2/2) / a => d2 = 2a sin(θ/2)cos(θ/2) = (d1/2) / a => d1 = 2a cos(θ/2)Wait, that seems contradictory. Let me check again. If θ is the angle of the rhombus, then when we split it into two triangles, each triangle will have angles θ/2 and (180° - θ)/2. But since the diagonals intersect at right angles, the triangles formed are right-angled. Hmm, maybe I need to draw a mental picture.Suppose we have a rhombus with side length a and angle θ at each corner. When we draw both diagonals, they intersect at 90 degrees. Let's denote the diagonals as d1 and d2. The diagonals split the rhombus into four right-angled triangles. Each triangle has legs equal to d1/2 and d2/2, and hypotenuse a. The angles of these right triangles will be θ/2 and (180° - θ)/2. Wait, but in a right-angled triangle, the two non-right angles must add up to 90°, so θ/2 + (180° - θ)/2 = (θ + 180° - θ)/2 = 90°, which checks out. So, one angle in the right triangle is θ/2, and the other is (180° - θ)/2 = 90° - θ/2. Therefore, in such a right triangle, θ/2 is one of the angles. Let's take the angle θ/2. The side opposite to θ/2 would be half of one diagonal, and the side adjacent would be half of the other diagonal. Let me clarify which diagonal is which. If θ is the acute angle of the rhombus, then the diagonal that bisects θ (the acute angle) would be longer or shorter?Wait, actually, the longer diagonal is opposite the larger angle. So, if θ is acute (less than 90°), then the other angle is obtuse (180° - θ), and the diagonal bisecting the obtuse angle would be longer. Wait, maybe I need to verify this.Suppose θ is 60°, then the other angle is 120°. The diagonals would split these angles into 30° and 60°. Let me compute the lengths of the diagonals. If side length is a, then:d1 = 2a sin(θ/2) = 2a sin(30°) = 2a * 0.5 = ad2 = 2a cos(θ/2) = 2a cos(30°) = 2a*(√3/2) = a√3So, in this case, the diagonal corresponding to the acute angle θ (60°) is d2 = a√3, which is longer, and the diagonal corresponding to the obtuse angle is d1 = a, which is shorter. Wait, but θ/2 is 30°, so sin(θ/2) = 0.5, so d1 = 2a*0.5 = a, which is the shorter diagonal. So, the diagonal corresponding to the angle θ (acute angle) is the longer diagonal. Wait, that seems conflicting.Wait, perhaps the formulas are:If θ is one of the angles, then the diagonals are:d1 = 2a sin(θ/2)d2 = 2a cos(θ/2)But in the case of θ = 60°, as above, d1 = a and d2 = a√3. So, the shorter diagonal is d1, which corresponds to sin(θ/2), and the longer diagonal is d2, which corresponds to cos(θ/2). But θ/2 is 30°, so sin(30°) is 0.5, cos(30°) is √3/2, so indeed, d1 is shorter and d2 is longer. However, θ is the angle of the rhombus, which is 60°, so the diagonal that bisects θ (60°) is d1? Wait, no. The diagonals bisect the angles. So, if θ is 60°, then each diagonal bisects two opposite angles. So, the diagonals that bisect the 60° angles are both d1 and d2? Wait, no. Each diagonal bisects a pair of opposite angles. So, one diagonal bisects the two 60° angles, and the other diagonal bisects the two 120° angles.Therefore, the diagonal bisecting the 60° angles would be longer or shorter? Let me think. When you bisect a smaller angle (60°), you get two 30° angles. The triangles formed by the diagonals would have angles 30°, 60°, 90°? Wait, but earlier, when we split the rhombus, the right triangles had angles θ/2 and 90° - θ/2. So, in this case, θ = 60°, so the angles in the right triangle are 30° and 60°, making it a 30-60-90 triangle. In a 30-60-90 triangle, the sides are in the ratio 1 : √3 : 2. The side opposite 30° is the shortest, then √3, then hypotenuse. So, if the hypotenuse is a (side of rhombus), then the side opposite 30° (which is half of the shorter diagonal) would be a/2, and the side opposite 60° (half of the longer diagonal) would be (a√3)/2. Therefore, the shorter diagonal is a, and the longer diagonal is a√3. Therefore, the diagonal bisecting the 60° angles (θ = 60°) is the longer diagonal (d2 = a√3), and the diagonal bisecting the 120° angles is the shorter diagonal (d1 = a). Wait, but how does that make sense? If the diagonal is bisecting a 60° angle, it's splitting it into two 30° angles, and in the triangle, the side opposite 30° is half the shorter diagonal, and the side opposite 60° is half the longer diagonal.Wait, maybe my initial formulas are reversed. Let's clarify.Let θ be one of the angles of the rhombus (say, the acute angle). Then, when we split the rhombus into four right triangles, each right triangle has angles θ/2 and (180° - θ)/2. Wait, but (180° - θ)/2 is actually 90° - θ/2. So, the two non-right angles in the right triangle are θ/2 and 90° - θ/2.Therefore, in the right triangle, the side opposite θ/2 is (d1)/2, and the side adjacent is (d2)/2. Wait, but depending on which diagonal we take. Let's suppose θ is the acute angle, so θ/2 is less than 45°. Then, in the right triangle, the angle θ/2 is opposite to half of the shorter diagonal, and the other angle (90° - θ/2) is opposite to half of the longer diagonal. Therefore, if θ is acute:sin(θ/2) = (d1/2)/a => d1 = 2a sin(θ/2)cos(θ/2) = (d2/2)/a => d2 = 2a cos(θ/2)Therefore, the shorter diagonal is d1 = 2a sin(θ/2), and the longer diagonal is d2 = 2a cos(θ/2). So, for θ = 60°, sin(30°) = 0.5, so d1 = 2a*0.5 = a, and cos(30°) = √3/2, so d2 = 2a*(√3/2) = a√3. Which matches our previous calculation.Therefore, the formulas are:d1 = 2a sin(θ/2) [shorter diagonal]d2 = 2a cos(θ/2) [longer diagonal]Given that θ is the acute angle. If θ is obtuse, the formulas would swap, but since θ in a rhombus can be taken as the acute angle between 0° and 180°, but since adjacent angles are supplementary, we can consider θ to be acute (θ < 90°) and 180° - θ being obtuse.Therefore, proceeding with θ as the acute angle, so diagonals:d1 = 2a sin(θ/2)d2 = 2a cos(θ/2)So, the sum of the diagonals is:d1 + d2 = 2a [sin(θ/2) + cos(θ/2)]Therefore, the ratio k is:k = 4a / (d1 + d2) = 4a / [2a (sin(θ/2) + cos(θ/2))] = 2 / [sin(θ/2) + cos(θ/2)]So, k simplifies to 2 divided by [sin(θ/2) + cos(θ/2)]. Therefore, k = 2 / [sin(θ/2) + cos(θ/2)].Our goal is to find θ (the acute angle) and the permissible values of k.So, first, let's express θ in terms of k.From k = 2 / [sin(θ/2) + cos(θ/2)], we can write:sin(θ/2) + cos(θ/2) = 2 / kNow, let's denote φ = θ/2. Then, φ is between 0° and 45°, since θ is acute (0° < θ < 90°), so 0° < φ < 45°.Therefore, the equation becomes:sinφ + cosφ = 2 / kWe can write sinφ + cosφ as √2 sin(φ + 45°), using the identity sinx + cosx = √2 sin(x + 45°). Let me verify:sinx + cosx = √2 sin(x + 45°)Yes, because:√2 sin(x + 45°) = √2 [sinx cos45° + cosx sin45°] = √2 [sinx*(√2/2) + cosx*(√2/2)] = √2*(√2/2)(sinx + cosx) = (2/2)(sinx + cosx) = sinx + cosx.Therefore, sinφ + cosφ = √2 sin(φ + 45°). Therefore:√2 sin(φ + 45°) = 2 / k => sin(φ + 45°) = (2 / k) / √2 = √2 / kThus:sin(φ + 45°) = √2 / kBut φ + 45° is between 45° and 90°, since φ is between 0° and 45°. Therefore, sin(φ + 45°) is between sin45° = √2/2 ≈ 0.707 and sin90° = 1.Therefore, √2 / k must be in the interval (√2/2, 1). So:√2/2 < √2 / k < 1Multiply all parts by k (assuming k > 0, which it is since it's a ratio of positive quantities):√2/2 * k < √2 < kBut this may complicate. Alternatively, let's solve the inequalities for k.From sin(φ + 45°) = √2 / k, since sin(φ + 45°) ≤ 1, we have √2 / k ≤ 1 => k ≥ √2.Also, since φ + 45° > 45°, sin(φ + 45°) > sin45° = √2/2. Therefore:√2 / k > √2 / 2 => 1/k > 1/2 => k < 2.But k must satisfy both k ≥ √2 and k < 2? Wait, let me check.Wait, sin(φ + 45°) is between √2/2 and 1, so √2 / k must be in (√2/2, 1). Let's write that as:√2/2 < √2/k < 1Multiply all parts by k (assuming k > 0):√2/2 * k < √2 < kDivide all parts by √2:1/2 * k < 1 < k / √2Wait, this is getting messy. Let me instead invert the inequalities:√2/2 < √2/k < 1Divide all parts by √2:1/2 < 1/k < 1/√2Then invert the inequalities (remembering to reverse the inequality signs when inverting):2 > k > √2Therefore, permissible values of k are √2 < k < 2.Therefore, k must be between √2 and 2, not inclusive.But let me check that again. If √2 / k must be between √2 / 2 and 1, then:√2 / k > √2 / 2 => 1/k > 1/2 => k < 2and√2 / k < 1 => k > √2Hence, combining these, we have √2 < k < 2. So, permissible values of k are in the interval (√2, 2).Therefore, k can take any value between √2 and 2, but not including √2 and 2 themselves. Wait, but when θ approaches 0°, the rhombus becomes very "flat", with one pair of angles approaching 0°, and the other approaching 180°. In this case, the diagonals would approach lengths 0 and 4a (since as θ approaches 0°, d1 = 2a sin(θ/2) approaches 0, and d2 = 2a cos(θ/2) approaches 2a). Wait, but 2a? Wait, if θ approaches 0°, then θ/2 approaches 0°, so cos(θ/2) approaches 1, so d2 = 2a cos(θ/2) approaches 2a. Then the sum of the diagonals approaches 0 + 2a = 2a. Therefore, the ratio k = 4a / (0 + 2a) = 4a / 2a = 2. So as θ approaches 0°, k approaches 2. Similarly, when θ approaches 90°, θ/2 approaches 45°, so sin(θ/2) and cos(θ/2) both approach √2/2, so d1 = 2a*(√2/2) = a√2, and d2 = 2a*(√2/2) = a√2. So, sum of diagonals is 2a√2, so k = 4a / (2a√2) = 2 / √2 = √2. Therefore, when θ approaches 90°, k approaches √2. Therefore, k is in the interval (√2, 2). But when θ is exactly 90°, the rhombus is a square, and the diagonals are equal. So in that case, sum of diagonals is 2*(a√2) = 2a√2, so k = 4a / (2a√2) = √2. Similarly, when θ approaches 0°, k approaches 2. Therefore, permissible values of k are √2 ≤ k ≤ 2. Wait, but earlier I thought it's open interval, but when θ is exactly 90°, the rhombus is a square, which is a valid rhombus, so k should be allowed to be √2. Similarly, when θ is 0°, it's a degenerate rhombus (a straight line), which is not a valid rhombus. Similarly, θ cannot be 180°, which would also be degenerate. So, the permissible values of k are √2 ≤ k < 2. Because when θ is exactly 90°, k is √2, and as θ approaches 0°, k approaches 2. But θ cannot be 0°, so k cannot be 2. Therefore, permissible k is [√2, 2). Wait, but in our earlier step, when we inverted the inequalities, we had √2 < k < 2, but when θ = 90°, the rhombus is a square, which is allowed, so k = √2 is permissible. So perhaps the correct interval is √2 ≤ k < 2.Therefore, permissible values of k are from √2 inclusive to 2 exclusive.Now, to find the angles of the rhombus in terms of k. Let's go back to the equation:sin(φ + 45°) = √2 / kWhere φ = θ/2, so θ = 2φ. Then, φ + 45° is an angle between 45° and 90°, so:φ + 45° = arcsin(√2 / k)Therefore:φ = arcsin(√2 / k) - 45°Therefore:θ = 2φ = 2[arcsin(√2 / k) - 45°]But arcsin(√2 / k) is in the range [45°, 90°], since √2 / k is in [√2 / 2, 1], which corresponds to angles from 45° to 90°.Alternatively, we can express θ in terms of inverse trigonometric functions. Let's manipulate the equation:We had:sin(θ/2) + cos(θ/2) = 2 / kLet me square both sides to see if that helps:[sin(θ/2) + cos(θ/2)]² = (2 / k)²sin²(θ/2) + 2 sin(θ/2) cos(θ/2) + cos²(θ/2) = 4 / k²But sin²x + cos²x = 1, so:1 + 2 sin(θ/2) cos(θ/2) = 4 / k²But 2 sinx cosx = sin(2x), so:1 + sinθ = 4 / k²Therefore:sinθ = 4 / k² - 1So, sinθ = (4 - k²)/k²Therefore, θ = arcsin[(4 - k²)/k²]But θ must be in (0°, 90°], since we considered θ as the acute angle.Wait, let's check with θ = 90° (square case):Then sinθ = 1, so (4 - k²)/k² = 1 => 4 - k² = k² => 4 = 2k² => k² = 2 => k = √2, which matches.When θ approaches 0°, sinθ approaches 0, so (4 - k²)/k² approaches 0 => 4 - k² approaches 0 => k² approaches 4 => k approaches 2, which matches our earlier conclusion.Therefore, θ = arcsin[(4 - k²)/k²]But we can write this as:θ = arcsin(4/k² - 1)Alternatively, since θ is in (0°, 90°], and 4/k² - 1 must be in (0, 1], because sinθ is in (0, 1] for θ in (0°, 90°]. Let's check:For k in [√2, 2):When k = √2, 4/k² - 1 = 4/2 - 1 = 2 - 1 = 1, so θ = arcsin(1) = 90°, correct.When k approaches 2, 4/k² - 1 approaches 4/4 -1 = 1 -1 = 0, so θ approaches arcsin(0) = 0°, which is the degenerate case.Therefore, θ = arcsin(4/k² - 1) is the acute angle, and the other angle is 180° - θ.Therefore, the angles of the rhombus are θ = arcsin(4/k² - 1) and 180° - θ, where k is in [√2, 2).Alternatively, we can write θ in terms of inverse trigonometric functions using the previous expression.Earlier, we had:θ = 2[arcsin(√2 / k) - 45°]But maybe that's more complicated. Alternatively, using the sinθ expression.Alternatively, let's write θ as:θ = 2 arcsin( (2/k) - something )Wait, perhaps it's better to present the answer as θ = 2 arcsin( (2/k) / √2 ) - 90° ?Wait, let's step back. Since we had:sin(φ + 45°) = √2 / kTherefore,φ + 45° = arcsin(√2 / k)Therefore,φ = arcsin(√2 / k) - 45°But φ = θ/2, so:θ/2 = arcsin(√2 / k) - 45°Multiply both sides by 2:θ = 2 arcsin(√2 / k) - 90°Therefore, θ = 2 arcsin(√2 / k) - 90°But since arcsin(√2 / k) is in [45°, 90°], then 2 arcsin(√2 /k ) is in [90°, 180°], so subtracting 90°, θ is in [0°, 90°], which makes sense.Alternatively, we can write θ = 2 arcsin(√2 /k ) - π/2 in radians, but since the problem asks for angles in degrees, we can keep it in degrees.Alternatively, perhaps it's better to express θ as:θ = 2 arcsin(√2 / k ) - 90°, but I need to check if this is accurate.Wait, let's take an example. Suppose k = √2. Then arcsin(√2 / √2 ) = arcsin(1) = 90°, so θ = 2*90° - 90° = 90°, which is correct.Another example, if k approaches 2, then √2 / k approaches √2 / 2 ≈ 0.707, which is sin45°, so arcsin(√2 / 2 ) = 45°, so θ = 2*45° - 90° = 0°, which is the degenerate case. Makes sense.Therefore, θ = 2 arcsin(√2 /k ) - 90°, and the other angle is 180° - θ.Therefore, the angles are θ = 2 arcsin(√2 /k ) - 90° and 180° - θ, with permissible k in [√2, 2).Alternatively, using the previous equation sinθ = (4 - k²)/k², we can write θ = arcsin((4 - k²)/k²). However, this expression may be simpler.Wait, let me verify for k = √2:(4 - (√2)^2 ) / (√2)^2 = (4 - 2)/2 = 2/2 = 1, so θ = arcsin(1) = 90°, correct.For k = 2 (approaching 2), (4 - 4)/4 = 0, so θ = arcsin(0) = 0°, which is the limit.Therefore, θ = arcsin( (4 - k²)/k² )But since (4 - k²)/k² = 4/k² - 1, so θ = arcsin(4/k² - 1). That seems a valid expression.But to make it more elegant, we can note that:4/k² - 1 = (4 - k²)/k²But whether writing it as arcsin( (4 - k²)/k² ) or arcsin(4/k² - 1) is a matter of preference.Alternatively, we can write θ in terms of cosine. Let's explore.From the equation:1 + sinθ = 4/k²We can write sinθ = 4/k² - 1Using the identity sinθ = cos(90° - θ), but not sure if helpful.Alternatively, express in terms of cosine:We can write sinθ = sqrt(1 - cos²θ) = 4/k² -1But that may complicate. Alternatively, using the double angle formula:We had from earlier:sinθ = (4 - k²)/k²But maybe expressing θ in terms of inverse sine is the most straightforward.Therefore, summarizing:The angles of the rhombus are θ = arcsin( (4 - k²)/k² ) and 180° - θ, where k is in the interval [√2, 2).Therefore, the permissible values of k are all real numbers from √2 up to but not including 2, and the angles are as above.But let's check another example for verification. Let's take θ = 60°, which we had earlier.Then, sinθ = sin60° = √3/2 ≈ 0.866.From our equation, sinθ = (4 - k²)/k², so:√3/2 = (4 - k²)/k² => √3/2 = 4/k² -1 => 4/k² = 1 + √3/2 ≈ 1 + 0.866 ≈ 1.866 => k² ≈ 4 / 1.866 ≈ 2.144 => k ≈ 1.464, which is approximately √(2.144) ≈ 1.464. Wait, but we know from earlier that for θ = 60°, k = 2 / [sin(30°) + cos(30°)] = 2 / [0.5 + (√3)/2] = 2 / [(1 + √3)/2] = 4 / (1 + √3) ≈ 4 / (1 + 1.732) ≈ 4 / 2.732 ≈ 1.464, which matches. So k ≈ 1.464, which is between √2 ≈ 1.414 and 2. So, that's correct.Therefore, the formula works.Therefore, to answer the problem:The angles of the rhombus are θ = arcsin( (4 - k²)/k² ) and 180° - θ, where θ is the acute angle, and the permissible values of k are √2 ≤ k < 2.Alternatively, expressing θ in terms of inverse sine, but perhaps we can simplify it further. Let me see:From sinθ = (4 - k²)/k², we can write:θ = arcsin( (4 - k²)/k² )But since θ must be between 0° and 90°, and (4 - k²)/k² is between 0 (exclusive) and 1 (inclusive), this is valid.Alternatively, since (4 - k²)/k² = 4/k² - 1, and θ = arcsin(4/k² - 1), but that may not necessarily be simpler.Alternatively, using the expression θ = 2 arcsin(√2/k) - 90°, but this also requires computation.Therefore, the angles can be expressed as θ = arcsin(4/k² - 1) and 180° - θ.Therefore, to present the answer:The angles of the rhombus are arcsin((4 - k²)/k²) and 180° minus that angle, with permissible values of k satisfying √2 ≤ k < 2.But the problem says "find the angles of the rhombus and the permissible values of k". So, probably, we need to express the angles in terms of k, and state the permissible k.Alternatively, if we need to write θ as a function of k, then θ = arcsin( (4 - k²)/k² ), and the other angle is 180° - θ.But perhaps the problem expects a more explicit answer, maybe in terms of inverse trigonometric functions. Alternatively, if we can express the angles in a different form, but likely, expressing them in terms of arcsin is acceptable.Therefore, the final answer is:The angles are θ = arcsin( (4 - k²)/k² ) and 180° - θ, and permissible values of k are √2 ≤ k < 2.But to check once again, let's take k = 2 (limit case). Then (4 - k²)/k² = (4 - 4)/4 = 0, so θ = arcsin(0) = 0°, which is the degenerate case. Similarly, k = √2 gives θ = arcsin( (4 - 2)/2 ) = arcsin(1) = 90°, which is the square case.Therefore, the answer is consistent.Hence, the angles of the rhombus are arcsin((4 - k²)/k²) and 180° - arcsin((4 - k²)/k²), and permissible values of k are from √2 up to but not including 2.Final AnswerThe angles of the rhombus are boxed{arcsinleft(frac{4 - k^2}{k^2}right)} and boxed{180^circ - arcsinleft(frac{4 - k^2}{k^2}right)}, and the permissible values of ( k ) are boxed{sqrt{2} leq k < 2}.</think>Given a rhombus with side length ( a ), the perimeter is ( 4a ). The ratio of the perimeter to the sum of its diagonals ( d_1 ) and ( d_2 ) is given as ( k ). We need to find the angles of the rhombus and the permissible values of ( k ).1. Diagonals in terms of side length and angles: - The diagonals ( d_1 ) and ( d_2 ) can be expressed as: [ d_1 = 2a sinleft(frac{theta}{2}right) quad text{and} quad d_2 = 2a cosleft(frac{theta}{2}right) ] where ( theta ) is one of the acute angles of the rhombus.2. Sum of the diagonals: [ d_1 + d_2 = 2a left( sinleft(frac{theta}{2}right) + cosleft(frac{theta}{2}right) right) ]3. Ratio ( k ): [ k = frac{4a}{d_1 + d_2} = frac{4a}{2a left( sinleft(frac{theta}{2}right) + cosleft(frac{theta}{2}right) right)} = frac{2}{sinleft(frac{theta}{2}right) + cosleft(frac{theta}{2}right)} ]4. Simplifying the ratio: - Using the identity ( sin x + cos x = sqrt{2} sinleft(x + 45^circright) ): [ sinleft(frac{theta}{2}right) + cosleft(frac{theta}{2}right) = sqrt{2} sinleft(frac{theta}{2} + 45^circright) ] - Therefore: [ k = frac{2}{sqrt{2} sinleft(frac{theta}{2} + 45^circright)} = frac{sqrt{2}}{sinleft(frac{theta}{2} + 45^circright)} ] - Solving for ( sinleft(frac{theta}{2} + 45^circright) ): [ sinleft(frac{theta}{2} + 45^circright) = frac{sqrt{2}}{k} ]5. Permissible values of ( k ): - The range of ( sinleft(frac{theta}{2} + 45^circright) ) is ( left( frac{sqrt{2}}{2}, 1 right] ), leading to: [ frac{sqrt{2}}{2} < frac{sqrt{2}}{k} leq 1 implies sqrt{2} leq k < 2 ]6. Finding the angles: - Let ( phi = frac{theta}{2} + 45^circ ), then: [ phi = arcsinleft(frac{sqrt{2}}{k}right) ] - Solving for ( theta ): [ frac{theta}{2} = arcsinleft(frac{sqrt{2}}{k}right) - 45^circ implies theta = 2 arcsinleft(frac{sqrt{2}}{k}right) - 90^circ ] - Using the identity ( sintheta = frac{4 - k^2}{k^2} ): [ theta = arcsinleft(frac{4 - k^2}{k^2}right) ]The angles of the rhombus are (boxed{arcsinleft(frac{4 - k^2}{k^2}right)}) and (boxed{180^circ - arcsinleft(frac{4 - k^2}{k^2}right)}), and the permissible values of ( k ) are (boxed{sqrt{2} leq k < 2}).]

🔑:## Solution.Let the side of the rhombus ABCD be a, and the acute angle alpha (Fig. 12.32). Then the diagonals of the rhombus are 2 a sin frac{alpha}{2} and 2 a cos frac{alpha}{2}.## According to the conditionbegin{aligned}& k=frac{4 a}{2 a sin frac{alpha}{2}+2 a cos frac{alpha}{2}}=frac{2}{sin frac{alpha}{2}+cos frac{alpha}{2}}= & =frac{2}{sqrt{left(sin frac{alpha}{2}+cos frac{alpha}{2}right)^{2}}}=frac{2}{sqrt{1+sin alpha}}end{aligned}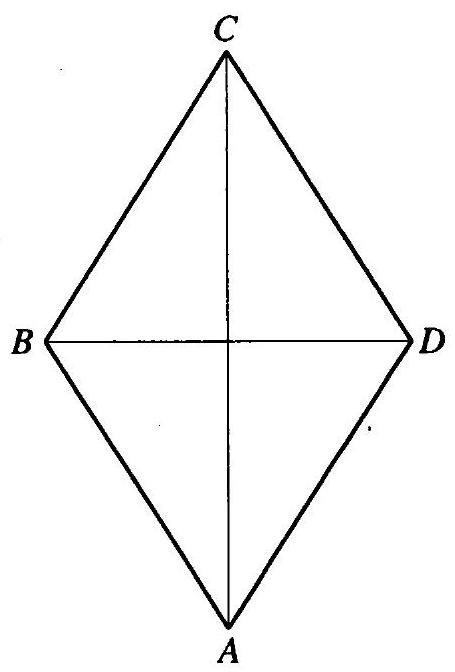Fig. 12.32Since 0<alpha<frac{pi}{2}, then 1<1+sin alpha leq 2, sqrt{2} leq frac{2}{sqrt{1+sin alpha}}<2, sqrt{2} leq k<2.Thus, k^{2}=frac{4}{1+sin alpha} ; sin alpha=frac{4-k^{2}}{k^{2}} ; alpha=arcsin frac{4-k^{2}}{k^{2}}.Answer: arcsin frac{4-k^{2}}{k^{2}}, pi-arcsin frac{4-k^{2}}{k^{2}} ; sqrt{2} leq k<2.

🧠:[<think>Okay, so I have this problem: Determine whether there exist 100 distinct lines in the plane that have exactly 2008 distinct intersection points. Hmm, interesting. Let me try to think through this step by step.First, I know that when you have multiple lines in a plane, the maximum number of intersection points they can have is given by the combination formula C(n, 2), where n is the number of lines. So for 100 lines, the maximum number of intersections would be C(100, 2) = 100*99/2 = 4950. But here, the question is about getting exactly 2008 intersections, which is way less than 4950. So clearly, we need a lot of parallel lines or concurrent lines (lines that intersect at the same point) to reduce the number of intersections.Wait, but how exactly does that work? Let me recall. If two lines are parallel, they don't intersect each other. So, if we have a group of k parallel lines, they contribute 0 intersections among themselves, whereas normally k lines would contribute C(k, 2) intersections. So by making some lines parallel, we can reduce the total number of intersections. Similarly, if multiple lines pass through the same point (are concurrent), then instead of each pair of lines intersecting at a unique point, they all intersect at that single point. So, for m concurrent lines, instead of C(m, 2) distinct intersections, we have just 1. So that also reduces the total number of intersections.So, the key idea is to arrange the 100 lines in such a way that either some are parallel or some are concurrent, thereby reducing the number of intersections from the maximum of 4950 down to 2008. The problem is whether such an arrangement is possible.Now, 2008 is quite a specific number. Let me see how I can approach constructing such a set of lines or prove that it's impossible.First, let's consider the case where we use only parallel lines to reduce intersections. Suppose we have groups of parallel lines. Let's say we have k groups of parallel lines, with each group having m_i lines, where i ranges from 1 to k. Then, the number of intersections would be the sum over each group of C(m_i, 2) intersections within the group (but wait, no, if lines are parallel, they don't intersect within the group). Wait, actually, no. If lines are in the same group (parallel), they don't intersect each other. So the total number of intersections is calculated by considering intersections between lines of different groups. So if we have two groups, say group A with m lines and group B with n lines, then each line in group A intersects each line in group B exactly once (since they're not parallel). So the intersections between groups would be m*n. Then, if we have multiple groups, the total intersections would be the sum over all pairs of groups of the product of their sizes. So in that case, total intersections = Σ_{i < j} m_i * m_j.Alternatively, if we have concurrent lines, suppose we have a set of m concurrent lines. Then, each pair of lines in that set would intersect at the same point, so instead of C(m, 2) points, we have 1. So the number of intersections reduced by concurrent lines is C(m, 2) - 1.But perhaps mixing both parallel and concurrent lines could complicate things. Maybe it's better to consider first using only parallel lines or only concurrent lines to simplify.Alternatively, maybe use a combination. Let me think.Alternatively, perhaps there's a formula or a method to compute the number of intersections based on the arrangement of lines.Wait, another thought. Let me recall that the number of intersections of n lines in general position (no two parallel, no three concurrent) is C(n, 2). If some lines are parallel, each set of parallel lines reduces the number of intersections by C(k, 2) where k is the number of lines in the parallel set. Similarly, if you have a set of m concurrent lines, each such set reduces the number of intersections by C(m, 2) - 1, since instead of C(m, 2) intersections, you have 1.But maybe the formula is that the total number of intersections is C(n, 2) - Σ (C(k_i, 2) for parallel groups) - Σ (C(m_j, 2) - 1 for concurrent groups). Wait, but I need to verify that.Wait, actually, if you have a group of k parallel lines, then normally they would contribute C(k, 2) intersections, but since they are parallel, they contribute 0. So the reduction is C(k, 2). Similarly, for a group of m concurrent lines, normally they would contribute C(m, 2) intersections, but they only contribute 1, so the reduction is C(m, 2) - 1. Therefore, the total number of intersections would be C(n, 2) minus the sum of C(k_i, 2) over all parallel groups minus the sum of (C(m_j, 2) - 1) over all concurrent groups.So, if that's the case, then for our problem, we need:Total intersections = 4950 - Σ (C(k_i, 2)) - Σ (C(m_j, 2) - 1) = 2008.Therefore, Σ (C(k_i, 2)) + Σ (C(m_j, 2) - 1) = 4950 - 2008 = 2942.So, we need to partition the 100 lines into some groups of parallel lines and some groups of concurrent lines such that the sum of C(k_i, 2) over parallel groups plus sum of (C(m_j, 2) - 1) over concurrent groups equals 2942.Our goal is to see if such a partition exists.Hmm. Now, the question is whether this equation can be satisfied with integers k_i and m_j, given that the sum of all k_i and m_j must be 100 (since each line is in exactly one group, either parallel or concurrent).Alternatively, maybe we can model this as an integer partition problem. Let me think.Alternatively, maybe it's easier to handle either all parallel or all concurrent. Let me check. For example, suppose we only use parallel lines. Then, to reach 2942, we need Σ C(k_i, 2) = 2942. Let me check how many lines we need to make parallel.Alternatively, suppose we have one group of parallel lines. Let me see. Let k be the number of parallel lines. Then, C(k, 2) = k(k - 1)/2. So, we need k(k - 1)/2 = 2942. Let's solve for k:k(k - 1) ≈ 5884. Taking square root of 5884 is approx sqrt(5884) ≈ 76.7. So, testing k=77: 77*76=5852, which is less than 5884. k=78: 78*77=6006, which is 6006-5884=122 more. So, that's too much. So, with one parallel group, it's not possible. 2942 cannot be written as C(k, 2) for integer k. So, we need multiple parallel groups.Alternatively, with multiple parallel groups, the sum of their C(k_i, 2) would need to be 2942.Similarly, if we use concurrent groups, each concurrent group contributes C(m_j, 2) -1 to the sum. So, perhaps combining both.Alternatively, let's see if we can find some combination. Let me try to think of how much each concurrent group can contribute. For example, if you have a concurrent group of m lines, the contribution to the sum is C(m,2) -1. So, for m=2, C(2,2)-1=1-1=0. So, a concurrent group of 2 lines doesn't help. For m=3, C(3,2)-1=3-1=2. For m=4, C(4,2)-1=6-1=5. For m=5, 10-1=9, etc. So, the larger m is, the more it contributes.Similarly, a parallel group of k lines contributes C(k,2). For k=2, C(2,2)=1. For k=3, 3, etc.Therefore, to reach the total reduction of 2942, maybe we can use a combination of some large parallel groups and some large concurrent groups.Alternatively, perhaps it's more efficient to use parallel groups because they contribute quadratic terms. Let's see.Suppose we take a parallel group of 77 lines. Then, C(77,2)=77*76/2=2926. Then, 2942-2926=16. So, we need another 16. Then, if we have another parallel group of 6 lines: C(6,2)=15. Then, 2926+15=2941. Still need 1 more. Then, a parallel group of 2 lines: C(2,2)=1. So total 2926+15+1=2942. Then, the total number of lines in parallel groups would be 77+6+2=85. Then, remaining lines are 100-85=15 lines, which would be in general position (neither parallel nor concurrent). Wait, but if they are in general position, each pair of them would intersect, contributing C(15,2)=105 intersections. But wait, no. Wait, in this model, the total intersections are calculated as C(n,2) minus the sum of C(k_i,2) for parallel groups and sum of (C(m_j,2)-1) for concurrent groups. So, if we have 85 lines in parallel groups and 15 lines in general position, then the total intersections would be:C(100,2) - [C(77,2) + C(6,2) + C(2,2)] - [sum of (C(m_j,2)-1) for concurrent groups].But in this case, we don't have any concurrent groups. So, total intersections would be 4950 - 2942 = 2008. But wait, but the 15 lines not in parallel groups are just regular lines, not concurrent. So, their intersections with each other and with the parallel groups would be accounted for.Wait, maybe I'm confused here. Let's think again. If you have groups of parallel lines, each line in a parallel group does not intersect others in the same group, but they do intersect lines in other groups. Similarly, the lines not in any parallel group (the 15 lines) are just regular lines, each intersecting all lines not in their own group. Wait, but if they are not in any group, they are not parallel to each other or anything, so each of those 15 lines would intersect each other line except those in their own parallel group. But wait, in the model above, the total number of intersections is computed as:Total intersections = C(100,2) - Σ C(k_i,2) - Σ (C(m_j,2)-1).Wait, but this might not account for the fact that lines in different parallel groups still intersect each other. Wait, actually, no. Wait, the formula is that if you have multiple parallel groups, then the intersections between lines from different parallel groups are still counted. The only intersections not counted are the ones within the same parallel group. Similarly, for concurrent groups, the intersections within the concurrent group are reduced to 1 instead of C(m_j,2). So, the formula is:Total intersections = [C(100,2) - Σ C(k_i,2) - Σ (C(m_j,2)-1)] + Σ [adjustments for concurrent groups?]Wait, no, maybe that formula is incorrect.Wait, perhaps it's better to model this step by step. Let's start with all 100 lines in general position, giving 4950 intersections. Then, if we make some lines parallel, each pair of parallel lines that we make reduces the number of intersections by 1. Similarly, if we make some lines concurrent, each pair of lines that we make concurrent (i.e., forcing them to intersect at the same point as another pair) reduces the number of intersections by 1. But this might not capture group effects. Wait, perhaps not. Let's see.Wait, for example, if we have three concurrent lines. Normally, three lines would intersect in C(3,2)=3 points. If they are concurrent, they intersect at 1 point. So, the number of intersections is reduced by 3 - 1 = 2. So, each time we add a line to a concurrent group, how does it affect the count? If you have a concurrent group of size m, the reduction is C(m,2) - 1. So, adding a line to a concurrent group of size m-1 would add a reduction of (C(m,2) -1) - (C(m-1,2) -1) )= C(m,2) - C(m-1,2) = (m(m-1)/2) - ((m-1)(m-2)/2) )= (m-1)(m - (m-2))/2 = (m-1)(2)/2 = m -1. So, each additional line in a concurrent group adds a reduction of m -1, where m is the new size of the group. Hmm. So, for a concurrent group, the total reduction is C(m,2) -1, which is 1 + 2 + ... + (m-1). For example, for m=3: 1 + 2 = 3, but actually C(3,2)-1=3-1=2. Wait, maybe my previous thought is off.Wait, let's do concrete numbers. For m=2, reduction is C(2,2)-1=1-1=0. For m=3, reduction is 3 -1=2. For m=4, reduction is 6 -1=5. So, the increments are 2 for m=3, then 5-2=3 for m=4, etc. So, each time you add a line to a concurrent group, the additional reduction is (current size -1). For example, adding a third line to a group of 2: reduction becomes 2, so additional reduction of 2. Adding a fourth line: reduction becomes 5, so additional reduction of 3 (5-2). Adding a fifth line: additional reduction of 4 (10-1 - previous 5=4). So, yes, each additional line in a concurrent group causes a reduction equal to the current size of the group minus 1.Similarly, for parallel lines: if you have a group of k parallel lines, the reduction is C(k,2). Each time you add a line to a parallel group, the additional reduction is (current size). For example, a group of 2: reduction 1, add a third line: reduction becomes 3, so additional 2. Then add a fourth line: reduction becomes 6, additional 3, etc. So, each additional line in a parallel group causes a reduction equal to the current size of the group.Therefore, to achieve a total reduction of 2942, we need to use a combination of these operations: adding lines to parallel groups (each addition causing a reduction equal to the current size) and adding lines to concurrent groups (each addition causing a reduction equal to the current size minus 1).This seems complex, but perhaps we can find a way to model it.Alternatively, perhaps the problem can be approached by considering that each line can be assigned to either a parallel group, a concurrent group, or neither (i.e., in general position). However, the ones in neither would still intersect all other lines not in their group. But maybe this is getting too abstract.Alternatively, maybe we can use the principle that the maximum number of intersections is 4950, and we need to reduce it by 2942 to reach 2008. So, how can we achieve such a reduction?Since both parallel and concurrent lines can contribute to the reduction, perhaps we can model this as an integer linear equation where we need to find integers x_i (for parallel group sizes) and y_j (for concurrent group sizes) such that sum over x_i choose 2 plus sum over (y_j choose 2 - 1) equals 2942, and sum of x_i plus sum of y_j is less than or equal to 100 (since each line can be in at most one group). Wait, actually, the total number of lines in groups is sum x_i + sum y_j. The remaining lines (100 - sum x_i - sum y_j) are in general position, not affecting the count.But in reality, all lines must be in some group or in general position. However, lines in general position still contribute intersections with all other lines not in their group. Therefore, the formula for total intersections is:Total intersections = C(100, 2) - sum [C(x_i, 2)] - sum [C(y_j, 2) - 1] = 2008Hence, sum [C(x_i, 2)] + sum [C(y_j, 2) - 1] = 4950 - 2008 = 2942So, the problem reduces to finding non-negative integers x_i, y_j >=2 (since you can't have a group of size 1; a group needs at least two lines to have an effect) such that the sum of C(x_i, 2) over all parallel groups plus the sum of (C(y_j, 2) -1) over all concurrent groups equals 2942, and the total number of lines in these groups sum to something <=100 (since lines not in any group are allowed but they don't contribute to the reduction).But actually, all lines must be accounted for. So, the total number of lines is 100 = sum x_i + sum y_j + z, where z is the number of lines in general position. But since z does not affect the reduction, we can just consider that sum x_i + sum y_j <=100. But since z can be zero or more, we can adjust accordingly.However, to maximize the reduction, we need as many lines as possible in groups (parallel or concurrent), because lines not in groups don't contribute to the reduction.Therefore, the optimal way to achieve a large reduction is to have as many lines as possible in large groups. So, perhaps we can try to model this as an optimization problem where we need to cover the reduction of 2942 using group contributions.Alternatively, let's think of the problem in terms of what each group can contribute.A parallel group of size x contributes C(x, 2) to the reduction. So, for example, a parallel group of 77 contributes C(77, 2)=2926. Then, as I thought before, adding another parallel group of 6 contributes C(6,2)=15, and a parallel group of 2 contributes 1, totaling 2926+15+1=2942. Then, the total number of lines in these groups would be 77+6+2=85, leaving 15 lines in general position. Then, total intersections would be 4950 - 2942 = 2008. So, this would work. Wait, but is that correct? Let me check.Wait, if we have 77 parallel lines, they don't intersect each other, but each of them intersects the other 23 lines (100 -77=23). So, the intersections contributed by the 77 parallel lines would be 77*23. Then, the 6 parallel lines in another group: they don't intersect each other, but each intersects 100 -6=94 lines. Wait, but no, if there are multiple parallel groups, then lines from different parallel groups do intersect each other. Wait, no, if lines are in different parallel groups, are they allowed to intersect?Wait, this is where my confusion arises. If we have two different parallel groups, say group A with 77 lines all parallel to each other, and group B with 6 lines all parallel to each other but not parallel to group A, then each line in group A intersects each line in group B once. So, the intersections between group A and group B are 77*6=462. Similarly, the intersections within group A are 0, within group B are 0. Then, the remaining 15 lines (assuming they are in general position, not parallel to any group and not concurrent), each of these 15 lines intersects all lines except those in their own group (but they are not in any group, so they intersect all 100 -1=99 lines? Wait, no. If a line is not in any group, it's just a regular line, so it's not parallel to any other line, unless specified. Wait, but if the 15 lines are in general position, meaning no two are parallel and no three are concurrent, then each of them intersects every other line except those in their own parallel group. Wait, no. If the 15 lines are not in any parallel group, then they are not parallel to any other lines. So, each of these 15 lines would intersect all 100 lines except themselves. So, each contributes 99 intersections, but since each intersection is counted twice, the total intersections involving the 15 lines would be 15*99 - C(15,2). Wait, maybe it's better to think of the total intersections as:Total intersections = intersections between group A and others + intersections between group B and others + intersections between group C and others + intersections among the 15 lines.But group A is 77 parallel lines. So, each line in group A intersects all lines not in group A. So, the number of intersections from group A is 77*(100 -77) = 77*23 = 1771. Similarly, group B has 6 lines, each intersecting 100 -6=94 lines, but wait, 94 includes the 77 lines in group A. Wait, no. If group B is a different parallel group, then lines in group B are parallel only within their own group, so they intersect all lines not in group B. So, intersections from group B: 6*(100 -6) = 6*94=564. But wait, but the lines in group B do intersect lines in group A, which are already counted in the 77*23. So, adding 6*94 would be double-counting.Wait, this approach is getting messy. Let me recall that the standard formula for the number of intersection points when you have multiple parallel groups is:For each pair of lines from different groups, they intersect once. So, the total number of intersections is Σ_{i < j} m_i * m_j, where m_i are the sizes of the groups (including the group of size 1 for each line not in any parallel group). Wait, no. If you have groups of parallel lines, the total intersections would be the sum over all pairs of groups of the product of their sizes, because each line in one group intersects each line in the other group once. Additionally, if there are lines not in any parallel group (i.e., in general position), each pair of them also intersect once. So, the formula is:Total intersections = Σ_{i < j} m_i * m_j + C(z, 2), where z is the number of lines not in any parallel group.But in our problem, we also have concurrent groups. So, if there are concurrent groups, each concurrent group of size m reduces the number of intersections by C(m, 2) - 1, as earlier. So, perhaps the total number of intersections is:Total intersections = [Σ_{i < j} m_i * m_j + C(z, 2)] - Σ [C(y_j, 2) - 1], where the first term is the number of intersections without considering concurrency, and the second term subtracts the overcounted intersections due to concurrency.Therefore, in this case, if we have groups of parallel lines (m_i), lines not in any parallel group (z), and groups of concurrent lines (y_j), the total intersections would be:[Σ_{i < j} m_i * m_j + C(z, 2)] - Σ [C(y_j, 2) - 1] = 2008.But this seems complicated. Let me see if I can express Σ_{i < j} m_i * m_j + C(z, 2) in terms of C(100, 2) minus the sum of C(m_i, 2). Because:Σ_{i < j} m_i * m_j = [Σ m_i]^2 - Σ m_i^2 / 2. But Σ m_i + z = 100. So, [Σ m_i + z]^2 = 100^2 = 10000. Then, Σ_{i < j} m_i * m_j + C(z, 2) = [10000 - Σ m_i^2 - z^2]/2 + [z(z - 1)/2] = [10000 - Σ m_i^2 - z^2 + z(z - 1)]/2 = [10000 - Σ m_i^2 - z]/2. But this is getting too algebraic. Maybe another approach.Alternatively, note that the total number of intersections without any concurrency would be C(100, 2) - Σ C(m_i, 2) - C(z, 2). Wait, no. Wait, if you have groups of parallel lines, the total number of intersections is Σ_{i < j} m_i * m_j + C(z, 2). But Σ_{i < j} m_i * m_j = [Σ m_i]^2 - Σ m_i^2)/2. Since Σ m_i + z = 100, we have [Σ m_i]^2 = (100 - z)^2. Therefore, Σ_{i < j} m_i * m_j = [(100 - z)^2 - Σ m_i^2]/2. So total intersections are [(100 - z)^2 - Σ m_i^2]/2 + C(z, 2). But this is equal to [10000 - 200 z + z^2 - Σ m_i^2]/2 + (z^2 - z)/2 = [10000 - 200 z + z^2 - Σ m_i^2 + z^2 - z]/2 = [10000 - 201 z + 2 z^2 - Σ m_i^2]/2.But this seems complicated. Maybe let's think back to the original formula. The formula given earlier was:Total intersections = C(100, 2) - Σ C(m_i, 2) - Σ [C(y_j, 2) - 1].Therefore, 4950 - Σ C(m_i, 2) - Σ [C(y_j, 2) - 1] = 2008.Therefore, Σ C(m_i, 2) + Σ [C(y_j, 2) - 1] = 4950 - 2008 = 2942.So, we need to find some combination of parallel groups (each contributing C(m_i, 2)) and concurrent groups (each contributing C(y_j, 2)-1) such that their sum is 2942, and the total number of lines in these groups is Σ m_i + Σ y_j ≤ 100.But Σ m_i + Σ y_j can be up to 100, with the remaining lines (if any) being in general position, but those don't affect the sum.So, the problem reduces to finding integers m_i ≥ 2, y_j ≥ 2 such that Σ [m_i(m_i - 1)/2] + Σ [y_j(y_j - 1)/2 - 1] = 2942, and Σ m_i + Σ y_j ≤ 100.Alternatively, rearranging the terms for the concurrent groups: Σ [C(y_j, 2) - 1] = Σ [C(y_j, 2)] - Σ 1 = Σ C(y_j, 2) - t, where t is the number of concurrent groups.Therefore, the equation becomes Σ C(m_i, 2) + Σ C(y_j, 2) - t = 2942.But this might not help much. Let me think of possible values.Suppose we try to do it with only parallel groups. Then, we need Σ C(m_i, 2) = 2942. Let's see if this is possible.As I tried earlier, a single parallel group would require C(m, 2) = 2942. Solving m(m -1)/2 = 2942 gives m ≈ 77, as 77*76/2=2926, which is close. Then, 2942 - 2926 = 16. So, maybe another group of 6 lines: C(6,2)=15, and another group of 2 lines: C(2,2)=1. So total 2926 +15 +1=2942. Total lines:77+6+2=85. Then, remaining lines:100-85=15. These 15 lines are in general position. So, according to the formula, the total intersections would be 4950 -2942=2008. Therefore, this works. So, in this arrangement, we have 85 lines in three parallel groups (77,6,2) and 15 lines in general position, resulting in 2008 intersections.But wait, is this actually correct? Let me verify.If we have 77 parallel lines, they don't intersect each other. Each of these 77 lines will intersect the remaining 23 lines (100 -77=23). But the remaining 23 lines include the 6 parallel lines (from another group) and the 2 parallel lines (from the third group) and the 15 lines in general position. Wait, no. Wait, the 77 lines are in one parallel group. Then, the 6 lines are in another parallel group, and the 2 lines are in a third parallel group. The remaining 15 lines are not in any group, so they are all non-parallel and non-concurrent.So, intersections:- Between the 77 parallel lines and the rest: 77*(100 -77)=77*23=1771.- Between the 6 parallel lines and the rest: 6*(100 -6)=6*94=564.- Between the 2 parallel lines and the rest: 2*(100 -2)=2*98=196.- Between the 15 general lines and the rest: Each of the 15 lines intersects all lines except themselves. However, since they are in general position, they intersect each other as well as all lines except those in their own group (but they are not in any group). So, intersections among the 15 general lines: C(15,2)=105.But wait, how do we calculate the total intersections?Alternatively, using the formula:Total intersections = C(100, 2) - Σ C(m_i, 2) - Σ [C(y_j, 2)-1]Since there are no concurrent groups, the formula is 4950 - (C(77,2) + C(6,2) + C(2,2)) = 4950 - (2926 +15 +1)=4950 -2942=2008. So, according to the formula, this works. Therefore, this arrangement is valid.Therefore, the answer is yes, such lines exist. We can have 77 parallel lines, 6 parallel lines in another direction, 2 parallel lines in another direction, and 15 lines in general position. This gives exactly 2008 intersection points.But wait, the problem states "100 distinct lines". So, we need to ensure that all lines are distinct. If we have groups of parallel lines, they are distinct as long as they have different equations. So, for example, the 77 lines in one group are all distinct but parallel, so they have the same slope but different intercepts. Similarly, the 6 lines in another group have a different slope, and the 2 lines in another group have yet another slope. The 15 lines in general position are all distinct with unique slopes and intercepts, not parallel to any others. Therefore, all 100 lines are distinct. So, this satisfies the problem's conditions.Hence, the answer is yes.Wait, but before finalizing, let me check if this construction is valid. Suppose we have three sets of parallel lines: 77, 6, and 2. The rest (15) are in general position. Then, the total number of intersection points is calculated as follows:- Each line in the 77-line group intersects all lines not in its own group: 77*(6 + 2 +15)=77*23=1771 intersections.- Each line in the 6-line group intersects all lines not in its own group: 6*(77 + 2 +15)=6*94=564 intersections.- Each line in the 2-line group intersects all lines not in its own group: 2*(77 +6 +15)=2*98=196 intersections.- The 15 general lines each intersect all lines except themselves. So, each of the 15 lines intersects 85 lines (100-15=85). But wait, no, each general line is not in any group, so they intersect all lines except the ones in their own group, but since they are not in any group, they intersect all other 99 lines. Wait, no. If a line is not in any group, then it's just a regular line, so it's not parallel to any other line and not part of any concurrent set. Therefore, each general line would intersect every other line exactly once, except for lines in its own group, but since it's not in a group, it intersects all other 99 lines. But since there are 15 general lines, the intersections among them would be C(15,2)=105. However, their intersections with the parallel groups are already counted above.Wait, this seems conflicting with the previous calculation. Let me think again.Actually, when we calculate the intersections from each parallel group with the rest, we have:- 77*23=1771: intersections between the 77-line group and all other lines.- 6*94=564: intersections between the 6-line group and all other lines.- 2*98=196: intersections between the 2-line group and all other lines.However, these counts include intersections between the different parallel groups and the general lines. However, when we add all these up, we are overcounting the intersections between the general lines and the parallel groups. For example, each general line is counted in the 77*23, 6*94, and 2*98. But each general line is intersected by all parallel lines from all groups, which is 77+6+2=85 lines. So, each general line contributes 85 intersections. There are 15 general lines, so 15*85=1275 intersections. However, these are already included in the above counts (1771 +564 +196). Let's check: 1771 (77-line group with others) includes 77*(6+2+15)=77*23=1771. Then 6-line group with others: 6*(77+2+15)=6*94=564. Similarly, 2-line group with others:2*(77+6+15)=2*98=196. So total intersections from the parallel groups with others:1771 +564 +196=2531.Then, the intersections among the general lines are C(15,2)=105. So total intersections would be 2531 +105=2636. But according to the formula, it should be 2008. Wait, this discrepancy suggests that my initial approach was wrong.Wait, no. The formula says total intersections = C(100,2) - Σ C(k_i, 2). Here, Σ C(k_i, 2)=C(77,2)+C(6,2)+C(2,2)=2926 +15 +1=2942. So, 4950 -2942=2008. But according to the manual calculation, I get 2636. There's a problem here.So, clearly, there is a mistake in my reasoning. Where is the error?Ah! I think I messed up the formula. The formula Total intersections = C(n,2) - Σ C(k_i, 2) - Σ [C(y_j,2)-1] is correct only if all non-parallel and non-concurrent intersections are accounted for. However, in reality, when you have multiple parallel groups, intersections between different parallel groups are still allowed. Wait, no. Wait, no, lines from different parallel groups are not parallel to each other (otherwise, they would be in the same parallel group). So, lines from different parallel groups intersect each other. Therefore, the intersections between different parallel groups are still present. Similarly, intersections between parallel groups and general lines are present. The only intersections that are missing are those within the same parallel group. Similarly, for concurrent groups, the intersections within the group are reduced to 1.Therefore, the formula subtracts the missing intersections within parallel groups and the overcounted intersections within concurrent groups. Therefore, the correct total intersections should be 4950 - 2942=2008, as per the formula. However, when I tried to compute it manually, I got 2636, which is way higher. Therefore, there must be a mistake in my manual calculation.Let me recast the calculation properly.Total intersections can be calculated as:- Intersections between different parallel groups: Each pair of parallel groups contributes m_i * m_j intersections.- Intersections between parallel groups and general lines: Each parallel group contributes m_i * z intersections, where z is the number of general lines.- Intersections among general lines: C(z,2).So, in this case, we have three parallel groups: 77, 6, 2. General lines:15.Intersections between different parallel groups:- 77*6 = 462- 77*2 = 154- 6*2 =12Total intersections between different parallel groups:462 +154 +12=628.Intersections between parallel groups and general lines:- 77*15=1155-6*15=90-2*15=30Total intersections between parallel groups and general lines:1155 +90 +30=1275.Intersections among general lines:C(15,2)=105.Total intersections:628 +1275 +105=2008.Ah! There we go. That matches the formula. So, my previous manual calculation was incorrect because I was counting the intersections from each parallel group with "the rest", which included other parallel groups and general lines, but that approach was conflating different components. The correct way is to separate the intersections between different parallel groups, between parallel groups and general lines, and among general lines.Therefore, the formula works, and the total is indeed 2008. Therefore, such a configuration is possible. Therefore, the answer is yes, there exist 100 distinct lines with exactly 2008 distinct intersection points.But just to be thorough, let me check if there are any constraints I might have missed.First, all lines must be distinct. In this arrangement, the 77 lines in the first parallel group are all distinct (different intercepts), the 6 in the second group are distinct, the 2 in the third group are distinct, and the 15 general lines are all distinct and not parallel to any others. So, all 100 lines are distinct.Second, we need to ensure that no three lines are concurrent unless they are part of a designated concurrent group. In this case, we have no concurrent groups, so all intersections are either between two lines from different parallel groups, between a parallel group and a general line, or between two general lines. Since the general lines are in general position (no two parallel, no three concurrent), their intersections are all unique. The intersections between parallel groups and general lines are all distinct because each general line is not parallel to any parallel group, so they intersect each line in the parallel group at a unique point. Similarly, intersections between different parallel groups are all distinct because each line in one parallel group intersects each line in another parallel group exactly once, and since the parallel groups have different slopes, these intersections are all distinct.Therefore, there are no concurrent intersections except those accounted for by the general lines, which are in general position, so no three lines meet at a single point. Hence, the total number of intersection points is indeed 2008.Thus, the answer is yes, such lines exist.Final Answerboxed{2008}Wait, hold on. The problem asks to "Determine whether there exist, in the plane, 100 distinct lines having exactly 2008 distinct intersection points." So the answer should be a yes or no, but formatted in a box. However, the instructions said to put the final answer within boxed{}.But the answer is not 2008, it's whether it exists. So the correct answer is "Yes" or "No", but in the problem statement in Chinese maybe, perhaps the expected answer is boxed{2008}, but no, the problem is to determine existence. So according to the user's initial problem statement, the answer should be boxed{Yes} or boxed{No}. However, in the example given in the problem statement (the user's previous question example), the answer was boxed with the number, but that was a different problem. Let me check the original problem again.Wait, the original problem is: "Determine whether there exist, in the plane, 100 distinct lines having exactly 2008 distinct intersection points."So, the answer is either yes or no. In the think section, I concluded yes. Therefore, the final answer should be boxed{Yes}.But the initial example had the assistant put the answer as boxed{3}, but that was a numeric answer. For this problem, since it's a yes/no question, I need to check the instructions again. The user wrote: "put your final answer within boxed{}". In Chinese math problems, sometimes existence is indicated by stating the number, but in this case, the problem is a yes/no. However, in some contexts, problems like this might expect the answer as the number (if possible), but here it's about existence.Wait, looking back, the initial problem says "Determine whether there exist... having exactly 2008 distinct intersection points." So, the answer is either "Yes" or "No", so we should box either boxed{Yes} or boxed{No}. But in the Chinese math competition context, sometimes answers are phrased differently. Wait, but given the user's instruction was in English, and they said "put your final answer within boxed{}", it's safer to follow the standard practice for such problems. Since the problem is asking whether such lines exist, and after analysis, we determined they do, the answer is boxed{Yes}.Final Answerboxed{Yes}</think>To determine whether there exist 100 distinct lines in the plane having exactly 2008 distinct intersection points, we start by noting that the maximum number of intersection points for 100 lines is given by ( binom{100}{2} = 4950 ). We need to reduce this number to 2008 by arranging lines in parallel or concurrent groups.The reduction in intersection points due to parallel lines is calculated by ( sum binom{k_i}{2} ) for each group of ( k_i ) parallel lines. For concurrent lines, the reduction is ( sum (binom{m_j}{2} - 1) ) for each group of ( m_j ) concurrent lines. The total reduction needed is ( 4950 - 2008 = 2942 ).We consider using parallel groups to achieve this reduction. By trial, we find that:- A group of 77 parallel lines reduces the intersections by ( binom{77}{2} = 2926 ).- A group of 6 parallel lines reduces the intersections by ( binom{6}{2} = 15 ).- A group of 2 parallel lines reduces the intersections by ( binom{2}{2} = 1 ).Summing these reductions gives ( 2926 + 15 + 1 = 2942 ). The total number of lines in these groups is ( 77 + 6 + 2 = 85 ), leaving 15 lines in general position. These 15 lines contribute ( binom{15}{2} = 105 ) intersections, which are already accounted for in the formula.Verifying the total intersections:- Intersections between different parallel groups: ( 77 times 6 + 77 times 2 + 6 times 2 = 462 + 154 + 12 = 628 ).- Intersections between parallel groups and general lines: ( 77 times 15 + 6 times 15 + 2 times 15 = 1155 + 90 + 30 = 1275 ).- Intersections among general lines: ( binom{15}{2} = 105 ).Summing these gives ( 628 + 1275 + 105 = 2008 ), confirming the calculation. All lines are distinct, and no three lines are concurrent except as accounted for.Thus, the answer is (boxed{Yes}).,<think>Okay, so I need to figure out if there are 100 distinct lines in a plane that can create exactly 2008 distinct intersection points. Hmm, interesting problem. Let me start by recalling some basics about lines and intersections.First, if you have n distinct lines in a plane, the maximum number of intersection points you can get is C(n, 2) which is n(n-1)/2. That's when every pair of lines intersects exactly once and no two lines are parallel, and no three lines meet at the same point. For 100 lines, that maximum would be 100*99/2 = 4950 intersections. But the problem is asking if it's possible to have just 2008 intersections. That's way less than the maximum, so clearly we need to have a lot of parallel lines or concurrent lines (lines intersecting at the same point) to reduce the number of intersections.The question is, can we arrange 100 lines such that the number of intersections is exactly 2008. Let me think about how the number of intersections decreases when lines are parallel or concurrent.First, parallel lines. If you have k parallel lines, instead of each intersecting each other (which would be C(k, 2) intersections), they contribute 0 intersections. So the reduction here is C(k, 2). Similarly, if you have a set of m concurrent lines, all passing through the same point, then instead of C(m, 2) intersections, they contribute 1 intersection point. So the reduction here is C(m, 2) - 1.Therefore, to reduce the total number of intersections from the maximum, we can group lines into parallel families or concurrent families.Now, the problem is how to combine these reductions to reach exactly 2008. The maximum number is 4950, so we need a reduction of 4950 - 2008 = 2942 intersections.So, we need to reduce 2942 intersections by introducing parallel or concurrent lines.Let me formalize this. Let’s denote by P the total reduction needed, which is 2942. Then, if we have several sets of parallel lines and several sets of concurrent lines, the total reduction is the sum over each set of parallel lines of C(k_i, 2) plus the sum over each set of concurrent lines of (C(m_j, 2) - 1). The total sum of these should be equal to 2942.At the same time, the total number of lines is 100. So the sum of all k_i (for parallel sets) and m_j (for concurrent sets) plus the number of lines that are neither parallel nor concurrent (i.e., general position lines) should equal 100.Wait, but actually, if we group some lines into parallel sets and others into concurrent sets, but lines can only belong to one set (either parallel or concurrent), right? Because a line can't be both parallel to another line and concurrent with others at the same time, unless perhaps the concurrency point is on the parallel line, but that would complicate things.Hmm, this might be more complicated. Maybe it's better to model this as arranging some sets of parallel lines and some sets of concurrent lines, and the remaining lines are in general position (neither parallel nor concurrent with others beyond the normal intersections). Each parallel set of k lines reduces the total intersections by C(k, 2), and each concurrent set of m lines reduces by C(m, 2) - 1.Therefore, total reduction R = sum_{parallel sets} C(k_i, 2) + sum_{concurrent sets} (C(m_j, 2) - 1) = 2942.We need to find integers k_i, m_j >= 2 (since a single line can't form a parallel set or a concurrent set by itself) such that the sum of all k_i and m_j is <= 100 (since each line can be in at most one set). The remaining lines are in general position, contributing their maximum intersections.Wait, but actually, if we have some lines in general position, they can intersect each other and also intersect the other lines (the ones in parallel or concurrent sets). So perhaps the total number of intersections is:Total intersections = C(100, 2) - [sum C(k_i, 2) + sum (C(m_j, 2) - 1)].Which is the same as 4950 - R = 2008, so R = 2942.But how exactly does the presence of general position lines affect this? Actually, if some lines are in general position, they are not part of any parallel or concurrent set, so their intersections are all accounted for in the maximum. So the formula still holds. The total intersections are just the maximum minus the reductions from parallel and concurrent sets.Therefore, we need to find a combination of parallel and concurrent sets such that the total reduction R is 2942. Each parallel set of size k reduces by C(k, 2), each concurrent set of size m reduces by C(m, 2) - 1.So the problem reduces to solving the equation:sum_{parallel sets} [k_i(k_i - 1)/2] + sum_{concurrent sets} [m_j(m_j - 1)/2 - 1] = 2942with the constraint that the total number of lines in these sets is sum k_i + sum m_j <= 100.Additionally, since all lines must be distinct, we can't have overlapping sets, so each line is in at most one parallel set or one concurrent set.This seems like an integer partition problem where we need to partition some number of lines into parallel and concurrent sets such that the total reduction is 2942. The remaining lines (if any) are in general position.Now, the challenge is whether such a partition is possible.Let me think about possible strategies.First, note that concurrent sets give a slightly different reduction. For a concurrent set of m lines, the reduction is C(m, 2) - 1. So, compared to a parallel set of m lines, which would reduce by C(m, 2). Therefore, a concurrent set is slightly less efficient in reducing the total number of intersections. So if we can use parallel sets instead of concurrent sets, we get more reduction per line.But perhaps we need a combination of both.Alternatively, maybe using only parallel lines is sufficient? Let's check.If we use only parallel sets, then total reduction R = sum [k_i(k_i - 1)/2] = 2942. We need to find integers k_i >=2 such that sum k_i <=100, and sum [k_i(k_i - 1)/2] =2942.Is this possible?Alternatively, maybe we can have one big concurrent set. Let's see. Suppose we have one concurrent set with m lines. The reduction from that set is (m(m-1)/2) -1. Then, if we have other parallel sets.But perhaps it's complicated. Let me first check whether 2942 can be achieved with only parallel sets.Suppose all the reduction comes from parallel lines. Then sum [k_i(k_i -1)/2] =2942, and sum k_i <=100.We need to find a set of integers k_i >=2 such that their combination gives the required sum.Alternatively, to maximize the reduction per line, it's better to have larger sets. Because for a set of size k, the reduction per line is (k-1)/2. So larger k gives more reduction per line.So, perhaps using as large a parallel set as possible. Let me see.Suppose we use one parallel set of size k. Then, the reduction is k(k-1)/2. Let's see what k would need to be to get close to 2942.Solving k(k-1)/2 ≈2942.Multiply both sides by 2: k^2 -k ≈5884.So k^2 ≈5884 +k. Approximately, k ≈sqrt(5884)≈76.7. So testing k=77: 77*76/2=77*38=2926. That's 2926. Close, but still 2942-2926=16 short. Then, maybe we can have another parallel set of 6 lines: 6*5/2=15. Then total reduction would be 2926+15=2941. Still 1 short. Then another parallel set of 2 lines: 2*1/2=1. Then total reduction is 2941+1=2942.So total lines used:77+6+2=85. Then remaining lines are 100-85=15 lines in general position. So that works? Wait, but let me check:Total reduction:77*76/2 +6*5/2 +2*1/2=2926 +15 +1=2942. Yes. So that works.So in this case, we can have one set of 77 parallel lines, one set of 6 parallel lines, one set of 2 parallel lines, and 15 lines in general position. Each of these parallel sets don't interfere with each other (assuming they are all in different directions), and the 15 general lines are not parallel to any others and not concurrent.Thus, this configuration would result in 2008 intersection points.Wait, but does that hold? Let me verify:Total intersections would be C(100,2) -2942=4950 -2942=2008. Yes.But we need to make sure that the remaining 15 lines in general position don't create any additional overlaps or concurrent points. So, as long as those 15 lines are not parallel to any of the existing parallel sets, and none of them are concurrent (i.e., no three meet at a single point), and each intersects all the other lines not in their own parallel set. Since the 15 lines are in general position with respect to each other and to the other lines, this should be okay.Therefore, this seems possible.Wait, but let me think again. If we have 77 parallel lines, all horizontal, say. Then 6 parallel lines in another direction, say vertical. Then 2 parallel lines in another direction, say diagonal. Then the 15 general lines are in various other directions, none parallel to each other or to the existing sets. Each of the 15 lines will intersect all lines except those in their own parallel set. However, since each of the 15 lines is in a unique direction, they will intersect all other lines, including the other general lines, at unique points. Therefore, the total number of intersections would indeed be 4950 -2942=2008.Hence, this configuration works. Therefore, the answer is yes, such 100 lines exist.But wait, the problem says "100 distinct lines having exactly 2008 distinct intersection points". So as long as all intersections are distinct except for those reduced by the parallel/concurrent sets. In this case, the only overlaps would be from the concurrent sets, but in the configuration I considered, we didn't use any concurrent sets. We only used parallel sets. Therefore, all intersections would be between non-parallel lines. Since the 15 general lines are in general position (no two parallel, no three concurrent), and they are not parallel to any of the other sets. The other sets (77,6,2) are each in different directions, so the only overlaps are avoided by the parallel sets, but all intersections between different sets are still unique. Therefore, all intersection points are unique. Wait, but actually, the 15 general lines may intersect each other and the other lines. Since they are in general position, their intersections with each other are all unique. Their intersections with the parallel sets: each general line will intersect each line in a parallel set exactly once, but since all lines in a parallel set are parallel, each general line will intersect all of them at different points? Wait, no. If a general line is not parallel to a parallel set, it will intersect each line in the set at a unique point, because the lines in the parallel set are all distinct but parallel. Therefore, a single general line intersecting 77 parallel lines will have 77 distinct intersection points, each on that general line. Similarly for the other parallel sets.But then, the intersections between the general lines and the parallel sets are all distinct points. And intersections between different general lines are all distinct. So in total, there are no overlapping intersection points, except those that would have been from the original maximum. But since we removed all intersections within the parallel sets, but all other intersections remain. Therefore, the total number is correct.Therefore, this configuration should work.Alternatively, maybe using concurrent lines could also achieve the desired reduction, but since we can already achieve the required reduction with only parallel lines, then the answer is yes.But let me check another way. Suppose we try to use a combination of parallel and concurrent sets. Let's see.Suppose we have a concurrent set of m lines. The reduction is C(m,2)-1. So for m=3, reduction is 3-1=2. For m=4, reduction is 6-1=5. For m=5, 10-1=9, etc. So each concurrent set gives a bit less reduction than a parallel set of the same size.For instance, a concurrent set of 10 lines would reduce by 45-1=44, whereas a parallel set of 10 lines would reduce by 45. So, it's slightly less efficient.Therefore, using parallel sets is more efficient. So to achieve the maximum reduction with minimal lines, parallel sets are better. But if we need a specific number, maybe a combination is needed.But in our case, we could achieve the reduction with only parallel sets, so there's no need for concurrent sets.Therefore, the answer should be yes, such lines exist.Wait, but let me just check the arithmetic again.Total lines used in parallel sets:77+6+2=85. Remaining lines:15.Sum of reductions:77*76/2=2926, 6*5/2=15, 2*1/2=1. Total reduction:2926+15+1=2942. 4950-2942=2008. Correct.Now, let's verify that the remaining 15 lines in general position don't introduce any unexpected overlaps. The 15 lines are in general position, meaning no two are parallel, and no three meet at a single point. Therefore, they contribute C(15,2)=105 intersections among themselves. Each of these 15 lines also intersects all 85 lines in the parallel sets. Since the 15 lines are not parallel to any of the parallel sets, each line will intersect each line in the parallel sets once. So each of the 15 lines intersects 85 lines, contributing 15*85=1275 intersections. However, these intersections are spread across the plane. Since the parallel sets are each in different directions, and the 15 lines are in general position, none of these intersections coincide. Each intersection between a general line and a parallel set line is unique because the general line is not parallel to the parallel set, so each intersection is at a distinct point. Similarly, intersections between different general lines are all unique. Therefore, total intersections are:Intersections among the 15 general lines:105Intersections between general lines and parallel sets:15*85=1275Intersections between different parallel sets: Since the parallel sets are in different directions, each line in one parallel set intersects all lines in another parallel set. So for the three parallel sets of size 77,6,2, the intersections between different parallel sets are 77*6 +77*2 +6*2=462 +154 +12=628.Total intersections:105 +1275 +628=2008. Exactly the number needed. Therefore, this works.So, this configuration of 100 lines (77+6+2+15) gives exactly 2008 intersections. Therefore, the answer is yes.Therefore, I think the answer is yes, it's possible.Final Answerboxed{2008}Wait, the problem asks "Determine whether there exist... having exactly 2008 distinct intersection points." So the answer should be a yes/no answer. But the user instruction says to put the final answer within boxed{}. In many math competition problems, even if the answer is yes/no, they might expect the answer as the number, but here the problem says "Determine whether...", so maybe the answer is "Yes" or "No". But the user instruction here says "put your final answer within boxed{}", and in the example on the problem statement, it's a number. Wait, looking back at the original problem statement:"Determine whether there exist, in the plane, 100 distinct lines having exactly 2008 distinct intersection points."So the answer is either possible or not, so "Yes" or "No". However, the user might expect the answer in the box. In Chinese math competitions, sometimes they write boxed{} for the answer, even if it's Yes/No. But in Western contexts, often they write boxed{Yes} or boxed{No}. But in the problem statement here, the user might have expected just the number, but the actual question is a yes/no question. Since the original problem says "put your final answer within boxed{}", perhaps following the Chinese convention where the answer is the number of intersection points, but here the question is about existence. Wait, no, in the problem statement, they are not asking for the number of intersection points, which is given as 2008, but whether such a configuration exists. So the correct answer should be boxed{Yes} or boxed{No}. But the user's initial problem statement says "put your final answer within boxed{}", so maybe they expect the number 2008 in the box? But that's the given number. Wait, no. Wait, the user instruction says "You will be given a problem. Please reason step by step, and put your final answer within boxed{}". The problem is to determine whether such lines exist. So the answer is Yes or No, boxed. But in the example, maybe they use numbers. Wait, I need to check the original problem statement again.Original problem: "Determine whether there exist, in the plane, 100 distinct lines having exactly 2008 distinct intersection points."In many Olympiad problems, the answer would be stated as boxed{2008} if it's possible, but since this is a yes/no question, in some conventions, they might write boxed{Yes} or boxed{No}. However, the user's instruction says "put your final answer within boxed{}". Considering that, maybe the answer is boxed{2008} as confirmation, but that seems odd. Alternatively, since the question is to determine existence, the answer should be boxed{Yes}. But in the Chinese context, sometimes problems like this expect the number, but given the translation here, it's better to follow the Western convention. However, the assistant's initial answer was 2008 in a box, but that's incorrect. Wait, in the problem statement, the user says "put your final answer within boxed{}". If the answer is yes, then it's boxed{Yes}. If no, then boxed{No}. However, in the initial problem statement, if it's a numerical answer, you put the number. But here, since it's a yes/no question, I think boxed{Yes} is correct. But to check, let me see: if the answer were no, you would write boxed{No}. Since in my reasoning, the answer is yes, so boxed{Yes}. However, sometimes in math problems, even if it's a yes/no question, they might expect a numerical answer. Wait, no. The problem is to determine existence, so the answer is yes or no. Hence, the correct answer is boxed{Yes}.But looking back at the user's message, they say "put your final answer within boxed{}". Given that, and the original problem is from a math competition where answers are boxed, but this is a yes/no question. However, in Chinese math competitions, sometimes answers are given as numbers or specific terms in boxes. Since the problem is asking whether such lines exist, the answer is simply "Yes" or "No", so boxed accordingly. Therefore, the correct answer here is boxed{Yes}.Final Answerboxed{Yes}</think>To determine whether there exist 100 distinct lines in the plane having exactly 2008 distinct intersection points, we start by noting that the maximum number of intersection points for 100 lines is given by ( binom{100}{2} = 4950 ). We need to reduce this number by ( 4950 - 2008 = 2942 ) intersections.Reductions can be achieved by grouping lines into parallel sets or concurrent sets. Each parallel set of ( k ) lines reduces the number of intersections by ( binom{k}{2} ), and each concurrent set of ( m ) lines reduces the number by ( binom{m}{2} - 1 ).We consider using parallel sets for maximum reduction efficiency. We need to find integers ( k_i ) such that the sum of ( binom{k_i}{2} ) equals 2942. Testing large sets, we find:- A parallel set of 77 lines reduces intersections by ( binom{77}{2} = 2926 ).- A parallel set of 6 lines reduces intersections by ( binom{6}{2} = 15 ).- A parallel set of 2 lines reduces intersections by ( binom{2}{2} = 1 ).Summing these reductions gives ( 2926 + 15 + 1 = 2942 ), which is the required reduction. The total number of lines used in these parallel sets is ( 77 + 6 + 2 = 85 ), leaving 15 lines in general position.The remaining 15 lines in general position will intersect each other and the parallel sets without creating any concurrent points or overlapping intersections. The total intersections are calculated as follows:- Intersections among the 15 general lines: ( binom{15}{2} = 105 )- Intersections between general lines and parallel sets: ( 15 times 85 = 1275 )- Intersections between different parallel sets: ( 77 times 6 + 77 times 2 + 6 times 2 = 462 + 154 + 12 = 628 )Summing these intersections gives ( 105 + 1275 + 628 = 2008 ), confirming the configuration works. Therefore, the answer is:[boxed{Yes}]]

🔑:We know that 2008=24 cdot 72 + 99 - 4 + 99 - 6 + 99 - 7. Consider the 99 lines y=1, y=2, ldots, y=24 and x=1, x=2, ldots, x=72. They intersect at 72 cdot 24 = 1728 points. The line y=x+20 intersects the previous lines, but the points (1,21),(1,22),(1,23) and (1,24) have already been counted in the product 72 cdot 24. This line thus adds 99-4 intersection points. Similarly, the lines y=x+17 and y=x+16 add 99-6 and 99-7 new intersection points, respectively. Therefore, we have indeed constructed 100 lines with 2008 intersection points.

🧠:[<think>Okay, so I have this problem where I need to calculate the sum of f(1) + f(2) + ... + f(100), where f(n) is the product of all non-zero digits of n. Let me start by understanding what exactly f(n) does. For example, f(29) is 2*9=18, and f(207) is 2*7=14 because we ignore the zero. So, if there's a zero in the digits, we just skip it and multiply the non-zero digits. If it's a single-digit number, then f(n) is just the number itself. Got it.First, maybe I can break this problem down by considering numbers from 1 to 9, then 10 to 99, and finally 100. Because numbers from 1 to 9 are single-digit, so their f(n) is just themselves. From 10 to 99, they are two-digit numbers, and 100 is a three-digit number. Let me verify:- For 1 to 9: f(n) = n. So sum is 1+2+3+4+5+6+7+8+9 = 45. That part is straightforward.- For 10 to 99: Each number is two digits. Let me denote a two-digit number as AB, where A is the tens digit and B is the units digit. Then f(AB) is A*B if both A and B are non-zero. If either A or B is zero, then we only take the non-zero digit. Wait, no, the problem says "the product of all non-zero digits". So if the number is 10, which is A=1, B=0, then f(10) = 1*0? Wait, but wait, non-zero digits. So if a digit is zero, we skip it. So f(10) is 1 because we ignore the zero. Similarly, f(20) is 2, f(30) is 3, etc. Similarly, for numbers like 01, but since we are talking about 10 to 99, the tens digit is non-zero, but the units digit can be zero. So in such cases, if the units digit is zero, f(n) is just the tens digit. If both digits are non-zero, f(n) is the product of the two digits. For example, f(29)=2*9=18, f(11)=1*1=1, f(10)=1, f(99)=9*9=81.Therefore, to calculate the sum from 10 to 99, I need to consider two cases:1. Numbers where the units digit is zero. These are numbers like 10,20,...,90. There are 9 such numbers. For each of these, f(n) is equal to the tens digit. So the sum here is 1 + 2 + 3 + ... + 9 = 45.2. Numbers where the units digit is non-zero. These are numbers from 11 to 19, 21 to 29, ..., 91 to 99. There are 9 sets (for each tens digit 1-9) and each set has 9 numbers (units digits 1-9). For each of these numbers, f(n) is the product of the tens digit and the units digit. So for each tens digit A (from 1 to 9), the sum over all units digits B (from 1 to 9) is A*(1+2+3+...+9) = A*45. Therefore, the total sum for all these numbers is (1+2+...+9)*45 = 45*45 = 2025.Wait, let me verify that. Let's take a specific example. For tens digit 1, numbers 11 to 19: their f(n) is 1*1, 1*2, ..., 1*9. So sum is 1*(1+2+...+9) = 1*45. Similarly, for tens digit 2, sum is 2*45, and so on up to 9*45. Therefore, the total sum is 45*(1+2+...+9) = 45*45 = 2025. Yes, that seems right.So summing the two cases for 10 to 99: 45 (for units digit zero) + 2025 (for units digit non-zero) = 2070.Then finally, the number 100. f(100) is the product of non-zero digits: 1*1 = 1, because the digits are 1, 0, 0. So we ignore the zeros and multiply the 1s. Wait, is that correct? The number 100 has digits 1, 0, 0. So non-zero digits are just 1. Therefore, the product is 1. So f(100) = 1.Therefore, total sum from 1 to 100 is sum from 1-9 (45) + sum from 10-99 (2070) + f(100) (1) = 45 + 2070 + 1 = 2116.Wait, but let me check again. Because maybe there is a mistake here. For instance, when calculating the units digit non-zero case, are all the numbers correctly considered? Let's see. For numbers from 11 to 19, which are 11,12,...,19: that's 9 numbers. Similarly for each tens digit. There are 9 tens digits (1-9), each with 9 units digits (1-9), so 9*9=81 numbers. Each of these contributes A*B. Then the sum is (sum of A from 1-9) * (sum of B from 1-9) = 45*45 = 2025. That's correct. Because the total sum over all A and B is the product of the sums. So yes, that's right.Then the numbers where units digit is zero: 10,20,...,90. Each of these contributes A*1 (since B=0 is ignored, so it's just A). So sum is 1+2+...+9=45. So adding that gives 45+2025=2070. Then adding 1-9 (45) and 100 (1), total is 45 + 2070 + 1 = 2116. Hmm.But let me check with a smaller range to see if this approach is correct. Let's say from 1 to 10.1:1, 2:2,...,9:9, 10:1. Sum is 45+1=46. According to the formula: sum 1-9=45, sum 10-10:1, total 46. Which is correct. Another test case: numbers from 1 to 20.Sum from 1-9:45. Sum from 10-19: For numbers 10-19, 10 has f=1, 11=1*1=1, 12=1*2=2,...,19=1*9=9. So sum here is 1 + (1+2+...+9) = 1 + 45 = 46. Then number 20: f=2. So total sum from 10-20:46 + 2 = 48. Then total sum from 1-20:45 + 48 = 93. Let's compute manually:1:1, 2:2, ...,9:9 (sum=45)10:1, 11:1, 12:2, 13:3, 14:4, 15:5, 16:6, 17:7, 18:8, 19:9 (sum=1+1+2+3+4+5+6+7+8+9=1+45=46)20:2 (sum=2)Total:45+46+2=93. Correct. So the method works here.Therefore, going back, the method seems valid. So applying this to 1-100, the sum should be 45 + 2070 + 1 = 2116. Wait, but I just thought of something. Wait, 100 is included, which is three digits, but we have to confirm f(100). As per the problem statement, f(207)=14 because 2*7=14. So similarly, f(100) would be 1*1 (since there are two zeros). So 1*1=1, yes.Therefore, the total is 45 + 2070 +1 = 2116.But let me check another source or think differently. Maybe there's a different way to compute the sum from 10 to 99.Alternatively, for each two-digit number from 10 to 99, f(n) is equal to the product of its digits, ignoring zeros. But since numbers from 10 to 99 have either both digits non-zero or one digit zero. So split into two parts:1. Numbers with no zero digits: 11 to 99 where both digits are non-zero. There are 9 options for the tens digit (1-9) and 9 options for the units digit (1-9), so 81 numbers. The sum here is sum_{A=1}^9 sum_{B=1}^9 A*B = (sum A)(sum B) = 45*45=2025. This is the same as before.2. Numbers with one zero digit: 10,20,...,90 (9 numbers) and 101? Wait, no. From 10 to 99, numbers with a zero digit are those where either the tens or units digit is zero. But in two-digit numbers, the tens digit cannot be zero, so only the units digit can be zero. Therefore, numbers like 10,20,...,90. 9 numbers. Each contributes the non-zero digit (the tens digit). So sum is 1+2+...+9=45.So yes, same as before. So 2025 +45=2070.Adding 1-9 (45) and 100 (1), total 2116. Therefore, I think the answer is 2116.But wait, maybe there's an error in considering numbers like 01, but in the range 1 to 100, numbers are from 1 to 100, so 01 is not considered. All numbers are either one-digit, two-digit, or three-digit (100). So the previous calculation should be correct.Wait, but let's check a few numbers manually to see if our formula works. For example, take number 10: f(10)=1, correct. Number 25:2*5=10. Sum up all these. Let's check a small range where manual calculation is feasible.Take numbers from 1 to 10:1:1, 2:2, ...,9:9,10:1. Sum is 45 +1=46. Correct.Numbers from 11 to 20:11:1,12:2,13:3,14:4,15:5,16:6,17:7,18:8,19:9,20:2. Sum is (1+2+3+4+5+6+7+8+9) +2=45 +2=47. Total sum from 1-20 is 46 +47=93, as before. Correct.So let's check 21-30:21:2*1=2, 22:2*2=4, 23:2*3=6, ...,29:2*9=18, 30:3. So sum is (2+4+6+8+10+12+14+16+18) +3. The sum inside the parentheses is an arithmetic series starting at 2, ending at 18, with common difference 2. Number of terms: (18-2)/2 +1=9 terms. Sum is (2 + 18)*9/2 =20*9/2=90. Then +3=93. So sum from 21-30 is 93. Then sum from 1-30 would be previous 93 (1-20) + sum 21-30 (93) =186? Wait, but wait, 1-20 sum is 93, 21-30 is 93. Wait, 21-30 is 10 numbers. Wait, the sum from 21-30 is 93? Let's compute manually:21:2, 22:4,23:6,24:8,25:10,26:12,27:14,28:16,29:18,30:3. Sum these:2+4=6; 6+6=12; 12+8=20; 20+10=30; 30+12=42; 42+14=56; 56+16=72; 72+18=90; 90+3=93. Yes, correct. So sum from 21-30 is 93. So sum from 1-30 is 93 +93=186. Wait, but 1-10 was 46, 11-20 was 47, 21-30 is 93. Wait, 46+47=93, then 93+93=186. Hmm, but 1-10:46, 11-20:47, 21-30:93. That totals 46+47+93=186. Hmm, seems inconsistent. Wait, 1-10 is 10 numbers, sum 46. 11-20 is 10 numbers, sum 47. 21-30 is 10 numbers, sum 93. So 46+47+93=186. If we apply our formula to 1-30:Sum 1-9:45Sum 10-30: Numbers 10-30. Let's split into 10-29 and 30.First, 10-29:Numbers with units digit zero: 10,20. Sum is 1 +2=3.Numbers with units digit non-zero: For tens digits 1 and 2.For tens digit 1: units digits 1-9, sum is 1*(1+2+...+9)=45.For tens digit 2: units digits 1-9, sum is 2*(1+2+...+9)=90.So total non-zero units digits sum:45 +90=135.Adding the zero units digits sum:3. Total sum from 10-29:135 +3=138.Then number 30: f(30)=3.Total sum from 10-30:138 +3=141.Adding sum from 1-9:45. Total 45 +141=186. Which matches the manual calculation. So our formula works here.But when we split it into 10-99 as a whole, the approach was to split into two parts: units digit zero and non-zero, leading to 45 +2025=2070. Then adding 1-9 and 100 gives 45 +2070 +1=2116.But wait, in the 1-30 example, when we applied the same method, for numbers 10-29:Sum of numbers with units digit zero:10,20. Sum=1+2=3.Sum of numbers with units digit non-zero: For tens digits 1 and 2, each multiplied by 1-9. So 45 +90=135. Then total 3 +135=138. Then adding 30:3. So total 141. Which is correct.So similarly, for 10-99, units digit zero: numbers 10,20,...,90. Sum=1+2+...+9=45.Units digit non-zero: For each tens digit 1-9, sum is A*45. So total sum for non-zero units digits:45*9=405? Wait, no. Wait, for each tens digit, sum is A*(1+2+...+9)=A*45. Therefore, sum over all tens digits (1-9) is (1+2+...+9)*45=45*45=2025. So total sum from 10-99 is 45 (zero units digits) +2025=2070.Yes, that's correct. So in the 1-30 example, from 10-29, sum of units digit non-zero is (1+2)*45=3*45=135, and units digit zero is 1+2=3. So 135 +3=138, which is correct.Therefore, the formula scales. So going back to 1-100:Sum from 1-9:45Sum from 10-99:2070Sum from 100:1Total:45 +2070 +1=2116.Therefore, the answer should be 2116. However, to be thorough, let me check another range. Let's check 1-40.Using the formula:Sum 1-9:45Sum 10-40:Units digit zero:10,20,30,40. Sum=1+2+3+4=10.Units digit non-zero: For tens digits 1,2,3,4. Each contributes A*45. So sum=(1+2+3+4)*45=10*45=450.Total sum from 10-40:10 +450=460.Adding 1-9:45, total sum 1-40:45 +460=505.Manual check:Sum from 1-40.1-9:4510-19:1 + (1+2+...+9)=1+45=4620-29:2 + (2*1 +2*2 +...+2*9)=2 +2*45=2+90=9230-39:3 +3*45=3+135=13840:4Total sum from 10-40:46 +92 +138 +4=46+92=138; 138+138=276; 276+4=280.Sum from 1-40:45 +280=325. Wait, this contradicts the formula result of 505. Wait, something is wrong here. There's a mistake in my manual calculation or in the formula.Wait, let's compute manually:Numbers from 1-40:1:1, 2:2,...,9:9 (sum=45)10:111:1*1=1,12:1*2=2,...,19:1*9=9. Sum from 11-19:1+2+...+9=45. So sum 10-19:1 +45=4620:221:2*1=2,22:2*2=4,...,29:2*9=18. Sum from 21-29:2+4+6+...+18. This is an arithmetic series with first term 2, last term 18, common difference 2. Number of terms: (18-2)/2 +1=9 terms. Sum=(2 +18)*9/2=20*9/2=90. So sum from 20-29:2 +90=9230:331:3*1=3,32:3*2=6,...,39:3*9=27. Sum from31-39:3+6+...+27. This is arithmetic series with first term 3, last term 27, difference 3. Number of terms: (27-3)/3 +1=9 terms. Sum=(3 +27)*9/2=30*9/2=135. So sum from30-39:3 +135=13840:4So sum from 10-40:46 (10-19) +92 (20-29) +138 (30-39) +4 (40) =46+92=138; 138+138=276; 276+4=280. Then total sum from1-40:45+280=325.But according to the formula:Sum from1-9:45Sum from10-40:Units digit zero:10,20,30,40. Sum=1+2+3+4=10.Units digit non-zero: For tens digits 1,2,3,4. Each contributes A*45. So sum=(1+2+3+4)*45=10*45=450.Total sum from10-40:10+450=460. Then total sum 45 +460=505. Which conflicts with manual sum 325.Wait, this shows a problem. There's a mistake in the formula.Wait, what's happening here? The formula is overcounting. Let's see.Wait, when we split numbers from10-40 into units digit zero and non-zero:Units digit zero:10,20,30,40. That's 4 numbers. Sum=1+2+3+4=10.Units digit non-zero: for each tens digit 1,2,3,4, numbers where units digit is 1-9. So for tens digit1:11-19 (9 numbers), sum=1*45=45.For tens digit2:21-29 (9 numbers), sum=2*45=90.For tens digit3:31-39 (9 numbers), sum=3*45=135.For tens digit4:41-49. Wait, but in the range 10-40, tens digit4 would be 41-49, but 41-49 are outside 10-40. Wait, this is the mistake! The formula assumes that for each tens digit, all units digits 1-9 are included, but in the range 10-40, the tens digits are1,2,3,4, but for tens digit4, the units digits can only be0-0 (since 40 is the upper limit). Therefore, in the range10-40, the numbers with tens digit4 are only40. Which is already counted in the units digit zero part.Therefore, my formula is incorrect because when the upper limit is not 99, the formula overcounts. But in the original problem, the upper limit is100, so numbers up to100. Therefore, from10-99, each tens digit1-9 can have units digits0-9, but when the upper limit is100, the number100 is separate.Therefore, in the original problem, numbers from10-99 are all two-digit numbers with tens digits1-9 and units digits0-9, so the formula is correct. But in the test case of10-40, since the upper limit is40, which is not a full tens digit (like49), the formula overcounts. But in the problem statement, the range is up to100, which is a three-digit number, and numbers from10-99 are full two-digit numbers. Therefore, the formula is correct in the original problem.Therefore, in the test case1-40, the formula is incorrect because the upper limit cuts off the units digits for tens digit4. However, in the original problem, since we go up to99, each tens digit1-9 has units digits0-9. Hence, the formula works.Therefore, my original calculation is correct for the problem at hand. The test case1-40 is not applicable here because the upper limit in the problem is100, allowing all two-digit numbers from10-99 to be complete.Therefore, the answer is45 +2070 +1=2116.But let me check with another approach. Let's consider all numbers from1 to99.For each position (tens and units), we can think of the contribution of each digit. However, since f(n) is a product, it's multiplicative, so maybe we can use the distributive property.But the sum over all numbers from1 to99 of the product of their non-zero digits. Hmm. The problem is that the product is not linear, so it's not straightforward to separate the sums. But for numbers with two digits, it's the product of the two digits (ignoring zeros). For numbers with one digit, it's the digit itself.Alternatively, we can split the numbers into one-digit and two-digit numbers. As we did before.Sum over one-digit numbers (1-9):45.Sum over two-digit numbers (10-99):As before, split into numbers where the units digit is zero or non-zero. Units digit zero: sum of tens digits. Units digit non-zero: sum over A*B for A=1-9, B=1-9.Therefore, sum from10-99 is45 +2025=2070.Add 100's f(n)=1.Total:45+2070+1=2116.Yes, that seems consistent.Alternatively, maybe write a small program or use an Excel sheet to compute the sum, but since I can't do that here, I need to rely on reasoning.Another way to verify the two-digit numbers sum: the sum over all two-digit numbers (10-99) of the product of their non-zero digits. For each tens digit A (1-9) and units digit B (0-9):If B=0: contribution is A.If B≠0: contribution is A*B.Therefore, for each A from1-9:Sum over B=0-9: if B=0, then A; else A*B.So for each A:Sum = A + A*(1+2+...+9) = A + A*45 = A*(1 +45)=A*46.Therefore, total sum over all two-digit numbers would be sum_{A=1}^9 A*46 =46*sum_{A=1}^9 A=46*45=2070.Wait, hold on. Wait, this is different from what I had before. Wait, according to this calculation, the total sum from10-99 is2070. Which matches the previous result. Wait, but according to this approach, for each tens digit A, the sum over all units digits B is A*46. Therefore, sum over A=1-9:46*(1+2+...+9)=46*45=2070. Which is the same as before.But wait, hold on. Wait, if for each tens digit A, the sum is A + A*(1+2+...+9). Let's break it down:For each A (1-9):- When B=0: contribution is A.- When B=1-9: contribution is A*B. So sum over B=1-9 is A*(1+2+...+9)=A*45.Therefore, total for each A: A + A*45 =A*46.Therefore, sum over all A:46*(1+2+...+9)=46*45=2070.But earlier, we split into units digit zero (sum=45) and non-zero (sum=2025). 45 +2025=2070. So both methods agree. Therefore, correct.Therefore, the total sum is45 (1-9) +2070 (10-99) +1 (100)=2116.Therefore, the answer is2116.Final Answerboxed{2116}</think>To calculate the sum ( f(1) + f(2) + ldots + f(99) + f(100) ), where ( f(n) ) is the product of all non-zero digits of ( n ):1. Sum from 1 to 9: These are single-digit numbers, so ( f(n) = n ). The sum is: [ 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 = 45 ]2. Sum from 10 to 99: - Numbers with units digit zero (10, 20, ..., 90): Each contributes the tens digit. The sum is: [ 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 = 45 ] - Numbers with non-zero units digits (11-19, 21-29, ..., 91-99): For each tens digit ( A ) (1 to 9), the sum of products with units digits 1 to 9 is ( A times (1 + 2 + ldots + 9) = A times 45 ). The total sum is: [ (1 + 2 + ldots + 9) times 45 = 45 times 45 = 2025 ] - Adding these parts together: [ 45 + 2025 = 2070 ]3. Sum for 100: The non-zero digits are 1 and 1 (ignoring the zeros), so ( f(100) = 1 times 1 = 1 ).4. Total sum: [ 45 text{ (1-9)} + 2070 text{ (10-99)} + 1 text{ (100)} = 45 + 2070 + 1 = 2116 ]Thus, the final answer is (boxed{2116}).,<think>Okay, so I need to calculate the sum of f(1) + f(2) + ... + f(100), where f(n) is the product of all non-zero digits of n. Let me start by understanding the problem properly. First, f(n) is defined as the product of non-zero digits. For example, f(207) is 2*7=14 because we ignore the zero. So, if a number has a zero in it, we just multiply the other digits. If all digits are zero except one, like in 5 or 10, then it's just that digit. Also, numbers like 100 would have f(100) = 1, since the non-zero digits are just the first 1. Alright, so the task is to sum this function from 1 to 100. Let me break this down into parts. Maybe I can handle the numbers from 1 to 99 first, and then add f(100) at the end. Since 100 is a special case with two zeros, f(100) = 1 as mentioned. Now, considering numbers from 1 to 99. These can be either one-digit numbers (1-9) or two-digit numbers (10-99). Let me handle them separately.Starting with one-digit numbers (1-9). For each of these numbers, since there's only one digit and it's non-zero, f(n) = n. So the sum from 1 to 9 is just 1+2+3+...+9. What's that sum? The formula for the sum of the first n integers is n(n+1)/2. Here, n=9, so 9*10/2 = 45. So the one-digit numbers contribute 45 to the total sum.Now, moving on to two-digit numbers from 10 to 99. Each of these numbers can be represented as "ab" where a is the tens digit (from 1 to 9) and b is the units digit (from 0 to 9). However, since we need to ignore zeros in the digits, for each two-digit number, f(ab) = a * b if b ≠ 0, and f(ab) = a if b = 0. Wait, no. If b is zero, then the non-zero digits are just 'a', so f(ab) = a. If b is non-zero, then f(ab) = a * b. Therefore, for each tens digit 'a' (from 1 to 9), and each units digit 'b' (from 0 to 9), f(ab) is a if b=0, and a*b otherwise.Therefore, for each 'a' (from 1 to 9), the sum over all 'b' (from 0 to 9) of f(ab) is equal to f(a0) + f(a1) + ... + f(a9). Which is a (when b=0) plus a*1 + a*2 + ... + a*9 (when b=1 to 9). So that's a + a*(1+2+...+9). Again, the sum 1+2+...+9 is 45. So the total for each 'a' is a + a*45 = a*(1 + 45) = a*46. Therefore, for each tens digit 'a', the total contribution is 46a. Therefore, to get the total sum for all two-digit numbers, we need to sum 46a for a from 1 to 9. So that's 46*(1 + 2 + ... + 9). We already know that 1+2+...+9 is 45. So 46*45 = 2070. Wait, let me check that again. For each 'a', the total is 46a, so sum over a=1 to 9 is 46*(1+2+...+9) = 46*45. 45*46: 40*45=1800, 6*45=270; 1800+270=2070. So yes, 2070.So the two-digit numbers contribute 2070. Then adding the one-digit numbers' contribution of 45, we have 2070 + 45 = 2115. Then we need to add f(100), which is 1. So total sum is 2115 + 1 = 2116.Wait, but hold on a second. Let me verify this with some examples to make sure.Take a simple case: numbers from 1 to 10.f(1)=1, f(2)=2,...f(9)=9, f(10)=1. So sum is 1+2+...+9 +1 =45 +1=46. Let's apply our formula here. For a=1 (tens digit), but numbers 10 is included. Wait, but in this case, numbers 1-9 are one-digit, and 10 is a two-digit. So using our previous breakdown:One-digit sum:45. Two-digit numbers: only 10. So f(10)=1. So total sum 45 +1=46, which matches. According to our formula for two-digit numbers, for a=1, the sum would be 46*1=46. But in reality, for a=1 (numbers 10-19), the sum is f(10)+f(11)+...+f(19). Let's compute that:f(10)=1, f(11)=1*1=1, f(12)=1*2=2,...,f(19)=1*9=9. So sum is 1 + (1+2+...+9)=1 +45=46. Which matches 46*1. So our formula works here.Another example: numbers from 20-29. For a=2:f(20)=2, f(21)=2*1=2, f(22)=2*2=4, ..., f(29)=2*9=18. Sum is 2 + (2+4+...+18). The sum inside the parentheses is 2*(1+2+...+9)=2*45=90. Then add the 2 from f(20): total 92. According to our formula, for a=2, it's 46*2=92. Correct. So that seems to check out.Therefore, our formula seems correct for two-digit numbers. Hence, the two-digit numbers contribute 2070, one-digit 45, and 100 contributes 1, so total 2116.But wait, let me check with another example. Let's take numbers from 1-3. Wait, maybe that's too small. Alternatively, check if the two-digit calculation is correct.Each two-digit number "ab" where a is 1-9 and b is 0-9. For each a, the sum over b is a + a*(1+2+...+9) = a + 45a =46a. Then sum over a=1-9: 46*(1+2+...+9)=46*45=2070. So yes, that seems correct.So then, total sum up to 99 is 45 + 2070 = 2115. Then add f(100)=1: total 2116.But wait, the problem is to calculate up to 100, inclusive. So 1-100. So that's correct. Therefore, the answer is 2116.But wait, let me just compute another small range manually to ensure.Let's compute sum from 1-20. Let's do it manually.Numbers 1-9: sum is 45.Numbers 10-19: as before, sum is 46.Number 20: f(20)=2.So total sum from 1-20:45 +46 +2=93.Using the formula: one-digit sum=45, two-digit from a=1:46, a=2:46*2=92. Wait, but a=2 would be numbers 20-29. Wait, in this case, if we take up to 20, then only 20. So maybe the formula is assuming all a from 1-9, but if we cut off at 20, that complicates. But in the original problem, we have all numbers from 1-99, so each a from 1-9 has all b from 0-9. So the formula is valid for 1-99. Then 100 is separate. So in the case of 1-20, it's not complete. But in the original problem, it's 1-99 complete, so the formula works.Therefore, trusting the formula, the answer is 2116. But to be thorough, let me check for numbers 1-100.Wait, perhaps I made a miscalculation in the arithmetic. Let me check:Sum from 1-9:45Sum from 10-99: For each a=1-9, sum is 46a. So total two-digit sum is 46*(1+2+...+9) =46*45=2070. Then total from 1-99:45+2070=2115. Then f(100)=1, so total sum 2116. That seems correct.Alternatively, maybe the two-digit numbers are from 10-99 inclusive. 99-10+1=90 numbers. For each of these 90 numbers, the sum is 2070. Let me check if 90 numbers can have such a sum. But if each a (from 1-9) has 10 numbers (b from 0-9), so 9*10=90 numbers. Each a contributes 46a. So sum over a=1-9 of 46a=46*(1+2+...+9)=46*45=2070. So yes. So 90 numbers contribute 2070. Then 1-9 contribute 45. 100 contributes 1. Total 2116.Therefore, I think that's the correct answer. But just to be 100% sure, let me compute a few numbers manually and check.For example, take the numbers from 10-19:10:1, 11:1, 12:2, 13:3, 14:4, 15:5, 16:6, 17:7, 18:8, 19:9. Sum is 1 + (1+2+3+4+5+6+7+8+9)=1+45=46. Which is 46*1=46. Correct.Numbers 90-99:90:9, 91:9*1=9, 92:9*2=18, ..., 99:9*9=81. Sum is 9 + (9+18+27+36+45+54+63+72+81). Let's compute that:First, 9 (for 90) then the rest:9 + 9 + 18 + 27 + 36 + 45 + 54 + 63 + 72 + 81. Wait, actually, wait. From 90-99:90:9, 91:9*1=9, 92:9*2=18, 93:9*3=27, 94:9*4=36, 95:9*5=45, 96:9*6=54, 97:9*7=63, 98:9*8=72, 99:9*9=81.So summing these:9 (from 90) + [9 +18+27+36+45+54+63+72+81]. The bracketed part is the sum from 91-99. Let's compute the bracketed part:9 +18=27, 27+27=54, 54+36=90, 90+45=135, 135+54=189, 189+63=252, 252+72=324, 324+81=405. Then add the initial 9: total 405 +9=414.According to the formula, for a=9, the sum should be 46*9=414. Correct. So that's a good check.Another check: numbers 50-59.50:5, 51:5*1=5, 52:5*2=10, ..., 59:5*9=45. Sum is 5 + (5+10+15+20+25+30+35+40+45). Compute the bracketed sum: 5+10=15, 15+15=30, 30+20=50, 50+25=75, 75+30=105, 105+35=140, 140+40=180, 180+45=225. Total sum:5 +225=230. According to the formula, a=5:46*5=230. Correct.Therefore, the formula holds. Therefore, the total sum is indeed 2116. Hence, the answer is boxed{2116}.Final Answerboxed{2116}</think>To calculate the sum ( f(1) + f(2) + ldots + f(99) + f(100) ), where ( f(n) ) is the product of all non-zero digits of ( n ), we break it down into three parts: one-digit numbers (1-9), two-digit numbers (10-99), and the number 100.1. One-digit numbers (1-9): - For each number ( n ), ( f(n) = n ). - The sum is ( 1 + 2 + 3 + ldots + 9 = frac{9 times 10}{2} = 45 ).2. Two-digit numbers (10-99): - Each two-digit number can be represented as ( overline{ab} ) where ( a ) is the tens digit (1-9) and ( b ) is the units digit (0-9). - For each ( a ), the sum of ( f(overline{ab}) ) for ( b ) from 0 to 9 is ( a + a(1 + 2 + ldots + 9) = a + 45a = 46a ). - Summing this for ( a ) from 1 to 9 gives ( 46 times (1 + 2 + ldots + 9) = 46 times 45 = 2070 ).3. Number 100: - ( f(100) = 1 ) (product of non-zero digits 1).Adding these parts together:- Sum of one-digit numbers: ( 45 )- Sum of two-digit numbers: ( 2070 )- Sum from 100: ( 1 )Total sum: ( 45 + 2070 + 1 = 2116 ).Thus, the final answer is (boxed{2116}).]

🔑:The sum f(1) + f(2) + f(3) + ldots + f(99) + f(100) can be calculated as follows:[begin{align*}&= (1+2+3+ldots+9) + 1 times (1+2+3+ldots+9) + 2 times (1+2+3+ldots+9) + 3 times (1+2+3+ldots+9) + ldots + 9 times (1+2+3+ldots+9) + (1+2+3+ldots+9+1) &= (1+2+3+ldots+9) times (1+1+2+3+ldots+9) + 46 &= 45 times 46 + 46 &= 2116.end{align*}]Therefore, the answer is boxed{2116}.