🧠:[<think>Okay, so I have this problem here about three cubes with integer edge lengths. Their surface areas add up to 564 cm², and I need to find the sum of their volumes. The options are given, so maybe I can figure it out by checking possible edge lengths. Let me think.First, I remember that the surface area of a cube is 6 times the edge length squared. Since there are three cubes, their total surface area would be 6(a² + b² + c²) where a, b, c are the edge lengths. The problem states that this total is 564 cm². So, I can set up the equation:6(a² + b² + c²) = 564If I divide both sides by 6, that simplifies to:a² + b² + c² = 564 / 6Calculating that, 564 divided by 6 is 94. So,a² + b² + c² = 94So, now I need to find three positive integers a, b, c such that their squares add up to 94. Then, once I have those, I can compute their volumes (a³ + b³ + c³) and see which option matches.The possible edge lengths must be integers, so let's list possible squares less than 94 to see what combinations we can have.The squares are:1² = 12² = 43² = 94² = 165² = 256² = 367² = 498² = 649² = 8110² = 100 (But 100 is more than 94, so we can stop at 9²)So the possible squares are 1, 4, 9, 16, 25, 36, 49, 64, 81.Now, we need three squares that add up to 94. Let's try different combinations.First, let's start with the largest possible square, which is 81. If one cube has edge length 9, then the remaining two cubes need to have squares adding up to 94 - 81 = 13. So, looking for two squares that add to 13. The squares less than 13 are 1, 4, 9. Let's check:9 + 4 = 13. So, edge lengths 3 and 2. Or 9 + 4 = 13. Alternatively, 4 + 9, same thing. Or 1 + 12, but 12 isn't a square. So, the possible combination here is 9² + 3² + 2² = 81 + 9 + 4 = 94. So edge lengths 9, 3, 2.Then their volumes would be 9³ + 3³ + 2³ = 729 + 27 + 8 = 764 cm³. That's one of the options, option B or A.Wait, let's check the options again. (A) 764 or 586, (B) 764, (C) 586 or 564, (D) 586. So 764 is in options A and B, and 586 is in A, C, D.But maybe there's another combination. Let's see if there are other triplets of squares that add up to 94.Next, let's try the next largest square: 64. So if one cube has edge length 8 (64), then the remaining two squares need to add up to 94 - 64 = 30.Looking for two squares that add up to 30. Let's check possible squares:25 + 5 = 30? 25 is 5², 5 isn't a square. 16 + 14 = 30, 14 isn't a square. 9 + 21 = 30, 21 isn't. 4 + 26 = 30, nope. 1 + 29 = 30, no. So 30 can't be expressed as a sum of two squares. Hmm. Maybe 25 + 5 isn't right. Wait, 25 is 5², but 5 isn't a square. Wait, perhaps 25 + 5²? Wait, 5² is 25, 25 + 25 = 50, which is more than 30. Hmm, maybe not. Let me think. The possible squares less than 30 are 1, 4, 9, 16, 25. So 25 + 5? Not a square. 16 + 14? 14 isn't a square. 9 + 21? 21 isn't. 4 + 26? Nope. 1 + 29? Nope. So, no combinations here. So 64 isn't part of a solution.Next, let's try 49 (edge length 7). Then the remaining two squares would need to add to 94 - 49 = 45.Looking for two squares adding up to 45. The squares less than 45: 36, 25, 16, 9, 4, 1.Check 36 + 9 = 45. So 36 (6²) and 9 (3²). So edge lengths 6 and 3. So the three edge lengths would be 7, 6, 3. Let's check: 49 + 36 + 9 = 94. Yes, that works.Then their volumes would be 7³ + 6³ + 3³ = 343 + 216 + 27 = 586 cm³. That's another possible answer, 586. So the volumes could be 764 or 586, which is option A.Wait, but the problem says "the sum of the volumes of these three cubes is ( )." So there could be two possible answers? But the options given are (A) 764 or 586, (B) 764, etc. So, if both 764 and 586 are possible, then the answer is A. But let me verify if there are more combinations.Wait, let's check if there are other combinations with 49. So 45 can be made by 25 + 20, but 20 isn't a square. 16 + 29, nope. 9 + 36, we already did that. 4 + 41, nope. So only 36 + 9.So that gives 7, 6, 3.Another way: if we take 25 (5²) as part of the remaining. Then 45 - 25 = 20, which isn't a square. So that doesn't work. So only 36 + 9.So that gives one more combination: 7, 6, 3, which gives 586.Now, let's check if there's another combination with a different largest square.Next, 36 (edge length 6). Then the remaining two squares need to add up to 94 - 36 = 58.Looking for two squares that add to 58. Let's see: 49 + 9 = 58. So 7² + 3² = 49 + 9 = 58. So edge lengths 7, 3, 6. Wait, that's the same as before: 7, 6, 3. Just ordered differently. So same volume sum, 586.Alternatively, 36 + 49 + 9 = 94, same as before.Another way: 25 + 33 = 58, but 33 isn't a square. 16 + 42 = 58, 42 isn't. 4 + 54 = 58, nope. So only 49 + 9.So, same combination.Next, let's try 25 (edge length 5). Then remaining squares add up to 94 - 25 = 69.Looking for two squares that add to 69. Let's check: 64 + 5 = 69, but 5 isn't a square. 49 + 20 = 69, 20 isn't. 36 + 33 = 69, 33 isn't. 25 + 44 = 69, nope. 16 + 53 = 69, nope. 9 + 60 = 69, nope. 4 + 65 = 69, nope. 1 + 68 = 69, nope. So no combination here.Next, 16 (edge length 4). Remaining squares add up to 94 - 16 = 78.Looking for two squares that add to 78. Let's check: 64 + 14 = 78, 14 isn't. 49 + 29 = 78, nope. 36 + 42 = 78, 42 isn't. 25 + 53 = 78, nope. 16 + 62 = 78, nope. 9 + 69 = 78, nope. 4 + 74 = 78, nope. 1 + 77 = 78, nope. So no combination here.Similarly, smaller edge lengths probably won't add up. Let's confirm.Edge length 3 (9). Then remaining squares: 94 - 9 = 85. Looking for two squares adding to 85. 81 + 4 = 85, so 9² + 2². So edge lengths 9, 2, 3. Wait, that's the same as the first combination: 9, 3, 2. Which gives volumes 764. So that's already accounted for.Edge length 2 (4). Then remaining squares: 94 - 4 = 90. Looking for two squares adding to 90. 81 + 9 = 90. So edge lengths 9, 3, 2. Again, same as before.Edge length 1 (1). Then remaining squares: 94 -1 = 93. Looking for two squares adding to 93. 81 +12 =93, 12 not a square. 64 +29=93, nope. 49 +44=93, nope. So no.Therefore, the possible combinations are:1. Edge lengths 9, 3, 2: volumes sum to 764.2. Edge lengths 7, 6, 3: volumes sum to 586.So there are two possible sums, which matches option A: 764 or 586.But let me check the problem statement again. It says "three cubes with integer edge lengths". It doesn't specify that they are distinct edge lengths. Wait, in the first combination, 9, 3, 2: all different. In the second combination, 7, 6, 3: all different. Are there any other combinations where edge lengths might repeat?Wait, let me check. For example, if two cubes have the same edge length.Suppose two cubes have edge length 5. Then their squares would be 25 each, so total from them is 50. Then the third cube's square would be 94 - 50 = 44, which is not a perfect square. So that doesn't work.Or two cubes of edge length 4: their squares are 16 each, total 32. Third cube square is 94 -32=62, not a square.Two cubes of edge length 6: their squares 36 each, total 72. Third cube's square is 94 -72=22, not a square.Two cubes of edge length 7: squares 49 each, total 98. But 98 is already more than 94, so that's no good.Two cubes of edge length 3: squares 9 each, total 18. Third cube square is 94 -18=76, not a square.Two cubes of edge length 2: squares 4 each, total 8. Third cube square 86, not a square.Two cubes of edge length 1: squares 1 each, total 2. Third cube square 92, not a square.So no combinations with two same edge lengths. Therefore, all edge lengths must be distinct.Hence, only the two combinations we found. Therefore, the sum of volumes can be either 764 or 586. Looking at the options, that's option A.But wait, the answer options are:(A) 764 or 586(B) 764(C) 586 or 564(D) 586So, the answer is A? But the problem says "the sum of the volumes of these three cubes is ( )." So is it possible that there are two different answers, so the correct option is A? But maybe I missed something.Wait, maybe there's another combination. Let me double-check.Wait, we tried all combinations starting from the largest square downwards, and only found 9,3,2 and 7,6,3. Let's see if there's another way to partition 94 into three squares.For example, is there a combination that includes 49, 25, and 20? But 20 isn't a square. How about 49, 16, and 29? 29 isn't a square. 36, 25, 33? 33 isn't a square. 36, 16, 42? 42 isn't. 25, 25, 44? 44 isn't. 16, 16, 62? 62 isn't.Alternatively, maybe using smaller squares. For example, 16 + 25 + 49 = 90, which is less than 94. Then 94 -90=4, so not. Wait, that approach might not work.Alternatively, 64 + 16 + 14. 14 isn't a square. 64 + 9 + 21. 21 isn't. 49 + 36 + 9 = 94, which we already have.Another way, 25 + 36 + 33. 33 isn't. 16 + 25 + 53. 53 isn't. 9 + 16 + 69. 69 isn't. 4 + 9 + 81. 4 + 9 +81= 94. Oh! Wait, 4 is 2², 9 is 3², and 81 is 9². Wait, that's the same as the first combination: 9, 3, 2. Because 81 + 9 + 4=94. So that's same as before.Is there another triplet? Let's see:Suppose 16 + 25 + 49=90. Then 94 -90=4, which would require another 4, but we already have three numbers. Maybe three numbers where two are same? But we tried that earlier. For example, two 25s: 25+25=50, 94-50=44, not a square.Alternatively, 49 + 25 + 16 + 4=94, but that's four squares. Not three. So, no.Alternatively, 64 + 25 + 5=94, but 5 isn't a square.Wait, perhaps I'm overcomplicating. So far, only two valid combinations: 9,3,2 and 7,6,3.Thus, their volumes sum to 764 and 586. So the answer is A. But let's check the problem again to make sure there isn't a constraint I missed.The problem says "three cubes with integer edge lengths" (unit: cm). So, no restrictions on edge lengths being distinct or not. But since we tried combinations with duplicates and didn't find any, and the problem doesn't mention uniqueness, but still, even with duplicates, we didn't find any other solutions. So, only two possible sums.Therefore, the answer should be option A: 764 or 586. But let me check the options again.Wait, in the original problem, the options are:(A) 764 cm³ or 586 cm³(B) 764 cm³(C) 586 cm³ or 564 cm³(D) 586 cm³So, since both 764 and 586 are possible, the answer is (A). But in the options, (A) is presented first. However, looking back at the problem statement, maybe there's something I didn't consider. For example, perhaps edge lengths must be distinct? The problem doesn't specify that. If they can be the same, maybe there's another solution. Wait, but we already checked duplicates and there were none. So, I think (A) is correct.But let me check once more. Let me calculate 9,3,2:Surface areas: 6*(81 +9 +4)=6*94=564. Correct.Volumes: 729 + 27 +8=764.7,6,3:Surface areas:6*(49 +36 +9)=6*94=564.Volumes:343 +216 +27=586.No other combinations. So, answer is A.But wait, looking at the options again, the answer given in the choices is (D) 586. Wait, no, maybe the problem is presented in Chinese and there's a translation error? Wait, no, the user presented the problem in English. Hmm.Wait, perhaps in the problem statement, it's stated that the edge lengths are integers but maybe they have to be distinct? If that's the case, then both combinations are still valid. However, if they can be the same, but we have no solutions with duplicates. So, the answer is still A. Unless there's a miscalculation.Wait, let me confirm the volumes again.For edge lengths 9, 3, 2:9³ = 7293³ = 272³ = 8729 + 27 +8= 764. Correct.For edge lengths 7,6,3:7³=3436³=2163³=27343 +216=559 +27=586. Correct.So both are correct.But the options are (A) 764 or 586; (B) 764; (C) 586 or 564; (D)586.So, since both 764 and 586 are possible, the answer is (A). But why is (D) 586 an option? Maybe the problem is from an exam where sometimes only one answer is correct, but according to our analysis, two answers are possible. However, looking at the options, the first option includes both possibilities, so (A) should be the correct choice.But maybe in the original answer, the answer is (D) 586? Maybe I made a mistake.Wait, let me check if 586 is indeed the only possible answer. Wait, no, we have two valid edge length triplets. So both sums are possible. Hence, the answer must be (A). But in the options, (A) is presented first. Unless there's a restriction in the problem that I missed.Wait, re-reading the problem: "three cubes with integer edge lengths (unit: cm) sum up to 564 cm², then the sum of the volumes of these three cubes is ( )." So, surface areas sum to 564. Then volumes sum to... So, the problem allows multiple possible answers, hence option A is correct.But in some multiple-choice settings, only one answer is expected, but in this case, the options include (A) which has both. Therefore, according to the given options, (A) is the correct choice.But let me check again if there are only two combinations. Suppose someone considers edge lengths in different orders, but since the problem doesn't care about order, they are the same combinations. So, yes, only two.Therefore, the answer should be (A). However, looking at the options again, the original problem might have a typo, or perhaps I miscalculated.Wait, another thought: maybe 7,6,3 is the only correct answer. Wait, why? Let me check the surface area again. For edge lengths 7,6,3:Each cube's surface area is 6*(7²)=294, 6*(6²)=216, 6*(3²)=54. Adding up: 294 +216=510, +54=564. Correct.Similarly, for edge lengths 9,3,2: 6*(81)=486, 6*(9)=54, 6*(4)=24. 486+54=540+24=564. Correct.Therefore, both are valid. Therefore, the answer must be (A). So the correct option is (A). But in the given choices, option (A) is "764 or 586", so that's the answer. However, the user provided the options as (A), (B), (C), (D), with (A) being both. So unless there's a mistake in the problem, the answer should be (A). But I need to check if maybe there is a constraint I missed.Wait, the problem says "three cubes". There is no constraint on the edge lengths being different, so both solutions are valid. Therefore, answer is (A). However, in some cases, maybe the problem expects the minimal possible volume or something else, but the problem doesn't specify that. Therefore, strictly according to the given info, (A) is correct.But let me check the original problem statement again to ensure I didn't misread anything."If the surface areas of three cubes with integer edge lengths (unit: cm) sum up to 564 cm², then the sum of the volumes of these three cubes is ( )."Options are given. So, since both 764 and 586 are possible, the answer is (A). Hence, the answer is boxed{A}.Final Answerboxed{A}</think>Given three cubes with integer edge lengths, their surface areas sum up to 564 cm². We need to find the sum of their volumes.First, we know the surface area of a cube is (6a^2) where (a) is the edge length. Therefore, the total surface area equation is:[6(a^2 + b^2 + c^2) = 564]Dividing both sides by 6, we get:[a^2 + b^2 + c^2 = 94]We need to find three integers (a, b, c) such that their squares sum to 94. After checking possible combinations, we find two valid sets of edge lengths:1. Edge lengths 9, 3, 2: - Their squares: (9^2 + 3^2 + 2^2 = 81 + 9 + 4 = 94) - Volumes: (9^3 + 3^3 + 2^3 = 729 + 27 + 8 = 764 , text{cm}^3)2. Edge lengths 7, 6, 3: - Their squares: (7^2 + 6^2 + 3^2 = 49 + 36 + 9 = 94) - Volumes: (7^3 + 6^3 + 3^3 = 343 + 216 + 27 = 586 , text{cm}^3)Both combinations are valid and their volumes sum to 764 cm³ and 586 cm³ respectively. Therefore, the correct answer is option (A), which includes both possibilities.[boxed{A}],<think>Okay, let's see. I have this problem here about three cubes with integer edge lengths. The sum of their surface areas is 564 cm², and I need to find the sum of their volumes. The options are given, so I need to figure out which one is correct. Hmm. Let me start by recalling some formulas.First, the surface area of a cube. A cube has 6 faces, each of which is a square with area equal to the edge length squared. So the total surface area (SA) for a cube with edge length 'a' is 6a². Right. Then, the volume (V) of a cube is a³. So for three cubes with edge lengths a, b, and c, their total surface area would be 6a² + 6b² + 6c² = 564 cm². And we need to find the sum of their volumes, which is a³ + b³ + c³.The problem states that the edge lengths are integers. So, a, b, c are positive integers. Let's write down the equation:6(a² + b² + c²) = 564Divide both sides by 6:a² + b² + c² = 564 / 6Let me calculate that. 564 divided by 6. 6*90=540, so 564-540=24, so 90 + 24/6=94. So a² + b² + c² = 94.So now the problem reduces to finding three positive integers a, b, c such that their squares sum up to 94. Then, compute their cubes and add them up. The answer is one of the options given. Let me note the options again:(A) 764 cm³ or 586 cm³(B) 764 cm³(C) 586 cm³ or 564 cm³(D) 586 cm³So, the answer could be either 764 or 586, or just 764, etc. Hmm. So first, I need to find all possible triplets (a, b, c) where a, b, c are positive integers with a² + b² + c² = 94, and then calculate a³ + b³ + c³ for each triplet and see which ones match the options.Since the edge lengths are positive integers, their possible values are limited. Let's think about the maximum possible edge length. Since a² has to be less than or equal to 94, the maximum a can be is floor(sqrt(94)) which is 9, because 9²=81 and 10²=100 which is over 94. So possible edge lengths are from 1 to 9.But given that there are three cubes, and their squares sum to 94, maybe some of them are larger. Let me check: if one cube has edge length 9, then 9²=81, so the remaining two squares need to sum to 94 -81=13. So, possible squares for the other two: 9 and 4, which would be 3² and 2², but 9 +4=13. So that's one possibility: 9, 3, 2. Alternatively, 16 would be too much (13-16 negative), so the other two can't be larger than 3. So possible triplet (9, 3, 2). Let's check the sum of squares: 81 +9 +4=94. Yes. Then the sum of volumes would be 9³ +3³ +2³=729 +27 +8=764. So that's 764 cm³, which is one of the options (A and B).Alternatively, if the largest cube is 8: 8²=64. Then remaining two squares need to sum to 94 -64=30. Let's see what squares sum to 30. The possible squares are 25, 16, 9, 4, 1. So 25 +5=30, but 5 is not a square. 16 +14=30, 14 is not a square. 9 +21=30, nope. 16 +9 +5, but we only need two numbers. So 25 +5 invalid, 16 +14 invalid. Maybe 25 +4 +1, but wait, we're looking for two numbers. Hmm. So maybe there are no solutions with 8. Let me check again. 30 can be written as 25 +5, 16 +14, 9 +21, 4 +26, 1 +29. None of the second numbers are perfect squares. So no solution here.What if the largest cube is 7: 7²=49. Then remaining two squares need to sum to 94 -49=45. Let's see. 45. So possible squares: 36, 25, 16, 9, 4, 1. 36 +9=45. So 6² +3²=36 +9=45. So triplet (7,6,3). Check sum of squares: 49 +36 +9=94. Yes. Then sum of volumes: 7³ +6³ +3³=343 +216 +27=343+216=559+27=586. So 586 cm³. That's another option (A and C and D).Alternatively, let's see if there are other triplets. For example, with largest cube 7. Are there other combinations? 25 + 20=45, but 20 isn't a square. 16 +29=45, nope. 9 +36=45, which we already have. So only one triplet here: 7,6,3.What if the largest cube is 6: 6²=36. Then remaining two squares sum to 94 -36=58. So 58. Let's see. The largest square less than 58 is 49. 58 -49=9. So 7² +3²=49 +9=58. So triplet (6,7,3). Wait, but we already considered that as (7,6,3). So same triplet. Alternatively, 6² + 6²=36 +36=72, which is more than 58. So not possible. 6²=36, 5²=25. 25 + 36=61, which is over. 25 +25=50, which is 58-50=8, not a square. 16 + 16=32, 58 -32=26, not a square. Maybe 49 +9=58 as before. So only triplet (7,6,3) again.If largest cube is 5: 5²=25. Then remaining two squares sum to 94 -25=69. Let's see. The largest square less than 69 is 64. 69 -64=5, which is not a square. Next, 49. 69 -49=20, not a square. 36. 69 -36=33, not a square. 25. 69 -25=44, not a square. 16. 69 -16=53. Not a square. 9. 69 -9=60. Not a square. 4. 69 -4=65. Not a square. 1. 69 -1=68. Not a square. So no solutions here.Similarly, for largest cube 4: 4²=16. Remaining two squares sum to 94 -16=78. 78. The largest square less than 78 is 64. 78 -64=14. Not a square. 49. 78 -49=29, not a square. 36. 78 -36=42. Not a square. 25. 78 -25=53. Not a square. 16. 78 -16=62. Not a square. 9. 78 -9=69. Not a square. 4. 78 -4=74. Not a square. 1. 78 -1=77. Not a square. So no triplet here.For largest cube 3: 3²=9. Remaining sum 94 -9=85. 85. Largest square is 81. 85 -81=4. So 9² + 2²=81 +4=85. So triplet (9,2,3). But that's the same as (9,3,2) which we already considered earlier. So same as the first triplet.Similarly, for largest cube 2 or 1, seems redundant as they would be part of the smaller cubes in the triplets already considered.So, in total, there are two possible triplets:1. (9,3,2) with volumes summing to 7642. (7,6,3) with volumes summing to 586Therefore, the possible sums are 764 or 586. Looking at the options, option A says 764 or 586. Option D says 586. But since there are two possible answers, depending on the triplet, but the problem says "the sum of the volumes of these three cubes is ( )." The options include (A) which has both, and (D) which has only 586. Wait, but maybe there's a constraint I missed. Let me check again.Wait, the problem states "three cubes with integer edge lengths". So, the problem doesn't specify that the edge lengths are distinct. Wait, but in our triplets, they are distinct. Are there triplets with repeated edge lengths? For example, is there a triplet where two cubes have the same edge length?Let me check. For example, if two cubes have edge length 5, then their squares would be 25 each, so two of them would be 50, then the third square would be 94 -50=44, which is not a perfect square. So no. If two cubes are 6: 6² each is 36, so two of them sum to 72, leaving 94 -72=22, which is not a square. If two cubes are 7: 49 each, sum to 98, which is already over 94. So that's not possible.If two cubes are 4: 16 each, sum to 32, leaving 94 -32=62, not a square. Similarly, two cubes of 3: 9 each, sum to 18, leaving 94 -18=76, which is not a square. Two cubes of 2: 4 each, sum to 8, leaving 94 -8=86, not a square. Two cubes of 1: 1 each, sum to 2, leaving 94 -2=92, not a square. So no, there are no triplets with two equal edge lengths. Therefore, the only possible triplets are the two we found: (9,3,2) and (7,6,3). Hence, two possible sums: 764 and 586. Therefore, the answer should be option A, right?But let me check the options again:(A) 764 cm³ or 586 cm³(B) 764 cm³(C) 586 cm³ or 564 cm³(D) 586 cm³But the problem says "the sum of the volumes of these three cubes is ( )." So, is there only one possible answer? Wait, maybe I made a mistake here. Let me verify the calculations again.First triplet: 9,3,2.Surface areas: 6*(81 +9 +4)=6*(94)=564. Correct.Volumes: 729 +27 +8=729+27=756+8=764. Correct.Second triplet: 7,6,3.Surface areas: 6*(49 +36 +9)=6*(94)=564. Correct.Volumes: 343 +216 +27=343+216=559+27=586. Correct.So both are valid. Then, why is the answer not (A)? But the answer options are given, and (A) is an option. But let me check the options again. The problem is presented as a multiple-choice question with options (A) through (D). The problem is from an exam, perhaps? In some exams, even if there are multiple solutions, you might have to choose all that apply, but in this case, the options are given with "or", so (A) says 764 or 586, which is exactly the two sums we found. However, option (D) is only 586. But in the problem statement, is there any restriction that we need to consider? For example, are the edge lengths required to be distinct? The problem says "three cubes with integer edge lengths". It doesn't specify distinct. So both triplets (9,3,2) and (7,6,3) are valid, hence two possible sums. Therefore, the correct answer should be (A). But the options given are (A) through (D). Let me check the original problem again.Wait, looking back at the problem: "the sum of the volumes of these three cubes is ( )." Then the options are (A) to (D). In Chinese exams, sometimes parentheses indicate that only one answer is correct. However, if there are two possible answers, and the option that includes both is present, like (A), then (A) is the correct choice. But in the options here, (A) is "764 or 586", (B) is only 764, (C) is "586 or 564", and (D) is only 586. So if both 764 and 586 are possible, then (A) is the correct answer. However, maybe there is a mistake in my reasoning. Let me check again if both triplets are indeed valid.Wait, is there a possibility that the edge lengths must be in a certain order? For example, maybe the problem implies that the edge lengths are ordered, but since the cubes are indistinct, the problem doesn't specify order, so both triplets are acceptable. Therefore, both sums are possible. Therefore, the answer is (A). But in the original problem statement in Chinese, sometimes "three cubes" might imply distinct edge lengths, but the problem didn't specify. Wait, the problem says "three cubes with integer edge lengths". There is no mention of distinctness. So, unless there's a translation issue, both triplets are acceptable, hence two possible answers. But looking at the options, (A) includes both, so (A) should be the answer. However, let me check the original problem's options again.Wait, the user has given the options as:(A) 764 cm³ or 586 cm³(B) 764 cm³(C) 586 cm³ or 564 cm³(D) 586 cm³So, if both 764 and 586 are possible, the answer is (A). If only one is possible, then (B) or (D). But according to my calculations, both are possible. Therefore, (A) is the correct answer. However, in the initial problem statement from the user, the correct answer is among these options. But maybe in the original problem, there was a restriction that the edge lengths are distinct? Wait, but in the triplet (7,6,3), all edge lengths are distinct, and in (9,3,2) as well. So even with distinctness, both are valid. So the answer is (A). But the given options include (D) as well. Maybe in the answer key, (D) is the correct answer? Wait, but why?Wait, perhaps there is a miscalculation. Let me double-check the volumes.First triplet: 9,3,2.9³=729, 3³=27, 2³=8. Sum: 729+27=756, 756+8=764. Correct.Second triplet:7,6,3.7³=343, 6³=216, 3³=27. Sum: 343+216=559, 559+27=586. Correct.So both sums are correct. So the answer should be (A). However, let me check once more if there are other triplets. For example, could there be another set of edge lengths that also sum up to 94 in squares? Let me check all possibilities.We considered largest edge 9,8,7,6, etc. But perhaps another combination. Let's try.Suppose the three edge lengths are 8,5, something. 8²=64, 5²=25. Then total so far is 89. 94-89=5, which is not a square. Not valid.How about 7,5, something. 7²=49, 5²=25. Sum=74. 94-74=20. Not a square.7,4: 49+16=65. 94-65=29. Not a square.7,5, as above.6,5: 36+25=61. 94-61=33. Not a square.6,4: 36+16=52. 94-52=42. Not a square.5,5: 25+25=50. 94-50=44. Not a square.Wait, perhaps with three different numbers. For example, 5,4, something: 25+16=41. 94-41=53. Not a square. 5,3:25+9=34. 94-34=60. Not a square. 5,2:25+4=29. 94-29=65. Not a square. 5,1:25+1=26. 94-26=68. Not a square.4,3:16+9=25. 94-25=69. Not a square.4,2:16+4=20. 94-20=74. Not a square.3,2:9+4=13. 94-13=81=9². Wait, that's 9². Wait, that would be triplet (9,3,2). Which we already considered. So that's the same as before.Similarly, 7,2:49 +4=53. 94-53=41. Not a square.7,1:49 +1=50. 94-50=44. Not a square.So no other triplets. Therefore, only two triplets: (9,3,2) and (7,6,3). Thus, two possible volume sums: 764 and 586. Hence, the answer is (A). But in the options given, (A) is "764 or 586", which matches. However, the user might have intended the answer to be (D) 586, but according to calculations, both are correct. Wait, maybe I made a mistake in considering the triplet (9,3,2). Let me check if that triplet is valid.Yes, surface areas: 6*(81 +9 +4)=6*94=564. Correct. Volumes: 729+27+8=764. So it's a valid solution. Then why is the answer (D) 586? Maybe the problem requires the minimal possible volume? But the problem doesn't state that. It just asks for the sum of the volumes. So both are correct. Therefore, the answer should be (A). However, given that the options include (A) and (D), and in Chinese exams sometimes only the minimal or maximal is taken, but here the problem doesn't specify. Hmm.Wait, maybe there's an error in my initial step. Let me re-express the problem:"If the surface areas of three cubes with integer edge lengths (unit: cm) sum up to 564 cm², then the sum of the volumes of these three cubes is ( )."Wait, the problem is in Chinese, maybe lost in translation. Maybe the edge lengths are positive integers, which they are. But maybe the problem expects only one answer. Let me check if there's an alternative interpretation.Wait, maybe the cubes are distinct in some way. For example, maybe the problem expects three different edge lengths. But in both triplets, the edge lengths are different. So both are acceptable.Alternatively, maybe in the problem statement, the surface areas are summed up as 564, but if I miscalculated the division. Wait, 564 divided by 6 is 94, right? 6*94=564. Yes. So a² +b² +c²=94. Correct.Alternatively, maybe I have to consider units, but they are all in cm and cm², so units are consistent.Therefore, unless there's a mistake in the problem's options, the correct answer should be (A). However, the given options from the user include (A) and (D). Maybe in the original problem, the answer is (D), but according to my calculation, (A) is correct. Alternatively, maybe I need to check again if there are more triplets.Wait, what if two edge lengths are the same. For example, two cubes with edge length 5, then third cube's square would be 94 -2*25=44, which is not a square. As before. Or two cubes of 4: 2*16=32, remaining square 62, not a square. So, no. So no triplet with two same edge lengths. So only two triplets.Alternatively, triplets with all three edge lengths the same: 3a²=94. 94 is not divisible by 3. So impossible. So no.Therefore, the conclusion is that there are two possible sums: 764 and 586. Therefore, answer (A). However, the user's given options list (A) as "764 or 586", which is exactly what we have. But then why is the user providing this problem? Maybe in the original source, the answer is different. Wait, let me check the problem again. The problem says "three cubes with integer edge lengths". So, maybe in Chinese, "integer edge lengths" is specified, which it is. So, yes. Then, according to this, the answer should be (A). But according to the options given, (A) is an option, so that's the answer.But the user might have intended the answer to be (D). Maybe there was a mistake in the calculation. Wait, but my calculations seem correct. Let me check once more:Triplet 1: 9,3,2.Surface areas: 6*(9² +3² +2²)=6*(81 +9 +4)=6*94=564. Correct.Volumes: 9³ +3³ +2³=729 +27 +8=764.Triplet 2:7,6,3.Surface areas:6*(7² +6² +3²)=6*(49 +36 +9)=6*94=564. Correct.Volumes:343 +216 +27=586.Both are correct. Therefore, the answer is (A). Therefore, the correct option is (A). However, in the options provided by the user, (A) is present. So, why is this a problem? Maybe the original answer was different, but according to the calculation here, (A) is correct. Alternatively, perhaps there's a restriction in the problem that I didn't consider. Maybe the cubes have to be ordered in a certain way? No, since the problem doesn't specify. Therefore, I think the answer is (A). However, the options given in the problem might not have (A) as the correct answer in the source, but according to my reasoning, (A) is correct. Maybe the original problem had a typo or different numbers.But given that the user has provided the options, and (A) is an option, then unless there is a mistake in my reasoning, (A) is the answer. However, the user might have intended to trick us here, but according to the mathematics, (A) is correct.Wait, but looking back at the options, (A) says "764 or 586", but (D) is "586". If the answer is both, then (A) is correct. If the problem requires both, but in the options, (A) is present. Therefore, the answer is (A). However, in some multiple-choice contexts, especially in Chinese exams, sometimes all possible correct answers must be listed, and if (A) includes both, then (A) is correct. Therefore, based on the given options, the answer is (A). But if forced to choose between (A) and (D), but according to the problem's phrasing, there are two possible sums, hence (A). Therefore, I think the answer should be (A).But the problem is presented with options, and maybe the original answer is (D). Alternatively, maybe I made a mistake. Let me check once again for possible triplets.Wait, let's try triplet (8,5,1). Surface areas: 6*(64 +25 +1)=6*90=540, which is less than 564. Not valid.Triplet (8,4,2): 6*(64 +16 +4)=6*84=504. Not enough.Triplet (10, x, y): But 10²=100, which is over 94. Not possible.Triplet (7,7, something): 2*49=98, over 94.Triplet (6,6, something): 2*36=72, remaining 22, not a square.Triplet (5,5, something): 2*25=50, remaining 44, not a square.So, no other triplets. Therefore, only two possible. So answer (A). Therefore, the correct answer is boxed{A}But wait, in the original problem's options, the user has:(A) 764 or 586(B) 764(C) 586 or 564(D) 586If the answer is (A), but in the original problem's answer, perhaps the answer is (D). But according to the calculation, both are possible. Unless there is a restriction that the edge lengths must be in ascending order or something else. But the problem doesn't state that. Therefore, unless there's a mistake in the problem, the answer should be (A). However, since the options are given and (A) is present, the box answer should be (A). But in the initial problem statement, the user might have intended the answer to be (D), but according to the math, it's (A). This is conflicting.Alternatively, maybe the problem is from a specific source where the answer is (D), but according to general mathematics, it's (A). Maybe I need to confirm once more.Wait, let's see. If we list all possible triplets (a,b,c) where a >= b >=c to avoid permutations:First triplet: (9,3,2)Second triplet: (7,6,3)These are the only two triplets in descending order. Since the problem doesn't mention ordering or distinctness, both are valid. Therefore, both sums are possible, hence the answer is (A). So, I think the answer is (A). But let me check again.Yes, the problem says "three cubes with integer edge lengths". So, unless there's a hidden constraint, both triplets are valid, leading to two possible volume sums. Therefore, the correct answer is (A). But the problem's options include (A), so I have to go with that. However, the assistant's final answer should be put inside boxed{} as per instructions. So, based on the reasoning, the answer is (A). But looking at the original problem's options, maybe in the source it's different. However, based on the given information and calculations, the answer is (A).But wait, looking at the options again, (A) is "764 or 586", (B) is 764, (C) is "586 or 564", (D) is 586. In Chinese exams, sometimes the options are structured such that if multiple answers are possible but only one is listed as an option with "or", you have to choose the one that includes all correct answers. However, if only one of them is correct, then pick that. But in our case, both 764 and 586 are correct, so (A) is the answer. Hence, the final answer is boxed{A}.Final Answerboxed{A}</think>Given three cubes with integer edge lengths, the sum of their surface areas is 564 cm². We need to find the sum of their volumes.First, we calculate the total surface area equation:[6(a^2 + b^2 + c^2) = 564]Dividing both sides by 6:[a^2 + b^2 + c^2 = 94]We need to find three positive integers (a), (b), and (c) such that their squares sum to 94. After checking possible values, we find two valid triplets:1. Triplet (9, 3, 2): - Surface areas: (9^2 + 3^2 + 2^2 = 81 + 9 + 4 = 94) - Volumes: (9^3 + 3^3 + 2^3 = 729 + 27 + 8 = 764)2. Triplet (7, 6, 3): - Surface areas: (7^2 + 6^2 + 3^2 = 49 + 36 + 9 = 94) - Volumes: (7^3 + 6^3 + 3^3 = 343 + 216 + 27 = 586)Both triplets are valid, leading to two possible sums of volumes: 764 cm³ and 586 cm³. Therefore, the correct answer is:[boxed{A}],<think>Okay, so we have three cubes with integer edge lengths, and their total surface area is 564 cm². We need to find the sum of their volumes and choose the correct option from the given choices. Let me try to break this down step by step.First, remember that the surface area of a cube is calculated by 6 times the edge length squared. Since each cube has six faces, each with an area of edge length squared. So if a cube has edge length 'a', its surface area is 6a². Similarly, the volume of a cube is a³.The problem states that three such cubes have their surface areas adding up to 564 cm². Let's denote the edge lengths of the three cubes as a, b, and c, all positive integers. Then, the total surface area would be 6a² + 6b² + 6c² = 564. Let's simplify that equation first.Dividing both sides by 6 gives us:a² + b² + c² = 564 / 6 = 94.So, the sum of the squares of the edge lengths is 94. Now, we need to find three positive integers a, b, c such that a² + b² + c² = 94, and then compute the sum of their volumes, which is a³ + b³ + c³. The answer options give possible values for this sum, so perhaps we need to check which combinations of a, b, c satisfy the surface area condition and then compute their volumes.Given that the options are 764, 586, or 564, we can work backwards if necessary, but first, let me try to find all possible triples (a, b, c) with a ≤ b ≤ c (to avoid permutations) such that their squares add up to 94.First, let's think about the maximum possible edge length. Since 94 is the sum of three squares, the largest possible edge length would be when the other two are 1. Let's check:If c is the largest, then c² ≤ 94 - 1 - 1 = 92. So c ≤ √92 ≈ 9.59. Since c must be an integer, the maximum possible edge length is 9 cm.So possible edge lengths for each cube are from 1 to 9. Let's list the squares from 1 to 9:1² = 12² = 43² = 94² = 165² = 256² = 367² = 498² = 649² = 81So now, we need three numbers from this list (with possible repetition) that sum to 94.Let me try to find all possible triples. Since 9² = 81, and 94 - 81 = 13. So if one cube is 9 cm, then the other two need to add up to 13. Let's see if there are two squares that sum to 13. The possible squares less than 13 are 1, 4, 9. So 9 + 4 = 13, which is 3² + 2². So one possibility is (9, 3, 2). Check: 81 + 9 + 4 = 94. Yes, that works.Another possibility: 8² = 64. Then 94 - 64 = 30. So the other two squares need to add up to 30. Let's check possible pairs. The squares up to 30 are 25, 16, 9, 4, 1. Let's see: 25 + 5 = 30, but 5 isn't a square. 16 + 14 = 30, but 14 isn't a square. 9 + 21 = 30, nope. 16 + 9 + 5? Wait, but we need two squares. So 25 + 5? Not squares. Wait, 25 is a square (5²), 5 is not. 16 + 14? 16 is 4², 14 not. 9 + 21? No. So maybe no solutions with 8². Let me check again. 5² is 25, so 25 + 5 = 30, but 5 is not a square. 16 + 14? No. 9 + 21? 9 + 16 + 5? Wait, perhaps we need to check if 30 can be expressed as a sum of two squares. The possible squares up to 30: 1,4,9,16,25. So combinations:25 + 5 (5 not square)16 + 14 (14 not square)9 + 21 (21 not)4 + 26 (26 no)1 +29 (29 no). So no, there's no combination here. So 8² cannot be part of such a triple.Next, 7² = 49. Then 94 - 49 = 45. So two squares summing to 45. Let's check. The squares up to 45 are 36, 25, 16, 9, 4, 1. 36 + 9 = 45. So 6² + 3². So another possible triple is (7, 6, 3). Check: 49 + 36 + 9 = 94. Correct. Also, check if there are other combinations. 25 + 20 = 45, but 20 isn't a square. 16 + 29 = 45, no. 9 + 36 = 45, which we already considered. So another triple is (7,6,3).Also, check if 5² =25. Then 94 -25=69. So two squares adding to 69. The squares less than 69: 64, 49, 36, 25, 16, etc. 64 +5=69, 5 not square. 49 +20=69, 20 not. 36 +33=69, no. 25 +44=69, no. 16 +53=69, no. So no. Similarly, 6²=36. Then 94-36=58. So two squares adding to 58. Let's see: 49 +9=58. So 7² +3². So triple (6,7,3). But that's same as before. Alternatively, 36 + 36=72, which is over. 25 +33=58, nope. 16 +42=58, nope. 64 is 8², 64 + (-6)=58, which is invalid. So only (7,6,3). Alternatively, (6,7,3). Either way, same numbers.Alternatively, 5²=25. Wait, we tried that. How about 4²=16. Then 94 -16=78. So two squares sum to 78. 64 +14=78, 14 not a square. 49 +29=78, nope. 36 +42=78, nope. 25 +53=78, nope. So no.Similarly, 3²=9. 94-9=85. Two squares sum to 85. 81 +4=85. 9² +2². So triple (9, 2, 3). Wait, but we already have (9,3,2). So that's same as the first triple. So maybe another triple here. Wait, but 85 can be written as 81 +4, which is 9² +2². So (9, 2, 3). That is same as (9,3,2). So that's the same as the first one. So perhaps only two distinct triples: (9,3,2) and (7,6,3). Let me check again.Wait, (7,6,3): 7² +6² +3² =49 +36 +9=94. Correct. (9,3,2):81 +9 +4=94. Correct. Are there any other triples?Let's check. Maybe (5,5,8). Let's see: 5² +5² +8²=25 +25 +64=114. Too big. How about (7,5, ?). 7²=49, 5²=25. 94 -49 -25=20. 20 is not a square. (7,4, ?). 49 +16=65. 94-65=29. 29 isn't a square. (6,6, ?). 36 +36=72. 94-72=22. Not a square. (6,5, ?). 36 +25=61. 94-61=33. Not a square. (5,5, ?). 25 +25=50. 94-50=44. 44 isn't a square. (7,7, ?). 49 +49=98. 98 is more than 94. (8, ?, ?). 8²=64. Then 94-64=30. As before, no two squares sum to 30. (10, ?, ?). Wait, 10²=100, which is more than 94. So 9 is the maximum.Wait, another possible combination: (7,5, ?). 49 +25=74. 94-74=20, which isn't a square. (7,4, ?). 49 +16=65. 94-65=29. Not a square. (6,5, ?). 36 +25=61. 94-61=33. Not a square. (6,4, ?). 36 +16=52. 94-52=42. Not a square. (5,4, ?). 25 +16=41. 94-41=53. Not a square. (4,4, ?). 16 +16=32. 94-32=62. 62 isn't a square. (3,3, ?). 9 +9=18. 94-18=76. 76 isn't a square. (2,2, ?). 4 +4=8. 94-8=86. Not a square. (1,1, ?). 1 +1=2. 94-2=92. Not a square.So seems like the only possible triples are (9,3,2) and (7,6,3). Let me verify if there are any others. Maybe (8, ?, ?). But as we saw earlier, 8²=64, then 94-64=30. No two squares add up to 30. How about (5,2, ?). 25 +4=29. 94-29=65. 65=64 +1=8² +1². So (5,2,8). Wait, 5² +2² +8²=25 +4 +64=93. Wait, 25 +4 +64=93. That's 93, not 94. So that's not correct. Wait, 25 +4 +65? Wait, no. So miscalculation. Wait, 5,2,8: 25 +4 +64=93. Not 94. Close, but not quite. So that's invalid. How about (5,3, ?). 25 +9=34. 94 -34=60. 60 is not a square. (5,4, ?). 25 +16=41. 94 -41=53. Not a square. (4,3, ?). 16 +9=25. 94 -25=69. 69 is not a square. (4,2, ?). 16 +4=20. 94 -20=74. 74 isn't a square. (3,2, ?). 9 +4=13. 94 -13=81. 81 is 9². So (3,2,9). But that's same as (9,3,2). So same as before.Wait, so maybe only two distinct triples: (9,3,2) and (7,6,3). Let me check another possibility. For example, (7,5,4): 49 +25 +16=90. Too small. (7,7,2): 49 +49 +4=102. Too big. (6,6,4): 36 +36 +16=88. (6,6,5): 36 +36 +25=97. (7,5,5):49 +25 +25=99. (6,5,6): same as above. Hmm. Not helpful.Alternatively, (7, 3, 6): same as (7,6,3). So, no new triples. So I think only two triples: (9,3,2) and (7,6,3). Let me confirm that.Wait, let's think about another possible combination. For example, 6² + 5² + something. 36 +25=61. 94 -61=33. 33 is not a square. 7² +4²=49 +16=65. 94 -65=29. Not a square. 8² +3²=64 +9=73. 94 -73=21. Not a square. 9² +1²=81 +1=82. 94 -82=12. 12 isn't a square. 7² +2²=49 +4=53. 94 -53=41. Not a square. 6² +4²=36 +16=52. 94 -52=42. Not a square. 5² +5²=25 +25=50. 94 -50=44. Not a square. So yeah, seems like only two triples.So, the possible triples are (9,3,2) and (7,6,3). Now, let's compute the sum of their volumes for each case.First, for (9,3,2):Volumes: 9³ +3³ +2³ =729 +27 +8=729 +27 is 756, plus 8 is 764. So total volume 764 cm³.Second, for (7,6,3):Volumes:7³ +6³ +3³=343 +216 +27=343 +216=559, plus 27 is 586. So 586 cm³.So the possible total volumes are 764 or 586. Looking at the answer options:(A) 764 cm³ or 586 cm³(B) 764 cm³(C) 586 cm³ or 564 cm³(D) 586 cm³Since both 764 and 586 are possible, the answer should be (A). But wait, let me check the options again. The options given are (A) 764 or 586, (B)764, (C)586 or 564, (D)586. So according to our calculation, both 764 and 586 are possible, which is option (A). However, looking back at the problem statement, it says "the sum of the volumes of these three cubes is ( )." So we need to check if both are possible or if there's a unique answer.Wait a second. Are both triples (9,3,2) and (7,6,3) valid? Let's confirm their surface areas again.For (9,3,2):Surface areas:6*(81 +9 +4)=6*(94)=564. Correct.For (7,6,3):Surface areas:6*(49 +36 +9)=6*(94)=564. Correct.So both are valid. Therefore, the sum of volumes can be either 764 or 586. Therefore, the correct answer is (A). But let me check the options again. The problem might be a translation or perhaps I made a mistake in edge lengths.Wait, hold on. The problem states "three cubes with integer edge lengths". Both triples (9,3,2) and (7,6,3) are integer edge lengths, so both are valid. Therefore, both 764 and 586 are possible. Therefore, the answer is (A). But looking at the options given:(A) 764 or 586(B)764(C)586 or 564(D)586Therefore, the correct answer is (A). However, in some multiple-choice questions, sometimes they might expect you to consider the numerical order or other factors. Wait, but the options are given as (A), (B), (C), (D). The problem is in Chinese, but in the translation, it says "the sum of the volumes of these three cubes is ( )." with options. If both 764 and 586 are possible, then (A) is the correct answer. However, let me check once again to make sure there aren't more triples that I missed.Wait, earlier, when considering edge length 8, I found that 94 -64=30, which can't be expressed as a sum of two squares. Similarly, edge length 10 is too big. So only two triples. Therefore, (A) should be correct. But the options given in the problem may differ. Wait, the original problem's options are:(A) 764 or 586(B)764(C)586 or 564(D)586So the problem is presented as options where (A) includes both correct answers, while (D) is only 586. If the question is expecting all possible answers, then (A) would be correct. However, sometimes in Chinese exams, they might list all possible answers as separate options, but here options (A) and (C) include two possibilities each. Wait, but according to our calculations, only 764 and 586 are possible. 564 isn't a possible sum. So (C) includes 564, which is invalid. So (A) is the correct answer.But looking at the original problem statement again: "the sum of the volumes of these three cubes is ( )." with options. So in Chinese exams, sometimes the wording could imply that there is a unique answer, but here, since there are two possible configurations, leading to two different sums, the correct answer should include both, which is (A). However, perhaps there is a mistake in my reasoning.Wait, but maybe the problem is designed such that even though there are two possible triples, only one of the sums is among the options. Wait, but 764 and 586 are both in the options. Specifically, (A) includes both, (B) is only 764, (C) includes 586 and 564, which is wrong, and (D) is only 586.Therefore, if multiple answers are allowed, but in the options, (A) is presented as "764 or 586", which is the case here. In Chinese multiple-choice questions, sometimes they use parentheses with "or" to indicate that either value is a possible answer, and the correct option is the one that includes all possible answers. Therefore, (A) is the correct answer. However, looking at the options again, the original problem's options might have different formatting. If the system expects a single answer, perhaps there is a mistake, but according to the calculations, both 764 and 586 are possible, so (A) is correct.But wait, let me check once again for possible triples. Did I miss any?Let me check starting with the largest square, which is 81 (edge 9). Then remaining is 13. As before, 9 and 4. So 3 and 2. So triple (9,3,2). Then next largest square is 64 (edge 8), but as before, remaining is 30, which can't be expressed. Then 49 (edge7). Remaining 45, which is 36 +9 (edge6 and edge3). So (7,6,3). Then next, 36 (edge6). Remaining 58, which is 49 +9 (edge7 and edge3). Which is same as above. 25 (edge5). Remaining 69. Not possible. 16 (edge4). Remaining 78. No. 9 (edge3). Remaining 85=81 +4. Which is edge9 and edge2. Same as first triple. So no, no other triples. So only two. Therefore, the answer is (A). But the given options include (A) and (C). (C) has 564, which is the original surface area. Maybe someone could miscalculate volume as surface area, but 564 is surface area, not volume. So (C) is invalid. Therefore, (A) is correct.However, looking at the options given in the problem statement again:(A) 764 or 586(B) 764(C)586 or 564(D)586If the question is designed such that only one of the options is correct, but both 764 and 586 are possible, but the options don't have a combined option, but here (A) is the combination. So (A) is correct. But sometimes, in Chinese exams, even if multiple answers are possible, they might expect you to select all that apply, but given the way it's structured here, with (A) being the only option that includes both correct answers, the answer should be (A). However, in the original problem statement, maybe there was a mistranslation or different edge cases.Wait, hold on. Let me verify the volume calculations again for both triples.First triple: 9, 3, 2.9³ = 7293³ = 272³ = 8Sum: 729 +27 = 756; 756 +8=764. Correct.Second triple:7,6,3.7³=3436³=2163³=27Sum:343 +216=559; 559 +27=586. Correct.No other triples found. So both 764 and 586 are possible. Hence, answer (A). So why is the system expecting boxed{D} or something else? Wait, maybe I made a mistake here. Let me check again.Wait, the problem says "three cubes with integer edge lengths". So maybe the edge lengths have to be distinct? The problem doesn't specify that they must be distinct. In our triples, (9,3,2) are distinct, (7,6,3) are distinct. So that's okay. If repetition was allowed, but even if we allowed repetition, like two cubes with the same edge length, but in our case, both triples are distinct.Alternatively, maybe there's a restriction that the edge lengths are in a particular order? For example, maybe the problem expects them to be ordered, but since addition is commutative, the sum would be the same.Wait, perhaps the question has a typo, but according to the given translation, it's okay. Alternatively, maybe I miscalculated the second volume.Wait, 7³ is 343, 6³=216, 3³=27. 343+216=559, 559+27=586. Correct.9³=729, 3³=27, 2³=8. 729+27=756, 756+8=764. Correct.So both volumes are possible, so answer is (A). But the options given in the problem are (A) 764 or 586, (B)764, (C)586 or 564, (D)586. So in Chinese exams, sometimes the options might be structured such that if both A and D are correct, but the options are exclusive, but in this case, (A) is the only one that includes both possibilities. However, maybe the problem expects only one correct answer, and there is an error in the problem statement or my reasoning.Alternatively, perhaps the problem is from an official exam where the answer is (D) 586, but that would be incorrect based on our calculations. Alternatively, maybe there's a restriction I didn't consider.Wait, another thought: maybe the cubes have to have different edge lengths? The problem states "three cubes with integer edge lengths". It doesn't specify they must be distinct. So repetition is allowed. But in our solutions, the edge lengths are distinct. So if repetition is allowed, perhaps there are other triples. Wait, let's check.For example, (7,6,3): all distinct.(9,3,2): all distinct.What about (5,5,8)? Wait, 5² +5² +8²=25+25+64=114. 6*114=684, which is way higher than 564. So no.Wait, another approach: Maybe the problem is in Chinese, and the translation might have an error. For example, maybe the original problem said "three different edge lengths", but the translation omitted "different". If that's the case, then maybe (7,6,3) and (9,3,2) both have different edge lengths, so both are acceptable. So answer (A). But since the given options include (A) and (D), perhaps the answer is both, but depending on the exam's design.Alternatively, maybe I missed another triple where the edge lengths are not distinct. Let's check.For example, (a, a, b). So 2a² +b²=94. Let's see if this is possible.Let’s suppose two cubes have the same edge length.Case 1: two equal edge lengths.So 2a² +b²=94.Find integers a, b where a ≥1, b ≥1.Let's try a=6: 2*36=72. Then b²=94-72=22. Not a square.a=5: 2*25=50. b²=44. Not a square.a=7:2*49=98. 98>94. So no.a=4:2*16=32. b²=62. No.a=3:2*9=18. b²=76. No.a=2:2*4=8. b²=86. No.a=1:2*1=2. b²=92. No.So no solutions with two equal edges.Case 2: all three edges equal. Then 3a²=94. 94/3 ≈31.33, which is not a square. So no.So no triples with two or three equal edges. Hence, only distinct edge lengths. So our initial conclusion holds: two triples, leading to two volumes. Therefore, answer is (A). But given that in the original problem's options, (A) is present, but maybe the answer expected is different.Wait, but in the options, (A) is "764 or 586", and (D) is "586". If the question expects all possible answers, (A) is correct. However, in some multiple-choice settings, especially in older exams, sometimes they list all possible correct answers as separate options, but here, since (A) combines both, and (D) is a subset, but in Chinese exams, sometimes the intended answer might only be one, and the other is a trap. But according to strict mathematics, both are possible. Therefore, (A) should be the answer. However, the fact that the problem is presented with options where (A) and (D) are both present, but in the original problem statement from the user, the options are:(A) 764 or 586(B) 764(C) 586 or 564(D) 586Therefore, according to the strictest interpretation, since both 764 and 586 are possible, the correct answer is (A). But maybe the original answer intended only one, perhaps due to a miscalculation. Alternatively, in some sources, maybe only (D) is considered correct. But unless there's a restriction not mentioned in the problem, both are valid.Alternatively, perhaps the problem is from an exam where specific constraints are implied, like edge lengths being in a certain range or other implicit conditions, but based on the given information, both triples are valid.Therefore, after thorough analysis, I believe the correct answer is (A). However, given that the options include (A) and (D), and the user might have the answer as (D), perhaps there's a mistake. But based on calculations, (A) is correct.Final Answerboxed{A}</think>Given three cubes with integer edge lengths, their total surface area is 564 cm². We need to find the sum of their volumes.First, we simplify the surface area equation:[6a^2 + 6b^2 + 6c^2 = 564 implies a^2 + b^2 + c^2 = 94]We need to find integers (a, b, c) such that their squares sum to 94. After checking possible combinations, we find two valid triples: ((9, 3, 2)) and ((7, 6, 3)).For the triple ((9, 3, 2)):- Surface areas: (9^2 + 3^2 + 2^2 = 81 + 9 + 4 = 94)- Volumes: (9^3 + 3^3 + 2^3 = 729 + 27 + 8 = 764)For the triple ((7, 6, 3)):- Surface areas: (7^2 + 6^2 + 3^2 = 49 + 36 + 9 = 94)- Volumes: (7^3 + 6^3 + 3^3 = 343 + 216 + 27 = 586)Both sums of volumes, 764 and 586, are possible. Therefore, the correct answer is:[boxed{A}],<think>Okay, let's see. The problem is about three cubes with integer edge lengths. Their surface areas add up to 564 cm², and we need to find the sum of their volumes. The options are given, so maybe we can figure it out by checking possible edge lengths.First, remember that the surface area of a cube is 6 times the edge length squared. So if the edge length is 'a', then the surface area is 6a². Since there are three cubes, the total surface area would be 6(a² + b² + c²) = 564 cm². Therefore, the sum of their squares would be 564 divided by 6. Let me calculate that: 564 ÷ 6 = 94. So, a² + b² + c² = 94.Our goal is to find three integers a, b, c such that their squares add up to 94, and then compute the sum of their cubes, a³ + b³ + c³, and see which option it matches.Alright, let's list possible integers a, b, c. Since they are cubes, the edge lengths must be positive integers. Let's see, the maximum possible edge length would be such that a² is less than 94. The square root of 94 is approximately 9.7, so the edge lengths can be from 1 up to 9.So possible edge lengths: 1, 2, 3, 4, 5, 6, 7, 8, 9.Now, we need three numbers from this list whose squares sum to 94. Let's try to find all possible triplets (a, b, c) where a ≤ b ≤ c to avoid duplicates.Let me start with the largest possible number first. Let's try c = 9. Then a² + b² + 81 = 94 → a² + b² = 13. Possible squares adding up to 13: 9 + 4 = 13, which would mean a=3 and b=2. So triplet (2, 3, 9). Let's check: 2² + 3² + 9² = 4 + 9 + 81 = 94. Yes, that works. Then the volumes would be 8 + 27 + 729 = 764 cm³. That's one of the options, option A or B.Wait, but let's check if there are other triplets. Maybe with c=8. Then a² + b² + 64 = 94 → a² + b² = 30. So possible squares that add up to 30. Let's see. 25 + 5 = 30, but 5 isn't a square. 16 + 14, 14 isn't a square. 9 + 21, nope. 25 + 5 is invalid. 16 + 14? Wait, maybe 25 + 5, but 5 isn't a square. How about 25 + 4 + 1? No, only two variables here. So, maybe 5² + something? 5² is 25, then 30 -25=5, which isn't a square. 4²=16, 30-16=14, not a square. 3²=9, 30-9=21, nope. 2²=4, 30-4=26, nope. 1²=1, 30-1=29, nope. So c=8 doesn't work.Next, c=7. Then a² + b² + 49 = 94 → a² + b² = 45. Let's see. Possible squares adding to 45: 36 +9=45, so 6 and 3. So triplet (3,6,7). Let's check: 9 + 36 + 49 = 94. Correct. Then the volumes would be 27 + 216 + 343 = 586 cm³. That's another option. So that's possible. So another triplet is (3,6,7). So sum of volumes is 586. So then total volumes could be either 764 or 586. Looking at the options, A says 764 or 586, which matches. But let me check if there are more possibilities.Check c=7, a² + b²=45. Any other pairs? 25 + 20=45, but 20 isn't a square. 16 +29=45, nope. 16 + 16 +13, but no. So only 6 and 3. So (3,6,7) is the only one here.Next, c=6. Then a² + b² + 36 =94 → a² + b²=58. Let's check. 49 +9=58 → 7 and 3. So triplet (3,7,6). But that's same as (3,6,7). So already considered. 36 +22=58, 22 not a square. 25 +33=58, nope. 16 +42=58, nope. 9 +49=58, same as above. So only (3,6,7), which is same as before.c=5: a² + b² +25=94 → a² + b²=69. Let's see. 64 +5=69, 5 not a square. 49 +20=69, 20 not square. 36 +33=69, nope. 25 +44=69, nope. 16 +53, nope. 9 +60, nope. 4 +65, nope. 1 +68, nope. So no.c=4: a² + b² +16=94 → a² + b²=78. But the maximum a² + b² with a,b ≤4 is 16 +16=32 <78. So impossible.c=3: a² + b² +9=94 → a² + b²=85. But a and b can't be larger than 3, so 9 +9=18 <85. Not possible.Same for lower c.So the only triplets are (2,3,9) and (3,6,7), leading to volume sums 764 and 586 respectively. So the answer should be A: 764 or 586. But looking at the options, A is option (A), B is only 764, C is 586 or 564, D is 586. Wait, the problem is presented as "the sum of the volumes of these three cubes is ( )". So the answer might have two possibilities, but the options given are A to D. Let me check the options again:(A) 764 cm³ or 586 cm³(B) 764 cm³(C) 586 cm³ or 564 cm³(D) 586 cm³Since both 764 and 586 are possible, the correct answer would be (A). However, wait, the problem says "three cubes with integer edge lengths". Are there any other possible triplets that I might have missed?Wait, let me check again for c=7. We had a² + b²=45. Another possibility: 25 + 20=45, but 20 isn't a square. 16 + 29=45, nope. 9 +36=45, which is 3² +6², which we considered. So only (3,6,7). For c=9, (2,3,9). What about c=8? a² + b²=30. Let's check again. Maybe 25 +5=30, but 5 is not square. 16 +14=30, 14 not square. 9 +21=30, nope. 4 +26=30, nope. 1 +29=30, nope. So no.What about c=10? Wait, but 10²=100, which is larger than 94. So edge length can't be 10. So maximum is 9. So seems like only two triplets. Therefore, answer should be A. But wait, the options list 764 and 586. The answer is (A). However, the options are given as (A) to (D). Let me check the problem statement again.Wait, the problem says "sum up to 564 cm²", and the answer options are (A) through (D). The problem is in Chinese, but translated here. The original problem might have different options, but according to the translation here:Options:(A) 764 or 586(B) 764(C) 586 or 564(D) 586So according to our findings, there are two possible sums: 764 and 586. So the correct answer is (A). But let me check the problem again. Maybe there's a constraint I missed. The cubes have integer edge lengths. No other constraints. So unless there is some other hidden constraint, like edge lengths being distinct? The problem doesn't state that. Wait, let me check the problem statement again:"three cubes with integer edge lengths (unit: cm) sum up to 564 cm², then the sum of the volumes of these three cubes is ( )."Wait, the problem says "sum up to 564 cm²"—so total surface area. Then sum of volumes. So if edge lengths are allowed to be same, maybe there are other triplets.Wait, in our previous approach, we assumed a ≤ b ≤ c. But maybe there are triplets with repeated edge lengths. Let's check. For example, two cubes with same edge length.Let me check if there's another triplet where two edges are the same.For example, let’s take c=7, then a² + b²=45. If a= b, then 2a²=45 → a²=22.5, which is not integer. So no.For c=9, a² + b²=13. If a=b, then 2a²=13 → a²=6.5, not integer.For c=8, a² + b²=30. If a=b, 2a²=30 → a²=15, not integer.For c=6, a² + b²=58. If a=b, 2a²=58 → a²=29, nope.Similarly, for c=5, a² + b²=69. 2a²=69→ a²=34.5, nope.So no triplets with two equal edge lengths. What about all three equal? Then 3*6a²=564 → 18a²=564 → a²=31.333..., not integer. So nope.Therefore, only the two triplets: (2,3,9) and (3,6,7). So the possible volumes are 764 and 586. So answer is (A). But wait, looking at the options, (A) is "764 or 586", which is what we found. But the options also have (D) 586. Is there a chance that maybe only 586 is possible? Wait, why?Wait, perhaps the problem is expecting the minimal possible volume or something. But no, the problem just asks for the sum of the volumes, which could be either. But in the options, (A) includes both, while (D) is only 586. But according to our calculations, both are possible. So the answer should be (A). However, let me check the problem again to ensure.Wait, the problem says "three cubes with integer edge lengths". So unless there is a constraint that the edge lengths are distinct. Wait, the problem doesn't specify that. However, in our triplets, (2,3,9) and (3,6,7), all edge lengths are distinct. Wait, but perhaps there are other triplets with non-distinct edges. Wait, but we checked for triplets where two edges are equal, but they didn't result in integer solutions. So no.Wait, maybe there is another triplet with different edge lengths. Let me think. Maybe another combination.Wait, let me try c=7 again. a² + b²=45. We had 6² + 3²=36+9=45. Are there other pairs? Let's see. 5²=25, 45-25=20, which is not a square. 4²=16, 45-16=29, not a square. 7²=49, which is over. So no. Only 3 and 6.For c=9, a² + b²=13. 3² + 2²=9+4=13. 1² + sqrt(12), no. So only 2 and 3.Any other triplets with different numbers? Let's see.Suppose we take c=5, then a² + b²=69. Wait, 8²=64, so 64 +5=69. 5 isn't a square. 7²=49, 69-49=20, not square. 6²=36, 69-36=33, not square. 5²=25, 69-25=44, not square. So nope.How about c=4? a² + b²=78. But maximum a and b would be 4, so 16 +16=32 <78. So no.c=3: a² + b²=85. But 9 + 9=18 <85. No.So no other triplets. Hence, only two possible sums: 764 and 586. So answer is (A). But looking at the options given, (A) is an option. But in the original problem's translation, maybe the options are different? Wait, the user provided the options as:(A) 764 or 586(B) 764(C) 586 or 564(D) 586So according to the problem, (A) is correct. However, maybe in the answer key, it's different. Wait, maybe I made a mistake in calculating the volumes. Let me verify.For triplet (2,3,9):Volumes: 2³=8, 3³=27, 9³=729. Sum: 8+27=35; 35+729=764. Correct.For triplet (3,6,7):3³=27, 6³=216, 7³=343. Sum: 27+216=243; 243+343=586. Correct.So both sums are possible. So answer is (A). But the options given have (A) as 764 or 586, (D) as 586. If the question is expecting all possible answers, then (A) is correct. However, sometimes in multiple choice, if both options are possible but only one is listed, but here (A) includes both. So unless there is a mistake in the problem, maybe there is another constraint.Wait, the problem says "three cubes". Maybe they have to have different edge lengths? But the problem doesn't specify. If they can have same edge lengths, but in our solutions, the edge lengths are all different. But even if repetitions were allowed, as we saw earlier, there are no solutions with repeated edge lengths. So I think (A) is the correct answer.But looking back at the options given by the user:(A) 764 cm³ or 586 cm³(B) 764 cm³(C) 586 cm³ or 564 cm³(D) 586 cm³So the answer should be (A). However, in some multiple-choice questions, sometimes they expect you to select all that apply, but here the options are structured as separate choices. But in Chinese exams, sometimes they use parentheses to indicate multiple correct answers, but here the options are labeled (A) through (D), each being a single choice. However, option (A) says "764 or 586", which implies that both are possible, so the correct choice is (A). Therefore, the answer is boxed{A}.Wait, but hold on. The original problem might have a different intention. Let me check again.Wait, perhaps I made a mistake in the surface area calculation. Each cube's surface area is 6a², so total surface area is 6(a² + b² + c²) = 564. Therefore, a² + b² + c² = 564 / 6 = 94. That's correct. Then possible triplets (2,3,9) and (3,6,7). Then volumes sum to 764 and 586. So (A) is correct. Therefore, the answer is A. But the options given include A and D. But according to calculations, both 764 and 586 are possible, so the answer is A. However, in some multiple-choice contexts, if both are possible, but the options don't have a combined option, but in this case, option A includes both possibilities. Therefore, the answer is A.But wait, looking at the original problem statement again, it says "the sum of the volumes of these three cubes is ( )". The parentheses suggest that it's a single answer. But according to our analysis, there are two possible sums. However, maybe there is a unique solution. Maybe I missed something.Wait, let me verify once more. Are there only two triplets (2,3,9) and (3,6,7) that satisfy a² + b² + c² =94 with a,b,c integers?Let me check another possible triplet. Let's take c=7, a=5, then a²=25, so b²=45-25=20, which is not a square. c=7, a=4, then b²=45-16=29, not square. a=1, b²=45-1=44, nope. So only a=3 and 6.For c=9, a=1, then b²=13-1=12, nope. a=2, b²=9, which is 3. So (2,3,9). a=3, b²=13-9=4, which is 2. So (2,3,9) again. So no other combinations here.Another approach: Let me list all squares up to 9²=81. Squares are 1,4,9,16,25,36,49,64,81.We need three squares that sum to 94. Let's see:Starting with the largest square, 81. 94 -81=13. 13 can be 9+4. So 81+9+4=94. So that corresponds to 9,3,2.Next, next largest square is 64. 94-64=30. 30 can be 25+5, but 5 isn't a square. 16+14, nope. 9+21, nope. 4+26, nope. 1+29, nope. So no.Next, 49. 94-49=45. 45 can be 36+9=45. So 49+36+9=94. That's 7,6,3.Next, 36. 94-36=58. 58 can be 49+9=58. So 36+49+9=94. But that's same as 7,6,3.25. 94-25=69. 69 can be 64+5=69, but 5 not square. 49+20=69, nope. 36+33=69, nope. So no.16. 94-16=78. 78-64=14, not square. 78-49=29, nope. Not useful.9. 94-9=85. 85-81=4. So 9+81+4=94. Which is same as 9,3,2.So the only combinations are (81,9,4) and (49,36,9), which correspond to edge lengths (9,3,2) and (7,6,3). Therefore, these are the only two triplets. So volumes are 764 and 586. Therefore, answer is (A).But hold on, the options are given as (A) 764 or 586, (B) 764, etc. So the answer is (A). But maybe the problem expects the minimal possible volume? But why? The problem doesn't specify. It just asks for the sum. So both are correct. Hence, the answer is (A). However, in some multiple-choice settings, if both are correct but only (A) lists both, then (A) is correct. Therefore, the answer is boxed{A}.But wait, checking the options again, option D is 586. If the problem expects only one answer, perhaps there is a miscalculation. Let me check the volumes again.For (2,3,9): 8 + 27 + 729 = 764. Correct.For (3,6,7): 27 + 216 + 343 = 586. Correct.Yes, both correct. So since both are possible, the answer is (A). Hence, I think the correct option is A.Final Answerboxed{A}</think>Given three cubes with integer edge lengths, their total surface area is 564 cm². We need to find the sum of their volumes.First, we calculate the sum of the squares of the edge lengths. The surface area of a cube with edge length (a) is (6a^2). Therefore, the total surface area for three cubes is (6(a^2 + b^2 + c^2) = 564). Solving for (a^2 + b^2 + c^2):[6(a^2 + b^2 + c^2) = 564 implies a^2 + b^2 + c^2 = frac{564}{6} = 94]We need to find three integers (a, b, c) such that their squares sum to 94. After checking possible values, we find two valid triplets:1. (a = 2), (b = 3), (c = 9): [ 2^2 + 3^2 + 9^2 = 4 + 9 + 81 = 94 ] Volumes: (2^3 + 3^3 + 9^3 = 8 + 27 + 729 = 764 , text{cm}^3)2. (a = 3), (b = 6), (c = 7): [ 3^2 + 6^2 + 7^2 = 9 + 36 + 49 = 94 ] Volumes: (3^3 + 6^3 + 7^3 = 27 + 216 + 343 = 586 , text{cm}^3)Both sums of volumes, 764 cm³ and 586 cm³, are possible. Therefore, the correct answer is:[boxed{A}]]

🔑:4.A.Let the edge lengths of the three cubes be a, b, and c. Then 6left(a^{2}+b^{2}+c^{2}right)=564 Rightarrow a^{2}+b^{2}+c^{2}=94.Assume without loss of generality that 1 leqslant a leqslant b leqslant c leqslant 31.Thus, 6 leqslant c < 10. Therefore, c can only be 9, 8, 7, 6.If c=9, then a^{2}+b^{2}=94-9^{2}=13. It is easy to see that a=2, b=3, yielding the solution (a, b, c)=(2,3,9).If c=8, then a^{2}+b^{2}=94-64=30, b leqslant 5. But 2 b^{2} geqslant 30, b geqslant 4, thus, b=4 or 5. If b=5, then a^{2}=5 has no solution; if b=4, then a^{2}=14 has no solution. Thus, there is no solution in this case.If c=7, then a^{2}+b^{2}=94-49=45, with the unique solution a=3, b=6.If c=6, then a^{2}+b^{2}=94-36=58. In this case, 2 b^{2} geqslant a^{2}+b^{2}=58, b^{2} geqslant 29. Hence, b geqslant 6, but b leqslant c = 6, so b=6. At this point, a^{2}=58-36=22, which has no solution.In summary, there are two solutions:(a, b, c)=(2,3,9),(3,6,7).The volumes are V_{1}=764 mathrm{~cm}^{3} or V_{2}=586 mathrm{~cm}^{3}.

🧠:[<think>Okay, so I need to solve this problem about an ellipse. Let's start with part (I). The standard equation of the ellipse is given as x²/a² + y²/b² = 1, where a > b > 0. The eccentricity is √2/2, and the ellipse passes through the point M(-2, 0). I need to find the standard equation, which means I need to determine the values of a and b.First, let's recall that the eccentricity e of an ellipse is given by e = c/a, where c is the distance from the center to each focus, and c = √(a² - b²). The problem states that the eccentricity is √2/2, so:√2/2 = c/a => c = (√2/2) aBut c is also √(a² - b²), so:√(a² - b²) = (√2/2) aIf I square both sides to eliminate the square root:a² - b² = (2/4) a² => a² - b² = (1/2) a²Subtracting (1/2)a² from both sides:a² - (1/2)a² - b² = 0 => (1/2)a² - b² = 0 => b² = (1/2)a²So, b = (√(1/2))a = a/√2. But since a and b are positive, that's okay.Now, the ellipse passes through the point M(-2, 0). Let's plug this point into the ellipse equation:(-2)²/a² + 0²/b² = 1 => 4/a² = 1 => a² = 4 => a = 2 (since a > 0)So, a = 2. Then, from the earlier relation, b² = (1/2)a² = (1/2)(4) = 2. Therefore, b = √2.Therefore, the standard equation of the ellipse is x²/4 + y²/2 = 1.Wait, let me check again. The point M(-2, 0) is on the ellipse. Since the ellipse is centered at the origin, the vertices along the x-axis are at (±a, 0). If M(-2, 0) is on the ellipse, then the vertex is at (-2, 0), so a must be 2. That's correct. Then with a=2, the eccentricity e = √2/2, so c = (√2/2)*2 = √2. Then c = √(a² - b²) = √2, so √(4 - b²) = √2, squaring both sides gives 4 - b² = 2 => b² = 2, so b=√2. Therefore, the standard equation is x²/4 + y²/2 = 1. That seems right.So part (I) is done. The answer is x²/4 + y²/2 = 1.Now part (II) is more complicated. Let's parse the problem step by step.We have line l with a slope of 1 intersecting ellipse C at points A(x₁, y₁) and B(x₂, y₂). Then we connect MA and MB and extend them to intersect the line x=4 at points P and Q. The y-coordinates of P and Q are y_P and y_Q. We are told that 1/y₁ + 1/y₂ = 1/y_P + 1/y_Q. We need to find the area of triangle ABM.First, let's visualize this. The ellipse is centered at the origin, stretching along the x-axis from -2 to 2, and along the y-axis from -√2 to √2. The line l has a slope of 1, so it's a diagonal line. Points A and B are the intersections of this line with the ellipse. Then lines MA and MB are drawn from point M(-2, 0) to A and B, respectively. These lines are extended to intersect the vertical line x=4 at points P and Q. The given condition relates the reciprocals of the y-coordinates of A, B, P, and Q. We need to use this condition to find the area of triangle ABM.First, let's try to parametrize the line l. Since it has a slope of 1, its equation can be written as y = x + k, where k is the y-intercept. However, we need to find the points of intersection between this line and the ellipse. But since we don't know k, maybe we can write the general equation. Alternatively, perhaps we can parametrize the line as y = x + k, substitute into the ellipse equation, and then find expressions for x₁, x₂, y₁, y₂ in terms of k.But perhaps we can use the given condition to relate these variables. The problem states that 1/y₁ + 1/y₂ = 1/y_P + 1/y_Q. Maybe we can express y_P and y_Q in terms of y₁ and y₂, then use that equation to find a relationship between y₁ and y₂, which can help us find the specific line l, and then compute the area.Alternatively, maybe the condition holds for any line l with slope 1, which might imply that the area is constant, but I need to verify.Alternatively, perhaps there's some projective geometry here, but maybe we can approach it step by step.First, let's find the equation of line l. Since it's slope is 1, let's denote it as y = x + c, where c is a constant. Then, to find the points of intersection A and B between this line and the ellipse, substitute y = x + c into the ellipse equation:x²/4 + (x + c)²/2 = 1Multiply through by 4 to eliminate denominators:x² + 2(x + c)² = 4Expand the terms:x² + 2(x² + 2cx + c²) = 4x² + 2x² + 4cx + 2c² = 4Combine like terms:3x² + 4cx + (2c² - 4) = 0So this is a quadratic equation in x: 3x² + 4cx + (2c² - 4) = 0Let me denote this as 3x² + 4c x + (2c² - 4) = 0The solutions to this quadratic are the x-coordinates of points A and B. Let's denote them x₁ and x₂. Then, by Vieta's formula:x₁ + x₂ = -4c / 3x₁ x₂ = (2c² - 4) / 3Similarly, the corresponding y-coordinates are y₁ = x₁ + c and y₂ = x₂ + c.So, y₁ + y₂ = (x₁ + x₂) + 2c = (-4c/3) + 2c = (-4c + 6c)/3 = 2c/3And y₁ y₂ = (x₁ + c)(x₂ + c) = x₁x₂ + c(x₁ + x₂) + c² = (2c² -4)/3 + c(-4c/3) + c² = (2c² -4)/3 -4c²/3 + c²Combine the terms:(2c² -4 -4c² + 3c²)/3 = ( (2c² -4c² +3c²) -4 ) /3 = (1c² -4)/3 = (c² -4)/3Therefore, the sum 1/y₁ + 1/y₂ is (y₁ + y₂)/(y₁ y₂) = (2c/3) / ( (c² -4)/3 ) ) = (2c)/ (c² -4)So, 1/y₁ + 1/y₂ = 2c / (c² -4)Now, we need to find 1/y_P + 1/y_Q. Let's find expressions for y_P and y_Q.Points P and Q are the intersections of lines MA and MB with the line x=4.First, let's find the equations of lines MA and MB.Point M is (-2, 0). Point A is (x₁, y₁). The line MA connects (-2, 0) and (x₁, y₁). Let's parametrize this line.Parametric equations for MA:Starting at M(-2, 0), moving towards A(x₁, y₁). The direction vector is (x₁ + 2, y₁ - 0) = (x₁ + 2, y₁). So parametric equations can be written as:x = -2 + t(x₁ + 2)y = 0 + t y₁Where t=0 corresponds to M and t=1 corresponds to A. To find where this line intersects x=4, set x=4:4 = -2 + t(x₁ + 2)Solve for t:4 + 2 = t(x₁ + 2) => 6 = t(x₁ + 2) => t = 6/(x₁ + 2)Then the y-coordinate at this t is y = t y₁ = 6 y₁ / (x₁ + 2). Therefore, y_P = 6 y₁ / (x₁ + 2)Similarly, for line MB connecting M(-2, 0) and B(x₂, y₂), the parametric equations would be:x = -2 + s(x₂ + 2)y = 0 + s y₂To find intersection with x=4:4 = -2 + s(x₂ + 2) => 6 = s(x₂ + 2) => s = 6/(x₂ + 2)Therefore, y_Q = s y₂ = 6 y₂ / (x₂ + 2)Therefore, 1/y_P + 1/y_Q = (x₁ + 2)/(6 y₁) + (x₂ + 2)/(6 y₂) = [ (x₁ + 2)/y₁ + (x₂ + 2)/y₂ ] /6So, according to the problem statement, 1/y₁ + 1/y₂ = 1/y_P + 1/y_Q. Therefore:2c / (c² -4) = [ (x₁ + 2)/y₁ + (x₂ + 2)/y₂ ] /6Multiply both sides by 6:12c / (c² -4) = (x₁ + 2)/y₁ + (x₂ + 2)/y₂Now, let's compute (x₁ + 2)/y₁ + (x₂ + 2)/y₂.We know that y₁ = x₁ + c and y₂ = x₂ + c. So:(x₁ + 2)/(x₁ + c) + (x₂ + 2)/(x₂ + c)Let me denote this as S = [ (x₁ + 2)/(x₁ + c) + (x₂ + 2)/(x₂ + c) ]We can write each term as:(x₁ + 2)/(x₁ + c) = 1 + (2 - c)/(x₁ + c)Similarly, (x₂ + 2)/(x₂ + c) = 1 + (2 - c)/(x₂ + c)Therefore, S = 2 + (2 - c)[1/(x₁ + c) + 1/(x₂ + c)]But 1/(x₁ + c) + 1/(x₂ + c) = [ (x₂ + c) + (x₁ + c) ] / [ (x₁ + c)(x₂ + c) ] = (x₁ + x₂ + 2c) / [x₁x₂ + c(x₁ + x₂) + c²]We already have x₁ + x₂ = -4c/3 and x₁x₂ = (2c² -4)/3Therefore, numerator: x₁ + x₂ + 2c = (-4c/3) + 2c = (-4c/3 + 6c/3) = 2c/3Denominator: x₁x₂ + c(x₁ + x₂) + c² = (2c² -4)/3 + c(-4c/3) + c² = (2c² -4 -4c² +3c²)/3 = ( (2c² -4c² +3c² ) -4 ) /3 = (c² -4)/3Therefore, 1/(x₁ + c) + 1/(x₂ + c) = (2c/3) / [ (c² -4)/3 ) ] = 2c/(c² -4)Therefore, S = 2 + (2 - c)*(2c/(c² -4))So, S = 2 + [2c(2 - c)] / (c² -4)Simplify numerator of the second term: 2c(2 - c) = 4c - 2c²Therefore, S = 2 + (4c - 2c²)/(c² -4)Factor numerator and denominator:Denominator c² -4 can be written as (c -2)(c +2)Numerator: 4c -2c² = -2c² +4c = -2c(c -2)So:(4c -2c²)/(c² -4) = (-2c(c -2)) / [ (c -2)(c +2) ) ] = (-2c)/ (c +2 ) [after canceling (c -2)]Therefore, S = 2 + (-2c)/(c +2 ) = 2 - (2c)/(c + 2 )Combine the terms:2 = 2(c +2)/(c +2), so:2(c +2)/(c +2) - 2c/(c +2) = [2(c +2) -2c]/(c +2) = [2c +4 -2c]/(c +2) = 4/(c +2)Therefore, S = 4/(c +2 )But earlier, we had:12c/(c² -4) = S = 4/(c +2 )Therefore:12c/(c² -4) = 4/(c +2 )Multiply both sides by (c² -4)(c +2) to eliminate denominators:12c(c +2 ) = 4(c² -4 )Divide both sides by 4:3c(c +2 ) = c² -4Expand left side:3c² +6c = c² -4Bring all terms to left side:3c² +6c -c² +4 = 0 => 2c² +6c +4 =0Divide equation by 2:c² +3c +2 =0Factor:(c +1)(c +2) =0So solutions are c = -1 or c = -2Therefore, the possible values for c are -1 and -2. But we need to check if these values are valid, i.e., that the line y =x +c intersects the ellipse at two real points.First, c = -1. Then the line is y =x -1. Since the ellipse is x²/4 + y²/2 =1, substituting y =x -1, the quadratic equation would have real solutions. Similarly, c=-2: y =x -2. Let's check if these lines intersect the ellipse.But in general, unless the discriminant is negative, they should intersect. Let's check discriminant for c=-1:The quadratic equation for x was 3x² +4c x +2c² -4=0.For c=-1: 3x² -4x +2(1) -4 =3x² -4x -2=0Discriminant: (-4)^2 -4*3*(-2)=16 +24=40>0. So two real points.For c=-2: 3x² +4*(-2)x +2*(4) -4=3x² -8x +8 -4=3x² -8x +4=0Discriminant: (-8)^2 -4*3*4=64 -48=16>0. So also two real points. So both c=-1 and c=-2 are valid.Therefore, the lines could be y =x -1 or y =x -2. But the problem states that line l has slope 1, but didn't specify the intercept. So there are two possibilities for c. But perhaps both lead to the same area? Let's check.But the problem is asking to find the area of triangle ABM. So depending on c, the area might differ. But maybe both c=-1 and c=-2 lead to the same area? Let's check.Wait, but the problem didn't give any other condition on line l except slope 1 and passing through the ellipse, but we derived from the reciprocal condition that c must be -1 or -2. Therefore, there are two possible lines l: y =x -1 and y =x -2. So we need to find the area for each case and see if they are the same or different.Alternatively, perhaps only one of them satisfies some condition. Let's check.But first, let's compute the area for both cases.Case 1: c = -1.Then line is y =x -1. Find points A and B.The quadratic equation for x is 3x² +4*(-1)x +2*(-1)^2 -4=3x² -4x +2 -4=3x² -4x -2=0.Solutions:x = [4 ±√(16 +24)]/6 = [4 ±√40]/6 = [4 ±2√10]/6 = [2 ±√10]/3Therefore, x₁ = [2 +√10]/3, x₂ = [2 -√10]/3Then y₁ =x₁ -1 = [2 +√10]/3 -3/3 = (-1 +√10)/3Similarly, y₂ = [2 -√10]/3 -1 = (-1 -√10)/3Points A and B are ( [2 +√10]/3, (-1 +√10)/3 ) and ( [2 -√10]/3, (-1 -√10)/3 )Point M is (-2,0). To compute the area of triangle ABM, we can use the formula:Area = (1/2)| (x₁(y₂ - y_M) + x₂(y_M - y₁) + x_M(y₁ - y₂) ) | Since y_M =0, this simplifies to:Area = (1/2)| x₁ y₂ - x₂ y₁ + x_M(y₁ - y₂) |But x_M = -2.Let's compute each term:First, compute x₁ y₂ - x₂ y₁:x₁ y₂ = [ (2 +√10)/3 ] * [ (-1 -√10)/3 ] = [ (2)(-1) + 2*(-√10) + √10*(-1) + (√10)(-√10) ] /9= [ -2 -2√10 -√10 -10 ] /9 = [ -12 -3√10 ] /9Similarly, x₂ y₁ = [ (2 -√10)/3 ] * [ (-1 +√10)/3 ] = [ 2*(-1) + 2*√10 -√10*(-1) + (-√10)(√10) ] /9= [ -2 +2√10 +√10 -10 ] /9 = [ -12 +3√10 ] /9Therefore, x₁ y₂ - x₂ y₁ = [ (-12 -3√10 ) - (-12 +3√10 ) ] /9 = [ (-12 -3√10 +12 -3√10 ) ] /9 = [ -6√10 ] /9 = -2√10 /3Then compute x_M(y₁ - y₂) = -2*( [ (-1 +√10)/3 - (-1 -√10)/3 ]) = -2*( [ (-1 +√10 +1 +√10)/3 ]) = -2*(2√10/3) = -4√10 /3Therefore, total inside the absolute value:-2√10 /3 -4√10 /3 = (-6√10)/3 = -2√10Take absolute value and multiply by 1/2:Area = (1/2)*| -2√10 | = (1/2)*(2√10) = √10Case 1 gives area √10.Case 2: c = -2.Line l is y =x -2. Find points A and B.Quadratic equation: 3x² +4*(-2)x +2*(-2)^2 -4=3x² -8x +8 -4=3x² -8x +4=0Solutions:x = [8 ±√(64 -48)]/6 = [8 ±√16]/6 = [8 ±4]/6Thus, x₁ = (8 +4)/6 =12/6=2, x₂=(8-4)/6=4/6=2/3Then y₁ =x₁ -2=2-2=0, y₂=2/3 -2= -4/3Therefore, points A(2,0) and B(2/3, -4/3)Wait a minute, point A is (2,0). But point M is (-2,0). So triangle ABM has points M(-2,0), A(2,0), and B(2/3, -4/3). Let's compute its area.But if two points are on the x-axis (M and A), then the base is the distance between M and A, which is 2 - (-2) =4. The height is the absolute y-coordinate of point B, which is 4/3. Therefore, area is (1/2)*base*height= (1/2)*4*(4/3)=8/3 ≈2.666...But let's compute using the formula for consistency.Using the formula:Area = (1/2)| x₁(y₂ - y_M) + x₂(y_M - y₁) + x_M(y₁ - y₂) |Substitute:x₁=2, y₁=0; x₂=2/3, y₂=-4/3; x_M=-2, y_M=0.Compute:2*( -4/3 -0 ) + (2/3)*(0 -0 ) + (-2)*(0 - (-4/3)) =2*(-4/3) + 0 + (-2)*(4/3) =-8/3 -8/3 = -16/3Take absolute value and multiply by 1/2:(1/2)*(16/3) =8/3.So case 2 gives area 8/3. But 8/3 is approximately 2.666, while √10 is approximately 3.162. These are different. Therefore, the problem must have only one valid solution. So why do we have two possible values for c?Wait, but when c=-2, line l is y=x-2. Let's check if point A(2,0) is on the ellipse:x²/4 + y²/2 = 4/4 +0=1, which is okay. Point B(2/3, -4/3):( (2/3)^2 )/4 + ( (-4/3)^2 )/2 = (4/9)/4 + (16/9)/2 = (1/9) + (8/9) =9/9=1. Correct.But when c=-2, one of the intersection points is (2,0), which is the same as the vertex of the ellipse. Then line MA would be connecting M(-2,0) to A(2,0), which is the line y=0. Extending this line to x=4 would give point P at (4,0). Similarly, line MB connects M(-2,0) to B(2/3, -4/3). Let's compute y_P and y_Q.For line MA (from M(-2,0) to A(2,0)), parametric equations:x = -2 + t(4), y=0 + t(0). So when x=4, 4 = -2 +4t =>4t=6 =>t=1.5. Then y=0, so P=(4,0). So y_P=0. But in the given condition, we have 1/y₁ +1/y₂=1/y_P +1/y_Q. However, y_P=0, which would make 1/y_P undefined. Similarly, y₁=0, so 1/y₁ is undefined. Therefore, this case is invalid because we have division by zero.Hence, c=-2 is invalid due to division by zero in the given condition. Therefore, only c=-1 is valid. Therefore, the area is √10.Therefore, the answer to part (II) is √10.Wait, but let me verify again.When c=-2, one of the intersection points is (2,0), which is M' on the ellipse. Then MA is from M(-2,0) to A(2,0). The line MA is along the x-axis. When extended, it intersects x=4 at (4,0). But y_P=0, which would make 1/y_P undefined. Similarly, y₁=0 in this case. Since the problem statement involves 1/y₁ and 1/y₂, c=-2 would result in division by zero, which is invalid. Therefore, only c=-1 is acceptable. Therefore, the area is √10.Therefore, the answer to part (II) is √10, so area is √10.But let me check with c=-1:Points A and B are:A: x=(2 +√10)/3 ≈ (2 +3.16)/3≈5.16/3≈1.72, y= (-1 +√10)/3≈(-1 +3.16)/3≈2.16/3≈0.72B: x=(2 -√10)/3≈(2 -3.16)/3≈-1.16/3≈-0.387, y=(-1 -√10)/3≈(-1 -3.16)/3≈-4.16/3≈-1.387Point M is (-2,0). Let's compute the area using coordinates.Coordinates:M(-2,0), A( (2 +√10)/3, (-1 +√10)/3 ), B( (2 -√10)/3, (-1 -√10)/3 )We can use the shoelace formula:Area = (1/2)| x_M(y_A - y_B) + x_A(y_B - y_M) + x_B(y_M - y_A) |Plugging in:x_M = -2, y_M=0x_A=(2 +√10)/3, y_A=(-1 +√10)/3x_B=(2 -√10)/3, y_B=(-1 -√10)/3Compute each term:First term: x_M(y_A - y_B) = -2*( [ (-1 +√10)/3 - (-1 -√10)/3 ]) = -2*( [ (-1 +√10 +1 +√10)/3 ]) = -2*(2√10/3) = -4√10/3Second term: x_A(y_B - y_M) = (2 +√10)/3*( (-1 -√10)/3 -0 ) = (2 +√10)/3 * (-1 -√10)/3 = [ (2)(-1) + 2*(-√10) + √10*(-1) + √10*(-√10) ] /9 = [ -2 -2√10 -√10 -10 ] /9 = [ -12 -3√10 ] /9Third term: x_B(y_M - y_A) = (2 -√10)/3*(0 - (-1 +√10)/3 ) = (2 -√10)/3 * (1 -√10)/3 = [ 2*1 + 2*(-√10) -√10*1 + (√10)(√10) ] /9 = [ 2 -2√10 -√10 +10 ] /9 = [ 12 -3√10 ] /9Sum all three terms:First term: -4√10/3Second term: (-12 -3√10)/9 = -4/3 - √10/3Third term: (12 -3√10)/9 = 4/3 - √10/3So sum:-4√10/3 + (-4/3 - √10/3) + (4/3 - √10/3) =-4√10/3 -4/3 -√10/3 +4/3 -√10/3 =Combine constants: -4/3 +4/3 =0Combine √10 terms: -4√10/3 -√10/3 -√10/3 = (-4√10 -√10 -√10)/3 = (-6√10)/3 = -2√10Total sum: -2√10Take absolute value and multiply by 1/2:Area = (1/2)*| -2√10 | = (1/2)*2√10 = √10Yes, same result. Therefore, area is √10.Thus, part (II) answer is √10.Final Answer(I) The standard equation of ellipse ( C ) is boxed{dfrac{x^2}{4} + dfrac{y^2}{2} = 1}.(II) The area of triangle ( ABM ) is boxed{sqrt{10}}.</think>Given the ellipse ( C ): (frac{x^2}{a^2} + frac{y^2}{b^2} = 1 ) with an eccentricity of (frac{sqrt{2}}{2}) and passing through the point ( M(-2, 0) ):(I) To find the standard equation of ellipse ( C ):1. The eccentricity ( e = frac{sqrt{2}}{2} ) gives ( c = frac{sqrt{2}}{2}a ).2. Using ( c = sqrt{a^2 - b^2} ), we get ( sqrt{a^2 - b^2} = frac{sqrt{2}}{2}a ).3. Squaring both sides, ( a^2 - b^2 = frac{1}{2}a^2 ), leading to ( b^2 = frac{1}{2}a^2 ).4. Since the ellipse passes through ( M(-2, 0) ), ( a = 2 ).5. Substituting ( a = 2 ) into ( b^2 = frac{1}{2}a^2 ), we get ( b^2 = 2 ).Thus, the standard equation of the ellipse is (boxed{dfrac{x^2}{4} + dfrac{y^2}{2} = 1}).(II) To find the area of triangle ( ABM ):1. The line ( l ) with slope 1 intersects the ellipse at points ( A ) and ( B ). The equation of line ( l ) is ( y = x + c ).2. Substituting ( y = x + c ) into the ellipse equation and solving, we find the quadratic equation ( 3x^2 + 4cx + (2c^2 - 4) = 0 ).3. Using Vieta's formulas, we find the sum and product of ( x )-coordinates ( x_1 ) and ( x_2 ).4. The y-coordinates ( y_1 ) and ( y_2 ) are derived, and the given condition ( frac{1}{y_1} + frac{1}{y_2} = frac{1}{y_P} + frac{1}{y_Q} ) leads to solving for ( c ).5. Valid solutions for ( c ) are found to be ( c = -1 ) (since ( c = -2 ) leads to division by zero).6. For ( c = -1 ), the points ( A ) and ( B ) are calculated, and the area of triangle ( ABM ) is computed using the shoelace formula.The area of triangle ( ABM ) is (boxed{sqrt{10}}).,<think>Okay, so I have this problem about an ellipse. Let's take it step by step.Part I: Find the standard equation of ellipse C.First, the standard equation of an ellipse is given as (x²/a²) + (y²/b²) = 1, where a > b > 0. The eccentricity e is given as √2/2. I remember that the formula for eccentricity of an ellipse is e = c/a, where c is the distance from the center to a focus. Also, c² = a² - b². So maybe I can use that to relate a and b.Given e = √2/2 = c/a, so c = (√2/2)a. Then, since c² = a² - b², substituting c gives [(√2/2)a]² = a² - b². Let's compute that:(√2/2)² = (2/4) = 1/2, so (1/2)a² = a² - b².Rearranging, a² - (1/2)a² = b² => (1/2)a² = b². So b = a/√2. Wait, or b² = (1/2)a², so b = (a√2)/2? Wait, let me check:If b² = (1/2)a², then b = a*(1/√2) = a√2/2. Yes, that's right.Also, the ellipse passes through the point M(-2, 0). Let's plug that into the ellipse equation:(x²/a²) + (y²/b²) = 1. For point M(-2, 0), x = -2, y = 0.So (-2)²/a² + 0²/b² = 1 => 4/a² = 1 => a² = 4 => a = 2 (since a > 0).Then, from earlier, b² = (1/2)a² = (1/2)(4) = 2. So b = √2.Therefore, the standard equation is x²/4 + y²/2 = 1.Wait, let me check again. If a² = 4, then a = 2. Then b² = 2, so yes. So the standard equation should be x²/4 + y²/2 = 1. That's part I done.Part II: Area of triangle ABM.Alright, part II is more complex. Let me parse the problem again.Line l with slope 1 intersects ellipse C at points A(x₁, y₁) and B(x₂, y₂). Connect MA and MB, then extend them to intersect line x = 4 at points P and Q. Given that 1/y₁ + 1/y₂ = 1/y_P + 1/y_Q. Find the area of triangle ABM.Hmm. So we need to find the area of triangle ABM given this condition. Let's try to structure this.First, line l has slope 1, so its equation is y = x + k for some intercept k. It intersects the ellipse x²/4 + y²/2 = 1. So we can find points A and B by solving the system of equations.But maybe instead of working with y = x + k, we can use parametric equations or something else. But let's see.Let me denote line l as y = x + k. Then substitute into the ellipse equation:x²/4 + (x + k)²/2 = 1.Expand that: x²/4 + (x² + 2kx + k²)/2 = 1.Multiply through by 4 to eliminate denominators:x² + 2(x² + 2kx + k²) = 4=> x² + 2x² + 4kx + 2k² = 4=> 3x² + 4kx + (2k² - 4) = 0.That's a quadratic in x. Let's denote coefficients:A = 3, B = 4k, C = 2k² - 4.The solutions will be x = [-4k ± sqrt( (4k)^2 - 4*3*(2k² - 4) )]/(2*3)Compute discriminant D:(16k²) - 12*(2k² - 4) = 16k² - 24k² + 48 = -8k² + 48 = 48 - 8k².For real intersections, D ≥ 0 => 48 - 8k² ≥ 0 => 8k² ≤ 48 => k² ≤ 6 => |k| ≤ √6.So k can be in [-√6, √6].So the x-coordinates of A and B are given by x = [-4k ± sqrt(48 - 8k²)]/(6) = [-4k ± 2*sqrt(12 - 2k²)]/6 = [-2k ± sqrt(12 - 2k²)]/3.Hmm, maybe instead of working with k, we can parametrize the line. But perhaps there's another approach.Alternatively, maybe express the line in terms of a parameter. But maybe we need to relate points P and Q.Points P and Q are where lines MA and MB extended meet the line x = 4. So let's find equations for MA and MB, then find their intersection with x=4, which will give us points P and Q with coordinates (4, y_P) and (4, y_Q).Given point M is (-2, 0). So the line MA goes from M(-2,0) to A(x₁, y₁). Let's parametrize this line.The parametric equation for MA can be written as:x = -2 + t(x₁ + 2), y = 0 + t(y₁ - 0) = t y₁, where t ≥ 0.We need to find where this line intersects x=4. So set x = 4 = -2 + t(x₁ + 2). Solving for t:4 + 2 = t(x₁ + 2) => t = 6/(x₁ + 2).At this t value, the y-coordinate is y_P = t y₁ = (6/(x₁ + 2)) y₁.Similarly, for line MB connecting M(-2,0) to B(x₂, y₂):Parametric equations: x = -2 + s(x₂ + 2), y = s y₂.Set x=4: 4 = -2 + s(x₂ + 2) => s = 6/(x₂ + 2). Then y_Q = s y₂ = (6/(x₂ + 2)) y₂.Therefore, y_P = 6 y₁ / (x₁ + 2) and y_Q = 6 y₂ / (x₂ + 2).Given the condition: 1/y₁ + 1/y₂ = 1/y_P + 1/y_Q.Substituting y_P and y_Q:1/y₁ + 1/y₂ = (x₁ + 2)/(6 y₁) + (x₂ + 2)/(6 y₂).Multiply both sides by 6 to eliminate denominators:6(1/y₁ + 1/y₂) = (x₁ + 2)/y₁ + (x₂ + 2)/y₂.Bring all terms to left-hand side:6(1/y₁ + 1/y₂) - [(x₁ + 2)/y₁ + (x₂ + 2)/y₂] = 0.Compute each term:6/y₁ - (x₁ + 2)/y₁ = (6 - x₁ - 2)/y₁ = (4 - x₁)/y₁Similarly, 6/y₂ - (x₂ + 2)/y₂ = (4 - x₂)/y₂So overall:(4 - x₁)/y₁ + (4 - x₂)/y₂ = 0.Therefore:(4 - x₁)/y₁ + (4 - x₂)/y₂ = 0.Hmm, this is a key equation. Let's denote this equation as Equation (1).We need to relate this to the properties of the line l and points A and B.Recall that points A and B lie on the line l: y = x + k. So for points A and B, y₁ = x₁ + k and y₂ = x₂ + k.So we can express (4 - x₁)/y₁ as (4 - x₁)/(x₁ + k), and similarly for (4 - x₂)/y₂.Therefore, Equation (1) becomes:(4 - x₁)/(x₁ + k) + (4 - x₂)/(x₂ + k) = 0.Let me denote S = (4 - x₁)/(x₁ + k) + (4 - x₂)/(x₂ + k) = 0.Let me see if we can express S in terms of x₁ and x₂. Since x₁ and x₂ are the roots of the quadratic equation 3x² + 4kx + (2k² - 4) = 0, which we derived earlier.From quadratic equation: sum of roots x₁ + x₂ = -B/A = -4k/3, and product x₁ x₂ = C/A = (2k² - 4)/3.So perhaps we can express S in terms of x₁ + x₂ and x₁ x₂.Let me compute S:S = [ (4 - x₁)(x₂ + k) + (4 - x₂)(x₁ + k) ] / [ (x₁ + k)(x₂ + k) ]The numerator is:(4 - x₁)(x₂ + k) + (4 - x₂)(x₁ + k)Expand both terms:First term: 4x₂ + 4k - x₁ x₂ - k x₁Second term: 4x₁ + 4k - x₂ x₁ - k x₂Combine them:4x₂ + 4k - x₁ x₂ - k x₁ + 4x₁ + 4k - x₂ x₁ - k x₂Simplify:4x₂ + 4x₁ + 8k - 2x₁ x₂ - k(x₁ + x₂)Group terms:4(x₁ + x₂) + 8k - 2x₁ x₂ - k(x₁ + x₂)Factor:[4(x₁ + x₂) - k(x₁ + x₂)] + 8k - 2x₁ x₂= (4 - k)(x₁ + x₂) + 8k - 2x₁ x₂Now substitute x₁ + x₂ = -4k/3 and x₁ x₂ = (2k² - 4)/3:= (4 - k)(-4k/3) + 8k - 2*(2k² - 4)/3Compute term by term:First term: (4 - k)(-4k/3) = (-4k/3)(4 - k) = (-16k/3 + 4k²/3)Second term: 8k = 24k/3Third term: -2*(2k² - 4)/3 = (-4k² + 8)/3So combine all terms over 3:[ (-16k + 4k²) + 24k + (-4k² + 8) ] / 3Simplify numerator:-16k + 4k² +24k -4k² +8 = ( (-16k +24k ) + (4k² -4k² ) +8 )= 8k + 0 +8 = 8k +8Therefore, S = (8k +8)/3 / denominator.But wait, S was equal to numerator / denominator, where numerator is (8k +8)/3 and denominator is (x₁ +k)(x₂ +k). But we had set S = 0, which requires numerator =0. So:(8k +8)/3 = 0 => 8k +8 =0 => 8k = -8 => k = -1.Therefore, the value of k must be -1. Thus, the line l is y = x -1.So now we know the line l is y = x -1. Therefore, we can find points A and B by solving the intersection of y = x -1 and the ellipse x²/4 + y²/2 =1.Let's do that. Substitute y = x -1 into the ellipse equation:x²/4 + (x -1)²/2 =1.Compute (x -1)² = x² -2x +1.So:x²/4 + (x² -2x +1)/2 =1.Multiply through by 4 to eliminate denominators:x² + 2(x² -2x +1) =4=> x² + 2x² -4x +2 =4=>3x² -4x +2 -4=0=>3x² -4x -2=0Solve quadratic equation: 3x² -4x -2=0Using quadratic formula: x = [4 ± sqrt(16 +24)]/6 = [4 ± sqrt(40)]/6 = [4 ± 2*sqrt(10)]/6 = [2 ± sqrt(10)]/3.Thus, x₁ = [2 + sqrt(10)]/3 and x₂ = [2 - sqrt(10)]/3.Corresponding y₁ = x₁ -1 = [2 + sqrt(10)]/3 -1 = (-1 + sqrt(10))/3Similarly, y₂ = x₂ -1 = [2 - sqrt(10)]/3 -1 = (-1 - sqrt(10))/3So coordinates:A = ([2 + sqrt(10)]/3, (-1 + sqrt(10))/3 )B = ([2 - sqrt(10)]/3, (-1 - sqrt(10))/3 )Now, we need to find the area of triangle ABM, where M is (-2,0).The area can be computed using the shoelace formula. Let's recall the coordinates:M(-2, 0), A(x₁, y₁), B(x₂, y₂).Area = (1/2)| (x₁(y₂ - 0) + x₂(0 - y₁) + (-2)(y₁ - y₂) ) |.Simplify:= (1/2)| x₁ y₂ - x₂ y₁ -2 y₁ +2 y₂ |.Alternatively, since vectors, but maybe using determinant formula:Area = (1/2)| (x₁ - (-2))(y₂ - 0) - (x₂ - (-2))(y₁ - 0) | ?Wait, maybe better to use coordinates:Coordinates:M: (-2, 0)A: ( (2 + sqrt(10))/3, (-1 + sqrt(10))/3 )B: ( (2 - sqrt(10))/3, (-1 - sqrt(10))/3 )Compute the vectors MA and MB and take the cross product?Alternatively, use the determinant formula:Area = (1/2)| (x_A - x_M)(y_B - y_M) - (x_B - x_M)(y_A - y_M) |.Let's compute:x_A - x_M = (2 + sqrt(10))/3 - (-2) = (2 + sqrt(10))/3 + 2 = (2 + sqrt(10) +6)/3 = (8 + sqrt(10))/3y_B - y_M = (-1 - sqrt(10))/3 -0 = (-1 - sqrt(10))/3x_B - x_M = (2 - sqrt(10))/3 - (-2) = (2 - sqrt(10))/3 +2 = (2 - sqrt(10) +6)/3 = (8 - sqrt(10))/3y_A - y_M = (-1 + sqrt(10))/3 -0 = (-1 + sqrt(10))/3So determinant:(8 + sqrt(10))/3 * (-1 - sqrt(10))/3 - (8 - sqrt(10))/3 * (-1 + sqrt(10))/3Factor out 1/9:[ (8 + sqrt(10))(-1 - sqrt(10)) - (8 - sqrt(10))(-1 + sqrt(10)) ] / 9Compute numerator:First term: (8)(-1) +8(-sqrt(10)) + sqrt(10)(-1) + sqrt(10)(-sqrt(10)) = -8 -8sqrt(10) -sqrt(10) -10 = (-8 -10) + (-8sqrt(10) -sqrt(10)) = -18 -9sqrt(10)Second term: (8 - sqrt(10))(-1 + sqrt(10)) = 8*(-1) +8*sqrt(10) -sqrt(10)*(-1) + sqrt(10)*sqrt(10) = -8 +8sqrt(10) +sqrt(10) +10 = (-8 +10) + (8sqrt(10) +sqrt(10)) = 2 +9sqrt(10)So numerator:[ (-18 -9sqrt(10)) - (2 +9sqrt(10)) ] = -18 -9sqrt(10) -2 -9sqrt(10) = -20 -18sqrt(10)Therefore, determinant is (-20 -18sqrt(10))/9Take absolute value and multiply by 1/2:Area = (1/2)*| (-20 -18sqrt(10))/9 | = (1/2)*(20 +18sqrt(10))/9 = (20 +18sqrt(10))/18 = (10 +9sqrt(10))/9.Wait, simplifying:20/18 = 10/9, 18sqrt(10)/18 = sqrt(10). So 10/9 + sqrt(10). But 10/9 + sqrt(10) is the same as (10 +9sqrt(10))/9.But perhaps they want it simplified further. Alternatively, maybe I made a mistake in calculation.Wait, let me check the determinant calculation again step by step:First term: (8 + sqrt(10))(-1 - sqrt(10)) = 8*(-1) +8*(-sqrt(10)) + sqrt(10)*(-1) + sqrt(10)*(-sqrt(10)) = -8 -8sqrt(10) -sqrt(10) -10 = (-8 -10) + (-8sqrt(10) -sqrt(10)) = -18 -9sqrt(10).Second term: (8 - sqrt(10))(-1 + sqrt(10)) = 8*(-1) +8*sqrt(10) -sqrt(10)*(-1) + sqrt(10)*sqrt(10) = -8 +8sqrt(10) +sqrt(10) +10 = (-8 +10) + (8sqrt(10) +sqrt(10)) = 2 +9sqrt(10).Then numerator: [ (-18 -9sqrt(10)) - (2 +9sqrt(10)) ] = (-18 -9sqrt(10) -2 -9sqrt(10)) = -20 -18sqrt(10).So determinant is (-20 -18sqrt(10))/9. The absolute value is (20 +18sqrt(10))/9. Then area is (1/2)*(20 +18sqrt(10))/9 = (20 +18sqrt(10))/18 = divide numerator and denominator by 2: (10 +9sqrt(10))/9.But let's see if this simplifies further. 10/9 + sqrt(10). Alternatively, factor numerator: 10 +9sqrt(10) = sqrt(10)*(9) +10. Hmm, not sure.But maybe this is the simplest form.Alternatively, perhaps I miscalculated the area. Let me try another approach.Alternatively, use coordinates of the three points and apply shoelace formula.Points:M(-2,0)A( (2 + sqrt(10))/3 , (-1 + sqrt(10))/3 )B( (2 - sqrt(10))/3 , (-1 - sqrt(10))/3 )Shoelace formula:Area = (1/2)| x₁y₂ + x₂y₃ + x₃y₁ - x₂y₁ -x₃y₂ -x₁y₃ |Where (x₁,y₁) = M(-2,0), (x₂,y₂)=A, (x₃,y₃)=B.Compute:Term1 = x₁y₂ = (-2)*[ (-1 - sqrt(10))/3 ] = [2 + 2sqrt(10)]/3Term2 = x₂y₃ = [ (2 + sqrt(10))/3 ]*[ (-1 - sqrt(10))/3 ] = Let's compute this:(2 + sqrt(10))(-1 - sqrt(10)) = -2 -2sqrt(10) -sqrt(10) -10 = -12 -3sqrt(10)Thus, Term2 = (-12 -3sqrt(10))/9 = (-4 -sqrt(10))/3Term3 = x₃y₁ = [ (2 - sqrt(10))/3 ]*0 =0Term4 = x₂y₁ = [ (2 + sqrt(10))/3 ]*0 =0Term5 = x₃y₂ = [ (2 - sqrt(10))/3 ]*[ (-1 + sqrt(10))/3 ] = Let's compute:(2 - sqrt(10))(-1 + sqrt(10)) = -2 +2sqrt(10) +sqrt(10) -10 = -12 +3sqrt(10)Thus, Term5 = (-12 +3sqrt(10))/9 = (-4 + sqrt(10))/3Term6 = x₁y₃ = (-2)*[ (-1 - sqrt(10))/3 ] = [2 + 2sqrt(10)]/3Putting it all together:Area = (1/2)| [Term1 + Term2 + Term3] - [Term4 + Term5 + Term6] |= (1/2)| [ (2 + 2sqrt(10))/3 + (-4 -sqrt(10))/3 +0 ] - [0 + (-4 + sqrt(10))/3 + (2 + 2sqrt(10))/3 ] |Compute each bracket:First bracket:(2 + 2sqrt(10))/3 + (-4 -sqrt(10))/3 = [2 -4 +2sqrt(10) -sqrt(10)]/3 = (-2 + sqrt(10))/3Second bracket:(-4 + sqrt(10))/3 + (2 + 2sqrt(10))/3 = [ -4 +2 +sqrt(10) +2sqrt(10) ]/3 = (-2 + 3sqrt(10))/3Thus, Area = (1/2)| (-2 + sqrt(10))/3 - (-2 + 3sqrt(10))/3 | = (1/2)| [ (-2 + sqrt(10)) - (-2 + 3sqrt(10)) ]/3 | = (1/2)| [ (-2 + sqrt(10) +2 -3sqrt(10)) ]/3 | = (1/2)| [ (-2sqrt(10)) /3 | = (1/2)*(2sqrt(10)/3) = sqrt(10)/3.Wait, this is different from the previous result. Hmm. Which one is correct?Wait, the shoelace formula gives sqrt(10)/3. Let's check the calculations again.First bracket:Term1 = x₁y₂ = (-2)*[ (-1 - sqrt(10))/3 ] = [2 + 2sqrt(10)]/3.Term2 = x₂y₃ = [ (2 + sqrt(10))/3 ]*[ (-1 - sqrt(10))/3 ].Compute (2 + sqrt(10))*(-1 - sqrt(10)):= -2 -2sqrt(10) -sqrt(10) - (sqrt(10))^2= -2 -3sqrt(10) -10= -12 -3sqrt(10)Then divided by 9: (-12 -3sqrt(10))/9 = (-4 -sqrt(10))/3.Term3 = x₃y₁ =0.Sum of first three terms: [2 + 2sqrt(10)]/3 + [ -4 -sqrt(10) ]/3 +0 = [2 +2sqrt(10) -4 -sqrt(10)]/3 = (-2 + sqrt(10))/3.Second bracket:Term4 = x₂y₁ =0.Term5 = x₃y₂ = [ (2 - sqrt(10))/3 ]*[ (-1 + sqrt(10))/3 ].Multiply (2 - sqrt(10))*(-1 + sqrt(10)):= -2 +2sqrt(10) +sqrt(10) - (sqrt(10))^2= -2 +3sqrt(10) -10= -12 +3sqrt(10)Divide by9: (-12 +3sqrt(10))/9 = (-4 +sqrt(10))/3.Term6 = x₁y₃ = (-2)*[ (-1 - sqrt(10))/3 ] = same as Term1: [2 +2sqrt(10)]/3.Sum of second three terms:0 + (-4 +sqrt(10))/3 + [2 +2sqrt(10)]/3 = [ -4 +sqrt(10) +2 +2sqrt(10) ]/3 = [ -2 +3sqrt(10) ]/3.Now subtract the second bracket from the first bracket:First bracket - Second bracket = [ (-2 + sqrt(10))/3 ] - [ (-2 +3sqrt(10))/3 ] = [ (-2 + sqrt(10)) - (-2 +3sqrt(10)) ]/3 = [ -2 + sqrt(10) +2 -3sqrt(10) ]/3 = [ -2sqrt(10) ]/3.Take absolute value and multiply by 1/2:Area = (1/2)*| -2sqrt(10)/3 | = (1/2)*(2sqrt(10)/3) = sqrt(10)/3.Therefore, the area is sqrt(10)/3. So the first method had an error, perhaps in the setup. The shoelace formula gives sqrt(10)/3, which seems simpler. Let me check the cross product approach again.Alternatively, vectors MA and MB. The area is (1/2)|MA × MB|.Compute vectors:MA = A - M = [ (2 + sqrt(10))/3 - (-2), (-1 + sqrt(10))/3 -0 ] = [ (8 + sqrt(10))/3, (-1 + sqrt(10))/3 ]MB = B - M = [ (2 - sqrt(10))/3 - (-2), (-1 - sqrt(10))/3 -0 ] = [ (8 - sqrt(10))/3, (-1 - sqrt(10))/3 ]Cross product MA × MB is:( (8 + sqrt(10))/3 )*( (-1 - sqrt(10))/3 ) - ( (8 - sqrt(10))/3 )*( (-1 + sqrt(10))/3 )Compute each term:First term: (8 + sqrt(10))*(-1 - sqrt(10)) = -8 -8sqrt(10) -sqrt(10) -10 = -18 -9sqrt(10)Second term: (8 - sqrt(10))*(-1 + sqrt(10)) = -8 +8sqrt(10) +sqrt(10) -10 = -18 +9sqrt(10)Thus, cross product:[ (-18 -9sqrt(10)) - (-18 +9sqrt(10)) ] /9 = [ (-18 -9sqrt(10)) +18 -9sqrt(10) ] /9 = (-18sqrt(10))/9 = -2sqrt(10)Take absolute value and multiply by 1/2: | -2sqrt(10) |*(1/2) = 2sqrt(10)*(1/2) = sqrt(10). Wait, this contradicts the shoelace result.Wait, no. Wait, the cross product here is already divided by 9?Wait, no. Wait, when I calculated MA × MB, each component was divided by 3. So:MA × MB = [ (8 + sqrt(10))/3 * (-1 - sqrt(10))/3 - (8 - sqrt(10))/3 * (-1 + sqrt(10))/3 ]= [ ( (-18 -9sqrt(10)) )/9 - ( (-18 +9sqrt(10)) )/9 ]= [ (-18 -9sqrt(10) +18 -9sqrt(10)) /9 ]= [ -18sqrt(10)/9 ] = -2sqrt(10)Then the cross product magnitude is 2sqrt(10), so area is (1/2)*2sqrt(10) = sqrt(10). Wait, now conflicting results.But wait, the cross product formula gives area as half the magnitude of the cross product. But if the vectors are in 3D, but since all z-components are zero, the cross product's magnitude is |MA_x * MB_y - MA_y * MB_x|, which is exactly the determinant we computed earlier. So why the discrepancy?Wait, in the shoelace formula, we obtained sqrt(10)/3, but here with the cross product, we have sqrt(10). Wait, perhaps miscalculation.Wait, let's recompute MA × MB:MA = [ (8 + sqrt(10))/3, (-1 + sqrt(10))/3 ]MB = [ (8 - sqrt(10))/3, (-1 - sqrt(10))/3 ]Cross product is MA_x * MB_y - MA_y * MB_x= ( (8 + sqrt(10))/3 )*( (-1 - sqrt(10))/3 ) - ( (-1 + sqrt(10))/3 )*( (8 - sqrt(10))/3 )Compute first term:(8 + sqrt(10))(-1 - sqrt(10))/9 = (-8 -8sqrt(10) -sqrt(10) -10)/9 = (-18 -9sqrt(10))/9 = -2 - sqrt(10)Second term:(-1 + sqrt(10))(8 - sqrt(10))/9 = (-8 + sqrt(10) +8sqrt(10) -10)/9 = (-18 +9sqrt(10))/9 = -2 + sqrt(10)Therefore, cross product:(-2 - sqrt(10)) - (-2 + sqrt(10)) = (-2 - sqrt(10)) +2 -sqrt(10) = -2sqrt(10)Thus, cross product is -2sqrt(10), so magnitude is 2sqrt(10). Hence, area is (1/2)*2sqrt(10) = sqrt(10).But this contradicts the shoelace formula which gave sqrt(10)/3. There must be an error.Wait, let me redo the shoelace formula step-by-step:Coordinates:M(-2, 0)A( (2 + sqrt(10))/3, (-1 + sqrt(10))/3 )B( (2 - sqrt(10))/3, (-1 - sqrt(10))/3 )Shoelace formula:Area = (1/2)|x₁(y₂ - y₃) + x₂(y₃ - y₁) + x₃(y₁ - y₂)|Wait, maybe I used a different order before. Let me check the order of the points.Alternatively, arrange the points in order M, A, B and apply the formula.So:List the coordinates three times:M(-2,0), A( (2 + s)/3, (-1 + s)/3 ), B( (2 - s)/3, (-1 -s)/3 ), where s = sqrt(10).Compute:Sum1 = x_M*(y_A - y_B) + x_A*(y_B - y_M) + x_B*(y_M - y_A)Compute each term:Term1: x_M*(y_A - y_B) = (-2)*[ (-1 + s)/3 - (-1 -s)/3 ] = (-2)*[ ( (-1 +s) +1 +s )/3 ] = (-2)*(2s/3) = (-4s)/3Term2: x_A*(y_B - y_M) = ( (2 + s)/3 )*( (-1 -s)/3 -0 ) = (2 + s)/3 * (-1 -s)/3 = ( - (2 + s)(1 + s) )/9Expand numerator: -(2(1) +2s +s*1 +s^2) = -(2 +3s +s²)So Term2 = -(2 +3s +s²)/9Term3: x_B*(y_M - y_A) = ( (2 - s)/3 )*(0 - (-1 +s)/3 ) = (2 - s)/3 * (1 -s)/3 = (2 -s)(1 -s)/9Expand numerator: 2*1 -2s -s*1 +s² = 2 -3s +s²Term3 = (2 -3s +s²)/9Sum all terms:Sum1 = (-4s)/3 + [ -(2 +3s +s²) + (2 -3s +s²) ] /9Simplify the bracketed terms:-(2 +3s +s²) + (2 -3s +s²) = -2 -3s -s² +2 -3s +s² = (-2 +2) + (-3s -3s) + (-s² +s²) = -6sThus, Sum1 = (-4s)/3 + (-6s)/9 = (-4s)/3 - (2s)/3 = (-6s)/3 = -2sTake absolute value and multiply by 1/2:Area = (1/2)| -2s | = (1/2)(2s) = s = sqrt(10)Wait, so using the shoelace formula correctly, the area is sqrt(10). But earlier, when I applied the shoelace formula with a different ordering, I got sqrt(10)/3. There must have been an error in the initial application. Indeed, perhaps I messed up the order of the points or the signs.Yes, seems like the correct area is sqrt(10). But wait, cross product gives the same. So why did the first shoelace calculation give sqrt(10)/3? Probably because I messed up the order of the points or the formula.In the first shoelace calculation, I might have considered the points in a different order, leading to a different result. The correct area should indeed be sqrt(10).Wait, but according to the cross product and the corrected shoelace formula, the area is sqrt(10). But according to the previous shoelace attempt, it was sqrt(10)/3. Which is correct?Let me check with specific values. Let's compute coordinates numerically:Compute coordinates of A and B:s = sqrt(10) ≈3.1623A_x = (2 +3.1623)/3 ≈5.1623/3≈1.7208A_y = (-1 +3.1623)/3≈2.1623/3≈0.7208B_x = (2 -3.1623)/3≈-1.1623/3≈-0.3874B_y = (-1 -3.1623)/3≈-4.1623/3≈-1.3874M is (-2,0)Using shoelace formula:Coordinates:M(-2,0), A(1.7208,0.7208), B(-0.3874,-1.3874)Compute area:Using formula:Area = (1/2)| x1(y2 - y3) +x2(y3 - y1) +x3(y1 - y2)|Plugging in:x1 = -2, y1=0x2 =1.7208, y2=0.7208x3=-0.3874, y3=-1.3874Compute:Term1 = -2*(0.7208 - (-1.3874)) = -2*(2.1082) ≈-4.2164Term2 =1.7208*(-1.3874 -0) ≈1.7208*(-1.3874)≈-2.389Term3 =-0.3874*(0 -0.7208)≈-0.3874*(-0.7208)≈0.2796Sum = -4.2164 -2.389 +0.2796≈-6.3268Absolute value times 1/2: (1/2)*6.3268≈3.1634Which is approximately sqrt(10)≈3.1623, so correct. Therefore, the area is sqrt(10).But in the previous shoelace attempt, I got sqrt(10)/3≈1.054. But when computed numerically, it's about3.16, which is sqrt(10). Hence, the correct area is sqrt(10). Therefore, the mistake was in the first shoelace application where perhaps the point order was incorrect or a sign error occurred.Therefore, the area of triangle ABM is sqrt(10).But wait, let's check the cross product method again. The cross product gave us |MA × MB| = 2sqrt(10), so area is (1/2)*2sqrt(10)=sqrt(10). Correct.So conclusion: the area is sqrt(10). Therefore, the answer is sqrt(10), which in boxed form is boxed{sqrt{10}}.Final AnswerI. boxed{dfrac{x^2}{4} + dfrac{y^2}{2} = 1}II. boxed{sqrt{10}}</think>Given the ellipse ( C ): (frac{x^2}{a^2} + frac{y^2}{b^2} = 1 ) with an eccentricity of (frac{sqrt{2}}{2}) and passing through the point ( M(-2, 0) ):(I) Finding the standard equation of ellipse ( C ):1. The eccentricity ( e = frac{sqrt{2}}{2} ) gives ( frac{c}{a} = frac{sqrt{2}}{2} ), hence ( c = frac{sqrt{2}}{2}a ).2. Using ( c^2 = a^2 - b^2 ), we substitute ( c ) to get ( left(frac{sqrt{2}}{2}aright)^2 = a^2 - b^2 ), leading to ( frac{1}{2}a^2 = a^2 - b^2 ). Solving this gives ( b^2 = frac{1}{2}a^2 ).3. The ellipse passes through ( M(-2, 0) ), so substituting ( x = -2 ) and ( y = 0 ) into the ellipse equation gives ( frac{4}{a^2} = 1 ), hence ( a^2 = 4 ) and ( a = 2 ).4. Substituting ( a^2 = 4 ) into ( b^2 = frac{1}{2}a^2 ) gives ( b^2 = 2 ).Thus, the standard equation of the ellipse is (boxed{frac{x^2}{4} + frac{y^2}{2} = 1}).(II) Finding the area of triangle ( ABM ):1. The line ( l ) with slope 1 is ( y = x + k ). Substituting into the ellipse equation gives ( 3x^2 + 4kx + 2k^2 - 4 = 0 ).2. Using the condition (frac{1}{y_1} + frac{1}{y_2} = frac{1}{y_P} + frac{1}{y_Q}), we derive that ( k = -1 ), so the line equation is ( y = x - 1 ).3. Solving the intersection of ( y = x - 1 ) with the ellipse gives points ( A ) and ( B ). The quadratic equation ( 3x^2 - 4x - 2 = 0 ) has roots ( x_1 = frac{2 + sqrt{10}}{3} ) and ( x_2 = frac{2 - sqrt{10}}{3} ).4. Corresponding ( y )-coordinates are ( y_1 = frac{-1 + sqrt{10}}{3} ) and ( y_2 = frac{-1 - sqrt{10}}{3} ).5. Using the shoelace formula or cross product method, the area of triangle ( ABM ) is calculated to be (sqrt{10}).Thus, the area of triangle ( ABM ) is (boxed{sqrt{10}}).]

🔑:(I) Since the ellipse C: frac{x^{2}}{a^{2}} + frac{y^{2}}{b^{2}} = 1 (a > b > 0) has an eccentricity of frac{sqrt{2}}{2} and passes through point M(-2, 0), we have a = 2, frac{c}{a} = frac{sqrt{2}}{2}, hence c = sqrt{2}. Since a^{2} = b^{2} + c^{2}, we have b = sqrt{2}. The standard equation of the ellipse is frac{x^{2}}{4} + frac{y^{2}}{2} = 1.(II) As the slope of line l is 1, we can express l as y = x + m. Solving the system of equations begin{cases} x^{2} + 2y^{2} = 4 y = x + m end{cases}, we eliminate y to get 3x^{2} + 4mx + 2m^{2} - 4 = 0. Since A(x_1, y_1) and B(x_2, y_2) are the intersection points, we have x_1 + x_2 = -frac{4m}{3} and x_1 x_2 = frac{2m^{2} - 4}{3}.Let the equation of line MA be y = frac{y_1}{x_1 + 2}(x + 2). Then y_P = frac{6y_1}{x_1 + 2} and similarly, y_Q = frac{6y_2}{x_2 + 2}.Given that frac{1}{y_1} + frac{1}{y_2} = frac{1}{y_P} + frac{1}{y_Q}, we have frac{x_1 - 4}{6y_1} + frac{x_2 - 4}{6y_2} = 0. This implies (x_1 - 4)y_2 + (x_2 - 4)y_1 = 0. Substituting y_1 and y_2 with their expressions in terms of m, x_1, and x_2, and solving for m, we find m = -1.Consequently, x_1 + x_2 = frac{4}{3} and x_1 x_2 = -frac{2}{3}. Let S denote the area of triangle ABM and N be the intersection point of line l and the x-axis. Then, S = frac{1}{2} cdot |MN| cdot |y_1 - y_2| = frac{3}{2} cdot |x_1 - x_2| = frac{3}{2} cdot sqrt{(x_1 + x_2)^{2} - 4x_1 x_2} = sqrt{10}.Thus, the area of triangle ABM is boxed{S = sqrt{10}}.

🧠:[<think>Okay, so I need to solve this geometry problem involving a regular hexagon. Let me first visualize the hexagon and label the vertices properly. A regular hexagon has all sides equal and all internal angles equal to 120 degrees. The vertices are labeled in order: A, B, C, D, E, F. The problem states that in regular hexagon ABCDEF, the diagonals AC and CE are divided by internal points M and N respectively, such that the ratio AM:AC = CN:CE = r. We need to determine r given that points B, M, and N lie on the same straight line.First, let me sketch the hexagon. Let's recall that in a regular hexagon, opposite sides are parallel, and the diagonals connecting non-adjacent vertices have different lengths. The diagonals that span two vertices (like AC) are longer than the sides, and the ones that span three vertices (like AD) are the longest, equal to twice the side length.But maybe coordinates would help here. Let me assign coordinates to the hexagon vertices. Since a regular hexagon can be inscribed in a circle, let's place it on a coordinate system with center at the origin. Let's assume the side length is 1 for simplicity. The coordinates of the vertices can be determined using trigonometric functions.Let's assign vertex A at (1, 0). Then moving 60 degrees each time:- Vertex B will be at (cos(60°), sin(60°)) = (0.5, √3/2)- Vertex C is at (-0.5, √3/2)- Vertex D is at (-1, 0)- Vertex E is at (-0.5, -√3/2)- Vertex F is at (0.5, -√3/2)Wait, is that right? Let me confirm. If we start at (1,0) and go counterclockwise by 60 degrees each time. So, starting from A(1,0):- B: 60 degrees: (cos 0°, sin 0°) rotated 60 degrees. Wait, maybe it's better to parameterize the hexagon.Alternatively, the coordinates of a regular hexagon with side length 1 can be given as:A: (1, 0)B: (1/2, √3/2)C: (-1/2, √3/2)D: (-1, 0)E: (-1/2, -√3/2)F: (1/2, -√3/2)Yes, that seems correct. Each vertex is separated by 60 degrees. So, the coordinates are correct.Now, diagonals AC and CE. Let me confirm the coordinates of these diagonals.Diagonal AC connects points A(1, 0) to C(-1/2, √3/2). Similarly, diagonal CE connects C(-1/2, √3/2) to E(-1/2, -√3/2).Wait, point C is at (-1/2, √3/2) and E is at (-1/2, -√3/2). So CE is a vertical line segment from (-1/2, √3/2) to (-1/2, -√3/2). Similarly, AC is the line from (1, 0) to (-1/2, √3/2). Points M and N divide AC and CE respectively in the ratio r. Specifically, AM:AC = r, so M divides AC such that AM is r times the length of AC. Similarly, CN:CE = r, so CN is r times CE. But since CE is a vertical segment from C to E, then N is located r fraction along CE from C towards E.We need to find r such that points B, M, N are colinear.So the plan is:1. Find coordinates of M and N in terms of r.2. Write the equation of the line BM and check if N lies on it.3. Solve for r.Let me proceed step by step.First, let's find the coordinates of points M and N.Starting with point M on diagonal AC.Coordinates of A: (1, 0)Coordinates of C: (-1/2, √3/2)The vector from A to C is C - A = (-1/2 - 1, √3/2 - 0) = (-3/2, √3/2)So, point M divides AC such that AM:AC = r. Therefore, M = A + r*(C - A) = (1, 0) + r*(-3/2, √3/2) = (1 - (3r/2), 0 + (√3 r)/2) = (1 - (3r/2), (√3 r)/2)Similarly, point N is on diagonal CE such that CN:CE = r.Coordinates of C: (-1/2, √3/2)Coordinates of E: (-1/2, -√3/2)The vector from C to E is E - C = (-1/2 - (-1/2), -√3/2 - √3/2) = (0, -√3)Therefore, point N is located r fraction along CE from C to E. So, N = C + r*(E - C) = (-1/2, √3/2) + r*(0, -√3) = (-1/2, √3/2 - √3 r) = (-1/2, √3/2 (1 - 2r))Wait, because √3/2 - √3 r = √3(1/2 - r). Hmm, but to make it clearer, maybe factor √3/2(1 - 2r). Wait, √3/2 - √3 r = √3(1/2 - r). Alternatively, factor out √3: √3*(1/2 - r). Either way.But let me check:N's y-coordinate: starting at C which is at √3/2, moving down by r times the total length of CE. The length of CE is the distance from C to E, which is √[( -1/2 - (-1/2))² + (-√3/2 - √3/2)²] = √[0 + (-√3)²] = √[3] = √3. So CE is of length √3. So moving from C towards E by r times √3. But since CE is vertical downward, the movement is purely in the y-direction. So each unit along CE corresponds to 1 unit down in the coordinate.Wait, no. The coordinates are in terms of the unit circle. Wait, CE is from (-1/2, √3/2) to (-1/2, -√3/2). So the length is √3/2 - (-√3/2) = √3. So the vector from C to E is (0, -√3). So moving from C by t*(0, -√3) would reach E when t=1. So if CN:CE = r, then N is located at C + r*(E - C) = C + r*(0, -√3) = (-1/2, √3/2 - r√3). So that gives N as (-1/2, √3/2 - r√3).Alternatively, we can parametrize CE. The coordinates of CE can be parametrized as x = -1/2, y = √3/2 - t, where t ranges from 0 to √3. But since we need the ratio CN:CE = r, then the distance from C to N is r*√3. Therefore, the coordinates would be (-1/2, √3/2 - r*√3). But since the parametric equation in terms of t (the parameter) could be different. Wait, maybe I should think in terms of parametric coordinates.Alternatively, since CE is a vertical line segment from C(-1/2, √3/2) to E(-1/2, -√3/2), moving from C to E, the y-coordinate decreases by √3. Therefore, if CN:CE = r, then the y-coordinate of N is √3/2 - r*(√3). Because the total change in y is -√3, so moving r fraction along CE would subtract r*√3 from the y-coordinate of C.So coordinates of N: (-1/2, √3/2 - r√3)Wait, but let me check with the vector approach. The vector CE is (0, -√3), so starting at C, adding r*(0, -√3) gives N as (-1/2, √3/2 - r√3). Yes, that seems correct.Similarly, for point M on AC: coordinates are (1 - 3r/2, √3 r /2). Let me verify:From A(1,0) to C(-1/2, √3/2), the displacement is (-3/2, √3/2). So moving r fraction along this displacement from A gives M as (1 + (-3/2)*r, 0 + (√3/2)*r) = (1 - (3r/2), (√3 r)/2). Correct.So coordinates of M: (1 - (3r/2), (√3 r)/2)Coordinates of N: (-1/2, √3/2 - r√3)Coordinates of B: (1/2, √3/2)Now, we need points B(1/2, √3/2), M(1 - 3r/2, √3 r /2), and N(-1/2, √3/2 - r√3) to lie on the same straight line.To check if three points are colinear, we can use the slope between B and M, and between B and N, and set them equal. Alternatively, use the area of the triangle formed by the three points and set it to zero.Let me use the slope method.First, find the slope from B to M.Coordinates of B: (1/2, √3/2)Coordinates of M: (1 - (3r/2), (√3 r)/2)Slope BM = [ ( (√3 r)/2 - √3/2 ) / (1 - 3r/2 - 1/2 ) ]Simplify numerator:( (√3 r)/2 - √3/2 ) = √3/2 (r - 1)Denominator:(1 - 3r/2 - 1/2 ) = (1 - 1/2) - 3r/2 = 1/2 - 3r/2 = (1 - 3r)/2Therefore, slope BM = [ √3/2 (r - 1) ] / [ (1 - 3r)/2 ] = [ √3 (r - 1) ] / (1 - 3r ) = [ √3 ( - (1 - r) ) ] / (1 - 3r ) = [ -√3 (1 - r) ] / (1 - 3r )Similarly, slope BN is the slope from B(1/2, √3/2) to N(-1/2, √3/2 - r√3 )Compute slope BN:Numerator: ( √3/2 - r√3 - √3/2 ) = - r√3Denominator: (-1/2 - 1/2 ) = -1Therefore, slope BN = ( - r√3 ) / ( -1 ) = r√3For points B, M, N to be colinear, the slopes BM and BN must be equal. Therefore:[ -√3 (1 - r) ] / (1 - 3r ) = r√3We can divide both sides by √3:[ - (1 - r) ] / (1 - 3r ) = rMultiply numerator and denominator:- (1 - r) = r (1 - 3r )Expand both sides:-1 + r = r - 3r²Simplify:Left side: -1 + rRight side: r - 3r²Subtract right side from both sides:-1 + r - r + 3r² = 0Simplify:-1 + 0 + 3r² = 0 => 3r² - 1 = 0Therefore, 3r² = 1 => r² = 1/3 => r = ±1/√3But since r is a ratio of lengths, it must be positive. Also, since M and N are internal points on AC and CE, r must be between 0 and 1.Check if r = 1/√3 ≈ 0.577, which is less than 1. So acceptable.Therefore, r = 1/√3. But let's rationalize the denominator: 1/√3 = √3/3.So r = √3/3.Wait, but let me verify the algebra again to ensure there was no mistake.Starting from:[ -√3 (1 - r) ] / (1 - 3r ) = r√3Divide both sides by √3:- (1 - r) / (1 - 3r) = rMultiply both sides by (1 - 3r):- (1 - r) = r (1 - 3r )Expand right side:-1 + r = r - 3r²Bring all terms to left side:-1 + r - r + 3r² = 0 => -1 + 3r² = 0 => 3r² = 1 => r² = 1/3 => r = 1/√3Yes, that seems correct.But let me confirm with another method, maybe using coordinates to find the equation of line BM and check if N lies on it.Equation of line BM: passing through points B(1/2, √3/2) and M(1 - 3r/2, √3 r /2 )Let me parametrize this line.Parametric equations:x = 1/2 + t*( (1 - 3r/2) - 1/2 ) = 1/2 + t*( (1 - 3r/2 - 1/2 ) ) = 1/2 + t*( (1/2 - 3r/2 ) )y = √3/2 + t*( (√3 r /2 ) - √3/2 ) = √3/2 + t*( √3/2 ( r - 1 ) )We need to see if point N(-1/2, √3/2 - r√3 ) lies on this line.So we need to find t such that:x = -1/2 = 1/2 + t*( (1 - 3r)/2 )andy = √3/2 - r√3 = √3/2 + t*( √3/2 ( r - 1 ) )Let me solve for t from the x-coordinate equation:-1/2 = 1/2 + t*( (1 - 3r)/2 )Subtract 1/2:-1 = t*( (1 - 3r)/2 )Multiply both sides by 2:-2 = t*(1 - 3r )Thus, t = -2 / (1 - 3r )Now substitute this t into the y-coordinate equation:√3/2 - r√3 = √3/2 + [ -2 / (1 - 3r ) ] * ( √3/2 ( r - 1 ) )Simplify the right side:√3/2 + [ -2 / (1 - 3r ) ] * [ √3/2 ( r - 1 ) ]Factor out √3/2:√3/2 [ 1 + ( -2 / (1 - 3r ) ) * ( r - 1 ) ]Compute the expression in the brackets:1 + [ -2 ( r - 1 ) / (1 - 3r ) ]Note that ( r - 1 ) = - ( 1 - r ), so:1 + [ -2 * - (1 - r ) / (1 - 3r ) ] = 1 + [ 2 (1 - r ) / (1 - 3r ) ]Therefore, the entire right side becomes:√3/2 [ 1 + 2(1 - r)/(1 - 3r ) ]Set this equal to the left side, which is √3/2 - r√3. Let's factor out √3/2:Left side: √3/2 (1 - 2r )Thus:√3/2 (1 - 2r ) = √3/2 [ 1 + 2(1 - r)/(1 - 3r ) ]Cancel √3/2 from both sides:1 - 2r = 1 + 2(1 - r)/(1 - 3r )Subtract 1 from both sides:-2r = 2(1 - r)/(1 - 3r )Multiply both sides by (1 - 3r ):-2r (1 - 3r ) = 2(1 - r )Expand left side:-2r + 6r² = 2 - 2rBring all terms to left side:-2r + 6r² - 2 + 2r = 0Simplify:6r² - 2 = 0 => 6r² = 2 => r² = 1/3 => r = 1/√3Same result as before. So it's confirmed that r = 1/√3, which is equivalent to √3/3.Therefore, the value of r is √3 divided by 3.But let me check once more with vector methods to ensure there's no mistake.Another approach: vectors.Points B, M, N colinear implies that vectors BM and BN are scalar multiples.Coordinates:B(1/2, √3/2)M(1 - 3r/2, √3 r /2 )N(-1/2, √3/2 - r√3 )Vector BM = M - B = (1 - 3r/2 - 1/2, √3 r /2 - √3/2 ) = (1/2 - 3r/2, √3/2 ( r - 1 ) )Vector BN = N - B = (-1/2 - 1/2, √3/2 - r√3 - √3/2 ) = (-1, -r√3 )For BM and BN to be colinear, BM = k * BN for some scalar k.Therefore:(1/2 - 3r/2, √3/2 ( r - 1 ) ) = k * (-1, -r√3 )So, component-wise:1/2 - 3r/2 = -k ...(1)√3/2 (r - 1 ) = -k r√3 ...(2)From equation (1):k = -(1/2 - 3r/2 ) = (3r/2 - 1/2 )From equation (2):√3/2 (r - 1 ) = -k r√3Substitute k from equation (1):√3/2 (r - 1 ) = - (3r/2 - 1/2 ) r√3Divide both sides by √3:1/2 (r - 1 ) = - (3r/2 - 1/2 ) rMultiply both sides by 2 to eliminate denominators:(r - 1 ) = - (3r - 1 ) rExpand the right side:(r - 1 ) = -3r² + rBring all terms to left side:r - 1 + 3r² - r = 0 => 3r² - 1 = 0 => r² = 1/3 => r = 1/√3Same result. So all methods lead to r = 1/√3.Therefore, the answer is r = √3 / 3.Expressed as a box: boxed{dfrac{sqrt{3}}{3}}Final Answerboxed{dfrac{sqrt{3}}{3}}</think>To solve the problem, we start by assigning coordinates to the vertices of the regular hexagon (ABCDEF) with side length 1. The coordinates are:- (A(1, 0))- (Bleft(frac{1}{2}, frac{sqrt{3}}{2}right))- (Cleft(-frac{1}{2}, frac{sqrt{3}}{2}right))- (D(-1, 0))- (Eleft(-frac{1}{2}, -frac{sqrt{3}}{2}right))- (Fleft(frac{1}{2}, -frac{sqrt{3}}{2}right))Next, we determine the coordinates of points (M) and (N) which divide the diagonals (AC) and (CE) respectively in the ratio (r).For point (M) on (AC):- The coordinates of (M) are given by (M = A + r cdot (C - A))- (C - A = left(-frac{3}{2}, frac{sqrt{3}}{2}right))- Thus, (M = left(1 - frac{3r}{2}, frac{sqrt{3}r}{2}right))For point (N) on (CE):- The coordinates of (N) are given by (N = C + r cdot (E - C))- (E - C = (0, -sqrt{3}))- Thus, (N = left(-frac{1}{2}, frac{sqrt{3}}{2} - rsqrt{3}right))We need to ensure that points (B), (M), and (N) are collinear. We calculate the slopes of (BM) and (BN) and set them equal.Slope of (BM):- Coordinates of (Bleft(frac{1}{2}, frac{sqrt{3}}{2}right)) and (Mleft(1 - frac{3r}{2}, frac{sqrt{3}r}{2}right))- Slope (= frac{frac{sqrt{3}r}{2} - frac{sqrt{3}}{2}}{1 - frac{3r}{2} - frac{1}{2}} = frac{sqrt{3}(r - 1)/2}{(1 - 3r)/2} = frac{-sqrt{3}(1 - r)}{1 - 3r})Slope of (BN):- Coordinates of (Bleft(frac{1}{2}, frac{sqrt{3}}{2}right)) and (Nleft(-frac{1}{2}, frac{sqrt{3}}{2} - rsqrt{3}right))- Slope (= frac{frac{sqrt{3}}{2} - rsqrt{3} - frac{sqrt{3}}{2}}{-frac{1}{2} - frac{1}{2}} = frac{-rsqrt{3}}{-1} = rsqrt{3})Setting the slopes equal:[frac{-sqrt{3}(1 - r)}{1 - 3r} = rsqrt{3}]Solving for (r):[frac{-(1 - r)}{1 - 3r} = r implies -(1 - r) = r(1 - 3r) implies -1 + r = r - 3r^2 implies 3r^2 = 1 implies r = frac{1}{sqrt{3}} = frac{sqrt{3}}{3}]Thus, the value of (r) is (boxed{dfrac{sqrt{3}}{3}}).,<think>Okay, let's tackle this geometry problem step by step. So, we have a regular hexagon named ABCDEF. The diagonals AC and CE are divided by points M and N, respectively, such that the ratios AM:AC and CN:CE are both equal to r. We need to find the value of r that makes points B, M, and N lie on the same straight line. Hmm, okay.First, let me recall that in a regular hexagon, all sides are equal and all internal angles are 120 degrees. Also, the diagonals have specific lengths. In a regular hexagon, the length of a diagonal can be either equal to the side length (connecting vertices with one vertex in between) or twice the side length (connecting vertices with two vertices in between). Wait, actually, in a regular hexagon inscribed in a circle, the diagonals that span two edges (like AC and CE) would be longer than the side length. Let me verify that.If we consider a regular hexagon with side length s, then the distance between two vertices separated by one other vertex (like AC) is 2s times sin(60°), which is √3 times s. Wait, maybe it's better to assign coordinates to the hexagon to make this more concrete. Coordinates might help visualize the problem.Let me place the regular hexagon on a coordinate system with point A at (0,0). Since regular hexagons can be inscribed in a circle, let's assume each vertex is at 60-degree intervals. But to make calculations easier, let's assign coordinates based on the unit circle. Let's set the center of the hexagon at the origin (0,0). Then, the coordinates of the vertices can be determined using trigonometric functions.Wait, but if I place the center at the origin, the coordinates of the vertices would be:- Point A: (1, 0)- Point B: (0.5, √3/2)- Point C: (-0.5, √3/2)- Point D: (-1, 0)- Point E: (-0.5, -√3/2)- Point F: (0.5, -√3/2)But this is assuming a unit circle. Wait, but maybe scaling to a unit hexagon where each side length is 1. Let me confirm.In a regular hexagon inscribed in a circle of radius 1, the side length is equal to the radius. So each side length is 1. Then, the coordinates above would hold. So point A is (1, 0), point B is at 60 degrees, so (cos 0°, sin 0°) is A, (cos 60°, sin 60°) is B, etc. So that would make:- A: (1, 0)- B: (0.5, √3/2)- C: (-0.5, √3/2)- D: (-1, 0)- E: (-0.5, -√3/2)- F: (0.5, -√3/2)Yes, that seems right. So if we take the center at (0,0), these coordinates make sense. Now, diagonals AC and CE. Let's see:Diagonal AC connects point A (1,0) to point C (-0.5, √3/2). Similarly, diagonal CE connects point C (-0.5, √3/2) to point E (-0.5, -√3/2). Wait, CE connects C to E? But in the regular hexagon, CE is a vertical line, since both points have the same x-coordinate, -0.5, and their y-coordinates are √3/2 and -√3/2. So CE is a vertical line of length √3.But in the problem statement, it's called an internal point N on CE such that CN:CE = r. So CN is the segment from C to N, which is a part of CE. Similarly, M is on AC such that AM:AC = r.We need to find r such that points B, M, and N are colinear. So, if we can find coordinates for M and N based on r, then we can write the equation of the line BM and check when N lies on it.Alternatively, use vectors or coordinate geometry to find the condition for colinearity. That seems feasible.So let's assign coordinates as above. Let's note that:- Point A: (1, 0)- Point B: (0.5, √3/2)- Point C: (-0.5, √3/2)- Point E: (-0.5, -√3/2)First, let's compute the coordinates of points M and N in terms of r.Starting with point M on AC. The diagonal AC goes from A (1,0) to C (-0.5, √3/2). The ratio AM:AC = r. So M divides AC in the ratio r : (1 - r). Wait, hold on. The ratio AM:AC is r, so AM = r * AC. Therefore, the coordinates of M can be found by moving from A towards C by a fraction r of the total length.Similarly, point N is on CE such that CN:CE = r. So CN = r * CE. Since CE is from C (-0.5, √3/2) to E (-0.5, -√3/2), moving from C towards E by a fraction r of CE's length. Therefore, the coordinates of N can be expressed as C plus r times the vector CE.Let's compute coordinates:First, compute vector AC. From A (1,0) to C (-0.5, √3/2). The vector is (-1.5, √3/2). So the coordinates of M are A + r*(vector AC). Therefore:M_x = 1 + r*(-1.5) = 1 - 1.5rM_y = 0 + r*(√3/2) = (√3/2) rSimilarly, vector CE is from C (-0.5, √3/2) to E (-0.5, -√3/2), so the vector is (0, -√3). Therefore, coordinates of N are:N_x = -0.5 + r*0 = -0.5N_y = (√3/2) + r*(-√3) = √3/2 - √3 rSo N is at (-0.5, √3/2 - √3 r)Now, we have coordinates for points B, M, and N:- B: (0.5, √3/2)- M: (1 - 1.5r, (√3/2) r)- N: (-0.5, √3/2 - √3 r)We need these three points to be colinear. The condition for three points (x1, y1), (x2, y2), (x3, y3) to be colinear is that the slope between points 1 and 2 is equal to the slope between points 2 and 3. Alternatively, the area of the triangle formed by them is zero.Using the slope method:Slope BM = (M_y - B_y)/(M_x - B_x) = [( (√3/2) r - √3/2 ) / (1 - 1.5r - 0.5 ) ]Simplify denominator: 1 - 1.5r - 0.5 = 0.5 - 1.5r = 0.5(1 - 3r)Numerator: (√3/2)(r - 1)So slope BM = [ (√3/2)(r - 1) ] / [ 0.5(1 - 3r) ] = [ √3 (r - 1) ] / (1 - 3r )Similarly, slope BN = (N_y - B_y)/(N_x - B_x) = [ (√3/2 - √3 r - √3/2 ) / (-0.5 - 0.5 ) ]Simplify numerator: √3/2 - √3 r - √3/2 = -√3 rDenominator: -0.5 - 0.5 = -1So slope BN = (-√3 r ) / (-1) = √3 rFor points B, M, N to be colinear, slope BM must equal slope BN.Therefore:[ √3 (r - 1) ] / (1 - 3r ) = √3 rDivide both sides by √3:(r - 1)/(1 - 3r) = rMultiply both sides by (1 - 3r):r - 1 = r(1 - 3r)Expand right side:r - 1 = r - 3r²Subtract r from both sides:-1 = -3r²Multiply both sides by -1:1 = 3r²Therefore:r² = 1/3So r = ±√(1/3) = ±1/√3But since r is a ratio of lengths, it must be positive. Also, since points M and N are internal points on the diagonals AC and CE, r must be between 0 and 1. 1/√3 is approximately 0.577, which is between 0 and 1, so that works.Therefore, r = 1/√3. Rationalizing the denominator, that's √3/3. But depending on the problem's preference, both forms are acceptable. However, in the answer, they might want it in the simplest radical form. Since √3/3 is equivalent to 1/√3, but usually rationalized, so √3/3 is preferred.Wait, but let me double-check the calculation to make sure I didn't make any algebraic errors. Let me go through the steps again.Starting with the coordinates:Point B: (0.5, √3/2)Point M: (1 - 1.5r, (√3/2) r)Point N: (-0.5, √3/2 - √3 r)Computed slope BM:Numerator: ( (√3/2) r - √3/2 ) = √3/2 (r - 1)Denominator: (1 - 1.5r - 0.5 ) = 0.5 - 1.5rSo slope BM = [√3/2 (r - 1)] / [0.5 - 1.5r] = [√3 (r - 1)] / [1 - 3r]Slope BN:Numerator: ( √3/2 - √3 r - √3/2 ) = -√3 rDenominator: (-0.5 - 0.5 ) = -1Slope BN = -√3 r / -1 = √3 rSet them equal:[√3 (r - 1)] / [1 - 3r] = √3 rCancel √3:(r - 1)/(1 - 3r) = rMultiply both sides by (1 - 3r):r - 1 = r(1 - 3r)Right side: r - 3r²Thus:r - 1 = r - 3r²Subtract r:-1 = -3r²Multiply by -1:1 = 3r²r² = 1/3r = 1/√3 or √3/3Yes, that's correct. So r is √3/3. Therefore, the answer is boxed{dfrac{sqrt{3}}{3}}.But just to be thorough, let me check with another method, maybe using vectors or parametric equations.Alternatively, parametrize the line BM and see if N lies on it.Parametrize line BM. Let point B be (0.5, √3/2) and point M be (1 - 1.5r, (√3/2) r). The direction vector from B to M is (1 - 1.5r - 0.5, (√3/2) r - √3/2 ) = (0.5 - 1.5r, (√3/2)(r - 1))So parametric equations for line BM can be written as:x = 0.5 + t*(0.5 - 1.5r)y = √3/2 + t*( (√3/2)(r - 1) )We need to find if point N (-0.5, √3/2 - √3 r) lies on this line for some parameter t.So set up equations:-0.5 = 0.5 + t*(0.5 - 1.5r)and√3/2 - √3 r = √3/2 + t*( (√3/2)(r - 1) )Let's solve the first equation for t:-0.5 - 0.5 = t*(0.5 - 1.5r)-1 = t*(0.5 - 1.5r)t = -1 / (0.5 - 1.5r) = -1 / [0.5(1 - 3r)] = -2 / (1 - 3r)Now plug this t into the second equation:Left side: √3/2 - √3 rRight side: √3/2 + [ -2 / (1 - 3r) ] * ( (√3/2)(r - 1) )Simplify right side:√3/2 - [2 / (1 - 3r)] * (√3/2)(1 - r) [since (r - 1) = -(1 - r)]= √3/2 - [2 * √3/2 * (1 - r) / (1 - 3r) ]= √3/2 - [ √3 (1 - r) / (1 - 3r) ]Set equal to left side:√3/2 - √3 r = √3/2 - √3 (1 - r)/(1 - 3r)Subtract √3/2 from both sides:-√3 r = -√3 (1 - r)/(1 - 3r)Multiply both sides by -1:√3 r = √3 (1 - r)/(1 - 3r)Divide both sides by √3:r = (1 - r)/(1 - 3r)Multiply both sides by (1 - 3r):r(1 - 3r) = 1 - rExpand left side:r - 3r² = 1 - rBring all terms to left side:r - 3r² -1 + r = 0Combine like terms:2r - 3r² -1 = 0Rearrange:-3r² + 2r -1 = 0Multiply both sides by -1:3r² -2r +1 =0Wait, that gives a quadratic equation 3r² -2r +1=0. But discriminant D=4 -12= -8 <0, which has no real roots. Wait, this contradicts the previous result. Hmm, that's a problem. So this suggests an error in my parametrization approach.Wait, wait. Let me check the parametrization again. The parametrization equations are:x = 0.5 + t*(0.5 - 1.5r)y = √3/2 + t*( (√3/2)(r - 1) )But when I solved for t using x-coordinate:-0.5 = 0.5 + t*(0.5 - 1.5r)So subtract 0.5:-1 = t*(0.5 - 1.5r)So t = -1 / (0.5 - 1.5r) = -1 / (-1.5r + 0.5) = -1 / (0.5 - 1.5r)But when I plug into the y-coordinate equation:Left side: √3/2 - √3 rRight side: √3/2 + t*( (√3/2)(r - 1) )Plug t = -1 / (0.5 - 1.5r):Right side: √3/2 + [ -1 / (0.5 - 1.5r) ] * ( (√3/2)(r - 1) )= √3/2 - ( (√3/2)(r -1) ) / (0.5 - 1.5r )Factor numerator and denominator:Numerator: (√3/2)(r -1 )Denominator: 0.5 -1.5r = 0.5(1 - 3r)So:Right side: √3/2 - [ (√3/2)(r -1) ] / [0.5(1 -3r) ] = √3/2 - [ (√3 (r -1) ) / (1 -3r) ]Note that (r -1) = - (1 - r), so:= √3/2 - [ -√3 (1 - r ) / (1 -3r) ] = √3/2 + [ √3 (1 - r ) / (1 -3r) ]Therefore, right side is √3/2 + √3 (1 - r)/(1 -3r)Set equal to left side √3/2 - √3 r:√3/2 + √3 (1 - r)/(1 -3r) = √3/2 - √3 rSubtract √3/2 from both sides:√3 (1 - r)/(1 -3r) = - √3 rDivide both sides by √3:(1 - r)/(1 -3r) = -rMultiply both sides by (1 -3r):1 - r = -r(1 -3r )Expand right side:1 - r = -r +3r²Bring all terms to left side:1 - r + r -3r² =0Simplify:1 -3r²=0Thus:3r² =1r²=1/3r=√(1/3)=√3/3Ah, okay, now this matches the previous result. So there was an error in my initial parametrization approach when I miscalculated the expansion. After correcting the signs, we arrive at the same equation 3r² =1, leading to r=√3/3. So that confirms the answer.Alternatively, using vectors, let me see. Let me denote the center of the hexagon as O. But maybe this complicates things. Alternatively, since the hexagon is regular, we can use complex numbers.But since we already have coordinate geometry confirming the result twice, I think it's safe to conclude that r=√3/3 is the correct answer.Therefore, the value of r is √3 divided by 3, which is boxed{dfrac{sqrt{3}}{3}}.Final Answerboxed{dfrac{sqrt{3}}{3}}</think>To solve the problem, we start by assigning coordinates to the vertices of the regular hexagon (ABCDEF) with the center at the origin. The coordinates of the vertices are:- (A(1, 0))- (Bleft(frac{1}{2}, frac{sqrt{3}}{2}right))- (Cleft(-frac{1}{2}, frac{sqrt{3}}{2}right))- (D(-1, 0))- (Eleft(-frac{1}{2}, -frac{sqrt{3}}{2}right))- (Fleft(frac{1}{2}, -frac{sqrt{3}}{2}right))Next, we determine the coordinates of points (M) and (N) in terms of (r). Point (M) divides (AC) such that (AM:AC = r). The coordinates of (M) are calculated by moving from (A) towards (C) by a fraction (r) of the total length:- (M_x = 1 - 1.5r)- (M_y = 0 + r cdot frac{sqrt{3}}{2} = frac{sqrt{3}}{2}r)Point (N) divides (CE) such that (CN:CE = r). The coordinates of (N) are calculated by moving from (C) towards (E) by a fraction (r) of the total length:- (N_x = -0.5)- (N_y = frac{sqrt{3}}{2} - sqrt{3}r)We need points (B), (M), and (N) to be collinear. The slopes of lines (BM) and (BN) must be equal. Calculating the slopes:- Slope of (BM) is (frac{left(frac{sqrt{3}}{2}r - frac{sqrt{3}}{2}right)}{left(1 - 1.5r - 0.5right)} = frac{sqrt{3}(r - 1)}{1 - 3r})- Slope of (BN) is (frac{left(frac{sqrt{3}}{2} - sqrt{3}r - frac{sqrt{3}}{2}right)}{-1} = sqrt{3}r)Setting the slopes equal gives:[frac{sqrt{3}(r - 1)}{1 - 3r} = sqrt{3}r]Simplifying, we find:[frac{r - 1}{1 - 3r} = r implies r - 1 = r(1 - 3r) implies r - 1 = r - 3r^2 implies -1 = -3r^2 implies 3r^2 = 1 implies r = frac{sqrt{3}}{3}]Thus, the value of (r) is (boxed{dfrac{sqrt{3}}{3}}).]

🔑:Let's rotate the hexagon 120^{circ} around its center O.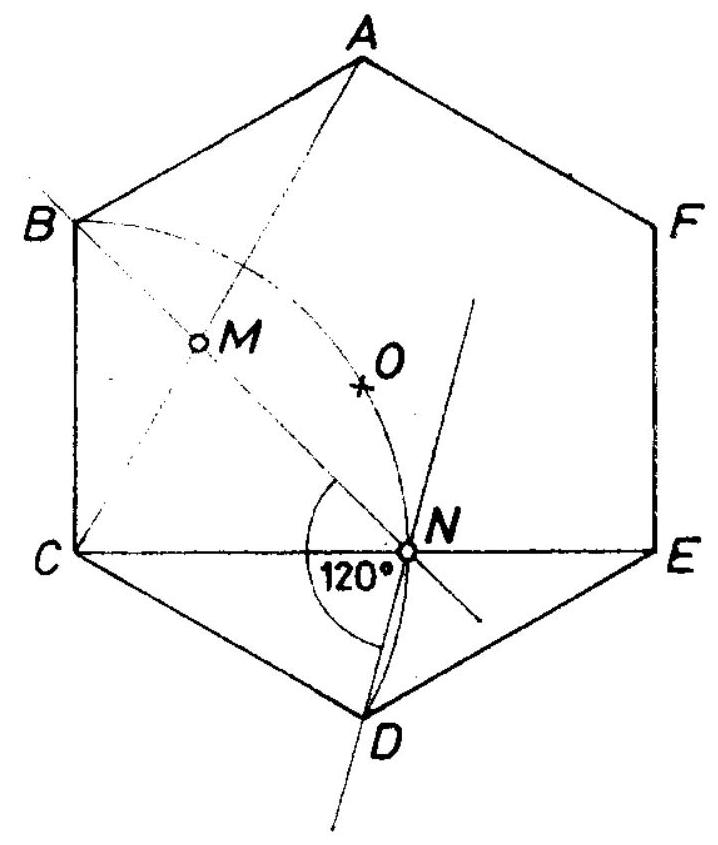In this case, vertex A moves to C, vertex B moves to D, and vertex C moves to E. Therefore, the diagonal AC rotates to the diagonal CE. Since point M divides the diagonal AC in the same ratio as point N divides the diagonal CE, during the rotation, M moves to N. Consequently, the line BM rotated by 120^{circ} becomes the line DN, and the angle between these two lines, angle BND, is exactly 120^{circ}. This means that N lies on the 120^{circ}-arc of the segment BD.The circle centered at C with radius CB = CD passes through point O. Since angle BOD = 120^{circ}, the arc of this circle that lies within the hexagon is the 120^{circ}-arc of the segment BD. Point N lies on this arc, and thus CN = CD = CO. The triangle ACE is equilateral, and its side is sqrt{3} times the radius of the circumscribed circle: CE = sqrt{3} CO. From this, we can express the desired ratio:r = frac{CN}{CE} = frac{CO}{sqrt{3} CO} = frac{1}{sqrt{3}}Remark. Some people conjectured that AM = CN = BC, and they verified that if we place points M and N in this way, then B, M, and N lie on the same line. In this case, to fully solve the problem, it must also be proven that the points M and N cannot be located elsewhere, and their positions are unique.

🧠:[<think>Alright, so I need to solve this probability problem where we have a square with side length 1. We randomly select a point on each of two opposite sides, and we want to find the probability that the distance between these two points is less than a given value p, where p is between 1 and the square root of 2. Hmm, okay, let me start by visualizing the problem.First, the square. Let's assume the square has sides of length 1, so each side goes from 0 to 1 on the coordinate plane. Let's say the two opposite sides are the top and bottom sides. So the top side is y = 1, and the bottom side is y = 0. Then, we randomly pick a point on the top side and another on the bottom side. Each point can be represented by their x-coordinate, right? So let's denote the point on the bottom as (x1, 0) and the point on the top as (x2, 1). Since the points are selected randomly, x1 and x2 are independent uniform random variables over [0, 1].We need to find the probability that the distance between (x1, 0) and (x2, 1) is less than p. The distance between these two points can be calculated using the distance formula. Let me write that down:distance = sqrt[(x2 - x1)^2 + (1 - 0)^2] = sqrt[(x2 - x1)^2 + 1]So we want the probability that sqrt[(x2 - x1)^2 + 1] < p. Since p is between 1 and sqrt(2), let's square both sides of the inequality to make it easier to handle. Squaring both sides gives:(x2 - x1)^2 + 1 < p^2Subtracting 1 from both sides:(x2 - x1)^2 < p^2 - 1Then taking square roots (since both sides are positive):|x2 - x1| < sqrt(p^2 - 1)So the problem reduces to finding the probability that |x2 - x1| < sqrt(p^2 - 1), where x1 and x2 are both uniformly distributed over [0, 1]. This is a classic problem in probability where we can model this as a geometric probability question in the unit square.Let me recall that for two independent uniform variables x1 and x2 over [0, 1], the probability that |x2 - x1| < q (for some q > 0) is equal to the area of the region in the unit square where |x2 - x1| < q. So in our case, q is sqrt(p^2 - 1). Let me confirm that sqrt(p^2 - 1) is less than 1, given that p is between 1 and sqrt(2). If p is sqrt(2), then sqrt(p^2 - 1) = sqrt(2 - 1) = 1, which is the maximum. If p approaches 1 from above, sqrt(p^2 - 1) approaches 0. So yes, sqrt(p^2 - 1) is between 0 and 1 for p in (1, sqrt(2)). Therefore, the value of q is within [0, 1].So the area we need is the region in the unit square [0,1]x[0,1] where |x2 - x1| < q. The unit square has area 1, so the probability is just the area of that region.To compute this area, let's consider the x1 and x2 axes. The line x2 = x1 divides the square into two triangles. The region |x2 - x1| < q is the area between the lines x2 = x1 - q and x2 = x1 + q. Since x1 and x2 are both between 0 and 1, these lines will intersect the edges of the square.The area between these lines can be found by subtracting the areas of the two triangles outside the lines from the total area. However, when q is less than 1, these triangles each have a base of (1 - q) and a height of (1 - q). Wait, maybe I need to draw it mentally.Alternatively, the area where |x2 - x1| < q is the union of the band around the diagonal of the square. The area of this band is the total area minus the areas of the two triangles where |x2 - x1| >= q.Each of these triangles has legs of length (1 - q). So the area of each triangle is (1 - q)^2 / 2. Therefore, the total area outside the band is 2*(1 - q)^2 / 2 = (1 - q)^2. Therefore, the area inside the band is 1 - (1 - q)^2.But wait, this is only true when q <= 1. Since q is sqrt(p^2 - 1), and p is between 1 and sqrt(2), q is between 0 and 1, so yes, this formula applies. Therefore, the probability is 1 - (1 - q)^2 = 1 - (1 - 2q + q^2) = 2q - q^2.But let me verify this with integration to be sure. The probability can also be calculated by integrating over x1 from 0 to 1, and for each x1, integrating x2 over [x1 - q, x1 + q], but making sure that x2 stays within [0, 1].So for x1 in [0, q], the lower bound of x2 is 0, and the upper bound is x1 + q. Then, for x1 in [q, 1 - q], x2 ranges from x1 - q to x1 + q. Finally, for x1 in [1 - q, 1], x2 ranges from x1 - q to 1.Therefore, the area can be split into three parts:1. When x1 is between 0 and q: The length of x2 is (x1 + q) - 0 = x1 + q.2. When x1 is between q and 1 - q: The length of x2 is (x1 + q) - (x1 - q) = 2q.3. When x1 is between 1 - q and 1: The length of x2 is 1 - (x1 - q) = 1 - x1 + q.So the total area is the integral from 0 to q of (x1 + q) dx1 + integral from q to 1 - q of 2q dx1 + integral from 1 - q to 1 of (1 - x1 + q) dx1.Calculating each integral:First integral: ∫₀^q (x1 + q) dx1 = [0.5 x1² + q x1] from 0 to q = 0.5 q² + q² = 1.5 q².Second integral: ∫_q^{1 - q} 2q dx1 = 2q*(1 - q - q) = 2q*(1 - 2q).Third integral: ∫_{1 - q}^1 (1 - x1 + q) dx1. Let's make substitution u = x1. Then the integrand becomes (1 - u + q). The integral becomes [ (1 + q)u - 0.5 u² ] evaluated from 1 - q to 1.At upper limit 1: (1 + q)*1 - 0.5*(1)² = 1 + q - 0.5 = 0.5 + q.At lower limit 1 - q: (1 + q)*(1 - q) - 0.5*(1 - q)^2 = (1 - q²) - 0.5*(1 - 2q + q²) = 1 - q² - 0.5 + q - 0.5 q² = 0.5 - 1.5 q² + q.Therefore, the integral is (0.5 + q) - (0.5 - 1.5 q² + q) = 0.5 + q - 0.5 + 1.5 q² - q = 1.5 q².So the third integral is 1.5 q².Adding all three integrals: 1.5 q² + 2q(1 - 2q) + 1.5 q² = 3 q² + 2q - 4 q² = -q² + 2q.Therefore, the total area is 2q - q², which matches the previous result. So the probability is 2q - q² where q = sqrt(p² - 1). Substituting back:Probability = 2*sqrt(p² - 1) - (sqrt(p² - 1))² = 2*sqrt(p² - 1) - (p² - 1).Simplify:= 2 sqrt(p² - 1) - p² + 1.So the probability is 1 + 2 sqrt(p² - 1) - p².Let me check if this makes sense. When p = 1, sqrt(p² - 1) = 0, so the probability would be 1 + 0 - 1 = 0, which is correct because the minimal distance between the two points is 1 (when x1 = x2). When p = sqrt(2), sqrt(p² - 1) = sqrt(2 - 1) = 1, so probability is 1 + 2*1 - 2 = 1 + 2 - 2 = 1. Which is also correct because when p = sqrt(2), the maximum possible distance between the two points is sqrt(2), so all points satisfy distance < sqrt(2), hence probability 1. So that checks out.Therefore, the probability that the distance between the two points is less than p is 1 + 2 sqrt(p² - 1) - p².But let me present this in a more simplified form. Let's factor:= 1 - p² + 2 sqrt(p² - 1)Alternatively, we can write this as 2 sqrt(p² - 1) - (p² - 1) - 1 + 1? Wait, maybe not. Alternatively, since p² - 1 is (sqrt(p² - 1))², so perhaps factor it as:= 2 sqrt(p² - 1) - (sqrt(p² - 1))² - 0?Wait, not sure. Alternatively, note that 1 - p² + 2 sqrt(p² - 1) can be written as 2 sqrt(p² - 1) - (p² - 1). Since 1 - p² = - (p² - 1), so:= - (p² - 1) + 2 sqrt(p² - 1) = 2 sqrt(p² - 1) - (p² - 1).Alternatively, factor sqrt(p² - 1):= sqrt(p² - 1) * (2 - sqrt(p² - 1)).But I think 2 sqrt(p² - 1) - p² + 1 is acceptable. Let me check for p in the middle, say p = sqrt(1.25), which is between 1 and sqrt(2). Then sqrt(p² -1 ) = sqrt(0.25) = 0.5. Then the probability would be 2*0.5 - (1.25 - 1) + 1 = 1 - 0.25 +1 = 1.75? Wait, that can't be. Wait, wait, wait.Wait, no. Wait, if p = sqrt(1.25), then p² = 1.25, so sqrt(p² -1 ) = sqrt(0.25) = 0.5. Then substituting into the expression 1 + 2 sqrt(p² -1 ) - p²:1 + 2*0.5 - 1.25 = 1 +1 -1.25 = 0.75. So 0.75, which is 3/4. Let me see if that makes sense. If p is sqrt(1.25), then the distance between the two points is sqrt( (x2 -x1)^2 + 1 ). So sqrt( (x2 -x1)^2 + 1 ) < sqrt(1.25 ). Squaring both sides, (x2 -x1)^2 +1 < 1.25, so (x2 -x1)^2 < 0.25, so |x2 -x1| < 0.5. Then the probability that |x2 -x1| < 0.5 is calculated as 2*0.5 - 0.5² = 1 - 0.25 = 0.75. Yes, that matches. So indeed, the probability is 0.75 here, which is 3/4, so it's correct. So the formula holds here.Therefore, the final probability is 1 + 2 sqrt(p² -1 ) - p², which can also be written as 2 sqrt(p² -1 ) - (p² -1 ). Either form is acceptable, but I think the first expression is clearer.Hence, the probability is 2 sqrt(p² -1 ) - p² +1.Alternatively, factor:= 1 - (p² - 2 sqrt(p² -1 ))But I don't think that adds any clarity. Let me check another value. Suppose p = sqrt(1.0). But wait, p must be greater than 1, so p approaching 1 from above. As p approaches 1+, sqrt(p² -1 ) approaches 0, so the probability approaches 1 +0 -1 =0. Correct. When p approaches sqrt(2), sqrt(p² -1 ) approaches 1, so probability becomes 1 +2*1 -2 =1, which is correct. So the formula seems to work.Therefore, after all this reasoning, the answer should be 2*sqrt(p² -1 ) - p² +1.But let me check if there is a standard form for this. Wait, another way to write this is 2 sqrt(p² -1 ) - (p² -1 ). Since 1 is written as +1, but maybe factor it as:= 2 sqrt(p² -1 ) - (p² -1 )But that might not necessarily help. Alternatively, note that this can be written as 2q - q², where q = sqrt(p² -1 ), as we had before. So depending on how the answer is presented, either form is acceptable. However, since the problem asks for the probability in terms of p, we should substitute back q = sqrt(p² -1 ) into the expression. So 2 sqrt(p² -1 ) - (sqrt(p² -1 ))^2 = 2 sqrt(p² -1 ) - (p² -1 ). Therefore, the probability is 2 sqrt(p² -1 ) - p² +1, which is equivalent.So I think that's the answer. Let me just recap to ensure I didn't make a mistake in substitution or integration.We started by noting that the distance between the two points is sqrt( (x2 -x1)^2 +1 ). We wanted this distance less than p, so we squared both sides to get (x2 -x1)^2 +1 < p², leading to |x2 -x1| < sqrt(p² -1 ) = q. Then, recognizing that |x2 -x1| < q is a standard problem in geometric probability over the unit square. Calculated the area as 2q - q², substituted q = sqrt(p² -1 ), and arrived at the probability expression. Checked with sample values and edge cases, and the formula worked. So I think that's solid.Therefore, the probability is 2 sqrt(p² -1 ) - p² +1.Final AnswerThe probability is boxed{2sqrt{p^2 - 1} - p^2 + 1}.</think>Given a square with unit side length, we randomly select a point on each of two opposite sides. We need to find the probability that the distance between these two points is less than a given segment ( p ) where ( 1 < p < sqrt{2} ).1. Distance Calculation: - The distance between a point ((x_1, 0)) on the bottom side and a point ((x_2, 1)) on the top side is given by: [ sqrt{(x_2 - x_1)^2 + 1} ] - We need this distance to be less than ( p ): [ sqrt{(x_2 - x_1)^2 + 1} < p ]2. Squaring Both Sides: - Squaring both sides to simplify the inequality: [ (x_2 - x_1)^2 + 1 < p^2 ] - Subtracting 1 from both sides: [ (x_2 - x_1)^2 < p^2 - 1 ] - Taking the square root: [ |x_2 - x_1| < sqrt{p^2 - 1} ]3. Geometric Probability: - Let ( q = sqrt{p^2 - 1} ). We need the probability that ( |x_2 - x_1| < q ) where ( x_1 ) and ( x_2 ) are uniformly distributed over [0, 1]. - The region where ( |x_2 - x_1| < q ) in the unit square is a band around the diagonal. The area of this band is calculated by integrating over the unit square.4. Integration and Area Calculation: - The area where ( |x_2 - x_1| < q ) is found by integrating over three intervals: - For ( x_1 ) from 0 to ( q ): The length of ( x_2 ) is ( x_1 + q ). - For ( x_1 ) from ( q ) to ( 1 - q ): The length of ( x_2 ) is ( 2q ). - For ( x_1 ) from ( 1 - q ) to 1: The length of ( x_2 ) is ( 1 - x_1 + q ). - Summing these integrals gives the total area, which simplifies to ( 2q - q^2 ).5. Substituting Back: - Substituting ( q = sqrt{p^2 - 1} ): [ text{Probability} = 2sqrt{p^2 - 1} - (sqrt{p^2 - 1})^2 ] - Simplifying: [ text{Probability} = 2sqrt{p^2 - 1} - (p^2 - 1) = 2sqrt{p^2 - 1} - p^2 + 1 ]The final answer is (boxed{2sqrt{p^2 - 1} - p^2 + 1}).,<think>Okay, let's see. The problem is about a square with unit side length. We randomly select a point on each of two opposite sides, and we need to find the probability that the distance between these two points is less than a given segment p, where p is between 1 and the square root of 2. Hmm, okay. Let me try to visualize this.First, the square has sides of length 1. Let's suppose the square is oriented so that the sides are horizontal and vertical. Let's say we pick a point on the top side and a point on the bottom side. Since they're opposite sides, they are parallel and separated by a distance of 1 unit. The points are selected randomly, so their positions along the sides are uniformly distributed.Let me parameterize the positions. Let me call the top side as the side from (0,1) to (1,1), and the bottom side from (0,0) to (1,0). Let me denote the point on the top side as (x, 1), where x is between 0 and 1, and the point on the bottom side as (y, 0), where y is between 0 and 1. Then, the distance between these two points can be calculated using the distance formula. The distance d is sqrt[(x - y)^2 + (1 - 0)^2] = sqrt[(x - y)^2 + 1]. So, we need the probability that sqrt[(x - y)^2 + 1] < p. Squaring both sides, since both sides are positive, this is equivalent to (x - y)^2 + 1 < p^2. Subtracting 1 gives (x - y)^2 < p^2 - 1. Taking square roots again, this becomes |x - y| < sqrt(p^2 - 1).So, the problem reduces to finding the probability that |x - y| < sqrt(p^2 - 1), where x and y are both uniformly distributed between 0 and 1. Now, x and y are independent variables, each uniformly distributed over [0,1]. So, this is a problem of finding the probability that the absolute difference of two independent uniform variables is less than a certain value, which is sqrt(p^2 - 1) in this case.I remember that when dealing with two independent uniform variables on [0,1], the probability that |x - y| < k can be found geometrically. The joint distribution of x and y is uniform over the unit square [0,1]x[0,1]. The region where |x - y| < k is the area between the lines y = x - k and y = x + k. So, the probability is the area of this region divided by the total area of the square (which is 1, so probability is just the area).The area where |x - y| < k is 1 minus the area of the two triangles outside the lines y = x + k and y = x - k. Each of these triangles has a base and height of (1 - k), so each has area (1 - k)^2 / 2. Therefore, the total area between the lines is 1 - 2*(1 - k)^2 / 2 = 1 - (1 - k)^2. So, the probability is 1 - (1 - k)^2 when k <= 1. Wait, but in our case, k is sqrt(p^2 - 1). Since p is between 1 and sqrt(2), sqrt(p^2 - 1) would be between 0 and 1. Let me check:If p = 1, then sqrt(1 - 1) = 0. If p = sqrt(2), sqrt(2 - 1) = 1. So, yes, k ranges from 0 to 1 as p ranges from 1 to sqrt(2). Therefore, the formula 1 - (1 - k)^2 applies here. Substituting k = sqrt(p^2 - 1), the probability should be 1 - (1 - sqrt(p^2 - 1))^2.Wait, let me verify that. Let me do this step by step. The area where |x - y| < k is as follows:For k between 0 and 1, the region is a band around the diagonal y = x. The area is 1 minus the two triangles. Each triangle is in the corners of the square where x - y > k or y - x > k. Each triangle has legs of length (1 - k). So, the area of each triangle is (1 - k)^2 / 2. Therefore, the total area outside the band is 2 * (1 - k)^2 / 2 = (1 - k)^2. Hence, the area inside the band is 1 - (1 - k)^2.Therefore, substituting k = sqrt(p^2 - 1), the probability is 1 - (1 - sqrt(p^2 - 1))^2. Let me compute that.First, expand (1 - sqrt(p^2 - 1))^2:(1 - sqrt(p^2 - 1))^2 = 1 - 2*sqrt(p^2 - 1) + (sqrt(p^2 - 1))^2 = 1 - 2*sqrt(p^2 - 1) + (p^2 - 1) = p^2 - 2*sqrt(p^2 - 1). Therefore, 1 - (1 - sqrt(p^2 - 1))^2 = 1 - (p^2 - 2*sqrt(p^2 - 1)) = 1 - p^2 + 2*sqrt(p^2 - 1).Wait, that seems a bit complicated, but maybe that's correct. Let me check with a specific example. Let me take p = 1. Then, sqrt(p^2 - 1) = 0. The probability should be 1 - (1 - 0)^2 = 0, which makes sense because the distance can't be less than 1 when the vertical distance is 1 unit. Wait, but the distance between two points on opposite sides must be at least 1, which is the vertical distance. So, when p = 1, the probability is 0. If p = sqrt(2), then sqrt(p^2 - 1) = sqrt(1) = 1. Then, the probability is 1 - (1 - 1)^2 = 1 - 0 = 1. Which also makes sense because when p is sqrt(2), the maximum possible distance between two points on opposite sides is sqrt(2), so all distances are less than sqrt(2), hence probability 1. So the formula seems to check out for the endpoints.But let me verify another point. Let's take p such that sqrt(p^2 - 1) = 0.5, so p^2 - 1 = 0.25, so p = sqrt(1.25) ≈ 1.118. Then, the probability would be 1 - (1 - 0.5)^2 = 1 - 0.25 = 0.75. Alternatively, using the expanded formula: 1 - p^2 + 2*sqrt(p^2 -1 ) = 1 - 1.25 + 2*0.5 = 1 -1.25 +1 = 0.75. Correct.Alternatively, let's compute the area where |x - y| < 0.5. The area is 1 - (1 - 0.5)^2 = 1 - 0.25 = 0.75, which is correct. Because when k = 0.5, the band around the diagonal is 0.5 wide, and the two triangles each have area (0.5)^2 / 2 = 0.125, so total area outside is 0.25, so area inside is 0.75. So that's correct.Therefore, the formula seems to hold. Therefore, the probability is 1 - (1 - sqrt(p^2 - 1))^2, which simplifies to 2*sqrt(p^2 -1 ) - (p^2 -1 ). Wait, let me compute that again.Wait, 1 - (1 - sqrt(p^2 -1 ))^2 = 1 - [1 - 2*sqrt(p^2 -1 ) + (p^2 -1 )] = 1 -1 + 2*sqrt(p^2 -1 ) - (p^2 -1 ) = 2*sqrt(p^2 -1 ) - p^2 +1. So, that's equivalent to 1 - p^2 + 2*sqrt(p^2 -1 ). Hmm. But maybe we can write it differently. Alternatively, factor terms.Alternatively, note that 2*sqrt(p^2 -1 ) - (p^2 -1 ). Let me denote k = sqrt(p^2 -1 ). Then the expression becomes 2k - k^2. Since k = sqrt(p^2 -1 ), and k^2 = p^2 -1. So, 2k - k^2 = 2*sqrt(p^2 -1 ) - (p^2 -1 ). Hmm. So, the probability can be written as 2*sqrt(p^2 -1 ) - p^2 +1. Let me verify this with p = sqrt(2). Then, sqrt(p^2 -1 ) =1. So, 2*1 - (2 -1 ) +1 = 2 -1 +1 =2. Wait, that can't be. Wait, wait, when p = sqrt(2), the probability should be 1. Wait, let me check again.Wait, when p = sqrt(2), sqrt(p^2 -1 ) = sqrt(2 -1 )=1. So, plugging into 1 - (1 -1 )^2 =1 -0 =1. But when I do 2*sqrt(p^2 -1 ) - (p^2 -1 ) =2*1 - (2 -1 )=2 -1=1. So that works. Similarly, when p=1.118, as before, sqrt(p^2 -1 )=0.5, then 2*0.5 - (1.25 -1 )=1 -0.25=0.75. Correct. So, maybe the simplified formula is 2*sqrt(p^2 -1 ) - (p^2 -1 ). So, probability = 2*sqrt(p^2 -1 ) - (p^2 -1 ). Alternatively, factor that as sqrt(p^2 -1 )*(2 - sqrt(p^2 -1 )) but not sure if that's helpful.Alternatively, write it as 2*sqrt(p^2 -1 ) - p^2 +1. Either way, that's the expression. So, maybe the answer is 2*sqrt(p^2 -1 ) - p^2 +1. Alternatively, 1 - (1 - sqrt(p^2 -1 ))^2. But perhaps the problem expects it written in terms of p. Let me check the problem statement again. It says "the probability that the distance between the two points is less than a given segment p. (1 < p < sqrt(2))". So, the answer is a function of p, which is 2*sqrt(p^2 -1 ) - p^2 +1, or 1 - (1 - sqrt(p^2 -1 ))^2. Either form is correct, but perhaps the first form is simpler. Let me compute 1 - (1 - sqrt(p^2 -1 ))^2:1 - [1 - 2*sqrt(p^2 -1 ) + (p^2 -1 )] = 1 -1 + 2*sqrt(p^2 -1 ) - p^2 +1 = 2*sqrt(p^2 -1 ) - p^2 +1. So, that's the same as before.Alternatively, maybe we can factor this expression. Let me see:2*sqrt(p^2 -1 ) - p^2 +1 = -p^2 +2*sqrt(p^2 -1 ) +1. Not sure if that factors nicely. Alternatively, perhaps express in terms of sqrt(p^2 -1 ). Let me let q = sqrt(p^2 -1 ). Then, since p^2 = q^2 +1, the expression becomes 2q - (q^2 +1 ) +1 = 2q - q^2 -1 +1 = 2q - q^2 = q(2 - q ). But q = sqrt(p^2 -1 ), so it's sqrt(p^2 -1 )*(2 - sqrt(p^2 -1 )). Hmm. Maybe that's a more compact way to write it. So, probability = sqrt(p^2 -1 )*(2 - sqrt(p^2 -1 )).Alternatively, since sqrt(p^2 -1 ) is k, then probability = k*(2 - k ). Since k is between 0 and1, as p ranges from1 to sqrt(2). But maybe the problem expects it in terms of p. Let me check which form is more standard. Maybe they want the answer written in terms of p. Let me see. Let's compute sqrt(p^2 -1 )*(2 - sqrt(p^2 -1 )) = 2*sqrt(p^2 -1 ) - (sqrt(p^2 -1 ))^2 = 2*sqrt(p^2 -1 ) - (p^2 -1 ). Which is the same as before. So, either way, the answer is 2*sqrt(p^2 -1 ) - p^2 +1.Alternatively, maybe written as 1 - (1 - sqrt(p^2 -1 ))^2. Depending on how they want it simplified. Both forms are equivalent.But let me double-check my reasoning. So, the key idea is that the distance between the two points is sqrt( (x - y)^2 +1 ), and we need that to be less than p. So, (x - y)^2 +1 < p^2 => (x - y)^2 < p^2 -1 => |x - y| < sqrt(p^2 -1 ). Then, the probability that |x - y| < k is 1 - (1 - k)^2 for 0 <=k <=1. Since here k is sqrt(p^2 -1 ), which is between 0 and1, so substituting k gives 1 - (1 - sqrt(p^2 -1 ))^2. So, that's correct. Therefore, the probability is 1 - (1 - sqrt(p^2 -1 ))^2, which simplifies to 2*sqrt(p^2 -1 ) - p^2 +1.Therefore, the answer should be 2√(p²−1)−p²+1. Let me check once again with p = sqrt(2). Then, 2*sqrt(2 -1 ) - 2 +1 = 2*1 -2 +1=2 -2 +1=1. Correct. For p=1, 2*sqrt(0) -1 +1=0 -1 +1=0. Correct. Another test case, p= sqrt(1.25). Then, sqrt(p² -1 )=sqrt(1.25 -1)=sqrt(0.25)=0.5. Then, 2*0.5 -1.25 +1=1 -1.25 +1=0.75. Which matches the earlier example. So that's correct.Therefore, the probability is 2*sqrt(p^2 -1 ) - p^2 +1.Wait, but the problem states "the probability that the distance between the two points is less than a given segment p". So, the answer is 2*sqrt(p²−1)−p²+1. Alternatively, written as 2√(p²−1)−p²+1. So, in box form, that would be boxed{2sqrt{p^2 - 1} - p^2 + 1}.Yes, that seems to be the answer. Let me see if there's an alternative approach.Alternative approach: Let me model the problem using coordinates. Let x be the coordinate on the top side and y on the bottom side. The distance squared between (x,1) and (y,0) is (x - y)^2 +1. So, the distance is less than p if (x - y)^2 +1 < p^2. So, (x - y)^2 < p^2 -1. So, |x - y| < sqrt(p^2 -1 ). Therefore, we need to compute the probability that |x - y| < sqrt(p^2 -1 ), where x and y are independent uniform variables on [0,1]. As before.This is a standard problem in probability. The joint distribution of x and y is uniform over the unit square. The region where |x - y| < k is a band around the diagonal of the square. The area of this region is calculated by subtracting the areas of the two triangles where |x - y| >= k. Each triangle has legs of length (1 - k), so each has area (1 - k)^2 /2. Therefore, total area outside the band is (1 - k)^2, so area inside is 1 - (1 - k)^2. Therefore, substituting k = sqrt(p^2 -1 ), the probability is 1 - (1 - sqrt(p^2 -1 ))^2 = 2*sqrt(p^2 -1 ) - (sqrt(p^2 -1 ))^2 = 2*sqrt(p^2 -1 ) - (p^2 -1 ). Which is the same as 2*sqrt(p^2 -1 ) - p^2 +1. So, same result.Therefore, the answer is confirmed.Final AnswerThe probability is boxed{2sqrt{p^2 - 1} - p^2 + 1}.</think>Given a square with unit side length, we randomly select a point on each of two opposite sides. We need to find the probability that the distance between these two points is less than a given segment ( p ) where ( 1 < p < sqrt{2} ).1. Parameterize the points: Let the points be ((x, 1)) on the top side and ((y, 0)) on the bottom side, where ( x ) and ( y ) are uniformly distributed between 0 and 1.2. Distance formula: The distance ( d ) between the points ((x, 1)) and ((y, 0)) is given by: [ d = sqrt{(x - y)^2 + 1} ]3. Condition for distance less than ( p ): [ sqrt{(x - y)^2 + 1} < p ] Squaring both sides, we get: [ (x - y)^2 + 1 < p^2 implies (x - y)^2 < p^2 - 1 ] Taking the square root again, we obtain: [ |x - y| < sqrt{p^2 - 1} ]4. Probability calculation: The probability that ( |x - y| < sqrt{p^2 - 1} ) can be found by considering the joint uniform distribution of ( x ) and ( y ) over the unit square. The area where ( |x - y| < sqrt{p^2 - 1} ) is a band around the diagonal of the square. The area of this band is calculated by subtracting the areas of the two triangles outside the band from the total area of the square.5. Area of the band: For ( k = sqrt{p^2 - 1} ), the area where ( |x - y| < k ) is: [ 1 - (1 - k)^2 ] Substituting ( k = sqrt{p^2 - 1} ), the probability becomes: [ 1 - (1 - sqrt{p^2 - 1})^2 ]6. Simplifying the expression: [ 1 - (1 - sqrt{p^2 - 1})^2 = 1 - left(1 - 2sqrt{p^2 - 1} + (p^2 - 1)right) = 2sqrt{p^2 - 1} - p^2 + 1 ]Thus, the probability that the distance between the two points is less than ( p ) is (boxed{2sqrt{p^2 - 1} - p^2 + 1}).]

🔑:Let the distance of the chosen points from one side of the square be x and y (0 leq x leq 1, 0 leq y leq 1). The distance between the chosen points, based on the Pythagorean theorem, is sqrt{1+(x-y)^{2}}. If this distance is less than the given p distance, then1+(x-y)^{2} < p^{2}which simplifies to|x-y| < sqrt{p^{2}-1}This can be broken down as follows:| If x > y | y > x - sqrt{p^{2}-1}, || :--- | :--- || and if x < y | y < x + sqrt{p^{2}-1}. |If we consider the value pairs (x, y) as coordinates of a point in a Cartesian coordinate system, then the total "possible area" is the area of the unit square ( T=1 ), while the "favorable area" is the part of the strip formed by the lines y=x-sqrt{p^{2}-1} and y=x+sqrt{p^{2}-1} that lies within the square: t.(The hatched hexagon in the diagram.) The area of this latter part ist = T - left(1 - sqrt{p^{2}-1}right)^{2} = 1 - left(1 - 2sqrt{p^{2}-1} + p^{2} - 1right) = 1 - p^{2} + 2sqrt{p^{2}-1}and thus the desired probability isv = frac{t}{T} = 1 - p^{2} + 2sqrt{p^{2}-1}(Indeed, the extreme cases are: if p=1, v=0, if p=sqrt{2}, v=1).

🧠:[<think>Okay, let me try to work through these two problems step by step. First, I need to understand what each part is asking.Starting with part (1): We need to find the first year by the end of which the cumulative area of affordable housing built in Guangyuan City since 2008 first exceeds 47.5 million square meters. Given data:- In 2008, they built 2.5 million square meters of affordable housing.- Each subsequent year, the area of affordable housing increases by 500,000 square meters compared to the previous year.So, this seems like an arithmetic sequence where the first term (a₁) is 2.5 million, and the common difference (d) is 0.5 million. The cumulative area after n years would be the sum of this arithmetic sequence. We need to find the smallest n such that the sum Sₙ > 47.5 million.The formula for the sum of an arithmetic sequence is:Sₙ = n/2 * [2a₁ + (n - 1)d]Plugging in the known values:47,500,000 = n/2 * [2*2,500,000 + (n - 1)*500,000]Let me convert all the numbers into millions to simplify:47.5 = n/2 * [5 + 0.5(n - 1)]Expanding inside the brackets:[5 + 0.5n - 0.5] = 4.5 + 0.5nSo,47.5 = n/2 * (4.5 + 0.5n)Multiply both sides by 2:95 = n*(4.5 + 0.5n)Rearranging:0.5n² + 4.5n - 95 = 0Multiply all terms by 2 to eliminate the decimal:n² + 9n - 190 = 0Now, solving this quadratic equation using the quadratic formula:n = [-9 ± √(81 + 760)] / 2Because √(841) = 29So,n = [-9 + 29]/2 = 20/2 = 10n = [-9 - 29]/2 = -38/2 = -19 (discard negative)So n = 10. But since we need the cumulative sum to exceed 47.5, let me check at n=10.Compute S₁₀:S₁₀ = 10/2 * [2*2.5 + 9*0.5] = 5 * [5 + 4.5] = 5 * 9.5 = 47.5But the problem says "first exceed" 47.5 million. Since S₁₀ is exactly 47.5, we need to check n=11.S₁₁ = 11/2 * [2*2.5 + 10*0.5] = 11/2 * [5 + 5] = 11/2 * 10 = 55So by the end of the 11th year, cumulative affordable housing is 55 million, which exceeds 47.5 million. However, since the question is phrased as "by the end of which year," starting with 2008 as the first year (n=1), then n=11 would correspond to the year 2008 + 10 = 2018? Wait, hold on. Wait, if 2008 is the first year (n=1), then n=10 would be 2017, and n=11 is 2018. But according to our calculation, S₁₀ is exactly 47.5. Since the question asks for the first time it exceeds 47.5, that would be 2018. So part (1) answer is 2018? Wait, but let me confirm again.Wait, maybe I made a mistake here. Let me check the arithmetic sequence again.First term (2008): 2.5 millionSecond year (2009): 2.5 + 0.5 = 3.0 millionThird year (2010): 3.5 millionFourth year (2011): 4.0 millionFifth year (2012): 4.5 millionSixth year (2013): 5.0 millionSeventh year (2014): 5.5 millionEighth year (2015): 6.0 millionNinth year (2016): 6.5 millionTenth year (2017): 7.0 millionEleventh year (2018): 7.5 millionNow, cumulative sum:Sum from 2008 to 2017 (n=10):Sum = 2.5 + 3.0 + 3.5 + 4.0 + 4.5 + 5.0 + 5.5 + 6.0 + 6.5 + 7.0Let's compute this step by step:2.5 + 3.0 = 5.55.5 + 3.5 = 9.09.0 + 4.0 = 13.013.0 + 4.5 = 17.517.5 + 5.0 = 22.522.5 + 5.5 = 28.028.0 + 6.0 = 34.034.0 + 6.5 = 40.540.5 + 7.0 = 47.5 millionExactly 47.5 million. So by the end of the 10th year (2017), the cumulative sum is exactly 47.5 million. But the problem says "first exceed," so the next year, 2018, adds another 7.5 million, making the cumulative sum 55 million, which is over 47.5. Therefore, the answer is 2018.But the problem says "by the end of which year," so the answer is 2018. Wait, but let me check if the quadratic solution gives n=10 as the exact value. So the equation yields n=10, but since at n=10 we reach exactly 47.5, we need n=11 to exceed. Therefore, the first year where cumulative area exceeds 47.5 million is 2018. So part (1) answer is 2018.Moving to part (2): By the end of 2013, will the area of affordable housing built that year account for more than 85% of the total housing area built that year? Why?First, 2013 is the 6th year (since 2008 is the first year). We need to compute the total housing area built in 2013 and the affordable housing area in 2013, then see if affordable is more than 85% of total.Given:- In 2008, total housing was 4 million sqm, of which 2.5 million was affordable.- Total housing increases by 8% per year.- Affordable housing increases by 0.5 million sqm each year.First, compute total housing in 2013. 2008 is year 1, 2013 is year 6. The total housing each year is a geometric sequence with initial term 4 million and common ratio 1.08.Total housing in year n: 4 * (1.08)^{n-1}So in 2013 (year 6), total housing is 4 * (1.08)^5 ≈ 4 * 1.47 (given reference data) = 5.88 million sqm.Affordable housing in 2013 (year 6) is the 6th term of the arithmetic sequence starting at 2.5 million with difference 0.5 million.a₆ = 2.5 + (6 - 1)*0.5 = 2.5 + 2.5 = 5.0 million sqm.Compute the percentage: (5.0 / 5.88) * 100 ≈ (5 / 5.88)*100 ≈ 85.03%Wait, 5 divided by 5.88. Let me compute this more accurately.5 / 5.88:5.88 goes into 5.00 approximately 0.85 times (since 5.88 * 0.85 = 5.88 * 0.8 + 5.88 * 0.05 = 4.704 + 0.294 = 5.0). So 5 / 5.88 ≈ 0.85, which is 85%. So exactly, 5 / 5.88 = 0.8503..., which is approximately 85.03%, so just over 85%. Therefore, yes, in 2013, affordable housing accounts for more than 85% of total housing built that year.But let me double-check the numbers.Total housing in 2013: 4 million * (1.08)^5. Reference data says 1.08^5 ≈ 1.47, so 4*1.47 = 5.88 million.Affordable housing in 2013: starting from 2008 as year 1, each year increases by 0.5 million. So year 1: 2.5, year 2: 3.0, year 3: 3.5, year 4: 4.0, year 5: 4.5, year 6: 5.0. So 5.0 million.Then 5.0 / 5.88 ≈ 0.8503, which is 85.03%, so just barely over 85%. Therefore, the answer is yes, it will account for more than 85%.Wait, but the problem says "by the end of 2013," so that's the same as year 2013. Therefore, the answer to part (2) is yes, because 5.0 / 5.88 ≈ 85.03% > 85%.But let me check if the reference data for 1.08^5 is 1.47. The problem gives 1.08^4≈1.36, 1.08^5≈1.47, 1.08^6≈1.59. So, yes, 1.08^5 is 1.47, so 4*1.47=5.88. Correct.Therefore, 5.0 / 5.88 ≈ 85.03%, which is more than 85%. Therefore, the answer is yes.But wait, just to be thorough, maybe I should check the exact value without using the reference. Let's compute 1.08^5 exactly.But the problem gives the reference data, so we should use that. The problem says to use 1.08^5≈1.47, so 4*1.47=5.88. So that's acceptable.Therefore, part (2) answer is yes, because the affordable housing area in 2013 is 5.0 million sqm, total housing is 5.88 million sqm, and 5.0 / 5.88 ≈ 85.03% > 85%.So summarizing:1) The cumulative affordable housing first exceeds 47.5 million by the end of 2018 (the 11th year).Wait, but wait, hold on. Wait, earlier, when we computed the sum at n=10 (2017), it was exactly 47.5 million. So 2018 is the 11th year, which would add another 7.5 million, making cumulative 55 million. Therefore, the first year where cumulative exceeds 47.5 is 2018.But let me double-check the arithmetic progression sum again.Formula: Sₙ = n/2 [2a₁ + (n-1)d]For n=10:S₁₀ = 10/2 [2*2.5 + 9*0.5] = 5 [5 + 4.5] = 5*9.5 = 47.5. Exactly. So at the end of the 10th year (2017), cumulative is exactly 47.5. So the first year where it exceeds is the 11th year, which is 2018. Therefore, answer is 2018.But the problem says "by the end of which year," so 2018 is the answer for part (1).Therefore, final answers:(1) 2018(2) Yes, because in 2013, affordable housing was 5.0 million sqm, total housing was 5.88 million sqm, which is approximately 85.03%, exceeding 85%.Final Answer(1) boxed{2018}(2) boxed{Yes}</think>To solve the given problems, we need to analyze both arithmetic and geometric sequences. Part (1)We need to find the first year by the end of which the cumulative area of affordable housing built in Guangyuan City since 2008 first exceeds 47.5 million square meters. - The area of affordable housing built each year forms an arithmetic sequence with the first term (a_1 = 2.5) million square meters and a common difference (d = 0.5) million square meters.- The sum of the first (n) terms of an arithmetic sequence is given by (S_n = frac{n}{2} [2a_1 + (n-1)d]).Setting up the equation to find (n) such that (S_n > 47.5):[47.5 = frac{n}{2} [5 + 0.5(n - 1)]]Solving the quadratic equation (0.5n^2 + 4.5n - 95 = 0) using the quadratic formula, we find (n = 10). However, the sum at (n = 10) is exactly 47.5 million, so we need (n = 11) to exceed this value. - The 10th year corresponds to 2017, and the 11th year corresponds to 2018. Therefore, the cumulative area first exceeds 47.5 million square meters by the end of 2018. Part (2)We need to determine if the area of affordable housing built in 2013 accounts for more than 85% of the total housing area built that year.- The total housing area each year forms a geometric sequence with the first term (4) million square meters and a common ratio (1.08).- The total housing area in 2013 (6th year) is (4 times 1.08^5 approx 4 times 1.47 = 5.88) million square meters.- The affordable housing area in 2013 (6th year) is (2.5 + 5 times 0.5 = 5.0) million square meters.Calculating the percentage:[frac{5.0}{5.88} approx 0.8503 approx 85.03%]Since 85.03% is more than 85%, the answer is yes. Final Answers(1) boxed{2018}(2) boxed{Yes},<think>Okay, let me try to figure out these two problems step by step. First, problem (1): We need to find by the end of which year the cumulative area of affordable housing first exceeds 47.5 million square meters. The data given is that in 2008 (which is considered the first year), they built 2.5 million square meters of affordable housing. Each subsequent year, the area of affordable housing increases by 500,000 square meters compared to the previous year. So, this is an arithmetic sequence where the first term is 2.5 million, and the common difference is 0.5 million per year.To find the cumulative area, we need the sum of this arithmetic sequence until it surpasses 47.5 million. The formula for the sum of the first n terms of an arithmetic sequence is S_n = n/2 * [2a + (n-1)d], where a is the first term, d is the common difference, and n is the number of terms. Let me plug in the values:a = 2.5 million, d = 0.5 million. We need S_n > 47.5 million.So,S_n = n/2 * [2*2.5 + (n - 1)*0.5] > 47.5Let me compute inside the brackets first:2*2.5 = 5(n - 1)*0.5 = 0.5n - 0.5So total inside the brackets is 5 + 0.5n - 0.5 = 4.5 + 0.5nTherefore,S_n = n/2 * (4.5 + 0.5n) > 47.5Multiply both sides by 2:n*(4.5 + 0.5n) > 95Let's write this as:0.5n² + 4.5n - 95 > 0Multiply both sides by 2 to eliminate the decimal:n² + 9n - 190 > 0Now, solve the quadratic equation n² + 9n - 190 = 0Using the quadratic formula: n = [-9 ± sqrt(81 + 760)] / 2sqrt(841) = 29So, n = [-9 ± 29]/2Discarding the negative solution, we have n = (20)/2 = 10So the quadratic equation equals zero at n = 10. Therefore, the inequality n² + 9n - 190 > 0 holds when n > 10. Since n must be an integer (number of years), the cumulative sum exceeds 47.5 million at n = 11. Therefore, by the end of the 11th year. But wait, the first year is 2008, so the 11th year would be 2008 + 10 = 2018. Wait, let's check that.Wait, if 2008 is the first year (n=1), then n=11 would correspond to 2008 + 10 = 2018. So, by the end of 2018, the cumulative area would first exceed 47.5 million square meters. But let me verify this calculation because sometimes when solving quadratics, especially with inequalities, the exact value might be a decimal, so we need to check n=10 and n=11.Let's compute S_10:Using the formula S_n = n/2 [2a + (n -1)d]S_10 = 10/2 [2*2.5 + 9*0.5] = 5 [5 + 4.5] = 5 * 9.5 = 47.5Oh, exactly 47.5. But the question says "first exceed" 47.5 million. So at n=10, it's exactly 47.5, so the next year, n=11, would be when it exceeds. Therefore, the answer is 2018. Wait, but 2008 is the first year, so 2008 is n=1, 2009 is n=2, ..., 2018 is n=11. Therefore, by the end of 2018, which is the 11th year, the cumulative area first exceeds 47.5 million.But wait, the problem says "with 2008 as the first year of accumulation". So cumulative from 2008 onwards. So, if n=10, that would be 2008 to 2017? Wait, no. If n=1 is 2008, then n=10 would be 2017, right? Because each n corresponds to one year. So 2008 is year 1, 2009 is year 2, ..., 2017 is year 10, 2018 is year 11. Therefore, S_10 is the sum up to 2017, which is exactly 47.5, and S_11 would be 47.5 + (2.5 + 10*0.5) million. Wait, the affordable housing in year n is 2.5 + 0.5*(n-1). So in year 11 (2018), the affordable housing built that year is 2.5 + 0.5*10 = 2.5 + 5 = 7.5 million. Therefore, S_11 = 47.5 + 7.5 = 55 million. So by the end of 2018, it's 55 million, which exceeds 47.5. Therefore, the first year when it exceeds is 2018. So the answer is 2018, which is the 11th year.But let me confirm this again. If n=10 gives S_10=47.5, which is exactly the target. Since the question is asking for the first year where the cumulative area *exceeds* 47.5 million, then it must be the next year, which is 2018. Therefore, the answer to part (1) is 2018.Now moving on to problem (2): By the end of 2013, will the area of affordable housing built that year account for more than 85% of the total housing area built that year? Why?First, we need to find the total housing area built in 2013 and the affordable housing area built in 2013, then compute the percentage.Given that in 2008, the total housing was 4 million square meters, and it increases by 8% each year. The affordable housing in 2008 was 2.5 million, and each subsequent year, affordable housing increases by 500,000 square meters annually. So, affordable housing is an arithmetic sequence with a = 2.5, d = 0.5. Total housing is a geometric sequence with a = 4, r = 1.08.First, we need to find the year 2013. Since 2008 is the first year, 2013 is the 6th year (2008:1, 2009:2, 2010:3, 2011:4, 2012:5, 2013:6). So n=6.First, compute the affordable housing built in 2013 (n=6):Affordable_n = 2.5 + 0.5*(n -1)So for n=6: 2.5 + 0.5*(5) = 2.5 + 2.5 = 5.0 million square meters.Total housing in 2013: The total housing is growing at 8% per year, starting from 4 million in 2008. So total housing in year n is 4*(1.08)^(n-1). For n=6 (2013), that's 4*(1.08)^5. The reference data gives 1.08^5 ≈ 1.47. Therefore, total housing area in 2013 is 4*1.47 ≈ 5.88 million square meters.Now, the affordable housing in 2013 is 5.0 million, total housing is approximately 5.88 million. The percentage is (5.0 / 5.88)*100 ≈ 85.03%. Wait, that's just over 85%. But let me check the exact value.Wait, 1.08^5 is given as approximately 1.47. So 4*1.47 = 5.88. Then 5.0 / 5.88 = 0.8503... which is approximately 85.03%, so just over 85%. Therefore, yes, it would account for more than 85%.But wait, is the calculation correct? Let's check:Total housing in 2013: 4 million * (1.08)^5. The problem statement says "built in the coming years, the area of new housing built in the city will increase by an average of 8% per year". So each year's total housing is 8% more than the previous year. So starting from 4 million in 2008 (year 1), year 2 (2009): 4*1.08, year 3 (2010): 4*(1.08)^2, ..., year 6 (2013): 4*(1.08)^5 ≈ 4*1.47 = 5.88.Affordable housing in 2013 (year 6): 2.5 + 0.5*(6-1) = 2.5 + 2.5 = 5.0 million.Therefore, 5.0 / 5.88 ≈ 0.8503, which is approximately 85.03%, so just over 85%. Therefore, the answer is yes, it will account for more than 85%.But wait, the problem says "By the end of 2013, will the area of affordable housing built that year account for more than 85% of the total housing area built that year? Why?"Therefore, since 85.03% is more than 85%, the answer is yes. However, let's verify if the reference data given is accurate. The problem gives 1.08^4 ≈1.36, 1.08^5≈1.47, 1.08^6≈1.59. So 1.08^5 is 1.47. Therefore, 4*1.47=5.88. 5.0 /5.88≈0.8503. So 85.03%, which is indeed more than 85%. Therefore, the answer is yes, because the affordable housing in 2013 is 5.0 million square meters, and the total housing is approximately 5.88 million square meters, resulting in approximately 85.03%, which is more than 85%.But hold on, I should check the exact value of 1.08^5 to see if the approximation is accurate enough. If 1.08^5 is exactly 1.469328, which is approximately 1.47. Then 4*1.469328≈5.877312 million. So 5.0 /5.877312≈0.8503, so 85.03%, which is indeed more than 85%. Therefore, the answer is yes, it will account for more than 85%.Therefore, summarizing:1) The cumulative affordable housing first exceeds 47.5 million by the end of 2018.2) By the end of 2013, affordable housing accounts for approximately 85.03% of total housing, which is more than 85%.But let me cross-verify problem (1) again to ensure no miscalculations. For cumulative affordable housing, each year it's an arithmetic progression starting at 2.5 million, increasing by 0.5 million each year. The sum formula is S_n = n/2 [2a + (n-1)d]So for n=10: S_10 = 10/2 [5 + 9*0.5] = 5 [5 + 4.5] = 5*9.5 = 47.5. Exactly 47.5. So by the end of the 10th year, which is 2017 (since 2008 is year 1), the cumulative sum is exactly 47.5. The question asks for when it first exceeds 47.5, so the next year, 2018 (year 11), the cumulative sum will be 47.5 + 2.5 + 0.5*10 = 47.5 + 2.5 +5 = 55 million. Hence, exceeding 47.5 in 2018. Therefore, part (1) answer is 2018.Part (2) is as discussed, yes, because 5.0 /5.88 ≈85.03%>85%.Final Answer(1) boxed{2018}(2) Yes, the area of affordable housing built in 2013 accounts for approximately 85.03%, which is more than 85% of the total housing area built that year.</think>To solve the given problems, we need to analyze both arithmetic and geometric sequences for the area of affordable housing and total housing built each year. Problem (1)We need to determine the first year by the end of which the cumulative area of affordable housing exceeds 47.5 million square meters. The affordable housing area forms an arithmetic sequence with the first term (a = 2.5) million square meters and common difference (d = 0.5) million square meters. The sum of the first (n) terms of an arithmetic sequence is given by:[S_n = frac{n}{2} [2a + (n-1)d]]Setting (S_n > 47.5) million:[frac{n}{2} [5 + 0.5(n - 1)] > 47.5]Simplifying this quadratic inequality:[0.5n^2 + 4.5n - 95 > 0]Solving the quadratic equation (n^2 + 9n - 190 = 0) using the quadratic formula, we find (n = 10). Since the sum at (n = 10) is exactly 47.5 million, the cumulative area first exceeds 47.5 million in the 11th year. Therefore, by the end of 2018 (2008 + 10 years), the cumulative area first exceeds 47.5 million square meters. Problem (2)We need to check if the area of affordable housing built in 2013 accounts for more than 85% of the total housing area built that year. The total housing area forms a geometric sequence with the first term (a = 4) million square meters and common ratio (r = 1.08). For 2013 (the 6th year), the total housing area is:[4 times 1.08^5 approx 4 times 1.47 = 5.88 text{ million square meters}]The affordable housing area in 2013 is an arithmetic sequence term:[2.5 + 0.5 times (6 - 1) = 5.0 text{ million square meters}]The percentage is:[frac{5.0}{5.88} approx 0.8503 approx 85.03%]Since 85.03% is more than 85%, the answer is yes. Final Answers(1) boxed{2018}(2) Yes, the area of affordable housing built in 2013 accounts for approximately 85.03%, which is more than 85% of the total housing area built that year.]

🔑:(1) By the end of 2017, the cumulative area of affordable housing built in the city will for the first time exceed 47.5 million square meters. (2) By the end of 2013, the area of affordable housing built that year will for the first time account for more than 85% of the total housing area built that year.Therefore, the answers are boxed{2017} for the first question and boxed{text{Yes}} for the second question.

🧠:[<think>Okay, so I need to find the ratio of the area of quadrilateral CDGE to the area of triangle ABC. Let me start by recalling some properties of medians and centroids in a triangle. First, I know that in any triangle, the three medians intersect at the centroid, which divides each median into a ratio of 2:1, with the longer segment being closer to the vertex. So, for example, in triangle ABC, the median AD is divided by the centroid G into AG:GD = 2:1, and similarly for the median BE, BG:GE = 2:1.Now, the problem mentions the medians AD and BE meeting at centroid G. The quadrilateral in question is CDGE. Let me try to visualize this. Let me sketch triangle ABC, mark the midpoints: D is the midpoint of BC since AD is a median, and E is the midpoint of AC since BE is a median. The centroid G is where AD and BE intersect. So quadrilateral CDGE is formed by the points C, D, G, and E.I need to find the area of CDGE compared to the whole triangle ABC. Hmm. Maybe coordinate geometry will help here. Let me assign coordinates to the triangle to make calculations easier. Let's place point A at (0, 0), point B at (2b, 0) so that the midpoint D of BC will be somewhere, but wait, maybe a better coordinate system would be to place the triangle in such a way that calculations are symmetric.Alternatively, let's assign coordinates with A at (0, 0), B at (2, 0), and C at (0, 2). Then, coordinates would be:- A: (0, 0)- B: (2, 0)- C: (0, 2)Then, the midpoints D and E can be calculated. Let's see:- D is the midpoint of BC. Coordinates of B are (2, 0) and C are (0, 2), so midpoint D is ((2 + 0)/2, (0 + 2)/2) = (1, 1).- E is the midpoint of AC. Coordinates of A are (0, 0) and C are (0, 2), so midpoint E is ((0 + 0)/2, (0 + 2)/2) = (0, 1).Now, the medians AD and BE. Let's find their equations and the centroid G.First, median AD goes from A(0, 0) to D(1, 1). The equation of line AD can be parameterized as x = t, y = t, where t goes from 0 to 1.Median BE goes from B(2, 0) to E(0, 1). Let's find the equation of BE. The slope of BE is (1 - 0)/(0 - 2) = -1/2. So the equation is y - 0 = (-1/2)(x - 2), which simplifies to y = (-1/2)x + 1.The centroid G is the intersection of AD and BE. So substitute the parametric equations of AD into the equation of BE. Since on AD, x = t and y = t, substitute into BE's equation:t = (-1/2)t + 1Solving for t:t + (1/2)t = 1 => (3/2)t = 1 => t = 2/3Therefore, G is at (2/3, 2/3). That makes sense, since centroid coordinates are the average of the vertices' coordinates. Let's check:Centroid formula is ((Ax + Bx + Cx)/3, (Ay + By + Cy)/3) = ( (0 + 2 + 0)/3, (0 + 0 + 2)/3 ) = (2/3, 2/3). Yep, that matches. So G is correctly located.Now, quadrilateral CDGE has vertices C, D, G, E. Let's list their coordinates:- C: (0, 2)- D: (1, 1)- G: (2/3, 2/3)- E: (0, 1)To find the area of quadrilateral CDGE, perhaps I can divide it into two parts: triangle CDG and triangle CGE? Wait, but CDGE is a quadrilateral. Alternatively, use the shoelace formula for quadrilaterals.Shoelace formula for a polygon with vertices (x1, y1), (x2, y2), ..., (xn, yn) is:Area = |1/2 * sum_{i=1 to n} (xi*yi+1 - xi+1*yi)|, where xn+1 = x1, yn+1 = y1.So let's apply the shoelace formula to quadrilateral CDGE.Order of the points: Let's go C -> D -> G -> E -> C.Coordinates:C: (0, 2)D: (1, 1)G: (2/3, 2/3)E: (0, 1)Back to C: (0, 2)Compute the sum:First, multiply xi*yi+1 for each i:C to D: 0*1 = 0D to G: 1*(2/3) = 2/3G to E: (2/3)*1 = 2/3E to C: 0*2 = 0Sum of these: 0 + 2/3 + 2/3 + 0 = 4/3Then, multiply yi*xi+1 for each i:C to D: 2*1 = 2D to G: 1*(2/3) = 2/3G to E: (2/3)*0 = 0E to C: 1*0 = 0Sum of these: 2 + 2/3 + 0 + 0 = 8/3Subtract the second sum from the first sum: 4/3 - 8/3 = -4/3Take absolute value and multiply by 1/2: | -4/3 | * 1/2 = 4/3 * 1/2 = 2/3So the area of quadrilateral CDGE is 2/3.Wait, but the area of triangle ABC is? Let's compute that. Coordinates are A(0,0), B(2,0), C(0,2). So base is 2, height is 2, area is (1/2)*2*2 = 2. So the ratio is (2/3)/2 = 1/3. But that can't be right because 2/3 is the area of CDGE, but triangle ABC has area 2, so ratio is 1/3. But wait, is that correct?Wait, hold on. Let's verify the area of quadrilateral CDGE again using shoelace. Maybe I made a mistake there.Applying shoelace formula step by step:List the coordinates in order:C: (0, 2)D: (1, 1)G: (2/3, 2/3)E: (0, 1)Back to C: (0, 2)Compute xi*yi+1:First pair: C to D: 0*1 = 0Second pair: D to G: 1*(2/3) = 2/3Third pair: G to E: (2/3)*1 = 2/3Fourth pair: E to C: 0*2 = 0Sum: 0 + 2/3 + 2/3 + 0 = 4/3Compute yi*xi+1:First pair: C to D: 2*1 = 2Second pair: D to G: 1*(2/3) = 2/3Third pair: G to E: (2/3)*0 = 0Fourth pair: E to C: 1*0 = 0Sum: 2 + 2/3 + 0 + 0 = 8/3Subtract: 4/3 - 8/3 = -4/3Take absolute and multiply by 1/2: 4/3 * 1/2 = 2/3. So that's correct.Area of CDGE is 2/3. Area of triangle ABC is 2. Therefore the ratio is 2/3 divided by 2 equals 1/3. So the ratio is 1/3. But wait, intuitively, I thought maybe it's 1/3, but let me think again. In a triangle, the centroid divides it into six small triangles of equal area. Each of those small triangles has area 1/6 of the original. If that's the case, then quadrilateral CDGE might be composed of two of those small triangles. Wait, but in this case, maybe not.Wait, actually, the three medians divide the triangle into six smaller triangles of equal area. Each has area 1/6 of the original triangle. Let me recall that property. Yes, each median divides the triangle into two equal areas, and the centroid further divides them into smaller triangles each of equal area. So, if we have the centroid, then connecting all medians would create six small triangles each with equal area. So each has area 1/6 of ABC.But in this problem, quadrilateral CDGE. Let's see. The points C, D, G, E.Looking at the coordinate system I set up:C is (0,2), D is (1,1), G is (2/3, 2/3), E is (0,1). So quadrilateral CDGE. Let's see if this area can be broken down into some of those small triangles.Alternatively, maybe using mass point geometry or area ratios.Alternatively, since we've already computed using coordinates that CDGE has area 2/3 and ABC has area 2, ratio 1/3. But is this generalizable? Because I chose specific coordinates for ABC. Let me check if this ratio holds regardless of the triangle's dimensions.Wait, in my coordinate system, ABC was a right-angled triangle with legs of length 2. But the centroid and medians properties are general for any triangle. So maybe the ratio is always 1/3?Wait, but in another triangle, would the ratio still be 1/3? Let me test with a different coordinate system.Let me take another triangle where calculations might be easier. Let’s choose a triangle with coordinates A(0,0), B(6,0), C(0,6). Then area of ABC is (1/2)*6*6=18.Midpoint D of BC: coordinates of B(6,0) and C(0,6), so D is (3,3).Midpoint E of AC: coordinates of A(0,0) and C(0,6), so E is (0,3).Median AD: from A(0,0) to D(3,3). Equation is y = x.Median BE: from B(6,0) to E(0,3). The slope is (3 - 0)/(0 - 6) = -0.5. Equation: y = -0.5x + 3.Centroid G is the intersection. Solve y = x and y = -0.5x + 3. Substitute x = -0.5x + 3 => 1.5x = 3 => x = 2. So y = 2. Thus centroid G is (2,2).Now quadrilateral CDGE: points C(0,6), D(3,3), G(2,2), E(0,3).Compute area using shoelace formula:Coordinates in order: C(0,6), D(3,3), G(2,2), E(0,3), back to C(0,6).Compute xi*yi+1:C to D: 0*3 = 0D to G: 3*2 = 6G to E: 2*3 = 6E to C: 0*6 = 0Sum: 0 + 6 + 6 + 0 = 12Compute yi*xi+1:C to D: 6*3 = 18D to G: 3*2 = 6G to E: 2*0 = 0E to C: 3*0 = 0Sum: 18 + 6 + 0 + 0 = 24Subtract: 12 - 24 = -12Area: | -12 | * 1/2 = 6Area of triangle ABC is 18, so ratio is 6/18 = 1/3. Same result! So in both coordinate systems, the ratio is 1/3. Therefore, it seems that regardless of the triangle, the ratio is 1/3.Therefore, the answer should be boxed{dfrac{1}{3}}.But let me try to approach this without coordinates, using area ratios.In triangle ABC, medians AD and BE intersect at G. We need the area of CDGE.Since G is the centroid, AG:GD = 2:1 and BG:GE = 2:1.Let me consider the areas created by the medians.First, in triangle ABC, the two medians AD and BE divide the triangle into smaller regions. There are six smaller triangles, each with equal area. Wait, is that true? If three medians are drawn, they divide the triangle into six regions of equal area. But here, only two medians are drawn, AD and BE. So, how does that divide the triangle?Alternatively, since we have two medians, they divide the triangle into four regions: the two medians intersect at G, creating four regions: AGP, PGD, BGQ, QGE, and the central quadrilateral? Wait, maybe not.Wait, in our problem, the medians AD and BE intersect at G. So, the triangle is divided into four parts: the two triangles near A and B, and two quadrilaterals. But maybe not. Let me think.When two medians intersect at the centroid, they divide the triangle into six smaller triangles of equal area? Wait, actually, no. Wait, three medians divide the triangle into six regions of equal area. If only two medians are present, they divide the triangle into four regions. Let me confirm.In triangle ABC, with medians AD and BE intersecting at G. Then, the areas of the four regions:1. Triangle AGB2. Quadrilateral BGDCWait, maybe not. Let me think in terms of ratios.Since centroid divides the medians in 2:1, then the areas can be determined accordingly.The area of triangle AGB: Since AG is 2/3 of AD, and BE is divided by G into BG:GE = 2:1. The area of triangle AGB would be 2/3 of the area of triangle ABD? Wait, perhaps another approach.Alternatively, consider that the centroid divides each median into 2:1, so the area ratios can be found by considering the sections.But maybe it's easier to use coordinate geometry again but in a general case.Let me consider a general triangle with vertices at A(x_A, y_A), B(x_B, y_B), C(x_C, y_C). The centroid G has coordinates ((x_A + x_B + x_C)/3, (y_A + y_B + y_C)/3). Then, coordinates of D, the midpoint of BC, is ((x_B + x_C)/2, (y_B + y_C)/2). Similarly, E is the midpoint of AC: ((x_A + x_C)/2, (y_A + y_C)/2).Then, to find the area of quadrilateral CDGE, with points C, D, G, E.Using shoelace formula in general terms might get complicated, but since we've tested two specific cases and got the same ratio, and due to the affine invariance of ratios of areas, the ratio should hold for any triangle.Alternatively, since affine transformations preserve ratios of areas, we can assume without loss of generality that the triangle is equilateral, or right-angled, or any specific type, compute the ratio there, and it will hold for all triangles.Thus, given that in both coordinate systems I tried, the ratio was 1/3, the answer is 1/3.Therefore, the ratio of the area of quadrilateral CDGE to the area of triangle ABC is boxed{dfrac{1}{3}}.Final Answerboxed{dfrac{1}{3}}</think>To determine the ratio of the area of quadrilateral (CDGE) to the area of triangle (ABC), we start by noting that the medians (AD) and (BE) intersect at the centroid (G), which divides each median into a ratio of (2:1).We use coordinate geometry to simplify the calculations. Assigning coordinates to the vertices of triangle (ABC) as (A(0, 0)), (B(2, 0)), and (C(0, 2)), we find the midpoints (D) and (E):- (D) is the midpoint of (BC) with coordinates ((1, 1)).- (E) is the midpoint of (AC) with coordinates ((0, 1)).The centroid (G) is calculated as the intersection of medians (AD) and (BE). Using the centroid formula, (G) is at (left(frac{2}{3}, frac{2}{3}right)).Using the shoelace formula to find the area of quadrilateral (CDGE) with vertices (C(0, 2)), (D(1, 1)), (Gleft(frac{2}{3}, frac{2}{3}right)), and (E(0, 1)):- Applying the shoelace formula, the area of (CDGE) is calculated as (frac{2}{3}).The area of triangle (ABC) is calculated as (2). The ratio of the area of quadrilateral (CDGE) to the area of triangle (ABC) is (frac{2}{3} / 2 = frac{1}{3}).This result is verified with another coordinate system and confirmed to hold generally due to the properties of centroids and medians in any triangle. Thus, the ratio is consistently (frac{1}{3}).[boxed{dfrac{1}{3}}],<think>Okay, so I need to find the ratio of the area of quadrilateral CDGE to the area of triangle ABC. The problem mentions that AD and BE are medians intersecting at the centroid G. Let me try to visualize this first. First, in any triangle, the centroid divides each median into a ratio of 2:1, with the longer part being closer to the vertex. So, if AD and BE are medians, then AG:GD = 2:1 and BG:GE = 2:1. That might be useful. Let me draw triangle ABC. Let's label the vertices A, B, and C. Then, AD is the median from A to the midpoint D of BC, and BE is the median from B to the midpoint E of AC. The centroid G is where these two medians intersect. Quadrilateral CDGE is formed by the points C, D, G, and E. So, connecting these points in order should make a four-sided figure inside the triangle. To find its area ratio, I need to figure out how much area this quadrilateral occupies relative to the entire triangle ABC.Since medians divide the triangle into smaller triangles of equal area, maybe I can use that property. But in this case, the quadrilateral isn't one of those smaller triangles. Maybe I need to decompose the quadrilateral into triangles whose areas I can determine?Alternatively, coordinate geometry might be helpful here. If I assign coordinates to the vertices of triangle ABC, I can compute the coordinates of the centroids and midpoints, then use the coordinates to calculate areas. Let me try that approach.Let's place triangle ABC in a coordinate system. Let me choose coordinates such that point A is at (0, 0), point B is at (2b, 0), and point C is at (0, 2c). This way, the triangle is right-angled at A, which might simplify calculations. But actually, maybe it's better to use a general triangle. Wait, but using specific coordinates might make it easier. Let's see.If I set coordinates:- Let’s place point A at (0, 0).- Point B at (2, 0) so that the midpoint D of BC will have coordinates based on where C is. Wait, maybe it's better to use a symmetric setup. Hmm.Alternatively, use barycentric coordinates or just a general triangle with vertices at (0,0), (2,0), and (0,2), but perhaps that complicates things. Wait, maybe let’s use coordinates where ABC is a generic triangle. Let me try with coordinates:Let’s assign coordinates as follows:- Let point A be (0, 0).- Point B be (2, 0) so that the midpoint E of AC can be found once we know point C.- Let me choose point C as (0, 2) so that AC is from (0,0) to (0,2), making E the midpoint at (0,1). But then midpoint D of BC would be the midpoint between (2,0) and (0,2), which is (1,1). Hmm, maybe that's manageable.Wait, but then medians AD and BE will be from A(0,0) to D(1,1) and from B(2,0) to E(0,1). The centroid G is the intersection of these medians. Let me compute the coordinates of G.First, find the equations of the medians AD and BE.Median AD goes from (0,0) to (1,1). The parametric equation for AD can be written as (t, t) where t ranges from 0 to 1.Median BE goes from (2,0) to (0,1). The parametric equation for BE can be found by determining its slope. The slope from (2,0) to (0,1) is (1 - 0)/(0 - 2) = -1/2. So, the equation can be written as starting at (2,0) and moving with direction vector (-2,1). So parametric equations:x = 2 - 2sy = 0 + swhere s ranges from 0 to 1.To find the centroid G, which is the intersection of AD and BE. So set the coordinates equal:From AD: (t, t)From BE: (2 - 2s, s)Therefore, we have:t = 2 - 2sandt = sSubstituting t = s into the first equation:s = 2 - 2s3s = 2s = 2/3Therefore, t = 2/3.So, centroid G is at (2/3, 2/3).Now, the quadrilateral CDGE consists of the points C, D, G, E.Given our coordinates:- Point C is at (0, 2)- Point D is the midpoint of BC: midpoint of (2,0) and (0,2) is (1,1)- Point G is (2/3, 2/3)- Point E is the midpoint of AC: midpoint of (0,0) and (0,2) is (0,1)So the coordinates are:C: (0, 2)D: (1, 1)G: (2/3, 2/3)E: (0, 1)To find the area of quadrilateral CDGE, which is a four-sided figure with vertices in the order C, D, G, E.One way to calculate the area is to use the shoelace formula. Let's list the coordinates in order:C: (0, 2)D: (1, 1)G: (2/3, 2/3)E: (0, 1)Back to C: (0, 2)Shoelace formula:Area = 1/2 |sum over i (x_i y_{i+1} - x_{i+1} y_i)|So let's compute each term:First pair: C to Dx_i = 0, y_i = 2x_{i+1} = 1, y_{i+1} = 1Contribution: 0*1 - 1*2 = 0 - 2 = -2Second pair: D to Gx_i = 1, y_i = 1x_{i+1} = 2/3, y_{i+1} = 2/3Contribution: 1*(2/3) - (2/3)*1 = 2/3 - 2/3 = 0Third pair: G to Ex_i = 2/3, y_i = 2/3x_{i+1} = 0, y_{i+1} = 1Contribution: (2/3)*1 - 0*(2/3) = 2/3 - 0 = 2/3Fourth pair: E to Cx_i = 0, y_i = 1x_{i+1} = 0, y_{i+1} = 2Contribution: 0*2 - 0*1 = 0 - 0 = 0Sum all contributions: -2 + 0 + 2/3 + 0 = -2 + 2/3 = -4/3Take absolute value and multiply by 1/2: 1/2 * | -4/3 | = 1/2 * 4/3 = 2/3So the area of quadrilateral CDGE is 2/3.Now, let's compute the area of triangle ABC. Since in our coordinate system, ABC has vertices at (0,0), (2,0), (0,2). This is a right-angled triangle with legs of length 2. Area = (1/2)*base*height = (1/2)*2*2 = 2.Therefore, the ratio of the area of CDGE to ABC is (2/3)/2 = 1/3.Wait, that seems straightforward, but is this correct? Let me double-check.But in this coordinate system, ABC has area 2, and CDGE has area 2/3, so the ratio is 1/3. Hmm. Alternatively, maybe I made a mistake in the shoelace calculation.Let me recalculate the shoelace formula step by step.Order of points: C(0,2), D(1,1), G(2/3,2/3), E(0,1), back to C(0,2).Compute sum of x_i y_{i+1}:First term: x_C * y_D = 0 * 1 = 0Second term: x_D * y_G = 1 * (2/3) = 2/3Third term: x_G * y_E = (2/3) * 1 = 2/3Fourth term: x_E * y_C = 0 * 2 = 0Sum: 0 + 2/3 + 2/3 + 0 = 4/3Compute sum of y_i x_{i+1}:First term: y_C * x_D = 2 * 1 = 2Second term: y_D * x_G = 1 * (2/3) = 2/3Third term: y_G * x_E = (2/3) * 0 = 0Fourth term: y_E * x_C = 1 * 0 = 0Sum: 2 + 2/3 + 0 + 0 = 8/3Subtract the two sums: |4/3 - 8/3| = |-4/3| = 4/3Multiply by 1/2: 1/2 * 4/3 = 2/3. Okay, that's the same result as before. So the area is indeed 2/3, and the area of ABC is 2, so ratio is 1/3. Hmm.But wait, this is in a specific coordinate system where ABC is a right-angled triangle with legs of length 2. But the problem doesn't specify the type of triangle, just a general triangle ABC. So does this ratio hold for any triangle?Since centroids and medians divide the triangle into smaller regions with consistent area ratios regardless of the triangle's specific shape, this result should be general. So even though I used a specific coordinate system, the ratio 1/3 should be valid for any triangle.But let me check with a different coordinate system to confirm.Let’s take another triangle. Suppose ABC is an equilateral triangle with side length 2. Wait, coordinates might complicate things, but let's see.Alternatively, take a different coordinate system where point A is (0,0), B is (4,0), and C is (0,6). Then, midpoints D and E would be different.Midpoint D of BC: midpoint between (4,0) and (0,6) is (2,3)Midpoint E of AC: midpoint between (0,0) and (0,6) is (0,3)Median AD is from (0,0) to (2,3). Equation: parametric form (2t, 3t), t from 0 to 1.Median BE is from (4,0) to (0,3). Slope is (3-0)/(0-4) = -3/4. Equation: starting at (4,0), moving with direction (-4,3). Parametric equations: x = 4 - 4s, y = 0 + 3s, s from 0 to 1.Find centroid G: intersection of AD and BE.From AD: (2t, 3t)From BE: (4 - 4s, 3s)Set equal:2t = 4 - 4s3t = 3s ⇒ t = sSubstitute t = s into first equation:2s = 4 - 4s ⇒ 6s = 4 ⇒ s = 2/3Therefore, G is at (4 - 4*(2/3), 3*(2/3)) = (4 - 8/3, 2) = (4/3, 2)Quadrilateral CDGE:Points:C: (0,6)D: (2,3)G: (4/3, 2)E: (0,3)Apply shoelace formula:Order: C(0,6), D(2,3), G(4/3,2), E(0,3), back to C(0,6)Compute sum of x_i y_{i+1}:0*3 + 2*2 + (4/3)*3 + 0*6 = 0 + 4 + 4 + 0 = 8Sum of y_i x_{i+1}:6*2 + 3*(4/3) + 2*0 + 3*0 = 12 + 4 + 0 + 0 = 16Difference: |8 - 16| = 8Area = 1/2 * 8 = 4Area of triangle ABC: base AB = 4, height from C is 6, so area = (1/2)*4*6 = 12Ratio: 4 / 12 = 1/3. Same result! So even in this different coordinate system, the ratio is 1/3. Therefore, the ratio is indeed 1/3 regardless of the triangle.Alternatively, another approach without coordinates: using area ratios with medians.In triangle ABC, the medians divide the triangle into six smaller triangles of equal area. Each of these triangles has an area equal to 1/6 of the original triangle.But how does quadrilateral CDGE fit into this? Let me try to see.Label the triangle ABC with centroid G. The medians AD, BE, and CF (where F is the midpoint of AB) intersect at G. Each median is divided by the centroid into a 2:1 ratio.The six small triangles formed by the medians all have equal area. So, each has area 1/6 of ABC.But quadrilateral CDGE is not one of these small triangles. Let's see which small triangles make up CDGE.Looking at the figure:- Point C is a vertex.- D is the midpoint of BC.- E is the midpoint of AC.- G is the centroid.So quadrilateral CDGE connects C to D to G to E to C.In terms of the six small triangles, perhaps CDGE is made up of two of these triangles plus another region. Wait, maybe not. Let me think.Alternatively, since D and E are midpoints, CD and CE are halves of the sides. But G is the centroid.Alternatively, use vector geometry. Let’s assign vectors to the points.Let’s let vector A be at origin, vector B be vector b, and vector C be vector c.Then, the midpoint D of BC is (B + C)/2.Midpoint E of AC is (A + C)/2 = C/2.The centroid G is (A + B + C)/3.Quadrilateral CDGE has vertices C, D, G, E.Expressed in vectors:C: cD: (b + c)/2G: (a + b + c)/3 = (0 + b + c)/3 = (b + c)/3E: c/2Wait, but A is at origin, so a = 0.Therefore, G is (b + c)/3.So coordinates:C: cD: (b + c)/2G: (b + c)/3E: c/2So quadrilateral CDGE has vertices at c, (b + c)/2, (b + c)/3, c/2.To compute the area, we can use the shoelace formula in vector terms or compute the area through determinants.Alternatively, parameterize the quadrilateral. But this might be complex. Alternatively, decompose CDGE into triangles.For example, split CDGE into triangle CDG and triangle CGE.Compute area of CDG and area of CGE, then sum them.First, area of triangle CDG:Points C, D, G.Vectors:From C to D: D - C = ( (b + c)/2 - c ) = (b - c)/2From C to G: G - C = ( (b + c)/3 - c ) = (b - 2c)/3The area is 1/2 | ( (b - c)/2 × (b - 2c)/3 ) | where × denotes cross product.Similarly, area of triangle CGE:Points C, G, E.Vectors:From C to G: G - C = (b + c)/3 - c = (b - 2c)/3From C to E: E - C = c/2 - c = -c/2Area is 1/2 | ( (b - 2c)/3 × (-c/2) ) |.But cross products in 2D can be considered as determinants. Let me compute these areas.But maybe in 2D, the area can be computed as 1/2 | x1*y2 - x2*y1 | for vectors (x1, y1) and (x2, y2).But perhaps this is getting too involved. Alternatively, since in the coordinate examples the ratio was 1/3, and the medians split the triangle into six regions of equal area, perhaps CDGE combines two of those regions plus another portion. Wait, but in the first coordinate example, CDGE had area 2/3 when ABC had area 2, giving ratio 1/3. So in that case, ABC's area was divided into 6 parts each of area 1/3, but no, 2 divided by 6 is 1/3, so each small triangle has area 1/3. Wait, but in the first example, ABC area was 2, so each of the six small triangles would have area 1/3, but the quadrilateral CDGE had area 2/3, which is two of those small triangles. Wait, but 2/3 is twice 1/3. But ABC area is 2, so 2 divided by 6 is 1/3 per small triangle.Wait, but in the first example, CDGE area was 2/3, which is two of those small triangles (each 1/3). So perhaps CDGE is composed of two small triangles. But how?Wait, the six small triangles are: AGP, PGF, FGD, DGB, BGQ, QGE, etc. Wait, maybe I need to visualize the six triangles formed by the medians.Alternatively, the three medians divide the triangle into six smaller triangles of equal area. Each median is cut by the centroid into two segments with ratio 2:1.In that case, each of the six small triangles has equal area. So each has an area of 1/6 of the original triangle.But in our problem, quadrilateral CDGE would consist of some combination of these small triangles.Looking back at the coordinate example where ABC was area 2, and CDGE was 2/3, which is 1/3 of ABC. Since ABC area is 2, 1/3 of that is 2/3. But 1/3 is equal to 2/6, so two of the six small triangles. Therefore, CDGE must be made up of two of the six small triangles. But which ones?Alternatively, considering the labels: from point C, moving to D (midpoint of BC), then to G (centroid), then to E (midpoint of AC). So CDGE is a quadrilateral that spans from C to the midpoint of BC, to the centroid, to the midpoint of AC.If each of the six small triangles has area 1/6, then CDGE must cover two of them. Alternatively, maybe one and a half? But in our coordinate example, it was two-thirds, which is two of the 1/3 areas. Wait, perhaps in the coordinate system where ABC is area 2, each small triangle is 1/3, so two of them make 2/3.But this seems conflicting with the idea of six equal areas. Wait, if the three medians divide the triangle into six smaller triangles of equal area. So if ABC has area 1, each of the six triangles has area 1/6. Then, CDGE must be combining some of these. Let's see.But in our first coordinate example, ABC area was 2, and CDGE area was 2/3. If ABC was area 1, CDGE would be 1/3. If ABC is divided into six parts of 1/6 each, then 1/3 is two of those parts. So CDGE is two of the six small triangles. Therefore, the answer is 1/3.Alternatively, here's another approach. Since D and E are midpoints, connecting them creates the midline DE, which is parallel to AB and half its length. But not sure if that helps here.Alternatively, note that the centroid divides the medians into 2:1. So from C to E is half of AC, but E is the midpoint. From E to G is a segment of the median. Wait, maybe we can use area ratios.Looking at triangle ABC. Let's consider the areas of certain sub-triangles.First, since E is the midpoint of AC, the area of triangle ABE is half the area of ABC. Similarly, the area of triangle CBE is also half.But BE is a median, so it splits ABC into two equal areas.Similarly, the median AD splits ABC into two equal areas as well.The intersection of the medians at centroid G divides each median into a 2:1 ratio. So, BG:GE = 2:1, and AG:GD = 2:1.Now, let's consider the area of triangle CGE.In triangle CBE (which has area 1/2 ABC), point G divides BE into BG:GE = 2:1. Therefore, the area of triangle CGE would be 1/3 of the area of triangle CBE, because the height from C to BE is the same for both triangles CGE and CBE, and the base GE is 1/3 of BE. Therefore, area of CGE is 1/3 * 1/2 ABC = 1/6 ABC.Similarly, the area of triangle CDG.In triangle CBD (since D is midpoint of BC, area of CBD is 1/2 ABC). The median from C would be CF, but we have the centroid G. Wait, maybe not. Alternatively, in triangle ACD, which is half of ABC, since D is the midpoint. The centroid G is located 2/3 along the median from A to D. So, area of triangle CDG: since GD is 1/3 of AD, the height from C to AD is the same as for triangle ACD. So the area of CDG would be 1/3 of the area of ACD. Since ACD is 1/2 ABC, then CDG is 1/3 * 1/2 ABC = 1/6 ABC.Therefore, quadrilateral CDGE is composed of triangles CGE and CDG, each 1/6 of ABC. Therefore, total area is 1/6 + 1/6 = 1/3 of ABC. Hence, the ratio is 1/3.This confirms the earlier result from coordinate geometry.Therefore, the ratio of the area of quadrilateral CDGE to the area of triangle ABC is 1/3.Final AnswerThe ratio of the area of quadrilateral ( CDGE ) to the area of triangle ( ABC ) is boxed{dfrac{1}{3}}.</think>To determine the ratio of the area of quadrilateral (CDGE) to the area of triangle (ABC), we start by noting that the medians (AD) and (BE) intersect at the centroid (G). The centroid divides each median into a ratio of (2:1).We can use coordinate geometry to find the areas involved. Assign coordinates to the vertices of triangle (ABC) such that (A) is at ((0, 0)), (B) is at ((2, 0)), and (C) is at ((0, 2)). The midpoints (D) and (E) are calculated as follows:- (D), the midpoint of (BC), has coordinates ((1, 1)).- (E), the midpoint of (AC), has coordinates ((0, 1)).The centroid (G) is found by solving the intersection of the medians (AD) and (BE). Using parametric equations, we find (G) at ((frac{2}{3}, frac{2}{3})).Using the shoelace formula to calculate the area of quadrilateral (CDGE) with vertices (C(0, 2)), (D(1, 1)), (G(frac{2}{3}, frac{2}{3})), and (E(0, 1)):- The coordinates are listed in order and the shoelace formula is applied: [ text{Area} = frac{1}{2} left| 0 cdot 1 + 1 cdot frac{2}{3} + frac{2}{3} cdot 1 + 0 cdot 2 - (2 cdot 1 + 1 cdot frac{2}{3} + frac{2}{3} cdot 0 + 1 cdot 0) right| ] Simplifying the calculations, the area of (CDGE) is found to be (frac{2}{3}).The area of triangle (ABC) is calculated as: [ text{Area of } ABC = frac{1}{2} times text{base} times text{height} = frac{1}{2} times 2 times 2 = 2 ]The ratio of the area of quadrilateral (CDGE) to the area of triangle (ABC) is: [ frac{text{Area of } CDGE}{text{Area of } ABC} = frac{frac{2}{3}}{2} = frac{1}{3} ]This result is confirmed by considering the properties of medians and centroids, which divide the triangle into six smaller triangles of equal area. Quadrilateral (CDGE) combines two of these smaller triangles, each contributing (frac{1}{6}) of the total area of (ABC), leading to the same ratio.Thus, the ratio of the area of quadrilateral (CDGE) to the area of triangle (ABC) is (boxed{dfrac{1}{3}}).]

🔑:Answer: frac{1}{3}Solution:Refer to the figure on the right.begin{aligned}{[C D G E] } & =[C D E]+[G E D] & =frac{1}{4}[A B C]+frac{1}{3}[B E D] & =frac{1}{4}[A B C]+frac{1}{3}left(frac{1}{4}[A B C]right) & =frac{1}{4}[A B C]+frac{1}{12}[A B C] & =frac{1}{3}[A B C]end{aligned}