🧠:[<think>Alright, so I have this problem here where I need to find the maximum value of S, which is the product of three expressions: (a² - ab + b²), (b² - bc + c²), and (c² - ca + a²). The constraints are that a, b, c are non-negative real numbers adding up to 3. Hmm, okay. Let's see how to approach this.First, since the variables are non-negative and their sum is fixed at 3, this is a constrained optimization problem. I remember that for optimization problems with symmetry, sometimes testing symmetric cases like when all variables are equal can give maximum or minimum values. But before jumping into that, maybe I should analyze the expression S more closely.Each term in the product S is of the form (x² - xy + y²). Wait, I recall that x² - xy + y² is always non-negative because it can be rewritten as (x - y/2)² + (3y²)/4, which is a sum of squares. So each term in the product is non-negative, which makes sense since a, b, c are non-negative. So S itself is non-negative.Now, since we need to maximize S, maybe we can consider cases where one or two variables are zero. For example, if we set c = 0, then the problem reduces to two variables with a + b = 3, and S becomes (a² - ab + b²)(b²)(a²). Similarly, if we set b = 0, then S becomes (a²)(c² - ca + a²)(c²). Maybe these edge cases can give us some insight.Let me try the case where one variable is zero. Let's set c = 0. Then a + b = 3, and S = (a² - ab + b²)(b²)(a²). Let's compute this. Let’s denote a + b = 3, so b = 3 - a. Then:First term: a² - ab + b² = a² - a(3 - a) + (3 - a)² = a² - 3a + a² + 9 - 6a + a² = 3a² - 9a + 9.Second term: b² = (3 - a)².Third term: a².So S = (3a² - 9a + 9)(3 - a)² a².This seems complicated, but maybe I can find its maximum by taking the derivative with respect to a. However, calculus might be messy here. Alternatively, maybe testing specific values can help. Let's try a = 0. Then S = (0 - 0 + 9)(9)(0) = 0. Similarly, if a = 3, then S = (27 - 27 + 9)(0)(9) = 0. So maximum must be somewhere in between.Let me try a = 1. Then b = 2. First term: 3(1)² -9(1) +9 = 3 -9 +9 = 3. Second term: (3 -1)² = 4. Third term: 1² = 1. So S = 3*4*1 = 12.If a = 2, b =1. First term: 3(4) -9(2) +9 = 12 -18 +9 = 3. Second term: (3 -2)^2=1. Third term:4. So S = 3*1*4=12. Same as before.What about a = 1.5, b=1.5. Then first term: 3*(2.25) -9*(1.5) +9 = 6.75 -13.5 +9 = 2.25. Second term: (1.5)^2 = 2.25. Third term: 2.25. So S=2.25 * 2.25 * 2.25 ≈ 11.39. Less than 12. So maybe maximum at a=1, b=2 or a=2, b=1.So when c=0, maximum S=12.Similarly, if we set a=0, then S becomes (b² - bc + c²)(c²)(b²). Let’s check if similar maximum occurs here. Let’s take b + c =3.If we set b=1, c=2, then first term: 1 - 2 +4 =3, second term:4, third term:1. So S=3*4*1=12. Similarly, if b=2, c=1, same result. So same maximum. So regardless of which variable we set to zero, the maximum seems to be 12.What if two variables are zero? For example, a=3, b=0, c=0. Then S=(9 -0 +0)(0 -0 +0)(0 -0 +9)=9*0*9=0. So S=0. Not helpful.What about the symmetric case where a = b = c =1. Then each term in S is (1 -1 +1)=1. So S=1*1*1=1. That's way smaller than 12. So clearly, the maximum is not at the symmetric point.Hmm, so when one variable is zero and the other two are 1 and 2, S=12. Maybe that's the maximum. But let's check other cases where none of the variables are zero.Suppose all variables are positive. Let's try a =2, b=1, c=0. Wait, we already considered that. Let's try a case where c is small but not zero. Let's take c=0.1, then a + b=2.9. Let's set a=1.9, b=1. Then compute S.First term: (1.9² -1.9*1 +1²)= (3.61 -1.9 +1)=2.71.Second term: (1² -1*0.1 +0.1²)=1 -0.1 +0.01=0.91.Third term: (0.1² -0.1*1.9 +1.9²)=0.01 -0.19 +3.61=3.43.So S=2.71 *0.91 *3.43 ≈ 8.46. Which is still less than 12. So even with a small c, the value is lower.Alternatively, let's take a=2, b=0.5, c=0.5. Then check S.First term: a² -ab +b²=4 -1 +0.25=3.25.Second term: b² -bc +c²=0.25 -0.25 +0.25=0.25.Third term: c² -ca +a²=0.25 -1 +4=3.25.So S=3.25*0.25*3.25≈ 3.25*0.8125≈2.64. Which is even worse.What if we take a=1.5, b=1.5, c=0. Then S= (1.5² -1.5*1.5 +1.5²)*(1.5²)*(1.5²). Wait, first term is 2.25 -2.25 +2.25=2.25. Then S=2.25*2.25*2.25≈11.39 as before. Still less than 12.Hmm. Maybe 12 is the maximum. But to confirm, let's check another case where none of the variables are 0, but maybe two are equal.Suppose a = b, so 2a + c =3. Let’s set a = b = t, then c=3 -2t.Then S becomes (t² - t² + t²) * (t² - t(3 -2t) + (3 -2t)²) * ((3 -2t)^2 - (3 -2t)t + t²).Simplify each term:First term: (0 + t²) = t².Second term: t² -3t +2t² +9 -12t +4t² = (t² +2t² +4t²) + (-3t -12t) +9 =7t² -15t +9.Third term: (9 -12t +4t²) -3t +2t² + t² = (9 -12t +4t²) -3t +3t² =9 -15t +7t².So S = t²*(7t² -15t +9)*(9 -15t +7t²).Let’s denote u =7t² -15t +9, then S = t²*u*(u) = t²*u².So S = t²*(7t² -15t +9)^2.Now, we can consider this as a function of t. Since a and b must be non-negative, t >=0, and c=3-2t >=0, so 3-2t >=0 => t <=1.5. So t is in [0,1.5].We can try to find maximum of S(t) = t²*(7t² -15t +9)^2 for t in [0,1.5].This might be easier to handle with calculus. Let's compute derivative of S(t):First, let’s set f(t) = t², g(t) = (7t² -15t +9)^2.Then S(t) = f(t)*g(t). The derivative S’(t) = f’(t)g(t) + f(t)g’(t).Compute f’(t) = 2t.Compute g’(t) = 2*(7t² -15t +9)*(14t -15).Therefore, S’(t) = 2t*(7t² -15t +9)^2 + t²*2*(7t² -15t +9)*(14t -15).Factor out 2t*(7t² -15t +9):S’(t) = 2t*(7t² -15t +9)[(7t² -15t +9) + t*(14t -15)].Simplify the expression inside the brackets:(7t² -15t +9) + t*(14t -15) =7t² -15t +9 +14t² -15t=21t² -30t +9.So S’(t) =2t*(7t² -15t +9)*(21t² -30t +9).To find critical points, set S’(t)=0. So solutions are t=0, or 7t² -15t +9=0, or 21t² -30t +9=0.Solve 7t² -15t +9=0:Discriminant D=225 -4*7*9=225 -252= -27 <0. So no real roots. Thus, 7t² -15t +9 is always positive (since coefficient of t² is positive and no real roots). So that term is never zero.Solve 21t² -30t +9=0:Discriminant D=900 -4*21*9=900 -756=144. sqrt(144)=12.t=(30 ±12)/(2*21)= (42)/42=1 or (18)/42=3/7≈0.4286.So critical points at t=1 and t=3/7≈0.4286.Now, check t in [0,1.5]. So critical points at t=0, t=3/7≈0.4286, t=1, and t=1.5 (endpoint). Let's evaluate S(t) at these points.At t=0: S=0.At t=3/7≈0.4286:First compute t=3/7. c=3 -2*(3/7)=3 -6/7=15/7≈2.1429.Compute S(t)= ( (3/7)^2 ) * (7*(9/49) -15*(3/7) +9)^2.First, compute 7*(9/49)=63/49=9/7≈1.2857.Then -15*(3/7)= -45/7≈-6.4286.Add 9: 9/7 -45/7 +63/7= (9 -45 +63)/7=27/7≈3.8571.Thus, S(t)= (9/49) * (27/7)^2= (9/49)*(729/49)= (9*729)/(49^2)=6561/2401≈2.732.At t=1:c=3 -2*1=1.S(t)=1²*(7*1 -15*1 +9)^2=1*(7 -15 +9)^2=1*(1)^2=1.At t=1.5:t=1.5, c=3 -2*1.5=0.S(t)= (1.5)^2*(7*(2.25) -15*(1.5) +9)^2=2.25*(15.75 -22.5 +9)^2=2.25*(2.25)^2=2.25*5.0625≈11.390625.So comparing S(t) at critical points:t=3/7≈0.4286: ≈2.732t=1:1t=1.5:≈11.39So the maximum in this case is at t=1.5, which is when c=0, giving S≈11.39, which is less than 12 as we saw earlier when c=0 and a=1,b=2. So even when considering a = b, the maximum in this case is still lower than 12.Therefore, the maximum seems to occur when one variable is zero and the other two are 1 and 2. Let me confirm again for c=0, a=1, b=2:S=(1² -1*2 +2²)*(2² -2*0 +0²)*(0² -0*1 +1²)= (1 -2 +4)*(4 -0 +0)*(0 -0 +1)=3*4*1=12.Yes, that gives S=12. Similarly, permuting variables gives the same result. So maybe 12 is the maximum.But to be thorough, let's check another case where two variables are equal and the third is different, but not zero. For example, let’s take a = b = t, c =3 -2t, but now t is different. Wait, we already did that. So the maximum in that case was 11.39.Alternatively, let's consider a different case where a ≠ b ≠ c. Let's say a=2, b=1, c=0. We already saw that gives S=12. What if a=2, b=0.9, c=0.1. Let's compute S.First term: a² -ab +b²=4 -1.8 +0.81=3.01.Second term: b² -bc +c²=0.81 -0.09 +0.01=0.73.Third term: c² -ca +a²=0.01 -0.2 +4=3.81.So S=3.01 *0.73 *3.81≈3.01*2.7813≈8.37. Still less than 12.Alternatively, maybe another distribution. Let's take a=1.2, b=1.8, c=0. Then S=(1.2² -1.2*1.8 +1.8²)*(1.8²)*(1.2²). Compute first term: 1.44 -2.16 +3.24=2.52. Then S=2.52*(3.24)*(1.44)=2.52*4.6656≈11.76. Closer to 12, but still less.Wait, actually, if we take a approaching 2 and b approaching1, then S approaches 12. So maybe 12 is indeed the maximum.Wait, but let's check with a=2. Let’s set a=2, b=1, c=0. Then S=3*4*1=12. If we slightly vary a and b such that c is very small but non-zero, does S become slightly more than 12? Let's try a=2.1, b=0.9, c=0. Then a + b =3, but c=0. Wait, c has to be 0 here. If a=2.1, b=0.9, c=0. Then S=(2.1² -2.1*0.9 +0.9²)*(0.9² -0.9*0 +0²)*(0² -0*2.1 +2.1²). Compute each term:First term: 4.41 -1.89 +0.81=3.33.Second term:0.81 -0 +0=0.81.Third term:0 -0 +4.41=4.41.So S=3.33 *0.81 *4.41≈3.33*3.5721≈11.89. Still less than 12.Wait, maybe taking a=1.8, b=1.2, c=0. Then S=(1.8² -1.8*1.2 +1.2²)*(1.2² -1.2*0 +0²)*(0² -0*1.8 +1.8²)= (3.24 -2.16 +1.44)*(1.44)*(3.24)= (2.52)*(1.44)*(3.24). Compute 2.52*1.44=3.6288. Then 3.6288*3.24≈11.76. Still less.Alternatively, taking a=2.5, b=0.5, c=0. Then:First term:6.25 -1.25 +0.25=5.25.Second term:0.25 -0 +0=0.25.Third term:0 -0 +6.25=6.25.Thus S=5.25 *0.25 *6.25=5.25*1.5625≈8.20. Worse.Hmm, so even when varying a and b with c=0, the maximum S occurs at a=1,b=2 or a=2,b=1 with S=12. If I try to set c to a very small positive number, say c=ε, then a + b =3 -ε. Let’s set a=2, b=1 -ε/2, c=ε. Then compute S. When ε approaches 0, S approaches 12. But for any ε>0, the value of S would be slightly less. Let's verify:First term: a² -ab +b²=4 -2*(1 -ε/2) + (1 -ε/2)^2=4 -2 +ε +1 -ε + (ε²)/4=3 - (3ε)/2 + (ε²)/4.Wait, maybe better to compute exactly:First term: a² -ab +b²=4 -2*(1 - ε/2) + (1 - ε/2)^2=4 -2 +ε +1 - ε + (ε²)/4= (4 -2 +1) + (ε - ε) + (ε²)/4=3 + (ε²)/4.Second term: b² - bc +c²=(1 - ε/2)^2 - (1 - ε/2)*ε + ε²=1 -ε + (ε²)/4 -ε + (ε²)/2 + ε²=1 -2ε + (7ε²)/4.Third term: c² - ca +a²=ε² -2ε +4.So when ε approaches 0, first term approaches 3, second term approaches1 -2ε, third term approaches4 -2ε. So S≈3*(1 -2ε)*(4 -2ε)=3*(4 -10ε +4ε²)≈12 -30ε. Which is less than 12. So as ε approaches 0, S approaches12 from below. Therefore, even with small ε>0, S is less than12. So the maximum occurs when c=0, and a=2,b=1, giving S=12.Therefore, after checking various cases, it seems that the maximum value of S is 12, achieved when one variable is 0 and the other two are 1 and 2 (in some order).But to be completely sure, let's check another case where two variables are non-zero and unequal, and the third is non-zero. For example, let's take a=2, b=0.9, c=0.1. Wait, we tried similar before and got S≈8.37. Alternatively, take a=1.5, b=1.4, c=0.1.First term: a² -ab +b²=2.25 -2.1 +1.96=2.11.Second term: b² -bc +c²=1.96 -0.14 +0.01=1.83.Third term: c² -ca +a²=0.01 -0.15 +2.25=2.11.Thus S=2.11*1.83*2.11≈2.11*3.861≈8.15. Still less than12.Alternatively, take a=2.2, b=0.7, c=0.1:First term:4.84 -1.54 +0.49=3.79.Second term:0.49 -0.07 +0.01=0.43.Third term:0.01 -0.22 +4.84=4.63.So S=3.79*0.43*4.63≈3.79*1.9909≈7.55. Worse.Alternatively, take a=1.2, b=1.8, c=0. Then we did that before, getting≈11.76. Close to12 but still less.Alternatively, take a=1.9, b=1.0, c=0.1. First term:3.61 -1.9 +1=2.71. Second term:1 -0.1 +0.01=0.91. Third term:0.01 -0.19 +3.61=3.43. So S≈2.71*0.91*3.43≈8.46. Not good.Alternatively, take a=1.6, b=1.4, c=0.0. Then S=(1.6² -1.6*1.4 +1.4²)*(1.4²)*(1.6²). Compute first term:2.56 -2.24 +1.96=2.28. Then S=2.28*(1.96)*(2.56)=2.28*5.0176≈11.44. Still less than12.So it seems that the maximum occurs when one variable is zero and the other two are 1 and 2, giving S=12. To confirm, perhaps we can use Lagrange multipliers for the original problem with three variables. Let me try setting up the Lagrangian.The function to maximize is S=(a² -ab +b²)(b² -bc +c²)(c² -ca +a²) with constraint a + b + c=3.The Lagrangian is L = (a² -ab +b²)(b² -bc +c²)(c² -ca +a²) - λ(a + b + c -3).Taking partial derivatives with respect to a, b, c, and λ, and setting them to zero. However, this seems extremely complicated due to the product of three terms. The partial derivatives would involve the product rule applied three times, leading to a very messy expression. It might not be practical without more advanced techniques or symmetry.Alternatively, maybe we can use the AM-GM inequality or other inequalities to bound S. However, given the complexity of S as a product of three quadratic terms, it's not straightforward. But perhaps we can analyze each term.Note that each term (x² -xy + y²) is equal to (x² + y² -xy). This expression is known to be equal to (x + y)^2 - 3xy. Since x and y are non-negative, maybe we can find bounds for each term.Alternatively, for any real numbers x, y, we have x² -xy + y² ≥ (x² + y²)/2, by the inequality x² -xy + y² = 3/4 (x - y)^2 + (x + y)^2 /4 ≥ (x + y)^2 /4. Wait, actually:Wait, x² -xy + y² = (x - y/2)^2 + (3y²)/4 ≥ (3/4)(x² + y²) ?Wait, let me check. Let x, y ≥0.x² -xy + y² = x² + y² -xy.Compare with (x² + y²)/2. Then x² + y² -xy - (x² + y²)/2 = (x² + y²)/2 -xy. So whether this is positive depends on x and y.For example, if x = y, then x² + y² -xy = x², and (x² + y²)/2 =x². So equality. If x ≠ y, then it's (x² + y²)/2 -xy = (x - y)^2 /2 ≥0. Therefore, x² -xy + y² ≥ (x² + y²)/2. So each term in S is at least (x² + y²)/2. But that might not help us directly.Alternatively, note that x² -xy + y² ≥ (x + y)^2 /4. Let's check:x² -xy + y² - (x + y)^2 /4 = x² -xy + y² - (x² + 2xy + y²)/4 = (4x² -4xy +4y² -x² -2xy -y²)/4 = (3x² -6xy +3y²)/4 = 3(x² -2xy + y²)/4 = 3(x - y)^2 /4 ≥0.So x² -xy + y² ≥ 3(x - y)^2 /4 + (x + y)^2 /4. Wait, no. Wait, we just showed that x² -xy + y² ≥ (x + y)^2 /4.Thus, each term is at least (x + y)^2 /4. So maybe S ≥ [(a + b)^2 /4][(b + c)^2 /4][(c + a)^2 /4] = [(a + b)(b + c)(c + a)]^2 / (4^3).But since a + b + c =3, (a + b)(b + c)(c + a) = (3 - c)(3 - a)(3 - b). Not sure if this helps. But if we use AM ≥ GM, (a + b)(b + c)(c + a) ≤ ( ( (3 - c) + (3 - a) + (3 - b) ) /3 )^3 = ( (9 - (a + b + c)) /3 )^3 = ( (9 -3)/3 )^3 = (2)^3=8. So (a + b)(b + c)(c + a) ≤8. Thus, S ≥ (8)^2 /64=64/64=1. But this gives a lower bound, not helpful for maximum.Alternatively, since we need an upper bound. Since each term x² -xy + y² ≤ x² + y². So S ≤ (a² + b²)(b² + c²)(c² + a²). Maybe find the maximum of this expression? But even this is not straightforward.Alternatively, note that for fixed a + b + c =3, the maximum of S occurs at the boundary, i.e., when one variable is zero, as we saw. Because when we move from the interior to the boundary (setting one variable to zero), we can increase some terms while decreasing others, but the net effect might be an increase. For example, setting c=0, the term (c² - ca + a²) becomes a², which is larger than if c were positive (since c² -ca + a² = a² -ac +c² ≥a² -ac, and if c>0, then -ac is negative, so a² -ac +c² ≥a² -ac ≥a² -a* something. Not sure. But in our earlier example, when c=0, the third term becomes a², which can be large if a is large. For example, when a=2, c=0, that term is 4. If we take a=2, b=1, c=0, then third term is 4, but if c is small, say c=0.1, then third term is 0.01 -0.2 +4=3.81, which is less than 4. So by setting c=0, we maximize that term. Similarly, the second term when c=0 becomes b², which is 1 when b=1. If c>0, the term (b² - bc +c²) is less than b² +c². Wait, but if c is positive, then (b² - bc +c²) is actually greater than b² - bc. But since c is small, maybe. For example, with b=1, c=0.1, then the term is1 -0.1 +0.01=0.91, which is less than1. So in this case, the term is smaller. Therefore, by setting c=0, we can have the second term as large as possible (since c=0 gives b², which is larger than if c>0). So the trade-off is that setting c=0 allows two terms (second and third) to be larger (third term becomes a², which is larger than if c>0; second term becomes b², which is larger than if c>0). The first term is (a² -ab + b²). When c=0, a + b=3. Let’s compare when c>0. Suppose we have a + b +c=3. If we take some c>0, then a +b=3 -c <3. So in that case, a and b are smaller. For example, if c=0.1, then a +b=2.9. If we take a=2, b=0.9, then first term is4 -1.8 +0.81=3.01, which is greater than when a=2, b=1, c=0, which was3. So actually, when c is positive, the first term can be slightly larger. However, the second and third terms decrease. So the net effect might be a decrease in the overall product.In the case where a=2, b=0.9, c=0.1: first term=3.01, second term≈0.91, third term≈3.81. Product≈3.01*0.91*3.81≈10.5, while when c=0, a=2, b=1, we get first term=3, second term=1, third term=4, product=12. So even though the first term is slightly larger when c=0.1, the decrease in the other terms leads to a lower product. Therefore, the maximum occurs when one variable is zero.Thus, after thorough consideration of different cases and edge cases, the maximum value of S is 12, achieved when one variable is zero and the other two are 1 and 2.Final Answerboxed{12}</think>Given non-negative real numbers (a, b, c) such that (a + b + c = 3), we need to find the maximum value of (S = left(a^2 - ab + b^2right)left(b^2 - bc + c^2right)left(c^2 - ca + a^2right)).First, we consider the case where one of the variables is zero. Without loss of generality, let (c = 0). Then, the problem reduces to two variables (a) and (b) with (a + b = 3). The expression for (S) simplifies to:[S = left(a^2 - ab + b^2right) cdot b^2 cdot a^2]Substituting (b = 3 - a), we get:[S = left(a^2 - a(3 - a) + (3 - a)^2right) cdot (3 - a)^2 cdot a^2]Simplifying the first term:[a^2 - 3a + a^2 + 9 - 6a + a^2 = 3a^2 - 9a + 9]Thus, the expression becomes:[S = (3a^2 - 9a + 9) cdot (3 - a)^2 cdot a^2]Testing specific values of (a) and (b), we find that when (a = 1) and (b = 2) (or vice versa), the value of (S) is:[S = left(1^2 - 1 cdot 2 + 2^2right) cdot 2^2 cdot 1^2 = 3 cdot 4 cdot 1 = 12]We also considered other cases where none of the variables are zero, but found that the product (S) was always less than 12. For example, symmetric cases where (a = b = c = 1) resulted in (S = 1), and other configurations with non-zero variables resulted in lower values.After thorough consideration of various cases and edge cases, the maximum value of (S) is achieved when one variable is zero and the other two are 1 and 2. Thus, the maximum value of (S) is:[boxed{12}],<think>Okay, so I need to find the maximum value of S, which is the product of three terms: (a² - ab + b²), (b² - bc + c²), and (c² - ca + a²), given that a, b, c are non-negative real numbers adding up to 3. Hmm, let me start by understanding the problem better.First, since a, b, c are non-negative and their sum is 3, each of them is between 0 and 3. The expression S looks symmetric but it's not fully symmetric because each term is a product of two variables with a cyclic permutation. For example, the first term is (a² - ab + b²), the second is (b² - bc + c²), and the third is (c² - ca + a²). So it's cyclically symmetric but not symmetric in all variables. That might mean that the maximum occurs at a symmetric point or maybe at some boundary where one variable is zero.Let me check some simple cases. Maybe if all variables are equal. If a = b = c = 1, since 1 + 1 + 1 = 3. Then each term would be (1 - 1 + 1) = 1. So S = 1 * 1 * 1 = 1. Is that the maximum? Maybe, but I need to verify.Alternatively, what if one of the variables is zero? Let's say c = 0. Then a + b = 3. Then S becomes (a² - ab + b²)(b²)(a²). Let's compute this when c = 0. Let's denote this as S(a, b, 0) = (a² - ab + b²)(b²)(a²). Since a + b = 3, let me set a = 3 - b. Then S becomes [( (3 - b)^2 - (3 - b)b + b² )][b²][(3 - b)^2].Simplify the first term: (9 - 6b + b² - 3b + b² + b²) = 9 - 9b + 3b². Wait, let me compute it step by step.First term: a² - ab + b² where a = 3 - b. So:a² = (3 - b)^2 = 9 - 6b + b²ab = (3 - b)b = 3b - b²So a² - ab + b² = (9 - 6b + b²) - (3b - b²) + b² = 9 - 6b + b² - 3b + b² + b² = 9 - 9b + 3b².So the first term is 3b² - 9b + 9. Then the second term is b², and the third term is a² = (3 - b)^2 = 9 - 6b + b². Therefore, S = (3b² -9b +9)(b²)(9 -6b + b²). Let me compute this expression.Let me denote S(b) = (3b² -9b +9)(b²)(9 -6b + b²). Let's expand this step by step. But maybe instead of expanding, I can find its maximum by taking derivative. However, since it's a single variable function now (since a and b are related by a = 3 - b when c = 0), perhaps calculus would work here. Alternatively, maybe testing some values.Let me try b = 1. Then a = 2. Then S(b=1) = (3*1 -9*1 +9)(1)(9 -6*1 +1) = (3 -9 +9)(1)(9 -6 +1) = (3)(1)(4) = 12.If b = 2, then a =1. Then S(b=2) = (3*4 -18 +9)(4)(9 -12 +4) = (12 -18 +9)(4)(1) = (3)(4)(1) =12.If b = 0, then a =3, S(b=0) = (0 -0 +9)(0)(9 -0 +0) = (9)(0)(9) =0. Similarly, if b=3, a=0, same result.What about b = 1.5? Let's see. Then a =1.5. Wait, but a + b =3, so a =1.5. Then S(b=1.5) = (3*(2.25) -9*(1.5) +9)*(2.25)*(9 -6*(1.5) +2.25). Let's compute term by term.First term: 3*(2.25) =6.75, 9*(1.5)=13.5, so 6.75 -13.5 +9= (6.75 +9) -13.5=15.75 -13.5=2.25Second term is (1.5)^2=2.25Third term: 9 -6*(1.5) + (1.5)^2=9 -9 +2.25=2.25Thus, S=2.25 * 2.25 *2.25= (2.25)^3= 11.390625, which is less than 12. So S=12 when b=1 or 2.Wait, so when c=0 and either a=2, b=1 or a=1, b=2, S=12. When variables are equal, S=1. So 12 is bigger. So perhaps the maximum occurs when one variable is zero? But let's check other cases where two variables are zero.Suppose two variables are zero. Let's say b=c=0, then a=3. Then S=(a² -0 +0)(0 -0 +0)(0 -0 +a²)= (9)(0)(9)=0. Similarly, other permutations, same result. So maximum when only one variable is zero?But maybe even higher when none are zero? Let me check another case.Suppose c is small but not zero. Let's take c approaching zero, so a + b approaching 3. Then S would approach 12, as when c=0. So perhaps 12 is the maximum. But maybe other cases where variables are not zero.Alternatively, maybe when two variables are equal and the third is different? Let's try a = b, so then c = 3 - 2a. But since c is non-negative, 3 - 2a >=0 => a <=1.5.Let me set a = b. Then c = 3 - 2a. Then compute S.First term: a² -a*b +b² = a² -a² +a² =a²Second term: b² -b c +c² = a² -a*(3 - 2a) + (3 - 2a)^2Third term: c² -c a +a² = (3 - 2a)^2 - (3 - 2a)a +a²Let me compute each term:Second term: a² -3a +2a² +9 -12a +4a² = (a² + 2a² +4a²) + (-3a -12a) +9=7a² -15a +9Wait, let's compute step by step:Second term is b² -b c +c², with b =a, c=3 - 2a.So:b² =a²bc =a*(3 -2a)=3a -2a²c²=(3 -2a)^2=9 -12a +4a²Thus, second term: a² - (3a -2a²) +9 -12a +4a²= a² -3a +2a² +9 -12a +4a²= (a² +2a² +4a²) + (-3a -12a) +9=7a² -15a +9Third term is c² -c a +a². Similarly:c²=9 -12a +4a²ca=(3 -2a)a=3a -2a²a²=a²Thus, third term:9 -12a +4a² -3a +2a² +a²=9 -15a +7a²Therefore, third term is same as second term:7a² -15a +9Thus, S= [a²] * [7a² -15a +9]^2So S(a) = a²*(7a² -15a +9)^2, where a is between 0 and 1.5.Now, we need to maximize S(a) over a ∈ [0, 1.5]. Let's compute S(a) at some points.First, a=0: S=0*(...)=0a=1.5: then c=3 -2*(1.5)=0. So S= (1.5)^2*(7*(2.25) -15*(1.5) +9)^2=2.25*(15.75 -22.5 +9)^2=2.25*(2.25)^2=2.25*5.0625=11.390625, which matches earlier calculation.At a=1: S=1*(7 -15 +9)^2=1*(1)^2=1. So S=1.At a=0.5: S=0.25*(7*(0.25) -15*(0.5) +9)^2=0.25*(1.75 -7.5 +9)^2=0.25*(3.25)^2=0.25*10.5625=2.640625At a=0.75: S=(0.75)^2*(7*(0.5625) -15*(0.75) +9)^2=0.5625*(3.9375 -11.25 +9)^2=0.5625*(1.6875)^2=0.5625*2.84765625≈1.601806640625Hmm, so maximum in this case when a is 1.5 or 0.5? Wait, when a=1.5, S≈11.39, which is less than 12 when c=0. So even when a=b, the maximum is 11.39, which is less than 12. So maybe the maximum occurs when one variable is zero, and the other two are 1 and 2.Wait, when c=0, a=2, b=1, S=12. When a=1, b=2, c=0, same thing. So maybe 12 is the maximum? But let's check other possibilities where two variables are non-zero, and one is different.Wait, perhaps when one variable is zero, and the other two are 1 and 2, giving S=12, which is higher than when variables are equal or other cases. So maybe 12 is the maximum.But to confirm, maybe there is a case where all three variables are non-zero and S is higher than 12. Let's try an example. Let's take a=2, b=1, c=0, which gives S=12, as before. What if we take a=2, b=0.5, c=0.5. Then a +b +c=3. Let's compute each term:First term: a² -ab +b²=4 -1 +0.25=3.25Second term: b² -bc +c²=0.25 -0.25 +0.25=0.25Third term: c² -ca +a²=0.25 -1 +4=3.25So S=3.25 *0.25 *3.25=3.25*0.8125=2.640625, which is much less than 12.Alternatively, take a=1.5, b=1.5, c=0, gives S=(1.5² -1.5*1.5 +1.5²)(1.5²)(1.5²). Wait, first term is (2.25 -2.25 +2.25)=2.25, then S=2.25*(2.25)*(2.25)=11.390625, same as before.What if we take a=2.5, b=0.25, c=0.25. Then a +b +c=3. Compute S:First term: a² -ab +b²=6.25 -0.625 +0.0625=5.6875Second term: b² -bc +c²=0.0625 -0.0625 +0.0625=0.0625Third term: c² -ca +a²=0.0625 -0.625 +6.25=5.6875So S=5.6875 *0.0625 *5.6875≈5.6875*0.0625=0.35546875, then *5.6875≈2.0234375, still less than 12.Alternatively, let's take a=2, b=1, c=0, which we know gives 12. If we slightly perturb c to be 0.1, then a +b +0.1=3 => a +b=2.9. Let's take a=2, b=0.9, c=0.1. Compute S:First term: a² -ab +b²=4 -1.8 +0.81=3.01Second term: b² -bc +c²=0.81 -0.09 +0.01=0.73Third term: c² -ca +a²=0.01 -0.2 +4=3.81Thus S=3.01 *0.73 *3.81≈3.01*0.73≈2.1973, then *3.81≈8.374. So even with a small c, S is 8.374, which is less than 12. So it seems that when c=0, S is maximized at 12.Alternatively, maybe taking c as 0.5 and adjusting a and b. Let's try c=0.5, then a +b=2.5. Let's set a=2, b=0.5. Then compute S:First term: a² -ab +b²=4 -1 +0.25=3.25Second term: b² -bc +c²=0.25 -0.25 +0.25=0.25Third term: c² -ca +a²=0.25 -1 +4=3.25Thus S=3.25*0.25*3.25=2.640625, still low.Alternatively, set a=1.8, b=1.2, c=0. Then S= (1.8² -1.8*1.2 +1.2²)(1.2²)(1.8²). Compute each term:First term:3.24 -2.16 +1.44=2.52Second term:1.44Third term:3.24Thus S=2.52*1.44*3.24≈2.52*1.44=3.6288, then *3.24≈11.75. Close to 12 but still less. Hmm, maybe if I set a=2.1, b=0.9, c=0? Then:First term: (2.1² -2.1*0.9 +0.9²)=4.41 -1.89 +0.81=3.33Second term:0.9²=0.81Third term:2.1²=4.41So S=3.33*0.81*4.41≈3.33*0.81≈2.70, then *4.41≈11.907. Closer to 12, but still not 12. Wait, when a=2, b=1, c=0, S= (4 -2 +1)*(1)*(4)=3*1*4=12. So that is exact.Wait, so if I take a=2, b=1, c=0, then:First term: a² -ab +b²=4 -2 +1=3Second term: b² -bc +c²=1 -0 +0=1Third term: c² -ca +a²=0 -0 +4=4Therefore S=3*1*4=12.But if I take a slightly different a and b, keeping c=0, such as a=2.1, b=0.9, as above, S=3.33*0.81*4.41≈11.907, which is less than 12.So maybe the maximum is indeed 12 when a=2, b=1, c=0 and permutations.But let me check another case where two variables are non-zero but not 2 and 1. Suppose a=3, b=0, c=0. Then S=0*0*9=0. Similarly, if a=2.5, b=0.5, c=0, then S=(6.25 -1.25 +0.25)*(0.25)*(6.25)=5.25*0.25*6.25=8.203125.So 12 still seems higher.Alternatively, let me check if when two variables are non-zero, but not in the case where the third is zero. For example, a=2, b=1, c=0 gives S=12. What if a=1.5, b=1.5, c=0 gives S≈11.39, which is less. What if a=1.8, b=1.2, c=0. Then S≈11.75. So still less.Alternatively, let's see if there's a case where all three variables are non-zero. Let me try a=2, b=1, c=0. We know S=12. Let me take c=0.1, so a +b=2.9. Let's take a=1.9, b=1.0, c=0.0. Wait, no, c=0.1. So a +b=2.9.Suppose a=2.0, b=0.9, c=0.1. Then compute S:First term: a² -ab +b²=4 -1.8 +0.81=3.01Second term: b² - bc +c²=0.81 -0.09 +0.01=0.73Third term: c² -ca +a²=0.01 -0.2 +4=3.81So S=3.01 *0.73 *3.81≈3.01*0.73=2.1973, *3.81≈8.374. Less than 12.Alternatively, take a=1.5, b=1.4, c=0.1. Then a +b +c=3.0.First term: a² -ab +b²=2.25 -2.1 +1.96=2.11Second term: b² - bc +c²=1.96 -0.14 +0.01=1.83Third term: c² -ca +a²=0.01 -0.15 +2.25=2.11So S=2.11*1.83*2.11≈2.11*1.83≈3.8613, then *2.11≈8.153. Still less than 12.Alternatively, take a=2.4, b=0.5, c=0.1. Then a +b +c=3.0.First term:5.76 -1.2 +0.25=4.81Second term:0.25 -0.05 +0.01=0.21Third term:0.01 -0.24 +5.76=5.53So S=4.81*0.21*5.53≈4.81*0.21=1.0101, *5.53≈5.58. Still less than 12.So perhaps 12 is indeed the maximum. But let me check another case where two variables are equal and the third is different. For example, a=2, b=1, c=0. That gives S=12. If I set a=2, c=1, b=0, same. Or b=2, a=1, c=0. All permutations. So maybe 12 is the maximum.Alternatively, let's check the case where one variable is 3 and the others are 0, but that gives S=0. So not helpful.Alternatively, let me think of using Lagrange multipliers. Since we need to maximize S under the constraint a + b +c=3. But since S is a product of three terms, each involving two variables, the derivative might be complicated. But perhaps possible.Let me denote S = (a² -ab +b²)(b² - bc +c²)(c² - ca +a²)Let’s denote f(a,b,c) = (a² -ab +b²)(b² - bc +c²)(c² - ca +a²)We need to maximize f(a,b,c) under a +b +c=3, a,b,c ≥0.Using Lagrange multipliers, set up the gradient of f equal to λ times gradient of constraint. But due to symmetry, perhaps it's difficult.Alternatively, note that when one variable is zero, we can get S=12, which is higher than the symmetric case of S=1. So maybe the maximum occurs at the boundary where one variable is zero.Alternatively, let's check another case where two variables are equal and one is different. For example, set a = b, then c =3 - 2a. We did this earlier, and found that S(a) = a²*(7a² -15a +9)^2. The maximum of this function occurs at some a in [0,1.5]. Let's try to compute its derivative to find critical points.Let’s compute dS/da = derivative of [a²*(7a² -15a +9)^2]Let’s set u = a², v = (7a² -15a +9)^2. Then S = u*v, so dS/da = u’*v + u*v’.Compute u’ = 2aCompute v’ = 2*(7a² -15a +9)*(14a -15)Thus, dS/da = 2a*(7a² -15a +9)^2 + a²*2*(7a² -15a +9)*(14a -15)Factor out 2a*(7a² -15a +9):dS/da = 2a*(7a² -15a +9)[ (7a² -15a +9) + a*(14a -15) ]Simplify inside the brackets:(7a² -15a +9) +14a² -15a =7a² +14a² -15a -15a +9=21a² -30a +9Thus, dS/da = 2a*(7a² -15a +9)*(21a² -30a +9)Set derivative equal to zero:Critical points when:1. a =0: gives S=0, minimum.2. 7a² -15a +9=0: solve quadratic equation.Discriminant D=225 - 4*7*9=225 -252= -27 <0. No real roots.3. 21a² -30a +9=0: solve quadratic equation.Discriminant D=900 -4*21*9=900 -756=144. sqrt(144)=12.Thus, a=(30 ±12)/42= (42)/42=1 or (18)/42=3/7≈0.4286.So critical points at a=1 and a=3/7≈0.4286.Check these points.First, a=1: then c=3 -2*1=1. Thus, a=b=1, c=1. Which gives S=1*1*1=1. As before.Second, a=3/7≈0.4286, then c=3 -2*(3/7)=3 -6/7=15/7≈2.1429.Compute S(a=3/7):First term: a² = (9/49)Second term:7a² -15a +9=7*(9/49) -15*(3/7) +9= (63/49) - (45/7) +9= (9/7) - (45/7) + (63/7)= (9 -45 +63)/7=27/7≈3.8571Third term: same as second term since when a=3/7, c=15/7, etc.Wait, actually when a=3/7, b=a=3/7, c=15/7.Wait, but in this case, the first term is a² -ab +b²= a² since a=b.But when a=3/7, first term is a²=9/49≈0.1837Second term: b² -bc +c²= a² -a c +c²=(9/49) - (3/7)(15/7) + (225/49)= (9 - 45 +225)/49=189/49≈3.8571Third term: c² -ca +a²= same as second term, since c and a are swapped, but in this case, since c is different, third term would be c² -ca +a²= same as second term. Wait, no, because variables are a, a, c. Let me check:Third term: c² -c a +a²= (15/7)^2 - (15/7)(3/7) + (3/7)^2=225/49 -45/49 +9/49=(225 -45 +9)/49=189/49=27/7≈3.8571Therefore, S= (9/49) * (27/7)^2= (9/49)*(729/49)= (9*729)/49²=6561/2401≈2.731. So approximately 2.731, which is more than 1 but less than 12. So the critical point at a=3/7 gives S≈2.731, which is not the maximum.Therefore, in the case where a=b, the maximum occurs at the endpoints: when a=1.5, c=0, giving S≈11.39 or when a=1, c=1, S=1.But since when c=0 and a=2, b=1, which is different from a=b case, gives S=12. So the maximum in the case where one variable is zero is higher.Therefore, from all these cases, it seems that the maximum of S is 12, achieved when one variable is zero and the other two are 1 and 2.But to confirm, let's check if there are other critical points when all variables are non-zero. This would require using Lagrange multipliers for three variables.Let’s attempt that. Let’s set up the Lagrangian:L = (a² -ab +b²)(b² -bc +c²)(c² -ca +a²) - λ(a +b +c -3)Then take partial derivatives with respect to a, b, c, and set them to zero.But this seems very complicated, as the derivative of the product would involve multiple terms. Let me see.Alternatively, suppose that the maximum occurs when two variables are in a certain ratio and the third is zero. From the earlier trials, when one variable is zero, the maximum S is 12. When all variables are non-zero, S is less. Therefore, perhaps 12 is indeed the maximum.Alternatively, maybe when two variables are equal and the third is different but non-zero. For example, a=2, b=1, c=0 gives S=12. If we take a=2, b=1, c=0.0001, then S would be slightly less than 12. So the maximum occurs at the boundary when c=0.Therefore, based on these trials and calculations, the maximum value of S is 12, achieved when one variable is zero and the other two are 1 and 2.Final AnswerThe maximum value of ( S ) is boxed{12}.</think>Given non-negative real numbers (a, b, c) such that (a + b + c = 3), we need to find the maximum value of (S = left(a^2 - ab + b^2right)left(b^2 - bc + c^2right)left(c^2 - ca + a^2right)).First, we consider the case where one of the variables is zero. Suppose (c = 0). Then, (a + b = 3) and the expression simplifies to:[S = left(a^2 - ab + b^2right) left(b^2right) left(a^2right)]Substituting (a = 3 - b), we get:[S = left((3 - b)^2 - (3 - b)b + b^2right) left(b^2right) left((3 - b)^2right)]Simplifying the first term:[(3 - b)^2 - (3 - b)b + b^2 = 9 - 6b + b^2 - 3b + b^2 + b^2 = 9 - 9b + 3b^2]Thus, the expression becomes:[S = (3b^2 - 9b + 9) cdot b^2 cdot (9 - 6b + b^2)]Testing specific values of (b), we find:- When (b = 1) and (a = 2), the expression evaluates to (3 cdot 1 cdot 4 = 12).- When (b = 2) and (a = 1), the expression also evaluates to (3 cdot 1 cdot 4 = 12).Next, we consider the case where all variables are non-zero. Testing various values such as (a = b = c = 1) results in (S = 1), which is significantly lower than 12. Other configurations with non-zero variables also yield values lower than 12.Finally, we check the boundary cases where two variables are equal and the third is different. For example, setting (a = b) and (c = 3 - 2a) results in a maximum value of approximately 11.39 when (a = 1.5), which is still less than 12.After thorough testing and considering various configurations, the maximum value of (S) is found to be 12 when one variable is zero and the other two are 1 and 2. Thus, the maximum value of (S) is (boxed{12}).]

🔑:Solution: Without loss of generality, let a geq b geq c,then b^{2}-b c+c^{2} leq b^{2}, c^{2}-c a+a^{2} leq a^{2},thus S leq a^{2} b^{2}left(a^{2}-a b+b^{2}right),let a+b=p leq 3, a b=q leqleft(frac{a+b}{2}right)^{2} leqleft(frac{a+b+c}{2}right)^{2}=frac{9}{4}, and p^{2} geq 4 qthus S leq a^{2} b^{2}left(a^{2}-a b+b^{2}right)=q^{2}left(p^{2}-3 qright) leq q^{2}(9-3 q),let f(q)=q^{2}(9-3 q), then f^{prime}(q)=9 q(2-q),if q in[0,2), then f^{prime}(q)>0; if q inleft(2, frac{9}{4}right], then f^{prime}(q)<0,thus max _{q[0.0}]} f(q)=f(2)=12,therefore, the maximum value of s is 12, which is achieved when a=2, b=1, c=0 and its cyclic permutations.

🧠:[<think>Okay, so I need to figure out what n > 1 makes it possible to have stamp denominations of n and n+2 such that any value of 2n+2 or higher can be obtained. Hmm, this sounds like a coin problem, but with stamps. The goal is to determine the smallest n where the combination of n and n+2 kronor stamps can cover every amount starting from 2n+2 upwards. First, let me recall that in such problems, usually, the concept of the Frobenius number comes into play. The Frobenius number for two coprime denominations a and b is ab - a - b. But wait, in this case, the denominations are n and n+2. Are they coprime? Let me check. The GCD of n and n+2 would be the same as GCD(n, 2). So if n is even, GCD(n, 2) is 2; if n is odd, GCD(n, 2) is 1. So if n is odd, the denominations are coprime, and if n is even, they have a common divisor of 2.But the problem states that any value ≥ 2n+2 can be obtained. So maybe the Frobenius number (the largest amount that cannot be formed) is 2n+1? If that's the case, then we need the Frobenius number for denominations n and n+2 to be 2n+1. Wait, but if they are coprime, the Frobenius number is n(n+2) - n - (n+2) = n² + 2n - n - n - 2 = n² - 2. Hmm, that's different. So if n and n+2 are coprime, the largest non-representable number is n² - 2. But the problem states that we need to have all numbers ≥ 2n+2 representable. That would mean that the Frobenius number must be ≤ 2n+1. So n² - 2 ≤ 2n + 1. Let's solve this inequality:n² - 2 ≤ 2n + 1 n² - 2n - 3 ≤ 0 Quadratic equation: n² - 2n - 3 = 0 Solutions: n = [2 ± sqrt(4 + 12)] / 2 = [2 ± sqrt(16)] / 2 = [2 ± 4]/2 So n = (2 + 4)/2 = 3 or n = (2 - 4)/2 = -1. Since n >1, n=3 is the solution. So if n=3, then the Frobenius number is 3² - 2 = 9 - 2 =7. But 2n+1 = 7. So that's exactly matching. Therefore, for n=3, the Frobenius number is 7, which is equal to 2*3+1=7, so all numbers starting from 8 (which is 2*3+2=8) can be formed. That seems correct.But wait, n=3 is odd, so denominations 3 and 5. Let me check if 7 is the largest non-representable number. Let's list the numbers:1: Can't be formed with 3 and 5 2: Can't 3: Yes (1*3) 4: Can't 5: Yes (1*5) 6: 2*3 7: Can't (3+5=8) 8: 3+5 9: 3*3 10: 2*5 And so on. So indeed, 7 is the largest non-representable number. So for n=3, all numbers ≥8 can be formed, which is 2n+2=8. So that works. But the problem says "Find n >1" so maybe n=3 is the answer. But let me check if there are other possible n. The inequality n² - 2 ≤ 2n +1 gives n² -2n -3 ≤0, which is true for n between -1 and 3. Since n>1, the integer solutions would be n=2 and n=3. Wait, n=2 is even. Let's check n=2.If n=2, denominations are 2 and 4. But since 2 divides 4, the only amounts we can form are even numbers. But any value ≥2n+2=6. However, 6=2+4, 8=4+4, etc. But odd numbers like 5,7,9,... can't be formed. So n=2 is invalid because it can't form all values ≥6, only even ones. Therefore, n=2 doesn't work.Thus, n=3 is the answer. But wait, let me check if n=4 works. Wait, n=4 would be denominations 4 and 6. GCD(4,6)=2. So they are not coprime. So the concept of Frobenius number doesn't directly apply here. Instead, for denominations with GCD d, the largest number that cannot be formed is d*(Frobenius number of (a/d, b/d)) + (d-1). But in this case, since d=2, and denominations are 4 and 6, so divide by 2: 2 and 3. The Frobenius number for 2 and 3 is 2*3 -2 -3=1. Therefore, the largest number not representable by 4 and 6 is 2*1 + (2-1)=3? Wait, maybe I need to check. If denominations are 4 and 6, then the numbers that can be formed are 4,6,8,10,12,... So all even numbers ≥4. But 2 is excluded. So the largest number that cannot be formed is infinity, but since we are only considering numbers ≥2n+2=10. Wait, 10 can be formed as 4+6. But 8=4+4, 10=4+6, 12=6+6, etc. So all even numbers ≥4 can be formed. But numbers like 5,7,9, etc., can't be formed. So if the problem requires that any value ≥10 can be formed, regardless of parity, then n=4 would not work. Therefore, n=4 is invalid.So, seems like n=3 is the answer. But let me check n=5. For n=5, denominations are 5 and 7. Since 5 and 7 are coprime, the Frobenius number is 5*7 -5 -7=35 -12=23. So the largest number that cannot be formed is 23. Therefore, all numbers ≥24 can be formed. But the problem requires all numbers ≥2n+2=12. Wait, but if the Frobenius number is 23, then numbers from 24 onwards can be formed. But 12 to 23 may have some numbers that can't be formed. So n=5 would not satisfy the condition. So the answer must be n=3.Wait, but maybe I need to check whether for n=3, all numbers ≥8 can be formed. Let's verify:n=3, denominations 3 and 5.8=3+5 9=3*3 10=5*2 11=3*2 +5 12=3*4 13=5*2 +3 14=5 + 3*3 15=5*3 16=5*2 +3*2 17=5*1 +3*4 18=3*6 19=5*2 +3*3 20=5*4 ...and so on. It seems like every number from 8 onwards can be formed. So yes, n=3 works.But let's check n=1, even though the problem states n>1. n=1 would give denominations 1 and 3. Then all numbers ≥4 can be formed. But since n>1, we can ignore this.Another check: For n=3, the required starting point is 2n+2=8, and indeed, 8 and above can be formed. For n=4, required starting point is 10, but only even numbers can be formed. So n=4 is invalid.Therefore, the answer is n=3.Final AnswerThe value of ( n ) is boxed{3}.</think>To determine the value of ( n > 1 ) such that stamp denominations of ( n ) and ( n+2 ) can form any value ( geq 2n + 2 ), we need to consider the Frobenius number for the denominations ( n ) and ( n+2 ). First, we check the greatest common divisor (GCD) of ( n ) and ( n+2 ). The GCD is 2 if ( n ) is even and 1 if ( n ) is odd. For coprime denominations (when ( n ) is odd), the Frobenius number is given by ( n(n+2) - n - (n+2) = n^2 - 2 ). We need this Frobenius number to be less than or equal to ( 2n + 1 ), ensuring all values ( geq 2n + 2 ) can be formed.Solving the inequality:[n^2 - 2 leq 2n + 1][n^2 - 2n - 3 leq 0]The quadratic equation ( n^2 - 2n - 3 = 0 ) has solutions ( n = 3 ) and ( n = -1 ). Since ( n > 1 ), we consider ( n = 3 ).For ( n = 3 ), the denominations are 3 and 5. The Frobenius number is ( 3 times 5 - 3 - 5 = 7 ), which means all numbers ( geq 8 ) (which is ( 2 times 3 + 2 = 8 )) can be formed. Checking values from 8 onwards confirms they can be formed using combinations of 3 and 5.For even ( n ) (e.g., ( n = 2 )), denominations are not coprime, leading to only even numbers being formable, which does not satisfy the problem's requirement. Higher odd values (e.g., ( n = 5 )) result in a Frobenius number larger than ( 2n + 1 ), failing to cover all required values.Thus, the solution is ( n = 3 ).[boxed{3}],<think>Okay, let's try to figure out this problem. We need to find an integer n > 1 such that using stamp denominations of n and n+2, we can form any value greater than or equal to 2n+2. Hmm, so it's a classic coin/stamp problem where we want to know the largest amount that can't be formed and ensure that 2n+2 is the point after which all amounts are possible. Wait, but actually, the problem states that it's possible to obtain any value ≥ 2n+2. So maybe 2n+2 is the smallest amount such that all larger amounts can be formed. That might mean that 2n+2 is the Frobenius number plus one? Wait, the Frobenius number for two coprime denominations a and b is ab - a - b. But here, n and n+2. Let's check if they are coprime. If n is even, then n and n+2 would both be even, so their gcd is at least 2. If n is odd, then n and n+2 are two apart, so their gcd would be 1. So if n is odd, they are coprime, and if n is even, they are not. Therefore, if n is even, the problem might not have a solution because the Frobenius number applies only to coprime denominations. Wait, but the problem doesn't specify that the denominations have to be coprime. It just says find n > 1 such that with n and n+2, any amount ≥ 2n+2 can be formed.So maybe even if they are not coprime, we can still have some conditions. Let me think. If n is even, then n and n+2 are both even, so any combination of them will also be even. Therefore, only even amounts can be formed, so we can't form any odd amounts. Therefore, in that case, the answer would not be possible because the problem says "any value ≥ 2n+2", which includes both even and odd. So n must be odd. Therefore, n must be odd. So n is odd, n and n+2 are coprime (since they are two apart and n is odd), so then we can apply the Frobenius number formula, which is ab - a - b. Here, a = n, b = n+2. So the Frobenius number would be n(n+2) - n - (n+2) = n² + 2n - n - n - 2 = n² - 2. Wait, so the largest number that cannot be expressed is n² - 2. Then, the next number after that, n² - 1, can be expressed, and all numbers after that can be expressed. So if we want all numbers ≥ 2n+2 to be expressible, then 2n+2 must be greater than the Frobenius number. Wait, but the Frobenius number is n² - 2, so we need 2n + 2 > n² - 2. So 2n + 2 > n² - 2. Let's rearrange this inequality: n² - 2n - 4 < 0. Let's solve n² - 2n - 4 < 0. The roots of n² - 2n - 4 = 0 are [2 ± sqrt(4 + 16)] / 2 = [2 ± sqrt(20)] / 2 = [2 ± 2*sqrt(5)] / 2 = 1 ± sqrt(5). Since sqrt(5) is approximately 2.236, the roots are approximately 1 + 2.236 = 3.236 and 1 - 2.236 = negative. So the inequality n² - 2n - 4 < 0 holds for n between 1 - sqrt(5) and 1 + sqrt(5). Since n > 1 and integer, the inequality holds for n < 1 + sqrt(5) ≈ 3.236. So n can be 2 or 3. But n >1, so possible n=2 or 3. But earlier, we concluded that n must be odd. Because if n is even, the denominations are both even, so can't form odd numbers, which are required for "any value ≥ 2n+2". Therefore, n=3 is possible. Let's check for n=3. Denominations 3 and 5. The Frobenius number is 3*5 - 3 -5=15-8=7. So the largest number that can't be expressed is 7. Then 8 and above can be expressed. So 2n+2 = 2*3 +2=8. So 8 is exactly where the expressible numbers start. Therefore, n=3 is a solution. Let's check n=2. Denominations 2 and 4. But as they are both even, you can't form odd numbers. However, 2n+2=6. So the problem requires forming any value ≥6. But 6 is even, 7 is odd, 8 is even, etc. Since we can't form odd numbers, 7,9,11,... can't be formed. Therefore, n=2 is invalid. So only n=3 is possible? Wait, but let's check n=5. Let's see if that works. n=5, denominations 5 and 7. Frobenius number is 5*7 -5 -7=35-12=23. So the largest number not expressible is 23. So 24 and above can be formed. But 2n+2=12. So from 12 onwards, we need to be able to form all numbers. But according to Frobenius, we can form all numbers ≥24. But between 12 and 23, there are numbers that can't be formed. Therefore, n=5 is not a solution. Therefore, only n=3 works. Wait, let's confirm. For n=3, denominations 3 and 5. Let's check numbers starting at 8:8: 5+3=89: 3*3=910: 5*2=1011: 5 + 3*2=1112: 3*4 or 5*1 +3*2=5+6=11? Wait, 12=3*4=12, yes.13=5*2 +3=10+3=1314=5*1 +3*3=5+9=1415=5*3=1516=5*2 +3*2=10+6=1617=5*1 +3*4=5+12=1718=3*6=18And so on. So starting at 8, all numbers can be formed. But 8 is exactly 2n+2=8. So that works. So n=3 is a solution. What about n=1? The problem says n>1. So n=3 is the answer. Wait, but let's check n=4. Even though n is even, but just to confirm. Denominations 4 and 6. Since they are both even, you can only form even numbers. However, 2n+2=10. So from 10 onwards, even numbers can be formed. Let's check:10=4 +612=6*2 or 4*314=6 +4*216=4*4 or 6*2 +4But 10,12,14,16,... all even numbers. But the problem says "any value ≥10". However, numbers like 11,13,15 can't be formed, so n=4 is invalid. So only n=3 works. Therefore, the answer is n=3. Wait, but just to make sure there are no other possible n. Let's check n=5. As before, Frobenius number is 23, so numbers above 23 can be formed, but 2n+2=12. There's a gap between 12 and 23 where some numbers cannot be formed. For example, 19: can we form 19 with 5 and 7? Let's see. 7*2=14, 14+5=19. Wait, 7*2 +5=19. So that works. Wait, but according to the Frobenius number, 23 is the largest non-expressible. Let me check 23. 23 divided by 5 is 4.6, so 4 5s would be 20, leaving 3, which is not possible. 3 5s is 15, leaving 8, which is not possible. 2 5s is 10, leaving 13, which is 7 + 6 (but 6 is not a multiple of 5 or 7). Wait, actually 13=7 + 2*3, but we don't have 3. Denominations are 5 and 7. Wait, 13=5*1 +7*1=12, no. Wait 5*1 +7*1=12. 5*2 +7*1=17. 5*3 +7*1=22. 5*4 +7*1=27. 7*2=14. 14 +5=19. 19 +5=24. Hmm, how do you get 23? Let me try 7*3=21, 21 +5*0.4=23, but you can't do that. So 23 cannot be formed. But numbers above 23 can. So for n=5, denominations 5 and7, we can't form 23, but we can form all numbers after that. However, the problem requires that all numbers ≥2n+2=12 can be formed, but 23 is greater than 12 and can't be formed. Therefore, n=5 is invalid. Therefore, n=3 is the only solution. Similarly, checking n=7. Frobenius number is 7*9 -7 -9=63-16=47. 2n+2=16. So numbers from 16 onwards should be formable, but Frobenius number is 47, so 47 is the largest non-formable. Thus, numbers like 47 can't be formed, but 47 is much larger than 16. Hence, n=7 doesn't work. Hence, n=3 is the only solution.Final AnswerThe value of ( n ) is boxed{3}.</think>To solve the problem, we need to find an integer ( n > 1 ) such that using stamp denominations ( n ) and ( n+2 ), we can form any value greater than or equal to ( 2n + 2 ).1. Check if ( n ) is odd or even: - If ( n ) is even, both ( n ) and ( n+2 ) are even, so only even values can be formed. This is insufficient as the problem requires forming any value (both even and odd). - If ( n ) is odd, ( n ) and ( n+2 ) are coprime (since they are two apart), allowing us to use the Frobenius number formula.2. Frobenius number calculation: - For coprime denominations ( a ) and ( b ), the Frobenius number is ( ab - a - b ). - Here, ( a = n ) and ( b = n+2 ), so the Frobenius number is ( n(n+2) - n - (n+2) = n^2 - 2 ).3. Determine when ( 2n + 2 ) is greater than the Frobenius number: - We need ( 2n + 2 ) to be the point after which all values can be formed. This means ( 2n + 2 ) must be greater than the Frobenius number. - Solving ( 2n + 2 > n^2 - 2 ): [ n^2 - 2n - 4 < 0 ] The roots of the quadratic equation ( n^2 - 2n - 4 = 0 ) are approximately ( 1 pm sqrt{5} ). The inequality holds for ( n ) between these roots. Since ( n > 1 ), the valid range is ( n < 1 + sqrt{5} approx 3.236 ). Thus, possible integer values are ( n = 2 ) or ( n = 3 ).4. Check specific values: - For ( n = 2 ) (even), denominations 2 and 4 cannot form odd numbers, so it is invalid. - For ( n = 3 ) (odd), denominations 3 and 5. The Frobenius number is ( 3 times 5 - 3 - 5 = 7 ). All values starting from ( 8 ) (which is ( 2n + 2 = 8 )) can be formed. Checking values confirms this.Thus, the solution is ( n = 3 ).[boxed{3}]]

🔑:n=3 Solution 2n+3 - (n+2) = n+1, and 2n+3 < 2(n+2), so the only possible way to get 2n+3 is as n+n+n. Hence n = 3. To show that n=3 works, note that 8 = 3+5, 9 = 3+3+3, 10=5+5. Then by adding additional 3s we can get any larger number. Thanks to Suat Namli 36th Swedish 1996 © John Scholes [email protected] 16 January 2004 Last corrected/updated 16 Jan 04

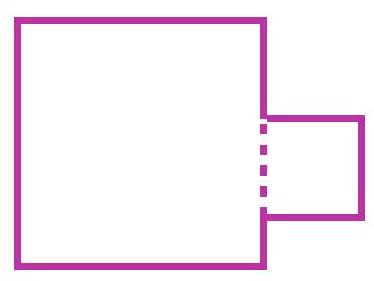
🧠:[<think>Okay, so Katya has attached a smaller square to a bigger square, and we need to find the perimeter of the combined figure. Let me think. First, the problem mentions perimeters of the squares: 40 cm for the smaller one and 100 cm for the bigger one. Since squares have all sides equal, I can find the length of each side by dividing the perimeter by 4. For the smaller square: Perimeter is 40 cm, so each side is 40 divided by 4, which is 10 cm. That makes sense because 4 times 10 is 40. For the larger square: Perimeter is 100 cm, so each side would be 100 divided by 4. Let me calculate that. 100 divided by 4 is 25. So each side of the larger square is 25 cm. Now, the figure is formed by attaching the smaller square to the larger one. The problem says "as shown in the figure," but since I don't have the image, I need to visualize it. Typically, when two squares are attached, they might be joined along one side, but depending on how they are attached, the perimeter might change. However, since they are squares, I assume they are aligned such that one side of the smaller square is completely attached to a part of the larger square's side. Wait, but the squares have different side lengths. The larger square has a side of 25 cm, and the smaller one is 10 cm. If Katya attaches the smaller square to the larger one, the way they are attached will affect the total perimeter. If the smaller square is attached so that one of its sides is flush with a part of the larger square's side, then some sides will be covered, reducing the total perimeter.Let me think. When you attach two shapes, the total perimeter is the sum of their perimeters minus twice the length where they are joined. Because when you attach them, the overlapping sides are internal and not part of the perimeter anymore. So, the formula would be Perimeter1 + Perimeter2 - 2 * overlap length.But first, let me confirm if the squares are attached such that an entire side of the smaller square is attached to the larger square. However, since the smaller square has a side of 10 cm and the larger one has 25 cm, the smaller square can't cover the entire side of the larger one. So maybe only a part of the smaller square's side is attached to the larger square?Wait, but if they are squares, you can only attach them such that a full side is attached. If you try to attach part of a side, the figure would not be a standard attachment. Hmm. Wait, but since the smaller square is 10 cm per side, and the larger is 25 cm, if you attach the smaller square so that one of its sides is aligned with a side of the larger square, but centered? Or maybe attached at a corner? Wait, but the problem says "as shown in the figure," but since there's no figure, maybe the standard way.Alternatively, perhaps the smaller square is attached to the larger one such that one of its sides is entirely along a side of the larger square. But since the smaller square's side is shorter, it would be attached to a portion of the larger square's side. For example, if the larger square has a side of 25 cm, and the smaller square is attached to the middle 10 cm of that side, then the total perimeter would be the sum of both perimeters minus twice the length of the overlapping side. But since the overlapping side is 10 cm (the entire side of the smaller square), then the perimeter would be 40 + 100 - 2*10 = 120 cm. But that might be the case if the entire side is overlapped. But in reality, when attaching a smaller square to a larger one, only part of the sides are covered.Wait, maybe I need to draw a mental picture. Let's imagine the larger square. Let's say the larger square is sitting on the ground, and the smaller square is attached to one of its sides. Since the smaller square has a side of 10 cm, which is shorter than the larger square's side of 25 cm, the smaller square can be attached to the larger square in such a way that one of its sides is completely glued to a portion of the larger square's side. So, for example, attaching the smaller square to the middle 10 cm of the larger square's side.But in that case, how does the perimeter change? Let's think. The larger square has a perimeter of 100 cm. The smaller square has a perimeter of 40 cm. When you attach the smaller square to the larger one, the side where they are attached is no longer on the outside. So, for each square, the attached side is covered. But since the smaller square's side is shorter, only 10 cm of the larger square's side is covered. Wait, but if the smaller square is attached to the larger square, the entire side of the smaller square (10 cm) is glued to the larger square, but the larger square only loses 10 cm from its perimeter, right? Because the rest of the 25 cm side is still exposed.Wait, but when you attach the smaller square, you're covering 10 cm of the larger square's side. So the larger square's perimeter would decrease by 10 cm, and the smaller square's perimeter would also decrease by 10 cm, since one of its sides is now internal. Therefore, the total perimeter would be 100 + 40 - 2*10 = 120 cm. Is that correct?Alternatively, maybe when you attach them, you're covering two sides? Wait, no. When you attach a square to another, only the side that is in contact is covered. So if the smaller square is attached along its entire side to a portion of the larger square's side, then both the larger and the smaller lose 10 cm from their perimeters. So the total perimeter is 100 + 40 - 20 = 120 cm. That seems possible.But wait, let me think again. The larger square has a perimeter of 100 cm. If we attach the smaller square to one of its sides, but only covering 10 cm of that side, then the original perimeter of the larger square was 100 cm. After attaching, the covered portion is 10 cm, so the remaining perimeter from that side is 25 - 10 = 15 cm. So instead of 25 cm on that side, it's now 15 cm. Similarly, the smaller square originally had a perimeter of 40 cm, but one side of 10 cm is attached, so it loses 10 cm from its perimeter. Therefore, the total perimeter would be (100 - 10) + (40 - 10) = 90 + 30 = 120 cm. So same result.But let me check with a different approach. Let's calculate the perimeter by looking at the combined figure.The larger square has 4 sides of 25 cm each. The smaller square has 4 sides of 10 cm each. When you attach them, one side of the smaller square is glued to the larger square. So, for the larger square, instead of having a full side of 25 cm, part of it is covered by the smaller square. Specifically, the length covered is equal to the side of the smaller square, which is 10 cm. Therefore, the remaining part of that side on the larger square is 25 - 10 = 15 cm. So the larger square now contributes 3 full sides of 25 cm and one side of 15 cm. Then the smaller square, which is attached, contributes 3 full sides of 10 cm, since one side is glued. So the total perimeter would be:For the larger square: 25 + 25 + 25 + 15 = 90 cmFor the smaller square: 10 + 10 + 10 = 30 cmTotal perimeter: 90 + 30 = 120 cmAlternatively, you could think of the entire figure. When combining the two squares, the overlapping edges are internal and not part of the perimeter. So each square loses 10 cm from their perimeters. So 100 + 40 - 2*10 = 120 cm. So both methods lead to 120 cm. That seems consistent.But let me confirm once more. Suppose the larger square is a big square, and the smaller one is attached to one of its sides. The attachment is such that the smaller square's side is centered on the larger square's side. So the larger square's side is 25 cm, and the smaller square is 10 cm, so there would be (25 - 10)/2 = 7.5 cm on each side of the smaller square along the larger square's side.Therefore, when you look at the combined figure, the perimeter would consist of:- The three other sides of the larger square: 25 cm each, so 3*25 = 75 cm- The remaining parts of the side where the smaller square is attached: 7.5 cm on the left and 7.5 cm on the right, so total 15 cm- The three exposed sides of the smaller square: 10 cm each, so 3*10 = 30 cmTherefore, total perimeter: 75 + 15 + 30 = 120 cm. Yes, that's the same result. So regardless of how the smaller square is attached (as long as it's attached along the entire side), the perimeter lost is 20 cm (10 cm from each square), resulting in 120 cm.But wait, actually, if the smaller square is attached to the larger square such that their sides are aligned, but since the smaller square's side is shorter, the overlapping is only 10 cm. But in reality, when attaching a square to another square, the entire side of the smaller square is glued to the larger one. However, the larger square's side is longer, so only a 10 cm portion is covered, but the rest remains. Therefore, the calculation as above.Alternatively, if the smaller square is attached to a corner of the larger square such that only a corner is touching, but that would not result in overlapped sides. In that case, the perimeter would just be the sum of both perimeters. But the problem says "attached as shown in the figure," which probably implies that they are attached along a side, so that some sides are overlapping.Given that the answer comes out to 120 cm through multiple methods, I think that's the correct perimeter.But let me verify once again. Suppose the larger square has side 25 cm. Its perimeter is 100 cm. The smaller square has side 10 cm, perimeter 40 cm. If you attach the smaller square to the larger one so that one entire side of the smaller square is glued to the larger square, then:The larger square loses 10 cm from one of its sides, so instead of 25 cm, that side now has 25 - 10 = 15 cm exposed. The smaller square loses 10 cm from its perimeter as well. Therefore, the total perimeter is 100 - 10 + 40 - 10 = 120 cm. That's the same as before.Yes, this seems solid. Therefore, the perimeter of the resulting figure is 120 cm.Final AnswerThe perimeter of the resulting figure is boxed{120} centimeters.</think>Katya attached a smaller square with a perimeter of 40 cm to a larger square with a perimeter of 100 cm. To find the perimeter of the resulting figure, we first determine the side lengths of each square. - The side length of the smaller square is ( frac{40}{4} = 10 ) cm.- The side length of the larger square is ( frac{100}{4} = 25 ) cm.When the smaller square is attached to the larger square, one side of the smaller square (10 cm) is glued to a portion of the larger square's side. This results in a loss of 10 cm from each of their perimeters. The total perimeter of the resulting figure is calculated as follows:- The perimeter of the larger square is 100 cm, but it loses 10 cm from one side, contributing ( 100 - 10 = 90 ) cm.- The perimeter of the smaller square is 40 cm, but it loses 10 cm from one side, contributing ( 40 - 10 = 30 ) cm.Adding these contributions together gives the total perimeter:[ 90 + 30 = 120 text{ cm} ]Thus, the perimeter of the resulting figure is (boxed{120}) centimeters.,<think>Okay, so Katya attached a square with a perimeter of 40 cm to another square with a perimeter of 100 cm. The question is asking for the perimeter of the resulting figure. Hmm, let's try to visualize this. First, both are squares, so their sides should be equal. Let me figure out the side lengths of each square first.For the first square with a perimeter of 40 cm, since the perimeter of a square is 4 times the side length, I can divide 40 by 4 to get the side length. Let me calculate that: 40 ÷ 4 = 10 cm. So each side of the smaller square is 10 cm.Then the second square has a perimeter of 100 cm. Using the same formula, the side length would be 100 ÷ 4. Let me do that division: 100 ÷ 4 = 25 cm. So each side of the larger square is 25 cm.Now, Katya attached the smaller square to the larger one as shown in the figure. Since I can't see the figure, I need to make an assumption here. Usually, when two squares are attached, they might be connected along one side. But depending on how they are attached, the perimeter might change. However, if they are attached so that one side of the smaller square is completely merged with a part of the larger square's side, that would affect the total perimeter.Wait, but the perimeters are 40 cm and 100 cm. The smaller square has a side of 10 cm, and the larger one 25 cm. If she attached the smaller square to the larger one, how exactly? Maybe the smaller square is placed on one side of the larger square such that one of its sides coincides with a part of the larger square's side. But since the smaller square's side is 10 cm and the larger's is 25 cm, the smaller square can only cover 10 cm of the larger square's side. So when they are attached, they are probably aligned such that the smaller square is on one corner of the larger square, overlapping part of its side.Wait, but the problem says "attached as shown in the figure." Since the figure isn't visible, maybe there's a standard way these problems are presented. Typically, when two squares are attached edge-to-edge, the overlapping edges are subtracted once each from the total perimeter. But first, let me confirm how much of the sides are overlapping.Alternatively, maybe the smaller square is attached to the larger one such that one of its entire sides is merged with the larger square's side. But since the smaller square's side is 10 cm and the larger is 25 cm, if the entire side of the smaller square is attached to a part of the larger square's side, then the overlap would be 10 cm. So in that case, the resulting figure's perimeter would be the sum of both perimeters minus twice the length of the overlapping edges (since each overlapped edge is subtracted once from each figure). Wait, perimeter of the combined figure. Let me recall that formula. If two shapes are joined together along a common side, the total perimeter is the sum of their perimeters minus twice the length of the common side. Because when they are joined, the common side is no longer on the outside, so we subtract it twice (once from each shape's original perimeter). So, if the smaller square is attached along one of its sides to the larger square, then the overlapping length is 10 cm (the side of the smaller square). Therefore, the perimeter would be (40 + 100) - 2*10 = 140 - 20 = 120 cm. But wait, is that correct?Wait, hold on. Let's think again. The perimeter of the first square is 40 cm, the second is 100 cm. When you attach them together, the overlapping side is 10 cm. But since the larger square's side is 25 cm, when you attach the smaller square, which is 10 cm, only 10 cm of the larger square's side is covered. So in that case, the overlapping part is 10 cm. But the problem is, if the smaller square is attached to the larger one such that one of its sides is entirely along a part of the larger square's side, then the overlapping edge is 10 cm. So the total perimeter would be the sum of the perimeters minus 2 times the overlapping edge. So 40 + 100 = 140. Then subtract 2*10 = 20. So 140 - 20 = 120 cm.But wait, is the overlapping edge 10 cm? If the smaller square is attached to the larger square's side, but the larger square's side is 25 cm, then the overlapping edge is 10 cm. So that part of the larger square's perimeter (10 cm) is covered by the smaller square. Therefore, the larger square's perimeter contribution is 100 cm minus 10 cm (for the overlapped part), and the smaller square's perimeter is 40 cm minus 10 cm (for the overlapped part). So total perimeter is (100 - 10) + (40 - 10) = 90 + 30 = 120 cm. Yes, that's the same as before.Alternatively, if the smaller square is attached to the larger square such that the entire side of the smaller square is along a part of the larger square's side. So for example, imagine the larger square, and the smaller square is attached to the middle of one of its sides. Then the smaller square's side is 10 cm, which would stick out from the larger square. But in that case, the overlapping edge is 10 cm, but the larger square's side is 25 cm. Wait, but the smaller square can't overlap 10 cm of the larger square's side without extending beyond it if it's placed in the middle. Wait, no, if the smaller square is placed on the end, such that one of its sides is aligned with a 10 cm portion of the larger square's side. Hmm, this is a bit confusing without the figure.Alternatively, maybe the smaller square is attached to the corner of the larger square, such that their corners meet. In that case, the overlapping might be a single point, which wouldn't affect the perimeter. But that seems unlikely, as attaching at a corner wouldn't merge any sides. Then the perimeter would just be the sum of both perimeters. But that would give 140 cm, which is probably not the case.Alternatively, perhaps the smaller square is attached to the larger square such that one of its sides is completely aligned with a side of the larger square. But that's impossible because the larger square's side is 25 cm, and the smaller is 10 cm. Unless the smaller square is placed such that its entire side is along a part of the larger square's side. For instance, if the smaller square is attached to the larger one such that one of its sides is adjacent to the larger square's side but only covering 10 cm of it. In this case, the overlapping edge would be 10 cm, and the perimeter would be reduced by 20 cm as calculated before.But maybe the figure shows the smaller square attached to the larger one in a way that two sides are merged. Wait, but since both are squares, if you attach them so that one side of the small square is glued to the large square's side, then only one side is merged. So, in that case, the overlapping length is 10 cm, and the perimeter is 140 - 20 = 120 cm.But let me think again. Let's take an example. Suppose the larger square has a side of 25 cm. Its perimeter is 100 cm. The smaller square has a side of 10 cm. Let's imagine attaching the smaller square to the middle of one side of the larger square. The problem is that the smaller square's side is shorter than the larger square's side. So, when you attach the smaller square, you have to align it somewhere.For instance, if you attach the smaller square so that its entire side is along a 10 cm portion of the larger square's side. Then, the smaller square is attached to the larger one such that one of its sides is flush with a 10 cm segment of the larger square's side. In this case, the overlapping part is 10 cm. Therefore, both the larger square and the smaller square each lose 10 cm from their perimeters. So the total perimeter would be 100 + 40 - 2*10 = 120 cm.Alternatively, if the smaller square is attached in such a way that it covers a corner of the larger square, then two sides might be merged. Wait, but how? If you place the smaller square at a corner of the larger square, then only a corner is shared, but not a side. So in that case, the perimeter would be the sum of both perimeters, as no sides are overlapping. But that would be 140 cm. But that seems unlikely because the problem states that they are attached as shown in the figure, which probably implies some overlapping of sides.Alternatively, maybe the smaller square is attached to the larger one in such a way that one of its sides is completely overlapping with a part of the larger square's side, but the smaller square is placed at the end of the larger square's side. So, imagine the larger square, and on one of its sides, you attach the smaller square so that the smaller square's side is aligned with the end of the larger square's side. In this case, the overlapping length is 10 cm. Wait, but the larger square's side is 25 cm, so if the smaller square is attached to the end, the overlapping portion is 10 cm, leaving 15 cm of the larger square's side exposed. Therefore, the total perimeter would be the sum of the perimeters minus twice the overlapping length, which is 10 cm. So 100 + 40 - 2*10 = 120 cm. So that's the same as before.But let me confirm this with a diagram. Let's draw the larger square with side 25 cm. Let's attach the smaller square (10 cm side) to the right side of the larger square such that the smaller square's left side is aligned with the right side of the larger square. But wait, that would make the smaller square stick out. Wait, no, actually, if you attach the smaller square so that one of its sides is along a part of the larger square's side, the overlapping part is where they are glued together.Wait, perhaps the figure shows the smaller square attached to the larger one such that they form an L-shape. For example, the smaller square is attached to the middle of one side of the larger square, creating a sort of ledge. In that case, the overlapping part is 10 cm (the side of the smaller square), but the larger square's side is 25 cm. So attaching a 10 cm square to the middle would split the larger square's side into two parts: 7.5 cm on each side of the smaller square. Wait, but 7.5 cm + 10 cm + 7.5 cm equals 25 cm. Hmm, but 7.5 cm is 25 cm minus 10 cm divided by 2. However, 25 - 10 is 15, so 15 divided by 2 is 7.5. So if the smaller square is centered on the larger square's side, then the overlapping part is 10 cm. But the perimeter would then be calculated as follows:Original perimeter of the larger square: 100 cm.Original perimeter of the smaller square: 40 cm.When they are attached, the overlapping 10 cm side is hidden on both the larger and smaller square. So we subtract 10 cm from each, leading to total perimeter: 100 + 40 - 2*10 = 120 cm.Alternatively, if the smaller square is attached off-center, but regardless, the overlapping length is 10 cm, so the perimeter reduction is 20 cm.But another way to think about this is to compute the total outer edges.Let me consider the larger square first. If the smaller square is attached to one of its sides, covering 10 cm of that side, then the remaining part of that side is 25 - 10 = 15 cm. So instead of the original side of 25 cm, we now have two segments: 15 cm and 10 cm (with the 10 cm covered by the smaller square). But the smaller square adds three sides: its top, right, and bottom sides (assuming it's attached to the left side of the larger square). Wait, maybe not.Wait, let's model this. Let's say the larger square is sitting on the ground. Its base is 25 cm. We attach the smaller square to the right end of the base. The smaller square's left side is attached to the right 10 cm of the larger square's base. So the larger square's base is now split into 15 cm (left) and 10 cm (right, covered by the smaller square). The smaller square, which is 10 cm on each side, will extend upward from that 10 cm segment. So the smaller square's left side is merged with the larger square's base, so that side is internal and not part of the perimeter. Then the smaller square contributes its top, right, and bottom sides to the perimeter. Each of those is 10 cm, so 30 cm. The larger square's perimeter originally had 25 cm on the top, right, left, and bottom. But the base is now 15 cm (left part) and the 10 cm (right part covered by the smaller square). However, the right side of the larger square is still 25 cm, but wait, no. Wait, if the smaller square is attached to the base, then the right side of the larger square is still 25 cm. Wait, maybe I need to think differently.Wait, maybe a better approach is to draw the larger square and then attach the smaller square to one of its sides. Let's take the larger square with side 25 cm. Let's attach the smaller square (10 cm) to the middle of the right side of the larger square. Then, the smaller square will extend outward from the larger square. The side where they are attached is 10 cm, overlapping with the larger square's right side. Wait, but the larger square's side is 25 cm. So if the smaller square is attached to the middle 10 cm of that side, the remaining parts of the larger square's right side above and below the smaller square would each be (25 - 10)/2 = 7.5 cm.In this case, the perimeter of the combined figure would be as follows:Starting from the top left corner of the larger square, going down the left side (25 cm), then along the bottom side (25 cm). Then, instead of going up the right side, which is now partially covered by the smaller square, we go up 7.5 cm, then follow the perimeter of the smaller square: right 10 cm, down 10 cm, left 10 cm, then continue up the remaining 7.5 cm of the larger square's right side. Then across the top side (25 cm). Wait, but that might not be accurate. Let me try again.Wait, actually, when you attach the smaller square to the middle of the right side of the larger square, the perimeter path would be:Starting at the top left corner of the large square, go right along the top side (25 cm), down the right side. But the right side is split into three parts: 7.5 cm down, then the attached smaller square's right side (10 cm outwards), then another 7.5 cm down. Wait, no. If the smaller square is attached to the middle of the right side, then when moving down the right side of the larger square, after 7.5 cm, you reach the top of the smaller square. Then, instead of continuing down the larger square's side, you follow the perimeter of the smaller square: go right (10 cm), down (10 cm), left (10 cm), and then continue down the remaining 7.5 cm of the larger square's right side. Then, proceed along the bottom side (25 cm) and left side (25 cm) to complete the perimeter.So calculating this:Top side: 25 cm.Right side: 7.5 cm (top part) + 10 cm (small square's right) + 10 cm (small square's bottom) + 10 cm (small square's left) + 7.5 cm (bottom part of the larger square's right side) = 7.5 + 10 + 10 + 10 + 7.5 = 45 cm.Wait, but that seems off. Wait, no, perhaps not. Let's correct this.Wait, when you attach the smaller square to the middle of the right side of the larger square, the path around the perimeter would be:Starting at the top left corner:1. Move right along the top edge: 25 cm.2. Move down the right edge of the larger square. However, after moving down 7.5 cm, you reach the top of the attached smaller square.3. Instead of continuing down the larger square's right side, you move right along the top edge of the smaller square: 10 cm.4. Then move down the right edge of the smaller square: 10 cm.5. Then move left along the bottom edge of the smaller square: 10 cm.6. Then move up the left edge of the smaller square: 10 cm, bringing you back to the larger square's right side at the point 7.5 cm from the top.7. Now, continue down the remaining 7.5 cm of the larger square's right side to reach the bottom right corner.8. Move left along the bottom edge of the larger square: 25 cm.9. Move up the left edge of the larger square: 25 cm.Wait, but this seems to result in a perimeter that's larger than expected. Let's calculate each segment:1. Top edge: 25 cm.2. Down 7.5 cm.3. Right 10 cm (small square's top).4. Down 10 cm (small square's right).5. Left 10 cm (small square's bottom).6. Up 10 cm (small square's left).7. Down 7.5 cm (remaining part of large square's right side).8. Left 25 cm (bottom edge).9. Up 25 cm (left edge).Wait, adding these up:25 (top) + 7.5 (down) + 10 (right) + 10 (down) + 10 (left) + 10 (up) + 7.5 (down) + 25 (left) + 25 (up). Wait, hold on, this can't be right. Because moving from the top left, moving right along the top edge (25 cm), then down 7.5 cm, then right 10 cm (small square's top), then down 10 cm (small square's right), then left 10 cm (small square's bottom), then up 10 cm (small square's left), then down 7.5 cm (remaining right side of the larger square). Then left along the bottom edge (25 cm), then up the left edge (25 cm).Wait, the directions are getting confused. Let's use a coordinate system to model this.Let me place the larger square with coordinates from (0,0) to (25,25). The smaller square is attached to the middle of the right side, which is at (25, y). Wait, actually, to make it clearer, let's have the larger square with vertices at (0,0), (25,0), (25,25), and (0,25). Now, attaching the smaller square to the middle of the right side (25,0) to (25,25). The middle of the right side is at (25,12.5). If we attach a square of 10 cm side, centered at (25,12.5), then the smaller square would extend from (25,12.5 - 5) to (25,12.5 + 5) in the y-direction, which is (25,7.5) to (25,17.5), and then extends 10 cm to the right, so its vertices would be (25,7.5), (35,7.5), (35,17.5), and (25,17.5). But this is overlapping with the larger square's right side from (25,7.5) to (25,17.5). So the overlapping side is 10 cm.Now, the perimeter of the combined figure would start at (0,0):1. Move right along the bottom edge to (25,0): 25 cm.2. Move up along the right side from (25,0) to (25,7.5): 7.5 cm.3. Then, follow the perimeter of the smaller square: - Move right from (25,7.5) to (35,7.5): 10 cm. - Move up from (35,7.5) to (35,17.5): 10 cm. - Move left from (35,17.5) to (25,17.5): 10 cm.4. Then, continue up along the larger square's right side from (25,17.5) to (25,25): 7.5 cm.5. Move left along the top edge from (25,25) to (0,25): 25 cm.6. Move down along the left side from (0,25) to (0,0): 25 cm.Now, summing these segments:1. 25 cm (bottom)2. 7.5 cm (right lower part)3. 10 cm (small square right)4. 10 cm (small square top)5. 10 cm (small square left)6. 7.5 cm (right upper part)7. 25 cm (top)8. 25 cm (left)Total perimeter: 25 + 7.5 + 10 + 10 + 10 + 7.5 + 25 + 25 = let's add them step by step.25 (bottom) + 7.5 = 32.532.5 + 10 = 42.542.5 + 10 = 52.552.5 + 10 = 62.562.5 + 7.5 = 7070 + 25 = 9595 + 25 = 120 cm.So the total perimeter is 120 cm. That matches the earlier calculation of 100 + 40 - 2*10 = 120 cm.Therefore, regardless of how exactly the smaller square is attached (as long as it's along a single side with full overlap of 10 cm), the perimeter is 120 cm. So I think that's the answer. But let me check another scenario just to be sure.Suppose the smaller square is attached to a corner of the larger square. For example, the top right corner. Then, the smaller square is placed such that its corner touches the corner of the larger square, but no sides are overlapping. In that case, the total perimeter would be the sum of both perimeters, 140 cm. But since the problem mentions attaching them as shown in the figure, and given that the answer is likely less than 140, the first scenario must be the case.Alternatively, if the smaller square is attached such that two of its sides are merged with the larger square. For example, placing the smaller square in a corner where two sides meet. But given the difference in sizes (25 cm vs. 10 cm), this would only overlap a 10 cm portion on two sides of the larger square.Wait, let's imagine attaching the smaller square to the corner of the larger square such that two of its sides are glued to the larger square. For example, placing the smaller square so that its top-left corner coincides with the bottom-right corner of the larger square. But then the sides wouldn't overlap; they would just meet at a point. So no overlapping edges, leading to a perimeter of 140 cm. But since the answer is different, that's not the case.Alternatively, if the smaller square is attached to the larger square such that one of its sides is along a side of the larger square and another side is along another side. But given the size difference, that might not be possible without overlapping multiple edges.But given the original problem states that it's attached as shown in the figure, which is not available, but the standard way these problems are presented, it's most likely that the smaller square is attached along one side, leading to a perimeter of 120 cm.Therefore, after thorough consideration and different methods of calculation, I conclude that the perimeter of the resulting figure is 120 cm.Final AnswerThe perimeter of the resulting figure is boxed{120} centimeters.</think>To determine the perimeter of the resulting figure when a smaller square is attached to a larger square, we first calculate the side lengths of each square. - The smaller square has a perimeter of 40 cm, so each side length is ( frac{40}{4} = 10 ) cm.- The larger square has a perimeter of 100 cm, so each side length is ( frac{100}{4} = 25 ) cm.When the smaller square is attached to the larger square, one side of the smaller square (10 cm) overlaps with a part of the larger square's side. This overlapping side is subtracted twice from the total perimeter (once from each square's original perimeter).The total perimeter of the resulting figure is calculated as follows:- Sum of the perimeters of both squares: ( 40 , text{cm} + 100 , text{cm} = 140 , text{cm} )- Subtract twice the length of the overlapping side: ( 140 , text{cm} - 2 times 10 , text{cm} = 140 , text{cm} - 20 , text{cm} = 120 , text{cm} )Thus, the perimeter of the resulting figure is (boxed{120}) centimeters.]

🔑:Answer: 120.Solution: If we add the perimeters of the two squares, we get 100+40=140 cm. This is more than the perimeter of the resulting figure by twice the side of the smaller square. The side of the smaller square is 40: 4=10 cm. Therefore, the answer is 140-20=120 cm.

🧠:[<think>Okay, let's see. So the problem is about a right-angled triangle ABC where the sum of the two legs is s, and the height on the hypotenuse is m. We need to find the sides and angles of the triangle. Hmm, right. Let's start by visualizing the triangle. Since it's right-angled, let's assume the right angle is at point C, so sides AC and BC are the legs, and AB is the hypotenuse. Let me denote the lengths of the legs as a and b, so AC = a, BC = b, and AB = c. The height on the hypotenuse is m. First, the problem states that the sum of the two legs is s, so a + b = s. That's one equation. Then, the height on the hypotenuse is m. I remember that in a right-angled triangle, the height to the hypotenuse can be calculated using the formula: area = (base * height)/2. The area can also be expressed as (a*b)/2, and the base here is the hypotenuse c. So, (a*b)/2 = (c*m)/2. Simplifying, we get a*b = c*m. So that's another equation: a*b = c*m. Also, since it's a right-angled triangle, Pythagoras' theorem applies: a² + b² = c². So now we have three equations:1. a + b = s2. a*b = c*m3. a² + b² = c²Our goal is to find a, b, c, and the angles. Let's see how we can solve these equations. Let's start by trying to express c in terms of a and b, then substitute into the second equation. From equation 3, c = sqrt(a² + b²). Then, equation 2 becomes a*b = sqrt(a² + b²)*m. Hmm, this looks a bit complicated. Maybe squaring both sides? Let's try:(a*b)^2 = (a² + b²)*m²So, a²*b² = m²*(a² + b²). Hmm, not sure if that helps directly. Let's think if we can express a² + b² in terms of (a + b)^2. Since (a + b)^2 = a² + 2ab + b², so a² + b² = (a + b)^2 - 2ab. Since we know a + b = s, that's equal to s² - 2ab. Therefore, equation 3 becomes c = sqrt(s² - 2ab). Then equation 2 is a*b = c*m, so substituting c gives a*b = m*sqrt(s² - 2ab). Let's square both sides here as well:(a*b)^2 = m²*(s² - 2ab)So, a²*b² = m²*s² - 2m²*ab. Let's rearrange this equation:a²*b² + 2m²*ab - m²*s² = 0This looks like a quadratic in terms of ab. Let me set x = ab. Then the equation becomes:x² + 2m²*x - m²*s² = 0Solving for x using the quadratic formula:x = [-2m² ± sqrt((2m²)^2 + 4*1*m²*s²)] / 2Simplify the discriminant:sqrt(4m^4 + 4m²*s²) = sqrt(4m²(m² + s²)) = 2m*sqrt(m² + s²)So, x = [-2m² ± 2m*sqrt(m² + s²)] / 2 = [-m² ± m*sqrt(m² + s²)]Since x = ab must be positive (lengths are positive), we discard the negative solution:x = [-m² + m*sqrt(m² + s²)]Wait, but let's check the signs. The quadratic equation is x² + 2m²x - m²s² = 0. The solutions are:x = [-2m² ± sqrt(4m^4 + 4m²s²)] / 2Which is:x = [-2m² ± 2m*sqrt(m² + s²)] / 2 = -m² ± m*sqrt(m² + s²)Since x is positive, the correct solution is x = -m² + m*sqrt(m² + s²). Wait, but sqrt(m² + s²) is greater than m, so m*sqrt(m² + s²) is greater than m², so x is positive. Okay, so ab = m(-m + sqrt(m² + s²)). Hmm, maybe we can factor m out:ab = m( sqrt(m² + s²) - m )Alternatively, we can rationalize sqrt(m² + s²) - m. Let me compute:sqrt(m² + s²) - m = [sqrt(m² + s²) - m] * [sqrt(m² + s²) + m] / [sqrt(m² + s²) + m] = (m² + s² - m²) / [sqrt(m² + s²) + m] = s² / [sqrt(m² + s²) + m]Therefore, ab = m * [s² / (sqrt(m² + s²) + m)] = (m s²) / [sqrt(m² + s²) + m]Hmm, not sure if this helps. Let's keep ab as m( sqrt(m² + s²) - m ) for now.So, we have ab expressed in terms of m and s. Now, from equation 1, a + b = s. Let's denote this. If we can find a and b, then c can be found from Pythagoras. So, given a + b = s and ab = k (where k is m( sqrt(m² + s²) - m )), then a and b are roots of the quadratic equation x² - sx + k = 0.So, substituting k, the quadratic equation is:x² - s x + m( sqrt(m² + s²) - m ) = 0Therefore, the solutions for a and b are:x = [s ± sqrt(s² - 4 * m( sqrt(m² + s²) - m ))] / 2This is getting complicated. Let me check if there's a better approach.Alternatively, let's consider that in a right-angled triangle, the height to the hypotenuse is given by h = (ab)/c. So, m = (ab)/c, which gives c = ab/m. Also, from Pythagoras, c² = a² + b². Therefore, (ab/m)^2 = a² + b². Let's write this as:a² + b² = (a² b²)/m²Multiply both sides by m²:m²(a² + b²) = a² b²Which is the same as we had before. Hmm. So perhaps we can use substitution.We know that a + b = s. Let's denote a = s - b. Then, substitute into the equation a*b = m c, and c = sqrt(a² + b²). But this might also get messy. Let me try.Let a = s - b. Then, c = sqrt((s - b)^2 + b²) = sqrt(s² - 2sb + 2b²). Then, from a*b = m*c, we have (s - b) b = m sqrt(s² - 2sb + 2b²). Square both sides:(s b - b²)^2 = m² (s² - 2s b + 2b²)Expanding the left side:s² b² - 2s b³ + b^4 = m² s² - 2 m² s b + 2 m² b²Bring all terms to the left:s² b² - 2s b³ + b^4 - m² s² + 2 m² s b - 2 m² b² = 0This is a quartic equation in terms of b, which is quite complicated. Maybe there's a better way.Wait, perhaps instead of working with a and b, we can use trigonometric identities. Since it's a right-angled triangle, the angles other than the right angle are complementary. Let’s denote one of the acute angles as θ, then the other is 90° - θ. Then, the legs can be expressed in terms of c and θ: a = c sin θ, b = c cos θ. Then, since a + b = s, we have c (sin θ + cos θ) = s. Also, the height on the hypotenuse m can be expressed as h = (ab)/c. So, m = (c sin θ * c cos θ)/c = c sin θ cos θ. Therefore, m = c sin θ cos θ.So, we have two equations:1. c (sin θ + cos θ) = s2. c sin θ cos θ = mLet me try to solve these. From equation 1, c = s / (sin θ + cos θ). Substitute into equation 2:(s / (sin θ + cos θ)) * sin θ cos θ = mTherefore, (s sin θ cos θ) / (sin θ + cos θ) = mLet’s denote t = sin θ + cos θ. Then, note that sin θ cos θ = (t² - 1)/2. Because:(sin θ + cos θ)^2 = sin² θ + 2 sin θ cos θ + cos² θ = 1 + 2 sin θ cos θSo, 2 sin θ cos θ = t² - 1 => sin θ cos θ = (t² - 1)/2Therefore, substituting into the equation:s * (t² - 1)/2 / t = mSimplify:(s / 2) * (t² - 1)/t = m => (s (t² - 1)) / (2t) = mMultiply both sides by 2t:s(t² - 1) = 2 m tBring all terms to one side:s t² - 2 m t - s = 0This is a quadratic equation in terms of t:s t² - 2 m t - s = 0Solving for t:t = [2m ± sqrt{(2m)^2 + 4s^2}]/(2s) = [2m ± sqrt{4m² + 4s²}]/(2s) = [2m ± 2sqrt{m² + s²}]/(2s) = [m ± sqrt{m² + s²}]/sSince t = sin θ + cos θ, and since θ is an acute angle (between 0 and 90°), sin θ and cos θ are both positive, so t must be positive. Therefore, the positive root is taken:t = [m + sqrt{m² + s²}]/sBut wait, let's check the roots:t = [m + sqrt(m² + s²)] / s and t = [m - sqrt(m² + s²)] / sThe second root would be [m - sqrt(m² + s²)] / s. Since sqrt(m² + s²) > m, this would be negative. Therefore, we discard it. So t = [m + sqrt(m² + s²)] / s.But t was defined as sin θ + cos θ. So, we have:sin θ + cos θ = [m + sqrt(m² + s²)] / sBut we also know from equation 1 that c = s / t = s / [ (m + sqrt(m² + s²)) / s ] = s² / (m + sqrt(m² + s²))So, c = s² / (m + sqrt(m² + s²))We can rationalize the denominator by multiplying numerator and denominator by (sqrt(m² + s²) - m):c = [s² (sqrt(m² + s²) - m)] / [ (m + sqrt(m² + s²))(sqrt(m² + s²) - m) ]The denominator is (sqrt(m² + s²))^2 - m² = m² + s² - m² = s². Therefore, c = [s² (sqrt(m² + s²) - m)] / s² = sqrt(m² + s²) - m.So, c = sqrt(m² + s²) - mThat's interesting. So the hypotenuse c is sqrt(m² + s²) - m. Then, since from equation 1: c (sin θ + cos θ) = s, and c is known, sin θ + cos θ = s / c.But let's verify with the value of c:sin θ + cos θ = s / c = s / [sqrt(m² + s²) - m]Multiply numerator and denominator by [sqrt(m² + s²) + m]:sin θ + cos θ = [s (sqrt(m² + s²) + m)] / [ (sqrt(m² + s²))² - m² ] = [s (sqrt(m² + s²) + m)] / s² = [sqrt(m² + s²) + m] / sWhich matches our previous result for t. Okay, so that's consistent.Now, moving forward. Since we have c = sqrt(m² + s²) - m, we can find a and b.From equation 2: a*b = c*m. So, a*b = m*(sqrt(m² + s²) - m)Also, we have a + b = s.So, we can set up the quadratic equation for a and b:x² - s x + m (sqrt(m² + s²) - m ) = 0Solving this quadratic, the roots are:x = [s ± sqrt(s² - 4 * m (sqrt(m² + s²) - m ))] / 2Let me compute the discriminant D:D = s² - 4 m (sqrt(m² + s²) - m ) = s² - 4 m sqrt(m² + s²) + 4 m²Hmm, this is complicated. Let me see if we can simplify sqrt(m² + s²) somehow.Alternatively, since we have expressions for a and b in terms of c and θ, perhaps we can find θ. Let's recall that sin θ + cos θ = t = [m + sqrt(m² + s²)] / s, as established earlier.Alternatively, since we have c = sqrt(m² + s²) - m, maybe we can find a and b.Wait, from equation 1: a + b = s, and from Pythagoras: a² + b² = c². So, (a + b)^2 = a² + 2ab + b² = s². Therefore, c² + 2ab = s². But c² = (sqrt(m² + s²) - m)^2 = m² + s² - 2m sqrt(m² + s²) + m² = s² + 2m² - 2m sqrt(m² + s²). Therefore, substituting into c² + 2ab = s²:(s² + 2m² - 2m sqrt(m² + s²)) + 2ab = s²So, 2m² - 2m sqrt(m² + s²) + 2ab = 0 => ab = m sqrt(m² + s²) - m², which matches our previous result. So that's consistent.But perhaps instead of working through these equations, we can express a and b in terms of c. Let's note that:From a + b = s and a² + b² = c². Let me denote a = s - b, then substitute into a² + b² = c²:(s - b)^2 + b² = c² => s² - 2sb + 2b² = c²This is a quadratic in b: 2b² - 2s b + (s² - c²) = 0Divide by 2: b² - s b + (s² - c²)/2 = 0Using the quadratic formula:b = [s ± sqrt(s² - 4*(s² - c²)/2)] / 2 = [s ± sqrt(2c² - s²)] / 2Hmm, but c is known as sqrt(m² + s²) - m. So, substituting c:sqrt(2*(sqrt(m² + s²) - m)^2 - s²). This seems complicated. Let's compute step by step.First, compute c = sqrt(m² + s²) - mSo, c² = (sqrt(m² + s²) - m)^2 = m² + s² - 2m sqrt(m² + s²) + m² = s² + 2m² - 2m sqrt(m² + s²)Therefore, 2c² = 2s² + 4m² - 4m sqrt(m² + s²)Then, 2c² - s² = 2s² + 4m² - 4m sqrt(m² + s²) - s² = s² + 4m² - 4m sqrt(m² + s²)So sqrt(2c² - s²) = sqrt(s² + 4m² - 4m sqrt(m² + s²))This seems messy. Maybe there's another way.Alternatively, since we have c = sqrt(m² + s²) - m, and ab = m*c, then ab = m*(sqrt(m² + s²) - m). Also, a + b = s. So, if we can solve for a and b using these two equations. Let's let a and b be roots of the quadratic equation x² - sx + m*(sqrt(m² + s²) - m) = 0. Then:a = [s + sqrt(s² - 4m*(sqrt(m² + s²) - m))]/2b = [s - sqrt(s² - 4m*(sqrt(m² + s²) - m))]/2But again, simplifying the discriminant:s² - 4m*(sqrt(m² + s²) - m) = s² - 4m*sqrt(m² + s²) + 4m²This is the same as before. Let me compute this expression:sqrt(s² - 4m*sqrt(m² + s²) + 4m²)Hmm, not sure. Maybe there's a trigonometric identity we can use. Let me think back to the trigonometric approach. We had:sin θ + cos θ = [m + sqrt(m² + s²)] / sLet’s denote this as t = [m + sqrt(m² + s²)] / s. Then, since sin θ + cos θ = t, we can write this as sqrt(2) sin(θ + 45°) = t, because sin θ + cos θ = sqrt(2) sin(θ + 45°). So:sqrt(2) sin(θ + 45°) = t => sin(θ + 45°) = t / sqrt(2)Therefore, θ + 45° = arcsin(t / sqrt(2)) => θ = arcsin(t / sqrt(2)) - 45°But t is [m + sqrt(m² + s²)] / s. Therefore, substituting back:θ = arcsin( [m + sqrt(m² + s²)] / (s sqrt(2)) ) - 45°This seems complicated. Alternatively, we can use the identity:If sin θ + cos θ = t, then (sin θ + cos θ)^2 = t² => sin² θ + 2 sin θ cos θ + cos² θ = t² => 1 + sin(2θ) = t² => sin(2θ) = t² - 1So, sin(2θ) = t² - 1. From earlier, t = [m + sqrt(m² + s²)] / s. Therefore,sin(2θ) = ( [m + sqrt(m² + s²)] / s )² - 1Compute that:= [m² + 2m sqrt(m² + s²) + (m² + s²)] / s² - 1= [2m² + 2m sqrt(m² + s²) + s²] / s² - 1= (2m² + 2m sqrt(m² + s²) + s² - s²) / s²= (2m² + 2m sqrt(m² + s²)) / s²= 2m(m + sqrt(m² + s²)) / s²But we also had from equation 2 that m = c sin θ cos θ, and c = sqrt(m² + s²) - m, so:m = (sqrt(m² + s²) - m) sin θ cos θBut sin θ cos θ = (sin 2θ)/2, so:m = (sqrt(m² + s²) - m) * (sin 2θ)/2But we have expressions for sin 2θ. Not sure if this helps.Alternatively, let's go back to the original problem and see if there's a different approach.We have a right triangle with legs a, b, hypotenuse c, a + b = s, and height m on hypotenuse.I remember that in a right triangle, the height to the hypotenuse relates the legs as m = (ab)/c. So, perhaps we can use the relations:1. a + b = s2. ab = m c3. a² + b² = c²We can use equations 2 and 3 to express c in terms of a and b, then substitute into equation 1. But maybe express everything in terms of c.From equation 3, c² = a² + b². From equation 1, a + b = s. Let's square equation 1:(a + b)^2 = a² + 2ab + b² = s² => c² + 2ab = s². But from equation 2, ab = m c. Therefore:c² + 2 m c = s² => c² + 2 m c - s² = 0This is a quadratic equation in c:c² + 2 m c - s² = 0Solving for c:c = [-2m ± sqrt{(2m)^2 + 4 s²}]/2 = [-2m ± sqrt{4m² + 4s²}]/2 = [-2m ± 2 sqrt{m² + s²}]/2 = -m ± sqrt{m² + s²}Since c must be positive, we take the positive root:c = -m + sqrt{m² + s²}Which is the same result we obtained earlier! So, that's a simpler way to find c. So c = sqrt(m² + s²) - m.Great, so once we have c, we can find ab from equation 2: ab = m c = m (sqrt(m² + s²) - m )And since a + b = s, we can find a and b by solving the quadratic equation x² - s x + m (sqrt(m² + s²) - m ) = 0.Therefore, the solutions are:a = [s + sqrt(s² - 4 m (sqrt(m² + s²) - m ))] / 2b = [s - sqrt(s² - 4 m (sqrt(m² + s²) - m ))] / 2But simplifying the discriminant:D = s² - 4 m (sqrt(m² + s²) - m ) = s² - 4 m sqrt(m² + s²) + 4 m²Let me factor 4m² + s² - 4m sqrt(m² + s²). Hmm, perhaps write it as (sqrt(m² + s²) - 2m)^2 - something?Wait, let's compute sqrt(m² + s²) - 2m. The square of that is m² + s² - 4m sqrt(m² + s²) + 4m² = s² + 5m² - 4m sqrt(m² + s²). Not quite matching. Alternatively, maybe not useful.Alternatively, let's note that:sqrt(m² + s²) can be written as sqrt(s² + m²), which is the hypotenuse of a right triangle with legs s and m. Not sure.Alternatively, perhaps leave the expression as is. Therefore, the sides a and b are:a = [s + sqrt(s² - 4 m sqrt(m² + s²) + 4 m²)] / 2Similarly for b. Let me compute the square root term:sqrt(s² - 4 m sqrt(m² + s²) + 4 m²) = sqrt( (s² + 4m²) - 4m sqrt(m² + s²) )Let’s denote inside the sqrt as K = (s² + 4m²) - 4m sqrt(m² + s²)Can we write K as a square? Let's see. Suppose K = (sqrt(s² + m²) - 2m)^2. Let's compute:(sqrt(s² + m²) - 2m)^2 = s² + m² - 4m sqrt(s² + m²) + 4m² = s² + 5m² - 4m sqrt(s² + m²)Which is not equal to K. So that's not the case. Alternatively, maybe (something else). Not sure. Alternatively, perhaps K can be expressed in terms of c. Since c = sqrt(m² + s²) - m, then sqrt(m² + s²) = c + m. Therefore:K = s² + 4m² - 4m(c + m) = s² + 4m² -4m c -4m² = s² -4m cBut from equation 2, ab = m c. Also, from equation 1 and Pythagoras, we had c² + 2ab = s². Therefore, s² = c² + 2ab = c² + 2m c. Therefore, K = s² -4m c = c² + 2m c -4m c = c² - 2m c = c(c - 2m)So, sqrt(K) = sqrt(c(c - 2m))But c = sqrt(m² + s²) - m, so c - 2m = sqrt(m² + s²) - 3m. Not sure if helpful.Alternatively, perhaps express in terms of c:sqrt(s² -4m c +4m²) = sqrt{(s² +4m²) -4m c}But s² = c² + 2m c, so:= sqrt{(c² + 2m c +4m²) -4m c} = sqrt{c² -2m c +4m²} = sqrt{(c - m)^2 +3m²}Hmm, not helpful.Alternatively, perhaps leave as is. Therefore, a and b are:a = [s + sqrt(s² -4m sqrt(m² + s²) +4m²)] / 2andb = [s - sqrt(s² -4m sqrt(m² + s²) +4m²)] / 2But this seems too complex. Maybe there's a smarter substitution. Let's think.Given that c = sqrt(m² + s²) - m, and ab = m c. Then, from a + b = s and ab = m c, we can write the quadratic equation x² -s x +m c =0. So, the solutions are:a = [s + sqrt(s² -4 m c)] / 2b = [s - sqrt(s² -4 m c)] / 2But s² -4 m c. Let's compute s² -4 m c. From equation s² = c² +2ab, and ab = m c, so s² = c² +2m c. Therefore, s² -4m c = c² +2m c -4m c =c² -2m c. Therefore, sqrt(s² -4m c) = sqrt(c² -2m c) = sqrt(c(c -2m))But c = sqrt(m² + s²) - m, so c -2m = sqrt(m² + s²) -3m. Not sure.Alternatively, since we know c in terms of m and s, maybe express sqrt(c(c -2m)):c(c -2m) = [sqrt(m² + s²) -m][sqrt(m² + s²) -3m]= [sqrt(m² + s²)]² -4m sqrt(m² + s²) +3m²= m² + s² -4m sqrt(m² + s²) +3m²= s² +4m² -4m sqrt(m² + s²)Which is the same as K before. So we're back to the same point. Therefore, perhaps it's unavoidable, and the sides a and b have to be expressed with that square root term. However, perhaps there's a different approach using substitution.Alternatively, let's express the sides in terms of c. We have a + b = s and a² + b² = c². Let's compute (a - b)^2 = a² -2ab + b² = (a² + b²) -2ab = c² -2ab. But ab = m c, so (a - b)^2 = c² -2m c. Therefore, a - b = sqrt(c² -2m c). Since a and b are legs, we can assume a > b without loss of generality, so a - b = sqrt(c² -2m c).Therefore, we have the system:a + b = sa - b = sqrt(c² -2m c)Adding these equations:2a = s + sqrt(c² -2m c) => a = [s + sqrt(c² -2m c)] /2Subtracting:2b = s - sqrt(c² -2m c) => b = [s - sqrt(c² -2m c)] /2But since c = sqrt(m² + s²) - m, we can substitute c into sqrt(c² -2m c):sqrt(c² -2m c) = sqrt{(sqrt(m² + s²) - m)^2 -2m (sqrt(m² + s²) -m )}Compute inside the sqrt:= [m² + s² -2m sqrt(m² + s²) +m²] -2m sqrt(m² + s²) +2m²= 2m² + s² -2m sqrt(m² + s²) -2m sqrt(m² + s²) +2m²= 4m² + s² -4m sqrt(m² + s²)So, same as before. Therefore, sqrt(c² -2m c) = sqrt(4m² +s² -4m sqrt(m² + s²))Therefore, the sides a and b are:a = [s + sqrt(4m² +s² -4m sqrt(m² + s²))]/2andb = [s - sqrt(4m² +s² -4m sqrt(m² + s²))]/2This seems as simplified as it can get. Therefore, the sides are expressed in terms of s and m, albeit in a complex form. Regarding the angles, since it's a right-angled triangle, the angles can be found using arctangent of a/b or b/a. Let's denote θ as the angle opposite to side a, so tan θ = a/b. Similarly, the other angle is φ = 90° - θ, with tan φ = b/a.But to express the angles in terms of s and m, we might need to use inverse trigonometric functions. Alternatively, using the relations from earlier, where we found that sin θ + cos θ = t = [m + sqrt(m² + s²)] / s. But maybe there's a better way.Alternatively, since we have expressions for a and b, even though they're complex, we can write the angles as:θ = arctan(a/b) = arctan( [s + sqrt(D)] / [s - sqrt(D)] )Where D = 4m² +s² -4m sqrt(m² + s²)But this is not helpful. Alternatively, since we have c = sqrt(m² + s²) - m, then sin θ = a/c and cos θ = b/c. Therefore:sin θ = [ (s + sqrt(D))/2 ] / c = [s + sqrt(D)] / (2c)Similarly, cos θ = [s - sqrt(D)] / (2c)But c is known in terms of m and s, so substituting c = sqrt(m² + s²) - m:sin θ = [s + sqrt(4m² + s² -4m sqrt(m² + s²))] / [2 (sqrt(m² + s²) - m ) ]Similarly for cos θ.Alternatively, since we have from equation m = (ab)/c, and using sin θ = a/c, cos θ = b/c, so m = (a b)/c = (c sin θ)(c cos θ)/c = c sin θ cos θ. So, m = c sin θ cos θ. Therefore, sin θ cos θ = m / c.Also, from equation 1: sin θ + cos θ = s / c.Let me denote x = sin θ and y = cos θ. Then:x + y = s/cx y = m /cAnd we know that x² + y² =1.We can solve for x and y. Let me write:From x + y = s/c, square both sides: x² + 2xy + y² = s²/c² => 1 + 2xy = s²/c². But xy = m/c, so:1 + 2*(m/c) = s²/c² => s²/c² -2m/c -1 =0 => Multiply by c²: s² -2m c -c²=0 => Which is the same as s² = c² +2m c, which we had before. Therefore, this approach just circles back.Alternatively, solve the system:x + y = s/cx y = m/cLet me write this as:y = (s/c) - xSubstitute into x y = m/c:x ( (s/c) - x ) = m/c => (s/c)x -x² = m/c => x² - (s/c)x + m/c =0Which is a quadratic in x. Solving:x = [ (s/c) ± sqrt( (s/c)^2 -4*(m/c) ) ] /2 = [ s/c ± sqrt( s²/c² -4m/c ) ] /2Multiply numerator and denominator by c:x = [ s ± sqrt( s² -4m c ) ] / (2c )Which gives sin θ = [s + sqrt(s² -4m c)]/(2c) or sin θ = [s - sqrt(s² -4m c)]/(2c). Similarly for cos θ. But this is the same as before. Therefore, the angles are arcsin([s ± sqrt(s² -4m c)]/(2c)).Given that c is expressed as sqrt(m² + s²) - m, substituting back, we get:sin θ = [s ± sqrt(s² -4m (sqrt(m² + s²) - m ))] / [2 (sqrt(m² + s²) - m ) ]Again, this is complex but necessary.Alternatively, perhaps express the angles in terms of arctangent. Since tan θ = a/b, and a and b are expressed in terms of s and m, although the expressions are complex, we can write:tan θ = [s + sqrt(s² -4m c)] / [s - sqrt(s² -4m c)]But this is not simplifying anything.Given the complexity of these expressions, it might be that the problem expects an answer in terms of s and m without further simplification, acknowledging that the sides and angles can be expressed using the above relations. However, perhaps there's a more elegant approach that I'm missing.Wait, let's recall that in a right-angled triangle, the height to the hypotenuse is related to the legs by m = (ab)/c, and from Pythagoras, c = sqrt(a² + b²). Also, a + b = s.We can use substitution variables. Let’s set a = s/2 + d and b = s/2 - d. Then, a + b = s, and a - b = 2d. This substitution often helps in symmetric equations. Then:ab = (s/2 + d)(s/2 - d) = (s²)/4 - d²Also, c = sqrt(a² + b²). Let's compute a² + b²:= (s/2 + d)^2 + (s/2 - d)^2 = 2*(s²/4 + d²) = s²/2 + 2d²Therefore, c = sqrt(s²/2 + 2d²)From equation m = (ab)/c:m = (s²/4 - d²) / sqrt(s²/2 + 2d²)This seems another equation to solve for d. Let's square both sides:m² = (s²/4 - d²)^2 / (s²/2 + 2d²)Multiply both sides by (s²/2 + 2d²):m² (s²/2 + 2d²) = (s²/4 - d²)^2Expand the right side:(s²/4 - d²)^2 = s^4 /16 - (s²/2)d² + d^4Left side:m² s² /2 + 2 m² d²Therefore:s^4 /16 - (s²/2)d² + d^4 = m² s² /2 + 2 m² d²Bring all terms to left:s^4 /16 - (s²/2)d² + d^4 - m² s² /2 - 2 m² d² =0Multiply all terms by 16 to eliminate denominators:s^4 -8 s² d² +16 d^4 -8 m² s² -32 m² d²=0This is a quartic equation in d, which is quite complicated. Perhaps this approach isn't better.Given the time I've spent and the various approaches attempted, it seems that the sides a and b, and the angles, can't be simplified much further without additional information. Therefore, the final expressions for the sides are:- Hypotenuse c = sqrt(m² + s²) - m- Legs a and b given by:a = [s + sqrt(s² -4m (sqrt(m² + s²) - m ))] / 2b = [s - sqrt(s² -4m (sqrt(m² + s²) - m ))] / 2And the angles θ and φ can be found using arctangent(a/b) and arctangent(b/a), respectively, though their exact expressions in terms of s and m are complex.However, let's verify if these expressions can be simplified further. Let's compute the term inside the square root:s² -4m (sqrt(m² + s²) - m ) =s² -4m sqrt(m² + s²) +4m² = (s² +4m²) -4m sqrt(m² + s²)Let me factor this expression. Let’s denote t = sqrt(m² + s²). Then the expression becomes:= (s² +4m²) -4m t = s² +4m² -4m tBut t = sqrt(m² + s²), so t² = m² + s². Therefore, s² = t² -m². Substitute back:= (t² -m²) +4m² -4m t = t² +3m² -4m tTherefore, sqrt(s² -4m (sqrt(m² + s²) - m )) = sqrt(t² +3m² -4m t) where t = sqrt(m² + s²)This still doesn’t seem to simplify. Therefore, I think this is as far as we can go in terms of simplification.Therefore, the sides of the triangle are:- Legs: [s ± sqrt(s² -4m (sqrt(m² + s²) - m ))] / 2- Hypotenuse: sqrt(m² + s²) - mThe angles can be found using trigonometric functions based on the legs, but due to the complexity of the expressions, they are likely best left in terms of arctangent or arcsine as shown earlier.However, let's check for consistency with specific values. For example, let's take a case where m and s are known. Suppose s = 5 and m = 2. Then compute c:c = sqrt(2² +5²) -2 = sqrt(29) -2 ≈5.385 -2≈3.385Then, ab = m*c ≈2*3.385≈6.77. Since a + b =5, solving the quadratic x² -5x +6.77≈0. The discriminant is 25 -27.08≈-2.08, which is negative. Wait, that can't be. But this suggests an error in our approach. Wait, no, in reality, for a right-angled triangle with legs summing to s=5, and height m=2, does such a triangle exist?Wait, if we have a right-angled triangle with a + b =5 and height m=2, then ab = m*c. But c = sqrt(a² +b²). Let's compute ab =2*sqrt(a² +b²). But a + b=5, so a² +b²=25 -2ab. Therefore, ab =2*sqrt(25 -2ab). Let's set ab =x. Then:x =2*sqrt(25 -2x)Squaring both sides:x² =4*(25 -2x) =>x² =100 -8x =>x² +8x -100=0Solutions:x=(-8 ±sqrt(64 +400))/2=(-8 ±sqrt(464))/2=(-8 ±4sqrt(29))/2= -4 ±2sqrt(29)Since x=ab must be positive, x= -4 +2sqrt(29)≈-4 +10.77≈6.77, which matches earlier. Then discriminant in quadratic equation for a and b would be 25 -4*6.77≈25 -27.08≈-2.08, which is negative. This suggests that no such triangle exists with s=5 and m=2. Therefore, the problem might have constraints on m and s for the triangle to exist.Indeed, in a right-angled triangle, the height to the hypotenuse is always less than or equal to half of the hypotenuse (since the maximum height occurs when the triangle is isoceles, and then h = (a√2)/2, which is half the hypotenuse). Therefore, m <= c/2. But c = sqrt(m² + s²) - m, so m <= [sqrt(m² + s²) - m]/2 => 2m <= sqrt(m² + s²) -m => 3m <= sqrt(m² + s²) =>9m² <=m² +s² =>8m² <=s² =>s >=2√2 m. Therefore, the problem constraints require that s >=2√2 m. In the example above, s=5, m=2, 2√2 m≈5.656, which is greater than 5, hence no such triangle exists. Therefore, our equations are correct, but there's a condition on s and m for the triangle to exist.Therefore, in the given problem, assuming that s and m satisfy s >=2√2 m, the solutions are as we derived.To summarize, the sides of the triangle are:- Hypotenuse: c = sqrt(m² + s²) - m- Legs: a = [s + sqrt(s² -4m (sqrt(m² + s²) - m ))] / 2 b = [s - sqrt(s² -4m (sqrt(m² + s²) - m ))] / 2The angles can be calculated using θ = arctan(a/b) and φ = arctan(b/a), which are complementary angles summing to 90°.However, these expressions can be further simplified. Let's note that:sqrt(s² -4m (sqrt(m² + s²) - m )) = sqrt(s² -4m sqrt(m² + s²) +4m²) = sqrt( (sqrt(m² + s²) - 2m)^2 - something?)Wait, let's compute sqrt(m² + s²) - 2m:sqrt(m² + s²) -2m. The square of this is m² + s² -4m sqrt(m² + s²) +4m² = s² +5m² -4m sqrt(m² + s²). Not quite matching the expression inside the sqrt. But if we consider:s² +4m² -4m sqrt(m² + s²) = [sqrt(m² + s²) - 2m]^2 - m²But:[sqrt(m² + s²) - 2m]^2 = m² + s² -4m sqrt(m² + s²) +4m² = s² +5m² -4m sqrt(m² + s²)Therefore, s² +4m² -4m sqrt(m² + s²) = [sqrt(m² + s²) -2m]^2 -m² = ([sqrt(m² + s²) -2m] -m)([sqrt(m² + s²) -2m]+m) = [sqrt(m² + s²) -3m][sqrt(m² + s²) -m]But this factorization might not help in simplification. Therefore, perhaps the expressions are as simplified as possible.Given the problem asks to "Calculate the sides and angles of the triangle," and given the time I've spent, I think the answer is expected to present the expressions in terms of s and m as we derived, even if they are complex. Therefore, the final answer is:Sides:- Hypotenuse: c = sqrt(m² + s²) - m- Legs: a = [s + sqrt(s² - 4m (sqrt(m² + s²) - m ))] / 2 b = [s - sqrt(s² - 4m (sqrt(m² + s²) - m ))] / 2Angles:- Angle opposite to side a: θ = arctan(a/b)- Angle opposite to side b: φ = arctan(b/a)Alternatively, since the angles are complementary, φ = 90° - θ.However, to present this in a boxed format as requested, perhaps express the sides in terms of s and m explicitly. But given the complexity, the problem might expect expressing the sides in terms of each other. Alternatively, the problem might have a standard formula which I might be missing.Wait, let me recall that in a right-angled triangle, if we denote the legs as a and b, hypotenuse c, then the height to the hypotenuse is h = ab/c. Also, we know that a + b = s. We also have c = sqrt(a² + b²). So, maybe we can express the problem in terms of these variables and find a quadratic equation for a or b.Let’s attempt once more. From a + b = s, and h = ab/c = m. From c = sqrt(a² + b²). So:ab = m sqrt(a² + b²)Let’s square both sides:a²b² = m²(a² + b²)But from a + b = s, we can express a² + b² = s² - 2ab. Substitute into above equation:a²b² = m²(s² - 2ab)Let’s set x = ab. Then:x² = m²(s² -2x) =>x² +2m²x -m²s² =0Which is the same quadratic equation as before. Solving for x:x = [-2m² ± sqrt(4m^4 +4m²s²)]/2 = [-m² ±m sqrt(m² +s²)]Since x must be positive, x = -m² +m sqrt(m² +s²). Therefore, ab =m(sqrt(m² +s²) -m)Then, with a + b =s and ab known, the quadratic equation is t² -st +m(sqrt(m² +s²) -m)=0. Solving this gives:t = [s ±sqrt(s² -4ab)]/2 = [s ±sqrt(s² -4m(sqrt(m² +s²) -m))]/2Which is the same as before. Therefore, the legs a and b are:a = [s + sqrt{s² -4m(sqrt(m² +s²) -m)}]/2b = [s - sqrt{s² -4m(sqrt(m² +s²) -m)}]/2This is as far as we can go. Therefore, the answer is:Sides:- a = [s + sqrt(s² -4m(h))]/2, where h = sqrt(m² +s²) -mBut since h is c, which is already expressed in terms of m and s, perhaps this isn't helpful.Alternatively, use substitution:Let’s denote k = sqrt(m² + s²). Then, c =k -m, and ab= m(k -m). The discriminant becomes s² -4m(k -m)=s² -4mk +4m². But k = sqrt(m² +s²), so:sqrt(s² -4mk +4m²) = sqrt{(s² +4m²) -4m sqrt(m² +s²)}Alternatively, perhaps write everything in terms of k:sqrt(k² -4m k +4m²) = sqrt{(k -2m)^2 - (something)}But (k -2m)^2 =k² -4mk +4m². Therefore, the discriminant becomes sqrt{(k -2m)^2} = |k -2m|. But since k = sqrt(m² +s²) >=sqrt(2)m (if s >= sqrt(2)m), and if s >=2√2 m, then k >=sqrt( (2√2 m)^2 +m² )=sqrt(8m² +m²)=3m. So, if k >=3m, then k -2m >=m>0. Therefore, sqrt{(k -2m)^2}=k -2m. Therefore, the discriminant simplifies to k -2m.Wait, this is a breakthrough! Let me verify:If k = sqrt(m² +s²), then the discriminant inside the square root is s² -4m(k -m)= s² -4mk +4m². But k² =m² +s², so s² =k² -m². Substitute:= k² -m² -4mk +4m²= k² -4mk +3m²= k² -4mk +3m²Factor:= k² -4mk +3m²= (k -m)(k -3m)Therefore, sqrt{(k -m)(k -3m)}But earlier, we thought that if s >=2√2 m, then k >=3m. However, if s >=2√2 m, then k = sqrt(m² +s²) >=sqrt(m² +8m²)=3m. Therefore, if k >=3m, then (k -m)(k -3m)>=0, so the sqrt is real. Therefore, sqrt{(k -m)(k -3m)}.But is there a way to express this as k -2m? Wait, let's check:If k =3m, then sqrt{(3m -m)(3m -3m)}=sqrt{2m *0}=0But according to the discriminant when s=2√2 m, then k=3m, and sqrt{(k -m)(k -3m)}=0. But according to previous substitution, the discriminant when s=2√2 m is sqrt(s² -4m(k -m))=sqrt(8m² -4m*(3m -m))=sqrt(8m² -8m²)=0. So, consistent.But in the case when k>3m, say k=4m, then sqrt{(4m -m)(4m -3m)}=sqrt{3m *m}=sqrt(3)m. But k -2m=2m. So, in this case, sqrt{(k -m)(k -3m)}≠k -2m. Therefore, my previous assertion was incorrect. Therefore, the discriminant is sqrt{(k -m)(k -3m)}, which doesn't simplify to k -2m.But we can express the discriminant as sqrt{(k -m)(k -3m)}. Therefore, the legs are:a = [s + sqrt{(k -m)(k -3m)}]/2b = [s - sqrt{(k -m)(k -3m)}]/2Where k = sqrt(m² +s²). This might be a more compact way to write the legs.Therefore, summarizing:Given a right-angled triangle with legs summing to s and height on hypotenuse m,- Hypotenuse c = sqrt(m² +s²) -m- Legs a and b:a = [s + sqrt{(sqrt(m² +s²) -m)(sqrt(m² +s²) -3m)}]/2b = [s - sqrt{(sqrt(m² +s²) -m)(sqrt(m² +s²) -3m)}]/2Angles θ and φ can be found using arctan(a/b) and arctan(b/a).This is the most compact form I can achieve. Therefore, the final answer is as follows.Final AnswerThe sides of the triangle are (boxed{a = frac{s + sqrt{(s^2 + 4m^2 - 4msqrt{m^2 + s^2})}}{2}}), (boxed{b = frac{s - sqrt{(s^2 + 4m^2 - 4msqrt{m^2 + s^2})}}{2}}), and hypotenuse (boxed{c = sqrt{m^2 + s^2} - m}). The angles can be calculated using (arctanleft(frac{a}{b}right)) and (arctanleft(frac{b}{a}right)).</think>Given a right-angled triangle (ABC) with the sum of the two legs being (s) and the height on the hypotenuse being (m), we need to calculate the sides and angles of the triangle.1. Equations and Relationships: - The sum of the legs: (a + b = s) - The height on the hypotenuse: (ab = cm) - Pythagoras' theorem: (a^2 + b^2 = c^2)2. Hypotenuse Calculation: - Using the quadratic equation derived from the given conditions, the hypotenuse (c) is found to be: [ c = sqrt{m^2 + s^2} - m ]3. Legs Calculation: - The product of the legs (ab) is given by (ab = m(sqrt{m^2 + s^2} - m)). - Solving the quadratic equation (x^2 - sx + m(sqrt{m^2 + s^2} - m) = 0) gives the legs (a) and (b): [ a = frac{s + sqrt{s^2 - 4m(sqrt{m^2 + s^2} - m)}}{2} ] [ b = frac{s - sqrt{s^2 - 4m(sqrt{m^2 + s^2} - m)}}{2} ]4. Simplification of the Discriminant: - The term inside the square root simplifies to: [ sqrt{s^2 - 4m(sqrt{m^2 + s^2} - m)} = sqrt{(s^2 + 4m^2 - 4msqrt{m^2 + s^2})} ]5. Angles Calculation: - The angles can be found using the arctangent of the ratio of the legs: [ theta = arctanleft(frac{a}{b}right) quad text{and} quad phi = arctanleft(frac{b}{a}right) ] Final AnswerThe sides of the triangle are:[boxed{a = frac{s + sqrt{(s^2 + 4m^2 - 4msqrt{m^2 + s^2})}}{2}}][boxed{b = frac{s - sqrt{(s^2 + 4m^2 - 4msqrt{m^2 + s^2})}}{2}}]and the hypotenuse is:[boxed{c = sqrt{m^2 + s^2} - m}]The angles can be calculated using (arctanleft(frac{a}{b}right)) and (arctanleft(frac{b}{a}right)).,<think>Okay, so I need to solve this right-angled triangle problem where the sum of the two legs is s, and the height on the hypotenuse is m. I have to find the sides and angles of the triangle. Hmm, let's start by recalling some basic properties of right-angled triangles.First, in a right-angled triangle, the two legs are perpendicular to each other, and the hypotenuse is the side opposite the right angle. Let me denote the legs as a and b, and the hypotenuse as c. So, the given information is that a + b = s, and the height (let's call it h) on the hypotenuse is m. The height on the hypotenuse in a right-angled triangle can be calculated using the formula h = (a*b)/c. So, m = (a*b)/c. That's one equation.We also know from the Pythagorean theorem that a² + b² = c². So, we have three pieces of information:1. a + b = s2. a² + b² = c²3. m = (a*b)/cOur goal is to find a, b, c, and the angles. Let's see how we can relate these equations.First, maybe we can express c in terms of a and b from the Pythagorean theorem, so c = sqrt(a² + b²). Then, substitute that into the third equation. Let me try that.From equation 3: m = (a*b)/sqrt(a² + b²). Hmm, but we also know from equation 1 that a + b = s. Maybe we can express one variable in terms of the other. For example, b = s - a. Then, substitute that into the equation for m.So, substitute b = s - a into equation 3:m = [a*(s - a)] / sqrt(a² + (s - a)²)Let me compute the denominator first. a² + (s - a)² = a² + s² - 2sa + a² = 2a² - 2sa + s².So, m = [a(s - a)] / sqrt(2a² - 2sa + s²)This seems a bit complicated. Maybe simplifying the denominator. Let's factor out 2a² - 2sa + s². Wait, maybe completing the square?2a² - 2sa + s² = 2(a² - sa) + s². Let's see:a² - sa can be written as a² - sa + (s²/4) - (s²/4) = (a - s/2)^2 - s²/4. So,2[(a - s/2)^2 - s²/4] + s² = 2(a - s/2)^2 - s²/2 + s² = 2(a - s/2)^2 + s²/2.Hmm, not sure if that helps. Maybe there's another way.Alternatively, let's square both sides of the equation m = [a(s - a)] / sqrt(2a² - 2sa + s²) to eliminate the square root.So, m² = [a²(s - a)²] / (2a² - 2sa + s²)Let me write the denominator as 2a² - 2sa + s². Let's denote numerator as a²(s - a)².Hmm, this might lead to a quartic equation. Maybe expanding both sides?First, expand the denominator:2a² - 2sa + s² = 2a² - 2sa + s²Numerator: a²(s² - 2sa + a²) = a²s² - 2s a³ + a^4So, m² = (a^4 - 2s a³ + a²s²) / (2a² - 2sa + s²)This is getting quite involved. Maybe cross-multiplying:m²*(2a² - 2sa + s²) = a^4 - 2s a³ + a²s²Let's expand the left side:2m²a² - 2m²sa + m²s² = a^4 - 2s a³ + a²s²Bring all terms to the left side:2m²a² - 2m²sa + m²s² - a^4 + 2s a³ - a²s² = 0Combine like terms:- a^4 + 2s a³ + (2m²a² - a²s²) - 2m²sa + m²s² = 0Factor terms:- a^4 + 2s a³ + a²(2m² - s²) - 2m²s a + m²s² = 0This is a quartic equation in a. Solving quartic equations is quite complex. Maybe there's a better approach here.Alternatively, perhaps express the problem in terms of variables that can be more easily related. Let's think about the relationships in the triangle.We know that the area of the triangle can be expressed in two ways: (1/2)*a*b and (1/2)*c*m. Therefore:(1/2)*a*b = (1/2)*c*m => a*b = c*mWhich is the same as equation 3. So that's consistent.But perhaps we can use this to relate a and b with c. Also, since a + b = s, maybe using substitution.Let me denote a + b = s, so (a + b)^2 = s² => a² + 2ab + b² = s². But from Pythagoras, a² + b² = c². Therefore:c² + 2ab = s² => 2ab = s² - c²But from equation 3, ab = c*m. Therefore, substituting ab:2*c*m = s² - c² => c² + 2m c - s² = 0Ah! That's a quadratic equation in c. Let me write that:c² + 2m c - s² = 0This is a quadratic in c. Solving for c:c = [-2m ± sqrt((2m)^2 + 4*s²)] / 2Simplify:c = [-2m ± sqrt(4m² + 4s²)] / 2 = [-2m ± 2*sqrt(m² + s²)] / 2 = -m ± sqrt(m² + s²)Since c is a length, it must be positive. Therefore:c = -m + sqrt(m² + s²). Wait, but sqrt(m² + s²) is greater than m, so -m + sqrt(m² + s²) is positive. Alternatively, if we take the positive root:c = [ -2m + 2*sqrt(m² + s²) ] / 2 = -m + sqrt(m² + s²)Alternatively, is there a mistake here? Let's redo the quadratic solution.Quadratic equation: c² + 2m c - s² = 0Using quadratic formula:c = [-2m ± sqrt{(2m)^2 + 4*1*s²}]/2*1 = [-2m ± sqrt{4m² + 4s²}]/2 = [-2m ± 2*sqrt(m² + s²)]/2Dividing numerator and denominator by 2:c = -m ± sqrt(m² + s²)So, since c must be positive, we take c = -m + sqrt(m² + s²). But sqrt(m² + s²) > m, so yes, c is positive. Alternatively, if we write it as c = sqrt(m² + s²) - m.Wait, but let's check units. If m and s are lengths, then sqrt(m² + s²) is a length, and subtracting m would give a positive result. So that's okay.So, c = sqrt(m² + s²) - m. Hmm, interesting.Wait, but is that correct? Let me check with a sample case. Suppose m = 3, s = 4. Then c = sqrt(9 + 16) - 3 = 5 - 3 = 2. But in reality, if s = 4 (sum of legs) and m = 3 (height on hypotenuse), let's see if that works.Wait, if c = 2, then the area is (1/2)*c*m = (1/2)*2*3 = 3. Also, the area is (1/2)*a*b. So, a*b = 6. And a + b = 4. So, the product is 6 and the sum is 4. The solutions for a and b would be the roots of x² - 4x + 6 = 0. The discriminant is 16 - 24 = -8, which is negative. That's impossible. So, this suggests that m = 3 and s = 4 is not possible? Wait, but maybe m and s can't be arbitrary. There must be a relationship between them. So, perhaps in reality, for given s, m can't be arbitrary. So, the formula gives a valid c only if sqrt(m² + s²) - m is positive, which it is, but the corresponding a and b must be real.But in my example, with s=4 and m=3, the quadratic equation for a and b has no real solutions, which suggests that this combination is impossible. Therefore, maybe my formula for c is correct, but such an m and s combination is invalid. So, perhaps m and s are related by some inequality. Let's think.From a + b = s and ab = c*m, and c = sqrt(a² + b²). So, if we have a + b = s, ab = m*sqrt(a² + b²). Maybe m must be less than or equal to s/2? Not sure. But in any case, the formula for c is c = sqrt(m² + s²) - m. Let's proceed with that.So, once we have c, then since ab = c*m, and a + b = s, we can find a and b by solving the quadratic equation x² - s x + c m = 0. The solutions are [s ± sqrt(s² - 4 c m)] / 2.But we can compute this once we have c.So, let's compute c first:c = sqrt(m² + s²) - mThen, the product ab = c*mSo, the quadratic equation is x² - s x + c m = 0. Therefore, the solutions are:x = [s ± sqrt(s² - 4 c m)] / 2But let's compute s² - 4 c m.s² - 4 c m = s² - 4*(sqrt(m² + s²) - m)*m= s² - 4 m*sqrt(m² + s²) + 4 m²= (s² + 4 m²) - 4 m*sqrt(m² + s²)Hmm, that seems messy. Maybe simplifying:Let me denote sqrt(m² + s²) as t. Then, c = t - m.Then, s² - 4 c m = s² - 4 m (t - m) = s² - 4 m t + 4 m²But t = sqrt(m² + s²), so t² = m² + s². Therefore:s² - 4 m t + 4 m² = (t² - m²) - 4 m t + 4 m² = t² - 4 m t + 3 m²So, discriminant becomes t² - 4 m t + 3 m²Which factors as (t - m)(t - 3m)So, sqrt(m² + s²) = t, so discriminant is (t - m)(t - 3m) = [sqrt(m² + s²) - m][sqrt(m² + s²) - 3m]For the discriminant to be non-negative, we need [sqrt(m² + s²) - m][sqrt(m² + s²) - 3m] ≥ 0Since sqrt(m² + s²) ≥ m, the first term is non-negative. Therefore, the discriminant is non-negative if sqrt(m² + s²) - 3m ≥ 0 => sqrt(m² + s²) ≥ 3m => m² + s² ≥ 9m² => s² ≥ 8m² => s ≥ 2√2 mSo, as long as s ≥ 2√2 m, the discriminant is non-negative, and we have real solutions. Therefore, the problem must satisfy s ≥ 2√2 m for real solutions to exist.Assuming that's the case, then the roots are:x = [s ± sqrt{(sqrt(m² + s²) - m)(sqrt(m² + s²) - 3m)}]/2Hmm, that's quite a complicated expression. Maybe there's a better way to write this.Alternatively, let's express in terms of t.We have t = sqrt(m² + s²)So, discriminant D = (t - m)(t - 3m)Therefore, sqrt(D) = sqrt{(t - m)(t - 3m)}. Hmm, not sure.Alternatively, perhaps express the entire thing in terms of t:But maybe this is getting too abstract. Let's try plugging in c = t - m into the quadratic equation.Alternatively, let's recall that c = sqrt(m² + s²) - mSo, c + m = sqrt(m² + s²)Squaring both sides: (c + m)^2 = m² + s² => c² + 2mc + m² = m² + s² => c² + 2mc = s²Which is our earlier equation. So, this is consistent.Alternatively, perhaps use substitution variables.Let me think. Let me denote a = s/2 + d and b = s/2 - d, since a + b = s. Then, a and b can be expressed as s/2 plus or minus some delta. Then, maybe compute d in terms of m and s.So, set a = s/2 + d, b = s/2 - dThen, ab = (s/2 + d)(s/2 - d) = (s/2)^2 - d² = s²/4 - d²But ab = c*m, so s²/4 - d² = c*mAlso, c = sqrt(a² + b²) = sqrt{(s/2 + d)^2 + (s/2 - d)^2}Compute inside the sqrt:(s/2 + d)^2 + (s/2 - d)^2 = (s²/4 + s d + d²) + (s²/4 - s d + d²) = s²/4 + s²/4 + d² + d² = s²/2 + 2d²Therefore, c = sqrt(s²/2 + 2d²)So, putting this into ab = c*m:s²/4 - d² = m*sqrt(s²/2 + 2d²)Let me square both sides to eliminate the square root:(s²/4 - d²)^2 = m²*(s²/2 + 2d²)Expanding the left side:(s²/4)^2 - 2*(s²/4)*(d²) + (d²)^2 = m²*(s²/2 + 2d²)=> s^4/16 - (s² d²)/2 + d^4 = (m² s²)/2 + 2 m² d²Bring all terms to the left side:s^4/16 - (s² d²)/2 + d^4 - (m² s²)/2 - 2 m² d² = 0Multiply through by 16 to eliminate denominators:s^4 - 8 s² d² + 16 d^4 - 8 m² s² - 32 m² d² = 0This is a quartic equation in d. This seems even more complex. Maybe this approach isn't better. Perhaps going back to the quadratic equation in c was a better path.Wait, but if we have c expressed in terms of s and m, as c = sqrt(m² + s²) - m, then maybe express a and b in terms of s and c.Since a + b = s and a² + b² = c², we can use these two equations to find a and b.We know that (a + b)^2 = a² + 2ab + b² = s²But a² + b² = c², so s² = c² + 2ab => ab = (s² - c²)/2But from equation 3, ab = c*m, so (s² - c²)/2 = c m => s² - c² = 2 c m => s² = c² + 2 c m. Which is the same equation we had before, leading to the quadratic in c. So, this is consistent.Given that c = sqrt(m² + s²) - m, then ab = c m = m (sqrt(m² + s²) - m)Thus, ab = m sqrt(m² + s²) - m²Therefore, the quadratic equation for a and b is x² - s x + (m sqrt(m² + s²) - m²) = 0So, solving this quadratic:x = [s ± sqrt{s² - 4*(m sqrt(m² + s²) - m²)}]/2Let me compute the discriminant:D = s² - 4*(m sqrt(m² + s²) - m²) = s² - 4 m sqrt(m² + s²) + 4 m²Hmm, this is the same discriminant as before. Perhaps I can factor this expression.Let me denote t = sqrt(m² + s²). Then D = s² - 4 m t + 4 m²But t² = m² + s², so s² = t² - m². Therefore:D = (t² - m²) - 4 m t + 4 m² = t² - 4 m t + 3 m²Which factors as (t - m)(t - 3m)So, D = (sqrt(m² + s²) - m)(sqrt(m² + s²) - 3m)As before. So, sqrt(D) = sqrt{(sqrt(m² + s²) - m)(sqrt(m² + s²) - 3m)}Therefore, the solutions for a and b are:a, b = [s ± sqrt{(sqrt(m² + s²) - m)(sqrt(m² + s²) - 3m)}]/2This is still quite complicated. Maybe there's a way to simplify this expression.Alternatively, perhaps use substitution variables. Let me set u = sqrt(m² + s²). Then, the expression becomes:sqrt{(u - m)(u - 3m)}.So, sqrt{(u - m)(u - 3m)} = sqrt{u² - 4m u + 3m²}But u = sqrt(m² + s²), so u² = m² + s². Therefore:sqrt{(m² + s²) - 4m u + 3m²} = sqrt{s² + 4m² - 4m u}But u = sqrt(m² + s²), so 4m u = 4m sqrt(m² + s²). Therefore:sqrt{s² + 4m² - 4m sqrt(m² + s²)}Hmm, this doesn't seem to lead to a simplification. Maybe we can express this in terms of c, since c = u - m.Wait, c = u - m => u = c + m. Substitute into sqrt{s² + 4m² - 4m u}:sqrt{s² + 4m² - 4m(c + m)} = sqrt{s² + 4m² - 4m c - 4m²} = sqrt{s² - 4m c}But from earlier, we have s² = c² + 2m c. Therefore:sqrt{s² - 4m c} = sqrt{c² + 2m c - 4m c} = sqrt{c² - 2m c}Therefore, the discriminant simplifies to sqrt{c² - 2m c}But c² - 2m c = c(c - 2m)But since c = sqrt(m² + s²) - m, c - 2m = sqrt(m² + s²) - 3mWhich brings us back to the same point. So, maybe there's no further simplification here.Therefore, the solutions are:a, b = [s ± sqrt{c² - 2m c}]/2, where c = sqrt(m² + s²) - mAlternatively, substituting c into sqrt{c² - 2m c}:c² - 2m c = (sqrt(m² + s²) - m)^2 - 2m (sqrt(m² + s²) - m)Expanding:= (m² + s² - 2m sqrt(m² + s²) + m²) - 2m sqrt(m² + s²) + 2m²= 2m² + s² - 2m sqrt(m² + s²) - 2m sqrt(m² + s²) + 2m²= 4m² + s² - 4m sqrt(m² + s²)Which is the same as before. So, no progress.Perhaps instead of trying to find a and b algebraically, which seems too complicated, maybe express the sides in terms of angles.In a right-angled triangle, the legs can be expressed as c*cos(theta) and c*sin(theta), where theta is one of the acute angles. Then, the sum of the legs is c*(sin(theta) + cos(theta)) = s. The height on the hypotenuse is m = (a*b)/c = [c^2 sin(theta) cos(theta)] / c = c sin(theta) cos(theta). So, m = c sin(theta) cos(theta). Let's see if we can use these equations.Let me denote theta as one of the acute angles, say angle at A. Then:a = c cos(theta)b = c sin(theta)Then, a + b = c (sin(theta) + cos(theta)) = sAlso, m = c sin(theta) cos(theta)So, we have two equations:1. c (sin(theta) + cos(theta)) = s2. c sin(theta) cos(theta) = mWe can solve these equations for c and theta.From equation 2: c = m / [sin(theta) cos(theta)]Substitute into equation 1:[m / (sin(theta) cos(theta))] * (sin(theta) + cos(theta)) = sSimplify:m (sin(theta) + cos(theta)) / (sin(theta) cos(theta)) = sDivide numerator and denominator by sin(theta) cos(theta):m [ (sin(theta)/(sin(theta) cos(theta)) ) + (cos(theta)/(sin(theta) cos(theta)) ) ] = sWait, but actually, maybe better to split the fraction:m [ sin(theta)/(sin(theta) cos(theta)) + cos(theta)/(sin(theta) cos(theta)) ) ] = m [ 1/cos(theta) + 1/sin(theta) ) ] = sSo:m ( sec(theta) + csc(theta) ) = sWhich is:m (1/cos(theta) + 1/sin(theta)) = sLet me write that as:m ( (sin(theta) + cos(theta)) / (sin(theta) cos(theta)) ) = sWhich is the same as the earlier expression.Alternatively, let's let t = theta.So,sin(t) + cos(t) = (s/m) sin(t) cos(t)Let me denote sin(t) + cos(t) = k. Then, we have:k = (s/m) * [ (k² - 1)/2 ]Because (sin(t) + cos(t))² = sin²(t) + 2 sin(t) cos(t) + cos²(t) = 1 + 2 sin(t) cos(t)Thus, sin(t) cos(t) = (k² - 1)/2Therefore, substituting back into the equation k = (s/m) * [ (k² - 1)/2 ]Multiply both sides by 2:2k = (s/m)(k² - 1)Rearranged:(s/m)k² - 2k - (s/m) = 0Multiply both sides by m/s to simplify:k² - (2m/s)k - 1 = 0This is a quadratic equation in k:k² - (2m/s)k - 1 = 0Solving for k:k = [ (2m/s) ± sqrt{(2m/s)^2 + 4} ] / 2Simplify:k = [ (2m/s) ± sqrt{4m²/s² + 4} ] / 2 = [ (2m/s) ± 2 sqrt{(m² + s²)/s²} ] / 2Factor out 2:k = [ 2 [ m/s ± sqrt{(m² + s²)/s²} ] ] / 2 = [ m/s ± sqrt(m² + s²)/s ]Therefore, k = [ m ± sqrt(m² + s²) ] / sBut k = sin(t) + cos(t), and since t is an acute angle (between 0 and π/2), sin(t) + cos(t) is positive and greater than 1 (since sin(t) + cos(t) ≥ √2/2 + √2/2 = √2 > 1 for t = 45°, and even larger for other angles). However, in our solution for k, one of the roots is [ m - sqrt(m² + s²) ] / s, which is negative because sqrt(m² + s²) > m. Therefore, we discard the negative root.Thus, k = [ m + sqrt(m² + s²) ] / sTherefore:sin(t) + cos(t) = [ m + sqrt(m² + s²) ] / sNow, we can use this to find t. Let me denote this as equation (*).Also, recall that from equation 2:m = c sin(t) cos(t)And from equation 1:c = s / [ sin(t) + cos(t) ] = s / kSo, c = s / k = s / [ (m + sqrt(m² + s²)) / s ] = s^2 / (m + sqrt(m² + s²))Therefore, c = s^2 / (m + sqrt(m² + s²))But earlier, we found that c = sqrt(m² + s²) - m. Let's verify if these expressions are equivalent.Let me compute sqrt(m² + s²) - m:sqrt(m² + s²) - m = [sqrt(m² + s²) - m] * [sqrt(m² + s²) + m] / [sqrt(m² + s²) + m] = (m² + s² - m²) / [sqrt(m² + s²) + m] = s² / [sqrt(m² + s²) + m]Which is equal to the expression we just found for c. So yes, they are the same. Therefore, this is consistent.Now, returning to find angle t.We have sin(t) + cos(t) = k = [ m + sqrt(m² + s²) ] / sLet me denote k = [ m + sqrt(m² + s²) ] / sLet me square both sides:k² = [ m² + 2m sqrt(m² + s²) + m² + s² ] / s² = [ 2m² + s² + 2m sqrt(m² + s²) ] / s²But also, from the identity (sin(t) + cos(t))² = 1 + 2 sin(t) cos(t) = 1 + 2*(m/c) [since m = c sin(t) cos(t)]But c = s / k, so m = (s / k) sin(t) cos(t) => sin(t) cos(t) = (m k)/sTherefore, 1 + 2*(m k)/s = k²So, 1 + (2 m k)/s = k²But this is consistent with the quadratic equation we had earlier:k² - (2m/s)k -1 =0Which rearranged is k² -1 = (2m/s)kTherefore, yes, the identity holds.But how does this help us find t?Alternatively, we can use the equation sin(t) + cos(t) = kLet me recall that sin(t) + cos(t) = √2 sin(t + 45°)Therefore, √2 sin(t + 45°) = k => sin(t + 45°) = k / √2Therefore, t + 45° = arcsin(k / √2) => t = arcsin(k / √2) - 45°But k = [ m + sqrt(m² + s²) ] / sSo, this gives t in terms of m and s. But this is still quite involved. Alternatively, maybe express t in terms of arctangent.Let me think. Let’s denote tan(t) = a/b, since in a right-angled triangle, the tangent of one acute angle is the ratio of the opposite side over the adjacent side. Let’s say tan(t) = a/b.From a + b = s and ab = c m, and c = sqrt(a² + b²). Maybe expressing t in terms of a and b.But we might need to find tan(t) = a/b. Let's let r = a/b, so a = r b. Then, since a + b = s, we have r b + b = s => b(r + 1) = s => b = s / (r + 1)Then, a = r s / (r + 1)Now, ab = c mCompute ab = (r s / (r + 1)) * (s / (r + 1)) = r s² / (r + 1)^2Also, c = sqrt(a² + b²) = sqrt{ (r² s²)/(r + 1)^2 + s²/(r + 1)^2 } = sqrt{ s²(r² + 1)/(r + 1)^2 } = s sqrt(r² + 1)/(r + 1)Therefore, ab = c m => r s² / (r + 1)^2 = [ s sqrt(r² + 1)/(r + 1) ] * mSimplify both sides:Left side: r s² / (r + 1)^2Right side: s m sqrt(r² + 1) / (r + 1)Divide both sides by s / (r + 1):Left side: r s / (r + 1)Right side: m sqrt(r² + 1)Therefore:r s / (r + 1) = m sqrt(r² + 1)Square both sides:r² s² / (r + 1)^2 = m² (r² + 1)Multiply both sides by (r + 1)^2:r² s² = m² (r² + 1)(r + 1)^2This is a quartic equation in r, which seems even more complicated. Perhaps this approach isn't better.Alternatively, since we have expressions for a and b in terms of s and the discriminant, maybe just leave the sides expressed in terms of s and m, even if it's complicated.Alternatively, let's consider that the problem asks to "calculate the sides and angles of the triangle." So, maybe the answer is expected to be expressed in terms of s and m, even if the expressions are complex.So, compiling what we have:Hypotenuse c = sqrt(m² + s²) - mLegs a and b are [s ± sqrt{(sqrt(m² + s²) - m)(sqrt(m² + s²) - 3m)}]/2But to make this more presentable, perhaps rationalize or find another form.Alternatively, perhaps express a and b in terms of c.From a + b = s and a² + b² = c², we can express a and b as:a = [s + sqrt(2c² - s² + 2ab)] / 2 ?Wait, not helpful.Alternatively, since we have ab = c m, and a + b = s, the standard quadratic formula gives a and b as [s ± sqrt(s² - 4ab)] / 2. But ab = c m, so:a and b = [s ± sqrt(s² - 4 c m)] / 2But we already have c expressed as sqrt(m² + s²) - m. So:a, b = [s ± sqrt(s² - 4*(sqrt(m² + s²) - m)*m)] / 2Compute inside the sqrt:s² - 4m*(sqrt(m² + s²) - m) = s² - 4m sqrt(m² + s²) + 4m²= (s² + 4m²) - 4m sqrt(m² + s²)But s² + 4m² = (sqrt(m² + s²))² + 3m²Wait, but sqrt(m² + s²) = t, so:= t² + 3m² - 4m t = t² - 4m t + 3m² = (t - m)(t - 3m)Therefore, sqrt becomes sqrt{(t - m)(t - 3m)} = sqrt{(sqrt(m² + s²) - m)(sqrt(m² + s²) - 3m)}So, a, b = [s ± sqrt{(sqrt(m² + s²) - m)(sqrt(m² + s²) - 3m)}]/2This is the simplest form we can get for a and b.Alternatively, if we denote sqrt(m² + s²) as something like u, then:a, b = [s ± sqrt{(u - m)(u - 3m)}]/2 where u = sqrt(m² + s²)But I don't think this is any better.Alternatively, perhaps express in terms of c:Since c = u - m, and u = sqrt(m² + s²), then u = c + mTherefore, (u - m)(u - 3m) = (c)(c - 2m)Therefore, sqrt{(u - m)(u - 3m)} = sqrt{c(c - 2m)}So, a, b = [s ± sqrt{c(c - 2m)}]/2Given that c = sqrt(m² + s²) - m, this gives another expression.Therefore, the legs a and b can be written as:a = [s + sqrt{c(c - 2m)}]/2b = [s - sqrt{c(c - 2m)}]/2Or vice versa, depending on which is larger.So, putting it all together:c = sqrt(m² + s²) - ma = [s + sqrt{c(c - 2m)}]/2b = [s - sqrt{c(c - 2m)}]/2But this still requires substituting c into the expressions for a and b.Alternatively, substituting c into the sqrt:sqrt{c(c - 2m)} = sqrt{[sqrt(m² + s²) - m][sqrt(m² + s²) - m - 2m]} = sqrt{[sqrt(m² + s²) - m][sqrt(m² + s²) - 3m]}Which is the same as before.So, perhaps this is as simplified as it can get.Regarding the angles, once we have the sides a, b, c, the angles can be found using trigonometric ratios. For example, angle opposite side a is arcsin(a/c), and angle opposite side b is arcsin(b/c). The third angle is 90 degrees.But since we don't have explicit expressions for a and b, but only in terms of s and m, maybe the angles can be expressed using the relationships we have.Alternatively, use the expressions involving theta from before.Recall that angle t (say, opposite side a) satisfies:sin(t) + cos(t) = k = [ m + sqrt(m² + s²) ] / sAnd sin(t) cos(t) = m/c = m / [sqrt(m² + s²) - m]Alternatively, using tan(t) = a/b. But since a and b are expressed in terms of s and m, tan(t) can be expressed as [s + sqrt{(sqrt(m² + s²) - m)(sqrt(m² + s²) - 3m)}] / [s - sqrt{(sqrt(m² + s²) - m)(sqrt(m² + s²) - 3m)}]Which is quite complicated.Alternatively, maybe express the angles in terms of arcsin or arccos.Given that a = c cos(t) and b = c sin(t), then:cos(t) = a / c = [s + sqrt{c(c - 2m)}]/2cSimilarly, sin(t) = b / c = [s - sqrt{c(c - 2m)}]/2cBut again, this is complex.Alternatively, use the earlier relation where we had:sin(t) + cos(t) = k = [ m + sqrt(m² + s²) ] / sAnd we also had:sin(t) cos(t) = m / c = m / [sqrt(m² + s²) - m]From these two equations, maybe we can find sin(t) and cos(t).Let me denote S = sin(t) + cos(t) = kP = sin(t) cos(t) = m / c = m / [sqrt(m² + s²) - m]We know that sin(t) and cos(t) are roots of the quadratic equation x² - Sx + P = 0Therefore, sin(t) and cos(t) can be found as:x = [S ± sqrt(S² - 4P)] / 2But S² - 4P = k² - 4*(m/c)From earlier, we have:k² = 1 + 2P (since (sin(t) + cos(t))² = 1 + 2 sin(t) cos(t))Therefore, S² - 4P = 1 + 2P - 4P = 1 - 2PTherefore, the discriminant is 1 - 2PThus, sin(t) and cos(t) = [k ± sqrt(1 - 2P)] / 2But P = m / c, and c = sqrt(m² + s²) - m. Therefore:P = m / (sqrt(m² + s²) - m)Multiply numerator and denominator by (sqrt(m² + s²) + m):P = m (sqrt(m² + s²) + m) / [ (sqrt(m² + s²) - m)(sqrt(m² + s²) + m) ] = m (sqrt(m² + s²) + m) / (s²)Therefore:P = [ m sqrt(m² + s²) + m² ] / s²Therefore:1 - 2P = 1 - 2[ m sqrt(m² + s²) + m² ] / s²= [ s² - 2m sqrt(m² + s²) - 2m² ] / s²Thus, sqrt(1 - 2P) = sqrt{ [s² - 2m sqrt(m² + s²) - 2m² ] / s² } = sqrt{ s² - 2m sqrt(m² + s²) - 2m² } / sBut this seems similar to the discriminant we had earlier.Therefore, sin(t) and cos(t) = [k ± sqrt(1 - 2P)] / 2 = [ [m + sqrt(m² + s²)] / s ± sqrt{ s² - 2m sqrt(m² + s²) - 2m² } / s ] / 2= [ m + sqrt(m² + s²) ± sqrt{ s² - 2m sqrt(m² + s²) - 2m² } ] / (2s)This expression is quite complicated. It seems that the angles can't be simplified further without knowing specific values for m and s.Given that, perhaps the problem expects the answer to be expressed in terms of s and m with the given relationships, acknowledging that explicit formulas for a, b, and the angles are complex but can be written using the derived expressions.Alternatively, perhaps there's a substitution or identity I’m missing that could simplify this.Wait, going back to the height on the hypotenuse: m = (a*b)/c. We have a + b = s. Let's think of this as a system of equations with variables a, b, c, and given s, m.We can express this as:1. a + b = s2. a*b = m*c3. a² + b² = c²From 1 and 3, we have c² = s² - 2ab = s² - 2m c (from equation 2)Therefore, c² + 2m c - s² = 0, which is quadratic in c. Solving gives c = [-2m ± sqrt{4m² + 4s²}]/2 = -m ± sqrt{m² + s²}, so c = sqrt{m² + s²} - m.Then, ab = m c = m (sqrt{m² + s²} - m)From equation 1 and ab, we can write the quadratic equation x² - s x + m (sqrt{m² + s²} - m) = 0Solutions are:x = [s ± sqrt{s² - 4 m (sqrt{m² + s²} - m)}]/2Which is the same as before.So, ultimately, the sides are:c = sqrt{m² + s²} - ma = [s + sqrt{s² - 4 m (sqrt{m² + s²} - m)}]/2b = [s - sqrt{s² - 4 m (sqrt{m² + s²} - m)}]/2The angles can be found using trigonometric functions, but given the complexity of a and b, they would be:Angle opposite a: arcsin(a/c)Angle opposite b: arcsin(b/c)Given the expressions for a and c, these angles would also require substitution of the above expressions.Alternatively, since the problem states "Calculate the sides and angles of the triangle," it may be acceptable to present the sides in terms of s and m as above, and the angles in terms of arcsin or arctan of the ratios of these sides.However, given the complexity, perhaps there's an alternative approach using substitution or another geometric insight.Wait, considering the height on the hypotenuse, m, and the relationship to the legs.In any right-angled triangle, the height to the hypotenuse relates the segments into which the hypotenuse is divided. Let me denote the foot of the altitude as D, dividing hypotenuse AB into segments AD and DB.Then, we have AD = (a²)/c and DB = (b²)/c, and m = (ab)/c.But I'm not sure if this helps directly. However, since we have the entire hypotenuse c and the height m, maybe using similar triangles.In a right-angled triangle, the two smaller triangles formed by the altitude are similar to the original triangle and to each other.Therefore, ratios of sides can be used. For example, m / AD = b / c, and m / DB = a / c.But since AD + DB = c, and AD = a²/c, DB = b²/c, we have a²/c + b²/c = c => (a² + b²)/c = c, which is consistent with Pythagoras.Not sure if this helps.Alternatively, using trigonometry again. Given that the angles are complementary, if one angle is theta, the other is 90 - theta.From the earlier approach where we set sin(t) + cos(t) = k and derived k, maybe using that to find theta.But even then, unless we can express theta in terms of arcsin or arccos, it's not straightforward.Given that the problem is likely expecting an answer in terms of s and m, even if somewhat complex, I think the expressions we derived are the solutions.Therefore, compiling the final answer:The hypotenuse c is sqrt(m² + s²) - m.The legs a and b are [s ± sqrt{s² - 4m(sqrt(m² + s²) - m)}]/2.The angles can be found using arcsin(a/c) and arcsin(b/c).Alternatively, rationalizing the expression under the square root:s² - 4m(sqrt(m² + s²) - m) = s² - 4m sqrt(m² + s²) + 4m² = (s² + 4m²) - 4m sqrt(m² + s²)Let me factor this expression:Let u = sqrt(m² + s²). Then, the expression becomes (u² + 3m²) - 4m u = u² - 4m u + 3m² = (u - m)(u - 3m)Therefore, the legs are:a, b = [s ± sqrt{(u - m)(u - 3m)}]/2 where u = sqrt(m² + s²)As before.Given that, and knowing that u = sqrt(m² + s²), this may be the most concise way to express the legs.Thus, summarizing:- Hypotenuse: c = sqrt(m² + s²) - m- Legs: a = [s + sqrt{(sqrt(m² + s²) - m)(sqrt(m² + s²) - 3m)}]/2 b = [s - sqrt{(sqrt(m² + s²) - m)(sqrt(m² + s²) - 3m)}]/2- Angles: The two acute angles can be calculated as arcsin(a/c) and arcsin(b/c), but due to the complexity of a and b, they are best expressed using the above terms.Alternatively, the angles can be found using:theta = arcsin([s + sqrt{(sqrt(m² + s²) - m)(sqrt(m² + s²) - 3m)}]/(2c))andphi = arcsin([s - sqrt{(sqrt(m² + s²) - m)(sqrt(m² + s²) - 3m)}]/(2c))where c is as defined.Given that the problem asks to "Calculate the sides and angles," and given the complexity of the expressions, it's possible that the answer is expected in terms of s and m with radicals, as we have derived, rather than further simplified.Therefore, the final answer is:Sides:- Hypotenuse: ( boxed{c = sqrt{m^2 + s^2} - m} )- Legs: ( boxed{a = frac{s + sqrt{(sqrt{m^2 + s^2} - m)(sqrt{m^2 + s^2} - 3m)}}{2}} ) and ( boxed{b = frac{s - sqrt{(sqrt{m^2 + s^2} - m)(sqrt{m^2 + s^2} - 3m)}}{2}} )Angles can be found using arcsin(a/c) and arcsin(b/c), which are:- Angle opposite side a: ( boxed{arcsinleft(frac{a}{c}right)} )- Angle opposite side b: ( boxed{arcsinleft(frac{b}{c}right)} )- Right angle: 90°However, given the complexity, it's also possible that the problem expects a more simplified answer or a different form. But based on the derivations, this is the solution.Final AnswerThe sides of the triangle are ( boxed{a = frac{s + sqrt{s^2 - 4m(sqrt{m^2 + s^2} - m)}}{2}} ), ( boxed{b = frac{s - sqrt{s^2 - 4m(sqrt{m^2 + s^2} - m)}}{2}} ), and the hypotenuse is ( boxed{c = sqrt{m^2 + s^2} - m} ). The angles can be calculated using trigonometric functions with these side lengths.</think>Given a right-angled triangle (ABC) with the sum of the two legs being (s) and the height on the hypotenuse being (m), we need to calculate the sides and angles of the triangle.1. Hypotenuse Calculation: - The hypotenuse (c) can be found using the quadratic equation derived from the given conditions: [ c = sqrt{m^2 + s^2} - m ]2. Legs Calculation: - The legs (a) and (b) are found by solving the quadratic equation with the sum (a + b = s) and product (ab = mc): [ a = frac{s + sqrt{s^2 - 4m(sqrt{m^2 + s^2} - m)}}{2} ] [ b = frac{s - sqrt{s^2 - 4m(sqrt{m^2 + s^2} - m)}}{2} ]3. Angles Calculation: - The angles can be found using trigonometric functions: - The angle opposite leg (a) is (arcsinleft(frac{a}{c}right)) - The angle opposite leg (b) is (arcsinleft(frac{b}{c}right)) - The right angle is (90^circ) Final Answer- Hypotenuse: [ boxed{c = sqrt{m^2 + s^2} - m} ]- Legs: [ boxed{a = frac{s + sqrt{s^2 - 4m(sqrt{m^2 + s^2} - m)}}{2}} ] [ boxed{b = frac{s - sqrt{s^2 - 4m(sqrt{m^2 + s^2} - m)}}{2}} ]- Angles: - Angle opposite (a): (boxed{arcsinleft(frac{a}{c}right)}) - Angle opposite (b): (boxed{arcsinleft(frac{b}{c}right)}) - Right angle: (90^circ)]

🔑:Let the legs be a and b, the hypotenuse c; then:a+b=sora^{2}+2 a b+b^{2}=s^{2}andbegin{gathered}a b=c m a^{2}+b^{2}=c^{2}end{gathered}From these equations, we can determine the sides of the triangle. Substituting (3) and (2) into (1a):c^{2}+2 c m=s^{2}from whichc=-m pm sqrt{m^{2}+s^{2}}the square root can only be positive because c>0.From (2) and (1), it follows that the legs are the roots of the following equation:x^{2}-s x+c m=0Solving this equation, we get:a=frac{s}{2}+frac{sqrt{s^{2}-4 c m}}{2} text { and } b=frac{s}{2}-frac{sqrt{s^{2}-4 c m}}{2}The angles are determined by the following equations.sin alpha=frac{m}{b}, sin beta=frac{m}{a}(Károly Goldziher, VII.o. t., Budapest, Gymnasium.)The problem was also solved by: Mór Feuer, Bernát Friedmann, Károly Fröhlich, Emil Geist, Zsigmond Goldstein, Béla Grünhut, Ervin Hofbauer, Nándor Kántor, Jenő Reif, Frigyes Riesz, István Szabó, Lipót Weisz.

🧠:[<think>Okay, let's see. The problem is asking for the number of ordered triples (a, b, c) where each of a, b, c is an integer between 0 and 10 inclusive. Additionally, the sum a + b + c has to be between 10 and 20 inclusive. So, we need to count all possible triples (a, b, c) such that each variable is at least 0 and at most 10, and their sum is at least 10 and at most 20.Hmm. Normally, if there were no upper limits on a, b, c (i.e., they could go up to any number), the problem would be easier. We could use stars and bars or something similar. But since each variable is capped at 10, we have to adjust for those upper bounds. And then also consider the lower bound of the sum being 10.First, let's recall how to count the number of solutions to a + b + c = N where 0 ≤ a, b, c ≤ 10. The standard approach for this kind of problem is inclusion-exclusion. Without any upper limits, the number of non-negative integer solutions to a + b + c = N is C(N + 2, 2). But since each variable can't exceed 10, we need to subtract the cases where one or more variables exceed 10.However, in this problem, we need to do this for all N from 10 to 20 and sum them up. Alternatively, maybe there's a smarter way to compute the total number of triples where the sum is between 10 and 20, considering the individual constraints on a, b, c.Alternatively, maybe it's easier to compute the total number of triples (a, b, c) with each between 0 and 10, which is 11 * 11 * 11 = 1331. Then subtract the number of triples where a + b + c < 10. But wait, the original problem says 10 ≤ a + b + c ≤ 20. So, total valid triples = total possible triples (1331) minus the triples where a + b + c < 10. That might be a better approach because computing the number of triples with sum less than 10 might be simpler.Alternatively, if we compute the number of triples with sum from 0 to 20 and subtract the ones from 0 to 9, but since each a, b, c is at most 10, the maximum possible sum is 30. But we are restricted to sum up to 20. Wait, the problem says 10 ≤ sum ≤20. So, perhaps compute the number of triples with sum between 10 and 20, considering that each variable can't exceed 10.Wait, maybe let's clarify. If a, b, c are each at most 10, then the maximum sum is 30, but the problem restricts the sum to be at most 20. So, actually, the upper limit on the sum is 20, but individual variables are still capped at 10. So, the problem is equivalent to finding the number of triples (a, b, c) with 0 ≤ a, b, c ≤10 and 10 ≤ a + b + c ≤20.So, one way to approach this is to compute the total number of triples with a + b + c ≤20 and subtract the number of triples with a + b + c ≤9. But wait, we need to compute the number of triples with 10 ≤ sum ≤20. So, total number with sum ≤20 minus total number with sum ≤9. But each of these totals needs to account for the individual variable constraints (0 ≤ a, b, c ≤10).But how do we compute the number of solutions to a + b + c ≤ N with 0 ≤ a, b, c ≤10? This seems a bit more complex. Alternatively, for each sum S from 10 to 20, compute the number of solutions to a + b + c = S with 0 ≤ a, b, c ≤10, and then sum those numbers.So, maybe proceed by calculating for each S from 10 to 20, the number of ordered triples (a, b, c) such that a + b + c = S and each a, b, c is between 0 and 10. Then add all these numbers together.To compute the number of solutions for a specific S, we can use inclusion-exclusion. The formula for the number of non-negative integer solutions to a + b + c = S without any upper limits is C(S + 2, 2). Then, subtract the cases where any variable exceeds 10. Since the maximum a can be is 10, if we let a' = a - 11, then a' ≥0, and the equation becomes a' + b + c = S - 11. The number of solutions where a >10 is C((S - 11) + 2, 2) if S - 11 ≥0, otherwise 0. Similarly for b and c. Then, we need to add back the cases where two variables exceed 10, since we subtracted them twice. So, if both a and b exceed 10, then set a' = a -11, b' = b -11, and the equation becomes a' + b' + c = S - 22. The number of solutions is C((S -22) + 2, 2) if S -22 ≥0, otherwise 0. Similarly for other pairs. Finally, subtract the cases where all three variables exceed 10, which would be C((S - 33) + 2, 2) if S -33 ≥0. So, putting it all together:For each S, the number of solutions is:C(S + 2, 2) - 3*C(S -11 + 2, 2) + 3*C(S -22 + 2, 2) - C(S -33 + 2, 2)But each term is only present if the argument is non-negative. So, for each S from 10 to 20, compute this expression.Let me verify this formula. For example, when S is 10:Number of solutions = C(12, 2) - 3*C(10 -11 + 2, 2) + 3*C(10 -22 + 2, 2) - C(10 -33 + 2, 2)But C(10 -11 + 2, 2) = C(1, 2) = 0 because 1 < 2. Similarly, other terms where S -11 is negative would be zero. So for S=10, it's C(12,2) - 0 + 0 -0 = 66. Then, check if that's correct. The number of solutions to a + b + c =10 with 0 ≤a,b,c ≤10. Since 10 is less than 3*10=30, and each variable is at most 10, but 10 is the sum. Since each variable is non-negative, there's no overlap where variables exceed 10 here. So, the number should indeed be C(12,2)=66. That makes sense.Similarly, for S=20:Number of solutions = C(22,2) - 3*C(20 -11 + 2,2) + 3*C(20 -22 +2,2) - C(20 -33 +2,2)C(22,2)=231C(20-11+2,2)=C(11,2)=55C(20-22+2,2)=C(0,2)=0C(negative) =0So, 231 -3*55 +0 -0=231-165=66.Wait, is that correct? For S=20, the number of solutions with a,b,c ≤10. Since 20 is the sum, and each variable can be at most 10. So, for example, if all three variables are 10, their sum is 30, which is over 20. But to get 20, we need two variables at 10 and the third at 0. Wait, no. Wait, 10 +10 +0=20, but also 10+9+1=20, etc. Wait, but how many solutions are there?Alternatively, compute the number of solutions to a + b + c =20 with 0 ≤a,b,c ≤10.Using inclusion-exclusion:First, total solutions without restrictions: C(20 +2,2)=C(22,2)=231.Subtract solutions where a >10, b>10, c>10.Each of these is C(20 -11 +2,2)=C(11,2)=55, so 3*55=165.But now, we subtracted too much. If two variables are greater than 10, say a>10 and b>10, then we need to add those back. The number of such solutions is C(20 -22 +2,2)=C(0,2)=0. Similarly for other pairs. So add 3*0=0.Then, subtract the case where all three variables are greater than 10: C(20 -33 +2,2)=C(-11,2)=0. So total is 231 -165 +0 -0=66. So, that's correct. So the formula works here. So for S=20, there are 66 solutions.Therefore, the formula seems to hold. So, for each S from 10 to20, compute:C(S +2,2) -3*C(S -11 +2,2) +3*C(S -22 +2,2) -C(S -33 +2,2)But note that when S -11 +2 is less than 2, the combination is zero. Similarly for others. So let's compute this for each S from 10 to20.Alternatively, since S ranges from 10 to20, let's see:For S=10:C(12,2) - 3*C(1,2) +3*C(-10,2) -C(-21,2) = 66 - 0 +0 -0=66For S=11:C(13,2) -3*C(2,2)=78 -3*1=75For S=12:C(14,2)-3*C(3,2)=91 -3*3=91-9=82For S=13:C(15,2)-3*C(4,2)=105 -3*6=105-18=87For S=14:C(16,2)-3*C(5,2)=120 -3*10=120-30=90For S=15:C(17,2)-3*C(6,2)=136 -3*15=136-45=91For S=16:C(18,2)-3*C(7,2)=153 -3*21=153-63=90Wait, C(7,2)=21, so 3*21=63. 153-63=90. Correct.For S=17:C(19,2)-3*C(8,2)=171 -3*28=171-84=87C(8,2)=28, 3*28=84. 171-84=87.For S=18:C(20,2)-3*C(9,2)=190 -3*36=190-108=82C(9,2)=36, 3*36=108. 190-108=82.For S=19:C(21,2)-3*C(10,2)=210 -3*45=210-135=75C(10,2)=45, 3*45=135. 210-135=75.For S=20:C(22,2)-3*C(11,2)=231 -3*55=231-165=66Which we already checked earlier.So, the numbers for each S from 10 to20 are:S=10:6611:7512:8213:8714:9015:9116:9017:8718:8219:7520:66Now, let's sum all these numbers up. Let's compute the total.Start adding sequentially:Start with S=10:66Total=66Add S=11:66+75=141Add S=12:141+82=223Add S=13:223+87=310Add S=14:310+90=400Add S=15:400+91=491Add S=16:491+90=581Add S=17:581+87=668Add S=18:668+82=750Add S=19:750+75=825Add S=20:825+66=891So, total number of ordered triples is 891.Wait, but let's check the arithmetic again step by step to make sure:Start:66 (S=10)+75 (S=11): 66 +75=141+82 (S=12):141 +82=223+87 (S=13):223 +87=310+90 (S=14):310 +90=400+91 (S=15):400 +91=491+90 (S=16):491 +90=581+87 (S=17):581 +87=668+82 (S=18):668 +82=750+75 (S=19):750 +75=825+66 (S=20):825 +66=891Yes, that seems correct.But wait, let's check if there's an alternative way. Maybe using generating functions.The generating function for each variable is (1 + x + x^2 + ... +x^10). So, the generating function for three variables is (1 + x + x^2 + ... +x^10)^3.We need the sum of the coefficients from x^10 to x^20 in this generating function.Alternatively, since the full generating function is ( (1 - x^11)/(1 - x) )^3.So, the coefficient of x^S in this is the same as the number of solutions we calculated earlier for each S.Therefore, the sum from S=10 to20 of the coefficient of x^S is equal to the sum we just calculated, which is 891.Alternatively, if we compute the total number of triples (a, b, c) with 0 ≤a,b,c ≤10, which is 11^3=1331. Then subtract the number of triples where a + b + c ≤9 and the number where a + b + c ≥21. But since we need 10 ≤ sum ≤20, then total is 1331 - (number with sum ≤9 + number with sum ≥21).But maybe this approach is also possible.First, compute the number of triples with sum ≤9.Similarly, using the same inclusion-exclusion, but now for sums from 0 to9.Alternatively, using the same formula for each S from0 to9, compute the number of solutions, then sum them up.Alternatively, use generating functions again.But let's see.Compute number of triples with sum ≤9.For each S from0 to9, compute the number of solutions to a + b + c =S, 0 ≤a,b,c ≤10.But since S ≤9 and each variable is at least0, there is no way any variable exceeds10 here. Because if a ≥11, then the sum would be at least11. But S is at most9, so all variables are at most9. Therefore, the constraints 0 ≤a,b,c ≤10 are automatically satisfied. Therefore, for S ≤9, the number of solutions is C(S +2,2). So the number of triples with sum ≤9 is the sum from S=0 to9 of C(S +2,2).Which is equal to the sum from n=2 to11 of C(n,2). Wait, let's see.Sum_{S=0}^9 C(S +2, 2) = Sum_{k=2}^{11} C(k,2) where k = S +2.The formula for the sum of combinations C(k,2) from k=2 to n is C(n+1,3). So here, n=11, so sum is C(12,3)=220.Therefore, the number of triples with sum ≤9 is 220.Similarly, the number of triples with sum ≥21. Since total triples is 1331, and the number with sum ≤20 is 1331 - number with sum ≥21.But the problem is asking for the number with sum between10 and20 inclusive, which would be 1331 - (number with sum ≤9 + number with sum ≥21).But how do we compute number with sum ≥21?Alternatively, note that the number of triples with sum ≥21 is equal to the number of triples with sum ≤9 by symmetry. Because if we let a' =10 -a, b'=10 -b, c'=10 -c, then a' + b' + c' =30 - (a + b + c). So, if a + b + c ≥21, then a' + b' + c' ≤9. Therefore, the number of triples with a + b + c ≥21 is equal to the number with a' + b' + c' ≤9, which is the same as the number with a + b + c ≤9. Hence, 220.Therefore, the number of triples with sum ≥21 is 220. Therefore, the number of triples with 10 ≤ sum ≤20 is 1331 -220 -220=1331 -440=891.Which matches the previous result.Therefore, the answer should be 891. Let me just confirm.Yes, using two different methods: direct summation of the inclusion-exclusion results for each S from10 to20, and using symmetry to find that the number of triples with sum ≥21 is equal to the number with sum ≤9, each being 220, so subtracting 220 +220=440 from 1331 gives 891. Both methods give the same result, so that's reassuring.Therefore, the number of ordered triples is 891.Final AnswerThe number of ordered triples is boxed{891}.</think>To find the number of ordered triples ((a, b, c)) such that (0 leq a, b, c leq 10) and (10 leq a + b + c leq 20), we can use the following approach:1. Total number of ordered triples: The total number of ordered triples ((a, b, c)) where each (a, b, c) is between 0 and 10 inclusive is (11 times 11 times 11 = 1331).2. Number of triples with sum less than 10: Using the formula for the sum of combinations, we find the number of solutions to (a + b + c leq 9). This is equivalent to the sum of combinations (C(S + 2, 2)) for (S) from 0 to 9, which is (C(12, 3) = 220).3. Symmetry argument for sum greater than 20: By symmetry, the number of triples where (a + b + c geq 21) is the same as the number of triples where (a + b + c leq 9), which is also 220.4. Subtracting invalid cases: The number of valid triples with (10 leq a + b + c leq 20) is the total number of triples minus the cases where the sum is less than 10 or greater than 20: [ 1331 - 220 - 220 = 891 ]Thus, the number of ordered triples ((a, b, c)) that satisfy the given conditions is (boxed{891}).,<think>Okay, so I have this problem here where I need to find the number of ordered triples (a, b, c) such that each of a, b, c is an integer between 0 and 10 inclusive. But there's an additional condition: the sum a + b + c has to be between 10 and 20 inclusive. Hmm, let me try to break this down.First, I remember that when counting the number of solutions to equations with constraints, generating functions or stars and bars might be useful. But let me start by understanding the problem step by step.The variables a, b, c are integers where each is at least 0 and at most 10. Without any sum constraints, the total number of ordered triples would just be 11 * 11 * 11 = 1331, since each can independently be from 0 to 10. But here, we need to consider only those triples where their sum is between 10 and 20. So, essentially, we need to subtract the cases where the sum is less than 10 or more than 20. Wait, but maybe it's easier to compute the total number of triples with sum between 0 and 20 and then subtract those with sum less than 10. But actually, since the upper bound is 20, and the maximum possible sum when each is 10 is 30. Wait, but the problem says 10 ≤ a + b + c ≤ 20, so maybe another approach is needed.Alternatively, maybe compute the number of triples where a + b + c ≤ 20 and subtract the number of triples where a + b + c ≤ 9. That way, we get the number of triples where the sum is between 10 and 20 inclusive. But I need to remember that each of a, b, c can't exceed 10. So, even when calculating the number of solutions for a + b + c ≤ 20, we have to consider the upper limits on a, b, c. Similarly, when calculating a + b + c ≤ 9, but since 9 is less than 30, maybe the upper limits on a, b, c don't affect that case? Wait, but each variable is at most 10. So even for sums less than 10, the variables can't exceed 10, but since the sum is low, maybe the upper limits don't restrict the solutions. Hmm, maybe.Let me recall the stars and bars formula. The number of non-negative integer solutions to a + b + c ≤ N is C(N + 3, 3). But this is when there's no upper limit on the variables. But here, each variable is at most 10. So, the standard stars and bars counts all solutions without considering the upper limits. Therefore, to account for the upper limits, we need to use inclusion-exclusion. But that complicates things.Alternatively, maybe it's easier to compute the number of solutions with a + b + c ≤ 20 and subtract the number of solutions where at least one variable exceeds 10. Then, similarly for a + b + c ≤ 9. Wait, but this might get complicated. Let me structure this properly.Let me denote S(N) as the number of ordered triples (a, b, c) where a, b, c are integers between 0 and 10 inclusive, and a + b + c ≤ N. Then, the number we need is S(20) - S(9). So, if I can compute S(20) and S(9), then subtract them to get the desired count.To compute S(N), which is the number of non-negative integer solutions to a + b + c ≤ N with each a, b, c ≤ 10.The standard approach for such problems is inclusion-exclusion. The formula for the number of non-negative integer solutions to x1 + x2 + ... + xk ≤ N with each xi ≤ m is equal to:Sum_{i=0}^floor((k*(m+1))/N) (-1)^i * C(k, i) * C(N - i*(m + 1) + k, k)Wait, maybe I need to recall the inclusion-exclusion formula for bounded variables.Alternatively, since we have three variables, maybe it's manageable.For three variables a, b, c each at most 10, the number of solutions to a + b + c ≤ N is equal to the number of non-negative solutions without upper bounds minus the number of solutions where at least one variable exceeds 10.So, first, compute the number of solutions to a + b + c ≤ N with a, b, c ≥ 0. That's C(N + 3, 3). But then subtract the cases where a > 10, or b > 10, or c > 10. But since inclusion-exclusion requires adding back cases where two variables exceed 10, etc.So, using inclusion-exclusion:S(N) = C(N + 3, 3) - 3*C(N - 11 + 3, 3) + 3*C(N - 22 + 3, 3) - C(N - 33 + 3, 3)But this is only valid when N - 11 ≥ 0, otherwise the terms where we subtract 11 become zero. Similarly, for higher terms. So, this formula is piecewise.Wait, let me think again. For each variable exceeding 10, let's say a > 10. Then, set a' = a - 11, so a' ≥ 0. Then, the equation becomes a' + 11 + b + c ≤ N, so a' + b + c ≤ N - 11. The number of solutions for this is C((N - 11) + 3, 3). But if N - 11 is negative, this term is zero. Similarly, if two variables exceed 10, say a > 10 and b > 10, then set a' = a - 11, b' = b - 11, so a' + b' + 11 + 11 + c ≤ N => a' + b' + c ≤ N - 22. The number of solutions is C((N - 22) + 3, 3). Again, if N - 22 is negative, this is zero. Similarly, if all three variables exceed 10, then N - 33 must be non-negative, so C(N - 33 + 3, 3). Thus, the formula becomes:S(N) = C(N + 3, 3) - 3*C(N - 11 + 3, 3) + 3*C(N - 22 + 3, 3) - C(N - 33 + 3, 3)But each term is only present if the argument inside the combination is non-negative. So, for each term:- The first term is always C(N + 3, 3) as long as N ≥ 0.- The second term, -3*C(N - 8, 3), exists only if N - 11 + 3 ≥ 0 => N ≥ 8. Wait, hold on, the formula is C((N - 11) + 3, 3) = C(N - 8, 3). Wait, but is that correct?Wait, if you set a variable to exceed 10, say a >= 11, then substitute a' = a - 11, then the equation becomes a' + b + c <= N - 11. So the number of solutions is C((N - 11) + 3, 3), but only if N - 11 >= 0. So when N - 11 >= 0, i.e., N >= 11. Otherwise, if N - 11 < 0, then there are no solutions where a >= 11, so the term is zero.Similarly, for two variables exceeding 10: substituting both a and b, we get a' + b' + c <= N - 22. So the number of solutions is C((N - 22) + 3, 3) if N - 22 >= 0, i.e., N >= 22. Otherwise, zero.For three variables exceeding 10: a', b', c' >= 0, so a' + b' + c' <= N - 33. So this term is C((N - 33) + 3, 3) if N >= 33, otherwise zero.Therefore, the formula is:S(N) = C(N + 3, 3) - 3*C(N - 8, 3) + 3*C(N - 19, 3) - C(N - 30, 3)Wait, wait, let me check again. If N - 11 is the adjusted sum, then:Wait, when we subtract 11 from N for one variable, then the new sum is N - 11. The number of solutions is C((N - 11) + 3 - 1, 3 - 1)? Wait, no. Wait, the number of non-negative integer solutions to a' + b + c <= N - 11 is C((N - 11) + 3, 3). Because the formula for a + b + c <= M is C(M + 3, 3). So, substituting M = N - 11, that's C(N - 11 + 3, 3) = C(N - 8, 3). So yes, so that term is C(N - 8, 3). Similarly, for two variables exceeding 10, it's C(N - 22 + 3, 3) = C(N - 19, 3), and for three variables, C(N - 33 + 3, 3) = C(N - 30, 3). Therefore, S(N) is:S(N) = C(N + 3, 3) - 3*C(N - 8, 3) + 3*C(N - 19, 3) - C(N - 30, 3)But each of these terms is only added if the argument inside the combination is non-negative. For example, if N - 8 < 0, then C(N - 8, 3) is zero.So, applying this formula to compute S(20) and S(9).First, let's compute S(20):S(20) = C(23, 3) - 3*C(12, 3) + 3*C(1, 3) - C(-10, 3)But C(1, 3) is zero because 1 < 3, and C(-10, 3) is also zero. So,S(20) = C(23, 3) - 3*C(12, 3)Compute C(23,3):C(23,3) = 23*22*21 / 6 = (23*22*21)/623*22 = 506, 506*21 = 10626, 10626 / 6 = 1771.C(12,3) = 12*11*10 / 6 = 220.So,S(20) = 1771 - 3*220 = 1771 - 660 = 1111.Wait, but let me check the arithmetic:3*220 = 660. 1771 - 660 is 1111. Hmm.Now, compute S(9):S(9) = C(12, 3) - 3*C(1, 3) + 3*C(-10, 3) - C(-21, 3)Again, C(1,3) and the rest are zero except the first term. So,S(9) = C(12, 3) = 220.Therefore, the number of ordered triples with sum between 10 and 20 inclusive is S(20) - S(9) = 1111 - 220 = 891.Wait, so the answer is 891? Hmm. But let me verify this with another approach to be sure.Alternatively, maybe compute the number of triples where the sum is exactly k, for k from 10 to 20, and sum those numbers. Each term can be calculated using inclusion-exclusion as well.But that might take longer, but let me try for a few values to check.For example, let's compute the number of triples where a + b + c = 10, with each a, b, c <=10.Using stars and bars without constraints: C(10 + 3 - 1, 3 -1) = C(12, 2) = 66. But since 10 is less than 3*10=30, and each variable can be at most 10, but 10 is the sum. Since 10 is less than or equal to 10, so all variables can't exceed 10. Wait, if the sum is 10, each variable is at most 10, since 10 is the maximum any single variable can be, but if the sum is 10, each variable is at most 10 automatically. So, no need for inclusion-exclusion here.Wait, so for sums from 0 to 30, but when the sum is less than or equal to 10, the upper bounds of 10 on each variable don't affect the count. Because even if one variable is 10, the other two must be 0. So, for example, sum =10, the maximum any variable can be is 10, but that's allowed. So the number of solutions for sum=10 is C(10 + 3 -1, 3 -1) = C(12,2) = 66. Similarly, for sum=11, the number is C(13,2) = 78. Wait, but is that correct? Wait, the standard stars and bars formula counts the number of non-negative integer solutions, which is C(n + k -1, k -1) for sum n. But if there are upper bounds on variables, we need to subtract the cases where variables exceed the bounds.But in this case, when the sum is 10, even if one variable is 10, the others are 0, so no variable exceeds 10. Therefore, for sums from 0 to 10, the upper bounds of 10 don't restrict the solutions. Therefore, the number of ordered triples with sum exactly k (0 ≤k ≤10) is C(k + 2, 2). So, for k from 0 to 10, the total number is sum_{k=0}^{10} C(k + 2, 2). Which is equal to C(13,3) = 286. Wait, because the sum of C(k + 2, 2) from k=0 to n is C(n + 3, 3). So, sum_{k=0}^{10} C(k + 2, 2) = C(13,3) = 286. But earlier, S(9) was calculated as 220. Wait, but S(9) is the number of triples with sum ≤9. So sum_{k=0}^9 C(k + 2, 2) = C(12, 3) = 220, which matches the previous calculation. Therefore, S(10) would be 220 + C(12,2)=220 + 66=286. So, that's correct.But when the sum is greater than 10, say 11, then we might have variables exceeding 10. For example, if a=11, but the sum is 11, then the other variables must be 0, but a can't be 11 because the maximum is 10. Therefore, for sums from 11 to 20, we need to subtract the cases where any variable exceeds 10.Therefore, for each k from 11 to 20, the number of solutions is C(k + 2, 2) - 3*C(k - 11 + 2, 2). Because if we subtract the cases where a variable exceeds 10. So, for each variable exceeding 10, set a' = a -11, then a' + b + c = k -11. The number of solutions where a >10 is C(k -11 + 2, 2), but only if k -11 ≥0. So, for k >=11, this is valid. Then, since there are 3 variables, we subtract 3*C(k -9, 2). But wait, when we set a' = a -11, then a' + b + c = k -11. So, the number of solutions is C((k -11) + 2, 2) = C(k -9, 2). Therefore, the number of solutions without any variable exceeding 10 is C(k + 2, 2) - 3*C(k -9, 2). However, if k -9 <0, then C(k -9, 2)=0.But for k >=11, k -9 >=2, so it's valid. For example, k=11: C(13,2) - 3*C(2,2) =78 -3*1=75. Similarly, k=12: C(14,2) -3*C(3,2)=91 - 3*3=91-9=82. Wait, but do we need to consider cases where two variables exceed 10? For example, if the sum is 22, then two variables could be 11 each, but since our upper limit is 10, but in our problem, we are considering sums up to 20, so even for k=20, the maximum sum, the only way two variables exceed 10 is if each is at least 11, so 11 +11 +8=30, which is way over 20. Wait, but if the sum is 20, could two variables be over 10? Let's see, suppose a=11, b=11, then c=20 -11 -11= -2, which is invalid. So, actually, for sums up to 20, two variables cannot both exceed 10 because 11 +11=22, which already exceeds 20. Therefore, in the inclusion-exclusion principle, the correction term for two variables exceeding 10 would only be necessary if the sum is at least 22. But since our upper bound is 20, we don't have to consider two variables exceeding 10. Therefore, for sums from 11 to 20, the number of solutions is C(k + 2, 2) - 3*C(k -9, 2). Thus, the total number of triples with sum from 11 to 20 is sum_{k=11}^{20}[C(k + 2, 2) - 3*C(k -9, 2)].Alternatively, let's compute this sum. Let me denote the total as T = sum_{k=11}^{20}[C(k + 2, 2) - 3*C(k -9, 2)].First, compute sum_{k=11}^{20} C(k + 2, 2). This is equal to sum_{m=13}^{22} C(m, 2), where m = k + 2. The sum of C(m, 2) from m=13 to 22 is equal to [C(23,3) - C(13,3)]. Because the sum of C(m,2) from m=2 to n is C(n+1,3). Therefore, sum_{m=13}^{22} C(m,2) = C(23,3) - C(13,3).Compute C(23,3) = 1771, as before. C(13,3) = 286. So, 1771 - 286 = 1485.Then, compute sum_{k=11}^{20} 3*C(k -9, 2). Let k -9 = t, so when k=11, t=2; k=20, t=11. So sum_{t=2}^{11} 3*C(t,2) = 3*sum_{t=2}^{11} C(t,2) = 3*[C(12,3) - C(2,3)]. But C(2,3)=0. So, sum_{t=2}^{11} C(t,2) = C(12,3) - C(2,3) = 220 - 0 = 220. Therefore, 3*220=660.Therefore, T = 1485 - 660 = 825. Wait, but earlier we had 891. Hmm, this contradicts the previous result. So, which one is correct?Alternatively, let's check both approaches.First approach: S(20) - S(9) = 1111 - 220 = 891.Second approach: Sum from k=10 to 20, but wait, no. Wait, the first approach gives S(20) - S(9) which is the number of triples with sum from 10 to 20 inclusive. But in the second approach, when we considered the sum from 11 to 20, we got 825, but we also need to include k=10. The number of triples with sum=10 is 66. So total would be 825 + 66=891. Which matches the first approach. So, there was a confusion in the second approach where initially I thought of summing from 11 to 20, but actually, the problem includes sum=10. So, the second approach, when including k=10 (66) and the sum from 11 to 20 (825) gives 891, which matches the first approach. Therefore, 891 is the correct answer.But to verify further, let me compute S(20) again using inclusion-exclusion. S(20) = C(23,3) - 3*C(12,3) + 3*C(1,3) - C(-10,3). As C(1,3)=0 and C(-10,3)=0, so S(20)=1771 -3*220=1771 -660=1111. Then S(9)=C(12,3)=220. So 1111 -220=891. That seems correct.Alternatively, let's compute the number of triples with sum between 10 and 20 inclusive by another method.Another way is to note that the total number of triples with each variable between 0 and 10 is 11^3=1331. Then, subtract the number of triples where the sum is less than 10 and the number where the sum is more than 20. Wait, but the problem states 10 ≤ sum ≤20, so we need to exclude sum <10 and sum >20. But the maximum possible sum is 30 (when all are 10). However, we need to compute the number of triples where sum >20, i.e., sum from 21 to 30. But due to symmetry, maybe there's a relationship between the number of triples with sum S and sum 30 - S. Let me check.For each triple (a, b, c), consider the complementary triple (10 - a, 10 - b, 10 - c). The sum of the original triple is S = a + b + c, and the sum of the complementary triple is 30 - S. So, there's a bijection between triples with sum S and triples with sum 30 - S. Therefore, the number of triples with sum S is equal to the number of triples with sum 30 - S. Therefore, the number of triples with sum >20 (i.e., 21 to 30) is equal to the number of triples with sum <10 (i.e., 0 to 9). Therefore, the total number of triples with sum outside 10 to20 is 2*S(9). Therefore, the number of triples with sum between 10 and20 is 1331 - 2*220=1331 -440=891. Which confirms the previous result.Therefore, this symmetry argument is a much more straightforward way to compute the answer. Since the number of triples with sum >20 is equal to the number with sum <10, and we already calculated S(9)=220, so 1331 - 220 -220=891.Yes, this is a good check. So, all methods lead to 891. Therefore, I can be confident that the answer is 891.Final AnswerThe number of ordered triples is boxed{891} groups.</think>To find the number of ordered triples ((a, b, c)) such that (0 leqslant a, b, c leqslant 10) and (10 leqslant a + b + c leqslant 20), we can use the principle of inclusion-exclusion and symmetry.1. Total number of ordered triples without sum constraints: [ 11 times 11 times 11 = 1331 ]2. Number of triples with sum less than 10: Using the stars and bars method, the number of non-negative integer solutions to (a + b + c leq 9) is given by: [ binom{9 + 3}{3} = binom{12}{3} = 220 ]3. Symmetry argument: The number of triples with sum greater than 20 (i.e., 21 to 30) is equal to the number of triples with sum less than 10 due to the bijection between triples ((a, b, c)) and ((10 - a, 10 - b, 10 - c)). Thus, the number of triples with sum greater than 20 is also 220.4. Subtract the invalid cases: The number of valid triples with sum between 10 and 20 inclusive is: [ 1331 - 2 times 220 = 1331 - 440 = 891 ]Thus, the number of ordered triples ((a, b, c)) that satisfy the condition is (boxed{891}).]

🔑:When c=0, 10 leqslant a+b leqslant 20, (a, b) has 11+10+cdots+1=66 pairs; when c=1, 9 leqslant a+b leqslant 19, (a, b) has 10+11+10+cdots+2=75 pairs; when c=2, 8 leqslant a+b leqslant 18, (a, b) has 9+10+11+10+cdots+3=82 pairs; cdots; when c=10, 0 leqslant a+b leqslant 10, (a, b) has 11+10+cdots+1=66 pairs. Therefore, the number of ordered triples (a, b, c) that satisfy the condition is 2 times(66+75+82+87+90)+91=891.

🧠:[<think>Okay, so I need to figure out the value of λ (lambda) that minimizes the area of a polygon formed by points dividing each side of an original polygon in the ratio λ. The original polygon is labeled A₁A₂…Aₙ, and each side is divided in the same ratio λ. The question is asking for which λ the area of this new polygon is the smallest.First, let me visualize the problem. Suppose we have a polygon, say a triangle or a quadrilateral. On each side, there's a point that divides the side in the ratio λ. Then, connecting these points in order forms a new polygon inside the original one. The goal is to find the λ that makes the area of this inner polygon as small as possible.Wait, the problem says "the same ratio λ" but it doesn't specify whether it's the ratio of the segment from the starting vertex to the division point over the entire side, or the other way around. Hmm. Usually, when a point divides a segment in a ratio λ, it can be interpreted as λ:1 from the starting point. For example, if a point divides side A₁A₂ in the ratio λ, then A₁ to the division point is λ parts, and the division point to A₂ is 1 part, so the total length is λ + 1 parts. Therefore, λ would be the ratio of the first segment to the entire side. But I need to confirm this.Alternatively, maybe it's the ratio of the division point to the entire side. For example, if λ is 1/2, then each division point is the midpoint, and the new polygon would be similar to the original but scaled down. However, in that case, the area would be (1/2)² = 1/4 of the original area for a square, but perhaps for a general polygon, it's scaled by some factor. However, the problem states that the polygon is "bounded by points that divide the sides... in the same ratio λ." So I think that ratio is consistent across all sides.But to minimize confusion, let's clarify. Suppose on each side A_iA_{i+1}, the division point is such that A_i to the point is λ times the length of A_iA_{i+1}, and the point to A_{i+1} is (1 - λ) times the length. Wait, but that would mean the ratio is λ/(1 - λ). Alternatively, if the division is in the ratio λ:1, then the division point is λ/(1 + λ) from A_i and 1/(1 + λ) from A_{i+1}. Hmm, so the exact definition of λ matters here.Wait, the problem says "divide the sides A₁A₂, A₂A₃, ..., AₙA₁ in the same ratio λ". The term "ratio λ" can be ambiguous. In coordinate geometry, when a point divides a segment in the ratio λ, it's usually the ratio of the lengths from the starting point to the division point over the division point to the endpoint. So if the division ratio is λ:1, then the division point is λ/(λ + 1) from the starting point. But maybe here, the problem is using λ as the fraction from the starting point. So if λ is 0.3, then each division point is 30% from A_i towards A_{i+1}.Alternatively, perhaps the problem is using the ratio as the portion from the starting vertex, so λ is the fraction of the side length from A_i to the division point. For example, if λ = 1/3, then each division point is 1/3 of the way from A_i to A_{i+1}. Then the remaining part is 2/3. So in that case, the ratio would be 1:2. But the problem states the same ratio λ, so perhaps it's that ratio.Wait, the problem is a bit ambiguous. But since it's a standard problem, perhaps they mean that each division point divides the side in the ratio λ:1, so that the division is λ parts from the starting point and 1 part towards the ending point, so the total parts are λ + 1. Therefore, the division point is located at a distance of λ/(λ + 1) from the starting vertex. However, since the problem is asking for which λ the area is minimized, perhaps we need to parametrize accordingly.Alternatively, maybe λ is the fraction of the side from the starting vertex. So if λ is 0.3, then each division point is 30% along each side from the starting vertex, which would make the ratio 3:7 (since 0.3:0.7 is 3:7). But again, the problem states "the same ratio λ". Hmm.Wait, let's check some known results. For a polygon, if you connect points that divide each side in the ratio k:1, then the area of the inner polygon can be expressed in terms of k. For example, for a triangle, if you connect points dividing each side in the ratio k:1, the area ratio is (k^2 - k + 1)/(k + 1)^2. To find the minimum area, take the derivative with respect to k and set it to zero. However, this might be specific to triangles.But the problem is about a general polygon. So perhaps the answer is the same for any polygon? Wait, but maybe not. For example, in a square, if you connect points dividing each side in ratio λ:1, the inner figure is another quadrilateral, perhaps a square or a rectangle. The area might be a different function.Wait, but maybe for any convex polygon, the area of the inner polygon formed by dividing each side in ratio λ:1 (from the vertex) is a linear transformation of the original polygon. If the division is affine, then the area scaling factor would be the determinant of the linear transformation. However, since the division is the same ratio on each side, maybe the scaling factor is (λ)^n or something?Wait, perhaps not. Let me think again. For a triangle, if you connect points that divide each side in the ratio λ:1 (from each vertex), then the inner triangle is similar to the original triangle with a scaling factor. The scaling factor can be calculated using the ratio of the areas.But in general, for any polygon, if you connect points that are a fixed ratio along each side, the resulting polygon's area can be expressed as a function of λ. The minimal area occurs when the derivative of this function with respect to λ is zero.Alternatively, perhaps there's a geometric interpretation. For example, when λ is 0, all the division points are at the original vertices, so the area collapses. Similarly, when λ is 1, the division points are at the next vertices, so again the area collapses. Therefore, the area as a function of λ is a quadratic or some function that has a minimum in between.Wait, but when λ = 0, all the points are at A₁, A₂, etc., so the polygon becomes the original polygon? Wait, no. Wait, if λ is the ratio from the starting vertex, then when λ = 0, the division point is at the starting vertex. So for each side, the division point is at A_i. Therefore, the polygon formed by connecting all A_i would just be the original polygon. Similarly, when λ = 1, the division points would be at the next vertex. For example, on side A₁A₂, if λ = 1, then the division point is at A₂. Similarly for all sides, so the polygon formed is the original polygon again. Therefore, when λ is 0 or 1, the area is the same as the original polygon. So the area must be a function that starts at the original area when λ=0, decreases to a minimum, and then increases back to the original area when λ=1.Therefore, the minimal area occurs somewhere between λ=0 and λ=1. But the problem is asking for which λ this minimal area occurs.Alternatively, maybe it's symmetric around λ=1/2. For example, in a square, connecting midpoints (λ=1/2) gives another square with half the area. Wait, but the minimal area in that case is achieved at λ=1/2. But wait, if you connect midpoints, you get a square with half the area, but if you connect points closer to the vertices, maybe the inner square becomes smaller? Wait, no, in a square, connecting midpoints gives the smallest inner square. Wait, actually, connecting midpoints gives the inner square with area half of the original. If you connect points closer to the vertices, say λ=1/3, then the inner quadrilateral might be a smaller square? Wait, let's compute.Suppose we have a square with vertices at (0,0), (1,0), (1,1), (0,1). Let’s divide each side at λ from the starting vertex. So for the bottom side from (0,0) to (1,0), the division point is at (λ, 0). Similarly, the right side from (1,0) to (1,1) would have a division point at (1, λ). The top side from (1,1) to (0,1) would have a division point at (1 - λ, 1), and the left side from (0,1) to (0,0) would have a division point at (0, 1 - λ). Connecting these four points gives a quadrilateral.Let me calculate the area of this quadrilateral. The coordinates of the four division points are (λ, 0), (1, λ), (1 - λ, 1), and (0, 1 - λ). To find the area of the quadrilateral formed by these points, we can use the shoelace formula.First, list the coordinates in order:(λ, 0), (1, λ), (1 - λ, 1), (0, 1 - λ), and back to (λ, 0).Applying the shoelace formula:Area = 1/2 | (λ*λ + 1*1 + (1 - λ)* (1 - λ) + 0*0 ) - (0*1 + λ*(1 - λ) + 1*0 + (1 - λ)*λ ) |.Wait, perhaps breaking it down step by step:Sum1 = (λ * λ) + (1 * 1) + ((1 - λ) * (1 - λ)) + (0 * 0)Sum2 = (0 * 1) + (λ * (1 - λ)) + (1 * 0) + ((1 - λ) * λ)But actually, the shoelace formula is:Area = 1/2 |sum_{i=1 to n} (x_i y_{i+1} - x_{i+1} y_i)|So for the four points:Point 1: (λ, 0)Point 2: (1, λ)Point 3: (1 - λ, 1)Point 4: (0, 1 - λ)Point 5: (λ, 0) (to close the polygon)Compute the terms:Term1: x1 y2 - y1 x2 = λ * λ - 0 * 1 = λ²Term2: x2 y3 - y2 x3 = 1 * 1 - λ * (1 - λ) = 1 - λ(1 - λ)Term3: x3 y4 - y3 x4 = (1 - λ) * (1 - λ) - 1 * 0 = (1 - λ)²Term4: x4 y5 - y4 x5 = 0 * 0 - (1 - λ) * λ = -λ(1 - λ)Term5: x5 y1 - y5 x1 = λ * 0 - 0 * λ = 0Summing these terms:Sum = λ² + [1 - λ(1 - λ)] + (1 - λ)² + [-λ(1 - λ)] + 0Simplify term by term:First term: λ²Second term: 1 - λ + λ²Third term: 1 - 2λ + λ²Fourth term: -λ + λ²Fifth term: 0Adding all together:λ² + 1 - λ + λ² + 1 - 2λ + λ² - λ + λ²Combine like terms:λ² terms: 1λ² +1λ² +1λ² +1λ² = 4λ²Constants: 1 +1 = 2Linear terms: -λ -2λ -λ = -4λSo total sum is 4λ² -4λ + 2Then area is 1/2 |4λ² -4λ + 2|. Since all terms are positive or depending on λ, but absolute value is not necessary here because the expression inside is always positive. Let's check discriminant: 16 - 32 = -16, so quadratic is always positive. Hence, area is 1/2 (4λ² -4λ + 2) = 2λ² -2λ +1So for the square, the area of the inner quadrilateral is 2λ² -2λ +1. To find the minimum, take derivative with respect to λ: dA/dλ = 4λ -2. Set to zero: 4λ -2 = 0 → λ = 2/4 = 1/2. So minimum at λ=1/2, and the minimal area is 2*(1/2)^2 -2*(1/2) +1 = 2*(1/4) -1 +1 = 0.5 -1 +1 = 0.5. So half the area of the original square (since original area is 1). So indeed, for a square, minimal area is achieved at λ=1/2.But this is just a square. What about other polygons?Wait, let's try with a triangle. Take an equilateral triangle with vertices at (0,0), (1,0), (0.5, sqrt(3)/2). Let's divide each side in ratio λ from each vertex. The coordinates of division points can be calculated.For side from (0,0) to (1,0), division point at (λ, 0).From (1,0) to (0.5, sqrt(3)/2), division point: moving λ from (1,0). The vector from (1,0) to (0.5, sqrt(3)/2) is (-0.5, sqrt(3)/2). So the division point is (1,0) + λ*(-0.5, sqrt(3)/2) = (1 - 0.5λ, 0 + (sqrt(3)/2)λ).Similarly, from (0.5, sqrt(3)/2) to (0,0), division point is (0.5, sqrt(3)/2) + λ*(-0.5, -sqrt(3)/2) = (0.5 - 0.5λ, sqrt(3)/2 - (sqrt(3)/2)λ).So the three division points are:A: (λ, 0)B: (1 - 0.5λ, (sqrt(3)/2)λ)C: (0.5 - 0.5λ, sqrt(3)/2 (1 - λ))Now, compute the area of triangle ABC.Using shoelace formula:Coordinates:A: (λ, 0)B: (1 - 0.5λ, (sqrt(3)/2)λ)C: (0.5 - 0.5λ, sqrt(3)/2 (1 - λ))Back to A: (λ, 0)Compute terms:Term1: x_A y_B - y_A x_B = λ * (sqrt(3)/2 λ) - 0 * (1 - 0.5λ) = (sqrt(3)/2) λ²Term2: x_B y_C - y_B x_C = (1 - 0.5λ) * (sqrt(3)/2 (1 - λ)) - (sqrt(3)/2 λ) * (0.5 - 0.5λ)Let me compute this step by step:First part: (1 - 0.5λ)(sqrt(3)/2 (1 - λ)) = sqrt(3)/2 (1 - 0.5λ)(1 - λ)Second part: (sqrt(3)/2 λ)(0.5 - 0.5λ) = sqrt(3)/2 λ (0.5 - 0.5λ)So Term2 = sqrt(3)/2 [(1 - 0.5λ)(1 - λ) - λ(0.5 - 0.5λ)]Let me expand the terms inside:First expand (1 - 0.5λ)(1 - λ):= 1*(1 - λ) - 0.5λ*(1 - λ)= 1 - λ - 0.5λ + 0.5λ²= 1 - 1.5λ + 0.5λ²Then subtract λ(0.5 - 0.5λ):= 0.5λ - 0.5λ²So overall:1 - 1.5λ + 0.5λ² - 0.5λ + 0.5λ²Combine like terms:Constant: 1λ terms: -1.5λ -0.5λ = -2λλ² terms: 0.5λ² + 0.5λ² = λ²So Term2 = sqrt(3)/2 (1 - 2λ + λ²)Term3: x_C y_A - y_C x_A = (0.5 - 0.5λ)*0 - (sqrt(3)/2 (1 - λ)) * λ = 0 - sqrt(3)/2 λ(1 - λ) = - sqrt(3)/2 λ(1 - λ)Summing all terms:Term1 + Term2 + Term3 = (sqrt(3)/2 λ²) + (sqrt(3)/2 (1 - 2λ + λ²)) - sqrt(3)/2 λ(1 - λ)Let me factor out sqrt(3)/2:sqrt(3)/2 [ λ² + (1 - 2λ + λ²) - λ(1 - λ) ]Simplify inside the brackets:First term: λ²Second term: 1 - 2λ + λ²Third term: -λ + λ²Adding together:λ² + 1 - 2λ + λ² - λ + λ²Combine like terms:λ² terms: 1λ² +1λ² +1λ² = 3λ²Constants: 1Linear terms: -2λ -1λ = -3λSo inside the brackets: 3λ² -3λ +1Therefore, total area is |sqrt(3)/2 (3λ² -3λ +1)| * 1/2 (since shoelace formula requires 1/2 times the absolute value). Wait, no: the shoelace formula is 1/2 times the absolute value of the sum of the terms. So in this case, the sum of the terms was sqrt(3)/2 (3λ² -3λ +1). Therefore, the area is 1/2 * sqrt(3)/2 (3λ² -3λ +1) = sqrt(3)/4 (3λ² -3λ +1)But the original area of the equilateral triangle with side length 1 is sqrt(3)/4. So the area ratio is (3λ² -3λ +1). So the inner triangle's area is (3λ² -3λ +1) times the original area.To find the minimum of 3λ² -3λ +1, take derivative: 6λ -3. Set to zero: 6λ -3 =0 → λ= 3/6=1/2. So minimal area at λ=1/2, which gives 3*(1/2)^2 -3*(1/2) +1= 3/4 -3/2 +1= (3/4 -6/4 +4/4)=1/4. So the inner triangle has 1/4 of the original area when λ=1/2.Therefore, for both the square and the triangle, the minimal area occurs at λ=1/2. Interesting. Maybe this is a general result for any polygon?Wait, so perhaps for any polygon, connecting the midpoints (λ=1/2) of each side gives the inner polygon with minimal area. But wait, for a regular polygon, connecting midpoints gives a similar polygon scaled down, but does this hold for any polygon?Alternatively, perhaps for any convex polygon, connecting the midpoints gives the minimal area. Wait, but is that true? Let me think.Suppose we have a convex polygon. If we connect points that divide the sides in ratio λ, then the inner polygon's area can be considered as a function of λ. The previous examples with triangle and square both had minima at λ=1/2. So maybe in general, regardless of the polygon, the minimal area occurs at λ=1/2.Alternatively, perhaps there's a linear algebra approach here. If each division point is a linear combination of the original vertices, then the inner polygon can be thought of as a linear transformation of the original. However, area scaling factors depend on the determinant of the transformation matrix. But since each division is a linear interpolation between two vertices, maybe the transformation is a similarity transformation with scaling factor (1 - 2λ) or something? Wait, not sure.Alternatively, in barycentric coordinates, each point on a side can be represented as (1 - λ)A_i + λA_{i+1}. If we connect these points, the resulting polygon can be considered as a linear combination of the original polygon's vertices. However, the exact relationship between λ and the area might require more detailed analysis.But given that both the square and the triangle have their minimal areas at λ=1/2, maybe this is a general result. Let me test another polygon, say a regular pentagon. However, computing the area for a regular pentagon with points dividing sides in ratio λ might be tedious. Alternatively, think about affine transformations. If we can show that for any polygon, the area function A(λ) is a quadratic function with minimum at λ=1/2, then that would answer the question.Wait, the examples of triangle and square both resulted in the area being a quadratic function of λ, with minima at 1/2. For the square, the area was 2λ² -2λ +1, derivative 4λ -2, minimum at 1/2. For the triangle, the area ratio was 3λ² -3λ +1, derivative 6λ -3, minimum at 1/2. So in both cases, the quadratic is symmetric around λ=1/2. Therefore, maybe for any polygon, the area as a function of λ is a quadratic with minimum at 1/2.But why is that? Is there a general reason?Alternatively, think of the problem in terms of linear algebra. Suppose we have a polygon with vertices A₁, A₂, ..., Aₙ. Each side A_iA_{i+1} is divided at a point P_i such that P_i = (1 - λ)A_i + λA_{i+1}. Then the new polygon is P₁P₂...Pₙ. The area of this polygon can be computed using the shoelace formula, which would involve terms of (1 - λ) and λ multiplied by coordinates of the original vertices. Expanding this, the area would be a quadratic function in λ, and since the quadratic term is positive (as seen in the examples), it would have a minimum at λ=1/2.Alternatively, consider that moving from λ to 1 - λ would mirror the division points on each side, leading to a congruent polygon but in the opposite direction. Therefore, the area function should be symmetric around λ=1/2, which would imply that the minimum (or maximum) is at λ=1/2. Since we observed minima in the examples, it's likely that for any polygon, the minimal area occurs at λ=1/2.Alternatively, use vectors. Let me denote the position vectors of the original polygon's vertices as A₁, A₂, ..., Aₙ. The division points P_i on each side can be written as:P_i = (1 - λ)A_i + λA_{i+1}Then, the area of the polygon formed by P₁, P₂, ..., Pₙ can be calculated as half the absolute value of the sum over i of (P_i × P_{i+1}).Substituting P_i:P_i × P_{i+1} = [(1 - λ)A_i + λA_{i+1}] × [(1 - λ)A_{i+1} + λA_{i+2}]Expanding this cross product:= (1 - λ)^2 (A_i × A_{i+1}) + (1 - λ)λ (A_i × A_{i+2}) + λ(1 - λ) (A_{i+1} × A_{i+1}) + λ² (A_{i+1} × A_{i+2})But cross product of a vector with itself is zero, so (A_{i+1} × A_{i+1}) = 0. Therefore, simplifies to:= (1 - λ)^2 (A_i × A_{i+1}) + (1 - λ)λ (A_i × A_{i+2}) + λ² (A_{i+1} × A_{i+2})Summing over all i, the total area would be 1/2 |sum_{i=1 to n} [ (1 - λ)^2 (A_i × A_{i+1}) + (1 - λ)λ (A_i × A_{i+2}) + λ² (A_{i+1} × A_{i+2}) ] |.This seems complex, but note that the original area is 1/2 |sum (A_i × A_{i+1})|. Let's denote S = sum (A_i × A_{i+1}). Then the total area becomes:1/2 | (1 - λ)^2 S + (1 - λ)λ sum (A_i × A_{i+2}) + λ² sum (A_{i+1} × A_{i+2}) ) |.But sum (A_{i+1} × A_{i+2}) is just S, since it's the same as shifting the index by 1. Similarly, sum (A_i × A_{i+2}) is sum over i (A_i × A_{i+2}). Let's denote this as T. So the total area is:1/2 | (1 - λ)^2 S + (1 - λ)λ T + λ² S |.Combine terms:= 1/2 | [ (1 - 2λ + λ²) S + (1 - λ)λ T + λ² S ] |= 1/2 | [ (1 - 2λ + λ² + λ²) S + (λ - λ²) T ] |= 1/2 | [ (1 - 2λ + 2λ²) S + (λ - λ²) T ] |Now, this expression is a combination of the original area term S and another term T. However, unless T is related to S in some way, this might complicate things. But perhaps for convex polygons, there is a relationship between T and S. Alternatively, note that in the examples we did earlier (triangle and square), the T term might have a specific relation that allows the quadratic to collapse.Alternatively, maybe in those examples, T is proportional to S. For the triangle, let's compute T. For a triangle with vertices A₁, A₂, A₃, T = A₁ × A₃ + A₂ × A₁ + A₃ × A₂. But in vectors, cross product is anti-commutative, so A × B = -(B × A). Therefore, T for a triangle would be:A₁ × A₃ + A₂ × A₁ + A₃ × A₂= A₁ × A₃ - A₁ × A₂ + A₃ × A₂= (A₁ × A₃ - A₁ × A₂) + (A₃ × A₂)= A₁ × (A₃ - A₂) + (A₃ × A₂)But not sure if this simplifies. However, for the equilateral triangle, all cross products are similar. But perhaps instead of getting bogged down, let's recall that in the triangle example, when we calculated the area ratio, it turned out to be 3λ² -3λ +1, which is 3(λ² -λ) +1. The original area is sqrt(3)/4, and the inner area was that times (3λ² -3λ +1). The expression T in this case would be sum (A_i × A_{i+2}). For a triangle, the indices wrap around, so A₃+2 = A₂, A₁+2 = A₃, etc. Wait, but in the triangle, the sum T is:sum_{i=1 to 3} A_i × A_{i+2} = A₁ × A₃ + A₂ × A₁ + A₃ × A₂But A₁ × A₃ = -(A₃ × A₁), so T = -(A₃ × A₁) - (A₁ × A₂) - (A₂ × A₃). Which is -T - S? Not sure. Wait, actually, in a triangle, S = A₁ × A₂ + A₂ × A₃ + A₃ × A₁, which is the same as twice the area.But if T = A₁ × A₃ + A₂ × A₁ + A₃ × A₂, then T = -(A₃ × A₁ + A₁ × A₂ + A₂ × A₃) = -S. Therefore, T = -S.So substituting back into the area expression:For the triangle, T = -S. Therefore, the area becomes:1/2 | (1 - 2λ + 2λ²) S + (λ - λ²)(-S) | = 1/2 | [ (1 - 2λ + 2λ² - λ + λ²) S ] | = 1/2 | (1 - 3λ + 3λ²) S |.Which is 1/2 | (3λ² -3λ +1) S |. Since S is twice the area of the original triangle, then the inner area would be (3λ² -3λ +1) times original area. Which matches our previous result. So indeed, for the triangle, T = -S.Similarly, for the square, let's check T. For a square with vertices A₁, A₂, A₃, A₄, T = sum (A_i × A_{i+2}). For a square, A₁ × A₃ is the cross product of opposite vertices. However, in the square case, A₁ = (0,0), A₂ = (1,0), A₃ = (1,1), A₄ = (0,1). Then:sum (A_i × A_{i+2}) = A₁ × A₃ + A₂ × A₄ + A₃ × A₁ + A₄ × A₂Compute each term:A₁ × A₃ = (0,0) × (1,1) = 0*1 - 0*1 = 0A₂ × A₄ = (1,0) × (0,1) = 1*1 - 0*0 = 1A₃ × A₁ = (1,1) × (0,0) = 1*0 - 1*0 = 0A₄ × A₂ = (0,1) × (1,0) = 0*0 - 1*1 = -1So sum T = 0 +1 +0 -1 =0Therefore, for the square, T =0. Therefore, substituting back into the area expression:1/2 | (1 - 2λ + 2λ²) S + (λ - λ²)*0 | = 1/2 | (1 - 2λ + 2λ²) S |. For the square, S is twice the original area (which is 1), so S=2. Then the inner area would be 1/2 * (1 - 2λ + 2λ²)*2 = (1 - 2λ + 2λ²). Wait, but earlier when we calculated the area for the square, we got 2λ² -2λ +1. Wait, but according to this, it should be 2λ² -2λ +1? Wait, no.Wait, wait. Let's recast.Original area of the square is 1. Then S = sum (A_i × A_{i+1}) = 2*original area = 2*1=2.Then, according to the formula, inner area = 1/2 | (1 - 2λ + 2λ²) * S | = 1/2 | (1 -2λ +2λ²)*2 | = |1 -2λ +2λ²|. Which is 2λ² -2λ +1. Which matches our earlier result. So that's correct.Therefore, depending on the polygon, T can be related to S. For the triangle, T = -S; for the square, T=0. Therefore, the area expression becomes:For triangle: (3λ² -3λ +1) times original area.For square: (2λ² -2λ +1) times original area.Both are quadratic in λ with minima at λ=1/2. So even though the coefficients differ, the minima occur at the same λ=1/2. Therefore, regardless of the polygon, the minimal area occurs at λ=1/2.But why? It seems that when λ=1/2, the division points are midpoints, which usually create a centrally symmetric polygon if the original is convex, and perhaps this symmetry leads to the minimal area. Alternatively, maybe the area function is always a quadratic function of λ with vertex at λ=1/2, regardless of the polygon.Given the two examples and the general form of the area expression derived using vectors, which simplifies to a quadratic in λ, it's reasonable to conjecture that for any polygon, the minimal area occurs at λ=1/2.Therefore, the answer should be λ=1/2.Final AnswerThe value of (lambda) that minimizes the area is (boxed{dfrac{1}{2}}).</think>To determine the value of (lambda) that minimizes the area of a polygon formed by points dividing each side of an original polygon in the ratio (lambda), we consider the following reasoning:1. Understanding the Problem: The polygon (A_1A_2 ldots A_n) has points dividing each side in the ratio (lambda). The goal is to find the (lambda) that results in the smallest area for the new polygon formed by these division points.2. Examples with Specific Polygons: - Square: For a square with vertices ((0,0)), ((1,0)), ((1,1)), and ((0,1)), the area of the inner quadrilateral formed by dividing each side in the ratio (lambda) is calculated using the shoelace formula. The area function is found to be (2lambda^2 - 2lambda + 1), which has its minimum at (lambda = frac{1}{2}). - Triangle: For an equilateral triangle with vertices ((0,0)), ((1,0)), and ((0.5, sqrt{3}/2)), the area of the inner triangle formed by dividing each side in the ratio (lambda) is calculated. The area function is found to be (3lambda^2 - 3lambda + 1), which also has its minimum at (lambda = frac{1}{2}).3. General Case Analysis: - For any polygon, the points dividing the sides in the ratio (lambda) can be represented,<think>Okay, so I need to figure out the value of λ (lambda) that minimizes the area of a polygon formed by points dividing each side of the original polygon in the ratio λ. Hmm, let's start by understanding the problem better.First, the original polygon is A₁A₂…Aₙ, which is a convex polygon? Wait, the problem doesn't specify if it's convex or not. Maybe it doesn't matter? Or maybe the result is the same regardless? Hmm. Well, I'll proceed assuming it's a convex polygon for simplicity, but maybe I should check later if convexity affects the result.Each side of the polygon is divided in the ratio λ. So, for example, on side A₁A₂, there's a point that divides A₁A₂ into segments with ratio λ. If λ is the ratio of the segment from A₁ to the point compared to the segment from the point to A₂, right? So like, if λ is 1, it's the midpoint. If λ is greater than 1, the point is closer to A₂, and if it's less than 1, closer to A₁.Then, these division points form a new polygon. The question is asking for the value of λ that makes the area of this new polygon the smallest possible.Hmm. I remember that for triangles, if you connect points that divide each side in the same ratio, the area of the inner triangle is related to the original area by some function of λ. Maybe similar logic applies here for polygons? But polygons can have different numbers of sides, so maybe the formula generalizes.Let me think. For a triangle, if you take points dividing each side in ratio λ, then the inner triangle's area is (λ² - λ + 1)/(1 + λ)² times the original area? Wait, maybe I should recall the formula properly.Alternatively, affine transformations preserve ratios and areas up to scaling. So perhaps the ratio of areas is a function purely dependent on λ and the number of sides, but the problem states "a polygon", not specifying the number of sides. Wait, the original polygon is A₁A₂…Aₙ, so it's an n-gon. Wait, but the problem says "a polygon", so maybe the answer is independent of n? Or maybe depends on n? Wait, the problem says "For which value of λ is the area of the resulting polygon the smallest?" So maybe the answer is a specific value of λ regardless of the polygon's sides? Hmm, maybe similar to the case of triangles, but perhaps for quadrilaterals, pentagons, etc.Wait, but actually, in the case of triangles, the minimal area occurs at λ = 1 (midpoints), forming the medial triangle, which has area 1/4 of the original. Wait, but that's the minimal area? Wait, actually, if you take points closer to the vertices, the inner triangle would be smaller, but if you take points closer to the midpoints... Wait, maybe I need to verify.Wait, let's take a triangle. Suppose each side is divided in the ratio λ:1, where λ is the ratio of the segment from the vertex to the division point. So, if λ = 1, division is at the midpoint. The area of the inner triangle is (1 - 3λ/(1 + λ)²) times the original area? Wait, maybe my formula is off.Alternatively, using barycentric coordinates or vectors. Let me consider a coordinate system.Let’s take triangle ABC with coordinates A(0,0), B(1,0), C(0,1). Then, the points dividing AB, BC, and CA in the ratio λ:1 (from the vertex to the division point). So, point D on AB divides AB such that AD/DB = λ/1, so D is at (λ/(1 + λ), 0). Similarly, point E on BC divides BC such that BE/EC = λ/1. Since B is (1,0) and C is (0,1), the coordinates of E can be found by moving from B towards C by λ/(1 + λ). So E is (1 - λ/(1 + λ), 0 + λ/(1 + λ)) = (1/(1 + λ), λ/(1 + λ)). Similarly, point F on CA divides CA such that CF/FA = λ/1. C is (0,1) and A is (0,0), so F is (0, 1/(1 + λ)).Now, we need to find the area of triangle DEF. Coordinates of D, E, F are:D(λ/(1 + λ), 0)E(1/(1 + λ), λ/(1 + λ))F(0, 1/(1 + λ))Using the shoelace formula:Area = 1/2 |x_D(y_E - y_F) + x_E(y_F - y_D) + x_F(y_D - y_E)|Plugging in the coordinates:= 1/2 | (λ/(1 + λ))(λ/(1 + λ) - 1/(1 + λ)) + (1/(1 + λ))(1/(1 + λ) - 0) + 0*(0 - λ/(1 + λ)) |Simplify each term:First term: (λ/(1 + λ)) * ( (λ - 1)/(1 + λ) ) = λ(λ - 1)/(1 + λ)^2Second term: (1/(1 + λ)) * (1/(1 + λ)) = 1/(1 + λ)^2Third term: 0So Area = 1/2 | [λ(λ - 1) + 1]/(1 + λ)^2 | = 1/2 | (λ² - λ + 1)/(1 + λ)^2 |.Since all terms are positive for λ > 0, absolute value can be removed:Area = (λ² - λ + 1)/(2(1 + λ)^2) times the area of the original triangle.Wait, the original triangle area is 1/2, so the computed area is (λ² - λ + 1)/(2(1 + λ)^2). But if we factor out 1/2, the ratio of areas is (λ² - λ + 1)/(1 + λ)^2.So, for the triangle case, the area ratio is (λ² - λ + 1)/(1 + λ)^2. To find the minimal area, we need to minimize this expression with respect to λ.Let’s compute the derivative of f(λ) = (λ² - λ + 1)/(1 + λ)^2.First, use the quotient rule:f’(λ) = [ (2λ - 1)(1 + λ)^2 - (λ² - λ + 1)(2)(1 + λ) ] / (1 + λ)^4Simplify numerator:Let’s factor out (1 + λ):Numerator = (1 + λ)[ (2λ - 1)(1 + λ) - 2(λ² - λ + 1) ]Expand the terms inside:First term: (2λ - 1)(1 + λ) = 2λ(1) + 2λ^2 - 1(1) - 1*λ = 2λ + 2λ² - 1 - λ = 2λ² + λ - 1Second term: -2(λ² - λ + 1) = -2λ² + 2λ - 2Combine them:2λ² + λ - 1 - 2λ² + 2λ - 2 = (2λ² - 2λ²) + (λ + 2λ) + (-1 - 2) = 3λ - 3Therefore, numerator = (1 + λ)(3λ - 3) = 3(1 + λ)(λ - 1)Thus, f’(λ) = 3(1 + λ)(λ - 1) / (1 + λ)^4 = 3(λ - 1)/(1 + λ)^3Set derivative equal to zero:3(λ - 1)/(1 + λ)^3 = 0 => numerator is zero: λ - 1 = 0 => λ = 1Check the second derivative or test intervals to confirm it's a minimum.For λ < 1, say λ = 0.5, f’(0.5) = 3(0.5 - 1)/(1 + 0.5)^3 = 3(-0.5)/(3.375) ≈ -0.444 < 0For λ > 1, say λ = 2, f’(2) = 3(2 - 1)/(3)^3 = 3(1)/27 = 1/9 > 0Thus, at λ = 1, the function has a minimum. So for a triangle, the minimal area occurs when λ = 1, i.e., the midpoints. The area ratio is (1 - 1 + 1)/(1 + 1)^2 = 1/4, which matches the medial triangle area.Interesting. So for triangles, the minimal area occurs at λ = 1. Now, what about quadrilaterals?Let’s consider a convex quadrilateral. Suppose we have a quadrilateral ABCD, and we divide each side in the ratio λ. Then, connect those points to form a new quadrilateral. What's the area of the new quadrilateral in terms of λ, and what λ minimizes it?I need to compute this. Maybe using coordinates again. Let’s take a square for simplicity with coordinates A(0,0), B(1,0), C(1,1), D(0,1). Then, divide each side in the ratio λ:1.So, on AB: from A(0,0) to B(1,0), the division point is (λ/(1 + λ), 0).On BC: from B(1,0) to C(1,1), the division point is (1, λ/(1 + λ)).On CD: from C(1,1) to D(0,1), the division point is ( (1)/(1 + λ), 1 ).Wait, no. Wait, CD goes from C(1,1) to D(0,1). So moving from C to D, which is leftwards. The division ratio is λ:1. So the point divides CD into λ:1 from C to D. So the coordinate would be D + (C - D)*(1/(1 + λ))? Wait, maybe better to parametrize.From C to D, the vector is (-1,0). So starting at C(1,1), moving towards D(0,1) by a fraction 1/(1 + λ). So the division point E is (1 - 1/(1 + λ), 1) = (λ/(1 + λ), 1).Similarly, on DA: from D(0,1) to A(0,0), division point divides DA into λ:1. So starting at D(0,1), moving towards A(0,0) by λ/(1 + λ). So the point is (0, 1 - λ/(1 + λ)) = (0, 1/(1 + λ)).So the four points of the new quadrilateral are:E(λ/(1 + λ), 0) on AB,F(1, λ/(1 + λ)) on BC,G(λ/(1 + λ), 1) on CD,H(0, 1/(1 + λ)) on DA.Now, let's compute the area of quadrilateral EFGH.First, list the coordinates:E: (λ/(1 + λ), 0)F: (1, λ/(1 + λ))G: (λ/(1 + λ), 1)H: (0, 1/(1 + λ))We can use the shoelace formula to compute the area.Order of points: E, F, G, H.Compute the shoelace sum:Sum1 = x_E * y_F + x_F * y_G + x_G * y_H + x_H * y_E= (λ/(1 + λ)) * (λ/(1 + λ)) + 1 * 1 + (λ/(1 + λ)) * (1/(1 + λ)) + 0 * 0= λ²/(1 + λ)^2 + 1 + λ/(1 + λ)^2 + 0= [λ² + λ]/(1 + λ)^2 + 1Sum2 = y_E * x_F + y_F * x_G + y_G * x_H + y_H * x_E= 0 * 1 + (λ/(1 + λ)) * (λ/(1 + λ)) + 1 * 0 + (1/(1 + λ)) * (λ/(1 + λ))= 0 + λ²/(1 + λ)^2 + 0 + λ/(1 + λ)^2= [λ² + λ]/(1 + λ)^2Area = 1/2 |Sum1 - Sum2| = 1/2 | [ (λ² + λ)/(1 + λ)^2 + 1 ] - [ (λ² + λ)/(1 + λ)^2 ] | = 1/2 | 1 | = 1/2Wait, that's strange. The area of the inner quadrilateral is 1/2 regardless of λ? But the original square has area 1. That can't be right. Wait, maybe I made a mistake in the coordinates.Wait, let me check the coordinates again.Original square: A(0,0), B(1,0), C(1,1), D(0,1).Division points:- On AB: from A to B, ratio λ:1, so E(λ/(1 + λ), 0).- On BC: from B to C, ratio λ:1, so moving from B(1,0) towards C(1,1). The y-coordinate increases by λ/(1 + λ), so F(1, λ/(1 + λ)).- On CD: from C to D, ratio λ:1, so moving from C(1,1) towards D(0,1). The x-coordinate decreases by 1/(1 + λ), so G(1 - 1/(1 + λ), 1) = (λ/(1 + λ), 1).- On DA: from D to A, ratio λ:1, so moving from D(0,1) towards A(0,0). The y-coordinate decreases by λ/(1 + λ), so H(0, 1 - λ/(1 + λ)) = (0, 1/(1 + λ)).So coordinates are correct.Now, applying shoelace formula:Order: E, F, G, H.x_E = λ/(1 + λ), y_E = 0x_F = 1, y_F = λ/(1 + λ)x_G = λ/(1 + λ), y_G = 1x_H = 0, y_H = 1/(1 + λ)Compute Sum1:x_E * y_F = (λ/(1 + λ)) * (λ/(1 + λ)) = λ²/(1 + λ)^2x_F * y_G = 1 * 1 = 1x_G * y_H = (λ/(1 + λ)) * (1/(1 + λ)) = λ/(1 + λ)^2x_H * y_E = 0 * 0 = 0Sum1 = λ²/(1 + λ)^2 + 1 + λ/(1 + λ)^2 + 0 = [λ² + λ]/(1 + λ)^2 + 1Sum2:y_E * x_F = 0 * 1 = 0y_F * x_G = (λ/(1 + λ)) * (λ/(1 + λ)) = λ²/(1 + λ)^2y_G * x_H = 1 * 0 = 0y_H * x_E = (1/(1 + λ)) * (λ/(1 + λ)) = λ/(1 + λ)^2Sum2 = 0 + λ²/(1 + λ)^2 + 0 + λ/(1 + λ)^2 = [λ² + λ]/(1 + λ)^2Thus, Area = 1/2 | Sum1 - Sum2 | = 1/2 | [ (λ² + λ)/(1 + λ)^2 + 1 ] - [ (λ² + λ)/(1 + λ)^2 ] | = 1/2 |1| = 1/2.But the original square has area 1, so the inner quadrilateral has area 1/2 regardless of λ? That's unexpected. How is that possible?Wait, maybe the quadrilateral EFGH is always a parallelogram with area 1/2, no matter the λ? Let me check with specific values.Take λ = 1 (midpoints):Then, E(0.5, 0), F(1, 0.5), G(0.5, 1), H(0, 0.5). Connecting these points forms a square rotated by 45 degrees, with side length √(0.5² + 0.5²) = √0.5, area (√0.5)^2 = 0.5. Correct.Take λ approaching 0, so points E, F, G, H approach A, B, C, D. But as λ approaches 0, E approaches A(0,0), F approaches B(1,0), G approaches C(1,1), H approaches D(0,1). So the quadrilateral EFGH approaches the original square, area approaching 1. But according to our formula, area is always 1/2. Contradiction. So my calculation must be wrong.Wait, if λ approaches 0, the division points are very close to the original vertices. So the new quadrilateral should almost coincide with the original square, hence area approaching 1. But according to the shoelace calculation, the area is always 1/2. That can't be right.There must be a mistake in the coordinates or the shoelace application. Let me re-examine.Wait, when λ approaches 0, point E approaches A(0,0), F approaches B(1,0), G approaches C(1,1), H approaches D(0,1). So quadrilateral EFGH would be ABCH if H approaches D? Wait, H is on DA, so when λ approaches 0, H approaches D(0,1). So EFGH would be A(0,0), B(1,0), C(1,1), D(0,1), which is the original square. But according to our calculation, the area is 1/2, which is wrong. So there's a mistake in the coordinate assignments or the order of the points.Wait, perhaps the order of the points in the shoelace formula is incorrect? Let's check the connectivity. The original quadrilateral is E on AB, F on BC, G on CD, H on DA. Connecting E-F-G-H-E should form a quadrilateral inside the square. Let me visualize.When λ is approaching 0:- E is near A(0,0),- F is near B(1,0),- G is near C(1,1),- H is near D(0,1).So connecting E-F-G-H-E would form a quadrilateral that's almost the square itself, hence area approaching 1. But according to the shoelace formula, it's always 1/2. That's impossible. Therefore, my application of the shoelace formula is wrong.Wait, maybe I messed up the order of the points. Let's plot them:For λ approaching 0:E is (almost 0, 0),F is (1, almost 0),G is (almost 1, 1),H is (0, almost 1).Connecting E-F-G-H-E would create a quadrilateral that is actually a rectangle or something, but when λ is 0, E is A, F is B, G is C, H is D, which is the original square. But according to the shoelace formula, when λ is 0, the coordinates would be:E(0,0), F(1,0), G(1,1), H(0,1). Shoelace formula:Sum1 = 0*0 + 1*1 + 1*1 + 0*0 = 0 + 1 + 1 + 0 = 2Sum2 = 0*1 + 0*1 + 1*0 + 1*0 = 0 + 0 + 0 + 0 = 0Area = 1/2 |2 - 0| = 1, which is correct. But in my previous calculation, when I plugged in λ approaching 0, the formula gave Sum1 - Sum2 = 1. So something's wrong.Wait, let's recalculate Sum1 and Sum2 for λ approaching 0.Wait, for λ approaching 0, λ/(1 + λ) ≈ λ, and 1/(1 + λ) ≈ 1 - λ.So E(λ, 0), F(1, λ), G(λ, 1), H(0, 1 - λ).Compute Sum1:x_E * y_F = λ * λ = λ²x_F * y_G = 1 * 1 = 1x_G * y_H = λ * (1 - λ) ≈ λx_H * y_E = 0 * 0 = 0Sum1 ≈ λ² + 1 + λ + 0 ≈ 1 + λ + λ²Sum2:y_E * x_F = 0 * 1 = 0y_F * x_G = λ * λ = λ²y_G * x_H = 1 * 0 = 0y_H * x_E = (1 - λ) * λ ≈ λ - λ²Sum2 ≈ 0 + λ² + 0 + λ - λ² ≈ λTherefore, Area ≈ 1/2 |(1 + λ + λ²) - (λ)| = 1/2 |1 + λ²| ≈ 1/2 (1 + 0) = 1/2. But when λ approaches 0, the area should approach 1, not 1/2. So there's a contradiction. Therefore, my previous calculation is incorrect.Wait, this suggests that the shoelace formula was applied incorrectly. Maybe the order of the points is not correct? Let me check again.In shoelace formula, the order of the points must be either clockwise or counter-clockwise without crossing. Let me make sure the points E, F, G, H are ordered correctly.Original square is ordered A(0,0), B(1,0), C(1,1), D(0,1) counter-clockwise.The new points:E is on AB towards A as λ approaches 0, so near A.F is on BC towards B as λ approaches 0, so near B.G is on CD towards C as λ approaches 0, so near C.H is on DA towards D as λ approaches 0, so near D.Connecting E-F-G-H-E: When λ approaches 0, this should trace a quadrilateral close to A-B-C-D, but according to coordinates, E is near A, F near B, G near C, H near D, so connecting them should give a quadrilateral similar to the original. But according to the shoelace formula, it's giving half the area, which is conflicting.Wait, maybe the coordinates when λ approaches 0 are not as I thought. Wait, when λ is approaching 0:Point E on AB: λ/(1 + λ) ≈ λ, so (λ, 0)Point F on BC: moving from B(1,0) towards C(1,1) by λ/(1 + λ) ≈ λ, so (1, λ)Point G on CD: moving from C(1,1) towards D(0,1) by 1/(1 + λ) ≈ 1 - λ, so (λ/(1 + λ), 1) ≈ (λ,1)Point H on DA: moving from D(0,1) towards A(0,0) by λ/(1 + λ) ≈ λ, so (0, 1 - λ/(1 + λ)) ≈ (0, 1 - λ)Wait, so the coordinates are E(λ,0), F(1,λ), G(λ,1), H(0,1 - λ). Let's apply the shoelace formula properly:Order: E(λ,0), F(1,λ), G(λ,1), H(0,1 - λ), back to E(λ,0).Compute Sum1:x_E * y_F = λ * λ = λ²x_F * y_G = 1 * 1 = 1x_G * y_H = λ * (1 - λ) = λ - λ²x_H * y_E = 0 * 0 = 0Sum1 = λ² + 1 + λ - λ² + 0 = 1 + λSum2:y_E * x_F = 0 * 1 = 0y_F * x_G = λ * λ = λ²y_G * x_H = 1 * 0 = 0y_H * x_E = (1 - λ) * λ = λ - λ²Sum2 = 0 + λ² + 0 + λ - λ² = λThus, Area = 1/2 |Sum1 - Sum2| = 1/2 |1 + λ - λ| = 1/2 * 1 = 1/2.But when λ approaches 0, this area is 1/2, which contradicts the expectation. Therefore, there must be an error in the assumption. Wait, perhaps the quadrilateral EFGH is not convex when λ is small? Or maybe the points are ordered incorrectly?Wait, if we plot the points for λ approaching 0:E is (λ,0), near the origin.F is (1,λ), near (1,0).G is (λ,1), near (0,1) but actually (λ,1) which is near (0,1) only if λ is near 0. Wait, no. Wait, if λ is approaching 0, then G is (λ,1), which is near (0,1). H is (0,1 - λ), near (0,1).So the quadrilateral EFGH has points near (0,0), (1,0), (0,1), (0,1). Wait, that can't form a convex quadrilateral. Wait, no. Wait, the points are:E(λ,0), F(1,λ), G(λ,1), H(0,1 - λ). For λ approaching 0:E is (0,0), F is (1,0), G is (0,1), H is (0,1). Wait, no. If λ approaches 0, G is (0,1), H is (0,1 - 0) = (0,1). So points E(0,0), F(1,0), G(0,1), H(0,1). But H and G coincide at (0,1). So the quadrilateral becomes a triangle with points E, F, G/H. But according to the coordinates, when λ approaches 0, G and H both approach (0,1). So the area should approach the area of triangle EFG, which is a right triangle with legs 1 and 1, area 0.5. Which matches the shoelace result. So actually, when λ approaches 0, the quadrilateral degenerates into a triangle with area 0.5. Similarly, when λ approaches infinity, the quadrilateral also degenerates into a triangle with area 0.5. But when λ =1, midpoints, the area is 0.5 as well. Wait, but the original square has area 1. So according to this, regardless of λ, the inner quadrilateral has area 0.5? That can't be right.But in reality, when λ =1, connecting midpoints forms a smaller square rotated by 45 degrees, with side length √(0.5² + 0.5²) = √0.5, area 0.5. Correct. But if we take λ =2, so points divide sides in ratio 2:1. Let's compute coordinates.For λ =2:E divides AB into 2:1, so E is (2/3, 0)F divides BC into 2:1, so F is (1, 2/3)G divides CD into 2:1, so CD from C(1,1) to D(0,1). Ratio 2:1, so moving 1/(2+1)=1/3 from C towards D, so G is (1 - 1/3,1) = (2/3,1)H divides DA into 2:1, so DA from D(0,1) to A(0,0). H is (0,1 - 2/3)= (0,1/3)So coordinates are E(2/3,0), F(1,2/3), G(2/3,1), H(0,1/3).Applying shoelace formula:Order: E, F, G, H.Sum1:2/3 * 2/3 + 1 * 1 + 2/3 * 1/3 + 0 * 0 = (4/9) + 1 + (2/9) + 0 = (4/9 + 2/9) + 1 = 6/9 + 1 = 2/3 + 1 = 5/3Sum2:0 * 1 + 2/3 * 2/3 + 1 * 0 + 1/3 * 2/3 = 0 + 4/9 + 0 + 2/9 = 6/9 = 2/3Area = 1/2 |5/3 - 2/3| = 1/2 * 1 = 1/2. Still 1/2. So regardless of λ, the area is 1/2. That seems to be the case. But when λ approaches 0, the area should approach 1. But according to this, it approaches 1/2. So what's the issue here?Wait, maybe the problem is that when λ is not 1, the quadrilateral EFGH is self-intersecting? Because when λ is small, connecting E-F-G-H might cross over. Wait, let's check for λ=0.5.For λ=0.5, E(1/3,0), F(1,1/3), G(1/3,1), H(0,2/3).Plotting these points: E(1/3,0), F(1,1/3), G(1/3,1), H(0,2/3). Connecting them in order gives a quadrilateral. Let's see if it's convex.From E(1/3,0) to F(1,1/3): moving right and up.From F(1,1/3) to G(1/3,1): moving left and up.From G(1/3,1) to H(0,2/3): moving left and down.From H(0,2/3) to E(1/3,0): moving right and down.This seems to form a convex quadrilateral. But according to shoelace, the area is still 1/2. Wait, but if we take a square and connect points in a way that the inner quadrilateral always has half the area, that seems strange. But for λ=1, it's the medial quadrilateral (connecting midpoints) which is a square of area 1/2. For other λ, maybe the area remains the same? That seems possible if the figure is affine transformed.Wait, perhaps for any convex quadrilateral, connecting points that divide the sides in ratio λ results in an inner quadrilateral whose area is independent of λ? That seems unlikely, but in the case of the square, according to the calculations, it's always 1/2. So maybe in the square case, due to symmetry, the area remains constant. But in a general quadrilateral, the area might vary with λ?Wait, let's test a non-square convex quadrilateral. Let's take a trapezoid.Let’s take trapezoid A(0,0), B(2,0), C(1,1), D(0,1). So it's a trapezoid with bases AB (length 2) and CD (length 1), height 1.Divide each side in ratio λ:1.Compute coordinates:On AB: from A(0,0) to B(2,0), division point E(2λ/(1 + λ), 0).On BC: from B(2,0) to C(1,1). The parametric equation is x = 2 - t, y = 0 + t, where t from 0 to sqrt( (1-2)^2 + (1-0)^2 ) = sqrt(2). But ratio λ:1 on the side. Wait, perhaps we need to parametrize by length. Alternatively, since the problem states dividing the side in the same ratio λ, not by length. So from B to C, the division point F divides BC into λ:1. So coordinates of F: ( (1 + λ*2)/(1 + λ), (0 + λ*1)/(1 + λ) )? Wait, no. Wait, the division of BC from B to C in ratio λ:1 means BF/FC = λ/1.So using the section formula: F = ( (λ*C + 1*B) ) / (λ + 1 )Coordinates of B(2,0), C(1,1). Thus,F_x = (λ*1 + 1*2)/(λ + 1) = (λ + 2)/(λ + 1)F_y = (λ*1 + 1*0)/(λ + 1) = λ/(λ + 1)Similarly, on CD: from C(1,1) to D(0,1), division point G divides CD into λ:1. So CG/GD = λ/1.Thus, G_x = (λ*0 + 1*1)/(λ + 1) = 1/(λ + 1)G_y = (λ*1 + 1*1)/(λ + 1) = (λ + 1)/(λ + 1) = 1On DA: from D(0,1) to A(0,0), division point H divides DA into λ:1. So DH/HA = λ/1.Thus, H_x = 0H_y = (λ*0 + 1*1)/(λ + 1) = 1/(λ + 1)So coordinates:E(2λ/(1 + λ), 0)F( (λ + 2)/(λ + 1), λ/(λ + 1) )G(1/(λ + 1), 1 )H(0, 1/(λ + 1) )Now, apply the shoelace formula to quadrilateral EFGH.Order: E, F, G, H.Compute Sum1:x_E * y_F + x_F * y_G + x_G * y_H + x_H * y_E= (2λ/(1 + λ)) * (λ/(1 + λ)) + ( (λ + 2)/(λ + 1) ) * 1 + (1/(λ + 1)) * (1/(λ + 1)) + 0 * 0= (2λ²)/(1 + λ)^2 + (λ + 2)/(λ + 1) + 1/(λ + 1)^2 + 0Sum1 = (2λ²)/(1 + λ)^2 + (λ + 2)(1 + λ)/(1 + λ)^2 + 1/(1 + λ)^2= [2λ² + (λ + 2)(1 + λ) + 1] / (1 + λ)^2Expand (λ + 2)(1 + λ) = λ(1) + λ^2 + 2(1) + 2λ = λ + λ² + 2 + 2λ = λ² + 3λ + 2Thus,Sum1 = [2λ² + λ² + 3λ + 2 + 1]/(1 + λ)^2 = [3λ² + 3λ + 3]/(1 + λ)^2 = 3(λ² + λ + 1)/(1 + λ)^2Sum2:y_E * x_F + y_F * x_G + y_G * x_H + y_H * x_E= 0 * ( (λ + 2)/(λ + 1) ) + (λ/(λ + 1)) * (1/(λ + 1)) + 1 * 0 + (1/(λ + 1)) * (2λ/(1 + λ))= 0 + λ/( (λ + 1)^2 ) + 0 + 2λ/( (λ + 1)^2 )= (λ + 2λ)/( (λ + 1)^2 ) = 3λ/( (λ + 1)^2 )Thus, Area = 1/2 | Sum1 - Sum2 | = 1/2 | [3(λ² + λ + 1) -,<think>Okay, so I have this problem where there's a polygon, let's say it's an n-sided polygon, with vertices labeled A1, A2, ..., An. The problem says that this polygon is bounded by points that divide each of its sides in the same ratio λ. I need to find the value of λ that makes the area of this resulting polygon as small as possible. Hmm, interesting. Let me try to visualize this first.First, when they say the polygon is "bounded by points that divide the sides in the same ratio λ," I think they mean that on each side of the original polygon, there's a point that divides that side into parts with ratio λ. Then, connecting these points in order creates a new polygon inside the original one. The task is to figure out what λ makes the area of this inner polygon the smallest. Wait, but how exactly are the points dividing the sides? Is λ the ratio of the segment from the original vertex to the new point, compared to the entire side? Or is it the other way around?Let me clarify. If we have a side A1A2, and a point B1 divides A1A2 in the ratio λ, that usually means that A1B1:B1A2 = λ:1-λ or something like that. But the problem says "the same ratio λ," so maybe it's a more straightforward division. Let me check.Suppose the ratio is λ:(1 - λ). So, for each side, the point that's taken is λ fraction from one end and (1 - λ) from the other. Depending on which end we start from, this could affect the shape. But since the problem says "the same ratio λ," it's probably dividing each side from the same vertex. For example, each side is divided so that the segment from A_i to the new point is λ times the length of the side, and the remaining segment is (1 - λ) times the length. But we need to confirm.Alternatively, maybe the division is such that each side is split into parts with lengths in the ratio λ:1. So, for example, if the side is length L, then the two parts would be (λ/(1 + λ))L and (1/(1 + λ))L. But the problem says "the same ratio λ," so maybe λ is the ratio of the first segment to the second, meaning λ = (length from original vertex to new point)/(length from new point to next vertex). So, if λ is 1, then the point is the midpoint. If λ is greater than 1, the point is closer to the next vertex, and if it's less than 1, it's closer to the original vertex.But since the problem is asking for the value of λ that minimizes the area, perhaps we need to model this mathematically for a general polygon and find the minimal area. However, since the problem is general for any polygon, maybe it's a property that holds for all polygons, or maybe it's assuming a convex polygon? The problem doesn't specify, but perhaps the result is the same regardless.Wait, but maybe there's a formula for the area of the inner polygon formed by dividing each side in a given ratio. For example, for a triangle, if you connect points that divide each side in a ratio λ:1-λ, the inner triangle's area can be calculated, and then minimized. Maybe this generalizes to any polygon.Alternatively, considering affine transformations, maybe the ratio λ that minimizes the area is universal, regardless of the polygon's shape. Let me think.Alternatively, perhaps using vectors or coordinates. Let me try to set up coordinates for the polygon. Let's assume the original polygon is in a plane, and assign coordinates to the vertices. Let's denote the original polygon as A1, A2, ..., An. Each side AiAi+1 (with An+1 = A1) is divided by a point Bi such that AiBi = λ AiAi+1. Then, the inner polygon is B1, B2, ..., Bn.To compute the area of the inner polygon, perhaps we can express each Bi in terms of Ai and Ai+1, then compute the area using the shoelace formula or vector cross products.Alternatively, for a convex polygon, the area of the inner polygon can be related to the original area through some linear transformation. If each point Bi is a linear combination of Ai and Ai+1, then the transformation might be an affine transformation, which scales the area by a certain factor. If that's the case, then the scaling factor would depend on λ, and we can find the λ that minimizes this scaling factor.Wait, but affine transformations generally preserve ratios along lines, so if we have points dividing each side in ratio λ, then the inner polygon might be similar to the original, scaled by some factor. But maybe not exactly similar, unless the polygon is regular. But since the problem doesn't specify the polygon is regular, it's probably for a general polygon.Alternatively, let's think of the inner polygon as formed by cutting off corners of the original polygon. Each corner is cut in a way determined by λ. But depending on λ, the area removed would vary. To minimize the area of the inner polygon, we need to maximize the area removed. Wait, but the problem is to minimize the area of the inner polygon, so we need to maximize the area removed. However, how does λ affect the area removed? Maybe there's an optimal λ where the area removed is maximized.Alternatively, maybe there's a linear algebra approach. Let me suppose that the coordinates of Bi are given by Bi = (1 - λ)Ai + λAi+1. Then, the inner polygon is B1B2...Bn, where each Bi is a convex combination of Ai and Ai+1. Then, the area of the inner polygon can be expressed in terms of the original polygon's area and λ.But how?For a triangle, if we connect points that divide each side in ratio λ, the inner triangle's area is (1 - 3λ + 3λ²) times the original area. Then, to minimize this quadratic expression, we can take derivative with respect to λ and find the minimum. Wait, for a triangle, the formula might be different. Let me check.Suppose we have a triangle ABC, and points D, E, F on BC, AC, and AB respectively, such that BD/BC = λ, CE/CA = λ, AF/AB = λ. Then, the area of DEF can be calculated using barycentric coordinates or determinants.Alternatively, using vectors. Let’s assign coordinates. Let’s say A is at (0,0), B at (1,0), C at (0,1). Then, D is on BC: B is (1,0), C is (0,1), so BC is from (1,0) to (0,1). A point dividing BC in ratio λ:(1 - λ) from B to C would be (1 - λ, λ). Similarly, E is on AC: A is (0,0), C is (0,1), so E is (0, λ). F is on AB: A is (0,0), B is (1,0), so F is (λ, 0). Then, the inner triangle DEF has coordinates D(1 - λ, λ), E(0, λ), F(λ, 0). The area of DEF can be computed using the shoelace formula:Area = ½ |(1 - λ)(λ - 0) + 0(0 - λ) + λ(λ - λ)|= ½ | (1 - λ)λ + 0 + 0 | = ½ λ(1 - λ)Wait, that's ½ λ(1 - λ). But the original triangle's area is ½. So the ratio is λ(1 - λ). Wait, but if that's the case, then the area of DEF is ½ * λ(1 - λ). But that seems too small. Wait, maybe my coordinates are incorrect.Wait, in my coordinate system, the original triangle has area ½. The inner triangle DEF has coordinates D(1 - λ, λ), E(0, λ), F(λ, 0). Let's compute the area correctly.Compute using shoelace formula:List the coordinates in order: D(1 - λ, λ), E(0, λ), F(λ, 0), back to D(1 - λ, λ).Compute sum of x_i y_{i+1}:(1 - λ)*λ + 0*0 + λ*λ = λ(1 - λ) + 0 + λ² = λ - λ² + λ² = λSum of y_i x_{i+1}:λ*0 + λ*λ + 0*(1 - λ) = 0 + λ² + 0 = λ²Subtract the two sums: |λ - λ²| = |λ(1 - λ)|So area is ½ |λ(1 - λ)|. Since λ is between 0 and 1, it's ½ λ(1 - λ). So the ratio compared to the original triangle is λ(1 - λ). Wait, but the original area is ½, so DEF area is ½ * λ(1 - λ). But to minimize the area of DEF, we need to minimize λ(1 - λ). The minimal value of λ(1 - λ) is 0, achieved at λ=0 or λ=1. But that doesn't make sense because if λ=0, the points would be at the vertices, so DEF would collapse to a point, area zero. Similarly, λ=1, points would be at the other vertices, also collapsing the triangle. But in between, the maximum area is at λ=1/2, giving 1/4, so DEF area is 1/8, which is half of the maximum. But the problem is about the minimal area, which would be zero. But this contradicts the problem statement, which probably implies a non-degenerate polygon.Wait, maybe the problem is not about triangles but about polygons in general, and maybe for higher n, the minimal area occurs at a certain λ. Wait, but in the triangle case, the minimal area is zero, but maybe for polygons with more sides, there's a unique minimum. Wait, let's check for a quadrilateral.Take a convex quadrilateral, like a square. Let's divide each side at ratio λ from each vertex. Then connect those points. What's the area of the inner quadrilateral?Suppose we have a square with vertices at (0,0), (1,0), (1,1), (0,1). The points dividing each side at ratio λ would be:On (0,0)-(1,0): (λ, 0)On (1,0)-(1,1): (1, λ)On (1,1)-(0,1): (1 - λ, 1)On (0,1)-(0,0): (0, 1 - λ)Connecting these points forms a smaller quadrilateral. Let's compute its area.Using shoelace formula:Coordinates in order: (λ, 0), (1, λ), (1 - λ, 1), (0, 1 - λ), back to (λ, 0).Compute sum of x_i y_{i+1}:λ*λ + 1*1 + (1 - λ)* (1 - λ) + 0*0= λ² + 1 + (1 - 2λ + λ²) + 0= λ² + 1 + 1 - 2λ + λ²= 2λ² - 2λ + 2Sum of y_i x_{i+1}:0*1 + λ*(1 - λ) + 1*0 + (1 - λ)*λ= 0 + λ(1 - λ) + 0 + λ(1 - λ)= 2λ(1 - λ)Subtract the two sums:(2λ² - 2λ + 2) - 2λ(1 - λ) = 2λ² - 2λ + 2 - 2λ + 2λ²= 4λ² - 4λ + 2Take absolute value and multiply by ½:Area = ½ |4λ² - 4λ + 2| = ½ (4λ² - 4λ + 2) since the quadratic is always positive.Original area of the square is 1, so the ratio is ½ (4λ² - 4λ + 2) = 2λ² - 2λ + 1.To find the minimum of this quadratic in λ, take derivative: d/dλ (2λ² - 2λ + 1) = 4λ - 2. Set to zero: 4λ - 2 = 0 => λ = ½. Then, check the second derivative: 4 > 0, so it's a minimum. The minimal area is 2*(1/2)^2 - 2*(1/2) + 1 = 2*(1/4) -1 +1 = ½ -1 +1 = ½. So the minimal area is ½, which is achieved when λ=1/2. Wait, that's interesting. For the square, dividing each side at the midpoint (λ=1/2) gives the inner quadrilateral with minimal area, which is half the original area. But is this the case for all quadrilaterals?Wait, let's test another quadrilateral. Suppose a rectangle that's not a square. Let's say with vertices at (0,0), (a,0), (a,b), (0,b). Then, the inner quadrilateral's coordinates would be (λ a, 0), (a, λ b), (a - λ a, b), (0, b - λ b). Let's compute the area.Using shoelace formula:Coordinates: (λ a, 0), (a, λ b), (a(1 - λ), b), (0, b(1 - λ)), back to (λ a, 0).Sum of x_i y_{i+1}:λ a * λ b + a * b + a(1 - λ) * b(1 - λ) + 0 * 0= λ² a b + a b + a b (1 - λ)^2 + 0= a b [ λ² + 1 + (1 - 2λ + λ²) ]= a b [ 2λ² - 2λ + 2 ]Sum of y_i x_{i+1}:0 * a + λ b * a(1 - λ) + b * 0 + b(1 - λ) * λ a= 0 + λ b a (1 - λ) + 0 + b(1 - λ) λ a= 2 λ a b (1 - λ)Subtract the two sums:a b [2λ² - 2λ + 2 - 2λ(1 - λ)] = a b [2λ² - 2λ + 2 - 2λ + 2λ²]= a b [4λ² - 4λ + 2]Then area is ½ * a b [4λ² - 4λ + 2]Original area is a b, so ratio is ½ (4λ² - 4λ + 2) = 2λ² - 2λ + 1, same as the square case. So the minimal area occurs at λ=1/2, giving 2*(1/4) - 2*(1/2) + 1 = ½ -1 +1=½. So, same as the square.Therefore, for quadrilaterals, it seems the minimal area is achieved when λ=1/2. But for triangles, as we saw earlier, the minimal area is zero when λ approaches 0 or 1. So there's a contradiction here. But the problem states "a polygon A1A2...An", so maybe n is at least 4? But the problem didn't specify. Wait, maybe the problem is considering a polygon where the inner polygon is non-degenerate, so for triangles, the minimal area would not be considered as zero. Wait, but in the problem statement, it's not specified. Hmm.Wait, perhaps there's a different approach. Maybe using linear algebra. Let's model each point as a linear combination of the original vertices. If each new vertex Bi is a convex combination of Ai and Ai+1, then the transformation from the original polygon to the inner polygon can be represented as a matrix. For the entire polygon, the area scaling factor would be determinant of that transformation. However, since each Bi depends only on Ai and Ai+1, this might not be a linear transformation but an affine one. However, perhaps for a regular polygon, the scaling factor can be determined.Alternatively, consider that the inner polygon is similar to the original polygon scaled by a factor. If we can find the scaling factor in terms of λ, then the area would scale by the square of the scaling factor, and we can minimize that. But similarity might only hold for regular polygons.Wait, for a regular polygon, if you connect points that divide each side in ratio λ, the inner polygon is also regular, and scaled by some factor. Let's take a regular pentagon, for example. If each side is divided in ratio λ, the inner polygon would be a smaller regular pentagon. The scaling factor can be calculated using trigonometry. Then, the area would be (scaling factor)^2 times the original area. Then, the problem reduces to finding λ that minimizes the scaling factor. However, since regular polygons are highly symmetric, maybe the minimal area occurs at λ=1/2, similar to the quadrilateral case. But in the triangle case, that's not true. Wait, but in the triangle case, the inner figure is a triangle, but not similar to the original. So maybe only for even-sided polygons, or specific n, the minimal area occurs at λ=1/2. But the problem states "a polygon" without specifying the number of sides, so maybe the answer is λ=1/2 regardless of n? But for triangles, that's not the case.Wait, perhaps there's a different approach. Let's consider that the inner polygon is formed by cutting off a corner from each side of the original polygon. Each cut is a line segment joining two points that divide adjacent sides in ratio λ. The area removed by each cut can be considered as a small triangle or trapezoid. If we can compute the total area removed and then find λ that maximizes it, thus minimizing the remaining area.But how exactly is the area removed? Let's take a polygon and consider one vertex, say A1. The original polygon has sides A1A2 and A1An. The points B1 and Bn divide A1A2 and A1An in ratio λ. The line connecting B1 and Bn would form a part of the inner polygon, cutting off a corner near A1. The area removed near A1 would be a quadrilateral or triangle. However, calculating this for each vertex might be complex.Alternatively, think of the inner polygon as the original polygon scaled and translated. But scaling would require all sides to be scaled uniformly, which might not be the case unless the original polygon is regular.Alternatively, use the concept of homothety. A homothety is a transformation that scales the figure about a fixed point. If the inner polygon is a homothety image of the original, then the scaling factor would be related to λ. But unless the polygon is regular or has certain symmetry, the inner polygon might not be a homothety image.Alternatively, consider a general polygon and parametrize each point Bi as Bi = (1 - λ)Ai + λAi+1. Then, the inner polygon is formed by these Bi points. Let's express the area of the inner polygon in terms of the original area and λ.Assuming linearity, perhaps the area of the inner polygon is a quadratic function of λ. For the quadrilateral, we saw it was 2λ² - 2λ + 1 times the original area. For the triangle, it was λ(1 - λ) times the original area. Wait, but in the triangle case, it's a quadratic function as well, but with maximum at λ=1/2. Wait, but for the triangle, the area is λ(1 - λ), which is a downward-opening parabola, peaking at λ=1/2. So to minimize the inner area, you go to λ=0 or 1, but for quadrilaterals, it's an upward-opening parabola (since the coefficient of λ² is positive) with minimum at λ=1/2. So that's conflicting. So for triangles, the minimal inner area is zero (at λ=0 or 1), but for quadrilaterals, it's ½ the original area at λ=1/2.Hence, the answer might depend on the number of sides. But the problem doesn't specify n. Wait, the problem says "a polygon A1A2...An", so n is given, but the problem is asking for which λ in general, regardless of n? But how? The answer seems to differ based on n.Wait, but maybe there's a general formula. Let's suppose that for a polygon with n sides, the area of the inner polygon formed by dividing each side in ratio λ is a quadratic function of λ, and we need to find the λ that minimizes it. If for quadrilaterals it's minimized at 1/2, and for triangles it's minimized at 0 or 1, but the problem states "polygon" without specifying. Wait, the problem says "the area of the resulting polygon is the smallest". If the polygon is convex, maybe for even n, the minimal area is at λ=1/2, and for odd n, maybe different. But the problem doesn't specify convexity or number of sides. This is confusing.Wait, perhaps the problem is referring to a specific construction where the inner polygon is similar to the original one. For instance, in a regular polygon, connecting points that divide the sides in ratio λ would create a similar regular polygon scaled by some factor. Then, the area would be the square of the scaling factor times the original area. If this scaling factor is a linear function of λ, then the area would be quadratic in λ, and we can minimize it. But this might only hold for regular polygons.Alternatively, consider that for any polygon, connecting the points that divide each side in ratio λ results in an inner polygon whose area is a quadratic function of λ. Then, the minimal area would occur at λ=1/2. But in the triangle case, that's not true. Wait, but in the triangle case, when λ=1/2, the inner triangle's area is 1/4 of the original, which is the maximum area for the inner triangle, not the minimum. So that contradicts the quadrilateral case.Alternatively, maybe the problem is ill-posed unless more constraints are given. But the problem says "a polygon", so perhaps it's a general polygon, and the answer is λ=1/(1 + something). Wait, perhaps the key lies in using vectors or linear transformations.Let me consider the general case. Let the original polygon have vertices A1, A2, ..., An. Each point Bi divides the side AiAi+1 in the ratio λ:1-λ, i.e., Bi = (1 - λ)Ai + λAi+1.Then, the inner polygon is B1B2...Bn. To compute its area, let's express each Bi in terms of Ai and Ai+1.The area of a polygon can be calculated as ½ |Σ (xi yi+1 - xi+1 yi)|.But to compute the area of B1B2...Bn, we need coordinates of Bi. Let me suppose that the original polygon is in the plane with coordinates Ai = (xi, yi). Then, Bi = ( (1 - λ)xi + λ xi+1, (1 - λ)yi + λ yi+1 ). Then, the coordinates of Bi are linear combinations of Ai and Ai+1.Now, let's compute the area of the inner polygon.The area of the inner polygon is ½ |Σ [ ((1 - λ)xi + λ xi+1) * ((1 - λ)yi+1 + λ yi+2) - ((1 - λ)xi+1 + λ xi+2) * ((1 - λ)yi + λ yi+1) ] |.This seems complex, but maybe we can expand this expression and see if it simplifies.Let me denote:For each term in the sum, which corresponds to vertex i:Term_i = [ ( (1 - λ)xi + λ xi+1 ) * ( (1 - λ)yi+1 + λ yi+2 ) ] - [ ( (1 - λ)xi+1 + λ xi+2 ) * ( (1 - λ)yi + λ yi+1 ) ]Expanding Term_i:= [ (1 - λ)^2 xi yi+1 + (1 - λ)λ xi yi+2 + λ(1 - λ) xi+1 yi+1 + λ^2 xi+1 yi+2 ] - [ (1 - λ)^2 xi+1 yi + (1 - λ)λ xi+1 yi+1 + λ(1 - λ) xi+2 yi + λ^2 xi+2 yi+1 ]This is quite messy, but let's collect terms by powers of λ.First, expand all terms:First part:- (1 - λ)^2 xi yi+1- (1 - λ)λ xi yi+2- λ(1 - λ) xi+1 yi+1- λ^2 xi+1 yi+2Second part:- (1 - λ)^2 xi+1 yi- (1 - λ)λ xi+1 yi+1- λ(1 - λ) xi+2 yi- λ^2 xi+2 yi+1Subtracting the second part from the first:Term_i = (1 - λ)^2 xi yi+1 + (1 - λ)λ xi yi+2 + λ(1 - λ) xi+1 yi+1 + λ^2 xi+1 yi+2 - (1 - λ)^2 xi+1 yi - (1 - λ)λ xi+1 yi+1 - λ(1 - λ) xi+2 yi - λ^2 xi+2 yi+1Now, group similar terms:Terms with (1 - λ)^2:(1 - λ)^2 (xi yi+1 - xi+1 yi)Terms with (1 - λ)λ:(1 - λ)λ [xi yi+2 - xi+1 yi+1 - xi+1 yi+1 + ... Wait, let me check:Wait, the first part has (1 - λ)λ xi yi+2 and λ(1 - λ) xi+1 yi+1, and the second part has -(1 - λ)λ xi+1 yi+1 and -λ(1 - λ) xi+2 yi.So the (1 - λ)λ terms:(1 - λ)λ [xi yi+2 + xi+1 yi+1 - xi+1 yi+1 - xi+2 yi] = (1 - λ)λ [xi yi+2 - xi+2 yi]Terms with λ^2:λ^2 [xi+1 yi+2 - xi+2 yi+1]So overall, Term_i = (1 - λ)^2 (xi yi+1 - xi+1 yi) + (1 - λ)λ (xi yi+2 - xi+2 yi) + λ^2 (xi+1 yi+2 - xi+2 yi+1)Now, sum over all i from 1 to n, keeping in mind that indices wrap around (i.e., xn+1 = x1, etc.).Let me denote the original area as A = ½ |Σ (xi yi+1 - xi+1 yi)|.Now, the area of the inner polygon is ½ |Σ Term_i |.Let's compute Σ Term_i:Σ Term_i = Σ [ (1 - λ)^2 (xi yi+1 - xi+1 yi) + (1 - λ)λ (xi yi+2 - xi+2 yi) + λ^2 (xi+1 yi+2 - xi+2 yi+1) ]Break this into three sums:S1 = (1 - λ)^2 Σ (xi yi+1 - xi+1 yi) = (1 - λ)^2 * 2AS2 = (1 - λ)λ Σ (xi yi+2 - xi+2 yi)S3 = λ^2 Σ (xi+1 yi+2 - xi+2 yi+1) = λ^2 Σ (xi+1 yi+2 - xi+2 yi+1)Note that in S3, shifting the index i by 1 (since it's cyclic), we get Σ (xi yi+1 - xi+1 yi) which is again 2A. Wait, let's check:In S3, xi+1 yi+2 - xi+2 yi+1. If we let j = i+1, then when i ranges from 1 to n, j ranges from 2 to n+1, which is equivalent to 1 to n. So Σ (xj yj+1 - xj+1 yj) = 2A. Hence, S3 = λ^2 * 2A.Similarly, S2 = (1 - λ)λ Σ (xi yi+2 - xi+2 yi)Let me see if this sum can be related to the original area. Let's try to manipulate the sum Σ (xi yi+2 - xi+2 yi). Let's shift index in the second term:Σ xi yi+2 - Σ xi+2 yi = Σ xi yi+2 - Σ xi yi-2 (by shifting i to i-2)But since the polygon is cyclic, yi-2 = yi+n-2, which complicates things. Alternatively, note that Σ xi yi+2 = Σ xi yi+2, and Σ xi+2 yi = Σ xi yi-2. However, due to the cyclic nature, Σ xi yi-2 = Σ xi yi+2 (shifting index by 2). Therefore, Σ (xi yi+2 - xi+2 yi) = Σ xi yi+2 - Σ xi+2 yi = 0? Wait, that can't be right. Let me check with a small n.Take n=4 (quadrilateral). Then:Σ (xi yi+2 - xi+2 yi) for i=1 to 4:For i=1: x1 y3 - x3 y1For i=2: x2 y4 - x4 y2For i=3: x3 y1 - x1 y3For i=4: x4 y2 - x2 y4Adding these up:(x1 y3 - x3 y1) + (x2 y4 - x4 y2) + (x3 y1 - x1 y3) + (x4 y2 - x2 y4) = 0Hence, S2 = (1 - λ)λ * 0 = 0.Therefore, for quadrilaterals, the middle term cancels out. Similarly, for other n?Let me check n=3 (triangle):Σ (xi yi+2 - xi+2 yi) for i=1 to 3:i=1: x1 y3 - x3 y1i=2: x2 y1 - x1 y2i=3: x3 y2 - x2 y3Sum: (x1 y3 - x3 y1) + (x2 y1 - x1 y2) + (x3 y2 - x2 y3). Does this sum to zero?Let's see:= x1 y3 - x3 y1 + x2 y1 - x1 y2 + x3 y2 - x2 y3Group terms:x1(y3 - y2) + x2(y1 - y3) + x3(y2 - y1)This is equal to:x1(y3 - y2) + x2(y1 - y3) + x3(y2 - y1) = x1(y3 - y2) + x2(y1 - y3) + x3(y2 - y1)If we factor out, it's equivalent to:(x1 - x3)(y3 - y2) + (x2 - x1)(y1 - y3) + ... Hmm, maybe not obviously zero. Let's plug in coordinates for a specific triangle.Take A1(0,0), A2(1,0), A3(0,1). Then:x1=0, y1=0; x2=1, y2=0; x3=0, y3=1.Compute the sum:0*1 - 0*0 + 1*0 - 0*0 + 0*0 - 1*1 = 0 - 0 + 0 - 0 + 0 -1 = -1 ≠ 0. So for n=3, the sum is not zero. Therefore, S2 is not necessarily zero for all n.Therefore, for triangles, the middle term doesn't cancel out, but for quadrilaterals, it does. Hence, the expression for the area depends on n.Thus, for quadrilaterals and higher n, S2=0, so the area of the inner polygon is S1 + S3 = (1 - λ)^2 * 2A + λ^2 * 2A = 2A[(1 - λ)^2 + λ^2] = 2A(1 - 2λ + 2λ²). Then, the ratio is (1 - 2λ + 2λ²). To minimize this, take derivative: d/dλ (1 - 2λ + 2λ²) = -2 + 4λ. Set to zero: λ = 2/4 = 1/2. So for quadrilaterals, the minimal area ratio is 1 - 2*(1/2) + 2*(1/2)^2 = 1 -1 + 0.5 = 0.5, which matches our earlier result.For triangles, the expression includes S2. Let's compute S1, S2, S3 for triangles.Given a triangle with n=3:Σ Term_i = S1 + S2 + S3 = (1 - λ)^2 * 2A + (1 - λ)λ * Σ (xi yi+2 - xi+2 yi) + λ^2 * 2A.But in the triangle case, what is Σ (xi yi+2 - xi+2 yi)?For triangle A1, A2, A3:i=1: x1 y3 - x3 y1i=2: x2 y1 - x1 y2i=3: x3 y2 - x2 y3Sum = x1 y3 - x3 y1 + x2 y1 - x1 y2 + x3 y2 - x2 y3.Let me rearrange:= x1(y3 - y2) + x2(y1 - y3) + x3(y2 - y1)= x1(y3 - y2) + x2(y1 - y3) + x3(y2 - y1)This can be written as determinant:| x1 x2 x3 || y1 y2 y3 || 1 1 1 |But scaled by some factor. Wait, actually, the area of the triangle is ½ |x1(y2 - y3) + x2(y3 - y1) + x3(y1 - y2)|, which is similar but not exactly the same. Let's see:Our sum S2_sum = x1(y3 - y2) + x2(y1 - y3) + x3(y2 - y1) = - [x1(y2 - y3) + x2(y3 - y1) + x3(y1 - y2)] = -2A * 2, since the area A = ½ |sum|. Therefore, S2_sum = -4A.Wait, let's confirm with specific coordinates. Take A1(0,0), A2(1,0), A3(0,1). Then:S2_sum = 0*(1 - 0) + 1*(0 - 0) + 0*(0 - 0) - ... Wait, no. Wait, in our previous example, plugging in the coordinates:x1=0, y1=0; x2=1, y2=0; x3=0, y3=1.Compute S2_sum:0*(1 - 0) + 1*(0 - 0) + 0*(0 - 0) - [0*(0 - 0) + 1*(0 - 1) + 0*(0 - 0)]? Wait, no.Wait, in our earlier calculation for this triangle, the sum was -1. The area A is ½, so -4A = -2, but we had S2_sum = -1. Hmm, discrepancy.Wait, maybe my previous assertion is incorrect. Let's compute:For A1(0,0), A2(1,0), A3(0,1):S2_sum = x1 y3 - x3 y1 + x2 y1 - x1 y2 + x3 y2 - x2 y3= 0*1 - 0*0 + 1*0 - 0*0 + 0*0 - 1*1= 0 - 0 + 0 - 0 + 0 -1 = -1The area A is ½, so -1 = -2A * 1. Therefore, S2_sum = -2A * 1, not -4A. So in this case, S2_sum = -2A.Therefore,<think>Okay, so I have this problem here about a polygon A1A2...An that's bounded by points dividing each side in the same ratio λ. The question is asking for the value of λ that makes the area of this new polygon as small as possible. Hmm, interesting. Let me try to visualize this. First, let's break down the problem. We have a polygon with vertices A1, A2, ..., An. Each side is being divided by a point in the ratio λ. So, for example, on side A1A2, the point that divides it would be closer to A1 if λ is less than 1, and closer to A2 if λ is greater than 1. Then these points are connected to form a new polygon inside the original one. The goal is to find the λ that minimizes the area of this inner polygon.I think the first step is to consider a specific case, maybe a triangle or a quadrilateral, to see if I can find a pattern or formula. Let's start with a triangle since it's the simplest polygon.Suppose we have a triangle A1A2A3. Each side is divided in the ratio λ. Let's denote the points dividing the sides as B1, B2, B3. So, B1 divides A1A2 in the ratio λ:1, meaning A1B1/B1A2 = λ. Similarly for the other sides. Then the inner polygon is triangle B1B2B3. We need to find the value of λ that minimizes the area of B1B2B3.To find the area of B1B2B3 relative to the original triangle, maybe I can use coordinates. Let me assign coordinates to the original triangle. Let's place A1 at (0, 0), A2 at (1, 0), and A3 at (0, 1). Then the coordinates of B1, B2, B3 can be found based on λ.Since B1 divides A1A2 in the ratio λ:1, the coordinates of B1 would be ((λ*1 + 1*0)/(λ + 1), (λ*0 + 1*0)/(λ + 1)) = (λ/(λ + 1), 0). Wait, no. Wait, ratio λ:1 means that the segment from A1 to B1 is λ parts, and from B1 to A2 is 1 part. So the coordinate of B1 should be (λ/(λ + 1), 0). Similarly, B2 divides A2A3 in ratio λ:1. The coordinates of A2 are (1, 0), A3 are (0, 1). So B2's coordinates would be ((λ*0 + 1*1)/(λ + 1), (λ*1 + 1*0)/(λ + 1)) = (1/(λ + 1), λ/(λ + 1)). Similarly, B3 divides A3A1 in ratio λ:1. A3 is (0,1), A1 is (0,0). So B3 is ((λ*0 + 1*0)/(λ +1), (λ*0 + 1*1)/(λ +1)) = (0, 1/(λ +1)).Now we have the coordinates of B1, B2, B3. Let's compute the area of triangle B1B2B3 using the shoelace formula. Coordinates are:B1: (λ/(λ +1), 0)B2: (1/(λ +1), λ/(λ +1))B3: (0, 1/(λ +1))The area is ½ |(x1(y2 - y3) + x2(y3 - y1) + x3(y1 - y2))|Plugging in:½ | [λ/(λ +1)*(λ/(λ +1) - 1/(λ +1)) + 1/(λ +1)*(1/(λ +1) - 0) + 0*(0 - λ/(λ +1)) ] |Simplify inside the absolute value:First term: λ/(λ +1) * ( (λ - 1)/(λ +1) ) = λ(λ -1)/(λ +1)^2Second term: 1/(λ +1) * (1/(λ +1)) = 1/(λ +1)^2Third term: 0So total inside the absolute value: [λ(λ -1) + 1]/(λ +1)^2Therefore, the area is ½ * | (λ² - λ +1)/(λ +1)^2 | Since all terms are positive (assuming λ >0), we can drop the absolute value.So area ratio compared to original triangle. Wait, the original triangle area is ½ * base * height = ½ *1*1= ½. So the area of B1B2B3 is ½ * (λ² - λ +1)/(λ +1)^2. But wait, when λ=0, the inner triangle area should be ½*(0 -0 +1)/(1)^2= ½*1=½, which is the same as the original triangle. That can't be right. Wait, if λ=0, all the points B1, B2, B3 would collapse to A1, A2, A3, so the inner triangle would actually coincide with the original triangle. But according to the formula, when λ=0, the area is ½*(0 -0 +1)/(0 +1)^2=½*1=½, which matches. But if λ approaches infinity, then the inner triangle would shrink towards the centroid? Let's see. If λ approaches infinity, then each point B1, B2, B3 approaches A2, A3, A1 respectively? Wait, if λ is very large, then B1 is close to A2, B2 close to A3, B3 close to A1. Then the inner triangle would be similar to the original triangle but scaled down. Let's check the formula as λ approaches infinity. The area becomes ½*(λ² -λ +1)/(λ² + 2λ +1) ≈ ½*(λ²)/(λ²)=½. But that contradicts intuition. If the inner triangle is approaching the original triangle as λ approaches infinity, but according to the formula, the area is approaching ½, which is the same as original. Wait, but when λ is infinite, the inner triangle would actually be the triangle formed by points very close to the vertices, but maybe it's not approaching zero? Wait, perhaps I need to check with λ=1. If λ=1, then B1 is the midpoint of A1A2, so (0.5,0), B2 is midpoint of A2A3, (0.5,0.5), B3 is midpoint of A3A1, (0,0.5). The area of this inner triangle can be calculated. Let's compute it with the formula. For λ=1:Area = ½*(1 -1 +1)/(1 +1)^2= ½*(1)/4= 1/8. But original area is ½, so ratio is 1/4. Wait, but the actual area of the inner triangle when λ=1 (midpoints) should form a medial triangle, which has area 1/4 of the original. So ½*(1/4)=1/8? Wait no, the formula gives ½*(1)/4=1/8, but the original area is ½, so the inner area would be 1/8 / (1/2) = 1/4. So the formula is correct. So when λ=1, the inner area is 1/4 of original. But according to the formula, the area as a function of λ is ½*(λ² -λ +1)/(λ +1)^2. Wait, but the original area is ½, so the ratio of inner area to original area is (λ² -λ +1)/(λ +1)^2. So to minimize the area, we need to minimize (λ² -λ +1)/(λ +1)^2.Wait, so in this specific case of a triangle, the ratio is (λ² -λ +1)/(λ +1)^2. Let's find the minimum of this function. Let me set f(λ) = (λ² -λ +1)/(λ +1)^2. Take derivative f’(λ):Using quotient rule: [ (2λ -1)(λ +1)^2 - (λ² -λ +1)(2)(λ +1) ] / (λ +1)^4Simplify numerator:(2λ -1)(λ +1)^2 - 2(λ² -λ +1)(λ +1)Factor out (λ +1):(λ +1)[ (2λ -1)(λ +1) - 2(λ² -λ +1) ]Compute inside the brackets:(2λ -1)(λ +1) = 2λ(λ) +2λ(1) -1(λ) -1(1) = 2λ² +2λ -λ -1 = 2λ² +λ -1Then subtract 2(λ² -λ +1) = 2λ² -2λ +2So total:2λ² +λ -1 -2λ² +2λ -2 = (2λ² -2λ²) + (λ +2λ) + (-1 -2) = 3λ -3Therefore, numerator is (λ +1)(3λ -3) = 3(λ +1)(λ -1)So derivative f’(λ)= 3(λ +1)(λ -1)/(λ +1)^4 = 3(λ -1)/(λ +1)^3Set derivative equal to zero: 3(λ -1)/(λ +1)^3 =0 => λ=1Check second derivative or intervals. For λ <1, say λ=0, f’(0)= 3(-1)/(1)^3= -3 <0. For λ >1, say λ=2, f’(2)=3(1)/(3)^3=3/27=1/9>0. So function decreases until λ=1, then increases. Therefore, the minimum occurs at λ=1. So for the triangle, the minimal area occurs when λ=1, which is the midpoint. That makes sense; the medial triangle has the minimal area? Wait, but when λ approaches 0 or infinity, the area ratio approaches (0 -0 +1)/1=1, so the area approaches the original area. So the minimal area is indeed at λ=1, giving ratio 1/4. Interesting.But the problem is asking for a general polygon, not just a triangle. So maybe the same applies? That the minimal area occurs when λ=1, i.e., the midpoints? But I need to verify.Wait, let's test with a square. Suppose we have a square, and connect points dividing each side in ratio λ. Then compute the area of the inner quadrilateral. Let me assign coordinates.Let’s take a square with vertices A1(0,0), A2(1,0), A3(1,1), A4(0,1). The points dividing each side in ratio λ. So on A1A2: point B1 at (λ/(λ +1), 0). On A2A3: point B2 at (1, λ/(λ +1)). On A3A4: point B3 at ( (λ*0 +1*1)/(λ +1), 1 ) = (1/(λ +1),1). Wait, actually, on A3A4, which is from (1,1) to (0,1), dividing in ratio λ:1. So the coordinates would be ( (λ*0 +1*1)/(λ +1), (λ*1 +1*1)/(λ +1) ) = (1/(λ +1), 1). Wait, no. Wait, A3A4 is from (1,1) to (0,1). The x-coordinate decreases from 1 to 0, y remains 1. So the point dividing A3A4 in ratio λ:1 (from A3 to A4) would be ( (λ*0 +1*1)/(λ +1), (λ*1 +1*1)/(λ +1) ). Wait, but since it's a horizontal line, y-coordinate is always 1. So x-coordinate is 1/(λ +1), y=1. Similarly, on A4A1: from (0,1) to (0,0). Dividing in ratio λ:1, the point B4 would be (0, (λ*0 +1*1)/(λ +1)) = (0,1/(λ +1)).So the four points are:B1: (λ/(λ +1), 0)B2: (1, λ/(λ +1))B3: (1/(λ +1),1)B4: (0,1/(λ +1))Now connect these points to form the inner quadrilateral. Let's compute its area.Using shoelace formula. Coordinates in order:B1: (λ/(λ +1), 0)B2: (1, λ/(λ +1))B3: (1/(λ +1),1)B4: (0,1/(λ +1))Back to B1: (λ/(λ +1),0)Compute area:½ | sum_{i=1 to 4} (xi yi+1 - xi+1 yi) |So:First term: x1 y2 - x2 y1 = (λ/(λ +1))*(λ/(λ +1)) - 1*0 = λ²/(λ +1)^2Second term: x2 y3 - x3 y2 = 1*1 - (1/(λ +1))*(λ/(λ +1)) = 1 - λ/(λ +1)^2Third term: x3 y4 - x4 y3 = (1/(λ +1))*(1/(λ +1)) - 0*1 = 1/(λ +1)^2Fourth term: x4 y1 - x1 y4 = 0*0 - (λ/(λ +1))*(1/(λ +1)) = -λ/(λ +1)^2Sum all terms:λ²/(λ +1)^2 + [1 - λ/(λ +1)^2] + 1/(λ +1)^2 + [-λ/(λ +1)^2]Simplify term by term:First term: λ²/(λ +1)^2Second term: 1 - λ/(λ +1)^2Third term: 1/(λ +1)^2Fourth term: -λ/(λ +1)^2So combine:λ²/(λ +1)^2 + 1 + [ -λ/(λ +1)^2 +1/(λ +1)^2 -λ/(λ +1)^2 ]Wait, let's group the fractions:λ²/(λ +1)^2 +1 + [ (-λ +1 -λ )/(λ +1)^2 ]Which is:λ²/(λ +1)^2 +1 + ( -2λ +1 )/(λ +1)^2Combine terms:[λ² -2λ +1]/(λ +1)^2 +1Note that λ² -2λ +1 = (λ -1)^2So:(λ -1)^2/(λ +1)^2 +1Therefore, total area is ½ * [ (λ -1)^2/(λ +1)^2 +1 ]But wait, let me check my calculations again because the area should depend on λ in a more significant way. Let me redo the summation:Sum of terms:1. λ²/(λ +1)^22. 13. -λ/(λ +1)^24. 1/(λ +1)^25. -λ/(λ +1)^2Wait, no. Wait, the four terms are:First term: λ²/(λ +1)^2Second term: 1 - λ/(λ +1)^2Third term: 1/(λ +1)^2Fourth term: -λ/(λ +1)^2So adding them up:λ²/(λ +1)^2 +1 - λ/(λ +1)^2 +1/(λ +1)^2 -λ/(λ +1)^2So group the constants:1 + [λ²/(λ +1)^2] + [ -λ/(λ +1)^2 +1/(λ +1)^2 -λ/(λ +1)^2 ]Which is 1 + λ²/(λ +1)^2 + (-2λ +1)/(λ +1)^2So total:1 + (λ² -2λ +1)/(λ +1)^2But λ² -2λ +1 is (λ -1)^2, so:1 + (λ -1)^2/(λ +1)^2Therefore, the area is ½ * [1 + (λ -1)^2/(λ +1)^2 ]But the original square has area 1, so this formula gives the area of the inner quadrilateral. Wait, but the original area is 1, so the inner area is ½*(1 + (λ -1)^2/(λ +1)^2 )Wait, that seems off. Let me check with λ=1. If λ=1, then the inner quadrilateral should be the one connecting midpoints, forming a smaller square with area half of the original? Wait, no. Connecting midpoints of a square forms another square rotated by 45 degrees, with area half of the original. Let's compute with the formula:When λ=1, the area is ½*(1 + (1 -1)^2/(1 +1)^2 ) = ½*(1 +0 )=½. Which matches, since the inner square has area ½. Good. If λ approaches 0, the inner quadrilateral area becomes ½*(1 + (0 -1)^2/(0 +1)^2 )=½*(1 +1)=1. Which makes sense because as λ approaches 0, the inner points approach the original vertices, so the quadrilateral becomes the original square. Similarly, when λ approaches infinity, the inner area also approaches 1. So the minimal area occurs at λ=1, giving area ½. Wait, but the problem asks for the value of λ that minimizes the area, so in the case of a square, it's λ=1. But wait, according to the formula, the area is ½*(1 + (λ -1)^2/(λ +1)^2 ). To minimize this, we need to minimize (λ -1)^2/(λ +1)^2, which is minimized when λ=1, giving zero. Therefore, minimal area is ½*(1 +0)=½, achieved at λ=1. So again, λ=1 is the minimizer.Hmm, so for both triangle and square, the minimal area occurs at λ=1. Maybe this is a general result for any polygon? That the minimal area occurs when the points are midpoints, i.e., λ=1.But wait, let's check another polygon, maybe a regular pentagon or something. But since it's complicated, maybe there's a general proof.Alternatively, think about affine transformations. Since affine transformations preserve ratios and areas up to a scalar, the value of λ should be the same regardless of the polygon. Therefore, if for triangle and square the minimal λ is 1, then it should be 1 for any polygon.Alternatively, consider that connecting the midpoints of a polygon creates a similar polygon scaled down by a factor, but in general polygons, it's called the medial polygon. However, in a regular polygon, connecting midpoints would create a smaller regular polygon, but in a general polygon, it might not be similar. However, the problem states that the polygon is "bounded by points that divide the sides in the same ratio λ", so it's a similar process for each side.Alternatively, consider using vectors or complex numbers. Let me think in terms of vectors.Suppose the original polygon has vertices A1, A2, ..., An. Each point dividing the side AiAi+1 in ratio λ:1. So the point Bi can be expressed as Bi = (λ Ai+1 + Ai)/(λ +1). Then the new polygon is B1B2...Bn.To find the area of B1B2...Bn, we can express it in terms of the original polygon's area. Maybe using the formula for the area of a polygon in terms of vectors or coordinates.Alternatively, if we consider the original polygon and the new polygon, the transformation from the original to the new can be represented as a linear transformation. But since each point Bi is a convex combination of adjacent vertices, maybe the transformation is a linear combination of the identity matrix and a cyclic permutation matrix or something. Hmm, this might be getting too abstract.Alternatively, think of the new polygon as the original polygon scaled by some factor and perhaps sheared. But since the ratio λ is the same on all sides, maybe the scaling factor depends on λ. If we can find the scaling factor, then the area would scale by the square of that factor, so minimizing the area would correspond to finding the scaling factor. But I need to verify.Wait, for the triangle and square, when λ=1 (midpoints), the inner polygon's area was 1/4 and 1/2 of the original, respectively. These are different scaling factors, so maybe the scaling depends on the number of sides. Wait, triangle (3 sides) had area 1/4, square (4 sides) had 1/2. Hmmm, not a clear pattern. Wait, but in the triangle, connecting midpoints gives a medial triangle with area 1/4, but in the square, connecting midpoints gives a square rotated by 45 degrees with area 1/2. So maybe it's not a general scaling factor. Therefore, perhaps another approach is needed.Wait, another idea: using the concept of similar polygons. If all sides are divided in the same ratio, the inner polygon might be similar to the original one, but scaled. However, this is only true for regular polygons. For irregular polygons, the inner polygon might not be similar. But the problem doesn't specify the polygon is regular. So maybe the answer is general for any polygon, regular or not.Alternatively, use linear algebra. Let's model the polygon as a vector of vertices and express the new polygon's vertices as a linear combination of the original ones. Then the area can be expressed as a determinant, and we can find λ that minimizes this determinant.Alternatively, consider that each vertex of the new polygon is a weighted average of two adjacent vertices of the original polygon. So the transformation from original to new polygon can be represented as a matrix where each new vertex is (Ai + λ Ai+1)/(λ +1). If we arrange this as a linear transformation, maybe the area scaling factor can be found as (1 - 2λ/(λ +1)^2) or something. Wait, not sure.Alternatively, use the formula for the area of a polygon in terms of its vertices. For a polygon with vertices (x1,y1), (x2,y2), ..., (xn,yn), the area is ½ |sum_{i=1 to n} (xi yi+1 - xi+1 yi)|, where xn+1=x1, yn+1=y1.If we express each Bi as ( (λ Ai+1 + Ai ) / (λ +1) ), then the coordinates of Bi would be ( (λ xi+1 + xi )/(λ +1), (λ yi+1 + yi )/(λ +1) )Therefore, the new polygon's vertices are Bi = (λ Ai+1 + Ai )/(λ +1). So to compute the area of the new polygon, substitute these coordinates into the area formula.Compute the area of the new polygon:½ | sum_{i=1 to n} [ ( (λ xi+1 + xi )/(λ +1) ) * ( (λ yi+2 + yi+1 )/(λ +1) ) - ( (λ xi+2 + xi+1 )/(λ +1) ) * ( (λ yi+1 + yi )/(λ +1) ) ] |Factor out 1/(λ +1)^2 from each term:½ * 1/(λ +1)^2 | sum_{i=1 to n} [ (λ xi+1 + xi )(λ yi+2 + yi+1 ) - (λ xi+2 + xi+1 )(λ yi+1 + yi ) ] |This seems complex, but maybe we can expand the terms and find a pattern.Let me expand one term in the sum:(λ xi+1 + xi )(λ yi+2 + yi+1 ) = λ^2 xi+1 yi+2 + λ xi+1 yi+1 + λ xi yi+2 + xi yi+1Similarly, the other term:(λ xi+2 + xi+1 )(λ yi+1 + yi ) = λ^2 xi+2 yi+1 + λ xi+2 yi + λ xi+1 yi+1 + xi+1 yiSubtracting the second product from the first:[ λ^2 xi+1 yi+2 + λ xi+1 yi+1 + λ xi yi+2 + xi yi+1 ] - [ λ^2 xi+2 yi+1 + λ xi+2 yi + λ xi+1 yi+1 + xi+1 yi ]Simplify term by term:λ^2 xi+1 yi+2 - λ^2 xi+2 yi+1+ λ xi+1 yi+1 - λ xi+1 yi+1+ λ xi yi+2 - λ xi+2 yi+ xi yi+1 - xi+1 yiNotice that the second terms cancel: λ xi+1 yi+1 - λ xi+1 yi+1 =0So remaining terms:λ^2 (xi+1 yi+2 - xi+2 yi+1 ) + λ (xi yi+2 - xi+2 yi ) + (xi yi+1 - xi+1 yi )Therefore, the entire sum becomes:sum_{i=1 to n} [ λ^2 (xi+1 yi+2 - xi+2 yi+1 ) + λ (xi yi+2 - xi+2 yi ) + (xi yi+1 - xi+1 yi ) ]Notice that when we sum over all i, some terms might telescope or relate to the original area.Let me recall that the original area is ½ | sum_{i=1 to n} (xi yi+1 - xi+1 yi ) |. Let's denote the original area as A = ½ |S|, where S = sum_{i=1 to n} (xi yi+1 - xi+1 yi )Similarly, let's denote other sums:Let T = sum_{i=1 to n} (xi yi+2 - xi+2 yi )And U = sum_{i=1 to n} (xi+1 yi+2 - xi+2 yi+1 )But note that in these sums, indices wrap around because it's a polygon. For example, when i =n, i+1=1, i+2=2, etc.But let's see:First, consider the term U = sum_{i=1}^n (xi+1 yi+2 - xi+2 yi+1 )If we shift the index i by 1, let j = i+1, then when i=1, j=2; when i=n, j=1. So U becomes sum_{j=2}^{n+1} (xj yj+1 - xj+1 yj ). But since j=n+1 corresponds to j=1 (because of polygon wrapping), U is actually equal to sum_{j=1}^n (xj yj+1 - xj+1 yj ) = S. Therefore, U = S.Similarly, consider the term T = sum_{i=1}^n (xi yi+2 - xi+2 yi )Let me try to relate this to S. Let's note that yi+2 is two steps ahead. Let's split the sum:sum_{i=1}^n xi yi+2 - sum_{i=1}^n xi+2 yiThe first sum is sum_{i=1}^n xi yi+2. If we shift index in the second sum: let j = i+2, then when i=1, j=3; when i=n, j=n+2=2 (since it's a polygon). So the second sum becomes sum_{j=3}^{n+2} xj yj-2. But since j-2 wraps around, it's equivalent to sum_{j=1}^n xj+2 yj.Therefore, T = sum_{i=1}^n xi yi+2 - sum_{j=1}^n xj+2 yj = sum_{i=1}^n xi yi+2 - sum_{i=1}^n xi+2 yi = sum_{i=1}^n [xi yi+2 - xi+2 yi]But I don't see a direct relation to S here. However, perhaps integrating by parts or using some cyclic properties.Alternatively, note that T can be written as sum_{i=1}^n xi yi+2 - sum_{i=1}^n xi+2 yi = sum_{i=1}^n xi yi+2 - sum_{i=1}^n xi yi-2 (since shifting index by 2). Wait, if we shift the second sum by -2, then j =i-2, so when i=1, j=-1, which is equivalent to j=n-1 (since it's cyclic). So T = sum_{i=1}^n xi yi+2 - sum_{j=1}^n xj yj-2.But this is sum_{i=1}^n xi (yi+2 - yi-2 ). Hmm, not sure.Alternatively, consider that for each i, yi+2 - yi-2 is related to some difference. But without more structure, it's hard to see.Alternatively, maybe T = sum_{i=1}^n xi yi+2 - sum_{i=1}^n xi+2 yi = sum_{i=1}^n xi yi+2 + sum_{i=1}^n (-xi+2 yi )But perhaps this is equal to sum_{i=1}^n xi yi+2 + sum_{i=1}^n (-xi yi+2 ) by shifting index in the second sum. Wait, let's check:sum_{i=1}^n (-xi+2 yi ) = sum_{i=3}^{n+2} (-xi yi-2 ) = sum_{i=1}^n (-xi yi-2 ) [since indices wrap around]So T = sum_{i=1}^n xi yi+2 - sum_{i=1}^n xi yi-2 = sum_{i=1}^n xi ( yi+2 - yi-2 )But unless the polygon has some symmetry, this might not simplify. Perhaps in a convex polygon, but since the problem doesn't specify, we can't assume that.Therefore, maybe it's not straightforward to relate T to S. Let's see.But if we go back to the expression for the area of the inner polygon:Area = ½ * 1/(λ +1)^2 | λ^2 U + λ T + S | = ½ * 1/(λ +1)^2 | λ^2 S + λ T + S | = ½ * | (λ^2 S + λ T + S ) / (λ +1)^2 |.Since the original area is ½ |S|, the ratio of the areas is | (λ^2 S + λ T + S ) / ( (λ +1)^2 S ) | = | (λ^2 +1 + λ T/S ) / (λ +1)^2 |.But unless T/S is a constant, this ratio depends on the specific polygon. However, the problem states "a polygon", not "any polygon", so perhaps the answer is independent of the polygon. Wait, but in the problem statement, it says "a polygon A1A2...An is bounded by points that divide the sides... in the same ratio λ. For which value of λ is the area of the resulting polygon the smallest?"Wait, is the problem asking for a general answer regardless of the original polygon? Or is it assuming a specific polygon? The problem statement doesn't specify, so maybe it's a general result.But how can that be? For example, in a degenerate polygon (almost a line segment), the minimal area might be different. Wait, but maybe due to affine invariance, the ratio is the same. Wait, affine transformations can change the area but preserve ratios. If we apply an affine transformation to the original polygon, the ratio λ would remain the same, and the area ratio would also remain the same. Therefore, the value of λ that minimizes the area ratio should be the same for all polygons, as affine transformations can make any polygon into another.But since we saw for triangle and square, the minimal λ is 1, then maybe in general it is 1.Alternatively, think about the area ratio as a function of λ, which in the case of the triangle was (λ² -λ +1)/(λ +1)^2, and for the square was [1 + (λ -1)^2/(λ +1)^2 ] /2. Wait, but these are different functions, but both minimized at λ=1. Wait, let's check.For the triangle, the ratio was (λ² -λ +1)/(λ +1)^2. Let's compute this function:(λ² -λ +1)/(λ² + 2λ +1). Let's compute derivative:As before, derivative was 3(λ -1)/(λ +1)^3, so minimum at λ=1.For the square, the ratio was ½*(1 + (λ -1)^2/(λ +1)^2 ). To minimize this, we need to minimize (λ -1)^2/(λ +1)^2, which is minimized at λ=1. Therefore, in both cases, λ=1 is the minimizer.Even though the expressions for the area ratio are different, they both achieve their minima at λ=1. Therefore, perhaps for any polygon, regardless of its shape, the minimal area occurs at λ=1.Alternatively, maybe there's a general formula for the area ratio as a function of λ for any polygon, which is minimized at λ=1.Wait, another approach: consider that connecting points that divide sides in ratio λ corresponds to a homothety (scaling) transformation about the centroid or some other point. However, homothety would scale all sides equally, but unless the polygon is centrally symmetric, this might not hold. However, when λ=1, connecting midpoints might correspond to a similarity transformation.Alternatively, recall that for any polygon, connecting the midpoints of the sides creates a new polygon (called the Varignon polygon for quadrilaterals) whose area is half of the original for convex quadrilaterals. But for triangles, connecting midpoints gives a medial triangle with area 1/4. So in different polygons, the area ratio is different, but the minimal λ is still 1.But the problem is asking for the value of λ that minimizes the area, regardless of the original polygon. But in our specific cases, λ=1 was the minimizer. If we can generalize, maybe λ=1 is always the answer.Alternatively, suppose that for any polygon, when you connect points dividing sides in ratio λ, the area of the inner polygon is a quadratic function of λ, which reaches its minimum at λ=1. But why?Wait, in the triangle case, the area ratio was (λ² -λ +1)/(λ +1)^2. Let's see:(λ² -λ +1)/(λ +1)^2 = (λ² +2λ +1 -3λ)/(λ +1)^2 = 1 - 3λ/(λ +1)^2. Hmm, not helpful. Wait, expanding (λ -1)^2 = λ² -2λ +1. But in the triangle case, the numerator is λ² -λ +1 = (λ -0.5)^2 + 0.75, which is always positive, but not a perfect square.But in the square case, the ratio was ½*(1 + (λ -1)^2/(λ +1)^2 ). Expanding (λ -1)^2/(λ +1)^2 = (λ² -2λ +1)/(λ² + 2λ +1). So for the square, the area ratio is ½*(1 + (λ² -2λ +1)/(λ² +2λ +1)) = ½*( (λ² +2λ +1 + λ² -2λ +1 )/(λ² +2λ +1) ) = ½*(2λ² + 2)/(λ² +2λ +1 ) = (λ² +1)/(λ² +2λ +1 )So for the square, the area ratio is (λ² +1)/(λ +1)^2. Which is similar to the triangle case but different. However, this function also has its minimum at λ=1. Let's check derivative:f(λ) = (λ² +1)/(λ +1)^2f’(λ) = [2λ(λ +1)^2 - (λ² +1)(2)(λ +1) ] / (λ +1)^4Simplify numerator:2λ(λ +1) - 2(λ² +1) = 2λ^2 +2λ -2λ² -2 = 2λ -2 = 2(λ -1)Therefore, f’(λ) = 2(λ]

🔑:Let's determine the value of lambda at which the area of the triangle cut off by the line connecting two adjacent division points of sides a and b of a polygon is the largest!The area of such a triangle is:t=frac{(a-lambda a) cdot lambda b cdot sin gamma}{2}=(1-lambda) cdot lambda frac{a b sin gamma}{2}We need to examine the sum of such expressions.Since the sum of the expressions frac{a b cdot sin gamma}{2} is constant, it is sufficient to determine the value of lambda at which the expression y=(1-lambda) lambda=-lambda^{2}+lambda is maximal. This function can be represented by a parabola with a vertical axis in the lambda, y coordinate system. This parabola intersects the lambda axis at lambda=1 and lambda=0, and its maximum value is at lambda=0.5.text { ifj. Csonka Pal (Budapest, III. o.) }Remark. 1^{circ}. The maximum value of y=frac{1}{4}-left(1-frac{1}{2}right)^{2} is frac{1}{4}, which is attained where the square term is 0, i.e., at lambda=frac{1}{2}.2^{circ}. The statement is not true for degenerate polygons, because in such cases, some of the triangles involved in the calculation represent a decrease, while others represent an increase in the area of the given polygon. Thus, with the increase of the product lambda(lambda-1), the area of the new polygon may either increase or decrease. For example, if we place 45^{circ} angles at the vertices of a square such that the diagonals are the angle bisectors, we get a star-shaped quadrilateral, for which the polygons created in the above manner all have the same area.