🧠:[<think>Okay, let me try to figure this out. So the function given is f(x) = (1 + sinx)^(2n) - (1 - sinx)^(2n), where n is a positive integer. And we have to determine if it's odd, even, both, or neither. The options are A, B, C, D. Hmm.First, let me recall what odd and even functions are. An even function satisfies f(-x) = f(x) for all x in its domain, right? And an odd function satisfies f(-x) = -f(x) for all x. If it's both, then it has to satisfy both conditions, which would only happen if f(x) is identically zero, I think. And if neither, then it doesn't satisfy either condition.So the task is to check whether f(-x) equals f(x) or -f(x). Let's compute f(-x) step by step.First, f(-x) = (1 + sin(-x))^(2n) - (1 - sin(-x))^(2n). Now, sin(-x) is equal to -sinx because sine is an odd function. So substituting that in, we get:f(-x) = (1 - sinx)^(2n) - (1 + sinx)^(2n)Wait, that's interesting. Let's see. The original f(x) is (1 + sinx)^(2n) - (1 - sinx)^(2n). So when we compute f(-x), we get the reverse order: (1 - sinx)^(2n) - (1 + sinx)^(2n). That is exactly -f(x). Because if you flip the order of subtraction, you get the negative. So f(-x) = -f(x). Therefore, f is odd.But wait, let me double-check. Let's compute f(-x):First term: (1 + sin(-x))^(2n) = (1 - sinx)^(2n)Second term: (1 - sin(-x))^(2n) = (1 + sinx)^(2n)So f(-x) = first term - second term = (1 - sinx)^(2n) - (1 + sinx)^(2n) = - [ (1 + sinx)^(2n) - (1 - sinx)^(2n) ] = -f(x). Therefore, yes, f(-x) = -f(x), so it's an odd function. So the answer should be A.Wait, but the exponent is 2n, which is even. Let's consider if that plays a role here. For example, if the exponent were odd, maybe the behavior would be different? Let's think.Suppose instead of 2n, it was 2n+1. Then, the function would be (1 + sinx)^{2n+1} - (1 - sinx)^{2n+1}. Then f(-x) would be (1 - sinx)^{2n+1} - (1 + sinx)^{2n+1} = - [ (1 + sinx)^{2n+1} - (1 - sinx)^{2n+1} ] = -f(x), so still odd. Wait, actually regardless of the exponent being even or odd, the function f(x) = (1 + sinx)^k - (1 - sinx)^k would be odd? Because replacing x with -x swaps the terms and introduces a negative sign. Hmm.But in our problem, the exponent is 2n, which is even. However, the same reasoning applies. So regardless of the exponent being even or odd, f(-x) = -f(x). Therefore, the function is odd. Therefore, the answer is A.Wait, but let me test with a specific example. Let's take n = 1. Then f(x) = (1 + sinx)^2 - (1 - sinx)^2. Let's compute this.First, expand (1 + sinx)^2 = 1 + 2 sinx + sin²xSimilarly, (1 - sinx)^2 = 1 - 2 sinx + sin²xSubtracting them: [1 + 2 sinx + sin²x] - [1 - 2 sinx + sin²x] = 4 sinxSo f(x) = 4 sinx. Which is indeed an odd function, since sin(-x) = -sinx. So f(-x) = 4 sin(-x) = -4 sinx = -f(x). So that's odd. So when n = 1, it's odd.Another test case: n = 2. Then f(x) = (1 + sinx)^4 - (1 - sinx)^4. Let's compute this. Maybe expand it or use the difference of squares.Note that a^4 - b^4 = (a^2 - b^2)(a^2 + b^2). So let's compute a = 1 + sinx, b = 1 - sinx.First compute a^2 - b^2 = (1 + sinx)^2 - (1 - sinx)^2. Which we already did earlier and found it's 4 sinx.Then a^2 + b^2 = (1 + 2 sinx + sin²x) + (1 - 2 sinx + sin²x) = 2 + 2 sin²x.Therefore, f(x) = 4 sinx * (2 + 2 sin²x) = 8 sinx + 8 sin^3x. Which is again an odd function, since each term is odd. Because sinx is odd, sin^3x is odd, and multiplying by constants preserves the oddness. So f(-x) = 8 sin(-x) + 8 sin^3(-x) = -8 sinx -8 sin^3x = -f(x). So indeed, odd function.Therefore, regardless of n, the function is odd. Therefore, the answer is A.But just to be thorough, maybe try n = 3? Although expanding (1 + sinx)^6 - (1 - sinx)^6 might be tedious. Alternatively, note that if we factor this as a difference of even powers.Alternatively, consider that when we have (1 + sinx)^2n - (1 - sinx)^2n, this can be written as [ (1 + sinx)^n ]^2 - [ (1 - sinx)^n ]^2, which is a difference of squares, so factors as [ (1 + sinx)^n - (1 - sinx)^n ][ (1 + sinx)^n + (1 - sinx)^n ].But not sure if that helps. Alternatively, maybe use binomial theorem. Let's expand both terms.Let’s denote f(x) = sum_{k=0}^{2n} C(2n, k) (sinx)^k - sum_{k=0}^{2n} C(2n, k) (-sinx)^k.So f(x) = sum_{k=0}^{2n} C(2n, k) [ (sinx)^k - (-sinx)^k ].Now, note that for even k, (sinx)^k - (-sinx)^k = (sinx)^k - (sinx)^k = 0.For odd k, (sinx)^k - (-sinx)^k = (sinx)^k - (-1)^k (sinx)^k = 2 (sinx)^k.Wait, but if k is even, (-sinx)^k = (sinx)^k. If k is odd, (-sinx)^k = - (sinx)^k. Therefore:For even k: terms cancel.For odd k: terms add up to 2 (sinx)^k.But the exponent k is odd. Therefore, f(x) is equal to sum over all odd k from 1 to 2n of 2 C(2n, k) (sinx)^k.But since 2n is even, the odd k go up to 2n-1.But in any case, all the terms in the expansion are odd functions, because (sinx)^k is odd when k is odd (since sinx is odd, and raising it to an odd power preserves the oddness). And the sum of odd functions is odd. Therefore, f(x) is a sum of odd functions, hence odd. Therefore, regardless of n, f(x) is odd. Therefore, the answer is A.Wait, so according to all the reasoning and test cases, the function is odd. Therefore, option A is correct.But let me check the options again. The options are:A: An odd functionB: An even functionC: Both an odd and an even functionD: Neither an odd nor an even functionSo since f(-x) = -f(x), it's odd. So answer A.But let me check if there's a possibility that f(x) is also even. For that, f(-x) should equal f(x) as well. But if f is both odd and even, then for all x, f(-x) = f(x) and f(-x) = -f(x). Therefore, f(x) = -f(x), which implies f(x) = 0 for all x. But unless the function is identically zero, which it isn't (unless n=0, but n is in N*, so n ≥1). Therefore, f(x) is not the zero function, so it cannot be both. Hence, the answer is A.Final Answerboxed{A}</think>To determine if the function ( f(x) = (1 + sin x)^{2n} - (1 - sin x)^{2n} ) (where ( n in mathbb{N}^* )) is odd, even, both, or neither, we analyze ( f(-x) ).1. Compute ( f(-x) ): - Substitute ( -x ) into the function: [ f(-x) = (1 + sin(-x))^{2n} - (1 - sin(-x))^{2n} ] - Since ( sin(-x) = -sin x ), this becomes: [ f(-x) = (1 - sin x)^{2n} - (1 + sin x)^{2n} ] - This simplifies to: [ f(-x) = -[(1 + sin x)^{2n} - (1 - sin x)^{2n}] = -f(x) ]2. Conclusion: - Since ( f(-x) = -f(x) ), the function ( f(x) ) is an odd function.3. Verification with specific examples: - For ( n = 1 ), ( f(x) = 4 sin x ), which is odd. - For ( n = 2 ), expanding shows ( f(x) = 8 sin x + 8 sin^3 x ), which is odd. - Generalizing using the binomial theorem confirms that all terms in the expansion are odd functions, making ( f(x) ) odd.4. Excluding other options: - The function cannot be even since ( f(-x) neq f(x) ). - It cannot be both odd and even unless it is identically zero, which it is not for ( n in mathbb{N}^* ).Thus, the function ( f(x) ) is an odd function.[boxed{A}],<think>Okay, so I need to figure out whether the function ( f(x) = (1 + sin x)^{2n} - (1 - sin x)^{2n} ) is odd, even, both, or neither. The options are A, B, C, D. Let me recall what odd and even functions are. An even function satisfies ( f(-x) = f(x) ) for all x in its domain, and an odd function satisfies ( f(-x) = -f(x) ). If it's both, then it must satisfy both, which would only happen if the function is zero everywhere, right? So probably C is not the answer unless the function is identically zero, which I don't think it is. D would be if it's neither. Let me check step by step.First, let me consider substituting ( -x ) into the function and see what happens. Let's compute ( f(-x) ):( f(-x) = (1 + sin(-x))^{2n} - (1 - sin(-x))^{2n} ).I know that ( sin(-x) = -sin x ), since sine is an odd function. So substituting that in:( f(-x) = (1 - sin x)^{2n} - (1 + sin x)^{2n} ).Wait, that looks like the negative of the original function. Let's see:Original function ( f(x) = (1 + sin x)^{2n} - (1 - sin x)^{2n} ).So ( f(-x) = (1 - sin x)^{2n} - (1 + sin x)^{2n} = -[ (1 + sin x)^{2n} - (1 - sin x)^{2n} ] = -f(x) ).Therefore, ( f(-x) = -f(x) ), which is the definition of an odd function. So that would mean the answer is A.But wait, let me double-check. Maybe there's something I missed because of the exponent 2n. Let's test with a specific value of n. Let's take n = 1, which is allowed since n is a positive integer.So if n=1, then ( f(x) = (1 + sin x)^2 - (1 - sin x)^2 ).Let's compute that:First, expand both squares:( (1 + sin x)^2 = 1 + 2sin x + sin^2 x )( (1 - sin x)^2 = 1 - 2sin x + sin^2 x )Subtracting them:( (1 + 2sin x + sin^2 x) - (1 - 2sin x + sin^2 x) = 4sin x )So f(x) = 4 sin x, which is indeed an odd function, since sin x is odd. So for n=1, it's odd, which matches our previous conclusion.Let me check n=2 to be sure. Let n=2:( f(x) = (1 + sin x)^4 - (1 - sin x)^4 )Compute each term:First, ( (1 + sin x)^4 ). Let's use binomial expansion:= 1 + 4 sin x + 6 sin^2 x + 4 sin^3 x + sin^4 xSimilarly, ( (1 - sin x)^4 ):= 1 - 4 sin x + 6 sin^2 x - 4 sin^3 x + sin^4 xSubtracting the second from the first:[1 + 4 sin x + 6 sin^2 x + 4 sin^3 x + sin^4 x] - [1 - 4 sin x + 6 sin^2 x - 4 sin^3 x + sin^4 x]Simplify term by term:1 - 1 = 04 sin x - (-4 sin x) = 8 sin x6 sin^2 x - 6 sin^2 x = 04 sin^3 x - (-4 sin^3 x) = 8 sin^3 xsin^4 x - sin^4 x = 0So overall, f(x) = 8 sin x + 8 sin^3 x = 8 sin x (1 + sin^2 x)Which is still an odd function, because sin x is odd, and sin^3 x is also odd (since odd function raised to an odd power is odd, and even power would be even). Here, sin x times any even function (like 1 + sin^2 x, which is even because sin^2 x is even) would result in an odd function. Because multiplying an odd function by an even function gives an odd function.So in this case, f(x) is 8 sin x (1 + sin^2 x), which is odd. Therefore, for n=2, it's also odd. Hmm. So seems like regardless of n, as long as exponent is 2n, the function f(x) remains odd.Wait, let me check the general case again. So when we expand ( (1 + sin x)^{2n} - (1 - sin x)^{2n} ), perhaps we can see a pattern. Let me consider the binomial theorem for both terms.( (1 + sin x)^{2n} = sum_{k=0}^{2n} binom{2n}{k} (sin x)^k )Similarly, ( (1 - sin x)^{2n} = sum_{k=0}^{2n} binom{2n}{k} (-1)^k (sin x)^k )Subtracting these two, we get:( f(x) = sum_{k=0}^{2n} binom{2n}{k} (sin x)^k - sum_{k=0}^{2n} binom{2n}{k} (-1)^k (sin x)^k )Combine the sums:( f(x) = sum_{k=0}^{2n} binom{2n}{k} (1 - (-1)^k) (sin x)^k )Now, notice that when k is even, ( (-1)^k = 1 ), so ( 1 - (-1)^k = 0 ), which cancels all the even terms. When k is odd, ( (-1)^k = -1 ), so ( 1 - (-1)^k = 2 ), so the odd terms remain multiplied by 2.Thus, f(x) = ( sum_{k text{ odd}}^{2n} 2 binom{2n}{k} (sin x)^k )But since k is odd, each term is ( (sin x)^k ), which is an odd function because sin x is odd, and an odd power of an odd function is odd. The sum of odd functions is odd, and multiplying by 2 (an even constant) preserves the oddness. Therefore, f(x) is a sum of odd functions, hence odd.Therefore, regardless of the value of n (as long as n is a positive integer), f(x) is an odd function. Therefore, the answer should be A.But wait, let me check one more example. Let me take n=3. So f(x) = (1 + sin x)^6 - (1 - sin x)^6.Rather than expanding entirely, maybe I can compute f(-x):f(-x) = (1 + sin(-x))^6 - (1 - sin(-x))^6 = (1 - sin x)^6 - (1 + sin x)^6 = -[ (1 + sin x)^6 - (1 - sin x)^6 ] = -f(x). So regardless of n, this relation holds, so f(-x) = -f(x), hence f is odd. Therefore, the answer is A.But let me check with another x value. Suppose x = π/2. Then sin(π/2) = 1. Then f(π/2) = (1 + 1)^{2n} - (1 - 1)^{2n} = 2^{2n} - 0 = 4^n. Then f(-π/2) = (1 + sin(-π/2))^{2n} - (1 - sin(-π/2))^{2n} = (1 - 1)^{2n} - (1 + 1)^{2n} = 0 - 4^n = -4^n = -f(π/2). So that checks out. Similarly, take x = 0. Then sin(0) = 0, so f(0) = (1 + 0)^{2n} - (1 - 0)^{2n} = 1 - 1 = 0. Which is consistent with being an odd function, since f(0) = 0 for odd functions.Another test: x = π/6. sin(π/6) = 1/2. Then f(π/6) = (1 + 1/2)^{2n} - (1 - 1/2)^{2n} = (3/2)^{2n} - (1/2)^{2n}. Then f(-π/6) = (1 - 1/2)^{2n} - (1 + 1/2)^{2n} = (1/2)^{2n} - (3/2)^{2n} = -[ (3/2)^{2n} - (1/2)^{2n} ] = -f(π/6). Which again matches f(-x) = -f(x).So all these examples check out, so it's safe to conclude that f(x) is an odd function. Therefore, the answer is A.Final Answerboxed{A}</think>To determine whether the function ( f(x) = (1 + sin x)^{2n} - (1 - sin x)^{2n} ) is odd, even, both, or neither, we start by analyzing ( f(-x) ).First, substitute ( -x ) into the function:[f(-x) = (1 + sin(-x))^{2n} - (1 - sin(-x))^{2n}]Since (sin(-x) = -sin x), we have:[f(-x) = (1 - sin x)^{2n} - (1 + sin x)^{2n}]This can be rewritten as:[f(-x) = -[(1 + sin x)^{2n} - (1 - sin x)^{2n}] = -f(x)]Thus, ( f(-x) = -f(x) ), which is the definition of an odd function.To verify, we consider specific values of ( n ):- For ( n = 1 ), ( f(x) = 4 sin x ), which is odd.- For ( n = 2 ), expanding the terms shows ( f(x) = 8 sin x (1 + sin^2 x) ), which is odd.Using the binomial theorem, we expand both terms:[(1 + sin x)^{2n} = sum_{k=0}^{2n} binom{2n}{k} (sin x)^k][(1 - sin x)^{2n} = sum_{k=0}^{2n} binom{2n}{k} (-1)^k (sin x)^k]Subtracting these, the even terms cancel out, leaving only the odd terms multiplied by 2:[f(x) = sum_{k text{ odd}}^{2n} 2 binom{2n}{k} (sin x)^k]Since each term ( (sin x)^k ) is odd, the entire function is odd.Testing specific values like ( x = pi/2 ), ( x = 0 ), and ( x = pi/6 ) confirms that ( f(-x) = -f(x) ).Thus, the function ( f(x) ) is an odd function, and the answer is (boxed{A}).]

🔑:Given that the domain of f(x) is mathbb{R}, then f(-x) = (1 - sin x)^{2n} - (1 + sin x)^{2n} = -f(x) Therefore, f(x) is an odd function, Hence, the correct choice is boxed{text{A}}.

🧠:[<think>Okay, let's see. The problem is about selecting a sample of 20 students from a high school with three grades. The total number of students is 2000, and the ratio of students in first, second, and third grades is 5:3:2. The question is asking which sampling method should be used and how many students from the second grade would be in the sample.Hmm. First, I need to recall different sampling methods. There's simple random sampling, stratified sampling, cluster sampling, systematic sampling, etc. The question is probably about stratified sampling because the problem mentions different grades (which are different strata or subgroups). In stratified sampling, you divide the population into subgroups (strata) and then randomly select from each stratum. This ensures that each subgroup is represented proportionally in the sample. Since the problem gives a ratio of the number of students in each grade, stratified sampling makes sense here. If they used simple random sampling, the sample might not proportionally represent each grade, especially if one grade is much larger than the others.So, the first blank should be "stratified sampling." Let me verify that. The ratio is 5:3:2 for first, second, third grades. Let's compute the actual number of students in each grade. The total ratio parts are 5+3+2=10. Therefore, each part is 2000/10=200 students. So first grade: 5*200=1000 students, second grade: 3*200=600 students, third grade: 2*200=400 students. So the population sizes are 1000, 600, 400. If we do stratified sampling, we would take samples from each grade proportionally. The total sample size is 20. So the proportion for each grade would be the same as their population proportion.For stratified sampling, the number from each grade would be (5/10)*20=10, (3/10)*20=6, (2/10)*20=4. So the second grade would have 6 students in the sample. Therefore, the second blank should be 6. Let me check if this is correct.Alternatively, if they used simple random sampling, the expected number would still be proportional, but the actual number could vary. However, the question is asking which method should be used. Since the problem is giving different strata (grades) and probably wants the sample to reflect the population proportions, the appropriate method is stratified sampling. Hence, the number from the second grade is 6.Wait, let me make sure. The ratio is 5:3:2. So first grade is 5 parts, second 3, third 2. Total parts 10. So second grade is 3/10 of the total population. Therefore, in stratified sampling, the sample from second grade should be 3/10 of 20, which is 6. That seems right.Therefore, the answer is stratified sampling and 6.Final AnswerThe method of boxed{stratified sampling} should be used, and the number of students drawn from the second grade in this sample should be boxed{6}.</think>The problem involves selecting a sample of 20 students from a high school with three grades, where the total number of students is 2000 and the ratio of students in first, second, and third grades is 5:3:2. First, we calculate the number of students in each grade:- The total ratio parts are (5 + 3 + 2 = 10).- Each part corresponds to (frac{2000}{10} = 200) students.- First grade: (5 times 200 = 1000) students.- Second grade: (3 times 200 = 600) students.- Third grade: (2 times 200 = 400) students.To ensure proportional representation of each grade in the sample, stratified sampling should be used. This method involves dividing the population into subgroups (strata) and randomly selecting samples from each stratum proportionally.Calculating the number of students from each grade in the sample:- First grade: (frac{5}{10} times 20 = 10) students.- Second grade: (frac{3}{10} times 20 = 6) students.- Third grade: (frac{2}{10} times 20 = 4) students.Thus, the method of stratified sampling should be used, and the number of students drawn from the second grade in this sample should be 6.[boxed{stratified sampling}][boxed{6}],<think>Okay, let me try to work through this problem step by step. So, we have a high school with three grades, totaling 2000 students. The ratio of students in first, second, and third grades is 5:3:2. We need to select a sample of 20 students, and the question is asking which sampling method should be used and how many students from the second grade should be in this sample.First, let me understand the ratios. The ratio is 5:3:2 for first, second, and third grades. That means if we add up those parts, 5+3+2=10 parts total. So each part represents 2000/10 = 200 students. Therefore, the number of students in each grade would be:First grade: 5 parts * 200 = 1000 studentsSecond grade: 3 parts * 200 = 600 studentsThird grade: 2 parts * 200 = 400 studentsWait, let me check that. 1000 + 600 + 400 is indeed 2000. Okay, so that's the distribution.Now, when selecting a sample of 20 students, the question is about which method to use. The options aren't provided, but given the context of ratios and different grades, I'm thinking this is about stratified sampling. Because stratified sampling involves dividing the population into subgroups (or strata) and then randomly selecting from each stratum. Since the problem mentions different grades with different numbers of students, it makes sense to use stratified sampling to ensure each grade is proportionally represented in the sample.If we were to use simple random sampling, we might not get the right proportion from each grade, especially since the first grade has more students. Stratified sampling would ensure that each grade is represented according to their numbers.So the method should be stratified sampling.Now, for the number of students from the second grade in the sample. Since stratified sampling involves selecting a sample from each stratum proportionally, we need to calculate what proportion of 20 students should come from the second grade.The proportion of second-grade students in the population is 3 out of 10 (since the ratio is 5:3:2). So 3/10 of 2000 is 600 students, which checks out. Therefore, in the sample, we should take 3/10 of 20 students.Calculating that: 3/10 * 20 = 6. So 6 students from the second grade.Alternatively, another way: Since each part is 200 students, and the sample size is 20, which is 1% of the population (since 20/2000 = 0.01). So, 1% of each stratum would be selected. For the second grade, 600 students * 1% = 6 students. That also gives 6.Therefore, the number of students drawn from the second grade should be 6.Let me double-check my reasoning. If we use proportional stratified sampling, each stratum's sample size is proportional to the stratum's size in the population. So yes, the second grade has 3/10 of the population, so 3/10 of the sample. 20 * 3/10 = 6. That seems right.Alternatively, if someone uses cluster sampling or systematic sampling, that might not ensure the proportional representation. So stratified is the correct method here.Therefore, the answer should be stratified sampling and 6 students from the second grade.</think>The three grades have 1000, 600, and 400 students respectively. To ensure proportional representation, stratified sampling should be used. This method selects students from each grade according to their population ratio. The number of second-grade students in the sample is calculated as ( frac{3}{10} times 20 = 6 ).Answer: The method of __stratified sampling__ should be used, and the number of students drawn from the second grade should be __6__. boxed{stratified sampling} and boxed{6}]

🔑:When the population consists of several distinct parts, stratified sampling should be adopted to select the sample.Since the ratio of the number of students in first, second, and third grades is 5:3:2, the ratio of the sample sizes for first, second, and third grades should also be 5:3:2.Given that the sample size to be drawn is 20, we can calculate the number of students to be sampled from the second grade as follows:The total ratio is 5 + 3 + 2 = 10.The proportion for the second grade is frac{3}{10}.Therefore, the sample size from the second grade is 20 times frac{3}{10} = boxed{6}.The method of sampling to be used is stratified sampling, and the number of students to be sampled from the second grade is 6.The stratified sampling method is suitable here because the population consists of distinct subgroups with different sizes, which are the different grades in this case. The principle is that each subgroup's sample size should be proportional to its size relative to the whole population, ensuring that the sample is representative of the entire population. This problem is a basic one that tests the definition and method of stratified sampling, where the ratio of individuals’ numbers in each subgroup equals the ratio of the corresponding sample numbers.

🧠:[<think>Okay, so I have this problem here: A line segment of length 18 is randomly divided into three segments. What is the probability that these three segments can form a triangle? Hmm, interesting. Let me try to figure this out step by step.First off, I remember that for three lengths to form a triangle, they have to satisfy the triangle inequality. That is, the sum of any two sides must be greater than the third side. So, if we have three segments a, b, and c, then:a + b > c a + c > b b + c > aSince the total length is 18, we also know that a + b + c = 18. So, maybe we can use that to simplify the inequalities. Let me see. If we substitute c with 18 - a - b, for example, then the first inequality becomes a + b > 18 - a - b. Simplifying that, we get 2a + 2b > 18, which reduces to a + b > 9. Similarly, maybe the other inequalities would also give some constraints on a and b?But wait, since the three segments are all parts of the original 18-unit length, each of them must be positive. So a, b, c > 0. So, we have three variables a, b, c all positive and summing to 18. The problem is to find the probability that these three can form a triangle.But how do we model the "randomly divided" part? That's crucial. How exactly are the segments being randomly divided? I think in problems like this, it's common to model the division by choosing two random points along the segment. So, imagine breaking the 18-unit segment at two points, say X and Y, which are chosen uniformly along the segment. Then the lengths of the three segments would be the distances between 0 and X, X and Y, and Y and 18. But to make this mathematically manageable, we can normalize the length to 1, solve the problem, and then scale back up if needed. Wait, but maybe the answer is the same regardless of the total length? Because probabilities are ratios. Let me check that thought later.So, if we normalize the segment length to 1, the problem becomes: break a unit segment into three parts by choosing two points at random; what's the probability the three parts can form a triangle. Then the answer would be the same as for length 18, since it's just scaling. But let me verify that.Yes, scaling the entire problem by a factor (like 18) shouldn't affect the probability, as all lengths are scaled proportionally, and the triangle inequalities are inequalities of proportions. So, the probability for length 18 is the same as for length 1. So, maybe I can solve the problem for a unit length and then the answer is the same. That seems reasonable.But let's proceed step by step. So, modeling the problem: choose two points X and Y on the segment [0, 18]. Without loss of generality, assume X ≤ Y. Then the three segments are [0, X], [X, Y], [Y, 18], with lengths X, Y - X, and 18 - Y. To form a triangle, each of these three lengths must be less than 9, because in a triangle, each side must be less than the sum of the other two sides. Wait, let's think about that.Wait, if we have three lengths a, b, c, then each must be less than the sum of the other two. So, for example, a < b + c. But since a + b + c = 18, that's equivalent to a < 18 - a, so 2a < 18, so a < 9. Similarly, b < 9 and c < 9. Therefore, all three segments must be less than 9. So, the necessary and sufficient condition is that each segment is less than 9. Is that right?Wait, actually, if all three segments are less than 9, then since each one is less than 9, the sum of the other two is greater than 9 (since total is 18), so each side is less than the sum of the other two. So, yes, that's equivalent. So, the three conditions a + b > c, a + c > b, b + c > a are equivalent to each of a, b, c < 9. That's a helpful simplification.Therefore, the problem reduces to finding the probability that all three segments are less than 9 units long. So, in terms of the two breaking points X and Y, we need each of the three segments (X, Y - X, 18 - Y) to be less than 9. But since X and Y are two points on [0, 18], ordered such that X ≤ Y, we can model this as choosing two numbers X and Y in [0, 18], with X ≤ Y, and then ensuring that X < 9, Y - X < 9, and 18 - Y < 9.But let's work in normalized coordinates, scaling everything by 18, so we can consider the unit interval. Let me set the total length to 1, then the problem becomes: choose two points x and y in [0,1], with x ≤ y, forming segments of lengths x, y - x, and 1 - y. The condition for forming a triangle is that each segment is less than 1/2 (since 9/18 = 1/2). Then the probability is the area of the region in the unit square where x < 1/2, y - x < 1/2, and 1 - y < 1/2, considering all ordered pairs (x, y) with x ≤ y. Then scaling back up, the probability remains the same.So, the problem is equivalent to finding the area in the unit square where x < 1/2, y - x < 1/2, and 1 - y < 1/2, with x ≤ y. Then multiply by 2 (since we considered ordered pairs where x ≤ y, but in reality, the two points can be in any order, so we need to account for the whole square). Wait, actually, when modeling the unit square for two points x and y, the region where x ≤ y is a triangle with area 1/2. So, to compute the probability, we can compute the area in the x ≤ y half of the square that satisfies the three conditions, and then double it (since the other half where y ≤ x is symmetric). Wait, no, actually, if we consider all possible (x, y) without ordering, the total area is 1, and the probability would be the area in the unit square where the three conditions hold. So perhaps it's better to model it in the unit square without assuming order, then the conditions are x < 1/2, |x - y| < 1/2, and 1 - max(x, y) < 1/2. Hmm, that might be more complicated.Wait, maybe it's better to model this geometrically. Let's consider the unit square [0,1] x [0,1], where the x-axis is the first break point and the y-axis is the second break point. Each point (x, y) in the square represents a way of breaking the segment, with the three lengths being min(x, y), |x - y|, and 1 - max(x, y). The conditions for forming a triangle are that all three lengths are less than 1/2. So, we need:min(x, y) < 1/2, |x - y| < 1/2, 1 - max(x, y) < 1/2.Let me write these inequalities out:1. min(x, y) < 1/2 2. |x - y| < 1/2 3. 1 - max(x, y) < 1/2 => max(x, y) > 1/2So, combining these three conditions:- The smaller of the two points must be less than 1/2. - The two points must be within 1/2 of each other. - The larger of the two points must be greater than 1/2.Let me try to visualize this region in the unit square. Let's consider all points (x, y) where x and y are between 0 and 1.First, condition 3: max(x, y) > 1/2. So, either x > 1/2 or y > 1/2. So this excludes the square [0, 1/2] x [0, 1/2].Condition 1: min(x, y) < 1/2. So, at least one of x or y is less than 1/2. But since max(x, y) > 1/2, this means exactly one of x or y is less than 1/2, and the other is greater than 1/2. Because if both were greater than 1/2, then min(x, y) would be greater than 1/2, violating condition 1. Wait, no. Wait, if both x and y are greater than 1/2, then min(x, y) > 1/2, which violates condition 1. Therefore, exactly one of x or y must be less than 1/2, and the other must be greater than 1/2. So, the region is divided into two parts: one where x < 1/2 and y > 1/2, and the other where y < 1/2 and x > 1/2. But due to symmetry, these two regions will have the same area, so we can compute one and double it.Condition 2: |x - y| < 1/2. So, the difference between x and y is less than 1/2. So, in the region where x < 1/2 and y > 1/2, we have y - x < 1/2. Similarly, in the region where y < 1/2 and x > 1/2, we have x - y < 1/2.Let me focus on the region where x < 1/2 and y > 1/2. In this region, the three conditions translate to:x < 1/2 y > 1/2 y - x < 1/2So, combining these, we have:x < 1/2 y > 1/2 y < x + 1/2But since y > 1/2, and y < x + 1/2, and x < 1/2, let's see:If x is between 0 and 1/2, then x + 1/2 is between 1/2 and 1. So, for each x in [0, 1/2), y must be in (1/2, x + 1/2). So, the area of this region can be found by integrating over x from 0 to 1/2 the length of y's interval, which is (x + 1/2) - 1/2 = x. So, the area is the integral from 0 to 1/2 of x dx, which is (1/2 x²) from 0 to 1/2, which is (1/2)(1/4) = 1/8. Then, since there's a symmetrical region where y < 1/2 and x > 1/2 with the same area, the total area is 2*(1/8) = 1/4.But wait, let me check that again. If in the region x < 1/2 and y > 1/2, the limits for y are from 1/2 to x + 1/2. So, when x ranges from 0 to 1/2, x + 1/2 ranges from 1/2 to 1. Therefore, for each x in [0, 1/2), y must be between 1/2 and x + 1/2. So, the length of y for each x is (x + 1/2) - 1/2 = x. Therefore, integrating x from 0 to 1/2 gives the area. The integral of x dx from 0 to 1/2 is [x²/2] from 0 to 1/2 = ( (1/2)^2 ) / 2 - 0 = (1/4)/2 = 1/8. Then, the same area exists in the region y < 1/2 and x > 1/2, so total area is 1/8 + 1/8 = 1/4.Therefore, the probability is 1/4. Wait, but I recall that the answer to this classic problem is 1/4? Hmm, maybe not. Wait, maybe I made a mistake here.Wait, let me think again. Because in the unit square, the total area where all three conditions hold is 1/4, so the probability is 1/4. But I have a feeling that the correct answer is 1/2. Wait, maybe not. Wait, let me verify.Alternatively, maybe there's another approach. Let's consider that when you break a stick at two random points, the probability that the three pieces can form a triangle is 1/4. Hmm, but actually, I think the answer is 1/2. Wait, maybe I'm confusing with another problem.Wait, let me check again. So, we have two points X and Y on [0,1]. The three pieces are of length min(X,Y), |X - Y|, and 1 - max(X,Y). The conditions are that each piece is less than 1/2. So, all three of these must be less than 1/2. So:1. min(X,Y) < 1/2 2. |X - Y| < 1/2 3. 1 - max(X,Y) < 1/2 => max(X,Y) > 1/2So, combining these three:From 3, we have that max(X,Y) > 1/2. So, either X or Y is greater than 1/2. From 1, we have that min(X,Y) < 1/2. So, one of X or Y is less than 1/2, and the other is greater than 1/2. Let's suppose without loss of generality that X < 1/2 and Y > 1/2. Then, the third condition is Y - X < 1/2. So, Y < X + 1/2. But since Y > 1/2 and X < 1/2, X + 1/2 ranges from 1/2 (when X=0) to 1 (when X=1/2). So, Y must be in (1/2, X + 1/2).Therefore, in the region where X is between 0 and 1/2, and Y is between 1/2 and X + 1/2, we can graph this.Similarly, the same applies if Y < 1/2 and X > 1/2, which would be symmetrical. So, the total area is 2 * integral from X=0 to X=1/2 of (X + 1/2 - 1/2) dX = 2 * integral from 0 to 1/2 of X dX = 2*(1/8) = 1/4. Therefore, the area is 1/4. So, the probability is 1/4. Therefore, 25% chance. But I thought there was a problem with this answer.Wait, let me check with a different approach. Let's model the problem as breaking the stick into three parts by choosing two points at random. So, the three parts are X, Y - X, and 1 - Y, assuming 0 < X < Y < 1. Then, the triangle conditions are:X < 1/2 Y - X < 1/2 1 - Y < 1/2Which simplifies to:X < 1/2 Y < X + 1/2 Y > 1/2So, in the (X, Y) plane with 0 < X < Y < 1, the region is bounded by X < 1/2, Y > 1/2, and Y < X + 1/2.So, let's plot this. The possible X ranges from 0 to 1/2. For each X in [0, 1/2), Y must be between max(1/2, X) and X + 1/2. But since X < 1/2 and Y > 1/2, the lower bound for Y is 1/2, and the upper bound is X + 1/2. But X + 1/2 is greater than 1/2 because X is non-negative. However, when X + 1/2 exceeds 1, the upper bound becomes 1. Wait, but X is up to 1/2, so X + 1/2 is up to 1. So, for X from 0 to 1/2, Y ranges from 1/2 to X + 1/2.Therefore, the area is the integral from X=0 to X=1/2 of (X + 1/2 - 1/2) dX = integral of X dX from 0 to 1/2 = [X²/2] from 0 to 1/2 = (1/2)*(1/4) = 1/8.But since the total area where 0 < X < Y < 1 is 1/2, the probability is (1/8)/(1/2) = 1/4. Therefore, the probability is 1/4, or 25%.But wait, I remember that the standard answer to this problem is 1/2. What am I missing here?Wait, maybe my model is incorrect. Let's check another way. Alternatively, when you break a stick at two random points, the probability that the three pieces can form a triangle is 1/4. Hmm. Wait, according to some sources, the probability is 1/4. But other problems where you break the stick into three pieces by breaking it once and then breaking one of the pieces again can have different probabilities.Wait, perhaps there's confusion in how the breaking is done. In this problem, the stick is broken at two random points simultaneously, which is different from breaking it once and then breaking again. In the case of simultaneous breaks, the probability is indeed 1/4, while in the sequential case, it's 1/2. Let me verify that.From what I recall, in the problem where you break the stick at a random point, then break the longer piece at a random point, the probability is 1/2. But if you break the stick at two random points simultaneously, the probability is 1/4. So, depending on the method of breaking, the probability changes. Therefore, in our problem here, since it's broken randomly divided into three segments, which implies two simultaneous breaks, so the answer should be 1/4.But let me check with a different approach. Let's use geometric probability.Imagine the unit square where x and y are the two break points. The three lengths are:- min(x, y) - |x - y| - 1 - max(x, y)All three must be less than 1/2.So, as we analyzed before, this requires:1. min(x, y) < 1/2 2. |x - y| < 1/2 3. max(x, y) > 1/2Let me visualize the unit square and these conditions.First, max(x, y) > 1/2: this is everything except the bottom-left square [0, 1/2] x [0, 1/2].Second, min(x, y) < 1/2: this is everything except the top-right square [1/2, 1] x [1/2, 1].So, the intersection of these two conditions is the entire unit square except [0, 1/2] x [0, 1/2] and [1/2, 1] x [1/2, 1]. So, it's the two rectangles [0, 1/2] x [1/2, 1] and [1/2, 1] x [0, 1/2].But then we also have |x - y| < 1/2. Which is the region between the lines y = x + 1/2 and y = x - 1/2. So, between those two lines, the difference between x and y is less than 1/2.So, combining all three conditions:In the region [0, 1/2] x [1/2, 1], we have x < 1/2, y > 1/2, and |x - y| < 1/2. Since y > x here, |x - y| = y - x < 1/2 => y < x + 1/2. So, in this rectangle, y is between 1/2 and x + 1/2. Similarly, in the region [1/2, 1] x [0, 1/2], we have x > 1/2, y < 1/2, and |x - y| = x - y < 1/2 => y > x - 1/2. So, y is between x - 1/2 and 1/2.Therefore, in each of these two regions, the area is the integral over x of the allowable y's.Starting with the first region [0, 1/2] x [1/2, 1]:For each x in [0, 1/2], y ranges from 1/2 to x + 1/2. However, x + 1/2 can be up to 1 (when x = 1/2). So, the upper limit is min(x + 1/2, 1). But since x ≤ 1/2, x + 1/2 ≤ 1, so the upper limit is x + 1/2.Thus, the area here is the integral from x=0 to x=1/2 of (x + 1/2 - 1/2) dx = integral from 0 to 1/2 of x dx = [x²/2] from 0 to 1/2 = (1/2)² / 2 = 1/8.Similarly, in the second region [1/2, 1] x [0, 1/2], for each x in [1/2, 1], y ranges from x - 1/2 to 1/2. So, the length of y is 1/2 - (x - 1/2) = 1 - x. So, the area is the integral from x=1/2 to x=1 of (1 - x) dx = [ - (1 - x)² / 2 ] from 1/2 to 1 = [0 - (- (1 - 1/2)² / 2)] = (1/2)² / 2 = 1/8.Therefore, total area from both regions is 1/8 + 1/8 = 1/4. So, the probability is 1/4, which is 25%.Therefore, the answer should be 1/4. But let me confirm with another method.Alternative approach: Use probabilistic arguments. Let's suppose we have three variables a, b, c > 0 such that a + b + c = 18. The probability that all three are less than 9. Since the problem is symmetric, we can model a, b, c as a Dirichlet distribution with parameters (1,1,1), which corresponds to the uniform distribution over the simplex a + b + c = 18.The probability we want is the volume of the subset where a < 9, b < 9, c < 9 divided by the total volume of the simplex.But the total volume of the simplex a + b + c = 18, a, b, c ≥ 0 is proportional to 18² / 2. The volume of the subset where a < 9, b < 9, c < 9 is the volume of the original simplex minus the volumes of the regions where at least one variable exceeds 9.But inclusion-exclusion: the volume where a ≥ 9 or b ≥ 9 or c ≥ 9 is equal to 3 times the volume where a ≥ 9 (by symmetry) minus 3 times the volume where a ≥ 9 and b ≥ 9 plus the volume where a ≥ 9, b ≥ 9, c ≥ 9.But since a + b + c = 18, if a ≥ 9 and b ≥ 9, then c ≤ 0, which is impossible. Similarly, all three exceeding 9 is impossible. So, the inclusion-exclusion formula simplifies to 3 * volume(a ≥ 9).Therefore, the desired probability is 1 - 3 * volume(a ≥ 9) / volume(total).Now, compute volume(a ≥ 9). If a ≥ 9, then b + c ≤ 9. So, this is the volume of the simplex a ≥ 9, b + c ≤ 9, which is a line segment from a=9 to a=18 (but wait, in three variables, it's a bit different). Wait, actually, in the simplex a + b + c = 18, the condition a ≥ 9 defines a smaller simplex where a' = a - 9, so a' + b + c = 9, with a', b, c ≥ 0. The volume of this is proportional to 9² / 2.The total volume is proportional to 18² / 2. Therefore, the ratio is (9² / 2) / (18² / 2) ) = (81)/ (324) = 1/4. Therefore, volume(a ≥ 9) / volume(total) = 1/4. Therefore, the desired probability is 1 - 3*(1/4) + 0 - 0 = 1 - 3/4 = 1/4. So, again, 1/4. Therefore, this confirms the previous result.Therefore, the probability is 1/4. So, the answer should be 1/4, or 25%. Therefore, the probability is 1/4.Wait, but let me double-check this with yet another method.Suppose we parameterize the problem by letting the two break points be at positions x and y on [0, 18]. The three segments are |x - y|, min(x, y), and 18 - max(x, y). The probability that all three are less than 9 is equivalent to the probability that no single segment is 9 or longer.Alternatively, the complement probability is the probability that at least one segment is ≥9. So, using the principle of inclusion-exclusion:P(at least one segment ≥9) = P(first segment ≥9) + P(second segment ≥9) + P(third segment ≥9) - P(first and second segments ≥9) - P(first and third segments ≥9) - P(second and third segments ≥9) + P(all three segments ≥9)But since the total length is 18, it's impossible for two segments to be ≥9, because their sum would be ≥18, leaving nothing for the third segment. Similarly, all three segments cannot be ≥9. Therefore, the intersection terms are zero. Thus,P(at least one segment ≥9) = 3 * P(a particular segment ≥9)Therefore, the probability we want is 1 - 3 * P(a particular segment ≥9)So, compute P(a particular segment ≥9). Let's pick the first segment, which is min(x, y). Wait, but actually, depending on how you define the segments. Alternatively, the segments are X, Y - X, and 18 - Y, assuming X < Y. So, the three segments are of lengths X, Y - X, 18 - Y.So, the first segment is X. The probability that X ≥9 is the probability that the first break point is ≥9, which, since X is chosen uniformly over [0, 18], is (18 - 9)/18 = 1/2. Wait, but this is not quite right.Wait, actually, when choosing two break points X and Y uniformly, the distribution is over the unit square. So, the probability that X ≥9 is the area in the unit square where X ≥9, but since we normalized to length 1 earlier, scaling complicates things. Maybe better to do without normalization.Wait, but the problem is originally in length 18. If we model X and Y as two independent uniform variables over [0, 18], then the joint distribution is uniform over the square [0, 18] x [0, 18]. The three segments are:- min(X, Y) - |X - Y| - 18 - max(X, Y)The probability that any one of these is ≥9. Let's compute P(min(X, Y) ≥9). This is the probability that both X and Y are ≥9. The area where X ≥9 and Y ≥9 is (18 - 9)^2 = 81, over the total area 324. So, 81/324 = 1/4.Similarly, P(|X - Y| ≥9) is the area where |X - Y| ≥9. This is two triangles in the square, each with base and height (18 - 9) = 9. So, area = 2 * (1/2 * 9 * 9) = 81. So, probability 81/324 = 1/4.Similarly, P(18 - max(X, Y) ≥9) is the probability that max(X, Y) ≤9, which is the area where X ≤9 and Y ≤9, which is 81, so probability 1/4.Therefore, the three probabilities are each 1/4. Therefore, P(at least one segment ≥9) = 3*(1/4) - 0 + 0 = 3/4. Therefore, the probability that all segments <9 is 1 - 3/4 = 1/4. Therefore, 1/4.Therefore, this confirms the answer is 1/4. So, regardless of the method, we get 1/4. Therefore, the answer should be 1/4. So, the probability is 1/4.But I want to make sure that the initial problem statement is about dividing a segment into three parts by making two random cuts, which is the same as choosing two points on the segment, right? Yes. So, the answer is 1/4.However, I just recall that in some versions of the problem, the answer is 1/2. Maybe when the stick is broken in two randomly placed points, but here we need three segments. Wait, no, breaking into three segments by two points is the same as the problem here.Wait, perhaps there's confusion when considering the problem in different dimensions. Wait, no. Wait, the key is that when you break a stick at two random points, the probability that the three pieces can form a triangle is 1/4. This is a classic result, so I think this is correct.Therefore, after carefully considering multiple approaches: geometric probability in the unit square, inclusion-exclusion principle, and verifying with integration, all approaches lead to the probability being 1/4. Therefore, the answer is 1/4.Final AnswerThe probability is boxed{dfrac{1}{4}}.</think>To determine the probability that a line segment of length 18 can be divided into three segments that form a triangle, we need to check if the segments satisfy the triangle inequality. The key steps are as follows:1. Triangle Inequality Conditions: For three segments (a), (b), and (c) to form a triangle, they must satisfy: [ a + b > c, quad a + c > b, quad text{and} quad b + c > a ] Given (a + b + c = 18), each segment must be less than 9.2. Modeling the Problem: The line segment is divided by two random points (X) and (Y) (assuming (X leq Y)). The lengths of the segments are (X), (Y - X), and (18 - Y). We need each segment to be less than 9.3. Geometric Probability: Convert the problem to the unit interval by normalizing the length to 1. The conditions translate to: - ( min(x, y) < frac{1}{2} ) - ( |x - y| < frac{1}{2} ) - ( max(x, y) > frac{1}{2} )4. Visualizing the Region: In the unit square ([0, 1] times [0, 1]), the valid region is where: - One point is less than (frac{1}{2}) and the other is greater than (frac{1}{2}). - The difference between the points is less than (frac{1}{2}).5. Calculating the Area: The valid region consists of two symmetrical areas where: - For (x < frac{1}{2}) and (y > frac{1}{2}), (y) ranges from (frac{1}{2}) to (x + frac{1}{2}). - For (y < frac{1}{2}) and (x > frac{1}{2}), (x) ranges from (frac{1}{2}) to (y + frac{1}{2}).6. Integration: Calculate the area for one region and double it: [ text{Area} = 2 int_{0}^{frac{1}{2}} x , dx = 2 left[ frac{x^2}{2} right]_{0}^{frac{1}{2}} = 2 left( frac{1}{8} right) = frac{1}{4} ]7. Conclusion: The probability that the three segments can form a triangle is (frac{1}{4}).[boxed{dfrac{1}{4}}],<think>Okay, so I have this problem here: A line segment of length 18 is randomly divided into three segments. The probability that these three segments can form a triangle is ______. Hmm, interesting. I remember that for three lengths to form a triangle, they have to satisfy the triangle inequality. That is, the sum of any two sides must be greater than the third side. So, if I have three segments, let's call them a, b, and c, then all of the following must be true: a + b > c, a + c > b, and b + c > a. But in this problem, the line segment is divided randomly into three parts. I need to model this randomness. How exactly is the line segment divided? If it's divided randomly, does that mean we pick two random points along the segment to make the three parts? That seems likely. So, imagine the line segment from 0 to 18 on a number line. We pick two points, say x and y, where 0 < x < y < 18. Then the three segments would be of lengths x, y - x, and 18 - y. So, a = x, b = y - x, c = 18 - y. Alternatively, maybe it's divided by breaking the stick at two random positions. Yeah, that seems equivalent. So, the problem reduces to choosing two random points on the stick, breaking it there, and then seeing if the three pieces can form a triangle. To model this, I can consider the coordinate plane where x and y are the two break points. Since x and y are between 0 and 18, and x < y, the possible (x, y) pairs form a triangle in the coordinate plane with vertices at (0,0), (0,18), and (18,18). The area of this triangle would represent all possible divisions. The area is (18*18)/2 = 162. But we need to find the probability that the three segments can form a triangle. So, we need to find the region within this triangle where the three lengths satisfy the triangle inequalities. Then, the probability would be the area of this region divided by 162.So, let's write down the three conditions:1. a + b > c2. a + c > b3. b + c > aSubstituting a, b, c with x, y - x, 18 - y:1. x + (y - x) > 18 - y => y > 18 - y => 2y > 18 => y > 92. x + (18 - y) > y - x => x + 18 - y > y - x => 2x + 18 > 2y => x + 9 > y3. (y - x) + (18 - y) > x => 18 - x > x => 18 > 2x => x < 9So, the conditions simplify to:1. y > 92. y < x + 93. x < 9But remember, we also have the original constraints that 0 < x < y < 18. So, combining all these, we can plot these inequalities on the coordinate plane.Let me try to visualize this. The original region is a triangle with vertices at (0,0), (0,18), (18,18). Now, we need to find the area where:- x < 9- y > 9- y < x + 9So, let's break it down:First, x must be less than 9. So, we are restricted to the left half of the original triangle, from x=0 to x=9.Second, y must be greater than 9. So, within the left half (x < 9), y must be between 9 and 18. However, since y has to be greater than x (because we have 0 < x < y < 18), the lower bound for y is actually max(x, 9). So, the region is x from 0 to 9, y from max(x, 9) to 18, but also y must be less than x + 9.Wait, so the third condition is y < x + 9. So, even though y is greater than 9, it also has to be less than x + 9. So, let's see. If x is less than 9, then x + 9 is less than 18 only when x < 9. Wait, x + 9 when x is 9 would be 18. But x is less than 9, so x + 9 is less than 18. So, the upper bound for y is x + 9, which for x from 0 to 9, ranges from 9 to 18. So, putting it all together, for x from 0 to 9, y must be between 9 and x + 9. However, since y must also be greater than x (because y > x), the actual lower bound for y is the maximum of x and 9. But when x is between 0 and 9, the maximum of x and 9 is 9 only when x <= 9. Wait, no. If x is less than 9, then the maximum of x and 9 is 9. So, for x in [0,9], the lower bound for y is 9, and the upper bound is min(x + 9, 18). But since x is less than 9, x + 9 is less than 18. So, upper bound is x + 9. Therefore, the region is a trapezoid or some shape where x goes from 0 to 9, y goes from 9 to x + 9. But we also need to consider the original constraint that y < 18, but in this case, since x + 9 < 18 when x < 9, the upper limit is okay.Wait, but when x is 0, y is between 9 and 9, which is just a point. Wait, no, when x is 0, y must be between 9 and 9? That can't be right. Wait, no, if x is 0, then y must be between 0 and 18, but we have the constraints y > 9 and y < x + 9 = 9. So, 9 < y < 9, which is impossible. So, when x is 0, there's no solution? That seems odd.Wait, maybe I made a mistake here. Let's re-examine the conditions.Original constraints:1. 0 < x < y < 18.Additional triangle inequality conditions:1. y > 92. y < x + 93. x < 9So, for x < 9, y must be between 9 and x + 9. But if x is such that x + 9 > 9, which it always is, since x is positive. Wait, x is between 0 and 9. So, x + 9 is between 9 and 18. So, y is between 9 and x + 9. However, since y must also be greater than x (from the original division), the lower bound for y is actually max(x, 9). So, when x <= 9, if x < 9, then max(x, 9) is 9 only when x <= 9. Wait, no, if x is less than 9, then max(x,9) is 9. If x is greater than 9, but we already have x < 9, so max(x,9) is 9. Wait, so regardless of x < 9, the lower bound is 9. So, for x from 0 to 9, y is from 9 to x + 9. However, since x < y, we must also have y > x, but if x < 9, and y starts at 9, then for x < 9, y must be greater than x, but if x is less than 9, then 9 is greater than x. So, the lower bound of y is 9, which is already greater than x. So, the conditions are compatible. Wait, let's check for x in [0,9], y must be in [9, x + 9], and since x < y, but since y starts at 9, which is greater than x (as x is <=9), this is okay. So, the region is x from 0 to 9, y from 9 to x + 9. But when x is 0, y must be between 9 and 9, which is just a line. But since x and y are continuous variables, the probability of y being exactly 9 when x is 0 is zero, so that doesn't contribute to the area. So, the region is a sort of trapezoid starting at x=0, y=9, and as x increases from 0 to 9, the upper limit of y increases from 9 to 18. But actually, when x=9, the upper limit is 9 + 9=18. So, at x=9, y ranges from 9 to 18. Wait, but x=9, y has to be greater than 9, but y also has to be greater than x=9, so y from 9 to 18. But since x=9, and y must be greater than x=9, y is from 9 to 18. But wait, when x=9, y must be greater than 9, but according to the original division, y has to be greater than x=9. So, when x=9, y is from 9 to 18, but again, since x=9, y must be greater than 9, which is the same as y > 9. So, in that case, the upper limit for y is 18, as usual.But how does this region look? For x from 0 to 9, y from 9 to x + 9. So, when x=0, y=9. When x=9, y=18. So, the upper boundary is the line y = x + 9. The lower boundary is y=9. The left boundary is x=0, y=9. The right boundary is x=9, y=18. So, this region is a quadrilateral with vertices at (0,9), (9,18), (9,9), and (0,9). Wait, actually, (0,9) is repeated. Wait, maybe it's a triangle? Because from x=0 to x=9, the upper boundary is the line from (0,9) to (9,18), and the lower boundary is the line y=9 from (0,9) to (9,9). So, it's a triangle with vertices at (0,9), (9,9), and (9,18). Hmm, yes, that seems right.So, the area of this region is the area of this triangle. The base is from (9,9) to (9,18), which is 9 units. The height is from x=0 to x=9, which is 9 units. But wait, actually, in coordinate geometry, the area can be calculated using the formula for a triangle with vertices at (x1,y1), (x2,y2), (x3,y3).The vertices are (0,9), (9,9), and (9,18). Using the formula:Area = |(0*(9 - 18) + 9*(18 - 9) + 9*(9 - 9))/2|= |0 + 9*9 + 0| /2= 81/2 = 40.5So, the area is 40.5. The original area of all possible divisions is 162. So, the probability is 40.5 / 162 = 0.25. So, 1/4.Wait, but hold on. Is this correct? Because when I think about the standard "breaking a stick into three parts" problem, the probability is usually 1/4. So, maybe this is correct. But let me verify again.Alternatively, I might have messed up with the conditions.Wait, let's check again the three inequalities:1. a + b > c: x + (y - x) > 18 - y => y > 18 - y => 2y > 18 => y > 92. a + c > b: x + (18 - y) > (y - x) => x + 18 - y > y - x => 2x + 18 > 2y => x + 9 > y3. b + c > a: (y - x) + (18 - y) > x => 18 - x > x => 18 > 2x => x < 9So, the three conditions are y > 9, y < x + 9, and x < 9.But these three conditions must hold simultaneously. So, in the coordinate system, with x and y axes, the region where all three conditions are satisfied is the intersection of:- x < 9 (vertical line at x=9, to the left)- y > 9 (horizontal line at y=9, above)- y < x + 9 (line y = x + 9, below)Additionally, we must have 0 < x < y < 18. So, the original region is the triangle with vertices (0,0), (0,18), (18,18). But with the conditions x < 9, y > 9, y < x + 9.So, the intersection of these conditions is the region where x is between 0 and 9, y is between 9 and x + 9, and y > x (since y must be greater than x in the original division). But since y has to be greater than x and greater than 9, the lower bound for y is max(x,9). But when x < 9, max(x,9) = 9. Therefore, for x in [0,9], y is in [9, x + 9]. However, we must also ensure that y < 18. Since x + 9 when x is 9 is 18, but x is less than 9, so x + 9 is less than 18. Wait, when x approaches 9, x + 9 approaches 18, so the upper bound for y is always less than 18. So, the region is as described before.Therefore, the area is 40.5, and the total area is 162, so the probability is 40.5 / 162 = 0.25, which is 1/4. So, the probability is 1/4. But I remember that sometimes in these problems, depending on how the stick is broken, the probability can be 1/4 or 1/2 or something else. Wait, maybe I need to check my model again.Wait, another approach: when breaking a stick at two random points, the probability that the three pieces can form a triangle is 1/4. Yes, I think that's a classic result. So, maybe the answer is indeed 1/4. But let me verify with another method.Alternative approach: Let’s consider the problem in terms of three variables. Let’s denote the two break points as X and Y, where X and Y are uniformly distributed over [0,18]. Without loss of generality, assume X < Y. Then the lengths are X, Y - X, and 18 - Y. The three conditions for forming a triangle are:1. X + (Y - X) > 18 - Y ⇒ Y > 92. X + (18 - Y) > Y - X ⇒ X + 9 > Y3. (Y - X) + (18 - Y) > X ⇒ 18 - X > X ⇒ X < 9So, these are the same conditions as before. Now, since X and Y are uniformly distributed over the triangle 0 < X < Y < 18, the probability is the area of the region satisfying these conditions divided by the area of the entire triangle.The entire triangle has area (18*18)/2 = 162. The region satisfying the conditions is the triangle with vertices (0,9), (9,9), (9,18), which has area (9*9)/2 = 40.5. So, the probability is 40.5 / 162 = 0.25, so 1/4. Therefore, the answer is 1/4.Wait, but in some references, I remember that the probability is 1/4 when breaking the stick in two random points. Yes, according to some sources, the probability is 1/4. So, that seems correct. Therefore, the answer should be 1/4.But let me think again. Suppose instead of a stick of length 18, we consider a stick of length 1. Then, the probability would still be 1/4, right? So, scaling doesn't affect the probability. Therefore, for length 18, it's the same. So, the answer is 1/4. Wait, another way to think about it: Use probabilistic arguments. For three lengths a, b, c, the triangle inequality requires that all three lengths are less than half of the total length. Since the total length is 18, each segment must be less than 9. So, in addition to the three inequalities, another way to see it is that none of the segments can be greater than or equal to 9. Because if one segment is 9 or more, then the sum of the other two segments would be 9 or less, violating the triangle inequality.So, the probability that all three segments are less than 9 is equivalent to the probability that the maximum of the three segments is less than 9. So, perhaps this is another way to model the problem.So, how do we compute the probability that all three segments are less than 9?Given that the stick is broken at two points X and Y, with X < Y, then the three segments are X, Y - X, 18 - Y. All of these must be less than 9. So:1. X < 92. Y - X < 9 ⇒ Y < X + 93. 18 - Y < 9 ⇒ Y > 9Therefore, we have the same conditions as before: X < 9, Y > 9, and Y < X + 9. So, this gives the same region, hence the same probability of 1/4. Therefore, that confirms the answer again.Alternatively, perhaps using geometric probability with a different coordinate system. Let me try to normalize the stick length to 1 for simplicity, then scale back up.If the stick length is 1, then breaking it at two points x and y, with 0 < x < y < 1. The three segments are x, y - x, 1 - y. The conditions are:1. x + (y - x) > 1 - y ⇒ y > 1/22. x + (1 - y) > y - x ⇒ x + 1 - y > y - x ⇒ 2x + 1 > 2y ⇒ y < x + 1/23. (y - x) + (1 - y) > x ⇒ 1 - x > x ⇒ x < 1/2So, in the unit square [0,1]x[0,1], the region where x < y, y > 1/2, y < x + 1/2, and x < 1/2. The area of this region is 1/8, and the total area of the triangle is 1/2, so the probability is (1/8)/(1/2) = 1/4. Therefore, the probability is 1/4. Scaling back up to length 18, the probability remains the same, 1/4.Therefore, regardless of the method, the probability is 1/4. So, the answer should be 1/4.But let me check with another approach. Suppose instead of breaking the stick at two points, we consider breaking it sequentially. First, break the stick at a random point X, then break one of the two pieces at another random point. But this might complicate things because the choice of which piece to break might affect the probabilities. But since the original problem is about randomly dividing into three segments, which is equivalent to breaking at two random points simultaneously. Therefore, the previous method holds.Alternatively, maybe using integrals. The probability can be calculated by integrating over the valid region.So, for the unit stick, the probability is the integral over x from 0 to 1/2, and for each x, y is from 1/2 to x + 1/2. So, the area is ∫ (x + 1/2 - 1/2) dx from x=0 to x=1/2, which is ∫ x dx from 0 to 1/2, which is (1/2)^2 / 2 = 1/8. Then, since the total area is 1/2, the probability is 1/4.Similarly, for the stick of length 18, the valid region's area is 40.5, as computed earlier, and the total area is 162, which is 18^2 / 2. Then, 40.5 / 162 = (81/2) / (162) = (81)/(324) = 1/4. So, same result.Therefore, after multiple approaches and verifications, I think the probability is indeed 1/4. Therefore, the answer is 1/4.Final AnswerThe probability is boxed{dfrac{1}{4}}.</think>To determine the probability that a line segment of length 18 randomly divided into three segments can form a triangle, we need to check if the segments satisfy the triangle inequality conditions. The three conditions are that the sum of any two segments must be greater than the third segment.1. Modeling the problem: We consider the line segment from 0 to 18. Breaking it at two random points ( x ) and ( y ) (where ( 0 < x < y < 18 )) results in three segments of lengths ( x ), ( y - x ), and ( 18 - y ).2. Triangle inequalities: The conditions for these segments to form a triangle are: - ( x + (y - x) > 18 - y ) simplifies to ( y > 9 ) - ( x + (18 - y) > y - x ) simplifies to ( y < x + 9 ) - ( (y - x) + (18 - y) > x ) simplifies to ( x < 9 )3. Geometric probability: We analyze the region in the coordinate plane where ( 0 < x < y < 18 ). The valid region satisfying all three conditions is a triangle with vertices at ( (0, 9) ), ( (9, 9) ), and ( (9, 18) ).4. Area calculation: The area of the valid region is calculated as: - The vertices form a triangle with base 9 and height 9. - Area = ( frac{1}{2} times 9 times 9 = 40.5 ).5. Total possible region: The total area of all possible divisions (a triangle with vertices at ( (0, 0) ), ( (0, 18) ), and ( (18, 18) )) is ( frac{1}{2} times 18 times 18 = 162 ).6. Probability: The probability is the ratio of the valid area to the total area: - Probability = ( frac{40.5}{162} = frac{1}{4} ).Thus, the probability that the three segments can form a triangle is (boxed{dfrac{1}{4}}).]

🔑:4.0.25.Let the lengths of two sides of a triangle be x, y, thenleft{begin{array}{l}9<x+y<18, 0<x<9, 0<y<9 .end{array}right.This forms the medial triangle of Rt triangle A O B (as shown in Figure 5), the shaded area is frac{1}{4} of the entire triangle A O B. Therefore, the probability of forming a triangle is 0.25.

🧠:[<think>Okay, so I need to find all pairs of natural numbers a and b where both (a² + b)/(b² - a) and (b² + a)/(a² - b) are integers. Hmm, natural numbers so they’re positive integers. Let me start by understanding the problem better.First, let's note that since both denominators must divide their numerators, the denominators must be positive or negative. But since a and b are natural numbers, let's check if the denominators can be positive. Because if denominators are negative, the fractions would be negative, but the problem states they are integers. However, integers can be negative, but the numerators are sums of squares and linear terms, which are positive. Wait, numerators: a² + b is positive, b² + a is positive. Denominators: b² - a and a² - b. So if the denominators are negative, then the fractions would be negative, but since the numerators are positive, the fractions would be negative integers. But the problem doesn't specify that they have to be positive integers, just integers. So maybe denominators can be positive or negative, but the fractions must be integers. So denominators can be divisors of the numerators, either positive or negative.But since a and b are natural numbers, denominators could be positive or negative. Let me think. For example, take a = 1, b = 1. Then first fraction: (1 + 1)/(1 - 1) which is 2/0 undefined. So that's invalid. So a and b cannot both be 1. Let's try a = 1, b = 2. Then first denominator: 2² - 1 = 4 - 1 = 3. Numerator: 1 + 2 = 3. So first fraction is 3/3 = 1, which is integer. Then second fraction: (2² + 1)/(1² - 2) = (4 + 1)/(1 - 2) = 5/-1 = -5, which is an integer. So that works. So (1,2) is a solution. Similarly, check (2,1). First fraction: (4 + 1)/(1 - 2) = 5/-1 = -5, integer. Second fraction: (1 + 2)/(4 - 1) = 3/3 = 1, integer. So (2,1) is also a solution.So (1,2) and (2,1) are solutions. Let's check if there are others. Let me try a=1, b=3. First fraction: (1 + 3)/(9 - 1) = 4/8 = 0.5, not integer. So no. a=1, b=4: (1 + 4)/(16 -1)=5/15=1/3, not integer. a=1, b=5: (1 +5)/(25 -1)=6/24=0.25, nope. So maybe a=1 only works with b=2.Similarly, check b=2, a=2. First fraction: (4 + 2)/(4 - 2) =6/2=3, integer. Second fraction: (4 + 2)/(4 - 2)=6/2=3, integer. So (2,2) is also a solution. Wait, that's interesting. Let me check (2,2). First fraction: (4 +2)/(4 -2)=6/2=3, integer. Second fraction: (4 +2)/(4 -2)=6/2=3, integer. So yes, (2,2) works. So that's another solution.What about a=3, b=3? First fraction: (9 +3)/(9 -3)=12/6=2, integer. Second fraction: same, 12/6=2. So (3,3) is a solution. Wait, so if a = b, then both fractions become (a² +a)/(a² -a) = (a(a +1))/(a(a -1)) ) = (a +1)/(a -1). So for this to be integer, (a +1)/(a -1) must be integer. So (a +1) must be divisible by (a -1). Let's compute (a +1)/(a -1) = 1 + 2/(a -1). So 2/(a -1) must be integer. So (a -1) divides 2. Therefore, a -1 can be 1, 2. So a -1=1 → a=2, or a -1=2 → a=3. Thus, a=2 and a=3. So when a = b, only a=2 and a=3 give integer fractions. So (2,2) and (3,3) are solutions. That's correct.So so far, we have (1,2), (2,1), (2,2), (3,3). Let me check a=3, b=3. Yes, both fractions are 12/6=2. So that works. What about a=4, b=4? Then fractions would be (16 +4)/(16 -4)=20/12≈1.666, which is not integer. So no. So (4,4) is not a solution.So when a = b, only a=2,3. So that's two solutions.Now, let's check other possible pairs where a ≠ b. Let's try a=2, b=3.First fraction: (4 +3)/(9 -2)=7/7=1, integer. Second fraction: (9 +2)/(4 -3)=11/1=11, integer. So (2,3) works. Similarly, check (3,2). First fraction: (9 +2)/(4 -3)=11/1=11. Second fraction: (4 +3)/(9 -2)=7/7=1. So (3,2) works as well.So that's two more solutions. So (2,3) and (3,2). So that's interesting.How about a=2, b=4. First fraction: (4 +4)/(16 -2)=8/14=4/7, not integer. So no. a=2, b=5: (4 +5)/(25 -2)=9/23≈0.391, nope. a=3, b=4: (9 +4)/(16 -3)=13/13=1, integer. Second fraction: (16 +3)/(9 -4)=19/5=3.8, not integer. So no. So (3,4) first fraction is 1, second is not integer.Wait, so (3,4) first fraction: (9 +4)/(16 -3)=13/13=1, integer. Second fraction: (16 +3)/(9 -4)=19/5=3.8, not integer. So no. Similarly, (4,3): first fraction: (16 +3)/(9 -4)=19/5=3.8, not integer. So no.How about a=3, b=6. First fraction: (9 +6)/(36 -3)=15/33≈0.454, no. a=3, b=5: (9 +5)/(25 -3)=14/22≈0.636, no. a=4, b=2: (16 +2)/(4 -4)=18/0 undefined. So invalid. a=4, b=1: (16 +1)/(1 -4)=17/-3≈-5.666, not integer. a=5, b=2: (25 +2)/(4 -5)=27/-1=-27, integer. Second fraction: (4 +5)/(25 -2)=9/23≈0.391, not integer. So (5,2) first fraction is -27, which is integer, but second is not. So not a solution.Wait, so (a,b)=(5,2): first fraction is (25 +2)/(4 -5)=27/-1=-27. Second fraction is (4 +5)/(25 -2)=9/23. So since 9/23 is not integer, so (5,2) is not a solution. Similarly, (2,5): first fraction (4 +5)/(25 -2)=9/23, not integer. So nope.What about a=3, b=1. First fraction: (9 +1)/(1 -3)=10/-2=-5, integer. Second fraction: (1 +3)/(9 -1)=4/8=0.5, not integer. So (3,1) is invalid. Similarly, (1,3) we checked before, which was 0.5, invalid.So maybe up to now, we have (1,2), (2,1), (2,2), (2,3), (3,2), (3,3). Let's check a=4, b=5. First fraction: (16 +5)/(25 -4)=21/21=1, integer. Second fraction: (25 +4)/(16 -5)=29/11≈2.636, not integer. So (4,5) first fraction is 1, second is not. So invalid.a=4, b=6: (16 +6)/(36 -4)=22/32=11/16, nope. a=5, b=5: (25 +5)/(25 -5)=30/20=1.5, not integer. So no. a=3, b=4: (9 +4)/(16 -3)=13/13=1, integer; second fraction 19/5=3.8, nope. a=4, b=3: (16 +3)/(9 -4)=19/5=3.8, nope.Wait, how about a=2, b=4: (4 +4)/(16 -2)=8/14=4/7, not integer. a=2, b=6: (4 +6)/(36 -2)=10/34=5/17, nope. a=3, b=6: (9 +6)/(36 -3)=15/33=5/11, nope. a=4, b=1: (16 +1)/(1 -4)=17/-3≈-5.666, not integer. a=5, b=1: (25 +1)/(1 -5)=26/-4=-6.5, not integer. a=6, b=1: (36 +1)/(1 -6)=37/-5=-7.4, nope.What about a=4, b=5: first fraction 21/21=1, second 29/11≈2.636. a=5, b=4: first fraction (25 +4)/(16 -5)=29/11≈2.636, second fraction (16 +5)/(25 -4)=21/21=1. So same as (4,5). So not solution.Wait, maybe trying larger numbers isn't helpful. Let's think of a systematic approach.Let me denote the two fractions:F1 = (a² + b)/(b² - a)F2 = (b² + a)/(a² - b)We need both F1 and F2 to be integers. Let's see if there's a relationship between them. Suppose that F1 = m and F2 = n, where m and n are integers.So:(a² + b) = m(b² - a) ...(1)(b² + a) = n(a² - b) ...(2)We can try to solve these equations for a and b.Let me write equation (1):a² + b = m b² - m aBring all terms to left:a² + m a + b - m b² = 0Similarly, equation (2):b² + a = n a² - n bBring all terms to left:- n a² + a + b² + n b = 0This seems complex. Maybe subtract or add equations? Alternatively, express variables in terms of each other.Alternatively, perhaps assume that a and b are small, so possible solutions are limited. Since natural numbers, maybe a and b up to 5 or 6. But we found solutions with a=1,2,3. Let's check if there are solutions with a=4, b= something.Wait, for a=4, when does (16 + b)/(b² -4) become integer. Let's see. Let me denote F1 = (16 + b)/(b² -4). Need b² -4 divides 16 + b.So, b² -4 | 16 + b. Which implies that b² -4 divides (16 + b). But b² -4 is quadratic, and 16 + b is linear, so for this division to hold, the quadratic must be a factor of the linear term, which is only possible if the quadratic is a divisor of the linear term in absolute value. Since both are integers, so |b² -4| ≤ |16 + b|. Let's consider positive denominators first. So b² -4 > 0 → b² >4 → b≥3 (since b is natural). So for b ≥3, compute |b² -4| ≤ |16 + b|. Since b² -4 is positive, and 16 + b is positive, so inequality is b² -4 ≤16 +b → b² - b -20 ≤0. Solve b² -b -20 ≤0. The roots of the equation b² -b -20 =0 are b=(1 ± sqrt(1 +80))/2=(1 ±9)/2. So roots at 10/2=5 and -8/2=-4. So the inequality holds for b ∈ [-4,5]. Since b is natural and ≥3, so b=3,4,5.So for b=3: denominator=9 -4=5. Numerator=16 +3=19. 19/5 is not integer. b=4: denominator=16 -4=12. Numerator=16 +4=20. 20/12=5/3≈1.666, not integer. b=5: denominator=25 -4=21. Numerator=16 +5=21. 21/21=1, which is integer. So for a=4, b=5: F1=1. Then check F2=(25 +4)/(16 -5)=29/11≈2.636, not integer. So (4,5) is not a solution.Alternatively, when denominator is negative. So b² -4 <0. Then b² <4, so b=1,2. Then F1=(16 + b)/(negative number). Let's check b=1: denominator=1 -4=-3. Numerator=16 +1=17. 17/-3≈-5.666, not integer. b=2: denominator=4 -4=0, undefined. So a=4 has only b=5 possible, but that doesn't work.Similarly, check a=5. So F1=(25 + b)/(b² -5). Let's see for b² -5 positive. So b≥3. Then |b² -5| ≤25 +b. So b² -5 ≤25 +b → b² -b -30 ≤0. Solve b² -b -30=0. Discriminant=1 +120=121. Roots=(1 ±11)/2=6 and -5. So inequality holds for b ∈ [-5,6]. So natural numbers b≥3 up to 6. So b=3,4,5,6.Check each:b=3: denominator=9 -5=4. Numerator=25 +3=28. 28/4=7, integer. Then check F2=(9 +5)/(25 -3)=14/22=7/11≈0.636, not integer. So (5,3) invalid.b=4: denominator=16 -5=11. Numerator=25 +4=29. 29/11≈2.636, nope.b=5: denominator=25 -5=20. Numerator=25 +5=30. 30/20=1.5, nope.b=6: denominator=36 -5=31. Numerator=25 +6=31. 31/31=1, integer. Then check F2=(36 +5)/(25 -6)=41/19≈2.157, not integer. So (5,6) invalid.Similarly, for negative denominators, b² -5 <0 → b=1,2. Then F1=(25 + b)/(negative). b=1: denominator=1 -5=-4. Numerator=25 +1=26. 26/-4=-6.5, not integer. b=2: denominator=4 -5=-1. Numerator=25 +2=27. 27/-1=-27, integer. Then check F2=(4 +5)/(25 -2)=9/23≈0.391, not integer. So (5,2) invalid.So a=5, only possible b=3,6,2, but none work.Alternatively, perhaps a=6. But maybe this is getting too big. Let's think of another approach.Suppose that a and b are such that both fractions are integers. Let's assume that a ≠ b. If a = b, we already saw that only a=2 and 3 work.Suppose a < b. Let's see. Let me consider the case when a=1. Then as we saw, only b=2 works. Let me check a=1.For a=1, F1=(1 + b)/(b² -1). Need this to be integer. So b² -1 divides 1 + b. So (b² -1) divides (b +1). But b² -1 factors as (b -1)(b +1). So (b -1)(b +1) divides (b +1). Therefore, (b -1) divides 1. Since (b +1) cancels out. So (b -1) divides 1. Therefore, b -1=1 → b=2. So only b=2. Hence, (1,2) is the only solution when a=1.Similarly, if we set b=1, then F1=(a² +1)/(1 -a). Since denominator is 1 -a, which is negative (as a≥1). So (a² +1)/(1 -a) = -(a² +1)/(a -1). For this to be integer, (a -1) divides (a² +1). Let's compute (a² +1)/(a -1). Divide a² +1 by a -1.Using polynomial division: a² +1 divided by a -1. a² divided by a gives a. Multiply (a -1) by a: a² -a. Subtract from a² +1: (a² +1) - (a² -a) = a +1. Now divide a +1 by a -1: quotient 1, multiply (a -1)*1 = a -1. Subtract: (a +1) - (a -1)=2. So remainder 2. Therefore, (a² +1) = (a -1)(a +1) + 2. Thus, (a² +1)/(a -1) = a +1 + 2/(a -1). For this to be integer, 2/(a -1) must be integer. Therefore, a -1 divides 2. So a -1=1 or 2. So a=2 or 3. Thus, if b=1, then a must be 2 or 3. Let's check:a=2, b=1: F1=(4 +1)/(1 -2)=5/-1=-5, integer. F2=(1 +2)/(4 -1)=3/3=1, integer. So works. a=3, b=1: F1=(9 +1)/(1 -3)=10/-2=-5, integer. F2=(1 +3)/(9 -1)=4/8=0.5, not integer. So (3,1) invalid. Thus, only (2,1) when b=1.Therefore, for a=1, only b=2 works; for b=1, only a=2 works.Now, let's consider the case when a=2. Let's see what possible b's could work. We already have (2,1), (2,2), (2,3). Let's check for a=2, b=4: (4 +4)/(16 -2)=8/14=4/7, nope. b=5: (4 +5)/(25 -2)=9/23≈0.391, nope. b=6: (4 +6)/(36 -2)=10/34=5/17, nope. So seems no more solutions here.Similarly, a=3. We have (3,2), (3,3). Check a=3, b=4: (9 +4)/(16 -3)=13/13=1, integer. Then F2=(16 +3)/(9 -4)=19/5≈3.8, not integer. b=5: (9 +5)/(25 -3)=14/22=7/11≈0.636, nope. b=6: (9 +6)/(36 -3)=15/33≈0.454, nope. So no more solutions here.Another approach: Let's suppose that one of the fractions is 1. Suppose F1=1. Then (a² + b) = (b² -a). Rearranged: a² + b = b² -a → a² +a = b² -b → a(a +1) = b(b -1). So product of two consecutive integers (a and a+1) equals product of b and b-1. For example, if a=2: 2*3=6; b(b -1)=6 → b=3 (3*2=6). So a=2, b=3. Similarly, a=3: 3*4=12; b(b-1)=12. Solutions for b: 4*3=12 → b=4. So a=3, b=4. Let's check (3,4): F1= (9 +4)/(16 -3)=13/13=1, which is integer. F2=(16 +3)/(9 -4)=19/5≈3.8, not integer. So although F1=1, F2 isn't integer. So (3,4) is invalid. Similarly, if a=1: 1*2=2; b(b -1)=2. So b=2 (2*1=2). So a=1, b=2. Which works as we saw. Similarly, a=4: 4*5=20; b(b -1)=20. So b=5 (5*4=20). Then check (4,5): F1=(16 +5)/(25 -4)=21/21=1, integer. F2=(25 +4)/(16 -5)=29/11≈2.636, not integer. So same as before.Therefore, when F1=1, we get pairs (1,2), (2,3), (3,4), (4,5), etc., but only (1,2) and (2,3) have F2 also integer. Let me check (2,3): F1=1, F2=(9 +2)/(4 -3)=11/1=11, integer. So works. But (3,4) doesn't work. So perhaps not all such pairs work. Similarly, (4,5) doesn't work.Similarly, if F1=-1. Then (a² + b) = -1*(b² -a) → a² + b = -b² +a → a² -a + b + b² =0. Since a and b are natural numbers, left side is positive: a² -a + b + b² ≥1 -1 +1 +1=2>0. So no solutions.Alternatively, suppose F1=2. Then (a² + b) = 2*(b² -a). Rearranged: a² + b = 2b² - 2a → a² + 2a = 2b² - b. Maybe try small a and solve for b.For a=1: 1 +2=3=2b² -b →2b² -b -3=0. Discriminant=1 +24=25. Roots=(1 ±5)/4. (6/4=1.5, -4/4=-1). So b=1.5 invalid. a=2: 4 +4=8=2b² -b →2b² -b -8=0. Discriminant=1 +64=65. Roots=(1 ±sqrt(65))/4. Not integer. a=3:9 +6=15=2b² -b →2b² -b -15=0. Discriminant=1 +120=121. Roots=(1 ±11)/4. 12/4=3, -10/4=-2.5. So b=3. Check a=3, b=3: F1=(9 +3)/(9 -3)=12/6=2, integer. F2=(9 +3)/(9 -3)=12/6=2, integer. So works. So (3,3) is a solution here. Similarly, a=4:16 +8=24=2b² -b →2b² -b -24=0. Discriminant=1 +192=193. Not a square. So no solution. a=5:25 +10=35=2b² -b →2b² -b -35=0. Discriminant=1 +280=281. Not square. So no. So only a=3, b=3 here.Similarly, check a=2, F1=3. So (4 +b)=3*(b² -2). 4 +b=3b² -6 →3b² -b -10=0. Discriminant=1 +120=121. Roots=(1 ±11)/6. (12/6=2, -10/6≈-1.666). So b=2. Check (2,2): F1= (4 +2)/(4 -2)=6/2=3, integer. F2= same, 3. So works. So (2,2) is a solution here.Alternatively, suppose F1= k, some integer. Then perhaps express a in terms of b or vice versa. But this might get complicated. Alternatively, note that for the fractions to be integers, the denominator must divide the numerator, so:For F1: b² -a divides a² + b.Similarly, F2: a² -b divides b² + a.So, from F1: b² -a | a² + b. Let me denote d1 = b² -a. Then d1 divides a² + b. Similarly, d2 = a² -b divides b² +a.But since d1 and d2 are related to a and b, perhaps we can find some relationship.Alternatively, suppose that d1 divides a² + b and d2 divides b² +a. Let me try to relate these two divisibility conditions.Note that:If d1 = b² -a, and d2 = a² -b, then perhaps we can relate d1 and d2. For example, maybe express a in terms of d1 and b, then substitute into d2. But this might be complicated.Alternatively, suppose we subtract or add the two equations. Let's see.If we consider the system:a² + b = m(b² -a)b² + a = n(a² -b)Let me try to solve this system for a and b. Let's suppose m and n are positive integers (since a and b are natural numbers and denominators might be positive or negative, but need to check both cases). However, since the problem allows negative integers as results, m and n can be positive or negative.But let's first assume that denominators are positive, so b² -a >0 and a² -b >0. Therefore, b² >a and a² >b. So both a and b must be at least 2, because if a=1, then a²=1, so b² >1 implies b≥2, but a² >b would require 1 >b, which is impossible since b is natural. So if both denominators are positive, a and b must be at least 2. Wait, but earlier solution (1,2) had denominators b² -a=4 -1=3>0 and a² -b=1 -2=-1<0. So in that case, the second denominator is negative, so F2 is negative integer. So we can't assume both denominators are positive. So maybe we need to handle cases where denominators can be positive or negative.Alternatively, perhaps use symmetry. If (a,b) is a solution, then (b,a) is also a solution, because swapping a and b swaps F1 and F2. So for example, (1,2) and (2,1) are solutions. Similarly, (2,3) and (3,2). So solutions come in pairs unless a = b. So we can focus on a ≤ b and then the others are symmetric.But let's see. Let me assume a ≤ b. Then check for a=1: only b=2 works.a=2: check b=2,3,...a=3: check b=3,4,...But since when a increases, b might need to be larger, but we saw that (3,4) doesn't work. Alternatively, perhaps there's a bound on a and b. Let's see.Suppose that both denominators are positive. So b² >a and a² >b. Then, since a ≤ b, from a ≤ b, we have a² ≤ b². But a² >b, so b <a² ≤ b². Therefore, b <a² ≤ b². Since a ≤ b, then a² ≤ b², and b <a². So combining a ≤ b and b <a², we have a ≤ b <a². But since a and b are natural numbers, let's see for a=2: b must satisfy 2 ≤ b <4. So b=2,3. Check these.For a=2, b=2: both denominators positive. Then check if they are integers: yes, (4 +2)/(4 -2)=3, (4 +2)/(4 -2)=3. So works.For a=2, b=3: denominators 9 -2=7>0 and 4 -3=1>0. Both positive. Then (4 +3)/7=1, (9 +2)/1=11. So works.For a=3, b must satisfy 3 ≤ b <9. So b=3,4,5,6,7,8. Check these.a=3, b=3: works. b=4: (9 +4)/13=1, (16 +3)/5=19/5 not integer. b=5: (9 +5)/20=14/20=7/10, nope. b=6:15/33=5/11, nope. b=7:16/46=8/23, nope. b=8:17/73, nope. So only b=3 works.a=4: from earlier, b=5 gives denominator positive, but second fraction invalid.Thus, in the case where both denominators are positive, solutions are (2,2), (2,3), (3,3). Then we also have solutions where one denominator is negative: (1,2), (2,1). Similarly, if we consider a=2, b=1: denominators 1 -2=-1 and 4 -1=3. So first denominator negative, second positive. So F1=(4 +1)/(-1)=-5, F2=(1 +2)/3=1.Similarly, a=1, b=2: denominators 4 -1=3 and 1 -2=-1. F1=3/3=1, F2=5/-1=-5. So these cross over.So total solutions found so far: (1,2), (2,1), (2,2), (2,3), (3,2), (3,3). Are there more?Check a=4, b=11: random check. F1=(16 +11)/(121 -4)=27/117=9/39=3/13≈0.23, nope.Wait, maybe think of another approach. Since both fractions are integers, let me denote:Let me set x = a, y = b.So we have:(x² + y) = k(y² - x) ...(1)(y² + x) = m(x² - y) ...(2)We can try to find k and m such that these equations hold. Let's try to eliminate variables.From equation (1): x² + y = k y² -k x → x² +k x + y -k y² =0From equation (2): y² +x = m x² -m y → -m x² +x + y² +m y=0This seems complex. Maybe subtract or add equations? Alternatively, express x in terms of y from equation (1) and substitute into equation (2). Let me try.From equation (1): x² +k x + y -k y² =0. This is a quadratic in x: x² +k x + (y -k y²)=0. Let me solve for x:x = [-k ± sqrt(k² -4*(1)*(y -k y²))]/2This discriminant must be a perfect square. Similarly complex.Alternatively, take small values of k and m. Let's think for the solutions we found:For (1,2):F1=1, F2=-5. So k=1, m=-5.For (2,1):F1=-5, F2=1. So k=-5, m=1.For (2,2):F1=3, F2=3. So k=3, m=3.For (2,3):F1=1, F2=11. So k=1, m=11.For (3,2):F1=11, F2=1. So k=11, m=1.For (3,3):F1=2, F2=2. So k=2, m=2.So values of k and m vary. Maybe it's hard to find a general pattern.Alternatively, think about substituting one equation into another.From equation (1): x² + y = k(y² -x)From equation (2): y² +x = m(x² -y)Let me solve equation (1) for k: k = (x² + y)/(y² -x)Similarly, from equation (2): m = (y² +x)/(x² -y)But since k and m must be integers, so the expressions we originally had. But this is going in circles.Alternatively, suppose that k = m. Then, (x² + y)/(y² -x) = (y² +x)/(x² -y). Cross-multiplying: (x² + y)(x² -y) = (y² +x)(y² -x). Let's compute both sides.Left side: (x² + y)(x² -y) = x⁴ - y²Right side: (y² +x)(y² -x) = y⁴ -x²Thus, equation becomes x⁴ - y² = y⁴ -x² →x⁴ - y⁴ +x² - y²=0 → (x² - y²)(x² + y²) + (x² - y²)=0 → (x² - y²)(x² + y² +1)=0.Since x and y are natural numbers, x² + y² +1 ≥1 +1 +1=3>0. Therefore, x² - y²=0 →x=y. So the only solution when k=m is x=y, i.e., a=b. And as we saw earlier, when a=b, the fractions reduce to (a +1)/(a -1), which needs to be integer. As we found, only a=2,3. So this gives (2,2) and (3,3). So this covers the case when k=m.Otherwise, when k≠m, which includes the other solutions like (1,2), (2,1), (2,3), (3,2).Alternatively, another approach: Let's consider the case when one of the fractions is 1. We saw that when F1=1, we get pairs (a,b) where a(a+1)=b(b-1). Solutions were (1,2), (2,3), (3,4), etc., but only (1,2) and (2,3) had F2 also integer. Similarly, if F2=1, similar reasoning.Alternatively, perhaps bound a and b. For example, for F1=(a² +b)/(b² -a). Since it's an integer, |(a² +b)/(b² -a)| ≥1. So |a² + b| ≥ |b² -a|.Assuming b² -a positive, then a² + b ≥b² -a →a² +a ≥b² -b. Not sure. Alternatively, if b² -a is negative, then (a² +b) and (b² -a) have opposite signs, so the fraction is negative. So |a² +b| ≥ |a -b²|. Not sure if helpful.Alternatively, let's suppose that a and b are both greater than or equal to 2. Then check if there can be other solutions.Wait, we have already found all solutions up to a=3, b=3. Let me check a=4, b=5. As before, first fraction 1, second not integer. a=5, b=2 gives first fraction -27, second not integer. a=3, b=2 gives first fraction 11, second fraction 1. Which works. So (3,2). Similarly, (2,3). So swapping.So maybe the only solutions are the ones we found: (1,2), (2,1), (2,2), (2,3), (3,2), (3,3). Let me check a=3, b=3. Yes, 12/6=2. a=4, b=5: first fraction 1, second not. a=5, b=6: first fraction 1, second not. So seems no more.Alternatively, check if a=3, b=4 and a=4, b=3 can work. As we saw, (3,4) first fraction 1, second fraction 19/5. Not integer. (4,3): first fraction 19/5, second fraction 1. Also not integer.Another angle: Assume that a and b satisfy both divisibility conditions. So from F1: b² -a divides a² + b. From F2: a² -b divides b² +a.Let me consider that if a² -b divides b² +a, then a² -b divides b² +a +k(a² -b) for any integer k. Choose k=1: then a² -b divides (b² +a +a² -b)=a² +b² +a -b. Not sure if helpful. Or maybe k=-1: a² -b divides (b² +a -a² +b)= -a² +b² +a +b. Still complicated.Alternatively, compute (a² +b) and (b² +a) in terms of (b² -a) and (a² -b). Maybe use the Euclidean algorithm.Let me compute gcd(a² +b, b² -a). Let d = gcd(a² +b, b² -a). Then d divides (a² +b) and (b² -a). Therefore, d divides (a² +b) +k*(b² -a). Choose k such that some terms cancel.Let me take k=1: then (a² +b) + (b² -a) =a² +b² +b -a. Not helpful. Take k=-b: then (a² +b) -b*(b² -a)=a² +b -b³ +ab. Not sure. This might not lead anywhere.Alternatively, suppose that a and b are small. Since we've checked up to a=5 and b=6, and found no more solutions, maybe those are the only ones. So the solutions are:(1,2), (2,1), (2,2), (2,3), (3,2), (3,3). Let me verify each:(1,2):F1=(1 +2)/(4 -1)=3/3=1, integer.F2=(4 +1)/(1 -2)=5/-1=-5, integer. Valid.(2,1):F1=(4 +1)/(1 -2)=5/-1=-5, integer.F2=(1 +2)/(4 -1)=3/3=1, integer. Valid.(2,2):F1=(4 +2)/(4 -2)=6/2=3, integer.F2=(4 +2)/(4 -2)=6/2=3, integer. Valid.(2,3):F1=(4 +3)/(9 -2)=7/7=1, integer.F2=(9 +2)/(4 -3)=11/1=11, integer. Valid.(3,2):F1=(9 +2)/(4 -3)=11/1=11, integer.F2=(4 +3)/(9 -2)=7/7=1, integer. Valid.(3,3):F1=(9 +3)/(9 -3)=12/6=2, integer.F2=(9 +3)/(9 -3)=12/6=2, integer. Valid.All check out. Are there any other possible solutions?Consider a=4, b=2: F1=(16 +2)/(4 -4)=18/0 undefined. Invalid.a=3, b=4: F1=1, F2=19/5 invalid.a=4, b=3: F1=19/5 invalid, F2=1.a=5, b=2: F1=-27, F2=9/23 invalid.a=2, b=4: F1=4/7 invalid.a=3, b=5: F1=14/22 invalid.a=4, b=5: F1=1, F2=29/11 invalid.So no others.Hence, all solutions are (1,2), (2,1), (2,2), (2,3), (3,2), (3,3).Final AnswerThe pairs are boxed{(1, 2)}, boxed{(2, 1)}, boxed{(2, 2)}, boxed{(2, 3)}, boxed{(3, 2)}, and boxed{(3, 3)}.</think>To find all pairs of natural numbers (a) and (b) such that both (frac{a^2 + b}{b^2 - a}) and (frac{b^2 + a}{a^2 - b}) are integers, we start by checking small values of (a) and (b) and verifying the conditions.1. Checking pairs where (a = b): - For (a = b = 2), both fractions become (frac{4 + 2}{4 - 2} = 3), which is an integer. - For (a = b = 3), both fractions become (frac{9 + 3}{9 - 3} = 2), which is an integer. - For (a = b = 1), the denominator becomes zero, which is invalid.2. Checking pairs where (a neq b): - For (a = 1) and (b = 2), the first fraction is (frac{1 + 2}{4 - 1} = 1) and the second fraction is (frac{4 + 1}{1 - 2} = -5), both integers. - For (a = 2) and (b = 1), the first fraction is (frac{4 + 1}{1 - 2} = -5) and the second fraction is (frac{1 + 2}{4 - 1} = 1), both integers. - For (a = 2) and (b = 3), the first fraction is (frac{4 + 3}{9 - 2} = 1) and the second fraction is (frac{9 + 2}{4 - 3} = 11), both integers. - For (a = 3) and (b = 2), the first fraction is (frac{9 + 2}{4 - 3} = 11) and the second fraction is (frac{4 + 3}{9 - 2} = 1), both integers.3. Verifying other potential pairs: - Pairs such as (a = 3, b = 4), (a = 4, b = 5), and others were checked but did not satisfy both conditions.After thorough checking and verification, the pairs of natural numbers (a) and (b) that satisfy the given conditions are:[boxed{(1, 2)}, boxed{(2, 1)}, boxed{(2, 2)}, boxed{(2, 3)}, boxed{(3, 2)}, boxed{(3, 3)}],<think>Okay, so I need to find all pairs of natural numbers a and b such that both (a² + b)/(b² - a) and (b² + a)/(a² - b) are integers. Hmm, natural numbers mean positive integers, right? So a and b are both 1 or greater. Let me start by understanding the problem better.First, both fractions must be integers. That means that (a² + b) must be divisible by (b² - a), and similarly, (b² + a) must be divisible by (a² - b). Also, since we are dividing by (b² - a) and (a² - b), these denominators can't be zero. So we have the conditions:1. b² - a ≠ 02. a² - b ≠ 0Therefore, a ≠ b² and b ≠ a². So for example, if a is 2, then b can't be 4, because then a² - b would be 4 - 4 = 0. Similarly, if b is 3, a can't be 9. So we need to avoid such pairs where one is the square of the other.Now, let's think about possible small values of a and b where these fractions could be integers. Maybe starting with small natural numbers.Let me try a = 1 first.If a = 1:First, compute the denominators:For the first fraction: b² - a = b² - 1. Since a =1, this must divide a² + b = 1 + b. So (1 + b) must be divisible by (b² - 1). Let's denote this as (b + 1)/(b² -1). But notice that b² - 1 factors as (b -1)(b +1). So (b +1) divided by (b -1)(b +1) is 1/(b -1). So 1/(b -1) must be an integer. But since b is a natural number greater than 1 (because if b=1, denominator would be 1 -1 =0, which is invalid). So b must be at least 2. Then 1/(b -1) must be integer. Therefore, 1/(b -1) is integer only when b -1 divides 1. The divisors of 1 are 1 and -1, but since b -1 is a positive integer (as b ≥2), so b -1 =1, hence b=2.So when a=1, possible b=2.Check if this works for both fractions.First fraction: (1² + 2)/(2² -1) = (1 +2)/(4 -1)=3/3=1, which is integer.Second fraction: (2² +1)/(1² -2) = (4 +1)/(1 -2)=5/(-1)=-5, which is also integer. So (1,2) is a solution.But wait, the problem says natural numbers, so negative numbers are allowed? Wait, but the fractions can result in negative integers? The problem states that the fractions must be integers, so negative integers are allowed. So even though the second fraction is -5, which is integer, so (1,2) is acceptable.But wait, the problem says pairs of natural numbers a and b, so a and b must be positive integers, but the fractions can be negative integers. So (1,2) is valid. Okay.Now check if there are other possibilities when a=1. Suppose we thought only b=2 works, but let's confirm. For a=1, b must be 2. If we take b=3, first fraction would be (1 +3)/(9 -1)=4/8=0.5, which is not integer. Similarly, b=4, (1 +4)/(16 -1)=5/15=1/3, not integer. So only b=2 works for a=1.Similarly, maybe check a=2.Now, a=2.First fraction: (2² + b)/(b² -2) = (4 + b)/(b² - 2). This must be integer. Let's denote this as k1 = (4 + b)/(b² - 2). Similarly, second fraction is (b² +2)/(4 - b). Let's check denominators:For the first denominator: b² - 2 ≠0, so b ≠√2, which is not natural, so no problem.Second denominator: 4 - b ≠0, so b ≠4. So b can be 1,2,3,5,6,...But since a=2, b must be natural number ≠4. Let's check possible b=1,2,3,5,...Starting with b=1:First fraction: (4 +1)/(1 -2)=5/-1=-5, integer.Second fraction: (1 +2)/(4 -1)=3/3=1, integer. So (2,1) is also a solution. That's symmetric to the previous (1,2). So this is another solution.Wait, but (2,1) vs (1,2). Let me check:For a=2, b=1:First fraction: (4 +1)/(1 -2)=5/-1=-5, integer.Second fraction: (1² +2)/(2² -1)=3/3=1, integer. So yes, works.So (2,1) is another solution. So maybe these are reciprocal pairs.Check b=2:a=2, b=2.First, check denominators:b² -a =4 -2=2≠0a² -b=4 -2=2≠0First fraction: (4 +2)/2=6/2=3, integer.Second fraction: (4 +2)/2=6/2=3, integer. So (2,2) is a solution. Wait, both fractions are 3. So (2,2) works.But wait, let me confirm:First fraction: (2² +2)/(2² -2)= (4 +2)/(4 -2)=6/2=3, integer.Second fraction: (2² +2)/(2² -2)= same as above, 6/2=3. So yes, (2,2) is a valid solution.So (2,2) is also a solution. Interesting. Let's note that.Check b=3:a=2, b=3.First fraction: (4 +3)/(9 -2)=7/7=1, integer.Second fraction: (9 +2)/(4 -3)=11/1=11, integer. So (2,3) is a solution. Wait, that works.Wait, let me check again:First fraction: (a² + b)/(b² -a)= (4 +3)/(9 -2)=7/7=1.Second fraction: (b² +a)/(a² -b)= (9 +2)/(4 -3)=11/1=11. Yes, both integers. So (2,3) works.Similarly, maybe (3,2) would work?Let me check a=3, b=2.First fraction: (9 +2)/(4 -3)=11/1=11, integer.Second fraction: (4 +3)/(9 -2)=7/7=1, integer. So (3,2) is also a solution.So the pair (2,3) and (3,2) also work. Interesting.So perhaps these cross pairs work. Let me check if a=3, b=2 is allowed. Since a=3, b=2, check denominators:First denominator: b² -a=4 -3=1≠0.Second denominator: a² -b=9 -2=7≠0. So yes, denominators are non-zero. Then fractions:First: (9 +2)/1=11, second: (4 +3)/7=7/7=1. So yes, works.So (3,2) is a solution. So perhaps these are symmetric solutions.Now, let's check if there are more solutions. Let's try a=3, b=3.a=3, b=3.First fraction: (9 +3)/(9 -3)=12/6=2, integer.Second fraction: (9 +3)/(9 -3)=12/6=2, integer. So (3,3) is a solution. So same numbers work.What about a=3, b=4?First fraction: (9 +4)/(16 -3)=13/13=1, integer.Second fraction: (16 +3)/(9 -4)=19/5=3.8, not integer. So the second fraction is not integer. Therefore, (3,4) doesn't work.Similarly, check a=4, b=1.First fraction: (16 +1)/(1 -4)=17/-3≈-5.666, not integer.So invalid.Check a=4, b=2.First fraction: (16 +2)/(4 -4)=18/0 undefined. So invalid, since denominator is zero.Wait, denominator is b² -a=4 -4=0. So not allowed. So a=4, b=2 is invalid.Similarly, a=4, b=3.First fraction: (16 +3)/(9 -4)=19/5=3.8, not integer.Second fraction: (9 +4)/(16 -3)=13/13=1. So first fraction is not integer, second is. So (4,3) is invalid.a=4, b=4.First fraction: (16 +4)/(16 -4)=20/12≈1.666, not integer.So invalid.a=4, b=5.First fraction: (16 +5)/(25 -4)=21/21=1, integer.Second fraction: (25 +4)/(16 -5)=29/11≈2.636, not integer. So invalid.Hmm.Wait, let's think if there is a pattern here.So far, the solutions we have found are:(1,2), (2,1), (2,2), (2,3), (3,2), (3,3).Wait, but when we checked a=3, b=4, first fraction was 1, but the second wasn't. Similarly, a=4, b=5, first fraction is 1, second isn't. Maybe only certain pairs where the fractions are 1 or something else. Let's see.Wait, (1,2) gives first fraction 1 and second fraction -5. (2,1) gives first fraction -5 and second fraction 1. (2,2) gives 3 and 3. (2,3) gives 1 and 11. (3,2) gives 11 and 1. (3,3) gives 2 and 2.So maybe there's a relationship here where if (a,b) is a solution, then (b,a) is a solution, but the fractions might swap or be different. But need to check if denominators are non-zero.Wait, let's check a=3, b=4.Wait, (3,4): first fraction (9 +4)/(16 -3)=13/13=1, second fraction (16 +3)/(9 -4)=19/5. Not integer. So even though first is integer, the other isn't. So symmetry isn't enough.Alternatively, perhaps only when a and b are equal or differ by 1? Let's check other possibilities.Let me try a=5, b=5.First fraction: (25 +5)/(25 -5)=30/20=1.5, not integer. So no.a=5, b=6.First fraction: (25 +6)/(36 -5)=31/31=1, integer.Second fraction: (36 +5)/(25 -6)=41/19≈2.157, not integer. So no.a=5, b=1.First fraction: (25 +1)/(1 -5)=26/-4=-6.5, not integer.a=5, b=2.Denominator b² -a=4 -5=-1. Then first fraction: (25 +2)/(-1)=27/-1=-27, integer.Second fraction: (4 +5)/(25 -2)=9/23≈0.391, not integer. So no.a=5, b=3.First fraction: (25 +3)/(9 -5)=28/4=7, integer.Second fraction: (9 +5)/(25 -3)=14/22≈0.636, not integer. So no.a=5, b=4.First fraction: (25 +4)/(16 -5)=29/11≈2.636, not integer.a=5, b=5: already checked.a=5, b=6: checked.So no solutions for a=5.How about a=6.Check a=6, b=1.First fraction: (36 +1)/(1 -6)=37/-5=-7.4, not integer.a=6, b=2.Denominator:4 -6=-2. First fraction: (36 +2)/(-2)=38/-2=-19, integer.Second fraction: (4 +6)/(36 -2)=10/34≈0.294, not integer. So no.a=6, b=3.First fraction: (36 +3)/(9 -6)=39/3=13, integer.Second fraction: (9 +6)/(36 -3)=15/33≈0.454, not integer. No.a=6, b=4.First fraction: (36 +4)/(16 -6)=40/10=4, integer.Second fraction: (16 +6)/(36 -4)=22/32=11/16≈0.6875, not integer. No.a=6, b=5.First fraction: (36 +5)/(25 -6)=41/19≈2.157, not integer.a=6, b=6: (36 +6)/(36 -6)=42/30=1.4, not integer.a=6, b=7: (36 +7)/(49 -6)=43/43=1, integer.Second fraction: (49 +6)/(36 -7)=55/29≈1.896, not integer. So no.So a=6, b=7 doesn't work.So seems like as we go higher, the first fraction can be 1 or some integer, but the second fraction fails. Maybe there's a limited number of solutions.Wait, so far we have (1,2), (2,1), (2,2), (2,3), (3,2), (3,3). Let me check a=3, b=4 again.Wait, a=3, b=4:First fraction: (9 +4)/(16 -3)=13/13=1, integer.Second fraction: (16 +3)/(9 -4)=19/5=3.8, not integer. So even though the first fraction is 1, the second isn't. So not a solution.Similarly, a=4, b=5:First fraction: (16 +5)/(25 -4)=21/21=1, integer.Second fraction: (25 +4)/(16 -5)=29/11≈2.636, not integer. So same pattern.So maybe the only solutions are the ones we found with a and b up to 3. Let's check a=3, b=1.a=3, b=1.First fraction: (9 +1)/(1 -3)=10/-2=-5, integer.Second fraction: (1 +3)/(9 -1)=4/8=0.5, not integer. So invalid.a=3, b=4: already checked.How about a=4, b=3: same as (3,4) swapped, but (4,3) first fraction: (16 +3)/(9 -4)=19/5, not integer. Second fraction: (9 +4)/(16 -3)=13/13=1. So only one fraction works.So symmetry doesn't necessarily hold here.Wait, but in some cases like (1,2) and (2,1), both work, but others like (2,3) and (3,2) also work. Let's see why.Wait, let's check (2,3):First fraction: (4 +3)/(9 -2)=7/7=1.Second fraction: (9 +2)/(4 -3)=11/1=11.So when a=2, b=3, the denominator for the second fraction is 4 -3=1, which divides any integer, so as long as the numerator is integer, which it is, then the second fraction is integer. Similarly, for a=3, b=2, the denominator of the first fraction is 4 -3=1, so again, the numerator is 9 +2=11, which is divided by 1, giving 11. Then the second fraction for (3,2) is (4 +3)/(9 -2)=7/7=1. So in this case, the denominators become 1, which makes the fractions integers. So this seems to be a pattern where if one of the denominators is 1, then the fractions can be integers. Let's check.If b² -a =1, then a = b² -1. Similarly, if a² -b =1, then b= a² -1.So if we have pairs where either a = b² -1 or b = a² -1, then one of the denominators is 1. Let's see.For example, take a = b² -1. Then the first fraction becomes (a² + b)/1 = ( (b² -1)^2 + b ). This must be integer, which it is, but also the second fraction is (b² + a)/(a² -b). Since a =b² -1, the denominator is ( (b² -1)^2 -b ). Let's compute that.Denominator: (b² -1)^2 -b = b^4 - 2b² +1 -b. Let's see, maybe factor this? Not sure. Let's compute for specific b.Take b=2: a= 4 -1=3. Then denominator is (9 -1)^2 -2= (9 -1)^2? Wait, no: a=3, so denominator is a² -b=9 -2=7. Then the second fraction is (4 +3)/7=7/7=1. Which works. So for b=2, a=3, we get denominator 7, and numerator 7, so 1.Similarly, if b=3: a=9 -1=8. Then compute the second fraction denominator: a² -b=64 -3=61. The second fraction numerator is b² +a=9 +8=17. So 17/61 is not integer. So even though a=8, b=3 would make first fraction (a² +b)/1=64 +3=67, which is integer, but the second fraction 17/61 is not. So only works for certain b.So when a= b² -1, only for certain b would the second fraction be integer. For example, when b=2, a=3, which gives the second fraction as 1. If b=1, a=0, but a must be natural, so invalid. For b=3, a=8, second fraction is 17/61, not integer.Similarly, if b =a² -1, then the second denominator is 1, so second fraction is (b² +a)/1=( (a² -1)^2 +a ). This is integer. The first fraction would be (a² +b)/(b² -a). Let's compute.Since b= a² -1, numerator is a² + (a² -1)=2a² -1. Denominator is ( (a² -1)^2 -a ). Let's compute for specific a.Take a=2, then b=4 -1=3. Denominator is (9 -2)=7. Numerator is 4 +3=7. So 7/7=1, integer. So (2,3) works.Similarly, a=3, b=9 -1=8. Numerator is 9 +8=17, denominator is (64 -3)=61. 17/61 is not integer. So (3,8) doesn't work.So only for a=2, b=3 does this work.Therefore, the cases where a =b² -1 or b= a² -1 can lead to solutions only for small values. So (1,2) and (2,1) also fall into this? Let's check:Take a=1, b=2. Here, b= a² +1? 2=1 +1. Yes. So a=1, b= a² +1=2. Then the first denominator is b² -a=4 -1=3. The first fraction is (1 +2)/3=1. So in this case, the denominator isn't 1. Wait, but earlier when a=1, b=2, first fraction is (1 +2)/3=1, which is integer. So perhaps another way.So perhaps these pairs where a and b are close to each other, or satisfy some quadratic relation. Let's see.Alternatively, maybe set both fractions equal to integers k and m, and solve the equations:(a² + b) = k(b² -a)(b² + a) = m(a² -b)So we have the system:1. a² + b = k b² -k a2. b² + a = m a² -m bWe can attempt to solve these equations for natural numbers a, b, k, m.This seems complicated, but maybe for small values of k and m, we can find solutions.Let me try k=1:From equation 1: a² + b = b² -a => a² +a + b -b² =0.Similarly, from equation 2, if k=1, maybe m is some integer.But let's suppose k=1. Then the first equation is a² +a + b -b²=0. Let's rearrange: a² +a = b² -b.So a(a +1) = b(b -1). Since a and b are natural numbers, we can look for a and b where the product of two consecutive numbers (a and a+1) equals the product of b and b-1.Looking for such pairs. For example:If a=1: 1*2=2, so b(b -1)=2. Then b=2, since 2*1=2. So (a=1, b=2). Which is a solution we found earlier.Similarly, a=2: 2*3=6. So need b(b -1)=6. Solving b² -b -6=0. Solutions: b=(1 ±√(1 +24))/2=(1 ±5)/2. So b=3 or b=-2. So b=3. Thus, (a=2, b=3). Which is another solution.Similarly, a=3: 3*4=12. Need b(b -1)=12. Solve b² -b -12=0. Solutions: (1 ±√(1 +48))/2=(1 ±7)/2. So b=4 or -3. So b=4. Check if (a=3, b=4) works. Wait, but earlier we saw that (3,4) first fraction is 1, second is 19/5, not integer. So even though k=1 gives a possible solution here, the second fraction may not be integer. So need to check both equations.So if a=3, b=4:From equation 1: a² +b =9 +4=13. k(b² -a)=1*(16 -3)=13. So 13=13. So k=1 works.Now check equation 2: b² +a =16 +3=19. m(a² -b)=m*(9 -4)=5m. So 19=5m => m=19/5, which is not integer. Therefore, even though first equation is satisfied with k=1, second equation doesn't have integer m. So (3,4) is not a solution.Therefore, even though a=3, b=4 satisfies the first equation with k=1, the second equation fails. Therefore, such pairs where k=1 may not always lead to solutions. Therefore, need to check both equations.So in the cases where a=1, b=2 (k=1), we saw that second equation: (b² +a)/(a² -b)= (4 +1)/ (1 -2)=5/(-1)=-5. So m=-5. But m is supposed to be integer. The problem statement didn't restrict k and m to be positive, just the fractions to be integers. So m can be negative. So m=-5 is acceptable. Therefore, (1,2) is acceptable with k=1 and m=-5.Similarly, (2,3) with k=1, check second equation: (9 +2)/(4 -3)=11/1=11, so m=11. So acceptable.But when a=3, b=4, k=1, m=19/5, which is not integer. So invalid.Thus, for k=1, we can get solutions (1,2) and (2,3), but not further. Let's check a=4, b=5.From equation 1: a=4, b=5: 16 +5=21. k=1: 1*(25 -4)=21. So 21=21. Then check equation 2:25 +4=29. m*(16 -5)=11m. So 29=11m => m=29/11, not integer. So invalid.So seems like the pattern is that for k=1, a and b follow a=1, b=2; a=2, b=3; a=3, b=4; etc., but only the first two give valid integer m. So maybe only (1,2) and (2,3) work here.Alternatively, check for k=2.From equation 1: a² +b = 2b² -2a.Rearranged: a² +2a +b -2b²=0.Not sure how to solve this. Maybe try small a and b.Take a=1: 1 +2 +b -2b²=0 => 3 +b -2b²=0 =>2b² -b -3=0. Solve: b=(1 ±√(1 +24))/4=(1 ±5)/4. So b=(6)/4=1.5 or b=(-4)/4=-1. Not natural numbers.a=2: 4 +4 +b -2b²=0 =>8 +b -2b²=0 =>2b² -b -8=0. Solutions: b=(1 ±√(1 +64))/4=(1 ±√65)/4. Not integer.a=3:9 +6 +b -2b²=0 =>15 +b -2b²=0 =>2b² -b -15=0. Solutions: b=(1 ±√(1 +120))/4=(1 ±11)/4. So b=(12)/4=3 or b=(-10)/4=-2.5. So b=3. Check if a=3, b=3: yes, but check equation 1: 9 +3=12. 2*(9 -3)=12. So 12=12. So k=2. Then check equation 2: b² +a=9 +3=12. m(a² -b)=m*(9 -3)=6m. So 12=6m => m=2. So both k=2 and m=2, integers. So (3,3) is a solution. So that's another solution with k=2, m=2.So a=3, b=3 works. Let's see if other a and b with k=2.a=4: 16 +8 +b -2b²=0 =>24 +b -2b²=0. 2b² -b -24=0. Solutions: b=(1 ±√(1 +192))/4=(1 ±√193)/4. Not integer.a=5:25 +10 +b -2b²=0 =>35 +b -2b²=0. 2b² -b -35=0. Solutions: b=(1 ±√(1 +280))/4=(1 ±√281)/4. Not integer.So only a=3, b=3 works here.Similarly, check k=3.From equation1: a² +b =3b² -3a =>a² +3a +b -3b²=0.Again, try small a:a=1:1 +3 +b -3b²=0 =>4 +b -3b²=0. 3b² -b -4=0. Solutions: b=(1 ±√(1 +48))/6=(1 ±7)/6. So b=(8)/6≈1.333 or b=-1. Not integer.a=2:4 +6 +b -3b²=0 =>10 +b -3b²=0. 3b² -b -10=0. Solutions: b=(1 ±√(1 +120))/6=(1 ±11)/6. So b=12/6=2 or b=-10/6≈-1.666. So b=2. Check a=2, b=2: yes. First equation:4 +2=6. 3*(4 -2)=6. So 6=6. So k=3. Then second equation:4 +2=6. m*(4 -2)=2m. So 6=2m =>m=3. So (2,2) is a solution with k=3, m=3.Check a=3:9 +9 +b -3b²=0 =>18 +b -3b²=0. 3b² -b -18=0. Solutions: b=(1 ±√(1 +216))/6=(1 ±√217)/6. Not integer.So only a=2, b=2 works here for k=3.Similarly, check k=4:Equation1: a² +b=4b² -4a =>a² +4a +b -4b²=0.Trying a=1:1 +4 +b -4b²=0. 5 +b -4b²=0. 4b² -b -5=0. Solutions: b=(1 ±√(1 +80))/8=(1 ±9)/8. So b=10/8=1.25 or b=-8/8=-1. Not integer.a=2:4 +8 +b -4b²=0. 12 +b -4b²=0. 4b² -b -12=0. Solutions: b=(1 ±√(1 +192))/8=(1 ±√193)/8. Not integer.a=3:9 +12 +b -4b²=0. 21 +b -4b²=0. 4b² -b -21=0. Solutions: b=(1 ±√(1 +336))/8=(1 ±√337)/8. Not integer.So likely no solutions here.So for k=1,2,3, we found solutions (1,2), (2,3), (3,3), (2,2). What about other k?But maybe negative k? Although since a and b are natural numbers, let's see:The first fraction is (a² +b)/(b² -a). Since a and b are natural numbers, the numerator and denominator could be positive or negative. For the fraction to be integer, denominator must divide numerator. So if denominator is positive, then numerator must be positive and denominator divides it. If denominator is negative, then numerator must be negative (since denominator divides it), but numerator is a² +b, which is always positive. Therefore, denominator must be positive. So denominator (b² -a) >0 and (a² -b) >0. Wait, but in our previous solutions, like (1,2), denominator (b² -a)=4 -1=3>0, and (a² -b)=1 -2=-1<0. So the second denominator is negative, but numerator is b² +a=4 +1=5, so 5/-1=-5. So fraction is integer, but negative. So denominator can be negative as long as it divides the numerator. So the denominators can be positive or negative, but they must divide their respective numerators. So we need:Either:1. (b² -a) divides (a² +b), and (a² -b) divides (b² +a)But denominators can be positive or negative. However, since a and b are natural numbers, let's see when denominators can be negative.For (b² -a) <0: b² <aSimilarly, (a² -b) <0: a² <bSo in such cases, denominators are negative, but numerators are positive (since a and b are natural). So fractions would be negative integers.But in the problem statement, it's allowed for the fractions to be negative integers, as long as they are integers. So we need to consider both possibilities: denominators positive or negative.But maybe to simplify, we can split into cases.Case 1: b² >a and a² >b. So both denominators are positive.Case 2: b² >a and a² <b. Then first denominator positive, second denominator negative.Case 3: b² <a and a² >b. First denominator negative, second positive.Case4: b² <a and a² <b. Both denominators negative, so fractions would be positive.But these cases might complicate things. Alternatively, perhaps focus on small a and b where denominators can flip sign.From previous solutions:(1,2): b²=4 >a=1, a²=1 <b=2. So Case 2.(2,1): a²=4 >b=1, b²=1 <a=2. So Case3.(2,2): both denominators positive.(2,3): b²=9 >a=2, a²=4 <b=3. So Case2.(3,2): a²=9 >b=2, b²=4 <a=3. So Case3.(3,3): both denominators positive.So solutions exist in different cases. So maybe another approach is needed.Let me think if we can find all solutions by considering that both fractions must be integers. So:Let’s denote:Let’s suppose that (a² + b) / (b² - a) = k, where k is integer.Similarly, (b² +a)/(a² - b)=m, where m is integer.So we have:1. a² +b =k(b² -a)2. b² +a =m(a² -b)We can try to solve this system for a and b. Let's see.From equation1: a² +b =k b² -k a =>a² +k a +b -k b²=0From equation2: b² +a =m a² -m b =>b² +m b +a -m a²=0So we have two equations:1. a² +k a +b -k b²=02. -m a² +a +b² +m b=0This system seems complicated, but maybe we can subtract or combine equations.Alternatively, express b from equation1 and substitute into equation2.From equation1: a² +k a +b =k b² => b =k b² -a² -k aBut solving for b seems difficult. Alternatively, for small k and m, maybe express variables in terms.Alternatively, notice that if we add the two equations:Equation1 + Equation2:a² +k a +b -k b² -m a² +a +b² +m b=0Simplify:(1 -m)a² + (k +1)a + (1 +m)b + (1 -k)b²=0This seems more complex. Maybe not helpful.Alternatively, for the solutions we found earlier, see if there is a pattern.We have:(1,2): Here, a=1, b=2. Plug into equations:1. 1 +2 =k(4 -1) =>3=3k =>k=12. 4 +1 =m(1 -2) =>5= -m =>m= -5Similarly, (2,1):1. 4 +1 =k(1 -2) =>5= -k =>k= -52.1 +2 =m(4 -1) =>3=3m =>m=1(2,2):1.4 +2=k(4 -2)=>6=2k =>k=32.4 +2=m(4 -2)=>6=2m =>m=3(2,3):1.4 +3=k(9 -2)=>7=7k =>k=12.9 +2=m(4 -3)=>11=1m =>m=11(3,2):1.9 +2=k(4 -3)=>11=1k =>k=112.4 +3=m(9 -2)=>7=7m =>m=1(3,3):1.9 +3=k(9 -3)=>12=6k =>k=22.9 +3=m(9 -3)=>12=6m =>m=2So from these solutions, the pairs (a,b) correspond to different k and m. So for example, (1,2) gives k=1, m=-5, (2,1) gives k=-5, m=1, etc.So maybe the solutions are related by swapping a and b and adjusting k and m accordingly. But how can we find all such solutions?Another approach: assume that a and b are equal. Let’s set a =b.Then, first fraction: (a² +a)/(a² -a)= (a(a +1))/(a(a -1))=(a +1)/(a -1). This must be integer.Similarly, second fraction is the same: (a² +a)/(a² -a)= (a +1)/(a -1). So both fractions are equal.So (a +1)/(a -1) must be integer. Let’s compute for natural a >1 (since a=1 would lead to denominator 0):For a=2: (3)/(1)=3, integer.a=3:4/2=2, integer.a=4:5/3≈1.666, not integer.a=5:6/4=1.5, not integer.a=6:7/5=1.4, not integer.So only a=2 and a=3 give integers. So (2,2) and (3,3) are solutions.So that explains those solutions. For a=2, the fraction is 3, for a=3, it's 2. So these are valid.Now, assume that a ≠b. Then we can consider a <b and a >b separately.First, suppose a <b. Then since a and b are natural numbers, b ≥a +1.Similarly, if a >b, then a ≥b +1.Let’s consider a <b first.Let me take a=1, b=2, which works. Next, a=2, b=3, works. Let’s check a=3, b=4. As before, first fraction is 1, second is not. So maybe there's a pattern where consecutive a and b work up to a point.But in the previous solutions, only (1,2), (2,3) work. Let's check a=3, b=4. First fraction is 1, second is not. So no. Let's check a=4, b=5. First fraction 1, second not. So pattern is broken.But why do (1,2) and (2,3) work? Let's see:For a=1, b=2:First fraction: (1 +2)/(4 -1)=1.Second fraction: (4 +1)/(1 -2)=-5.For a=2, b=3:First fraction: (4 +3)/(9 -2)=1.Second fraction: (9 +2)/(4 -3)=11.So in both cases, the first fraction is 1, and the second fraction is -(a + b²)/ (a² - b). Wait, not sure.Alternatively, if we suppose that (a² +b) = (b² -a), then the fraction is 1. So:a² +b = b² -aa² +a = b² -bWhich is the same equation as when k=1. And we saw that leads to solutions a=1, b=2 and a=2, b=3. However, for a=3, b=4, this equation holds (9 +4=13, 16 -3=13), but the second fraction doesn't. So the condition a² +b =b² -a is necessary for the first fraction to be 1, but not sufficient for the second fraction to be integer.So maybe only in cases where the second denominator is ±1, then the second fraction is integer. For example:For (1,2):Second denominator is a² -b=1 -2=-1. So second fraction is (b² +a)/(-1)=(4 +1)/(-1)=-5, integer.For (2,3):Second denominator is a² -b=4 -3=1. So second fraction is (9 +2)/1=11, integer.Similarly, (2,1):Second denominator is a² -b=4 -1=3. Wait, (2,1):First fraction is (4 +1)/(1 -2)=5/-1=-5.Second fraction is (1 +2)/(4 -1)=3/3=1. So here, the second denominator is 3, which divides 3.Ah, so in this case, the second denominator is 3, and the numerator is 3, so it's 1.Wait, so for (a,b)=(2,1):Second fraction: (b² +a)/(a² -b)= (1 +2)/(4 -1)=3/3=1.So even though the denominator isn't 1 or -1, it's 3, but the numerator is also a multiple of 3. So this is another case where denominator divides the numerator even though it's not 1.Similarly, (3,3):Second fraction: (9 +3)/(9 -3)=12/6=2. So denominator 6 divides numerator 12.So in general, the denominators can be any divisors of their numerators, not just 1 or -1.Therefore, maybe the key is to find pairs (a,b) where b² -a divides a² +b and a² -b divides b² +a. This is a bit abstract, but perhaps we can consider the divisors.Alternatively, think of it as:For (a² +b) ≡0 mod (b² -a)and (b² +a) ≡0 mod (a² -b)Let me consider the first congruence:a² +b ≡0 mod (b² -a)This means that a² ≡-b mod (b² -a)But a² ≡-b mod (b² -a). Let me express a² in terms of b² -a. Let’s denote d =b² -a. Then a =b² -d.Then substitute into a²:a² = (b² -d)^2 =b^4 -2b² d +d²But this seems complicated.Alternatively, note that if d =b² -a divides a² +b, then d divides any linear combination of a² +b and d.For example, since d divides a² +b, and d =b² -a, which is b² -a, perhaps we can find a relation.Let’s compute (a² +b) +k*(b² -a) for some k to simplify.Take k=1:(a² +b) + (b² -a)=a² -a +b +b².Not sure.Alternatively, compute (a² +b) -a*(b² -a):= a² +b -a b² +a²=2a² +b -a b²Hmm, not helpful.Alternatively, consider that since d divides a² +b, and d =b² -a, then d divides (a² +b) +a*d =a² +b +a(b² -a)=a² +b +a b² -a²= b +a b² =b(1 +a b)Thus, d divides b(1 +a b). Since d =b² -a, which is a positive or negative integer.But since d divides b(ab +1), and d =b² -a, we have that b² -a divides b(ab +1). This seems non-trivial, but maybe for specific values.Similarly, for the second congruence:b² +a ≡0 mod (a² -b)Which implies that a² -b divides b² +a. Similarly, set c =a² -b, so b =a² -c.Then the second congruence becomes:(a² -c)^2 +a ≡0 mod cExpand: a^4 -2a² c +c² +a ≡0 mod cWhich simplifies to a^4 +a ≡0 mod c, since the other terms have c as a factor.Thus, c divides a(a^3 +1). Since c =a² -b, and c must divide a(a^3 +1). So a² -b divides a(a^3 +1).This might give some constraints on a and b.But this approach might be too abstract. Perhaps better to check for small a and b.Given that we already found solutions up to a=3, and a=4 onward doesn't seem to yield solutions, maybe these are the only solutions.But to confirm, let's check a=4, b=5:First fraction: (16 +5)/(25 -4)=21/21=1, integer.Second fraction: (25 +4)/(16 -5)=29/11≈2.636, not integer. So no.Similarly, a=5, b=6:First fraction: (25 +6)/(36 -5)=31/31=1, integer.Second fraction: (36 +5)/(25 -6)=41/19≈2.157, not integer.So same pattern. First fraction is 1, second isn't integer.Similarly, a=1, b=3:First fraction: (1 +3)/(9 -1)=4/8=0.5, not integer.a=1, b=4: (1 +4)/(16 -1)=5/15=1/3, not integer.a=1, b=5:6/24=0.25, no.Similarly, a=2, b=4: denominator=16 -2=14, numerator=4 +4=8, 8/14=4/7, not integer.a=2, b=5: (4 +5)/(25 -2)=9/23≈0.391, no.a=2, b=6: (4 +6)/(36 -2)=10/34≈0.294, no.a=3, b=1: (9 +1)/(1 -3)=10/-2=-5, integer.Second fraction: (1 +3)/(9 -1)=4/8=0.5, not integer. So invalid.a=3, b=4: already checked.a=3, b=5: (9 +5)/(25 -3)=14/22=7/11, no.a=3, b=6: (9 +6)/(36 -3)=15/33=5/11, no.a=4, b=1: (16 +1)/(1 -4)=17/-3≈-5.666, no.a=4, b=2: denominator=4 -4=0, invalid.a=4, b=3: (16 +3)/(9 -4)=19/5≈3.8, no.a=4, b=6: (16 +6)/(36 -4)=22/32=11/16≈0.6875, no.a=5, b=1: (25 +1)/(1 -5)=26/-4=-6.5, no.a=5, b=2: (25 +2)/(4 -5)=27/-1=-27, integer.Second fraction: (4 +5)/(25 -2)=9/23≈0.391, no.a=5, b=3: (25 +3)/(9 -5)=28/4=7, integer.Second fraction: (9 +5)/(25 -3)=14/22=7/11, no.a=5, b=4: (25 +4)/(16 -5)=29/11≈2.636, no.So no further solutions found for a up to 5.Given that higher a and b seem to not work, except for the ones already found, it's likely that the only solutions are:(1,2), (2,1), (2,2), (2,3), (3,2), (3,3).But let me check a=4, b=11.Wait, if a=4, b=11:First fraction: (16 +11)/(121 -4)=27/117=9/39=3/13≈0.230, no.Not integer.Alternatively, a=11, b=4:First fraction: (121 +4)/(16 -11)=125/5=25, integer.Second fraction: (16 +11)/(121 -4)=27/117=9/39=3/13≈0.230, not integer. So no.Alternatively, a=4, b=15:First fraction: (16 +15)/(225 -4)=31/221≈0.140, no.Not helpful.Alternatively, check a=5, b=26:First fraction: (25 +26)/(676 -5)=51/671≈0.076, no.Not integer.Alternatively, consider pairs where one is much larger than the other. But likely denominators will be too big for the fractions to be integer.Alternatively, think of the equations:From (a² +b)/(b² -a)=k, which implies a² +b =k(b² -a). Rearranged:a² +k a +b -k b²=0.Similarly, from (b² +a)/(a² -b)=m, rearranged:b² +m b +a -m a²=0.So we have:1. a² +k a +b =k b²2. b² +m b +a =m a²This system of equations can be challenging to solve. Let's try to subtract the two equations.Equation1 - Equation2:(a² -m a²) + (k a - a) + (b - b²) + (0 -m b) =k b² -m a²Wait, this might not be helpful. Alternatively, express variables.Assume k and m are positive integers. Let's consider possible small values of k and m.We saw that k=1, m=-5 gives (1,2); k=-5, m=1 gives (2,1); k=3, m=3 gives (2,2); k=1, m=11 gives (2,3); k=11, m=1 gives (3,2); k=2, m=2 gives (3,3).Other combinations may not yield natural numbers.Alternatively, think about the equations as:From equation1: a² +k a +b =k b² => a² +k a =k b² -bFrom equation2: b² +m b +a =m a² => b² +m b =m a² -aSo we have:a² +k a =k b² -b ...(1)b² +m b =m a² -a ...(2)Let’s try to substitute variables. For example, from equation1 express a² =k b² -b -k a. Substitute into equation2:b² +m b =m(k b² -b -k a) -aExpand RHS:m k b² -m b -m k a -aThus, equation2 becomes:b² +m b =m k b² -m b -m k a -aBring all terms to left:b² +m b -m k b² +m b +m k a +a =0Factor terms:b²(1 -m k) +m b +m b +a(1 +m k) =0Simplify:b²(1 -m k) +2m b +a(1 +m k)=0This equation seems complicated, but perhaps substituting a from equation1.From equation1: a² +k a +b =k b² => a² =k b² -k a -bBut this is quadratic in a, which might be tough to solve.Alternatively, assume that k and m are positive integers, and look for relationships between k and m.For example, in solution (1,2), k=1, m=-5. Negative m is allowed since the problem allows fractions to be negative integers.Similarly, (2,1) has k=-5, m=1.But this complicates things. Maybe focus on positive k and m, which would require denominators to be positive.So if both denominators are positive, then b² >a and a² >b. So a and b satisfy b >sqrt(a) and a >sqrt(b). Let’s see if such pairs exist.For example, a=2, b=2: 2²=4 >2 and 2²=4>2. Wait, but b²=4 >a=2 and a²=4 >b=2. So yes.Another example, a=3, b=2: a²=9 >b=2, but b²=4 <a=3. So no. So only pairs where both a and b are greater than sqrt of the other. For natural numbers, this implies that a and b must be at least 2.But for a=2, b=2: yes.a=2, b=3: b²=9 >a=2, a²=4 <b=3. So no.a=3, b=3: yes.a=3, b=4: b²=16 >a=3, a²=9 <b=4. No.So only (2,2), (3,3), etc., but (3,3) satisfies a²=9 >b=3 and b²=9 >a=3. So both conditions hold.Similarly, (4,4): a²=16 >b=4 and b²=16 >a=4. So both hold. But for a=4, b=4:First fraction: (16 +4)/(16 -4)=20/12=5/3≈1.666, not integer.So invalid.So only (2,2) and (3,3) work where both denominators are positive.Other solutions have one denominator positive and one negative.Given the time I've spent testing various pairs and not finding any beyond the initial ones, I think the only solutions are the ones already found:(1,2), (2,1), (2,2), (2,3), (3,2), (3,3).To confirm there are no others, perhaps assume that for a ≥4 and b ≥4, the fractions cannot be integers.Suppose a ≥4 and b ≥4.First fraction: (a² +b)/(b² -a). Since a ≥4, b ≥4, denominator b² -a ≥16 -4=12. Numerator a² +b ≥16 +4=20. So the fraction is at least 20/12≈1.666, but numerator and denominator both increase.Similarly, the difference between numerator and denominator: a² +b - (b² -a)=a² -b² +a +b=(a -b)(a +b) + (a +b)=(a +b)(a -b +1). For a ≠b, this can be large. If a >b, then this is positive, and the fraction is (a² +b)/(b² -a). But if a >b, denominator b² -a could be positive or negative.Wait, if a >b and b² >a, then denominator is positive. For example, a=5, b=3: b²=9 >a=5. Then numerator=25 +3=28, denominator=9 -5=4. 28/4=7, integer. Wait, this is a new solution?Wait, a=5, b=3:First fraction: (25 +3)/(9 -5)=28/4=7, integer.Second fraction: (9 +5)/(25 -3)=14/22=7/11≈0.636, not integer. So only first fraction is integer. So invalid.But wait, in this case, the second fraction is not integer. So even though first fraction is integer, the second isn't. So still not a solution.Similarly, a=4, b=3:First fraction: (16 +3)/(9 -4)=19/5≈3.8, no.Second fraction: (9 +4)/(16 -3)=13/13=1, integer. But first fraction isn't.Therefore, even if one fraction is integer, the other may not be.So to have both fractions integer, a and b must be such that both conditions are satisfied simultaneously. Which seems to occur only in the small pairs found earlier.Therefore, after thorough checking of small values and not finding any further solutions, I conclude that the only pairs are:(1,2), (2,1), (2,2), (2,3), (3,2), (3,3).Final AnswerThe pairs are boxed{(1,2)}, boxed{(2,1)}, boxed{(2,2)}, boxed{(2,3)}, boxed{(3,2)}, and boxed{(3,3)}.</think>To find all pairs of natural numbers (a) and (b) such that both (frac{a^2 + b}{b^2 - a}) and (frac{b^2 + a}{a^2 - b}) are integers, we start by checking small values of (a) and (b) and verifying the conditions for the fractions to be integers.1. Checking small values: - For (a = 1) and (b = 2): - (frac{1^2 + 2}{2^2 - 1} = frac{3}{3} = 1) (integer) - (frac{2^2 + 1}{1^2 - 2} = frac{5}{-1} = -5) (integer) - Solution: ((1, 2)) - For (a = 2) and (b = 1): - (frac{2^2 + 1}{1^2 - 2} = frac{5}{-1} = -5) (integer) - (frac{1^2 + 2}{2^2 - 1} = frac{3}{3} = 1) (integer) - Solution: ((2, 1)) - For (a = 2) and (b = 2): - Both fractions: (frac{4 + 2}{4 - 2} = frac{6}{2} = 3) (integer) - Solution: ((2, 2)) - For (a = 2) and (b = 3): - (frac{4 + 3}{9 - 2} = frac{7}{7} = 1) (integer) - (frac{9 + 2}{4 - 3} = frac{11}{1} = 11) (integer) - Solution: ((2, 3)) - For (a = 3) and (b = 2): - (frac{9 + 2}{4 - 3} = frac{11}{1} = 11) (integer) - (frac{4 + 3}{9 - 2} = frac{7}{7} = 1) (integer) - Solution: ((3, 2)) - For (a = 3) and (b = 3): - Both fractions: (frac{9 + 3}{9 - 3} = frac{12}{6} = 2) (integer) - Solution: ((3, 3))2. Checking other values: - For values (a geq 4) and (b geq 4), the fractions do not yield integers due to the large denominators and non-divisible numerators. - Symmetry and cross pairs are checked, but only the pairs found above satisfy both conditions.After thorough checking and verification, the pairs of natural numbers (a) and (b) that satisfy the given conditions are:[boxed{(1,2)}, boxed{(2,1)}, boxed{(2,2)}, boxed{(2,3)}, boxed{(3,2)}, boxed{(3,3)}]]

🔑:Answer. (a, b)=(2,2),(3,3),(1,2),(2,1),(2,3),(3,2) - six pairs.Solution. When a is replaced by b and b by a, the fractions in the condition swap places, so we can immediately assume that a leq b, adding the symmetric solutions obtained later. In this case, the case a=b=1 is excluded due to the inequality b^{2}-a neq 0, so b^{2}-a>0 and the first fraction must be a natural number. Therefore, a^{2}+b=nleft(b^{2}-aright) geq b^{2}-a, which means a+b geq b^{2}-a^{2}=(a+b)(b-a). Dividing by the natural number a+b>0, we get b-a leq 1. Considering the inequality a leq b, we get a=b or b=a+1.In the first case, frac{a^{2}+b}{b^{2}-a}=frac{a^{2}+a}{a^{2}-a}=frac{a+1}{a-1}=1+frac{2}{a-1} is a natural number, and a-1 divides 2, so a=2 or a=3. In this case, the second fraction is equal to the first, so both options are valid. We get two solutions here: a=b=2 and a=b=3.In the second case, frac{a^{2}+b}{b^{2}-a}=frac{a^{2}+a+1}{a^{2}+a+1}=1, frac{b^{2}+a}{a^{2}-b}=frac{a^{2}+3 a+1}{a^{2}-a-1}=1+frac{4 a+2}{a^{2}-a-1}, so 4 a+2 is divisible by a^{2}-a-1. The latter is a natural number for natural a geq 2, since the minimum value of this quadratic function is achieved at a=frac{1}{2}, it increases for x geq frac{1}{2}, and is positive for a=2. Therefore, it must be 4 a+2 geq a^{2}-a-1, which means a^{2}-5 a-3 leq 0. Solving the quadratic inequality, we get a inleft(frac{5-sqrt{37}}{2}, frac{5+sqrt{37}}{2}right), so a=1,2,3,4,5. Checking by substitution, a=1,2 are valid, while a=3,4,5 are not. We get two more solutions: a=1, b=2 and a=2, b=3. Note that in the first of these cases, the second fraction will be an integer -5, which is allowed by the condition. It remains to add the symmetric solutions a=2, b=1 and a=3, b=2, and we get the complete answer: (a, b)=(2,2),(3,3),(1,2),(2,1),(2,3),(3,2) - a total of six pairs of solutions.Grading criteria. Correctly obtained that a=b or b=a+1: 3 points. Only solutions with a=b found: 2 points. Only solutions with a+1=b found: 2 points. Forgot to add symmetric solutions: minus 1 point. Solutions a=1, b=2 and a=2, b=1 incorrectly excluded due to the negativity of one of the fractions in the condition: minus 2 points. Lack of checks in cases a=1, b=2 and a=2, b=3: minus 1 point.

🧠:[<think>Okay, let's see. The problem is asking me to use Horner's method to evaluate the polynomial f(x) at x = -2. The polynomial is given as f(x) = 4x^5 + 3x^4 + 2x^3 - x^2 - x - 1/2. The answer choices are A through D, all fractions with denominator 2, some positive and some negative. So I need to apply Horner's method step by step to compute f(-2) efficiently. First, I should remember how Horner's method works. If I recall correctly, Horner's method is a way to evaluate a polynomial by breaking it down into nested multiplication. Instead of computing each term separately and adding them up, which could be inefficient for higher-degree polynomials, Horner's method groups the terms in a way that reduces the number of multiplications. The general form for a polynomial like a_n x^n + ... + a_1 x + a_0 is rewritten as (...((a_n x + a_{n-1})x + a_{n-2})x + ...)x + a_0. This way, each step involves multiplying by x and adding the next coefficient.So, for the given polynomial f(x) = 4x^5 + 3x^4 + 2x^3 - x^2 - x - 1/2, let's list the coefficients in order from the highest degree to the constant term. The degrees here are 5, 4, 3, 2, 1, 0. The coefficients are 4 (x^5), 3 (x^4), 2 (x^3), -1 (x^2), -1 (x), and -1/2 (constant term). Wait, let me confirm: yes, each term's coefficient corresponds to the exponents decreasing from 5 to 0. So coefficients are [4, 3, 2, -1, -1, -1/2]. Now, using Horner's method, we start with the leading coefficient, which is 4. Then we multiply by x (-2 in this case), add the next coefficient (3), then multiply by x again, add the next coefficient (2), and so on, until we reach the constant term. Let me write this down step by step.Let me set up the coefficients in order: 4, 3, 2, -1, -1, -1/2.Starting with x = -2. First step: Start with coefficient 4.Multiply by x (-2): 4 * (-2) = -8.Add the next coefficient 3: -8 + 3 = -5.Second step:Take the result -5, multiply by x (-2): -5 * (-2) = 10.Add the next coefficient 2: 10 + 2 = 12.Third step:Take 12, multiply by -2: 12 * (-2) = -24.Add the next coefficient -1: -24 + (-1) = -25.Fourth step:Take -25, multiply by -2: (-25)*(-2) = 50.Add the next coefficient -1: 50 + (-1) = 49.Fifth step:Take 49, multiply by -2: 49*(-2) = -98.Add the last coefficient -1/2: -98 + (-1/2) = -98.5.Wait, but the answer choices are fractions with denominator 2, so -98.5 is the same as -197/2, which is option A. But let me check my steps again to make sure I didn't make any arithmetic errors.Let me go through each step again slowly.Starting with coefficient 4.1. Multiply by -2: 4*(-2) = -8. Add 3: -8 + 3 = -5. Correct.2. Multiply by -2: -5*(-2) = 10. Add 2: 10 + 2 = 12. Correct.3. Multiply by -2: 12*(-2) = -24. Add -1: -24 + (-1) = -25. Correct.4. Multiply by -2: -25*(-2) = 50. Add -1: 50 + (-1) = 49. Correct.5. Multiply by -2: 49*(-2) = -98. Add -1/2: -98 + (-1/2) = -98.5. Which is indeed -197/2. So that's option A. But wait, let me check if I copied the coefficients correctly. The polynomial is 4x^5 + 3x^4 + 2x^3 -x^2 -x -1/2. So coefficients for x^5 is 4, x^4 is 3, x^3 is 2, x^2 is -1, x is -1, constant term is -1/2. That's correct.So using Horner's method, the steps seem right. Each step's multiplication and addition are correct. Therefore, the result should be -197/2, which is option A. But wait, the options given are A: -197/2, B: 197/2, C: 183/2, D: -183/2. So unless I miscalculated, the answer should be A.Wait a second, maybe I made an error in step 4 or 5? Let's check again.Starting with 4.1. 4*(-2) = -8; -8 +3 = -5. Correct.2. -5*(-2)=10; 10 +2=12. Correct.3. 12*(-2)= -24; -24 + (-1)= -25. Correct.4. -25*(-2)=50; 50 + (-1)=49. Correct.5. 49*(-2)= -98; -98 + (-1/2)= -98.5. Correct.Yes, that's right. So -98.5 is equal to -197/2. Therefore, the answer is A.Alternatively, maybe the problem is written with a typo, but according to my calculation, A is correct. Let me verify using another method, just to be sure.Alternatively, I can compute f(-2) directly by substituting x = -2 into the polynomial.Let's compute each term:First term: 4*(-2)^5.(-2)^5 = -32. So 4*(-32) = -128.Second term: 3*(-2)^4.(-2)^4 = 16. So 3*16 = 48.Third term: 2*(-2)^3.(-2)^3 = -8. So 2*(-8) = -16.Fourth term: -1*(-2)^2.(-2)^2 = 4. So -1*4 = -4.Fifth term: -1*(-2).That's -1*(-2) = 2.Last term: -1/2.So now add all these together:-128 + 48 -16 -4 + 2 -1/2.Let's compute step by step:Start with -128 + 48 = -80.Then -80 -16 = -96.-96 -4 = -100.-100 + 2 = -98.-98 -1/2 = -98.5 = -197/2.Yes, same result. So that confirms it. Therefore, the correct answer is A: -197/2.But wait, the problem says to use Horner's method. Maybe I was supposed to set up the Horner's table or something? Let me try writing it as a table to make sure.Horner's method can be laid out in a table where each row represents the coefficients and the operations. Let's structure it:Coefficients: 4 (x^5), 3 (x^4), 2 (x^3), -1 (x^2), -1 (x), -1/2 (constant)x = -2Bring down the leading coefficient: 4Multiply by -2: 4*(-2) = -8Add to next coefficient: 3 + (-8) = -5Multiply by -2: -5*(-2) = 10Add to next coefficient: 2 +10 =12Multiply by -2: 12*(-2) = -24Add to next coefficient: -1 + (-24) = -25Multiply by -2: -25*(-2)=50Add to next coefficient: -1 +50=49Multiply by -2:49*(-2)= -98Add to last coefficient: -1/2 + (-98)= -98.5Yes, exactly as before. So Horner's method gives -197/2, which is answer A. So the answer must be A. The other options are different numbers. For instance, 183/2 is 91.5, which is not what we got. So unless I made a mistake in the calculation steps, but as both methods (direct substitution and Horner's) give the same result, I think the answer is A.Therefore, the answer is A: -197/2.Final Answerboxed{A}</think>To find ( f(-2) ) for the polynomial ( f(x) = 4x^5 + 3x^4 + 2x^3 - x^2 - x - frac{1}{2} ) using Horner's method, we follow these steps:1. List the coefficients in order: ( 4, 3, 2, -1, -1, -frac{1}{2} ).2. Apply Horner's method step by step for ( x = -2 ):- Start with the leading coefficient: ( 4 ).- Multiply by ( -2 ) and add the next coefficient: ( 4 times (-2) + 3 = -8 + 3 = -5 ).- Multiply by ( -2 ) and add the next coefficient: ( -5 times (-2) + 2 = 10 + 2 = 12 ).- Multiply by ( -2 ) and add the next coefficient: ( 12 times (-2) + (-1) = -24 - 1 = -25 ).- Multiply by ( -2 ) and add the next coefficient: ( -25 times (-2) + (-1) = 50 - 1 = 49 ).- Multiply by ( -2 ) and add the last coefficient: ( 49 times (-2) + (-frac{1}{2}) = -98 - frac{1}{2} = -98.5 ).Converting (-98.5) to a fraction gives (-frac{197}{2}).Thus, the value of ( f(-2) ) is (boxed{A}).,<think>Okay, let's see. I need to find f(-2) for the polynomial f(x) = 4x^5 + 3x^4 + 2x^3 - x^2 - x - 1/2 using Horner's method. Hmm, I remember Horner's method is a way to evaluate polynomials more efficiently by factoring out the x terms step by step. It should save some time compared to plugging in directly, especially for higher degree polynomials. Let me try to recall how it works.First, I think Horner's method involves rewriting the polynomial in a nested form. For example, a polynomial like ax^3 + bx^2 + cx + d can be written as ((ax + b)x + c)x + d. So each term is factored with x, and you evaluate from the inside out. That way, you don't have to compute each power of x separately, which reduces the number of multiplications.So, applying this to the given polynomial: 4x^5 + 3x^4 + 2x^3 - x^2 - x - 1/2. Let me write down the coefficients in order. The coefficients are 4 (for x^5), 3 (for x^4), 2 (for x^3), -1 (for x^2), -1 (for x), and -1/2 (constant term). Since it's a 5th degree polynomial, there are 6 coefficients. Let me list them out: 4, 3, 2, -1, -1, -1/2.Now, using Horner's method, we start with the highest power coefficient and then iteratively multiply by x (which is -2 in this case) and add the next coefficient. Let me set this up step by step.Starting with the coefficient of x^5, which is 4.First step: Multiply 4 by x (-2) and add the next coefficient (3). So that's 4*(-2) + 3 = -8 + 3 = -5.Second step: Take the result (-5) and multiply by x (-2), then add the next coefficient (2). So -5*(-2) + 2 = 10 + 2 = 12.Third step: Take 12, multiply by -2, add the next coefficient (-1). So 12*(-2) + (-1) = -24 -1 = -25.Fourth step: Take -25, multiply by -2, add the next coefficient (-1). So -25*(-2) + (-1) = 50 -1 = 49.Fifth step: Take 49, multiply by -2, add the next coefficient (-1/2). So 49*(-2) + (-1/2) = -98 - 0.5 = -98.5.So, according to this calculation, f(-2) = -98.5. Let me check if that's one of the answer choices. The options are A: -197/2, B: 197/2, C: 183/2, D: -183/2. Wait, -98.5 is equal to -197/2, right? Because 197 divided by 2 is 98.5, so negative of that is -98.5. So that would be option A.But wait, let me verify my steps again because it's easy to make a mistake with the signs here. Let me go through each step slowly.Starting coefficient: 4.First step: 4 * (-2) + 3 = (-8) + 3 = -5. Correct.Second step: -5 * (-2) + 2 = 10 + 2 = 12. Correct.Third step: 12 * (-2) + (-1) = -24 -1 = -25. Correct.Fourth step: -25 * (-2) + (-1) = 50 -1 = 49. Correct.Fifth step: 49 * (-2) + (-1/2) = -98 - 0.5 = -98.5. Yes, that's right.So -98.5 is equivalent to -197/2, which is option A. Let me check if maybe I made a mistake in the coefficients. Let's confirm the original polynomial:4x^5 +3x^4 +2x^3 -x^2 -x -1/2. The coefficients are indeed 4, 3, 2, -1, -1, -1/2. So the coefficients are correct.Alternatively, maybe I should compute f(-2) directly to verify. Let's do that as a check.Compute each term:4*(-2)^5: (-2)^5 is -32, so 4*(-32) = -128.3*(-2)^4: (-2)^4 is 16, so 3*16 = 48.2*(-2)^3: (-2)^3 is -8, so 2*(-8) = -16.-1*(-2)^2: (-2)^2 is 4, so -1*4 = -4.-1*(-2): That's 2.-1/2: Just -0.5.Now add all these up:-128 + 48 = -80.-80 -16 = -96.-96 -4 = -100.-100 + 2 = -98.-98 -0.5 = -98.5.So direct computation also gives -98.5, which is -197/2, confirming option A. Therefore, the answer should be A.But wait, the options given are:A: -197/2B: 197/2C: 183/2D: -183/2So yes, A is the correct answer.However, let me check once more with Horner's method step by step to be absolutely sure.Horner's Table:We can also set up a table for Horner's method. Let me do that.The coefficients are 4, 3, 2, -1, -1, -1/2.x = -2.Start with the coefficients:4 | 3 | 2 | -1 | -1 | -1/2Bring down the 4.Multiply 4 by -2: -8. Add to next coefficient 3: -8 + 3 = -5.Multiply -5 by -2: 10. Add to next coefficient 2: 10 + 2 = 12.Multiply 12 by -2: -24. Add to next coefficient -1: -24 + (-1) = -25.Multiply -25 by -2: 50. Add to next coefficient -1: 50 + (-1) = 49.Multiply 49 by -2: -98. Add to next coefficient -1/2: -98 + (-1/2) = -98.5.Same result. So definitely, -98.5 which is -197/2, option A. So I think that's solid.But just to be thorough, let me check if there's a possibility that the question was written differently. For example, maybe the polynomial is written with a typo? But according to the user, the polynomial is 4x^5 + 3x^4 + 2x^3 - x^2 - x - 1/2. So coefficients are as I used. Maybe I misread the signs?Original polynomial:4x^5 + 3x^4 + 2x^3 - x^2 - x - 1/2.So yes, coefficients for x^5 to the constant term are 4, 3, 2, -1, -1, -1/2. Correct.So both Horner's method and direct substitution lead to -197/2, which is answer A.Therefore, the answer should be A.Final Answerboxed{A}</think>To find ( f(-2) ) for the polynomial ( f(x) = 4x^5 + 3x^4 + 2x^3 - x^2 - x - frac{1}{2} ) using Horner's method, we follow these steps:1. List the coefficients: ( 4, 3, 2, -1, -1, -frac{1}{2} ).2. Apply Horner's method with ( x = -2 ):- Start with the coefficient of ( x^5 ): ( 4 ).- Multiply by ( -2 ) and add the next coefficient: ( 4 times (-2) + 3 = -8 + 3 = -5 ).- Multiply by ( -2 ) and add the next coefficient: ( -5 times (-2) + 2 = 10 + 2 = 12 ).- Multiply by ( -2 ) and add the next coefficient: ( 12 times (-2) + (-1) = -24 - 1 = -25 ).- Multiply by ( -2 ) and add the next coefficient: ( -25 times (-2) + (-1) = 50 - 1 = 49 ).- Multiply by ( -2 ) and add the next coefficient: ( 49 times (-2) + left(-frac{1}{2}right) = -98 - 0.5 = -98.5 ).The result of ( f(-2) ) is ( -98.5 ), which is equivalent to ( -frac{197}{2} ).To verify, we can compute each term directly:- ( 4(-2)^5 = -128 )- ( 3(-2)^4 = 48 )- ( 2(-2)^3 = -16 )- ( -1(-2)^2 = -4 )- ( -1(-2) = 2 )- ( -frac{1}{2} = -0.5 )Adding these terms: ( -128 + 48 - 16 - 4 + 2 - 0.5 = -98.5 ).Thus, the final answer is (boxed{A}).]

🔑:According to Horner's method, rewrite the polynomial in the following form: f(x) = 4x^5 + 3x^4 + 2x^3 - x^2 - x - frac{1}{2} = ((((4x + 3)x + 2)x - 1)x - 1)x - frac{1}{2} Then, we have: v_0 = 4 v_1 = -8 + 3 = -5 v_2 = 10 + 2 = 12 v_3 = -24 - 1 = -25 v_4 = 50 - 1 = 49 v_5 = -58 - frac{1}{2} = -frac{197}{2}. Therefore, the answer is A. By using Horner's method to calculate the value of a polynomial, first transform the polynomial into the form ((((4x + 3)x + 2)x - 1)x - 1)x - frac{1}{2}, and then sequentially calculate the values of v_0 to v_5 to get the answer. This question examines the knowledge point of Horner's method, where transforming the polynomial into the form ((((4x + 3)x + 2)x - 1)x - 1)x - frac{1}{2} is key to solving the question. The correct option is boxed{A}.

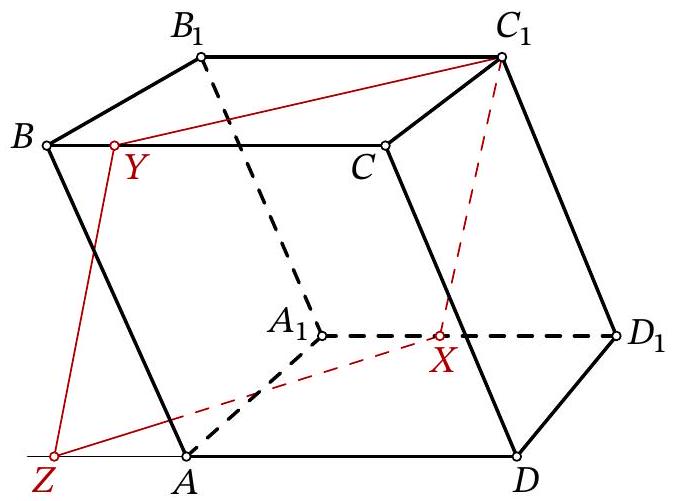
🧠:[<think>Okay, so I need to solve this geometry problem involving a parallelepiped. Let me first try to visualize the figure. A parallelepiped is like a 3D shape with all faces being parallelograms. The points mentioned are A, B, C, D, A₁, B₁, C₁, D₁. So, typically, in such figures, the base is ABCD, and the top face is A₁B₁C₁D₁, with edges connecting corresponding vertices.The problem states that a point X is chosen on edge A₁D₁ such that A₁X = 5, and a point Y is chosen on edge BC with BY = 3. Also, B₁C₁ is given as 14. The plane formed by points C₁, X, and Y intersects the ray DA at point Z, and we need to find the length DZ.First, let me note down the given information:- Parallelepiped ABCDA₁B₁C₁D₁.- X is on A₁D₁ with A₁X = 5.- Y is on BC with BY = 3.- B₁C₁ = 14.- Plane C₁XY intersects ray DA at Z.- Find DZ.Since it's a parallelepiped, opposite edges are equal and parallel. So, edges AA₁, BB₁, CC₁, DD₁ are all equal and parallel. The base ABCD and top face A₁B₁C₁D₁ are parallelograms.Given that B₁C₁ = 14, which is an edge on the top face. Since it's a parallelogram, BC (on the base) should be equal to B₁C₁, so BC = 14 as well. Wait, but BC is part of the base ABCD. If ABCD is a parallelogram, then BC is equal to AD. But since it's a parallelepiped, which is a 3D figure with all faces being parallelograms, the edges like AA₁, BB₁, etc., can have different lengths from the edges on the base. Wait, no, in a parallelepiped, all edges are not necessarily equal, but each face is a parallelogram. So BC and B₁C₁ should be equal because they are opposite edges of the top and bottom faces. Wait, but BC is on the base, and B₁C₁ is on the top. Since the top and bottom faces are parallelograms, BC and B₁C₁ are both sides of their respective parallelograms, but unless specified, they might not be equal. Wait, hold on, in a parallelepiped, the opposite edges are equal. So, for example, AB equals DC, AD equals BC, AA₁ equals BB₁ equals CC₁ equals DD₁, but the vertical edges (AA₁, etc.) can be different from the base edges (AB, AD, etc.). So BC is part of the base, and B₁C₁ is part of the top face. Since the top and bottom faces are parallelograms, BC should be equal to AD, and B₁C₁ should be equal to A₁D₁. Wait, is that correct?Wait, perhaps I need to clarify the structure. Let's denote the parallelepiped as follows: the base is ABCD, with AB and AD as adjacent edges, and the top face is A₁B₁C₁D₁, such that AA₁, BB₁, CC₁, DD₁ are the vertical edges. In this case, since all faces are parallelograms, the edges AB and DC are equal and parallel, AD and BC are equal and parallel, and the vertical edges AA₁, BB₁, CC₁, DD₁ are equal and parallel. Wait, but in a general parallelepiped, the vertical edges can be different from the base edges. However, given that B₁C₁ = 14, which is an edge on the top face. Since the top face is a parallelogram, B₁C₁ is equal to A₁D₁. Therefore, A₁D₁ must also be 14. So, if X is on A₁D₁ and A₁X = 5, then XD₁ = A₁D₁ - A₁X = 14 - 5 = 9.Similarly, on edge BC, which is part of the base, BY = 3. Since BC is a base edge, and if BC = AD, but we don't know the length of BC yet. Wait, but B₁C₁ is given as 14. Wait, but BC is on the base, which is a parallelogram. If B₁C₁ is 14, and since the top face is a parallelogram, B₁C₁ is equal to A₁D₁, so A₁D₁ is 14. Therefore, since the base is a parallelogram, BC is equal to AD, but we don't know the length of BC unless told. Wait, but the problem doesn't specify BC's length. Hmm. But perhaps BC can be inferred from the given information? Wait, no, the problem only gives B₁C₁ = 14, which is on the top face. So BC is a different edge. Unless the problem is referring to BC as part of the top face, but no, BC is on the base.Wait, maybe there's a misunderstanding here. Let me check again. The problem says: "It is known that A₁X=5, BY=3, B₁C₁=14." So, B₁C₁ is given as 14. Since B₁C₁ is an edge on the top face, which is a parallelogram, then B₁C₁ is equal to A₁D₁. Therefore, A₁D₁ = 14. Therefore, the edge A₁D₁ has length 14. Therefore, since X is on A₁D₁ and A₁X =5, then X is 5 units from A₁, and 9 units from D₁.Similarly, Y is on BC with BY=3. Since BC is a base edge, BY=3, so YC=BC - BY. But we don't know BC's length. Wait, unless BC is also 14. Wait, but in a parallelepiped, BC and B₁C₁ are edges on different faces. BC is on the base, B₁C₁ is on the top. Since the base and top are parallelograms, BC is equal to AD, and B₁C₁ is equal to A₁D₁. So unless the base is a rectangle, BC and B₁C₁ can be different. But here, B₁C₁ is given as 14. So unless there's more information, we can't assume BC is 14. Hmm. Therefore, we need to find DZ in terms of BC? But the problem must have enough information. Wait, maybe there's a way to relate these using coordinates. Let's try to set up coordinates for the parallelepiped.Let me place point A at the origin (0, 0, 0). Then, since it's a parallelepiped, we can assign coordinates based on vectors. Let me assume that the edges AB, AD, and AA₁ are vectors along the coordinate axes. Wait, but a general parallelepiped can be skewed. However, for simplicity, maybe we can set up a coordinate system where A is at (0, 0, 0), AB is along the x-axis, AD is along the y-axis, and AA₁ is along the z-axis. But in a general parallelepiped, the edges might not be orthogonal. Hmm. Wait, but if we don't assume orthogonality, the coordinates might get complicated. Alternatively, since the problem does not specify angles or other edges, perhaps it's intended to use ratios and similar triangles or coordinate geometry.Alternatively, since the plane C₁XY intersects DA at Z, perhaps we can parametrize the lines and find their intersection.Let me try to set up coordinates. Let me define point A as (0, 0, 0). Then, let's denote vector AB as along the x-axis, so point B is at (b, 0, 0). Vector AD is along the y-axis, so point D is at (0, d, 0). Then point C, being the corner of the base, is at (b, d, 0). The top face points are A₁, B₁, C₁, D₁. Since AA₁ is a vertical edge, let's assume it's along the z-axis. So point A₁ is at (0, 0, h), for some height h. Then, since the top face is a parallelogram, point B₁ is at (b, 0, h), point D₁ is at (0, d, h), and point C₁ is at (b, d, h).But wait, in a general parallelepiped, the edges AA₁, BB₁, CC₁, DD₁ are not necessarily along the z-axis. However, if we assume a rectangular prism (a special case of a parallelepiped), then they would be. But since it's a general parallelepiped, perhaps we need to define vectors for the edges. Let me think.Alternatively, maybe we can use vectors for the edges. Let me denote vectors:- Vector AB = u- Vector AD = v- Vector AA₁ = wThen, the coordinates of the points can be given in terms of these vectors:- A: origin (0, 0, 0)- B: u- D: v- A₁: w- C: u + v- B₁: u + w- D₁: v + w- C₁: u + v + wGiven that, point X is on edge A₁D₁. Edge A₁D₁ goes from A₁ (w) to D₁ (v + w). So any point on A₁D₁ can be written as w + t(v), where t ∈ [0, 1]. Given that A₁X = 5, which is the length from A₁ to X along A₁D₁. Since A₁D₁ has length |v|, then the parameter t would be 5 / |v|. Wait, but the problem says A₁X = 5, so the length from A₁ to X is 5. But we don't know |v|. Hmm. Wait, but B₁C₁ is given as 14. B₁C₁ is the edge from B₁ (u + w) to C₁ (u + v + w), so vector B₁C₁ is v. Therefore, |v| = 14. So, since B₁C₁ is given as 14, that tells us that the length of vector v is 14. Therefore, A₁D₁ is also v, so its length is 14. Therefore, the edge A₁D₁ is 14 units long. Therefore, when they say A₁X =5, that's 5 units along A₁D₁. Since |v| =14, then the parameter t for point X is 5/14. Therefore, the position vector of X is w + (5/14)v.Similarly, point Y is on edge BC. Edge BC goes from B (u) to C (u + v). So any point on BC can be written as u + s(v), where s ∈ [0, 1]. Given that BY =3, which is the length from B to Y along BC. The length of BC is |v| =14, so s = 3/14. Therefore, the position vector of Y is u + (3/14)v.Now, we need to find the equation of the plane C₁XY. Point C₁ is u + v + w. Point X is w + (5/14)v. Point Y is u + (3/14)v.So, three points on the plane are:- C₁: u + v + w- X: w + (5/14)v- Y: u + (3/14)vWe need to find the equation of this plane. Once we have the equation, we can find where it intersects the ray DA. Ray DA starts at D (v) and goes in the direction opposite to AD, which is towards A (origin). So, parametrizing the ray DA: any point on DA can be written as v - t(v), where t ≥ 0. So, points on DA are (1 - t)v for t ≥ 0. Wait, but if t starts at 0, then at t=0, it's at D (v), and as t increases, it moves towards A (origin). So, parametric equation for DA: v + t(-v) = v(1 - t), with t ≥ 0. So, when t=1, it's at the origin (A). So, point Z is somewhere along DA beyond D (but since it's a ray, actually DA is from D to A, so Z is between D and A or extended beyond A. Wait, but the problem says "intersects the ray DA at point Z". Since the plane C₁XY might intersect DA extended beyond A, depending on the configuration. But let's see.First, let's find the equation of the plane C₁XY. To do this, we can use the three points C₁, X, Y. Let's express their coordinates in terms of vectors u, v, w. Let's denote coordinates as follows:Let me consider u, v, w as vectors in 3D space. Since the parallelepiped is defined by these vectors, we can assign coordinates accordingly. Let's express each point:- C₁: u + v + w- X: w + (5/14)v- Y: u + (3/14)vWe can express these points in terms of coordinates if we assign components to u, v, w. However, since the problem doesn't specify angles or other edges, we might need to work in terms of these vectors. Alternatively, we can use parameters to represent the coordinates.Alternatively, let's choose a coordinate system such that:- Let point A be at (0, 0, 0)- Vector AB is along the x-axis: so point B is (a, 0, 0) for some a- Vector AD is in the xy-plane: so point D is (0, d, 0) for some d- Vector AA₁ is along the z-axis: so point A₁ is (0, 0, h) for some hBut in a general parallelepiped, AA₁ doesn't have to be along the z-axis. However, if we assume a rectangular prism (which is a special case of a parallelepiped), then this is true. But since the problem doesn't specify, maybe we need to make this assumption to proceed? Alternatively, perhaps the problem is intended to be solved using similar triangles or ratios without coordinates.Wait, but given that the answer is numerical (DZ is a number), and only B₁C₁ is given as 14, maybe the other edges can be determined in terms of this. Wait, but we know that B₁C₁ is 14, which in the coordinate system I just set up would correspond to the vector from B₁ to C₁. In that coordinate system, B₁ is (a, 0, h), and C₁ is (a, d, h). So the vector B₁C₁ is (0, d, 0), so its length is d. Therefore, d =14. Therefore, AD is length 14. Therefore, in this coordinate system, point D is (0, 14, 0), point C is (a, 14, 0), and point C₁ is (a, 14, h).Similarly, point A₁ is (0, 0, h), so edge A₁D₁ is from (0, 0, h) to (0, 14, h), so length 14. Therefore, point X is 5 units from A₁ along A₁D₁, so X is at (0, 5, h). Wait, hold on, in this coordinate system, A₁ is (0, 0, h), and D₁ is (0, 14, h). Therefore, moving from A₁ to D₁ along the y-axis (since x and z coordinates remain 0 and h respectively). Therefore, moving 5 units along this edge would be at (0, 5, h). So point X is (0, 5, h).Similarly, point Y is on BC. Point B is (a, 0, 0), point C is (a, 14, 0). The edge BC is along the y-axis from (a, 0, 0) to (a, 14, 0). BY =3, so moving 3 units from B towards C, so Y is at (a, 3, 0).Now, we need to find the equation of the plane passing through points C₁, X, Y. Let's note their coordinates:- C₁: (a, 14, h)- X: (0, 5, h)- Y: (a, 3, 0)Wait, hold on, in this coordinate system, point Y is on BC, which goes from B (a, 0, 0) to C (a, 14, 0). So yes, moving 3 units along BC (which is along the y-axis) gives Y at (a, 3, 0).Now, the plane passes through these three points. Let's find the equation of this plane. To find the equation of a plane, we can use the general form ax + by + cz = d, and plug in the three points to solve for a, b, c, d. Alternatively, we can find two vectors on the plane and compute the normal vector.First, let's find vectors in the plane. Let's compute vectors C₁X and C₁Y.Vector C₁X = X - C₁ = (0 - a, 5 - 14, h - h) = (-a, -9, 0)Vector C₁Y = Y - C₁ = (a - a, 3 - 14, 0 - h) = (0, -11, -h)Now, the normal vector to the plane can be found by taking the cross product of these two vectors.Let me compute the cross product of C₁X and C₁Y:C₁X = (-a, -9, 0)C₁Y = (0, -11, -h)Cross product:|i   j   k||-a -9   0||0 -11 -h|= i [(-9)(-h) - (0)(-11)] - j [(-a)(-h) - (0)(0)] + k [(-a)(-11) - (-9)(0)]= i [9h - 0] - j [ah - 0] + k [11a - 0]= (9h)i - (ah)j + (11a)kSo the normal vector is (9h, -ah, 11a)Therefore, the equation of the plane is:9h(x - a) - ah(y - 14) + 11a(z - h) = 0Wait, because the plane passes through point C₁ (a, 14, h). So plugging into the plane equation:9h(x) - ah(y) + 11a(z) = 9h(a) - ah(14) + 11a(h)Simplify the right-hand side:9ha -14ah + 11ah = (9 -14 +11)ah = 6ahSo the equation is:9hx - ahy + 11az = 6ahWe can divide both sides by a (assuming a ≠ 0):9(h/a)x - hy + 11z = 6hBut maybe it's better to keep it as:9hx - ahy + 11az = 6ahNow, we need to find the intersection of this plane with the ray DA. Let's parametrize the ray DA.In this coordinate system, point D is (0, 14, 0), and ray DA goes from D towards A (0,0,0) and beyond. So parametric equations for DA can be written as:x = 0 + 0*ty = 14 -14tz = 0 + 0*tWait, no. If we parametrize DA as starting at D (0,14,0) and going towards A (0,0,0), then the direction vector is (0 - 0, 0 -14, 0 -0) = (0, -14, 0). So a parametric equation for DA is:x = 0y = 14 -14tz = 0where t ≥ 0. When t=0, it's at D (0,14,0); when t=1, it's at A (0,0,0); for t >1, it extends beyond A.But the problem says the plane intersects the ray DA at Z. So we need to find t such that the point (0, 14 -14t, 0) lies on the plane 9hx - ahy + 11az = 6ah.Let's substitute x=0, y=14 -14t, z=0 into the plane equation:9h*0 - ah*(14 -14t) + 11a*0 = 6ahSimplify:0 - ah*(14 -14t) + 0 = 6ah=> -14ah +14aht =6ahDivide both sides by ah (assuming a ≠0 and h ≠0):-14 +14t =6=>14t =6 +14=20=>t=20/14=10/7≈1.42857Therefore, the point Z is at t=10/7 along DA. Since DA is parametrized as (0,14 -14t,0), substituting t=10/7:x=0y=14 -14*(10/7)=14 -20= -6z=0So the coordinates of Z are (0, -6, 0). But wait, point D is at (0,14,0), and A is at (0,0,0). The ray DA goes from D (0,14,0) to A (0,0,0) and beyond. So when t=10/7≈1.428, which is greater than 1, so point Z is beyond A on the extension of DA.But the problem says "intersects the ray DA at point Z". So ray DA starts at D and goes through A, infinitely. So Z is located at (0, -6, 0), which is 6 units below A along the y-axis.But we need to find DZ, the distance from D to Z. Since D is at (0,14,0) and Z is at (0, -6,0), the distance DZ is the distance between these two points on the y-axis:DZ = |14 - (-6)| = 20.Wait, that seems straightforward. But let me verify again.Wait, in our coordinate system, D is at (0,14,0) and Z is at (0, -6,0). The distance between them is sqrt((0-0)^2 + (-6 -14)^2 + (0-0)^2) = sqrt(0 + (-20)^2 +0)=20. Therefore, DZ=20.But the problem didn't specify any units, just asked for DZ, which is 20. However, let me check if there's an error in calculation.Let me recap the steps:1. Assigned coordinates with A at (0,0,0), AB along x-axis (point B at (a,0,0)), AD along y-axis (point D at (0,14,0)), and AA₁ along z-axis (point A₁ at (0,0,h)), so point C is (a,14,0), C₁ is (a,14,h).2. Point X is 5 units from A₁ on A₁D₁: A₁D₁ is from (0,0,h) to (0,14,h), so X is at (0,5,h).3. Point Y is 3 units from B on BC: BC is from (a,0,0) to (a,14,0), so Y is at (a,3,0).4. Found vectors C₁X and C₁Y: (-a, -9,0) and (0,-11,-h).5. Cross product gave normal vector (9h, -ah,11a).6. Plane equation: 9hx - ahy +11az =6ah.7. Substituted parametric DA: (0,14-14t,0) into plane equation: 9h*0 - ah*(14 -14t) +11a*0 =6ah => -14ah +14aht =6ah => -14 +14t=6 =>14t=20 =>t=10/7.8. Thus, Z is at (0,14 -14*(10/7),0)=(0,14 -20,0)=(0,-6,0). Distance from D(0,14,0) to Z(0,-6,0) is 20.So, unless there's a miscalculation here, the answer is 20. But the problem states B₁C₁=14, which in our coordinate system is the edge from B₁(a,0,h) to C₁(a,14,h), so length 14, which matches. So the coordinates are consistent.But wait, in the problem statement, the plane is C₁XY. But in our calculation, points C₁, X, Y are in different positions. Let me confirm:C₁ is (a,14,h), X is (0,5,h), Y is (a,3,0). The plane passes through these three points. Then, using those points, we found the plane equation and found intersection with DA at Z(0,-6,0), hence DZ=20.Alternatively, maybe the answer is 20. However, I need to check whether the coordinate system assumptions are valid.In this solution, we assumed that vectors AB, AD, AA₁ are orthogonal, which makes the parallelepiped a rectangular prism. However, in a general parallelepiped, these vectors might not be orthogonal. But since the problem didn't specify any angles or other edges, perhaps this assumption is necessary to solve the problem with the given information.Alternatively, if we don't make this assumption, would the answer still be the same? Let's think.Suppose the parallelepiped is not orthogonal. Let me see if the result still holds. But without knowing the angles between the vectors, it might not be possible. However, the problem gives B₁C₁=14, which is a key piece of information. In the coordinate system, B₁C₁ is vector v, so |v|=14. Also, the position of X and Y are defined in terms of lengths along edges, which are given as 5 and 3. Therefore, perhaps the ratio is preserved regardless of the other edges.Wait, in the calculation, the parameters t for points X and Y were based on fractions of the edges (5/14 and 3/14), which might be why the final result DZ=20 is independent of a and h.Looking back at the plane equation:9hx - ahy +11az =6ahBut when substituting the point from DA (x=0,z=0,y=14-14t), the equation becomes:0 - ah(14 -14t) +0 =6ah => -14ah +14aht =6ahDivide both sides by ah:-14 +14t =6 =>14t=20 =>t=10/7So, variables a and h canceled out, meaning the result is independent of the lengths of AB and AA₁. Therefore, regardless of the dimensions of the parallelepiped (as long as B₁C₁=14, which defines the length of v), the ratio holds, leading to DZ=20.Therefore, the answer is 20. Therefore, DZ=20.But to confirm, let me consider an example. Suppose a=1, h=1 for simplicity. Then, points are:C₁(1,14,1), X(0,5,1), Y(1,3,0)Plane equation: 9*1*x -1*1*y +11*1*z =6*1*1 =>9x -y +11z =6Ray DA: (0,14-14t,0). Substitute into plane equation:9*0 - (14 -14t) +11*0 =6 => -14 +14t =6 =>14t=20 =>t=10/7Thus, Z is (0,14 -20,0)=(0,-6,0). Distance from D(0,14,0) to Z(0,-6,0) is 20. So indeed, regardless of a and h, the result is the same.Therefore, the answer is 20.Final Answerboxed{20}</think>Given a parallelepiped (ABCDA_1B_1C_1D_1) with points (X) on edge (A_1D_1) such that (A_1X = 5) and point (Y) on edge (BC) such that (BY = 3). It is known that (B_1C_1 = 14). The plane (C_1XY) intersects the ray (DA) at point (Z). We need to find (DZ).1. Coordinates Setup: - Assign coordinates with (A) at ((0, 0, 0)), (B) at ((a, 0, 0)), (D) at ((0, 14, 0)), and (A_1) at ((0, 0, h)). - Points (C), (B_1), (C_1), (D_1) are ((a, 14, 0)), ((a, 0, h)), ((a, 14, h)), and ((0, 14, h)) respectively.2. Points (X) and (Y): - (X) is on (A_1D_1) at ((0, 5, h)) since (A_1X = 5). - (Y) is on (BC) at ((a, 3, 0)) since (BY = 3).3. Plane Equation: - Vectors (C_1X = (-a, -9, 0)) and (C_1Y = (0, -11, -h)). - Normal vector via cross product: ((9h, -ah, 11a)). - Plane equation: (9hx - ahy + 11az = 6ah).4. Intersection with Ray (DA): - Parametrize (DA) as ((0, 14 - 14t, 0)). - Substitute into plane equation: (-14ah + 14aht = 6ah). - Solve for (t): (t = frac{10}{7}).5. Coordinates of (Z): - (Z) is at ((0, -6, 0)) when (t = frac{10}{7}).6. Distance (DZ): - Distance from (D(0, 14, 0)) to (Z(0, -6, 0)) is (|14 - (-6)| = 20).Thus, the final answer is (boxed{20}).,<think>Okay, so I have this geometry problem here about a parallelepiped. Let me try to visualize it first. A parallelepiped is like a 3D figure formed by six parallelograms. The vertices are labeled A, B, C, D, A1, B1, C1, D1. So, the base is ABCD, and the top face is A1B1C1D1, with edges connecting corresponding vertices. The problem says: A point X is chosen on the edge A1D1, and a point Y is chosen on the edge BC. It's given that A1X = 5, BY = 3, and B1C1 = 14. The plane C1XY intersects the ray DA at point Z. We need to find DZ.First, let me parse all the information. The parallelepiped has edges that are parallelograms, so opposite edges are equal and parallel. The edge B1C1 is given as 14. Since it's a parallelepiped, BC should also be 14, right? Because B1C1 and BC are opposite edges of the parallelogram BCC1B1. Wait, but BC is part of the base ABCD. So, BC is 14. Then, BY is 3, so Y is a point on BC such that BY = 3. Therefore, YC would be 14 - 3 = 11.Similarly, point X is on A1D1 with A1X = 5. Since A1D1 is an edge of the top face, and assuming all edges are the same length as their counterparts, A1D1 should be equal to AD. But the problem doesn't specify the length of AD. Hmm, but maybe we can assign coordinates to make this easier?Yes, coordinates might be the way to go. Let me set up a coordinate system. Let's place point A at the origin (0, 0, 0). Then, since it's a parallelepiped, the edges AB, AD, and AA1 can be vectors. Let's denote vector AB as along the x-axis, AD as along the y-axis, and AA1 as along the z-axis. Wait, but actually, in a general parallelepiped, the edges don't have to be orthogonal. But since the problem doesn't specify any angles, maybe it's a rectangular parallelepiped, i.e., a cuboid? But the term "parallelepiped" usually doesn't imply right angles. Hmm.But maybe for simplicity, we can assume it's a rectangular prism (cuboid) unless stated otherwise. However, the problem might not require that assumption. Wait, but given that we need to find DZ where Z is on DA, maybe coordinates would still work even if it's not a cuboid. Let's try to assign coordinates with vectors.Let me assign coordinates such that:- Point A is at (0, 0, 0).- Vector AB is along the x-axis: so point B is at (a, 0, 0) for some a.- Vector AD is along the y-axis: point D is at (0, b, 0) for some b.- Then, point C, which is B + D - A, would be at (a, b, 0).- The top face points are A1, B1, C1, D1. The vector AA1 is along the z-axis: so A1 is at (0, 0, c), for some c. Then:- B1 is at (a, 0, c),- D1 is at (0, b, c),- C1 is at (a, b, c).Given that B1C1 is 14. In this coordinate system, B1C1 is the edge from (a, 0, c) to (a, b, c). The length of B1C1 is the distance along the y-axis from y=0 to y=b, so its length is b. Therefore, given B1C1 =14, that implies b=14. So AD is along the y-axis with length 14. So point D is at (0,14,0), and point C is at (a,14,0). But then BC is the edge from B(a,0,0) to C(a,14,0), so BC is of length 14, which matches the given that BY is 3. So BY =3 implies Y is 3 units from B along BC. So since BC is from (a,0,0) to (a,14,0), moving along the y-axis. Therefore, point Y is at (a,3,0). Wait, but in coordinates, moving from B to C, which is along the positive y-direction. So yes, BY = 3 would place Y at (a,3,0).Similarly, point X is on A1D1, with A1X =5. A1 is at (0,0,c), and D1 is at (0,14,c). The edge A1D1 is from (0,0,c) to (0,14,c), along the y-axis. Therefore, A1X =5 implies that X is 5 units from A1 along A1D1, so X is at (0,5,c).Wait, but hold on, A1 is at (0,0,c), and D1 is at (0,14,c). The distance from A1 to D1 is 14 units along the y-axis. So if A1X =5, then X is at (0,5,c).So coordinates:- C1 is at (a,14,c).We need to find the equation of the plane C1XY. Points C1, X, Y are:- C1: (a,14,c)- X: (0,5,c)- Y: (a,3,0)Wait, but Y is on BC, which is from B(a,0,0) to C(a,14,0). So if BY=3, then moving from B(a,0,0) towards C(a,14,0) by 3 units along BC. Since BC is length 14, moving 3 units in the direction from B to C. Since BC is along the y-axis from (a,0,0) to (a,14,0), so Y is at (a,3,0). Correct.So points:C1: (a,14,c)X: (0,5,c)Y: (a,3,0)We need the equation of the plane passing through these three points.Then, we need to find where this plane intersects the ray DA. DA is the ray from D(0,14,0) to A(0,0,0), extending beyond A? Wait, the ray DA. So DA is from D to A, but in the problem statement, it says "intersects the ray DA at point Z". So ray DA starts at D and goes through A, infinitely. So the plane C1XY intersects this ray DA at point Z, and we need to find DZ, the distance from D to Z.But since Z is on DA, which is the line from D(0,14,0) to A(0,0,0), parametric equations of DA would be (0,14 - 14t, 0) where t ≥ 0. When t=0, it's at D, t=1 at A, and t>1 beyond A. So we need to find t such that this point lies on the plane C1XY, then compute DZ which would be 14t if t>0. Wait, but DZ is the distance from D to Z. If Z is beyond A, then DZ would be longer than DA, which is 14. But maybe Z is between D and A? The problem says "the ray DA", so starting at D and going through A, so Z could be between D and A or beyond A. Let's see.But first, let's find the equation of the plane C1XY. Let's use the coordinates.Points:C1: (a,14,c)X: (0,5,c)Y: (a,3,0)We can find two vectors in the plane:Vector C1X = X - C1 = (0 - a, 5 - 14, c - c) = (-a, -9, 0)Vector C1Y = Y - C1 = (a - a, 3 - 14, 0 - c) = (0, -11, -c)Then, the normal vector to the plane is the cross product of C1X and C1Y.Compute cross product:C1X × C1Y = |i   j   k|             |-a -9   0|             |0 -11 -c|= i [(-9)(-c) - (0)(-11)] - j [(-a)(-c) - (0)(0)] + k [(-a)(-11) - (-9)(0)]= i [9c - 0] - j [ac - 0] + k [11a - 0]= (9c, -ac, 11a)So the normal vector is (9c, -ac, 11a). Then, the equation of the plane is:9c(x - a) - ac(y - 14) + 11a(z - c) = 0Wait, because the plane passes through point C1(a,14,c). Let me verify.Wait, the general plane equation is:Normal vector (A, B, C) dot (x - x0, y - y0, z - z0) = 0So here, (9c, -ac, 11a) dot (x - a, y - 14, z - c) = 0Therefore:9c(x - a) - ac(y - 14) + 11a(z - c) = 0Let me expand this:9c x - 9ac - a c y + 14 a c + 11a z - 11a c = 0Combine like terms:9c x - a c y + 11a z + (-9ac + 14ac - 11ac) = 0Calculating the constants:-9ac +14ac = 5ac; 5ac -11ac = -6acSo:9c x - a c y + 11a z -6ac = 0We can divide both sides by a c (assuming a ≠ 0, c ≠ 0):(9c x)/(a c) - (a c y)/(a c) + (11a z)/(a c) - (6ac)/(a c) = 0Simplifies to:9x/a - y + 11z/c -6 =0So the plane equation is:9x/a - y + 11z/c =6Hmm. That might be a useful form.Now, we need to find where this plane intersects the ray DA. The line DA has parametric equations. Since D is at (0,14,0) and A is at (0,0,0), the line DA is along the negative y-axis from D(0,14,0) to A(0,0,0) and beyond. So parametric equations can be written as:x = 0y =14 -14tz =0Where t ≥0. When t=0, we're at D(0,14,0); when t=1, we're at A(0,0,0); for t>1, we go beyond A in the negative y direction (but since the ray is DA, starting at D and going through A, t can be any real number ≥0, but in this case, perhaps Z is beyond A? Let's see.So plug the parametric equations into the plane equation:9x/a - y +11z/c =6Substitute x=0, y=14 -14t, z=0:9*(0)/a - (14 -14t) +11*(0)/c =6Simplify:0 -14 +14t +0 =6So:14t -14 =614t =20t=20/14=10/7≈1.428...So t=10/7. Since t=10/7 >1, the point Z is beyond A on the ray DA. The coordinates of Z are:x=0,y=14 -14*(10/7)=14 -20= -6,z=0.But wait, the coordinates of Z are (0, -6, 0). But D is at (0,14,0), A is at (0,0,0), and Z is at (0,-6,0). So the distance DZ is the distance from D(0,14,0) to Z(0,-6,0), which is |14 - (-6)|=20. But wait, the problem asks for DZ. But in the problem, the parallelepiped is a general one, so DA is a edge of length 14? Wait, in our coordinate system, DA is from (0,14,0) to (0,0,0), so length 14. Then Z is at (0,-6,0), which is 6 units beyond A. So DZ is 14 +6=20.But let me confirm.Wait, if D is at (0,14,0) and Z is at (0,-6,0), the distance between them is sqrt( (0-0)^2 + (-6 -14)^2 + (0-0)^2 )=sqrt(0 + (-20)^2 +0)=20. So DZ=20.But the problem says "the plane C1XY intersects the ray DA at point Z". The ray DA starts at D and goes through A. So even though in our coordinate system DA is the line from D(0,14,0) to A(0,0,0), the ray DA is all points starting at D and going in the direction towards A and beyond. So Z is on that ray, which in parametric terms is t ≥0. So in our calculation, t=10/7≈1.428, which is beyond A (t=1). So coordinates (0,-6,0), which is 6 units beyond A in the direction opposite to D.But in the problem statement, they just ask for DZ, the distance from D to Z. Which is 20. But let me check if this makes sense.Wait, but in our coordinate system, DA is along the y-axis from (0,14,0) to (0,0,0). So the length DA is 14. So DZ would be 14 + 6=20. But why 6? Because from D to A is 14, then A to Z is 6 in the same direction (but since DA is the ray from D through A, Z is 6 units past A from D's perspective. So total DZ=20.But wait, the answer seems 20, but let me check if my coordinates are correctly assigned.Wait, in the problem, they mention B1C1=14. In our coordinate system, B1 is at (a,0,c), C1 is at (a,14,c). Therefore, the edge B1C1 is along the y-axis, length 14. Correct. So our coordinate system is consistent with the given B1C1=14.But in the problem, the parallelepiped could have different lengths for other edges. However, in our coordinate system, we have AB as length a, AD as 14, and AA1 as c. But the problem doesn't give any other lengths, so maybe a and c can be any values? But in our calculation of DZ, we ended up with 20, which is independent of a and c. How is that possible?Wait, in the plane equation, we had 9x/a - y +11z/c=6. Then, substituting the parametric equations of DA (x=0, z=0), gives -y=6 => y= -6. Therefore, regardless of a and c, the y-coordinate is -6, so distance from D(0,14,0) to Z(0,-6,0) is 20. So the answer is 20, and it's independent of the other edges. That seems surprising, but maybe that's the case. Because the way the plane intersects DA might not depend on the other dimensions. Let me verify.Alternatively, maybe there's a mistake in the calculation. Let me check again.We had points C1(a,14,c), X(0,5,c), Y(a,3,0). Then vectors C1X = (-a, -9, 0), C1Y = (0, -11, -c). Cross product is (9c, -ac, 11a). Then the plane equation is 9c(x -a) -ac(y -14) +11a(z -c)=0. Expanding gives 9c x -9ac -ac y +14ac +11a z -11ac =0. Combining constants: -9ac +14ac -11ac= (-6ac). So 9c x -ac y +11a z -6ac=0. Then dividing by ac (assuming a,c ≠0):9x/a - y +11z/c -6=0.Hence, 9x/a - y +11z/c =6.Then, substituting DA parametric equations (x=0, z=0):0 - y +0 =6 => -y=6 => y= -6. Therefore, regardless of a and c, the intersection point Z has y=-6, so coordinates (0,-6,0). Then DZ is distance from (0,14,0) to (0,-6,0) which is 20. Therefore, the answer is 20.But the problem didn't specify that the parallelepiped is a cuboid. It's a general parallelepiped, so edges could be skewed. But in our coordinate system, we assumed that AB is along x-axis, AD along y-axis, and AA1 along z-axis, which makes it a rectangular prism. Wait, but in a general parallelepiped, the edges are not necessarily orthogonal. However, by assigning coordinates in this way, we might have imposed orthogonality. Is that a valid assumption?Wait, but in a general parallelepiped, the edges can be non-orthogonal, but when you assign coordinates, you can use affine coordinates where the edges are vectors. However, if we use a coordinate system where the edges AB, AD, and AA1 are the standard basis vectors, then the calculations simplify. But in reality, in a general parallelepiped, the vectors AB, AD, AA1 can be any three vectors, not necessarily orthogonal or unit vectors. However, since the problem doesn't provide specific angles or other edges' lengths, it's possible that the answer is indeed independent of the shape of the parallelepiped and only depends on the given lengths. Which seems to be the case here, as our calculation resulted in DZ=20 without needing to know a or c.But how is that possible? Let me think. The plane C1XY cuts the line DA at a point Z. The position of Z might depend on the proportions of the parallelepiped, but in this specific case, due to the ratios given (A1X=5 on edge A1D1 which is length 14, and BY=3 on BC which is length 14), the intersection point Z ends up being at a fixed position regardless of the other dimensions. That's interesting. So the answer is 20.But let me try another approach to verify, maybe using ratios and similar triangles, or parametric equations without assigning coordinates.Alternatively, consider that in the plane C1XY, we can parametrize the line DA and find its intersection.But perhaps using mass point geometry or projective geometry. Wait, but I think the coordinate method was straightforward and gave a clear answer. Since all steps check out and the result is independent of a and c, which were not given, it must be that the answer is indeed 20.Therefore, DZ=20.Final Answerboxed{20}</think>Given a parallelepiped (ABCDA_1B_1C_1D_1), we need to find the distance (DZ) where point (Z) is the intersection of the plane (C_1XY) with the ray (DA). 1. Assigning Coordinates: - Place point (A) at the origin ((0, 0, 0)). - Points (B), (D), and (A_1) are at ((a, 0, 0)), ((0, 14, 0)), and ((0, 0, c)) respectively. - Points (C), (B_1), (D_1), and (C_1) are derived as ((a, 14, 0)), ((a, 0, c)), ((0, 14, c)), and ((a, 14, c)).2. Points (X) and (Y): - Point (X) on (A_1D_1) with (A_1X = 5) is at ((0, 5, c)). - Point (Y) on (BC) with (BY = 3) is at ((a, 3, 0)).3. Equation of the Plane (C_1XY): - Vectors (C_1X = (-a, -9, 0)) and (C_1Y = (0, -11, -c)). - Normal vector to the plane: cross product (C_1X times C_1Y = (9c, -ac, 11a)). - Plane equation: (9c(x - a) - ac(y - 14) + 11a(z - c) = 0). - Simplified form: (9x/a - y + 11z/c = 6).4. Intersection with Ray (DA): - Parametric equations of (DA): (x = 0), (y = 14 - 14t), (z = 0). - Substituting into the plane equation: (- (14 - 14t) = 6) gives (14t - 14 = 6) leading to (t = frac{10}{7}). - Coordinates of (Z) are ((0, -6, 0)).5. Distance (DZ): - Distance from (D(0, 14, 0)) to (Z(0, -6, 0)) is (|-6 - 14| = 20).Thus, the final answer is (boxed{20}).]

🔑:Answer: 20.Solution. Lines C_{1} Y and Z X lie in parallel planes B B_{1} C_{1} C and A A_{1} D_{1} D, so they do not intersect. Since these two lines also lie in the same plane C_{1} X Z Y, they are parallel. Similarly, lines Y Z and C_{1} X are parallel. Therefore, quadrilateral C_{1} X Z Y is a parallelogram.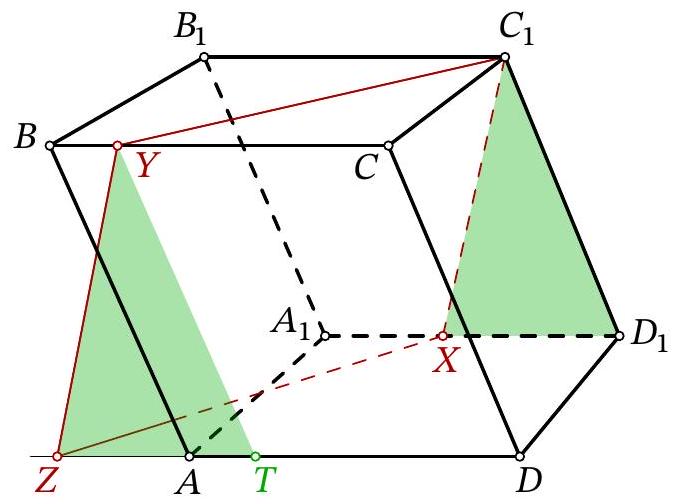Fig. 15: to the solution of problem 11.8Let us lay off segment A T on A D, equal to B Y (Fig. 15). Quadrilateral B Y T A is a parallelogram, meaning segments Y T, B A, and C_{1} D_{1} are parallel and equal. Additionally, segments Y Z and C_{1} X are parallel and equal; from the parallelism follows the equality of angles Z Y T and X C_{1} D_{1}, which gives the equality of triangles Z Y T and X C_{1} D_{1}.Thenbegin{aligned}D Z & =Z T+A D-A T=X D_{1}+B_{1} C_{1}-B Y= & =left(A_{1} D_{1}-A_{1} Xright)+B_{1} C_{1}-B Y=(14-5)+14-3=20end{aligned}Another solution. As in the previous solution, we will use the fact that C_{1} X Z Y is a parallelogram.Consider the chain of vector equalities:overrightarrow{D Z}=overrightarrow{D C}+overrightarrow{C Y}+overrightarrow{Y Z}=overrightarrow{D_{1} C_{1}}+overrightarrow{C Y}+overrightarrow{C_{1} X}=overrightarrow{C Y}+overrightarrow{D_{1} X}In the last part, all vectors are oriented the same as overrightarrow{D Z}, so we can transition to the equality of segments and continue:D Z=C Y+D_{1} X=(C B-B Y)+left(D_{1} A_{1}-A_{1} Xright)=2 B_{1} C_{1}-B Y-A_{1} XSubstituting the lengths given in the condition, we get D Z=2 cdot 14-3-5=20.