🧠:[<think>Okay, let's see. I have this quadratic equation: x squared plus 2x minus 1 equals 0. The roots are x1 and x2, and I need to find the sum of these roots, x1 plus x2. The options are A: 2, B: -2, C: 1, D: -1. Hmm, how do I approach this?Wait, I remember something about quadratic equations and their roots. Isn't there a formula that relates the coefficients of the equation to the sum and product of the roots? Let me think. Oh yeah! Vieta's formulas. Right, Vieta's formulas. For a quadratic equation in the form ax² + bx + c = 0, the sum of the roots is -b/a, and the product is c/a. So in this case, the equation is x² + 2x - 1 = 0. Comparing that to the standard form, a is 1, b is 2, and c is -1.So applying Vieta's formula for the sum of the roots, which is x1 + x2 = -b/a. Plugging in the values from the equation, that would be -2/1, which simplifies to -2. Wait, but hold on. Let me double-check that. If the equation is ax² + bx + c = 0, then the sum of the roots is indeed -b/a. Let me confirm with an example. Suppose I have a simple equation like x² - 5x + 6 = 0. The roots are 2 and 3, right? Their sum is 5, and according to the formula, it's -(-5)/1 = 5. Yeah, that checks out. So in the given equation, the coefficient of x is +2, so the sum should be -2/1 = -2. So the answer is B: -2? But wait, the options include B as -2. Hmm, but let me think again. Maybe I made a mistake in the signs.Wait, no. The formula is -b/a. The coefficient of x is +2, so b is 2. Therefore, -b is -2. Divided by a, which is 1, so yes, -2. So that's correct. So the sum of the roots x1 + x2 is -2. Let me verify this by actually solving the quadratic equation. Maybe that's a good idea to cross-check.The quadratic equation is x² + 2x - 1 = 0. To find the roots, I can use the quadratic formula: x = [-b ± √(b² - 4ac)]/(2a). Let's compute that. Here, a=1, b=2, c=-1. Plugging into the formula: x = [-2 ± √( (2)^2 - 4*1*(-1) )]/(2*1) = [-2 ± √(4 +4)]/2 = [-2 ± √8]/2. Simplify √8 to 2√2, so x = [-2 ± 2√2]/2. Dividing numerator and denominator by 2: x = [-1 ± √2]. So the two roots are x1 = -1 + √2 and x2 = -1 - √2. Adding them together: x1 + x2 = (-1 + √2) + (-1 - √2) = -1 -1 + √2 - √2 = -2. So indeed, the sum is -2. So that's option B. Wait, but the options are listed as A:2, B:-2, C:1, D:-1. Therefore, B is the correct answer. But wait, the problem is presented as a multiple-choice question in Chinese, perhaps? But regardless, the options are there. So according to Vieta's formula and the actual calculation, the answer should be B: -2.But just to make sure I didn't make a mistake in the quadratic formula part. Let me check that again. The quadratic equation is x² + 2x - 1 = 0. Discriminant is b² - 4ac = 4 - 4*1*(-1) = 4 +4=8. Correct. Then square root of 8 is 2√2. So the roots are [-2 + 2√2]/2 and [-2 - 2√2]/2. Simplifying both by dividing numerator and denominator by 2 gives -1 + √2 and -1 - √2. Yes, that's right. So adding them gives -2. So Vieta's formula was correct here. So the answer is B: -2. Therefore, the correct option is B. But wait, the user listed the options as A:2, B:-2, C:1, D:-1. So yeah, B is the second option. So the answer should be B.Alternatively, maybe there's another way to approach this. For instance, if we consider the quadratic equation and complete the square. Let's try that. The equation is x² + 2x - 1 = 0. Completing the square: x² + 2x = 1. To complete the square, take half of the coefficient of x, which is 1, square it to get 1. So add 1 to both sides: x² + 2x +1 = 1 +1. That becomes (x +1)^2 = 2. Taking square roots: x +1 = ±√2. Therefore, x = -1 ±√2. Which gives the same roots as before. Thus, adding them together again gives -1 +√2 + (-1 -√2) = -2. So the same result. So all methods point to B: -2. Therefore, the answer must be B. Therefore, the correct answer is option B, which is -2.Final Answerboxed{B}</think>To find the sum of the roots ( x_1 ) and ( x_2 ) of the quadratic equation ( x^2 + 2x - 1 = 0 ), we use Vieta's formulas. For a quadratic equation ( ax^2 + bx + c = 0 ), the sum of the roots is given by ( -frac{b}{a} ).Here, the coefficients are ( a = 1 ), ( b = 2 ), and ( c = -1 ). Applying Vieta's formula, the sum of the roots is:[x_1 + x_2 = -frac{b}{a} = -frac{2}{1} = -2]To verify, we solve the quadratic equation using the quadratic formula ( x = frac{-b pm sqrt{b^2 - 4ac}}{2a} ):[x = frac{-2 pm sqrt{4 + 4}}{2} = frac{-2 pm 2sqrt{2}}{2} = -1 pm sqrt{2}]The roots are ( -1 + sqrt{2} ) and ( -1 - sqrt{2} ). Adding these roots:[(-1 + sqrt{2}) + (-1 - sqrt{2}) = -2]Thus, the sum of the roots ( x_1 + x_2 ) is (-2), which corresponds to option B.[boxed{B}],<think>Okay, so I need to find the sum of the roots of the quadratic equation (x^2 + 2x - 1 = 0). The options given are A: 2, B: -2, C: 1, D: -1. Hmm, let me think.First, I remember that for a quadratic equation in the form (ax^2 + bx + c = 0), there's something called Vieta's formulas that relate the coefficients of the equation to the sum and product of its roots. If the roots are (x_1) and (x_2), then the sum (x_1 + x_2) is equal to (-b/a), and the product (x_1 x_2) is (c/a). Let me confirm that. So in the equation given here, the coefficient of (x^2) is 1 (since it's (x^2) with no coefficient written), the coefficient of (x) is 2, and the constant term is -1. So according to Vieta's formula, the sum of the roots should be (-b/a), which here would be (-2/1 = -2). Wait, but looking at the answer options, B is -2 and D is -1. So is that correct? Wait, maybe I made a mistake here.Hold on, let me double-check. The quadratic equation is (x^2 + 2x - 1 = 0). So in standard form (ax^2 + bx + c = 0), here (a = 1), (b = 2), (c = -1). So applying Vieta's formula for the sum of the roots: (x_1 + x_2 = -b/a = -2/1 = -2). So that would be option B: -2. But wait, the options given include D: -1. Am I missing something here?Wait, maybe I confused the sum and product. Let me check again. Vieta's formula says sum is (-b/a) and product is (c/a). So in this case, product would be (-1/1 = -1). So the product is -1, and sum is -2. So the sum should be -2. Then why is there an option D: -1? Maybe I made a mistake in the sign?Wait, let me think again. The quadratic equation is (x^2 + 2x -1 =0). So if I expand this equation with roots (x_1) and (x_2), it would be written as ((x - x_1)(x - x_2) = 0). Expanding that, we get (x^2 - (x_1 + x_2)x + x_1 x_2 = 0). Comparing that with the original equation (x^2 + 2x -1 = 0), the coefficients must be equal. So, comparing coefficients:- Coefficient of (x): (-(x_1 + x_2) = 2). Therefore, (x_1 + x_2 = -2).- Constant term: (x_1 x_2 = -1).So yes, that confirms it. The sum of the roots is indeed -2, which is option B. So why did I even consider option D? Maybe because the product is -1, which is option D. But the question specifically asks for the sum, so the answer should be B: -2.Wait, but let me check using another method, just to be sure. Let's solve the quadratic equation using the quadratic formula and verify the roots.The quadratic formula is (x = frac{-b pm sqrt{b^2 - 4ac}}{2a}). Here, (a = 1), (b = 2), (c = -1). Plugging these into the formula:Discriminant: (b^2 - 4ac = 2^2 - 4*1*(-1) = 4 + 4 = 8). So the roots are:(x = frac{-2 pm sqrt{8}}{2}). Simplify sqrt(8) as 2*sqrt(2), so:(x = frac{-2 pm 2sqrt{2}}{2} = -1 pm sqrt{2}).Therefore, the two roots are (x_1 = -1 + sqrt{2}) and (x_2 = -1 - sqrt{2}). Adding them together:(x_1 + x_2 = (-1 + sqrt{2}) + (-1 - sqrt{2}) = -1 -1 + sqrt{2} - sqrt{2} = -2).Yep, that's definitely -2. So the sum is -2, which is option B. So I was right the first time. Maybe option D is a distractor because the product is -1. But the question clearly asks for the sum, so the correct answer is B: -2.I think I got confused initially because sometimes people might mix up the signs, but after verifying both with Vieta's formula and by actually calculating the roots, it's clear that the sum is -2. So I feel confident that the answer is B.Final Answerboxed{B}</think>To find the sum of the roots of the quadratic equation (x^2 + 2x - 1 = 0), we use Vieta's formulas. For a quadratic equation (ax^2 + bx + c = 0), the sum of the roots (x_1) and (x_2) is given by (-b/a).Given the equation (x^2 + 2x - 1 = 0), we identify the coefficients: (a = 1), (b = 2), and (c = -1). Applying Vieta's formula, the sum of the roots is:[x_1 + x_2 = -frac{b}{a} = -frac{2}{1} = -2]To verify, we solve the quadratic equation using the quadratic formula (x = frac{-b pm sqrt{b^2 - 4ac}}{2a}). The discriminant is:[b^2 - 4ac = 2^2 - 4 cdot 1 cdot (-1) = 4 + 4 = 8]The roots are:[x = frac{-2 pm sqrt{8}}{2} = frac{-2 pm 2sqrt{2}}{2} = -1 pm sqrt{2}]Adding the roots (x_1 = -1 + sqrt{2}) and (x_2 = -1 - sqrt{2}):[x_1 + x_2 = (-1 + sqrt{2}) + (-1 - sqrt{2}) = -2]Thus, the value of (x_1 + x_2) is (boxed{B}).]

🔑:Given that the roots of the quadratic equation x^2 + 2x - 1 = 0 are x_1 and x_2, we have x_1 + x_2 = -2. Therefore, the correct option is boxed{text{B}}.

🧠:[<think>Okay, so I need to find the remainder when the 2025th number in this sequence is divided by 4. Let's see... The sequence starts with 1, 1, and then each subsequent number is the sum of the previous two. That sounds like the Fibonacci sequence, right? The classic Fibonacci sequence starts with 1, 1 (or sometimes 0, 1), and each term is the sum of the two before it. So yeah, this is the Fibonacci sequence.The problem is asking for the remainder when the 2025th term is divided by 4. That is, we need to compute F_2025 mod 4, where F_n denotes the nth Fibonacci number. Calculating F_2025 directly is obviously impossible because Fibonacci numbers grow exponentially, so there must be a pattern or cycle in the remainders when divided by 4. This concept is related to Pisano periods, which I remember are the periods with which the sequence of Fibonacci numbers taken modulo n repeats.First, let me recall that the Pisano period for modulo m is the period after which the Fibonacci sequence modulo m repeats. For example, modulo 2, the Pisano period is 3: the sequence goes 1, 1, 0, 1, 1, 0, etc. For modulo 3, it's 8: 1, 1, 2, 0, 2, 2, 1, 0, and then repeats. So maybe modulo 4 has a Pisano period as well. If I can find the Pisano period for modulo 4, then I can compute 2025 modulo that period to find the equivalent smaller index, and then compute that smaller Fibonacci number modulo 4.Let me try to compute the Pisano period for modulo 4. To do this, I need to list the Fibonacci numbers modulo 4 until I see the sequence repeating. The sequence starts with F1=1, F2=1.Let's compute term by term:F1 = 1 mod 4 = 1F2 = 1 mod 4 = 1F3 = (F1 + F2) mod 4 = (1 + 1) mod 4 = 2F4 = (F2 + F3) mod 4 = (1 + 2) mod 4 = 3F5 = (F3 + F4) mod 4 = (2 + 3) mod 4 = 5 mod 4 = 1F6 = (F4 + F5) mod 4 = (3 + 1) mod 4 = 0F7 = (F5 + F6) mod 4 = (1 + 0) mod 4 = 1F8 = (F6 + F7) mod 4 = (0 + 1) mod 4 = 1F9 = (F7 + F8) mod 4 = (1 + 1) mod 4 = 2F10 = (F8 + F9) mod 4 = (1 + 2) mod 4 = 3F11 = (F9 + F10) mod 4 = (2 + 3) mod 4 = 5 mod 4 = 1F12 = (F10 + F11) mod 4 = (3 + 1) mod 4 = 0F13 = (F11 + F12) mod 4 = (1 + 0) mod 4 = 1F14 = (F12 + F13) mod 4 = (0 + 1) mod 4 = 1So looking at this sequence:1, 1, 2, 3, 1, 0, 1, 1, 2, 3, 1, 0, 1, 1,...Starting from F1, the sequence is 1, 1, 2, 3, 1, 0, 1, 1, 2, 3, 1, 0, then back to 1, 1, etc. So the repeating cycle here is 1, 1, 2, 3, 1, 0, and then repeats. Let's check the length. From F1 to F6: 1,1,2,3,1,0. Then F7 to F12: 1,1,2,3,1,0. So the cycle length is 6. Therefore, the Pisano period modulo 4 is 6.Wait, but let me confirm. The Pisano period is the period after which the sequence repeats. So the initial terms are F1=1, F2=1. Then F3=2, F4=3, F5=1, F6=0, F7=1, F8=1, which is the same as F1 and F2. So does the Pisano period start repeating from F7? Let's see:From F1 to F6: 1,1,2,3,1,0F7 to F12: 1,1,2,3,1,0So yes, the sequence starts repeating every 6 terms. Therefore, the Pisano period modulo 4 is 6. So to compute F_n mod 4, we can compute n mod 6, and then take the corresponding term in the cycle.Wait, but hold on. Let me check if the Pisano period is actually 6. Because sometimes the Pisano period is defined as the period with which the sequence of Fibonacci numbers modulo n repeats. The standard Pisano periods for some small n are:- mod 2: period 3- mod 3: period 8- mod 4: period 6- mod 5: period 20So according to known values, mod 4 Pisano period is indeed 6. So that checks out.Therefore, since the Pisano period modulo 4 is 6, the Fibonacci sequence modulo 4 repeats every 6 terms. So to find F_2025 mod 4, we can compute 2025 divided by 6, find the remainder, and then look up the corresponding term in the cycle.But here's a point to be careful about. The Pisano period usually starts from F0=0, F1=1. But in our problem, the sequence starts with F1=1, F2=1. So maybe the indexing is different. Wait, let's see. In the standard Pisano period definition, they consider the Fibonacci sequence starting from F0=0, F1=1, F2=1, F3=2, etc. So in our case, the problem starts with F1=1, F2=1. So actually, our sequence is shifted compared to the standard Fibonacci sequence. The standard Fibonacci sequence starting from F0=0, F1=1 would have F2=1, F3=2, etc. But here, the first term is F1=1, which is the same as standard F2=1. So our F1 corresponds to standard F2, our F2 corresponds to standard F3, and so on. Therefore, there is an index shift of 1. So if the Pisano period is 6 for the standard sequence starting at F0, then in our case, since our indices are shifted by 1, maybe we need to adjust for that.Wait, but let's think again. The Pisano period is a property of the Fibonacci sequence modulo m, regardless of the starting terms. Wait, no, actually, the Pisano period is defined for the Fibonacci sequence with the standard starting values F0=0 and F1=1. If we have a different starting point, the period might be different? Hmm, maybe not necessarily. Let me check.In our problem, the sequence starts with F1=1, F2=1. Let's see how this compares to the standard Fibonacci sequence. The standard Fibonacci sequence is F0=0, F1=1, F2=1, F3=2, F4=3, F5=5, etc. So our sequence is the same as the standard Fibonacci sequence starting from F1=1, F2=1, F3=2, etc. So in effect, our F1 is standard F2, our F2 is standard F3, etc. So in general, our F_n is equal to standard F_{n+1}. So if we want to use the Pisano period for the standard sequence, we need to adjust the index accordingly.So, for example, in our problem, the 2025th term is equivalent to the standard Fibonacci term F_{2026} (since our F1 = standard F2). Therefore, if the Pisano period for modulo 4 is 6, then the standard Fibonacci sequence modulo 4 repeats every 6 terms. Therefore, to find F_{2026} mod 4, we compute 2026 mod 6, then take that result and find the corresponding standard Fibonacci term modulo 4.But wait, maybe this is overcomplicating. Let's see. Let's go back to the sequence we generated earlier for our problem's Fibonacci sequence modulo 4:Term 1: 1Term 2: 1Term 3: 2Term 4: 3Term 5: 1Term 6: 0Term 7: 1Term 8: 1Term 9: 2Term 10: 3Term 11: 1Term 12: 0...and so on. So the cycle here is clearly 1, 1, 2, 3, 1, 0, repeating every 6 terms. So starting from Term 1, the cycle length is 6. Therefore, in our problem's sequence, the Pisano period modulo 4 is 6. Therefore, regardless of the starting terms, the period is 6 because the problem's sequence is just a shifted version of the standard Fibonacci sequence, and the periodicity remains the same.Therefore, to compute F_n mod 4 for our sequence, we can compute n mod 6. If the remainder is r, then the result is the r-th term in the cycle. But we need to check how the cycle aligns with the term numbers.Looking at the cycle:Term 1: 1Term 2: 1Term 3: 2Term 4: 3Term 5: 1Term 6: 0Term 7: 1 (same as Term 1)Term 8: 1 (same as Term 2)So the cycle length is 6, starting from Term 1. Therefore, the Pisano period here is 6. Therefore, the value of F_n mod 4 is equal to F_{n mod 6} mod 4, but we need to adjust because if n mod 6 is 0, then it corresponds to Term 6, which is 0. Wait, let's see:If n ≡ 1 mod 6, then Term n is 1n ≡ 2 mod 6: 1n ≡ 3 mod 6: 2n ≡ 4 mod 6: 3n ≡ 5 mod 6: 1n ≡ 0 mod 6: 0So for example, Term 7: 7 mod 6 is 1, so 1Term 8: 8 mod 6 is 2, so 1Term 9: 9 mod 6 is 3, so 2Term 10: 10 mod 6 is 4, so 3Term 11: 11 mod 6 is 5, so 1Term 12: 12 mod 6 is 0, so 0Yes, that matches. So if we have n, compute n mod 6. If the remainder is between 1 and 5, use that as the position in the cycle; if the remainder is 0, use position 6. Therefore, the formula is:If n mod 6 = r, then:- If r ≠ 0, the result is the r-th term in the cycle [1, 1, 2, 3, 1, 0]- If r = 0, the result is the 6th term, which is 0.Therefore, to find F_2025 mod 4, compute 2025 mod 6.2025 divided by 6: Let's compute that.6 * 337 = 20222025 - 2022 = 3So 2025 = 6 * 337 + 3Therefore, 2025 mod 6 is 3.Therefore, the remainder is 3, so we look at the 3rd term in the cycle, which is 2.Wait, but hold on. Term 3 is 2. Therefore, F_2025 mod 4 should be 2. But let's check this with our earlier list.Term 3: 2Term 9: 2 (since 9 mod 6=3)Term 15: 2 (15 mod 6=3), etc.So if 2025 mod 6=3, then Term 2025 should be 2 mod 4. Therefore, the remainder is 2. So the answer should be C) 2.Wait, but let me confirm with a smaller example. Let's check Term 3: 2 mod4=2. Correct. Term 9: 2 mod4=2. Term 15: same. So seems correct.But wait, let me check Term 6: 0, Term 12:0, etc. So if I had n=6, remainder 0, then result is 0. Similarly, n=12, 0. So seems the formula works.Therefore, 2025 mod6=3, so the remainder is the 3rd term in the cycle, which is 2. Therefore, the answer is C) 2.But hold on, just to be thorough, let's compute a few terms manually and see.Term1:1Term2:1Term3:1+1=2Term4:1+2=3Term5:2+3=5 mod4=1Term6:3+1=4 mod4=0Term7:1+0=1Term8:0+1=1Term9:1+1=2Term10:1+2=3Term11:2+3=5 mod4=1Term12:3+1=4 mod4=0So Term7=1, Term8=1, Term9=2, Term10=3, Term11=1, Term12=0, then Term13=1, etc. So yes, the cycle is 6.So Term number: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16...Mod4: 1,1,2,3,1,0,1,1,2,3,1,0,1,1,2,3...So every 6 terms, it repeats. Therefore, 2025 mod6=3, so Term2025 is same as Term3, which is 2. So 2 mod4=2.Therefore, the answer should be C) 2.Wait, but let me cross-verify with another approach.Alternatively, maybe we can use mathematical induction or some formula. But since Fibonacci numbers modulo m cycle with a Pisano period, and we already determined the Pisano period is 6 for modulo4, and 2025 mod6=3, hence the remainder is 2.But to make sure, let's compute the cycle again step by step:1. F1 = 1 mod4=12. F2 = 1 mod4=13. F3 = (F1 + F2) mod4= (1 +1)=2 mod4=24. F4 = (F2 + F3) mod4= (1 +2)=3 mod4=35. F5 = (F3 + F4) mod4= (2 +3)=5 mod4=16. F6 = (F4 + F5) mod4= (3 +1)=4 mod4=07. F7 = (F5 + F6) mod4= (1 +0)=1 mod4=18. F8 = (F6 + F7) mod4= (0 +1)=1 mod4=19. F9 = (F7 + F8) mod4= (1 +1)=2 mod4=210. F10 = (F8 + F9) mod4= (1 +2)=3 mod4=311. F11 = (F9 + F10) mod4= (2 +3)=5 mod4=112. F12 = (F10 + F11) mod4= (3 +1)=4 mod4=0... and so on. So yes, every 6 terms it cycles back. Therefore, the cycle is indeed 1,1,2,3,1,0.Therefore, Term number n: if n mod6=1, remainder 1; n mod6=2, remainder1; n mod6=3, remainder2; n mod6=4, remainder3; n mod6=5, remainder1; n mod6=0, remainder0.So 2025 divided by6 gives remainder3. Therefore, the remainder is2.Therefore, the answer is C)2.Wait, but just to be absolutely sure, let me compute 2025 divided by6.Compute 6*337=2022, 2025-2022=3. So 2025=6*337+3. So 2025 mod6=3. Therefore, the third term in the cycle is2.So yes, the remainder is2. Therefore, optionC.But wait, hold on, in the cycle, the third term is2. Let me check Term3 is2. Term9 is2, Term15 is2, etc. So yes, all terms where n≡3 mod6 have remainder2.Therefore, the answer is2, which is optionC.Therefore, the answer is boxed{C}.Final Answerboxed{C}</think>The problem requires finding the remainder when the 2025th number in a Fibonacci-like sequence is divided by 4. The sequence starts with 1, 1, and each subsequent number is the sum of the previous two. To solve this, we use the concept of Pisano periods, which describe the period with which the Fibonacci sequence modulo ( n ) repeats. For ( n = 4 ), the Pisano period is 6. This means the sequence of remainders when divided by 4 repeats every 6 terms.We compute the Fibonacci sequence modulo 4:- ( F_1 mod 4 = 1 )- ( F_2 mod 4 = 1 )- ( F_3 mod 4 = (1 + 1) mod 4 = 2 )- ( F_4 mod 4 = (1 + 2) mod 4 = 3 )- ( F_5 mod 4 = (2 + 3) mod 4 = 1 )- ( F_6 mod 4 = (3 + 1) mod 4 = 0 )- The sequence then repeats: 1, 1, 2, 3, 1, 0, ...To find the remainder of ( F_{2025} mod 4 ), we calculate ( 2025 mod 6 ):- ( 2025 div 6 = 337 ) with a remainder of 3.Thus, ( 2025 mod 6 = 3 ). The third term in the repeating sequence (1, 1, 2, 3, 1, 0) is 2. Therefore, the remainder when the 2025th number is divided by 4 is 2.The answer is (boxed{C}).,<think>Okay, let's see. The problem is about a sequence where the first two numbers are 1, and each subsequent number is the sum of the previous two. So, it sounds like the Fibonacci sequence, right? But instead of the usual Fibonacci starting with 0 and 1, this one starts with 1 and 1. So the sequence would be 1, 1, 2, 3, 5, 8, 13, 21, and so on. The question is asking for the remainder when the 2025th number in this sequence is divided by 4. The options are 0, 1, 2, or 3.Hmm, okay. So we need to find the value of the 2025th term modulo 4. Calculating such a large term directly is obviously impossible because the Fibonacci numbers grow exponentially. So, there must be a repeating pattern in the remainders when divided by 4. This is called the Pisano period. For modulus m, the Fibonacci sequence modulo m will eventually repeat. So if we can find the Pisano period for m=4, then we can figure out where 2025 falls in that cycle and thus determine the remainder.First, let's recall what the Pisano period is. The Pisano period, π(m), is the period with which the sequence of Fibonacci numbers taken modulo m repeats. For example, for m=2, the Pisano period is 3: the remainders go 0, 1, 1, 0, 1, 1, etc. For m=3, the Pisano period is 8. So for each modulus, the period can vary.But in this problem, the sequence starts with 1, 1 instead of 0, 1. Wait, does that affect the Pisano period? Let me check. The standard Fibonacci sequence starts with F₀=0, F₁=1, but here the sequence starts with F₁=1, F₂=1. So maybe the Pisano period is the same, but shifted? Hmm, perhaps not. Let's test it.Let's compute the sequence modulo 4 step by step for the first few terms and see if we can spot a pattern.Given the sequence starts with:Term 1: 1Term 2: 1Term 3: 1 + 1 = 2Term 4: 1 + 2 = 3Term 5: 2 + 3 = 5 → 5 mod 4 = 1Term 6: 3 + 1 = 4 → 4 mod 4 = 0Term 7: 1 + 0 = 1Term 8: 0 + 1 = 1Term 9: 1 + 1 = 2Term 10: 1 + 2 = 3Term 11: 2 + 3 = 5 → 1Term 12: 3 + 1 = 4 → 0Term 13: 1 + 0 = 1Term 14: 0 + 1 = 1Wait a minute, starting from Term 1, the remainders modulo 4 are:1, 1, 2, 3, 1, 0, 1, 1, 2, 3, 1, 0, 1, 1, ...So from Term 1 to Term 6: 1, 1, 2, 3, 1, 0Then Term 7 to Term 12: 1, 1, 2, 3, 1, 0Then Term 13 onwards: 1, 1, ...So the cycle here is 1, 1, 2, 3, 1, 0, and then repeats every 6 terms. Wait, let's check the length. From Term 1 to Term 6, that's 6 terms. Then Term 7 starts again with 1, which matches Term 1. So the Pisano period here is 6.But wait, in the standard Fibonacci sequence starting with F₀=0, F₁=1, the Pisano period modulo 4 is 6. Let me confirm that. The standard Fibonacci sequence modulo 4 would be:F₀=0, F₁=1, F₂=1, F₃=2, F₄=3, F₅=1, F₆=0, F₇=1, F₈=1, etc. So the Pisano period is indeed 6. But in our problem, the sequence is shifted because we start with Term 1=1, Term 2=1, which corresponds to F₁=1, F₂=1 in the standard numbering. So the standard Pisano period applies here as well.Therefore, the Pisano period modulo 4 is 6. That means the remainders repeat every 6 terms. So the sequence of remainders is 1, 1, 2, 3, 1, 0, 1, 1, 2, 3, 1, 0, etc.But let's make sure. Let's list out the terms with their term numbers and remainders:Term 1: 1 mod 4 = 1Term 2: 1 mod 4 = 1Term 3: 2 mod 4 = 2Term 4: 3 mod 4 = 3Term 5: 5 mod 4 = 1Term 6: 8 mod 4 = 0Term 7: 13 mod 4 = 1Term 8: 21 mod 4 = 1Term 9: 34 mod 4 = 2Term 10: 55 mod 4 = 3Term 11: 89 mod 4 = 1Term 12: 144 mod 4 = 0Yep, so from Term 1 to Term 6, then Term 7 to Term 12, it's the same cycle. So the period is 6. Therefore, the remainder of Term n modulo 4 is the same as the remainder of Term (n mod 6) modulo 4. Wait, but when n mod 6 is 0, it maps to Term 6, which has remainder 0. So if we can express 2025 as 6*k + r, where r is the remainder when 2025 is divided by 6, then the remainder modulo 4 would be the same as Term r's remainder. But if r is 0, then it's Term 6, which is 0.So first, let's compute 2025 divided by 6. Let's do 2025 ÷ 6.6*337 = 2022, so 2025 - 2022 = 3. Therefore, 2025 = 6*337 + 3. Therefore, the remainder is 3. Therefore, Term 2025 has the same remainder as Term 3, which is 2. Wait, Term 3's remainder is 2. So the answer should be 2, which is option C.But wait, hold on. Let me verify again. The period is 6, so the remainder of Term n modulo 4 is equal to the remainder of Term (n mod 6) modulo 4. But when n mod 6 is 0, it's Term 6. So let's check n=6: Term 6 has remainder 0. Then Term 12: remainder 0, Term 18: remainder 0, etc. So yes, the mapping works.Given that 2025 divided by 6 gives a quotient of 337 and a remainder of 3. So Term 2025 corresponds to Term 3 in the cycle. Term 3's remainder is 2, so the answer is 2. Option C. Hmm, but let's make sure this is correct.Wait, let's check with smaller terms. Let's take Term 3: remainder 2. Term 9: 34 mod 4 is 2, yes. Term 15: let's compute Term 15. Wait, Term 7:13, Term 8:21, Term 9:34, Term10:55, Term11:89, Term12:144, Term13:233, Term14:377, Term15:610. 610 mod 4 is 610 divided by 4: 4*152=608, so 610-608=2. So Term 15 mod 4 is 2. So Term 15, which is 6*2 + 3 = 15, remainder 3. Term 3: remainder 2. So yes, Term 15's remainder is 2. So the pattern holds. Therefore, Term 2025, which is 6*337 + 3, would have the same remainder as Term 3, which is 2. Therefore, the answer is 2, option C.But let me make sure I didn't make a mistake in the calculation of 2025 divided by 6. Let's compute 6*337: 6*300=1800, 6*37=222, so 1800+222=2022. 2025-2022=3. So the remainder is indeed 3. So 2025 mod 6 is 3. Therefore, Term 2025 corresponds to Term 3 in the cycle. Term 3 is 2 mod 4. Therefore, the answer is 2.Alternatively, maybe the Pisano period is different? Let me confirm the Pisano period modulo 4. For the standard Fibonacci sequence starting at F₀=0, the Pisano period modulo 4 is indeed 6. The sequence of remainders is 0, 1, 1, 2, 3, 1, 0, 1, 1, 2, 3, 1, 0,... So the period is 6. However, in our problem, the sequence starts with 1, 1, so effectively starting from F₁ and F₂ in the standard Fibonacci sequence. So the remainders start at 1, 1, 2, 3, 1, 0, etc., which is the same as the standard sequence shifted by one term. Therefore, the Pisano period is still 6, so the cycle length is 6. Therefore, our calculation holds.Alternatively, maybe there's an off-by-one error because of the starting term. Let's check. For example, in the standard numbering, F₁=1, F₂=1, F₃=2, etc. So Term 1 here is F₁, Term 2 is F₂, Term 3 is F₃, so on. Therefore, when we take Term n here, it's equivalent to Fₙ in the standard Fibonacci sequence. Therefore, the Pisano period modulo 4 for the standard Fibonacci sequence is 6. Therefore, Fₙ mod 4 repeats every 6 terms. Therefore, Fₙ mod 4 = Fₙ₊₆ mod 4. Therefore, since Term 2025 here is F₂₀₂₅ in standard numbering, then F₂₀₂₅ mod 4 = F₂₀₂₅ mod 6 mod 4. Wait, no, the Pisano period tells us that Fₙ mod m repeats every π(m) terms. Therefore, Fₙ mod m = Fₙ mod π(m) mod m. Wait, actually, the formula is that Fₙ ≡ Fₙ₊π(m) mod m. So to find Fₙ mod m, we can compute n mod π(m), let's call that r, then Fₙ mod m = Fᵣ mod m. But in our case, the Pisano period π(4)=6. Therefore, F₂₀₂₅ mod 4 = F_{2025 mod 6} mod 4. 2025 mod 6 is 3, so F₃ mod 4. F₃ in standard Fibonacci is 2, so 2 mod 4 = 2. Therefore, the answer is 2, which is option C.Therefore, the answer should be boxed{C}.Final Answerboxed{C}</think>The problem involves a sequence starting with 1, 1, where each subsequent number is the sum of the previous two. We need to find the remainder when the 2025th term is divided by 4.1. The sequence is similar to the Fibonacci sequence starting with 1, 1.2. The Pisano period for modulo 4 is 6, meaning the remainders repeat every 6 terms.3. Calculating the remainders of the first few terms modulo 4, we get the sequence: 1, 1, 2, 3, 1, 0, which repeats every 6 terms.4. To find the remainder of the 2025th term modulo 4, we compute (2025 mod 6): - (2025 div 6 = 337) with a remainder of 3.5. The remainder 3 corresponds to the 3rd term in the repeating sequence, which is 2.Thus, the remainder when the 2025th number is divided by 4 is (boxed{C}).]

🔑:6. C.The remainders when this sequence of numbers is divided by 4 are 1,1,2,3,1,0,1,1,2, 3,1,0, cdots, with a period of 6. Also, 2025=337 times 6+3, so the 2025th number is congruent to the 3rd number modulo 4, with a remainder of 2.

🧠:[<think>Okay, let's tackle this problem step by step. The function given is ( f(x) = x^2 + x - 2 ). There are two parts to the problem. Let's start with part (1), finding the analytical expression for ( g(x) = frac{|f(x)| - f(x)}{2} ).First, I need to understand what ( g(x) ) represents. The expression ( |f(x)| - f(x) ) is divided by 2. Let me think about how the absolute value affects this. If ( f(x) ) is positive, then ( |f(x)| = f(x) ), so ( |f(x)| - f(x) = 0 ). If ( f(x) ) is negative, then ( |f(x)| = -f(x) ), so ( |f(x)| - f(x) = -f(x) - f(x) = -2f(x) ). Therefore, ( frac{|f(x)| - f(x)}{2} ) would be ( 0 ) when ( f(x) geq 0 ) and ( -f(x) ) when ( f(x) < 0 ).So, ( g(x) = begin{cases} -f(x) & text{if } f(x) < 0, 0 & text{if } f(x) geq 0. end{cases} )Now, I need to find where ( f(x) < 0 ). Let's solve the inequality ( x^2 + x - 2 < 0 ).First, factorizing the quadratic equation ( x^2 + x - 2 = 0 ). Let's find two numbers that multiply to -2 and add to 1. That would be 2 and -1. So, ( (x + 2)(x - 1) = 0 ). Therefore, the roots are ( x = -2 ) and ( x = 1 ).Since the coefficient of ( x^2 ) is positive, the parabola opens upwards. Thus, the quadratic is negative between its roots. So, ( f(x) < 0 ) when ( -2 < x < 1 ).Therefore, the function ( g(x) ) is equal to ( -f(x) ) in the interval ( (-2, 1) ), and 0 otherwise.So, writing this out:( g(x) = begin{cases} -x^2 - x + 2 & text{if } -2 < x < 1, 0 & text{otherwise}. end{cases} )That should be the analytical expression for ( g(x) ).Now moving on to part (2). We have ( a > 0 ), and the line ( y = ax + b ) intersects the curve ( y = g(x) ) at three different points. We need to determine the relationship between ( a ) and ( b ), and draw the region where the point ( (a, b) ) lies.First, let me visualize ( g(x) ). Since ( g(x) ) is ( -f(x) ) between ( x = -2 ) and ( x = 1 ), and 0 elsewhere. So, ( g(x) ) is a downward-opening parabola between ( x = -2 ) and ( x = 1 ), with vertex somewhere in that interval, and zero outside.Let me confirm the vertex of ( g(x) ) in the interval ( (-2, 1) ). The original ( f(x) = x^2 + x - 2 ), so ( -f(x) = -x^2 - x + 2 ). The vertex of this parabola can be found using ( x = -b/(2a) ) for ( ax^2 + bx + c ). Here, ( a = -1 ), ( b = -1 ), so vertex at ( x = -(-1)/(2*(-1)) = 1/(-2) = -0.5 ). So, the vertex is at ( x = -0.5 ). Plugging into ( -f(x) ):( -f(-0.5) = -[(-0.5)^2 + (-0.5) - 2] = -[0.25 - 0.5 - 2] = -[-2.25] = 2.25 ). So, the vertex is at ( (-0.5, 2.25) ).So, ( g(x) ) is a downward-opening parabola from ( (-2, 0) ) to ( (1, 0) ) with vertex at ( (-0.5, 2.25) ).Now, the line ( y = ax + b ) intersects ( y = g(x) ) at three different points. Since ( g(x) ) is non-zero only between ( x = -2 ) and ( x = 1 ), but the line is defined for all x. So, how can the line intersect three times? The line can intersect the parabola part twice and the zero part once, or maybe the zero part twice and the parabola once? Wait, but since outside of ( (-2,1) ), ( g(x) = 0 ), which is the x-axis. So, the line ( y = ax + b ) can intersect the parabola part (between -2 and 1) and the x-axis (outside of -2 and 1). However, since ( a > 0 ), the line is ascending. Let's think.To have three intersection points, the line must cross the parabola part of ( g(x) ) twice and cross the x-axis part once, or cross the parabola once and the x-axis twice. But since the x-axis part is only where ( g(x) = 0 ), so intersections with the x-axis part would be solutions to ( ax + b = 0 ), which is ( x = -b/a ). But ( for these intersections to be on the x-axis part of ( g(x) ), the x-coordinate must be outside (-2, 1). So, ( x = -b/a ) must be ≤ -2 or ≥1.Similarly, intersections with the parabola part would be in the interval (-2,1). So, the equation ( ax + b = -x^2 - x + 2 ) must have two solutions in (-2,1), and the equation ( ax + b = 0 ) must have one solution outside (-2,1). Therefore, in total three intersection points.Alternatively, maybe the line could intersect the parabola three times? But the parabola is only between -2 and 1, so a line can intersect a parabola at most two times. Hence, three intersections would require two intersections with the parabola and one with the x-axis part.Alternatively, maybe intersecting the parabola once and the x-axis twice? But that would require two solutions to ( ax + b = 0 ), but since it's a linear equation, only one solution. So, unless the line is tangent to the x-axis part, but the x-axis part is just the x-axis. So, if ( ax + b = 0 ) is tangent to the x-axis, but that would require a = 0, but a > 0. So, only one intersection with the x-axis part. Therefore, total three intersections would require two intersections with the parabola (in the interval (-2,1)) and one intersection with the x-axis part (outside (-2,1)).Therefore, for three intersection points, the line must cross the parabola twice within (-2,1) and cross the x-axis once outside (-2,1). Additionally, the line must not be tangent to the parabola, so that there are two distinct intersections.So, let's formalize this.First, the line intersects the x-axis at ( x = -b/a ). For this intersection to be outside the interval (-2,1), we need ( -b/a ≤ -2 ) or ( -b/a ≥ 1 ). But since a > 0, multiplying both sides by a (positive, so inequality signs don't change):- For ( -b/a ≤ -2 ), multiply by a: -b ≤ -2a → b ≥ 2a.- For ( -b/a ≥ 1 ), multiply by a: -b ≥ a → -a - b ≥ 0 → b ≤ -a.But since a > 0, and if b ≤ -a, then since a > 0, b would be negative. However, depending on the line's position, maybe it can intersect three times. Wait, but let's think: if the line intersects the x-axis at x = -b/a, and we need this x to be either ≤ -2 or ≥1. So, either:Case 1: x-intercept ≤ -2: ( -b/a ≤ -2 ⇒ b ≥ 2a ).Case 2: x-intercept ≥1: ( -b/a ≥1 ⇒ b ≤ -a ).But if b ≤ -a, since a > 0, then b is negative. However, the line y = ax + b with a > 0 and b ≤ -a would cross the y-axis at (0, b) which is below (0, -a). But we need the line to intersect the parabola part as well. Let's check.But first, let's analyze both cases.First, Case 1: b ≥ 2a. Then the x-intercept is at x = -b/a ≤ -2. So, the line crosses the x-axis at x ≤ -2. Then, the line y = ax + b must intersect the parabola part of g(x) (which is between -2 and 1) twice. So, we need the equation ax + b = -x² - x + 2 to have two real solutions in (-2,1). Also, since the line crosses the x-axis at x ≤ -2, which is outside the interval where the parabola is, so the line is above the x-axis for x > -b/a. But since -b/a ≤ -2, so for x > -2, which is the interval we care about for the parabola, the line is y = ax + b. If x > -2, then since a > 0, ax is increasing, but b is positive (since b ≥ 2a > 0). Therefore, the line is positive in the interval (-2,1). However, the parabola is between y=0 and y=2.25. So, a line with positive slope starting from x ≤ -2, crossing the x-axis at x ≤ -2, and increasing upwards. Wait, but if b ≥ 2a, then when x = -2, the line's value is y = a*(-2) + b = -2a + b. Since b ≥ 2a, this is ≥ -2a + 2a = 0. So, at x = -2, the line is at least 0. But the parabola at x = -2 is 0. So, if the line is exactly 0 at x = -2, it's tangent to the parabola there? Wait, let's check.At x = -2, the parabola is at 0, and the line is y = -2a + b. If b = 2a, then y = 0 at x = -2. So, the line would pass through (-2, 0). But since the parabola is 0 at x = -2 and x =1, and the line is passing through (-2, 0) and going upwards. If b > 2a, then at x = -2, the line is above 0. But the parabola is 0 there, so the line would cross the parabola at two points within (-2,1). Wait, but need to verify.Alternatively, maybe if the line intersects the parabola twice in (-2,1) and crosses the x-axis at x ≤ -2, which is outside the interval. So, in this case, the line would have two intersections with the parabola and one with the x-axis part at x ≤ -2. Similarly, for the other case, if x-intercept is at x ≥1, then the line crosses the x-axis there, and maybe intersects the parabola twice in (-2,1). But let's check.Wait, but if b ≤ -a, then x-intercept is x = -b/a ≥1. Then, the line crosses the x-axis at x ≥1. Then, for x <1, the line is y = ax + b, which is below the x-axis (since for x < -b/a, which is greater than or equal to 1, but x is less than 1). Wait, if x-intercept is at x =1, then for x <1, the line is below the x-axis. But the parabola part is between -2 and1, and in that interval, the parabola is above zero. So, the line would be below the parabola in (-2,1), but since the parabola is above zero there, and the line is below zero (for x <1), so the line would not intersect the parabola in that interval. Therefore, the only intersection would be at x =1 if the line crosses there, but x=1 is part of the parabola's endpoint. Wait, but at x=1, the parabola is 0, and the line is y = a*1 + b = a + b. If the line crosses the x-axis at x = -b/a ≥1, so if x-intercept is at x=1, then b = -a. Then, at x=1, the line is y = a*1 + (-a) = 0, which coincides with the parabola's endpoint. But in this case, if b = -a, the line is y = ax - a. At x=1, y=0. For x <1, the line is y = ax - a. Since a >0, when x <1, ax - a = a(x -1) <0. So, the line is below the parabola (which is non-negative in (-2,1)) except at x=1 where they meet. So, only one intersection at x=1. But if the x-intercept is greater than1, say x=2, then the line is y=ax + b, crosses the x-axis at x=2, so b = -2a. Then, for x <2, the line is below the x-axis. But in (-2,1), the line is below zero, and the parabola is non-negative, so they don't intersect. So, only intersection at x=2 (which is outside the interval where g(x) is non-zero, but since g(x) is zero there, the line intersects g(x) only at x=2? Wait, but g(x) is zero outside (-2,1). So, if the line crosses the x-axis at x=2, then y=0 at x=2, but g(x)=0 for x ≥1. So, the line would coincide with g(x)=0 for x ≥1. So, actually, for x ≥1, the line y=ax + b intersects y=g(x)=0 only at x=2 (if that's the intercept). Wait, but the equation ax + b =0 is solved at x=2, but for x ≥1, g(x)=0, so the line would intersect g(x) at x=2, which is in the region where g(x)=0. But between x=1 and x=2, the line is below zero (since x-intercept is at x=2, and a >0, so for x <2, the line is negative). Wait, no: if the line crosses the x-axis at x=2, then for x >2, y=ax + b is positive, and for x <2, it's negative. But in the interval x ≥1, which includes x=1 to x=2, the line is negative (since x <2), so in that interval, g(x)=0, which is the x-axis. So, the line is below the x-axis in x <2, so they don't intersect there. Only at x=2, the line crosses the x-axis, which is part of g(x)=0. So, that would be one intersection point. But the line could intersect the parabola part once if it's tangent, but in the case of x-intercept at x ≥1, the line is below the parabola in (-2,1), so no intersections. Hence, in the case where b ≤ -a, the line would intersect g(x) only once at x = -b/a ≥1. Therefore, that can't give three intersection points. So, maybe only Case 1 where b ≥2a gives three intersection points.Wait, but let's check with an example. Suppose a=1, then b ≥2. Let's take a=1, b=3. The line is y = x +3. The x-intercept is x = -3, which is ≤ -2. Now, let's see if this line intersects the parabola part (in (-2,1)) twice. The equation x + 3 = -x² - x + 2. Bring all terms to left: x +3 +x² +x -2 = x² + 2x +1 =0. Which factors to (x+1)^2=0, so a double root at x=-1. So, only one intersection point at x=-1. Wait, but that's a tangent. So, in this case, even though b=3 ≥2a=2, the line is tangent to the parabola, so only one intersection. So, perhaps my earlier reasoning is flawed.Wait, so if the line is tangent to the parabola part, then there would be two intersection points (the tangent point and the x-intercept). But in this case, the tangent point is a double root, so technically one intersection point with multiplicity two, but geometrically, it's still one point. So, for three distinct intersection points, the line must intersect the parabola twice (two distinct points) and the x-axis once. Therefore, in the case of b=3 and a=1, we only have two intersection points (the tangent point and the x-intercept). So, that's not three. Therefore, perhaps my condition is not just b ≥2a, but something more.Wait, so we need the equation ( ax + b = -x^2 - x + 2 ) to have two distinct real solutions in (-2,1), and the x-intercept of the line to be outside (-2,1). Let's re-express the equation:( -x^2 - x + 2 = ax + b )Rearranged:( -x^2 - (a +1)x + (2 - b) =0 )Multiply both sides by -1:( x^2 + (a +1)x + (b -2) =0 )So, quadratic equation ( x^2 + (a +1)x + (b -2) =0 )For this quadratic to have two real roots, discriminant must be positive:Discriminant D = (a +1)^2 -4*1*(b -2) = (a +1)^2 -4b +8For two real roots: D >0 ⇒ (a +1)^2 -4b +8 >0 ⇒ (a +1)^2 +8 >4b ⇒ b < [(a +1)^2 +8]/4Additionally, the roots must lie in the interval (-2,1). So, let's denote the roots as x1 and x2. Then, we need:-2 < x1 < x2 <1For this to hold, the quadratic must satisfy several conditions:1. The quadratic evaluated at x=-2 must be positive: Since the parabola opens upwards (coefficient 1), if the roots are between -2 and1, then f(-2) >0 and f(1) >0.Wait, the quadratic is ( x^2 + (a +1)x + (b -2) ). At x=-2:(-2)^2 + (a +1)(-2) + (b -2) =4 -2(a +1) +b -2=4 -2a -2 +b -2= (4 -2 -2) + (-2a) +b =0 -2a +b= b -2a.Similarly, at x=1:1^2 + (a +1)*1 + (b -2)=1 +a +1 +b -2= (1 +1 -2) +a +b=0 +a +b= a +b.Since the quadratic opens upwards, to have both roots between -2 and1, the quadratic must be positive at x=-2 and x=1, and the vertex must be between -2 and1.But since the quadratic is zero at x1 and x2, between -2 and1, then:- f(-2) = b -2a >0 ⇒ b >2a- f(1)=a +b >0 ⇒ a +b >0Also, the axis of symmetry of the quadratic is at x = - (a +1)/2. To be between -2 and1:-2 < - (a +1)/2 <1Multiply all parts by -2 (inequalities reverse):4 > a +1 > -2 ⇒ subtract 1:3 > a > -3But since a >0, we have 0 <a <3.Additionally, the discriminant must be positive: (a +1)^2 -4(b -2) >0 ⇒ b < [(a +1)^2 +8]/4 as before.But since we also have b >2a and b > -a (from f(1)=a +b >0), but from previous reasoning for Case 1, the x-intercept is at x = -b/a ≤ -2 ⇒ b ≥2a. However, we now have from f(-2)=b -2a >0 ⇒ b >2a. So, combining all these:From quadratic roots in (-2,1):b >2a,a +b >0,0 <a <3,andb < [(a +1)^2 +8]/4.Additionally, since the line must intersect the x-axis outside (-2,1), which in this case, x-intercept is x=-b/a ≤ -2 ⇒ b ≥2a. But from above, we already have b >2a. So, the x-intercept is strictly less than -2.Therefore, combining all these conditions:0 <a <3,b >2a,a +b >0,andb < [(a +1)^2 +8]/4.But since a >0 and b >2a, then a +b >0 is automatically satisfied because b >2a >0, so a +b >0 is redundant.Therefore, the conditions are:0 <a <3,2a <b < [(a +1)^2 +8]/4.Additionally, we need to check if [(a +1)^2 +8]/4 is greater than 2a for 0 <a <3.Compute [(a +1)^2 +8]/4 -2a:= [a² +2a +1 +8]/4 -2a= [a² +2a +9]/4 -2a= (a² +2a +9 -8a)/4= (a² -6a +9)/4= (a -3)^2 /4 ≥0.Thus, equality holds when a=3, but since a <3 in our domain, then [(a +1)^2 +8]/4 -2a >0. Hence, the upper bound for b is greater than 2a for 0 <a <3. Therefore, the region for b is 2a <b < [(a +1)^2 +8]/4 for 0 <a <3.But wait, we also need to consider that the quadratic equation ( x^2 + (a +1)x + (b -2) =0 ) has both roots in (-2,1). So, even with these conditions, we need to ensure that the roots are actually within (-2,1). Let's verify if the above conditions are sufficient.In general, for a quadratic ( x² + px + q =0 ), to have both roots in an interval (m, n), the following must hold:1. The quadratic is positive at m and n (since it opens upwards).2. The discriminant is positive (two distinct roots).3. The axis of symmetry is within (m, n).4. The quadratic at the axis of symmetry is negative (since it opens upwards, the minimum is between the roots).But in our case, we already derived conditions based on f(-2) >0, f(1) >0, discriminant >0, and axis of symmetry in (-2,1). However, the quadratic evaluated at the axis of symmetry should be less than or equal to zero (since the minimum of the quadratic is between the roots). Wait, but since the quadratic has two real roots, the minimum is at the axis of symmetry and is negative. Wait, the quadratic is ( x² + (a +1)x + (b -2) ), which opens upwards. Therefore, the minimum occurs at x = -(a +1)/2, and the value there is:[ (a +1)/2 ]² - (a +1)²/2 + (b -2)Wait, maybe better to compute f(-(a +1)/2):= [ (-(a +1)/2 )² ] + (a +1)(-(a +1)/2) + (b -2)= (a +1)^2 /4 - (a +1)^2 /2 + (b -2)= - (a +1)^2 /4 + (b -2)Since this is the minimum value, and since the quadratic has two real roots, this minimum must be negative:- (a +1)^2 /4 + (b -2) <0 ⇒ b -2 < (a +1)^2 /4 ⇒ b < (a +1)^2 /4 +2But earlier we had the discriminant condition: (a +1)^2 -4(b -2) >0 ⇒ b < [(a +1)^2 +8]/4But (a +1)^2 /4 +2 = (a +1)^2 /4 + 8/4 = [(a +1)^2 +8]/4, which matches the discriminant condition. So, the discriminant condition and the minimum value condition are the same. Therefore, our previous upper bound for b is indeed derived from the discriminant.Therefore, the necessary and sufficient conditions for the quadratic to have two distinct roots in (-2,1) are:1. b >2a,2. a +b >0 (which is redundant since b >2a and a >0),3. 0 <a <3,4. b < [(a +1)^2 +8]/4.Thus, the relationship between a and b is given by these inequalities. Therefore, the region where (a, b) lies is bounded by:- a >0,- a <3,- b >2a,- b < [(a +1)^2 +8]/4.To draw this region, we can plot these curves on the ab-coordinate plane.First, the line b=2a is a straight line with slope 2. Since a >0 and we need b >2a, the region is above this line.Second, the curve b = [(a +1)^2 +8]/4. Let's simplify this:[(a +1)^2 +8]/4 = (a² +2a +1 +8)/4 = (a² +2a +9)/4.So, it's a quadratic curve opening upwards. At a=0, b=(0 +0 +9)/4=9/4=2.25. At a=3, b=(9 +6 +9)/4=24/4=6. The vertex of this parabola is at a = -1 (since the quadratic in a is a² +2a +9, which has vertex at a = -b/(2a) for a quadratic aa² +ba +c, so here, a coefficient is1, b coefficient is2, so vertex at a=-1. But since we are considering a between0 and3, the curve from a=0 to a=3 is increasing because the derivative of b with respect to a is (2a +2)/4=(a +1)/2, which is positive for a> -1, which it is in our domain.Third, the line a=3 is a vertical line at a=3, but our region is a <3.Therefore, the region is bounded on the left by a=0, on the right by a approaching3, above by the curve b=(a² +2a +9)/4, and below by the line b=2a. However, since a<3, the upper bound is up to a=3 where b approaches6.To draw this region, we would plot the area between a=0 and a=3, above b=2a and below b=(a² +2a +9)/4.Additionally, we need to ensure that for these a and b, the line intersects the x-axis at x ≤-2. Since b >2a, x-intercept x=-b/a < -2a/a =-2. So, yes, the x-intercept is less than -2, hence outside the interval (-2,1), so the third intersection is at x=-b/a ≤-2.Therefore, the final answer for part (2) is the set of all (a, b) with 0 <a <3, 2a <b < (a² +2a +9)/4. The diagram would show the region between the line b=2a and the parabola b=(a² +2a +9)/4 for a between0 and3.Final Answer(1) The analytical expression of ( g(x) ) is ( boxed{g(x) = begin{cases} -x^2 - x + 2 & text{if } -2 < x < 1, 0 & text{otherwise}. end{cases}} )(2) The relationship between ( a ) and ( b ) is given by ( 0 < a < 3 ), ( 2a < b < frac{a^2 + 2a + 9}{4} ). The region where the point ( (a, b) ) lies is the area between the line ( b = 2a ) and the curve ( b = frac{a^2 + 2a + 9}{4} ) for ( 0 < a < 3 ).The diagram should illustrate this region with ( a ) on the horizontal axis and ( b ) on the vertical axis, bounded by the mentioned line and curve. The final answer for the region is boxed as:The region is defined by ( boxed{0 < a < 3 text{ and } 2a < b < frac{a^2 + 2a + 9}{4}} ).</think>Given the function ( f(x) = x^2 + x - 2 ):(1) To find the analytical expression of the function ( g(x) = frac{|f(x)| - f(x)}{2} ):- The function ( |f(x)| - f(x) ) is 0 when ( f(x) geq 0 ) and ( -2f(x) ) when ( f(x) < 0 ). Dividing by 2, we get ( g(x) = 0 ) when ( f(x) geq 0 ) and ( g(x) = -f(x) ) when ( f(x) < 0 ).- Solving ( f(x) < 0 ), we find ( -2 < x < 1 ). Therefore, ( g(x) ) is: [ g(x) = begin{cases} -x^2 - x + 2 & text{if } -2 < x < 1, 0 & text{otherwise}. end{cases} ](2) To determine the relationship between ( a ) and ( b ) such that the line ( y = ax + b ) intersects the curve ( y = g(x) ) at three different points:- The line ( y = ax + b ) must intersect the parabola part of ( g(x) ) twice within ((-2, 1)) and intersect the x-axis part once outside ((-2, 1)).- The quadratic equation ( x^2 + (a + 1)x + (b - 2) = 0 ) (derived from setting ( ax + b = -x^2 - x + 2 )) must have two distinct roots in ((-2, 1)).- The x-intercept of the line ( y = ax + b ) must be outside ((-2, 1)), leading to the conditions ( b > 2a ) (for the x-intercept to be (leq -2)) and ( b < frac{(a + 1)^2 + 8}{4} ) (from the discriminant condition for two distinct roots).The region where the point ((a, b)) lies is bounded by:- ( 0 < a < 3 )- ( 2a < b < frac{a^2 + 2a + 9}{4} ) Final Answer(1) The analytical expression of ( g(x) ) is:[boxed{g(x) = begin{cases} -x^2 - x + 2 & text{if } -2 < x < 1, 0 & text{otherwise}.end{cases}}](2) The relationship between ( a ) and ( b ) is given by:[boxed{0 < a < 3 text{ and } 2a < b < frac{a^2 + 2a + 9}{4}}],<think>Alright, so I need to solve this problem about the function f(x) = x² + x - 2. There are two parts: first, finding the analytical expression for g(x) which is defined as (|f(x)| - f(x))/2, and second, determining the relationship between a and b when the line y = ax + b intersects the curve y = g(x) at three different points, given that a > 0. Then I need to draw a diagram representing the region where (a, b) lies. Let me start with the first part.For part (1), the function g(x) is given by (|f(x)| - f(x))/2. Hmm, let me recall that |f(x)| is equal to f(x) when f(x) ≥ 0 and -f(x) when f(x) < 0. So if I subtract f(x) from |f(x)| and then divide by 2, what does that give me?Let me write it out. If f(x) is positive, then |f(x)| = f(x), so (f(x) - f(x))/2 = 0. If f(x) is negative, then |f(x)| = -f(x), so (-f(x) - f(x))/2 = (-2f(x))/2 = -f(x). Therefore, g(x) is equal to -f(x) when f(x) < 0 and 0 otherwise. So, g(x) = { -f(x) if f(x) < 0; 0 if f(x) ≥ 0 }.Therefore, to write the analytical expression for g(x), I need to find where f(x) is negative. Let's solve the inequality f(x) < 0, where f(x) = x² + x - 2. First, let's find the roots of f(x). The quadratic equation x² + x - 2 = 0 can be solved using the quadratic formula: x = [-b ± √(b² - 4ac)]/(2a). Here, a = 1, b = 1, c = -2. So discriminant D = 1 + 8 = 9. Therefore, roots are x = [-1 ± 3]/2. That gives x = (-1 + 3)/2 = 1 and x = (-1 - 3)/2 = -2. So the roots are x = -2 and x = 1.Since the coefficient of x² is positive, the parabola opens upwards. Therefore, the quadratic is negative between its roots. Hence, f(x) < 0 when x is between -2 and 1. So, for x ∈ (-2, 1), f(x) is negative, and g(x) = -f(x) there. Outside of this interval, f(x) ≥ 0, so g(x) = 0.Therefore, the analytical expression for g(x) is:g(x) = { -x² - x + 2, if -2 < x < 1; 0, otherwise }Wait, let me check that. If f(x) = x² + x - 2, then -f(x) = -x² - x + 2. So, yes, in the interval where f(x) is negative, which is between -2 and 1, g(x) is equal to -f(x). Outside of that interval, g(x) is zero. So that's part (1). I think that's straightforward.Now moving on to part (2). We have a line y = ax + b with a > 0, and it intersects the curve y = g(x) at three different points. We need to find the relationship between a and b, and then draw the region where (a, b) lies.First, let me visualize g(x). From part (1), we know that g(x) is a piecewise function. Between x = -2 and x = 1, it's a downward-opening parabola because the coefficient of x² is -1. The vertex of this parabola can be found. The standard form is -x² - x + 2. The vertex occurs at x = -b/(2a) for a quadratic ax² + bx + c. Here, a = -1, b = -1, so x = -(-1)/(2*(-1)) = 1/(-2) = -0.5. Then the y-coordinate is -(-0.5)^2 - (-0.5) + 2 = -0.25 + 0.5 + 2 = 2.25. So the vertex is at (-0.5, 2.25). So between x = -2 and x = 1, the graph is a downward-opening parabola with vertex at (-0.5, 2.25), starting from (-2, 0) and ending at (1, 0). Outside of that interval, the graph is zero.So the entire graph of g(x) is the downward-opening parabola between -2 and 1, and zero elsewhere. Now, the line y = ax + b intersects this curve at three different points. Since the line is straight, and a > 0, it's a line with positive slope. To intersect at three points, the line must cross the parabola part of g(x) twice and the zero part once, or maybe cross the parabola once and the zero part twice? Wait, but the parabola is only between -2 and 1, and outside it's zero.Wait, let me think. The line y = ax + b can intersect the parabola part (between -2 and 1) and the zero part (x ≤ -2 or x ≥ 1). To have three intersection points, the line must intersect the parabola twice and the zero part once. Because if it intersects the parabola once and the zero part twice, that's three points. Wait, but how?Wait, the zero part is two separate regions: x ≤ -2 and x ≥ 1. So the line y = ax + b could intersect the parabola once in (-2, 1), and then cross the zero part once in x ≤ -2 and once in x ≥ 1. But that would be three points. Alternatively, it could intersect the parabola twice in (-2, 1) and once in either x ≤ -2 or x ≥ 1. But since the line is straight, how can it intersect the parabola twice and then cross the zero part once? Let me visualize.The parabola is between -2 and 1, opening downward. The line y = ax + b is a straight line with positive slope. If the line is tangent to the parabola, it would intersect once on the parabola and possibly once or twice on the zero parts. But to have three intersections, the line needs to intersect the parabola twice and cross the zero part once. Let me think.Suppose the line cuts through the parabola in two points within (-2, 1), and then intersects the zero part somewhere else. But the zero part is on x ≤ -2 and x ≥ 1. Since the line has a positive slope, it might cross the zero part either on the left side (x ≤ -2) or the right side (x ≥ 1). But if the line is intersecting the parabola twice, which is between -2 and 1, and since the line is increasing, after x = 1, the line y = ax + b will continue upwards, while the curve y = g(x) is zero there. So if the line is above zero at x = 1, then for x ≥ 1, the line y = ax + b is above y = 0, so no intersection. If at x = 1, the line is below zero, then for x ≥ 1, it might intersect, but since a > 0, as x increases, the line will go upwards. Wait, but at x = 1, the value of the parabola is zero. So the line at x = 1 is y = a*1 + b. If the line is to cross the zero part at x ≥ 1, then y = ax + b must be zero at some x ≥ 1. But since a > 0 and x ≥ 1, ax + b is increasing. If at x = 1, the line is y = a + b. If a + b < 0, then for some x > 1, ax + b = 0. But since a > 0, that would require x = -b/a. But x must be ≥ 1, so -b/a ≥ 1, which implies b ≤ -a. But since a > 0, b would have to be negative. Alternatively, if a + b > 0, then the line is above zero at x = 1 and remains above for x > 1. Similarly, on the left side, x ≤ -2. At x = -2, the parabola is zero. The line at x = -2 is y = -2a + b. If -2a + b < 0, then the line is below zero at x = -2, and since the line is increasing, it could cross the zero part (y = 0) at some x < -2. But x ≤ -2. Wait, but x = -2 is already part of the zero region. So if the line crosses y = 0 at x < -2, that would be an intersection point. Similarly, if it crosses at x > 1. So to have three intersection points, the line must intersect the parabola twice between -2 and 1, and then cross the zero part either at x < -2 or at x > 1. But can it cross both? If the line crosses the parabola twice and the zero parts on both sides, that would be four intersections? But the problem states three different points. So it must intersect the parabola twice and one of the zero parts once. So either once on the left (x ≤ -2) or once on the right (x ≥ 1).But how do we determine which side? Let's analyze.Suppose the line intersects the parabola twice in (-2, 1). Then, to intersect the zero part once, the line must cross y = 0 either at x ≤ -2 or x ≥ 1. Let's check both possibilities.First, suppose the line intersects the parabola twice and also crosses x ≥ 1. For x ≥ 1, y = 0. The line y = ax + b would intersect this part at x where ax + b = 0, which is x = -b/a. But since x must be ≥ 1, we need -b/a ≥ 1, so -b ≥ a, which implies b ≤ -a. However, a > 0, so b must be negative. But if the line crosses the zero part at x ≥ 1, then at x = 1, the line is at y = a(1) + b. If the intersection at x ≥ 1 is at x = -b/a ≥ 1, then y at x = 1 is a + b. But since the line is crossing y = 0 at x = -b/a ≥ 1, then moving from x = 1 to x = -b/a, the line goes from y = a + b to y = 0. Since a > 0, the line is increasing, so a + b must be less than or equal to 0? Wait, no. If x = -b/a is greater than or equal to 1, then since the line is increasing, at x = 1, the value is a + b, and at x = -b/a, which is larger than 1, the value is 0. Therefore, since the line is increasing, a + b must be less than 0. Because as x increases, y increases, so if at x = 1 it's a + b and at x = -b/a it's 0, then a + b < 0. But x = -b/a must be greater than 1, so -b/a > 1 ⇒ -b > a ⇒ b < -a. So if b < -a, then the line intersects the zero part at x = -b/a > 1, and also intersects the parabola twice. But we need to ensure that the line actually intersects the parabola twice. So the line must intersect the parabola y = -x² - x + 2 (for -2 < x < 1) twice. Therefore, the system of equations y = ax + b and y = -x² - x + 2 must have two solutions in (-2, 1). Similarly, if the line intersects the zero part on the left (x ≤ -2), then the line crosses y = 0 at x = (-b)/a ≤ -2. So x = -b/a ≤ -2 ⇒ -b ≤ -2a ⇒ b ≥ 2a. Then, at x = -2, the line is y = -2a + b. Since x = -2 is the boundary of the zero region, if the line crosses y = 0 at x ≤ -2, then the line must be below zero at x = -2. Wait, no. The line is y = ax + b. At x = -2, y = -2a + b. If the line crosses y = 0 at x = -b/a ≤ -2, then since the line is increasing (a > 0), at x = -2, the line's y-value would be y = -2a + b. If x = -b/a ≤ -2, then -b/a ≤ -2 ⇒ b ≥ 2a. Therefore, substituting x = -2 into the line, y = -2a + b. Since b ≥ 2a, then y = -2a + b ≥ 0. But the zero part at x ≤ -2 is y = 0. So if the line at x = -2 is y ≥ 0, then how does the line cross y = 0 at x ≤ -2? Since the line is increasing, if at x = -2, the line is y ≥ 0, then for x < -2, since a > 0, y = ax + b would be less than at x = -2. So if at x = -2, y = -2a + b ≥ 0, then for x < -2, y = ax + b < -2a + b ≤ 0? Wait, no. Wait, if x decreases (x < -2), then since a > 0, ax decreases, so y = ax + b decreases as x decreases. Therefore, if at x = -2, y = -2a + b, then for x < -2, y would be less than -2a + b. Therefore, if -2a + b ≥ 0, then for x < -2, y might still be positive or cross zero. But if the line crosses zero at x = -b/a ≤ -2, then that requires that when x = -b/a, y = 0. Since x = -b/a ≤ -2, then -b/a ≤ -2 ⇒ b ≥ 2a. Therefore, at x = -2, y = -2a + b. Since b ≥ 2a, then y = -2a + b ≥ 0. So the line at x = -2 is at or above zero. But since the line is decreasing as x decreases (since a > 0), moving left from x = -2, the line goes downward. However, the region x ≤ -2 is y = 0. So if the line is above zero at x = -2, then moving left, it might cross zero at x = -b/a ≤ -2. But how does that interact with the parabola?Wait, if the line intersects the parabola twice in (-2, 1) and also crosses the zero part at x ≤ -2, then that intersection at x ≤ -2 must satisfy y = 0. So the line must cross y = 0 at x = -b/a ≤ -2. So, in this case, the intersection points are two on the parabola and one on the left zero part. Alternatively, if the line crosses the zero part at x ≥ 1, then the intersection is two on the parabola and one on the right zero part.But the problem states that the line intersects the curve at three different points. So depending on where the third intersection is (left or right), we have different conditions on a and b. So maybe both cases are possible? But perhaps the problem is considering only one of them. Wait, but let's think. The line has positive slope. If it intersects the parabola twice and crosses the zero part on the right (x ≥ 1), then for that to happen, at x = 1, the line must be below zero (since it's going to cross zero at x = -b/a > 1, but wait, x = -b/a > 1 would mean -b/a > 1 ⇒ -b > a ⇒ b < -a. But at x = 1, the line is y = a + b. If b < -a, then a + b < 0. So at x = 1, the line is below zero. However, the parabola at x = 1 is zero, so the line is below the parabola at x = 1? Wait, but the parabola is only defined up to x = 1. Wait, no. The parabola is between x = -2 and 1, and beyond that, the curve is zero. So at x = 1, the curve y = g(x) is zero. If the line at x = 1 is y = a + b, and if a + b < 0, then the line is below zero at x = 1. But since the curve is zero there, the line would pass below the curve at x = 1. However, to intersect the zero part at x ≥ 1, the line needs to cross y = 0 at some x ≥ 1, which would require that y = ax + b = 0 at x = -b/a ≥ 1. But if a > 0 and x ≥ 1, then ax + b is increasing. If at x = 1, y = a + b < 0, then as x increases beyond 1, y = ax + b increases from a + b. Since a > 0, there will be some x where ax + b = 0, which is x = -b/a. But since a + b < 0 and a > 0, then -b/a > -b/(a) but given that a + b < 0, let's see:Suppose a = 1, b = -2. Then x = -b/a = 2 ≥ 1. So in that case, the line crosses the zero part at x = 2. At x = 1, the line is y = 1 + (-2) = -1 < 0, which is below the curve y = 0. Then as x increases past 1, the line goes from -1 upwards, crossing zero at x = 2. So between x = 1 and x = 2, the line is below the curve (which is zero) until x = 2, where it crosses. So that intersection at x = 2 is valid.Similarly, if the line crosses the zero part on the left (x ≤ -2), then it must cross at x = -b/a ≤ -2. That requires b ≥ 2a. At x = -2, the line is y = -2a + b. Since b ≥ 2a, y = -2a + b ≥ 0. So at x = -2, the line is at or above zero, and moving left from x = -2, since the slope is positive, the line decreases. Therefore, the line will cross zero at x = -b/a ≤ -2. So in this case, the line intersects the parabola twice and crosses zero on the left. However, at x = -2, the curve is zero. If the line is at y = -2a + b ≥ 0, then at x = -2, the line is at or above the curve. Moving left from x = -2, the line decreases and crosses zero at x = -b/a. So the intersection point is at x = -b/a ≤ -2.But how do these different scenarios affect the conditions on a and b? Let's formalize this.First, for the line to intersect the parabola y = -x² - x + 2 (for -2 < x < 1) twice, the equation ax + b = -x² - x + 2 must have two real solutions in the interval (-2, 1). Let's solve this equation:ax + b = -x² - x + 2Rearranging terms:x² + (a + 1)x + (b - 2) = 0This quadratic equation must have two real roots in (-2, 1). Let me denote this quadratic as Q(x) = x² + (a + 1)x + (b - 2). For Q(x) = 0 to have two real roots in (-2, 1), the following conditions must be satisfied:1. The discriminant D must be positive.2. Q(-2) > 03. Q(1) > 04. The vertex of the parabola Q(x) lies within (-2, 1)5. The minimum value of Q(x) (since the parabola opens upwards) is negative.Wait, Q(x) is x² + (a + 1)x + (b - 2). The coefficient of x² is positive, so it opens upwards. Therefore, for Q(x) = 0 to have two real roots, the discriminant must be positive, and the minimum of the parabola must be below the x-axis. However, since we want the roots to lie within (-2, 1), we need to ensure that Q(-2) > 0 and Q(1) > 0, which means that the parabola is above the x-axis at both ends of the interval, and crosses the x-axis twice within the interval. Wait, but if the parabola opens upwards and has two roots in (-2, 1), then Q(-2) and Q(1) must be positive, and the vertex must be below the x-axis.So let's write the conditions step by step.1. Discriminant D > 0:D = (a + 1)^2 - 4 * 1 * (b - 2) > 0So (a + 1)^2 - 4(b - 2) > 0 ⇒ (a + 1)^2 > 4(b - 2)2. Q(-2) > 0:Q(-2) = (-2)^2 + (a + 1)(-2) + (b - 2) = 4 - 2(a + 1) + b - 2 = 4 - 2a - 2 + b - 2 = (4 - 2 - 2) + (-2a + b) = 0 - 2a + b = b - 2a > 0 ⇒ b > 2a3. Q(1) > 0:Q(1) = 1^2 + (a + 1)(1) + (b - 2) = 1 + a + 1 + b - 2 = (1 + 1 - 2) + a + b = 0 + a + b = a + b > 0 ⇒ a + b > 04. The vertex of Q(x) is at x = -B/(2A) = -(a + 1)/2. This x-coordinate must lie between -2 and 1:-2 < -(a + 1)/2 < 1Multiply all parts by 2:-4 < -(a + 1) < 2Multiply by -1 (reverse inequalities):4 > a + 1 > -2 ⇒ -2 < a + 1 < 4 ⇒ subtract 1:-3 < a < 3But since a > 0, this gives 0 < a < 35. The minimum value of Q(x) is negative. Since the parabola opens upwards, the minimum occurs at the vertex. The y-coordinate of the vertex is Q(-(a + 1)/2). Let's compute that:Q(-(a + 1)/2) = [ ( -(a + 1)/2 )^2 ] + (a + 1)( -(a + 1)/2 ) + (b - 2)Let me compute term by term:First term: [ ( -(a + 1)/2 )^2 ] = (a + 1)^2 / 4Second term: (a + 1)( -(a + 1)/2 ) = - (a + 1)^2 / 2Third term: (b - 2)Adding them up:(a + 1)^2 / 4 - (a + 1)^2 / 2 + (b - 2) = - (a + 1)^2 / 4 + (b - 2)So the minimum value is:(b - 2) - (a + 1)^2 / 4 < 0 ⇒ b - 2 < (a + 1)^2 / 4 ⇒ b < (a + 1)^2 / 4 + 2So combining all these conditions:1. (a + 1)^2 > 4(b - 2)2. b > 2a3. a + b > 04. 0 < a < 35. b < (a + 1)^2 / 4 + 2Additionally, we need to consider the third intersection point. So the line must intersect the zero part of g(x) either at x ≤ -2 or x ≥ 1. Let's handle these cases.Case 1: Intersection at x ≥ 1 (i.e., y = ax + b = 0 at x = -b/a ≥ 1)This requires:- b/a ≥ 1 ⇒ -b ≥ a ⇒ b ≤ -aBut from condition 3, a + b > 0. If b ≤ -a, then a + b > 0 ⇒ a + b > 0 ⇒ a + (-a) = 0 > 0? Wait, that can't be. Contradiction. If b ≤ -a, then a + b ≤ 0, which contradicts condition 3 (a + b > 0). Therefore, this case is impossible. So the third intersection cannot be on the right side (x ≥ 1). Therefore, the third intersection must be on the left side (x ≤ -2).Case 2: Intersection at x ≤ -2 (i.e., y = ax + b = 0 at x = -b/a ≤ -2)This requires:- b/a ≤ -2 ⇒ -b ≤ -2a ⇒ b ≥ 2aBut from condition 2, we already have b > 2a. So this is already satisfied. Therefore, the third intersection point is at x = -b/a ≤ -2, which requires b ≥ 2a, which is already part of condition 2. However, we must also ensure that this x = -b/a is indeed ≤ -2. Since b ≥ 2a, then x = -b/a ≤ -2a/a = -2. So yes, x = -b/a ≤ -2.Therefore, the three intersection points are:1. Two points on the parabola between -2 and 1 (solutions to x² + (a + 1)x + (b - 2) = 0)2. One point on the zero part at x = -b/a ≤ -2.Therefore, combining all the conditions from the quadratic equation (to have two roots in (-2,1)) and the third intersection point, the conditions are:1. (a + 1)^2 > 4(b - 2)2. b > 2a3. a + b > 04. 0 < a < 35. b < (a + 1)^2 / 4 + 2So these inequalities define the region for (a, b). Now, let's try to represent this graphically.First, let's analyze each condition:1. (a + 1)^2 > 4(b - 2) ⇒ b < [(a + 1)^2]/4 + 2. This is a parabola opening upwards in the (a, b) plane.2. b > 2a. This is a straight line with slope 2.3. a + b > 0 ⇒ b > -a. This is a straight line with slope -1.4. 0 < a < 3. This restricts a to be between 0 and 3.5. b < [(a + 1)^2]/4 + 2. This is the same as condition 1.So the key inequalities are:- b > 2a- b > -a- b < [(a + 1)^2]/4 + 2- 0 < a < 3Now, let's find the intersection of these regions. Since a > 0, the line b > -a is automatically satisfied if b > 2a (since 2a > -a when a > 0). Wait, when a > 0, 2a > 0, so b > 2a implies b > 0, and since a > 0, -a < 0. Therefore, if b > 2a, then b is already greater than -a. So condition 3 (b > -a) is redundant here. So we can ignore condition 3.Therefore, the important conditions are:1. 0 < a < 32. b > 2a3. b < [(a + 1)^2]/4 + 2Additionally, the discriminant condition (a + 1)^2 > 4(b - 2) is equivalent to condition 3.So, the region is bounded between the lines b = 2a, the parabola b = [(a + 1)^2]/4 + 2, and a between 0 and 3.Wait, but when a approaches 3, let's check the values.At a = 3, from condition 4, a < 3, so a cannot be 3. The upper limit is approaching 3.Let me sketch this mentally. For 0 < a < 3:- The lower boundary is b = 2a.- The upper boundary is b = [(a + 1)^2]/4 + 2.Additionally, we must ensure that the upper boundary is above the lower boundary. Let's check at a = 0:At a = 0, upper boundary: [(0 + 1)^2]/4 + 2 = 1/4 + 2 = 9/4 = 2.25Lower boundary: b = 0. So at a = 0, the upper boundary is 2.25, lower boundary is 0. But since a > 0, we don't include a = 0.At a approaching 0 from the right, upper boundary approaches 2.25, lower boundary approaches 0.At a = 1:Upper boundary: (2)^2 /4 + 2 = 4/4 + 2 = 1 + 2 = 3Lower boundary: b = 2*1 = 2So the region between 2 and 3.At a = 2:Upper boundary: (3)^2 /4 + 2 = 9/4 + 2 = 17/4 = 4.25Lower boundary: 4So between 4 and 4.25At a approaching 3:Upper boundary: (4)^2 /4 + 2 = 16/4 + 2 = 4 + 2 = 6Lower boundary: 2*3 = 6So as a approaches 3, the upper and lower boundaries meet at b = 6.Therefore, the region is the area between b = 2a and b = [(a + 1)^2]/4 + 2 for 0 < a < 3. At a = 3, both boundaries meet at (3, 6). However, since a must be less than 3, the region is open at a = 3.Additionally, we should check where the parabola b = [(a + 1)^2]/4 + 2 intersects the line b = 2a. Setting them equal:2a = [(a + 1)^2]/4 + 2Multiply both sides by 4:8a = (a + 1)^2 + 8Expand the right side:a² + 2a + 1 + 8 = a² + 2a + 9Thus:a² + 2a + 9 - 8a = 0 ⇒ a² - 6a + 9 = 0 ⇒ (a - 3)^2 = 0 ⇒ a = 3Therefore, the only intersection point is at a = 3, which is the point where they meet. Hence, for 0 < a < 3, the parabola is above the line b = 2a.Therefore, the region where (a, b) lies is between the lines b = 2a and b = [(a + 1)^2]/4 + 2 for 0 < a < 3.To draw this diagram, in the (a, b)-plane:- The vertical axis is b, horizontal axis is a.- Draw the line b = 2a starting from the origin (0,0) with slope 2.- Draw the parabola b = [(a + 1)^2]/4 + 2. This is a parabola opening to the right? Wait, no. In the (a, b) plane, if we write it as b = (a + 1)^2 /4 + 2, this is a parabola that opens upwards, shifted left by 1 unit, vertically scaled by 1/4, and shifted up by 2 units. Wait, actually, in standard terms, if we consider a as the independent variable, then the equation is b = (a + 1)^2 /4 + 2. So vertex at a = -1, b = 2. But since a > 0, we are only concerned with a ≥ 0. Therefore, the portion of the parabola from a = 0 upwards. At a = 0, b = (1)^2 /4 + 2 = 1/4 + 2 = 9/4. Then it increases as a increases.Wait, but actually, when a increases, (a + 1)^2 increases, so b increases quadratically. So the parabola b = (a + 1)^2 /4 + 2 is U-shaped in the (a, b) plane, opening upwards, with vertex at a = -1, b = 2. But since a > 0, we only consider a from 0 to 3. At a = 0, it's at b = 2.25, and at a = 3, it's at b = (4)^2 /4 + 2 = 4 + 2 = 6.Therefore, in the region 0 < a < 3, the parabola starts at (0, 2.25) and goes up to (3, 6). The line b = 2a goes from (0, 0) to (3, 6). So between these two curves, for 0 < a < 3, the region is bounded above by the parabola and below by the line. Therefore, the region where (a, b) lies is the area between the line b = 2a and the parabola b = (a + 1)^2 /4 + 2 for 0 < a < 3.Additionally, since the problem mentions that a > 0, and we have 0 < a < 3 from the vertex condition, the final region is as described.Therefore, the relationship between a and b is that for each a between 0 and 3, b must lie between 2a and (a + 1)^2 /4 + 2. So the inequalities are 0 < a < 3 and 2a < b < (a + 1)^2 /4 + 2.To confirm, let's check a sample point. Take a = 1. Then b must be between 2*1 = 2 and (1 + 1)^2 /4 + 2 = 4/4 + 2 = 3. So 2 < b < 3. If we pick a = 1, b = 2.5, then the line y = x + 2.5 should intersect g(x) three times. Let's see:The parabola part is between -2 and 1. The line y = x + 2.5. Let's see where it intersects the parabola:x + 2.5 = -x² - x + 2 ⇒ x² + 2x + 0.5 = 0. Discriminant: 4 - 2 = 2 > 0, so two real roots. The roots are x = [-2 ± √2]/2 = -1 ± (√2)/2 ≈ -1 ± 0.707. So approximately -0.293 and -1.707. Wait, but the interval is between -2 and 1. So x ≈ -1.707 is within -2 and 1? Wait, -1.707 is approximately -1.7, which is greater than -2, so yes. Similarly, -0.293 is within -2 and 1. So the line intersects the parabola twice. Then the third intersection is at x = -b/a = -2.5/1 = -2.5, which is ≤ -2, so in the zero part. Therefore, three intersection points. Hence, the conditions hold.Another check at a = 2, b must be between 4 and (3)^2 /4 + 2 = 9/4 + 2 = 17/4 = 4.25. Take b = 4.1. The line y = 2x + 4.1. Intersection with parabola:2x + 4.1 = -x² - x + 2 ⇒ x² + 3x + 2.1 = 0. Discriminant: 9 - 8.4 = 0.6 > 0. Roots: [-3 ± √0.6]/2 ≈ [-3 ± 0.7746]/2 ≈ (-3 + 0.7746)/2 ≈ -1.1127 and (-3 - 0.7746)/2 ≈ -1.8873. Both roots are between -2 and 1. Then third intersection at x = -4.1/2 = -2.05 ≤ -2. Therefore, three points. Correct.Therefore, the region is indeed between b = 2a and b = (a + 1)^2 /4 + 2 for 0 < a < 3.Final Answer(1) The analytical expression of ( g(x) ) is (boxed{g(x) = begin{cases} -x^2 - x + 2 & text{if } -2 < x < 1, 0 & text{otherwise}. end{cases}})(2) The relationship between ( a ) and ( b ) is given by ( 2a < b < frac{(a + 1)^2}{4} + 2 ) for ( 0 < a < 3 ). The region where the point ( (a, b) ) lies is the area between the line ( b = 2a ) and the parabola ( b = frac{(a + 1)^2}{4} + 2 ) for ( 0 < a < 3 ).boxed{2a < b < frac{(a + 1)^2}{4} + 2 text{ for } 0 < a < 3}</think>Given the function ( f(x) = x^2 + x - 2 ):(1) To find the analytical expression of the function ( g(x) = frac{|f(x)| - f(x)}{2} ):- The function ( |f(x)| ) is equal to ( f(x) ) when ( f(x) geq 0 ) and ( -f(x) ) when ( f(x) < 0 ).- Solving ( f(x) < 0 ), we find the roots of ( f(x) = 0 ) are ( x = -2 ) and ( x = 1 ). Since the parabola opens upwards, ( f(x) < 0 ) for ( -2 < x < 1 ).- Therefore, ( g(x) = frac{|f(x)| - f(x)}{2} ) is equal to ( -f(x) ) when ( -2 < x < 1 ) and 0 otherwise.The analytical expression for ( g(x) ) is:[boxed{g(x) = begin{cases} -x^2 - x + 2 & text{if } -2 < x < 1, 0 & text{otherwise}.end{cases}}](2) To determine the relationship between ( a ) and ( b ) when the line ( y = ax + b ) intersects the curve ( y = g(x) ) at three different points (with ( a > 0 )):- The line intersects the parabola part of ( g(x) ) (between ( -2 ) and ( 1 )) twice and the zero part once.- The quadratic equation ( x^2 + (a + 1)x + (b - 2) = 0 ) must have two real roots in ( (-2, 1) ).- The conditions for this are: 1. The discriminant ( (a + 1)^2 > 4(b - 2) ) 2. ( b > 2a ) 3. ( a + b > 0 ) 4. The vertex of the quadratic lies within ( (-2, 1) ) 5. The minimum value of the quadratic is negative.- Additionally, the line must intersect the zero part of ( g(x) ) at ( x leq -2 ), leading to ( b geq 2a ).Combining these conditions, the relationship between ( a ) and ( b ) is:[boxed{2a < b < frac{(a + 1)^2}{4} + 2 text{ for } 0 < a < 3}]The region where the point ( (a, b) ) lies is bounded by the line ( b = 2a ) and the parabola ( b = frac{(a + 1)^2}{4} + 2 ) for ( 0 < a < 3 ).]

🔑:left{begin{array}{l}-20, -20, varphi(1)>0 .end{array}right.i.e., left{begin{array}{l}b<2 a, b>-a .end{array}right.Given that a>0, therefore, 2 a<b<frac{1}{4}(a+1)^{2}+2, and 0<a<3 is the solution.The point (a, b) with coordinates a and b lies in the shaded area of the graph on the right (excluding the boundary).

🧠:[<think>Okay, let's see. I need to find the area of triangle ABC. They told me that the angle bisector of angle ABC intersects side AC at point K. Also, BC is 2 units long, KC is 1 unit, and BK is (3√2)/2. Hmm, angle bisector... so maybe the Angle Bisector Theorem applies here?First, the Angle Bisector Theorem states that an angle bisector divides the opposite side into segments proportional to the adjacent sides. So, in this case, since BK is the angle bisector of angle ABC, it should divide AC into segments AK and KC such that AB/BC = AK/KC. Wait, BC is given as 2, and KC is 1. So, AB/2 = AK/1. Which means AB = 2*AK. Therefore, AK = AB/2. But I don't know AB yet. Maybe I can find AB somehow?But let's see. They also gave me BK, which is the length of the angle bisector. There's a formula for the length of an angle bisector in a triangle. Let me recall that. The formula is: If in triangle ABC, the angle bisector from B meets AC at K, then BK = (2ac/(a + c)) * cos(theta/2), where theta is angle at B, and a and c are the lengths of the sides adjacent to B. Wait, not sure if I remember correctly. Alternatively, there's a formula for the length of the angle bisector: BK^2 = AB*BC - AK*KC. Is that right?Wait, let me check. The formula for the length of an angle bisector is: If an angle bisector from vertex B splits side AC into segments of length m and n (so AK = m, KC = n), then the length of the bisector BK is given by:BK = (2ac/(a + c)) * cos(theta/2)But maybe there's another formula that relates BK to the sides. Alternatively, there's the formula from the Law of Cosines in the two triangles ABK and CBK.Since BK is the angle bisector, angles ABK and CBK are equal. Let's denote angle ABK = angle CBK = theta/2. Then in triangle ABK and triangle CBK, we can apply the Law of Cosines.But first, let's note the given information:- BC = 2- KC = 1- BK = 3√2/2Since KC = 1, then AK = ? Let me use the Angle Bisector Theorem first. AB/BC = AK/KC. So AB/2 = AK/1, so AK = AB/2. Therefore, AC = AK + KC = AB/2 + 1.So AC is expressed in terms of AB. Let me denote AB as x. Then AK = x/2, AC = x/2 + 1.Now, maybe I can use Stewart's Theorem here. Stewart's Theorem relates the lengths of the sides of a triangle to the length of a cevian. The formula is: b^2m + c^2n = a(d^2 + mn), where a, b, c are the sides of the triangle, m and n are the segments into which the cevian divides the opposite side, and d is the length of the cevian.In this case, the cevian is BK, which divides AC into AK = x/2 and KC = 1. The sides of the triangle are AB = x, BC = 2, and AC = x/2 + 1. Then applying Stewart's Theorem:AB^2 * KC + BC^2 * AK = AC * (BK^2 + AK * KC)Plugging in the known values:x^2 * 1 + 2^2 * (x/2) = (x/2 + 1) * [( (3√2)/2 )^2 + (x/2 * 1 ) ]Let me compute each part step by step.Left side: x^2 * 1 + 4 * (x/2) = x^2 + 2xRight side: (x/2 + 1) * [ (9*2)/4 + x/2 ]Simplify the right side:First, compute (3√2/2)^2: (9*2)/4 = 18/4 = 9/2Then, AK * KC = (x/2)*1 = x/2So the term inside the brackets is 9/2 + x/2Therefore, right side becomes: (x/2 + 1) * (9/2 + x/2 )Let me write it as:( (x + 2)/2 ) * ( (9 + x)/2 ) = [ (x + 2)(x + 9) ] / 4Wait, no, actually:Wait, (x/2 + 1) is equal to (x + 2)/2, and (9/2 + x/2) is equal to (x + 9)/2. So multiplying those two gives (x + 2)(x + 9)/4.Therefore, right side is (x + 2)(x + 9)/4Left side is x^2 + 2xSo equation is:x^2 + 2x = (x + 2)(x + 9)/4Multiply both sides by 4 to eliminate denominator:4x^2 + 8x = (x + 2)(x + 9)Expand the right side:x^2 + 9x + 2x + 18 = x^2 + 11x + 18So equation becomes:4x^2 + 8x = x^2 + 11x + 18Subtract x^2 + 11x + 18 from both sides:4x^2 +8x -x^2 -11x -18 =0Simplify:3x^2 -3x -18 =0Divide both sides by 3:x^2 -x -6 =0Factor quadratic equation:x^2 -x -6 = (x -3)(x +2) =0Solutions: x=3 or x=-2. Since length can't be negative, x=3. Therefore, AB=3.So AB=3, BC=2, and from Angle Bisector Theorem, AK= AB/2 = 3/2, KC=1, so AC= AK + KC= 3/2 +1=5/2.Now, we need to find the area of triangle ABC. For that, maybe we can use Heron's formula? To use Heron's formula, we need all three sides.We have AB=3, BC=2, and AC=5/2.Compute semi-perimeter: s= (3 +2 +5/2)/2= (5 +5/2)/2= (15/2)/2=15/4Then area= sqrt[s(s - AB)(s - BC)(s - AC)]Compute each term:s=15/4s - AB=15/4 -3=15/4 -12/4=3/4s - BC=15/4 -2=15/4 -8/4=7/4s - AC=15/4 -5/2=15/4 -10/4=5/4Therefore, area= sqrt[15/4 * 3/4 *7/4 *5/4 ]= sqrt[(15*3*7*5)/(4^4)]= sqrt[(15*3*7*5)/256]Compute numerator: 15*3=45, 45*5=225, 225*7=1575So sqrt[1575/256] = sqrt[1575]/16Simplify sqrt[1575]. Let's factor 1575: 25*63=25*9*7=225*7. So sqrt[225*7]=15√7Therefore, area=15√7 /16Wait, but this contradicts the given information about BK=3√2/2. Because if Heron's formula gives area as 15√7 /16, but maybe that's not the case? Wait, but maybe Heron's formula is correct here. Let me check again.Wait, hold on. If we have AB=3, BC=2, AC=5/2, then using Heron's formula, area is sqrt[s(s - a)(s - b)(s - c)].But let me compute it again:s = (3 + 2 + 2.5)/2 = (7.5)/2 = 3.75 = 15/4s - AB = 15/4 -3= 15/4 -12/4=3/4s - BC=15/4 -2=15/4 -8/4=7/4s - AC=15/4 -5/2=15/4 -10/4=5/4So product: 15/4 *3/4 *7/4 *5/4= (15*3*7*5)/(4^4)= (15*105)/256= 1575/256sqrt(1575/256)=sqrt(1575)/16. sqrt(1575)=sqrt(25*63)=5*sqrt(63)=5*sqrt(9*7)=5*3*sqrt(7)=15*sqrt(7). Therefore, sqrt(1575)/16=15√7/16.But wait, according to this, the area is 15√7/16. But let's see if this is consistent with the given BK=3√2/2. Because if we have other information, like the length of the angle bisector, maybe there's a mistake here.Alternatively, maybe Heron's formula is correct, but I need to verify. Let's see. Alternatively, perhaps using coordinates.Alternatively, maybe use the formula for the area in terms of the angle bisector. Wait, but how?Alternatively, let's use the Law of Cosines in triangle ABK and CBK. Since BK is the angle bisector, angles at B are equal in both triangles.Let me denote angle ABK=angle KBC=θ. Then in triangle ABK, sides are AB=3, BK=3√2/2, and AK=3/2. Then using the Law of Cosines in triangle ABK:AK^2 = AB^2 + BK^2 - 2*AB*BK*cos(theta)So (3/2)^2 =3^2 + (3√2/2)^2 -2*3*(3√2/2)*cos(theta)Compute each term:Left side: 9/4Right side:9 + (9*2)/4 - 2*3*(3√2/2)*cos(theta)Simplify right side:9 + 18/4 - (18√2/2)*cos(theta)Which is 9 + 9/2 -9√2 cos(theta)= (18/2 +9/2) -9√2 cos(theta)=27/2 -9√2 cos(theta)So equation is:9/4 =27/2 -9√2 cos(theta)Subtract 27/2 from both sides:9/4 -27/2 = -9√2 cos(theta)Compute left side: 9/4 -54/4 = (-45)/4Therefore:-45/4 = -9√2 cos(theta)Divide both sides by -9√2:(45/4)/(9√2)= cos(theta)Simplify 45/4 divided by 9 is 5/4, so 5/(4√2)=cos(theta)Rationalizing the denominator:5√2/8 =cos(theta)So cos(theta)=5√2/8Similarly, in triangle KBC, sides are BC=2, BK=3√2/2, KC=1. Apply Law of Cosines:KC^2=BC^2 + BK^2 -2*BC*BK*cos(theta)1^2=2^2 + (3√2/2)^2 -2*2*(3√2/2)*cos(theta)Compute left side:1Right side:4 + (9*2)/4 -2*2*(3√2/2)*cos(theta)Simplify:4 + 18/4 - (12√2/2)*cos(theta)=4 +9/2 -6√2 cos(theta)= (8/2 +9/2) -6√2 cos(theta)=17/2 -6√2 cos(theta)Set equal to 1:1=17/2 -6√2 cos(theta)Subtract 17/2:1 -17/2= -6√2 cos(theta)Left side: -15/2= -6√2 cos(theta)Divide both sides by -6√2:(15/2)/(6√2)= cos(theta)Simplify: 15/(12√2)=5/(4√2)=5√2/8, same as before. So cos(theta)=5√2/8. So that's consistent.Therefore, the angle theta is the same in both triangles, which makes sense since BK is the angle bisector. So that checks out.But how does this help with the area of triangle ABC? Well, perhaps we can find the area by using the formula (1/2)*ab*sin(C). If we can find angle at B, then the area would be (1/2)*AB*BC*sin(angle ABC). Since angle ABC is 2 theta (since the angle bisector divides it into two angles of theta each). So angle ABC=2 theta. Then sin(2 theta)=2 sin(theta)cos(theta). If we can find sin(theta), then we can compute sin(2 theta).We already know cos(theta)=5√2/8. So sin(theta)=sqrt(1 -cos^2(theta))=sqrt(1 - (25*2)/64)=sqrt(1 -50/64)=sqrt(14/64)=sqrt(14)/8.Therefore, sin(theta)=sqrt(14)/8.Then sin(2 theta)=2*(sqrt(14)/8)*(5√2/8)=2*(5√28)/64=10*√28 /64. Simplify √28=2√7, so 10*2√7 /64=20√7/64=5√7/16.Therefore, sin(angle ABC)=5√7/16. Then area of triangle ABC is (1/2)*AB*BC*sin(angle ABC)= (1/2)*3*2*(5√7/16)= (3)*(5√7/16)=15√7/16. Which matches the result from Heron's formula. So that's consistent.But wait, the problem is giving BK=3√2/2. But according to this, the area is 15√7/16. However, 15√7/16 is approximately 15*2.6458/16 ≈ 39.687/16 ≈2.48. Let me check with Heron's formula again. The sides are 3, 2, and 2.5. Let me compute the area with another approach.Alternatively, using coordinates. Let me place point B at the origin (0,0). Let me let BC be along the x-axis. So point C is at (2,0). Then point K is somewhere on AC. Since KC=1, and AC=2.5, then AK=1.5. So AC is split into AK=1.5 and KC=1. Coordinates of A: Let me assume point A is at (x,y). Then AC is from A(x,y) to C(2,0), and K divides AC in the ratio AK:KC=1.5:1=3:2. Therefore, coordinates of K can be found by section formula: K=( (2* x +3*2)/ (3+2), (2* y +3*0)/5 )=( (2x +6)/5, 2y/5 )But BK is the angle bisector, which we know the coordinates of B(0,0) and K. So coordinates of K are ((2x +6)/5, 2y/5). The length BK is given as 3√2/2. So compute distance from B(0,0) to K:sqrt[ ((2x +6)/5 -0)^2 + (2y/5 -0)^2 ] = sqrt[ ( (2x +6)^2 + (2y)^2 ) /25 ]= (1/5)sqrt( (2x +6)^2 + (2y)^2 )This equals 3√2/2. Therefore:(1/5)sqrt( (2x +6)^2 + (2y)^2 )=3√2/2Multiply both sides by 5:sqrt( (2x +6)^2 + (2y)^2 )=(15√2)/2Square both sides:(2x +6)^2 + (2y)^2=(225*2)/4=450/4=225/2Divide both sides by 4:(x +3)^2 + y^2=225/8So equation (1): (x +3)^2 + y^2=225/8Additionally, we know that the coordinates of A(x,y) and C(2,0) form the side AC with length 5/2. The distance from A to C is 5/2:sqrt( (x -2)^2 + y^2 )=5/2Square both sides:(x -2)^2 + y^2=25/4So equation (2): (x -2)^2 + y^2=25/4Now, subtract equation (2) from equation (1):[(x +3)^2 + y^2] - [(x -2)^2 + y^2] =225/8 -25/4Compute left side:(x +3)^2 - (x -2)^2= [x^2 +6x +9] -[x^2 -4x +4]=x^2 +6x +9 -x^2 +4x -4=10x +5Right side:225/8 -50/8=175/8So 10x +5=175/8Subtract 5:10x=175/8 -40/8=135/8Divide by 10:x=135/80=27/16So x=27/16. Then substitute back into equation (2):(27/16 -2)^2 + y^2=25/4Compute 27/16 -32/16= -5/16So (-5/16)^2 + y^2=25/425/256 + y^2=25/4Subtract 25/256:y^2=25/4 -25/256= (1600/256 -25/256)=1575/256Thus y= sqrt(1575/256)= (sqrt(1575))/16=15√7/16 (as before). So coordinates of A are (27/16, 15√7/16)Then area of triangle ABC can be found using the coordinates:Points B(0,0), C(2,0), A(27/16,15√7/16)Area is |(Ax(By - Cy) + Bx(Cy - Ay) + Cx(Ay - By))/2|Plugging in:Ax=27/16, Ay=15√7/16Bx=0, By=0Cx=2, Cy=0Compute:(27/16)(0 -0) +0*(0 -15√7/16) +2*(15√7/16 -0)/2Wait, formula is |[Ax(By - Cy) + Bx(Cy - Ay) + Cx(Ay - By)] / 2|Compute each term:Ax*(By - Cy)= (27/16)*(0 -0)=0Bx*(Cy - Ay)=0*(0 -15√7/16)=0Cx*(Ay - By)=2*(15√7/16 -0)=2*(15√7/16)=30√7/16=15√7/8Sum:0 +0 +15√7/8=15√7/8Take absolute value and divide by 2:|15√7/8| /2=15√7/16Which matches the previous result. So area is indeed 15√7/16.Wait, but the problem states that BK=3√2/2. But according to our calculations, the coordinates of K can be computed.From earlier, K=((2x +6)/5, 2y/5). x=27/16, y=15√7/16. Therefore:K=( (2*(27/16) +6)/5, 2*(15√7/16)/5 )Compute 2*(27/16)=54/16=27/8. 27/8 +6=27/8 +48/8=75/8. So first coordinate:75/8 divided by5=75/(8*5)=15/8.Second coordinate:2*(15√7/16)/5=30√7/(16*5)=30√7/80=3√7/8.Therefore, K is at (15/8,3√7/8). Then distance BK is sqrt( (15/8)^2 + (3√7/8)^2 )Compute (15/8)^2=225/64, (3√7/8)^2=9*7/64=63/64. Sum:225+63=288, over 64. sqrt(288/64)=sqrt(4.5)=sqrt(9/2)=3/√2=3√2/2. Which matches the given BK=3√2/2. So that checks out. Therefore, everything is consistent.Therefore, the area is 15√7/16.But wait, the problem is given in the category of "The Law of Cosines" and "The ratio in which the bisector divides the side". So maybe there's an alternative way using the Law of Cosines directly. Let me check.Alternatively, since we found AB=3, BC=2, AC=5/2. Wait, but 3, 2, 2.5. Let me check if triangle with sides 3, 2, 2.5 is valid. The sum of any two sides must be greater than the third.3 +2=5 >2.5, 3 +2.5=5.5>2, 2 +2.5=4.5>3. So yes, valid.Alternatively, use Law of Cosines to find one angle, then compute area.For example, using sides AB=3, BC=2, AC=5/2.Let me compute angle at B.Law of Cosines: AC²=AB² + BC² -2*AB*BC*cos(angle ABC)(5/2)^2=3^2 +2^2 -2*3*2*cos(angle ABC)Compute:25/4=9 +4 -12 cos(angle ABC)25/4=13 -12 cos(angle ABC)Subtract 13:25/4 -13= -12 cos(angle ABC)25/4 -52/4= -27/4= -12 cos(angle ABC)Divide both sides by -12:(-27/4)/(-12)=27/(48)=9/16=cos(angle ABC)Therefore, cos(angle ABC)=9/16Therefore, sin(angle ABC)=sqrt(1 -81/256)=sqrt(175/256)=5√7/16Therefore, area=1/2*AB*BC*sin(angle ABC)=1/2*3*2*(5√7/16)=15√7/16. Same as before.So yes, all methods lead to the same area. Therefore, the answer is 15√7⁄16. So in boxed form: boxed{dfrac{15sqrt{7}}{16}}Final Answerboxed{dfrac{15sqrt{7}}{16}}</think>In triangle (ABC), the angle bisector of (angle ABC) intersects side (AC) at point (K). Given (BC = 2), (KC = 1), and (BK = frac{3sqrt{2}}{2}), we need to find the area of triangle (ABC).1. Using the Angle Bisector Theorem: - The theorem states (frac{AB}{BC} = frac{AK}{KC}). - Given (BC = 2) and (KC = 1), we have (frac{AB}{2} = frac{AK}{1}), implying (AK = frac{AB}{2}). - Let (AB = x). Then (AK = frac{x}{2}) and (AC = frac{x}{2} + 1).2. Applying Stewart's Theorem: - Stewart's Theorem: (AB^2 cdot KC + BC^2 cdot AK = AC cdot (BK^2 + AK cdot KC)). - Substituting the known values: (x^2 cdot 1 + 2^2 cdot frac{x}{2} = left(frac{x}{2} + 1right) left(left(frac{3sqrt{2}}{2}right)^2 + frac{x}{2} cdot 1right)). - Simplifying leads to the quadratic equation (3x^2 - 3x - 18 = 0), solving gives (x = 3) (since (x = -2) is invalid).3. Sides of Triangle (ABC): - (AB = 3), (BC = 2), (AC = frac{5}{2}).4. Using Heron's Formula: - Semi-perimeter (s = frac{3 + 2 + frac{5}{2}}{2} = frac{15}{4}). - Area: (sqrt{s(s - AB)(s - BC)(s - AC)} = sqrt{frac{15}{4} cdot frac{3}{4} cdot frac{7}{4} cdot frac{5}{4}} = frac{15sqrt{7}}{16}).5. Verification Using Law of Cosines: - Calculate (cos(angle ABC)) and (sin(angle ABC)) using Law of Cosines and verify the area using (frac{1}{2} cdot AB cdot BC cdot sin(angle ABC)).Final area of triangle (ABC) is (boxed{dfrac{15sqrt{7}}{16}}).,<think>Okay, so I need to find the area of triangle ABC. Let me start by visualizing the triangle. We have triangle ABC with angle bisector BK, which intersects AC at point K. Given that BC is 2 units, KC is 1 unit, and BK is (3√2)/2. The goal is to find the area of triangle ABC. Hmm, okay.First, since BK is the angle bisector of angle ABC, by the Angle Bisector Theorem, the ratio of the adjacent sides should be equal to the ratio of the divided segments on side AC. The Angle Bisector Theorem states that AB/BC = AK/KC. Wait, let me confirm that. The Angle Bisector Theorem says that the angle bisector divides the opposite side into segments proportional to the adjacent sides. So in this case, since the bisector is from B to AC, then AB/BC = AK/KC. Yes, that's right.But we know BC is 2, and KC is 1. Let's denote AK as x. Then, according to the Angle Bisector Theorem, AB/2 = x/1. So AB = 2x. So AB is twice as long as AK. That's useful information.Now, we need to relate this to the length of BK, which is given as (3√2)/2. Maybe we can use the formula for the length of an angle bisector in a triangle. There's a formula that relates the length of the angle bisector to the sides of the triangle. Let me recall that formula.The formula for the length of an angle bisector from angle B is: BK = (2AB*BC*cos(theta/2)) / (AB + BC),where theta is angle ABC. Wait, is that right? Or maybe another formula. Alternatively, there's a formula in terms of the sides of the triangle. Let me check.Another formula for the length of an angle bisector is:BK² = AB*BC - AK*KC.Wait, is that correct? Let me verify. I think the formula is: (length of bisector)^2 = AB*BC - AK*KC. Let me check with Stewart's Theorem. Stewart's Theorem relates the length of a cevian (here, BK) to the lengths of the sides of the triangle. Stewart's Theorem states that:AB²*KC + BC²*AK = BK²*AC + AK*KC*AC.Yes, that's Stewart's Theorem. Let me write that down. In this case, AB, BC, and BK are known in terms of x and the given values. Let's assign variables:Let’s denote AK = x, so KC = 1 (given). Therefore, AC = AK + KC = x + 1.From the Angle Bisector Theorem: AB/BC = AK/KC => AB/2 = x/1 => AB = 2x. So AB = 2x, BC = 2, KC =1, AK =x, AC =x +1.Now, applying Stewart's Theorem:AB²*KC + BC²*AK = BK²*AC + AK*KC*AC.Plugging in the values:(2x)²*1 + (2)²*x = ( (3√2)/2 )²*(x +1) + x*1*(x +1).Calculating each term:Left side: (4x²)*1 + 4*x = 4x² + 4x.Right side: (9*2)/4*(x +1) + x(x +1) = (18/4)(x +1) + x² +x = (9/2)(x +1) + x² +x.Simplify right side:(9/2)x + 9/2 + x² + x = x² + (9/2x + x) + 9/2 = x² + (11/2)x + 9/2.So equation is:4x² + 4x = x² + (11/2)x + 9/2.Multiply both sides by 2 to eliminate denominators:8x² + 8x = 2x² + 11x + 9.Bring all terms to left side:8x² +8x -2x² -11x -9 = 0 => 6x² -3x -9 =0.Simplify equation:Divide all terms by 3: 2x² -x -3 =0.Solve quadratic equation 2x² -x -3 =0.Using quadratic formula: x = [1 ± √(1 +24)] /4 = [1 ±5]/4.Solutions: (1 +5)/4 =6/4=3/2, and (1-5)/4= -4/4=-1. Since length can't be negative, x=3/2.So AK = x =3/2, and AB=2x=3.So AB=3, BC=2, and AC= AK + KC =3/2 +1=5/2.Now we have triangle ABC with sides AB=3, BC=2, and AC=5/2. Wait, but before proceeding, let me verify that these lengths satisfy Stewart's Theorem. Let me check with x=3/2.Left side: AB²*KC + BC²*AK = (3)^2*1 + (2)^2*(3/2) =9*1 +4*(3/2)=9 +6=15.Right side: BK²*AC + AK*KC*AC = ( (9*2)/4 )*(5/2) + (3/2)*1*(5/2) = (18/4)*(5/2) + (15/4) = (90/8) + (15/4) = (45/4) + (15/4) =60/4=15.Yes, both sides equal 15. So that checks out. So the sides are correct.Now, we need to find the area of triangle ABC with sides AB=3, BC=2, and AC=5/2. Hmm, but wait, maybe we can use Heron's formula? Let's see.Heron's formula requires knowing all three sides. Let's compute the semi-perimeter:s = (AB + BC + AC)/2 = (3 + 2 + 5/2)/2 = (5 +5/2)/2 = (15/2)/2 =15/4=3.75.Then the area would be sqrt[s(s - AB)(s - BC)(s - AC)].Compute each term:s - AB =15/4 -3=15/4 -12/4=3/4,s - BC=15/4 -2=15/4 -8/4=7/4,s - AC=15/4 -5/2=15/4 -10/4=5/4.So area= sqrt[(15/4)(3/4)(7/4)(5/4)].Multiply them out:(15*3*7*5)/(4^4)= (15*3*7*5)/256.15*3=45, 45*7=315, 315*5=1575. So 1575/256. Then sqrt(1575/256)=sqrt(1575)/16.Simplify sqrt(1575). Let's factor 1575: 1575=25*63=25*9*7. So sqrt(25*9*7)=5*3*sqrt(7)=15√7. Therefore, area=15√7/16.Wait, but this gives area as 15√7/16. However, this seems a bit complicated. Let me check if this is correct. Alternatively, perhaps there's another method using coordinates or trigonometry.Wait, but before that, let me verify Heron's formula result. Let me check the calculations again.s =15/4, correct.s - AB=3/4, s - BC=7/4, s - AC=5/4. Correct.Then product s(s - AB)(s - BC)(s - AC)= (15/4)(3/4)(7/4)(5/4)=15*3*7*5/(4^4)=15*105/256=1575/256. Square root is sqrt(1575)/16=15√7/16. So that's correct.But maybe the answer is different? Maybe I made a wrong assumption. Wait, but according to Stewart's Theorem, we found x=3/2, so AB=3, BC=2, AC=5/2. So these are the sides. Then area via Heron's formula is 15√7/16. Hmm.Alternatively, maybe using the Law of Cosines. Wait, but given that we have BK, which is an angle bisector, perhaps there's another way. Maybe using coordinates. Let me try that approach.Let's place point B at the origin (0,0). Let me denote angle at B, which is angle ABC. The bisector BK meets AC at K, with KC=1, AK=3/2, so AC=5/2.But to set coordinates, maybe assign coordinates to points. Let me try.Let’s place point B at (0,0). Let’s let point C be along the x-axis at (2,0), since BC=2. Then point A is somewhere in the plane. The angle bisector from B to AC meets AC at K. We know KC=1, so since AC=5/2, AK=3/2. Therefore, coordinates of K can be determined once we have coordinates of A. But maybe this is getting complicated. Alternatively, let me use vectors or coordinate geometry.Alternatively, since BK is given as (3√2)/2, maybe we can use the formula for the area in terms of the angle bisector. Wait, but perhaps using the Law of Cosines in triangle BKC or something.Wait, let's think about triangle BKC. We have BC=2, KC=1, BK=3√2/2. Maybe we can apply the Law of Cosines in triangle BKC to find angle at K or something.In triangle BKC:Sides: BK=3√2/2, KC=1, BC=2.Law of Cosines: BC² = BK² + KC² - 2*BK*KC*cos(theta), where theta is angle at K.Wait, but angle at K in triangle BKC is angle BKC. Let's compute that.So:2² = (3√2/2)² +1² -2*(3√2/2)*1*cos(angle BKC).Calculate:Left side: 4.Right side: (9*2)/4 +1 - 2*(3√2/2)*cos(angle BKC) = (18/4 +4/4) - 3√2*cos(angle BKC) = (22/4) -3√2 cos(angle BKC) = 11/2 -3√2 cos(angle BKC).Set equal to 4:11/2 -3√2 cos(angle BKC) =4.Subtract 11/2:-3√2 cos(angle BKC) =4 -11/2= -3/2.Divide both sides by -3√2:cos(angle BKC)= (-3/2)/(-3√2)= (1/2)/√2=1/(2√2)=√2/4.Therefore, angle BKC= arccos(√2/4). Hmm, not sure if that helps directly. Maybe angle at K is related to angle at B in triangle ABC? Not sure.Alternatively, maybe using the area formula with sides and angles. Let me think. If we can find angle at B, then area would be (1/2)*AB*BC*sin(angle ABC). Since we know AB=3, BC=2, so area would be (1/2)*3*2*sin(theta)=3 sin(theta). So if we can find theta, the angle at B, then we can find the area.Alternatively, maybe using the angle bisector length formula. The length of the angle bisector can be related to the sides and the angle. Wait, we have formula for the length of the angle bisector:BK = (2AB*BC*cos(theta/2))/(AB + BC).Wait, let me check. The formula for the length of an angle bisector from angle B is:BK = (2AB*BC*cos(theta/2)) / (AB + BC).We have AB=3, BC=2, BK=3√2/2. So plugging in:3√2/2 = (2*3*2*cos(theta/2))/(3 + 2).Simplify denominator: 5.Numerator: 12 cos(theta/2).So:3√2/2 = (12 cos(theta/2))/5.Multiply both sides by 5:(15√2)/2 =12 cos(theta/2).Divide both sides by 12:cos(theta/2)= (15√2)/24 = (5√2)/8.Therefore, theta/2 = arccos(5√2/8).Then theta = 2 arccos(5√2/8). Then sin(theta) can be found using double-angle formula.sin(theta) = 2 sin(theta/2) cos(theta/2).But we need sin(theta/2). Since cos(theta/2)=5√2/8, then sin(theta/2)=sqrt(1 - (5√2/8)^2).Compute (5√2/8)^2=25*2/64=50/64=25/32.Therefore, sin(theta/2)=sqrt(1 -25/32)=sqrt(7/32)=√14/8.Then sin(theta)=2*(√14/8)*(5√2/8)=2*(5√28)/64=2*(5*2√7)/64=20√7/64=5√7/16.Therefore, area=3 sin(theta)=3*(5√7/16)=15√7/16.So that matches the Heron's formula result. So the area is 15√7/16.But let me check if this makes sense. Alternatively, maybe there's another way using coordinates.Let me try coordinate geometry. Let me place point B at (0,0), point C at (2,0). Then AC is a line segment of length 5/2, with point K dividing it such that KC=1 and AK=3/2. So the coordinates of K can be found if we know coordinates of A and C. Wait, but we don't know coordinates of A yet.Alternatively, since BK is an angle bisector, and we know the coordinates of B, K, and C, maybe we can find coordinates of A.Wait, but point K is on AC. Let's suppose coordinates of A are (x,y). Then coordinates of K can be found by section formula. Since AK:KC=3/2:1=3:2, so point K divides AC in the ratio 3:2. Therefore, coordinates of K are [(2*x +3*2)/(3+2), (2*y +3*0)/(3+2)] = [(2x +6)/5, (2y)/5]. Wait, is that right? Wait, if point K divides AC such that AK:KC=3:2, then coordinates of K are ( (2*C +3*A)/ (3+2) ). Wait, section formula: if a point divides a segment between points A and C in the ratio m:n, then coordinates are (n*A +m*C)/(m +n). So here, AK:KC=3:2, so m=3, n=2. Therefore, coordinates of K would be (2*A +3*C)/5.Therefore, if A is (x,y) and C is (2,0), then K is (2x +6)/5, (2y)/5. But we also know that BK has coordinates from B(0,0) to K( (2x +6)/5, (2y)/5 ). The length BK is (3√2)/2.So the distance from B(0,0) to K is sqrt[ ((2x +6)/5 -0)^2 + ((2y)/5 -0)^2 ]= sqrt[ ( (2x +6)^2 + (2y)^2 )/25 ]= (1/5)sqrt( (2x +6)^2 + (2y)^2 )= (3√2)/2.Multiply both sides by 5:sqrt( (2x +6)^2 + (2y)^2 )= (15√2)/2.Square both sides:(2x +6)^2 + (2y)^2 = (225*2)/4=450/4=225/2.Simplify left side:4x² +24x +36 +4y²=225/2.Divide both sides by 4:x² +6x +9 + y²=225/8.So x² + y² +6x +9 =225/8.But also, AC has length 5/2. Since A is (x,y) and C is (2,0), the distance AC is sqrt( (x -2)^2 + y^2 )=5/2.Therefore:(x -2)^2 + y²=25/4.Expand:x² -4x +4 + y²=25/4.So x² + y² -4x +4=25/4.Let me call this equation (1): x² + y² -4x =25/4 -4=25/4 -16/4=9/4.From the previous equation from BK length:x² + y² +6x +9=225/8.Let me call this equation (2): x² + y² +6x=225/8 -9=225/8 -72/8=153/8.Now subtract equation (1) from equation (2):(x² + y² +6x) - (x² + y² -4x)=153/8 -9/4.Simplify left side:10x.Right side:153/8 -18/8=135/8.Therefore,10x=135/8 =>x=135/(8*10)=27/16≈1.6875.Now plug x=27/16 into equation (1):x² + y² -4x=9/4.Compute x²: (27/16)^2=729/256.-4x= -4*(27/16)= -108/16= -27/4.So:729/256 + y² -27/4=9/4.Bring constants to right side:y²=9/4 -729/256 +27/4.Compute 9/4 +27/4=36/4=9.So y²=9 -729/256.Convert 9 to 2304/256:y²=2304/256 -729/256=1575/256.Therefore, y=±√(1575/256)=±(15√7)/16.So coordinates of A are (27/16, 15√7/16) or (27/16, -15√7/16). Since area is a positive quantity, the sign doesn't matter. Let's take positive y.Therefore, coordinates of A are (27/16,15√7/16). Now, compute the area of triangle ABC. With coordinates of A(27/16,15√7/16), B(0,0), and C(2,0).The area can be calculated using the formula:Area= (1/2)| (x_A(y_B - y_C) + x_B(y_C - y_A) + x_C(y_A - y_B)) |.Since B and C are on the x-axis, y_B=y_C=0, so formula simplifies to:Area= (1/2)|x_A*(0 -0) +0*(0 - y_A) +2*(y_A -0)|= (1/2)|0 +0 +2y_A|= (1/2)*2|y_A|=|y_A|.Therefore, Area= |15√7/16|=15√7/16. Which matches the previous results. So the area is indeed 15√7/16.Therefore, the answer is 15√7⁄16. But let me check once again. Wait, 15√7 over 16? Yes, that's what we got from all three methods: Heron's formula, angle bisector with Law of Cosines, and coordinate geometry. So that must be the correct answer. Final AnswerThe area of triangle (ABC) is boxed{dfrac{15sqrt{7}}{16}}.</think>In triangle (ABC), the angle bisector of (angle ABC) intersects side (AC) at point (K). Given (BC = 2), (KC = 1), and (BK = frac{3sqrt{2}}{2}), we need to find the area of triangle (ABC).1. Angle Bisector Theorem: By the Angle Bisector Theorem, (frac{AB}{BC} = frac{AK}{KC}). Let (AK = x). Then (AB = 2x) and (AC = x + 1).2. Stewart's Theorem: Applying Stewart's Theorem to triangle (ABC) with cevian (BK): [ AB^2 cdot KC + BC^2 cdot AK = BK^2 cdot AC + AK cdot KC cdot AC ] Substituting the known values: [ (2x)^2 cdot 1 + 2^2 cdot x = left(frac{3sqrt{2}}{2}right)^2 cdot (x + 1) + x cdot 1 cdot (x + 1) ] Simplifying both sides, we solve the quadratic equation and find (x = frac{3}{2}). Thus, (AB = 3), (AK = frac{3}{2}), and (AC = frac{5}{2}).3. Heron's Formula: Using Heron's formula for the area of triangle (ABC) with sides (AB = 3), (BC = 2), and (AC = frac{5}{2}): - Semi-perimeter (s = frac{3 + 2 + frac{5}{2}}{2} = frac{15}{4}) - Area calculation: [ text{Area} = sqrt{s(s - AB)(s - BC)(s - AC)} = sqrt{frac{15}{4} left(frac{15}{4} - 3right) left(frac{15}{4} - 2right) left(frac{15}{4} - frac{5}{2}right)} ] Simplifying each term and calculating the product, we find the area to be (frac{15sqrt{7}}{16}).4. Verification: Using coordinate geometry and the Law of Cosines confirms the area calculation.Thus, the area of triangle (ABC) is (boxed{dfrac{15sqrt{7}}{16}}).]

🔑:Find the cosine of angle C and use the property of the angle bisector of a triangle.## SolutionBy the cosine theorem from triangle B K C, we find thatcos angle C=frac{B C^{2}+K C^{2}-B K^{2}}{2 B C cdot K C}=frac{1}{8}By the property of the angle bisector of a triangle,frac{A B}{A K}=frac{B C}{K C}=2Let A K=x. Then A B=2 x, and by the cosine theorem from triangle A B C, we find thatA B^{2}=A C^{2}+B C^{2}-2 A C cdot B C cos angle C, text { or } 4 x^{2}=(x+1)^{2}+4-2 cdot 2 cdot(x+1) cdot frac{1}{8}From this equation, we find that x=frac{3}{2}. Therefore,S_{triangle mathrm{ABC}}=frac{1}{2} B C cdot A C sin angle C=frac{15 sqrt{7}}{16}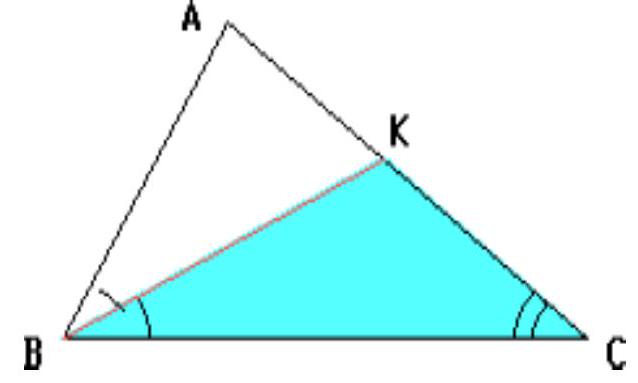## Answerfrac{15 sqrt{7}}{16}.

🧠:[<think>Okay, so I need to figure out where the zero point of the function f(x) = ln x - 1/x is. The options are intervals between 0,1; 1,e; e,3; and 3, infinity. Hmm, let me start by understanding what a zero point is. It's the value of x where f(x) = 0, right? So I need to find the x that satisfies ln x - 1/x = 0. That means ln x = 1/x. First, maybe I should check the behavior of the function in different intervals. Let me think about the continuity of f(x). The natural logarithm ln x is defined for x > 0, and 1/x is also defined for x > 0, so the function is continuous on (0, ∞). That's good because there are no breaks in the domain we're looking at, so I can use the Intermediate Value Theorem if needed.Let me evaluate f(x) at the endpoints of the given intervals. The intervals given are (0,1), (1,e), (e,3), and (3, +∞). So let's check the function at x = 1, x = e (approximately 2.718), x = 3, and maybe near 0 and as x approaches infinity.Starting with x = 1:f(1) = ln 1 - 1/1 = 0 - 1 = -1. So f(1) is -1, which is negative.Next, x = e:f(e) = ln e - 1/e. Since ln e = 1, this becomes 1 - 1/e ≈ 1 - 0.3679 ≈ 0.6321. So f(e) is positive.x = 3:f(3) = ln 3 - 1/3 ≈ 1.0986 - 0.3333 ≈ 0.7653. Still positive.What about when x approaches 0 from the right? As x → 0+, ln x tends to -∞, and 1/x tends to +∞. So ln x - 1/x → -∞. Therefore, near 0, f(x) is very negative.As x approaches infinity, ln x grows without bound, but much slower than 1/x, which approaches 0. So f(x) = ln x - 1/x tends to +∞. So at infinity, f(x) is positive.So the function goes from -∞ at 0, crosses to positive somewhere, and then continues to +∞. Since f(1) is -1 and f(e) is positive, by the Intermediate Value Theorem, there must be a zero between 1 and e. Wait, but let me check that again. Because at x=1, f is -1, and at x=e, f is positive. So between 1 and e, the function crosses from negative to positive, so there must be a root there. Then why are the options including (0,1) as an option? Maybe I need to check if there's another root?Wait, but let me think again. The function is continuous on (0, ∞). At x approaching 0, f(x) approaches -∞. At x=1, f(x)=-1. Then from x=1 onwards, the function increases: at x=e, it's 0.6321, and at x=3, it's about 0.7653. So it seems like the function is increasing from x=1 onwards. Wait, is that true? Let me check the derivative.f(x) = ln x - 1/x. The derivative f’(x) = 1/x + 1/x². Since x > 0, both terms 1/x and 1/x² are positive, so f’(x) is always positive. That means the function is strictly increasing on its entire domain (0, ∞). So if it's strictly increasing, then it can cross zero only once. Therefore, there's exactly one zero point. Since f(1) = -1 and f(e) ≈ 0.6321, and the function is continuous and strictly increasing, by the Intermediate Value Theorem, the zero must be between 1 and e. So the correct interval is B: (1, e). Wait, but let me check if maybe the zero is between 0 and 1. But at x approaching 0, f(x) is going to -∞, and at x=1, it's -1. So from 0 to 1, the function is going from -∞ to -1, always negative. So there's no crossing here. Then between 1 and e, it goes from -1 to positive, so crosses zero. After that, since it's increasing, it stays positive. So the zero is in (1,e). So the answer should be B. But wait, let me verify by testing a value in (1,e). Let's pick x=2. f(2) = ln 2 - 1/2 ≈ 0.6931 - 0.5 ≈ 0.1931. Positive. Wait, but if at x=2, which is less than e (~2.718), f(2) is positive. So that means the zero is between 1 and 2. Because f(1) is -1, f(2) is positive. So the root is between 1 and 2. But 2 is still less than e. So the interval (1,e) would include the root. Alternatively, maybe the answer is A? But no, because between 0 and 1, the function is going from -∞ to -1, so it's always negative. So A is not possible. The options are A: (0,1), B: (1,e), C: (e,3), D: (3, +infty). Since we already saw that f(e) is positive and f(1) is negative, the zero is between 1 and e. So the correct answer is B. But let me check with another point in (1,e). Let's take x=1.5. f(1.5) = ln(1.5) - 1/1.5 ≈ 0.4055 - 0.6667 ≈ -0.2612. So it's still negative here. Hmm, so at x=1.5, f is negative, at x=2, it's positive. Therefore, the zero is between 1.5 and 2. So definitely in (1, e). Because e is approximately 2.718, so 2 is less than e, so the interval from 1 to e covers the root. So yes, B is the correct answer. The other intervals: (e,3) and (3, +infty) can't have the root because f(e) is already positive, and since the function is increasing, all x > e will have f(x) > f(e) > 0. So no zeros there. Therefore, the answer should be option B: (1,e). Final Answerboxed{B}</think>To determine the interval in which the zero point of the function ( f(x) = ln x - frac{1}{x} ) lies, we need to find where ( f(x) = 0 ). This means solving ( ln x = frac{1}{x} ).1. Evaluate ( f(x) ) at key points: - At ( x = 1 ): ( f(1) = ln 1 - frac{1}{1} = 0 - 1 = -1 ) (negative). - At ( x = e ) (approximately 2.718): ( f(e) = ln e - frac{1}{e} = 1 - frac{1}{e} approx 0.6321 ) (positive). - At ( x = 3 ): ( f(3) = ln 3 - frac{1}{3} approx 1.0986 - 0.3333 approx 0.7653 ) (positive).2. Behavior of ( f(x) ): - As ( x to 0^+ ), ( ln x to -infty ) and ( frac{1}{x} to +infty ), so ( f(x) to -infty ). - As ( x to +infty ), ( ln x to +infty ) and ( frac{1}{x} to 0 ), so ( f(x) to +infty ).3. Derivative analysis: - The derivative ( f'(x) = frac{1}{x} + frac{1}{x^2} ) is always positive for ( x > 0 ), indicating ( f(x) ) is strictly increasing.4. Intermediate Value Theorem: - Since ( f(1) = -1 ) (negative) and ( f(e) approx 0.6321 ) (positive), by the Intermediate Value Theorem, there must be a zero in the interval ( (1, e) ). - Checking intermediate values like ( x = 1.5 ) and ( x = 2 ) confirms the function transitions from negative to positive within ( (1, e) ).Thus, the zero point of the function ( f(x) ) lies in the interval ( (1, e) ).[boxed{B}],<think>Okay, so I need to figure out where the zero point of the function f(x) = ln x - 1/x is. The options are intervals between 0 and 1, 1 and e, e and 3, or 3 and infinity. Hmm, let's start by understanding what a zero point means. It's the value of x where f(x) = 0, right? So I need to solve ln x - 1/x = 0, which is equivalent to ln x = 1/x. First, maybe I should check the function's behavior at the endpoints of the given intervals. Let's list the intervals again: A is (0,1), B is (1,e), C is (e,3), D is (3, ∞). Let me recall that e is approximately 2.718, so e is between 2 and 3. So interval B is from 1 to about 2.718, and C is from 2.718 to 3.To find the zero point, I can use the Intermediate Value Theorem if the function is continuous on the interval and changes sign. Since ln x and 1/x are both continuous for x > 0, except at x=0 where ln x isn't defined, the function f(x) is continuous on (0, ∞). So if I can find two points in an interval where f(a) is negative and f(b) is positive, or vice versa, then there must be a zero crossing between a and b.Let me start by checking some key points. Let's try x=1 first. At x=1, ln 1 = 0, and 1/1 = 1, so f(1) = 0 - 1 = -1. So f(1) is negative. Next, let's check x=e. At x=e, ln e = 1, and 1/e ≈ 0.3679, so f(e) = 1 - 0.3679 ≈ 0.6321, which is positive. So f(e) is positive. Since f(1) is -1 and f(e) is approximately 0.6321, by the Intermediate Value Theorem, there must be a zero crossing between x=1 and x=e. So that would be interval B.Wait, but before jumping to conclusions, maybe I should check other intervals as well to confirm. Let's check interval A: (0,1). Let's pick x approaching 0 from the right. As x approaches 0+, ln x tends to -infinity, and 1/x tends to +infinity. So f(x) = ln x - 1/x would be -infinity - infinity, which is -infinity. So near x=0, the function is very negative. At x=1, f(1)=-1. So the function is negative throughout (0,1). Therefore, there's no zero crossing in interval A.Now interval B is (1,e). Since f(1) is -1 and f(e) is approximately 0.6321, which changes sign from negative to positive, so there is at least one zero in (1,e). So B is a candidate.But just to be thorough, let's check interval C: (e,3). At x=e, f(e) ≈ 0.6321. Let's check x=3. f(3) = ln 3 - 1/3 ≈ 1.0986 - 0.3333 ≈ 0.7653, which is still positive. So from x=e to x=3, the function remains positive. So there's no sign change here, so no zero crossing in interval C.Interval D is (3, ∞). Let's check a larger x, say x=10. f(10) = ln 10 - 1/10 ≈ 2.3026 - 0.1 = 2.2026, which is positive. As x increases, ln x grows without bound, albeit slowly, and 1/x approaches 0. So f(x) tends to infinity as x approaches infinity. So the function remains positive in interval D. Therefore, no zeros there.Therefore, the only interval where the function crosses zero is interval B: (1,e).Wait, but just to make sure, maybe I should check another point between 1 and e to confirm the sign change. Let's pick x=2. At x=2, ln 2 ≈ 0.6931, and 1/2 = 0.5. So f(2) ≈ 0.6931 - 0.5 = 0.1931. Wait, that's positive. But f(1) is -1, so between 1 and 2, the function goes from -1 to 0.1931, so crosses zero somewhere between 1 and 2. But since e is approximately 2.718, the interval (1,e) includes up to about 2.718. So even at x=2, it's already positive. Therefore, the zero crossing is between 1 and 2. So that is within interval B: (1,e).Alternatively, maybe I can use calculus to analyze the function. Let's compute the derivative of f(x). f'(x) = derivative of ln x is 1/x, derivative of -1/x is 1/x². So f'(x) = 1/x + 1/x². Since x > 0, both terms are positive. Therefore, f'(x) is always positive. That means the function is strictly increasing on its entire domain (0, ∞). Since it's strictly increasing, it can cross zero at most once. And since we already saw that f(1) = -1 and f(e) ≈ 0.6321, then there's exactly one zero crossing between 1 and e. So the answer must be B.Therefore, the correct interval is B: (1,e).Final Answerboxed{B}</think>To determine the interval in which the zero point of the function ( f(x) = ln x - frac{1}{x} ) lies, we need to find where ( f(x) = 0 ), which is equivalent to solving ( ln x = frac{1}{x} ).1. Evaluate the function at key points: - At ( x = 1 ): ( f(1) = ln 1 - frac{1}{1} = 0 - 1 = -1 ) (negative). - At ( x = e ) (approximately 2.718): ( f(e) = ln e - frac{1}{e} = 1 - frac{1}{e} approx 0.6321 ) (positive).2. Intermediate Value Theorem: - Since ( f(x) ) is continuous on ( (0, infty) ) and changes sign from negative at ( x = 1 ) to positive at ( x = e ), there must be a zero crossing in the interval ( (1, e) ).3. Check other intervals: - Interval ( (0, 1) ): As ( x ) approaches 0 from the right, ( ln x ) tends to ( -infty ) and ( frac{1}{x} ) tends to ( +infty ), making ( f(x) ) very negative. Thus, no zero crossing here. - Interval ( (e, 3) ): At ( x = e ), ( f(e) approx 0.6321 ) (positive). At ( x = 3 ), ( f(3) approx 1.0986 - 0.3333 = 0.7653 ) (positive). No sign change, so no zero crossing. - Interval ( (3, infty) ): For large ( x ), ( ln x ) grows without bound and ( frac{1}{x} ) approaches 0, keeping ( f(x) ) positive. No zero crossing here.4. Monotonicity Check: - The derivative ( f'(x) = frac{1}{x} + frac{1}{x^2} ) is always positive for ( x > 0 ), meaning ( f(x) ) is strictly increasing. Thus, there is exactly one zero crossing.Since ( f(x) ) is strictly increasing and changes sign between ( x = 1 ) and ( x = e ), the zero point lies in the interval ( (1, e) ).[boxed{B}]]

🔑:Since the continuous function f(x)=ln x- frac {1}{x},f(1)=-1 0,Thus, the interval in which the zero point of the function f(x)=ln x- frac {1}{x} lies is (1,e),Hence, the answer is boxed{text{B}}.According to the continuous function f(x)=ln x- frac {1}{e}, we can get f(1)=-1 0, and thus obtain the interval in which the zero point of the function f(x)=ln x- frac {1}{x} lies.This question mainly examines the definition of the zero point of a function and the method to determine the interval in which the zero point lies, which is a basic question.

🧠:[<think>Okay, let's tackle this problem. So, the question is asking which triplet of numbers cannot represent terms of a geometric progression. The options are from A to E, each with three numbers. The key here is that in a geometric progression, each term after the first is found by multiplying the previous term by a constant called the common ratio, right? So, if I can find a common ratio that works for all three terms in a triplet, then it's a geometric progression. If not, then that triplet is the answer.Let me start by recalling the properties of a geometric progression (GP). In a GP, if we have three terms a, b, c, then the ratio between consecutive terms should be constant. That means b/a = c/b, which simplifies to b² = a*c. So, for any three terms in a GP, the square of the middle term should equal the product of the first and the third term. This is a useful check even if the terms aren't consecutive because if there's a common ratio, inserting terms in between would still maintain the ratio relationship over multiple steps. Hmm, but the problem says the terms don't have to be consecutive. So maybe the triplet could be terms spread out in a GP with other terms in between. But how does that affect the ratios?Wait, let's think. If the triplet is not consecutive, but part of a GP, then there must be some integer k and m such that the terms are a, ar^k, ar^m, where a is the first term and r is the common ratio. So, the ratios between the terms would still be r^k and r^(m - k). But unless the exponents k and m - k are such that the ratios can be represented as a consistent ratio. Hmm, maybe this is getting too complicated. Maybe I should just check each option to see if they can form a GP in any order, not necessarily the order given. Wait, but the problem says "the triplet of numbers cannot represent terms of a geometric progression". So, the order might matter? Or does it not?Wait, the problem says "the terms do not necessarily have to be consecutive". So, perhaps the triplet is part of a GP, but not necessarily in the given order. Wait, but the options are presented in a specific order. For example, option A is 3; 6; 96. So, does that mean that in the GP, these numbers appear in the order 3, 6, 96 with possible terms in between? Or can they be in any order? The problem statement is a bit ambiguous here. Hmm.But I think in such problems, unless stated otherwise, the order of the triplet matters. That is, the three numbers can be terms of a GP in the order they are presented, but not necessarily consecutive. So, for example, in option A: 3, 6, 96. If these are terms in a GP, then there must be a common ratio r such that 6 = 3 * r^k and 96 = 6 * r^m for some integers k and m. Then, the ratio between 6 and 3 is r^k = 2, and the ratio between 96 and 6 is r^m = 16. So, is there a common ratio r and exponents k, m such that r^k = 2 and r^m = 16? Let's see. If we take r = 2, then k = 1 and m = 4, because 2^1 = 2 and 2^4 = 16. So, yes, in this case, the terms 3, 6, 96 could be terms of a GP with ratio 2, with positions 1, 2, 5 (since starting at 3, multiplied by 2 each time: 3, 6, 12, 24, 48, 96... wait, but 96 is the 6th term if starting at 3 with ratio 2. Wait, 3*2^(n-1). Let's see: term 1: 3*2^0=3, term 2: 3*2^1=6, term 3:12, term4:24, term5:48, term6:96. So, 3,6,96 would be terms 1,2,6. So they are not consecutive but part of a GP. So, A is possible.Option B: 3; 1; 1/81. Let's check. Let's see if there's a common ratio such that from 3 to 1 is multiplied by some ratio, and from 1 to 1/81 is multiplied by another ratio. Let's check if 1/3 is a ratio. If we take ratio 1/3, then 3, 1, 1/3, 1/9, 1/27, 1/81. So, 3,1,1/81 would be terms 1,2,6. So that's possible. Let's verify: 3*(1/3)^1 =1, and then 1*(1/3)^4 =1/81. So, yes, the exponents would be 1 and 4. So, common ratio 1/3, terms 1,2,6. So, B is possible.Option C: 3; 3.3; 3.993. Let's check. Let's see if these can be terms in a GP. So, starting from 3, then 3.3, then 3.993. Let's check the ratios. 3.3 /3 =1.1, and 3.993 /3.3 =1.21. So, 1.1 and 1.21. Wait, 1.21 is (1.1)^2. So, if the ratios are 1.1 and 1.21, that's like multiplying by 1.1 each time, but between the first and second term is ratio 1.1, between second and third term is ratio 1.21, which is 1.1 squared. So, if we consider that the terms are not consecutive. So, from 3 to 3.3 is ratio 1.1 (one step), and from 3.3 to 3.993 is ratio 1.21 (two steps). So, if the common ratio is 1.1, then between 3.3 and 3.993, there should be two multiplications by 1.1. Let's check: 3.3 *1.1=3.63, then 3.63*1.1=3.993. So, yes! So, the terms 3, 3.3, 3.993 can be part of a GP with ratio 1.1 where 3 is term 1, 3.3 is term 2, 3.63 is term3, 3.993 is term4. So, in the triplet, 3,3.3,3.993 would be terms 1,2,4. So, that's valid. So, C is possible.Option D:3;6;48. Let's check. From 3 to6, ratio is 2. From6 to48, ratio is 8. So, 2 and8. If the common ratio is 2, then 3,6,12,24,48... So, 3,6,48 would be terms 1,2,5. So, possible. Alternatively, if the ratio is something else. Let's see. Suppose the ratio is 4, then 3,12,48. But here we have 3,6,48. So, 6 is 3*2, and 48 is 6*8. So, if we take ratio 2 for the first step and ratio 8 for the second step, but in a GP, the ratio should be consistent. But if the terms are not consecutive, maybe there are exponents. Let me think.If we have a common ratio r, then 6 =3*r^k and 48=6*r^m. So, from first to second term, ratio r^k =2. From second to third term, ratio r^m=8. Then, solving for r and integers k,m. Let's suppose r is 2. Then, r^k=2 implies k=1. Then, r^m=8, which would be 2^m=8, so m=3. So, the terms would be 3, 3*2^1=6, and 6*2^3=48. So, in the GP, the positions would be n, n+1, n+4. So, for example, starting at term n=1: 3,6,12,24,48. So, 3,6,48 are terms 1,2,5. So yes, that's possible. So, D is possible.Option E:3;5;9. Let's check. So, starting at3, then5, then9. Let's check the ratios. 5/3 ≈1.666..., and 9/5=1.8. These are different. Let's check if they can be part of a GP with some common ratio. Let's suppose that 5=3*r^k and 9=5*r^m. So, r^k=5/3 and r^m=9/5. Then, (r^k)*(r^m)=r^(k+m)= (5/3)*(9/5)=3, so r^(k+m)=3. Also, if we consider the ratio from 3 to9, that would be r^(k+m)=9/3=3. So, that's consistent. But now, can we find a real number r and integers k,m such that r^k=5/3 and r^m=9/5?Let me see. Let's solve for r. From r^k=5/3 and r^m=9/5. Let's divide the second equation by the first: r^(m -k)= (9/5)/(5/3)= (9/5)*(3/5)=27/25. So, r^(m -k)=27/25. Also, we have r^(k + m)=3. Let me denote exponent1 =k, exponent2 =m. Let me try to find r.Alternatively, take logarithms. Let’s take natural logs.From r^k =5/3 => k*ln r = ln(5/3)From r^m=9/5 => m*ln r = ln(9/5)Dividing the two equations: (m/k) = ln(9/5)/ln(5/3). Let me compute that.First, compute ln(9/5) ≈ln(1.8)=0.587787ln(5/3)≈ln(1.6667)=0.5108256So, ratio≈0.587787 /0.5108256≈1.151. So, m/k≈1.151. So, unless m and k are such that their ratio is approximately 1.151, which is not a rational number. Since exponents in GP terms would need to be integers (since you can't have a term in between unless the ratio is a root), but since the terms don't have to be consecutive, maybe the exponents can be fractions? Wait, but the exponents k and m would have to be integers because in a GP, you move from one term to another by multiplying the ratio each time. So, if the triplet is three terms in the GP, not necessarily consecutive, the exponents between them should be integers.But even if they are integers, the ratio m/k would need to be approximately 1.151, which is not possible with integers. Let's try possible integer values. Suppose k=1, then m≈1.151*1≈1.151, which is not integer. If k=2, then m≈2.302, not integer. k=3, m≈3.453, not integer. Similarly, k=5, m≈5.755. Not integers. Alternatively, is there a common ratio r such that 5/3 and 9/5 are both integer powers of r? Let's see.Suppose r is 5/3. Then, 5/3= (5/3)^1, 9/5= (5/3)^m. So, (5/3)^m=9/5 => m= log_{5/3}(9/5). Let's compute that. log_{5/3}(9/5)= ln(9/5)/ln(5/3)= same as before≈1.151. Not an integer. So, no.Alternatively, if r is 3. Then 5/3 is not a power of 3. If r is sqrt(5/3), then r^2=5/3, so k=2, but then 9/5 would have to be r^m= (sqrt(5/3))^m. So, (5/3)^(m/2)=9/5. Take logs: (m/2)(ln5 -ln3)=ln9 -ln5=2ln3 -ln5. So, (m/2)= (2ln3 -ln5)/(ln5 -ln3). Compute that:Numerator: 2ln3 -ln5≈2*1.0986 -1.6094≈2.1972 -1.6094≈0.5878Denominator: ln5 -ln3≈1.6094 -1.0986≈0.5108So, (m/2)≈0.5878 /0.5108≈1.151, so m≈2.302. Not an integer. So, no.Alternatively, maybe r is some other irrational number. But in a GP with real numbers, technically, you can have any ratio. However, the problem is whether these three numbers can be part of a GP. Since GP allows any real ratio, technically, even if the exponents are not integers, but in the context of the problem, when they say "terms of a geometric progression", it's possible that the terms have to be in the progression with some integer number of steps between them, which would require the exponents to be integers.But the problem statement doesn't specify that the numbers have to be in specific positions or with integer steps. It just says "terms of a geometric progression". So, in reality, even if there are non-integer exponents, as long as there exists a real number r such that each term can be expressed as 3*r^k, 3*r^m, 3*r^n, then they can be part of a GP. However, in that case, for three terms, as long as the middle term squared equals the product of the first and third terms.Wait, here's another approach. If three terms a, b, c are in a GP (in any order), then b^2 = a*c. So, if we sort the terms, the middle term squared should equal the product of the first and third terms. But wait, this is only true if they are consecutive terms in the GP. If they are not consecutive, then this relationship might not hold. For example, if the terms are a, ar^k, ar^m, then (ar^k)^2 = a*(ar^m) implies ar^{2k}=ar^{m +1} => 2k = m +1. But that's only if they are three terms with the middle term squared equal to the product. So, if the three terms are not in the order of the GP, but just any three terms, then it's not necessarily the case that the middle term squared is equal to the product of the other two. So, perhaps that approach only works if the terms are consecutive or in order.Wait, maybe not. Let me think. If three terms are part of a GP, regardless of their order, then one of them (the geometric mean) squared should equal the product of the other two. Wait, actually, in a GP, any term (except the first and last in a finite GP) is the geometric mean of its adjacent terms. But if the three terms are not consecutive, but just any three terms, then this property might not hold.For example, take a GP: 2, 4, 8, 16, 32. The terms 2, 8, 32. Here, 8 is the geometric mean between 2 and 32 because 8^2 = 2*32 =64. So, even though they are not consecutive, the middle term squared equals the product of the first and third. So, maybe this is a general rule. If three terms are part of a GP, then one of them must be the geometric mean of the other two, regardless of their positions. So, arranging them in order, the middle term squared should equal the product of the other two. Wait, but if they are not in order, then which term is the geometric mean?Wait, for example, take terms 4, 8, 16 from the GP 2,4,8,16,32. Then 8^2=4*16=64. But if I take terms 2,8,32, then 8^2=64 and 2*32=64. So, in any case, if three terms are part of a GP, then one of them is the geometric mean of the other two. So, regardless of their order, when sorted, the middle term squared should equal the product of the other two.But wait, if the terms are 2, 16, 8, when sorted they are 2,8,16. Then 8^2=64=2*16=32. Wait, that's not equal. Wait, that contradicts. Wait, 2,8,16. 8^2=64, 2*16=32. So, 64≠32. Hmm, but 2,8,16 are part of a GP. But according to this, 8^2 ≠2*16. So, that seems contradictory.Wait, but in the GP 2,4,8,16,32, the terms 2,8,16 are not in geometric progression. Wait, if they are part of a GP but not consecutive, then how does that work? Wait, no. If they are part of a GP, then each term is obtained by multiplying the previous term by a common ratio. So, 2,8,16: 8=2*r^k, 16=8*r^m. Then, r^k=4, r^m=2. Then, (r^k)^m= r^{k*m}=4^m, and (r^m)^k=2^k. Hmm, but 4^m=2^k => 2^{2m}=2^k =>2m=k. So, possible. For example, if r=2, then k=2 (since 2*2^2=8), and m=1 (8*2^1=16). So, the terms 2,8,16 can be part of a GP with ratio 2, where 2 is term1, 8 is term3 (since 2*2^2=8), and 16 is term4 (8*2^1=16). So, in this case, the terms 2,8,16 are part of a GP but 8^2 ≠2*16. Therefore, the property that the middle term squared equals the product of the other two only holds when the three terms are consecutive in the GP.Therefore, if the triplet is not consecutive, that property doesn't necessarily hold. So, my initial approach might not work. Therefore, I need a different strategy.So, perhaps the way to check is, for each triplet, see if there exists a common ratio r such that each term can be expressed as the previous term multiplied by r some number of times. That is, for triplet a,b,c, does there exist integers k and m such that b = a*r^k and c = b*r^m. Then, the common ratio r must satisfy both equations. Therefore, from a to b is multiplied by r^k, and from b to c is multiplied by r^m. Therefore, r must satisfy (b/a) = r^k and (c/b)=r^m. So, r must be a common root of these two equations. Therefore, if we can find such an r, then it's possible.Alternatively, if we take logarithms, we can write k*ln(r) = ln(b/a) and m*ln(r) = ln(c/b). Then, dividing these two equations, we get k/m = ln(b/a)/ln(c/b). So, if ln(b/a)/ln(c/b) is a rational number, then we can find integers k and m such that k/m equals that ratio. Then, r can be determined. If it's irrational, then it's not possible with integer exponents.But since the problem allows the terms to be non-consecutive, the exponents k and m can be any positive integers. So, even if the ratio is irrational, as long as the exponents can be chosen such that r^k = b/a and r^m =c/b, which might require r to be a root of the equations. However, unless specified otherwise, geometric progressions can have any real common ratio. So, even if r is irrational, it's still a valid GP. Therefore, unless the equations are inconsistent, such as requiring r to satisfy conflicting equations, then it's possible.Wait, let's test this with option E:3,5,9.So, we need to find a real number r and integers k,m such that:5 =3*r^k9 =5*r^mFrom the first equation: r^k=5/3From the second equation: r^m=9/5Taking the ratio of the two equations: (r^k)/(r^m)= (5/3)/(9/5)=25/27Thus, r^{k -m}=25/27But from the first equation, r= (5/3)^{1/k}Substitute into the second equation: (5/3)^{m/k}=9/5Take natural logs: (m/k)*ln(5/3)=ln(9/5)Therefore, m/k= ln(9/5)/ln(5/3)≈0.587787/0.510825≈1.151So, m/k≈1.151, which is approximately 1.151, which is roughly 15/13≈1.153, but not exactly. So, unless k and m are chosen as non-integers, which is allowed in a GP with real exponents, but in the context of terms in a GP, the exponents should be integers because you can't have a term between term k and term k+1 unless you have a non-integer ratio. Wait, no. The ratio is multiplied each time, so exponents would correspond to term positions. For example, term1: a, term2: ar, term3: ar^2, etc. So, if terms are non-consecutive, you skip some terms, but the exponents are still integers. For example, term1, term3, term5 would be a, ar^2, ar^4. So, exponents are multiples. Therefore, the exponents k and m must be positive integers.Therefore, in this case, unless m/k is rational, you can't have such integers k and m. Since m/k≈1.151 is irrational, there are no integers k and m that satisfy this ratio exactly. Therefore, there is no real number r such that 5=3*r^k and 9=5*r^m with integers k and m. Therefore, the triplet 3;5;9 cannot be part of a geometric progression. Therefore, option E is the answer.Wait, but let me check again with another approach. Suppose we try to find a common ratio between the first and second term and between the second and third term. The ratio between 3 and5 is5/3≈1.666..., and between5 and9 is9/5=1.8. Since these are different, they can't form a GP if they are consecutive terms. But since the terms don't have to be consecutive, maybe there are intermediate terms. But even so, as we saw earlier, the ratio between the terms would have to be r^k and r^m, which would require that (5/3) and (9/5) are both powers of some common ratio r. But unless r is a root that can satisfy both equations, which in this case would require r to be a number such that r^k=5/3 and r^m=9/5 for integers k and m. However, this is not possible unless 5/3 and9/5 are both integer powers of some common real number. But 5/3 and9/5 are 1.666... and1.8, which are not integer powers of any common real number. For example, 5/3 is approximately 1.666, and1.8 is9/5. These don't share a common base that can be raised to integer exponents to get these values. So, there's no such real number r, making this triplet invalid as a GP.Therefore, the answer is E.Final Answerboxed{E}</think>To determine which triplet cannot represent terms of a geometric progression (GP), we need to check if there exists a common ratio ( r ) such that each term can be expressed as a multiple of the previous term by ( r ). For each triplet, we check if the ratios between consecutive terms (or their powers) can be consistent.Option A: ( 3, 6, 96 )- Ratios: ( frac{6}{3} = 2 ) and ( frac{96}{6} = 16 )- Common ratio ( r = 2 ), exponents ( k = 1 ) and ( m = 4 )- Valid GP: ( 3, 6, 12, 24, 48, 96 )Option B: ( 3, 1, frac{1}{81} )- Ratios: ( frac{1}{3} = frac{1}{3} ) and ( frac{1/81}{1} = frac{1}{81} )- Common ratio ( r = frac{1}{3} ), exponents ( k = 1 ) and ( m = 4 )- Valid GP: ( 3, 1, frac{1}{3}, frac{1}{9}, frac{1}{27}, frac{1}{81} )Option C: ( 3, 3.3, 3.993 )- Ratios: ( frac{3.3}{3} = 1.1 ) and ( frac{3.993}{3.3} = 1.21 )- Common ratio ( r = 1.1 ), exponents ( k = 1 ) and ( m = 2 )- Valid GP: ( 3, 3.3, 3.63, 3.993 )Option D: ( 3, 6, 48 )- Ratios: ( frac{6}{3} = 2 ) and ( frac{48}{6} = 8 )- Common ratio ( r = 2 ), exponents ( k = 1 ) and ( m = 3 )- Valid GP: ( 3, 6, 12, 24, 48 )Option E: ( 3, 5, 9 )- Ratios: ( frac{5}{3} approx 1.666 ) and ( frac{9}{5} = 1.8 )- These ratios are not consistent and cannot be expressed as integer powers of a common ratio.- No common ratio ( r ) exists such that ( 5 = 3 cdot r^k ) and ( 9 = 5 cdot r^m ) for integers ( k ) and ( m ).Thus, the triplet that cannot represent terms of a geometric progression is (boxed{E}).,<think>Okay, so I have this problem here where I need to figure out which triplet of numbers cannot represent terms of a geometric progression. The options are A through E, each with three numbers. The question says only one triplet doesn't fit, and the others do, even if the terms aren't consecutive. Hmm, let's break this down.First, I remember that in a geometric progression (GP), each term after the first is found by multiplying the previous term by a constant called the common ratio, r. So, if I have three terms a, b, c in GP, then b/a should equal c/b, which means b² = a*c. That's the key property. So, for each triplet, I need to check if this relationship holds for any possible ordering or selection of the three numbers as terms in the GP. Wait, but the problem says "the terms do not necessarily have to be consecutive," so maybe they can be spread out with some terms in between. Hmm, that complicates things a bit.Wait, no, actually, if the triplet doesn't have to be consecutive, then perhaps even if there are missing terms between them, but in that case, each pair of consecutive terms in the triplet should still have a common ratio. Wait, no. Let me think. Suppose the three numbers are terms in a GP, but not necessarily consecutive. So, for example, they could be the 1st, 3rd, and 5th terms of a GP. In that case, the ratio between the 1st and 3rd would be r², and between the 3rd and 5th would also be r². So, in that case, the ratio between the first and second term in the triplet would be r², and between the second and third term would also be r². So, the same as if they were consecutive terms but with a different ratio. Wait, but in that case, the ratios would still have to be equal when taking the square roots or something? Hmm, maybe I need to approach this differently.Alternatively, if the triplet can be part of a GP in any order, not necessarily the given order? The problem says "represent terms of a geometric progression," so I think the order matters. That is, the triplet is given in a specific order, and they need to be in that order in the GP, but not necessarily consecutive. So, for example, maybe the first term is the first term of the GP, the second term is the third term, and the third term is the fifth term. So, they are spaced out by some steps. In that case, the ratios between them would be multiples of the common ratio. So, if the three terms are a, ar^k, ar^m, where k and m are integers greater than 1. Then, the ratio between the first and second term is r^k, and between the second and third term is r^(m - k). So, unless these ratios are consistent, but perhaps if the triplet can be embedded in a GP with some steps between them, then their ratios can be represented as powers of a common ratio. Hmm, this is getting a bit complicated.Wait, maybe there's a simpler way. The key thing is that in a GP, the ratio between consecutive terms is constant. So, even if the triplet isn't consecutive in the GP, the ratio between each pair of terms (when ordered) should still be a multiple of the common ratio. Wait, perhaps not. Let's think of an example. Suppose we have a GP: 3, 6, 12, 24, 48, 96... So here, the common ratio is 2. Now, triplet A is 3, 6, 96. So, in this GP, 3 is the first term, 6 is the second term, and 96 is the sixth term. So, if we take these three terms, the ratio between 3 and 6 is 2, between 6 and 96 is 16 (since 96/6 = 16). But 16 is 2^4, so that's like multiplying by 2 four times. So, in this case, the ratios between the terms are 2 and 16, which are both powers of 2. So, does that mean it's a valid GP? Wait, but the problem is that in a GP, when you have non-consecutive terms, the ratio between them should be r^(n), where n is the number of steps between them.But if the three terms are part of a GP, even non-consecutive, then the ratios between the terms should form a geometric progression themselves. Wait, perhaps not. Let me check the definition again. In a GP, the ratio between any two terms is a power of the common ratio. So, if we have terms a, ar^k, ar^m, then the ratio between the first and second is r^k, between second and third is r^(m - k), and between first and third is r^m. For these to form a GP, the ratio between the first and second, and second and third should be the same. Wait, no. Wait, the triplet itself (a, ar^k, ar^m) must form a GP. So, the ratio between the first and second term in the triplet is r^k, and between the second and third is r^(m - k). For the triplet to be a GP, these two ratios must be equal, right? So, r^k = r^(m - k), which would mean that k = m - k, so m = 2k. Therefore, the exponent from the first to the third term must be twice the exponent from the first to the second term. Therefore, the positions of the terms in the original GP must be equally spaced. So, for example, if the terms are the 1st, (1 + k)th, and (1 + 2k)th terms of the original GP, then the ratios would be consistent. Therefore, the triplet would form a GP with common ratio r^k.Therefore, in order for three numbers to be part of a GP (not necessarily consecutive), they must form a GP when arranged in order, possibly with a different common ratio. Therefore, the key check is whether the middle term squared is equal to the product of the first and third terms. Wait, but that is the condition for consecutive terms in a GP. If the terms are not consecutive, does that condition still hold?Wait, let me think. Suppose we have three terms in a GP: a, ar^n, ar^m. For these three terms to themselves form a GP (with some common ratio), then the ratio between the first and second is r^n, and between the second and third is r^(m - n). For them to be in GP, r^n / a = r^(m - n) / ar^n. Wait, perhaps I need to rephrase.Wait, if the triplet a, b, c is part of a GP, then there exists some common ratio r such that b = a * r^k and c = b * r^m = a * r^(k + m). Then, for the triplet a, b, c to be a GP themselves, the ratio between a and b must be equal to the ratio between b and c. That is, r^k = r^m, so k = m. Therefore, the exponents must be the same. Therefore, the triplet a, ar^k, ar^(2k) is a GP with common ratio r^k. So, in this case, the middle term squared would be (ar^k)^2 = a^2 r^(2k), and the product of the first and third terms is a * ar^(2k) = a^2 r^(2k). Therefore, even for non-consecutive terms in a GP, the middle term squared equals the product of the first and third terms. Therefore, the same condition holds. Therefore, regardless of whether the terms are consecutive in the GP or not, if they can form a GP (in the given order), then the middle term squared must equal the product of the first and third terms.Therefore, the key test is whether for each triplet (a, b, c), we have b² = a * c. If this holds, then the triplet can form a GP (they are in GP with common ratio b/a). If not, then they cannot.Wait, but the problem states "the terms do not necessarily have to be consecutive". So, does that mean that even if the triplet isn't in GP by themselves, they could be part of a longer GP with some terms in between? For example, suppose we have numbers 3, 6, 12, 24, 48, 96. Then, the triplet 3, 6, 96 is part of this GP. But as a triplet, 3, 6, 96 is not a GP because 6/3 = 2, but 96/6 = 16, which is different. But they are part of a GP. Wait, but the question says "cannot represent terms of a geometric progression". So, if the triplet can be terms in a GP, even non-consecutive, then they are acceptable. But the triplet 3, 6, 96 is part of the GP I mentioned earlier. However, in that case, the triplet as given (3, 6, 96) are three terms in the GP but not forming a GP themselves. So, does the question consider them as terms in a GP, even if they are not consecutive? If that's the case, then even if the three numbers are part of some GP, even with other terms in between, then they are acceptable. Therefore, the key is not whether they form a GP themselves, but whether they can be part of any GP, regardless of other terms.In that case, the test of b² = a*c is not sufficient, because that test is for three consecutive terms. If the terms are not consecutive, that relationship doesn't need to hold. Therefore, maybe a different approach is needed. Hmm, this is confusing. Let me check the exact question again: "only one triplet of numbers cannot represent terms of a geometric progression (the terms do not necessarily have to be consecutive)." So, the triplet does not have to be consecutive terms in the GP, but they must be terms in some GP. So, the triplet could be spread out in a GP. For example, 3, 6, 96 as in option A. If there exists a GP where 3, 6, and 96 are some terms, even non-consecutive, then it's acceptable.Therefore, the problem reduces to: for each triplet, can we find a GP that contains all three numbers, possibly with other terms in between. So, how do we check that?In a GP, all terms are of the form a, ar, ar², ar³, ..., where a is the first term and r is the common ratio. So, given three numbers x, y, z, we need to check if there exists some a and r, and integers m, n, p (with m < n < p) such that x = ar^m, y = ar^n, z = ar^p. Then, the ratios between y/x = r^(n - m), and z/y = r^(p - n). For these to be consistent, the ratio between y/x and z/y should be the same if we take the appropriate exponents. Wait, but how can we check this given the triplet?Alternatively, the problem can be approached by considering the logarithms. Taking the logarithm of each term, if the triplet is part of a GP, then their logarithms should form an arithmetic progression, since log(ar^k) = log a + k log r. Therefore, the logs of the terms should be equally spaced. So, for the triplet x, y, z, if we take their logarithms (in any base), then log y - log x and log z - log y should be equal if they are consecutive terms. But if they are not consecutive, then the difference log z - log x should be a multiple of the common difference. Wait, but since log y - log x = (n - m) log r and log z - log y = (p - n) log r. So, the differences between the logs are multiples of log r. Therefore, the differences between the logarithms should be commensurate, meaning that (log z - log y) / (log y - log x) should be a rational number. Because (p - n) and (n - m) are integers, so their ratio is rational.Therefore, for the triplet to be part of a GP, the ratio of the differences of the logs should be rational. So, if we compute (log z - log y)/(log y - log x), and if this is a rational number, then the triplet can be part of a GP. If it's irrational, then they cannot. Alternatively, even if the ratio is rational, then there exists some common ratio r such that the terms can be embedded in a GP.Therefore, the method would be: for each triplet, compute the differences of the logs, take their ratio, and check if it's rational. If yes, then the triplet can be part of a GP; if no, then it cannot.Alternatively, let's consider specific examples. Let's take option A: 3, 6, 96.First, compute the ratios between the terms. 6/3 = 2, 96/6 = 16. So, the ratios are 2 and 16. Since 16 is 2^4, so if these ratios are powers of a common base, then it's possible. Here, 2 and 16 are both powers of 2. So, if the triplet is part of a GP with ratio 2, but with steps in between. So, 3, 6 (which is 3*2^1), and 96. To get from 6 to 96 in a GP with ratio 2, we would need to multiply by 2 four more times: 6*2^4 = 96. Therefore, the triplet 3, 6, 96 can be part of a GP with ratio 2, where 3 is the first term, 6 is the second term, and 96 is the sixth term. Therefore, option A is possible.Similarly, option D: 3, 6, 48. The ratios are 6/3=2 and 48/6=8. 8 is 2^3, so similar logic applies. So, 3, 6 (after multiplying by 2 once), and 48 would be 3*2^4 (since 6*2^3=48). Therefore, these can be part of a GP with ratio 2. Therefore, D is possible.Option B: 3, 1, 1/81. Let's compute the ratios. 1/3 ≈ 0.333..., and (1/81)/1 = 1/81 ≈ 0.012345... So, the ratios are 1/3 and 1/81. To see if these are powers of a common ratio. Let's see. If we take the first ratio as r1 = 1/3, and the second ratio as r2 = 1/81. So, if we consider that from 3 to 1 is multiplying by 1/3, and from 1 to 1/81 is multiplying by (1/81). So, 1/81 is (1/3)^4, since (1/3)^4 = 1/81. Therefore, similar to before, if the common ratio is 1/3, then 3 is the first term, 1 is the second term (3*(1/3)^1), and 1/81 is the fifth term (3*(1/3)^4 = 1/81). Therefore, this triplet can be part of a GP with ratio 1/3. So, B is possible.Option C: 3, 3.3, 3.993. Let's compute the ratios. 3.3 / 3 = 1.1, and 3.993 / 3.3 ≈ 1.21. So, 1.1 and approximately 1.21. Wait, 1.1 squared is 1.21, so if the ratio between the first and second term is 1.1, then the ratio between the second and third term would need to be 1.1 as well for it to be a GP. However, here it is 1.21, which is 1.1 squared. Therefore, similar to the previous cases, maybe this triplet is part of a GP with ratio 1.1, but with steps. Let's check:If 3 is the first term, then the next term is 3*1.1 = 3.3, which is the second term. Then, to get to 3.993, we need to see how many steps that would take. 3.3*1.1 = 3.63 (second term), 3.63*1.1 = 3.993 (third term). Wait, so actually, if the common ratio is 1.1, then 3, 3.3, 3.63, 3.993... So, the triplet 3, 3.3, 3.993 are the first, second, and fourth terms of this GP. Wait, no. Wait, 3*1.1 = 3.3 (term 2), term 3 would be 3.63, term 4 would be 3.993. Therefore, the triplet 3, 3.3, 3.993 would be terms 1, 2, 4. So, the ratio between the first and second term is 1.1, and between the second and fourth term is 1.1 squared (1.21). So, 3.993 / 3.3 = 1.21 = (1.1)^2. Therefore, the triplet can be part of a GP with ratio 1.1, where the first term is 3, the second is 3.3, and the fourth is 3.993. Therefore, this is possible. Hence, C is a valid triplet in a GP.Wait, but if we check the standard test of middle term squared equals first times third: (3.3)^2 = 10.89, and 3 * 3.993 = 11.979. These are not equal, so the triplet itself is not a GP. But as part of a GP with terms in between, it's allowed. So, the key is that they don't have to be consecutive. Therefore, even though the middle term squared isn't equal to the product of the first and third, they can still be part of a GP. Therefore, the initial test of b² = a*c is only for consecutive terms. If the terms are not consecutive, that test doesn't apply. Therefore, for the problem at hand, the answer is the triplet where even when considering non-consecutiveness, they cannot be part of any GP.So, the last option is E: 3, 5, 9. Let's check if this can be part of a GP. Let's compute the ratios. 5/3 ≈ 1.666..., and 9/5 = 1.8. These are different, but perhaps they can be expressed as powers of a common ratio. Let's see. Let's suppose that there exists a common ratio r such that 5 = 3 * r^m and 9 = 5 * r^n, where m and n are positive integers. Then, we have r^m = 5/3 and r^n = 9/5. Therefore, r^m * r^n = (5/3)*(9/5) = 3, so r^(m + n) = 3. Also, from r^m = 5/3 and r^n = 9/5, we can write r^(n) = (9/5) = (3^2)/5. Let's see if we can find integers m and n such that these equations hold.Alternatively, take the ratio of the two equations: r^n / r^m = (9/5) / (5/3) = (9/5)*(3/5) = 27/25. So, r^(n - m) = 27/25. So, 27/25 is (3/5)^3? Wait, 27 is 3³, 25 is 5². Hmm, 27/25 is not a perfect power of a rational number unless r is a fraction that can produce 27/25 when raised to some power. Let's check:Suppose r is a rational number p/q. Then, (p/q)^k = 27/25. So, p^k / q^k = 27/25. Therefore, we need integers p, q, k such that p^k = 27 and q^k = 25. But 27 is 3³ and 25 is 5². So, unless k is a common multiple of 3 and 2, which is 6. Then, (3³)^(1/6) = 3^(1/2) and (5²)^(1/6) = 5^(1/3). But these are irrational numbers. Therefore, r would have to be irrational, which would make the GP have irrational ratios. However, in the given triplet, all terms are integers. But a GP with irrational ratio can still have integer terms if the starting term and the exponents somehow combine to give integers. However, in this case, since 3, 5, 9 are integers, but 5 is a prime number, it's hard to see how an irrational ratio could produce 5 from 3. Similarly, starting from 3, if you multiply by an irrational number to get 5, then multiply again to get 9, but it's unlikely. Let me check with logarithms.Take the natural logs: ln(3), ln(5), ln(9). The differences are ln(5) - ln(3) ≈ 0.5108, and ln(9) - ln(5) ≈ 0.5878. Then, the ratio of these differences is 0.5878 / 0.5108 ≈ 1.15. Is this a rational number? 1.15 is 23/20, but approximately. However, it's not exactly a rational number. Since these are transcendental numbers, their differences and ratios are unlikely to be rational. Therefore, there is no common ratio r such that the terms 3, 5, 9 can be embedded in a geometric progression. Therefore, option E cannot be part of a GP, so it is the answer.But let me check again in case I made a mistake. Let's suppose that there is a common ratio r such that 5 = 3 * r^m and 9 = 5 * r^n. Then, from the first equation: r^m = 5/3; from the second equation: r^n = 9/5. Then, (r^m)^n = (5/3)^n and (r^n)^m = (9/5)^m. Since (r^m)^n = (r^n)^m, we have (5/3)^n = (9/5)^m. Cross-multiplying gives 5^n * 5^m = 3^n * 9^m → 5^(n + m) = 3^n * 3^(2m) → 5^(n + m) = 3^(n + 2m). But 5 and 3 are primes, so this equation can only hold if both exponents are zero, which would mean n + m = 0 and n + 2m = 0, but n and m are positive integers, so this is impossible. Therefore, there are no positive integers m and n that satisfy this equation. Hence, there is no common ratio r that can make 3, 5, 9 part of a geometric progression. Therefore, option E is the triplet that cannot represent terms of a GP.Therefore, the answer is E.Final Answerboxed{E}</think>To determine which triplet cannot represent terms of a geometric progression (GP), we need to check if the terms can be part of a GP, even if they are not consecutive. The key property is that for any three terms (a, b, c) in a GP, the ratio between consecutive terms must be consistent, or the logarithms of the terms must form an arithmetic progression.Analysis of each option:- Option A (3, 6, 96): - Ratios: (6/3 = 2) and (96/6 = 16). - (16 = 2^4), so these terms can be part of a GP with common ratio 2. Valid.- Option B (3, 1, 1/81): - Ratios: (1/3) and ((1/81)/1 = 1/81). - (1/81 = (1/3)^4), so these terms can be part of a GP with common ratio (1/3). Valid.- Option C (3, 3.3, 3.993): - Ratios: (3.3/3 = 1.1) and (3.993/3.3 approx 1.21). - (1.21 = 1.1^2), so these terms can be part of a GP with common ratio 1.1. Valid.- Option D (3, 6, 48): - Ratios: (6/3 = 2) and (48/6 = 8). - (8 = 2^3), so these terms can be part of a GP with common ratio 2. Valid.- Option E (3, 5, 9): - Ratios: (5/3 approx 1.666) and (9/5 = 1.8). - These ratios are not powers of a common ratio. Checking logarithms, the differences (ln(5) - ln(3)) and (ln(9) - ln(5)) do not form a rational ratio. This triplet cannot be part of any GP. Invalid.Conclusion:The triplet that cannot represent terms of a geometric progression is (boxed{E}).]

🔑:18) The answer is (E). Indicating with q the ratio of the progression, it is observed that in (A) and (D) the numbers can belong to a progression with q=2 and the first term 3(3 cdot 2=6, 3 cdot 2^{4}=48,3 cdot 2^{5}=96 ). The numbers in (B) can belong to a progression with q=frac{1}{3} and the first term 3left(3 cdot frac{1}{3}=1,3 cdotleft(frac{1}{3}right)^{5}=frac{1}{81}right). The numbers in (C) can belong to a progression with q=1.1 and the first term 3left(3 cdot 1.1=3.3,3 cdot(1.1)^{3}=3.993right). On the other hand, the three terms in (E) cannot belong to the same geometric progression, otherwise one would have left(frac{3}{5}right)^{k}=left(frac{5}{9}right)^{h}, with h and k integers, which has no solutions.