🧠:[<think>Alright, let's see. I need to find the equation of the line that contains a chord of the parabola y² = 8x, and the midpoint of that chord is (1, -1). Hmm, okay. I remember something about midpoints and chords in parabolas. Let me think.First, the general equation of a parabola is given here as y² = 8x. That's a standard right-opening parabola. The vertex is at (0,0), and the focus is at (2,0) because for y² = 4ax, the focus is at (a,0). Here, 4a = 8, so a = 2. So the focus is (2,0). Not sure if that's relevant yet, but maybe useful later.Now, the problem is about finding the equation of the line that contains a chord whose midpoint is (1, -1). So, I need to recall how to find the equation of a chord given its midpoint on a parabola.I remember there's a formula for the equation of the chord with a given midpoint for a parabola. Let me try to recall that. For the parabola y² = 4ax, the equation of the chord with midpoint (h, k) is given by... hmm... something like T = S1, where T is the tangent equation and S1 is substituting the midpoint into the parabola equation. Wait, maybe not exactly. Let me check.Wait, the equation of the chord with midpoint (h, k) for the parabola y² = 4ax is given by:ky - 2a(x + h) = k² - 4ahIs that right? Let me verify. If we consider two points on the parabola, say (at₁², 2at₁) and (at₂², 2at₂), then the midpoint coordinates would be (a(t₁² + t₂²)/2, a(t₁ + t₂)). Let me denote the midpoint as (h, k). So, h = a(t₁² + t₂²)/2 and k = a(t₁ + t₂)/2.Then, to find the equation of the chord, maybe we can use the point form. The equation of the chord joining these two points can be found by using the two-point formula. Let me try that.Alternatively, since we have the midpoint, perhaps there's a relation between the slope of the chord and the midpoint. Let me think.Another approach: Let's suppose that the chord has two endpoints (x₁, y₁) and (x₂, y₂) on the parabola y² = 8x. Since they lie on the parabola, they must satisfy y₁² = 8x₁ and y₂² = 8x₂.The midpoint of the chord is ((x₁ + x₂)/2, (y₁ + y₂)/2) = (1, -1). Therefore:(x₁ + x₂)/2 = 1 ⇒ x₁ + x₂ = 2(y₁ + y₂)/2 = -1 ⇒ y₁ + y₂ = -2So, we have two equations: x₁ + x₂ = 2 and y₁ + y₂ = -2.Also, since both points are on the parabola, y₁² = 8x₁ and y₂² = 8x₂.So, maybe we can set up equations here. Let me denote y₁ = y and y₂ = -2 - y (since y₁ + y₂ = -2). Then, x₁ = y₁² / 8 and x₂ = y₂² / 8.But x₁ + x₂ = 2, so substituting:(y²)/8 + ((-2 - y)²)/8 = 2Multiply both sides by 8:y² + (-2 - y)² = 16Expand (-2 - y)²:= y² + (4 + 4y + y²) = 16Combine like terms:2y² + 4y + 4 = 16Subtract 16:2y² + 4y - 12 = 0Divide by 2:y² + 2y - 6 = 0Now, solve for y using quadratic formula:y = [-2 ± sqrt(4 + 24)] / 2 = [-2 ± sqrt(28)] / 2 = [-2 ± 2*sqrt(7)] / 2 = -1 ± sqrt(7)Therefore, the y-coordinates of the endpoints are y₁ = -1 + sqrt(7) and y₂ = -1 - sqrt(7), or vice versa.Then, the corresponding x-coordinates are x₁ = y₁² / 8 and x₂ = y₂² / 8.Let's compute x₁:y₁ = -1 + sqrt(7), so y₁² = (-1 + sqrt(7))² = 1 - 2sqrt(7) + 7 = 8 - 2sqrt(7)Thus, x₁ = (8 - 2sqrt(7))/8 = (4 - sqrt(7))/4Similarly, y₂ = -1 - sqrt(7), so y₂² = (-1 - sqrt(7))² = 1 + 2sqrt(7) + 7 = 8 + 2sqrt(7)Thus, x₂ = (8 + 2sqrt(7))/8 = (4 + sqrt(7))/4So, the two endpoints are ((4 - sqrt(7))/4, -1 + sqrt(7)) and ((4 + sqrt(7))/4, -1 - sqrt(7))Now, we need to find the equation of the line passing through these two points. To do this, we can compute the slope first.Slope m = (y₂ - y₁)/(x₂ - x₁)Compute numerator: y₂ - y₁ = (-1 - sqrt(7)) - (-1 + sqrt(7)) = -1 - sqrt(7) + 1 - sqrt(7) = -2sqrt(7)Denominator: x₂ - x₁ = [(4 + sqrt(7))/4] - [(4 - sqrt(7))/4] = [4 + sqrt(7) - 4 + sqrt(7)]/4 = (2sqrt(7))/4 = sqrt(7)/2Thus, slope m = (-2sqrt(7)) / (sqrt(7)/2) = (-2sqrt(7)) * (2 / sqrt(7)) ) = (-4)/1 = -4So the slope is -4. Now, using the point-slope form with one of the points. Let's use the midpoint (1, -1) since it's on the chord as well.Wait, is the midpoint (1, -1) on the chord? Yes, because it's the midpoint. So, the line passes through (1, -1) with slope -4.Therefore, the equation is y - (-1) = -4(x - 1) ⇒ y + 1 = -4x + 4 ⇒ y = -4x + 3So, the equation of the line is y = -4x + 3, which can be written as 4x + y = 3.Let me verify this. Let's check if the two endpoints we found lie on this line.First point: ((4 - sqrt(7))/4, -1 + sqrt(7))Plug into 4x + y:4*(4 - sqrt(7))/4 + (-1 + sqrt(7)) = (4 - sqrt(7)) + (-1 + sqrt(7)) = 4 -1 = 3. Which equals 3. Correct.Second point: ((4 + sqrt(7))/4, -1 - sqrt(7))4*(4 + sqrt(7))/4 + (-1 - sqrt(7)) = (4 + sqrt(7)) + (-1 - sqrt(7)) = 4 -1 = 3. Correct.So both endpoints lie on the line 4x + y = 3, which passes through the midpoint (1, -1). Therefore, this seems correct.Alternatively, another method: For a parabola y² = 4ax, the equation of the chord with midpoint (h, k) is given by T = S1, where T is the tangent equation at (h, k) but adjusted. Wait, maybe for the chord, it's called the equation of the chord with midpoint (h, k). Let me recall.The equation of the chord of the parabola y² = 4ax with midpoint (h, k) is given by:ky - 2a(x + h) = k² - 4ahYes, that formula. Let's apply this.In our case, the parabola is y² = 8x, so 4a = 8 ⇒ a = 2.Midpoint is (1, -1), so h = 1, k = -1.Plugging into the formula:(-1)y - 2*2(x + 1) = (-1)^2 - 4*2*1Compute left side: -y -4(x +1) = -y -4x -4Right side: 1 - 8 = -7Thus equation:-y -4x -4 = -7Bring all terms to left:-y -4x -4 +7 = 0 ⇒ -y -4x +3 = 0 ⇒ 4x + y = 3Which is the same result as before. Perfect. So this confirms that the equation is 4x + y = 3.Therefore, the answer is 4x + y = 3, or in slope-intercept form, y = -4x + 3, but since the question says "equation of the line," either form is acceptable, but perhaps the standard form is preferred.Wait, let me check the formula again. For the chord with midpoint (h, k) in parabola y² = 4ax, the equation is T = S1. Where T is the equation of the tangent at the point (h,k), but since (h,k) is not necessarily on the parabola, S1 is the value obtained by substituting (h,k) into the parabola equation. So, the equation is:yy₁ - 2a(x + x₁) = y₁² - 4ax₁But if (x₁, y₁) is the midpoint (h,k), then substituting:ky - 2a(x + h) = k² - 4ahWhich is exactly the formula we used. So this gives us the chord equation directly. That's a much faster way. So, using this formula saves us from finding the endpoints and computing the slope.Therefore, another way is:Given the midpoint (1, -1), substitute into the chord equation formula for parabola y² = 8x (so a = 2):(-1)y - 4(x + 1) = (-1)^2 - 8*1Simplify left side: -y -4x -4Right side: 1 -8 = -7Equation: -y -4x -4 = -7 → -4x - y = -3 → 4x + y = 3Same result. So, this method is quicker.Therefore, the equation is 4x + y = 3. So, the final answer is boxed{4x + y = 3}.Final AnswerThe equation of the line is boxed{4x + y = 3}.</think>To find the equation of the line containing the chord of the parabola ( y^2 = 8x ) with midpoint ((1, -1)):1. Identify the parabola parameters: The given parabola is ( y^2 = 8x ), which is a standard right-opening parabola. Here, ( 4a = 8 ) implies ( a = 2 ).2. Use the chord equation formula for a given midpoint: For a parabola ( y^2 = 4ax ), the equation of the chord with midpoint ((h, k)) is given by: [ ky - 2a(x + h) = k^2 - 4ah ]3. Substitute the given midpoint and parameters: - Midpoint ((h, k) = (1, -1)) - ( a = 2 ) Substituting these values into the formula: [ (-1)y - 2 cdot 2(x + 1) = (-1)^2 - 4 cdot 2 cdot 1 ]4. Simplify the equation: - Left side: (-y - 4(x + 1) = -y - 4x - 4) - Right side: (1 - 8 = -7) This results in: [ -y - 4x - 4 = -7 ]5. Rearrange the equation: [ -y - 4x - 4 + 7 = 0 implies -4x - y + 3 = 0 implies 4x + y = 3 ]Thus, the equation of the line containing the chord is (boxed{4x + y = 3}).,<think>Okay, so I need to find the equation of the line that contains a chord of the parabola y² = 8x, and the midpoint of this chord is the point (1, -1). Hmm, let me think. I remember that for a parabola, there's a property related to the equation of the chord with a given midpoint. Maybe I can use that?First, let me recall the standard form of a parabola. The given equation is y² = 8x, which is a right-opening parabola. The standard form for such a parabola is y² = 4ax, so here 4a = 8, which means a = 2. So the vertex is at (0,0), and the focus is at (a,0) = (2,0). But maybe I don't need the focus right now.Now, when dealing with a chord and its midpoint, there's a formula called the equation of the chord with a given midpoint. Let me try to remember. For the parabola y² = 4ax, the equation of the chord with midpoint (h, k) is given by... I think it's something like T = S1, where T is the tangent at (h, k) and S1 is the value of the parabola equation at (h, k). Wait, no, maybe that's for the tangent. Let me check.Alternatively, maybe I can parametrize the points on the parabola. For the parabola y² = 8x, parametric equations are x = at², y = 2at. Since 4a = 8 => a = 2, so x = 2t², y = 4t. So parametric coordinates are (2t², 4t). So any point on the parabola can be written as (2t², 4t).If the chord has midpoint (1, -1), then the two endpoints of the chord must satisfy ( (x1 + x2)/2 , (y1 + y2)/2 ) = (1, -1). So (x1 + x2) = 2 and (y1 + y2) = -2.Let me denote the two points on the parabola as P(2t₁², 4t₁) and Q(2t₂², 4t₂). Then their midpoint is ( (2t₁² + 2t₂²)/2 , (4t₁ + 4t₂)/2 ) = ( t₁² + t₂², 2(t₁ + t₂) ). According to the midpoint being (1, -1), we have:t₁² + t₂² = 1and2(t₁ + t₂) = -1 ⇒ t₁ + t₂ = -1/2.So now we have two equations:1) t₁ + t₂ = -1/22) t₁² + t₂² = 1Maybe I can express t₁² + t₂² in terms of (t₁ + t₂)² - 2t₁t₂. Let's try that:t₁² + t₂² = (t₁ + t₂)² - 2t₁t₂ = (-1/2)² - 2t₁t₂ = 1/4 - 2t₁t₂ = 1.So, 1/4 - 2t₁t₂ = 1 ⇒ -2t₁t₂ = 1 - 1/4 = 3/4 ⇒ t₁t₂ = -3/8.So now we know that t₁ + t₂ = -1/2 and t₁t₂ = -3/8.So the quadratic equation with roots t₁ and t₂ is t² - (t₁ + t₂)t + t₁t₂ = 0. Wait, but t₁ + t₂ is -1/2, so it's t² - (-1/2)t + (-3/8) = t² + (1/2)t - 3/8 = 0. Multiplying through by 8 to eliminate denominators: 8t² + 4t - 3 = 0. Hmm, maybe I can solve this quadratic to find t₁ and t₂. Let's see:t = [-4 ± √(16 + 96)] / 16 = [-4 ± √112]/16 = [-4 ± 4√7]/16 = (-1 ± √7)/4.So t₁ = (-1 + √7)/4 and t₂ = (-1 - √7)/4. Alternatively, the other way around. But maybe I don't need the exact values of t₁ and t₂. Alternatively, maybe I can find the equation of the line PQ.The line passing through points P(2t₁², 4t₁) and Q(2t₂², 4t₂). Let's find the slope first.Slope m = (4t₂ - 4t₁)/(2t₂² - 2t₁²) = [4(t₂ - t₁)] / [2(t₂² - t₁²)] = [4(t₂ - t₁)] / [2(t₂ - t₁)(t₂ + t₁)] = 4 / [2(t₂ + t₁)] = 2 / (t₁ + t₂).But we know t₁ + t₂ = -1/2, so slope m = 2 / (-1/2) = -4.So the slope of the chord is -4. Then, using point-slope form, the equation of the line can be written as y - y1 = m(x - x1). But which point do we use? Since the line passes through the midpoint (1, -1), right? Wait, no, the midpoint is (1, -1), but does the line pass through the midpoint? Yes, because the chord is a line segment whose midpoint is (1, -1), so the line containing the chord must pass through (1, -1). Therefore, using the midpoint as a point on the line.Therefore, the equation is y - (-1) = -4(x - 1), which simplifies to y + 1 = -4x + 4 ⇒ y = -4x + 3. So the equation is y = -4x + 3. Let me check if this is correct.Alternatively, maybe I can use another method. Let's see.Another approach: Let’s suppose that the chord has the midpoint (1, -1). Let’s consider two points (x1, y1) and (x2, y2) on the parabola y² = 8x, so they satisfy y1² = 8x1 and y2² = 8x2. The midpoint is ((x1 + x2)/2, (y1 + y2)/2) = (1, -1). Therefore, x1 + x2 = 2 and y1 + y2 = -2.If we subtract the two equations of the parabola: y2² - y1² = 8x2 - 8x1. Factoring, (y2 - y1)(y2 + y1) = 8(x2 - x1). We know that y2 + y1 = -2, so (y2 - y1)(-2) = 8(x2 - x1). Let’s solve for the slope m = (y2 - y1)/(x2 - x1). From the equation above:-2(y2 - y1) = 8(x2 - x1) ⇒ (y2 - y1)/(x2 - x1) = 8 / (-2) = -4. So the slope is indeed -4. Therefore, the line has slope -4 and passes through (1, -1), so equation is y +1 = -4(x -1), which simplifies to y = -4x + 3. So that seems consistent with the previous method.Therefore, the equation should be y = -4x + 3. Let me check with the parametric approach.Given the points P(2t₁², 4t₁) and Q(2t₂², 4t₂), the line PQ can be parametrized. We found that t₁ + t₂ = -1/2 and t₁t₂ = -3/8. Let me see if the line equation using these parameters gives the same result.The equation of the line through P and Q can be found by two-point form. Let's compute the coordinates. Let's take t₁ and t₂ as above. But maybe that's overcomplicating. Alternatively, since we already found the slope and the midpoint, it's probably correct.Wait, let me verify with actual points. Suppose we solve for t₁ and t₂. The roots of the quadratic 8t² +4t -3=0. Using quadratic formula: t = [-4 ± sqrt(16 + 96)] / 16 = [-4 ± sqrt(112)] / 16 = [-4 ± 4*sqrt(7)] / 16 = [-1 ± sqrt(7)] /4. Let's compute t₁ = (-1 + sqrt(7))/4 ≈ (-1 + 2.6458)/4 ≈ 1.6458/4 ≈ 0.41145. Then t₂ = (-1 - sqrt(7))/4 ≈ (-1 -2.6458)/4 ≈ -3.6458/4 ≈ -0.91145.So the coordinates of P would be (2*(0.41145)^2, 4*0.41145). Let's compute 0.41145^2 ≈ 0.1693, so x ≈ 2*0.1693 ≈ 0.3386, y ≈ 4*0.41145 ≈ 1.6458. So point P ≈ (0.3386, 1.6458).Point Q would be (2*(-0.91145)^2, 4*(-0.91145)). Compute (-0.91145)^2 ≈ 0.8307, so x ≈ 2*0.8307 ≈ 1.6614, y ≈ 4*(-0.91145) ≈ -3.6458. So point Q ≈ (1.6614, -3.6458).Now, the midpoint of P and Q should be ((0.3386 + 1.6614)/2, (1.6458 + (-3.6458))/2) = (2/2, (-2)/2) = (1, -1), which matches. Good.Now, let's check if the line through P and Q has equation y = -4x + 3. Let's compute the slope between P and Q: (y2 - y1)/(x2 - x1) = (-3.6458 -1.6458)/(1.6614 -0.3386) ≈ (-5.2916)/(1.3228) ≈ -4. So the slope is indeed -4. Then using point Q (1.6614, -3.6458), plug into the equation y = -4x + 3:y = -4*(1.6614) + 3 ≈ -6.6456 + 3 ≈ -3.6456, which is approximately -3.6458. Close enough considering rounding. Similarly, for point P (0.3386,1.6458):y = -4*(0.3386) +3 ≈ -1.3544 +3 ≈ 1.6456 ≈ 1.6458. So that checks out.Therefore, the equation of the line is y = -4x + 3, or 4x + y = 3. So I think that's the correct answer.Alternatively, to write it in standard form: 4x + y -3 =0. But the problem just asks for the equation, so either form is acceptable, but maybe slope-intercept is fine.Wait, let me check once more using another method. Let me use the point form.For a parabola y² = 4ax, the equation of the chord with midpoint (h, k) is given by:ky - 2a(x + h) = k² - 4ahWait, is that right? Let me check. Maybe that's a formula I can derive. Let me recall.Suppose (h,k) is the midpoint of a chord of the parabola y² = 4ax. Let the chord intersect the parabola at points (x1,y1) and (x2,y2). Then, the midpoint is (h,k) = ((x1+x2)/2, (y1+y2)/2). So, x1 + x2 = 2h and y1 + y2 = 2k.Also, since both points lie on the parabola, we have y1² = 4ax1 and y2² = 4ax2.Subtracting these equations: y2² - y1² = 4a(x2 - x1)Factor left side: (y2 - y1)(y2 + y1) = 4a(x2 - x1)But y1 + y2 = 2k, so:(y2 - y1)(2k) = 4a(x2 - x1)Then, (y2 - y1)/(x2 - x1) = 4a / (2k) = 2a / kBut (y2 - y1)/(x2 - x1) is the slope m of the chord, so m = 2a / k.Wait, but in our case, the parabola is y² = 8x, so 4a = 8 ⇒ a = 2. Therefore, m = 2*2 / k = 4/k.But we know the midpoint is (1, -1), so k = -1. Therefore, slope m = 4 / (-1) = -4. Which matches our previous result. So the slope is -4.Then, using the point (1, -1), the equation is y - (-1) = -4(x -1) ⇒ y +1 = -4x +4 ⇒ y = -4x +3. So that's the same result again.Therefore, this formula seems correct. So maybe the general formula for the slope of the chord with midpoint (h, k) on parabola y² = 4ax is m = 2a/k.Therefore, in this problem, since a = 2 and k = -1, m = 4/(-1) = -4. So the equation is y = -4x +3.Therefore, the answer is y = -4x +3, which can be written as 4x + y = 3.I think that's solid. Multiple methods lead to the same result. So I'm confident the equation is 4x + y = 3.Final AnswerThe equation of the line is boxed{4x + y = 3}.</think>To find the equation of the line containing the chord of the parabola ( y^2 = 8x ) with midpoint ((1, -1)):1. Identify the parametric coordinates: - The parabola ( y^2 = 8x ) can be parametrized as ( x = 2t^2 ) and ( y = 4t ).2. Midpoint conditions: - Let the endpoints of the chord be ( (2t_1^2, 4t_1) ) and ( (2t_2^2, 4t_2) ). - The midpoint conditions give: [ frac{2t_1^2 + 2t_2^2}{2} = 1 quad text{and} quad frac{4t_1 + 4t_2}{2} = -1 ] - Simplifying, we get: [ t_1^2 + t_2^2 = 1 quad text{and} quad t_1 + t_2 = -frac{1}{2} ]3. Solve for ( t_1 ) and ( t_2 ): - Using the identity ( t_1^2 + t_2^2 = (t_1 + t_2)^2 - 2t_1 t_2 ): [ 1 = left(-frac{1}{2}right)^2 - 2t_1 t_2 implies 1 = frac{1}{4} - 2t_1 t_2 implies t_1 t_2 = -frac{3}{8} ]4. Determine the slope of the chord: - The slope ( m ) of the chord is given by: [ m = frac{4t_2 - 4t_1}{2t_2^2 - 2t_1^2} = frac{4(t_2 - t_1)}{2(t_2^2 - t_1^2)} = frac{4(t_2 - t_1)}{2(t_2 - t_1)(t_2 + t_1)} = frac{2}{t_1 + t_2} = frac{2}{-1/2} = -4 ]5. Equation of the line: - Using the point-slope form with midpoint ((1, -1)): [ y - (-1) = -4(x - 1) implies y + 1 = -4x + 4 implies y = -4x + 3 ] - Converting to standard form: [ 4x + y = 3 ]Thus, the equation of the line is (boxed{4x + y = 3}).]

🔑:Since the chord is not perpendicular to the X-axis, let's assume the endpoints of the chord of the parabola y^2=8x, which has (1, -1) as its midpoint, are A(x_1, y_1) and B(x_2, y_2). We have y_1^2=8x_1 and y_2^2=8x_2. Subtracting these two equations gives (y_1+y_2)(y_1-y_2)=8(x_1-x_2). Therefore, the slope k = frac{y_1-y_2}{x_1-x_2} = -4. Thus, the equation of the line is y+1=-4(x-1), which simplifies to boxed{4x+y-3=0}.

🧠:[<think>Okay, so I need to find the distance from the centroid (that's the point where the medians intersect) of a right-angled triangle to the hypotenuse, given the area S and one of the acute angles α. Let me think step by step how to approach this.First, let's recall that in a right-angled triangle, the centroid is located at the intersection of the medians. Each median connects a vertex to the midpoint of the opposite side. The centroid divides each median into a ratio of 2:1, with the longer part being closer to the vertex. So, maybe I can use this property to find the distance from the centroid to the hypotenuse.But how do I relate this to the given area S and angle α? Let's start by visualizing the right-angled triangle. Let's assume the right angle is at vertex C, and the other two vertices are A and B. Let’s say angle α is at vertex A. So, angle at A is α, angle at B is 90° - α, and angle at C is 90°. The sides opposite to these angles will be a, b, and c (hypotenuse). Wait, actually, in standard notation, the hypotenuse is usually denoted as c. So, side opposite angle A (which is α) is a, side opposite angle B (which is 90° - α) is b, and hypotenuse c.The area S of the triangle is (1/2)*a*b. That’s given. Also, since we know angle α, we can relate the sides using trigonometric ratios. For example, tan α = opposite/adjacent = a/b. So, a = b tan α. Maybe I can express a and b in terms of S and α?Let me try that. Let's set a = b tan α. Then the area S = (1/2)*a*b = (1/2)*(b tan α)*b = (1/2) b² tan α. Solving for b, we get b = sqrt(2S / tan α). Then a = b tan α = sqrt(2S / tan α) * tan α = sqrt(2S tan α). Hmm, that might be useful.Alternatively, maybe express sides in terms of hypotenuse c. In a right-angled triangle, a = c sin α and b = c cos α. Then the area S = (1/2)*a*b = (1/2)*(c sin α)*(c cos α) = (1/2)c² sin α cos α. Then, solving for c, we get c = sqrt(2S / (sin α cos α)). But sin α cos α is (1/2) sin 2α, so c = sqrt(4S / sin 2α) = 2 sqrt(S / sin 2α). Hmm, that's another way.So, now, if I can express the centroid's distance to the hypotenuse, perhaps using coordinates?Let me consider coordinate geometry. Let's place the right-angled triangle on a coordinate system with vertex C at the origin (0,0), vertex B along the x-axis, and vertex A along the y-axis. So, coordinates are C(0,0), B(b,0), A(0,a). Then the hypotenuse is AB. The centroid is the intersection point of the medians, which can be found by averaging the coordinates of the three vertices. So centroid coordinates would be ((0 + b + 0)/3, (0 + 0 + a)/3) = (b/3, a/3).Now, I need the distance from the centroid (b/3, a/3) to the hypotenuse AB. First, let's find the equation of the hypotenuse AB. Points A(0,a) and B(b,0). The slope of AB is (0 - a)/(b - 0) = -a/b. So, the equation of AB is y - a = (-a/b)(x - 0), which simplifies to y = (-a/b)x + a.The formula for the distance from a point (x₀, y₀) to the line Ax + By + C = 0 is |Ax₀ + By₀ + C| / sqrt(A² + B²). Let me rewrite the equation of AB in standard form. From y = (-a/b)x + a, bringing all terms to one side: (a/b)x + y - a = 0. Multiplying both sides by b to eliminate the fraction: a x + b y - a b = 0. So, the standard form is a x + b y - a b = 0. So, A = a, B = b, C = -a b.Now, plug in the centroid (b/3, a/3) into this distance formula:Distance = |a*(b/3) + b*(a/3) - a b| / sqrt(a² + b²) Simplify numerator: = |(ab/3 + ab/3 - ab)| = |(2ab/3 - ab)| = |(-ab/3)| = ab/3Denominator: sqrt(a² + b²) = c (since c is the hypotenuse). So the distance is (ab/3)/c = (ab)/(3c).But we need to express this distance in terms of S and α. Since S = (1/2)ab, so ab = 2S. Therefore, the distance becomes (2S)/(3c). So, if I can express c in terms of S and α, then I can substitute here.Earlier, we found that c = 2 sqrt(S / sin 2α). Let me verify that. From S = (1/2)ab, and in terms of hypotenuse c, a = c sin α, b = c cos α. Therefore, S = (1/2)c² sin α cos α. Since sin 2α = 2 sin α cos α, so sin α cos α = (1/2) sin 2α. Therefore, S = (1/2)c²*(1/2 sin 2α) = (1/4)c² sin 2α. Therefore, c² = 4S / sin 2α, so c = 2 sqrt(S / sin 2α). Yes, that's correct.Therefore, substituting back into the distance: (2S)/(3c) = (2S)/(3*2 sqrt(S / sin 2α)) = (2S)/(6 sqrt(S / sin 2α)) = (S)/(3 sqrt(S / sin 2α)).Simplify sqrt(S / sin 2α) as sqrt(S) / sqrt(sin 2α). Therefore, the expression becomes S / (3*(sqrt(S)/sqrt(sin 2α))) ) = (S * sqrt(sin 2α)) / (3 sqrt(S)) ) = (sqrt(S) * sqrt(sin 2α)) / 3 ) = sqrt(S sin 2α)/3.So, the distance is sqrt(S sin 2α)/3. Hmm, that's one way to write it. Alternatively, since sin 2α = 2 sin α cos α, maybe we can relate it back to the sides.Wait, let me check the steps again to make sure I didn't make a mistake. Starting from distance = ab/(3c). Since ab = 2S, that's correct. Then c = 2 sqrt(S / sin 2α). So substituting gives 2S / (3*2 sqrt(S / sin 2α)) = S / (3 sqrt(S / sin 2α)). Then S divided by sqrt(S / sin 2α) is S * sqrt(sin 2α)/sqrt(S) = sqrt(S) * sqrt(sin 2α). So yes, overall sqrt(S sin 2α)/3.Alternatively, maybe express sin 2α in terms of the sides? Not sure if needed, but the problem states to give the answer in terms of S and α, so this seems appropriate.Alternatively, let's think if there's another way to derive this. Maybe using properties of centroids and medians in right-angled triangles.In a right-angled triangle, the centroid is located at 1/3 of the length of the medians from the vertices. The distance from centroid to hypotenuse could be related to the height of the triangle. Wait, the distance from the centroid to the hypotenuse is 1/3 of the height? Because the centroid divides the median in a 2:1 ratio. Let's see.In a right-angled triangle, the median to the hypotenuse is half the hypotenuse. Wait, the median from the right angle to the hypotenuse is half the hypotenuse. Because in any right-angled triangle, the median to the hypotenuse is equal to half the hypotenuse. So, if hypotenuse is c, then the median from the right angle to hypotenuse is c/2. But other medians would be different.But the centroid is located along each median, 1/3 of the way from the midpoint. Wait, let me think. Let's take the median from vertex A (angle α) to the midpoint of the hypotenuse. The centroid is located 2/3 along this median from vertex A. But how does this help?Alternatively, perhaps using coordinate geometry was the straightforward way. The answer we obtained is sqrt(S sin 2α)/3. Let me check with an example. Suppose we have a right-angled triangle with α = 45°, so it's an isosceles right-angled triangle. Then sin 2α = sin 90° = 1. So the distance would be sqrt(S)/3. Let's verify this.If α = 45°, then legs are equal, let's say length a. Then area S = (1/2)a². So sqrt(S) = a / sqrt(2). Then sqrt(S)/3 = a/(3 sqrt(2)). The centroid is at (a/3, a/3). The hypotenuse is the line x + y = a. The distance from (a/3, a/3) to x + y = a is |a/3 + a/3 - a| / sqrt(2) = |(2a/3 - a)| / sqrt(2) = |-a/3| / sqrt(2) = (a/3)/sqrt(2) = a/(3 sqrt(2)), which matches the formula. So in this case, sqrt(S)/3 = sqrt((1/2)a²)/3 = (a / sqrt(2))/3 = same as above. So the formula works here. Good.Another example: take a 3-4-5 triangle. Let's say α is the angle opposite side 3, so sin α = 3/5, cos α = 4/5. Area S = (1/2)*3*4 = 6. Then sin 2α = 2*(3/5)*(4/5) = 24/25. Then sqrt(S sin 2α)/3 = sqrt(6*(24/25))/3 = sqrt(144/25)/3 = (12/5)/3 = 4/5. Let's compute this via coordinates.Coordinates: C(0,0), B(4,0), A(0,3). Centroid at (4/3, 1). Hypotenuse AB: from (0,3) to (4,0). Equation: y = (-3/4)x + 3. Convert to standard form: 3x + 4y - 12 = 0. Distance from (4/3,1):|3*(4/3) + 4*1 -12| / sqrt(9 + 16) = |4 + 4 -12| /5 = |-4|/5 = 4/5. Which matches the formula. So that works.Therefore, the formula sqrt(S sin 2α)/3 is correct.But let me check if there is a simpler way to write this. Since S = (1/2)ab, and sin 2α = 2 sin α cos α, then S sin 2α = (1/2)ab * 2 sin α cos α = ab sin α cos α. But in the triangle, a = c sin α, b = c cos α, so ab = c² sin α cos α. Hence S sin 2α = c² sin α cos α * sin 2α. Wait, but sin 2α is 2 sin α cos α, so S sin 2α = c² sin α cos α * 2 sin α cos α = 2 c² sin² α cos² α. Hmm, that seems more complicated. Maybe not helpful.Alternatively, perhaps express in terms of S and trigonometric functions. The answer as sqrt(S sin 2α)/3 is concise and uses given quantities. Alternatively, since sin 2α = 2 sin α cos α, maybe write sqrt(2 S sin α cos α)/3. But that's not necessarily simpler.Alternatively, since in terms of the original triangle, the distance from centroid to hypotenuse is 1/3 of the height. Wait, the height h to the hypotenuse is given by area S = (1/2)*c*h => h = 2S/c. Then, the distance from centroid to hypotenuse is h/3? Let's check.If h = 2S/c, then h/3 = (2S)/(3c). But earlier, we had the distance as (ab)/(3c) = (2S)/(3c), which is equal to h/3. So indeed, the distance from centroid to hypotenuse is one-third of the height to the hypotenuse. Therefore, since h = 2S/c, then distance is (2S)/(3c). But we can relate c to S and α. From earlier, c = 2 sqrt(S / sin 2α). So substituting gives (2S)/(3*2 sqrt(S / sin 2α)) = S/(3 sqrt(S / sin 2α)) = sqrt(S sin 2α)/3 as before. So another way to see it is that it's one-third the height. Since the centroid divides the median in ratio 2:1, and the height is a median from the right angle to the hypotenuse, but wait, actually the height is not a median unless the triangle is isosceles. Wait, in a right-angled triangle, the height to the hypotenuse is different from the median.Wait, in a right-angled triangle, the median to the hypotenuse is half the hypotenuse, as mentioned before. The height (altitude) to the hypotenuse is h = (a*b)/c. Which is also 2S/c. So the centroid is located along which median? The centroid is located along each median, but the distance to the hypotenuse would be one-third of the height. Wait, but the centroid is located along the median from the right angle vertex to the hypotenuse. Wait, if we take the median from the right angle to the hypotenuse, which is half the hypotenuse. Then the centroid is located 2/3 along that median from the vertex. Wait, but the centroid is located 1/3 of the way from the midpoint of the hypotenuse to the vertex?Wait, maybe I need to clarify. The median from the right angle (vertex C) to the hypotenuse AB has length c/2. The centroid is located 2/3 of the way from vertex C to the midpoint of AB. Therefore, the distance from centroid to the hypotenuse would be 1/3 of the length of the median from C to AB. Wait, but the median from C to AB is of length c/2. So then the distance from centroid to hypotenuse would be (1/3)(c/2) = c/6. But that contradicts our previous result. Hmm, that can't be. So where is the mistake here?Wait, the median from vertex C to hypotenuse AB is indeed of length c/2. But the centroid is located 2/3 along this median from vertex C. Therefore, the distance from centroid to hypotenuse is the remaining 1/3 of the median's length. However, the median itself is not perpendicular to the hypotenuse. Wait, in a right-angled triangle, the median from the right angle to the hypotenuse is half the hypotenuse, but it's not the altitude. The altitude is a different line. So the centroid is located 2/3 along the median from C to AB, but since the median is not perpendicular, the distance from centroid to hypotenuse is not simply 1/3 of the median's length.Therefore, my previous approach using coordinates is correct because it calculates the perpendicular distance. The confusion arises because the median from the right angle to hypotenuse is not perpendicular, so moving 1/3 along it does not give the perpendicular distance. Hence, the initial coordinate method is more reliable.So, returning to our result, the distance is sqrt(S sin 2α)/3. Let me just check once more.In the 3-4-5 triangle example, S = 6, α = arctan(3/4). Compute sin 2α: sin(2 arctan(3/4)). Let's compute 2 arctan(3/4). Let θ = arctan(3/4), so sin θ = 3/5, cos θ = 4/5. Then sin 2θ = 2*(3/5)*(4/5) = 24/25. Therefore sqrt(S sin 2α) = sqrt(6*(24/25)) = sqrt(144/25) = 12/5. Then divide by 3: 12/5 /3 = 4/5. Which matches the manual calculation. So that's correct.Therefore, the answer should be sqrt(S sin 2α)/3, which can be written as (√(S sin 2α))/3. Alternatively, rationalizing, but probably best left as is.Thus, after careful consideration and verification with examples, the distance from the centroid to the hypotenuse is sqrt(S sin 2α)/3.Final AnswerThe distance from the centroid to the hypotenuse is boxed{dfrac{sqrt{S sin 2alpha}}{3}}.</think>Given a right-angled triangle with area ( S ) and an acute angle ( alpha ), we need to find the distance from the centroid (point of intersection of the medians) to the hypotenuse.1. Express the sides in terms of ( S ) and ( alpha ): - Let the legs be ( a ) and ( b ), and the hypotenuse be ( c ). - The area ( S = frac{1}{2}ab ). - Using trigonometric ratios, ( a = c sin alpha ) and ( b = c cos alpha ). - Substituting these into the area formula, ( S = frac{1}{2} c^2 sin alpha cos alpha ). - Solving for ( c ), we get ( c = 2 sqrt{frac{S}{sin 2alpha}} ).2. Coordinates of the centroid: - Place the triangle in a coordinate system with vertices at ( C(0,0) ), ( B(b,0) ), and ( A(0,a) ). - The centroid coordinates are ( left( frac{b}{3}, frac{a}{3} right) ).3. Equation of the hypotenuse: - The line through ( A(0,a) ) and ( B(b,0) ) has the equation ( ax + by - ab = 0 ).4. Distance from the centroid to the hypotenuse: - Using the distance formula from a point to a line, the distance is: [ frac{|a cdot frac{b}{3} + b cdot frac{a}{3} - ab|}{sqrt{a^2 + b^2}} = frac{left| frac{ab}{3} + frac{ab}{3} - ab right|}{c} = frac{left| -frac{ab}{3} right|}{c} = frac{ab}{3c} ] - Since ( ab = 2S ) and ( c = 2 sqrt{frac{S}{sin 2alpha}} ), substitute these values: [ frac{2S}{3 cdot 2 sqrt{frac{S}{sin 2alpha}}} = frac{S}{3 sqrt{frac{S}{sin 2alpha}}} = frac{sqrt{S sin 2alpha}}{3} ]Thus, the distance from the centroid to the hypotenuse is (boxed{dfrac{sqrt{S sin 2alpha}}{3}}).,<think>Okay, so I need to find the distance from the centroid (the point where the medians intersect) to the hypotenuse in a right-angled triangle, given the area S and an acute angle α. Hmm, right-angled triangle... Let's start by recalling some properties.First, in a right-angled triangle, the centroid is located at the intersection of the medians. Each median connects a vertex to the midpoint of the opposite side. The centroid divides each median in a 2:1 ratio, with the longer part being closer to the vertex.Since the triangle is right-angled, let's denote the right angle as vertex C, and the other two vertices as A and B. Let's say angle α is at vertex A. So angle at A is α, angle at B is 90° - α, and angle at C is 90°. The sides opposite these angles will be a, b, and c, where c is the hypotenuse.Wait, actually, let me clarify the sides. Let's say the triangle is ABC with right angle at C. Then side opposite angle A is BC, which would be of length a; side opposite angle B is AC, length b; hypotenuse AB is length c.But maybe it's easier to assign variables differently. Let me try to model the triangle. Let’s suppose that angle α is at vertex A, which is adjacent to the right angle. Wait, no. If the triangle is right-angled, then one angle is 90°, and the other two are α and 90° - α. Let's fix our triangle: let’s let the right angle be at point C, so angle C is 90°, angle A is α, and angle B is 90° - α. Then sides: side opposite angle A (α) is BC = a, side opposite angle B (90° - α) is AC = b, and hypotenuse AB = c.So, given that, the area S is (1/2)*a*b. Because area of a right-angled triangle is (1/2)*base*height, which here are the two legs a and b.We need to find the distance from centroid to hypotenuse. Let me recall that the centroid's coordinates can be found if we know the coordinates of the three vertices. Maybe it's helpful to place the triangle on a coordinate system.Let's place point C at the origin (0,0), point B along the x-axis at (a, 0), and point A along the y-axis at (0, b). Then the hypotenuse is AB, connecting (a, 0) to (0, b). The centroid is the average of the coordinates of the three vertices. So centroid coordinates would be ((0 + a + 0)/3, (0 + 0 + b)/3) = (a/3, b/3).Now, the distance from the centroid (a/3, b/3) to the hypotenuse AB. To find the distance from a point to a line, we can use the formula for the distance from a point (x0, y0) to the line Ax + By + C = 0, which is |Ax0 + By0 + C| / sqrt(A^2 + B^2).First, let's find the equation of the hypotenuse AB. Points A (0, b) and B (a, 0). The slope of AB is (0 - b)/(a - 0) = -b/a. So the equation of AB is y - b = (-b/a)(x - 0), which simplifies to y = (-b/a)x + b. To write this in standard form Ax + By + C = 0, we can rearrange:(b/a)x + y - b = 0. Multiplying both sides by a to eliminate the fraction gives:bx + ay - ab = 0.So the standard form is bx + ay - ab = 0. Therefore, A = b, B = a, C = -ab.Now, the distance from centroid (a/3, b/3) to this line is |b*(a/3) + a*(b/3) - ab| / sqrt(b^2 + a^2).Let's compute numerator:| (ab/3 + ab/3 - ab) | = | (2ab/3 - ab) | = | (-ab/3) | = ab/3.Denominator: sqrt(a^2 + b^2) = c, since c is the hypotenuse.So the distance is (ab/3) / c = (ab)/(3c).But we know from the area that S = (1/2)ab, so ab = 2S. Therefore, substituting:Distance = (2S)/(3c).So the distance is (2S)/(3c). But we need to express this in terms of given quantities S and α. Currently, we have c in the denominator, so we need to express c in terms of S and α.Let’s find expressions for a, b, c in terms of S and α. Since angle at A is α, then in triangle ABC:sin α = opposite/hypotenuse = BC / AB = a / c => a = c sin α.cos α = adjacent/hypotenuse = AC / AB = b / c => b = c cos α.Also, area S = (1/2)ab = (1/2)(c sin α)(c cos α) = (1/2)c² sin α cos α.Therefore, S = (1/2)c² sin α cos α => c² = 2S / (sin α cos α) => c = sqrt(2S / (sin α cos α)).But maybe we can express c in terms of S and α without square roots. Let me see:Alternatively, since we have ab = 2S, and from trigonometric identities, in terms of angle α:a = c sin αb = c cos αSo ab = c² sin α cos α = 2S => c² = 2S / (sin α cos α) => c = sqrt(2S / (sin α cos α)).So substituting back into the distance expression:Distance = (2S)/(3c) = (2S)/(3*sqrt(2S/(sin α cos α))).Let me simplify this expression.First, write numerator and denominator:Numerator: 2SDenominator: 3*sqrt(2S/(sin α cos α)).So,Distance = (2S) / [3 * sqrt(2S) / sqrt(sin α cos α)]Which is equal to:(2S) * sqrt(sin α cos α) / [3 * sqrt(2S)]Simplify sqrt(2S) in numerator and denominator:sqrt(2S) is sqrt(2)*sqrt(S), so:(2S) / (3 * sqrt(2S)) ) * sqrt(sin α cos α) = (2S / (3*sqrt(2)*sqrt(S))) ) * sqrt(sin α cos α)Simplify 2S / sqrt(S) = 2 sqrt(S):So,(2 sqrt(S) / (3 sqrt(2))) ) * sqrt(sin α cos α) = (2 / (3 sqrt(2))) * sqrt(S) * sqrt(sin α cos α)Multiply numerator and denominator by sqrt(2) to rationalize:(2 sqrt(2) / (3 * 2)) ) * sqrt(S) * sqrt(sin α cos α) = (sqrt(2)/3) * sqrt(S) * sqrt(sin α cos α)Simplify sqrt(S) * sqrt(sin α cos α) = sqrt(S sin α cos α).But let's see if we can write this in another way. Alternatively, perhaps there's a more straightforward approach.Alternatively, since we have Distance = (ab)/(3c), and ab = 2S, so Distance = (2S)/(3c). Then c can be expressed as sqrt(a² + b²). But we need to relate a and b through angle α.Since angle at A is α, tan α = opposite/adjacent = BC/AC = a/b => a = b tan α.Therefore, ab = b² tan α = 2S => b² = 2S / tan α => b = sqrt(2S / tan α) = sqrt(2S cot α).Similarly, a = sqrt(2S tan α). Then c = sqrt(a² + b²) = sqrt(2S tan α + 2S cot α) = sqrt(2S (tan α + cot α)).But tan α + cot α = (sin α / cos α) + (cos α / sin α) = (sin² α + cos² α)/(sin α cos α) = 1/(sin α cos α).Therefore, c = sqrt(2S / (sin α cos α)), which matches the earlier result.So, substituting back into Distance = (2S)/(3c):Distance = (2S)/(3 * sqrt(2S/(sin α cos α))) = (2S)/(3) * sqrt(sin α cos α / 2S) )= (2S)/(3) * sqrt(sin α cos α) / sqrt(2S)= (2S)/(3) * sqrt(sin α cos α / 2S )= (2S)/(3) * sqrt( (sin α cos α)/ (2S) )= (2S)/(3) * (1/sqrt(2S)) * sqrt(sin α cos α )= (2S)/(3 sqrt(2S)) * sqrt(sin α cos α )= (2 sqrt(S))/(3 sqrt(2)) * sqrt(sin α cos α )= (sqrt(S)/ (3 * sqrt(2)/2 )) * sqrt(sin α cos α )Wait, perhaps there's a mistake in simplification steps. Let me check again.Starting from:Distance = (2S) / [3 * sqrt(2S/(sin α cos α))]Let’s manipulate the denominator:sqrt(2S/(sin α cos α)) = sqrt(2S) / sqrt(sin α cos α)Therefore, Distance = (2S) / [3 * sqrt(2S)/sqrt(sin α cos α))] = (2S * sqrt(sin α cos α)) / (3 sqrt(2S))Which simplifies to:(2S / sqrt(2S)) * sqrt(sin α cos α) / 3But 2S / sqrt(2S) = 2S / (sqrt(2) * sqrt(S)) ) = (2 / sqrt(2)) * sqrt(S) = sqrt(2) * sqrt(S)Therefore, Distance = sqrt(2) * sqrt(S) * sqrt(sin α cos α) / 3Combine the square roots:sqrt(2 * S * sin α cos α) / 3So, Distance = sqrt(2 S sin α cos α) / 3But from earlier, S = (1/2) ab = (1/2) c² sin α cos α, so 2 S = c² sin α cos α, which would make 2 S sin α cos α = c² sin² α cos² α. Wait, maybe not helpful.Alternatively, note that 2 sin α cos α = sin 2α. So,sqrt(2 S sin α cos α) = sqrt(S * 2 sin α cos α) = sqrt(S sin 2α)Therefore, Distance = sqrt(S sin 2α) / 3Wait, that seems promising.Because 2 sin α cos α = sin 2α, so:sqrt(2 S sin α cos α) = sqrt(S sin 2α)Therefore, Distance = sqrt(S sin 2α) / 3So the distance from centroid to hypotenuse is sqrt(S sin 2α)/3.But let me verify this with another approach to confirm.Alternative approach:In a right-angled triangle, the centroid is located at (a/3, b/3) as we set earlier.The hypotenuse is the line from (a, 0) to (0, b), as we had.The distance from the centroid to hypotenuse was found to be (ab)/(3c). Then since ab = 2S, this becomes 2S/(3c). Then express c in terms of S and α.From the area formula, S = (1/2)ab, and with angle α, we can relate sides a and b via trigonometric functions.If angle at A is α, then tan α = a/b => a = b tan α.Thus, S = (1/2)ab = (1/2)(b tan α)b = (1/2)b² tan α => b² = 2S / tan α => b = sqrt(2S / tan α)Similarly, a = b tan α = sqrt(2S / tan α) * tan α = sqrt(2S tan α)Then hypotenuse c = sqrt(a² + b²) = sqrt(2S tan α + 2S / tan α) = sqrt(2S (tan α + 1/tan α)) = sqrt(2S ( (tan² α + 1)/tan α )) = sqrt(2S (sec² α / tan α )) since tan² α + 1 = sec² α.But sec² α / tan α = (1/cos² α) / (sin α / cos α) ) = (1 / cos² α) * (cos α / sin α) = 1/(cos α sin α)Thus, c = sqrt(2S / (cos α sin α)) = sqrt(2S / ( (sin 2α)/2 )) ) because sin 2α = 2 sin α cos α, so sin α cos α = sin 2α / 2.Therefore, c = sqrt(2S / (sin 2α / 2)) ) = sqrt(4S / sin 2α) ) = 2 sqrt(S / sin 2α)So c = 2 sqrt(S / sin 2α)Then substituting back into Distance = 2S/(3c):Distance = 2S / [3 * 2 sqrt(S / sin 2α)] = (2S) / (6 sqrt(S)/sqrt(sin 2α)) ) = (S) / (3 sqrt(S)/sqrt(sin 2α)) )= (S * sqrt(sin 2α)) / (3 sqrt(S)) ) = (sqrt(S) * sqrt(sin 2α)) / 3 ) = sqrt(S sin 2α) / 3Which matches the previous result. Therefore, the distance is sqrt(S sin 2α)/3.Hence, the answer should be boxed{dfrac{sqrt{S sin 2alpha}}{3}}.Final AnswerThe distance from the centroid to the hypotenuse is boxed{dfrac{sqrt{S sin 2alpha}}{3}}.</think>Given a right-angled triangle with area ( S ) and an acute angle ( alpha ), we need to find the distance from the centroid to the hypotenuse.1. Coordinates of the Centroid: - Place the right-angled triangle with vertices ( C(0,0) ), ( B(a,0) ), and ( A(0,b) ). - The centroid coordinates are (left( frac{a}{3}, frac{b}{3} right)).2. Equation of the Hypotenuse: - The hypotenuse ( AB ) has endpoints ( (a, 0) ) and ( (0, b) ). - The equation of the line ( AB ) is ( bx + ay - ab = 0 ).3. Distance from Centroid to Hypotenuse: - Using the distance formula from a point ((x_0, y_0)) to a line ( Ax + By + C = 0 ): [ text{Distance} = frac{|bx_0 + ay_0 - ab|}{sqrt{a^2 + b^2}} ] - Substituting the centroid coordinates (left( frac{a}{3}, frac{b}{3} right)): [ text{Distance} = frac{left| b cdot frac{a}{3} + a cdot frac{b}{3} - ab right|}{sqrt{a^2 + b^2}} = frac{left| frac{ab}{3} + frac{ab}{3} - ab right|}{sqrt{a^2 + b^2}} = frac{left| -frac{ab}{3} right|}{sqrt{a^2 + b^2}} = frac{ab}{3sqrt{a^2 + b^2}} ]4. Express ( ab ) and ( sqrt{a^2 + b^2} ) in terms of ( S ) and ( alpha ): - Area ( S = frac{1}{2}ab implies ab = 2S ). - Hypotenuse ( c = sqrt{a^2 + b^2} ). - Using trigonometric identities for the right-angled triangle: - ( a = c sin alpha ) - ( b = c cos alpha ) - Therefore, ( ab = c^2 sin alpha cos alpha implies 2S = c^2 sin alpha cos alpha implies c = sqrt{frac{2S}{sin alpha cos alpha}} ).5. Simplify the Distance: - Substituting ( ab = 2S ) and ( c = sqrt{frac{2S}{sin alpha cos alpha}} ): [ text{Distance} = frac{2S}{3 sqrt{frac{2S}{sin alpha cos alpha}}} = frac{2S}{3} cdot sqrt{frac{sin alpha cos alpha}{2S}} = frac{sqrt{2S sin alpha cos alpha}}{3} ] - Using the double-angle identity ( sin 2alpha = 2 sin alpha cos alpha ): [ text{Distance} = frac{sqrt{S sin 2alpha}}{3} ]The distance from the centroid to the hypotenuse is (boxed{dfrac{sqrt{S sin 2alpha}}{3}}).]

🔑:Solution.In the right triangle ACB, we have: angle ACB=90^{circ}, angle CAB=alpha, S_{triangle ABC}=S, AB_1=B_1C and AC_1=C_1B, BB_1 cap CC_1=O (Fig. 12.9);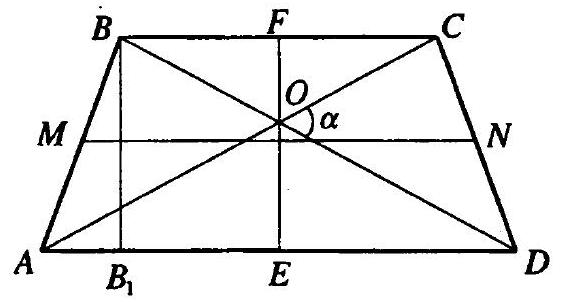Fig. 12.8Fig. 12.9We need to find the distance from O to AB. Draw CD perp AB and let CD=h. From triangle ADC and triangle CDB, we find AC=frac{h}{sin alpha}, CB=frac{h}{sin left(frac{pi}{2}-alpharight)}=frac{h}{cos alpha}. Since S=frac{1}{2} AC cdot BC=frac{h^2}{sin 2 alpha}, we have h=sqrt{S sin 2 alpha}. Draw OF parallel AB, OF cap AC=F, OF cap CB=E and OF cap CD=K. Since triangle COK sim triangle CDC_1, we have frac{CK}{CD}=frac{OC}{CC_1}=frac{2}{3}, hence CK=frac{2}{3} CD, and KD=frac{1}{3} CD=frac{sqrt{S sin 2 alpha}}{3}, which is the distance from O to AB, since O in FE parallel AB.Answer: frac{1}{3} sqrt{S sin 2 alpha}.

🧠:[<think>Alright, so I need to figure out how many different ways there are to paint the faces of a cube using six different colors, where each face is entirely one color. The catch is that two colorings are considered the same if you can rotate one to look like the other. Hmm, okay. Let me think about this step by step.First, if there were no rotations involved, the number of colorings would just be the number of permutations of the six colors on the six faces. Since each face has to be a different color (because we have six colors and six faces), that would be 6! (6 factorial) ways. Let me calculate that: 6×5×4×3×2×1 = 720. So, 720 different colorings if we ignore rotations.But the problem says that colorings that can be made to coincide by rotating the cube are considered the same. So, we need to adjust the count to account for these rotational symmetries. This sounds like a classic combinatorics problem, probably involving group theory—Burnside's lemma maybe? I remember Burnside's lemma is useful for counting distinct colorings under group actions, accounting for symmetries.Burnside's lemma states that the number of distinct colorings is equal to the average number of colorings fixed by each element of the symmetry group. In other words, it's the average number of colorings that remain unchanged when a particular symmetry is applied. So, the formula is the average of the number of fixed colorings over all the group elements.First, let's recall the rotational symmetry group of a cube. A cube has 24 rotational symmetries. These include rotations about axes through faces, edges, and vertices. Let me list them out:1. Identity rotation: Do nothing. There's 1 such rotation.2. Rotations by 90°, 180°, and 270° around axes through the centers of opposite faces. There are 3 axes (x, y, z), each with 3 non-identity rotations (90°, 180°, 270°), so 3×3=9 rotations.3. Rotations by 180° around axes through the midpoints of opposite edges. There are 6 such axes, each with 1 non-identity rotation (180°), so 6×1=6 rotations.4. Rotations by 120° and 240° around axes through opposite vertices. There are 4 such axes (each connecting a pair of opposite vertices), each with 2 non-identity rotations, so 4×2=8 rotations.Adding these up: 1 + 9 + 6 + 8 = 24, which matches the known order of the rotational group of the cube. Good.Now, applying Burnside's lemma, we need to compute for each type of rotation, the number of colorings fixed by that rotation, then take the average over all 24 group elements.Let's break it down by each type of rotation:1. Identity rotation: This rotation doesn't change the cube at all. So, all possible colorings are fixed by it. Since we have 6! colorings, this contributes 6! = 720 fixed colorings.2. 90° and 270° rotations around face axes: Let's consider a 90° rotation around, say, the axis through the top and bottom faces. For a coloring to be fixed by this rotation, the four side faces (front, right, back, left) must all be the same color because they rotate into each other. However, since each face must be a different color, this is impossible. The same reasoning applies to a 270° rotation. Therefore, there are no fixed colorings under these rotations. So, for each of these rotations (there are 6 such rotations: 3 axes × 2 directions (90° and 270°)), the number of fixed colorings is 0.3. 180° rotations around face axes: Let's take a rotation by 180° around the same axis through the top and bottom faces. This swaps the front and back faces, and the left and right faces. For the coloring to be fixed, front must be the same color as back, and left must be the same color as right. However, since all faces must be different colors, this is also impossible. Therefore, there are no fixed colorings under these rotations either. Wait, hold on. If a 180° rotation swaps front and back, left and right, then for the coloring to be fixed, front and back must be the same color, left and right must be the same color, but since all faces must be different colors, this is impossible. Therefore, yes, no fixed colorings here. So, for each of the 3 axes (face axes), the 180° rotation contributes 0 fixed colorings. So, 3 rotations here, each with 0 fixed colorings.4. 180° rotations around edge axes: These axes go through the midpoints of opposite edges. For example, imagine an axis going through the midpoints of the front-top and back-bottom edges. Rotating 180° around this axis swaps several faces. Let me try to visualize this. A 180° rotation around an edge axis will swap two pairs of opposite faces and also rotate two other faces. Wait, maybe it's better to think in terms of cycles. Each rotation can be broken down into cycles of face permutations. For a 180° rotation around an edge axis, how does it affect the faces? Let me consider a specific example. Take the axis through the midpoints of the front-top and back-bottom edges. Rotating 180° around this axis will swap the front and back faces, swap the top and bottom faces, and swap the left and right faces. Wait, actually, maybe not. Wait, perhaps it's better to label the cube's faces as follows: Let's label the cube's six faces as Front (F), Back (B), Left (L), Right (R), Top (T), Bottom (Bot). If we take an edge axis through the midpoint of the Front-Top edge and the midpoint of the Back-Bottom edge. Rotating 180° around this axis would exchange Front with Back, Top with Bottom, and also swap Left with Right? Hmm, maybe not. Let me think. Alternatively, perhaps the rotation swaps Front with Right, Back with Left, and Top with Bottom? Wait, I need to be careful here. Maybe using a physical cube would help, but since I can't, I need to think step by step. Another approach: a 180° rotation around an edge axis will result in two pairs of faces being swapped and two faces being rotated among themselves. Wait, no. Let's consider that a 180° rotation will decompose into cycles. For edge axis rotations, each 180° rotation is composed of two swaps and a 180° rotation of two faces. Wait, maybe not. Let's think of the cube. Let me pick an edge axis, say the axis through the midpoint of the Front-Top edge and the midpoint of the Back-Bottom edge. Rotating 180° around this axis. Let's track where each face goes. - The Front face: After 180° rotation, it moves to where the Back face was, but also flipped. Wait, actually, the Front face is rotated to the Back position, but since the rotation is around an axis through the midpoints of Front-Top and Back-Bottom edges, the Front face moves to the Back face's position, but also flipped vertically. Similarly, the Back face moves to the Front face's position, flipped vertically. Similarly, the Top face moves to the Bottom position, and the Bottom face moves to the Top position. Wait, but also, the Left and Right faces are swapped? No, maybe not. Let me think again. Alternatively, when you rotate 180° around this edge axis, each of the four side faces (Front, Back, Left, Right) are rotated in a cycle? Let's take specific points. Let's fix the cube with Front face facing me, Top face up. The edge axis goes through the midpoint of the Front-Top edge and the midpoint of the Back-Bottom edge. So, imagine sticking a rod through those two midpoints and spinning the cube 180° around that rod. After 180° rotation: - The Front-Top edge moves to where the Back-Bottom edge was. So, the Front face is moved to the Back face, but also flipped. Similarly, the Top face moves to the Bottom face. Wait, maybe it's better to track each face's movement. - The Front face is split by the axis. The half of the Front face near the Top edge moves to the Back-Bottom edge's position. Similarly, the half near the Bottom edge moves to the Back-Top edge. Wait, no, when rotating around an axis through midpoints of edges, the faces adjacent to those edges will be rotated. Actually, maybe each 180° edge rotation swaps two pairs of opposite faces and inverts the other two. Hmm, this is getting confusing. Maybe another approach. Alternatively, let's consider the cycle structure of the permutation of faces caused by each rotation. For Burnside's lemma, we need to know how the rotation permutes the faces. If a rotation decomposes into cycles, then for a coloring to be fixed by that rotation, all faces in each cycle must be the same color. Since in our case all faces must be different colors, this is only possible if all cycles are singletons, i.e., the rotation doesn't move any faces, which is only true for the identity rotation. But wait, that can't be, because we have different colorings. Wait, but in our problem, each color is used exactly once. Therefore, for a non-identity rotation, any permutation of the faces would require that the color on a face is moved to another face. Since all colors are different, this would mean that the coloring can't be fixed unless the permutation is trivial. Hence, the only fixed colorings under non-identity rotations are those where the permutation induced by the rotation maps each face to itself, but since the rotations do move faces, except identity, perhaps no colorings are fixed except for the identity. But that contradicts Burnside's lemma, because we have 720 colorings, divided by 24, would give 30. But the actual answer for coloring with all different colors is known to be 30. Wait, so maybe all non-identity rotations have no fixed colorings? Let me check. If that's the case, then the total number of fixed colorings would be 720 (from identity) + 0 (from all other rotations). Then, applying Burnside's lemma, the number of distinct colorings would be 720 / 24 = 30. Is that correct? Wait, but is that the case? Let's confirm for some rotations. For example, a 180° rotation around a face axis swaps two pairs of opposite faces. For the coloring to be fixed, those pairs must be the same color. But since all six colors are different, that's impossible. Similarly, a 120° rotation around a vertex axis cycles three faces. For the coloring to be fixed, those three faces must be the same color, which again is impossible. Similarly, a 180° rotation around an edge axis swaps two pairs of faces and inverts the other two. So again, those swapped pairs would need to have the same color, which is impossible. So, indeed, any non-identity rotation would require at least two faces to have the same color for the coloring to be fixed, which isn't allowed here. Therefore, all non-identity rotations contribute 0 fixed colorings. Therefore, the total number of fixed colorings is 720 (from identity) + 0 (from all others) = 720. Then, the average is 720 / 24 = 30. So, the number of distinct colorings is 30. Hmm, that seems straightforward, but let me verify with another approach to be sure. Alternatively, the formula for the number of distinct colorings of a cube with all different colors assigned to each face is indeed 6! divided by the order of the rotation group, which is 24. So, 720 / 24 = 30. That's a common result in combinatorics. For example, when you have n colors and n objects with symmetry, you divide by the size of the symmetry group. But this is only valid when all the colorings are free (no color is repeated), which is exactly our case here. So, yes, 6! / 24 = 30. Therefore, the answer should be 30. Wait, but let me just cross-validate once more. Suppose we consider a simpler case, like coloring the cube with 3 colors. The formula would be different, right? But in our case, since all colors are different and we have as many colors as faces, the count is indeed 6! divided by the number of rotational symmetries. That makes sense because each distinct coloring can be rotated into 24 different arrangements, all of which are considered the same. So, 720 total divided by 24 equivalent arrangements gives 30 unique colorings. So, yes, I think that's correct. Therefore, the answer is 30.Final AnswerThe number of distinct colorings is boxed{30}.</think>To determine the number of distinct ways to paint the faces of a cube using six different colors (where each face must be a different color and rotations are considered equivalent), we use Burnside's lemma. First, we calculate the number of permutations of the six colors on the six faces, which is (6! = 720).Next, we consider the rotational symmetries of the cube. The cube has 24 rotational symmetries, which include:1. The identity rotation (1 symmetry).2. Rotations by 90°, 180°, and 270° around axes through the centers of opposite faces (9 symmetries).3. Rotations by 180° around axes through the midpoints of opposite edges (6 symmetries).4. Rotations by 120° and 240° around axes through opposite vertices (8 symmetries).Using Burnside's lemma, we need to count the number of colorings fixed by each type of rotation:1. Identity rotation: All 720 colorings are fixed.2. 90° and 270° rotations around face axes: No colorings are fixed because the four side faces would need to be the same color.3. 180° rotations around face axes: No colorings are fixed because pairs of faces would need to be the same color.4. 180° rotations around edge axes: No colorings are fixed because pairs of faces would need to be the same color.5. 120° and 240° rotations around vertex axes: No colorings are fixed because three faces would need to be the same color.Summing the fixed colorings for all symmetries, we get 720 (from the identity) and 0 from all other rotations. The average number of fixed colorings is then:[frac{720}{24} = 30]Thus, the number of distinct colorings is (boxed{30}).,<think>Okay, so I have this problem here: In how many different ways can the faces of a cube be painted using six given colors, with each face painted entirely one color, and considering two colorings different if they can't be made to coincide by rotating the cube. Hmm, interesting. Let me try to figure this out step by step.First, let me understand the problem correctly. We have a cube, and each of its six faces needs to be painted with one of six colors. Each face must be entirely one color, and we can use all six colors, right? So, each face gets a unique color? Wait, hold on. The problem says "using six given colors," but it doesn't specify that each color must be used exactly once. Hmm. Wait, but the cube has six faces. If we have six colors, and each face must be painted with one color, then if we use each color exactly once, that's one scenario. But if we can use the colors more than once, that's a different scenario. Wait, the problem says "using six given colors," so maybe we can use each color any number of times, but we have six different colors available? Or does it mean we have to use each color exactly once?This is a crucial point because it affects the total number of colorings. Let me re-read the problem: "each face must be painted entirely with one color", "using six given colors". The wording is a bit ambiguous. If it had said "six different colors," that would mean each face is a different color. But it says "using six given colors," which might mean that we have six colors to choose from, but we can use them any number of times. However, the cube has six faces, so if we have to use each color exactly once, that's a permutation. But if we can use colors multiple times, that's different.Wait, actually, given that it's a combinatorics problem about counting colorings up to rotation, and given that it's mentioned "each face must be painted entirely with one color," and "using six given colors," I think the standard interpretation here is that each color is used exactly once. Because if you can repeat colors, then the answer would be different, and usually in such problems, if you have as many colors as the number of objects (faces here), it's typical to assume each color is used once. But let me verify.Suppose we have six colors, each used exactly once on the six faces. Then, the number of colorings is the number of distinct colorings under rotation. But if we can repeat colors, then the problem becomes more complicated. However, the problem says "using six given colors," which might imply that each color is available, but not necessarily that each color must be used. Wait, but in that case, the problem would say "using up to six colors." Hmm.Alternatively, maybe "using six given colors" just means that we have six colors to choose from, and each face is painted with one of them, possibly repeating. So the total number of colorings without considering rotation would be 6^6. But considering rotation, we need to divide by the number of rotations or use Burnside's lemma. But the problem is in the wording. If it's "using six given colors" without specifying that each color must be used exactly once, then repetition is allowed.Wait, but the original problem is stated as: "each face must be painted entirely with one color", "using six given colors". So, each face is painted with one color, and the six colors are given. If the six colors are given, does that mean we have to use each color exactly once? For example, if you have six cans of paint, each of different colors, and you must use all of them, then each face gets a different color. But if it's just that you have six colors available, and you can choose any color for each face, with repetition allowed, then the count is different.This is a critical point. Let me check standard problems. In standard cube coloring problems, when they mention using n colors, it usually allows repetition unless specified otherwise. However, when the number of colors is equal to the number of faces, sometimes the problem assumes that each color is used once. But since the problem here says "using six given colors," without specifying "each color exactly once," I think repetition is allowed. However, since there are six faces and six colors, if we use each color once, the problem becomes counting the number of distinct colorings where each color is used exactly once, accounting for cube rotations. Alternatively, if repetition is allowed, the count is different.Wait, but if repetition is allowed, the problem would be similar to counting colorings up to rotation with possible color repetitions, which is a classic Burnside's lemma application. But given that the problem says "using six given colors," and each face is painted with one color, I think the problem is in the first category: assigning a color from six to each face, allowing repeats. Then, considering two colorings the same if one can be rotated to the other.But the problem is a bit ambiguous. Wait, maybe the problem is from a textbook or a standard question, so maybe I can recall similar problems. For example, if you have a cube and color each face with one of six colors, how many distinct colorings are there considering rotations. Then, the answer is calculated using Burnside's lemma. But in that case, when you can repeat colors, the formula is different than when you can't.Wait, actually, the problem says "using six given colors", each face painted entirely with one color. So, if you have six colors, and you can paint each face with any of the six, possibly repeating, then the number of colorings without considering rotation is 6^6. But when considering rotation, we need to use Burnside's lemma to count the distinct colorings. But if the problem requires that each color is used exactly once, then the number of colorings without considering rotation is 6! (since it's permutations of six colors on six faces), and then divided by the number of rotations? Wait, no. When considering rotational symmetries, even if all colors are distinct, the count isn't simply divided by the number of rotations. Instead, you still need to use Burnside's lemma.Therefore, perhaps the problem is ambiguous, but given that the number of colors is equal to the number of faces, it's likely that the intended interpretation is that each color is used exactly once. So, we have six different colors, each assigned to one face, and we need to count the number of distinct colorings up to rotation. So, in that case, the answer is the number of distinct colorings where each color is used exactly once, considering cube rotations.Alternatively, if repetition is allowed, the answer would be different, but given that the problem states "using six given colors," and there are six faces, the problem is likely asking for colorings where each color is used exactly once. So, let's proceed with that assumption.Therefore, the problem is equivalent to counting the number of distinct colorings of a cube's faces with six different colors, where two colorings are considered the same if one can be rotated to coincide with the other. The formula for this is given by Burnside's lemma, which averages the number of fixed colorings under each symmetry of the cube.Burnside's lemma states that the number of distinct colorings is equal to the average number of colorings fixed by each group element (each symmetry). So, first, we need to enumerate all the rotational symmetries of the cube, then for each symmetry, determine how many colorings are fixed by that symmetry, sum those numbers, and divide by the total number of symmetries.The cube has 24 rotational symmetries: 6 faces can be on top, and for each face on top, there are 4 possible rotations. So 6*4=24.Now, the rotational symmetries of the cube can be divided into different types based on their axes and rotation angles. The types are:1. Identity rotation: doing nothing.2. 90-degree rotations around axes through the centers of opposite faces.3. 180-degree rotations around axes through the centers of opposite faces.4. 270-degree rotations around axes through the centers of opposite faces.5. 180-degree rotations around axes through the midpoints of opposite edges.6. 120-degree rotations around axes through opposite vertices.7. 240-degree rotations around axes through opposite vertices.Wait, let me recall the standard classification. The cube's rotation group has several conjugacy classes:1. Identity: 1 element.2. 90-degree rotations about face axes: There are 6 face axes (3 axes, each with two directions), but each axis has rotations of 90°, 180°, 270°. However, the conjugacy classes are separated by rotation angles. So, 90° and 270° rotations are in the same class, and 180° rotations are in another. Wait, no. Let me check again.Actually, in the cube's rotation group, the conjugacy classes are:1. Identity: 1 element.2. 180-degree rotations about face axes: There are 3 axes (through centers of opposite faces), each axis has one non-identity rotation of 180°, so 3 elements.3. 120-degree rotations about vertex axes: There are 4 axes (through opposite vertices), each axis allows for 120° and 240° rotations, so 8 elements.4. 180-degree rotations about edge axes: There are 6 axes (through midpoints of opposite edges), each axis allows a 180° rotation, so 6 elements.5. 90-degree and 270-degree rotations about face axes: For each of the 3 face axes, we have rotations of 90° and 270°, which are distinct conjugacy classes? Wait, no. Actually, 90° and 270° rotations about the same axis are conjugate in the rotation group?Wait, maybe it's better to look up the standard conjugacy classes for the cube's rotation group. From what I remember, the rotation group of the cube (which is isomorphic to S4) has the following conjugacy classes:1. Identity: 1 element.2. 180-degree rotations about face axes: 3 axes × 1 rotation each = 3 elements.3. 120-degree rotations about vertex axes: 8 elements (each of 120° and 240° for 4 axes).4. 180-degree rotations about edge axes: 6 elements.5. 90-degree and 270-degree rotations about face axes: 6 elements (3 axes × 2 directions each).Wait, but that sums up to 1 + 3 + 8 + 6 + 6 = 24 elements, which matches the total number of rotational symmetries. But I might have misremembered. Let me check:- Identity: 1- 90° and 270° rotations about face axes: 6 total (3 axes, each with two non-trivial rotations)- 180° rotations about face axes: 3- 120° and 240° rotations about vertex axes: 8 (4 axes, each with two rotations)- 180° rotations about edge axes: 6Yes, that's correct. So:1. Identity: 12. 180-degree face rotations: 33. 180-degree edge rotations: 64. 120/240-degree vertex rotations: 85. 90/270-degree face rotations: 6So these are the conjugacy classes.Now, for Burnside's lemma, we need to compute, for each conjugacy class, the number of colorings fixed by any element in that class, multiply by the size of the conjugacy class, sum them all, and divide by the group size (24).Given that the colorings are with six distinct colors assigned to the six faces, a fixed coloring under a group element is a coloring where the permutation induced by that group element doesn't change the coloring. Since all colors are distinct, this requires that the permutation induced by the group element leaves the color labels unchanged, i.e., the permutation must be the identity permutation on the faces. Therefore, for a given rotation, the number of colorings fixed by that rotation is equal to the number of colorings that are invariant under that rotation. Since all colors are distinct, the only way a coloring is fixed is if the rotation permutes faces of the same color. But since all colors are distinct, this can only happen if the rotation permutes faces that have the same color. However, since all colors are distinct, this requires that the permutation induced by the rotation is trivial, i.e., the rotation doesn't move any face. Wait, no. Wait, if all colors are distinct, then for a rotation to fix a coloring, it must map each face to itself. Otherwise, if it permutes faces, since the colors are all different, the coloring would change.Therefore, if a rotation permutes the faces, then the coloring can only be fixed by that rotation if the permutation induced by the rotation maps each face to itself. Therefore, only the identity rotation fixes all possible colorings. All other rotations cannot fix any coloring with all distinct colors because they would require that some faces have the same color, which they don't. Wait, but that seems counterintuitive. Let me think.Suppose we have a coloring where all faces are different colors. Then, if we apply a non-identity rotation, the coloring will change because the rotation moves the faces to different positions, which now have different colors. Therefore, the only symmetry that fixes such a coloring is the identity. Therefore, the number of colorings fixed by the identity is 6! (all possible colorings), and the number fixed by any non-identity rotation is 0. Therefore, applying Burnside's lemma, the number of distinct colorings is (6! + 0 + 0 + ... + 0)/24 = 720 / 24 = 30.But wait, that seems too straightforward. However, I need to verify if this is correct. Let me check with another example. Suppose we have a cube and we want to color its faces with all distinct colors. Then, the number of distinct colorings up to rotation is indeed 6! divided by the number of rotations? Wait, no, that's not necessarily correct because Burnside's lemma says it's the average number of fixed colorings per group element.But in this case, since only the identity element fixes any colorings (as all colorings are distinct), then yes, the total number of fixed colorings is 6! for the identity and 0 for all others. Therefore, the average is 6! / 24 = 720 / 24 = 30. So the answer would be 30.But wait, I've heard before that the number of distinct colorings of a cube with six different colors is 30. So that seems correct.But let me just verify with a different approach. Suppose we fix one face to a particular color to account for rotations. For example, fix the top face to color 1. Then, there are 5 remaining colors for the bottom face. However, the bottom face can be any of the remaining 5 colors, but rotations around the vertical axis (the axis through the top and bottom faces) can rotate the cube, so the four side faces can be arranged in 3! ways. Wait, no. Wait, if we fix the top face to color 1, then the bottom face can be any of the remaining 5 colors. Then, the four lateral faces form a cycle. Since we can rotate the cube around the vertical axis, the number of distinct colorings for the lateral faces is (4-1)! = 6 (circular permutations). Wait, but with four distinct colors, the number of distinct arrangements considering rotation is indeed (4-1)! = 6. So, total colorings would be 5 (choices for bottom) * 6 (arrangements of lateral faces) = 30. So that matches. Therefore, the answer is 30.But hold on, this method gives 30, and Burnside's lemma also gives 30. So that's consistent.Alternatively, if we didn't assume that all colors are distinct, but allowed repetition, the answer would be different. But given the problem statement, since there are six colors and six faces, it's reasonable to assume that each color is used once. Therefore, the answer should be 30.Wait, but just to be thorough, let's go back to Burnside's lemma and confirm.Total group size: 24 rotations.For each conjugacy class:1. Identity: 1 element. Each coloring is fixed by the identity. Number of fixed colorings: 6! = 720.2. 180-degree face rotations: 3 elements. Each rotation is 180 degrees around an axis through the centers of two opposite faces. For a coloring to be fixed by this rotation, the pairs of opposite faces swapped by the rotation must be the same color. However, since all colors are distinct, this is impossible unless the two pairs are fixed. But since all colors are distinct, the four faces around the axis (the ones being swapped in pairs) must each have unique colors, but after a 180 rotation, their colors must match. Since they are distinct, this is impossible. Therefore, fixed colorings: 0.3. 180-degree edge rotations: 6 elements. These are rotations by 180 degrees around axes through the midpoints of opposite edges. Such a rotation swaps two pairs of opposite faces. Again, for the coloring to be fixed, the swapped faces must have the same color. But since all colors are distinct, this is impossible. Therefore, fixed colorings: 0.4. 120/240-degree vertex rotations: 8 elements. These rotations cycle three faces around a vertex. For a coloring to be fixed, the three cycled faces must have the same color. But since all colors are distinct, this is impossible. Therefore, fixed colorings: 0.5. 90/270-degree face rotations: 6 elements. These rotations cycle four faces around a face axis. For the coloring to be fixed, those four faces must have the same color. But since all colors are distinct, this is impossible. Therefore, fixed colorings: 0.Therefore, summing over all conjugacy classes:(1*720 + 3*0 + 6*0 + 8*0 + 6*0)/24 = 720/24 = 30.Yes, that's correct. Therefore, the number of distinct colorings is 30.So, the answer is 30, which in boxed form is boxed{30}.Final Answerboxed{30}</think>To determine the number of distinct ways to paint the faces of a cube using six given colors (each face painted entirely with one color), considering rotations, we use Burnside's lemma. The key steps are as follows:1. Identify the rotational symmetries of the cube: The cube has 24 rotational symmetries, which can be classified into different conjugacy classes: - Identity: 1 element - 180-degree rotations about face axes: 3 elements - 180-degree rotations about edge axes: 6 elements - 120/240-degree rotations about vertex axes: 8 elements - 90/270-degree rotations about face axes: 6 elements2. Calculate fixed colorings for each conjugacy class: - Identity: All 6! colorings are fixed. - Fixed colorings: (6! = 720) - 180-degree face rotations: No colorings can be fixed since all colors are distinct. - Fixed colorings: (0) - 180-degree edge rotations: No colorings can be fixed since all colors are distinct. - Fixed colorings: (0) - 120/240-degree vertex rotations: No colorings can be fixed since all colors are distinct. - Fixed colorings: (0) - 90/270-degree face rotations: No colorings can be fixed since all colors are distinct. - Fixed colorings: (0)3. Apply Burnside's lemma: - Sum of fixed colorings: (1 cdot 720 + 3 cdot 0 + 6 cdot 0 + 8 cdot 0 + 6 cdot 0 = 720) - Average number of fixed colorings: (frac{720}{24} = 30)Thus, the number of distinct colorings of the cube's faces, considering rotations, is (boxed{30}).]

🔑:4. Suppose the faces of a cube are painted green, blue, red, yellow, white, and black. Let's place the cube so that the green face is at the bottom. In this case, the top face can be painted one of the five remaining colors. It is clear that no two colorings, in which the top (i.e., opposite the green) face is painted different colors, can be aligned with each other by rotation. Now let's determine the number of colorings in which the top face is painted a certain color (say, blue); the total number of colorings is five times this number (since the top face can be painted any of the 5 remaining colors).Choose one of the four colors remaining after removing green and blue (say, red) and place our cube so that the red face is the back face; this can always be achieved by rotating the cube around the vertical axis. We have 3 colors left - yellow, white, and black, with which we need to paint the 3 faces (the front and two side faces). Clearly, none of the resulting colorings can be aligned with each other by rotation - with any rotation, either the bottom face will no longer be green, or the back face will no longer be red. The three faces can be painted with the three colors in six different ways (the front face can be painted any of the three colors, and for each of these colorings, we can choose the color of the left face in two ways).Therefore, the total number of colorings that cannot be aligned by rotating the cube is 5 cdot 6=30.

🧠:[<think>Okay, so I need to figure out the range of values for m such that whenever x is between m and m+1, the inequality x² - 7x + 10 ≤ 0 holds true. That means q being true should guarantee that p is also true. Let me break this down step by step.First, let me recall what the inequality x² - 7x + 10 ≤ 0 represents. This is a quadratic inequality. To solve such inequalities, it's usually helpful to factor the quadratic or find its roots and then determine the intervals where the inequality holds.Let me start by factoring the quadratic expression x² - 7x + 10. Let me see, I need two numbers that multiply to 10 and add up to -7. Hmm, the factors of 10 are 1 and 10, 2 and 5. Let's check 2 and 5. If both are negative, they would add up to -7. Yes, (-2) * (-5) = 10 and (-2) + (-5) = -7. So the quadratic factors as (x - 2)(x - 5) ≤ 0. So the roots are x = 2 and x = 5. Since the coefficient of x² is positive (1), the parabola opens upwards. Therefore, the quadratic will be ≤ 0 between its roots. So the solution to the inequality p is x ∈ [2, 5]. That is, for any x between 2 and 5 inclusive, the inequality holds.Now, the problem states that q: m ≤ x ≤ m + 1 is a sufficient condition for p. That means if q is true (i.e., x is in [m, m + 1]), then p must also be true (i.e., x is in [2, 5]). Therefore, the interval [m, m + 1] must be entirely contained within [2, 5]. If even a part of [m, m + 1] is outside [2, 5], then q might be true but p would be false, which violates the sufficiency condition.So, to ensure that [m, m + 1] is entirely within [2, 5], two conditions must be satisfied:1. The left endpoint of q, which is m, must be greater than or equal to the left endpoint of p, which is 2. So m ≥ 2.2. The right endpoint of q, which is m + 1, must be less than or equal to the right endpoint of p, which is 5. So m + 1 ≤ 5, which implies m ≤ 4.Therefore, combining these two inequalities, m must satisfy 2 ≤ m ≤ 4. So the range of m is [2, 4].Wait, let me double-check. If m = 2, then the interval is [2, 3], which is within [2, 5]. If m = 4, the interval is [4, 5], which is also within [2, 5]. If m is between 2 and 4, say m = 3, the interval is [3, 4], which is still within [2, 5]. So that seems correct.But let me verify if there's any other consideration. For instance, if m is less than 2, say m = 1, then the interval would be [1, 2], which is partially outside [2, 5]. Specifically, x = 1 would satisfy q but not p. Similarly, if m is greater than 4, say m = 5, the interval would be [5, 6], which is entirely outside [2, 5], so q would not imply p. Therefore, the correct range for m is indeed [2, 4].Another way to think about it: the entire interval [m, m + 1] must lie within [2, 5]. Therefore, m must be at least 2 to start at or after 2, and m + 1 must be at most 5, so m can be up to 4. So m ∈ [2, 4].Yes, that seems right. So the answer should be that m is between 2 and 4, inclusive.Final AnswerThe range of values for ( m ) is boxed{[2, 4]}.</think>To determine the range of values for ( m ) such that ( q ): ( m leqslant x leqslant m + 1 ) is a sufficient condition for ( p ): ( x^2 - 7x + 10 leqslant 0 ), we start by solving the quadratic inequality ( x^2 - 7x + 10 leqslant 0 ).First, we factor the quadratic expression:[x^2 - 7x + 10 = (x - 2)(x - 5)]The roots are ( x = 2 ) and ( x = 5 ). Since the quadratic opens upwards (the coefficient of ( x^2 ) is positive), the inequality ( (x - 2)(x - 5) leqslant 0 ) holds for ( x ) in the interval ([2, 5]).Next, we need the interval ([m, m + 1]) to be entirely contained within ([2, 5]). This requires:1. The left endpoint ( m ) to be at least 2: [ m geqslant 2 ]2. The right endpoint ( m + 1 ) to be at most 5: [ m + 1 leqslant 5 implies m leqslant 4 ]Combining these two conditions, we get:[2 leqslant m leqslant 4]Thus, the range of values for ( m ) is (boxed{[2, 4]}).,<think>Okay, let's see. The problem says that if q is a sufficient condition for p, then we need to find the range of values for m. So, first, I need to understand what p and q represent. Starting with p: the inequality is x² - 7x + 10 ≤ 0. I remember that quadratic inequalities can be solved by finding the roots of the equation x² - 7x + 10 = 0 and then determining the intervals where the quadratic expression is less than or equal to zero. Let me factor that quadratic. Looking at x² - 7x + 10, I need two numbers that multiply to 10 and add up to -7. Hmm, factors of 10 are 1 and 10, 2 and 5. Let's see: 2 and 5 add up to 7. Since the middle term is -7x, both numbers should be negative: -2 and -5. So, the quadratic factors as (x - 2)(x - 5) ≤ 0. Wait, let me check that: (x - 2)(x - 5) = x² -7x +10, yes, that's correct. So, the roots are x = 2 and x = 5. Since the coefficient of x² is positive, the parabola opens upwards. Therefore, the inequality (x - 2)(x - 5) ≤ 0 holds between the roots. So, the solution to p is x ∈ [2, 5]. Okay, so p is true when x is between 2 and 5, inclusive. Now, q is given as m ≤ x ≤ m + 1. So, q defines an interval of length 1 starting at m. The problem states that q is a sufficient condition for p. That means if q is true, then p must also be true. In other words, whenever x is in [m, m + 1], it must also be in [2, 5]. So, the interval [m, m + 1] must be entirely contained within [2, 5]. Therefore, we need [m, m + 1] ⊆ [2, 5]. To satisfy this inclusion, the entire interval [m, m + 1] must lie within [2, 5]. So, two conditions must hold: 1. The left endpoint m must be greater than or equal to 2. 2. The right endpoint m + 1 must be less than or equal to 5. So, if I set up those inequalities: 1. m ≥ 22. m + 1 ≤ 5Solving the second inequality: m ≤ 5 - 1 => m ≤ 4. Therefore, combining both inequalities, m must satisfy 2 ≤ m ≤ 4. Wait, but let me double-check that. If m is 2, then the interval is [2, 3], which is within [2, 5]. If m is 4, the interval is [4, 5], which is also within [2, 5]. If m is between 2 and 4, say 3, then the interval is [3, 4], which is still within [2,5]. So, this seems correct. But maybe I need to consider if m is less than 2 or greater than 4. Let's see. If m is less than 2, say m = 1, then the interval is [1, 2]. But [1, 2] is not entirely within [2, 5], because 1 is less than 2. So, q would include x values not in p, which would mean q isn't a sufficient condition for p. Similarly, if m is greater than 4, say m = 4.5, then the interval is [4.5, 5.5]. The upper part of this interval, from 5 to 5.5, is outside of p's interval [2, 5], so again, q would not be entirely within p. Hence, m can't be less than 2 or greater than 4. Therefore, the range of m is from 2 to 4, inclusive. So, m ∈ [2, 4]. But wait, let me also verify for the edges. If m is exactly 2, then the interval is [2,3], which is within [2,5]. If m is exactly 4, the interval is [4,5], which is within [2,5]. So, the endpoints are allowed. Therefore, the answer should be m is between 2 and 4, inclusive. So, 2 ≤ m ≤ 4. I think that's it, but let me make sure I didn't miss anything. Another way to think about it: for q to be sufficient for p, every x that satisfies q must satisfy p. So, the interval [m, m + 1] must be entirely inside [2,5]. So, the smallest m can be is 2, so that the interval starts at 2. If m were any smaller, part of [m, m +1] would be left of 2. Similarly, the largest m can be is 4, because then the interval ends at 5. If m were any larger, part of [m, m +1] would be right of 5. Yep, that makes sense. So, m has to be between 2 and 4. I don't think there's any other constraints here. The interval [m, m+1] is length 1, so as long as it's entirely within [2,5], m is okay. So, final answer: m ∈ [2,4].Final AnswerThe range of values for ( m ) is boxed{[2, 4]}.</think>Given ( p ): ( x^{2} - 7x + 10 leqslant 0 ), we first solve the quadratic inequality. Factoring the quadratic expression, we get:[x^{2} - 7x + 10 = (x - 2)(x - 5) leqslant 0]The roots are ( x = 2 ) and ( x = 5 ). Since the quadratic opens upwards, the solution to the inequality is the interval where the expression is non-positive, which is:[x in [2, 5]]Next, we consider ( q ): ( m leqslant x leqslant m + 1 ). For ( q ) to be a sufficient condition for ( p ), the interval ([m, m + 1]) must be entirely contained within ([2, 5]). This requires:1. The left endpoint ( m ) to be at least 2: [ m geqslant 2 ]2. The right endpoint ( m + 1 ) to be at most 5: [ m + 1 leqslant 5 implies m leqslant 4 ]Combining these inequalities, we find the range of values for ( m ):[2 leqslant m leqslant 4]Thus, the range of values for ( m ) is (boxed{[2, 4]}).]

🔑:Solving (x^{2} - 7x + 10 leqslant 0) yields (2 leqslant x leqslant 5), which means (p): (2 leqslant x leqslant 5).Let (A = { x | 2 leqslant x leqslant 5 }) due to (p).From proposition (q), we know: (m leqslant x leqslant m + 1),Let (B = { x | m leqslant x leqslant m + 1 }),Since (q) is a sufficient condition for (p),It follows that (B subseteq A), which leads to the system of inequalities:[begin{cases} m geqslant 2 m + 1 leqslant 5 end{cases}]Solving this, we find: (2 leqslant m leqslant 4).Therefore, the range of values for (m) is boxed{2 leqslant m leqslant 4}.

🧠:[<think>Okay, so I need to figure out the range of the real number m such that the inequality (m²x - 1)/(mx + 1) < 0 holds for all x ≥ 4. Hmm, let's start by understanding the problem step by step.First, the inequality given is a rational function in terms of x. The numerator is m²x - 1, and the denominator is mx + 1. The inequality is less than zero, so we're looking for when the rational function is negative. And this has to be true for all x greater than or equal to 4. Also, m is not zero.Since this needs to hold for all x ≥ 4, the expression must stay negative throughout that interval. That suggests that either the numerator and denominator have opposite signs for all x ≥ 4. So, the key is to analyze the signs of the numerator and denominator for x ≥ 4 and find m such that one is positive and the other is negative throughout that interval.Let me consider the numerator and denominator separately.Numerator: m²x - 1Denominator: mx + 1For the rational expression to be negative, the numerator and denominator must have opposite signs. So either:1. Numerator > 0 and Denominator < 0 for all x ≥ 4, or2. Numerator < 0 and Denominator > 0 for all x ≥ 4.But since x is going to infinity, as x increases, the terms with x will dominate. So we need to check the behavior as x approaches infinity and ensure that the inequality holds for all x ≥ 4, including as x becomes very large.Let me first check the leading terms. The leading term in the numerator is m²x, and in the denominator, it's mx. So as x becomes very large, the numerator behaves like m²x and the denominator behaves like mx. Therefore, the rational function behaves like (m²x)/(mx) = m. So, as x approaches infinity, the expression tends to m. Therefore, if the limit is m, and the inequality requires the expression to be negative for all x ≥ 4, then m must be negative. Because if m were positive, then as x approaches infinity, the expression would approach m, which is positive, contradicting the inequality. Therefore, m must be negative. That's a key point. So m < 0.But let's not jump to conclusions yet. Let's verify.So if m is negative, then the denominator mx + 1. Since m is negative, mx is negative, and when x increases, mx becomes more negative. So denominator mx + 1 would be 1 + (negative number). When does denominator become zero? Let's find x such that mx + 1 = 0. Then x = -1/m. Since m is negative, -1/m is positive. So the denominator is zero at x = -1/m, which is a positive number. For x > -1/m, since m is negative, mx + 1 becomes more negative as x increases. Wait, no. Wait, if m is negative, then mx + 1 is a linear function with slope m (negative). So as x increases, mx + 1 decreases. So when x crosses -1/m (which is positive), the denominator changes sign. For x < -1/m, denominator is positive, and for x > -1/m, denominator is negative.But in our problem, x starts at 4 and goes to infinity. So if -1/m is less than 4, then for all x ≥ 4, denominator is negative (since x > -1/m). If -1/m is greater than or equal to 4, then for x ≥ 4, the denominator would be positive or zero. But since denominator cannot be zero (as x ≥ 4 and -1/m would have to be ≥ 4, so m ≥ -1/4. But m is negative, so m ∈ (-1/4, 0). Wait, let me clarify.Wait, denominator mx + 1. If we need denominator to be negative for all x ≥ 4, then we need mx + 1 < 0 for all x ≥ 4. Let's see. If m is negative, then mx + 1 < 0 when x > -1/m. But if x ≥ 4, then to have mx + 1 < 0 for all x ≥ 4, we need that 4 ≥ -1/m. Because if -1/m ≤ 4, then x ≥ 4 would be greater than -1/m, so denominator is negative. Wait, no. Wait, if m is negative, then mx +1 < 0 is equivalent to x > -1/m. So to have mx +1 <0 for all x ≥4, we must have that -1/m ≤4. Because if -1/m ≤4, then x ≥4 implies x ≥ -1/m, so mx +1 ≤0. But since x ≥4 and -1/m ≤4, then x ≥ -1/m, so mx +1 ≤0. However, if -1/m >4, then for x in [4, -1/m), mx +1 would be positive, and for x > -1/m, it would be negative. Therefore, to have denominator negative for all x ≥4, we need that -1/m ≤4, which implies that m ≥ -1/4. But m is negative, so m ∈ [-1/4, 0). But m ≠0, so m ∈ [-1/4, 0).Wait, let's check this. If m is negative, then -1/m is positive. So the denominator is negative when x > -1/m. So if we need denominator negative for all x ≥4, then all x ≥4 must satisfy x > -1/m. Therefore, 4 > -1/m. But since m is negative, multiplying both sides by m (negative) reverses inequality:4 > -1/mMultiply both sides by m (negative):4m < -1Divide by 4:m < -1/4Wait, this contradicts the earlier conclusion. Hmmm. Let me be careful here.Wait, solving 4 > -1/m when m is negative. Let's do it step by step.If m is negative, then 4 > -1/m.Multiply both sides by m (which is negative), so inequality flips:4m < -1Then, 4m < -1 ⇒ m < -1/4.But since m is negative, that's okay. So m must be less than -1/4.Wait, that seems conflicting with previous thought.Wait, original inequality: denominator mx +1 <0 for all x ≥4.Which is equivalent to mx +1 <0 for all x ≥4.If m is negative, then mx +1 is a decreasing function. So the maximum value of mx +1 on x ≥4 occurs at x=4. So, if at x=4, mx +1 <0, then for all x ≥4, mx +1 ≤ mx=4 +1 <0. Wait, but if m is negative, then as x increases, mx +1 decreases. So the maximum value is at x=4. Therefore, if mx +1 <0 at x=4, then it will be less than 0 for all x ≥4. Therefore, the condition is m*4 +1 <0 ⇒ 4m +1 <0 ⇒ 4m < -1 ⇒ m < -1/4.Therefore, if m < -1/4, then denominator is negative for all x ≥4.If m > -1/4, then at x=4, denominator is 4m +1. If m > -1/4, then 4m > -1, so 4m +1 >0. Then, as x increases, mx +1 increases if m is positive, but m is positive here? Wait, no. If m is positive, then mx +1 is increasing. But if m is positive, denominator is increasing, and at x=4, it's 4m +1. If m is positive, 4m +1 is positive, so denominator is positive for all x ≥4. However, numerator is m²x -1. If m is positive, numerator is m²x -1. Since m² is positive, numerator is increasing. At x=4, numerator is 4m² -1. Depending on m, it could be positive or negative.But wait, the original problem states that the inequality must hold for all x ≥4. If m is positive, then denominator is positive for all x ≥4 (since m >0, mx +1 is positive for x ≥4). Then, numerator must be negative for all x ≥4. But numerator is m²x -1. If m is positive, then m² is positive, so numerator is increasing. Therefore, if numerator is negative for all x ≥4, then it must be negative at x approaching infinity. But as x approaches infinity, numerator m²x -1 approaches infinity, which is positive. Contradiction. Therefore, m cannot be positive.Therefore, m must be negative. Then, as established, to have denominator negative for all x ≥4, we need m < -1/4.Therefore, m is in (-∞, -1/4). But we need to check the numerator.Wait, so denominator is negative (since m < -1/4), and for the rational function to be negative, numerator must be positive. Therefore, numerator m²x -1 must be positive for all x ≥4.So, numerator m²x -1 >0 for all x ≥4.So, m²x -1 >0 ⇒ m²x >1 ⇒ x >1/m². So, for x ≥4, we need 4 >1/m². So 1/m² <4 ⇒ m² >1/4 ⇒ |m|>1/2.But m is negative and m < -1/4. So |m|>1/2 implies m < -1/2 or m >1/2. But m is negative and m < -1/4, so combining these, m < -1/2.Therefore, m must be less than -1/2.Wait, let me check this again.Numerator: m²x -1 >0 for all x ≥4. Since x is increasing, the minimal value of numerator occurs at x=4. Therefore, if m²*4 -1 >0, then for all x ≥4, numerator will be greater than that, hence positive. So:4m² -1 >0 ⇒ m² >1/4 ⇒ |m| >1/2. Since m is negative, this gives m < -1/2.Therefore, combining both conditions:Denominator negative for all x ≥4 requires m < -1/4.Numerator positive for all x ≥4 requires m < -1/2.So the intersection is m < -1/2.Therefore, m must be in (-∞, -1/2).But let's verify this.Take m = -1 (which is less than -1/2). Then numerator is m²x -1 = (1)x -1 = x -1. Denominator is mx +1 = -x +1. So for x ≥4, numerator x -1 is positive (since x ≥4, x -1 ≥3), denominator -x +1 is negative (since x ≥4, -x +1 ≤ -3). So positive divided by negative is negative. So the inequality holds. So for m = -1, it works.Take m = -0.6 (which is between -1/2 and -1/4). Then m = -3/5.Numerator: m²x -1 = (9/25)x -1. At x=4, this is (36/25) -1 = 11/25 >0. However, as x increases, numerator (9/25)x -1 increases, so stays positive. Denominator: mx +1 = (-3/5)x +1. At x=4, denominator is (-12/5) +1 = -7/5 <0. So numerator is positive, denominator is negative, so expression is negative. So for m = -0.6, which is in (-1/2, -1/4), the inequality holds. Wait, but according to previous reasoning, m must be less than -1/2. But here, m = -0.6 is between -1/2 and -1/4, and it seems to work. Hmm, contradiction. Therefore, my previous reasoning was flawed.Wait, so perhaps my conclusion that m < -1/2 is incorrect. Let me check again.Wait, in the numerator, if m is between -1/2 and -1/4, say m = -0.6, then m² = 0.36, so m²x -1 = 0.36x -1. At x=4, 0.36*4 -1 = 1.44 -1 = 0.44 >0. As x increases, 0.36x -1 increases, so numerator is positive for all x ≥4. The denominator is mx +1 = -0.6x +1. At x=4, denominator is -2.4 +1 = -1.4 <0. So numerator is positive, denominator is negative, so expression is negative. So why was my previous conclusion m < -1/2?Ah, here's the mistake. The condition for the numerator to be positive for all x ≥4 is m²x -1 >0 for all x ≥4. The minimal value of the numerator is at x=4, so 4m² -1 >0 ⇒ m² >1/4 ⇒ |m| >1/2. But if m is negative, |m| >1/2 ⇒ m < -1/2. But in the example above, m = -0.6 is less than -1/2? Wait, -0.6 is -3/5, which is -0.6, and -1/2 is -0.5. So -0.6 is less than -0.5, so m = -0.6 is actually less than -1/2. Wait, -1/2 is -0.5, so m = -0.6 is indeed less than -1/2. Wait, but in my example, m = -0.6 is less than -1/2, so it's included in the range. Wait, perhaps I confused the numbers.Wait, wait. Let's take m = -0.4, which is between -1/2 (-0.5) and -1/4 (-0.25). Let's check this.m = -0.4, numerator m²x -1 = (0.16)x -1. At x=4, 0.16*4 -1 = 0.64 -1 = -0.36 <0. So numerator is negative here. But denominator is mx +1 = -0.4x +1. At x=4, denominator is -1.6 +1 = -0.6 <0. So both numerator and denominator are negative, so their ratio is positive, which contradicts the inequality (needs to be <0). Therefore, m = -0.4 doesn't work.But if m = -0.6, which is less than -0.5 (i.e., m < -1/2), then numerator is positive for x ≥4. So in this case, numerator positive and denominator negative, so ratio is negative. So m = -0.6 works.But m = -0.4 (between -1/4 and -1/2) leads to numerator negative at x=4, denominator negative, so ratio positive, which violates the inequality.Therefore, the key is that the numerator must be positive for all x ≥4. The minimal value of the numerator occurs at x=4. So, 4m² -1 must be greater than 0. Therefore, m² >1/4 ⇒ |m|>1/2. Since m is negative, m < -1/2.Therefore, combining the two conditions:1. Denominator negative for all x ≥4: m < -1/4.2. Numerator positive for all x ≥4: m < -1/2.Hence, the intersection is m < -1/2.Therefore, the range of m is (-∞, -1/2).But let's check another example. Let m = -1/2. Then:Numerator: m²x -1 = (1/4)x -1. At x=4, (1/4)*4 -1 = 1 -1 =0. So at x=4, the numerator is zero. But the inequality is (m²x -1)/(mx +1) <0. At x=4, the expression is 0/(denominator) =0, which is not less than zero. Hence, m = -1/2 is excluded. Therefore, the range is m < -1/2.But also, for m = -1/2, we need to check whether the expression is less than zero for all x ≥4. At x=4, it's zero, which violates the inequality. Hence, m must be strictly less than -1/2.Therefore, the range is (-∞, -1/2).Wait, but let's check m = -1/2. Let me compute the expression at x=4:Numerator: ( (-1/2)^2 )*4 -1 = (1/4)*4 -1 = 1 -1 =0.Denominator: (-1/2)*4 +1 = -2 +1 = -1.So the expression is 0 / -1 =0, which is not less than zero. Therefore, m=-1/2 is excluded. So the correct interval is m < -1/2.Hence, the answer is m ∈ (-∞, -1/2).But let's verify for m < -1/2. Take m = -2, which is less than -1/2.Numerator: m²x -1 = 4x -1. For x ≥4, this is ≥ 16 -1 =15 >0.Denominator: mx +1 = -2x +1. For x ≥4, this is ≤ -8 +1 = -7 <0. So numerator positive, denominator negative, expression negative. So inequality holds.Another test, m = -3/4 (which is less than -1/2). Then m = -0.75.Numerator: m²x -1 = (0.5625)x -1. At x=4, 0.5625*4 -1 =2.25 -1=1.25>0. Denominator: -0.75x +1. At x=4, -3 +1=-2<0. So expression is positive/negative = negative. So holds.At x=1000, numerator≈0.5625*1000=562.5 -1≈561.5>0. Denominator≈-0.75*1000= -750 +1≈-749<0. So expression negative.Hence, works.If m = -1/2, as before, numerator at x=4 is zero. So invalid. Hence, m must be less than -1/2.Therefore, the range is m ∈ (-∞, -1/2).Final AnswerThe range of the real number ( m ) is boxed{(-infty, -dfrac{1}{2})}.</think>To determine the range of the real number ( m ) such that the inequality (dfrac{m^{2}x-1}{mx+1} < 0) holds for all ( x geq 4 ), we analyze the behavior of the numerator and denominator separately.1. Denominator Analysis: - The denominator ( mx + 1 ) must be negative for all ( x geq 4 ). Since ( m ) is negative, the denominator is a decreasing function. The maximum value of the denominator at ( x = 4 ) must be negative: [ 4m + 1 < 0 implies m < -frac{1}{4} ]2. Numerator Analysis: - The numerator ( m^2x - 1 ) must be positive for all ( x geq 4 ). Since ( m ) is negative, ( m^2 ) is positive, making the numerator an increasing function. The minimum value of the numerator at ( x = 4 ) must be positive: [ 4m^2 - 1 > 0 implies m^2 > frac{1}{4} implies |m| > frac{1}{2} ] - Since ( m ) is negative, this implies ( m < -frac{1}{2} ).Combining both conditions, we find that ( m ) must be less than (-frac{1}{2}). Therefore, the range of ( m ) is (boxed{(-infty, -dfrac{1}{2})}).,<think>Okay, so I need to find the range of real numbers m (where m is not zero) such that the inequality (m²x - 1)/(mx + 1) < 0 holds for all x ≥ 4. Hmm, let me start by understanding what this inequality means and how to approach it.First, the inequality is a rational expression. The sign of a rational expression depends on the signs of the numerator and the denominator. So, the expression (m²x - 1)/(mx + 1) will be negative when the numerator and denominator have opposite signs. Therefore, the inequality (m²x - 1)/(mx + 1) < 0 is equivalent to (m²x - 1) and (mx + 1) having opposite signs.So, there are two cases to consider:1. Numerator positive and denominator negative.2. Numerator negative and denominator positive.Our goal is to find m such that for all x ≥ 4, one of these two cases holds. Let me analyze each case separately.First, let's consider the denominator: mx + 1. Since x can be as large as needed (x ≥ 4), the behavior of mx + 1 as x increases depends on the sign of m. If m is positive, then mx + 1 will increase without bound as x increases. If m is negative, mx + 1 will decrease without bound as x increases. So, the sign of the denominator is crucial here.Similarly, the numerator is m²x - 1. Since m² is always non-negative (because it's squared), m²x will be non-negative for all x ≥ 0, and since m ≠ 0, m²x is actually positive for x > 0. Therefore, m²x - 1 is a linear function in x with a positive slope (because m² is positive). So, as x increases, the numerator m²x - 1 will increase. Therefore, there will be a point where the numerator crosses zero. Let's find that point.Setting numerator equal to zero: m²x - 1 = 0 => x = 1/m². So, for x < 1/m², the numerator is negative, and for x > 1/m², it's positive. But since x is starting from 4, we need to know whether 1/m² is less than 4 or greater than 4. If 1/m² < 4, then for x ≥ 4, the numerator is positive. If 1/m² ≥ 4, then the numerator is negative for x = 4 and becomes positive once x passes 1/m². But if 1/m² is very large, like greater than 4, then for x between 4 and 1/m², the numerator is negative, and beyond that, it's positive. However, since our inequality needs to hold for all x ≥ 4, if 1/m² > 4, then there will be some x in [4, 1/m²) where the numerator is negative, and for x > 1/m², it becomes positive. Therefore, the sign of the numerator changes depending on x, which complicates things because the denominator's sign also depends on m.So, perhaps the key is to ensure that for all x ≥ 4, the numerator and denominator have opposite signs. Let me structure this.Case 1: Numerator > 0 and Denominator < 0 for all x ≥ 4.Case 2: Numerator < 0 and Denominator > 0 for all x ≥ 4.We need either Case 1 or Case 2 to hold for all x ≥ 4. Let's explore each case.Starting with Case 1: Numerator > 0 and Denominator < 0 for all x ≥ 4.First, Numerator > 0 for all x ≥ 4. As we saw earlier, the numerator m²x -1 is a linear function increasing in x. So, if we want m²x -1 > 0 for all x ≥ 4, the minimal value of the numerator occurs at x = 4. Therefore, m²*4 -1 > 0 => 4m² >1 => m² > 1/4 => |m| > 1/2.Second, Denominator < 0 for all x ≥4. The denominator is mx + 1. If we want mx + 1 < 0 for all x ≥4, let's analyze this. For x ≥4, mx +1 < 0.If m is positive, then as x increases, mx +1 increases to infinity, so mx +1 can't be <0 for all x ≥4. Therefore, m must be negative.If m is negative, then mx +1 is decreasing in x. So, the maximum value of mx +1 on x ≥4 occurs at x =4. Therefore, to have mx +1 <0 for all x ≥4, it suffices that the maximum value at x=4 is <0. So, m*4 +1 <0 => 4m < -1 => m < -1/4.But from the numerator condition, we have |m| >1/2. Since m is negative here, |m| >1/2 translates to m < -1/2.Therefore, in Case 1, we need m < -1/2 (since m must satisfy both m < -1/4 and m < -1/2, the stricter condition is m < -1/2). So, m < -1/2.Now, moving to Case 2: Numerator <0 and Denominator >0 for all x ≥4.First, Numerator <0 for all x ≥4. The numerator is m²x -1, which is increasing in x. If we want m²x -1 <0 for all x ≥4, then the numerator must be negative even at x approaching infinity. But since the numerator is m²x -1, which is a linear function with slope m² >0 (since m ≠0), as x approaches infinity, the numerator tends to infinity. Therefore, it's impossible for the numerator to remain negative for all x ≥4 because eventually, it will become positive as x increases. Hence, Case 2 cannot hold for all x ≥4 unless the numerator is never positive, which is impossible because the slope is positive. Therefore, Case 2 is impossible. Therefore, the only possible case is Case 1.But wait, let me check that again. If we want the numerator to be negative for all x ≥4, but since the numerator is increasing, the latest point where it could be negative is at x=4. If the numerator is negative at x=4, then for x >4, it will become more positive. Therefore, if we require the numerator to be negative at x=4, then m²*4 -1 <0 => m² <1/4 => |m| <1/2. But then, if |m| <1/2, and m is positive or negative. However, in Case 2, we also need the denominator to be positive for all x ≥4.So, denominator >0 for all x ≥4. The denominator is mx +1. Let's see. If m is positive, then mx +1 is increasing in x, so its minimum value is at x=4. Therefore, denominator >0 for all x ≥4 if 4m +1 >0 => m > -1/4. But since m is positive here, m >0, which already satisfies m > -1/4. But if m is positive, and |m| <1/2 (from the numerator condition), then m is between 0 and 1/2. Wait, but if m is positive, then the denominator is mx +1, which is positive for all x ≥4, because m is positive. So, for m positive, denominator is positive. The numerator is m²x -1. For x ≥4, m²x -1. If m is between 0 and 1/2, then m² <1/4, so m²x < (1/4)x. At x=4, m²x <1. Therefore, m²x -1 <0 at x=4, and since m²x increases with x, at some point x =1/m², the numerator becomes zero. So, for x ≥4, if 1/m² >4, i.e., m² <1/4, which is already our case (m between 0 and 1/2), then the numerator is negative for x=4 and becomes positive at x=1/m². Therefore, between x=4 and x=1/m², the numerator is negative, but beyond x=1/m², it becomes positive. But since 1/m² >4, as m² <1/4, then 1/m² >4. Therefore, if x can be up to infinity, but the numerator becomes positive once x exceeds 1/m². Therefore, the numerator is positive for x >1/m². Therefore, for x in [4, 1/m²), the numerator is negative, and for x >1/m², it's positive. But our inequality must hold for all x ≥4. Therefore, even if the numerator is positive for x >1/m², the denominator is positive (since m is positive), so the entire expression would be positive, violating the inequality (we need it to be negative). Therefore, even if m is between 0 and 1/2, the inequality (m²x -1)/(mx +1) <0 would hold only when numerator is negative and denominator is positive, which is in the interval x ∈ [4, 1/m²). But beyond x=1/m², the numerator becomes positive, making the expression positive, which violates the inequality. Therefore, Case 2 cannot hold for all x ≥4 if m is positive, because after x=1/m², the expression becomes positive. Therefore, Case 2 is invalid. If m is negative, let's check.Wait, in Case 2, denominator must be positive for all x ≥4. So, if m is negative, denominator is mx +1. For x ≥4, mx is negative (since m is negative), so mx +1. The denominator would be positive if mx +1 >0. Since m is negative, as x increases, mx becomes more negative, so mx +1 decreases. Therefore, the minimal value occurs as x approaches infinity, which is negative infinity. Therefore, mx +1 will eventually become negative. Therefore, if m is negative, the denominator cannot be positive for all x ≥4. Therefore, only if m is positive can the denominator be positive for all x ≥4, but as we saw earlier, even then the numerator becomes positive for x >1/m², which breaks the inequality. Therefore, Case 2 is impossible.Therefore, the only possible case is Case 1, where numerator is positive and denominator is negative for all x ≥4. As previously established, for this case, m must be negative, with |m| >1/2, so m < -1/2. Wait, but let me check if that's sufficient.So, if m < -1/2, then:- Numerator: m²x -1. Since m² >1/4, then at x=4, m²*4 -1 > (1/4)*4 -1 =1 -1=0. Therefore, numerator is positive at x=4 and increasing for x >4, so numerator remains positive for all x ≥4.- Denominator: mx +1. Since m is negative, mx is negative for all x. As x increases, denominator mx +1 becomes more negative. However, at x=4, denominator is 4m +1. Since m < -1/2, 4m +1 <4*(-1/2) +1= -2 +1= -1 <0. Therefore, at x=4, denominator is negative, and for x >4, since m is negative, denominator becomes more negative (i.e., even smaller). Therefore, denominator is negative for all x ≥4.Therefore, in this case, numerator is positive and denominator is negative for all x ≥4, so the expression (m²x -1)/(mx +1) is negative for all x ≥4. Therefore, the inequality holds.Thus, the conclusion is that m must be less than -1/2.But let me verify with a specific example. Let's take m = -1. Then m² =1. Then numerator is x -1. For x ≥4, x -1 is positive. Denominator is -x +1. For x ≥4, -x +1 is negative. So, (x -1)/(-x +1) = -(x -1)/(x -1) = -1 (for x ≠1). Wait, but x ≥4, so x ≠1. Therefore, the expression simplifies to -1 for all x ≥4. Therefore, (m²x -1)/(mx +1) = -1 <0, which holds. So, m = -1 is valid.Another example, m = -0.6, which is less than -0.5. Then m² = 0.36. The numerator is 0.36x -1. At x=4, 0.36*4 -1 =1.44 -1=0.44>0. Denominator is -0.6x +1. At x=4, denominator is -2.4 +1= -1.4 <0. So, positive over negative gives negative, so the inequality holds. For x=10, numerator is 3.6 -1=2.6>0, denominator is -6 +1= -5 <0, so still negative. So, works.Now, check m=-0.4, which is greater than -0.5 (i.e., |m| <0.5). Then m²=0.16. Numerator:0.16x -1. At x=4, 0.64 -1= -0.36 <0. Denominator: -0.4x +1. At x=4, denominator is -1.6 +1= -0.6 <0. So numerator negative and denominator negative, making the expression positive, which violates the inequality. Hence, m=-0.4 is invalid.Similarly, if m is between -0.5 and 0, say m=-0.3. Then m²=0.09. Numerator at x=4: 0.09*4 -1=0.36 -1= -0.64 <0. Denominator: -0.3x +1. At x=4, denominator is -1.2 +1= -0.2 <0. So again, numerator and denominator both negative, expression positive, which violates the inequality. Hence, invalid.If m is positive, say m=0.3. Then numerator is 0.09x -1. At x=4:0.36 -1= -0.64 <0. Denominator:0.3x +1=1.2 +1=2.2>0. So, numerator negative and denominator positive, so expression negative. Wait, but hold on. For x=4, the expression is negative. But when x exceeds 1/m²≈11.11, the numerator becomes positive. For example, x=12, numerator=0.09*12 -1=1.08 -1=0.08>0. Denominator=0.3*12 +1=3.6 +1=4.6>0. So, numerator and denominator both positive, expression positive. Therefore, for x=12, the expression is positive, which violates the inequality. Therefore, m=0.3 is invalid even though at x=4 it works.Therefore, for positive m, even though at x=4 the expression is negative, once x crosses 1/m², the expression becomes positive, which violates the requirement that it must hold for all x≥4. Therefore, positive m's are invalid.Therefore, only m < -1/2 works. Therefore, the range of real numbers m is (-∞, -1/2).But let me check another edge case. What if m = -1/2 exactly? Then m²=1/4. The numerator is (1/4)x -1. At x=4, (1/4)*4 -1=1 -1=0. So, at x=4, the numerator is zero, making the expression zero, which is not less than zero. Therefore, m=-1/2 is excluded. Therefore, m must be strictly less than -1/2.Therefore, the range is m ∈ (-∞, -1/2).Final AnswerThe range of the real number ( m ) is boxed{(-infty, -dfrac{1}{2})}.</think>To determine the range of real numbers ( m ) (where ( m neq 0 )) such that the inequality (dfrac{m^{2}x - 1}{mx + 1} < 0) holds for all ( x geq 4 ), we analyze the signs of the numerator and denominator.The inequality holds when the numerator and denominator have opposite signs. We consider two cases:1. Numerator positive and denominator negative for all ( x geq 4 ): - The numerator ( m^2x - 1 ) must be positive for all ( x geq 4 ). This requires ( m^2 cdot 4 - 1 > 0 ), leading to ( m^2 > frac{1}{4} ) or ( |m| > frac{1}{2} ). - The denominator ( mx + 1 ) must be negative for all ( x geq 4 ). For ( m ) negative, the maximum value of the denominator at ( x = 4 ) must be negative: ( 4m + 1 < 0 ), leading to ( m < -frac{1}{4} ). Combining with ( |m| > frac{1}{2} ), we get ( m < -frac{1}{2} ).2. Numerator negative and denominator positive for all ( x geq 4 ): - The numerator ( m^2x - 1 ) is increasing and will eventually become positive as ( x ) increases, making this case impossible for all ( x geq 4 ).Thus, the valid case is when ( m ) is negative and ( |m| > frac{1}{2} ). Checking edge cases confirms that ( m = -frac{1}{2} ) is excluded because the numerator becomes zero at ( x = 4 ).Therefore, the range of the real number ( m ) is (boxed{(-infty, -dfrac{1}{2})}).]

🔑:AnalysisThis problem examines the issue of a quadratic inequality always being true. It involves converting a fractional inequality into a polynomial inequality and then discussing and solving it using knowledge of quadratic functions.SolutionGiven: dfrac{m^{2}x-1}{mx+1} 0, the inequality cannot always hold true for all x geqslant 4,Therefore, m -dfrac{1}{m},Then, dfrac{1}{m^{2}} < 4,Solving gives -1 < m < -dfrac{1}{2},When m=-1, it is obviously true,When m < -1, dfrac{1}{m^{2}} < -dfrac{1}{m},Then, -dfrac{1}{m} < 4,Solving gives m < -1,Summarizing, the range of m is m < -dfrac{1}{2}.Therefore, the answer is boxed{m < -dfrac{1}{2}}.

🧠:[<think>Okay, let's try to figure out this problem. So, there's a magical tree with 46 fruits. Each day, starting from day 1, the number of fruits that fall increases by 1 each day. But if there aren't enough fruits left to drop the required number, it starts over by dropping 1 fruit the next day. We need to find out on which day all the fruits will have fallen.Hmm, let me break this down. On day 1, 1 fruit falls. Day 2, 2 fruits. Day 3, 3, and so on. But if, say, on day n, there are fewer fruits left than n, then instead of dropping n fruits, it resets and drops 1 fruit that day. Then the next day, it would try to drop 2 fruits again, right?So the process is like 1, 2, 3, ..., until the remaining fruits are less than the next day's required number. Then it starts back at 1, 2, 3, etc., until all fruits are gone.Let me try to simulate this step by step. Maybe create a table of days, fruits fallen each day, total fallen, and remaining.Starting with 46 fruits.Day 1: Drop 1. Remaining: 45. Total fallen: 1.Day 2: Drop 2. Remaining: 43. Total fallen: 3.Day 3: Drop 3. Remaining: 40. Total fallen: 6.Day 4: Drop 4. Remaining: 36. Total fallen: 10.Day 5: Drop 5. Remaining: 31. Total fallen: 15.Day 6: Drop 6. Remaining: 25. Total fallen: 21.Day 7: Drop 7. Remaining: 18. Total fallen: 28.Day 8: Drop 8. Remaining: 10. Total fallen: 36.Day 9: Now, next day would be day 9, which requires dropping 9 fruits. But remaining is 10. Wait, 10 is more than 9, so we can drop 9. Then remaining would be 1. Total fallen: 36 + 9 = 45. Remaining: 1.Wait, but hold on. Day 9: If we drop 9, remaining is 1. Then day 10 would require dropping 10 fruits, but only 1 is left. Since 1 < 10, we reset. So on day 10, we drop 1, which brings remaining to 0. So total days would be 10?Wait, but let me check that again. Let's step through each day carefully.Starting with 46.Day 1: Drop 1. Remaining: 45.Day 2: Drop 2. Remaining: 43.Day 3: 3. Remaining: 40.Day 4: 4. Remaining: 36.Day 5: 5. Remaining: 31.Day 6: 6. Remaining: 25.Day 7: 7. Remaining: 18.Day 8: 8. Remaining: 10.Day 9: 9. Remaining: 1.Day 10: Next day, supposed to drop 10, but only 1 left. So reset to 1. Drop 1. Remaining: 0.So total days would be 10. But wait, let me verify this step by step.Wait, after day 8, remaining is 10. So day 9: drop 9, remaining 1. Then day 10: need to drop 10, but only 1 left. So on day 10, drop 1, which finishes it. So day 10 is the last day. So the answer is day 10? But let me check another way.Alternatively, maybe there's a formula or a way to calculate this without simulating each day. Let's think about the triangular numbers. The sum 1 + 2 + 3 + ... + n = n(n + 1)/2. If the total fruits were a triangular number, then the days needed would be exactly n. But 46 isn't a triangular number. The triangular numbers near 46 are:For n=9: 45. For n=10: 55. So 46 is between 45 and 55. So if we use the normal sequence, up to day 9, we would have dropped 45 fruits. Then on day 10, we need to drop 10, but only 1 left. So the problem says if the number is less, we start over by dropping 1. So instead of day 10 being 10, it becomes 1. So day 10: drop 1, remaining 0. So total days 10.Wait, but in the problem statement, if on a certain day the number of fruits is less than the number that should fall, then on that day it will start over by dropping 1. So when the remaining fruits is less than the next day's number, we start over. So let's see, after day 9, we have 1 fruit left. The next day, day 10, we were supposed to drop 10, but since 1 < 10, we drop 1 instead. So day 10 is the last day.Therefore, the answer is day 10. But wait, let me check again. Let me simulate step by step:Day 1: 1 fallen, remaining 45Day 2: 2, total 3, remaining 43Day 3: 3, total 6, remaining 40Day 4: 4, total 10, remaining 36Day 5: 5, total 15, remaining 31Day 6: 6, total 21, remaining 25Day 7: 7, total 28, remaining 18Day 8: 8, total 36, remaining 10Day 9: 9, total 45, remaining 1Day 10: Need to drop 10, but only 1 left. So start over by dropping 1, total 46, remaining 0.Yes, so day 10. But wait, but maybe the problem is different. Let me check the problem statement again."On the first day, 1 fruit will fall from the tree, and the number of fruits that fall each day is 1 more than the previous day. However, if the number of fruits on the tree is less than the number that should fall on a certain day, then on that day it will start over by dropping 1 fruit and continue according to the original rule."Wait, does "start over" mean that after that day, the next day will be 2, then 3, etc., or does it mean that on the day when it's not enough, we drop 1, and then the next day we try to drop 2 again? Let me parse the original Chinese to check.Original problem: "如果树上某一天剩下的果子数少于这一天应该掉落的果子数, 那么在那天，它会重新开始从掉1个果子，并继续按照原来的规则进行。如此继续，直到树上的果子都掉光为止。"Translation: "If on a certain day the number of fruits remaining on the tree is less than the number of fruits that should fall on that day, then on that day it will start over by dropping 1 fruit and continue according to the original rule. This continues until all the fruits on the tree have fallen."So "start over" refers to starting the sequence over from 1 on that day. So if the required number is more than the remaining fruits, on that day you drop 1, and then the next day you would drop 2, etc.So in the case where on day 9, after dropping 9, you have 1 left. Then day 10 requires dropping 10, but since 1 < 10, you drop 1 instead (which clears the tree), so that day is day 10. The sequence would have been 1,2,3,4,5,6,7,8,9,1. But since after day 10, there are 0 left, it stops.Therefore, the total days are 10.Wait, but in my earlier simulation, day 10 is the day when 1 fruit is dropped, finishing the total. So the answer is day 10.Alternatively, maybe the problem is considering that after dropping 9 on day 9, there's 1 left. Then day 10: supposed to drop 10, but only 1 left, so you drop 1, which takes the total to 46. So day 10 is the last day. Hence, 10 days.But let me test with a smaller number to see if this logic holds. Suppose there are 2 fruits.Day 1: drop 1, remaining 1.Day 2: supposed to drop 2, but only 1 left. So drop 1. Now remaining 0. So total days 2.Alternatively, if the answer was 3 days, but no, in this case, it's 2 days. So the formula works here. Similarly, if there are 3 fruits:Day1: 1, remaining 2.Day2: 2, remaining 0. So days 2.Wait, but if 3 fruits:Wait day1: 1, remaining 2.Day2: 2, remaining 0. So that's 2 days.But if there were 4 fruits:Day1:1, remaining3.Day2:2, remaining1.Day3: supposed to drop3, but only1 left. So drop1, remaining0. So days3.Yes, so 1+2+1=4.Similarly, for 46, following the same logic, the answer would be day10.Alternatively, maybe using the formula for the sum until the last full sequence.Let's see, the sum S = n(n+1)/2. Find the largest n where S <= 46.n=9: 9*10/2=45 <=46.So after day9, 45 fruits have fallen, 1 remaining.Then day10: supposed to drop10, but only1 left. So drop1, total46. So day10.Thus, the answer is 10 days.Alternatively, another approach: the total number of days is equal to the largest triangular number less than total fruits, then add the days needed to finish the remaining fruits with the reset sequence.But in this case, after 45 (triangular number 9), remaining 1. Then the next day, drop1. So total days 9 +1=10.Alternatively, if remaining fruits after triangular number is r, then the days needed would be n + ceil(r /1), but since after triangular number n, we have r fruits left, and the next day we can drop 1, so days n +1 if r=1.Wait, but in the case where remaining fruits is r, and we have to drop 1 each day until they are gone. But according to the problem, when you can't drop the required number, you drop 1 and continue the sequence. So if you have r remaining, and the next required is k, where k > r, you drop 1 on that day (k is set to 1), and then the next day you would try to drop 2, etc. But in the case of r=1, after dropping 1, you finish. So in the case of r=1, it's just 1 more day.So total days: n +1, where n is the triangular number just below total fruits.But in our case, n=9, since 45 is the triangular number. Then 46-45=1. So days=9+1=10.Similarly, if total fruits were 47, then after day9, 45, remaining 2. Day10: need to drop10, but 2<10, so drop1, remaining1. Then day11: next day, drop2, but only1 left, so drop1, remaining0. So days=9+2=11.But in our case, remaining is 1, so days=9+1=10.Therefore, the answer is 10 days. So I think that's correct.But let me check another example. If total fruits are 10.Triangular number n=4: 10. So days=4. Wait, 1+2+3+4=10, so days=4.If total fruits are 11.Triangular number n=4:10, remaining1. Then day5: drop1, total11. So days=5.Yes. So formula works.Therefore, applying to 46: triangular number 45 (n=9), remaining1, days=9+1=10.So the answer is day10.Final Answerboxed{10}</think>The problem involves a magical tree with 46 fruits. Each day, the number of fruits that fall increases by 1 from the previous day. If the remaining fruits are less than the number that should fall on a certain day, the sequence resets to dropping 1 fruit the next day. We need to determine the day when all fruits will have fallen.1. Day-by-Day Simulation: - Day 1: 1 fruit falls, remaining = 45 - Day 2: 2 fruits fall, remaining = 43 - Day 3: 3 fruits fall, remaining = 40 - Day 4: 4 fruits fall, remaining = 36 - Day 5: 5 fruits fall, remaining = 31 - Day 6: 6 fruits fall, remaining = 25 - Day 7: 7 fruits fall, remaining = 18 - Day 8: 8 fruits fall, remaining = 10 - Day 9: 9 fruits fall, remaining = 1 - Day 10: Need to drop 10 fruits, but only 1 left. Therefore, drop 1 fruit, remaining = 02. Triangular Number Approach: - The largest triangular number less than 46 is 45 (sum of 1 to 9). - After 9 days, 45 fruits have fallen, leaving 1 fruit. - On the 10th day, since only 1 fruit is left, the sequence resets to dropping 1 fruit, which finishes all remaining fruits.Thus, the day when all fruits will have fallen is day 10.[boxed{10}],<think>Okay, so there's this magical tree with 46 fruits. Every day, starting from day one, a certain number of fruits fall. The first day, 1 fruit falls. Each subsequent day, the number of fruits that fall is 1 more than the previous day. But there's a catch: if on any day the number of fruits left on the tree is less than the number that should fall that day, then instead of that number, it resets and starts again from 1 fruit falling. This process continues until all the fruits have fallen off. The question is asking on which day the tree will have no fruits left.Alright, let me try to break this down. So initially, there are 46 fruits. On day 1, 1 fruit falls. Then day 2, 2 fruits fall, day 3, 3 fruits, and so on. However, if on day n, the number of fruits remaining is less than n, then instead of n fruits falling, it resets to 1, and the cycle continues. So we need to track day by day how many fruits are left and adjust the number of falling fruits accordingly if we hit the reset condition.Let me start by writing down the days and the number of fruits that fall each day, keeping track of the remaining fruits.Starting with 46 fruits.Day 1: 1 fruit falls. Remaining: 46 - 1 = 45.Day 2: 2 fruits fall. Remaining: 45 - 2 = 43.Day 3: 3 fruits fall. Remaining: 43 - 3 = 40.Day 4: 4 fruits fall. Remaining: 40 - 4 = 36.Day 5: 5 fruits fall. Remaining: 36 - 5 = 31.Day 6: 6 fruits fall. Remaining: 31 - 6 = 25.Day 7: 7 fruits fall. Remaining: 25 - 7 = 18.Day 8: 8 fruits fall. Remaining: 18 - 8 = 10.Day 9: Now, according to the sequence, 9 fruits should fall. But there are only 10 left. 10 is more than 9, so does it still proceed? Wait, the problem says if the number of fruits is less than the number that should fall, then it resets. Since 10 is not less than 9, we can go ahead. So 9 fruits fall. Remaining: 10 - 9 = 1.Day 10: Now, the next day would be day 10, and according to the original rule, 10 fruits should fall. However, only 1 fruit is left. Since 1 is less than 10, we reset. So on day 10, instead of 10 fruits, only 1 fruit falls. Remaining: 1 - 1 = 0.Wait, so after day 9, we have 1 fruit left. Then day 10, since 1 < 10, reset to 1 fruit falling. Therefore, day 10: 1 fruit falls, and the tree is empty. So does that mean it takes 10 days?But let me check again because maybe I made a mistake in the day counts. Let me go step by step.Day 1: 1 falls, remaining 45.Day 2: 2 falls, remaining 43.Day 3: 3 falls, remaining 40.Day 4: 4 falls, remaining 36.Day 5: 5 falls, remaining 31.Day 6: 6 falls, remaining 25.Day 7: 7 falls, remaining 18.Day 8: 8 falls, remaining 10.Day 9: 9 falls, remaining 1.Day 10: Need to drop 10, but only 1 left. So reset to 1. 1 falls, remaining 0.Therefore, day 10 is the last day. So total of 10 days. But wait, the problem says "the day the tree's fruits will all be gone." So if on day 10, the last fruit falls, then the answer is day 10.But let me confirm. Let me recount each day:Start with 46.1: 1 -> 452: 2 -> 433: 3 -> 404: 4 -> 365: 5 -> 316: 6 -> 257: 7 -> 188: 8 -> 109: 9 -> 110: 1 (because 1 < 10) -> 0Yes, that seems correct. So 10 days in total.But let me check another way. The sum of the first n numbers is n(n+1)/2. But in this case, since the sequence can reset, the total days might not follow the triangular number.But let's see. The first 9 days would have the sum 1+2+3+4+5+6+7+8+9 = 45. So 45 fruits would have fallen by day 9. But the total fruits are 46, so day 10 would need to drop 1 fruit, which is exactly the remaining one. But wait, wait. Wait, if we didn't reset, on day 10 we would need to drop 10, but since only 1 is left, we reset to 1. Therefore, day 10, 1 fruit falls. So total days are 10.Alternatively, if there were 45 fruits, then day 9 would have finished. But since there are 46, day 9 leaves 1, then day 10 drops 1. So total days 10.But let me see if there's another way to approach this problem. Suppose we model the days as sequences where each time we have a cycle: start dropping 1, 2, 3,... until the remaining fruits are less than the next number, then reset.So the first cycle: 1,2,3,...,k where the sum is <=46. Wait, but actually, since each day you check if the remaining is less than the next number. So it's not cycles, but each day you increment the number to drop by 1, unless you can't, then reset.This is similar to the problem where you try to subtract 1, then 2, then 3, etc., but if you can't subtract the next number, you reset to 1. So the total days would be the number of days until the sum reaches 46, considering resets when needed.Alternatively, perhaps we can think of it as follows: the number of fruits fallen after n days is the sum of a sequence where each term is either incrementing by 1 each day or resetting to 1 when needed.But maybe it's easier to simulate day by day, as I did before.Let me try another approach. Let's see how much is being subtracted each day until we reach the total of 46.Days 1-9: 1+2+3+4+5+6+7+8+9 = 45. Then on day 10, we have 1 left, so we subtract 1. Total days: 10.Wait, that seems too straightforward. But in reality, when we subtract each day's amount, the total would be 45 after day 9, and then 1 on day 10. So 45 +1 = 46. So 10 days. Therefore, the answer is day 10.But let me check if there's a case where after resetting, the sequence continues again. For example, suppose that after a reset, the next day it starts again from 1, 2, 3, etc. But in this problem, it seems that whenever a reset happens (because the remaining fruits are less than the next number), it starts over by dropping 1 fruit and continues according to the original rule. So after resetting, the next day would be 1, then 2, etc.But in our case, when we reset on day 10, we only need to drop 1 fruit, which is the last one. So day 10 is the last day. Therefore, total days are 10.But let me consider another scenario where after resetting, you might have more days. For example, suppose that if you reset, you start again from 1, but if after resetting again, you can continue.But let's take the problem statement again: "if the number of fruits on the tree is less than the number that should fall on a certain day, then on that day it will start over by dropping 1 fruit and continue according to the original rule."So when a reset occurs, you drop 1 fruit that day, and then the next day you would try to drop 2 fruits again. But in our case, after day 9, we have 1 fruit left. Day 10: supposed to drop 10, but only 1 left. So reset to 1. Then drop 1, remaining 0. So day 10 is the last day.Another example: suppose after day n, you have 2 fruits left. The next day, you are supposed to drop n+1 fruits. But since 2 < n+1, you reset to 1. Then drop 1 fruit, remaining 1. Then the next day, you try to drop 2 again, but only 1 left, so reset to 1 again. So drop 1, remaining 0. So in that case, it would take two more days.But in our problem, after day 9, we have 1 fruit. Then on day 10, reset to 1, dropping 1, remaining 0. So only one day needed. Therefore, day 10.Wait, but according to this, if after resetting, the next day you continue the original rule, meaning that after dropping 1 on the reset day, the next day you try to drop 2, unless you can't. But in our case, after day 10, all fruits are gone. So there is no day 11. So day 10 is the last day.Therefore, the answer should be day 10. But let me verify once more with the day-by-day count.Day 1: 1 (remaining: 45)Day 2: 2 (43)Day 3: 3 (40)Day 4: 4 (36)Day 5: 5 (31)Day 6: 6 (25)Day 7: 7 (18)Day 8: 8 (10)Day 9: 9 (1)Day 10: 1 (0)Yes, that's 10 days. So the answer is 10. Therefore, the tree will be empty on day 10. So the final answer is boxed{10}.But wait, let me check again in case I miscounted. Let's list the days and subtract each time:Start: 46Day 1: 46 -1 =45Day 2: 45 -2=43Day3:43-3=40Day4:40-4=36Day5:36-5=31Day6:31-6=25Day7:25-7=18Day8:18-8=10Day9:10-9=1Day10:1-1=0Yes, exactly. So day 10 is when it's all gone. So the answer is 10. Therefore, boxed answer is boxed{10}.Final Answerboxed{10}</think>Starting with 46 fruits on the tree, each day the number of fruits that fall increases by 1 from the previous day. If the number of fruits remaining is less than the number that should fall, it resets to 1. We track the number of fruits remaining each day:- Day 1: 1 fruit falls, remaining: (46 - 1 = 45)- Day 2: 2 fruits fall, remaining: (45 - 2 = 43)- Day 3: 3 fruits fall, remaining: (43 - 3 = 40)- Day 4: 4 fruits fall, remaining: (40 - 4 = 36)- Day 5: 5 fruits fall, remaining: (36 - 5 = 31)- Day 6: 6 fruits fall, remaining: (31 - 6 = 25)- Day 7: 7 fruits fall, remaining: (25 - 7 = 18)- Day 8: 8 fruits fall, remaining: (18 - 8 = 10)- Day 9: 9 fruits fall, remaining: (10 - 9 = 1)- Day 10: 10 fruits should fall, but only 1 is left. Reset to 1 fruit falling, remaining: (1 - 1 = 0)All fruits fall by day 10. Therefore, the answer is (boxed{10}).]

🔑:6. (10 points) There is a magical tree with 46 fruits on it. On the first day, 1 fruit will fall from the tree, and the number of fruits that fall each day is 1 more than the previous day. However, if the number of fruits on the tree is less than the number that should fall on a certain day, then that day it will start over by dropping 1 fruit and continue according to the original rule. This continues, so by the 10th day, all the fruits on the tree will have fallen.【Solution】Since 1+2+3+4+5+6+7+8+9=45 (fruits)By the tenth day, it is not enough to start over and drop 1 fruit. It ends exactly then.45+1=46 text { (fruits) }Therefore, the answer is: 10