🧠:[<think>Okay, let's see. I have this problem here: the equation is x² - 45x + m = 0, and the roots are prime numbers. We need to find the value of d, which is the sum of the squares of the roots. Hmm, okay, let's start breaking this down.First, I remember that for a quadratic equation ax² + bx + c = 0, the sum of the roots is -b/a and the product is c/a. So in this case, the equation is x² - 45x + m = 0. That means a is 1, b is -45, and c is m. So the sum of the roots should be -b/a = -(-45)/1 = 45. And the product of the roots is c/a = m/1 = m.Alright, so the two roots are prime numbers, let's call them p and q. Then we have:p + q = 45andp * q = m.We need to find d = p² + q².Hmm, how do I relate that to the given information? Well, I know that (p + q)² = p² + 2pq + q². So, if I subtract 2pq from both sides, I get p² + q² = (p + q)² - 2pq. Therefore, d = (45)² - 2m. But wait, do I know what m is? Not yet. But maybe since p and q are primes, there's only a certain pair of primes that add up to 45. Then once I find p and q, I can compute d directly.So, the key is to find two prime numbers that add up to 45, and then multiply them to get m. Then compute d. Let's focus on finding those primes.We need two primes p and q such that p + q = 45. Let's list primes less than 45 and see which pairs add up to 45.First, list primes less than 45:2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43.Now, let's check which pairs add up to 45.Start with the smallest prime, 2:45 - 2 = 43. Is 43 a prime? Yes. So 2 and 43 are primes adding to 45.Next, 3:45 - 3 = 42. 42 is not a prime.5:45 - 5 = 40. Not prime.7:45 - 7 = 38. Not prime.11:45 - 11 = 34. Not prime.13:45 - 13 = 32. Not prime.17:45 - 17 = 28. Not prime.19:45 - 19 = 26. Not prime.23:45 - 23 = 22. Not prime.29:45 - 29 = 16. Not prime.31:45 - 31 = 14. Not prime.37:45 - 37 = 8. Not prime.41:45 - 41 = 4. Not prime.43:45 - 43 = 2. Already considered that pair (2 and 43).So the only pair of primes that add up to 45 are 2 and 43.Wait, is that right? Let me check again. Maybe I missed a pair.Wait, for example, 17 and 28: 28 isn't prime. 19 and 26: 26 isn't prime. 7 and 38: 38 isn't prime. 13 and 32: 32 isn't prime. 5 and 40: 40 isn't prime. 3 and 42: 42 isn't prime. 11 and 34: 34 isn't prime. 23 and 22: 22 isn't prime. 29 and 16: 16 isn't prime. 31 and 14: 14 isn't prime. 37 and 8: 8 isn't prime. 41 and 4: 4 isn't prime. 43 and 2: already covered.So indeed, the only primes that add up to 45 are 2 and 43.Therefore, the roots are 2 and 43. Then, the sum of their squares is d = 2² + 43² = 4 + 1849 = 1853.Wait, but let me check if that's correct. Let me compute 43 squared: 43*43. 40*40 is 1600, plus 2*40*3=240, plus 3*3=9. So 1600 + 240 + 9 = 1849. Then 1849 + 4 is 1853. That seems right.But wait, hold on. Let me confirm once again if 2 and 43 are primes. 2 is the only even prime, and 43 is a well-known prime. Yes, both are primes. So that pair is valid.Hence, d = 1853. Therefore, the answer should be 1853.Alternatively, perhaps I can verify using Vieta's formula. If the roots are 2 and 43, then the equation is (x - 2)(x - 43) = x² - (2+43)x + (2*43) = x² -45x +86. So m is 86. Then the sum of the squares is 4 + 1849 = 1853. So that checks out.Alternatively, maybe the problem expects me to compute d as (p + q)² - 2pq. Let's see: (45)² - 2*86. 45 squared is 2025. 2*86 is 172. Then 2025 - 172 = 2025 - 172.2025 - 100 is 1925, then subtract 72 more: 1925 - 72 = 1853. So that also gives the same answer. Therefore, regardless of the method, d is 1853.Therefore, the answer is 1853.Final Answerboxed{1853}</think>Given the quadratic equation (x^2 - 45x + m = 0) with prime number roots, we need to find the sum of the squares of the roots, denoted as (d).First, we use Vieta's formulas:- The sum of the roots (p) and (q) is (p + q = 45).- The product of the roots is (pq = m).We need to find two prime numbers that add up to 45. Checking pairs of primes less than 45, we find that the only pair is 2 and 43. Both are prime numbers and their sum is 45.Next, we calculate the sum of their squares:[d = p^2 + q^2 = 2^2 + 43^2 = 4 + 1849 = 1853]We can verify this using the identity (p^2 + q^2 = (p + q)^2 - 2pq):[d = (45)^2 - 2m = 2025 - 2 times 86 = 2025 - 172 = 1853]Thus, the value of (d) is (boxed{1853}).,<think>Okay, so I have this problem here: the quadratic equation x² - 45x + m = 0 has roots that are prime numbers. I need to find the value of d, which is the sum of the squares of the roots. Hmm, let's break this down step by step.First, I remember that for a quadratic equation of the form ax² + bx + c = 0, the sum of the roots is -b/a and the product is c/a. In this case, the equation is x² - 45x + m = 0, so a is 1, b is -45, and c is m. Therefore, the sum of the roots should be -b/a, which would be -(-45)/1 = 45. So the two prime numbers that are the roots add up to 45. Their product is c/a, which is m/1 = m. So m is the product of those two primes.Now, the problem says the roots are prime numbers. So we need two prime numbers that add up to 45. Then, once we find those primes, we can compute their squares and add them together to get d.Wait, but primes except for 2 are odd. The sum of two odd numbers is even. But 45 is odd. So if the sum is 45, which is odd, one of the primes must be even, and the only even prime is 2. Therefore, one of the primes is 2, and the other is 45 - 2 = 43. Let me check if 43 is a prime number.43 is a prime number because it's not divisible by 2, 3, 5. Let's see: 43 divided by 2 is 21.5, not integer. 43 divided by 3 is around 14.333, not integer. Divided by 5 is 8.6, not integer. Then primes up to sqrt(43) which is around 6.557, so check primes up to 7. Next prime is 7: 43 divided by 7 is about 6.14, not integer. So yes, 43 is prime. So the two primes are 2 and 43.Therefore, the roots are 2 and 43. Then the sum of their squares is 2² + 43². Let me compute that. 2 squared is 4, and 43 squared is 43*43. Let me calculate 43 squared. 40 squared is 1600, plus 3 squared is 9, and then cross terms 2*40*3 = 240. So (40 + 3)^2 = 40² + 2*40*3 + 3² = 1600 + 240 + 9 = 1849. So 43 squared is 1849. Then 4 + 1849 = 1853. So d is 1853.Wait, but just to make sure there are no other pairs of primes that add up to 45. Let me check. Let's suppose instead of 2 and 43, maybe there are other primes. Let's list primes less than 45 and see if any pair adds to 45.Primes less than 45: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43.So start with 2: 45 - 2 = 43, which is prime, as we saw.Next, check 3: 45 - 3 = 42. 42 is not prime (divisible by 2, 3, etc.)5: 45 - 5 = 40. Not prime (ends with 0).7: 45 - 7 = 38. Not prime (even, greater than 2).11: 45 - 11 = 34. Not prime (even).13: 45 -13 =32. Not prime.17: 45 -17=28. Not prime.19: 45-19=26. Not prime.23: 45-23=22. Not prime.29: 45-29=16. Not prime.31: 45-31=14. Not prime.37: 45-37=8. Not prime.41: 45-41=4. Not prime.43: 45-43=2. Which is prime, but that's the same pair as before.So indeed, the only pair of primes that add up to 45 are 2 and 43. Therefore, those are the roots.Therefore, sum of squares is 2² +43²=4 +1849=1853. So d is 1853.But wait, just to make sure I didn't make a mistake in the arithmetic. Let's verify 43 squared again. 43*43: 40*40=1600, 40*3=120, 3*40=120, 3*3=9. So (40+3)(40+3)=1600+120+120+9=1600+240+9=1849. Yes, that's correct. Then 1849 +4 is 1853.So I think that's the correct answer. The problem didn't ask for m, but if it did, m would be 2*43=86. But since they just want d, the sum of the squares, it's 1853. So I think that's the answer. Let me check again if there's another possible pair of primes adding to 45. Hmm, 2 and 43 are the only ones. So yes, 1853 is the correct value for d.Final AnswerThe value of ( d ) is boxed{1853}.</think>Given the quadratic equation (x^2 - 45x + m = 0) with prime number roots, we need to find the value of (d), which is the sum of the squares of the roots.First, we use Vieta's formulas:- The sum of the roots is (45).- The product of the roots is (m).Since the roots are prime numbers and their sum is (45) (an odd number), one of the primes must be (2) (the only even prime). The other root is (45 - 2 = 43). We verify that (43) is a prime number.The roots are (2) and (43). We calculate the sum of their squares:[2^2 + 43^2 = 4 + 1849 = 1853]Thus, the value of (d) is (boxed{1853}).]

🔑:Let the roots be alpha, beta. alpha+beta=45, alpha beta=mThe sum of two prime numbers alpha+beta=45 alpha=2, beta=43 (2 is the only even prime number)d=alpha^{2}+beta^{2}=4+43^{2}=1853

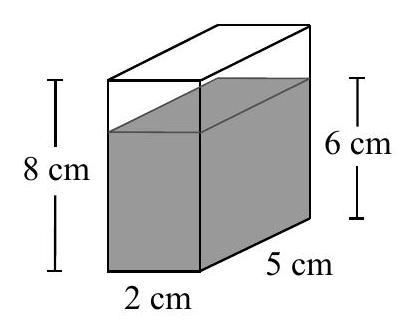
🧠:[<think>Okay, so there's this rectangular prism, which is like a box, right? It's closed, so no open faces. The problem says it's standing on a face with dimensions 2 cm by 5 cm. So, the base is 2 cm by 5 cm, and the height of the prism is 8 cm. Got that. The prism contains water with a depth of 6 cm. Then, when we tip the prism so that it stands on a face with the greatest area, we need to find the new depth of the water. The options are from 0.75 cm up to 1.75 cm. Hmm.First, let me visualize this. When it's standing on the 2 cm by 5 cm face, that's the base. The height of the prism is 8 cm, so the other dimensions must be 2 cm, 5 cm, and 8 cm. Wait, no. Wait, hold on. A rectangular prism has three dimensions: length, width, and height. If it's standing on a face with dimensions 2 cm by 5 cm, then the height of the prism (the dimension perpendicular to the base) is 8 cm. So the three dimensions are 2 cm, 5 cm, and 8 cm. So the other faces would have areas: 2×8, 5×8, and 2×5. So when they tip it to stand on the face with the greatest area, that would be the face with the largest area. The areas of the faces are 2×5=10, 2×8=16, and 5×8=40. Wait, 5×8 is 40 cm², which is the largest. So the greatest area is 40 cm², so they tip it onto the 5 cm by 8 cm face. So the new base is 5 cm by 8 cm, and the height of the prism when it's standing on that base would be 2 cm. Wait, no. Wait, the original prism has three dimensions: 2 cm, 5 cm, and 8 cm. So depending on which face it's standing on, the height (the dimension perpendicular to the base) changes. So when standing on the 2×5 face, the height is 8 cm. If we tip it onto the 5×8 face, then the height becomes 2 cm. Wait, no, that doesn't make sense. Wait, no. Wait, the prism's height when standing on a particular face is the dimension perpendicular to that face. So the original position: base is 2×5, height is 8. If we tip it onto the 5×8 face, then the new height (the dimension perpendicular to the new base) would be 2 cm. So when they tip the prism, the height becomes 2 cm? But that seems contradictory because tipping it onto a face with a larger area would make it shorter? Hmm, maybe.But let me not get confused. Let's think step by step. The original volume of water is the area of the base times the depth. The base is 2×5=10 cm², and the depth is 6 cm. So the volume of water is 10×6=60 cm³. When we tip the prism, the volume remains the same, right? Because the water is just being sloshed around, not added or removed. So the new volume will still be 60 cm³. Now, when it's tipped onto the face with the greatest area, which is 5×8=40 cm². So the new base is 40 cm². The depth of the water will be the volume divided by the base area. Wait, but that's only if the water fills the prism uniformly, but depending on how it's tipped, maybe the shape of the water changes. Wait, maybe not. Wait, if we tip it so that it stands on the 5×8 face, then the original height of the prism in this orientation is 2 cm. But the water's depth was 6 cm in the original orientation. Wait, but in the original orientation, the height of the prism was 8 cm, so 6 cm of water. If we tip it onto the 5×8 face, the height is now 2 cm. But 6 cm was in the original height. Hmm, maybe I need to think differently.Wait, perhaps when tipping the prism, the water level will adjust so that the volume remains the same, but the shape of the water might not be a rectangular prism anymore. Maybe it forms a slanted surface? Wait, but if we tip it until it's standing on the 5×8 face, then the water will settle so that its surface is horizontal, right? So in the new orientation, the water will form a horizontal surface. So the depth of the water will be measured vertically from the new base. Hmm.Let me try to sketch mentally. Original position: prism is standing on 2x5 base, height 8 cm. Water is 6 cm deep. So the water forms a rectangular prism with base 2x5 and height 6. Volume 60 cm³. Then, when tipped onto the 5x8 face, which is the largest face. So the new base is 5x8, and the height (the dimension perpendicular to the base) is 2 cm. Wait, but how can the height be 2 cm? Because the original dimensions are 2, 5, 8. So when standing on 5x8, the height is 2 cm. But the water volume is 60 cm³, so if the base area is 40 cm², then the depth would be 60/40 = 1.5 cm. But 1.5 cm is one of the options, option D. But wait, is that the case? Wait, but if the height of the prism in the new orientation is only 2 cm, how can the water depth be 1.5 cm? It seems possible. But let me check again.Wait, maybe when tipping the prism, the height isn't 2 cm. Wait, confusion arises here. Let me think about the dimensions. The prism has three dimensions: length 2 cm, width 5 cm, and height 8 cm. So when it's standing on the 2x5 face, the vertical dimension is 8 cm. If we tip it onto the 5x8 face, then the vertical dimension (height) becomes 2 cm. So the prism is now lying on its side, so to speak, with the 5x8 face as the base, and the height is 2 cm. So the maximum possible depth of water in this orientation would be 2 cm. But we have 60 cm³ of water. If we pour 60 cm³ into a base of 5x8=40 cm², then the depth would be 60/40=1.5 cm. But since the height is 2 cm, 1.5 cm is less than 2 cm, so it's possible. So then the answer is D) 1.5 cm. But let me check if this is correct.Wait, but I might be oversimplifying. When you tip the prism, the water might not just form a rectangular prism in the new orientation. Because tipping could cause the water to spread out differently. Wait, but if the prism is a rectangular prism, when you tip it so that it's standing on a different face, and the water level is horizontal, then the water would still form a rectangular prism with the same volume, just with different dimensions. So as long as the new depth is less than the height in the new orientation, then it's just volume divided by the base area. But let's confirm.Original volume: 2*5*6=60 cm³. New base area: 5*8=40 cm². So if the water forms a rectangular prism with base 5*8 and depth h, then 40*h=60 => h=1.5 cm. Since the height in the new orientation is 2 cm, 1.5 cm is possible, so the depth is 1.5 cm. So answer D. But let me check the answer options. The options are A) 0.75, B)1, C)1.25, D)1.5, E)1.75. So D is an option. But wait, is this correct?Alternatively, maybe the problem is more complicated. Maybe when you tip the prism, the water doesn't just stay as a rectangular prism. For example, if you tilt the prism, the water level might adjust such that it forms a slant, but since the problem says "the depth of the water", which is the vertical depth when it's resting on the new base.Wait, maybe the key here is that when you tip the prism onto the 5x8 face, the height of the prism (i.e., the vertical dimension) becomes 2 cm. But the original water volume is 60 cm³. If the base area is 5x8=40 cm², then the depth would be 60/40=1.5 cm. But wait, the height is only 2 cm, so 1.5 cm is 3/4 of the height. But in the original orientation, the water was 6 cm out of 8 cm, which is 3/4 as well. Wait, 6/8 is 0.75, so 3/4. So 3/4 of the height in each orientation? Wait, in the original, the height is 8 cm, water is 6 cm. 6 is 3/4 of 8. If in the tipped orientation, the height is 2 cm, then 3/4 of that is 1.5 cm. So maybe that's the connection. So perhaps the answer is D)1.5 cm. But is this just a coincidence?Alternatively, perhaps when tipping, the percentage of the height filled remains the same? But that might not hold. Let me think with another example. Suppose we have a cube with side 10 cm, filled with water to 5 cm. If we tip it onto another face, would the water level be 5 cm? No, it would depend on the orientation and the volume. But in that case, the volume is 10x10x5=500 cm³. If tipped onto a different face, say a 10x10 face, then the depth would be 500/(10x10)=5 cm. Wait, same as before. But if the cube is a rectangular prism, not a cube. Suppose a prism with sides 10, 20, 30. If filled to a certain depth on one face, and then tipped onto another face. The depth would depend on the volume divided by the base area. But in this problem, the original volume is 60 cm³. When tipped onto the 5x8 face, the base area is 40 cm², so depth is 60/40=1.5 cm. That seems straightforward. So maybe the answer is D)1.5 cm. But let me check again.Wait, but perhaps when tipping, the water doesn't just spread out as a rectangular prism. For example, if you have a container that's taller than the water level, when you tilt it, the water can form a slanted surface, but the problem states that after tipping, the prism is standing on the new face, so the water would settle to a horizontal surface. Therefore, the depth would be measured vertically from the base, and the volume would be base area times depth. Therefore, since the volume remains the same, the depth is 60/40=1.5 cm, which is 1.5 cm. Therefore, the answer is D. So maybe that's the answer.Wait, but let me verify once more. Let's consider the original position: base 2x5, height 8. Water depth 6. Volume 2*5*6=60. When tipped onto 5x8 base, the height becomes 2 cm. So the entire capacity of the prism is 5*8*2=80 cm³. The water is 60 cm³. So the ratio is 60/80=3/4. Therefore, the depth in the new orientation is 3/4 of the height. Since the height is 2 cm, 3/4 of 2 cm is 1.5 cm. So that also gives 1.5 cm. So that's the same answer. Therefore, whether you calculate it as volume divided by base area or as the same fraction of the height, you get 1.5 cm. So the answer is D.But let me check if there's a different approach. Suppose instead, when tipping the prism, the dimensions change. Wait, the prism is the same, just oriented differently. So the three dimensions remain 2,5,8. When standing on 2x5, height is 8. When standing on 5x8, height is 2. The water volume is 60. So in the new orientation, the base is 5x8=40, so depth is 60/40=1.5. So that's straightforward.But maybe I need to consider that the height of the water is along the original height when tipping. Wait, no. When you tip the prism, the "depth" is measured perpendicular to the new base. So if the new base is 5x8, then depth is vertical from that base. Since the prism is now 2 cm tall (in the vertical direction), the depth can't exceed 2 cm. Since 1.5 is less than 2, it's okay. So it's 1.5 cm. So the answer should be D.Alternatively, let's think about the problem differently. The original cross-sectional area is 2x5=10, depth 6. Volume 60. When tipped onto the largest face, which is 5x8. The cross-sectional area is 5x8=40. So if the water is spread over 40 cm², then depth is 60/40=1.5. So yes, that's the same.Alternatively, maybe the problem is a trick question where you have to consider that when tipping, some dimensions change. Wait, but all dimensions stay the same. The prism isn't being stretched or compressed, just reoriented. So the volume remains 60. The base area when tipped is 40, so depth is 1.5. So answer D. Therefore, I think the answer is D) 1.5 cm.Final Answerboxed{D}</think>The problem involves a closed rectangular prism with dimensions 2 cm, 5 cm, and 8 cm. Initially, the prism is standing on a face with dimensions 2 cm by 5 cm, and the water depth is 6 cm. We need to determine the depth of the water when the prism is tipped to stand on the face with the greatest area.1. Calculate the volume of water: - The base area when standing on the 2 cm by 5 cm face is (2 times 5 = 10 , text{cm}^2). - The volume of water is (10 times 6 = 60 , text{cm}^3).2. Determine the face with the greatest area: - The areas of the faces are (2 times 5 = 10 , text{cm}^2), (2 times 8 = 16 , text{cm}^2), and (5 times 8 = 40 , text{cm}^2). - The face with the greatest area is (5 times 8 = 40 , text{cm}^2).3. Calculate the new depth of water: - When tipped onto the 5 cm by 8 cm face, the new base area is (5 times 8 = 40 , text{cm}^2). - The volume of water remains (60 , text{cm}^3). - The new depth of the water is (frac{60}{40} = 1.5 , text{cm}).Thus, the depth of the water when the prism is tipped to stand on the face with the greatest area is (boxed{D}).,<think>Okay, so I need to solve this problem about a rectangular prism (which is basically a box shape) that's being tipped over, and figure out the new depth of the water inside. Let me try to visualize this step by step.First, the problem says it's a closed rectangular prism with height 8 cm. It's standing on a face that has dimensions 2 cm by 5 cm. So, when it's standing on that 2x5 face, the height of the prism is 8 cm. Then, there's water inside with a depth of 6 cm. Then, when we tip the prism so that it stands on the face with the greatest area, we need to find the new depth of the water. The options are given from 0.75 cm up to 1.75 cm.Alright, let's start by understanding the dimensions of the prism. Since it's a rectangular prism, it has three dimensions: length, width, and height. But depending on how it's oriented, which face is the base, the other dimensions become the height.Originally, the prism is standing on a face with dimensions 2 cm by 5 cm. So, that must be the base, and the height is 8 cm. Wait, but the height is 8 cm, so that would mean the third dimension (the one that's vertical when standing on the 2x5 base) is 8 cm. So the three dimensions of the prism are 2 cm, 5 cm, and 8 cm. Let me confirm: when it's standing on the 2x5 face, the height is 8 cm. That makes sense. So the prism has length 2 cm, width 5 cm, and height 8 cm.But then, when it's tipped over to stand on the face with the greatest area, which would be the largest face. The faces of a rectangular prism are pairs of sides. The areas of the faces are length×width, length×height, and width×height. So the areas would be:- 2×5 = 10 cm²- 2×8 = 16 cm²- 5×8 = 40 cm²Wait, but hold on. Wait, if the original base is 2x5, which has area 10 cm², then the other faces would be 2x8 and 5x8. So 2x8 is 16 cm², and 5x8 is 40 cm². So the largest face is 5x8, which is 40 cm². So when we tip it onto the 5x8 face, that becomes the new base. So the prism is now standing on the 5x8 face. Then the height of the prism in this orientation would be 2 cm, right? Because the dimensions are 2, 5, 8. So when standing on 5x8, the height becomes 2 cm. Wait, but that seems contradictory, because the height can't be 2 cm. Wait, no, the height is the vertical dimension when standing on a particular face.Wait, perhaps I need to clarify. Let's think of the prism as having dimensions length, width, height as 2 cm, 5 cm, 8 cm. When it's standing on the 2x5 face, the height is 8 cm. If we tip it onto the 5x8 face, then the height becomes 2 cm? Wait, that can't be. Wait, maybe not. Wait, the height is determined by which face you stand it on. So, if the original base is 2x5, then the vertical dimension is 8 cm. If we tip it onto the 5x8 face, then the vertical dimension (height) would be 2 cm. But that seems like the prism is now lying on its side with the shortest dimension as the height. Hmm.But the problem says it's a closed rectangular prism, so regardless of how it's oriented, the dimensions stay the same. So the prism's actual dimensions are 2, 5, and 8. So when standing on 2x5, the height is 8. When standing on 5x8, the height is 2. But when we tip it, we have to be careful about how the water redistributes.Wait, but maybe the height when standing on the 5x8 face is 2 cm? That seems too short. Wait, but the original height was 8 cm. If you tip it so that the 5x8 face is the base, then the vertical dimension (height) would be the remaining dimension, which is 2 cm. But how can the prism have a height of 2 cm in that orientation? Wait, perhaps the term "height" here is relative to the base. So depending on which face is the base, the height is the dimension perpendicular to that base.So, if the base is 2x5, the height is 8. If the base is 5x8, then the height is 2. Similarly, if the base is 2x8, the height is 5. That makes sense. So each face has an area, and the corresponding height is the remaining dimension.So, the problem states that initially, the prism is on the 2x5 base, with height 8 cm, and water depth 6 cm. Then it's tipped onto the base with the greatest area, which is 5x8. So in that case, the height becomes 2 cm. But how does the water depth change?Wait, but when you tip the prism, the water level will adjust according to the new orientation. The volume of water remains the same, but the base area changes, so the depth will change accordingly. Wait, but also, the shape of the water's surface might change if it's not filling the entire base when tipped. Hmm. Wait, but depending on how much water there is, when you tip the prism, the water might not reach the top of the new base, or it might spill over. Wait, but since the original depth is 6 cm, which is less than the original height of 8 cm, maybe when we tip it, the water will spread out over a larger base area, resulting in a shallower depth.But let's compute the volume of water first. The original volume is the area of the base times the depth. The original base is 2x5=10 cm², and the depth is 6 cm. So the volume is 10*6=60 cm³.When we tip the prism onto the 5x8 base, which has an area of 40 cm². So if we assume that the water forms a rectangular prism in the new orientation, the depth would be volume divided by base area: 60 / 40 = 1.5 cm. But 1.5 cm is one of the options (option D). But wait, maybe that's too simplistic? Because when you tip the prism, the water might not just form a rectangular prism; depending on the angle, it could form a slanted surface, but since we are tipping it until it stands on the new base, maybe the water surface becomes horizontal again. Wait, but in that case, the depth would just be the volume divided by the new base area.Wait, but if the prism is tipped so that it stands on the 5x8 face, then the new "height" (vertical dimension) is 2 cm. But if the water depth in this orientation is 1.5 cm, then since 1.5 cm is less than 2 cm, it's okay. So the water would form a rectangular prism with base 5x8 and depth 1.5 cm, which has volume 60 cm³, matching the original. So maybe that's the answer. But why is the answer not 1.5 cm? Wait, but let me check the answer choices. The options are A) 0.75, B)1, C)1.25, D)1.5, E)1.75. So D is 1.5 cm. But is this correct?Wait, but hold on. Maybe the problem is more complicated. Because when you tip the prism, the water might not just simply spread out over the entire base. Maybe when you tip it, the height of the water in the new orientation is constrained by the original dimensions.Wait, let's think again. The original prism is standing on the 2x5 face with height 8 cm. The water is at 6 cm depth. So the water fills up the prism to 6 cm in the vertical direction, which is 8 cm. So the volume is 2*5*6 = 60 cm³. When we tip the prism onto the 5x8 face, which is the largest face. The question is, what is the depth of the water now?But if we tip the prism so that it stands on the 5x8 face, then the vertical dimension (height) becomes 2 cm. So the maximum possible depth of water in this orientation is 2 cm. But the volume of water is 60 cm³. The base area is 5*8=40 cm². So if we pour 60 cm³ into a base of 40 cm², the depth would be 60/40 = 1.5 cm, which is less than 2 cm, so it's possible. So the water would form a layer of 1.5 cm depth in the new orientation. So the answer is D) 1.5 cm. But wait, the options include that. So that seems straightforward, but maybe the problem is trickier.Wait, maybe when tipping the prism, the water doesn't just stay as a rectangular prism. Maybe the axis along which you tip affects the distribution. Wait, but if you tip the prism so that it stands on the 5x8 face, then the original height of 8 cm becomes the depth, and the 2 cm becomes the vertical height. Wait, no. Wait, when you tip the prism, the dimensions don't change. The prism is rigid. So tipping it would reorient which face is the base, but the water would adjust to fill the space up to a certain height in the new base.Wait, but actually, when you tip the prism, the water level will adjust such that the volume remains the same. So as long as in the new orientation, the water forms a rectangular prism with the new base, the depth can be calculated as volume divided by base area. However, this is only true if the water doesn't overfill the new height. Since in the new orientation, the height is 2 cm, and the calculated depth is 1.5 cm, which is less than 2 cm, so it's okay.But maybe there's something wrong with this approach. Let me think again. If the original container is standing on 2x5 with height 8, and filled to 6 cm, the water is in the shape of a rectangular prism with base 2x5 and height 6. When tipped onto the 5x8 base, which is the largest face, the water would now have a base of 5x8 and some depth h. The volume is 5*8*h = 40h = 60 cm³, so h = 60 / 40 = 1.5 cm. So the answer is D) 1.5 cm. But let me check again, maybe the orientation is different.Wait, but maybe when you tip the prism, the height of the water is not along the vertical direction? Wait, no, when you tip it so that it stands on the 5x8 face, the vertical direction is now the original 2 cm. So the depth of the water should be measured along this vertical direction. But the base area is 5x8, and the depth is 1.5 cm. But is this correct?Wait, another way to think about it is: the original volume is 2*5*6 = 60. After tipping, the base is 5*8, so the depth is 60/(5*8) = 60/40 = 1.5. So that seems straightforward. But maybe the answer is different because when tipping, the water might form a different shape? For example, if the container is not full, tipping it might cause the water to occupy a different portion of the prism, not just a simple rectangular prism.Wait, but if the prism is a rectangular container, when you tip it so that a different face is the base, the water should still form a rectangular prism with the new base, as long as the depth is less than the new height. Since the new height is 2 cm, and the calculated depth is 1.5 cm, which is less, it's okay.Wait, but let me confirm with another approach. Let's consider the dimensions of the prism. Originally, the base is 2x5, height 8, water depth 6. So the water occupies a volume of 2*5*6=60. When tipped onto the 5x8 base, the dimensions of the prism are now: base 5x8, height 2. So the maximum volume of the prism is 5*8*2=80, which is larger than the water volume of 60. Therefore, the water will occupy a depth h in this new orientation such that 5*8*h=60, so h=1.5. So the answer is 1.5 cm, which is option D.But wait, the answer choices have 1.5 cm as D, so that's probably the answer. But why is the problem considered difficult then? Maybe I'm missing something.Alternatively, perhaps when tipping the prism, the water doesn't just stay as a rectangular prism. Maybe the tipping process causes the water to slosh, but the problem states "when the prism is tipped so that it stands on a face with the greatest area," which implies that it's placed stably on that face, and the water settles into a horizontal level. So in that case, the depth would be the volume divided by the base area. Hence, 60/40=1.5.Alternatively, maybe the problem is not as straightforward because the cross-sectional area changes during the tipping, and the height of the water is measured along a different axis. Wait, but when you tip the prism onto its largest face, the water level must adjust to maintain the same volume, so it's still just a matter of dividing the volume by the base area.Wait, perhaps the confusion comes from the orientation. Let me draw a diagram mentally. Original position: the prism is standing on 2x5 base, height 8 cm. The water is filled to 6 cm. So from the bottom (2x5 face), up to 6 cm in the vertical direction (which is the 8 cm dimension). So the water is a rectangular prism 2x5x6.When we tip it onto the 5x8 face. So now, the 5x8 face is the base. The height of the prism is now 2 cm. So the vertical direction is 2 cm. So the water needs to occupy a volume of 60 cm³ in this new orientation. The base is 5x8=40 cm², so the depth h is 60/40=1.5 cm. Since 1.5 cm is less than the height of 2 cm, the water doesn't spill, and forms a depth of 1.5 cm. Therefore, the answer is D) 1.5 cm.But wait, the options given are A) 0.75, B)1, C)1.25, D)1.5, E)1.75. So D is the fourth option. But in the original problem statement, they mention "as shown" with a diagram. Since I don't have the diagram, maybe there's a different configuration. Wait, the original prism is standing on 2x5, height 8 cm. The depth of water is 6 cm. When tipped onto the largest face (5x8), which is 40 cm². The height in that orientation is 2 cm. So if the water depth is 1.5 cm, which is 3/4 of the height. Hmm. But maybe the problem is that when tipping, the water's "depth" is measured along a different axis. Wait, but depth should be measured vertically. When you tip the prism, the vertical direction changes. So if the prism is now standing on the 5x8 face, the vertical direction is the original 2 cm dimension. Therefore, the depth of water is 1.5 cm in that vertical direction.But perhaps another way to think about it is that the length and width of the water's surface change when tipping. Wait, no. If the prism is a rigid container, the base when tipped is 5x8, and the water's depth is measured perpendicularly to that base. So that would be along the 2 cm dimension. So the depth is 1.5 cm. So the answer should be D.Alternatively, maybe the problem is referring to the depth along the original vertical axis when tipped? That is, even after tipping, the depth is measured from the original top. Wait, but no, when you tip the prism, the depth should be measured with respect to the new base. So if the prism is now standing on the 5x8 face, the depth is measured from that face upwards.Therefore, I think the answer is D) 1.5 cm.But let me check once again. Original volume is 2*5*6=60. New base area is 5*8=40. So 60=40*h => h=1.5. Since the height in the new orientation is 2 cm, 1.5 is less than 2, so it works. Therefore, the answer is D.But wait, maybe the question is trying to trick us by the way it's tipped. For example, if you tip the prism so that it's resting on the 5x8 face, but the water level is not just a simple division of volume by base area. For example, if the prism is only partially filled, maybe the water forms a different shape.Wait, but in reality, when you tip a rectangular container, the water level remains horizontal. So if the container is now resting on the 5x8 face, the water will form a horizontal surface. The volume of water is the area of the base times the height, but in this case, the base is 5x8, and the height (depth) is h. So the volume is 5*8*h. Since the volume must remain the same, 5*8*h=60 => h=1.5. So unless there's some other constraint, this should be correct.Alternatively, maybe when tipping the prism onto its largest face, the height of the water is measured along the original vertical axis. Wait, but that doesn't make sense. The depth should be measured with respect to the new base.Alternatively, perhaps the problem is considering that when you tip the prism onto the 5x8 face, the original 8 cm height is now horizontal. So the length of the container in the direction of the original height is 8 cm. So when you tip it, the water might spread out along that 8 cm length. Wait, but this requires a different approach.Wait, maybe I need to model the tipping as a rotation. Let's consider that the prism is being rotated from standing on the 2x5 face to standing on the 5x8 face. The rotation would be such that the 8 cm edge becomes horizontal. So during tipping, the water level would tilt, but once it's resting on the 5x8 face, the water would settle with a horizontal surface. The key is to find the height of this water level in the new orientation.But perhaps the confusion arises because the dimensions are 2, 5, and 8. So when it's standing on the 5x8 face, the height is 2 cm. So the container is only 2 cm tall in this orientation. So if the water's depth is 1.5 cm, then it's 3/4 of the height, which is 2 cm. That's possible. But in the original orientation, the water was 6 cm out of 8 cm, which is 3/4 as well. Wait, interesting. So the ratio of water depth to container height is the same? 6/8 = 3/4, and 1.5/2 = 3/4. So that's a coincidence. But maybe not, since the volume is the same. Wait, volume is base area times height. Original base area is 10 cm², height 6 cm, volume 60. New base area is 40 cm², height h, volume 40h=60 => h=1.5. So that's consistent.Alternatively, perhaps the problem is designed such that even if you tip the prism onto a different face, the depth changes according to the ratio of the base areas. But in this case, the base area increases by a factor of 4 (from 10 to 40), so the depth decreases by a factor of 4. But 6 divided by 4 is 1.5. So that's the same answer.Wait, but in that case, the answer is D. But why do the other answer choices exist? Maybe there is a different way to interpret the problem.Wait, let's think again. Maybe when tipping the prism onto the largest face (which is 5x8), the height of the prism in that orientation is not 2 cm. Wait, but the prism's dimensions are 2x5x8. When standing on the 5x8 face, the height must be the remaining dimension, which is 2 cm, right? Because the three dimensions are 2, 5, and 8. So depending on which face is the base, the height is the third dimension. So if the base is 5x8, the height is 2 cm. If the base is 2x8, the height is 5 cm. If the base is 2x5, the height is 8 cm.Therefore, when standing on the largest face (5x8), the height is 2 cm. Therefore, the maximum depth of water possible is 2 cm. Since our calculated depth is 1.5 cm, which is less than 2 cm, the water doesn't spill, and the depth is 1.5 cm. Therefore, the answer is D) 1.5 cm.I think that's solid. The key is that the volume remains the same, and when you tip the prism onto a different face, the base area changes, so the depth changes accordingly. Since 5x8 is four times larger than 2x5 (original base area 10 vs new base area 40), the depth is 6 divided by 4, which is 1.5. Therefore, the answer is D.Final Answerboxed{D}</think>The problem involves a closed rectangular prism with dimensions 2 cm, 5 cm, and 8 cm. Initially, the prism stands on a face with dimensions 2 cm by 5 cm, with a water depth of 6 cm. When tipped to stand on the face with the greatest area (5 cm by 8 cm), we need to determine the new depth of the water.1. Calculate the volume of water: The original volume of water is given by the base area multiplied by the depth: [ text{Volume} = 2 , text{cm} times 5 , text{cm} times 6 , text{cm} = 60 , text{cm}^3 ]2. Determine the new base area: When the prism is tipped onto the face with the greatest area (5 cm by 8 cm), the new base area is: [ text{New base area} = 5 , text{cm} times 8 , text{cm} = 40 , text{cm}^2 ]3. Calculate the new depth of water: The volume of water remains the same. Using the new base area, the depth ( h ) is calculated by: [ text{Volume} = text{New base area} times text{New depth} implies 60 , text{cm}^3 = 40 , text{cm}^2 times h ] Solving for ( h ): [ h = frac{60 , text{cm}^3}{40 , text{cm}^2} = 1.5 , text{cm} ]Thus, the depth of the water when the prism is tipped onto the face with the greatest area is (boxed{D}).]

🔑:The water is in the shape of a rectangular prism with a 2 mathrm{~cm} by 5 mathrm{~cm} base and depth 6 mathrm{~cm}.Therefore, the volume of water is 2 mathrm{~cm} times 5 mathrm{~cm} times 6 mathrm{~cm}=60 mathrm{~cm}^{3}.A face of the prism having the greatest area has dimensions 5 mathrm{~cm} by 8 mathrm{~cm}.When the prism is tipped so that it stands on a 5 mathrm{~cm} by 8 mathrm{~cm} face, the water is once again in the shape of a rectangular prism with a 5 mathrm{~cm} by 8 mathrm{~cm} base and unknown depth.Suppose that after the prism is tipped, the water's depth is d mathrm{~cm}.Since the volume of water is still 60 mathrm{~cm}^{3} when the prism is tipped, then 5 mathrm{~cm} times 8 mathrm{~cm} times d mathrm{~cm}=60 mathrm{~cm}^{3} or 40 d mathrm{~cm}^{3}=60 mathrm{~cm}^{3}, and so d=frac{60}{40}=frac{3}{2}.When the prism is tipped so that it stands on a face with the greatest area, the depth of the water is frac{3}{2} mathrm{~cm}=1.5 mathrm{~cm}.ANSWER: (D)#

🧠:[<think>Okay, so I need to find the intersection of sets A and B. Let me first remember what intersection means. From what I recall, the intersection of two sets A and B, written as A ∩ B, is the set that contains all elements that are common to both A and B. That is, the elements that are in both sets.Alright, let me check the given sets. The problem states that set A is {1, 2} and set B is {2, 3}. Hmm, so set A has elements 1 and 2, and set B has elements 2 and 3. I need to see which elements are in both sets.Looking at set A: 1, 2.Looking at set B: 2, 3.Now, let's compare each element. The first element in A is 1. Is 1 in set B? Set B has 2 and 3, so no, 1 is not in B. Then the next element in A is 2. Is 2 in set B? Yes, set B has 2 as its first element. So 2 is common to both sets.Now checking set B's elements. The elements are 2 and 3. We already checked 2 is in A. What about 3? Is 3 in set A? Set A has 1 and 2, so no, 3 is not in A. Therefore, the only common element is 2.So the intersection A ∩ B should be the set containing just 2. Let me write that as {2}. Wait, let me double-check. Maybe I made a mistake in reading the sets. The problem says A = {1,2} and B = {2,3}. Yes, that's correct. So 2 is the only element present in both. Therefore, their intersection is {2}.Is there a possibility I missed something? Let me think. Sometimes sets can have multiple instances of the same element, but in standard set theory, sets don't have duplicate elements. So even if an element was listed more than once, it's still considered once. But in this case, both sets A and B have only single instances of their elements, so there's no issue here. Another thing to check: sometimes intersections can be empty. For example, if there were no common elements between A and B, then A ∩ B would be the empty set. But here, since 2 is in both, the intersection is non-empty.Just to visualize, if I draw a Venn diagram with two overlapping circles, one labeled A and the other B. The overlapping region would contain the elements common to both. In this case, only 2 would be in that overlapping part.So, summarizing my thought process: elements of A are 1 and 2; elements of B are 2 and 3. The common element is 2. Hence, A ∩ B = {2}. I don't see any errors in this reasoning.Final AnswerThe intersection of sets (A) and (B) is boxed{{2}}.</think>To find the intersection of sets (A) and (B), we need to identify the elements common to both sets. Set (A) is given as ({1, 2}) and set (B) is given as ({2, 3}). - The elements of set (A) are 1 and 2.- The elements of set (B) are 2 and 3.Checking each element:- The element 1 is in set (A) but not in set (B).- The element 2 is in both set (A) and set (B).- The element 3 is in set (B) but not in set (A).Thus, the only common element is 2. Therefore, the intersection (A cap B) is the set containing the element 2.[A cap B = boxed{{2}}],<think>Okay, so I have to find the intersection of sets A and B. Let me recall what intersection means. The intersection of two sets, A and B, written as A ∩ B, is the set that contains all elements that are common to both A and B. That is, elements that are in A and also in B.First, let me make sure I understand the given sets. The problem states that set A is {1, 2} and set B is {2, 3}. Hmm, wait, actually, the original problem has the sets written with equals signs instead of colons or something. Let me check: "Given the sets A={1,2} and B={2,3}, find the intersection A cap B." Oh, maybe that's a typo in the formatting. Usually, sets are defined with colons like A = {1, 2}, but here it's written with equals signs. Maybe it's just a LaTeX formatting issue. So I think A is the set containing 1 and 2, and B is the set containing 2 and 3. That seems to make sense.So set A has elements 1 and 2. Set B has elements 2 and 3. Now, I need to find which elements are in both sets. Let's list out the elements of each set again for clarity.Set A: 1, 2.Set B: 2, 3.Looking at these, the number 1 is only in set A, the number 3 is only in set B, and the number 2 is in both sets A and B. Therefore, the intersection should be the set containing the element 2.Wait, let me double-check to make sure I haven't missed anything. Intersection is about common elements, so any element that is present in both A and B. Let's go through each element of A and check if it's in B.First element of A is 1. Is 1 in set B? Set B is {2, 3}, so no, 1 is not in B. Next element of A is 2. Is 2 in set B? Yes, because B has 2 and 3. So 2 is common to both sets.Similarly, if I check elements of B against A: 2 is in A, 3 is not in A. So only 2 is common.Therefore, the intersection A ∩ B should be {2}.Hmm, seems straightforward. Let me make sure there's no trick here. Sometimes problems might have sets with more elements or different data types, but in this case, both sets are simple with integers. No duplicates or anything, since sets don't allow duplicates. So the intersection is just the shared element.Alternatively, if I was unsure, I could write down the sets again:A = {1, 2}B = {2, 3}Visually, overlapping element is 2. So yes, A ∩ B = {2}.I think that's the answer. Not sure where I could have gone wrong here. Maybe if there was a misinterpretation of the original sets, but the problem clearly states A is {1,2} and B is {2,3}. So, yeah, the intersection is {2}.Final AnswerThe intersection of sets ( A ) and ( B ) is boxed{{2}}.</think>Given the sets ( A = {1, 2} ) and ( B = {2, 3} ), we need to find the intersection ( A cap B ).The intersection of two sets ( A ) and ( B ), denoted ( A cap B ), is the set of elements that are common to both ( A ) and ( B ).- Set ( A ) contains the elements 1 and 2.- Set ( B ) contains the elements 2 and 3.Checking each element:- The element 1 is in set ( A ) but not in set ( B ).- The element 2 is in both set ( A ) and set ( B ).- The element 3 is in set ( B ) but not in set ( A ).Thus, the only common element between sets ( A ) and ( B ) is 2. Therefore, the intersection ( A cap B ) is the set containing 2.[boxed{{2}}]]

🔑:We have sets A={1,2} and B={2,3}. To find their intersection A cap B, we look for the common elements between the two sets:A cap B = {1,2} cap {2,3} = {2}So the answer is boxed{{2}}.This problem can be solved directly by applying the definition of the intersection operation on sets. It assesses understanding of intersections and their operations, making it a fundamental and commonly tested topic.

🧠:[<think>Okay, so I need to find the smallest natural number z that has exactly four divisors between 1 and z!, right? Wait, no, the problem says "exactly four divisors t₁, t₂, t₃, t₄ with 1 < t₁ < t₂ < t₃ < t₄ < z!" So, actually, the divisors are between 1 and z! but not including 1 and z! itself? Hmm, let me make sure I parse that correctly.The problem states: "Determine the smallest natural number z that has exactly four divisors t₁, t₂, t₃, t₄ with 1 < t₁ < t₂ < t₃ < t₄ < z!" So, z must have exactly four divisors, each greater than 1 and less than z! (which is z factorial). The divisors must be ordered as t₁ through t₄, each increasing. And we need the smallest such z.Wait, but hold on. If z is a natural number, and we're looking for divisors of z, then typically the divisors of z are numbers that divide z without a remainder. The usual divisors include 1 and z itself. But here, the problem specifies four divisors t₁ to t₄ where each is greater than 1 and less than z! So, z must have four divisors (excluding 1 and z!) that are all less than z!.But z! is a very large number for any z ≥ 4. For example, if z is 4, z! is 24. The divisors of z=4 are 1, 2, 4. But here, we need four divisors between 1 and z! So, if z=4, its divisors are 1,2,4. But between 1 and 24, 4 has divisors 2 and 4. But 4 is equal to z, so the problem says t₄ < z!, so 4 is less than 24, so maybe 2 and 4 are divisors. But then, how many divisors does z=4 have between 1 and z!? Let's see.Wait, the problem is a bit ambiguous. Wait, let's re-read it: "the smallest natural number z that has exactly four divisors t₁, t₂, t₃, t₄ with 1 < t₁ < t₂ < t₃ < t₄ < z!". So, z has four divisors, each greater than 1, each less than z!.But z's divisors are numbers that divide z. So, divisors of z must be ≤ z. Therefore, the divisors t₁, t₂, t₃, t₄ must be between 1 and z!, but they are divisors of z, so they must also divide z. Therefore, the divisors t₁, t₂, t₃, t₄ must be in (1, z!) but also divide z. Since z divides itself, z is a divisor of z, but z! is much larger than z for z ≥ 3. So, z is less than z! for z ≥ 2. Therefore, the divisors of z are all ≤ z, so the divisors t₁ to t₄ must be in (1, z!) but since z < z!, they are actually just in (1, z). Therefore, the problem reduces to finding the smallest z such that z has exactly four divisors between 1 and z, which is equivalent to z having exactly six divisors in total (since we include 1 and z). Wait, but no. Wait, the problem says "exactly four divisors t₁, t₂, t₃, t₄ with 1 < t₁ < t₂ < t₃ < t₄ < z!". So excluding 1 and z. But since all divisors of z except 1 and z must be exactly four. Therefore, z must have exactly six divisors in total (since the count is 1, t₁, t₂, t₃, t₄, z). Therefore, z must be a number with exactly six divisors.Wait, but numbers with exactly six divisors can be of two forms: either p^5 where p is prime (since the number of divisors is 5 + 1 = 6), or p^2 * q where p and q are distinct primes (since the number of divisors is (2+1)*(1+1) = 6). So, which is smaller? The smallest p^5 is 32 (2^5), and the smallest p^2*q is 12 (2^2*3). So, 12 is smaller. Therefore, if z=12, then it has six divisors: 1, 2, 3, 4, 6, 12. So excluding 1 and 12, we have four divisors: 2, 3, 4, 6. These are the t₁ to t₄. Now, check whether each of them is less than z! For z=12, z! is 12 factorial, which is a huge number, 479001600. So obviously 2,3,4,6 are all less than 12!. So z=12 satisfies the condition. But is there a smaller z?Wait, maybe z=12 is not the answer. Wait, let's check for smaller numbers. Let's check numbers with exactly six divisors. The next smallest is 18 (2*3^2). Its divisors are 1, 2, 3, 6, 9, 18. Excluding 1 and 18, the divisors are 2,3,6,9. So four divisors. So z=18 would have t₁=2, t₂=3, t₃=6, t₄=9. Each less than 18! which is even bigger. So 18! is way larger, so they are all less. But 18 is larger than 12, so 12 is smaller.Wait, but 12 is the smallest number with six divisors. Then, maybe z=12 is the answer. But wait, is there a number smaller than 12 with exactly six divisors? Let's check. The numbers and their number of divisors:- 1: 1 divisor- 2: 2 divisors- 3: 2 divisors- 4: 3 divisors (1,2,4)- 5: 2 divisors- 6: 4 divisors (1,2,3,6)- 7: 2- 8: 4 divisors (1,2,4,8)- 9: 3 divisors- 10: 4 divisors- 11: 2- 12: 6 divisorsSo yes, 12 is the first number with six divisors. So z=12 is the smallest number with exactly four proper divisors (excluding 1 and itself). But the problem states that the divisors must be less than z! So since z! is huge, all the divisors (which are less than z) are automatically less than z! So the only constraint is that z must have exactly four divisors between 1 and z!, which is equivalent to z having exactly six divisors in total. Therefore, the answer is the smallest z with six divisors, which is 12.Wait, but wait, let me check again. The problem says "exactly four divisors t₁, t₂, t₃, t₄ with 1 < t₁ < t₂ < t₃ < t₄ < z!". So the four divisors are between 1 and z! but z! is factorial of z, so for z=12, the four divisors are 2,3,4,6, which are all less than 12!.But perhaps there's a smaller z where the four divisors happen to be less than z! For example, take z=6. z=6 has divisors 1,2,3,6. So excluding 1 and 6, it has two divisors: 2 and 3. So only two, which is less than four. So z=6 doesn't work. z=8 has divisors 1,2,4,8. Excluding 1 and 8, two divisors: 2 and 4. Still two. z=10: divisors 1,2,5,10. Excluding 1 and 10, two divisors. So not enough. z=12 is the first with four such divisors.Wait, but let's check if z=16. z=16 is 2^4, so divisors are 1,2,4,8,16. Excluding 1 and 16, there are three divisors: 2,4,8. So three, which is still less than four. So z=16 doesn't work. Next, z=18: as before, divisors 1,2,3,6,9,18. Excluding 1 and 18, four divisors: 2,3,6,9. So that's four, but z=18 is larger than 12, so 12 is smaller.So, seems like z=12 is the answer. Wait, but let me check another form. The other form for six divisors is p^5. The smallest such is 32. 32 has divisors 1,2,4,8,16,32. Excluding 1 and 32, four divisors: 2,4,8,16. So z=32 also meets the criteria, but it's larger than 12, so 12 is still the smallest.Therefore, the answer is z=12.But wait, let me check if there is any number smaller than 12 which might have four divisors between 1 and z! even if it has more than six total divisors. Wait, the problem says "exactly four divisors". So z must have exactly four divisors t₁ to t₄ between 1 and z! So total number of divisors of z would be six (including 1 and z). Because if z had more than six divisors, then even excluding 1 and z, there would be more than four. So, z must have exactly six divisors in total, which implies exactly four proper divisors (excluding 1 and z). Therefore, the only numbers with exactly four proper divisors are those with exactly six total divisors, which are either p^5 or p^2*q. The smallest of which is 12. So indeed, z=12 is the answer.Therefore, the answer should be 12, boxed as boxed{12}.Final Answerboxed{12}</think>To determine the smallest natural number ( z ) that has exactly four divisors ( t_1, t_2, t_3, t_4 ) with ( 1 < t_1 < t_2 < t_3 < t_4 < z! ), we need to find the smallest ( z ) such that ( z ) has exactly six divisors in total. This is because the four divisors ( t_1, t_2, t_3, t_4 ) must be between 1 and ( z! ), excluding 1 and ( z ) itself.A number with exactly six divisors can be either of the form ( p^5 ) (where ( p ) is a prime) or ( p^2 cdot q ) (where ( p ) and ( q ) are distinct primes). The smallest number of the form ( p^2 cdot q ) is ( 12 ) (since ( 2^2 cdot 3 = 12 )), and the smallest number of the form ( p^5 ) is ( 32 ) (since ( 2^5 = 32 )).For ( z = 12 ), the divisors are 1, 2, 3, 4, 6, and 12. Excluding 1 and 12, the divisors are 2, 3, 4, and 6, which are exactly four divisors. These divisors are all less than ( 12! ), which is a very large number.Checking smaller numbers than 12, we find that none of them have exactly six divisors. Therefore, the smallest ( z ) that satisfies the condition is 12.Thus, the answer is (boxed{12}).,<think>Okay, let's see. The problem is asking for the smallest natural number z that has exactly four divisors t1, t2, t3, t4, where each of these divisors is greater than 1 and less than z. So, essentially, z must have exactly six divisors in total because we're excluding 1 and z itself. Wait, no, hold on. Wait, the problem says exactly four divisors t1, t2, t3, t4 with 1 < t1 < t2 < t3 < t4 < z. So, that means including 1 and z, the total number of divisors would be six? Because 1, t1, t2, t3, t4, z. So yes, z must have six divisors in total. So, the problem reduces to finding the smallest natural number with exactly six divisors.But let me confirm. The problem states "exactly four divisors t1, t2, t3, t4" where each is between 1 and z. So, 1 and z are not counted among these four. Therefore, z has exactly six divisors. So, I need to find the smallest z with exactly six divisors. So, how do we approach this?First, recall that the number of divisors of a number is determined by its prime factorization. If z can be written as a product of primes raised to exponents, like z = p1^a1 * p2^a2 * ... * pn^an, then the number of divisors is (a1 + 1)(a2 + 1)...(an + 1). So, we need this product to be 6 because we want six divisors in total. So, we need to find exponents a1, a2, etc., such that when each is incremented by 1 and multiplied together, the result is 6.So, possible factorizations of 6 (since exponents are positive integers, the exponents plus 1 must multiply to 6). The possible factorizations of 6 are:1) 6 = 6 * 12) 6 = 3 * 23) 6 = 2 * 34) 6 = 1 * 6But since the order of the exponents doesn't matter (since multiplication is commutative), we can consider the different cases:Case 1: The number is of the form p^5, where p is prime. Then, the number of divisors is 5 + 1 = 6. The smallest such number would be 2^5 = 32.Case 2: The number is of the form p^2 * q, where p and q are distinct primes. Then, the number of divisors is (2 + 1)(1 + 1) = 3*2 = 6. The smallest such number would be 2^2 * 3 = 12.Case 3: The number is of the form p * q^2, which is similar to case 2. The smallest here would be 3^2 * 2 = 18, which is larger than 12.Case 4: The number is of the form p * q * r, three distinct primes. Then, the number of divisors is (1 + 1)(1 + 1)(1 + 1) = 2*2*2 = 8, which is more than 6. So that's not our case.So, the two possibilities are either p^5 or p^2 * q. The smallest numbers for these cases are 32 and 12, respectively. So, 12 is smaller than 32. Therefore, the smallest z with exactly six divisors is 12. Let's check.Divisors of 12: 1, 2, 3, 4, 6, 12. So, the four divisors between 1 and 12 are 2, 3, 4, 6. That's four divisors. So, 12 fits the description. Then, 12 is the answer. But wait, let's check if there is a smaller number.Wait, let's check numbers less than 12. Let's check 8: divisors are 1, 2, 4, 8. Only two divisors between 1 and 8, which are 2 and 4. Not enough. 9: divisors 1, 3, 9. Only one divisor between 1 and 9. 10: divisors 1, 2, 5, 10. Two divisors between 1 and 10. 11: prime number, so only 1 and 11. 12 we already checked. 6: divisors 1, 2, 3, 6. Two divisors between 1 and 6. 7: prime. 5: prime. 4: divisors 1, 2, 4. So, only one divisor between 1 and 4. 3, 2, 1: primes or 1. So, yes, 12 is indeed the smallest number with exactly six divisors. Therefore, the answer is 12.But wait, hold on. Let me make sure. Let's check 16. Wait, no, 16 is 2^4, which would have five divisors: 1, 2, 4, 8, 16. So, that's five divisors. Not six. So, 16 has five divisors. Then, 12 is indeed the smallest with six divisors. Wait, 24? No, 24 is larger. 18 is 2 * 3^2, which has (1+1)(2+1) = 6 divisors. Divisors of 18: 1, 2, 3, 6, 9, 18. So, the divisors between 1 and 18 are 2, 3, 6, 9. That's four. So, 18 also has six divisors, but since it's larger than 12, 12 is still the smallest.Wait, but 12's divisors between 1 and 12 are 2, 3, 4, 6. So, four divisors. Correct. So, z=12.But wait, let's check 24. 24 has more divisors. 1,2,3,4,6,8,12,24. So, eight divisors. Therefore, more than six. So, no.Wait, is there a number smaller than 12 with six divisors? Let's check 8: already checked, four divisors. 9: three. 10: four. 11: two. 12: six. So, yes, 12 is the first one with six divisors.But just to confirm, let's check the number of divisors for each number up to 12:1: 1 divisor.2: 2 (1,2).3: 2.4: 3 (1,2,4).5: 2.6: divisors are 1,2,3,6. So four.7: 2.8: 4 (1,2,4,8).9: 3 (1,3,9).10: 4 (1,2,5,10).11: 2.12: 6 (1,2,3,4,6,12). So yes, 12 is the first number with six divisors. So, the answer should be 12.But let me check again the prime factorization approach. The possible numbers with six divisors are either p^5 or p^2*q. The smallest p^5 is 2^5=32, and the smallest p^2*q is 2^2*3=12. So, 12 is indeed the smallest. Therefore, the answer is 12.But wait, hold on. Let me check if 12's divisors are all correct. 1,2,3,4,6,12. Yes. So, between 1 and 12, we have 2,3,4,6. Exactly four. So, this meets the problem's requirement. So, z=12 is the answer. Therefore, the minimal z is 12.Final AnswerThe smallest natural number ( z ) is boxed{12}.</think>To determine the smallest natural number ( z ) that has exactly four divisors ( t_1, t_2, t_3, t_4 ) with ( 1 < t_1 < t_2 < t_3 < t_4 < z ), we need to find a number ( z ) with exactly six divisors in total (since we exclude 1 and ( z ) itself).The number of divisors of a number ( z ) is determined by its prime factorization. If ( z ) has a prime factorization ( p_1^{a_1} cdot p_2^{a_2} cdot ldots cdot p_n^{a_n} ), the number of divisors is given by ( (a_1 + 1)(a_2 + 1) cdots (a_n + 1) ). We need this product to be 6.Possible factorizations of 6 are:1. ( 6 = 6 times 1 ): This corresponds to a number of the form ( p^5 ) where ( p ) is a prime. The smallest such number is ( 2^5 = 32 ).2. ( 6 = 3 times 2 ): This corresponds to a number of the form ( p^2 cdot q ) where ( p ) and ( q ) are distinct primes. The smallest such number is ( 2^2 cdot 3 = 12 ).Checking the divisors of 12, we find they are 1, 2, 3, 4, 6, and 12. The four divisors between 1 and 12 are 2, 3, 4, and 6, which meets the requirement.Thus, the smallest natural number ( z ) is (boxed{12}).]

🔑:}If the natural number (z) has the prime factorization[z=p_{1}^{a_{1}} cdot p_{2}^{a_{2}} cdot ldots cdot p_{n}^{a_{n}}]where the (p_{i}(i=1,2, ldots, n)) are distinct prime factors and the (a_{i}) are their frequencies in the factorization, then the number of divisors (t) of (z) (including 1 and (z) itself) is given by[t=left(a_{1}+1right) cdotleft(a_{2}+1right) cdot ldots cdotleft(a_{n}+1right)]Since the number (z) is supposed to have 6 divisors (including 1 and (z)), we have[6=left(a_{1}+1right) cdotleft(a_{2}+1right) cdot ldots cdotleft(a_{n}+1right)]Each factor (left(a_{i}+1right)) is greater than 1, so the only possible product is (6=3 cdot 2), meaning (z) has exactly 2 prime factors, one of which appears twice and the other once, i.e.,[z=p_{1}^{2} cdot p_{2}]If we substitute the smallest prime numbers 2 and 3 for (p_{1}) and (p_{2}), we get (z=2^{2} cdot 3=12). 12 is the number we are looking for. Its divisors, excluding 1 and (z) itself, are: 2, 3, 4, and 6.

🧠:[<think>Okay, so I have this problem here: 7 wolves eat 7 sheep in 7 days. How many days will it take for 9 wolves to eat 9 sheep? Hmm, let's see. At first glance, it seems like a proportion problem, maybe related to rates. Let me break it down step by step.First, I need to figure out the rate at which the wolves are eating the sheep. If 7 wolves can eat 7 sheep in 7 days, that means each wolf is eating a certain number of sheep per day. Let me think. If 7 wolves take 7 days to eat 7 sheep, then collectively, they eat 1 sheep per day. Wait, 7 wolves eating 7 sheep in 7 days – so over 7 days, each wolf would have eaten 1 sheep. So each wolf eats 1 sheep every 7 days. Therefore, the rate per wolf is 1/7 sheep per day. Let me confirm that.If one wolf eats 1/7 of a sheep per day, then 7 wolves would eat 7*(1/7) = 1 sheep per day. So in 7 days, they would eat 7*1 = 7 sheep. That checks out. So each wolf's eating rate is 1/7 sheep per day.Now, the question is about 9 wolves eating 9 sheep. How many days would that take? Let's apply the same logic. If each wolf eats 1/7 sheep per day, then 9 wolves would eat 9*(1/7) = 9/7 sheep per day. So their combined rate is 9/7 sheep per day.We need to find how many days it takes for them to eat 9 sheep. Let's denote the number of days as D. So, the total sheep eaten would be rate multiplied by time: (9/7) * D = 9. Solving for D: D = 9 / (9/7) = 7 days. Wait, so the answer is also 7 days?But that seems counterintuitive. Let me check again. If 7 wolves eat 7 sheep in 7 days, each wolf effectively eats 1 sheep over 7 days. So, each wolf's consumption is 1 sheep per 7 days. Therefore, the number of wolves and the number of sheep are the same here. So, if you have 9 wolves and 9 sheep, each wolf would still need 7 days to eat 1 sheep. Therefore, with 9 wolves, each eating 1 sheep over 7 days, they would collectively eat 9 sheep in 7 days. So yes, the answer is 7 days.Alternatively, think about the ratio. The number of wolves and sheep are increasing proportionally. From 7 to 9, both increase by the same factor (9/7). So, if the number of wolves and sheep scale by the same factor, the time remains the same. Because more wolves can eat more sheep in the same amount of time. So, if originally 7 wolves eat 7 sheep in 7 days, then 9 wolves would eat 9 sheep in 7 days. It's a classic problem where the quantities scale proportionally, so the time doesn't change.Wait, but let me make sure there isn't a trick here. Sometimes these problems can have nuances. For example, maybe the wolves have to eat a whole sheep, or maybe they can share? But in the original problem, 7 wolves eat 7 sheep in 7 days. That suggests that each wolf is eating one sheep over the 7 days. So, it's as if each wolf eats a sheep over 7 days. Therefore, even with 9 wolves, each would take 7 days to eat a sheep, so together, 9 wolves would eat 9 sheep in 7 days. Alternatively, maybe the rate is different. Let's model it using rates. Let's say the rate at which a wolf eats a sheep is r sheep per day. Then, 7 wolves eating for 7 days would consume 7 * r * 7 = 7 sheep. So, solving for r: 49r = 7 ⇒ r = 7/49 = 1/7 sheep per day. So each wolf eats 1/7 sheep per day. Then, for 9 wolves, the time D needed to eat 9 sheep would be 9 * (1/7) * D = 9. So again, (9/7) D = 9 ⇒ D = 7. So the same answer.Therefore, regardless of the approach, the answer seems to be 7 days. The key is that the number of wolves and sheep are increasing by the same factor, so the time required remains the same. This is similar to problems like "If 3 cats catch 3 mice in 3 minutes, how long for 100 cats to catch 100 mice?" The answer is still 3 minutes because each cat catches one mouse in that time, so scaling both cats and mice keeps the time the same.So, in conclusion, the answer should be 7 days. The proportional reasoning holds here, and the calculations check out both through rate equations and logical deduction.</think>It takes 7 wolves 7 days to eat 7 sheep, meaning each wolf eats 1 sheep every 7 days. If there are 9 wolves and 9 sheep, each wolf still needs 7 days to consume one sheep. Since the number of wolves and sheep increases proportionally (both multiplied by ( frac{9}{7} )), the time required remains unchanged. Thus, 9 wolves will eat 9 sheep in 7 days.[boxed{7}],<think>Okay, let me try to figure out this problem. So, the question is: 7 wolves eat 7 sheep in 7 days. How many days will it take for 9 wolves to eat 9 sheep? Hmm, interesting. At first glance, it seems like a proportion problem, but maybe there's a catch here. Let me break it down step by step.First, let's parse the given information. We have 7 wolves eating 7 sheep over 7 days. The question is asking about 9 wolves and 9 sheep. So, maybe I need to find the rate at which wolves eat sheep and then apply that rate to the new numbers. Let me think about rates.If 7 wolves eat 7 sheep in 7 days, then how many sheep does one wolf eat in one day? That might be a good starting point. Let's calculate the rate per wolf per day.If 7 wolves eat 7 sheep in 7 days, then collectively, they eat 1 sheep per day (since 7 sheep divided by 7 days equals 1 sheep per day). So, 7 wolves eat 1 sheep per day. Therefore, each wolf eats 1/7 of a sheep per day. Wait, that seems a bit strange, since wolves can't really eat a fraction of a sheep, but maybe in terms of rate, it's okay. Let's go with that for now.So, one wolf eats 1/7 of a sheep each day. Now, if we have 9 wolves, how many sheep would they eat in one day? That would be 9 times 1/7, which is 9/7 sheep per day. So, 9 wolves eat 9/7 sheep each day. But the question is, how many days will it take for them to eat 9 sheep?Wait, hold on. If 9 wolves eat 9/7 sheep per day, then to eat 9 sheep, it would take 9 divided by (9/7) days. Let me calculate that. Dividing by a fraction is the same as multiplying by its reciprocal, so 9 * (7/9) = 7 days. Hmm, so does that mean it takes 7 days for 9 wolves to eat 9 sheep? But that's the same as the original problem. That seems counterintuitive. Let me check again.Original problem: 7 wolves eat 7 sheep in 7 days. So, each wolf's eating rate is (7 sheep) / (7 wolves * 7 days) = 1/7 sheep per wolf per day. So, each wolf eats 1/7 of a sheep per day. Therefore, 9 wolves would eat 9 * 1/7 = 9/7 sheep per day. To eat 9 sheep, the time required would be 9 / (9/7) = 7 days. So, same answer.Alternatively, maybe there's another way to look at it. If 7 wolves take 7 days to eat 7 sheep, that suggests that each wolf is eating one sheep every 7 days. Wait, so if each wolf eats 1 sheep in 7 days, then 7 wolves would eat 7 sheep in 7 days. Similarly, 9 wolves would eat 9 sheep in 7 days as well. Because each wolf takes 7 days to eat one sheep. So, increasing the number of wolves and sheep proportionally keeps the time the same. That makes sense. So, the answer is 7 days. But let me think again. Suppose we have more wolves and more sheep. If the number of wolves and sheep increases by the same factor, does the time stay the same? Let's test with another example. If 1 wolf eats 1 sheep in 7 days, then 2 wolves would eat 2 sheep in 7 days. So, yes, scaling both up keeps the time constant. So, the key here is that the ratio of wolves to sheep is the same, so the time remains 7 days. Therefore, the answer is 7.But wait, maybe I need to consider if the wolves are working together or independently. If they are working together, maybe they can eat the sheep faster? But in the original problem, 7 wolves take 7 days to eat 7 sheep. So, if each wolf is responsible for one sheep, then each wolf takes 7 days to eat their own sheep. So, if you have 9 wolves and 9 sheep, each wolf can take 7 days to eat their own sheep. Therefore, the time remains 7 days. That makes sense. Alternatively, if we thought that all the wolves are eating all the sheep together, maybe there's some overlap. But in the original scenario, 7 wolves take 7 days to eat 7 sheep. If they were eating the same sheep, they would finish faster. But since it takes 7 days, it must be that each wolf is eating one sheep over 7 days. So, they're each eating their own sheep. So, the time it takes for a wolf to eat a sheep is 7 days. Therefore, regardless of the number of wolves and sheep, as long as the number is the same, each wolf takes 7 days to eat one sheep. Therefore, the answer is 7 days.But wait, another way to think about it: if 7 wolves eat 7 sheep in 7 days, the rate is 1 sheep per wolf per 7 days. So, each wolf consumes 1 sheep every 7 days. Therefore, 9 wolves would consume 9 sheep in 7 days, each wolf eating one sheep. So, even with more wolves and sheep, the time remains the same. So, the answer is 7 days.Alternatively, let's use the man-days concept. For the first problem: 7 wolves * 7 days = 49 wolf-days to eat 7 sheep. So, 49 wolf-days per 7 sheep, which is 7 wolf-days per sheep. So, each sheep requires 7 wolf-days to be eaten. Therefore, if you have 9 sheep, you need 9 * 7 = 63 wolf-days. If you have 9 wolves, then the number of days is 63 / 9 = 7 days. So, that's another way to see it. So, regardless of the method, the answer comes to 7 days. So, even though the numbers of wolves and sheep have increased, the ratio remains the same, so the time required remains the same. Therefore, the answer is 7 days.Final AnswerThe number of days it will take is boxed{7}.</think>Given that 7 wolves eat 7 sheep in 7 days, we need to determine how many days it will take for 9 wolves to eat 9 sheep.First, we calculate the rate at which the wolves eat the sheep. If 7 wolves eat 7 sheep in 7 days, the rate can be broken down as follows:- Collectively, the 7 wolves eat 1 sheep per day (7 sheep divided by 7 days).- Therefore, each wolf eats (frac{1}{7}) of a sheep per day.Next, we consider 9 wolves:- The rate at which 9 wolves eat sheep is (9 times frac{1}{7} = frac{9}{7}) sheep per day.- To eat 9 sheep, the time required is (frac{9}{frac{9}{7}} = 7) days.Another way to approach this is by using the concept of wolf-days:- 7 wolves eating 7 sheep in 7 days results in (7 text{ wolves} times 7 text{ days} = 49 text{ wolf-days}) to eat 7 sheep.- This means each sheep requires (7 text{ wolf-days}) to be eaten.- For 9 sheep, the total wolf-days needed is (9 times 7 = 63 text{ wolf-days}).- With 9 wolves, the number of days required is (frac{63 text{ wolf-days}}{9 text{ wolves}} = 7 text{ days}).In both approaches, the key insight is that the ratio of wolves to sheep remains the same, leading to the same number of days required.[boxed{7}]]

🔑:The number of wolves has increased by the same factor as the number of sheep, so the time of consumption will not change.## AnswerIn 7 days.

🧠:[<think>Okay, let's see. I have this problem here where I need to find the value of n given two vectors, a and b. The vectors are a = (1,1) and b = (2,n). The condition given is that the magnitude of the vector sum a + b is equal to the dot product of a and b. Hmm, that seems interesting. Alright, let me break this down step by step.First, let's recall some vector operations. The vector addition of a and b would be done component-wise, right? So, if a is (1,1) and b is (2,n), then adding them together should give (1+2, 1+n) which simplifies to (3, 1+n). So, the vector a + b is (3, 1 + n). Got that.Now, the magnitude of a vector, denoted by |v|, is calculated by taking the square root of the sum of the squares of its components. So, for the vector a + b = (3, 1 + n), its magnitude |a + b| would be sqrt(3² + (1 + n)²). Let me compute that. 3 squared is 9, and (1 + n) squared is (n + 1)^2. So, the magnitude is sqrt(9 + (n + 1)^2). Okay, that's the left side of the equation.On the other side of the equation, we have the dot product of vectors a and b. The dot product is calculated by multiplying the corresponding components and then adding them together. So, for vectors a = (1,1) and b = (2,n), the dot product a · b would be (1)(2) + (1)(n) = 2 + n. So, the right side of the equation is 2 + n.The problem states that these two expressions are equal: sqrt(9 + (n + 1)^2) = 2 + n. So, now I need to solve this equation for n. Let me write that down clearly:sqrt(9 + (n + 1)^2) = 2 + nTo solve for n, I can start by squaring both sides of the equation to eliminate the square root. Squaring both sides gives:[ sqrt(9 + (n + 1)^2) ]² = (2 + n)²Which simplifies to:9 + (n + 1)^2 = (2 + n)^2Alright, now expand both sides. Let's start with the left side:Left side: 9 + (n + 1)^2 = 9 + (n² + 2n + 1) = 9 + n² + 2n + 1 = n² + 2n + 10Right side: (2 + n)^2 = (n + 2)^2 = n² + 4n + 4So now, the equation becomes:n² + 2n + 10 = n² + 4n + 4Hmm, okay. Let's subtract n² from both sides to simplify:n² + 2n + 10 - n² = n² + 4n + 4 - n²Which simplifies to:2n + 10 = 4n + 4Now, let's bring all terms to one side. Let's subtract 2n and 4 from both sides:2n + 10 - 2n - 4 = 4n + 4 - 2n - 4Simplifying both sides:6 = 2nSo, dividing both sides by 2:n = 3Wait, so n is 3? Let me check this solution to make sure it's valid. Sometimes when we square both sides of an equation, we might introduce extraneous solutions, so it's important to verify.First, let's plug n = 3 back into the original equation:Left side: |a + b| = sqrt(9 + (3 + 1)^2) = sqrt(9 + 16) = sqrt(25) = 5Right side: a · b = 2 + 3 = 5So, both sides equal 5. That works! Therefore, n = 3 is indeed the correct solution.Wait, but just to make sure I didn't make a mistake in the algebra, let me go through the steps again.Original equation:sqrt(9 + (n + 1)^2) = 2 + nSquare both sides:9 + (n + 1)^2 = (2 + n)^2Expanding:Left side: 9 + n² + 2n + 1 = n² + 2n + 10Right side: n² + 4n + 4Subtract right side from left side:(n² + 2n + 10) - (n² + 4n + 4) = 0This simplifies to:-2n + 6 = 0 ⇒ -2n = -6 ⇒ n = 3Yep, same result. So, that's consistent. Therefore, n = 3 is the correct answer.I think that's it. The solution checks out both algebraically and when substituting back into the original equation. So, n must be 3.Final AnswerThe value of ( n ) is boxed{3}.</think>Given vectors (overrightarrow{a} = (1, 1)) and (overrightarrow{b} = (2, n)), we need to find (n) such that (|overrightarrow{a} + overrightarrow{b}| = overrightarrow{a} cdot overrightarrow{b}).First, we calculate the vector sum (overrightarrow{a} + overrightarrow{b}):[overrightarrow{a} + overrightarrow{b} = (1 + 2, 1 + n) = (3, 1 + n)]Next, we find the magnitude of this vector:[|overrightarrow{a} + overrightarrow{b}| = sqrt{3^2 + (1 + n)^2} = sqrt{9 + (1 + n)^2}]We also calculate the dot product (overrightarrow{a} cdot overrightarrow{b}):[overrightarrow{a} cdot overrightarrow{b} = 1 cdot 2 + 1 cdot n = 2 + n]According to the problem, these two expressions are equal:[sqrt{9 + (1 + n)^2} = 2 + n]Squaring both sides to eliminate the square root:[9 + (1 + n)^2 = (2 + n)^2]Expanding both sides:[9 + (n^2 + 2n + 1) = n^2 + 4n + 4]Simplifying both sides:[n^2 + 2n + 10 = n^2 + 4n + 4]Subtracting (n^2 + 4n + 4) from both sides:[2n + 10 = 4n + 4]Solving for (n):[10 - 4 = 4n - 2n implies 6 = 2n implies n = 3]Verification by substituting (n = 3) back into the original equation confirms the solution is correct. Therefore, the value of (n) is (boxed{3}).,<think>Okay, let's see. I need to find the value of n given the vectors a and b, and the condition that the magnitude of their sum equals their dot product. Hmm. Let me start by recalling some vector operations. First, vectors a and b are given as (1,1) and (2,n) respectively. So vector a has components (1,1) and vector b has components (2,n). The problem states that the magnitude of a + b is equal to the dot product of a and b. Let me write down the given vectors and the equation:Vector a = (1, 1)Vector b = (2, n)|a + b| = a · bSo, I need to compute both the magnitude of a + b and the dot product of a and b, then set them equal and solve for n.Let me compute a + b first. When adding vectors, you add their corresponding components. So:a + b = (1 + 2, 1 + n) = (3, 1 + n)Now, the magnitude of this vector is |a + b|. The magnitude of a vector (x, y) is sqrt(x² + y²). So:|a + b| = sqrt(3² + (1 + n)²) = sqrt(9 + (1 + n)²)Now, the dot product a · b is computed by multiplying corresponding components and then adding them. So:a · b = (1)(2) + (1)(n) = 2 + nAccording to the problem, these two quantities are equal. So:sqrt(9 + (1 + n)²) = 2 + nNow, I need to solve this equation for n. Let me square both sides to eliminate the square root. But before that, maybe I should check if squaring both sides is valid. Since the left side is a square root, it's non-negative, and the right side is 2 + n. Therefore, 2 + n must also be non-negative. So, 2 + n ≥ 0 => n ≥ -2. I'll keep that in mind to check later if the solution satisfies this condition.So, squaring both sides:[ sqrt(9 + (1 + n)²) ]² = (2 + n)²9 + (1 + n)² = (2 + n)²Now, let's expand both sides.Left side: 9 + (1 + n)²First, expand (1 + n)²: 1² + 2*1*n + n² = 1 + 2n + n²So left side becomes 9 + 1 + 2n + n² = 10 + 2n + n²Right side: (2 + n)²Expand this: 2² + 2*2*n + n² = 4 + 4n + n²So the equation now is:10 + 2n + n² = 4 + 4n + n²Hmm, let's subtract the right side from both sides to bring all terms to the left:10 + 2n + n² - 4 - 4n - n² = 0Simplify term by term:10 - 4 = 62n - 4n = -2nn² - n² = 0So the equation simplifies to:6 - 2n = 0Solve for n:-2n = -6Divide both sides by -2:n = (-6)/(-2) = 3So n = 3. Now, I need to check if this satisfies the earlier condition that 2 + n ≥ 0. Since n = 3, 2 + 3 = 5, which is positive. So squaring both sides was valid here. Also, let's verify the original equation to make sure.Compute |a + b| when n = 3:a + b = (3, 1 + 3) = (3, 4)|a + b| = sqrt(3² + 4²) = sqrt(9 + 16) = sqrt(25) = 5Compute a · b when n = 3:a · b = 1*2 + 1*3 = 2 + 3 = 5Yes, both sides equal 5. So n = 3 is indeed the solution.Wait, but let me just think again. The equation after expanding was:10 + 2n + n² = 4 + 4n + n²Subtracting 4 + 4n + n² from both sides gives 6 - 2n = 0. That's correct.So I don't think there's a mistake here. The solution n = 3 works. Let me check if there could be any other solutions. When we squared both sides of the equation sqrt(9 + (1 + n)^2) = 2 + n, sometimes squaring can introduce extraneous solutions. But since we derived n = 3 and checked it in the original equation, and there's only one solution here, I think that's the only answer.Alternatively, maybe there's another approach. Let me try solving the equation again step by step.Original equation:sqrt(9 + (1 + n)^2) = 2 + nLet me let x = n for simplicity. Then:sqrt(9 + (1 + x)^2) = 2 + xSquare both sides:9 + (1 + x)^2 = (2 + x)^2Expand both sides:9 + 1 + 2x + x² = 4 + 4x + x²Left side: 10 + 2x + x²Right side: 4 + 4x + x²Subtract right side from left:10 + 2x + x² - 4 - 4x - x² = 0 => 6 - 2x = 0 => x = 3Same result. So n = 3 is the only solution.Alternatively, if I consider the equation sqrt(9 + (1 + n)^2) = 2 + n. Let's note that the left side is sqrt((1 + n)^2 + 9), and the right side is 2 + n. For real numbers, sqrt of something is non-negative, so 2 + n must be non-negative. Therefore, n >= -2. So any solution must satisfy n >= -2.But in this case, we found n = 3, which is within the valid range. Therefore, the solution is valid.Another sanity check: Let's suppose n was something else, like n = 0. Then |a + b| would be sqrt(9 + 1) = sqrt(10), and the dot product would be 2 + 0 = 2. Not equal. If n = -1, |a + b| = sqrt(9 + 0) = 3, and the dot product would be 2 + (-1) = 1. Not equal. If n = 1, |a + b| = sqrt(9 + 4) = sqrt(13), dot product = 3. Not equal. So 3 is the only number that works here.Therefore, I think the answer is n = 3.Final AnswerThe value of ( n ) is boxed{3}.</think>Given vectors (overrightarrow{a} = (1, 1)) and (overrightarrow{b} = (2, n)), we need to find (n) such that (|overrightarrow{a} + overrightarrow{b}| = overrightarrow{a} cdot overrightarrow{b}).First, we compute the sum of the vectors:[overrightarrow{a} + overrightarrow{b} = (1 + 2, 1 + n) = (3, 1 + n)]Next, we find the magnitude of this sum:[|overrightarrow{a} + overrightarrow{b}| = sqrt{3^2 + (1 + n)^2} = sqrt{9 + (1 + n)^2}]We also calculate the dot product (overrightarrow{a} cdot overrightarrow{b}):[overrightarrow{a} cdot overrightarrow{b} = 1 cdot 2 + 1 cdot n = 2 + n]According to the problem, these two expressions are equal:[sqrt{9 + (1 + n)^2} = 2 + n]Squaring both sides to eliminate the square root:[9 + (1 + n)^2 = (2 + n)^2]Expanding both sides:[9 + 1 + 2n + n^2 = 4 + 4n + n^2]Simplifying the equation:[10 + 2n + n^2 = 4 + 4n + n^2]Subtracting (4 + 4n + n^2) from both sides:[6 - 2n = 0]Solving for (n):[-2n = -6 implies n = 3]Verification shows that (n = 3) satisfies the original equation. Therefore, the value of (n) is (boxed{3}).]

🔑:Since we know overrightarrow{a}=(1,1) and overrightarrow{b}=(2,n), we have overrightarrow{a}+ overrightarrow{b}=(3,1+n) and overrightarrow{a}cdot overrightarrow{b}=2+n.From the condition |overrightarrow{a}+ overrightarrow{b}|= overrightarrow{a}cdot overrightarrow{b}, we get sqrt{9+(1+n)^{2}}=2+n. Solving this equation, we find n=3.Therefore, the answer is boxed{3}.This problem involves calculating the coordinates of overrightarrow{a}+ overrightarrow{b} and the value of overrightarrow{a}cdot overrightarrow{b} from the coordinates of two vectors. Then, using the condition |overrightarrow{a}+ overrightarrow{b}|= overrightarrow{a}cdot overrightarrow{b}, we solve for the value of n. This question mainly tests the formula for the dot product of two vectors and the operations on vectors in coordinate form, and is considered a medium-level problem.