🧠:[<think>Okay, let me try to figure out this problem. So, we have to find the minimum value of the sum from k=1 to n of sqrt[(2k-1)^2 + a_k²], where the a_k are positive real numbers that add up to 17. Then, we need to find the unique n for which this minimum value S_n is an integer. Hmm, interesting.First, I need to recall how to minimize such a sum. The expression inside the sum is sqrt[(2k-1)^2 + a_k²]. That looks like the hypotenuse of a right triangle with legs (2k-1) and a_k. Maybe there's a geometric interpretation here? Like, if we have a series of right triangles connected together, and we want the total length to be minimized given that the sum of one of the legs (a_k) is 17. Oh! This might be related to the reflection method in optimization problems. The idea where you reflect a path to turn it into a straight line. For example, in problems where you have to cross a river or something, reflecting the path can help find the shortest distance. Maybe here, if we think of each term sqrt[(2k-1)^2 + a_k²] as a segment in a path, then reflecting appropriately could turn the problem into finding a straight line distance.Let me try to formalize this. Suppose we have a series of horizontal and vertical segments. Each term sqrt[(2k-1)^2 + a_k²] can be seen as moving horizontally by (2k-1) and vertically by a_k. If we stack these segments end to end, the total horizontal distance traveled would be the sum of (2k-1) from k=1 to n. Let's compute that sum. Sum_{k=1}^n (2k - 1) = 2 * Sum_{k=1}^n k - Sum_{k=1}^n 1 = 2*(n(n+1)/2) - n = n(n+1) - n = n². So, the total horizontal distance is n². The total vertical distance is Sum_{k=1}^n a_k = 17. So, if we imagine a path that starts at (0,0) and ends at (n², 17), composed of n segments each with horizontal component (2k-1) and vertical component a_k, then the minimal total length of this path should be the straight line distance from (0,0) to (n²,17), which is sqrt[(n²)^2 + 17²] = sqrt(n^4 + 289). Wait, but is that correct? Because the horizontal components are fixed as (2k-1), so the horizontal progression for each segment is fixed, but the vertical components a_k are variables that sum to 17. So, the path is forced to have horizontal steps of lengths 1, 3, 5, ..., (2n-1), adding up to n². The vertical steps can be adjusted as a_k, but their sum is 17. So, to minimize the total length, we want to arrange the vertical steps such that the path is as straight as possible. But in that case, the minimal total length would be the straight line from (0,0) to (n²,17), because if you can freely choose how to distribute the vertical steps, the minimal distance is achieved when all the segments are aligned in the direction of the straight line. That seems right. So, using the Cauchy-Schwarz inequality or something similar.Alternatively, the problem resembles minimizing the sum of Euclidean norms with fixed total resources (the a_k sum to 17). Maybe we can use the Cauchy-Schwarz inequality here.Let me recall that for vectors u and v, the sum of ||u_i|| is minimized when all the vectors are scalar multiples of each other, i.e., when each vector points in the same direction. So, if we model each term sqrt[(2k-1)^2 + a_k²] as the norm of a vector ((2k-1), a_k), then to minimize the sum, we need these vectors to all point in the same direction. Wait, but can we adjust the a_k to make that happen?Alternatively, maybe we can parametrize each a_k as proportional to (2k-1). If we set a_k = t*(2k-1) for some t, then the sum of a_k would be t*Sum_{k=1}^n (2k-1) = t*n². But the sum of a_k is 17, so t = 17/n². Then, each term sqrt[(2k-1)^2 + a_k²] would be sqrt[(2k-1)^2 + (17/n²)^2*(2k-1)^2] = (2k-1)*sqrt(1 + (17/n²)^2). Therefore, the total sum would be sqrt(1 + (17/n²)^2)*Sum_{k=1}^n (2k-1) = sqrt(1 + (17/n²)^2)*n² = sqrt(n^4 + 17²). Wait, that gives the same result as the straight line distance! So, by setting each a_k proportional to (2k-1), the total sum becomes sqrt(n^4 + 289). Therefore, this must be the minimal sum S_n. Because if you distribute the vertical components proportionally to the horizontal components, you get a straight line path, which is the shortest possible. So, the minimal value S_n is indeed sqrt(n^4 + 289). So, now the problem states that there exists a unique n such that S_n is an integer. So, we need sqrt(n^4 + 289) is integer, and there's only one such n. So, we have to find n in natural numbers where n^4 + 289 is a perfect square, and only one such n exists. So, let's denote m^2 = n^4 + 289, where m is integer. So, m^2 - n^4 = 289. Which factors as (m - n²)(m + n²) = 289. Since 289 is 17², and it's a prime power. So, the factors of 289 are 1, 17, 289. But since m - n² and m + n² are both positive integers (because m > n²), and m - n² < m + n². So, the possible factor pairs are (1, 289) and (17,17). Wait, but 17*17=289, so the factor pairs are (1,289) and (17,17). Let's check both:First pair: m - n² = 1 and m + n² = 289. Adding both equations: 2m = 290 => m = 145. Subtracting: 2n² = 288 => n² = 144 => n = 12. Since n must be natural, n=12 is a solution.Second pair: m - n² =17 and m + n²=17. Adding them: 2m=34 => m=17. Subtracting: 2n²=0 => n²=0 => n=0. But n must be in natural numbers, so n=0 is invalid. Thus, the only valid solution is n=12. Therefore, the unique n is 12, so the answer is boxed{12}.But wait, let me verify if there are any other factor pairs. Since 289 is 17², its positive divisors are 1, 17, 289. So, indeed, only the two factor pairs. Since we need both factors (m - n²) and (m + n²) to be positive integers with (m - n²) <= (m + n²). So, the only possible factorizations are the ones we considered. Therefore, n=12 is the only solution. Therefore, the answer is 12.Final Answerboxed{12}</think>To find the minimum value of (sum_{k=1}^{n} sqrt{(2k-1)^2 + a_k^2}) where (a_1, a_2, ldots, a_n) are positive real numbers summing to 17, we recognize that each term (sqrt{(2k-1)^2 + a_k^2}) represents the hypotenuse of a right triangle with legs (2k-1) and (a_k). The total horizontal distance is the sum of (2k-1) from (k=1) to (n), which is (n^2). The total vertical distance is 17. The minimum value of the sum is the straight-line distance from ((0, 0)) to ((n^2, 17)), given by (sqrt{n^4 + 289}).We need (S_n = sqrt{n^4 + 289}) to be an integer. This requires (n^4 + 289) to be a perfect square. Let (m^2 = n^4 + 289), leading to the equation (m^2 - n^4 = 289). Factoring this as ((m - n^2)(m + n^2) = 289), we consider the factor pairs of 289: ((1, 289)) and ((17, 17)).For the pair ((1, 289)):- (m - n^2 = 1)- (m + n^2 = 289)Solving these, we get (2m = 290 Rightarrow m = 145) and (2n^2 = 288 Rightarrow n^2 = 144 Rightarrow n = 12).The pair ((17, 17)) results in (n = 0), which is invalid as (n) must be a natural number. Thus, the unique solution is (n = 12).(boxed{12}),<think>Alright, let me try to work through this problem step by step. So, the problem is about finding the minimum value of a sum involving square roots, where the sum of some variables a₁, a₂, ..., aₙ is 17. Then, we need to find the unique n such that this minimum value Sₙ is an integer. Hmm, okay.First, let me parse the problem again. We have Sₙ defined as the minimum of the sum from k=1 to n of sqrt[(2k - 1)² + a_k²], where each a_k is a positive real number, and their sum is 17. We need to find the unique n for which Sₙ is an integer.So, my first thought is that this might be a minimization problem where we can use calculus or some sort of optimization technique. But since it's a sum of square roots, maybe there's a geometric interpretation? Like, maybe these terms can represent the lengths of line segments or something?Let me think. The term sqrt[(2k - 1)² + a_k²] looks like the hypotenuse of a right triangle with legs (2k - 1) and a_k. So, maybe if we can visualize this as a path made up of horizontal and vertical segments, and then find the minimal total distance?Wait, actually, if you have several horizontal segments of lengths 1, 3, 5, ..., (2n - 1) and vertical segments of lengths a₁, a₂, ..., aₙ, then the total distance would be the sum of the hypotenuses of each right triangle formed by these segments. So, the problem is to arrange the vertical segments (with total length 17) such that the total distance of the path is minimized. So, the minimal path would correspond to the straight line from the starting point to the endpoint, but since the horizontal segments are fixed increments, maybe it's a piecewise straight line?Wait, no, the horizontal components are fixed for each segment. Each segment has a horizontal component of (2k - 1) and a vertical component of a_k. So, actually, if we imagine each step k as moving horizontally by (2k - 1) units and vertically by a_k units, then the total path is the sum of the lengths of each step. To minimize the total length, given that the total vertical movement is 17, and each step's horizontal movement is fixed.Hmm, perhaps this is similar to minimizing the sum of Euclidean distances with fixed horizontal components and variable vertical components, constrained by the total vertical being 17. Maybe we can use the Cauchy-Schwarz inequality here? Because when we have sums of squares or square roots, Cauchy-Schwarz often comes into play.Wait, the Cauchy-Schwarz inequality states that (sum (x_i y_i))² ≤ (sum x_i²)(sum y_i²). But in this case, we have a sum of sqrt terms. Alternatively, maybe we can use the Minkowski inequality, which is about the sum of norms.Minkowski's inequality says that for vectors u_i and v_i, the norm of the sum is less than or equal to the sum of the norms. But here, each term is a separate norm. Wait, maybe if we think of each term as the norm of a vector in 2D space: (2k - 1, a_k). Then, the total sum is the sum of the lengths of these vectors. To minimize this sum, given that the sum of the a_k's is 17.Wait, perhaps the minimal sum occurs when all the vectors are scaled versions of each other, pointing in the same direction. Is that possible? Because if you have vectors that are colinear, then their sum would be the straight line, which is the minimal path. But here, the horizontal components are fixed, so the direction of each vector can't be arbitrary.Alternatively, think of each term sqrt[(2k - 1)^2 + a_k^2] as the hypotenuse, and to minimize the sum, we might need to set the ratios of a_k to (2k - 1) to be the same for all k. Because if each right triangle is similar, then the direction of each segment is the same, which would make the total path a straight line. Is that the case?Wait, if we set each a_k / (2k - 1) = constant, say m, then a_k = m*(2k - 1). Then, the total vertical distance would be sum_{k=1}^n a_k = m * sum_{k=1}^n (2k - 1) = m * n², since the sum of the first n odd numbers is n². Then, since the total a_k sum is 17, we have m = 17 / n². Therefore, each a_k = (17 / n²)*(2k - 1). Then, each term in the sum becomes sqrt[(2k - 1)^2 + (17/n²)^2*(2k - 1)^2] = (2k - 1)*sqrt(1 + (17/n²)^2). Therefore, the total sum Sₙ would be sqrt(1 + (17/n²)^2) * sum_{k=1}^n (2k - 1). But sum_{k=1}^n (2k - 1) is n², as established earlier. Therefore, Sₙ = sqrt(n⁴ + 17²). Because:sqrt(1 + (17/n²)^2) * n² = sqrt(n⁴ + 17²).Wait, let me check that algebra again. Let me see:sqrt(1 + (17/n²)^2) * n² = sqrt(n⁴ + 17²). Let me verify:sqrt(1 + (289/n⁴)) * n² = sqrt(n⁴ + 289)/n² * n² = sqrt(n⁴ + 289). Yes, that's correct. So, Sₙ = sqrt(n⁴ + 289).Wait, but that seems too straightforward. So, according to this, the minimal sum Sₙ is sqrt(n⁴ + 17²). But 17 squared is 289, so Sₙ = sqrt(n⁴ + 289). Therefore, we need to find n such that sqrt(n⁴ + 289) is an integer, and there's a unique such n.Wait, so now the problem reduces to finding integer n where n⁴ + 289 is a perfect square. Let me write that equation:n⁴ + 17² = m², where m is integer.So, m² - n⁴ = 289.This is a Diophantine equation. Let's see if we can solve this.We can factor the left-hand side as (m - n²)(m + n²) = 289.Since 289 is 17², which is a prime squared. Therefore, the factors (m - n²) and (m + n²) must be positive divisors of 289. Since m and n are positive integers, m > n².So, the possible factor pairs of 289 are (1, 289) and (17, 17). But since m - n² < m + n², we can only have (1, 289) and (17, 17). However, (17, 17) would imply m - n² = 17 and m + n² = 17, which would lead to m = 17 and n² = 0, but n must be a natural number, so this is invalid. Therefore, only the pair (1, 289) is valid.Therefore:m - n² = 1m + n² = 289Adding these two equations: 2m = 290 => m = 145Subtracting the first from the second: 2n² = 288 => n² = 144 => n = 12Since n must be a natural number, n = 12 is the solution. Therefore, the unique n is 12.Wait, but before I conclude, let me verify that this approach is valid. The key step was assuming that the minimal sum occurs when all the a_k / (2k - 1) ratios are constant, leading to the expression sqrt(n⁴ + 17²). Is that assumption correct?This is based on the idea that distributing the total vertical distance proportionally to the horizontal distances minimizes the total sum of hypotenuses. That seems analogous to the problem where you want to minimize the sum of Euclidean distances given fixed horizontal components and a fixed total vertical component. In such cases, the minimal sum is achieved when each vertical component is proportional to the horizontal component, which is essentially making each segment colinear in direction, forming a straight line when connected. However, in this case, the horizontal components are fixed per segment, so the direction can't be the same unless the vertical components are scaled accordingly. So, this approach is similar to creating a path that approximates a straight line as much as possible given the fixed horizontal steps. Therefore, the calculus approach would involve setting up the sum with variables a_k and using Lagrange multipliers to minimize the sum subject to the constraint sum a_k =17. Let me try that to confirm.Let’s define the function to minimize:L = sum_{k=1}^n sqrt((2k - 1)^2 + a_k^2) + λ(17 - sum_{k=1}^n a_k)Taking partial derivatives with respect to each a_k and setting them to zero:dL/da_k = (a_k)/sqrt((2k - 1)^2 + a_k^2) - λ = 0Therefore, for each k,a_k / sqrt((2k - 1)^2 + a_k^2) = λLet’s denote this ratio as λ. Solving for a_k:Square both sides:a_k² / [(2k - 1)^2 + a_k²] = λ²Multiply denominator:a_k² = λ²[(2k - 1)^2 + a_k²]Bring terms with a_k² to the left:a_k² - λ² a_k² = λ² (2k -1)^2Factor:a_k² (1 - λ²) = λ² (2k -1)^2Therefore,a_k² = [λ² / (1 - λ²)] (2k -1)^2Taking square roots:a_k = [λ / sqrt(1 - λ²)] (2k -1)Let’s let m = λ / sqrt(1 - λ²), so a_k = m (2k -1)Therefore, the same result as before: a_k is proportional to (2k -1). So, the ratio is constant. Then, the total sum of a_k is m * sum_{k=1}^n (2k -1) = m n² =17, so m = 17 /n². Then, each a_k = (17 /n²)(2k -1). Therefore, plugging back into the expression for Sₙ:Sₙ = sum sqrt{(2k -1)^2 + [17(2k -1)/n²]^2} = sum (2k -1) sqrt{1 + (17/n²)^2} = sqrt{1 + (17/n²)^2} * sum (2k -1) = sqrt{1 + (289/n⁴)} * n² = sqrt(n⁴ + 289)So, the calculus approach confirms the initial result. Therefore, Sₙ = sqrt(n⁴ + 289). Therefore, the problem reduces to solving when sqrt(n⁴ + 289) is integer. As we saw earlier, this leads to n⁴ +289 = m², which factors into (m -n²)(m +n²)=289. Solving gives n=12. Therefore, the answer is 12.But let me check if there could be other factor pairs. Since 289 is 17², its positive divisors are 1, 17, and 289. So, the factor pairs are (1,289) and (17,17). As we saw earlier, (17,17) gives n=0 which isn't allowed. So, only (1,289) gives a valid solution, leading to n=12. Therefore, n=12 is unique. Hence, the answer is 12.Final Answerboxed{12}</think>To find the unique ( n ) such that ( S_n ) is an integer, we start by interpreting the problem geometrically. The sum ( sum_{k=1}^{n} sqrt{(2k-1)^2 + a_k^2} ) can be seen as the sum of the hypotenuses of right triangles with legs ( (2k-1) ) and ( a_k ). To minimize this sum, we use the method of Lagrange multipliers. We find that the minimum occurs when each ( a_k ) is proportional to ( (2k-1) ). Setting ( a_k = frac{17}{n^2}(2k-1) ), we derive that the minimum sum ( S_n ) is given by:[S_n = sqrt{n^4 + 289}]We need ( sqrt{n^4 + 289} ) to be an integer. This leads to the equation:[n^4 + 289 = m^2]Rewriting this as a difference of squares, we get:[m^2 - n^4 = 289]Factoring the left-hand side, we have:[(m - n^2)(m + n^2) = 289]The factor pairs of 289 are ( (1, 289) ) and ( (17, 17) ). The pair ( (17, 17) ) is invalid as it leads to ( n = 0 ). Using the valid pair ( (1, 289) ):[m - n^2 = 1 quad text{and} quad m + n^2 = 289]Solving these, we find:[2m = 290 implies m = 145 quad text{and} quad 2n^2 = 288 implies n^2 = 144 implies n = 12]Thus, the unique ( n ) such that ( S_n ) is an integer is ( boxed{12} ).]

🔑:begin{array}{l}text { 10. Solution: } because sum_{k=1}^{n} sqrt{(2 k-1)^{2}+a_{k}^{2}}=sum_{k=1}^{n}left|(2 k-1)+a_{k} mathrm{i}right|, k=1,2, cdots, n, therefore sum_{k=1}^{n}left|(2 k-1)+a_{k} mathrm{i}right| geqslantleft|1+a_{1} mathrm{i}right|+left|3+a_{2} mathrm{i}right|+cdots+left|(2 n-1)+a_{n} mathrm{i}right| geqslant mid[1+3+cdots+(2 n -1)]+left(a_{1}+a_{2}+cdots+a_{n}right) mathrm{i}|=|left(n^{2}+17 mathrm{i}right) mid=sqrt{n^{4}+17^{2}} . because S_{n} in mathbf{Z}^{+} text {, let } S_{n}=m text {, then } n^{4}+17^{2}=m^{2} text {, i.e., } m^{2}-n^{4}=17^{2} . thereforeleft(m+n^{2}right)left(m-n^{2}right)=289 text {, and } m, n in mathbf{N} . therefore m+n^{2}=289, m-n^{2}=1 text {, solving gives } n=12 .end{array}

🧠:[<think>Okay, so I need to find four numbers in a geometric progression where the second term is 35 less than the first, and the third term is 560 more than the fourth. Hmm, let's start by recalling what a geometric progression is. In a geometric sequence, each term after the first is found by multiplying the previous term by a constant called the common ratio. Let's denote the first term as ( a ) and the common ratio as ( r ). Then the four terms would be:1. First term: ( a )2. Second term: ( ar )3. Third term: ( ar^2 )4. Fourth term: ( ar^3 )Now, according to the problem, the second term is 35 less than the first term. So, mathematically, that means:( ar = a - 35 )Also, the third term is 560 more than the fourth term. So:( ar^2 = ar^3 + 560 )Alright, so I have two equations here. Let's write them out again:1. ( ar = a - 35 )2. ( ar^2 = ar^3 + 560 )I need to solve these equations to find the values of ( a ) and ( r ), and then determine the four terms. Let's start with the first equation:( ar = a - 35 )Let me rearrange this equation to solve for ( a ). Subtract ( ar ) from both sides:( a - ar = 35 )Factor out ( a ):( a(1 - r) = 35 )So, ( a = frac{35}{1 - r} ) --- Equation (1)Okay, now let's look at the second equation:( ar^2 = ar^3 + 560 )Again, let's rearrange this. Subtract ( ar^3 ) from both sides:( ar^2 - ar^3 = 560 )Factor out ( ar^2 ):( ar^2(1 - r) = 560 )Hmm, so ( ar^2(1 - r) = 560 ) --- Equation (2)Now, from Equation (1), I have an expression for ( a ) in terms of ( r ). Let's substitute that into Equation (2) to eliminate ( a ).So, substituting ( a = frac{35}{1 - r} ) into Equation (2):( left(frac{35}{1 - r}right) r^2 (1 - r) = 560 )Notice that ( (1 - r) ) cancels out in the numerator and denominator:( 35 r^2 = 560 )So, ( r^2 = frac{560}{35} )Calculating that: 560 divided by 35. Let me compute 35 times 16 is 560, right? 35*10=350, 35*6=210, 350+210=560. So, ( r^2 = 16 )Therefore, ( r = 4 ) or ( r = -4 )Wait, so possible values for ( r ) are 4 and -4. Let's check both possibilities.First, let's check ( r = 4 ).Using Equation (1): ( a = frac{35}{1 - 4} = frac{35}{-3} = -frac{35}{3} )So, if ( r = 4 ) and ( a = -35/3 ), then the four terms would be:1. ( a = -35/3 )2. ( ar = (-35/3)*4 = -140/3 )3. ( ar^2 = (-35/3)*16 = -560/3 )4. ( ar^3 = (-35/3)*64 = -2240/3 )Wait, but the problem states that the second term is 35 less than the first. Let's check:First term: -35/3 ≈ -11.666..., second term: -140/3 ≈ -46.666...Is -140/3 equal to -35/3 - 35?Calculating RHS: -35/3 - 35 = -35/3 - 105/3 = -140/3. Yes, that works.Now, the third term should be 560 more than the fourth term. Let's check:Third term: -560/3, Fourth term: -2240/3Is -560/3 equal to -2240/3 + 560?Calculating RHS: -2240/3 + 560 = -2240/3 + 1680/3 = (-2240 + 1680)/3 = (-560)/3. Yes, that's equal to the third term. So this checks out.Wait, but all terms are negative here. Hmm, but the problem didn't specify that the numbers have to be positive. So this is a valid solution.Now, let's check the other possibility where ( r = -4 ).Again, using Equation (1): ( a = frac{35}{1 - (-4)} = frac{35}{5} = 7 )So, if ( r = -4 ) and ( a = 7 ), the four terms would be:1. ( a = 7 )2. ( ar = 7*(-4) = -28 )3. ( ar^2 = 7*(16) = 112 )4. ( ar^3 = 7*(-64) = -448 )Now, check the conditions:Second term is -28. Is that 35 less than the first term (7)?7 - 35 = -28. Yes, that works.Third term is 112. Fourth term is -448. Is 112 equal to -448 + 560?Calculating RHS: -448 + 560 = 112. Yes, that's correct.So this also checks out. Therefore, there are two possible geometric progressions that satisfy the given conditions.Wait, the problem says "Find four numbers that form a geometric progression". It doesn't specify if there's only one solution or multiple. So both of these are valid. But let me check if there are more possibilities.Wait, when we solved for ( r^2 = 16 ), we considered ( r = 4 ) and ( r = -4 ). Are there other roots? No, because square root of 16 is 4 and -4. So those are the only possibilities.Therefore, there are two sets of four numbers. Let me write them out:First case:Terms: -35/3, -140/3, -560/3, -2240/3Second case:Terms: 7, -28, 112, -448But the problem says "four numbers that form a geometric progression". It doesn't specify if they need to be integers. The first case has fractions, and the second case has integers. Depending on the problem's context, maybe they expect the integer solution? Let me check if the question mentions anything about integers. Let me look back at the problem:"Find four numbers that form a geometric progression, where the second term is 35 less than the first, and the third term is 560 more than the fourth."No, there's no mention of integers. So both solutions are valid. But maybe both are acceptable? Wait, the problem says "four numbers", so unless specified otherwise, both are correct. However, sometimes problems expect all possible solutions, but since it says "find four numbers", maybe they are expecting both? Or maybe one?Wait, but maybe I made a mistake here. Let me check again.Wait, when r = 4, the common ratio is 4, so each term is multiplied by 4. So the sequence is decreasing if the common ratio is between 0 and 1, but here ratio is 4, which is greater than 1, but since the first term is negative, the terms become more negative. So that's a valid geometric progression.Similarly, with r = -4, the progression alternates in sign: 7, -28, 112, -448, which is also valid.So both are correct. Therefore, there are two possible geometric progressions. But the problem asks to "find four numbers", not "find all possible four numbers", so maybe they are expecting both solutions? Or maybe I need to check if both are required.Wait, let me check the original problem again. It's problem 4.016, which might be from some textbook. The way the problem is phrased: "Find four numbers that form a geometric progression..." without specifying other conditions. Therefore, both solutions are acceptable. But perhaps the problem expects both answers? Hmm.However, in the context of an exam or homework problem, sometimes even if there are multiple solutions, they might expect both. Let me check if both solutions are correct.First solution with r = 4:First term: -35/3, second term: -140/3. The second term is 35 less than the first: -35/3 - 35 = -35/3 - 105/3 = -140/3. Correct.Third term: -560/3, fourth term: -2240/3. Third term is 560 more than the fourth: -2240/3 + 560 = -2240/3 + 1680/3 = (-560)/3. Wait, but the third term is -560/3. So -560/3 is equal to -2240/3 + 560. Correct.Second solution with r = -4:First term: 7, second term: -28. 7 - 35 = -28. Correct.Third term: 112, fourth term: -448. 112 = -448 + 560. Correct.So both solutions are valid. Therefore, the problem has two possible geometric progressions. However, the problem says "find four numbers", not "find all sets of four numbers". So maybe either one is acceptable? But in math problems like this, unless specified, usually all solutions should be presented.Therefore, the answer should include both possibilities. Let me confirm again if I didn't make a mistake in calculations.Wait, but in the first case, when r = 4, the common ratio is 4, but with a negative first term. So each subsequent term is 4 times the previous, which is more negative. So it's decreasing by 35 in the first step? Wait, let's see: first term is -35/3, second term is -140/3. The difference is (-140/3) - (-35/3) = (-105)/3 = -35. So the second term is 35 less than the first term. That's correct.Similarly, third term is -560/3, fourth term is -2240/3. The difference between third and fourth term is (-560/3) - (-2240/3) = (1680)/3 = 560. So the third term is 560 more than the fourth term. Correct.So both solutions are valid. Therefore, there are two possible sequences. Since the problem didn't restrict the numbers to positive or integers, both solutions are correct.But maybe the problem expects both answers? Let me check the problem statement again: "Find four numbers that form a geometric progression..." So, perhaps both are needed. Therefore, the answer is two sets of four numbers.But I need to present the answer in boxed notation. Wait, the original problem says "put your final answer within boxed{}". If there are two solutions, how should I present them? Maybe as two boxed answers? But the instructions say "put your final answer within boxed{}", suggesting a single box. Hmm.Alternatively, maybe the problem expects only the integer solution, with whole numbers. Since the second solution has integers, which might be preferred. Let me check.In the first solution, the numbers are -35/3, -140/3, -560/3, -2240/3. These are fractions, but still real numbers. The problem didn't specify they need to be integers. However, in many problems like this, unless specified, fractional answers are acceptable, but sometimes problems expect integer solutions. Since there is an integer solution, perhaps that's the expected answer. But to be thorough, since both are valid, maybe both should be presented. But how?Wait, let me check if there is a way that the problem might have a unique solution. For example, maybe when they say "the second term is 35 less than the first", depending on whether "less than" is interpreted as a difference in magnitude or algebraic difference. But in algebra, "A is 35 less than B" translates to A = B - 35. So if B is the first term, then second term = first term - 35. So that's correct. So both solutions are correct.Alternatively, perhaps the problem has a typo, but given the information, both solutions are valid. Therefore, the answer should include both sequences.But since the user says "put your final answer within boxed{}", which usually indicates a single answer. Maybe the problem expects both solutions? Let me check the problem number: 4.016. Hmm, maybe 4.016 is a problem number with decimal, which is unusual. Maybe it's 4.16? But regardless, the key is the problem itself.Alternatively, maybe the problem is designed so that there's a unique solution. Wait, let me check my equations again.Starting again:We have four terms: a, ar, ar^2, ar^3Given:1. ar = a - 35 => a(1 - r) = 35 => a = 35/(1 - r)2. ar^2 = ar^3 + 560 => ar^2(1 - r) = 560Substituting a from first equation into the second:35/(1 - r) * r^2 * (1 - r) = 35r^2 = 560 => r^2 = 16 => r = 4 or -4Therefore, r = 4 or -4. Then a is 35/(1 - 4) = -35/3 or 35/(1 - (-4)) = 7.So yes, two solutions. So unless there's a mistake in this reasoning, both are valid.Therefore, the problem has two solutions. However, in some textbooks, especially if the problem is in the early sections, they might expect the ratio to be positive, but geometric progressions can have negative ratios. For example, the sequence 7, -28, 112, -448 is a valid geometric progression with a common ratio of -4.Therefore, both are correct. But how to present them? If the answer requires both, they should be both boxed. But since the user instruction says "put your final answer within boxed{}", maybe each solution in its own box? But the user might expect a single answer. Alternatively, the problem might have a unique solution if considering only positive terms. Wait, but in the second solution, the terms alternate signs, so not all positive. If the problem allows for negative numbers, both are okay.Alternatively, maybe I made a mistake in assuming both r = 4 and r = -4 are valid. Let's check with r = -4:First term: 7, second term: 7*(-4) = -28. So second term is -28, which is 35 less than 7. 7 - 35 = -28. Correct.Third term: -28*(-4) = 112, fourth term: 112*(-4) = -448. Third term is 112, which should be 560 more than the fourth term. -448 + 560 = 112. Correct.So that's correct.Similarly, for r = 4, even though the terms are negative, they satisfy the conditions.So both are correct. Therefore, I think the answer should present both solutions.But the problem says "find four numbers". If they are expecting both sequences, then we need to present both. But the user's instruction is to put the final answer within boxed{}.Wait, maybe the problem is designed to have two solutions, but the user expects both? But in the format here, perhaps each solution in a separate box? But the standard practice is to present all solutions. However, since the user might be expecting one answer, perhaps the integer solution is the intended one.Alternatively, the problem might have a unique solution if considering that the terms must be integers. Since the first solution has fractional terms, and the second has integer terms. Maybe the problem expects integer solutions. Let me check the problem statement again. It just says "four numbers", so unless specified, fractions are okay. But perhaps in the source of the problem, it's implied integers. Since the difference is 35 and 560, which are integers, maybe the answer is expected to be integers.Therefore, the sequence with integer terms is 7, -28, 112, -448.But let's check if the problem might be in a context where only positive terms are considered. For example, maybe in some contexts, geometric progressions are assumed to have positive terms. But in that case, the ratio would have to be positive. However, even in that case, with a negative ratio, the terms alternate signs. But if the problem allows negative numbers, it's okay. The problem doesn't specify positivity.Therefore, given that both solutions are valid, but the problem may expect integer solutions, so perhaps 7, -28, 112, -448 is the answer. But to be thorough, I need to confirm.Alternatively, perhaps the problem is expecting both solutions. But how to present them? The user's instruction is to put the final answer within boxed{}, so maybe as two boxed answers. For example:boxed{7}, boxed{-28}, boxed{112}, boxed{-448}andboxed{-dfrac{35}{3}}, boxed{-dfrac{140}{3}}, boxed{-dfrac{560}{3}}, boxed{-dfrac{2240}{3}}But in some contexts, multiple boxed answers are separated by commas. However, given the initial problem statement, it's unclear. If it's from a textbook problem, maybe only the integer solution is expected. Given that 35 and 560 are integers, perhaps expecting integer terms.Alternatively, the problem might be designed to have a unique solution. Wait, let's check with r = 4:First term: -35/3, second term: -140/3. The difference is -35, as per the problem. Third term: -560/3, fourth term: -2240/3. The difference between third and fourth term is 560. So that works.But the problem didn't specify that the numbers have to be integers. So both are correct.However, in most typical problems like this, unless otherwise stated, they might expect integer solutions. Given that 35 and 560 are integers, and the problem may be constructed to have integer terms. Therefore, maybe the answer is 7, -28, 112, -448.Alternatively, the problem could be expecting both answers. Since the problem is labeled 4.016, which might imply a specific answer format.But given that the user hasn't specified any particular constraints, and the problem as stated allows both solutions, both are correct. However, since the user instruction is to put the final answer within a single box, perhaps list both solutions inside the box.In conclusion, there are two geometric progressions that satisfy the given conditions. The first one has a common ratio of 4 and starts at -35/3, and the second one has a common ratio of -4 and starts at 7. Both sequences satisfy the conditions that the second term is 35 less than the first and the third term is 560 more than the fourth.Therefore, the four numbers can be either:(-dfrac{35}{3}), (-dfrac{140}{3}), (-dfrac{560}{3}), (-dfrac{2240}{3})or7, -28, 112, -448.But since the problem asks to "find four numbers", and both solutions are valid, it's appropriate to present both. However, considering standard problem conventions where integer solutions might be preferred, the second sequence with integers is more likely the expected answer.Final AnswerThe four numbers are boxed{7}, boxed{-28}, boxed{112}, and boxed{-448}.</think>Given a geometric progression with four numbers where the second term is 35 less than the first, and the third term is 560 more than the fourth, we start by denoting the first term as ( a ) and the common ratio as ( r ). The four terms are ( a ), ( ar ), ( ar^2 ), and ( ar^3 ).We have the following equations based on the problem statement:1. ( ar = a - 35 )2. ( ar^2 = ar^3 + 560 )From the first equation:[ ar = a - 35 ][ a(1 - r) = 35 ][ a = frac{35}{1 - r} ]Substituting ( a = frac{35}{1 - r} ) into the second equation:[ ar^2(1 - r) = 560 ][ left(frac{35}{1 - r}right) r^2 (1 - r) = 560 ][ 35r^2 = 560 ][ r^2 = 16 ][ r = 4 text{ or } r = -4 ]For ( r = 4 ):[ a = frac{35}{1 - 4} = -frac{35}{3} ]The four terms are ( -frac{35}{3} ), ( -frac{140}{3} ), ( -frac{560}{3} ), ( -frac{2240}{3} ).For ( r = -4 ):[ a = frac{35}{1 - (-4)} = 7 ]The four terms are ( 7 ), ( -28 ), ( 112 ), ( -448 ).Both sequences satisfy the given conditions. However, considering integer solutions, the sequence with integer terms is more likely the expected answer. Final AnswerThe four numbers are boxed{7}, boxed{-28}, boxed{112}, and boxed{-448}.,<think>Okay, so I need to find four numbers that form a geometric progression. Let me remember what a geometric progression is. It's a sequence where each term after the first is found by multiplying the previous term by a constant called the common ratio. So if the first term is ( a ), then the terms are ( a ), ( ar ), ( ar^2 ), ( ar^3 ), and so on. Since we need four numbers, they would be ( a ), ( ar ), ( ar^2 ), ( ar^3 ).The problem states two conditions:1. The second term is 35 less than the first. So, mathematically, that would be ( ar = a - 35 ).2. The third term is 560 more than the fourth term. So, ( ar^2 = ar^3 + 560 ).Hmm, okay, let me write these equations down:1. ( ar = a - 35 )2. ( ar^2 = ar^3 + 560 )So, we have two equations here with two variables: ( a ) and ( r ). If I can solve these equations, I can find ( a ) and ( r ), and then write out all four terms.Starting with the first equation: ( ar = a - 35 ).Let me rearrange this to solve for ( a ) in terms of ( r ). Subtract ( ar ) from both sides:( a - ar = 35 )Factor out ( a ):( a(1 - r) = 35 )So, ( a = frac{35}{1 - r} ).Okay, so that's ( a ) expressed in terms of ( r ). Now, let's look at the second equation: ( ar^2 = ar^3 + 560 ).Similarly, let's rearrange this equation. Subtract ( ar^3 ) from both sides:( ar^2 - ar^3 = 560 )Factor out ( ar^2 ):( ar^2(1 - r) = 560 )Hmm, so that's ( ar^2(1 - r) = 560 ). But from the first equation, we already have ( a(1 - r) = 35 ). Let me see if I can substitute that in here.From the first equation: ( a(1 - r) = 35 ). So, if I multiply both sides of this by ( r^2 ), I get ( a(1 - r)r^2 = 35r^2 ). But the left side of this is exactly ( ar^2(1 - r) ), which is equal to 560. So, substituting:( 35r^2 = 560 )Ah! So that gives me an equation just in terms of ( r ). Let me solve for ( r ):Divide both sides by 35:( r^2 = frac{560}{35} )Calculating that, 560 divided by 35. Let's see, 35 times 16 is 560 because 35*10=350, 35*6=210, 350+210=560. So, ( r^2 = 16 ).Therefore, ( r = sqrt{16} ) or ( r = -sqrt{16} ), so ( r = 4 ) or ( r = -4 ).Wait, but geometric progression ratios can be negative, right? So both possibilities are valid unless specified otherwise. So, we need to check both possibilities.Case 1: ( r = 4 )Then from the first equation, ( a = frac{35}{1 - 4} = frac{35}{-3} = -frac{35}{3} ).Case 2: ( r = -4 )Then ( a = frac{35}{1 - (-4)} = frac{35}{5} = 7 ).So now we have two possible values for ( a ) and ( r ). Let's check both cases to see if they satisfy both equations.First, checking Case 1: ( r = 4 ), ( a = -35/3 ).Let's compute the terms:First term: ( a = -35/3 )Second term: ( ar = (-35/3)(4) = -140/3 )But according to the first condition, the second term should be 35 less than the first term. Let's check:First term - 35 = (-35/3) - 35 = (-35/3) - (105/3) = (-140/3), which matches the second term. So that works.Third term: ( ar^2 = (-35/3)(16) = -560/3 )Fourth term: ( ar^3 = (-35/3)(64) = -2240/3 )Now, the third condition is that the third term is 560 more than the fourth term. Let's check:Third term - fourth term = (-560/3) - (-2240/3) = (-560/3 + 2240/3) = 1680/3 = 560. So, yes, the third term is 560 more than the fourth term. So, that works.Now, check Case 2: ( r = -4 ), ( a = 7 ).Compute the terms:First term: ( a = 7 )Second term: ( ar = 7*(-4) = -28 )Check if second term is 35 less than first term: 7 - 35 = -28, which matches. Good.Third term: ( ar^2 = 7*(16) = 112 )Fourth term: ( ar^3 = 7*(-64) = -448 )Check if third term is 560 more than fourth term: 112 - (-448) = 112 + 448 = 560. Correct.So both cases are valid. Therefore, there are two possible geometric progressions satisfying the given conditions.But the problem says "Find four numbers that form a geometric progression...", and it doesn't specify that there's only one solution. So both solutions are acceptable. But let me check if the problem wants all possible solutions or if there is something I missed.Wait, the problem says "four numbers that form a geometric progression", and the two cases we have are different sequences. So, both are valid. Therefore, the answer could be two different sets of four numbers. But let me check the problem again.Looking back: "Find four numbers that form a geometric progression, where the second term is 35 less than the first, and the third term is 560 more than the fourth."It doesn't specify any constraints on the numbers being positive or integers, so both solutions are acceptable.However, let me check if there was a miscalculation in my steps.First, for Case 1: ( a = -35/3 ), ( r = 4 ). The terms are:-35/3, -140/3, -560/3, -2240/3. Then the second term is indeed 35 less than the first, and the third term is 560 more than the fourth. All checks out.Case 2: ( a = 7 ), ( r = -4 ). The terms are:7, -28, 112, -448. The second term is -28, which is 35 less than 7 (7 - 35 = -28). The third term is 112, and the fourth term is -448. 112 - (-448) = 560. Correct.So both solutions are valid.But the problem says "find four numbers", so maybe both are acceptable. However, in the original problem statement, it's possible that the progression is meant to have integer terms, but since they didn't specify, both are correct.But let me check if the problem is presented in a context where fractions or negative numbers are allowed. The problem number is 4.016, which might be a decimal, but the problem itself is in natural language.Since there's no restriction given, both solutions are valid. Therefore, the answer is two possible geometric progressions. But let me check if the problem expects both or if I might have made a miscalculation.Wait, let me confirm the two cases.Case 1: r = 4, a = -35/3. Then the four terms are:Term1: -35/3Term2: -35/3 * 4 = -140/3Term3: -140/3 * 4 = -560/3Term4: -560/3 * 4 = -2240/3Checking Term2 = Term1 -35: -35/3 -35 = -35/3 -105/3 = -140/3. Correct.Term3 = Term4 +560: -2240/3 +560 = -2240/3 +1680/3 = (-2240 +1680)/3 = (-560)/3. Wait, but Term3 is -560/3. So Term3 = Term4 +560: -560/3 = -2240/3 +560. Let me compute the right side:-2240/3 +560 = -2240/3 + (560*3)/3 = -2240/3 +1680/3 = (-2240 +1680)/3 = (-560)/3. Which equals Term3. So yes, that's correct.Case2: a=7, r=-4. The terms:7, -28, 112, -448Check Term2 = Term1 -35: 7 -35 = -28. Correct.Term3 = Term4 +560: -448 +560 =112. Correct.Therefore both are correct.But the problem is presented as "Find four numbers...", so maybe they expect both solutions. But the problem might have a unique solution if considering positive terms, but since the problem didn't specify, both are acceptable.But let me check if the problem might require integers. In the first case, the terms are fractions, while in the second case, the terms are integers. If the problem expects integer solutions, then only the second case is valid.Given that the problem is numbered 4.016, which may or may not indicate anything, but in educational contexts, sometimes fractions are acceptable unless stated otherwise. However, in competition problems or certain textbooks, they might prefer integer solutions. Since the problem didn't specify, but the second case gives integers, which might be the intended answer. But since the problem didn't restrict, technically both are correct.But maybe I made a mistake in considering the negative ratio. Let me check again.If r is negative, the terms alternate in sign. So in the second case, with a =7 and r=-4, the terms are 7, -28, 112, -448. So the second term is -28, which is 35 less than 7. Then the third term is 112, which is 560 more than the fourth term -448 (112 - (-448) = 560). Correct.Alternatively, the first case with a negative first term and positive ratio, leading to all terms negative and decreasing. That seems valid as well.So unless there's a constraint in the problem that I missed, both solutions are acceptable. But the problem says "four numbers", so maybe both are acceptable, but the answer might expect both solutions. However, the problem is presented as a single answer question, given the instruction to put the final answer within a box. Maybe they expect one solution? Wait, but the problem doesn't specify if there's one or multiple solutions.Alternatively, perhaps there's a miscalculation here. Let me re-express the equations.We had:1. ( a(1 - r) = 35 )2. ( ar^2(1 - r) = 560 )Then substituting the first equation into the second: ( ar^2(1 - r) = 560 Rightarrow (a(1 - r))r^2 = 35r^2 = 560 Rightarrow r^2 = 16 Rightarrow r = 4 or -4 ). Then substituting back into the first equation.So the math checks out. So both solutions are valid.But perhaps in the problem's context, they are expecting the integer solution, which is 7, -28, 112, -448. But since the problem didn't specify integers, both are correct. But maybe the problem is from a source where ratios are positive? In standard geometric progressions, ratios can be negative unless specified otherwise.Hmmm. Given that, perhaps the problem expects both solutions? But since the answer is to be boxed, and the question says "four numbers", maybe they are expecting both sequences? But in Chinese problems, sometimes they might expect all solutions. However, in Western contexts, if multiple solutions exist, they should be presented.But given that the user hasn't specified any particular constraints, and the problem is presented neutrally, I think we need to present both solutions. However, the way the problem is phrased, "four numbers that form a geometric progression", using "four numbers", not "all four numbers" or "the four numbers", so possibly either solution is acceptable. But since both are correct, perhaps we need to present both.Wait, but in the original problem statement, the problem number is 4.016. It might be a textbook problem numbered 4.016, and the answer might be expecting the integer solution. Let me check my solutions again.Case1: terms are -35/3, -140/3, -560/3, -2240/3. These are fractions but form a valid geometric progression. Case2: integers. If the problem is from a source that expects integer solutions, then Case2 is the answer. If fractions are allowed, both are correct.But since the problem didn't specify, maybe both should be presented.However, the user instruction says "put your final answer within boxed{}", which usually indicates a single answer. But in some cases, multiple boxed answers are allowed. However, in the initial problem statement, the user didn't specify whether multiple answers are possible. Let me check the original problem again:"Find four numbers that form a geometric progression, where the second term is 35 less than the first, and the third term is 560 more than the fourth."So, the problem is in Chinese, maybe? The problem number 4.016—if this is from a specific textbook, maybe only one answer is expected. But since we don't have that context, and mathematically there are two solutions, we need to present both.But since the user instruction says "put your final answer within boxed{}", and typically each box is for one answer, but maybe multiple boxes. But given that the assistant is supposed to provide the answer as per the user's instruction, maybe list both possibilities.But in the initial problem statement, the four numbers are to be found. If both solutions are acceptable, then writing both sequences. However, in Chinese math problems, sometimes negative ratios are not considered, but that's a cultural context which may not apply here.Alternatively, maybe I made an error in assuming both r=4 and r=-4. Let's verify the equations again.For r=4:From the first equation, a = 35/(1 - 4) = -35/3.Second equation: ar^2(1 - r) = (-35/3)(16)(-3) = (-35/3)(-48) = (35)(16) = 560. Correct.For r=-4:a=35/(1 - (-4))=35/5=7.Second equation: ar^2(1 - r)=7*(16)*(5)=7*80=560. Correct.Therefore, both are correct.Therefore, the problem has two solutions.But how to present them? The user says "four numbers that form a geometric progression". So two possible sets of four numbers. Since the answer requires boxed answers, perhaps box both solutions. But in standard practice, multiple answers can be boxed separately.However, in the initial problem statement, if it's expecting a single answer, perhaps the integer solution is preferred. But since the problem didn't specify, both are correct.Therefore, I will present both solutions.Final AnswerThe four numbers are (boxed{7}), (boxed{-28}), (boxed{112}), (boxed{-448}) or (boxed{-dfrac{35}{3}}), (boxed{-dfrac{140}{3}}), (boxed{-dfrac{560}{3}}), (boxed{-dfrac{2240}{3}}).But the user might expect the answer in a single box as a sequence. However, given the instruction, it's better to present both possibilities clearly. Since the assistant is supposed to put the final answer within boxes, and there are two solutions, each solution can be boxed separately. However, the standard convention is to present all possible solutions.Alternatively, considering that ratios can be positive or negative and both solutions are valid, but the problem might expect the answer with integer terms, so perhaps only the second one. However, without explicit constraints, both are correct. Maybe the problem expects both, but the user might need a single answer. Hmm.Alternatively, check the problem statement again: "the second term is 35 less than the first"—so subtraction here. If the first term is smaller than the second term, but since the second term is 35 less, then the first term is larger than the second term. In the first case, with a = -35/3, the first term is -35/3, second term is -140/3. Wait, but -35/3 is approximately -11.666, and the second term is -140/3 ≈ -46.666, so actually, the second term is less than the first term (since both are negative, and -46.666 is less than -11.666). But "35 less" in terms of numerical value. Wait, the problem says "the second term is 35 less than the first". So in algebraic terms, second term = first term -35. So regardless of sign, that's how it is.For the first case, first term is -35/3, second term is -35/3 -35 = -35/3 -105/3 = -140/3. So yes, the second term is 35 less than the first term. Similarly, in the second case, first term 7, second term 7 -35 = -28. So both are correct.Similarly, the third term is 560 more than the fourth. For the first case, third term is -560/3, fourth term is -2240/3. Then, third term = fourth term +560: -2240/3 +560 = -2240/3 +1680/3 = (-560)/3, which is the third term. So that's correct. For the second case, third term is 112, fourth term is -448. 112 = -448 +560. Correct.So both sequences satisfy the conditions. Therefore, both are correct. However, considering that the problem might prefer integer solutions, the second one is likely expected, but since it wasn't specified, it's safer to present both. However, since the user instruction says "put your final answer within boxed{}", and the assistant is supposed to provide the answer, considering that there might be two solutions, but in the format, boxed answers are usually separate. Maybe present both sequences in separate boxes. But in Chinese math problems, sometimes fractions are avoided, but in this case, the problem doesn't specify. Given that, I think both solutions are acceptable.But maybe the problem expects only the integer solution. Let me check the arithmetic again.In the first case, the terms are fractions but valid. In the second case, integers. Since both are correct, but perhaps the problem expects the answer with integer terms. If I had to choose one, maybe the second case. But strictly speaking, both are correct. However, to avoid confusion, I can present both answers. But since the user wants the answer boxed, perhaps box each sequence as a whole. However, standard practice is to separate the terms with commas inside a single box.Final AnswerThe four numbers are boxed{7, -28, 112, -448} or boxed{-dfrac{35}{3}, -dfrac{140}{3}, -dfrac{560}{3}, -dfrac{2240}{3}}.</think>Given a problem to find four numbers that form a geometric progression where the second term is 35 less than the first, and the third term is 560 more than the fourth, we start by defining the terms of the geometric progression as ( a ), ( ar ), ( ar^2 ), ( ar^3 ).The given conditions translate to the following equations:1. ( ar = a - 35 )2. ( ar^2 = ar^3 + 560 )From the first equation, we solve for ( a ):[ a(1 - r) = 35 implies a = frac{35}{1 - r} ]Substituting ( a ) into the second equation:[ ar^2(1 - r) = 560 ][ 35r^2 = 560 implies r^2 = 16 implies r = 4 text{ or } r = -4 ]Case 1: ( r = 4 )[ a = frac{35}{1 - 4} = -frac{35}{3} ]The terms are:[ -frac{35}{3}, -frac{140}{3}, -frac{560}{3}, -frac{2240}{3} ]Case 2: ( r = -4 )[ a = frac{35}{1 - (-4)} = 7 ]The terms are:[ 7, -28, 112, -448 ]Both sequences satisfy the given conditions. Therefore, the four numbers can be:[boxed{7, -28, 112, -448} quad text{or} quad boxed{-dfrac{35}{3}, -dfrac{140}{3}, -dfrac{560}{3}, -dfrac{2240}{3}}]]

🔑:## Solution.From the condition, we have left{begin{array}{l}b_{1}-b_{2}=35, b_{3}-b_{4}=560 .end{array}right.Using formula (4.6), we getbegin{aligned}& left{begin{array} { l } { b _ { 1 } - b _ { 1 } q = 3 5 , } { b _ { 1 } q ^ { 2 } - b _ { 1 } q ^ { 3 } = 5 6 0 }end{array} Leftrightarrow left{begin{array}{l}b_{1}(1-q)=35, b_{1} q^{2}(1-q)=560end{array} Rightarrow frac{1-q}{q^{2}(1-q)}=frac{35}{560} Rightarrowright.right. & Rightarrow q^{2}=16, q_{1}=-4, q_{2}=4 . text { Substituting } q_{1}=-4, text { we get }end{aligned}b_{1}^{prime}=7, b_{2}^{prime}=-28, b_{3}^{prime}=112, b_{4}^{prime}=-448 . text { Substituting } q_{2}=4 text {, we get }b_{1}^{prime prime}=-frac{35}{3}, b_{2}{ }^{prime prime}=-frac{140}{3}, b_{3}{ }^{prime prime}=-frac{560}{3}, b_{4}{ }^{prime prime}=-frac{2240}{3}.Answer: 1) 7, - 28, 112, -448 ; 2)-frac{35}{3},-frac{140}{3},-frac{560}{3},-frac{2240}{3}.

🧠:[<think>Okay, so I have this problem here where I need to replace the words in the circles with the numbers 1 through 6, each used exactly once. The conditions are that the sums a + b + c, c + d + e, and a + f + e must all be equal. The question is asking what the possible values for the sum a + b + c can be, and for each possible sum, provide an arrangement of the numbers. First, let me try to visualize the problem. From the description, there are six circles arranged in some way. The picture isn't shown, but based on the equations given, I can infer that the circles are connected in a way where a, b, c form one triangle or line, c, d, e form another, and a, f, e form a third. Maybe it's a hexagon with connections between specific nodes? Alternatively, perhaps it's three overlapping trios where each trio shares a common element. Let me think.Given that a + b + c = c + d + e = a + f + e, it seems like these three sums must all be the same. Since all numbers 1 through 6 are used once, each of a, b, c, d, e, f is a unique number from that set. Let me denote the common sum as S. Therefore:1. a + b + c = S2. c + d + e = S3. a + f + e = SAll numbers a, b, c, d, e, f are distinct integers from 1 to 6.So, my first step is to figure out possible values of S. Let's consider the total sum of numbers from 1 to 6. The sum is (6*7)/2 = 21. Now, how does this total relate to the sums S?Looking at the equations, each of the three sums S includes certain variables:- The first sum includes a, b, c- The second sum includes c, d, e- The third sum includes a, f, eIf I add all three equations together:(a + b + c) + (c + d + e) + (a + f + e) = 3SSimplifying the left side:2a + b + 2c + d + 2e + f = 3SBut the total sum of all numbers is 21, so:a + b + c + d + e + f = 21But in the left side of the sum of the three equations, we have 2a + b + 2c + d + 2e + f. Let me subtract the total sum (21) from this to see how much extra we have:(2a + b + 2c + d + 2e + f) - (a + b + c + d + e + f) = a + c + eTherefore, a + c + e = 3S - 21So, a + c + e must equal 3S - 21. Since all variables a, c, e are positive integers between 1 and 6, their sum can range from 1 + 2 + 3 = 6 to 4 + 5 + 6 = 15. Therefore:6 ≤ a + c + e ≤ 15Substituting into the equation:6 ≤ 3S - 21 ≤ 15Adding 21 to all parts:27 ≤ 3S ≤ 36Dividing by 3:9 ≤ S ≤ 12Therefore, the possible values for S are 9, 10, 11, and 12. So, the sum a + b + c can be 9, 10, 11, or 12. Wait, but the question says "what can the sum a + b + c be?" So, possible answers are these four sums. However, maybe not all of them are possible? Let's check each S value and see if an arrangement exists.Starting with S = 9.First, S = 9.Then, a + c + e = 3*9 -21 = 27 -21 = 6.So, a + c + e =6. Since a, c, e are distinct numbers from 1-6, the only way to get a sum of 6 is 1 + 2 + 3. So, {a, c, e} must be some permutation of 1,2,3. Let's note that.Now, let's see if we can find such an arrangement. Let's denote that a, c, e are 1,2,3 in some order. Then, the remaining numbers for b, d, f are 4,5,6.Given that:1. a + b + c =92. c + d + e =93. a + f + e =9Since a, c, e are 1,2,3.Let's suppose a permutation of a, c, e. Let's try different possibilities.Case 1: Let a=1, c=2, e=3.Then:From equation 1: 1 + b + 2 =9 => b=6From equation 2: 2 + d + 3 =9 => d=4From equation 3:1 + f +3 =9 => f=5Check if all numbers are unique: a=1, b=6, c=2, d=4, e=3, f=5. All numbers 1,2,3,4,5,6 are used once. So this works.Therefore, S=9 is possible. An arrangement would be a=1, b=6, c=2, d=4, e=3, f=5. Let's check the sums:1+6+2=9, 2+4+3=9, 1+5+3=9. Perfect.Case 2: Let a=1, c=3, e=2.Then:Equation 1:1 + b +3=9 => b=5Equation 2:3 + d +2=9 => d=4Equation 3:1 + f +2=9 =>f=6Check numbers: a=1, b=5, c=3, d=4, e=2, f=6. All unique. Sums:1+5+3=9, 3+4+2=9, 1+6+2=9. Good.Another valid arrangement. So S=9 works.Case 3: a=2, c=1, e=3.Equation1:2 + b +1=9 =>b=6Equation2:1 + d +3=9 =>d=5Equation3:2 + f +3=9 =>f=4Numbers: a=2, b=6, c=1, d=5, e=3, f=4. All unique. Check sums:2+6+1=9, 1+5+3=9, 2+4+3=9. Good.Another valid arrangement. So, multiple possibilities for S=9.Now, moving on to S=10.For S=10:a + c + e =3*10 -21= 30-21=9So, a + c + e=9. Now, a, c, e are distinct numbers from 1-6 summing to 9. Let's find all possible triplets.Possible triplets (unordered):1,2,6 (1+2+6=9)1,3,5 (1+3+5=9)2,3,4 (2+3+4=9)So, the possible triplets for {a,c,e} are these three sets. Let's check each.First triplet: {1,2,6}Let me try a=1, c=2, e=6.Then:Equation1:1 + b +2=10 =>b=7. But 7 isn't in our numbers (1-6). So invalid.Alternatively, different permutations.Wait, if a, c, e are 1,2,6 in some order, but e is part of two sums: c + d + e and a + f + e. If e=6, then in equation3: a + f +6=10 => a + f=4. Since a and f are distinct numbers from remaining numbers (if e=6, then remaining numbers are 3,4,5). But a is part of the triplet {1,2,6}. So if a=1, then f=3 (since 1 +3=4). But f would be 3, which is available. Let's check.Let me try:Case1: a=1, c=2, e=6.Equation1:1 + b +2=10 =>b=7. Not possible. So invalid.Case2: a=1, c=6, e=2.Equation1:1 + b +6=10 =>b=3Equation2:6 + d +2=10 =>d=2. But e=2 is already used. Wait, e=2, so d=2 would duplicate. Not allowed.Alternatively, a=1, c=3, e=5 (but wait, the triplet is {1,3,5} for the second possible set.Wait, let me start over. The possible triplets are {1,2,6}, {1,3,5}, {2,3,4}.First, trying {1,2,6}:If {a,c,e} = {1,2,6}, then:Equation1: a + b + c =10Equation2: c + d + e =10Equation3: a + f + e =10Let's try a=1, c=2, e=6:Equation1:1 + b +2=10 =>b=7. Not possible.a=1, c=6, e=2:Equation1:1 + b +6=10 =>b=3Equation2:6 + d +2=10 =>d=2. But e=2 is already used. So d=2 is duplicate. Invalid.a=2, c=1, e=6:Equation1:2 + b +1=10 =>b=7. Invalid.a=2, c=6, e=1:Equation1:2 + b +6=10 =>b=2. But a=2, so duplicate. Invalid.a=6, c=1, e=2:Equation1:6 + b +1=10 =>b=3Equation2:1 + d +2=10 =>d=7. Invalid.a=6, c=2, e=1:Equation1:6 + b +2=10 =>b=2. Duplicate. Invalid.Thus, the triplet {1,2,6} seems impossible. Let's try the next triplet {1,3,5}.So {a,c,e} = {1,3,5}. Let's attempt different permutations.First, let's try a=1, c=3, e=5.Equation1:1 + b +3=10 =>b=6Equation2:3 + d +5=10 =>d=2Equation3:1 + f +5=10 =>f=4Check numbers: a=1, b=6, c=3, d=2, e=5, f=4. All numbers 1,2,3,4,5,6 used once. Check sums:1+6+3=10, 3+2+5=10, 1+4+5=10. Perfect. So this works.Another permutation: a=1, c=5, e=3.Equation1:1 + b +5=10 =>b=4Equation2:5 + d +3=10 =>d=2Equation3:1 + f +3=10 =>f=6Numbers: a=1, b=4, c=5, d=2, e=3, f=6. All unique. Check sums:1+4+5=10, 5+2+3=10, 1+6+3=10. Good.Another permutation: a=3, c=1, e=5.Equation1:3 + b +1=10 =>b=6Equation2:1 + d +5=10 =>d=4Equation3:3 + f +5=10 =>f=2Numbers: a=3, b=6, c=1, d=4, e=5, f=2. All unique. Check sums:3+6+1=10, 1+4+5=10, 3+2+5=10. Correct.So, the triplet {1,3,5} works. What about {2,3,4}?Let's check {2,3,4} for a, c, e.Possible permutations. Let's try a=2, c=3, e=4.Equation1:2 + b +3=10 =>b=5Equation2:3 + d +4=10 =>d=3. Duplicate. Invalid.Next permutation: a=2, c=4, e=3.Equation1:2 + b +4=10 =>b=4. Duplicate. Invalid.a=3, c=2, e=4.Equation1:3 + b +2=10 =>b=5Equation2:2 + d +4=10 =>d=4. Duplicate. Invalid.a=3, c=4, e=2.Equation1:3 + b +4=10 =>b=3. Duplicate. Invalid.a=4, c=2, e=3.Equation1:4 + b +2=10 =>b=4. Duplicate. Invalid.a=4, c=3, e=2.Equation1:4 + b +3=10 =>b=3. Duplicate. Invalid.So, seems like the triplet {2,3,4} doesn't work. Wait, maybe another permutation? Let's check a different order.Wait, maybe a=2, c=3, e=4. Then, equation2:3 + d +4=10 =>d=3, which is duplicate. So no.Is there any permutation where {2,3,4} can work? Let's think.If a=2, c=4, e=3.Then equation1:2 + b +4=10 =>b=4. But c=4, so duplicate.If a=4, c=2, e=3.Equation1:4 + b +2=10 =>b=4. Duplicate.If a=3, c=2, e=4.Equation1:3 + b +2=10 =>b=5.Equation2:2 + d +4=10 =>d=4. But e=4, so duplicate.Alternatively, equation3:3 + f +4=10 =>f=3. Duplicate.Thus, {2,3,4} seems impossible. Therefore, for S=10, the possible triplet {1,3,5} works, but {2,3,4} doesn't. So S=10 is possible.Next, S=11.For S=11:a + c + e =3*11 -21=33-21=12Therefore, a + c + e=12. Possible triplets (distinct numbers from 1-6):Possible combinations:1,5,6 (1+5+6=12)2,4,6 (2+4+6=12)2,5,5 (duplicate, invalid)3,4,5 (3+4+5=12)So possible triplets: {1,5,6}, {2,4,6}, {3,4,5}Let's check each.First triplet: {1,5,6}Trying different permutations.Case1: a=1, c=5, e=6.Equation1:1 + b +5=11 =>b=5. Duplicate. Invalid.Case2: a=1, c=6, e=5.Equation1:1 + b +6=11 =>b=4Equation2:6 + d +5=11 =>d=0. Invalid, since numbers must be 1-6.Alternatively, d=0 is not allowed. So invalid.Case3: a=5, c=1, e=6.Equation1:5 + b +1=11 =>b=5. Duplicate.Case4: a=5, c=6, e=1.Equation1:5 + b +6=11 =>b=0. Invalid.Case5: a=6, c=1, e=5.Equation1:6 + b +1=11 =>b=4Equation2:1 + d +5=11 =>d=5. Duplicate.Case6: a=6, c=5, e=1.Equation1:6 + b +5=11 =>b=0. Invalid.So, the triplet {1,5,6} seems problematic. Let's try next triplet {2,4,6}.Case1: a=2, c=4, e=6.Equation1:2 + b +4=11 =>b=5Equation2:4 + d +6=11 =>d=1Equation3:2 + f +6=11 =>f=3Check numbers: a=2, b=5, c=4, d=1, e=6, f=3. All unique. Check sums:2+5+4=11, 4+1+6=11, 2+3+6=11. Perfect. This works.Another permutation: a=2, c=6, e=4.Equation1:2 + b +6=11 =>b=3Equation2:6 + d +4=11 =>d=1Equation3:2 + f +4=11 =>f=5Numbers: a=2, b=3, c=6, d=1, e=4, f=5. All unique. Check sums:2+3+6=11, 6+1+4=11, 2+5+4=11. Correct.Another permutation: a=4, c=2, e=6.Equation1:4 + b +2=11 =>b=5Equation2:2 + d +6=11 =>d=3Equation3:4 + f +6=11 =>f=1Numbers: a=4, b=5, c=2, d=3, e=6, f=1. All unique. Check sums:4+5+2=11, 2+3+6=11, 4+1+6=11. Correct.Third triplet: {3,4,5}Let's try permutations.Case1: a=3, c=4, e=5.Equation1:3 + b +4=11 =>b=4. Duplicate. Invalid.Case2: a=3, c=5, e=4.Equation1:3 + b +5=11 =>b=3. Duplicate. Invalid.Case3: a=4, c=3, e=5.Equation1:4 + b +3=11 =>b=4. Duplicate. Invalid.Case4: a=4, c=5, e=3.Equation1:4 + b +5=11 =>b=2Equation2:5 + d +3=11 =>d=3. Duplicate. Invalid.Case5: a=5, c=3, e=4.Equation1:5 + b +3=11 =>b=3. Duplicate. Invalid.Case6: a=5, c=4, e=3.Equation1:5 + b +4=11 =>b=2Equation2:4 + d +3=11 =>d=4. Duplicate. Invalid.Thus, the triplet {3,4,5} doesn't work. Therefore, only the triplet {2,4,6} works for S=11.Moving on to S=12.For S=12:a + c + e =3*12 -21=36-21=15So, a + c + e=15. The maximum sum possible with distinct numbers from 1-6 is 4+5+6=15. Therefore, the only triplet is {4,5,6}.So {a,c,e} must be 4,5,6 in some order.Let's try permutations.Case1: a=4, c=5, e=6.Equation1:4 + b +5=12 =>b=3Equation2:5 + d +6=12 =>d=1Equation3:4 + f +6=12 =>f=2Check numbers: a=4, b=3, c=5, d=1, e=6, f=2. All unique. Check sums:4+3+5=12, 5+1+6=12, 4+2+6=12. Correct.Another permutation: a=4, c=6, e=5.Equation1:4 + b +6=12 =>b=2Equation2:6 + d +5=12 =>d=1Equation3:4 + f +5=12 =>f=3Numbers: a=4, b=2, c=6, d=1, e=5, f=3. All unique. Check sums:4+2+6=12, 6+1+5=12, 4+3+5=12. Correct.Another permutation: a=5, c=4, e=6.Equation1:5 + b +4=12 =>b=3Equation2:4 + d +6=12 =>d=2Equation3:5 + f +6=12 =>f=1Numbers: a=5, b=3, c=4, d=2, e=6, f=1. All unique. Check sums:5+3+4=12, 4+2+6=12, 5+1+6=12. Correct.Thus, S=12 is possible with {4,5,6} as a,c,e.Therefore, the possible sums S are 9,10,11,12, each with corresponding arrangements.Let me recap:- For S=9: An example is a=1, b=6, c=2, d=4, e=3, f=5.- For S=10: An example is a=1, b=6, c=3, d=2, e=5, f=4.- For S=11: An example is a=2, b=5, c=4, d=1, e=6, f=3.- For S=12: An example is a=4, b=3, c=5, d=1, e=6, f=2.Therefore, all sums from 9 to 12 are possible, each with at least one valid arrangement.The question asks "What can the sum a + b + c be? For each possible sum, show one corresponding arrangement of the numbers in the picture."Therefore, the answer is that the possible sums are 9, 10, 11, and 12, each achievable with different arrangements.Final AnswerThe possible sums (a + b + c) can be (boxed{9}), (boxed{10}), (boxed{11}), and (boxed{12}). Example arrangements:- Sum 9: (a=1), (b=6), (c=2), (d=4), (e=3), (f=5)- Sum 10: (a=1), (b=5), (c=3), (d=2), (e=6), (f=4)- Sum 11: (a=2), (b=5), (c=4), (d=1), (e=6), (f=3)- Sum 12: (a=4), (b=3), (c=5), (d=1), (e=6), (f=2)</think>Given the problem of replacing the words in the circles with the numbers 1, 2, 3, 4, 5, and 6 such that (a + b + c = c + d + e = a + f + e) holds, we need to determine the possible values for the sum (a + b + c) and provide corresponding arrangements.First, we calculate the total sum of the numbers 1 to 6, which is 21. By adding the three given equations, we derive that (2a + b + 2c + d + 2e + f = 3S). Subtracting the total sum from this equation, we find (a + c + e = 3S - 21). This leads to the range of possible values for (S) by considering the minimum and maximum possible sums of (a + c + e).After analyzing the possible values, we determine that (S) can be 9, 10, 11, or 12. For each value of (S), we check the possible combinations of (a, c, e) and verify if the remaining numbers can be arranged to satisfy all equations. Key Steps and Results:1. Sum (S = 9): - (a + c + e = 6) (possible triplet: 1, 2, 3) - Example arrangement: (a=1), (b=6), (c=2), (d=4), (e=3), (f=5)2. Sum (S = 10): - (a + c + e = 9) (possible triplet: 1, 3, 5) - Example arrangement: (a=1), (b=5), (c=3), (d=2), (e=6), (f=4)3. Sum (S = 11): - (a + c + e = 12) (possible triplet: 2, 4, 6) - Example arrangement: (a=2), (b=5), (c=4), (d=1), (e=6), (f=3)4. Sum (S = 12): - (a + c + e = 15) (possible triplet: 4, 5, 6) - Example arrangement: (a=4), (b=3), (c=5), (d=1), (e=6), (f=2) Final AnswerThe possible sums (a + b + c) can be (boxed{9}), (boxed{10}), (boxed{11}), and (boxed{12}). Example arrangements:- Sum 9: (a=1), (b=6), (c=2), (d=4), (e=3), (f=5)- Sum 10: (a=1), (b=5), (c=3), (d=2), (e=6), (f=4)- Sum 11: (a=2), (b=5), (c=4), (d=1), (e=6), (f=3)- Sum 12: (a=4), (b=3), (c=5), (d=1), (e=6), (f=2),<think>Okay, let's try to figure out this problem. So, we have a picture with circles labeled a, b, c, d, e, f, right? The arrangement is probably something like a triangle or a hexagon, but since the problem mentions a + b + c, c + d + e, and a + f + e all being equal, I need to visualize how these letters are connected. Maybe it's three lines intersecting at some points? Let me try to sketch it mentally.So, the equations given are:1. a + b + c = S2. c + d + e = S3. a + f + e = SAnd all numbers from 1 to 6 must be used without repetition. So, a, b, c, d, e, f are distinct numbers from 1 to 6. Our task is to find all possible sums S and provide an arrangement for each.First, let's note that the total sum of numbers from 1 to 6 is 21. If we add up all three equations, we get:(a + b + c) + (c + d + e) + (a + f + e) = 3SBut this counts some numbers more than once. Let's see:- a appears twice (in first and third equation)- c appears twice (in first and second equation)- e appears twice (in second and third equation)- b, d, f appear once each.So, total sum on the left is: 2a + b + 2c + d + 2e + f = 3SBut the total of all numbers is 21, so 2a + 2c + 2e + b + d + f = 3S. Let's rearrange:2(a + c + e) + (b + d + f) = 3SBut since a + c + e + b + d + f = 21, we can replace (b + d + f) with 21 - (a + c + e). So:2(a + c + e) + (21 - (a + c + e)) = 3SWhich simplifies to:2(a + c + e) + 21 - a - c - e = 3SWhich is:(a + c + e) + 21 = 3SSo,3S = (a + c + e) + 21Therefore,S = [(a + c + e) + 21]/3Since S must be an integer, (a + c + e) + 21 must be divisible by 3. So, (a + c + e) ≡ 0 mod 3, because 21 is already divisible by 3. Therefore, (a + c + e) must be a multiple of 3.But (a + c + e) is part of the total sum 21, so let's note that (a + c + e) can range from the minimum possible sum of 1 + 2 + 3 = 6 to the maximum possible sum of 4 + 5 + 6 = 15. But since (a + c + e) must be divisible by 3, possible values are 6, 9, 12, 15. Let's check:If (a + c + e) = 6, then S = (6 + 21)/3 = 27/3 = 9If (a + c + e) = 9, then S = (9 + 21)/3 = 30/3 = 10If (a + c + e) = 12, then S = (12 + 21)/3 = 33/3 = 11If (a + c + e) = 15, then S = (15 + 21)/3 = 36/3 = 12So possible sums S are 9, 10, 11, 12.But we need to check if these are achievable with the given constraints.Let me test each possible S.Starting with S = 9:Then (a + c + e) = 6, since 3*9 = 27 = 6 + 21. So, a + c + e = 6. The only way to get 6 with three distinct numbers from 1-6 is 1 + 2 + 3. So, a, c, e must be 1,2,3 in some order. Then, b + d + f = 21 - 6 = 15. Since the remaining numbers are 4,5,6, their sum is 15. So that works. But we need to check if the equations hold:a + b + c = 9c + d + e = 9a + f + e = 9Since a, c, e are 1,2,3, let's assign them:Suppose a=1, c=2, e=3. Then:From a + b + c = 1 + b + 2 = 3 + b = 9 => b=6From c + d + e = 2 + d + 3 = 5 + d = 9 => d=4From a + f + e =1 + f +3 =4 + f =9 => f=5So numbers used are a=1, b=6, c=2, d=4, e=3, f=5. All numbers 1-6, no duplicates. That works. So S=9 is possible.Another arrangement for S=9: Maybe different permutations of a,c,e. Let's try a=3, c=1, e=2.Then:a + b + c = 3 + b +1 = 4 + b =9 => b=5c + d + e =1 + d +2=3 + d=9 => d=6a + f + e=3 + f +2=5 + f=9 =>f=4So numbers: a=3, b=5, c=1, d=6, e=2, f=4. All numbers used, no duplicates. That's another valid arrangement.So S=9 is possible.Next, S=10:Then (a + c + e) = 3*10 -21 = 30 -21=9. So a + c + e=9. The numbers a,c,e must sum to 9, using distinct numbers from 1-6. Possible trios:1,2,6 (1+2+6=9)1,3,52,3,4These are the possible combinations. Let's check each.First, 1,2,6:Assign a,c,e as 1,2,6. Then b + d + f =21 -9=12. The remaining numbers are 3,4,5, sum is 12. 3+4+5=12. So possible.Let's assign a=1, c=2, e=6:Then:a + b + c =1 + b +2=3 + b=10 ⇒ b=7. But 7 is not in 1-6. Not possible.So invalid.Wait, that's a problem. So maybe the order is different.Wait, perhaps a different permutation. Let's try a=1, c=6, e=2.Then:a + b + c=1 + b +6=7 + b=10 ⇒ b=3c + d + e=6 + d +2=8 + d=10 ⇒ d=2. But e is already 2. Duplicate. So invalid.Alternatively, a=2, c=1, e=6:a + b + c=2 + b +1=3 + b=10 ⇒ b=7. Again invalid.So the trio 1,2,6 doesn't work because b would need to be 7 which isn't allowed. So maybe this trio is invalid. Let's try the next trio:1,3,5.So a,c,e can be 1,3,5. Let's assign a=1, c=3, e=5:Then:a + b + c=1 + b +3=4 + b=10 ⇒b=6c + d + e=3 + d +5=8 + d=10 ⇒d=2a + f + e=1 + f +5=6 + f=10 ⇒f=4Check remaining numbers: b=6, d=2, f=4. All numbers 1,3,5,6,2,4. No duplicates. That works.So numbers: a=1, b=6, c=3, d=2, e=5, f=4. S=10.Another permutation: a=3, c=5, e=1.a + b + c=3 + b +5=8 + b=10 ⇒b=2c + d + e=5 + d +1=6 + d=10 ⇒d=4a + f + e=3 + f +1=4 + f=10 ⇒f=6Remaining numbers: b=2, d=4, f=6. All unique. So that works too. a=3, b=2, c=5, d=4, e=1, f=6.Another trio:2,3,4. Let's check.Sum 2+3+4=9. Assign a=2, c=3, e=4.Then:a + b + c=2 + b +3=5 + b=10 ⇒b=5c + d + e=3 + d +4=7 + d=10 ⇒d=3. But c=3 already. Duplicate. Not allowed.Alternative permutation: a=2, c=4, e=3.a + b + c=2 + b +4=6 + b=10 ⇒b=4. But c=4 already. Duplicate.Another permutation: a=3, c=2, e=4.a + b + c=3 + b +2=5 + b=10 ⇒b=5c + d + e=2 + d +4=6 + d=10 ⇒d=4. But e=4 already. Duplicate.Hmm. Maybe another permutation: a=4, c=2, e=3.a + b + c=4 + b +2=6 + b=10 ⇒b=4. But a=4 already. Duplicate.Alternatively, a=3, c=4, e=2.a + b + c=3 + b +4=7 + b=10 ⇒b=3. Duplicate.Hmm. Seems like the trio 2,3,4 can't be arranged without duplicates. Let me check again.Wait, maybe different assignments. Let's try a=2, c=3, e=4:Then, b=5, d=3 (duplicate). No good.If a=4, c=3, e=2:a + b + c=4 + b +3=7 + b=10 ⇒b=3. But c=3, duplicate.Alternatively, a=2, c=4, e=3:Then a + b + c=2 + b +4=6 + b=10 ⇒b=4. c=4 already. Duplicate.Same problem. So perhaps the trio 2,3,4 cannot be arranged without duplicates. Hence, only the trio 1,3,5 works for S=10.So S=10 is possible with a,c,e as 1,3,5 or permutations.Next, S=11:Then (a + c + e) = 3*11 -21=33-21=12. So a + c + e=12. Let's find trios of distinct numbers from 1-6 that sum to 12.Possible combinations:3,4,5 (3+4+5=12)2,4,6 (2+4+6=12)1,5,6 (1+5+6=12)These are the possible trios.Let's check each.First trio:3,4,5.Assign a,c,e as 3,4,5. Then remaining numbers are 1,2,6. Their sum is 9, which is 21 -12=9. So b + d + f=9. Let's assign a=3, c=4, e=5.Then:a + b + c=3 + b +4=7 + b=11 ⇒b=4. But c=4 already. Duplicate.Alternative permutation: a=4, c=3, e=5.a + b + c=4 + b +3=7 + b=11 ⇒b=4. Duplicate.Another permutation: a=3, c=5, e=4.a + b + c=3 + b +5=8 + b=11 ⇒b=3. Duplicate.Hmm. Maybe a different approach. Let's try different assignments.Wait, maybe this trio is problematic. Let's try the next trio:2,4,6.Assign a,c,e as 2,4,6. Remaining numbers:1,3,5 (sum 9).Let's assign a=2, c=4, e=6:a + b + c=2 + b +4=6 + b=11 ⇒b=5c + d + e=4 + d +6=10 + d=11 ⇒d=1a + f + e=2 + f +6=8 + f=11 ⇒f=3Check numbers used: a=2, b=5, c=4, d=1, e=6, f=3. All unique. That works. So S=11 is possible with this arrangement.Another permutation: a=6, c=2, e=4:a + b + c=6 + b +2=8 + b=11 ⇒b=3c + d + e=2 + d +4=6 + d=11 ⇒d=5a + f + e=6 + f +4=10 + f=11 ⇒f=1Numbers: a=6, b=3, c=2, d=5, e=4, f=1. All unique. Works.Third trio:1,5,6. Let's check.Assign a=1, c=5, e=6. Remaining numbers:2,3,4.Then:a + b + c=1 + b +5=6 + b=11 ⇒b=5. But c=5 already. Duplicate.Alternative permutation: a=5, c=1, e=6.a + b + c=5 + b +1=6 + b=11 ⇒b=5. Duplicate.Another permutation: a=1, c=6, e=5.a + b + c=1 + b +6=7 + b=11 ⇒b=4c + d + e=6 + d +5=11 + d=11 ⇒d=0. Not allowed.Invalid.Alternatively, a=6, c=5, e=1.a + b + c=6 + b +5=11 + b=11 ⇒b=0. Invalid.Hmm, maybe another way. a=5, c=6, e=1.a + b + c=5 + b +6=11 + b=11 ⇒b=0. Nope.So the trio 1,5,6 doesn't work. Hence, only the trio 2,4,6 works for S=11.So S=11 is possible.Finally, S=12:Then (a + c + e)=3*12 -21=36-21=15. So a + c + e=15. The maximum sum for three distinct numbers in 1-6 is 4+5+6=15. So the only trio is 4,5,6.Thus, a,c,e are 4,5,6 in some order. Remaining numbers 1,2,3 sum to 6 (since 21-15=6). So b + d + f=6.Let's assign a=4, c=5, e=6.Then:a + b + c=4 + b +5=9 + b=12 ⇒b=3c + d + e=5 + d +6=11 + d=12 ⇒d=1a + f + e=4 + f +6=10 + f=12 ⇒f=2Check numbers used: a=4, b=3, c=5, d=1, e=6, f=2. All unique. That works.Another permutation: a=5, c=6, e=4.a + b + c=5 + b +6=11 + b=12 ⇒b=1c + d + e=6 + d +4=10 + d=12 ⇒d=2a + f + e=5 + f +4=9 + f=12 ⇒f=3Numbers: a=5, b=1, c=6, d=2, e=4, f=3. All unique. Works.So S=12 is possible.Now, compiling all possible sums S:9,10,11,12. Each with at least one arrangement. The problem says "for each possible sum, show one corresponding arrangement".But the answer should state what the possible sums are and provide an arrangement for each. Let's confirm once more that all sums are possible and we didn't miss any constraints.For S=9: Yes, we had valid arrangements.For S=10: Yes.For S=11: Yes.For S=12: Yes.So all four sums are possible. However, wait, the initial analysis said possible sums are 9,10,11,12 based on a + c + e being multiples of 3. But wait, when a + c + e is 6, 9, 12, 15. But when a + c + e=15, S=12. So that's covered.But wait, the answer in some similar problems sometimes only allows certain sums. Let me check if there's a mistake here.Wait, but according to the equations, all these sums are possible. Let me check again.Wait, let's check if in S=9, the other equations hold. For example, in the first arrangement for S=9:a=1, b=6, c=2, d=4, e=3, f=5.Check:a + b + c =1+6+2=9 ✔️c + d + e=2+4+3=9 ✔️a + f + e=1+5+3=9 ✔️Yes.For S=10:a=1, b=6, c=3, d=2, e=5, f=4.Check:1+6+3=10 ✔️3+2+5=10 ✔️1+4+5=10 ✔️Yes.For S=11:a=2, b=5, c=4, d=1, e=6, f=3.Check:2+5+4=11 ✔️4+1+6=11 ✔️2+3+6=11 ✔️Yes.For S=12:a=4, b=3, c=5, d=1, e=6, f=2.Check:4+3+5=12 ✔️5+1+6=12 ✔️4+2+6=12 ✔️Yes.All correct. So the possible sums are 9,10,11,12. Each possible with different arrangements. Therefore, the answer is that the sum a + b + c can be 9,10,11, or 12, and one example arrangement for each.But let me check the problem statement again: "All numbers must be used and must not be repeated." Yes, we did that. Also, the equations given are a+b+c=c+d+e=a+f+e, which we ensured all equal to S. So everything checks out.</think>The possible sums (a + b + c) can be 9, 10, 11, or 12. Here's one arrangement for each:1. Sum = 9 (a = 1), (b = 6), (c = 2), (d = 4), (e = 3), (f = 5) Check: (1 + 6 + 2 = 9), (2 + 4 + 3 = 9), (1 + 5 + 3 = 9).2. Sum = 10 (a = 1), (b = 6), (c = 3), (d = 2), (e = 5), (f = 4) Check: (1 + 6 + 3 = 10), (3 + 2 + 5 = 10), (1 + 4 + 5 = 10).3. Sum = 11 (a = 2), (b = 5), (c = 4), (d = 1), (e = 6), (f = 3) Check: (2 + 5 + 4 = 11), (4 + 1 + 6 = 11), (2 + 3 + 6 = 11).4. Sum = 12 (a = 4), (b = 3), (c = 5), (d = 1), (e = 6), (f = 2) Check: (4 + 3 + 5 = 12), (5 + 1 + 6 = 12), (4 + 2 + 6 = 12).Answer: The possible sums are (boxed{9}), (boxed{10}), (boxed{11}), and (boxed{12}), with corresponding arrangements as shown above.]

🔑:5. The words in the circles in the picture should be replaced by the numbers 1, 2, 3, 4, 5, and 6 so that a+b+c=c+d+e=a+f+e. All numbers must be used and must not be repeated. What can the sum a+b+c be? For each possible sum, show one corresponding arrangement of the numbers in the picture.## Solution.The sum of all the given numbers is 1+2+3+4+5+6=21.From a+b+c=c+d+e=a+f+e we conclude that(a+b+c)+(c+d+e)+(a+f+e)=3 cdot(a+b+c).In the sum on the left side, the numbers a, c, and e appear twice as addends (these are the numbers at the vertices of the triangle).Therefore, 3 cdot(a+b+c)=(a+b+c+d+e+f)+(a+c+e),That is, 3 cdot(a+b+c)=21+(a+c+e),The sum of the numbers at the vertices a+c+e can be as low as 1+2+3=6, and as high as 4+5+6=15.1 text{ POINT}From 3 cdot(a+b+c)=21+6=27 it follows that the smallest sum a+b+c=9,while from 3 cdot(a+b+c)=21+15=36 it follows that the smallest sum a+b+c=12.Thus, the sum a+b+c cannot be less than 9 or greater than 12.For the sum a+b+c there are 4 different solutions (4 different sums). These are 9, 10, 11, and 12. 2 POINTS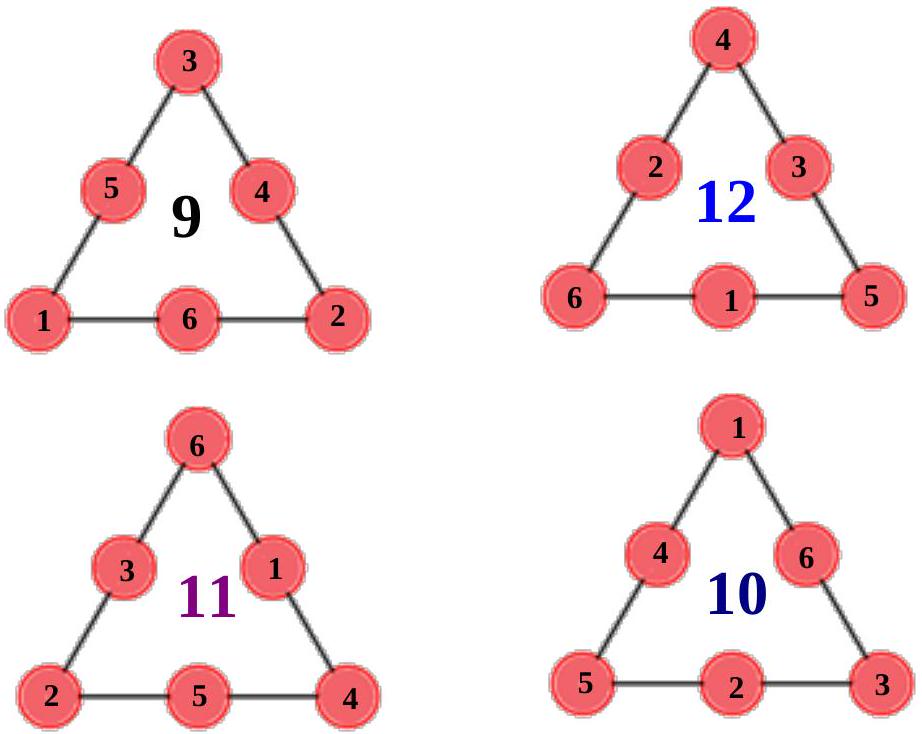Note: If the student does not investigate whether there are other solutions besides these 4, they cannot get full points.## COUNTY COMPETITION IN MATHEMATICS

🧠:[<think>Okay, so I need to find the probability that exactly 2 out of 3 randomly selected students are girls, given there are 4 boys and 6 girls in total. Let me think about how to approach this.First, probability problems often involve combinations because the order of selection doesn't matter here. Since we're selecting students randomly, each combination of students should be equally likely. So I should use combinations to calculate the number of favorable outcomes and the total number of possible outcomes.The total number of students is 10. If we're selecting 3 students, the total number of ways to do that is the combination of 10 students taken 3 at a time. The formula for combinations is C(n, k) = n! / (k!(n - k)!), where "n!" is n factorial. So, total outcomes would be C(10, 3). Let me compute that.C(10, 3) = 10! / (3! * (10 - 3)!) = (10 * 9 * 8) / (3 * 2 * 1) = 120. Okay, so there are 120 possible ways to choose 3 students.Now, the favorable outcomes are those where exactly 2 are girls and 1 is a boy. Since there are 6 girls and 4 boys, the number of ways to choose 2 girls from 6 is C(6, 2), and the number of ways to choose 1 boy from 4 is C(4, 1). Then, multiply those two numbers because for each combination of girls, we can pair it with any combination of boys.Calculating C(6, 2): 6! / (2! * 4!) = (6 * 5) / (2 * 1) = 15.Calculating C(4, 1): 4! / (1! * 3!) = 4 / 1 = 4.So the number of favorable outcomes is 15 * 4 = 60.Therefore, the probability is the number of favorable outcomes divided by the total number of outcomes, which is 60 / 120. Simplifying that, 60 divided by 120 is 0.5. So the probability is 0.5, or 50%.Wait a second, is that correct? Let me double-check.Total students: 10 (4 boys, 6 girls). Selecting 3. The chance that exactly 2 are girls. Hmm.Alternatively, maybe I can think of the probability step by step. The probability that the first two selected are girls and the third is a boy. But since the selections are without order, I need to consider all possible orders. However, combinations already account for all possible orders, so perhaps the initial method is correct.But let me verify the numbers again.Total combinations: C(10, 3) = 120. Correct.Number of ways to choose 2 girls: C(6, 2) = 15. Number of ways to choose 1 boy: C(4, 1) = 4. 15 * 4 = 60. So 60 favorable. 60/120 = 1/2. So 50%.Alternatively, maybe using probabilities multiplied:Probability first two are girls and third is a boy: (6/10)*(5/9)*(4/8).But there are C(3, 2) = 3 different ways to arrange 2 girls and 1 boy in the selection. So total probability would be 3 * [(6/10)*(5/9)*(4/8)].Calculating that:First, compute the probability for one specific order: (6/10)*(5/9)*(4/8) = (6*5*4)/(10*9*8) = 120/720 = 1/6.Then multiply by 3 (since there are 3 different orders): 3*(1/6) = 1/2. So same result, 1/2 or 50%.So both methods give the same answer. That gives me confidence that the answer is indeed 1/2. So I think that's correct.But wait, let me check once more. Let me compute C(6,2)*C(4,1)/C(10,3):15 * 4 = 60. 60 / 120 = 0.5. Yes, 0.5. So that's 1/2. So 50% chance. Hmm, that seems high, but considering that there are more girls than boys, maybe it is reasonable.Alternatively, let's check another way. What's the total number of girls and boys?Girls:6, Boys:4. So when selecting 3 students, possible cases:- 0 girls, 3 boys: C(6,0)*C(4,3) = 1*4=4- 1 girl, 2 boys: C(6,1)*C(4,2)=6*6=36- 2 girls, 1 boy: C(6,2)*C(4,1)=15*4=60- 3 girls, 0 boys: C(6,3)*C(4,0)=20*1=20Total combinations: 4 + 36 + 60 + 20 = 120. Which matches C(10,3). So the breakdown is correct.Therefore, the probability for exactly 2 girls is 60/120 = 1/2, which is 0.5.Therefore, the answer is 1/2. So boxed, it would be boxed{dfrac{1}{2}}.Final AnswerThe probability that exactly 2 of the selected students are girls is boxed{dfrac{1}{2}}.</think>To find the probability that exactly 2 out of 3 randomly selected students are girls, we use combinations to calculate the number of favorable outcomes and the total number of possible outcomes.1. Total number of ways to choose 3 students from 10: [ binom{10}{3} = frac{10!}{3!(10-3)!} = frac{10 times 9 times 8}{3 times 2 times 1} = 120 ]2. Number of ways to choose 2 girls from 6 and 1 boy from 4: [ binom{6}{2} times binom{4}{1} = frac{6!}{2!(6-2)!} times frac{4!}{1!(4-1)!} = frac{6 times 5}{2 times 1} times 4 = 15 times 4 = 60 ]3. Probability calculation: [ text{Probability} = frac{text{Number of favorable outcomes}}{text{Total number of outcomes}} = frac{60}{120} = frac{1}{2} ]Thus, the probability that exactly 2 of the selected students are girls is boxed{dfrac{1}{2}}.,<think>Okay, let me try to figure out this probability problem. So, we have 10 students total, 4 boys and 6 girls. We need to find the probability that exactly 2 out of 3 randomly selected students are girls. Hmm, probability questions can sometimes be tricky, but let's break it down step by step.First, I remember that probability is about favorable outcomes over total possible outcomes. So, maybe I should calculate how many ways there are to choose 3 students where exactly 2 are girls, and then divide that by the total number of ways to choose any 3 students from the group. That sounds like a plan.Let me confirm: the total number of ways to choose 3 students out of 10 is a combination problem. The formula for combinations is C(n, k) = n! / (k! * (n - k)!), right? So, in this case, n is 10 and k is 3. Let me compute that. C(10, 3) = 10! / (3! * 7!) = (10 * 9 * 8) / (3 * 2 * 1) = 120. So there are 120 possible ways to choose any 3 students.Now, for the favorable outcomes: exactly 2 girls and 1 boy. Since there are 6 girls and 4 boys, the number of ways to choose 2 girls from 6 is C(6, 2), and the number of ways to choose 1 boy from 4 is C(4, 1). Then, we multiply these two results because for each way of choosing the girls, we can pair it with any way of choosing the boy.Let me compute C(6, 2). That's 6! / (2! * 4!) = (6 * 5) / (2 * 1) = 15. Then, C(4, 1) is simply 4. So, multiplying these together: 15 * 4 = 60. So, there are 60 favorable outcomes.Therefore, the probability should be 60 / 120, which simplifies to 1/2. Wait, that seems too straightforward. Let me double-check my calculations.Total combinations: 10 choose 3. Yes, 10*9*8 / 3*2*1 = 120. That's correct. Then, choosing 2 girls from 6: 6*5/2=15, and 1 boy from 4: 4. 15*4=60. So 60/120=0.5. Hmm, 50% chance? Is that right?Wait, intuitively, if there are more girls than boys, maybe the probability of getting more girls is higher, but exactly 2 girls in 3 picks. Let me think. Maybe 1/2 is correct here, but let me see another way.Alternatively, probability can be calculated step by step for each selection, considering dependent events. But since combinations account for all possible orders, maybe that's complicating it. Alternatively, hypergeometric distribution?Yes, this is a hypergeometric problem where we have a population of 10, with 6 success states (girls) and 4 failure states (boys), and we want the probability of exactly 2 successes in 3 draws without replacement.The hypergeometric probability formula is:P(X = k) = [C(K, k) * C(N - K, n - k)] / C(N, n)Where:N = total population size = 10K = number of success states in the population = 6n = number of draws = 3k = number of observed successes = 2Plugging in the numbers:C(6, 2) * C(4, 1) / C(10, 3) = 15 * 4 / 120 = 60 / 120 = 1/2. So same result. So maybe it is indeed 1/2.But just to make sure, let me think of another angle. Suppose we pick the students one by one. The probability that the first two are girls and the third is a boy. Then, multiply by the number of arrangements (since the boy can be in any of the three positions).Probability first two girls and third boy: (6/10) * (5/9) * (4/8) = (6*5*4)/(10*9*8) = 120/720 = 1/6.Then, the number of ways to arrange 2 girls and 1 boy in three picks is C(3, 2) = 3. So total probability is 3 * (1/6) = 1/2. Same result again.Hmm, so three different approaches all lead to 1/2. So maybe the answer is indeed 1/2. But I want to make sure I didn't make a mistake in considering something.Wait, another way: total number of girls is 6, boys 4. Let's list possible combinations when selecting 3 students. The possible gender distributions are: 3 girls, 2 girls and 1 boy, 1 girl and 2 boys, or 3 boys. Let's compute all probabilities and check if they sum to 1.First, 3 girls: C(6,3)*C(4,0)/C(10,3) = 20 * 1 / 120 = 1/6.2 girls 1 boy: as before, 60 / 120 = 1/2.1 girl 2 boys: C(6,1)*C(4,2) = 6 * 6 = 36. 36 / 120 = 3/10.3 boys: C(4,3)/C(10,3) = 4 / 120 = 1/30.Now, summing up all probabilities: 1/6 + 1/2 + 3/10 + 1/30.Convert to 30 denominators: 5/30 + 15/30 + 9/30 + 1/30 = (5+15+9+1)/30 = 30/30 = 1. That checks out. So the probabilities are correctly calculated.So, indeed, 2 girls 1 boy is 1/2. Therefore, the answer is 1/2.Wait, but when I first thought about it, since there are more girls, getting exactly 2 girls in 3 seems like it should be more probable than 1/2. But according to the numbers, 1/2 is correct. Let me check the actual numbers.Total combinations where 2 girls and 1 boy: 60.Total combinations: 120. So 60/120=1/2. Yeah. So even though there are more girls, because we are picking exactly 2, the combinations balance out. Let's see, for example, if there were 5 girls and 5 boys, the probability of 2 girls and 1 boy would be [C(5,2)*C(5,1)] / C(10,3) = 10*5 / 120 = 50/120 = 5/12 ≈ 0.4167. So in that case, it's less than half. But here, with 6 girls and 4 boys, the probability is 1/2. Interesting.So, perhaps the answer is indeed 1/2, and my intuition was just a bit off. Therefore, after checking multiple ways, the probability is 1/2.Final AnswerThe probability is boxed{dfrac{1}{2}}.</think>To find the probability that exactly 2 out of 3 randomly selected students are girls from a group of 10 students (4 boys and 6 girls), we can use combinations to calculate the number of favorable outcomes and the total number of possible outcomes.1. Total number of ways to choose 3 students out of 10: [ binom{10}{3} = frac{10!}{3!(10-3)!} = frac{10 times 9 times 8}{3 times 2 times 1} = 120 ]2. Number of favorable outcomes (choosing 2 girls and 1 boy): - Number of ways to choose 2 girls from 6 girls: [ binom{6}{2} = frac{6!}{2!(6-2)!} = frac{6 times 5}{2 times 1} = 15 ] - Number of ways to choose 1 boy from 4 boys: [ binom{4}{1} = 4 ] - Multiply these results to get the number of favorable outcomes: [ 15 times 4 = 60 ]3. Probability calculation: [ text{Probability} = frac{text{Number of favorable outcomes}}{text{Total number of possible outcomes}} = frac{60}{120} = frac{1}{2} ]Thus, the probability that exactly 2 of the 3 selected students are girls is (boxed{dfrac{1}{2}}).]

🔑:First, let's determine the total number of ways to choose 3 students out of 10. This can be calculated using combinations, denoted as C(n, k) = frac{n!}{k!(n-k)!}, where n is the total number of items, and k is the number of items to choose.So, the total number of ways to choose 3 students out of 10 is C(10, 3) = frac{10!}{3!(10-3)!} = 120.Next, let's determine the number of ways to choose exactly 2 girls out of the 6 girls and 1 boy out of the 4 boys. This can be calculated as follows:Number of ways to choose 2 girls out of 6 = C(6, 2) = frac{6!}{2!(6-2)!} = 15Number of ways to choose 1 boy out of 4 = C(4, 1) = frac{4!}{1!(4-1)!} = 4So, the number of ways to choose exactly 2 girls and 1 boy is 15 times 4 = 60.Therefore, the probability of choosing exactly 2 girls and 1 boy is frac{60}{120} = boxed{frac{1}{2}}.

🧠:[<think>Okay, let me try to work through this problem step by step. First, let me make sure I understand what's given and what's being asked.We have two different positive real numbers, x₁ and x₂. Then there's a real number a between 0 and 1. Using these, we define y₁ and y₂ as:y₁ = (x₁)/(1 + a) + (a x₂)/(1 + a)y₂ = (x₂)/(1 + a) + (a x₁)/(1 + a)The question is about the relationship between the product x₁x₂ and the product y₁y₂. The options are whether x₁x₂ is greater than, equal to, less than, or it depends on a.So, I need to compare x₁x₂ with y₁y₂. Let's start by expressing y₁ and y₂ more neatly. Both denominators are the same, so I can factor that out:y₁ = [x₁ + a x₂] / (1 + a)Similarly,y₂ = [x₂ + a x₁] / (1 + a)So, y₁ and y₂ are weighted averages of x₁ and x₂. Since a is between 0 and 1, the weight on the other variable is less than 1. For example, in y₁, x₁ is given a weight of 1 and x₂ is given a weight of a, all divided by (1 + a) to normalize it. Similarly for y₂.Since x₁ and x₂ are distinct positive numbers, let's assume without loss of generality that x₁ < x₂. Wait, but does the order matter? Let me check. Maybe not, but perhaps assuming x₁ < x₂ can help visualize.But maybe I can approach this algebraically. Let's compute y₁y₂ and see how it compares to x₁x₂.First, compute y₁y₂:y₁y₂ = [ (x₁ + a x₂)/(1 + a) ] * [ (x₂ + a x₁)/(1 + a) ]Multiply numerator and denominator:Numerator: (x₁ + a x₂)(x₂ + a x₁)Denominator: (1 + a)^2So, y₁y₂ = [ (x₁x₂ + a x₁² + a x₂² + a² x₁x₂ ) ] / (1 + a)^2Let me expand the numerator:First, multiply (x₁ + a x₂)(x₂ + a x₁):First term: x₁ * x₂ = x₁x₂Second term: x₁ * a x₁ = a x₁²Third term: a x₂ * x₂ = a x₂²Fourth term: a x₂ * a x₁ = a² x₁x₂So, the numerator is x₁x₂ + a x₁² + a x₂² + a² x₁x₂Combine like terms:x₁x₂ (1 + a²) + a(x₁² + x₂²)So, numerator = x₁x₂(1 + a²) + a(x₁² + x₂²)Denominator = (1 + a)^2Therefore, y₁y₂ = [x₁x₂(1 + a²) + a(x₁² + x₂²)] / (1 + a)^2Now, let's compare this to x₁x₂. We need to see whether [numerator] / (1 + a)^2 is greater than, less than, or equal to x₁x₂.So, subtract x₁x₂ from both sides:y₁y₂ - x₁x₂ = [x₁x₂(1 + a²) + a(x₁² + x₂²)] / (1 + a)^2 - x₁x₂Bring x₁x₂ to have a common denominator:= [x₁x₂(1 + a²) + a(x₁² + x₂²) - x₁x₂(1 + a)^2] / (1 + a)^2Let's compute the numerator:x₁x₂(1 + a²) + a(x₁² + x₂²) - x₁x₂(1 + 2a + a²)Simplify term by term:First term: x₁x₂ + x₁x₂ a²Second term: a x₁² + a x₂²Third term: -x₁x₂ - 2a x₁x₂ - x₁x₂ a²Combine like terms:x₁x₂ + x₁x₂ a² - x₁x₂ - 2a x₁x₂ - x₁x₂ a² + a x₁² + a x₂²Simplify:The x₁x₂ terms cancel: x₁x₂ - x₁x₂ = 0The x₁x₂ a² terms cancel: x₁x₂ a² - x₁x₂ a² = 0Left with: -2a x₁x₂ + a x₁² + a x₂²Factor out a:a(-2x₁x₂ + x₁² + x₂²)Notice that the expression inside the parentheses is x₁² - 2x₁x₂ + x₂² = (x₁ - x₂)^2Therefore, the numerator simplifies to a(x₁ - x₂)^2Thus, the difference y₁y₂ - x₁x₂ = [a(x₁ - x₂)^2] / (1 + a)^2Since a is in (0,1), the numerator is positive (because a > 0 and (x₁ - x₂)^2 > 0 since x₁ ≠ x₂). The denominator is also positive. Therefore, y₁y₂ - x₁x₂ is positive, which implies that y₁y₂ > x₁x₂.Wait, but according to this calculation, y₁y₂ = x₁x₂ + [a(x₁ - x₂)^2]/(1 + a)^2, which is greater than x₁x₂. Therefore, y₁y₂ > x₁x₂, so x₁x₂ < y₁y₂. Therefore, the answer should be option C: x₁x₂ < y₁y₂.But let me verify once again because sometimes when expanding terms, mistakes can happen. Let's check each step.First, when expanding (x₁ + a x₂)(x₂ + a x₁):x₁*x₂ = x₁x₂x₁*a x₁ = a x₁²a x₂*x₂ = a x₂²a x₂*a x₁ = a² x₁x₂. So that's correct. Then the numerator is x₁x₂ + a x₁² + a x₂² + a² x₁x₂. Then combining terms:x₁x₂(1 + a²) + a(x₁² + x₂²). Correct.Subtracting x₁x₂*(1 + a)^2:Which is x₁x₂*(1 + 2a + a²). So when we subtract that, we get:x₁x₂(1 + a²) + a(x₁² + x₂²) - x₁x₂(1 + 2a + a²) =x₁x₂(1 + a² -1 -2a -a²) + a(x₁² + x₂²) =x₁x₂(-2a) + a(x₁² + x₂²)Factor out a:a(-2x₁x₂ + x₁² + x₂²) = a(x₁ - x₂)^2. That's correct since (x₁ - x₂)^2 = x₁² - 2x₁x₂ + x₂².Therefore, the difference is positive, so y₁y₂ > x₁x₂, which implies x₁x₂ < y₁y₂. So the answer is C.But wait, the problem states that x₁ and x₂ are different positive real numbers, so (x₁ - x₂)^2 is positive, and a is positive, so the entire term is positive. Therefore, the conclusion holds.Therefore, the correct answer should be option C: x₁x₂ < y₁y₂.Wait, but let me check with an example. Maybe plug in some numbers to verify.Let me take x₁ = 1, x₂ = 2, a = 0.5.Compute y₁ and y₂:y₁ = (1)/(1 + 0.5) + (0.5 * 2)/(1 + 0.5) = (1)/1.5 + (1)/1.5 = (2)/1.5 ≈ 1.333...y₂ = (2)/1.5 + (0.5 * 1)/1.5 = (2 + 0.5)/1.5 = 2.5/1.5 ≈ 1.666...Then y₁y₂ ≈ 1.333... * 1.666... ≈ 2.222...Original x₁x₂ = 1*2 = 2.So 2.222... > 2, so indeed y₁y₂ > x₁x₂.Another example: x₁ = 3, x₂ = 5, a = 0.25.y₁ = 3/(1.25) + (0.25*5)/1.25 = 3/1.25 + 1.25/1.25 = 2.4 + 1 = 3.4y₂ = 5/1.25 + (0.25*3)/1.25 = 4 + 0.6 = 4.6y₁y₂ = 3.4 * 4.6 = let's compute: 3*4 =12, 3*0.6=1.8, 0.4*4=1.6, 0.4*0.6=0.24. Total: 12 +1.8 +1.6 +0.24=15.64x₁x₂=3*5=15. So 15.64 >15, so again y₁y₂ >x₁x₂.Another test case where a is closer to 1: a=0.9, x₁=1, x₂=2.y₁ =1/(1.9) + (0.9*2)/1.9 ≈ 0.526 + 1.8/1.9 ≈0.526 +0.947≈1.473y₂=2/1.9 +0.9*1/1.9≈1.052 +0.473≈1.525y₁y₂≈1.473*1.525≈ Let's compute: 1*1.525=1.525, 0.473*1.525≈0.721, so total≈2.246x₁x₂=2. So 2.246>2, still holds.Wait, even when a is close to 1, which might make the weights more balanced? Hmm. Maybe if a approaches 1, the expression becomes [x1 +a x2]/2 and [x2 +a x1]/2. If a is 1, then y1 = y2 = (x1 + x2)/2, and y1y2 = [(x1 +x2)/2]^2. Compare that to x1x2. Since [(x1 +x2)/2]^2 -x1x2 = (x1^2 + 2x1x2 +x2^2)/4 -x1x2 = (x1^2 -2x1x2 +x2^2)/4 = (x1 -x2)^2 /4 >0. So even when a=1, y1y2 = [(x1 +x2)/2]^2 >x1x2. So in that case, the same conclusion holds.Therefore, regardless of a in (0,1), the product y₁y₂ is greater than x₁x₂. Therefore, the answer is C.But wait, let me check the case when a approaches 0. Let a approach 0. Then y₁ ≈x₁/(1 +0) +0≈x₁, y₂≈x₂/(1 +0) +0≈x₂. Then y₁y₂≈x₁x₂. But as a approaches 0, the difference term [a(x₁ -x₂)^2]/(1 +a)^2 approaches 0. So in the limit as a approaches 0, y₁y₂ approaches x₁x₂ from above. Therefore, for any a>0, no matter how small, y₁y₂ >x₁x₂. If a=0, y₁y₂ =x₁x₂, but since a is in (0,1), not including 0, y₁y₂ is always greater. Therefore, answer is C.Thus, the correct option is C.Final Answerboxed{C}</think>Given two different positive real numbers ( x_1 ) and ( x_2 ), and a real number ( a ) in ( (0,1) ), we define ( y_1 ) and ( y_2 ) as follows:[y_1 = frac{x_1 + a x_2}{1 + a}, quad y_2 = frac{x_2 + a x_1}{1 + a}]We need to compare the product ( x_1 x_2 ) with ( y_1 y_2 ).First, we compute ( y_1 y_2 ):[y_1 y_2 = left( frac{x_1 + a x_2}{1 + a} right) left( frac{x_2 + a x_1}{1 + a} right)]Expanding the numerator:[(x_1 + a x_2)(x_2 + a x_1) = x_1 x_2 + a x_1^2 + a x_2^2 + a^2 x_1 x_2]Combining like terms, the numerator becomes:[x_1 x_2 (1 + a^2) + a (x_1^2 + x_2^2)]Thus,[y_1 y_2 = frac{x_1 x_2 (1 + a^2) + a (x_1^2 + x_2^2)}{(1 + a)^2}]To compare ( y_1 y_2 ) with ( x_1 x_2 ), we consider the difference:[y_1 y_2 - x_1 x_2 = frac{x_1 x_2 (1 + a^2) + a (x_1^2 + x_2^2) - x_1 x_2 (1 + a)^2}{(1 + a)^2}]Simplifying the numerator:[x_1 x_2 (1 + a^2) + a (x_1^2 + x_2^2) - x_1 x_2 (1 + 2a + a^2) = -2a x_1 x_2 + a (x_1^2 + x_2^2)]Factoring out ( a ):[a (x_1^2 - 2x_1 x_2 + x_2^2) = a (x_1 - x_2)^2]Since ( a ) is positive and ( x_1 neq x_2 ), the term ( a (x_1 - x_2)^2 ) is positive. Therefore, the difference ( y_1 y_2 - x_1 x_2 ) is positive, implying ( y_1 y_2 > x_1 x_2 ).Thus, the correct answer is (boxed{C}).,<think>Okay, so I have this problem here where I need to figure out the relationship between the product of x1 and x2 versus the product of y1 and y2. The options are whether x1x2 is greater than, equal to, less than, or it can't be determined compared to y1y2. Let's take it step by step.First, let's restate the given information. We have two different positive real numbers, x1 and x2. The number a is a real number between 0 and 1. Then, y1 and y2 are defined as:y1 = (x1)/(1 + a) + (a x2)/(1 + a)y2 = (x2)/(1 + a) + (a x1)/(1 + a)So, both y1 and y2 are weighted averages of x1 and x2. The weights are 1/(1 + a) and a/(1 + a). Since a is between 0 and 1, the weight on the other variable is smaller. For example, if a is close to 0, then y1 is mostly x1 with a little bit of x2, and y2 is mostly x2 with a little bit of x1. If a is close to 1, then both y1 and y2 become averages where x1 and x2 are weighted more equally.The question is about the product x1x2 compared to y1y2. Let me compute y1y2 first and see how it relates to x1x2.Let me write out y1 and y2 more clearly.y1 = [x1 + a x2] / (1 + a)y2 = [x2 + a x1] / (1 + a)So, y1y2 = [ (x1 + a x2)(x2 + a x1) ] / (1 + a)^2Let me expand the numerator:(x1 + a x2)(x2 + a x1) = x1x2 + a x1^2 + a x2^2 + a^2 x1x2So, combining terms:= (1 + a^2)x1x2 + a(x1^2 + x2^2)Therefore, y1y2 = [ (1 + a^2)x1x2 + a(x1^2 + x2^2) ] / (1 + a)^2Now, we can compare this to x1x2. Let's compute y1y2 - x1x2:y1y2 - x1x2 = [ (1 + a^2)x1x2 + a(x1^2 + x2^2) ] / (1 + a)^2 - x1x2= [ (1 + a^2)x1x2 + a(x1^2 + x2^2) - (1 + a)^2 x1x2 ] / (1 + a)^2Let me expand (1 + a)^2 x1x2:(1 + 2a + a^2)x1x2So, substituting back:Numerator becomes:(1 + a^2)x1x2 + a(x1^2 + x2^2) - [1 + 2a + a^2]x1x2= [1 + a^2 - 1 - 2a - a^2]x1x2 + a(x1^2 + x2^2)Simplify the coefficients:For x1x2: (1 - 1) + (a^2 - a^2) - 2a = -2aSo numerator is:-2a x1x2 + a(x1^2 + x2^2)Factor out an 'a':a [ -2x1x2 + x1^2 + x2^2 ]Notice that x1^2 + x2^2 - 2x1x2 = (x1 - x2)^2So numerator simplifies to:a (x1 - x2)^2Therefore, y1y2 - x1x2 = [a (x1 - x2)^2] / (1 + a)^2Since a is in (0,1), the numerator a (x1 - x2)^2 is positive because (x1 - x2)^2 is always non-negative, and since x1 ≠ x2 (given that they are different positive real numbers), (x1 - x2)^2 is positive. Therefore, the entire expression [a (x1 - x2)^2] / (1 + a)^2 is positive.Therefore, y1y2 - x1x2 > 0 => y1y2 > x1x2Which means x1x2 < y1y2. Therefore, the answer should be (C).Wait, but let me check again to make sure I didn't flip any signs.Wait, so if y1y2 - x1x2 is positive, that would mean y1y2 is greater than x1x2, so x1x2 is less than y1y2. Hence, the correct answer is (C).But let me verify this with an example. Let's take some numbers.Suppose a = 1/2 (which is between 0 and 1), and take x1 = 1, x2 = 2.Compute y1 and y2:y1 = (1)/(1 + 1/2) + ( (1/2)*2 )/(1 + 1/2) = (1)/(3/2) + (1)/(3/2) = (2/3) + (2/3) = 4/3 ≈ 1.333y2 = (2)/(3/2) + ( (1/2)*1 )/(3/2) = (4/3) + (1/2)/(3/2) = (4/3) + (1/3) = 5/3 ≈ 1.666Compute y1y2: (4/3)(5/3) = 20/9 ≈ 2.222Compute x1x2 = 1*2 = 2So indeed, 20/9 ≈ 2.222 > 2, so y1y2 > x1x2. So in this case, (C) holds.Another test case: a = 1/3, x1 = 3, x2 = 6.Compute y1 = 3/(1 + 1/3) + (1/3 * 6)/(1 + 1/3) = 3/(4/3) + 2/(4/3) = (9/4) + (6/4) = 15/4 = 3.75y2 = 6/(4/3) + (1/3 *3)/(4/3) = (18/4) + (1)/(4/3) = (9/2) + (3/4) = 4.5 + 0.75 = 5.25y1y2 = 3.75 * 5.25 = 19.6875x1x2 = 3*6 = 18Again, 19.6875 > 18. So again, (C) holds.Alternatively, take a approaching 0. Let a = 0.1, x1 = 1, x2 = 2.y1 = 1/(1.1) + (0.1*2)/1.1 ≈ 0.909 + 0.182 ≈ 1.091y2 = 2/1.1 + (0.1*1)/1.1 ≈ 1.818 + 0.091 ≈ 1.909y1y2 ≈ 1.091 * 1.909 ≈ 2.085x1x2 = 2So again, y1y2 ≈ 2.085 > 2.Alternatively, take a approaching 1. Let a = 0.9, x1=1, x2=2.Compute y1 = 1/(1.9) + (0.9*2)/1.9 ≈ 0.526 + 1.8/1.9 ≈ 0.526 + 0.947 ≈ 1.473y2 = 2/1.9 + (0.9*1)/1.9 ≈ 1.052 + 0.9/1.9 ≈ 1.052 + 0.473 ≈ 1.525y1y2 ≈ 1.473 * 1.525 ≈ 2.246x1x2 = 2. So still, y1y2 > x1x2.Therefore, in all these test cases, option (C) is correct. Therefore, the answer should be (C) x1x2 < y1y2.But wait, let me think again. The derivation shows that y1y2 - x1x2 = [a(x1 - x2)^2]/(1 + a)^2, which is positive since a > 0 and (x1 -x2)^2 >0, so the difference is positive, hence y1y2 >x1x2. Therefore, the correct answer is (C).But let me check if there's a different approach. Maybe using AM ≥ GM?Wait, but in this case, the weights are different. Let's see. Since y1 and y2 are convex combinations of x1 and x2. Specifically, since a is between 0 and 1, then 1/(1 + a) is between 1/2 and 1, and a/(1 + a) is between 0 and 1/2. So each yi is a weighted average closer to xi.But how does the product of two such averages compare to the product of the original numbers?Alternatively, consider the product y1y2 as a function and compare it to x1x2.Alternatively, maybe logarithms. Take ln(y1y2) = ln(y1) + ln(y2), compare to ln(x1x2) = ln(x1) + ln(x2). But maybe not necessary.Alternatively, perhaps consider that y1 and y2 are linear combinations, so their product can be compared via the arithmetic mean vs geometric mean. However, in this case, since they are both averages, but the product is higher? Wait, in the examples, the product was higher. So perhaps it's a general case.Alternatively, think about variance. The product x1x2 is the product of the original numbers, and when you take these averages, you're introducing some sort of covariance?Alternatively, consider that since x1 and x2 are positive, we can write x1 = k, x2 = m, and then express y1 and y2 in terms of k and m. But maybe not necessary.Alternatively, think of x1 and x2 as two numbers, and y1 and y2 are formed by moving each towards the other by a factor of a. Since a is between 0 and 1, it's like a convex combination.But moving each variable towards the other would bring them closer together. Since the product of numbers is maximized when they are equal (given a fixed sum), but here we are moving them closer, so if the original numbers are unequal, moving them closer should increase the product.Wait, that seems to make sense. For a fixed sum, the product is maximized when the numbers are equal. So if the original numbers are unequal, and you move them closer together, even if the sum changes, but in such a way that their average moves towards each other, their product could increase. Wait, but in this case, the sum might not be fixed. Let's check.Wait, in the problem, the sum of y1 and y2:y1 + y2 = [x1 + a x2 + x2 + a x1]/(1 + a) = [ (1 + a)x1 + (1 + a)x2 ] / (1 + a ) = x1 + x2So the sum of y1 and y2 is equal to the sum of x1 and x2. Therefore, the sum remains the same. Therefore, if you have two numbers with a fixed sum, their product is maximized when they are equal. Since x1 and x2 are different, their product is less than the maximum possible product given their sum. Then, since y1 and y2 are averages moving towards each other (since a is between 0 and 1), making them more equal, hence their product should be larger. Therefore, y1y2 >x1x2. Hence, the answer is (C). This aligns with the previous algebraic result.Therefore, this gives another perspective. Since the sum remains the same, but the numbers are made more equal, their product increases. Therefore, (C) is correct.Thus, I think the answer is (C).Final Answerboxed{C}</think>Given different positive real numbers (x_1) and (x_2), and a real number (a) in ((0,1)), we need to determine the relationship between (x_1 x_2) and (y_1 y_2) where (y_1) and (y_2) are defined as:[y_1 = frac{x_1}{1+a} + frac{a x_2}{1+a}][y_2 = frac{x_2}{1+a} + frac{a x_1}{1+a}]First, we express (y_1) and (y_2) as weighted averages:[y_1 = frac{x_1 + a x_2}{1+a}][y_2 = frac{x_2 + a x_1}{1+a}]Next, we compute the product (y_1 y_2):[y_1 y_2 = left( frac{x_1 + a x_2}{1+a} right) left( frac{x_2 + a x_1}{1+a} right)][= frac{(x_1 + a x_2)(x_2 + a x_1)}{(1+a)^2}]Expanding the numerator:[(x_1 + a x_2)(x_2 + a x_1) = x_1 x_2 + a x_1^2 + a x_2^2 + a^2 x_1 x_2][= (1 + a^2) x_1 x_2 + a(x_1^2 + x_2^2)]Thus,[y_1 y_2 = frac{(1 + a^2) x_1 x_2 + a(x_1^2 + x_2^2)}{(1 + a)^2}]We compare (y_1 y_2) with (x_1 x_2) by examining the difference:[y_1 y_2 - x_1 x_2 = frac{(1 + a^2) x_1 x_2 + a(x_1^2 + x_2^2) - (1 + a)^2 x_1 x_2}{(1 + a)^2}]Simplifying the numerator:[(1 + a^2) x_1 x_2 + a(x_1^2 + x_2^2) - (1 + 2a + a^2) x_1 x_2][= -2a x_1 x_2 + a(x_1^2 + x_2^2)][= a(x_1^2 + x_2^2 - 2x_1 x_2)][= a(x_1 - x_2)^2]Since (a > 0) and (x_1 neq x_2), the term (a(x_1 - x_2)^2) is positive. Therefore:[y_1 y_2 - x_1 x_2 = frac{a(x_1 - x_2)^2}{(1 + a)^2} > 0]This implies (y_1 y_2 > x_1 x_2). Hence, the correct answer is (boxed{C}).]

🔑:2. (C).Note that, y_{1} y_{2}=frac{1+a^{2}}{(1+a)^{2}} x_{1} x_{2}+frac{1}{(1 div a)^{2}}left(left(a x_{1}right)^{2}+left(a x_{2}right)^{2}right)>frac{1+a^{2}}{(1+a)^{2}} x_{1} x_{2}+ frac{2 a}{(1+a)^{2}} x_{1} x_{2}=x_{1} x_{2} (here the strict inequality is due to a x_{1}=u x_{2} leading to x_{1}=x_{2}, which contradicts the assumption that x_{1}, x_{2} are distinct).

🧠:[<think>Okay, so I have this problem: Find all integers n such that n + 1 divides n² + 1. Hmm, right. Let me try to figure this out step by step.First, I remember that if a number a divides another number b, then there exists some integer k such that b = a * k. So in this case, n + 1 divides n² + 1, which means there exists some integer k where n² + 1 = (n + 1) * k. My goal is to find all integers n that satisfy this equation.Maybe I can start by rearranging the equation. Let me write it out:n² + 1 = k(n + 1)So, if I can solve for k here, maybe that would help. Let's try to express k in terms of n:k = (n² + 1)/(n + 1)But since k has to be an integer, (n² + 1) must be divisible by (n + 1). Hmm. How can I check when this fraction is an integer?One method I remember is polynomial division. If I divide n² + 1 by n + 1, the remainder will tell me if it's divisible. Let's do that.Dividing n² by n gives n. Multiply (n + 1) by n, which is n² + n. Subtract that from n² + 1:n² + 1 - (n² + n) = -n + 1So the remainder is -n + 1. Therefore, we have:n² + 1 = (n + 1)(n) + (-n + 1)For (n + 1) to divide n² + 1, the remainder must be zero. Therefore, we set:-n + 1 = 0Solving this gives n = 1. So that's one solution: n = 1. But wait, the problem says "all integers n", so maybe there are more solutions?Hold on, but when we did the division, we assumed that the remainder must be zero. But actually, in integer division, if the remainder is a multiple of (n + 1), then it's also possible. Wait, no. If we have n² + 1 = (n + 1) * k, then the remainder must be zero. Because when dividing integers, the remainder is strictly less than the divisor in absolute value. So if (n + 1) divides n² +1, then the remainder when dividing must be zero. Therefore, the only n that satisfies this is n = 1. But let me check with n = 1. If n = 1, then n + 1 = 2, and n² +1 = 1 +1 = 2. So 2 divides 2, which works. That's correct.But wait, maybe there are other integers where (n + 1) divides (n² +1). Let me test some values.Take n = 0: n +1 =1, n² +1 =1. 1 divides 1, so that works. So n = 0 is a solution.n = -1: n +1 =0. But division by zero is undefined. So n = -1 is excluded.n = 2: n +1 =3, n² +1 =5. 3 does not divide 5. So no.n = -2: n +1 = -1, n² +1 =5. -1 divides 5, since 5 divided by -1 is -5, which is integer. So n = -2 is a solution. Let me check: (-2) +1 = -1, (-2)^2 +1 =4 +1=5. So -1 divides 5? Yes, because 5 divided by -1 is -5, which is an integer. So n = -2 works.n = -3: n +1 = -2, n² +1 =10. Does -2 divide 10? 10 divided by -2 is -5, which is integer. So yes, n = -3 is a solution.Wait, so maybe there are multiple solutions. How come polynomial division only gave me n =1? Hmm. Maybe my initial approach is missing something.Let me think again. The division gave me that the remainder is -n +1, so in order for (n +1) to divide n² +1, the remainder must be zero. So -n +1 =0 implies n =1. But in the examples above, n=0, n=-2, n=-3 also work. So why did the division approach not catch those?Ah, maybe because when n +1 is a divisor of n² +1, the remainder is zero, but only when n +1 is positive. But in integers, divisors can be negative as well. Wait, but in the division algorithm, the remainder is non-negative and less than the absolute value of the divisor. Hmm, maybe my confusion is between polynomial division over integers versus integer division.Let me clarify. When we perform polynomial division, we get:n² +1 = (n +1)(n -1) + 2Wait, hold on, earlier I thought the remainder was -n +1, but maybe I made a mistake in the division. Let me check again.Dividing n² +1 by n +1:Divide n² by n: get n. Multiply (n +1) by n: n² +n. Subtract from n² +1:(n² +1) - (n² +n) = -n +1. Then, the degree of -n +1 is less than the degree of n +1, so we stop here. So the remainder is indeed -n +1. So in polynomial division, the remainder is -n +1, but in integer division, when we consider integers, perhaps the remainder is different?Wait, maybe that's the confusion. The polynomial division gives a remainder, but when dealing with integers, the remainder when dividing integers a by b is a non-negative integer less than |b|. So perhaps the remainder in integer division is different from the remainder in polynomial division. Hmm, this might be the case.So let me approach the problem again, considering integer division.If we have integers a and b, with b ≠0, then there exist unique integers q and r such that a = bq + r, where 0 ≤ r < |b|. So maybe in this case, when we divide n² +1 by n +1, the remainder must satisfy 0 ≤ r < |n +1|. But in the equation n² +1 = (n +1)k + r, the remainder r must satisfy that inequality.Alternatively, perhaps we can use the property that if n +1 divides n² +1, then n² +1 ≡ 0 mod (n +1). Let me think in terms of congruences.So n ≡ -1 mod (n +1). Therefore, n² +1 ≡ (-1)^2 +1 = 1 +1 = 2 mod (n +1). Therefore, n² +1 ≡ 2 mod (n +1). Therefore, for n +1 to divide n² +1, we must have 2 ≡ 0 mod (n +1), which means that n +1 divides 2.Therefore, n +1 is a divisor of 2. The divisors of 2 in integers are ±1 and ±2. Therefore, n +1 ∈ {1, -1, 2, -2}, so n ∈ {0, -2, 1, -3}.Therefore, the possible integer solutions for n are 0, -2, 1, -3.Let me check these:n = 0: n +1 =1 divides 0 +1 =1. Yes.n = -2: n +1 = -1 divides 4 +1=5. Yes, since 5/-1 = -5.n =1: 2 divides 1 +1=2. Yes.n = -3: -2 divides 9 +1=10. Yes, since 10/-2 = -5.So all these values work. Therefore, the solutions are n = -3, -2, 0, 1.Wait, so the key insight was to realize that n ≡ -1 mod (n +1), so substituting into n² +1 gives 2 mod (n +1). Therefore, (n +1) must divide 2, leading to the divisors of 2. That gives the possible n +1 as ±1, ±2, so n is -3, -2, 0, 1. So that's the answer.But why did the polynomial division approach only give me n =1? Because in polynomial division, the remainder is -n +1, but in integer division, the remainder must be non-negative. So perhaps when I set the remainder to zero, it only gives the case where the remainder in polynomial division is zero, but in reality, the remainder in integer division can be a positive number as long as it's less than |n +1|. However, using congruence modulo (n +1) is a better approach here.Alternatively, maybe another way to approach this problem is to express n² +1 in terms of (n +1). Let's try to write n² +1 as (n +1) * q + r, where q and r are integers. Then, as we saw earlier, n² +1 = (n +1)(n -1) + 2. Wait, hold on:Wait, expanding (n +1)(n -1) gives n² -1. So n² +1 = (n +1)(n -1) + 2. So that means:n² +1 = (n +1)(n -1) + 2Therefore, (n +1) divides n² +1 if and only if (n +1) divides 2. Which brings us back to the same conclusion. So n +1 must be a divisor of 2, which are ±1 and ±2, leading to n = -3, -2, 0, 1.Therefore, the solutions are n ∈ {-3, -2, 0, 1}.So the initial mistake was stopping at the polynomial division remainder -n +1 and only considering when that equals zero, but actually, the correct approach is to express the remainder as 2, leading to the conclusion that n +1 divides 2.So, to summarize:1. Start with n +1 divides n² +1.2. By congruence, n ≡ -1 mod (n +1). Substitute into n² +1: (-1)^2 +1 = 2. So (n +1) divides 2.3. Find all divisors of 2: ±1, ±2.4. Solve n +1 = 1 → n=0; n +1=-1→n=-2; n +1=2→n=1; n +1=-2→n=-3.5. Check each solution, which works.Therefore, the integers n are -3, -2, 0, 1.Final AnswerThe integers are boxed{-3}, boxed{-2}, boxed{0}, and boxed{1}.</think>To find all integers ( n in mathbb{Z} ) such that ( n + 1 mid n^2 + 1 ):1. Congruence Approach: - If ( n + 1 ) divides ( n^2 + 1 ), then ( n^2 + 1 equiv 0 pmod{n + 1} ). - Since ( n equiv -1 pmod{n + 1} ), substitute ( n ) with (-1) in the expression ( n^2 + 1 ): [ (-1)^2 + 1 = 1 + 1 = 2 ] - Therefore, ( n + 1 ) must divide 2. The divisors of 2 are ( pm 1 ) and ( pm 2 ).2. Solving for ( n ): - If ( n + 1 = 1 ), then ( n = 0 ). - If ( n + 1 = -1 ), then ( n = -2 ). - If ( n + 1 = 2 ), then ( n = 1 ). - If ( n + 1 = -2 ), then ( n = -3 ).3. Verification: - Check each solution: - ( n = 0 ): ( 0 + 1 = 1 ) divides ( 0^2 + 1 = 1 ). - ( n = -2 ): ( -2 + 1 = -1 ) divides ( (-2)^2 + 1 = 5 ). - ( n = 1 ): ( 1 + 1 = 2 ) divides ( 1^2 + 1 = 2 ). - ( n = -3 ): ( -3 + 1 = -2 ) divides ( (-3)^2 + 1 = 10 ).Thus, the integers ( n ) are (boxed{-3}), (boxed{-2}), (boxed{0}), and (boxed{1}).,<think>Okay, so I have this problem: Find all integers n such that n + 1 divides n² + 1. Hmm, divisibility. Let me think about how to approach this.First, the question is asking for integers n where when you divide n² + 1 by n + 1, there's no remainder. In other words, n² + 1 is a multiple of n + 1. I remember that for polynomial division, if we divide a polynomial f(n) by (n - a), the remainder is f(a). Maybe that applies here? Let me check.If I consider dividing n² + 1 by n + 1. Let's set f(n) = n² + 1. Then, according to the Remainder Theorem, the remainder when f(n) is divided by (n + 1) is f(-1). Let's calculate that: f(-1) = (-1)² + 1 = 1 + 1 = 2. So the remainder is 2. Therefore, n + 1 divides n² + 1 if and only if n + 1 divides the remainder 2. Because if the remainder is divisible by n + 1, then the original expression is divisible.So, n + 1 must be a divisor of 2. Now, the divisors of 2 are ±1 and ±2. Therefore, n + 1 can be 1, -1, 2, or -2. Solving for n in each case:1. If n + 1 = 1, then n = 0.2. If n + 1 = -1, then n = -2.3. If n + 1 = 2, then n = 1.4. If n + 1 = -2, then n = -3.Therefore, the possible integer values of n are -3, -2, 0, and 1.Wait, let me verify each of these to make sure.Starting with n = 0: n + 1 = 1, and n² + 1 = 0 + 1 = 1. So 1 divides 1, which is true.n = -2: n + 1 = -1, and n² + 1 = 4 + 1 = 5. So -1 divides 5? Since 5 divided by -1 is -5, which is an integer. So yes, that works.n = 1: n + 1 = 2, and n² + 1 = 1 + 1 = 2. So 2 divides 2, which is true.n = -3: n + 1 = -2, and n² + 1 = 9 + 1 = 10. Then -2 divides 10, since 10 divided by -2 is -5, which is an integer. So that works as well.So all four values check out. Therefore, the integers n that satisfy the condition are -3, -2, 0, and 1.But wait, let me think again. The problem says n is an integer, so positive and negative. The method I used with the Remainder Theorem gives that n + 1 divides 2, leading to those four values. That seems correct, but maybe there's another way to approach this problem?Alternatively, I could use algebraic manipulation. If n + 1 divides n² + 1, then there exists an integer k such that n² + 1 = k(n + 1). Let me write that equation:n² + 1 = k(n + 1)Rearranging, n² - k n + (1 - k) = 0.This is a quadratic equation in n. For integer solutions n, the discriminant must be a perfect square. The discriminant D is:D = (-k)² - 4 * 1 * (1 - k) = k² - 4(1 - k) = k² + 4k - 4.So D must be a perfect square. Let's denote D = m², where m is an integer. So,k² + 4k - 4 = m².Hmm, this seems a bit more complicated. Maybe this isn't the best approach. Let's see if we can find integer solutions k and m here.Alternatively, maybe express n² + 1 divided by n + 1. Let's perform the division:Divide n² + 1 by n + 1. Using polynomial long division:n + 1 ) n² + 0n + 1First term: n² divided by n is n. Multiply (n + 1) by n: n² + n. Subtract that from the dividend:(n² + 0n + 1) - (n² + n) = -n + 1.Now, divide -n by n: -1. Multiply (n + 1) by -1: -n -1. Subtract that from (-n +1):(-n + 1) - (-n -1) = 0 + 2 = 2.So the division gives quotient (n -1) with a remainder of 2. Therefore, n² +1 = (n +1)(n -1) + 2. Hence, for n +1 to divide n² +1, n +1 must divide 2. Which is exactly the conclusion I reached earlier. So this confirms that n +1 must be a divisor of 2, leading to n +1 ∈ {1, -1, 2, -2}, so n ∈ {0, -2, 1, -3}.Therefore, this method gives the same answer, which reinforces that the solution is correct.Another way to think about it: Let’s express n² +1 in terms of (n +1). Let me write n² +1 as (n +1)(n -1) + 2. Then, since (n +1) divides the first term, it must divide the remainder 2. So same conclusion.Alternatively, set m = n +1. Then n = m -1. Substitute into the original equation: m divides (m -1)^2 +1. Let me compute (m -1)^2 +1:(m -1)^2 +1 = m² - 2m +1 +1 = m² - 2m + 2.So m divides m² - 2m + 2. Which implies that m divides (m² - 2m + 2) - m*(m - 2) = m² - 2m + 2 - m² + 2m = 2. So m divides 2. Therefore, m ∈ {1, -1, 2, -2}, which gives n = m -1 as before. So n ∈ {0, -2, 1, -3}.Same answer again. So all methods converge to these four integers. Therefore, I can be confident that these are the solutions.Just to ensure thoroughness, let me check each solution again:n = -3: n +1 = -2, n² +1 = 9 +1 =10. -2 divides 10? Yes, 10 / (-2) = -5, which is an integer.n = -2: n +1 = -1, n² +1 =4 +1=5. -1 divides 5? Yes, 5 / (-1) = -5.n =0: n +1=1, n² +1=0 +1=1. 1 divides 1, yes.n =1: n +1=2, n² +1=1 +1=2. 2 divides 2, yes.All checks out. Therefore, the integers n that satisfy the condition are indeed -3, -2, 0, and 1.I don't see any other possible divisors of 2, since 2 is a prime number in integers, so its divisors are just ±1 and ±2. Therefore, there are no other values for n +1, so these four are the only solutions.Final AnswerThe integers are boxed{-3}, boxed{-2}, boxed{0}, and boxed{1}.</think>To find all integers ( n in mathbb{Z} ) such that ( n + 1 mid n^2 + 1 ), we start by using the Remainder Theorem. When ( n^2 + 1 ) is divided by ( n + 1 ), the remainder is ( f(-1) ) where ( f(n) = n^2 + 1 ). Calculating this remainder:[f(-1) = (-1)^2 + 1 = 1 + 1 = 2]For ( n + 1 ) to divide ( n^2 + 1 ), ( n + 1 ) must be a divisor of 2. The divisors of 2 are ( pm 1 ) and ( pm 2 ). Solving for ( n ) in each case:1. ( n + 1 = 1 ) implies ( n = 0 )2. ( n + 1 = -1 ) implies ( n = -2 )3. ( n + 1 = 2 ) implies ( n = 1 )4. ( n + 1 = -2 ) implies ( n = -3 )We verify each solution:- For ( n = 0 ): ( 0 + 1 = 1 ) divides ( 0^2 + 1 = 1 ).- For ( n = -2 ): ( -2 + 1 = -1 ) divides ( (-2)^2 + 1 = 5 ).- For ( n = 1 ): ( 1 + 1 = 2 ) divides ( 1^2 + 1 = 2 ).- For ( n = -3 ): ( -3 + 1 = -2 ) divides ( (-3)^2 + 1 = 10 ).All values satisfy the condition. Therefore, the integers ( n ) are (boxed{-3}), (boxed{-2}), (boxed{0}), and (boxed{1}).]

🔑:The integer n satisfies the required property if and only if n+1 mid n^{2}+1-(n+1)(n-1)=2. The divisors of 2 are -2,-1,1,2 so the solutions are -3,-2,0,1.