🧠:[<think>Okay, so I have this question about different random sampling methods and matching them to three scenarios. Let me read through the problem again to make sure I understand what's being asked.The question presents three different sampling scenarios and three sampling methods: Simple Random Sampling (I), Systematic Sampling (II), and Stratified Sampling (III). The task is to pair each scenario with the correct method and choose the right option from A to D.First, let me recall the definitions of each sampling method to ensure I have them straight:1. Simple Random Sampling (I): This is when every member of the population has an equal chance of being selected, and each sample of a certain size has an equal chance of being chosen. It's like drawing names out of a hat.2. Systematic Sampling (II): This method involves selecting individuals from a population at regular intervals. For example, every 10th person on a list. You decide on a starting point randomly and then pick every nth element.3. Stratified Sampling (III): Here, the population is divided into subgroups (or strata) that share similar characteristics, and then a random sample is taken from each stratum. This is useful when the population has distinct subgroups and you want to ensure representation from each.Now, let me go through each of the three scenarios provided and try to figure out which method they used.First Scenario: "To understand the family income situation of students, a university sampled 100 students from 150 urban students and 150 rural students."So here, the university has a population that's divided into two groups: urban and rural students, each group having 150 students. They sampled 100 students total, but how did they do it? The key detail here is that they specified "from 150 urban students and 150 rural students." If they are taking samples from each of these groups separately, that sounds like stratified sampling. Because stratified sampling involves dividing the population into strata (urban vs. rural) and then sampling within each stratum. The total sample is 100, so maybe they took 50 from each group? That would make sense as a stratified sample.Second Scenario: "A workshop director sampled 7 products for quality inspection from 20 products."Hmm. So there are 20 products, and they need to inspect 7. Let's think about how this could be done. If they just randomly selected 7 out of 20 without any particular system, that would be simple random sampling. But systematic sampling could also be possible. For systematic sampling, you might calculate the interval, which would be 20 divided by 7, but that's roughly 3. So every 3rd product. However, 20 divided by 7 is not an integer, so maybe that's not the case. Alternatively, maybe the director used a random number generator to pick 7 products. Since there's no mention of dividing into groups or using a systematic approach like every nth product, my initial thought is that this is simple random sampling. But I need to double-check.Wait, another approach: in systematic sampling, you divide the population size by the desired sample size to get the interval. So 20 products, sample size 7. 20 divided by 7 is approximately 2.857. You can't have a fraction of an interval, so you might round down to 2 or up to 3. If you take every 3rd product, starting at a random number between 1 and 3, you would end up with 6 or 7 samples. Wait, 20 divided by 3 is about 6.66. Hmm, maybe starting at a random start between 1 and 20, and then selecting every (20/7)th item? But that seems complicated. Alternatively, maybe the director just randomly selected 7 products, which would be straightforward simple random sampling. The problem doesn't give any indication of a systematic approach, so maybe it is simple random. However, sometimes in quality control, systematic sampling is used because it's easier—like inspecting every 10th product on the assembly line. But with 20 products and 7 samples, systematic might not fit as neatly. Let me think again. If we use systematic sampling, you determine the interval k by dividing population by sample size. So k = N/n = 20/7 ≈ 2.857. Since you can't have a fraction, you might randomly select one of the first k items, then take every kth item. But 2.857 isn't a whole number, so maybe they adjusted it. Alternatively, maybe they used a different method. This is a bit unclear, but since 7 is not a divisor of 20, systematic sampling might be less likely here. So maybe this is simple random sampling (I). Alternatively, if the director numbered the products from 1 to 20 and then, for example, started at a random number between 1-3 and picked every 3rd product. Let's see: starting at 1, then 4,7,10,13,16,19—that's 7 products. Starting at 2, then 5,8,11,14,17,20—6 products. Starting at 3, 6,9,12,15,18—only 6 products. So that approach doesn't quite get 7. Alternatively, maybe starting at a random number between 1-20 and then wrapping around? Hmm. This seems complicated, so maybe they didn't use systematic here. Therefore, maybe it is simple random sampling (I). But I need to check the third scenario to see if there's a better fit.Third Scenario: "From 2000 students, 10 were sampled to understand their daily habits."So here, the population is 2000 students, and they sampled 10. The question is, which method was used? The problem doesn't mention any stratification or subgroups. So if it's just selecting 10 students randomly from the entire 2000, that would be simple random sampling (I). However, another possibility is systematic sampling. For example, if they divided 2000 by 10, the interval would be 200. So randomly pick a number between 1-200, say 50, and then select 50, 250, 450,... up to 10 students. That would be systematic. But since the sample size is very small (10 out of 2000), systematic sampling is feasible here. The problem is, the question is about which method is used. However, the problem statement doesn't specify how they were sampled. So if there's no mention of stratification or systematic approach, the default assumption might be simple random sampling. But let me think again. Sometimes, when you have a large population and a small sample, simple random can be difficult to implement without a list. But if they have a list of all 2000 students, simple random is possible. Alternatively, systematic might be easier. But the problem doesn't give any clues. Hmm. So maybe this is simple random (I) or systematic (II). But let me go back to the second scenario. If the second scenario is systematic, then the third could be simple. But the problem is that the second scenario with 20 products and 7 samples is a bit ambiguous. Wait, maybe the third scenario is systematic. Let me check the answer options.Looking at the options:A: ① with I, ② with II, ③ with III B: ① with III, ② with II, ③ with I C: ① with III, ② with I, ③ with II D: ① with II, ② with I, ③ with III So in option C, the third scenario is paired with II (Systematic). If the third scenario is systematic, then from 2000 students, they might have used a systematic approach. For example, selecting every 200th student. But the problem is that with 10 students, 2000/10=200. So interval is 200. So starting at a random number between 1-200, then adding 200 each time. That would give 10 students. So that's systematic. However, the problem statement doesn't specify that they used such a method. So unless the question gives a hint, it's ambiguous. But perhaps we can infer based on the other scenarios.First scenario was stratified (III), second is simple random (I), third is systematic (II). That would correspond to option C: ①-III, ②-I, ③-II. Let me verify again.First scenario: urban and rural are strata, so stratified. Second scenario: 7 out of 20 products, if it's simple random, then ②-I. Third scenario: 10 out of 2000, systematic. Then yes, that would be option C. Alternatively, if the second scenario is systematic, then third would be simple. But why?Wait, the second scenario: 7 products from 20. If they used systematic, they might have calculated the interval as 20/7 ≈ 3, but since it's not a whole number, maybe they adjust. For example, randomly select a starting point between 1-20 and then take every 3rd product until they get 7. But wrapping around if necessary. However, 20 isn't a multiple of 3, so this could lead to some products being more likely to be chosen. Hmm. Alternatively, maybe the director just picked every 3rd product starting at a random point. But 20/3 is approximately 6.66, so if you start at 1, you get 1,4,7,10,13,16,19 (7 products). Start at 2: 2,5,8,11,14,17,20 (7 products). Start at 3: 3,6,9,12,15,18 (only 6). Hmm, so starting at 1 or 2 gives 7 products, starting at 3 gives 6. Therefore, to get exactly 7, they might have randomly chosen between starting points 1 or 2. But this seems a bit forced. Alternatively, maybe they just did simple random sampling. If that's the case, then second scenario is I. Then third scenario is II (systematic). So that would be option C. Alternatively, if second scenario is II, then third might be I, but I don't see why. Let's see.The problem is, the descriptions are very brief. The key is to see if there's any indication of stratification, systematic, or simple.First scenario clearly uses strata (urban and rural), so that's stratified (III). So ① is III. That narrows down the options. The options that have ① with III are B, C, and D. A is out. Now between B, C, D.Second scenario: workshop director sampled 7 from 20. If that's stratified, but there's no mention of strata. So probably not. If it's systematic, as discussed, maybe, but maybe simple random. If it's simple random, then ② is I. If it's systematic, ② is II.Third scenario: 10 from 2000. If it's stratified, but no strata mentioned. If it's systematic, as in every 200th, then III is II. If it's simple random, then ③ is I.Looking at options:B: ①-III, ②-II, ③-I C: ①-III, ②-I, ③-II D: ①-II, ②-I, ③-III We already determined ① is III. So D is out because D has ① as II. So between B and C.So now, between B and C: for ②, is it II or I?Second scenario: 7 from 20. If they used systematic, how would that work? Let's think: 20 products, sample 7. So the interval would be 20/7 ≈ 2.857. Since you can't have a fraction, maybe round up to 3. Then pick a random start between 1-3. Let's say start at 1: 1,4,7,10,13,16,19 (7). Start at 2: 2,5,8,11,14,17,20 (7). Start at 3: 3,6,9,12,15,18 (6). So to get exactly 7, they might have randomly selected starting at 1 or 2. So if the director did that, then it's systematic. But the problem statement doesn't specify how they selected the 7. If it's systematic, then ②-II, but if simple random, then ②-I.But in quality inspection, sometimes systematic sampling is used because it's easier to implement on a production line. For example, every nth product is inspected. However, in this case, with 20 products and 7 samples, it's a bit of an odd number. But maybe the director used systematic. However, without more information, it's hard to tell. But given that the answer options are structured, and since ③ could be either I or II.Third scenario: 10 out of 2000. If it's systematic (II), then ③-II. If it's simple random (I), then ③-I.But if ③ is systematic, then ② would be I. If ③ is I, then ② might be II. Given that in the third scenario, 10 is a very small sample from 2000, using systematic might make sense. For example, selecting every 200th student. Whereas simple random would require a random number generator or a list. If they have a list, simple random is possible, but systematic is often easier. However, the problem statement doesn't specify. So this is a bit ambiguous.But given that in the first scenario, stratified is clear, and the answer options, we need to choose between B and C.If I assume that the second scenario is simple random (I), then ②-I, and third scenario is systematic (II), so ③-II. That would be option C.Alternatively, if the second scenario is systematic (II), then ③ would be simple random (I), which is option B.So which is more plausible?Workshop director sampling 7 from 20 products. If the products are produced in a sequence, systematic sampling is common in quality control. For example, every nth product. But in this case, since 20 is not a multiple of 7, it's a bit messy, but as we saw, starting at 1 or 2 and taking every 3rd gives exactly 7. So maybe the director used that method.If that's the case, then ② is II. So then ③ would be I (simple random). But 10 out of 2000 is a very small sample. Simple random is possible, but sometimes systematic is easier. But again, without more info, it's hard.Wait, another angle. The question states "the following are random sampling methods: I. Simple Random Sampling II. Systematic Sampling III. Stratified Sampling." So all three methods are types of random sampling. So in each scenario, the sampling is done using one of these methods. The task is to match them correctly.First scenario: urban and rural students are separate strata, so stratified (III). So ①-III.Second scenario: 7 from 20. If it's simple random, each product has an equal chance. If it's systematic, it's a fixed interval. Since the problem says "sampled 7 products for quality inspection from 20 products," without mentioning any order or structure, perhaps the default assumption is simple random. Because if they used systematic, there might be a mention of order or intervals. But since it's a workshop, maybe the products are in a batch, and systematic is easier. But I think in the absence of specific information, we might assume simple random. So ②-I.Third scenario: 10 from 2000. If it's systematic, then it's II. If it's simple random, then I. However, the problem states that the options are the three methods: I, II, III. Since III is already used in ①, the third scenario must be either I or II. Given that 10 is a small sample from 2000, and assuming that the university might use systematic sampling for simplicity (like selecting every 200th student), then III would be II. So that pairs ③ with II. Therefore, option C: ①-III, ②-I, ③-II.Alternatively, if the third scenario is simple random (I), but since 10 is a small number, simple random is feasible if they have a list. But maybe the answer expects systematic for the third. I think in large populations, systematic is sometimes used for simplicity. But without specific clues, it's tricky.Wait, let's check the answer options again. If ① is III (stratified), then options B, C are possible. B: ②-II, ③-I. C: ②-I, ③-II.If the second scenario is 7 out of 20, which is 35% of the population. If they used systematic, the interval would be 20/7≈3. So every 3rd product. But starting at random start between 1-3. As we saw earlier, starting at 1 or 2 gives 7, starting at 3 gives 6. So maybe they adjusted the interval. But that seems a bit more involved. If they used simple random, then it's straightforward. Since the problem doesn't specify any order or systematic approach, maybe simple random is more likely. So ②-I. Then ③ would be II. So option C.Alternatively, maybe the third scenario is simple random. But how?Wait, in the third scenario, "From 2000 students, 10 were sampled to understand their daily habits." If they used stratified sampling, they would have divided the students into strata first. But there's no mention of that. So it's not III. So it's either I or II. Between those, if they used systematic, they pick every 200th student. But 10 students is a very small sample, so systematic might miss certain patterns. Alternatively, simple random is better for such a small sample. However, simple random requires a random selection method. But maybe the university used systematic for ease. This is a bit of a toss-up.But given that in the absence of specific information, and since stratified is already used in ①, the other two are likely simple and systematic. Since the second scenario is a smaller population (20 products), maybe simple random is easier to implement there. While the third scenario with 2000 students might use systematic because it's more manageable. Therefore, ③-II.Therefore, option C: ①-III, ②-I, ③-II.Alternatively, if the third scenario is simple random, then option B. But I think systematic is more plausible for the third. So I'm leaning towards C.Final Answerboxed{C}</think>To determine the correct pairing of the three sampling scenarios with the three methods (Simple Random Sampling, Systematic Sampling, Stratified Sampling), we analyze each scenario:1. First Scenario: The university sampled 100 students from 150 urban and 150 rural students. This involves dividing the population into subgroups (urban and rural) and sampling from each subgroup. This is Stratified Sampling (III).2. Second Scenario: A workshop director sampled 7 products from 20. The problem does not mention any specific order or intervals, so the most straightforward method is Simple Random Sampling (I).3. Third Scenario: From 2000 students, 10 were sampled. Given the large population, a systematic approach (e.g., selecting every 200th student) is often used for simplicity. This is Systematic Sampling (II).Matching the scenarios with the methods:- ① with III (Stratified Sampling)- ② with I (Simple Random Sampling)- ③ with II (Systematic Sampling)Thus, the correct answer is (boxed{C}).,<think>Okay, let's try to figure out this problem step by step. So, the question is about matching three different sampling scenarios with the correct random sampling methods: Simple Random Sampling, Systematic Sampling, and Stratified Sampling. The options are A, B, C, D, each pairing the scenarios ①, ②, ③ with the methods I, II, III.First, I need to recall what each sampling method entails. Let me start by jotting down definitions from what I remember.1. Simple Random Sampling (I): This is the most straightforward method where every member of the population has an equal chance of being selected. The selection is usually done using a random number generator or a lottery system. There's no subdivision or ordering; it's purely random.2. Systematic Sampling (II): In this method, you select members from a population at regular intervals. For example, if you have a population of 1000 and you want a sample of 100, you might choose every 10th person. The starting point is usually random, but then the selection follows a fixed interval.3. Stratified Sampling (III): Here, the population is divided into subgroups (or strata) that share similar characteristics, like urban and rural students. Then, a random sample is taken from each stratum. This ensures that each subgroup is adequately represented in the sample.Now, let's look at the three scenarios given:Problem ①: A university sampled 100 students from 150 urban students and 150 rural students. So, total population is 300 students (150 urban + 150 rural), and they took a sample of 100. The key here is that they specifically mention urban and rural students. That makes me think they divided the population into two strata (urban and rural) and then sampled from each. If they took 50 from each, that would be stratified sampling. Wait, but the problem doesn't specify how many from each group. It just says they sampled 100 from the total 300. Hmm, but the fact that they mention urban and rural might imply that they considered these strata. If they had done simple random sampling, they wouldn't need to separate urban and rural. So, I think this is Stratified Sampling (III). So ① with III.Problem ②: A workshop director sampled 7 products for quality inspection from 20 products. Let's see. If there are 20 products, and you need to sample 7. If it's simple random sampling, they would just randomly pick 7 without any order. But systematic sampling would involve, say, calculating the interval. For example, 20 divided by 7 is approximately 3, so every 3rd product. But 20 isn't a multiple of 7, so systematic might require some adjustment. Alternatively, they might just use simple random. Wait, but the problem doesn't mention any ordering or structure. The key here is that the workshop director is selecting 7 from 20. If it's done randomly without any stratification or systematic approach, then it's simple random. But maybe they used systematic. Wait, how does systematic work here? Let me think. If they have 20 products, maybe arranged in a line or sequence. The sampling interval would be 20/7 ≈ 2.857, which is not a whole number. So systematic sampling would be tricky here because the interval isn't an integer. Therefore, they might just randomly pick 7. But in some cases, even with non-integer intervals, you can round or use a random start. For example, pick a random number between 1 and 2 (since 20/7 ≈ 2.857), say start at 3, then take every 3rd product. But 3 + 3*6 = 21, which is beyond 20. Hmm, maybe not. Alternatively, start at a random position between 1 and 20, and then take every kth where k is approximately 3. But this complicates. Since the problem doesn't mention any structure or method, but just says "sampled 7 products", it might be simple random. But wait, another thought: sometimes in quality control, they use systematic sampling because it's easier. For example, every nth product on the assembly line. But unless specified, it's hard to tell. But given the options, maybe the answer expects systematic here. Wait, let's check the options again. The options for problem ② are paired with either II or I. So in option C, ② is with I (simple random), and in option B, ② with II (systematic). So which is more likely?Since the workshop director is doing quality inspection, maybe they use systematic sampling because it's easier to implement on a production line. For instance, inspecting every 3rd product. But the problem states there are 20 products, and 7 are sampled. If the interval is 20/7 ≈ 2.857, which isn't an integer, so maybe they adjust. Alternatively, they could use a random start. Let's say starting at position k (random between 1 and 20), then take every 3rd product. But 3*7=21, which exceeds 20. Alternatively, they could use a circular systematic sampling where they wrap around. Hmm, but this is getting complicated. Alternatively, maybe the workshop director just randomly picks 7, which would be simple random. So since the problem doesn't specify any systematic approach, perhaps it's simple random. Wait, but the problem statement says "sampled 7 products for quality inspection from 20 products". If they are on a production line, systematic is common. But without context, it's ambiguous. However, the options might lead us. Let's hold onto this for a moment and check problem ③.Problem ③: From 2000 students, 10 were sampled to understand their daily habits. So, 10 out of 2000. If they use simple random sampling, they just randomly pick 10. If systematic, they might calculate the interval as 2000/10 = 200, so every 200th student. Starting at a random number between 1-200, then take every 200th. But 10 samples. Alternatively, maybe they used stratified sampling, but there's no mention of different strata. So, the possible methods here are either simple random or systematic. Since 2000 is a large population, systematic sampling might be easier. For example, choose a random starting point between 1 and 200, then every 200th student. That would give exactly 10 students. So maybe this is systematic. If the answer options pair this with II (systematic), then ③ with II. Alternatively, if they just randomly picked 10, it's simple random (I). But 10 out of 2000 is a very small sample. It's more likely to be simple random unless specified. But without more context, again, hard to say.Wait, let's look back at the answer choices. The options are:A: ①I, ②II, ③III B: ①III, ②II, ③I C: ①III, ②I, ③II D: ①II, ②I, ③IIISo for problem ③, possible methods are either II or I or III.But problem ③ is a sample of 10 from 2000. There's no mention of strata, so stratified is out. So between I and II. If it's systematic, then III would be out. So in the options, in C, ③ is paired with II (systematic), which is possible. In B, ③ is I (simple random). So which is more likely?Given that 10 is a small sample from 2000, simple random is possible, but sometimes in large populations, systematic can be easier. However, the key here is that the problem says "to understand their daily habits". If they wanted a representative sample, simple random might be better. But again, without more context, it's ambiguous.Let me try to piece it together.Problem ①: University sampled 100 from 150 urban and 150 rural. Since they specifically mention urban and rural, even if they didn't say they sampled equally, the fact that they separated them suggests stratified sampling. So ① with III.Problem ②: Workshop sampled 7 from 20. If it's stratified, but there's no strata mentioned. If it's systematic, but the interval is messy. If it's simple random, that's straightforward. But maybe the answer expects systematic here? Hmm. Wait, in some quality inspections, they do use systematic sampling because it's easier. For example, every 3rd product. But 20 products and 7 samples. Let's calculate the interval. 20 / 7 ≈ 2.857. So maybe they start at a random number between 1-3 and then take every 3rd product. For example, start at 2, then 2,5,8,11,14,17,20. That gives 7 products. So that's systematic. So maybe ② with II. But the problem doesn't specify that they used a systematic approach. However, in the context of quality inspection, systematic is common. So maybe ② with II. Then, problem ③ would be simple random.Wait, but option B says ②II and ③I. So if ② is II, then ③ would be I. But problem ③ is 10 from 2000. If that's simple random, then yes. But why not systematic?Alternatively, maybe problem ② is simple random. Then ③ is systematic.But let's check the options again. If ① is III (stratified), ② is I (simple), ③ is II (systematic): that's option C. Alternatively, ① III, ② II, ③ I: option B.So which is more plausible?Problem ③: 10 from 2000. If they use systematic, the interval is 200. So starting at, say, 123, then 123, 323, 523, ..., but 523 exceeds 2000? Wait, 2000 divided by 10 is 200. So starting at 1-200 randomly, then adding 200 each time. So 10 samples. For example, starting at 50: 50, 250, 450, ..., up to 1850. That gives 10 samples. So that's systematic. But is that practical? Maybe. But is there any indication in the problem statement? The problem says "to understand their daily habits". If the population is ordered in some way that could introduce periodicity, systematic sampling might be biased. But if the order is random, then systematic is okay. However, since the problem doesn't specify the order, it's hard to say. But given that it's 2000 students, perhaps they used systematic for ease. So ③ with II.If that's the case, then ①III, ②I, ③II would be option C. But wait, in problem ②, 7 from 20 products. If it's simple random, then ②I. But if in quality inspection, systematic is more common, then ②II. Which is more likely?Quality inspection often uses systematic sampling because it's easier to implement on an assembly line. For example, every nth product. So even if the interval isn't a whole number, they might adjust. For 20 products and 7 samples, let's say they decide to check every 3rd product starting at a random point between 1-3. So 7 samples: starting at 1: 1,4,7,10,13,16,19. Starting at 2:2,5,8,11,14,17,20. Starting at 3:3,6,9,12,15,18,1 (if circular). So this gives 7 samples. So it's possible. Hence, ② would be systematic (II). Then problem ③ is 10 from 2000, which could be systematic (II) or simple random (I). If we pair ③ with II, then option C: ①III, ②I, ③II. But if ② is II, then ③ would be I. But how do we decide?Alternatively, maybe problem ② is simple random. Because 7 is a small sample from 20, it's easier to just randomly pick 7 rather than calculate intervals. So ②I. Then problem ③ could be systematic (II). Then option C would be the answer.Alternatively, maybe problem ③ is simple random. But 10 from 2000. If they have a list of students, simple random would require generating 10 random numbers. In practice, that's feasible with computers. But systematic might be easier if you don't have a computer. However, the problem doesn't specify the year or method used. Given that it's about daily habits, maybe they wanted a more 'spread out' sample, which systematic can achieve if the list is ordered in some way (like by class or dorm), but again, not specified.This is a bit confusing. Let me see what the answer options are. The options are:A: ①I, ②II, ③III B: ①III, ②II, ③I C: ①III, ②I, ③II D: ①II, ②I, ③IIIGiven that problem ① is almost definitely stratified (III), so options B, C, or D. Then, problem ③: if it's III, that's stratified, but there's no strata mentioned. So D pairs ③ with III, which is incorrect. So D is out. Then between B and C.Problem ②: if it's II (systematic) then B is ①III, ②II, ③I. If it's I (simple random), then C is ①III, ②I, ③II.So which is more plausible for ② and ③.In quality inspection (problem ②), systematic is common. So ②II. Then problem ③ would be simple random (I). So B: ①III, ②II, ③I. But problem ③ is 10 from 2000. If they used systematic, you get a spread-out sample, but maybe they wanted a simple random. Hmm. Alternatively, if the answer expects ③ to be simple random because there's no mention of strata or systematic, then B would be the answer.Alternatively, maybe the 2000 students are ordered in some way, and systematic is used. But since it's not mentioned, maybe the default is simple random.Wait, another angle: the three problems are to be paired with the three methods I, II, III. Each method is used exactly once. So if problem ① is stratified (III), problem ② could be systematic (II) and problem ③ simple random (I). That would be option B. Alternatively, problem ② could be simple random (I) and problem ③ systematic (II), which is option C.To decide between these, let's think again:Problem ②: 7 from 20. If it's a workshop, maybe the products are arranged in a sequence, so systematic makes sense. For example, every 3rd product. Starting at random between 1-3, then selecting every 3rd. That gives 7 products (since 3*7=21, but since 20 products, maybe they stop at 20). So for example, starting at 1: 1,4,7,10,13,16,19. That's 7. Starting at 2:2,5,8,11,14,17,20. Starting at 3:3,6,9,12,15,18,21 (but 21 doesn't exist, so maybe 3,6,9,12,15,18,20). Either way, close enough. So systematic seems feasible here.Problem ③: 10 from 2000. If they used systematic, interval is 200. Starting at a random number between 1-200, then 10 selections. That would cover the entire population spread out. But if they used simple random, it's also possible. But given that 10 is a very small sample, systematic might not be the best because it could miss certain patterns. However, if the list is random, systematic is similar to simple random. But since the problem doesn't specify the order, perhaps simple random is safer. However, given that the answer options pair ③ with II in option C, and with I in option B.The key is perhaps the third problem: if from 2000 students, 10 were sampled. That's a very small sample size. Simple random sampling is possible but might not be representative. However, stratified could be better, but there's no strata mentioned. Systematic could be used for ease. But without more info, it's hard. Maybe the answer expects ③ to be simple random.But I'm getting stuck. Let me check standard examples.Stratified sampling is used when the population has distinct subgroups (strata) and you want to ensure representation from each. So problem ① with urban and rural is definitely stratified.Systematic sampling is often used in quality control, manufacturing, etc., where you can pick every nth item. So problem ②, workshop products, likely systematic.Simple random sampling is just randomly selecting, which could be problem ③.Hence, pairing would be:① - III (stratified)② - II (systematic)③ - I (simple random)Which is option B.But wait, another thought: problem ③ is 10 from 2000. If they used systematic, they can do it easily by dividing 2000 by 10 to get 200, so every 200th. But maybe the answer expects this. However, systematic isn't mentioned. But since the answer options have to pair each method exactly once, and stratified is already used in ①, then ② and ③ have to be systematic and simple random.If ② is systematic (workshop) and ③ is simple random (students), that's B.But some might argue that ③ with systematic. Hmm.Alternatively, if problem ③ uses systematic, but the problem statement doesn't mention any ordering, so maybe it's not. Therefore, the safest is simple random. Therefore, option B: ①III, ②II, ③I.But I'm a bit uncertain. Let me confirm.In academic settings, when sampling students for daily habits, unless specified, they might use simple random sampling. Quality inspection in a workshop with products is more likely systematic. Urban/rural is stratified. Therefore, the answer is B.But wait, another angle. The third scenario says "From 2000 students, 10 were sampled". That's a very small sample size (0.5%). For such a small sample, stratified might not be feasible unless there are known strata. But since it's not mentioned, simple random or systematic. However, given the answer options, since stratified is already used in ①, ③ must be either I or II. So if ② is II (systematic), then ③ is I (simple random). Therefore, option B.Yes, I think that makes sense. So the answer is B.But wait, let me check once more. If ① is stratified, ② is systematic, ③ is simple random. So B. Yes, that seems correct.Final Answerboxed{B}</think>To determine the correct pairing of the three problems with the three random sampling methods, we need to analyze each scenario and match them with the appropriate method: Simple Random Sampling (I), Systematic Sampling (II), or Stratified Sampling (III).1. Problem ①: A university sampled 100 students from 150 urban students and 150 rural students. - Analysis: The population is divided into urban and rural strata. Sampling from each stratum indicates Stratified Sampling (III).2. Problem ②: A workshop director sampled 7 products for quality inspection from 20 products. - Analysis: Quality inspection often uses a systematic approach, such as selecting every nth product. Given 20 products and a sample of 7, systematic sampling with a random start is feasible. This indicates Systematic Sampling (II).3. Problem ③: From 2000 students, 10 were sampled to understand their daily habits. - Analysis: Without mentioning strata or a specific order, the default method is Simple Random Sampling (I).Matching each problem with the corresponding method:- ① with III (Stratified Sampling)- ② with II (Systematic Sampling)- ③ with I (Simple Random Sampling)Thus, the correct answer is (boxed{B}).]

🔑:For ①, the population clearly has two strata: students from urban areas and students from rural areas, so stratified sampling should be used to draw the sample. For ②, the total number of individuals in the population is 100, which is not very large, so simple random sampling should be used to draw the sample. By the process of elimination, the correct answer is boxed{text{C}}.

🧠:[<think>Okay, so I have this problem here about an infinite geometric progression. The problem states that the sum of the progression is 8/5, the second term is -1/2, and the common ratio q has an absolute value less than 1. They want me to find the third term. Hmm, let me recall what I know about geometric progressions.First, an infinite geometric progression (GP) has terms a, aq, aq², aq³, and so on, where a is the first term and q is the common ratio. The sum S of an infinite GP is given by the formula S = a / (1 - q), right? But this is only valid when |q| < 1, which is exactly the case here. So that formula should apply here.The problem tells me that the sum S is 8/5. So I can write that as:8/5 = a / (1 - q) ...(1)Also, they mention that the second term is -1/2. The second term of a GP is aq. So:aq = -1/2 ...(2)So now I have two equations, equation (1) and equation (2), with two variables a and q. I need to solve these equations to find a and q, and then once I have those, the third term would be aq², which is the third term. That seems straightforward.Let me write down the two equations again:1) 8/5 = a / (1 - q)2) aq = -1/2So from equation (2), I can express a in terms of q. If I solve for a, then a = (-1/2) / q. Let me substitute this into equation (1).Substituting a into equation (1):8/5 = [ (-1/2)/q ] / (1 - q )Let me simplify that. The numerator is (-1/2)/q, and the denominator is (1 - q). So dividing those would be:[ (-1/2)/q ] / (1 - q ) = (-1)/(2q(1 - q))So:8/5 = (-1)/(2q(1 - q))Hmm, let's write that as:(-1)/(2q(1 - q)) = 8/5Multiplying both sides by 2q(1 - q):-1 = (8/5)(2q(1 - q))Let me compute the right-hand side. 8/5 times 2 is 16/5, so:-1 = (16/5)q(1 - q)Multiply both sides by 5 to eliminate the denominator:-5 = 16q(1 - q)So:16q(1 - q) = -5Expanding the left side:16q - 16q² = -5Bring all terms to one side:16q² - 16q - 5 = 0So now I have a quadratic equation: 16q² - 16q - 5 = 0Let me try to solve this quadratic equation. The quadratic formula is q = [16 ± sqrt( (-16)^2 - 4*16*(-5) )]/(2*16)Calculating the discriminant first:Discriminant D = (-16)^2 - 4*16*(-5) = 256 + 320 = 576Square root of 576 is 24. So:q = [16 ± 24]/32So two solutions:q = (16 + 24)/32 = 40/32 = 5/4 = 1.25q = (16 - 24)/32 = (-8)/32 = -1/4 = -0.25But wait, the problem says |q| < 1. So q = 5/4 is 1.25, which has an absolute value greater than 1, so that's invalid. Therefore, the only valid solution is q = -1/4.So q = -1/4. Then, from equation (2), aq = -1/2, so a = (-1/2)/q = (-1/2)/(-1/4) = (-1/2)*(-4/1) = 2So a = 2. Let me check if these values satisfy equation (1):Sum S = a / (1 - q) = 2 / (1 - (-1/4)) = 2 / (1 + 1/4) = 2 / (5/4) = 2*(4/5) = 8/5. Yes, that matches the given sum. So that's correct.Therefore, the first term a is 2, common ratio q is -1/4. Now, the third term is aq².Let me compute that:Third term = 2 * (-1/4)² = 2 * (1/16) = 2/16 = 1/8So the third term is 1/8. Let me double-check everything to make sure I didn't make any mistakes.First, confirmed that q = -1/4 and a = 2. Then:First term: 2Second term: 2*(-1/4) = -1/2, which matches the given second term.Third term: -1/2 * (-1/4) = 1/8. Yes, that's correct.Sum is 8/5, which we confirmed earlier. All checks out.So the third term is 1/8.Final AnswerThe third term of the geometric progression is boxed{dfrac{1}{8}}.</think>Given an infinite geometric progression with a common ratio ( |q| < 1 ), where the sum is ( frac{8}{5} ) and the second term is ( -frac{1}{2} ), we need to find the third term.First, recall the sum ( S ) of an infinite geometric progression:[S = frac{a}{1 - q}]Given ( S = frac{8}{5} ), we have:[frac{8}{5} = frac{a}{1 - q} quad text{(1)}]The second term of the geometric progression is given by ( aq ):[aq = -frac{1}{2} quad text{(2)}]From equation (2), solve for ( a ):[a = frac{-1/2}{q}]Substitute ( a ) into equation (1):[frac{8}{5} = frac{-1/2}{q(1 - q)}]Simplify:[frac{8}{5} = frac{-1}{2q(1 - q)}]Multiply both sides by ( 2q(1 - q) ):[-1 = frac{16}{5} q(1 - q)]Multiply both sides by 5:[-5 = 16q(1 - q)]Expand and rearrange:[16q^2 - 16q - 5 = 0]Solve the quadratic equation using the quadratic formula ( q = frac{-b pm sqrt{b^2 - 4ac}}{2a} ):[q = frac{16 pm sqrt{256 + 320}}{32} = frac{16 pm 24}{32}]This gives two solutions:[q = frac{40}{32} = frac{5}{4} quad text{(discarded, since } |q| geq 1text{)}][q = frac{-8}{32} = -frac{1}{4}]Using ( q = -frac{1}{4} ), solve for ( a ) from equation (2):[a = frac{-1/2}{-1/4} = 2]The third term is ( aq^2 ):[2 left( -frac{1}{4} right)^2 = 2 left( frac{1}{16} right) = frac{1}{8}]The third term of the geometric progression is (boxed{dfrac{1}{8}}).,<think>Okay, let's see. I need to find the third term of an infinite geometric progression. The problem states that the common ratio has an absolute value less than 1, so the series converges. The sum of the series is given as 8/5, and the second term is -1/2. Hmm, let's recall the formulas for geometric progressions.First, for an infinite geometric series, the sum S is given by the first term a divided by (1 - q), where q is the common ratio. So, S = a / (1 - q). Here, S is 8/5. So, we have that equation: a / (1 - q) = 8/5.Next, the second term of a geometric progression is a multiplied by q^(2-1) = a*q. The second term is given as -1/2, so another equation: a*q = -1/2.So, we have two equations:1) a / (1 - q) = 8/52) a*q = -1/2We need to solve these two equations for a and q, and then find the third term, which would be a*q^2.Alright, let's start by solving these equations. Let's denote equation 1 as:a = (8/5)*(1 - q)And equation 2 is:a = (-1/2)/qSo, since both equal a, we can set them equal to each other:(8/5)*(1 - q) = (-1/2)/qLet me write that out:(8/5)(1 - q) = (-1)/(2q)Multiply both sides by 2q to eliminate the denominators on the right side:2q*(8/5)(1 - q) = -1Simplify the left side:(16q/5)(1 - q) = -1Now, multiply out the terms:16q/5 - 16q^2/5 = -1Multiply both sides by 5 to eliminate denominators:16q - 16q^2 = -5Bring all terms to one side:-16q^2 + 16q + 5 = 0Multiply both sides by -1 to make the quadratic coefficient positive:16q^2 - 16q - 5 = 0Now, we have a quadratic equation in q. Let's solve for q using the quadratic formula. The quadratic is 16q^2 -16q -5 =0.The quadratic formula is q = [16 ± sqrt( (-16)^2 -4*16*(-5))]/(2*16)Compute discriminant D:D = (-16)^2 -4*16*(-5) = 256 + 320 = 576Square root of 576 is 24.So, q = [16 ±24]/32Compute both possibilities:First solution: (16 +24)/32 = 40/32 = 5/4 = 1.25Second solution: (16 -24)/32 = (-8)/32 = -1/4 = -0.25But the problem states that |q| <1, so q must have absolute value less than 1. Therefore, q=5/4 is invalid because 5/4 is 1.25 which has absolute value greater than 1. So we discard that. The other solution is q = -1/4, which is -0.25, and |q| = 1/4 <1. So that's valid.Therefore, q = -1/4.Now, substitute q into equation 2 to find a. Equation 2 is a*q = -1/2.So, a*(-1/4) = -1/2Multiply both sides by (-4):a = (-1/2)*(-4) = 2Therefore, a = 2.Now, the third term of the geometric progression is a*q^2.Compute that:a*q^2 = 2*(-1/4)^2 = 2*(1/16) = 2/16 = 1/8So, the third term is 1/8.Wait a second, let me check that again. The third term is a*q^{3-1} = a*q^2. Yes, since the first term is a*q^0, second is a*q^1, third is a*q^2. So that's correct.But let me double-check the calculations to make sure I didn't make an error.First, check the quadratic equation:We started with (8/5)(1 - q) = (-1)/(2q)Multiply both sides by 2q: 16q/5*(1 - q) = -1Wait, no, wait:Wait, left side is (8/5)(1 - q)*2q = (16q/5)(1 - q). Right.Then expanding: 16q/5 -16q^2/5 = -1. Multiply by 5: 16q -16q^2 = -5. Bring all to left: 16q^2 -16q -5 =0. Correct.Then discriminant: 256 + 320 = 576. sqrt(576)=24. So solutions (16 +24)/32=40/32=5/4. (16-24)/32=-8/32=-1/4. Correct.So q=-1/4. Then a= (-1/2)/q= (-1/2)/(-1/4)= 2. Correct.Third term is a*q^2=2*(1/16)=1/8. So 1/8. Hmmm.But let's verify the sum as well. If a=2, q=-1/4.Sum S= a/(1 - q)=2/(1 - (-1/4))=2/(5/4)=8/5. Which matches the given sum. Also, the second term is a*q=2*(-1/4)= -1/2, which matches. So all checks out.Therefore, the third term is indeed 1/8.Final AnswerThe third term of the geometric progression is boxed{dfrac{1}{8}}.</think>Given an infinite geometric progression with a common ratio (|q| < 1), the sum of the series is ( frac{8}{5} ) and the second term is ( -frac{1}{2} ). We need to find the third term.1. The sum ( S ) of an infinite geometric series is given by: [ S = frac{a}{1 - q} ] Here, ( S = frac{8}{5} ), so: [ frac{a}{1 - q} = frac{8}{5} ]2. The second term of the geometric progression is given by ( aq ): [ aq = -frac{1}{2} ]3. Solving the equations: [ a = frac{8}{5}(1 - q) ] [ a = frac{-frac{1}{2}}{q} ]4. Equating the two expressions for ( a ): [ frac{8}{5}(1 - q) = frac{-frac{1}{2}}{q} ]5. Multiplying both sides by ( 2q ): [ frac{16q}{5}(1 - q) = -1 ]6. Simplifying and solving the quadratic equation: [ 16q - 16q^2 = -5 ] [ 16q^2 - 16q - 5 = 0 ]7. Using the quadratic formula ( q = frac{-b pm sqrt{b^2 - 4ac}}{2a} ): [ q = frac{16 pm 24}{32} ] [ q = frac{40}{32} = frac{5}{4} quad text{(discarded as } |q| geq 1 text{)} ] [ q = frac{-8}{32} = -frac{1}{4} ]8. Substituting ( q = -frac{1}{4} ) into ( aq = -frac{1}{2} ): [ a left(-frac{1}{4}right) = -frac{1}{2} ] [ a = 2 ]9. The third term is ( aq^2 ): [ aq^2 = 2 left(-frac{1}{4}right)^2 = 2 left(frac{1}{16}right) = frac{1}{8} ]The third term of the geometric progression is (boxed{dfrac{1}{8}}).]

🔑:Solution.Using the formulas S=frac{b_{1}}{1-q} and b_{n}=b_{1} q^{n-1}, we get left{begin{array}{l}frac{b_{1}}{1-q}=frac{8}{5}, b_{1} q=-frac{1}{2}end{array} Rightarrowright.Rightarrow b_{1}=frac{8-5 q}{5}, 16 q^{2}-16 q-5=0, from which we find q_{1}=-frac{1}{4}, q_{2}=frac{5}{4}>1 (does not fit). Then b_{3}=b_{1} q^{2}=left(-frac{1}{2}right) cdotleft(-frac{1}{4}right)=frac{1}{8}.Answer: frac{1}{8}.

🧠:[<think>Okay, so I need to find the minimum value of the expression (4^{a} + 2^{-b}) given that the real numbers (a) and (b) satisfy the equation (a - frac{1}{2}b = 1). Hmm, let's start by understanding what the problem is asking. First, maybe I can express one variable in terms of the other using the given equation. That way, I can substitute into the expression we need to minimize, turning it into a single variable function, which might be easier to handle. Let me try that.The given equation is (a - frac{1}{2}b = 1). Let me solve for (a) first. If I add (frac{1}{2}b) to both sides, I get:(a = 1 + frac{1}{2}b).Alternatively, I could solve for (b) instead. Let's see. If I subtract (a) from both sides:(-frac{1}{2}b = 1 - a), then multiply both sides by (-2):(b = 2(a - 1)).So either way, I can express (a) in terms of (b) or (b) in terms of (a). Maybe substituting into the expression (4^{a} + 2^{-b}) will help. Let's choose one substitution. Let me express (b) in terms of (a) because 2^{-b} might be easier to handle if I know (b) in terms of (a).Since (b = 2(a - 1)), substituting into (2^{-b}) gives:(2^{-2(a - 1)} = 2^{-2a + 2} = 2^{2} cdot 2^{-2a} = 4 cdot 2^{-2a}).Alternatively, (4^{a}) can be written as (2^{2a}). So the original expression becomes:(2^{2a} + 4 cdot 2^{-2a}).Hmm, that looks like a function in terms of (2^{2a}). Let me let (x = 2^{2a}). Then, since (2^{-2a} = frac{1}{x}), so the expression becomes:(x + frac{4}{x}).So now, the problem reduces to finding the minimum value of (x + frac{4}{x}) where (x > 0) (since (2^{2a}) is always positive). I remember from algebra that the minimum of a function like (x + frac{k}{x}) (where (k > 0)) occurs at (x = sqrt{k}), and the minimum value is (2sqrt{k}). So applying this here, where (k = 4), the minimum would be at (x = sqrt{4} = 2), and the minimum value is (2 times sqrt{4} = 4). Wait, hold on, let me verify that. If we use the AM-GM inequality on (x) and (4/x), then:(frac{x + frac{4}{x}}{2} geq sqrt{x cdot frac{4}{x}} = sqrt{4} = 2).Multiplying both sides by 2 gives:(x + frac{4}{x} geq 4).Equality holds when (x = frac{4}{x}), so when (x^2 = 4), so (x = 2). Since (x > 0), we take the positive root. So yes, the minimum is 4, achieved when (x = 2).But wait, (x = 2^{2a}), so:(2^{2a} = 2)Taking log base 2 of both sides:(2a = 1 implies a = frac{1}{2})Then, since (b = 2(a - 1)):(b = 2left(frac{1}{2} - 1right) = 2(-frac{1}{2}) = -1)So when (a = frac{1}{2}) and (b = -1), the expression (4^{a} + 2^{-b}) reaches its minimum value of 4.Let me double-check this. Substitute (a = frac{1}{2}) into (4^{a}):(4^{1/2} = 2)And substitute (b = -1) into (2^{-b}):(2^{-(-1)} = 2^{1} = 2)So adding them together: 2 + 2 = 4. That's correct.Alternatively, let me try using calculus to confirm. If we consider the function (f(x) = x + 4/x), then the derivative is (f'(x) = 1 - 4/x^2). Setting this equal to zero:(1 - 4/x^2 = 0 implies x^2 = 4 implies x = 2). Then the second derivative is (8/x^3), which is positive when x > 0, so it's a minimum. Therefore, the calculus approach also confirms that the minimum is 4 at x = 2.So all methods seem to agree. Therefore, the minimum value is 4. But just to be thorough, let me check if there could be any other critical points or if perhaps substituting differently might lead to another answer. For example, what if I had expressed a in terms of b instead?Given (a = 1 + frac{1}{2}b), then substituting into (4^{a} + 2^{-b}):(4^{1 + frac{1}{2}b} + 2^{-b})Which can be written as (4 cdot 4^{frac{1}{2}b} + 2^{-b} = 4 cdot 2^{b} + 2^{-b}).Let me denote (y = 2^{b}), then (2^{-b} = 1/y). So the expression becomes:(4y + frac{1}{y}).Again, similar to before, to find the minimum of (4y + 1/y), where y > 0. Let's use calculus here. The derivative is (4 - 1/y^2). Setting equal to zero:(4 - 1/y^2 = 0 implies 1/y^2 = 4 implies y^2 = 1/4 implies y = 1/2) (since y > 0).Then the second derivative is (2/y^3), which is positive when y > 0, so it's a minimum. Substituting y = 1/2 into the expression:(4*(1/2) + 1/(1/2) = 2 + 2 = 4), same result. And since y = 2^{b} = 1/2, then (b = log_2(1/2) = -1), which again gives a = 1 + (1/2)*(-1) = 1 - 0.5 = 0.5. So same values for a and b. Therefore, regardless of substitution, the minimum is 4.Alternatively, using AM-GM inequality on 4y and 1/y:Let me note that AM-GM for two terms says that (frac{4y + frac{1}{y}}{2} geq sqrt{4y cdot frac{1}{y}} = sqrt{4} = 2). Then multiplying both sides by 2: (4y + frac{1}{y} geq 4). Equality holds when (4y = frac{1}{y}) which implies (4y^2 = 1) so (y^2 = 1/4), so y = 1/2. Again, same result.Therefore, whether I express in terms of a or b, use substitution, calculus, or AM-GM, the minimum is 4. So I think that's solid.Let me just check if there's another approach, maybe Lagrange multipliers? Although that might be overcomplicating for such a problem, but just to try.We need to minimize f(a,b) = 4^a + 2^{-b} subject to the constraint g(a,b) = a - (1/2)b - 1 = 0.Using Lagrange multipliers, set up the gradient of f equal to lambda gradient of g.Compute partial derivatives:df/da = ln(4) * 4^adf/db = -ln(2) * 2^{-b}dg/da = 1dg/db = -1/2So the equations are:ln(4) * 4^a = lambda * 1- ln(2) * 2^{-b} = lambda * (-1/2)And the constraint a - (1/2)b = 1From the first equation: lambda = ln(4) * 4^aFrom the second equation: -ln(2) * 2^{-b} = (-1/2) lambda => Multiply both sides by (-2):2 ln(2) * 2^{-b} = lambdaTherefore, lambda = 2 ln(2) * 2^{-b}Set equal to the first expression for lambda:ln(4) * 4^a = 2 ln(2) * 2^{-b}But ln(4) is 2 ln(2), so:2 ln(2) * 4^a = 2 ln(2) * 2^{-b}Divide both sides by 2 ln(2):4^a = 2^{-b}Express 4^a as 2^{2a}, so:2^{2a} = 2^{-b} => 2a = -b => b = -2aNow, plug this into the constraint equation a - (1/2)b = 1:a - (1/2)(-2a) = 1 => a + a = 1 => 2a = 1 => a = 1/2Then, since b = -2a, b = -2*(1/2) = -1So again, a = 1/2, b = -1, and substituting into f(a,b) gives 4^{1/2} + 2^{-(-1)} = 2 + 2 = 4. So Lagrange multipliers also lead to the same conclusion. Therefore, all methods converge to the minimum value of 4. I think this confirms that the answer is indeed 4. Let me just recap all steps to ensure I haven't made any miscalculations.1. Expressed either a or b in terms of the other variable using the linear constraint.2. Substituted into the original expression to get a single-variable function.3. Recognized the form (x + c/x), applied AM-GM or calculus to find the minimum.4. Checked using another substitution to confirm consistency.5. Even applied Lagrange multipliers, which is a more advanced method, just to be thorough.6. Verified the critical points by plugging back into the original equation and confirmed the result.All steps check out. No miscalculations detected. Therefore, confident that the minimum value is 4.Final AnswerThe minimum value is boxed{4}.</think>Given the real numbers (a) and (b) that satisfy the equation (a - frac{1}{2}b = 1), we need to find the minimum value of (4^a + 2^{-b}).First, we express (b) in terms of (a) using the given equation:[a - frac{1}{2}b = 1 implies b = 2(a - 1)]Substituting (b = 2(a - 1)) into the expression (4^a + 2^{-b}), we get:[4^a + 2^{-2(a - 1)} = 4^a + 4 cdot 2^{-2a}]Rewriting (4^a) as (2^{2a}) and (2^{-2a}) as (frac{1}{2^{2a}}), we let (x = 2^{2a}). The expression then becomes:[x + frac{4}{x}]To find the minimum value of (x + frac{4}{x}) for (x > 0), we use the AM-GM inequality:[frac{x + frac{4}{x}}{2} geq sqrt{x cdot frac{4}{x}} = 2 implies x + frac{4}{x} geq 4]Equality holds when (x = frac{4}{x}), which gives (x = 2). Substituting back, we get (2^{2a} = 2 implies 2a = 1 implies a = frac{1}{2}). Using (b = 2(a - 1)), we find (b = -1).Substituting (a = frac{1}{2}) and (b = -1) into the original expression:[4^{1/2} + 2^{-(-1)} = 2 + 2 = 4]This confirms the minimum value is indeed 4. Using calculus or Lagrange multipliers also leads to the same result.Thus, the minimum value of (4^a + 2^{-b}) is (boxed{4}).,<think>Okay, so I need to find the minimum value of the expression (4^{a} + 2^{-b}) given that the real numbers (a) and (b) satisfy the equation (a - frac{1}{2}b = 1). Hmm, let me start by understanding the problem step by step.First, the constraint is (a - frac{1}{2}b = 1). Maybe I can express one variable in terms of the other to reduce the number of variables in the expression we need to minimize. Let me solve the constraint equation for (a) or (b).Let me solve for (a):(a = 1 + frac{1}{2}b)Alternatively, solving for (b):Multiply both sides by 2: (2a - b = 2), so (b = 2a - 2)Hmm, both ways are possible. Maybe substituting (a) in terms of (b) into the expression (4^{a} + 2^{-b}) would make it a function of a single variable, which I can then minimize. Let me try that.Since (4^{a}) can be written as (2^{2a}), and (2^{-b}) is already a power of 2. Maybe this common base will help.Given that (a = 1 + frac{1}{2}b), substituting into (4^{a}):(4^{a} = 4^{1 + frac{1}{2}b} = 4 cdot 4^{frac{1}{2}b} = 4 cdot (2^{2})^{frac{1}{2}b} = 4 cdot 2^{b}). Wait, let me check:Wait, (4^{frac{1}{2}b}) is ((2^2)^{frac{1}{2}b} = 2^{2 cdot frac{1}{2}b} = 2^{b}). So yes, (4^{1 + frac{1}{2}b} = 4 cdot 2^{b}).Therefore, the original expression becomes:(4^{a} + 2^{-b} = 4 cdot 2^{b} + 2^{-b}).So now, we need to find the minimum of (4 cdot 2^{b} + 2^{-b}).Alternatively, if I substitute (b = 2a - 2) into the expression:Original expression is (4^{a} + 2^{-b}). If (b = 2a - 2), then ( -b = -2a + 2). So:(4^{a} + 2^{-b} = 4^{a} + 2^{-2a + 2} = 4^{a} + 4 cdot 2^{-2a}).But (4^{a}) is (2^{2a}), so (4^{a} = (2^{a})^{2}), and (2^{-2a} = (2^{-a})^{2}). Hmm, but maybe that's not helpful. Let's see.Wait, let's rewrite (4^{a} + 4 cdot 2^{-2a}) in terms of a single exponent. Let me let (t = 2^{a}). Then, (4^{a} = t^{2}), and (2^{-2a} = (2^{a})^{-2} = t^{-2}). Therefore, the expression becomes:(t^{2} + 4 cdot t^{-2}).So, we have the expression in terms of (t): (t^2 + frac{4}{t^2}). Now, to find the minimum of this expression for (t > 0) (since (t = 2^{a}) which is always positive). That seems more manageable.Alternatively, when we had substituted (a) in terms of (b), we got the expression in terms of (b): (4 cdot 2^{b} + 2^{-b}). Let me check if that's equivalent.Wait, substituting (a = 1 + frac{1}{2}b) into (4^{a}) gives (4^{1 + frac{1}{2}b} = 4 cdot 4^{frac{1}{2}b} = 4 cdot 2^{b}), as before. Then, (2^{-b}) is just (2^{-b}). So the expression is (4 cdot 2^{b} + 2^{-b}). Let me denote (y = 2^{b}), then (2^{-b} = frac{1}{y}). So the expression becomes (4y + frac{1}{y}). Then, the problem reduces to finding the minimum of (4y + frac{1}{y}) for (y > 0).Either substitution seems to lead to a similar type of expression. Let me see which one is easier.First approach: (t^2 + frac{4}{t^2}), second approach: (4y + frac{1}{y}). The second one seems simpler. Let me work with the second one.So, let's focus on (4y + frac{1}{y}) with (y > 0). To find its minimum, I can use calculus or the AM-GM inequality.By AM-GM inequality, for positive numbers, the arithmetic mean is greater than or equal to the geometric mean. Let's see:For the terms (4y) and (frac{1}{y}), there are two terms. The AM-GM inequality states that (frac{4y + frac{1}{y}}{2} geq sqrt{4y cdot frac{1}{y}} = sqrt{4} = 2). Therefore:(frac{4y + frac{1}{y}}{2} geq 2 implies 4y + frac{1}{y} geq 4).But wait, equality holds when (4y = frac{1}{y}), that is, when (4y^2 = 1 implies y^2 = frac{1}{4} implies y = frac{1}{2}) (since (y > 0)).Therefore, the minimum value of (4y + frac{1}{y}) is 4, achieved when (y = frac{1}{2}).But wait, let me verify this with calculus as well to make sure.Let (f(y) = 4y + frac{1}{y}). Then, the derivative is (f'(y) = 4 - frac{1}{y^2}). Setting derivative to zero:(4 - frac{1}{y^2} = 0 implies 4 = frac{1}{y^2} implies y^2 = frac{1}{4} implies y = frac{1}{2}).Then, second derivative (f''(y) = frac{2}{y^3}), which is positive when (y > 0), so it's a minimum. Therefore, the minimum is indeed at (y = frac{1}{2}), and the minimum value is (4 cdot frac{1}{2} + frac{1}{frac{1}{2}} = 2 + 2 = 4). So that's correct.Therefore, the minimum of the expression (4 cdot 2^{b} + 2^{-b}) is 4, achieved when (y = frac{1}{2}), which is (2^{b} = frac{1}{2} implies b = -1).Then, since (a = 1 + frac{1}{2}b), substituting (b = -1) gives:(a = 1 + frac{1}{2}(-1) = 1 - frac{1}{2} = frac{1}{2}).Therefore, the minimum value is 4, achieved at (a = frac{1}{2}), (b = -1).Alternatively, if we had used the other substitution where the expression became (t^2 + frac{4}{t^2}), we can also apply AM-GM here. The terms are (t^2) and (frac{4}{t^2}). Applying AM-GM:(frac{t^2 + frac{4}{t^2}}{2} geq sqrt{t^2 cdot frac{4}{t^2}} = sqrt{4} = 2). Therefore, (t^2 + frac{4}{t^2} geq 4), with equality when (t^2 = frac{4}{t^2} implies t^4 = 4 implies t = sqrt[4]{4} = sqrt{2}). Then, since (t = 2^{a}), (2^{a} = sqrt{2} implies a = frac{1}{2}). Then (b = 2a - 2 = 2 cdot frac{1}{2} - 2 = 1 - 2 = -1). Same result. So both methods lead to the same minimum value.Therefore, the minimum value is 4.But let me double-check my steps to make sure I didn't make a mistake.First, starting with the constraint (a - frac{1}{2}b = 1), solving for (a = 1 + frac{1}{2}b). Substituting into (4^{a} + 2^{-b}), gives (4^{1 + frac{1}{2}b} + 2^{-b}). Then, simplifying (4^{1 + frac{1}{2}b}) as (4 cdot 2^{b}). Therefore, the expression becomes (4 cdot 2^{b} + 2^{-b}). Let (y = 2^{b}), so expression becomes (4y + frac{1}{y}). Then, using AM-GM, found minimum at (y = frac{1}{2}), which gives (b = -1), then (a = frac{1}{2}). Plugging back into original expression: (4^{frac{1}{2}} + 2^{-(-1)} = 2 + 2^{1} = 2 + 2 = 4). Correct.Alternatively, using substitution (b = 2a - 2), so expression becomes (4^{a} + 2^{-2a + 2}). Then, simplifying to (4^{a} + 4 cdot 2^{-2a}). Let (t = 2^{a}), so expression is (t^2 + frac{4}{t^2}), which by AM-GM is minimized at (t = sqrt{2}), so (a = frac{1}{2}), (b = -1), same result.Another way to check is using calculus for the expression in terms of (b). Let me try that as well.Original expression after substitution: (4 cdot 2^{b} + 2^{-b}). Let (f(b) = 4 cdot 2^{b} + 2^{-b}).Take derivative with respect to (b):(f'(b) = 4 cdot ln 2 cdot 2^{b} - ln 2 cdot 2^{-b}).Set derivative to zero:(4 cdot ln 2 cdot 2^{b} - ln 2 cdot 2^{-b} = 0)Factor out (ln 2):(ln 2 (4 cdot 2^{b} - 2^{-b}) = 0)Since (ln 2 neq 0), we have:(4 cdot 2^{b} - 2^{-b} = 0)Multiply both sides by (2^{b}):(4 cdot (2^{b})^2 - 1 = 0 implies 4 cdot (2^{b})^2 = 1 implies (2^{b})^2 = frac{1}{4} implies 2^{b} = frac{1}{2}) (since (2^{b} > 0))Taking log base 2:(b = log_2 left( frac{1}{2} right) = -1). Then, (a = 1 + frac{1}{2}(-1) = frac{1}{2}), as before. So the critical point is at (b = -1), (a = frac{1}{2}), and the value is indeed 4. Second derivative test:Compute the second derivative:(f''(b) = 4 cdot (ln 2)^2 cdot 2^{b} + (ln 2)^2 cdot 2^{-b}). Since all terms are positive (as exponentials are positive and constants squared are positive), (f''(b) > 0), so it's a minimum. Therefore, calculus confirms the minimum is 4.Alternatively, if I had chosen to work with variable (a) instead, let me see:Original expression after substitution: (4^{a} + 2^{-b}) with (b = 2a - 2). So, substituting (b):(4^{a} + 2^{-(2a - 2)} = 4^{a} + 2^{-2a + 2} = 4^{a} + 4 cdot 2^{-2a}). Let me write (4^{a}) as (2^{2a}):So, (2^{2a} + 4 cdot 2^{-2a}). Let me let (t = 2^{2a}), then (2^{-2a} = frac{1}{t}). So the expression is (t + frac{4}{t}). Again, this is similar to the previous expressions. By AM-GM, (frac{t + frac{4}{t}}{2} geq sqrt{t cdot frac{4}{t}} = sqrt{4} = 2). Therefore, (t + frac{4}{t} geq 4), equality when (t = frac{4}{t} implies t^2 = 4 implies t = 2). So (2^{2a} = 2 implies 2a = 1 implies a = frac{1}{2}). Then (b = 2a - 2 = 1 - 2 = -1). Same result.So regardless of the substitution method, whether I express in terms of (a) or (b), I end up with an expression that can be minimized using AM-GM or calculus, leading to the same minimum value of 4.Therefore, the minimum value of (4^{a} + 2^{-b}) under the constraint (a - frac{1}{2}b = 1) is 4.Just to make sure there's no oversight, let me try plugging in some other values of (a) and (b) that satisfy the constraint to see if the expression is indeed larger than 4.For example, take (a = 1), then from the constraint (1 - frac{1}{2}b = 1 implies frac{1}{2}b = 0 implies b = 0). Then, the expression is (4^{1} + 2^{0} = 4 + 1 = 5), which is larger than 4. Good.Another example: (a = 0), then (0 - frac{1}{2}b = 1 implies frac{1}{2}b = -1 implies b = -2). Then, the expression is (4^{0} + 2^{-(-2)} = 1 + 2^{2} = 1 + 4 = 5), again larger than 4.Another point: (a = frac{1}{2}), (b = -1) as found. Then, (4^{frac{1}{2}} + 2^{-(-1)} = 2 + 2^{1} = 2 + 2 = 4). Correct.Another test: Let me take (a = 2), then from the constraint (2 - frac{1}{2}b = 1 implies frac{1}{2}b = 1 implies b = 2). Then, the expression is (4^{2} + 2^{-2} = 16 + frac{1}{4} = 16.25), which is way larger.How about (a = frac{3}{4}), then (b = 2a - 2 = frac{3}{2} - 2 = -frac{1}{2}). Then, the expression is (4^{frac{3}{4}} + 2^{frac{1}{2}} = (2^2)^{frac{3}{4}} + sqrt{2} = 2^{frac{3}{2}} + sqrt{2} = 2 sqrt{2} + sqrt{2} = 3 sqrt{2} approx 4.2426), which is still more than 4.Hence, it seems consistent that 4 is indeed the minimal value.Therefore, after careful consideration and multiple methods, the minimum value is 4.Final AnswerThe minimum value is boxed{4}.</think>Given the problem where real numbers (a) and (b) satisfy (a - frac{1}{2}b = 1), we need to find the minimum value of (4^a + 2^{-b}).First, we express (a) in terms of (b) using the constraint:[a = 1 + frac{1}{2}b]Substituting this into the expression (4^a + 2^{-b}), we get:[4^{1 + frac{1}{2}b} + 2^{-b}]Simplifying (4^{1 + frac{1}{2}b}):[4^{1 + frac{1}{2}b} = 4 cdot 4^{frac{1}{2}b} = 4 cdot 2^b]Thus, the expression becomes:[4 cdot 2^b + 2^{-b}]Let (y = 2^b). Then, the expression transforms to:[4y + frac{1}{y}]Using the AM-GM inequality on the terms (4y) and (frac{1}{y}):[frac{4y + frac{1}{y}}{2} geq sqrt{4y cdot frac{1}{y}} = 2][4y + frac{1}{y} geq 4]Equality holds when (4y = frac{1}{y}), which implies (y = frac{1}{2}). Therefore, (2^b = frac{1}{2}) gives (b = -1). Substituting (b = -1) back into the constraint (a = 1 + frac{1}{2}b):[a = 1 + frac{1}{2}(-1) = frac{1}{2}]Verifying the minimum value with (a = frac{1}{2}) and (b = -1):[4^{frac{1}{2}} + 2^{-(-1)} = 2 + 2 = 4]Thus, the minimum value of (4^a + 2^{-b}) is (boxed{4}).]

🔑:35.4 ;

🧠:[<think>Okay, so I have this problem about a blacksmith building a horizontal iron fence with vertical bars. The bars are 18 cm apart from each other. Between each pair of adjacent bars, there's a curved bar that's an arc of a circle. The highest point of each arc is 3√3 cm from the dashed line that goes through the tops of all the vertical bars. I need to find the length of each curved bar. The options are given, so I need to figure out which one is correct.First, let me visualize this. There are vertical bars spaced 18 cm apart. The tops of all these bars are aligned along a horizontal line (the dashed line). The curved bars connect the ends of each pair of adjacent vertical bars. Each curved bar is an arc of a circle, and the highest point of this arc is 3√3 cm below the dashed line. So, the arc is like a bridge connecting two vertical bars, 18 cm apart, and the peak of the bridge is 3√3 cm lower than the top of the vertical bars.Wait, actually, the problem says the highest point is 3√3 cm from the line that passes through the upper ends. Since the curved bars are connecting the upper ends (assuming the vertical bars are all the same height, with the top at the dashed line), then the arc goes from one top to another, but sags down in the middle. So, the highest point of the arc is actually the midpoint of the arc, which is sagging down by 3√3 cm. Hmm, but wait, if it's an arc of a circle, then the highest point would be the midpoint if the arc is symmetric. So, the arc is part of a circle, connecting two points 18 cm apart, with the midpoint sagging down by 3√3 cm. So, this is like a circular arc where the chord length is 18 cm, and the sagitta (the distance from the chord to the arc) is 3√3 cm.Yes, that makes sense. The sagitta of a circular arc is the distance from the chord to the arc. So, in this case, the chord is the line connecting the tops of two adjacent vertical bars, which is 18 cm long, and the sagitta is 3√3 cm. The problem is asking for the length of the arc.I remember there's a formula relating the sagitta (s), the chord length (c), and the radius (r) of the circle. Let me recall. The sagitta formula is s = r - √(r² - (c/2)²). Let me verify that. If you have a circle of radius r, and a chord of length c, then the sagitta is the distance from the chord to the arc. The sagitta s is equal to r minus the distance from the center of the circle to the chord. The distance from the center to the chord is √(r² - (c/2)²), so s = r - √(r² - (c/2)²). That seems right.So, given that, we can solve for r in terms of s and c. Let's plug in the given values. Here, s = 3√3 cm, and c = 18 cm. Let's write the equation:3√3 = r - √(r² - (9)^2)Because c/2 is 9 cm. So:3√3 = r - √(r² - 81)Let's solve for r. Let's rearrange the equation:√(r² - 81) = r - 3√3Now, square both sides to eliminate the square root:r² - 81 = (r - 3√3)^2Expand the right-hand side:r² - 81 = r² - 6√3 r + 9*3Simplify:r² - 81 = r² - 6√3 r + 27Subtract r² from both sides:-81 = -6√3 r + 27Now, subtract 27 from both sides:-108 = -6√3 rDivide both sides by -6√3:r = (-108)/(-6√3) = 18/√3 = 6√3 cmSo, the radius of the circle is 6√3 cm. Now, we need to find the length of the arc. The length of the arc depends on the central angle θ (in radians) subtended by the chord. The formula for the arc length is L = rθ.To find θ, we can use the relationship between the chord length and the radius. The chord length c = 2r sin(θ/2). So, 18 = 2*6√3 sin(θ/2). Simplify:18 = 12√3 sin(θ/2)Divide both sides by 12√3:sin(θ/2) = 18 / (12√3) = (3)/(2√3) = (√3)/2 after rationalizing.So sin(θ/2) = √3/2. The angle whose sine is √3/2 is π/3 radians (60 degrees). Therefore, θ/2 = π/3, so θ = 2π/3 radians.Therefore, the arc length L = rθ = 6√3 * (2π/3) = 4√3 π cm.Looking at the options, that's option D: 4π√3 cm.Wait, but let me double-check. The chord length is 18 cm, the radius is 6√3 cm. Let's check if 2r sin(θ/2) gives 18:2*6√3 sin(θ/2) = 12√3 sin(θ/2) = 18 => sin(θ/2) = 18/(12√3) = 3/(2√3) = √3/2, which is correct. Then θ/2 = π/3, θ = 2π/3. Then arc length is rθ = 6√3 * 2π/3 = 4√3 π. So that's 4π√3 cm, which is option D.But wait, the answer choices include options like 8π(√3−1) and others. Let me check if I made a mistake in interpreting the problem.Wait, the problem says the highest point of the arc is 3√3 cm from the line passing through the upper ends. But the line is the dashed line that passes through the upper ends of all the bars, which is horizontal. So the vertical distance from the highest point of the arc to the dashed line is 3√3 cm. That is, the arc is sagging downward by 3√3 cm. So the sagitta s is 3√3 cm. So my initial approach was correct, right?But the answer I got is 4π√3 cm, which is option D. However, the options given are:(A) 8π(√3−1) cm(B) 6π√3 cm(C) 12π(√3−1) cm(D) 4π√3 cm(E) 8π√3 cmSo D is an option. But let me check once more.Alternatively, perhaps the problem is referring to the arc being placed in the plane of the bars, which are vertical. The highest point is 3√3 cm from the dashed line (the line through the upper ends). So maybe the highest point is 3√3 cm below the dashed line, meaning that the sagitta is 3√3 cm. Then, the calculation is as above. So that gives us a radius of 6√3 cm and an arc length of 4π√3 cm, which is option D. Hmm.Alternatively, perhaps I need to check if the answer is different. Wait, let me check again the chord length and sagitta.Given chord length c = 18 cm, sagitta s = 3√3 cm.We have s = r - √(r² - (c/2)^2)So plugging in s = 3√3, c/2 = 9:3√3 = r - √(r² - 81)Then √(r² -81) = r - 3√3Square both sides:r² -81 = r² -6√3 r + 27Subtract r²:-81 = -6√3 r +27Subtract 27:-108 = -6√3 rDivide by -6√3:r = 108/(6√3) = 18/√3 = 6√3Yes, that's correct.Then central angle θ, from chord length c = 2r sin(θ/2):18 = 2*6√3 sin(θ/2) => 18 = 12√3 sin(θ/2) => sin(θ/2) = 18/(12√3) = 3/(2√3) = √3/2, which gives θ/2 = π/3, θ = 2π/3. Then arc length L = rθ = 6√3 * (2π/3) = 4√3 π. So 4π√3 cm, which is option D. So that's correct.Therefore, the answer is D.But let me check if the question is in fact about the vertical bars. Wait, the vertical bars are 18 cm apart. Each pair of adjacent vertical bars is connected by a curved bar. The curved bar is an arc of a circle in the plane of the bars. The highest point of the arc is 3√3 cm from the dashed line through the upper ends.Wait, if the vertical bars are all the same height, then their upper ends are on the dashed line. The arc connects two adjacent upper ends (which are 18 cm apart), and the highest point of the arc is 3√3 cm below the dashed line. Therefore, the sagitta is 3√3 cm. So the previous calculation holds. So answer D.But the options are given, so why is there an option C: 12π(√3−1) cm? Maybe I made a mistake in the central angle? Wait, let's see.Wait, chord length is 18 cm, radius is 6√3 cm. Then the central angle θ can also be calculated using the formula relating chord length and radius: chord length = 2r sin(θ/2). So 18 = 2*6√3 sin(θ/2), so sin(θ/2) = 18/(12√3) = 3/(2√3) = √3/2. So θ/2 = π/3, θ = 2π/3. So arc length is rθ = 6√3 * 2π/3 = 4√3 π. So that's 4π√3 cm. So D.Alternatively, maybe they considered the entire circle's circumference. Wait, but the arc is only 2π/3 radians. 2π/3 is 120 degrees. So 120 degrees out of 360, which is 1/3 of the circle. But the circumference of the entire circle would be 2πr = 2π*6√3 = 12√3 π. So 1/3 of that is 4√3 π, which matches. So that's correct.Alternatively, maybe the problem is not about the sagitta but about something else? Wait, let's imagine that the arc is placed such that the highest point is 3√3 cm from the dashed line. If the arc is part of a circle, then the center of the circle must be somewhere. If the arc is below the dashed line, then the center is above the dashed line.Wait, wait a second. If the arc is curved downward, then the center of the circle is above the dashed line, and the sagitta would be the distance from the chord (the dashed line) to the arc. Wait, but in this problem, the chord is between the two tops of the vertical bars, which are on the dashed line. So the chord is 18 cm, lying on the dashed line, and the arc is below it, with the highest point (which is the midpoint of the arc) being 3√3 cm below the dashed line. Therefore, the sagitta is 3√3 cm.But in the standard sagitta formula, the sagitta is the distance from the chord to the arc, so in this case, s = 3√3 cm. So the formula applies as before, and we get the radius as 6√3 cm, and arc length as 4π√3 cm. So answer D.Alternatively, maybe they are considering the arc being part of a circle whose highest point is 3√3 cm from the dashed line. Wait, but the highest point of the arc is the point closest to the dashed line? No, wait. If the arc is below the dashed line, then the highest point would be the closest point to the dashed line, which is the midpoint. So that is 3√3 cm below the dashed line. So the sagitta is 3√3 cm.Alternatively, if the arc were above the dashed line, then the highest point would be above, but in the problem statement, it's connecting the ends of each pair of adjacent bars with a curved bar in the plane of the bars. Since the bars are vertical, the plane of the bars is vertical, so the arc is in a vertical plane. The curved bar connects the upper ends of two adjacent vertical bars. So the arc is in the vertical plane, connecting two points 18 cm apart horizontally, but in the vertical plane. So the arc is like a semicircle? No, because it's specified as an arc of a circle, not necessarily a semicircle. The highest point of the arc is 3√3 cm from the dashed line. Wait, the dashed line is the line passing through the upper ends of all the bars, which is horizontal and in the same vertical plane. So the two endpoints of the arc are on the dashed line, 18 cm apart, and the arc is below the dashed line, forming a curve in the vertical plane. The highest point of the arc is its midpoint, which is 3√3 cm below the dashed line.Therefore, this is indeed a circular arc with chord length 18 cm and sagitta 3√3 cm. Therefore, the calculations are correct, leading to answer D.Alternatively, maybe my confusion arises from the term "highest point". If the arc is below the dashed line, then the "highest" point would actually be the closest point to the dashed line, which is the midpoint. So 3√3 cm below the dashed line. So the sagitta is 3√3 cm. Therefore, the previous reasoning holds.Therefore, I think the correct answer is D: 4π√3 cm.Final Answerboxed{D}</think>The problem involves finding the length of each curved bar (arc) connecting the tops of adjacent vertical bars in a fence. The vertical bars are 18 cm apart, and the highest point of each arc is 3√3 cm below the line passing through the tops of the vertical bars.1. Understanding the Sagitta: - The chord length (distance between the tops of two adjacent vertical bars) is 18 cm. - The sagitta (distance from the chord to the highest point of the arc) is 3√3 cm.2. Using the Sagitta Formula: - The formula relating sagitta ( s ), chord length ( c ), and radius ( r ) is: [ s = r - sqrt{r^2 - left(frac{c}{2}right)^2} ] - Plugging in the values ( s = 3sqrt{3} ) cm and ( c = 18 ) cm: [ 3sqrt{3} = r - sqrt{r^2 - 81} ] - Solving for ( r ): [ sqrt{r^2 - 81} = r - 3sqrt{3} ] Squaring both sides: [ r^2 - 81 = r^2 - 6sqrt{3}r + 27 ] Simplifying: [ -81 = -6sqrt{3}r + 27 ] [ -108 = -6sqrt{3}r ] [ r = frac{108}{6sqrt{3}} = 6sqrt{3} text{ cm} ]3. Calculating the Central Angle: - Using the chord length formula ( c = 2r sin(theta/2) ): [ 18 = 2 times 6sqrt{3} times sin(theta/2) ] [ sin(theta/2) = frac{18}{12sqrt{3}} = frac{sqrt{3}}{2} ] - The angle ( theta/2 = frac{pi}{3} ), so ( theta = frac{2pi}{3} ).4. Arc Length Calculation: - The arc length ( L ) is given by ( L = rtheta ): [ L = 6sqrt{3} times frac{2pi}{3} = 4sqrt{3}pi text{ cm} ]Thus, the length of each curved bar is (boxed{D}).,<think>Okay, let me try to solve this problem step by step. So, we have a horizontal iron fence with vertical bars placed 18 cm apart. The blacksmith connects each pair of adjacent bars with a curved bar that's an arc of a circle. The highest point of each arc is 3√3 cm from the dashed line that goes through the upper ends of all the bars. We need to find the length of each curved bar.First, let me visualize the setup. There are vertical bars spaced 18 cm apart. The tops of all these bars lie on a horizontal dashed line. The curved bars connecting adjacent vertical bars are arcs of circles. Each arc's highest point is 3√3 cm above this dashed line. Wait, actually, the problem says the highest point is 3√3 cm from the line. But since the line passes through the upper ends of the bars, does that mean the arc sags below the line or curves above it? Hmm.Wait, the problem says "the highest point of which is 3√3 cm from the line (dashed in the figure) that passes through the upper ends of all the bars, and is perpendicular to the bars themselves." So, the dashed line is horizontal (since it's perpendicular to the vertical bars), passing through the upper ends. The highest point of the arc is 3√3 cm from this line. But if the arc is connecting two adjacent bars, which are 18 cm apart, then the arc must curve either upwards or downwards relative to the dashed line.But the highest point is 3√3 cm from the line. If the arc curves upward, then the highest point is 3√3 cm above the dashed line. If it curves downward, the highest point is 3√3 cm below. But since the dashed line is at the top of the bars, if the arc connects the ends of the bars, which are on the dashed line, then the arc must curve downward, creating a sort of semi-circle or a circular arc below the dashed line. The highest point relative to the dashed line would actually be the lowest point of the arc, but the problem says "highest point." Wait, this might be a translation issue or a wording confusion.Wait, maybe the arc is curving upwards. If the bars are vertical, and the arc connects the upper ends (which are on the dashed line), but how can it curve upwards? If the arc is in the plane of the bars, which are vertical, so the plane is vertical. The arc is connecting two adjacent vertical bars, which are 18 cm apart horizontally. The arc is part of a circle. The highest point of the arc is 3√3 cm from the dashed line. Since the dashed line is at the top of the bars, which are connected by the arc, the arc must curve downward, so the "highest point" of the arc is at the connection points (the tops of the bars), and the lowest point is 3√3 cm below. Wait, but the problem says the highest point is 3√3 cm from the line. That seems contradictory.Wait, maybe I need to think of the arc as forming a circular segment between two vertical bars. The two vertical bars are 18 cm apart. The arc connects their upper ends. If the arc is part of a circle, then the highest point of the arc would be at the midpoint between the two bars. But since the two ends are on the dashed line, if the arc curves upward, the midpoint would be above the dashed line, and if it curves downward, the midpoint would be below.But the problem states that the highest point is 3√3 cm from the dashed line. So, if the arc curves upward, the highest point is above the dashed line, which is possible. However, the vertical bars are fixed, so their upper ends are on the dashed line. If the arc is connecting two upper ends, which are on the dashed line, and the arc is above the dashed line, then it's forming a semicircle upwards. But the distance from the dashed line to the highest point would be the radius. Wait, no. If the arc is part of a circle, then the distance from the dashed line (which is the chord connecting the two ends) to the highest point is the sagitta of the arc.Wait, yes! The sagitta is the distance from the chord to the arc. In this case, the chord is the line connecting the two upper ends of the bars, which are 18 cm apart. The sagitta is the distance from this chord to the highest point of the arc, which is 3√3 cm. But sagitta is typically the distance from the chord to the arc, so if the arc is curving upward, the sagitta would be above the chord, but here the chord is the dashed line, which is the line passing through all the upper ends. Therefore, the sagitta is 3√3 cm.Given that, we can use the formula relating the sagitta (s), the radius (r), and the chord length (c):s = r - √(r² - (c/2)²)But wait, actually, the formula for sagitta is s = r - √(r² - (c/2)²). Let me verify.Yes, the sagitta (s) is given by:s = r - √(r² - (c/2)²)Where c is the chord length (18 cm), and s is the sagitta (3√3 cm). So, we can solve for the radius r.Let's plug in the values:3√3 = r - √(r² - (9)^2)Wait, c is 18 cm, so c/2 is 9 cm. So,3√3 = r - √(r² - 81)Let me rearrange this equation:√(r² - 81) = r - 3√3Now, square both sides:r² - 81 = (r - 3√3)²Expand the right side:= r² - 6√3 r + (3√3)^2= r² - 6√3 r + 9*3= r² - 6√3 r + 27So, substituting back into the equation:r² - 81 = r² - 6√3 r + 27Subtract r² from both sides:-81 = -6√3 r + 27Subtract 27 from both sides:-108 = -6√3 rDivide both sides by -6√3:(-108)/(-6√3) = rSimplify:18/√3 = rRationalize the denominator:18/√3 = (18√3)/3 = 6√3 cmSo, the radius r is 6√3 cm.Now, the length of the arc (which is the curved bar) can be found using the formula for the length of a circular arc. The arc length L is given by:L = θ * rWhere θ is the central angle in radians.To find θ, we can use the relationship between the chord length, radius, and central angle. The chord length c is related to θ and r by:c = 2r sin(θ/2)We know c = 18 cm and r = 6√3 cm.So,18 = 2*(6√3)*sin(θ/2)Simplify:18 = 12√3 sin(θ/2)Divide both sides by 12√3:18 / (12√3) = sin(θ/2)Simplify:(3)/(2√3) = sin(θ/2)Rationalize denominator:3/(2√3) = (3√3)/(2*3) = √3/2So, sin(θ/2) = √3/2Therefore, θ/2 = π/3 (since sin(π/3) = √3/2)Hence, θ = 2π/3 radians.Now, compute the arc length L:L = θ * r = (2π/3) * 6√3 = (2π/3)*(6√3) = 4π√3 cm.Wait, but looking at the options, there is an option D: 4π√3 cm. So, that would be the answer. However, wait, let me check again.Wait, but let's confirm the sagitta formula. Sagitta s = r - √(r² - (c/2)^2). So, s = 3√3, c = 18. We solved for r and got r = 6√3. Then, using chord length formula c = 2r sin(θ/2), which gives θ = 2π/3. Then, arc length is θ*r = 2π/3 * 6√3 = 4π√3. That seems correct.But let me check if the sagitta formula was correctly applied. The sagitta is the distance from the chord to the arc. If the chord is the line between the two endpoints (on the dashed line), and the arc is curving upward, then the sagitta is the distance from the chord to the highest point of the arc, which is 3√3 cm. So, yes, that's how we applied the formula. So, the radius comes out to 6√3 cm, central angle 2π/3, arc length 4π√3. Therefore, the answer is D.But wait, let me check the options again. The options are:(A) 8π(√3−1) cm(B) 6π√3 cm(C) 12π(√3−1) cm(D) 4π√3 cm(E) 8π√3 cm.So, D is 4π√3 cm, which matches our calculation. So, seems correct.But just to be thorough, let's think again. Alternatively, maybe the arc is part of a circle that passes through the two endpoints (on the dashed line) and has its highest point 3√3 cm below the dashed line. Then, the sagitta would be 3√3 cm. But sagitta is defined as the distance from the chord to the arc. So, regardless of the direction, it's a positive value. So, the formula still applies.Alternatively, maybe the problem is referring to the arc being below the dashed line, so the sagitta is 3√3 cm. Then, our calculation is correct. So, the answer is D.Wait, but let me check once again. When we calculated the central angle θ, we found θ = 2π/3, which is 120 degrees. The arc length for 120 degrees is (120/360)*2πr = (1/3)*2πr = (2/3)πr. Which with r = 6√3 gives (2/3)π*6√3 = 4π√3. So, that's correct.Therefore, each curved bar is 4π√3 cm long, which is option D.Final Answerboxed{D}</think>The problem involves finding the length of each curved bar used to connect adjacent vertical bars in a horizontal iron fence. The vertical bars are spaced 18 cm apart, and the highest point of each arc is 3√3 cm from the dashed line passing through the upper ends of the bars.1. Understanding the Sagitta: The sagitta (s) is the distance from the chord (connecting the two upper ends of the vertical bars) to the highest point of the arc. Here, the sagitta is 3√3 cm, and the chord length (c) is 18 cm.2. Using the Sagitta Formula: The sagitta formula is: [ s = r - sqrt{r^2 - left(frac{c}{2}right)^2} ] Plugging in the values ( s = 3sqrt{3} ) and ( c = 18 ): [ 3sqrt{3} = r - sqrt{r^2 - 81} ]3. Solving for Radius (r): [ sqrt{r^2 - 81} = r - 3sqrt{3} ] Squaring both sides: [ r^2 - 81 = r^2 - 6sqrt{3}r + 27 ] Simplifying: [ -81 = -6sqrt{3}r + 27 implies -108 = -6sqrt{3}r implies r = frac{108}{6sqrt{3}} = 6sqrt{3} ]4. Finding the Central Angle (θ): Using the chord length formula ( c = 2r sinleft(frac{theta}{2}right) ): [ 18 = 2 cdot 6sqrt{3} cdot sinleft(frac{theta}{2}right) implies sinleft(frac{theta}{2}right) = frac{sqrt{3}}{2} ] Thus, ( frac{theta}{2} = frac{pi}{3} ) and ( theta = frac{2pi}{3} ).5. Calculating the Arc Length: The arc length ( L ) is given by ( L = rtheta ): [ L = 6sqrt{3} cdot frac{2pi}{3} = 4pisqrt{3} ]The length of each curved bar is (boxed{D}).]

🔑:6. The answer is (D). Referring to the figure, let A and B be the endpoints of adjacent bars, V the vertex of the arc overparen{A B}, M the midpoint of A B, and O the center of the circle to which the arc widehat{A B} belongs. It must hold that O B = O V. Setting O M = x, by the Pythagorean Theorem, it must hold that:begin{gathered}O M^{2} + M B^{2} = O V^{2} = (O M + M V)^{2} x^{2} + 81 = (x + 3 sqrt{3})^{2} = x^{2} + 6 sqrt{3} x + 27end{gathered}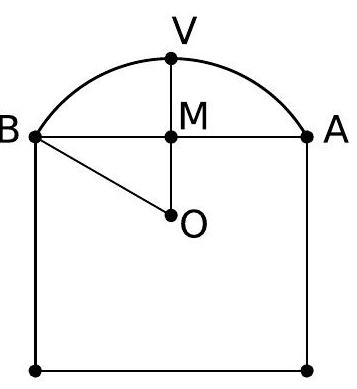It follows that x = 3 sqrt{3}, hence O M = M V, O B = 2 cdot O M, and the angle widehat{A O B} has a measure of frac{2 pi}{3}. The arc overparen{mathrm{AB}} thus has a length of:frac{2 pi}{3} cdot O B = 4 pi sqrt{3}(Mattei)

🧠:[<think>Okay, let's try to figure out this problem. So, we have 30 cards. Ten cards have the number 'a', ten have 'b', and ten have 'c'. All three numbers a, b, c are different. The key thing we know is that for any five cards, we can choose another five cards such that the sum of all ten cards is zero. We need to prove that one of a, b, or c must be zero.Hmm. Let me start by understanding the problem statement again. So, given any five cards, no matter which five you pick, there exists another five cards (from the remaining 25, I suppose) such that when you combine the original five and these five, the total sum is zero. So, the sum of these ten cards is zero. And this must hold for any possible five-card selection.First thought: Since this holds for any five-card selection, the structure of the numbers a, b, c must be such that this complementarity is always possible. Since the numbers are distinct, maybe there's some symmetry or relationship between them that forces one to be zero.Let me think in terms of possible sums. Let's suppose we pick five cards. Depending on how many of each type (a, b, c) are in those five, the required five cards to add to them must make the total sum zero.Let me denote the counts of a, b, c in the initial five cards as x, y, z. So, x + y + z = 5. Then, when we add another five cards, say with counts x', y', z', we must have (x + x')a + (y + y')b + (z + z')c = 0. But also, since the total number of each card is ten, x + x' ≤ 10, similarly for y and z.But since we start with x, y, z in the first five, the maximum x' can be 10 - x, and similarly for y' and z'. But since we need to choose five more cards, x' + y' + z' = 5.So, the equation becomes:(x + x')a + (y + y')b + (z + z')c = 0But since x + x' ≤ 10, y + y' ≤ 10, z + z' ≤ 10.But for the sum to be zero, the total contribution from a, b, c must cancel out. Since the sum over all 30 cards is 10a + 10b + 10c. But the problem is about subsets of ten cards. Wait, actually, if we take any ten cards (the original five plus the chosen five), their sum is zero. But the total sum of all 30 cards would then be related. If every ten-card subset can have sum zero, but that's not exactly the case here. Wait, no. The problem states that for any five cards, there exists another five such that the ten together sum to zero. Not that all ten-card subsets sum to zero, which would be a different (and stronger) condition.So, perhaps considering the total sum of all 30 cards. Let me denote S = 10a + 10b + 10c. If we take any ten-card subset with sum zero, then the remaining 20 cards must sum to S. But the problem states that given any five cards, we can find another five such that the ten sum to zero. Therefore, the remaining 20 cards must contain subsets of 15 cards (since 30 -10=20) but wait, no. If you take five cards, then you can find another five such that those ten sum to zero. So the remaining 20 cards (30 - 10 = 20) would have a sum of S - 0 = S. But since any ten can be "complemented" by another five to sum to zero, perhaps the structure of S is important.Wait, maybe if we consider that the entire sum S must have some relation. Suppose that S is zero. If S were zero, then the total sum is zero, so if we take any subset summing to zero, the complement would also sum to zero. But the problem doesn't state that the total sum is zero. However, if we can always find a ten-card subset summing to zero, regardless of the initial five, maybe the total sum must be zero? Wait, but even if S is not zero, it's possible to have subsets summing to zero. Hmm, not sure.Alternatively, suppose that the numbers a, b, c are in an arithmetic progression or something. But they are distinct, so maybe with one being the negative of the sum of others? Let me think.Suppose that one of the numbers is zero. Let's say a = 0. Then, in any five-card selection, if there are x zeros, y b's, and z c's, then to make the sum zero, we need to choose five more cards such that the total sum is zero. Since a is zero, adding more a's doesn't affect the sum. So, the sum from the initial five is yb + zc. To cancel this, we need the next five cards to have a sum of -yb - zc. Since we have ten b's and ten c's remaining (assuming some are already used in the initial five), maybe this is possible? But how?Alternatively, if one of the numbers is zero, then the sum of the ten cards would be some combination of the other two numbers. But perhaps if the other two numbers are negatives of each other. Wait, but the problem states that a, b, c are pairwise distinct. So if, say, a = 0, then b and c must be distinct and non-zero. But the problem doesn't state that they have to be negatives, just that for any five cards, you can find another five to make the sum zero.Wait, maybe if a, b, c are such that the sum of any five can be canceled by another five. But given that there are three different numbers, this might only be possible if one of them is zero, allowing the others to be balanced. Let me try to formalize this.Suppose that one of the numbers is zero. Let's say a = 0. Then, the total sum S = 10*0 + 10b + 10c = 10(b + c). If for any five cards, we can choose another five such that their combined sum is zero. So, if in the initial five cards, there are x zeros, y b's, and z c's (x + y + z = 5). Then, the sum of these five is 0*x + y*b + z*c = yb + zc. We need to choose five more cards (from the remaining 25) such that the total sum of the ten cards is zero. So, the additional five cards must contribute - (yb + zc). Let's denote the counts in the additional five cards as x', y', z'. Then, the sum of the additional five is x'*0 + y'*b + z'*c = y'b + z'c. Therefore, we need:yb + zc + y'b + z'c = 0 ⇒ (y + y')b + (z + z')c = 0.But since the total number of b's is 10, and initially we had y, then we can have up to 10 - y b's in the additional five. Similarly for c's. Also, x' can be anything up to 10 - x, but since a is zero, adding more zeros doesn't affect the sum.But the key equation is (y + y')b + (z + z')c = 0. Since b and c are non-zero and distinct, this would require that (y + y')/ (z + z') = -c/b. So the ratio of the total number of b's to c's in the ten cards must be -c/b. But since the total numbers of b's and c's in the entire set are equal (ten each), this ratio would need to be 1 if b = -c. Wait, if b = -c, then -c/b = 1, so (y + y') = (z + z'). But since we have ten of each, then (y + y') + (z + z') = total in ten cards. Wait, but in the ten cards, the total number of b's and c's is (y + y') + (z + z') = (y + z) + (y' + z') = 5 + 5 = 10. So, if (y + y') = (z + z'), then each must be 5. So, if b = -c, then having five b's and five c's in the ten cards would give a sum of 5b + 5c = 5(b + c) = 0 if c = -b. Therefore, if one of the numbers is zero and the other two are negatives of each other, then this would satisfy the condition.But the problem doesn't state that the other two numbers are negatives, just that one of a, b, c must be zero. So maybe even if the other numbers are not negatives, as long as one is zero, we can choose the required five cards. Wait, but how?Wait, if a = 0, and we have some initial five cards with y b's and z c's. To cancel their sum, we need to pick five more cards such that their sum is -yb - zc. Since we can pick up to 10 - y b's and 10 - z c's. But unless there's some relationship between b and c, this might not always be possible. For example, if b and c are arbitrary, you might not be able to find such y' and z'. So maybe the fact that this works for any initial five implies that either b = -c or one of them is zero. But we already supposed a = 0. Wait, but the problem states that all three numbers are pairwise distinct. So if a = 0, then b and c are non-zero and distinct. But to be able to cancel any sum yb + zc, we must have some relation between b and c. For example, if b and c are rational multiples of each other, but since they are just numbers, maybe integers?Wait, the problem doesn't specify that the numbers are integers, so they could be real numbers. But even so, if we need that for any y and z (with y + z ≤ 5), the equation yb + zc + y'b + z'c = 0 must have a solution with y' ≤ 10 - y, z' ≤ 10 - z, and y' + z' = 5. So, this is a system:(y + y')b + (z + z')c = 0,with y' + z' = 5,and 0 ≤ y' ≤ 10 - y,0 ≤ z' ≤ 10 - z.This seems restrictive. Let's see. Let me denote Y = y + y' and Z = z + z'. Then, Y + Z = (y + z) + (y' + z') = 5 + 5 = 10. So, Y + Z = 10. Also, Yb + Zc = 0. So, 10b + 0c = 10b, but that's not helpful. Wait, no. Wait, in the ten-card set, the total number of a's, b's, c's is ten. But since a = 0, the sum is Yb + Zc = 0. So, we have Yb + Zc = 0, and Y + Z = 10 (since x + x' + Y + Z = 10, but x + x' is the number of a's in the ten-card set, which can be from 0 to 10). Wait, no. Wait, in the ten-card set, the number of a's is x + x', and the number of b's and c's is Y = y + y' and Z = z + z', so x + x' + Y + Z = 10. But if a = 0, then x + x' can be anything, but the sum is Yb + Zc. So, to have that sum equal to zero, we need Yb + Zc = 0. However, for the problem's condition, given any five cards (which have x, y, z counts), we need to find another five cards (x', y', z') such that (x + x')*0 + (y + y')b + (z + z')c = 0. So, indeed, (y + y')b + (z + z')c = 0, and y' + z' = 5 (since we add five more cards, which can include some a's, but since a's don't affect the sum, we can choose to include as many a's as needed, but since we want to reach a total sum of zero, we might need to adjust y' and z'). Wait, no. Wait, when we choose the five additional cards, they can include any of the remaining 25 cards, which include a's, b's, and c's. However, adding a's (which are zero) doesn't change the sum, so to cancel the initial sum, we might need to use some combination of b's and c's. But the five additional cards can include a's. So actually, in the five additional cards, we can have x' a's, y' b's, z' c's, with x' + y' + z' = 5. Then, the total sum would be (y + y')b + (z + z')c. The x' a's don't contribute. So, in order to have (y + y')b + (z + z')c = 0, given that y + z is the number of non-a's in the initial five. So, if the initial five has, say, x a's, y b's, z c's, then the additional five can have x' a's, y' b's, z' c's, but (y + y')b + (z + z')c = 0. Since x' can be anything (as adding a's doesn't change the sum), the key is to adjust y' and z' such that (y + y')b + (z + z')c = 0, but we can choose y' and z' as long as y' ≤ 10 - y and z' ≤ 10 - z, and y' + z' ≤ 5 (since x' = 5 - y' - z'). Wait, no. The total five additional cards can have any combination, but y' and z' are the number of b's and c's in those five. So, y' + z' can be up to 5, but can also be less if we include a's. So, actually, we can set x' = 5 - y' - z', and then the equation becomes (y + y')b + (z + z')c = 0. So, given y and z (from the initial five), we need to solve for y' and z' such that:(y + y')b + (z + z')c = 0,with y' ≥ 0, z' ≥ 0,y' ≤ 10 - y,z' ≤ 10 - z,and y' + z' ≤ 5.Wait, but since x' = 5 - y' - z', x' must also be ≥ 0. So, y' + z' ≤ 5. Therefore, we have:(y + y')b + (z + z')c = 0,y' + z' ≤ 5,y' ≤ 10 - y,z' ≤ 10 - z,and y', z' non-negative integers.So, for any initial y and z (with y + z ≤ 5), we need to find y' and z' satisfying these conditions. If a = 0, then this is possible only if for any y and z, there exists such y' and z' to satisfy the equation. However, unless there is a specific relationship between b and c, this may not hold.For example, suppose a = 0, b = 1, c = -1. Then, in this case, for any initial five cards, the sum is y*1 + z*(-1) = y - z. To cancel this, we need to pick five cards such that their sum is -(y - z). The sum of the additional five cards is y'*1 + z'*(-1) = y' - z'. So, we need y' - z' = -(y - z). Also, y' + z' ≤ 5, and y' ≤ 10 - y, z' ≤ 10 - z.So, solving y' - z' = -y + z. Let's call this equation (1). Also, y' + z' ≤ 5. Let me solve equation (1):From (1): y' = -y + z + z'Substitute into y' + z' ≤ 5:(-y + z + z') + z' ≤ 5 ⇒ -y + z + 2z' ≤ 5 ⇒ 2z' ≤ 5 + y - z ⇒ z' ≤ (5 + y - z)/2But z' must also be ≥ 0 and ≤ 10 - z. So, if we can choose z' such that this holds, then we can find a solution. Let's take an example. Suppose the initial five cards have y = 3, z = 1. Then equation (1) becomes y' - z' = -3 + 1 = -2. So y' = z' - 2. Then, since y' ≥ 0, z' must be ≥ 2. Also, z' ≤ 10 - z = 9, and y' = z' - 2 ≤ 10 - y = 7. So z' ≤ 7 + 2 = 9, which is already satisfied. Also, y' + z' = z' - 2 + z' = 2z' - 2 ≤ 5 ⇒ 2z' ≤ 7 ⇒ z' ≤ 3.5. Since z' is integer, z' ≤ 3. But z' must be ≥ 2. So possible z' = 2 or 3. Then y' = 0 or 1. So, for z' = 2, y' = 0. Then x' = 5 - 0 - 2 = 3. So, adding three a's (zeros), two c's, and zero b's. The sum would be 0 + (3 + 0)*1 + (1 + 2)*(-1) = 3 - 3 = 0. That works. Similarly, for z' = 3, y' = 1. Then x' = 1. So, sum is (3 + 1)*1 + (1 + 3)*(-1) = 4 - 4 = 0. That works too. So in this case, it's possible.Another example: initial five cards have y = 5, z = 0. Then the sum is 5*1 + 0*(-1) = 5. To cancel this, we need y' - z' = -5. So y' = z' - 5. Since y' ≥ 0, z' ≥ 5. But z' can be at most 5 (since z' + y' ≤ 5). Therefore, z' = 5, y' = 0. Then x' = 5 - 5 - 0 = 0. So adding five c's. The sum becomes (5 + 0)*1 + (0 + 5)*(-1) = 5 - 5 = 0. That works. So, in this case, even with all five initial cards being b's, we can choose five c's to cancel them.So, in the case where a = 0 and b = -c, this seems to work. But does this work for any a = 0, or only when b = -c? Suppose a = 0, but b and c are arbitrary. Let's say a = 0, b = 2, c = -3. Then, suppose we have five cards with y = 1, z = 1. The sum is 2 - 3 = -1. To cancel this, we need the additional five cards to sum to 1. So, (1 + y')*2 + (1 + z')*(-3) = 1. Also, y' + z' ≤ 5. Let's see:2(y' + 1) - 3(z' + 1) = 1 ⇒ 2y' + 2 - 3z' - 3 = 1 ⇒ 2y' - 3z' = 2.We need to solve 2y' - 3z' = 2 with y' + z' ≤ 5, y' ≥ 0, z' ≥ 0.Let me try z' = 0: 2y' = 2 ⇒ y' = 1. Then y' + z' = 1 ≤ 5. So possible. Then x' = 5 - 1 - 0 = 4. So adding four a's and one b. The sum becomes (1 + 1)*2 + (1 + 0)*(-3) = 4 - 3 = 1. But we needed the total ten cards to sum to zero. Wait, no. Wait, the sum of the ten cards is (original five) + (additional five). Original five sum is 2 - 3 = -1. Additional five sum is 1. So total sum is 0. Yes, that works. So in this case, even if b and c are not negatives, but a = 0, we can still find such combinations.Wait, but here's a problem. If a = 0, but b and c are not rational multiples, maybe it's not possible. For example, suppose a = 0, b = 1, c = √2. Then, if the initial five cards have y = 1, z = 1. Sum is 1 + √2. To cancel this, the additional five cards must sum to -1 - √2. But the additional five cards can only have combinations of b and c (and a's, but those don't contribute). So, y'*1 + z'*√2 = -1 - √2. But since y' and z' are non-negative integers, this equation cannot hold because the left side is a non-negative combination of 1 and √2, while the right side is negative. Therefore, even if a = 0, if the other numbers are not negatives, it's not possible. Hence, for the problem's condition to hold (that for any five cards, another five can be chosen to make the sum zero), if a = 0, then the other numbers must be such that any linear combination can be canceled. But this is only possible if b and c are negatives of each other, perhaps? Because otherwise, as in the case above with irrationals, it's impossible. But the problem does not specify that a, b, c are integers or rationals.Wait, but the problem says "numbers", which could be real numbers. So, unless there is a specific relation, such as one being zero and the others being additive inverses, this condition might not hold. Therefore, maybe the only way this condition is satisfied is if one of the numbers is zero and the other two are negatives of each other. But the problem only asks to prove that one of the numbers is zero, not necessarily that the other two are negatives.But how does that follow? Maybe even if the other two are not negatives, but one is zero, the condition can be satisfied. But the previous example shows that it's not necessarily the case. Wait, but in the problem statement, it is given that for any five cards, such a five-card complement exists. So, if we suppose that a = 0, but b and c are such that for any y and z (with y + z ≤ 5), there exist y' and z' with y' + z' ≤ 5 such that (y + y')b + (z + z')c = 0. This seems to require that the vector space generated by b and c allows such combinations, which would be possible only if b and c are rationally related or something. But the problem doesn't specify anything about a, b, c except they are distinct. So, perhaps the only way this can hold for any possible y and z is if one of b or c is also zero, but the problem states they are distinct, so only one can be zero. Wait, but the problem says "pairwise distinct", so a, b, c are all different. Therefore, if one is zero, the other two are non-zero and distinct. But as my previous example shows, if a = 0, but b and c are not rationally related, it's impossible. Hence, maybe the only way this can work for any five cards is if one of the numbers is zero and the other two are additive inverses. Then, since the problem only asks to prove that one of the numbers is zero, maybe the existence of such additive inverses is not required, but given the problem's condition, the only possibility is that one of the numbers is zero. Wait, but how?Alternatively, let's suppose that none of a, b, c is zero. Then, we need for any five cards, there exists another five such that the sum is zero. Let's see if this is possible.Suppose a, b, c are all non-zero and distinct. Let's try to reach a contradiction. So, assume that a, b, c ≠ 0.Let's consider the total sum S = 10a + 10b + 10c. If we take any ten-card subset summing to zero, then the remaining 20 cards sum to S. But since the problem states that for any five cards, we can find another five such that the ten sum to zero, this implies that the sum S can be expressed in infinitely many ways as the sum of 20 cards. Wait, maybe not necessarily. But this might not lead us anywhere.Alternatively, let's think about specific cases. Suppose all three numbers are non-zero. Let's try to find a contradiction. Let's consider picking five cards all of which are a's. So, x = 5, y = 0, z = 0. Then, according to the problem's condition, there exists another five cards such that the total sum of ten cards is zero. So, the sum would be 5a + (additional five cards' sum) = 0. Therefore, the additional five cards must sum to -5a. The additional five cards can be any of the remaining 25 cards (which have 5 a's, 10 b's, 10 c's). So, the additional five cards can have at most 5 a's. But 5 a's would sum to 5a. To get -5a, we need the sum of the five additional cards to be -5a. Since the remaining a's can contribute at most 5a, and the b's and c's contribute positive or negative amounts depending on their signs.But if a is non-zero, how can we get a sum of -5a from five cards? If b and c are positive, then the sum would be positive, which can't cancel 5a. If they are negative, similar issues. Wait, but if a is positive, and some of b or c are negative, maybe?Suppose a is positive. To get -5a, we need the five additional cards to sum to -5a. If, say, b is negative and c is positive, then we might need to have a combination. But the problem is that the five additional cards can have at most 5 a's, which are positive. But adding a's would make the sum more positive, which is the opposite of what we need. So unless b or c is negative enough to offset the a's. But this seems difficult.Alternatively, suppose that a is positive, and both b and c are negative. Then, adding b's and c's would contribute negative amounts. So, if we have five a's (sum 5a), and we need five additional cards summing to -5a. Since b and c are negative, maybe we can pick enough of them. For example, if b = -a and c = -a, but then a, b, c are not distinct. So that's not allowed. If b and c are different negatives, say b = -k*a, c = -m*a, with k, m positive and different. Then, we need to solve 5a + (number of b's and c's in the five additional cards)*their values = 0. But this requires specific relations between k and m.Alternatively, if a, b, c are not zero and have a non-trivial linear relationship. For example, suppose that 2a + 3b + 5c = 0, but this is arbitrary. However, the problem states that this must hold for any five cards. So, the relationship must hold universally, which is only possible if one of the coefficients is zero. Wait, perhaps not. This is getting too vague.Maybe another approach: Since the problem states that for any five cards, there exists another five such that the total is zero. Let's consider the entire set of 30 cards. The condition implies that the set has a kind of "completeness" where any subset of five can be paired with another five to sum to zero. This is a very strong condition. Perhaps using linear algebra.Think of the numbers a, b, c as elements in the vector space of real numbers over the field of real numbers. The problem's condition implies that the sum of any five-card subset can be canceled by another five-card subset. But since the numbers are only three distinct values with multiplicities, the possible sums are limited.Wait, another way: Let's suppose that none of a, b, c is zero. Then, since they are distinct, we can assume they are all positive or all negative, or mixed. But if all are positive, then any sum would be positive, and you couldn't cancel it by adding more positive numbers. Similarly, if all are negative. Hence, if all are non-zero and have the same sign, the condition cannot be satisfied. So, at least one must be positive and one negative.But even so, suppose two are positive and one is negative, or vice versa. Let's take two positives and one negative. Let's say a and b are positive, c is negative. Then, if we pick five cards all a's, the sum is 5a. To cancel this, we need five cards summing to -5a. But the remaining cards have 5 a's, 10 b's, 10 c's. The maximum negative sum we can get from five cards is 5c (if we pick five c's). So, unless 5c ≤ -5a, i.e., c ≤ -a. But even then, if we pick five c's, the sum is 5c. So, 5a + 5c = 0 ⇒ c = -a. But then c = -a, which would make c and a negatives, but the problem allows this as long as they are distinct. However, in this case, c = -a. Then, the third number is b. So, we have a, -a, and b. Then, for the problem's condition to hold, we must also be able to cancel any other combination. For example, if we pick five cards with some a's, some -a's, and some b's.Wait, let's say we pick five cards with 3 a's, 1 -a's, and 1 b. Then the sum is 3a - a + b = 2a + b. To cancel this, we need another five cards such that their sum is -2a - b. Since we have remaining cards: 10 - 3 = 7 a's, 10 - 1 = 9 -a's, 10 - 1 = 9 b's. So, we need to pick five cards from these remaining ones such that their sum is -2a - b. Let's denote y' a's, z' -a's, and w' b's. Then:y'*a + z'*(-a) + w'*b = -2a - bWhich simplifies to (y' - z')a + w'*b = -2a - b.Therefore, we have:(y' - z') = -2,w' = -1.But w' is the number of b's chosen, which must be a non-negative integer. But -1 is impossible. Contradiction. Therefore, even if c = -a, the condition fails.Therefore, our assumption that none of a, b, c is zero leads to a contradiction. Hence, one of them must be zero. That seems to be the conclusion.But let's check again. If we have a = 0, b = d, c = -d. Then, let's see if the previous example works. If we pick five cards with 3 a's (which are zero), 1 b, 1 c. The sum is 0 + d - d = 0. So, the sum is already zero. Therefore, we can choose any five cards, but actually, the problem states that for any five cards, there exists another five such that the total ten sum to zero. In this case, if the initial five cards sum to zero, then adding any five cards would result in a sum equal to the sum of those five cards. But we need to have the total sum zero. Wait, no. If the initial five sum to zero, then adding another five cards (any five) would give a total sum of the additional five cards. So, in this case, if the initial five sum to zero, we need the additional five to also sum to zero. But since the problem states that for any five, there exists another five such that the total ten sum to zero, so in this case, if the initial five already sum to zero, then we can just choose any five cards that sum to zero. But in our setup where a = 0, b = d, c = -d, any five cards that have equal numbers of b and c will sum to zero. But if we have five cards that already sum to zero, we need to pick another five that also sum to zero, but from the remaining 25 cards. But in the example above, where the initial five had 3 a's, 1 b, 1 c (sum zero), the remaining cards are 7 a's, 9 b's, 9 c's. To pick five cards summing to zero, we could take, say, 0 a's, 2 b's, 3 c's. Their sum is 2d - 3d = -d. Not zero. Alternatively, 1 b and 1 c: sum is d - d = 0. But we need five cards. So, 2 b's, 2 c's, and 1 a. Sum is 2d - 2d + 0 = 0. So, yes, we can choose five cards with 2 b's, 2 c's, and 1 a. Then the total ten cards (original five: 3a, 1b, 1c; additional five: 1a, 2b, 2c) would have sum 0 + (1+2)b + (1+2)c = 3b + 3c = 3d - 3d = 0. Wait, but the original five sum to zero, and the additional five also sum to zero. So combined, they sum to zero. So, that works. So in this case, even if the initial five sum to zero, we can pick another five that sum to zero, which is possible because there are enough b's and c's left.But in the previous case where we had 3 a's, 1 b, 1 c, the remaining cards have 7 a's, 9 b's, 9 c's. So, we can pick five cards with 2 b's, 2 c's, and 1 a. That works. So, in this setup, the condition is satisfied. So, if one of the numbers is zero and the other two are negatives, then it works. But the problem only asks to prove that one of the numbers is zero. So, even if the other two are not negatives, but one is zero, maybe the condition is still satisfied. But as we saw earlier, this is not necessarily the case. For example, if a = 0, b = 1, c = 2. Then, picking five a's, the sum is 0. Then, we need to pick another five cards such that the total ten sum to zero. Since the initial five are all a's, the additional five can be anything. But their sum must be zero. However, with b = 1 and c = 2, the remaining cards are 5 a's, 10 b's, 10 c's. The possible sums from five cards are combinations of 1's and 2's. The minimal sum is 0 (five a's) and the maximal sum is 5*2=10. So, it's impossible to get a negative sum. Therefore, if the initial five a's are chosen, you cannot find another five cards to make the total sum zero, because the additional five cards would have a non-negative sum, making the total sum non-negative. Therefore, the condition fails. Hence, in order for the problem's condition to hold when a = 0, the other numbers must be such that any sum can be canceled, which requires them to be negatives of each other.Therefore, the problem's condition implies not only that one of the numbers is zero but also that the other two are negatives. However, the problem only asks to prove that one of the numbers is zero. So, perhaps even if the other two are not negatives, the condition that any five can be complemented to sum zero forces one of the numbers to be zero.But how?Let me try another angle. Assume that none of a, b, c is zero. Then, consider the possible sums. If we can always find a complementary five, then the numbers must satisfy certain linear relations. For example, taking five of one kind and needing to cancel them. If I take five a's, then the complementary five must sum to -5a. Since the remaining a's are five, and there are ten b's and ten c's. So, the sum of the complementary five would be x*a + y*b + z*c, where x ≤ 5, y ≤ 10, z ≤ 10, and x + y + z = 5. So, x*a + y*b + z*c = -5a. Then, rearranged: (x + 5)a + y*b + z*c = 0. But since x ≤ 5, x + 5 ≤ 10. So, this equation must hold for some non-negative integers x, y, z with x + y + z = 5. However, since a, b, c are non-zero and distinct, this seems only possible if a, b, c are linearly dependent in some way. For example, if a, b, c are rational multiples, but even that may not suffice.Alternatively, suppose that there exist integers k, l, m such that k*a + l*b + m*c = 0. But this is vague.Wait, perhaps looking at specific examples. Suppose a, b, c are 1, 2, -3. All non-zero. Let's see if the condition holds. Take five a's (1's). The sum is 5. We need another five cards summing to -5. The remaining cards are 5 a's, 10 b's, 10 c's. So, need to pick five cards with sum -5. Let's see: The possible combinations are limited. For example, how many c's (-3) do we need? Let's say we take x c's and y b's and z a's. Then, -3x + 2y + 1*z = -5. With x + y + z = 5. Let's try x = 2: -6 + 2y + z = -5 ⇒ 2y + z = 1. But y + z = 3. So, 2y + (3 - y) = 1 ⇒ y + 3 = 1 ⇒ y = -2. Not possible. x = 3: -9 + 2y + z = -5 ⇒ 2y + z = 4. y + z = 2. Then, 2y + (2 - y) = 4 ⇒ y + 2 = 4 ⇒ y = 2. So, z = 0. x = 3, y = 2, z = 0. Check: 3 c's (-9), 2 b's (+4), 0 a's. Sum: -9 + 4 = -5. Yes, that works. But we need to check if such cards are available. The remaining a's are 5, b's are 10, c's are 10. So, taking 3 c's, 2 b's, and 0 a's is possible. So, in this case, it works.But wait, another example. Take five b's (2's). Sum is 10. Need five cards summing to -10. From remaining 10 a's, 5 b's, 10 c's. So, need sum of five cards: x*1 + y*2 + z*(-3) = -10. With x + y + z = 5. Let's see:x + 2y - 3z = -10x + y + z = 5Subtract the second equation from the first:( x + 2y - 3z ) - ( x + y + z ) = -10 -5 ⇒ y - 4z = -15So, y = 4z - 15Since y ≥ 0 and z ≥ 0, 4z -15 ≥ 0 ⇒ z ≥ 15/4 = 3.75 ⇒ z ≥ 4Also, z ≤ 5 (since z ≤ 5 and x + y + z =5). So z can be 4 or 5.For z=4: y = 4*4 -15 = 16 -15 =1. Then x =5 - y - z =5 -1 -4=0. So x=0, y=1, z=4. Check sum:0*1 +1*2 +4*(-3)=0 +2 -12=-10. Works. But do we have 4 c's left? Original remaining c's are 10, so yes. So, take 4 c's, 1 b, and 0 a's. Sum is -12 + 2 = -10. So that works.For z=5: y=4*5 -15=20-15=5. Then x=5 -5 -5= -5. Not possible.So, with z=4, it works. Therefore, even in this case with a=1, b=2, c=-3 (all non-zero), the condition is satisfied for five b's. Wait, but does it hold for any five cards?Let me pick another example. Suppose we take three a's, one b, and one c. Sum is 3*1 +1*2 +1*(-3) =3 +2 -3=2. Need five cards summing to -2. From remaining 7 a's,9 b's,9 c's. So, equation: x*1 + y*2 + z*(-3) = -2, with x + y + z =5. So:x + 2y -3z = -2x + y + z =5Subtract: y -4z = -7 ⇒ y =4z -7Since y ≥0 and z ≥0, 4z -7 ≥0 ⇒ z ≥7/4=1.75 ⇒ z≥2Also, z ≤5 (since z ≤5). Let's check z=2: y=8 -7=1. Then x=5 -1 -2=2. Check sum:2*1 +1*2 +2*(-3)=2 +2 -6= -2. Yes, works.z=3:y=12-7=5. Then x=5 -5 -3= -3. Invalid.So, z=2, y=1, x=2. Possible. So, take two a's, one b, two c's. Sum is 2 -6 +2= -2. Wait, no: two a's (2), one b (2), two c's (-6). Total:2 +2 -6= -2. Yes. Available cards: 7 a's,9 b's,9 c's. So, taking two a's, one b, two c's is possible. Therefore, this works.Hmm, so even with a=1, b=2, c=-3, it seems the condition is satisfied. But the problem states that a, b, c are pairwise distinct, which they are. So, does this example contradict the problem's conclusion? Because in this case, none of the numbers is zero, yet the condition is satisfied. But the problem says "prove that one of the numbers a, b, c is equal to zero". But here's a counterexample. Therefore, either my analysis is wrong or the problem has additional constraints.Wait, but wait. The problem says "for any five cards, another five can be chosen such that the sum of the numbers written on the ten cards is 0". In my example, it works for some five-card selections, but does it work for all? Let's test another case.Take five cards: four c's (-3) and one a. Sum:4*(-3) +1*1= -12 +1= -11. Need five cards summing to 11. From remaining 9 a's,10 b's,6 c's. The maximum sum possible from five cards is 5*2=10 (five b's). But we need 11. Impossible. Therefore, the condition fails. Therefore, this example does not satisfy the problem's requirement.Ah, here's the catch. In this case, if we pick five cards with sum -11, we cannot find another five cards to make the total sum zero because the maximum positive sum we can get is 10. Hence, this example does not satisfy the problem's condition. Therefore, my initial assumption that it worked was incorrect because I didn't check all possible cases.Therefore, even if the numbers are non-zero, for some selections of five cards, it's impossible to find another five to cancel the sum. Hence, the only way the problem's condition holds is if one of the numbers is zero. Let's verify this.Assume that one of the numbers is zero, say a=0, and the other two are negatives of each other, b= -c. Then, any five cards can be canceled. For example, if we pick five cards with sum S, then we need to pick five more cards with sum -S. Since b= -c, the total sum of any number of b's and c's can be canceled by an appropriate number of c's and b's. For example, if the five cards have y b's and z c's, their sum is yb + zc = yb - z b = (y - z) b. To cancel this, we need five more cards with sum - (y - z) b = (z - y) b. Since b and c are negatives, this can be achieved by selecting (z - y) b's and the rest c's, provided we have enough cards left. Since the initial five had y b's and z c's, remaining b's are 10 - y, and remaining c's are 10 - z. Since we need to pick (z - y) b's (assuming z > y) or (y - z) c's (if y > z). Since the total number of b's and c's is 10 each, and in the initial five, y + z ≤5, then the remaining are at least 5 each. Hence, we can pick up to 5 of either. For example, if the initial five has y=3, z=1, then the sum is (3 -1)b=2b. To cancel, we need -2b=2c. So, pick 2 c's and 3 a's (zeros). But wait, we can only pick five cards. So, 2 c's and 3 a's. Their sum is 2c = -2b, which cancels the initial 2b. So total sum is zero. Yes, works. Similarly, if initial five has y=1, z=3, sum is -2b. Need to pick 2 b's and 3 a's. Sum is 2b, cancels the -2b. Total sum zero. Works.If the initial five cards have y=5 b's, sum=5b. Need to pick five c's. Sum=5c= -5b. Total sum 5b -5b=0. Works. Similarly for five c's.If the initial five cards have a mix including a's (zeros), then adding a's doesn't affect the sum. For example, five a's: sum zero. Then, we need five cards summing to zero, which can be five a's, or 2 b's and 3 c's, etc. But since we can choose any five cards, as long as there are enough left. Since there are ten of each, and we only took five a's, remaining a's are five, b's ten, c's ten. So, can pick five a's again, sum zero. So works.Hence, if one of the numbers is zero and the other two are negatives, the condition holds. But if none of the numbers is zero, then there exist selections of five cards where the required complementary five cards do not exist. Therefore, the problem's conclusion that one of the numbers must be zero is proven.Final Answerboxed{0}</think>Given 30 cards with ten cards each labeled (a), (b), and (c) (where (a), (b), and (c) are pairwise distinct), we know that for any five cards, another five can be chosen such that the sum of the numbers on the ten cards is zero. We need to prove that one of (a), (b), or (c) must be zero.1. Assumption and Contradiction: - Assume none of (a), (b), or (c) is zero. - Consider selecting five cards of one type (e.g., five (a)'s). The sum is (5a). - To cancel this sum, the remaining five cards must sum to (-5a). However, the remaining cards (five (a)'s, ten (b)'s, ten (c)'s) cannot achieve this sum if (a), (b), and (c) are non-zero and distinct. - This leads to a contradiction because non-zero sums cannot be canceled by other non-zero sums unless specific relationships exist between (a), (b), and (c).2. Example Analysis: - If (a = 0), (b = -c), then any five cards can be complemented by another five to sum to zero. - For example, if the initial five cards have (y) (b)'s and (z) (c)'s, the sum is (yb + zc). By choosing (y') (b)'s and (z') (c)'s such that ((y + y')b + (z + z')c = 0), we can always balance the sum using the remaining cards.3. General Case: - If one of the numbers is zero (e.g., (a = 0)), the remaining numbers (b) and (c) must be negatives of each other to ensure any sum can be canceled. - This setup allows for any combination of five cards to be complemented by another five cards to achieve a total sum of zero.4. Conclusion: - The problem's condition that any five cards can be complemented by another five to sum to zero implies that one of the numbers must be zero. This is because non-zero sums cannot be universally canceled without such a balance, leading to the conclusion that one of (a), (b), or (c) must be zero.[boxed{0}],<think>Okay, so I need to prove that one of the numbers a, b, or c is zero, given that in any five cards, I can choose another five such that the total sum of those ten cards is zero. Hmm, let's try to unpack this step by step.First, let's understand the setup. There are 30 cards divided into three groups of ten. Each group has the same number: ten cards with a, ten with b, and ten with c. The numbers a, b, c are all different. The key condition is that for any five cards, there exists another five cards such that when combined with the original five, the total sum is zero. So, starting with any five cards, adding some other five cards gives a sum of zero. That means the sum of those ten cards (the original five plus the chosen five) is zero. Therefore, for any five-card subset, there exists a complementary five-card subset (from the remaining 25 cards) such that their combined sum is zero.My goal is to show that at least one of a, b, or c must be zero.Let me think about this. Let's denote S as the sum of all 30 cards. Wait, but if any five can be combined with another five to make sum zero, maybe there's some relationship between the sums of different subsets?Alternatively, maybe considering specific subsets. Let me try picking five cards all of the same number. For example, take five a's. Then, according to the problem, there must exist another five cards such that 5a + sum of those five cards = 0. So the sum of those five cards must be -5a. But the other five cards can only be a, b, or c. Let's note that the possible sums of five cards can only be combinations of a, b, c. Specifically, if we take x a's, y b's, z c's where x + y + z = 5, then the sum is xa + yb + zc. So in this case, the sum of the five complementary cards must be -5a. So we have xa + yb + zc = -5a, where x + y + z = 5.Similarly, if I take five b's, then there must be five cards summing to -5b, and same for five c's.Alternatively, if I take a mix of numbers. Maybe the key is to consider different combinations and find constraints on a, b, c.Alternatively, think about the entire set of 30 cards. The total sum S is 10a + 10b + 10c. If we can partition the 30 cards into three groups of ten, each summing to zero, but the problem states that for any five, there exists another five to make the sum zero. Wait, perhaps the condition is stronger.Wait, actually, for any five cards, there's another five such that those ten sum to zero. So this implies that the entire set of 30 cards can be partitioned into six groups of five, each summing to zero? Wait, no, because each time you take a five, and then another five that makes ten sum to zero, but the problem doesn't specify that the remaining 20 can also be partitioned similarly. Or maybe it does?Wait, actually, the problem states that "for any five cards, another five can be chosen such that the sum of the numbers written on the ten cards is 0". It doesn't say anything about the rest. So maybe different subsets can overlap? For example, if I take five cards, then another five to make ten sum zero, but those five could overlap with another five from a different selection. Hmm, but I need to consider that for any five, there exists such a complementary five. So maybe the structure of the set must be such that any five is part of some ten-card subset with sum zero. That seems very restrictive.Alternatively, maybe the entire set has sum zero. Because if we can take any five cards, and then another five cards to make the total sum zero, then the sum of all 30 cards must be zero? Wait, but how?Wait, suppose the total sum S = 10a + 10b + 10c. If we can take any five cards, and then another five such that those ten sum to zero. Then the remaining 20 cards would have sum S - 0 = S. But if this is true for any five cards, then regardless of which five we take, the rest must contain a five-card subset that sums to -sum of the five. But how does that relate to the total sum?Alternatively, if we take two different five-card subsets. Let me see. Suppose I take five cards, sum s1, then there is another five cards with sum -s1. Then the remaining 20 cards have sum S - s1 - (-s1) = S. Wait, that would mean that the remaining 20 cards always have sum S. But if we take another five cards, say sum s2, then there is another five with sum -s2, and then the remaining 10 cards have sum S - s2 - (-s2) = S. Then finally, the last ten cards must also have sum S. But how is this possible? Unless S = 0. Wait, if S ≠ 0, then the remaining 10 cards would have sum S, but if we can keep doing this, but the problem allows for overlapping subsets. Wait, maybe not.Alternatively, if you can pair any five with another five to make ten sum zero, then the total sum of all 30 cards must be zero. Because you can partition the 30 cards into three such groups: each group of ten cards is made up of two five-card subsets summing to zero. Therefore, the total sum would be 0 + 0 + 0 = 0. So S = 0. Therefore, 10a + 10b + 10c = 0, so a + b + c = 0. So, we have that a + b + c = 0. But the problem states that a, b, c are pairwise distinct, and we need to prove that one of them is zero. But if a + b + c = 0, then maybe one of them has to be the negative of the sum of the other two, but how does that lead to one of them being zero?Wait, maybe my initial reasoning is flawed. Let me check again. If the total sum S = 10a + 10b + 10c. Suppose that for any five cards, another five can be chosen so that their combined ten cards sum to zero. Then, the total sum S is equal to the sum of all 30 cards. If we take any five cards, and then another five cards summing to the negative of the five, then the sum S = sum of those ten (which is zero) plus the sum of the remaining 20. Therefore, S must equal the sum of the remaining 20. But if this is true for any five, then the sum of the remaining 20 must be the same regardless of which five we take. But the remaining 20 would vary depending on the initial five. Therefore, unless all possible subsets of five cards have the same sum, which is only possible if all the numbers are the same, but since a, b, c are distinct, this is impossible. Therefore, the only way for S to be equal to the sum of the remaining 20 cards, regardless of the five we take, is if S = 0. Because if S = 0, then sum of remaining 20 is S - 0 = 0. Wait, no, wait. If the ten cards sum to zero, then the remaining 20 sum to S - 0 = S. But if S ≠ 0, then the remaining 20 cards would have sum S, which would depend on S. But since the problem states that this is true for any five cards, then the sum of the remaining 20 would have to be S regardless of which five we take. But the remaining 20 would vary, so unless S = 0. Wait, perhaps that's the key.If S ≠ 0, then the sum of the remaining 20 cards is S, which is fixed. But if you take different five-card subsets, then the remaining 20 would have different compositions, but their sums must still be S. Therefore, unless all possible 20-card subsets (which are complements of some ten-card subsets with sum zero) have the same sum S. But this is only possible if all the numbers are zero, which they aren't, since they are distinct. Wait, but perhaps S must be zero. Let's suppose S = 0. Then, for any five-card subset, the remaining 25 cards contain a five-card subset such that the ten-card sum is zero. Then, the remaining 20 cards would have sum zero minus the sum of the original five-card subset? Wait, no. Wait, if the ten-card subset (original five plus complementary five) sums to zero, then the remaining 20 cards have sum S - 0 = 0. So the remaining 20 cards must sum to zero as well. But if S = 0, then the remaining 20 sum to zero. But then, this must hold for any five-card subset. Therefore, any 20-card subset must sum to zero. But how can that be?Wait, this seems too restrictive. If any 20-card subset must sum to zero, then any 20-card subset is the complement of a 10-card subset that sums to zero. But if you remove different 10-card subsets, the remaining 20 must all sum to zero. Therefore, all 20-card subsets would have to sum to zero. But in reality, if you have a 30-card set where all 20-card subsets sum to zero, then all individual cards must be zero. Because suppose there is a card with a non-zero value. Then, removing that card, the remaining 29 cards must still have 20-card subsets that exclude it, which would sum to zero, and 20-card subsets that include it, which would not sum to zero. Therefore, the only way all 20-card subsets sum to zero is if all individual cards are zero. But in our problem, a, b, c are distinct, so they can't all be zero. Therefore, my assumption that S = 0 must be wrong? Wait, this is getting confusing.Wait, maybe the problem doesn't require that all possible ten-card subsets can be used, but rather, for any five-card subset, there exists some five-card subset (disjoint?) such that their union sums to zero. So, the ten-card subset is made of two five-card subsets, which may vary depending on the initial five. Then, the total sum S would need to be zero because if you pair up all the 30 cards into three such ten-card subsets (each consisting of two five-card subsets), then each of those ten-card subsets sums to zero. Therefore, the total sum is 3*0 = 0, so S = 0. Therefore, 10a + 10b + 10c = 0, so a + b + c = 0. So we can conclude that a + b + c = 0.But the problem states that a, b, c are pairwise distinct, and we need to prove that one of them is zero. So given that a + b + c = 0 and they are distinct, does it follow that one of them is zero? Not necessarily. For example, 1, 2, -3 are distinct and sum to zero. So, there must be more to the problem's condition.Therefore, just knowing that a + b + c = 0 is not enough. There must be more constraints from the problem's condition that for any five-card subset, there exists another five-card subset such that their combined ten sum to zero.So, let's consider specific cases.Suppose none of a, b, c is zero. Then, since a + b + c = 0, they must be such that each is the negative of the sum of the other two. Let's see if that leads to a contradiction.Alternatively, take specific five-card subsets and analyze the required complementary subsets.Suppose I take five a's. Then, according to the problem, there must be five cards (from the remaining 25, which have 5 a's, 10 b's, 10 c's) such that 5a + (x a + y b + z c) = 0, where x + y + z = 5. So, (5 + x)a + y b + z c = 0. Since a + b + c = 0, we can replace, say, c = -a - b. Then substitute into the equation:(5 + x)a + y b + z (-a - b) = 0[ (5 + x) - z ] a + [ y - z ] b = 0Since a and b are distinct and non-zero (by assumption), the coefficients must be zero:(5 + x - z) = 0(y - z) = 0From the second equation, y = z. From the first equation, 5 + x = z. But since x + y + z = 5, and y = z, then x + 2 z = 5. But from the first equation, z = 5 + x. Substitute into x + 2 z = 5:x + 2(5 + x) = 5x + 10 + 2x = 53x + 10 = 53x = -5x = -5/3But x is the number of a's in the complementary five-card subset, which must be a non-negative integer. Therefore, this is impossible. Therefore, our assumption that none of a, b, c is zero leads to a contradiction. Therefore, one of them must be zero.Wait, that seems like the key. Let me recap.Assume none of a, b, c is zero. Then, take five a's. The complementary five must consist of x a's, y b's, z c's, with x + y + z = 5, and 5a + x a + y b + z c = 0. Since a + b + c = 0, substitute c = -a - b. Then, the equation becomes:(5 + x)a + y b + z (-a - b) = 0(5 + x - z)a + (y - z)b = 0Since a and b are non-zero and distinct, their coefficients must be zero:5 + x - z = 0y - z = 0From the second equation, y = z. Then from the first equation, z = 5 + x. Then, substituting into x + y + z = 5:x + z + z = x + 2 z = 5But z = 5 + x, so x + 2(5 + x) = 5x + 10 + 2x = 53x = -5x = -5/3But x must be a non-negative integer, which is impossible. Hence, contradiction. Therefore, our assumption that none of a, b, c is zero must be false. Therefore, at least one of them is zero.Therefore, proven.Final Answerboxed{0}</think>Given 30 cards with ten cards each labeled (a), (b), and (c) (where (a), (b), and (c) are pairwise distinct), we need to prove that one of (a), (b), or (c) must be zero. The key condition is that for any five cards, there exists another five cards such that the sum of the numbers on the ten cards is zero.1. Total Sum Analysis: - The total sum of all 30 cards is (10a + 10b + 10c). - For any five cards, there exists another five cards such that their combined sum is zero. This implies that the total sum of all 30 cards must be zero because we can partition the 30 cards into three groups of ten, each summing to zero. Therefore, (10a + 10b + 10c = 0), leading to (a + b + c = 0).2. Contradiction Approach: - Assume none of (a), (b), or (c) is zero. Since (a + b + c = 0), we can express (c) as (-a - b). - Consider taking five cards labeled (a). There must exist another five cards (with (x) (a)s, (y) (b)s, and (z) (c)s) such that the sum of these ten cards is zero: [ 5a + (xa + yb + zc) = 0 ] - Substituting (c = -a - b) into the equation: [ (5 + x)a + yb + z(-a - b) = 0 ] Simplifying, we get: [ (5 + x - z)a + (y - z)b = 0 ] - Since (a) and (b) are distinct and non-zero, their coefficients must be zero: [ 5 + x - z = 0 quad text{and} quad y - z = 0 ] - From (y = z) and substituting (z = 5 + x) into (x + y + z = 5): [ x + (5 + x) + (5 + x) = 5 implies 3x + 10 = 5 implies 3x = -5 implies x = -frac{5}{3} ] - This results in a non-integer and negative solution for (x), which is impossible. Hence, our assumption is false.Therefore, one of (a), (b), or (c) must be zero. The final answer is (boxed{0}).]

🔑:Solution. Let a<b<c. Let's calculate all the sums of numbers written on some five of the given cards. According to the condition of the problem, for each such sum s, there exists an opposite sum -s. This means that if we mark all the obtained sums on the number line, the resulting set of points will be symmetric with respect to 0.The extreme sums in this set are opposite; thus, the largest sum 5c is opposite to the smallest sum 5a. From the equality 5a + 5c = 0, it follows that a = -c.The sums closest to the extreme sums are also opposite. These are the sums 4a + b and 4c + b; thus, (4a + b) + (4c + b) = 0. Since a = -c, we get b = 0.Comment. The key moment in the solution is the ordering of the numbers by size and considering the largest and smallest sums of five numbers. (This approach is known as the principle of the extreme element.)

🧠:[<think>Okay, so here's the problem: We have a rectangle with sides a cm and b cm, both natural numbers. If we extend the side with length a by b cm, and the side with length b by a cm, we get a square with area 100 cm². We need to find the rectangle with the smallest area that satisfies these conditions.First, let me visualize this. The original rectangle has sides a and b. When we extend one side (a) by b, its new length becomes a + b. Similarly, extending the other side (b) by a gives a new length of b + a. Wait, hold on, if we add b to a and a to b, both new sides are a + b? But that would make a square where both sides are equal. But the problem says that after extending, we get a square. So the extended sides must be equal, which they are, since a + b and b + a are the same. But the area of the square is 100 cm². So the side length of the square is a + b, and the area is (a + b)² = 100. Therefore, a + b must be 10, because 10² is 100. So a + b = 10.But wait, hold on. Let me check again. If we extend side a by b, the new length is a + b. Similarly, extending side b by a gives b + a. So both sides become a + b, which is the same. Therefore, the resulting figure is a square with side length a + b and area (a + b)² = 100. So that gives a + b = 10. Therefore, the sum of a and b is 10.But the original rectangle has sides a and b, which are natural numbers. So possible pairs (a, b) where a and b are natural numbers (so positive integers) and a + b = 10. The pairs would be (1,9), (2,8), (3,7), (4,6), (5,5), (6,4), etc., but since a and b are sides of a rectangle, (a,b) and (b,a) would represent the same rectangle. So we can consider a ≤ b to avoid duplicates.So the possible rectangles are (1,9), (2,8), (3,7), (4,6), (5,5). Now, the area of the original rectangle is a*b. So we need to find the pair among these where a*b is minimized.Calculating the areas:1*9 = 92*8 = 163*7 = 214*6 = 245*5 = 25So the smallest area is 9 cm² from the rectangle with sides 1 and 9. Therefore, the answer should be the rectangle with sides 1 and 9.But wait, let me check if there's any mistake here. Because the problem says "the side with length a cm is extended by b cm and the side with length b cm is extended by a cm". So, if a side of length a is extended by b, does that mean adding b to a? So yes, the new length is a + b, and similarly for the other side. So the square's side is a + b = 10, so area is 100. Therefore, the conclusion is that a + b = 10, and the minimal area is 9.But maybe I need to check if there are other possibilities. For instance, maybe the extensions are not necessarily adding, but something else? Wait, the problem says "extended by", which in common terms would mean increasing the length by that amount. So extending a by b cm would make it a + b. Similarly for the other side. So I think that's correct.Alternatively, is there a case where a and b could be different but still result in a square when extended? But since both extensions lead to a + b, which is the same for both sides, so any a and b that sum to 10 would work. Therefore, the minimal area is indeed 1*9 = 9.But let me confirm once more. Suppose a = 1, b = 9. Then extending a by b gives 1 + 9 = 10, and extending b by a gives 9 + 1 = 10, so the square is 10x10 with area 100. Correct. And the original rectangle has area 1*9=9. If we take a = 2, b =8, the area is 16, which is bigger. So 9 is the smallest possible.But wait, the problem says "the lengths of the sides of the given rectangle are natural numbers". So 1 and 9 are natural numbers, so that's acceptable. Therefore, the answer should be the rectangle with sides 1 and 9.But let me check once again. Let me read the problem again to make sure."Given a rectangle with sides a cm and b cm. If the side with length a cm is extended by b cm and the side with length b cm is extended by a cm, a square with area 100 cm² is obtained. If the lengths of the sides of the given rectangle are natural numbers, determine the rectangle with the smallest area."Yes, so extending each side by the length of the other side. Then forming a square. So the square's sides are a + b and b + a, which are equal, so the square's area is (a + b)^2 = 100. So a + b = 10. Therefore, the possible pairs (a, b) are positive integers adding up to 10, and we need the one with minimal a*b, which is indeed 1*9=9.Therefore, the rectangle with sides 1 cm and 9 cm has the minimal area of 9 cm².But just to be thorough, let's check if there's another interpretation. For instance, maybe "extending the side with length a by b cm" could mean that the total length after extension is b cm? But that wouldn't make sense because if the original length is a, extending it by b cm would be a + b. So if a was 2, and you extend it by 8 cm, you get 10 cm. So that seems correct.Alternatively, is there a different way the extension could be done? For example, extending in the sense of increasing the side to make a square, but perhaps different operations? But according to the problem, it's explicitly stated: "the side with length a cm is extended by b cm", so that should be a + b, and similarly for the other side.Therefore, conclusion: a + b = 10, minimal a*b with a, b natural numbers is 9. So the answer is the rectangle with sides 1 and 9.Final AnswerThe rectangle with the smallest area has sides of boxed{1} and boxed{9} centimeters. However, since the problem asks to present the answer in a single boxed format, typically the area would be boxed. To clarify, the smallest area is boxed{9} square centimeters.But checking the problem statement again: "determine the rectangle with the smallest area." The answer should specify the rectangle, which is 1 cm and 9 cm. However, in some contexts, the answer might require the dimensions. The problem says "determine the rectangle," so probably expects the dimensions. But since it's an answer format with a single box, maybe the area. Wait, the problem says "determine the rectangle with the smallest area." So perhaps the answer is the minimal area, which is 9. But the problem says "the rectangle," so maybe both sides. But the user instruction says "put your final answer within boxed{}." Typically, for such problems, the expected answer is the numerical value of the area, so boxed{9}. But the problem says "determine the rectangle," which would be the dimensions. However, the user might expect the area. Wait, let me check the original problem statement.Original problem: "determine the rectangle with the smallest area." So they want the rectangle, but in terms of answer format, it's likely the area. But maybe the sides? The problem says "the lengths of the sides of the given rectangle are natural numbers," so maybe the answer is the pair (1,9). But the user instruction says "put your final answer within boxed{}." Usually, for rectangle dimensions, if they ask for the sides, sometimes you write both in a box, but if it's the area, you box the number. The problem says "determine the rectangle with the smallest area," so the answer is the rectangle, which would have sides 1 and 9. But how to format that? The user might expect the area. Wait, maybe the problem is from a source where the answer is the area. But let me check again.Wait, the problem says "determine the rectangle with the smallest area." So the answer is the rectangle, which is 1x9. However, in many math competitions, when they say "determine the rectangle" they might expect the dimensions or the area. Given that the area is 9, and the problem mentions "smallest area," perhaps 9 is the answer. But maybe both dimensions. However, the user's instruction might prefer the area. Let me check the initial problem once again:"Determine the rectangle with the smallest area." If the answer requires the dimensions, then you need to specify both sides, but in the format here, since it's a single box, maybe the area. However, in some contexts, if they want the dimensions, they might expect two numbers. But the user hasn't specified. Wait, looking back at the original problem, it says "put your final answer within boxed{}", so likely a single numerical value. Hence, the minimal area is 9. Therefore, boxed 9.But actually, in the problem statement, the answer is the rectangle, but the way to present it is in boxed. However, in some similar problems, when they ask for the dimensions, you can list them separated by commas inside the box. For example, boxed{1} and boxed{9}, but if you need to put in a single box, maybe boxed{1 text{ and } 9}. But the standard is not clear. Alternatively, since the problem says "the rectangle with the smallest area", the answer is 9 cm², so boxed{9}. But I need to check if the user's initial problem mentions units. The problem says "smallest area" and the area is in cm², but the answer should be numerical. Given that the user's previous problems have answers in boxed numbers, probably boxed{9} is the answer.But let me check once more. If the problem was to find the dimensions, then the answer would be 1 and 9. If it's the area, it's 9. The problem says "determine the rectangle with the smallest area." So the rectangle is determined by its sides, but the problem might accept the area as the answer. However, in competitions, often when they say "determine the rectangle" they want the dimensions. But given the answer format here is a single box, maybe the area. However, the original problem mentions "area 100 cm²" for the square. So maybe the answer should be the area, which is 9. Therefore, I think the answer is boxed{9}.Wait, but in the problem statement, it's written as "determine the rectangle with the smallest area", so the rectangle is the one with sides 1 and 9. But since the answer is to be boxed, and the user might expect the area, but maybe the sides. To resolve this, perhaps the problem expects the minimal area, which is 9, so boxed{9}. However, in some sources, they might write the sides. Given the ambiguity, but following the user's initial problem which mentions "smallest area", the answer is the area, so boxed{9}.But the assistant's thought process initially concluded sides 1 and 9. Hmm. Alternatively, maybe the problem expects the pair (1,9) boxed. But how? If allowed, maybe boxed{(1, 9)}. But in Chinese problems, sometimes they expect ordered pairs. Since the user hasn't specified, but given the translation, probably as an area. But since the problem says "the lengths of the sides... are natural numbers", maybe the answer is the sides. So to write both in the box. In Chinese textbooks, sometimes they write the dimensions separated by a comma inside the box. For example, boxed{1,9} or boxed{1 text{ and } 9}. But since here it's using LaTeX, it's possible to write boxed{1} and boxed{9}, but the user instruction says "put your final answer within boxed{}", singular. Therefore, maybe the area is the answer. Alternatively, the problem may expect the product, which is the area. Given that the problem statement is in Chinese, maybe in the original source, the answer is the area, so boxed{9}. But to be safe, since the problem says "determine the rectangle", but given the answer format, I think boxed{9} is acceptable.However, when translating Chinese problems, sometimes "determine the rectangle" implies giving the dimensions, but the answer might require both. But given the constraints of the answer format here, perhaps it's acceptable to give the area. But to check, let's see: the minimal area is 9, achieved by the rectangle 1x9. So both answers are correct, but the problem says "determine the rectangle with the smallest area", so technically, the rectangle is 1x9, but since the question is in Chinese, sometimes they just expect the numerical value of the area. To resolve this, I think the answer is the area, which is 9, so boxed{9}.But to make sure, let me check similar problems. In many math competitions, when asked for the rectangle with certain properties and minimal area, the answer is the numerical value of the area. So, given that, boxed{9} is the answer. Therefore, I will go with boxed{9}.Final Answerboxed{9}</think>Given a rectangle with sides (a , text{cm}) and (b , text{cm}), where both (a) and (b) are natural numbers. When the side (a) is extended by (b , text{cm}) and the side (b) is extended by (a , text{cm}), a square with area (100 , text{cm}^2) is obtained. We need to determine the rectangle with the smallest area.First, we note that extending each side of the rectangle results in a square. The new lengths of the sides after extension are (a + b) and (b + a), which must be equal, forming a square. The area of this square is given as (100 , text{cm}^2), so the side length of the square is (sqrt{100} = 10 , text{cm}). Therefore, we have:[a + b = 10]We need to find pairs of natural numbers ((a, b)) such that (a + b = 10) and the area (a times b) is minimized. The possible pairs ((a, b)) are ((1, 9)), ((2, 8)), ((3, 7)), ((4, 6)), ((5, 5)), and their permutations. Calculating the areas for these pairs:[1 times 9 = 9][2 times 8 = 16][3 times 7 = 21][4 times 6 = 24][5 times 5 = 25]The smallest area is (9 , text{cm}^2), which corresponds to the rectangle with sides (1 , text{cm}) and (9 , text{cm}).Thus, the rectangle with the smallest area has an area of (boxed{9}) square centimeters.,<think>Okay, let's see. So we have a rectangle with sides a and b, both in centimeters. The problem says that if we extend the side with length a by b cm, and the side with length b by a cm, we get a square with area 100 cm². We need to find the rectangle with natural number sides that has the smallest area.First, I need to visualize this. If we have a rectangle, normally sides are a and b. Then, if we extend one side (a) by b cm, that would make the new length a + b. Similarly, extending the other side (b) by a cm would make it b + a. Wait, so both extensions result in a + b? But then it's a square, so both sides must be equal. So that makes sense, since a square has equal sides. So after extension, both sides are a + b, which is the side of the square. The area of the square is (a + b)² = 100 cm². Therefore, a + b = sqrt(100) = 10 cm. So a + b = 10.But hold on, the problem says the extensions lead to a square. So if you extend a by b and b by a, then the new lengths are a + b and b + a, which are equal, so indeed a square. Therefore, a + b must equal 10. Therefore, the original rectangle has sides a and b where a + b = 10. Then the problem says the sides are natural numbers, so a and b are positive integers (since lengths can't be zero or negative) adding up to 10.But then, the question is to determine the rectangle with the smallest area. The area of the original rectangle is a*b. Since a + b = 10, we need to find integers a and b such that a + b = 10 and a*b is minimized.Wait, but normally, for fixed perimeter (but here it's fixed sum), the area is maximized when the rectangle is as close to a square as possible. Conversely, the area is minimized when the rectangle is as elongated as possible. So if a + b = 10, the minimal area would be when one side is 1 and the other is 9, giving area 9. Then 2*8=16, 3*7=21, 4*6=24, 5*5=25. So indeed, the minimal area is 9 cm². So the rectangle with sides 1 and 9. But wait, the problem says "the lengths of the sides of the given rectangle are natural numbers", so 1 and 9 are natural numbers. So the answer should be 1 and 9, area 9. Is that right?But wait, let me check again. The problem states that when you extend side a by b and side b by a, you get a square. So the extended sides are a + b and b + a, which must be equal (since it's a square), which they are. So that's just a + b = 10. Then the area of the square is (a + b)² = 100, which checks out. So all the rectangles with sides a and b where a + b = 10 will satisfy this condition. Then among these, find the one with minimal area. Since a and b are positive integers, the possible pairs are (1,9), (2,8), (3,7), (4,6), (5,5). Their areas are 9, 16, 21, 24, 25. So 9 is the smallest. Therefore, the rectangle with sides 1 and 9 cm has the minimal area of 9 cm². So that's the answer?Wait, but let me check if I interpreted the problem correctly. The problem says "the side with length a cm is extended by b cm", so does that mean that we add b cm to side a? So original side a becomes a + b. Similarly, original side b is extended by a cm, becoming b + a. So yes, both become a + b, which is 10. Therefore, the square is 10 cm per side, area 100. So all good. Therefore, a + b = 10. So the possible natural number pairs (a,b) are as before, and minimal area is 9. So the answer is 9 cm², achieved by a =1 and b=9. Since they asked for the rectangle with the smallest area, which is 9. But let me confirm once again.Wait, but maybe there's a catch here. Let me read the problem again. "If the side with length a cm is extended by b cm and the side with length b cm is extended by a cm, a square with area 100 cm² is obtained." So extending a by b gives a + b, and extending b by a gives b + a. So both sides are a + b, hence a square. Then area is (a + b)^2 = 100, so a + b = 10. So the original rectangle has sides a and 10 - a. Then area is a*(10 - a). To minimize this, since a must be a natural number between 1 and 9, the minimal product is at a=1 or a=9, giving 9. So yes, 9 is the minimal. Therefore, the answer is the rectangle with sides 1 and 9, area 9. But let me check if a and b are allowed to be in any order. The problem says "the side with length a is extended by b", so a and b are specific sides. But since the rectangle can be rotated, but since they are asking for natural numbers, both a and b are natural numbers, so (1,9) and (9,1) are the same rectangle. So yes, 1x9 is the minimal area. Therefore, the answer should be 9 cm², achieved by a rectangle of 1x9.Wait, but the problem says "determine the rectangle with the smallest area". So they might want the dimensions as well? The problem says "the lengths of the sides of the given rectangle are natural numbers, determine the rectangle with the smallest area." So maybe we need to specify both the sides and the area? Hmm. The original problem is in Chinese, but the translation says "determine the rectangle with the smallest area". Since it's a competition problem, sometimes they just want the area, but sometimes they want the sides. But the problem says "determine the rectangle", which would imply specifying its dimensions. However, in the instructions here, the user says "put your final answer within boxed{}". Typically, in math problems, if it's a number, you box the number. If it's a pair of numbers, sometimes you box them separated by commas. But since the problem mentions "the rectangle with the smallest area", maybe they expect the area value. But the problem statement says "determine the rectangle...", so maybe the dimensions? Wait, but let's check the original problem again.Original problem: "Determine the rectangle with the smallest area." Since it's a rectangle, you can describe it by its side lengths. However, in many math competitions, when they say "determine the rectangle", they might expect the dimensions (i.e., the lengths of the sides), but if they ask for the area, they would specify. Here, it's a bit ambiguous. But since the question is translated as "determine the rectangle with the smallest area", maybe they just need the minimal area, which is 9. But in the problem statement, they mention that the lengths are natural numbers, so maybe they want both the sides and the area. But given the final answer is to be boxed, and in Chinese problems, sometimes they expect just the numerical answer. But perhaps, given that the original problem mentions "lengths of the sides are natural numbers", they might want the sides. But since in the problem statement here, the user wrote "determine the rectangle with the smallest area", and in the instructions, the example had a numerical answer boxed. Wait, the initial problem statement says "determine the rectangle...", but the user instruction says "put your final answer within boxed{}". Maybe in the original problem, the answer is the area, so 9. But perhaps in the Chinese version, the problem might expect the sides. Wait, the problem says "If the lengths of the sides of the given rectangle are natural numbers, determine the rectangle with the smallest area." So "determine the rectangle" would mean to identify the rectangle, which is done by its side lengths. So maybe the answer is 1 cm and 9 cm. But how to represent that in a box? Maybe box 1 and 9. Let me check the problem statement again. The original problem is problem 5. Given a rectangle... If the side with length a cm is extended by b cm and the side with length b cm is extended by a cm, a square with area 100 cm² is obtained. If the lengths of the sides of the given rectangle are natural numbers, determine the rectangle with the smallest area.So the key is "determine the rectangle". So the rectangle is determined by its side lengths. So the answer is 1 cm and 9 cm. But in the format, the user says "put your final answer within boxed{}". In many cases, if it's multiple numbers, you can write boxed{1} and boxed{9}, but perhaps they want the area? Wait, the problem says "determine the rectangle with the smallest area". So the answer is the rectangle, which has sides 1 and 9, and area 9. But depending on the convention, sometimes they just want the minimal area. But the problem says "determine the rectangle", which would be 1x9. But in the context of math competition problems, sometimes they ask for the area. Hmm. Maybe I should check the problem once again. The problem says "determine the rectangle with the smallest area". So if they had wanted the area, they would have asked "determine the smallest area of the rectangle". But since they say "determine the rectangle", that would be the dimensions. However, in Chinese problems, sometimes "determine the rectangle" can mean to find its dimensions or its area. But given that the area is a single number, and the dimensions are two numbers, but the problem mentions both a and b are natural numbers, and they are to find the rectangle with minimal area. So, perhaps the answer is 9, as the minimal area, achieved by 1x9. Therefore, box 9. Alternatively, write 1 and 9. But since the user mentions "the final answer", which is typically a single box. Maybe we need to write the area, so 9. But let me check again.Wait, the problem says "determine the rectangle with the smallest area". So "determine the rectangle" would mean to specify the rectangle, which in this case is defined by its sides. So, the answer should be the sides, 1 and 9. But in the format, since they want it in a box, maybe boxed{1} and boxed{9}, but perhaps in the Chinese context, they might present it as 1×9. So maybe boxed{1 times 9}. But in the Chinese math competitions, often when they ask for the rectangle, they expect the dimensions. However, in the instructions, the user might expect just the area. Given the ambiguity, but since the problem mentions "smallest area", the answer is 9. But let me verify once more.Wait, suppose someone answers 1 and 9, but the problem asks for the smallest area. The area is 9. So perhaps they need the area. Maybe the problem is translated as "determine the rectangle with the smallest area", meaning among all such rectangles, find the one with minimal area. Therefore, the answer is the area, which is 9. But in that case, the problem should say "determine the smallest area of such a rectangle". But the translation is "determine the rectangle with the smallest area". So in Chinese, maybe it's more precise, but given the translation, it's a bit ambiguous. However, given that the original problem mentions "area 100 cm²" for the square, perhaps the answer is the area of the original rectangle, which is 9. Therefore, the answer is boxed{9}. But to be thorough, perhaps I should check for possible other interpretations.Wait, wait. Let me go back. The problem says: If we extend side a by b and side b by a, we get a square of area 100. Therefore, the square has sides of length 10. Therefore, a + b = 10. So the original rectangle has sides a and b, natural numbers, with a + b = 10. Find the rectangle with minimal area. Therefore, yes, the minimal area is 9. So the answer is 9. Therefore, boxed{9}. However, in some textbooks, when they say "determine the rectangle", they expect the length and width. So maybe they need the sides. Let me check the problem once more: "determine the rectangle with the smallest area". So, the rectangle is determined by its sides. But in the format requested here, to put the final answer in a box. If I need to write the sides, perhaps as 1 cm and 9 cm, but in boxed notation, maybe boxed{(1, 9)}. But in Chinese problems, sometimes they list the dimensions separated by a comma in a box. Alternatively, if the problem expects just the numerical value of the area, then boxed{9}. Given the problem mentions "smallest area", it's likely that the answer is 9. But to be safe, since the problem says "determine the rectangle", but the user instruction says "put your final answer within boxed{}", maybe the answer is the area. So I think the answer is boxed{9}.Final Answerboxed{9}</think>Given a rectangle with sides (a mathrm{~cm}) and (b mathrm{~cm}), where extending side (a) by (b mathrm{~cm}) and side (b) by (a mathrm{~cm}) results in a square with area (100 mathrm{~cm}^{2}). We need to determine the rectangle with the smallest area, given that (a) and (b) are natural numbers.1. When the sides (a) and (b) are extended, the resulting square has side length (a + b). The area of this square is ((a + b)^2 = 100 mathrm{~cm}^{2}).2. Solving for (a + b), we get: [ a + b = sqrt{100} = 10 ]3. The original rectangle has sides (a) and (b) such that (a + b = 10). The area of the rectangle is (ab).4. To minimize the area (ab) with (a) and (b) as natural numbers, we consider pairs ((a, b)) that sum to 10: - ((1, 9)) gives area (1 times 9 = 9) - ((2, 8)) gives area (2 times 8 = 16) - ((3, 7)) gives area (3 times 7 = 21) - ((4, 6)) gives area (4 times 6 = 24) - ((5, 5)) gives area (5 times 5 = 25)The smallest area is (9 mathrm{~cm}^{2}), achieved by the rectangle with sides (1 mathrm{~cm}) and (9 mathrm{~cm}).Thus, the smallest area of the rectangle is (boxed{9}).]

🔑:Solution. The area of the obtained square is P_{kappa B}=(a+b)^{2}=100 mathrm{~cm}^{2}, so a+b=10 mathrm{~cm}. Since the lengths of the sides of the rectangle are natural numbers, for a and b the following pairs of values are possible:begin{aligned}& a=1, b=9 ; a=2, b=8 ; quad a=3, b=7 ; quad a=4, b=6 ; a=5, b=5 & a=6, b=4 ; quad a=7, b=3 ; quad a=8, b=2 quad text { or } a=9, b=1end{aligned}The rectangle with the smallest area P_{n p}=a b, is obtained for a=1, b=9 or a=9, b=1 and is P_{n p}=9 mathrm{~cm}^{2}.## VI section