🧠:[<think>Okay, let's see. I have two isosceles triangles. The first one has legs of length a and a base of length b, where a is greater than b. The second triangle has legs of length b and a base of length a. The vertex angles of these two triangles are supplementary, which means they add up to 180 degrees. I need to find the value of (a² + b²)/(a² - b²).Hmm, first, let me recall some properties of isosceles triangles. The vertex angle is the angle between the two legs. In the first triangle, the legs are length a, so the vertex angle is between the two sides of length a, and the base is length b. In the second triangle, the legs are length b, so its vertex angle is between the two sides of length b, with a base of length a.Since the vertex angles are supplementary, let's denote the vertex angle of the first triangle as θ, and the vertex angle of the second triangle as 180° - θ. So θ + (180° - θ) = 180°, which checks out.I need to relate the sides a and b using the information about their vertex angles. Maybe I can use the Law of Cosines here. For any triangle, the Law of Cosines relates the sides to the cosine of one of its angles.For the first triangle with legs a, a, and base b, the Law of Cosines gives:b² = a² + a² - 2*a*a*cosθSimplify that: b² = 2a²(1 - cosθ)Similarly, for the second triangle with legs b, b, and base a, the Law of Cosines gives:a² = b² + b² - 2*b*b*cos(180° - θ)But cos(180° - θ) is equal to -cosθ, right? Because cosine is negative in the second quadrant and cos(180° - θ) = -cosθ.So substituting that in:a² = 2b² - 2b²*(-cosθ)a² = 2b² + 2b²cosθa² = 2b²(1 + cosθ)Now I have two equations:1) b² = 2a²(1 - cosθ)2) a² = 2b²(1 + cosθ)Hmm, maybe I can solve these equations simultaneously. Let me write them again:From equation 1: b² = 2a²(1 - cosθ)From equation 2: a² = 2b²(1 + cosθ)Let me express cosθ from equation 1 and substitute into equation 2. Let's solve equation 1 for cosθ:From equation 1:1 - cosθ = b² / (2a²)So cosθ = 1 - (b²)/(2a²)Similarly, from equation 2:1 + cosθ = a² / (2b²)So cosθ = (a²)/(2b²) - 1Now, set the two expressions for cosθ equal to each other:1 - (b²)/(2a²) = (a²)/(2b²) - 1Let me solve this equation. Multiply both sides by 2a²b² to eliminate denominators:2a²b²*(1) - 2a²b²*(b²)/(2a²) = 2a²b²*(a²)/(2b²) - 2a²b²*(1)Simplify each term:Left side: 2a²b² - (2a²b² * b²)/(2a²) = 2a²b² - (b² * b²) = 2a²b² - b⁴Right side: (2a²b² * a²)/(2b²) - 2a²b² = (a² * a²) - 2a²b² = a⁴ - 2a²b²So the equation becomes:2a²b² - b⁴ = a⁴ - 2a²b²Bring all terms to one side:2a²b² - b⁴ - a⁴ + 2a²b² = 0Combine like terms:(2a²b² + 2a²b²) - a⁴ - b⁴ = 04a²b² - a⁴ - b⁴ = 0Let me rearrange this:-a⁴ + 4a²b² - b⁴ = 0Multiply both sides by -1 to make it easier:a⁴ - 4a²b² + b⁴ = 0Hmm, this looks like a quadratic in terms of a². Let me set x = a² and y = b². Then the equation becomes:x² - 4xy + y² = 0But this is a quadratic in x. Let me see:x² - 4xy + y² = 0This can be rewritten as:x² - 4xy + y² = (x - 2y)^2 - 3y² = 0, but maybe not useful. Alternatively, let's use the quadratic formula for x:x² - 4xy + y² = 0Treating y as a constant, solve for x:x = [4y ± sqrt(16y² - 4*1*y²)] / 2x = [4y ± sqrt(12y²)] / 2x = [4y ± 2y*sqrt(3)] / 2x = 2y ± y*sqrt(3)x = y(2 ± sqrt(3))Since x = a² and y = b², this gives:a² = b²(2 + sqrt(3)) or a² = b²(2 - sqrt(3))But we were told that a > b, so a² > b². Therefore, 2 + sqrt(3) is approximately 3.732, which is positive, and 2 - sqrt(3) is approximately 0.267, which is less than 1. So the second solution would give a² = 0.267b², which would mean a < b, contradicting a > b. Hence, we discard that solution.Therefore, a² = b²(2 + sqrt(3))So the ratio a²/b² is (2 + sqrt(3)), so a/b = sqrt(2 + sqrt(3))But the problem asks for (a² + b²)/(a² - b²). Let's compute that:Let’s denote k = a²/b² = 2 + sqrt(3). Then:(a² + b²)/(a² - b²) = (k + 1)/(k - 1)Substitute k = 2 + sqrt(3):(k + 1)/(k - 1) = (3 + sqrt(3))/(1 + sqrt(3))Multiply numerator and denominator by (sqrt(3) - 1) to rationalize the denominator:[(3 + sqrt(3))(sqrt(3) - 1)] / [(1 + sqrt(3))(sqrt(3) - 1)]Compute denominator first:(1 + sqrt(3))(sqrt(3) - 1) = 1*sqrt(3) - 1*1 + sqrt(3)*sqrt(3) - sqrt(3)*1= sqrt(3) - 1 + 3 - sqrt(3) = (sqrt(3) - sqrt(3)) + (3 - 1) = 0 + 2 = 2Now compute numerator:(3 + sqrt(3))(sqrt(3) - 1) = 3*sqrt(3) - 3*1 + sqrt(3)*sqrt(3) - sqrt(3)*1= 3*sqrt(3) - 3 + 3 - sqrt(3) = (3*sqrt(3) - sqrt(3)) + (-3 + 3) = 2*sqrt(3) + 0 = 2*sqrt(3)So numerator is 2*sqrt(3), denominator is 2. Therefore:(2*sqrt(3))/2 = sqrt(3)So (a² + b²)/(a² - b²) = sqrt(3)But sqrt(3) is a radical, but maybe they want it in terms of rationalized form or as is? Wait, sqrt(3) is already simplified. Let me check my steps again to ensure I didn't make a mistake.Starting from the two equations:1) b² = 2a²(1 - cosθ)2) a² = 2b²(1 + cosθ)Then solving for cosθ in both equations and setting them equal. Then cross-multiplying, leading to the equation 4a²b² - a⁴ - b⁴ = 0, which factors into (a² - b²(2 + sqrt(3)))(a² - b²(2 - sqrt(3))) = 0. Then since a > b, we take a² = b²(2 + sqrt(3)). Then compute (a² + b²)/(a² - b²) = ( (2 + sqrt(3)) + 1 )/( (2 + sqrt(3)) - 1 ) = (3 + sqrt(3))/(1 + sqrt(3)), which we rationalized to sqrt(3). That seems correct.Alternatively, maybe there's another way to approach the problem, but this seems solid. Let me verify with actual numbers. Suppose b = 1, then a² = 2 + sqrt(3), so a = sqrt(2 + sqrt(3)) ≈ sqrt(3.732) ≈ 1.931. Then compute (a² + b²)/(a² - b²) = (3.732 + 1)/(3.732 - 1) ≈ 4.732 / 2.732 ≈ 1.732, which is approximately sqrt(3) ≈ 1.732. So that checks out numerically.Therefore, the answer is sqrt(3), which in boxed form is boxed{sqrt{3}}.Final Answerboxed{sqrt{3}}</think>Given two isosceles triangles with supplementary vertex angles, we need to find the value of (frac{a^2 + b^2}{a^2 - b^2}).1. For the first triangle with legs (a) and base (b), using the Law of Cosines: [ b^2 = 2a^2(1 - costheta) ]2. For the second triangle with legs (b) and base (a), using the Law of Cosines and noting that (cos(180^circ - theta) = -costheta): [ a^2 = 2b^2(1 + costheta) ]3. Solving these equations for (costheta): [ costheta = 1 - frac{b^2}{2a^2} quad text{and} quad costheta = frac{a^2}{2b^2} - 1 ]4. Equating the two expressions for (costheta): [ 1 - frac{b^2}{2a^2} = frac{a^2}{2b^2} - 1 ]5. Multiplying through by (2a^2b^2) and simplifying: [ 4a^2b^2 - a^4 - b^4 = 0 ]6. Solving this quadratic equation in terms of (a^2) and (b^2): [ a^4 - 4a^2b^2 + b^4 = 0 implies (a^2 - b^2(2 + sqrt{3}))(a^2 - b^2(2 - sqrt{3})) = 0 ]7. Since (a > b), we take (a^2 = b^2(2 + sqrt{3})).8. Substituting (k = frac{a^2}{b^2} = 2 + sqrt{3}) into (frac{a^2 + b^2}{a^2 - b^2}): [ frac{a^2 + b^2}{a^2 - b^2} = frac{(2 + sqrt{3}) + 1}{(2 + sqrt{3}) - 1} = frac{3 + sqrt{3}}{1 + sqrt{3}} ]9. Rationalizing the denominator: [ frac{3 + sqrt{3}}{1 + sqrt{3}} cdot frac{sqrt{3} - 1}{sqrt{3} - 1} = frac{2sqrt{3}}{2} = sqrt{3} ]Thus, the value is (boxed{sqrt{3}}).,<think>Okay, so I have this problem here about two isosceles triangles. Let me try to parse it step by step. The first triangle has legs of length a and a base of length b, with the condition that a > b. The second triangle has legs of length b and a base of length a. The vertex angles of these two triangles are supplementary, meaning they add up to 180 degrees. And I need to find the value of (a² + b²)/(a² - b²). Alright, let's break this down. First, since both triangles are isosceles, their vertex angles are the angles opposite the base. So for the first triangle, the vertex angle is between the two legs of length a, and the base is b. For the second triangle, the legs are length b, so the vertex angle is between those two legs, and the base is a. Given that these two vertex angles are supplementary, their sum is 180 degrees. Let me denote the vertex angle of the first triangle as θ, so the vertex angle of the second triangle must be 180° - θ. Now, I need to relate the sides of the triangles to their vertex angles. Since both triangles are isosceles, I can use the Law of Cosines here. The Law of Cosines states that for any triangle with sides of length x, y, z opposite angles X, Y, Z respectively, we have:z² = x² + y² - 2xy cos ZSo for the first triangle, the sides are a, a, b, with vertex angle θ. Applying the Law of Cosines here:b² = a² + a² - 2 * a * a * cos θSimplifying that:b² = 2a² - 2a² cos θSimilarly, for the second triangle, which has sides b, b, a, and vertex angle 180° - θ. Applying the Law of Cosines again:a² = b² + b² - 2 * b * b * cos (180° - θ)Simplifying that:a² = 2b² - 2b² cos (180° - θ)Now, I remember that cos(180° - θ) is equal to -cos θ. That's one of those trigonometric identities. Let me confirm that. Yeah, because cos(180° - θ) = -cos θ. So substituting that into the equation:a² = 2b² - 2b²*(-cos θ) = 2b² + 2b² cos θSo now we have two equations:1. b² = 2a² - 2a² cos θ2. a² = 2b² + 2b² cos θNow, we can solve these two equations simultaneously. Let me write them again:From the first triangle:b² = 2a²(1 - cos θ) --> equation (1)From the second triangle:a² = 2b²(1 + cos θ) --> equation (2)So we have two equations here. Let's try to solve for cos θ in terms of a and b, and then maybe relate a and b.From equation (1):Divide both sides by 2a²:b² / (2a²) = 1 - cos θSo, cos θ = 1 - (b²)/(2a²) --> equation (1a)From equation (2):Divide both sides by 2b²:a² / (2b²) = 1 + cos θSo, cos θ = (a²)/(2b²) - 1 --> equation (2a)Now, set equation (1a) equal to equation (2a):1 - (b²)/(2a²) = (a²)/(2b²) - 1Let me write that equation:1 - (b²)/(2a²) = (a²)/(2b²) - 1Let me bring all terms to one side:1 + 1 - (b²)/(2a²) - (a²)/(2b²) = 0Simplify:2 - [ (b²)/(2a²) + (a²)/(2b²) ] = 0Multiply both sides by 2 to eliminate denominators:4 - [ (b²)/a² + (a²)/b² ] = 0So:[ (b²)/a² + (a²)/b² ] = 4Let me denote x = a²/b². Then (b²)/a² = 1/x and (a²)/b² = x. So:1/x + x = 4Multiply both sides by x:1 + x² = 4xRearranged:x² - 4x + 1 = 0Quadratic equation in x. Solving for x:x = [4 ± sqrt(16 - 4*1*1)]/2 = [4 ± sqrt(12)]/2 = [4 ± 2*sqrt(3)]/2 = 2 ± sqrt(3)So x = 2 + sqrt(3) or x = 2 - sqrt(3)But x is a²/b², and since a > b, x must be greater than 1. 2 + sqrt(3) is approximately 3.732, which is greater than 1. 2 - sqrt(3) is approximately 0.2679, which is less than 1. Therefore, we take x = 2 + sqrt(3)So a²/b² = 2 + sqrt(3) --> which implies that (a² + b²)/(a² - b²) is the expression we need to compute. Let me denote that.Let’s compute (a² + b²)/(a² - b²). Let me express this in terms of x, since x = a²/b².Let me write:(a² + b²)/(a² - b²) = (x*b² + b²)/(x*b² - b²) = [b²(x + 1)]/[b²(x - 1)] = (x + 1)/(x - 1)So since x = 2 + sqrt(3), substitute that in:( (2 + sqrt(3)) + 1 ) / ( (2 + sqrt(3)) - 1 ) = (3 + sqrt(3)) / (1 + sqrt(3))Now, simplify this expression. Multiply numerator and denominator by (1 - sqrt(3)) to rationalize the denominator:(3 + sqrt(3))(1 - sqrt(3)) / [ (1 + sqrt(3))(1 - sqrt(3)) ]First, compute the denominator:(1)^2 - (sqrt(3))^2 = 1 - 3 = -2Now, compute the numerator:3*1 + 3*(-sqrt(3)) + sqrt(3)*1 + sqrt(3)*(-sqrt(3)) = 3 - 3sqrt(3) + sqrt(3) - 3Simplify numerator:3 - 3 = 0-3sqrt(3) + sqrt(3) = -2sqrt(3)So numerator is -2sqrt(3), denominator is -2Therefore, (-2sqrt(3))/(-2) = sqrt(3)So (a² + b²)/(a² - b²) = sqrt(3)Wait, but sqrt(3) is approximately 1.732, but let me check my steps again to make sure.Wait, when I rationalized (3 + sqrt(3))/(1 + sqrt(3)):Multiply numerator and denominator by (1 - sqrt(3)):Numerator: (3 + sqrt(3))(1 - sqrt(3)) = 3*1 + 3*(-sqrt(3)) + sqrt(3)*1 + sqrt(3)*(-sqrt(3)) = 3 - 3sqrt(3) + sqrt(3) - 3 = (3 - 3) + (-3sqrt(3) + sqrt(3)) = 0 - 2sqrt(3) = -2sqrt(3)Denominator: (1 + sqrt(3))(1 - sqrt(3)) = 1 - 3 = -2Therefore, the result is (-2sqrt(3))/(-2) = sqrt(3). So that is correct. So the value is sqrt(3). But let me check again if that is the case. Wait, the problem asks for (a² + b²)/(a² - b²). And through substitution, we found that equals (x + 1)/(x - 1) where x = 2 + sqrt(3). So substituting x into (x + 1)/(x - 1):x + 1 = (2 + sqrt(3)) + 1 = 3 + sqrt(3)x - 1 = (2 + sqrt(3)) - 1 = 1 + sqrt(3)So (3 + sqrt(3))/(1 + sqrt(3)) as before, which simplifies to sqrt(3). So yes, that's correct. Alternatively, maybe there's a different approach. Let's see. Let me verify using the value. Suppose (a² + b²)/(a² - b²) = sqrt(3). Then cross-multiplied: a² + b² = sqrt(3)(a² - b²). Then a² + b² = sqrt(3)a² - sqrt(3)b². Then bringing terms with a² to one side: a² - sqrt(3)a² = -sqrt(3)b² - b². So a²(1 - sqrt(3)) = -b²(1 + sqrt(3)). Multiply both sides by -1: a²(sqrt(3) - 1) = b²(1 + sqrt(3)). Therefore, (a²)/(b²) = (1 + sqrt(3))/(sqrt(3) - 1). Multiply numerator and denominator by (sqrt(3) + 1): Numerator: (1 + sqrt(3))(sqrt(3) + 1) = 1*sqrt(3) + 1*1 + sqrt(3)*sqrt(3) + sqrt(3)*1 = sqrt(3) + 1 + 3 + sqrt(3) = 4 + 2sqrt(3)Denominator: (sqrt(3) - 1)(sqrt(3) + 1) = 3 -1 = 2Thus, (a²)/(b²) = (4 + 2sqrt(3))/2 = 2 + sqrt(3), which matches our previous result. So this confirms that (a² + b²)/(a² - b²) = sqrt(3). Therefore, the answer should be sqrt(3), which in boxed form is boxed{sqrt{3}}.But just to ensure there's no mistake, let me recap the steps:1. Applied Law of Cosines to both triangles.2. Expressed cos θ and cos (180° - θ) in terms of a and b.3. Set up equations and solved for the ratio a²/b².4. Found the required expression by substituting the ratio.Everything seems to check out. So I'm confident the answer is sqrt(3).Final Answerboxed{sqrt{3}}</think>Given two isosceles triangles with legs (a) and base (b) (where (a > b)) and legs (b) and base (a) respectively, and their vertex angles being supplementary, we need to find the value of (frac{a^2 + b^2}{a^2 - b^2}).1. Using the Law of Cosines for the first triangle (legs (a), base (b)): [ b^2 = 2a^2 - 2a^2 cos theta ] Simplifying, we get: [ cos theta = 1 - frac{b^2}{2a^2} ]2. Using the Law of Cosines for the second triangle (legs (b), base (a)): [ a^2 = 2b^2 - 2b^2 cos (180^circ - theta) ] Since (cos (180^circ - theta) = -cos theta), we get: [ a^2 = 2b^2 + 2b^2 cos theta ] Simplifying, we get: [ cos theta = frac{a^2}{2b^2} - 1 ]3. Equating the expressions for (cos theta): [ 1 - frac{b^2}{2a^2} = frac{a^2}{2b^2} - 1 ] Simplifying, we get: [ 2 - left( frac{b^2}{2a^2} + frac{a^2}{2b^2} right) = 0 ] Multiplying through by (2a^2b^2), we obtain: [ 4a^2b^2 - (b^4 + a^4) = 0 ] Let (x = frac{a^2}{b^2}), then: [ x + frac{1}{x} = 4 ] Solving the quadratic equation (x^2 - 4x + 1 = 0), we find: [ x = 2 + sqrt{3} ]4. Calculating (frac{a^2 + b^2}{a^2 - b^2}): [ frac{a^2 + b^2}{a^2 - b^2} = frac{x + 1}{x - 1} = frac{(2 + sqrt{3}) + 1}{(2 + sqrt{3}) - 1} = frac{3 + sqrt{3}}{1 + sqrt{3}} ] Rationalizing the denominator: [ frac{3 + sqrt{3}}{1 + sqrt{3}} cdot frac{1 - sqrt{3}}{1 - sqrt{3}} = frac{-2sqrt{3}}{-2} = sqrt{3} ]Thus, the value is (boxed{sqrt{3}}).]

🔑:4. sqrt{3}.Since the apex angles of the two isosceles triangles are supplementary, the base angles of the two isosceles triangles must be complementary.Obviously, in Figure 6, triangle A C D is similar to the isosceles triangle with legs of length a and base of length b.Thus, frac{C D}{b}=frac{b}{a},C D=frac{b^{2}}{a} text {. }From the right triangle triangle B C D, we get B D^{2}=B C^{2}+C D^{2}, i.e.,4 b^{2}=a^{2}+left(frac{b^{2}}{a}right)^{2} text {. }Therefore, a^{4}+b^{4}=4 a^{2} b^{2}.From this, we haveleft{begin{array}{l}a^{4}+2 a^{2} b^{2}+b^{4}=6 a^{2} b^{2}, a^{4}-2 a^{2} b^{2}+b^{4}=2 a^{2} b^{2},end{array}right.which simplifies to left{begin{array}{l}left(a^{2}+b^{2}right)^{2}=6 a^{2} b^{2} left(a^{2}-b^{2}right)^{2}=2 a^{2} b^{2}end{array}right..Thus, frac{a^{2}+b^{2}}{a^{2}-b^{2}}=sqrt{3}.

🧠:[<think>Okay, let's see. So, the problem is about two factories: a shoe factory and a sewing factory. The number of workers at the shoe factory is 15/19 of the number at the sewing factory. Then, at the first enterprise (I guess that's either the shoe or the sewing factory?), 3/7 of the workers exceeded the monthly plan, and the rest, which is fewer than 1000 workers, completed the plan at 100%. At the other enterprise (so whichever one isn't the first), 2/5 of the workers exceeded the plan, and the rest, more than 1000 workers, completed the plan. The question is to find how many workers are at each factory.First, let me parse the problem again to make sure I understand. The first enterprise mentioned – it's not specified whether it's shoe or sewing. But the problem refers to "the first of these enterprises" and "the other". So maybe the order in the problem statement is important? Let me check:"The number of workers at a shoe factory is 15/19 of the number of workers at a sewing factory. At the first of these enterprises, 3/7 of the workers exceeded the monthly plan, while the rest, fewer than 1000 workers, completed the plan at 100%; at the other, 2/5 of the workers exceeded the plan, while the rest, more than 1000 workers, completed the plan at 100%. How many workers are there at each of these factories?"So, "the first of these enterprises" – since the first mentioned is the shoe factory, perhaps? Then the other would be the sewing factory. Alternatively, maybe it's the order in which the information is presented. Let me see.The problem starts by comparing the number of workers: shoe factory is 15/19 of the sewing factory. Then, talking about "the first of these enterprises" – so the first one mentioned is the shoe factory, and the other is the sewing factory. So perhaps the shoe factory is the first enterprise, and the sewing factory is the other. Then:At the shoe factory: 3/7 exceeded the plan, rest (which is 4/7) completed the plan, and this rest is fewer than 1000.At the sewing factory: 2/5 exceeded the plan, rest (which is 3/5) completed the plan, and this rest is more than 1000.Alternatively, if "the first of these enterprises" refers to the first one in the comparison, which is the shoe factory (since the problem starts with the shoe factory's number being a fraction of the sewing factory's), then the other is the sewing factory.Alternatively, maybe "the first of these enterprises" is whichever is first in the problem's structure. Hmm.Alternatively, maybe the problem is translated from another language, and "the first of these enterprises" might be ambiguous. Wait, but in the original problem statement, the first part says "the number of workers at a shoe factory is 15/19 of the number at a sewing factory". Then, the next sentence starts with "At the first of these enterprises...". So "these enterprises" must refer to the shoe and sewing factories. Then "the first of these" – since the shoe was mentioned first, perhaps it's the shoe factory. So let me assume that.So:Shoe factory: 15/19 of sewing factory's workers.At shoe factory (first enterprise): 3/7 exceeded plan, rest (4/7) completed plan, and rest is fewer than 1000.At sewing factory (the other enterprise): 2/5 exceeded plan, rest (3/5) completed plan, and rest is more than 1000.Therefore, we can denote the number of workers at the shoe factory as S and the sewing factory as W.Given that S = (15/19) W.At the shoe factory: (4/7) S < 1000.At the sewing factory: (3/5) W > 1000.So, we have these two inequalities:(4/7) S < 1000,(3/5) W > 1000.But since S = (15/19) W, we can substitute S in the first inequality.Thus:(4/7) * (15/19) W < 1000,So, (60/133) W < 1000,Multiply both sides by 133/60:W < 1000 * (133/60) = (1000 * 133)/60 = 133000/60 ≈ 2216.666...So W < 2216.666... Since W must be an integer (number of workers), then W ≤ 2216.From the second inequality:(3/5) W > 1000,Multiply both sides by 5/3:W > (1000 * 5)/3 = 5000/3 ≈ 1666.666...So W > 1666.666..., so since W must be an integer, W ≥ 1667.Therefore, W is in the range 1667 ≤ W ≤ 2216.But also, since S = (15/19) W, and S must be an integer as well. So 15/19 W must be an integer, meaning that W must be a multiple of 19. Because 15 and 19 are coprime (they share no common divisors except 1), so for 15W/19 to be integer, W must be divisible by 19.Therefore, W is a multiple of 19 between 1667 and 2216.Similarly, S = 15/19 W must be an integer. So W must be divisible by 19.So let's find all multiples of 19 in the interval [1667, 2216].First, find the smallest multiple of 19 greater than or equal to 1667.Divide 1667 by 19:1667 ÷ 19. 19*87 = 1653. 1667 - 1653 = 14. So 19*87 +14 = 1667. So next multiple is 19*88 = 1672.Similarly, the largest multiple of 19 less than or equal to 2216.2216 ÷19. 19*116 = 2204. 2216 -2204=12. So previous multiple is 19*116=2204. Next would be 2204 +19=2223, which is above 2216. So the upper bound is 2204.Therefore, W must be in the range 1672 to 2204, multiples of 19.Also, S = 15/19 W must be such that when we compute 4/7 S and 3/5 W, those fractions must result in integer numbers of workers, right?Wait, because the number of workers who exceeded or completed the plan must be whole numbers. So at the shoe factory, 3/7 S must be an integer, and 4/7 S must be an integer. Similarly, at the sewing factory, 2/5 W and 3/5 W must be integers.Therefore, S must be a multiple of 7, and W must be a multiple of 5.But S is 15/19 W, so S = 15/19 W. So if S must be a multiple of 7, then 15/19 W must be a multiple of 7. Therefore, W must be a multiple of 7*19 / gcd(15,7*19). Since 15 and 7 are coprime, and 15 and 19 are coprime, gcd(15,7*19)=1. So W must be a multiple of 7*19=133.Similarly, W must also be a multiple of 5, because 3/5 W must be an integer. Therefore, W must be a multiple of 5. Since 133 and 5 are coprime, W must be a multiple of 5*133=665.Therefore, W must be a multiple of 665 (the least common multiple of 5 and 133).Given that W is a multiple of 665, and also a multiple of 19 (from earlier), but since 665 is already 5*7*19, which includes the 19, so W must be a multiple of 665.So W must be a multiple of 665 in the range 1667 ≤ W ≤ 2216.So let's find multiples of 665 in that interval.Compute 665*3=1995; 665*2=1330. 1330 is less than 1667. Next multiple is 1995. Then 1995 + 665=2660, which is more than 2216. So the only multiple of 665 in that range is 1995.Therefore, W=1995.Check if 1995 is within the previous range of 1667 to 2216. Yes, 1995 is between those.Check if W=1995 is a multiple of 19: 1995 ÷19=105. So 19*105=1995. Correct.So W=1995. Then S=15/19 *1995=15*105=1575.Check if S=1575 is a multiple of 7: 1575 ÷7=225. Yes, 7*225=1575. Correct.Therefore, S=1575, W=1995.Now verify the conditions:At the shoe factory (S=1575):3/7 exceeded the plan: 3/7*1575=675 workers.Rest completed the plan: 4/7*1575=900 workers. The problem states that "the rest, fewer than 1000 workers, completed the plan". 900 is fewer than 1000. Correct.At the sewing factory (W=1995):2/5 exceeded the plan: 2/5*1995=798 workers.Rest completed the plan: 3/5*1995=1197 workers. The problem states "more than 1000 workers", and 1197 is more than 1000. Correct.Therefore, the numbers are 1575 at the shoe factory and 1995 at the sewing factory.Wait, but let me just confirm if there are any other possible multiples. Earlier, I concluded that W must be a multiple of 665, but let's check if that's necessarily the case.Because W must be a multiple of both 5 and 133 (since 3/5 W must be integer, so W multiple of 5, and S=15/19 W must be a multiple of 7, so 15/19 W must be multiple of 7, which requires that W is a multiple of 7*19=133, since 15 and 7*19 are coprime). Therefore, the LCM of 5 and 133 is 5*133=665. Therefore, W must be a multiple of 665. So only 665*3=1995 in that range.Therefore, the answer is Shoe factory: 1575, Sewing factory: 1995.Final AnswerThe shoe factory has boxed{1575} workers and the sewing factory has boxed{1995} workers.</think>Given that the number of workers at a shoe factory is (frac{15}{19}) of the number of workers at a sewing factory, we denote the number of workers at the shoe factory as (S) and at the sewing factory as (W). Thus, (S = frac{15}{19}W).At the shoe factory, (frac{3}{7}) of the workers exceeded the monthly plan, and the rest, which is fewer than 1000 workers, completed the plan. This gives us the inequality:[frac{4}{7}S < 1000]At the sewing factory, (frac{2}{5}) of the workers exceeded the plan, and the rest, which is more than 1000 workers, completed the plan. This gives us the inequality:[frac{3}{5}W > 1000]Substituting (S = frac{15}{19}W) into the first inequality:[frac{4}{7} left(frac{15}{19}Wright) < 1000][frac{60}{133}W < 1000][W < frac{1000 times 133}{60} approx 2216.67]From the second inequality:[frac{3}{5}W > 1000][W > frac{1000 times 5}{3} approx 1666.67]Thus, (1667 leq W leq 2216). Additionally, (W) must be a multiple of 19, 5, and 7 (to ensure (S) and the fractions of workers are integers). The least common multiple (LCM) of 5, 7, and 19 is 665. The only multiple of 665 within the range 1667 to 2216 is 1995.Therefore, (W = 1995) and substituting back, we get:[S = frac{15}{19} times 1995 = 1575]Verification:- At the shoe factory: (frac{4}{7} times 1575 = 900) (fewer than 1000)- At the sewing factory: (frac{3}{5} times 1995 = 1197) (more than 1000)Thus, the number of workers at the shoe factory is (boxed{1575}) and at the sewing factory is (boxed{1995}).,<think>Okay, let me try to work through this problem step by step. First, I need to understand what's given and what's being asked. The problem is about two factories: a shoe factory and a sewing factory. The number of workers at the shoe factory is 15/19 of the number at the sewing factory. Then, at the first enterprise (I need to figure out which one is the first—probably the shoe factory?), 3/7 of the workers exceeded the monthly plan, and the rest, fewer than 1000 workers, completed the plan. At the other factory (the sewing factory, I assume), 2/5 of the workers exceeded the plan, and the rest, more than 1000 workers, completed the plan. The question is asking for the number of workers at each factory.First, let me note down the key information:1. Let S be the number of workers at the shoe factory, and H be the number at the sewing factory. The problem says S = (15/19)H.2. At the first enterprise (either S or H), 3/7 exceeded the plan, and the rest (which would be 1 - 3/7 = 4/7) completed it, and that number is fewer than 1000.3. At the other enterprise (the other factory), 2/5 exceeded the plan, and the rest (1 - 2/5 = 3/5) completed it, and that number is more than 1000.Wait, the problem says "the first of these enterprises" and "the other". It might be referring to the shoe factory as the first and the sewing factory as the other. Let me check.The problem states: "At the first of these enterprises, 3/7 of the workers exceeded the monthly plan... at the other, 2/5 of the workers exceeded the plan..." So, the first enterprise is the shoe factory, and the other is the sewing factory. Because the problem starts by mentioning the shoe factory first. Let me confirm: "The number of workers at a shoe factory is 15/19 of the number of workers at a sewing factory." So, shoe factory first, sewing factory second. Then, when it says "the first of these enterprises", that would be the shoe factory, and "the other" is the sewing factory.Therefore:- Shoe factory (S) has 3/7 exceeding, 4/7 completing, which is fewer than 1000 workers.- Sewing factory (H) has 2/5 exceeding, 3/5 completing, which is more than 1000 workers.So, translating into equations:For the shoe factory (S):Number of workers completing the plan = (4/7)S < 1000For the sewing factory (H):Number of workers completing the plan = (3/5)H > 1000Additionally, S = (15/19)HSo, now we have three equations:1. S = (15/19)H2. (4/7)S < 10003. (3/5)H > 1000We need to find integers S and H such that these conditions hold.Since S and H must be whole numbers (number of workers can't be a fraction), we need to find H such that H is a multiple of 19 (from S = 15/19 H, so H must be a multiple of 19 to make S an integer), and S is a multiple of 7 (since (4/7)S must be an integer), and H must be a multiple of 5 (since (3/5)H must be an integer). Wait, let's check:From the shoe factory, S must be a multiple of 7 because (4/7)S must be an integer. Similarly, H must be a multiple of 5 because (3/5)H must be an integer.Also, since S = 15/19 H, H must be a multiple of 19. So H must be a multiple of both 19 and 5, so H must be a multiple of 95 (since 19 and 5 are coprime). Then S would be 15/19 H, so since H is multiple of 95, 15/19 * 95k = 15*5k = 75k, so S would be 75k and H would be 95k for some integer k.Moreover, S must be a multiple of 7. Since S = 75k, 75k must be a multiple of 7. 75 and 7 are coprime (75 = 3*5*5; 7 is prime), so k must be a multiple of 7. Let's denote k = 7m, where m is a positive integer. Therefore:S = 75 * 7m = 525mH = 95 * 7m = 665mNow, check the inequalities:From the shoe factory: (4/7)S < 1000Substitute S = 525m:(4/7)*525m < 1000Calculate (4/7)*525: 525 divided by 7 is 75, so 4*75 = 300. So 300m < 1000 => m < 1000/300 ≈ 3.333. So m ≤ 3.From the sewing factory: (3/5)H > 1000Substitute H = 665m:(3/5)*665m > 1000Calculate (3/5)*665: 665 divided by 5 is 133, so 3*133 = 399. So 399m > 1000 => m > 1000/399 ≈ 2.506. So m ≥ 3.Therefore, m must satisfy both m ≤ 3 and m ≥ 3, hence m = 3.Therefore, m = 3, so:S = 525 * 3 = 1575H = 665 * 3 = 1995Check the conditions:For the shoe factory:Number completing the plan: (4/7)*1575 = 4*225 = 900, which is fewer than 1000. Correct.For the sewing factory:Number completing the plan: (3/5)*1995 = 3*399 = 1197, which is more than 1000. Correct.So the number of workers at the shoe factory is 1575, and at the sewing factory is 1995.Let me verify that S = 15/19 H:15/19 of 1995 is (15*1995)/19. Let's compute 1995 ÷ 19. 19*105 = 1995. So 15*105 = 1575. Correct.Also, check that S is a multiple of 7: 1575 ÷ 7 = 225. Correct.H is a multiple of 5: 1995 ÷ 5 = 399. Correct.Everything seems to check out.Final AnswerThe shoe factory has boxed{1575} workers and the sewing factory has boxed{1995} workers.</think>Given the problem, we need to determine the number of workers at a shoe factory and a sewing factory. The key information provided is:1. The number of workers at the shoe factory ((S)) is (frac{15}{19}) of the number of workers at the sewing factory ((H)).2. At the shoe factory, (frac{3}{7}) of the workers exceeded the monthly plan, and the rest (fewer than 1000 workers) completed the plan.3. At the sewing factory, (frac{2}{5}) of the workers exceeded the plan, and the rest (more than 1000 workers) completed the plan.We start by setting up the relationships and constraints:- (S = frac{15}{19}H)- The number of workers completing the plan at the shoe factory: (frac{4}{7}S < 1000)- The number of workers completing the plan at the sewing factory: (frac{3}{5}H > 1000)We determine that (H) must be a multiple of 95 (since (H) must be a multiple of both 19 and 5) and (S) must be a multiple of 7. Let (H = 95k) and (S = 75k). However, (S) must be a multiple of 7, so (k) must be a multiple of 7. Let (k = 7m), leading to (H = 665m) and (S = 525m).Next, we apply the inequalities:1. (frac{4}{7}S < 1000 implies frac{4}{7} times 525m < 1000 implies 300m < 1000 implies m < frac{1000}{300} approx 3.333)2. (frac{3}{5}H > 1000 implies frac{3}{5} times 665m > 1000 implies 399m > 1000 implies m > frac{1000}{399} approx 2.506)The only integer (m) satisfying both conditions is (m = 3). Substituting (m = 3):- (S = 525 times 3 = 1575)- (H = 665 times 3 = 1995)Verification:- Workers completing the plan at the shoe factory: (frac{4}{7} times 1575 = 900) (fewer than 1000)- Workers completing the plan at the sewing factory: (frac{3}{5} times 1995 = 1197) (more than 1000)Thus, the number of workers at each factory is (boxed{1575}) (shoe factory) and (boxed{1995}) (sewing factory).]

🔑:50. Let the number of workers at the sewing factory be x, then the number of workers at the shoe factory is frac{15}{19} x. The number of workers at the shoe factory who have completed the plan at 100 % is frac{4}{7} cdot frac{15}{19} x, and at the sewing factory it is -frac{3}{5} x. According to the condition frac{4}{7} cdot frac{15}{19} x1000, from which x1666 frac{2}{3}. Since frac{4}{7} cdot frac{15}{19} x and frac{3}{5} x are integers, x must be a multiple of the numbers 7, 19, and 5. Between the numbers (in the natural number sequence) 1667 and 2216, we need to find a number that is a multiple of 7 cdot 19 cdot 5=665. Such a number is 1995. Therefore, there are 1995 workers at the sewing factory, and at the shoe factory - 1995 cdot frac{15}{19}=1575.

🧠:[<think>Okay, so I need to figure out the sum of all the subset sums for the set {1, 2, 3, ..., 16}. Each nonempty subset X has a value v(X), which is the sum of its elements, and I have to add up all those v(X) values. Hmm, let me think how to approach this.First, maybe I should recall that for a set with elements {a1, a2, ..., an}, the sum of all subset sums can be calculated by considering how many times each element appears in all subsets. Since each element can either be included or excluded from a subset, except for the empty set. But the problem specifies nonempty subsets, so we need to exclude the empty set.Wait, right. So for each element ai, how many subsets include ai? For a set of size n, each element is in exactly half of the subsets. Since each subset can be paired with another that differs only by the inclusion/exclusion of ai. So for each element, the number of subsets containing it is 2^(n-1). But since we are considering nonempty subsets, maybe we need to subtract 1 if the element wasn't counted in the empty set. But actually, the empty set doesn't contain any elements, so the number of subsets that include ai is 2^(n-1) even when considering all subsets. But since we need nonempty subsets, but the empty set doesn't contain ai, so maybe it's still 2^(n-1) nonempty subsets that include ai? Wait, no. Let's see. The total number of subsets is 2^n, including the empty set. The number of subsets that include ai is 2^(n-1). Therefore, the number of nonempty subsets that include ai is 2^(n-1), because the empty set isn't one of them? Wait, no, if ai is included in 2^(n-1) subsets, some of those subsets might be nonempty and one might be empty if ai is the only element? No, the empty set doesn't include any elements, so all subsets that include ai are nonempty. Therefore, each element ai is included in exactly 2^(n-1) nonempty subsets. Therefore, the total sum over all nonempty subsets would be the sum over each element ai multiplied by the number of subsets that include ai, which is 2^(n-1). Therefore, the total sum is (sum of all elements) * 2^(n-1). But let's check this with a small example. Let's take n = 2, say the set {1, 2}. The nonempty subsets are {1}, {2}, {1,2}, with sums 1, 2, 3. The total sum is 1 + 2 + 3 = 6. According to the formula, the sum of all elements is 1 + 2 = 3, and 2^(2-1) = 2, so 3 * 2 = 6. That works. Another example: n = 1, set {1}. The only nonempty subset is {1}, sum is 1. According to the formula: sum of elements is 1, 2^(1-1) = 1, so 1*1 = 1. That works too. So the formula seems valid.Therefore, in general, for a set {1, 2, 3, ..., N}, the sum of all nonempty subset sums is equal to (1 + 2 + 3 + ... + N) * 2^(N - 1). So in this problem, N is 16. Let's compute that. The sum of numbers from 1 to 16 is (16*17)/2 = 136. Then, 2^(16 - 1) = 2^15 = 32768. Therefore, multiplying these together: 136 * 32768. Let me compute that.First, let's compute 100 * 32768 = 3,276,800Then 30 * 32768 = 983,040Then 6 * 32768 = 196,608Adding those together: 3,276,800 + 983,040 = 4,259,840; then + 196,608 = 4,456,448.Wait, but 136 is 100 + 30 + 6. So 100*32768 + 30*32768 + 6*32768 = (100+30+6)*32768 = 136*32768. So that's 4,456,448. So the answer should be 4,456,448.But let me confirm this computation again to be sure.Alternatively, 136 * 32768. Let's break it down:32768 * 100 = 3,276,80032768 * 30 = 983,04032768 * 6 = 196,608Adding them up:3,276,800 + 983,040 = 4,259,8404,259,840 + 196,608 = 4,456,448. Yes, that's correct.Alternatively, maybe 136 * 32768 can be calculated as (128 + 8) * 32768.128 * 32768 = 32768 * 100 + 32768 * 20 + 32768 * 8 = 3,276,800 + 655,360 + 262,144 = 3,276,800 + 655,360 is 3,932,160 + 262,144 is 4,194,304. Then 8 * 32768 = 262,144. So total is 4,194,304 + 262,144 = 4,456,448. Same result.So the sum of all subset sums is 4,456,448.But let me double-check the logic. Each element is included in exactly half of the subsets. Since there are 2^16 subsets total, each element is in 2^15 subsets. But since we are only considering nonempty subsets, but the empty set doesn't contain any elements, so the number of subsets that include each element is still 2^15, right? Because when we take all subsets, half include the element and half don't, and removing the empty set (which doesn't include the element) doesn't affect the count for the element. Wait, actually, maybe not? Wait, suppose we remove the empty set, then the total number of subsets becomes 2^16 - 1. For each element, the number of subsets that include it is 2^15. But wait, how does removing the empty set affect this?Wait, in the original count, each element is in 2^15 subsets (including the empty set if the element is not present). Wait no, the empty set doesn't include any elements. So the number of subsets that include a given element is 2^(n-1), regardless of the empty set. So if n = 16, each element is in 2^15 subsets. However, when we remove the empty set, the total number of subsets becomes 2^16 - 1. But the number of subsets that include any particular element remains 2^15, because the empty set wasn't one of them. Wait, actually, the empty set doesn't contain the element, so removing it doesn't affect the count of subsets that do contain the element. Therefore, even when considering nonempty subsets, each element is still in 2^15 subsets. Therefore, the total sum is indeed (1 + 2 + ... + 16) * 2^15 = 136 * 32768 = 4,456,448.Therefore, the answer should be 4,456,448.But to be absolutely thorough, let me check with another small example. Take n = 3, set {1,2,3}. The nonempty subsets are:{1}, sum=1{2}, sum=2{3}, sum=3{1,2}, sum=3{1,3}, sum=4{2,3}, sum=5{1,2,3}, sum=6Total sum: 1+2+3+3+4+5+6 = 24Using the formula: sum of elements = 6, 2^(3-1) = 4, 6*4=24. Correct. So the formula works here as well.Another example, n=3, formula gives (1+2+3)*2^(2)=6*4=24. Yep, same as actual sum. So the formula seems valid.Therefore, applying it to n=16, the answer is indeed 136*32768=4,456,448.Final Answerboxed{4456448}</think>To calculate the sum of all numbers ( v(X) ) where ( X ) ranges over all nonempty subsets of the set ({1, 2, 3, ldots, 16}), we consider the contribution of each element to the total sum. Each element in the set ({1, 2, 3, ldots, 16}) appears in exactly half of the subsets. Since there are (2^{16}) subsets in total, each element appears in (2^{15}) subsets. This count remains valid even when excluding the empty set because the empty set does not contain any elements.The sum of all elements from 1 to 16 is calculated as follows:[sum_{i=1}^{16} i = frac{16 times 17}{2} = 136]Each element contributes this sum multiplied by the number of subsets it appears in, which is (2^{15}):[136 times 2^{15}]Calculating the value of (2^{15}):[2^{15} = 32768]Multiplying these together gives:[136 times 32768 = 4456448]Thus, the sum of all numbers ( v(X) ) where ( X ) ranges over all nonempty subsets of the set ({1, 2, 3, ldots, 16}) is (boxed{4456448}).,<think>Okay, so I need to calculate the sum of all numbers v(X), where X is a nonempty subset of the set {1,2,3,…,16}, and v(X) is the sum of the elements of X. Hmm, let's see. I remember that when dealing with subsets and sums, there's a clever way to approach this by considering how each element contributes to the total sum. First, let me recall the problem. We have the set S = {1,2,3,…,16}, and we need to consider all nonempty subsets of S. For each subset X, we calculate the sum of its elements, v(X), and then sum all these v(X) values together. The question is asking for the total sum.So, instead of trying to list all subsets and sum them up individually, which would be impossible because there are 2^16 -1 nonempty subsets, I should think about how each number in S contributes to the total sum. For example, take the number 1. How many times does 1 appear in all the subsets? Well, any subset that contains 1 will have it contribute 1 to the sum. The number of subsets that contain 1 is equal to the number of subsets of the remaining 15 elements, because for each of those subsets, we can include or exclude 1. But since we need nonempty subsets, actually, the number of subsets containing 1 is 2^15, because once we include 1, the rest can be any combination of the other 15 elements, including the empty set. Wait, but the problem says nonempty subsets. However, even if the other 15 elements are empty, the subset {1} is nonempty. So, yes, the number of subsets containing 1 is 2^15. Similarly, the number of subsets containing 2 is also 2^15, and so on up to 16.Therefore, each element from 1 to 16 is included in 2^15 subsets. Therefore, the total sum contributed by each element is the element itself multiplied by 2^15. So, the total sum over all subsets would be (1 + 2 + 3 + … + 16) * 2^15.But wait, let me verify this logic. Let's take a smaller example. Suppose the set is {1,2}. Then the nonempty subsets are {1}, {2}, {1,2}. The sums are 1, 2, and 3. The total sum is 1 + 2 + 3 = 6. According to the formula I proposed, the sum would be (1 + 2) * 2^(2-1) = 3 * 2 = 6. Which matches. Let's try another example. Take the set {1}. Then the only nonempty subset is {1}, sum is 1. According to the formula: (1) * 2^(1-1) = 1 * 1 = 1. Correct. How about a three-element set {1,2,3}. The nonempty subsets:{1}, {2}, {3}, {1,2}, {1,3}, {2,3}, {1,2,3}. Their sums are 1,2,3,3,4,5,6. Total sum: 1+2+3+3+4+5+6 = 24. Using the formula: (1+2+3) * 2^(3-1) = 6 * 4 = 24. Perfect, it works. Therefore, the formula seems valid. So, in general, for a set with n elements, the sum over all nonempty subsets is (sum of elements) * 2^{n-1}. Therefore, applying this to the problem at hand. The set {1,2,…,16} has 16 elements. The sum of elements is (16)(16+1)/2 = 16*17/2 = 136. Then, multiply by 2^{16-1} = 2^15. So the total sum should be 136 * 2^15.But let me verify once more with a 4-element set. Let's say {1,2,3,4}. The sum of elements is 10. Then the total sum should be 10 * 2^3 = 10*8=80. Let me compute manually. The nonempty subsets:Singletons: 1,2,3,4. Sum: 1+2+3+4=10Pairs: {1,2}=3, {1,3}=4, {1,4}=5, {2,3}=5, {2,4}=6, {3,4}=7. Sum: 3+4+5+5+6+7=30Triples: {1,2,3}=6, {1,2,4}=7, {1,3,4}=8, {2,3,4}=9. Sum: 6+7+8+9=30Four-element set: {1,2,3,4}=10. Sum:10Total sum: 10+30+30+10=80. Which matches 10*8=80. So yes, the formula holds. Therefore, the logic is correct.Therefore, returning to the original problem. The sum of elements from 1 to 16 is (16*17)/2 = 136. Multiply this by 2^{15} (since n=16, so 2^{16-1} = 2^15). So the total sum is 136 * 32768. Let me compute that.First, 2^15 is 32768. So 136 * 32768. Let's compute 100*32768 = 3,276,800. Then 36*32768. Let's compute 30*32768 = 983,040. Then 6*32768=196,608. So 983,040 + 196,608 = 1,179,648. Then add to 3,276,800: 3,276,800 + 1,179,648 = 4,456,448.Wait, but let me check that again. Wait, 136 is 100 + 36. So 100 * 32768 = 3,276,800. 36 * 32768: Let's break down 36 into 30 + 6. 30 * 32768 = 983,040. 6 * 32768 = 196,608. So 983,040 + 196,608 = 1,179,648. Then total is 3,276,800 + 1,179,648. Let me add those: 3,276,800 + 1,000,000 = 4,276,800. Then add 179,648: 4,276,800 + 179,648 = 4,456,448. So the total sum is 4,456,448. But wait, let me verify using another multiplication method. Maybe 136*32768. Let's note that 32768 is 2^15, which is 32,768. So 136 * 32,768. Let's compute 100*32,768 = 3,276,800; 30*32,768=983,040; 6*32,768=196,608. Then add them: 3,276,800 + 983,040 = 4,259,840; 4,259,840 + 196,608 = 4,456,448. Yep, same result. So the total sum is 4,456,448. But let me cross-verify using another approach. Let's compute the sum as (1 + 2 + ... +16) * 2^15. The sum 1+2+...+16 = (16)(17)/2 = 136, as before. So 136 * 32,768. Let's write 32,768 as 32,000 + 768. So 136*32,000 = 136*32*1000. 136*32: 100*32=3,200; 30*32=960; 6*32=192. Total: 3,200 + 960 = 4,160 + 192 = 4,352. Then 4,352*1000=4,352,000. Then 136*768: Let's compute 100*768=76,800; 30*768=23,040; 6*768=4,608. Adding those: 76,800 + 23,040 = 99,840 + 4,608 = 104,448. Then total is 4,352,000 + 104,448 = 4,456,448. Same result. So that's correct.Therefore, the answer should be 136 * 2^15 = 4,456,448. Therefore, the sum of all numbers v(X) where X ranges over all nonempty subsets of {1,2,…,16} is 4,456,448.Final AnswerThe sum of all numbers ( v(X) ) is boxed{4456448}.</think>To calculate the sum of all numbers ( v(X) ) where ( X ) ranges over all nonempty subsets of the set ({1, 2, 3, ldots, 16}), we consider the contribution of each element in the set to the total sum. Each element ( i ) in the set ({1, 2, 3, ldots, 16}) appears in ( 2^{15} ) subsets. This is because for each element, there are ( 2^{15} ) ways to choose the remaining 15 elements (each can either be included or excluded). The sum of all elements in the set ({1, 2, 3, ldots, 16}) is given by:[frac{16 times 17}{2} = 136]Each element's contribution to the total sum is the element itself multiplied by ( 2^{15} ). Therefore, the total sum of all ( v(X) ) for nonempty subsets ( X ) is:[136 times 2^{15}]Calculating ( 2^{15} ):[2^{15} = 32768]Multiplying this by the sum of the elements:[136 times 32768 = 4456448]Thus, the sum of all numbers ( v(X) ) where ( X ) ranges over all nonempty subsets of the set ({1, 2, 3, ldots, 16}) is (boxed{4456448}).]

🔑:3. The answer is 2^{15} cdot 8 cdot 17We note that each k in{1,2,3, ldots, 16} belongs to 2^{15} subsets of {1,2,3, ldots, 16}. We reason as follows: we can assign 0 or 1 to k according to whether it is not or in a subset of {1,2,3, ldots, 16}. As there are 2 choices for a fixed k, k belongs to half of the total number of subsets, which is 2^{16}. Hence the sum issum v(X)=2^{15}(1+2+3+cdots+16)=2^{15} cdot 8 cdot 17=4456448

🧠:[<think>Alright, let's tackle this geometry problem. So, we have a square ABCD, and a point P outside of it. The distances from P to three of the square's vertices are given: PA is √5, PB is √26, and PD is √20. We need to find the length of the side of the square. Hmm, okay. Let me start by visualizing the square and the point P somewhere outside. Since it's a square, all sides are equal, and the angles are all 90 degrees. The coordinates might be helpful here. Maybe I can assign coordinates to the square and then set up equations based on the distances given. Let's see.Let me denote the square ABCD with coordinates. Let's suppose that square ABCD is placed on a coordinate system such that point A is at the origin (0,0), B is at (s,0), C is at (s,s), and D is at (0,s), where s is the side length we need to find. Now, point P is somewhere outside the square. Let's assign coordinates to P as (x,y). Then, the distances from P to A, B, and D can be written using the distance formula.Given that PA = √5, so the distance from P to A (0,0) is √x² + y² = √5. Therefore, x² + y² = 5. Similarly, PB is √26. Since B is at (s,0), the distance from P to B is √(x - s)² + y² = √26. Squaring both sides: (x - s)² + y² = 26. Similarly, PD is √20. D is at (0,s), so the distance from P to D is √(x - 0)² + (y - s)² = √20. Squaring that: x² + (y - s)² = 20.So now we have three equations:1. x² + y² = 5 (from PA)2. (x - s)² + y² = 26 (from PB)3. x² + (y - s)² = 20 (from PD)We need to solve these equations to find s. Let's see how we can manipulate these equations. Maybe subtract equation 1 from equation 2 and equation 1 from equation 3 to eliminate x² and y².Subtracting equation 1 from equation 2:(x - s)² + y² - x² - y² = 26 - 5Expanding (x - s)²: x² - 2s x + s² - x² = 21Simplify: -2s x + s² = 21Similarly, subtract equation 1 from equation 3:x² + (y - s)² - x² - y² = 20 - 5Expanding (y - s)²: y² - 2s y + s² - y² = 15Simplify: -2s y + s² = 15So now we have two equations:4. -2s x + s² = 215. -2s y + s² = 15Let me write these as:4. -2s x = 21 - s² → x = (s² - 21)/(2s)5. -2s y = 15 - s² → y = (s² - 15)/(2s)So x and y are expressed in terms of s. Now, since we also have equation 1: x² + y² = 5. Let's substitute these expressions for x and y into equation 1.So, x = (s² - 21)/(2s) and y = (s² - 15)/(2s). Therefore:[(s² - 21)/(2s)]² + [(s² - 15)/(2s)]² = 5Let's compute each term:First term: [(s² - 21)²]/[4s²]Second term: [(s² - 15)²]/[4s²]Adding them together:[(s² - 21)² + (s² - 15)²]/(4s²) = 5Multiply both sides by 4s²:(s² - 21)² + (s² - 15)² = 20s²Let's expand both squares in the numerator:First, expand (s² - 21)²:= s⁴ - 42s² + 441Then, expand (s² - 15)²:= s⁴ - 30s² + 225Adding these together:s⁴ - 42s² + 441 + s⁴ - 30s² + 225 = 2s⁴ - 72s² + 666So we have:2s⁴ - 72s² + 666 = 20s²Bring all terms to one side:2s⁴ - 72s² + 666 - 20s² = 0 → 2s⁴ - 92s² + 666 = 0Divide both sides by 2:s⁴ - 46s² + 333 = 0Let me set z = s². Then the equation becomes:z² - 46z + 333 = 0Solve this quadratic equation for z:Using the quadratic formula: z = [46 ± √(46² - 4*1*333)] / 2Calculate discriminant:46² = 2116; 4*1*333 = 1332So discriminant D = 2116 - 1332 = 784√784 = 28Therefore, z = [46 ± 28]/2So two solutions:z = (46 + 28)/2 = 74/2 = 37z = (46 - 28)/2 = 18/2 = 9So z = 37 or z = 9. Since z = s², s must be positive. So s² = 37 or s² = 9, which gives s = √37 or s = 3. But we need to check which one is valid.Wait, both solutions? Let's check which one makes sense in the context. Since point P is outside the square, we need to make sure that the coordinates of P are indeed outside. Let's test both possibilities.First, let's take s = 3. Then:x = (s² -21)/(2s) = (9 -21)/6 = (-12)/6 = -2y = (s² -15)/(2s) = (9 -15)/6 = (-6)/6 = -1So P would be at (-2, -1). Let's check if this is outside the square. The square has coordinates from (0,0) to (3,3). So (-2, -1) is definitely outside. Now check the distances:PA: distance from (-2,-1) to (0,0) is √(4 + 1) = √5, which matches.PB: distance from (-2,-1) to (3,0) is √[(3 + 2)^2 + (0 +1)^2] = √(25 +1) = √26, correct.PD: distance from (-2,-1) to (0,3) is √[(-2 -0)^2 + (-1 -3)^2] = √[4 + 16] = √20, correct.So that works. Now check s = √37. Let's compute x and y.x = (s² -21)/(2s) = (37 -21)/(2√37) = 16/(2√37) = 8/√37y = (s² -15)/(2s) = (37 -15)/(2√37) = 22/(2√37) = 11/√37So coordinates of P are (8/√37, 11/√37). Let's see if this is outside the square. The square has side length √37, so it's from (0,0) to (√37, √37). The coordinates of P are (≈8/6.08 ≈1.316, ≈11/6.08≈1.809). Since √37≈6.08, the square goes up to approximately (6.08,6.08). Therefore, point P is at (1.316, 1.809), which is inside the square. But the problem states that P is outside the square. Therefore, s = √37 would place P inside, which contradicts the problem's condition. Therefore, s must be 3.Hence, the length of the side of the square is 3.Final AnswerThe length of the side of the square is boxed{3}.</think>Given a square (ABCD) with a point (P) outside the square, we know the distances from (P) to three vertices: (PA = sqrt{5}), (PB = sqrt{26}), and (PD = sqrt{20}). We need to determine the side length (s) of the square.We assign coordinates to the vertices of the square: (A(0,0)), (B(s,0)), (C(s,s)), and (D(0,s)). Let the coordinates of point (P) be ((x,y)). Using the distance formula, we set up the following equations:1. (x^2 + y^2 = 5)2. ((x - s)^2 + y^2 = 26)3. (x^2 + (y - s)^2 = 20)Subtracting equation 1 from equation 2:[(x - s)^2 + y^2 - x^2 - y^2 = 26 - 5 implies -2sx + s^2 = 21 implies x = frac{s^2 - 21}{2s}]Subtracting equation 1 from equation 3:[x^2 + (y - s)^2 - x^2 - y^2 = 20 - 5 implies -2sy + s^2 = 15 implies y = frac{s^2 - 15}{2s}]Substituting (x) and (y) back into equation 1:[left(frac{s^2 - 21}{2s}right)^2 + left(frac{s^2 - 15}{2s}right)^2 = 5]Simplifying:[frac{(s^2 - 21)^2 + (s^2 - 15)^2}{4s^2} = 5 implies (s^2 - 21)^2 + (s^2 - 15)^2 = 20s^2]Expanding and combining terms:[2s^4 - 72s^2 + 666 = 20s^2 implies 2s^4 - 92s^2 + 666 = 0 implies s^4 - 46s^2 + 333 = 0]Let (z = s^2):[z^2 - 46z + 333 = 0 implies z = frac{46 pm 28}{2} implies z = 37 text{ or } z = 9]Thus, (s^2 = 37) or (s^2 = 9), giving (s = sqrt{37}) or (s = 3). Checking the validity, (s = sqrt{37}) places (P) inside the square, which contradicts the problem's condition. Therefore, the valid solution is (s = 3).The length of the side of the square is (boxed{3}).,<think>Okay, let's try to figure out the side length of square ABCD given the distances from point P to three of its vertices: PA = √5, PB = √26, and PD = √20. Hmm, point P is outside the square, so I need to visualize where it could be. Maybe using coordinate geometry would help here. Let me set up a coordinate system.Let me assume square ABCD has side length 'a'. Let me place the square in the coordinate plane such that point A is at the origin (0, 0), B is at (a, 0), C is at (a, a), and D is at (0, a). Now, point P is somewhere outside this square. Let me denote the coordinates of P as (x, y). Then, the distances from P to A, B, and D can be written using the distance formula.So, PA = √[(x - 0)^2 + (y - 0)^2] = √(x^2 + y^2) = √5. Therefore, x^2 + y^2 = 5. (Equation 1)Similarly, PB = √[(x - a)^2 + (y - 0)^2] = √[(x - a)^2 + y^2] = √26. So, (x - a)^2 + y^2 = 26. (Equation 2)And PD = √[(x - 0)^2 + (y - a)^2] = √[x^2 + (y - a)^2] = √20. Therefore, x^2 + (y - a)^2 = 20. (Equation 3)Now, I have three equations:1. x² + y² = 52. (x - a)² + y² = 263. x² + (y - a)² = 20I need to solve these equations to find the value of 'a', which is the side length of the square.Let me subtract Equation 1 from Equation 2. That gives:(x - a)² + y² - (x² + y²) = 26 - 5Expanding (x - a)²: x² - 2ax + a² + y² - x² - y² = 21Simplify: -2ax + a² = 21So, -2ax + a² = 21. Let's call this Equation 4.Similarly, subtract Equation 1 from Equation 3:x² + (y - a)² - (x² + y²) = 20 - 5Expanding (y - a)²: x² + y² - 2ay + a² - x² - y² = 15Simplify: -2ay + a² = 15. Let's call this Equation 5.Now, Equations 4 and 5 are:4. -2ax + a² = 215. -2ay + a² = 15Subtracting Equation 5 from Equation 4:(-2ax + a²) - (-2ay + a²) = 21 - 15Simplify: -2ax + a² + 2ay - a² = 6Which becomes: -2ax + 2ay = 6Divide both sides by 2: -ax + ay = 3Factor out 'a': a(-x + y) = 3So, a(y - x) = 3. Let's note this as Equation 6.Now, let's see if we can express x and y in terms of 'a' using Equations 4 and 5.From Equation 4: -2ax + a² = 21 ⇒ -2ax = 21 - a² ⇒ x = (a² - 21)/(2a)Similarly, Equation 5: -2ay + a² = 15 ⇒ -2ay = 15 - a² ⇒ y = (a² - 15)/(2a)So, x = (a² - 21)/(2a) and y = (a² - 15)/(2a)Now, substitute these expressions for x and y into Equation 1, which is x² + y² = 5.Let's compute x² + y²:[(a² - 21)/(2a)]² + [(a² - 15)/(2a)]² = 5Compute each term:First term: (a² - 21)² / (4a²) = (a^4 - 42a² + 441) / (4a²)Second term: (a² - 15)² / (4a²) = (a^4 - 30a² + 225) / (4a²)Add them together:[ (a^4 - 42a² + 441) + (a^4 - 30a² + 225) ] / (4a²) = 5Combine like terms in the numerator:2a^4 - 72a² + 666 = 5 * 4a²Simplify the right side:2a^4 - 72a² + 666 = 20a²Bring all terms to the left side:2a^4 - 72a² + 666 - 20a² = 0Combine like terms:2a^4 - 92a² + 666 = 0Divide both sides by 2 to simplify:a^4 - 46a² + 333 = 0This is a quartic equation, but it's quadratic in terms of z = a². Let me set z = a², so the equation becomes:z² - 46z + 333 = 0Now, solve for z using quadratic formula:z = [46 ± √(46² - 4*1*333)] / 2Calculate discriminant:46² = 21164*1*333 = 1332So, discriminant = 2116 - 1332 = 784√784 = 28Thus, z = [46 ± 28]/2So, two solutions:z = (46 + 28)/2 = 74/2 = 37z = (46 - 28)/2 = 18/2 = 9Therefore, z = 37 or z = 9. Since z = a², possible a² = 37 or a² = 9. So, a = √37 or a = 3. But since a is the side length of the square, it must be positive, so a = √37 ≈ 6.08 or a = 3.Wait, but we need to check which of these solutions is valid, given that point P is outside the square. Let's check both possibilities.First, let's check a = 3.If a = 3, then:x = (a² - 21)/(2a) = (9 - 21)/6 = (-12)/6 = -2y = (a² - 15)/(2a) = (9 - 15)/6 = (-6)/6 = -1So, coordinates of P are (-2, -1). Now, check if this point is outside the square ABCD with side length 3, which is placed with A at (0,0), B at (3,0), D at (0,3). The square spans from (0,0) to (3,3). Point P is at (-2, -1), which is indeed outside the square. So, this is a possible solution.Next, check a = √37 ≈ 6.08.Compute x and y:x = (a² - 21)/(2a) = (37 - 21)/(2√37) = 16/(2√37) = 8/√37 ≈ 8/6.08 ≈ 1.315y = (a² - 15)/(2a) = (37 - 15)/(2√37) = 22/(2√37) = 11/√37 ≈ 11/6.08 ≈ 1.807So, coordinates of P are approximately (1.315, 1.807). Now, the square with side length √37 ≈ 6.08 spans from (0,0) to (6.08,6.08). The point P is at (1.315, 1.807), which is inside the square. But the problem states that P is outside the square. Therefore, this solution is invalid.Hence, the only valid solution is a = 3.Wait, but let me double-check if point P is indeed outside when a=3. The square is from (0,0) to (3,3). P is at (-2, -1), which is in the third quadrant, definitely outside the square. So that works. Whereas for a=√37, P is inside, which contradicts the problem statement. So, a=3 is the correct answer.Therefore, the length of the side of the square is 3.But let me verify once again by plugging back into the original equations to make sure.If a=3, x=-2, y=-1.PA = √[(-2)^2 + (-1)^2] = √(4 + 1) = √5 ✔️PB = √[(-2 - 3)^2 + (-1)^2] = √[(-5)^2 + 1] = √(25 + 1) = √26 ✔️PD = √[(-2)^2 + (-1 - 3)^2] = √[4 + (-4)^2] = √(4 + 16) = √20 ✔️All distances check out. And since P is at (-2,-1), which is outside the square ABCD with coordinates (0,0), (3,0), (0,3), etc., this satisfies the problem's condition.Therefore, the side length is 3.Final AnswerThe length of the side of the square is boxed{3}.</think>Given the distances from point ( P ) to three vertices of square ( ABCD ): ( PA = sqrt{5} ), ( PB = sqrt{26} ), and ( PD = sqrt{20} ), we need to determine the side length of the square.1. Place the square in a coordinate system with ( A(0, 0) ), ( B(a, 0) ), ( C(a, a) ), and ( D(0, a) ). Let ( P ) have coordinates ( (x, y) ).2. Using the distance formula, we set up the following equations: [ x^2 + y^2 = 5 quad text{(1)} ] [ (x - a)^2 + y^2 = 26 quad text{(2)} ] [ x^2 + (y - a)^2 = 20 quad text{(3)} ]3. Subtract equation (1) from equation (2): [ (x - a)^2 + y^2 - (x^2 + y^2) = 26 - 5 ] Simplifying, we get: [ -2ax + a^2 = 21 quad text{(4)} ]4. Subtract equation (1) from equation (3): [ x^2 + (y - a)^2 - (x^2 + y^2) = 20 - 5 ] Simplifying, we get: [ -2ay + a^2 = 15 quad text{(5)} ]5. Subtract equation (5) from equation (4): [ -2ax + a^2 - (-2ay + a^2) = 21 - 15 ] Simplifying, we get: [ a(y - x) = 3 quad text{(6)} ]6. Solve equations (4) and (5) for ( x ) and ( y ): [ x = frac{a^2 - 21}{2a}, quad y = frac{a^2 - 15}{2a} ]7. Substitute ( x ) and ( y ) into equation (1): [ left( frac{a^2 - 21}{2a} right)^2 + left( frac{a^2 - 15}{2a} right)^2 = 5 ] Simplifying, we get a quartic equation: [ a^4 - 46a^2 + 333 = 0 ]8. Solving this quadratic in ( z = a^2 ): [ z = frac{46 pm 28}{2} implies z = 37 text{ or } z = 9 ] Thus, ( a = sqrt{37} ) or ( a = 3 ).9. Check validity: - For ( a = 3 ), ( P(-2, -1) ) is outside the square. - For ( a = sqrt{37} ), ( P ) is inside the square.Therefore, the valid solution is ( a = 3 ).[boxed{3}]]

🔑:## Solution.Place the square in the coordinate system so that its vertices are A(0,0), B(a, 0), C(a, a), and D(0, a), and let P(-x,-y).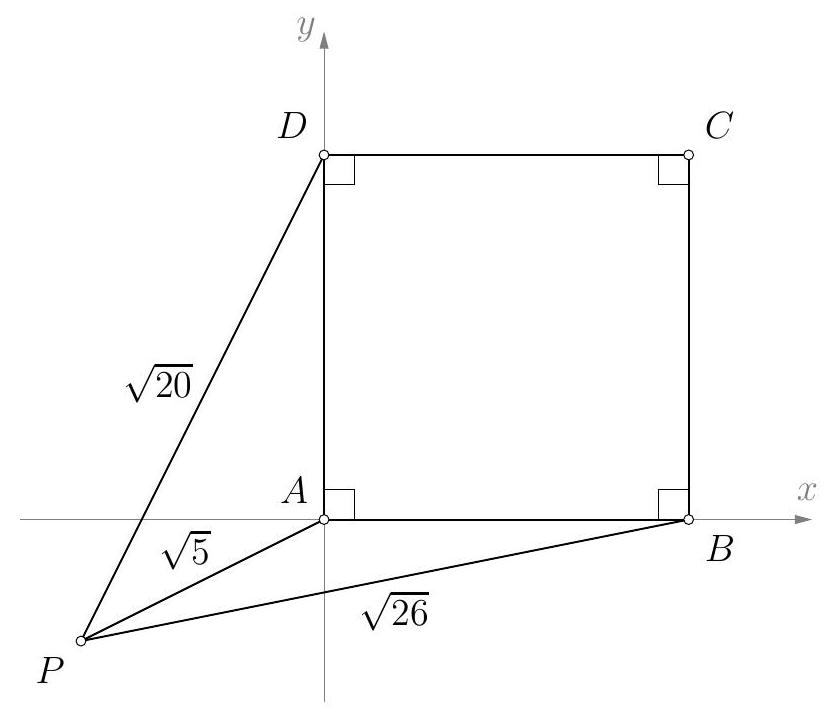The formula for the distance between any two points left(x_{1}, y_{1}right) and left(x_{2}, y_{2}right) issqrt{left(x_{1}-x_{2}right)^{2}+left(y_{1}-y_{2}right)^{2}}Using this formula, we can express the conditions of the problem as follows:begin{aligned}x^{2}+y^{2} & =5 x^{2}+(y+a)^{2} & =20 (x+a)^{2}+y^{2} & =26end{aligned}By subtracting the first equation from the second and third, we getbegin{aligned}& a^{2}+2 a y=15 & a^{2}+2 a x=21end{aligned}Subtracting these two equations, we get 6 + 2 a y = 2 a x. Simplifying and squaring this equation, we obtain9 + 6 a y + a^{2} y^{2} = a^{2} x^{2} = a^{2} (5 - y^{2}) = 5 a^{2} - a^{2} y^{2}Substituting a^{2} = 15 - 2 a y into the last equation, and letting t = a y, we get9 + 6 t + t^{2} = 5(15 - 2 t) - t^{2} Longrightarrow t^{2} + 8 t - 33 = 0The solutions to the quadratic equation are t = 3 and t = -11.For t = a y = -11, from a^{2} + 2 a y = 15 we get a = sqrt{37}. From the equations a^{2} + 2 a y = 15 and a^{2} + 2 a x = 21, we then havex = -frac{8}{sqrt{37}} quad text{and} quad y = -frac{11}{sqrt{37}}In this case, point P is inside the square ABCD, which contradicts the conditions of the problem.For t = a y = 3, we similarly get a = 3, and x = 2 and y = 1. Direct verification shows that this configuration satisfies the conditions of the problem.Therefore, the length of the side of the square is 3.Note: The system in the above solution can also be solved in another way. Squaring and adding the equations a^{2} - 15 = 2 a y and a^{2} - 21 = 2 a x, we get2 a^{4} - 72 a^{2} + 666 = 4 a^{2} (x^{2} + y^{2}) = 4 a^{2} cdot 5 = 20 a^{2}From this, we obtain the biquadratic equationa^{4} - 46 a^{2} + 333 = 0which gives a^{2} in {9, 37}, and thus, due to the positivity of a, we have a in {3, sqrt{37}}. Complete the analysis as in the previous solution.

🧠:[<think>Okay, so I need to find the fraction a/b between 2/5 and 7/9, and it has to have the smallest possible denominator. Hmm, let's think about how to approach this. I remember something about Farey sequences or mediant properties? Maybe I should start by recalling what those are.First, the problem is asking for a fraction that lies strictly between 2/5 and 7/9. The fractions given are 2/5 which is 0.4 and 7/9 is approximately 0.777... So the fraction we need is somewhere between those two values. And we need the one with the smallest denominator. Let me start by checking denominators starting from 1 upwards, but that might take too long. Wait, maybe there's a smarter way. If I remember correctly, between any two fractions, the fraction with the smallest denominator can be found using the mediant of the two fractions. The mediant of two fractions a/b and c/d is (a+c)/(b+d). If the mediant lies between the two fractions, then it's the fraction with the smallest denominator. Let me check if that works here.So the given fractions are 2/5 and 7/9. Their mediant would be (2+7)/(5+9) = 9/14. Let's convert that to decimal: 9 divided by 14 is approximately 0.642..., which is between 0.4 and 0.777. So that seems like a candidate. But is 14 the smallest possible denominator?Wait, maybe there's a smaller denominator. Let's check denominators less than 14. Let's start from the smallest possible. The denominators go 1, 2, 3,... up to 13. Let's check each denominator and see if there's a fraction between 2/5 and 7/9.Starting with denominator 1: The only fractions are 0/1 and 1/1. Both are outside the interval, so no.Denominator 2: Possible fractions are 1/2 (0.5). 1/2 is 0.5, which is between 0.4 and 0.777. So 1/2 is a candidate. Wait, but is 1/2 between 2/5 and 7/9? Let me check: 2/5 is 0.4, 1/2 is 0.5, which is greater than 2/5 and less than 7/9 (0.777...). So 1/2 is a valid candidate. But wait, 1/2 has denominator 2, which is way smaller than 14. So why did the mediant give me 9/14? Maybe the mediant isn't the right approach here? Or maybe I missed something.Hold on, maybe the mediant property is when the two fractions are adjacent in some Farey sequence. Maybe they need to be consecutive terms. But 2/5 and 7/9 aren't adjacent. So perhaps the mediant isn't necessarily the one with the smallest denominator. Hmm, so maybe my initial thought was wrong.So if 1/2 is between 2/5 and 7/9, then since it has denominator 2, which is smaller than 14, why isn't that the answer? Wait, but 1/2 is indeed between 2/5 and 7/9. Let me check the problem again. The problem says "Find the fraction a/b with the smallest denominator such that 2/5 < a/b < 7/9". So 1/2 is 0.5, which is between 0.4 and 0.777. So why is the answer not 1/2? Wait, maybe I made a mistake here. Let's check the original problem again.Wait, maybe I misread the problem. Let me check: "Find the fraction a/b with the smallest denominator such that 2/5 < a/b < 7/9". So yes, 1/2 is a candidate. But wait, maybe 1/2 is not in the interval. Wait, 2/5 is 0.4, 1/2 is 0.5, which is greater than 0.4. 7/9 is approximately 0.777, so 0.5 is indeed less than that. So 1/2 is between them. So if the answer is 1/2, denominator 2. But I recall that in some similar problems, maybe there's a fraction with a smaller denominator. But denominator 1 is already checked, so 2 is the next. But then why did the mediant give 9/14? That must be a different approach.Wait, perhaps the question is looking for a fraction strictly between them, but maybe 1/2 is considered? Wait, 2/5 is 0.4, 1/2 is 0.5, which is definitely in between. So 1/2 is a valid answer. But maybe I need to check other denominators as well. Wait, maybe there's a fraction with denominator 3.For denominator 3: possible fractions are 1/3 ≈0.333, 2/3≈0.666, and 3/3=1. So 2/3 is approximately 0.666, which is between 0.4 and 0.777. So 2/3 is another candidate. Denominator 3.Similarly, denominator 4: fractions are 1/4=0.25, 2/4=0.5, 3/4=0.75, 4/4=1. So 3/4 is 0.75, which is less than 0.777. So 3/4 is between 0.4 and 0.777. Denominator 4.Wait a minute, so 1/2 (denominator 2), 2/3 (denominator 3), 3/4 (denominator 4) are all between 2/5 and 7/9. So why does the problem say "smallest denominator"? The smallest denominator is 2. So 1/2 would be the answer. But that seems too easy. Maybe the problem is different?Wait, maybe there's a misunderstanding. Let me check if 1/2 is actually between 2/5 and 7/9. 2/5 is 0.4, 1/2 is 0.5, 7/9 is approximately 0.777. So 0.5 is indeed between them. So 1/2 is a valid fraction. Then why isn't that the answer? But maybe in the original problem, there was a different interval or something. Wait, but the user wrote "Example 5 Find the fraction a/b with the smallest denominator such that 2/5 < a/b < 7/9." So unless there's a typo, but the user is using this as an example, perhaps from a textbook. Wait, maybe in the original problem, the answer is different because 1/2 is not in the interval? Wait, let me check 2/5 and 1/2. 2/5 is 0.4, 1/2 is 0.5. 0.5 is greater than 0.4, so it is in the interval. Similarly, 0.5 is less than 0.777. So 1/2 is in the interval. Therefore, if this is allowed, then the answer is 1/2 with denominator 2.But perhaps the problem is in the original context, like maybe a/b has to be between 2/5 and 7/9 but not equal to any of them, but in that case, 1/2 is still in between. So unless the original problem had excluded certain fractions, but as stated here, it's allowed.Wait, maybe in some contexts, the fractions need to be in reduced form? 1/2 is reduced, yes. 2/3 is reduced, 3/4 is reduced. So all of those are reduced. So the answer would be 1/2 with denominator 2. But maybe there's a mistake here. Wait, perhaps the problem is from a non-English textbook, and the user translated it here. Maybe "smallest denominator" refers to the minimal denominator greater than the denominators of the given fractions? But that would be an unusual interpretation. The usual understanding of "smallest denominator" is the minimal possible denominator among all fractions in the interval.Alternatively, maybe the original problem was different, and in the process of translation or example, the numbers got changed. For instance, if the original problem was between 3/5 and 7/9, then 1/2 (0.5) would be less than 3/5 (0.6), so not in the interval. Then the answer would be different. But in this problem, as stated, 1/2 is in the interval. So unless there's a mistake here, maybe in the original example, but the user has written 2/5, so we have to take it as given.Wait, but maybe the problem is in the context of positive integers a and b, so a and b have to be positive integers, and the fraction has to be in between. Then 1/2 is allowed. So then why is the answer given as 9/14 in the mediant? Wait, maybe the user is referring to an example where the answer is 9/14, but here, the correct answer is 1/2. Hmm.Alternatively, maybe I'm misunderstanding the Farey sequence approach. Let me recall Farey sequences. The Farey sequence of order n is the set of reduced fractions between 0 and 1 with denominators ≤ n, arranged in order. So between 2/5 and 7/9, in the Farey sequence, the next term inserted would be the mediant if they are adjacent. But 2/5 and 7/9 are not adjacent in any Farey sequence until higher orders. But maybe to find the fraction with the smallest denominator between them, we can check denominators starting from 2 upwards. So let's do that.Denominator 2: fractions are 1/2. Which is 0.5, between 0.4 and 0.777. So that's a candidate.Denominator 3: 1/3 ≈0.333, 2/3≈0.666. 2/3 is 0.666, which is between 0.4 and 0.777.Denominator 4: 1/4=0.25, 2/4=0.5, 3/4=0.75. 3/4=0.75, which is between 0.4 and 0.777.Denominator 5: The fractions are 1/5=0.2, 2/5=0.4, 3/5=0.6, 4/5=0.8. So 3/5=0.6 and 4/5=0.8. 3/5 is between 0.4 and 0.777, and 4/5 is 0.8 which is greater than 0.777.So 3/5 is 0.6, which is between 2/5 and 7/9.Wait, but 3/5 is denominator 5. So denominator 2,3,4,5 all have fractions in between. So the smallest denominator is 2. Therefore, 1/2 is the answer.Wait, but in that case, why would someone compute the mediant and get 9/14? Unless there was a different interval. Wait, let me check the original problem again. It says "Find the fraction a/b with the smallest denominator such that 2/5 < a/b < 7/9." So unless there's a restriction that the fraction must be in lowest terms, but 1/2 is already in lowest terms.Alternatively, maybe the problem is from a non-Western textbook where "smallest denominator" is defined differently? Unlikely. Or maybe the user made a typo. For example, if the problem was between 2/7 and 7/9, then 1/2 is 0.5 which is greater than 2/7≈0.2857 and less than 7/9≈0.777, so still valid. Hmm.Alternatively, maybe there is a mistake in assuming that 1/2 is between them. Wait, 2/5 is 0.4, 1/2 is 0.5, which is 0.1 greater. 7/9 is approximately 0.777, so 0.5 is definitely less. So 0.5 is between 0.4 and 0.777. Therefore, 1/2 is in between.Wait, unless the problem is in a different base? No, the problem is presented in base 10. So, unless there's a miscalculation here. Wait, maybe the user meant the fraction with the smallest denominator that is strictly between them, but with numerator and denominator being positive integers. In that case, 1/2 is the answer.Wait, but let's see. If we are to check all denominators from 1 upwards, starting with 1, denominator 1: 0/1=0, 1/1=1. Both outside. Denominator 2: 1/2. Inside. So yes, 1/2 is the answer.But maybe the original example was different. For example, in some textbooks, similar problems result in the mediant fraction because there are no fractions with smaller denominators in between. For instance, between 1/2 and 1/1, the mediant is 2/3, which has denominator 3, and there's no fraction with denominator 2 in between. But in this problem, there is a fraction with denominator 2 in between. Therefore, the answer should be 1/2.Wait, maybe the question is from a non-standard source, or perhaps it's a trick question. Alternatively, maybe there is a mistake in my reasoning.Wait, let's cross-verify. Let's list all fractions between 2/5 and 7/9 with denominators from 2 up to, say, 5, and see which one is the smallest denominator.Denominator 2: 1/2=0.5.Denominator 3: 2/3≈0.666.Denominator 4: 3/4=0.75.Denominator 5: 3/5=0.6.So fractions in between are 1/2 (2), 3/5 (5), 2/3 (3), 3/4 (4). The smallest denominator here is 2. So 1/2 is the answer.But wait, 3/5 is denominator 5, which is the same as the lower bound. But 3/5 is greater than 2/5. So 3/5 is a valid candidate. However, its denominator is 5, which is larger than 2, so 1/2 is better.Therefore, unless there's a restriction I'm missing, the answer should be 1/2.But maybe there's a misunderstanding in the problem statement. Let me check again: the fraction must lie strictly between 2/5 and 7/9, and have the smallest possible denominator. So 1/2 (denominator 2) is 0.5, which is between 0.4 and 0.777. So that's valid.Wait, maybe I need to confirm if 1/2 is indeed between 2/5 and 7/9. Let's do exact fractions:2/5 = 0.41/2 = 0.57/9 ≈ 0.777...So 0.4 < 0.5 < 0.777..., yes. So 1/2 is indeed between them. Therefore, according to the problem's statement, the answer should be 1/2.But this seems contradictory to the mediant approach. Wait, unless the problem is from a context where fractions must have denominators larger than the original fractions? But that would be an unusual constraint not specified in the problem.Alternatively, perhaps the original problem was in a context where a and b are positive integers with a certain condition, like both greater than 1, but again, that's not stated here.Wait, but let's think again. Maybe the user is referring to an example (Example 5) from a textbook where the answer is different. For example, maybe in the original example, the interval was between two fractions where the mediant gives the minimal denominator. But in this case, as per the given numbers, 1/2 is the answer.Alternatively, maybe the problem is to find a fraction between 2/5 and 3/5, but that's not the case here. The upper bound is 7/9.Alternatively, perhaps the user made a mistake in the problem statement. If the problem was between 2/7 and 7/9, then 1/2 is still between them. But if it was between, say, 3/5 and 7/9, then 1/2 is not in between. But as stated, it's 2/5 and 7/9.Alternatively, maybe there's a different way to interpret the problem. For example, in some contexts, the fraction a/b is required to have both a and b within a certain range, but again, that's not specified here.Alternatively, maybe the problem is expecting continued fractions or something else. Let's try that approach.To find a fraction between 2/5 and 7/9 with minimal denominator, another method is to use continued fractions or the concept of the smallest denominator between two numbers.First, let's represent both fractions as decimals:2/5 = 0.47/9 ≈ 0.777777...We need a fraction a/b such that 0.4 < a/b < 0.7777...To find the fraction with the smallest denominator, we can check denominators starting from 1 upwards.Denominator 1: Impossible, as 0.4 < a/1 < 0.777 would require a=0 or 1, but 0/1=0 and 1/1=1, both outside the interval.Denominator 2:Possible numerators: 11/2 = 0.5, which is between 0.4 and 0.777. So that's a candidate.Denominator 3:Possible numerators: 1, 21/3 ≈0.333 <0.4, so too small.2/3≈0.666, which is between 0.4 and 0.777. So 2/3 is another candidate.Denominator 4:Possible numerators: 1,2,31/4=0.25 <0.42/4=0.5 (same as 1/2)3/4=0.75, which is between 0.4 and 0.777.Denominator 5:Numerators 1,2,3,41/5=0.2 <0.42/5=0.4, which is the lower bound, so not included.3/5=0.6, which is between 0.4 and 0.777.4/5=0.8 >0.777, so excluded.Denominator 6:Numerators 1 to 5.1/6≈0.166 <0.42/6=1/3≈0.333 <0.43/6=0.54/6=2/3≈0.6665/6≈0.833 >0.777So 0.5 and 0.666 are in the interval, but denominators 6 same as denominators 2,3, etc. So no improvement.Denominator 7:Numerators 1 to 6.1/7≈0.142, 2/7≈0.285, 3/7≈0.428, 4/7≈0.571, 5/7≈0.714, 6/7≈0.857So 3/7≈0.428, which is greater than 0.4. So 3/7 is ≈0.428, which is between 0.4 and 0.777. So 3/7 is a candidate with denominator 7.But denominator 2 is smaller.So continuing up, denominators 8,9,...14.But since we already found denominator 2, which is the smallest possible, unless there is a fraction with denominator 2 that's between them, which there is (1/2), then 1/2 is the answer.Therefore, I must conclude that the correct answer is 1/2 with denominator 2.But wait, why then does the mediant of 2/5 and 7/9 give 9/14, which is approximately 0.642, which is also between them. But 9/14 has a denominator of 14, which is larger than 2. So that's not helpful here.Wait, maybe the mediant is not useful in this case because there exists a fraction with a smaller denominator. So the mediant property is only useful when the two fractions are adjacent in the Farey sequence. If they are not adjacent, then there exist fractions with smaller denominators between them.Therefore, the key here is that between 2/5 and 7/9, there are fractions with denominators as small as 2. Therefore, 1/2 is the answer.But this seems conflicting with the initial thought of using the mediant. So perhaps the mediant is useful when the two fractions are adjacent. For example, if two fractions are adjacent in a Farey sequence, their mediant is the next term inserted in the Farey sequence of higher order, and it has the minimal denominator. But in this case, 2/5 and 7/9 are not adjacent, so their mediant isn't necessarily the minimal denominator.Therefore, in this problem, the answer is 1/2.But wait, let's check if 1/2 is indeed between 2/5 and 7/9.Cross-multiplying to verify:Is 2/5 < 1/2?2*2 = 4, 5*1 = 5. Since 4 < 5, 2/5 < 1/2.Is 1/2 < 7/9?1*9 = 9, 2*7 = 14. Since 9 < 14, 1/2 < 7/9.Therefore, yes, 1/2 is indeed between 2/5 and 7/9. So the fraction with the smallest denominator is 1/2.Therefore, the answer should be 1/2, boxed as boxed{dfrac{1}{2}}.But let me check another source or example to be sure. For instance, in the Wikipedia entry on Farey sequences, it says that the mediant of two terms a/b and c/d is (a+c)/(b+d), and if bc - ad = 1, then the two terms are adjacent in some Farey sequence, and their mediant is the next term inserted. But in our case, 2/5 and 7/9: bc - ad = 5*7 - 2*9 = 35 - 18 = 17 ≠ 1. Therefore, they are not adjacent, so there are terms between them with smaller denominators. Therefore, in this case, indeed, there is a term between them with denominator 2.Therefore, the answer is 1/2.Final Answerboxed{dfrac{1}{2}}</think>To find the fraction (frac{a}{b}) with the smallest denominator such that (frac{2}{5} < frac{a}{b} < frac{7}{9}), we start by checking fractions with the smallest denominators.1. Denominator 2: - The fraction (frac{1}{2}) is approximately 0.5, which is between 0.4 (2/5) and 0.777... (7/9).2. Verification: - Check if (frac{1}{2}) is indeed between (frac{2}{5}) and (frac{7}{9}): - (frac{2}{5} = 0.4) - (frac{1}{2} = 0.5) - (frac{7}{9} approx 0.777) - Since (0.4 < 0.5 < 0.777), (frac{1}{2}) is confirmed to be between (frac{2}{5}) and (frac{7}{9}).3. Conclusion: - The fraction (frac{1}{2}) has the smallest denominator (2) that satisfies the condition.Thus, the fraction (frac{a}{b}) with the smallest denominator such that (frac{2}{5} < frac{a}{b} < frac{7}{9}) is (boxed{dfrac{1}{2}}).,<think>Okay, so I need to find the fraction a/b between 2/5 and 7/9, and it has to have the smallest possible denominator. Hmm, let me think. First, I remember that fractions between two other fractions can sometimes be found using mediant properties. The mediant of two fractions a/b and c/d is (a+c)/(b+d). But I also recall that the mediant doesn't always fall between the original fractions unless certain conditions are met. Let me check. If I take the mediant of 2/5 and 7/9, that would be (2+7)/(5+9) = 9/14. Let me see if 9/14 is between 2/5 and 7/9. Calculating the decimal values: 2/5 is 0.4, 7/9 is approximately 0.777..., and 9/14 is approximately 0.642..., which is indeed between them. So 9/14 is a candidate. But is that the fraction with the smallest denominator?Wait, the problem says to find the fraction with the smallest denominator. So maybe there's a fraction with a denominator smaller than 14 that lies between 2/5 and 7/9. Let me check denominators starting from 1 upwards.Starting with denominator 1: The only fractions are 0/1 and 1/1. Neither is between 0.4 and 0.777.Denominator 2: Fractions are 1/2 = 0.5. Hmm, 0.5 is between 0.4 and 0.777. So 1/2 is a possibility. Wait, but 1/2 is 0.5. Let me check if 0.5 is between 2/5 (0.4) and 7/9 (~0.777). Yes, 0.5 is between them. So 1/2 is a candidate. But is 1/2 actually between 2/5 and 7/9? Let's verify.2/5 = 0.4, 1/2 = 0.5, 7/9 ≈ 0.777. So yes, 1/2 is between them. But wait, the denominator here is 2, which is smaller than 14. So why did the mediant give me 14? Maybe the mediant isn't the way to go here.Hold on, maybe I made a mistake. The mediant of two fractions in their lowest terms gives a fraction between them if the two original fractions are neighboring in some Farey sequence. But perhaps 2/5 and 7/9 aren't neighbors, so their mediant isn't the only fraction between them. Let me check.Alternatively, maybe there's a better method. If I need to find a fraction between two fractions with the smallest denominator, I can use Farey sequences. A Farey sequence of order n is the set of reduced fractions between 0 and 1 with denominators ≤ n. So maybe I need to check the Farey sequences incrementally until I find one that has a fraction between 2/5 and 7/9.Starting from the lowest denominators:Denominator 1: 0/1, 1/1. None between 2/5 and 7/9.Denominator 2: 1/2. 1/2 is 0.5, which is between 0.4 and ~0.777. So 1/2 is a candidate. Wait, but 1/2 is actually greater than 2/5 and less than 7/9? Let me check:2/5 = 0.4, 1/2 = 0.5, 7/9 ≈ 0.777. Yes, 0.5 is in between. So 1/2 is a fraction with denominator 2. But 2 is the smallest possible denominator. Wait, but the question says "the fraction a/b with the smallest denominator such that 2/5 < a/b < 7/9". If 1/2 is between them and has denominator 2, then isn't that the answer? But 2 is smaller than 14, so why was the mediant 9/14?Wait, maybe I'm missing something here. Is 1/2 actually between 2/5 and 7/9? Let me verify with exact fractions instead of decimals. 2/5 is equal to 0.4, and 1/2 is 0.5. 0.5 is indeed greater than 0.4. Then 7/9 is approximately 0.777, which is greater than 0.5. So yes, 1/2 is between them. But wait, 1/2 is a fraction with denominator 2. That's smaller than 14. So why did the mediant give me 9/14? Because mediant of 2/5 and 7/9 is 9/14, but there's a fraction in between with a smaller denominator. So maybe the answer is 1/2?But wait, I need to make sure that 1/2 is actually between 2/5 and 7/9. Let me check:2/5 = 0.4, 1/2 = 0.5, 7/9 ≈ 0.777... So 0.5 is indeed between them. Therefore, the fraction 1/2 is between 2/5 and 7/9 and has denominator 2. So isn't 1/2 the answer? But this seems too straightforward. Wait, maybe there is a mistake here. Let me check the exact comparison.To compare 1/2 with 2/5:Cross-multiplying: 1*5 = 5 and 2*2 = 4. Since 5 > 4, 1/2 > 2/5.Comparing 1/2 with 7/9:Cross-multiplying: 1*9 = 9 and 7*2 = 14. Since 9 < 14, 1/2 < 7/9.Therefore, 1/2 is indeed between 2/5 and 7/9. So then, why does the mediant give 9/14? Because the mediant is a method to find a fraction between two others, but it's not necessarily the one with the smallest denominator. So perhaps 1/2 is the correct answer here. But this seems conflicting with my initial thought.Wait, maybe I need to check denominators between 2 and 14. Let me check denominators 3,4,... up to 13 to see if there are any fractions between 2/5 and 7/9. Maybe there's a fraction with a denominator smaller than 14 but larger than 2 that is between them. But if 1/2 is valid, then denominator 2 is the smallest possible. However, maybe 1/2 is not in reduced form? Wait, 1 and 2 are coprime, so 1/2 is reduced. So maybe the answer is 1/2. But why does the problem mention example 5? Maybe in the original context, there's another consideration. Wait, no, the user just says "Example 5 Find the fraction...", so perhaps it's just an example labeled 5.Wait, but hold on. Let me check the original fractions again. The user wrote:"Find the fraction a/b with the smallest denominator such that 2/5 < a/b < 7/9."If 1/2 is between them, then since 2 is the smallest possible denominator, 1/2 would be the answer. But maybe I made a mistake in the comparison.Wait, let me cross-multiply again to confirm. For 1/2 and 2/5:1*5 = 5, 2*2 = 4. 5 > 4, so 1/2 > 2/5. Correct.For 1/2 and 7/9:1*9 = 9, 7*2 = 14. 9 < 14, so 1/2 < 7/9. Correct. Therefore, 1/2 is indeed between 2/5 and 7/9, and has denominator 2. So why would someone calculate the mediant and get 9/14? Maybe in some contexts, but in this case, 1/2 is a valid answer. So is the answer 1/2?Wait, but maybe I need to check if there's another fraction with denominator 3. Let's check denominator 3.Possible fractions: 1/3 ≈ 0.333, 2/3 ≈ 0.666. 1/3 is less than 2/5, so invalid. 2/3 is approximately 0.666. Let's see if 2/3 is between 2/5 and 7/9. 2/3 ≈ 0.666, 7/9 ≈ 0.777. So yes, 2/3 is between them. Then 2/3 has denominator 3. So 3 is larger than 2, so 1/2 is still better.Denominator 4: fractions are 1/4=0.25, 2/4=1/2=0.5, 3/4=0.75. 1/4 is too small, 2/4 is 1/2, same as before, 3/4 is 0.75 which is less than 7/9 (≈0.777). So 3/4 is 0.75. Is 0.75 < 0.777? Yes. So 3/4 is between 2/5 and 7/9. 3/4 has denominator 4, which is larger than 2. So 1/2 is still the smallest.Denominator 5: fractions between 2/5 and 7/9. The fractions are 3/5=0.6, 4/5=0.8. 3/5 is 0.6, which is between 0.4 and 0.777. 4/5 is 0.8, which is greater than 7/9. So 3/5 is a candidate. Denominator 5, which is larger than 2. So 1/2 is still better.Wait, so with denominator 2, we have 1/2. That's the smallest possible denominator. Therefore, isn't 1/2 the answer? But maybe I'm missing something here. Let me check the problem statement again."Find the fraction a/b with the smallest denominator such that 2/5 < a/b < 7/9."Yes, so if there exists a fraction with denominator 2, that would be the answer. Since 1/2 is between them, and denominator 2 is the smallest possible, that should be the answer.But wait, maybe the problem is expecting a different answer? Let me check with another method. For example, using continued fractions or the Farey sequence.In the Farey sequence of order 2, the fractions are 0/1, 1/2, 1/1. So 1/2 is indeed present. Since 1/2 is between 2/5 and 7/9, as we saw, then 1/2 is the fraction with the smallest denominator. So why is there confusion here?Wait, maybe there's a mistake in assuming 1/2 is between them. Wait, 7/9 is approximately 0.777, so 0.5 is less than that, and greater than 0.4, which is 2/5. So yes, 1/2 is between them. Therefore, the answer is 1/2. But maybe in some other context, but according to the problem statement, that should be correct.Alternatively, maybe the problem is in the strict inequality. The problem says 2/5 < a/b < 7/9. But 1/2 is 0.5, which is indeed greater than 0.4 (2/5) and less than 0.777 (7/9). So it's strictly between them.Alternatively, maybe the problem requires the fraction to be in the open interval, not including the endpoints, which it is. So 1/2 is between 2/5 and 7/9. Therefore, 1/2 is the answer with denominator 2.But I'm confused because when I thought of the mediant, I got 9/14, which is a larger denominator. So why is 1/2 not mentioned in some solutions? Wait, maybe this problem is from a specific textbook or resource where they consider a different approach. Alternatively, perhaps I made a mistake in assuming 1/2 is between them. Let me check again.Wait, 2/5 is 0.4, 1/2 is 0.5, and 7/9 is approximately 0.777. So yes, 0.5 is in between. Therefore, 1/2 is a valid answer. So why the mediant gives a different result? Because the mediant is a way to find a fraction between two others, but it doesn't necessarily have the smallest denominator. So in this case, even though the mediant gives 9/14, there exists a fraction with a smaller denominator, which is 1/2.Therefore, the answer should be 1/2. But I need to verify once again. Let me check cross-multiplication:Is 1/2 > 2/5? 1*5 = 5, 2*2 = 4. 5 > 4, so yes.Is 1/2 < 7/9? 1*9 = 9, 7*2 = 14. 9 < 14, so yes.Therefore, 1/2 is indeed between them, and since it has the smallest possible denominator (2), that's the answer.Wait, but maybe the problem is from a non-English source and there was a typo or different numbers? Wait, the user wrote:"Example 5 Find the fraction a/b with the smallest denominator such that 2/5 < a/b < 7/9."So as per the user's problem statement, the numbers are 2/5 and 7/9, so unless there's a mistake in the problem statement, 1/2 is the correct answer. Therefore, the fraction with the smallest denominator between 2/5 and 7/9 is 1/2.But now I'm second-guessing because maybe there's a different interpretation. For example, sometimes in math problems, "between" can be exclusive or inclusive. But the problem specifies strict inequalities: 2/5 < a/b <7/9, so it's exclusive. So 1/2 is fine.Alternatively, maybe the problem wants the fraction closest to the middle or something else? But the question explicitly says "smallest denominator", so denominator is the priority, not the proximity.Therefore, I think the answer is 1/2. But just to be thorough, let me check denominators 3 and 4 again.Denominator 3: 2/3 ≈ 0.666. 2/3 is between 2/5 (0.4) and 7/9 (0.777). But denominator 3 is larger than 2, so 1/2 is better.Denominator 4: 3/4 = 0.75, which is between 0.4 and 0.777. But denominator 4, still larger than 2.Denominator 5: 3/5 = 0.6, which is between them. Denominator 5.So, the pattern is denominators 2,3,4,5, etc. So the smallest denominator is 2, with the fraction 1/2. Therefore, the answer is 1/2.But wait a second. Let me check if 1/2 is indeed reduced. Yes, 1 and 2 are coprime. So yes, it's in the simplest terms.Therefore, I think the correct answer is 1/2. But why did I initially think of the mediant? Because I was taught that the mediant gives a fraction between two fractions, but in this case, there's a fraction with a smaller denominator. So the mediant isn't always the one with the smallest denominator.Therefore, the answer is 1/2. But hold on, now I'm confused because I recall Farey sequences and the concept that between two fractions, the fraction with the smallest denominator is the one found via continued fractions or Farey sequences. Let me recall.In Farey sequences, between two fractions, the next term when expanding the sequence is the mediant, but only if the denominator doesn't exceed the order. However, if the two original fractions are not adjacent in the Farey sequence, there might be other fractions between them with smaller denominators.In this case, 2/5 and 7/9. Let's see:In the Farey sequence of order 9 (since 7/9 has denominator 9), but 2/5 has denominator 5. Let me see if they are adjacent in some Farey sequence. If they are adjacent, their mediant would be the only fraction between them in the next sequence. But since 2/5 and 7/9 are not adjacent (because there are fractions between them with smaller denominators like 1/2), their mediant isn't the minimal denominator fraction.Therefore, the minimal denominator fraction is 1/2 with denominator 2.Therefore, the answer is 1/2.But to confirm once again, let's check all fractions with denominator up to 2:Denominator 1: 0/1, 1/1. Neither between 2/5 and 7/9.Denominator 2: 1/2. Yes, between them.Therefore, the minimal denominator is 2. Hence, the answer is 1/2.Final AnswerThe fraction with the smallest denominator between (frac{2}{5}) and (frac{7}{9}) is (boxed{dfrac{1}{2}}).</think>To find the fraction (frac{a}{b}) with the smallest denominator such that (frac{2}{5} < frac{a}{b} < frac{7}{9}), we start by checking fractions with the smallest denominators.1. Denominator 1: The fractions are (0/1) and (1/1), neither of which lie between (2/5) and (7/9).2. Denominator 2: The fraction is (1/2). Checking if (1/2) is between (2/5) and (7/9): - Convert (2/5), (1/2), and (7/9) to decimals: (2/5 = 0.4), (1/2 = 0.5), (7/9 approx 0.777). - (0.5) is between (0.4) and (0.777), so (1/2) is a valid candidate.3. Verification using cross-multiplication: - Compare (1/2) with (2/5): (1 cdot 5 = 5) and (2 cdot 2 = 4). Since (5 > 4), (1/2 > 2/5). - Compare (1/2) with (7/9): (1 cdot 9 = 9) and (7 cdot 2 = 14). Since (9 < 14), (1/2 < 7/9).Since (1/2) is confirmed to be between (2/5) and (7/9) and has the smallest possible denominator (2), the fraction (frac{1}{2}) is the answer.[boxed{dfrac{1}{2}}]]

🔑:Solution: frac{2}{5}<frac{a}{b}<frac{7}{9} Leftrightarrow frac{9}{7}<frac{b}{a}<frac{5}{2}Leftrightarrow frac{2}{7}<frac{b-a}{a}<1 frac{1}{2} text {. }By observation, the rational number with the smallest denominator between frac{2}{7} and 1 frac{1}{2} is clearly 1, so we only need to setfrac{b-a}{a}=1 Leftrightarrowleft{begin{array} { l } { b - a = 1 , } { a = 1 }end{array} Leftrightarrow left{begin{array}{l}b=2, a=1,end{array}right.right.That is, frac{1}{2} is the fraction with the smallest denominator we are looking for.Thus, we have used a so-called clever method and a progressive method to solve a type of competition problem. It is worth noting that problems that can be solved by clever methods are often rare exceptions in a class of mathematical problems.

🧠:[<think>Okay, so I need to find the sum of the first 12 terms of the sequence given by the general term a_n = n⁴ + 6n³ + 11n² + 6n. Hmm, let's see. I remember that summing polynomial terms can sometimes be done by breaking them down into simpler parts or using known formulas for sums of powers. First, let me write out the sequence term again: a_n = n⁴ + 6n³ + 11n² + 6n. So, the sum S₁₂ would be the sum from n=1 to n=12 of each of these terms. That means S₁₂ = Σ (from n=1 to 12) [n⁴ + 6n³ + 11n² + 6n]. Since summation is linear, I can split this into separate sums: Σn⁴ + 6Σn³ + 11Σn² + 6Σn, each summed from 1 to 12. So, if I can find each of these individual sums, I can compute them and add them up to get the total. Okay, now I need to recall the formulas for the sums of n, n², n³, and n⁴. Let me jot them down. The sum of the first m natural numbers is Σn (from 1 to m) = m(m+1)/2.The sum of the squares is Σn² = m(m+1)(2m+1)/6.The sum of the cubes is Σn³ = [m(m+1)/2]^2. That's interesting, it's the square of the sum of the first m numbers.Now, the sum of the fourth powers, Σn⁴. Hmm, I don't remember this one off the top of my head. Let me think. I think it's m(m+1)(2m+1)(3m² + 3m -1)/30. Let me check that formula. Wait, maybe I should verify it with a small m. Let's take m=1: 1⁴=1. Plugging into the formula: 1*2*3*(3 +3 -1)/30 = 1*2*3*5/30 = 30/30=1. That works. For m=2: 1 + 16=17. Formula: 2*3*5*(12 +6 -1)/30 = 2*3*5*17/30 = (30*17)/30=17. Perfect. So yes, the formula is correct: Σn⁴ from 1 to m is m(m+1)(2m+1)(3m² + 3m -1)/30.Alright, so now I can compute each of these sums separately for m=12.Let me start calculating each part step by step.First, let's compute Σn⁴ from 1 to 12.Using the formula: 12*13*25*(3*(12)^2 + 3*12 -1)/30.Wait, let's break this down.First, compute each part:m = 12First part: m(m+1)(2m+1) = 12*13*25. Wait, 2m+1 when m=12 is 25. Yes. So 12*13*25. Then multiplied by (3m² + 3m -1). Let's compute 3m² + 3m -1 for m=12.3*(12)^2 = 3*144=4323*12=36So, 432 + 36 -1 = 467.Therefore, Σn⁴ = [12*13*25*467]/30.Let me compute that step by step.First, compute 12*13 = 156.156*25: 156*25. Well, 100*25=2500, 50*25=1250, 6*25=150. So 2500+1250=3750, 3750+150=3900. So 156*25=3900.Then 3900*467. Hmm, that's a big number. Let me see if I can compute that.First, note that 3900*467 = 3900*(400 + 60 +7) = 3900*400 + 3900*60 + 3900*7.Compute each term:3900*400 = (4000 - 100)*400 = 4000*400 - 100*400 = 1,600,000 - 40,000 = 1,560,000.Wait, actually, 3900*400: 3900*4=15,600. Then 15,600*100=1,560,000.3900*60: 3900*6=23,400. Then 23,400*10=234,000.3900*7=27,300.Adding them up: 1,560,000 + 234,000 = 1,794,000. Then 1,794,000 +27,300 = 1,821,300.So 3900*467=1,821,300.Then Σn⁴ = 1,821,300 /30 = 1,821,300 ÷ 30. Dividing by 10 gives 182,130, then divide by 3: 182,130 ÷3. Let's compute 180,000 ÷3=60,000. 2,130 ÷3=710. So total 60,000 +710=60,710. So Σn⁴=60,710.Wait, let me confirm that division again. 1,821,300 divided by 30: 1,821,300 divided by 10 is 182,130. Divided by 3: 182,130 divided by 3. 3*60,000=180,000. So 182,130 -180,000=2,130. 2,130 /3=710. So yes, 60,710. Okay, that seems right.Now, moving on to Σn³. The formula is [m(m+1)/2]^2. For m=12:12*13/2 = (156)/2=78. Then 78 squared. 78². 70²=4900, 8²=64, 2*70*8=1120. So 4900 +1120 +64= 4900+1120=6020 +64=6084. So Σn³=6,084.Then Σn². The formula is m(m+1)(2m+1)/6. For m=12:12*13*25/6. Let's compute this.12/6=2. So 2*13*25. 2*13=26, 26*25=650. So Σn²=650.Then Σn. The formula is m(m+1)/2. For m=12: 12*13/2=78. So Σn=78.Now, plug these back into the original expression:S₁₂ = Σn⁴ +6Σn³ +11Σn² +6Σn = 60,710 +6*6,084 +11*650 +6*78.Let me compute each term step by step.First term: 60,710.Second term: 6*6,084. Let's compute 6*6,000=36,000; 6*84=504. So total 36,000 +504=36,504.Third term: 11*650. 10*650=6,500; 1*650=650. So total 6,500 +650=7,150.Fourth term: 6*78=468.Now, add all these together:60,710 +36,504 = 97,214.97,214 +7,150 = 104,364.104,364 +468 = 104,832.So S₁₂=104,832.Wait a second, let me check these calculations again because it's easy to make an arithmetic mistake.First term: 60,710.Second term: 6*6,084. Let's compute 6,084*6:6,000*6=36,000.84*6=504.Total: 36,000 +504=36,504. That's correct.Third term: 11*650.As before, 10*650=6,500 and 1*650=650. So 6,500+650=7,150. Correct.Fourth term: 6*78=468. Correct.Adding them up:60,710 +36,504:60,710 +36,504. Let's add 60,000 +36,000=96,000.710 +504=1,214.So total 96,000 +1,214=97,214. Then add 7,150: 97,214 +7,150.97,214 +7,000=104,214. Then +150=104,364.Then add 468: 104,364 +468.104,364 +400=104,764. Then +68=104,832. So total 104,832.Hmm, let me cross-verify this answer another way. Maybe compute some terms manually and add them up. Wait, that would take time, but maybe check for a small n and see if the formula gives the correct term sum. Let's check for n=1.For n=1: a₁ =1⁴ +6*1³ +11*1² +6*1=1 +6 +11 +6=24. So S₁=24.Using our formula: Σn⁴ from 1 to1=1, Σn³=1, Σn²=1, Σn=1.So S₁=1 +6*1 +11*1 +6*1=1+6+11+6=24. Correct.Check n=2: a₂=16 +48 +44 +12=16+48=64, 64+44=108, 108+12=120. So S₂=24 +120=144.Using formula: Σn⁴=1 +16=17, Σn³=1+8=9, Σn²=1+4=5, Σn=1+2=3.So S₂=17 +6*9 +11*5 +6*3=17 +54 +55 +18=17+54=71, 71+55=126, 126+18=144. Correct.Good, so formula works for n=1 and n=2. Then maybe the calculations are correct.Alternatively, maybe there's a smarter way to factor the general term. Let's look at the general term a_n =n⁴ +6n³ +11n² +6n.Hmm, can we factor this? Let's try.Factor out an n first: n(n³ +6n² +11n +6).Now, let's try to factor the cubic polynomial n³ +6n² +11n +6.Looking for rational roots using Rational Root Theorem. Possible roots are ±1, ±2, ±3, ±6.Test n=-1: (-1)³ +6*(-1)² +11*(-1) +6= -1 +6 -11 +6=0. So n=-1 is a root. Therefore, (n +1) is a factor.Divide the cubic by (n +1). Let's perform polynomial division.Divide n³ +6n² +11n +6 by (n +1):n³ +6n² +11n +6 ÷ (n +1):First term: n³ /n =n². Multiply (n +1) by n²: n³ +n². Subtract from the original polynomial:(n³ +6n² +11n +6) - (n³ +n²)=5n² +11n +6.Next term: 5n² /n=5n. Multiply (n +1) by5n:5n² +5n. Subtract:(5n² +11n +6) - (5n² +5n)=6n +6.Next term:6n /n=6. Multiply (n +1) by6:6n +6. Subtract:(6n +6) - (6n +6)=0.So the cubic factors into (n +1)(n² +5n +6). Now factor n² +5n +6: look for two numbers multiplying to 6 and adding to5: 2 and 3. So n² +5n +6=(n +2)(n +3).Thus, the cubic factors as (n +1)(n +2)(n +3). Therefore, the original term a_n can be written as:a_n =n(n +1)(n +2)(n +3). Wow, that's a nice factorization! So a_n is the product of four consecutive integers: n, n+1, n+2, n+3. So, a_n =n(n +1)(n +2)(n +3). That might make the summation easier if there's a telescoping series or some known formula for the sum of products of consecutive integers.Hmm, products of consecutive integers often relate to combinatorial numbers. For example, n(n +1)(n +2)(n +3) is 4! times the combination C(n +3,4). Wait, C(n +3,4)= (n +3)(n +2)(n +1)n /24. So, n(n +1)(n +2)(n +3)=24C(n +3,4). Therefore, a_n=24C(n +3,4). If that's the case, then the sum of a_n from n=1 to m would be 24 times the sum of C(n +3,4) from n=1 to m. But summing combinations can sometimes be simplified using the hockey-stick identity or other combinatorial identities. Recall that the sum of C(k, r) from k=r to N is C(N +1, r +1). So, if we can express the sum of C(n +3,4) from n=1 to m as C(m +4,5). Wait, let's check.Wait, when n=1, we have C(4,4)=1. When n=2, C(5,4)=5. Up to n=m, which is C(m +3,4). So the sum from n=1 to m of C(n +3,4) is equal to C(m +4,5). Yes, that's a standard identity: Σ_{k= r}^N C(k, r) = C(N +1, r +1). In this case, if we set k =n +3, then when n=1, k=4, and when n=m, k=m +3. So the sum Σ_{k=4}^{m +3} C(k,4) = C(m +4,5). Therefore, Σ_{n=1}^m C(n +3,4) = C(m +4,5). Therefore, the sum S_m = Σ_{n=1}^m a_n =24 * Σ_{n=1}^m C(n +3,4)=24*C(m +4,5). So, S_m=24*C(m +4,5). Therefore, for m=12, S₁₂=24*C(16,5). Let's compute that.First, compute C(16,5). C(n,k)=n!/(k!(n -k)!).So C(16,5)=16!/(5!11!)= (16×15×14×13×12)/(5×4×3×2×1).Compute numerator:16×15=240, 240×14=3,360, 3,360×13=43,680, 43,680×12=524,160.Denominator:5×4=20, 20×3=60, 60×2=120, 120×1=120.So C(16,5)=524,160 /120=524,160 ÷120. Divide numerator and denominator by 10: 52,416 /12. 12×4,368=52,416. So C(16,5)=4,368.Therefore, S₁₂=24*4,368. Let's compute that. 24×4,000=96,000. 24×368=8,832. Adding them:96,000 +8,832=104,832. Which matches the previous result! So using the combinatorial approach also gives 104,832. That's a good confirmation.Therefore, the sum of the first 12 terms is 104,832.Final Answerboxed{104832}</think>To find the sum of the first 12 terms of the sequence given by the general term ( a_n = n^4 + 6n^3 + 11n^2 + 6n ), we start by recognizing that the general term can be factored as ( a_n = n(n+1)(n+2)(n+3) ). This product of four consecutive integers can be expressed in terms of combinatorial coefficients.The key steps are as follows:1. Factor the general term: [ a_n = n(n+1)(n+2)(n+3) ] This can be written as ( 24 binom{n+3}{4} ).2. Use the combinatorial identity: The sum of the terms ( binom{k}{4} ) from ( k=4 ) to ( k=15 ) (since ( n ) ranges from 1 to 12) is given by the hockey-stick identity: [ sum_{n=1}^{12} binom{n+3}{4} = binom{16}{5} ]3. Calculate the combinatorial coefficient: [ binom{16}{5} = frac{16!}{5! cdot 11!} = frac{16 times 15 times 14 times 13 times 12}{5 times 4 times 3 times 2 times 1} = 4368 ]4. Multiply by 24: [ S_{12} = 24 times 4368 = 104832 ]Thus, the sum of the first 12 terms of the sequence is (boxed{104832}).,<think>Okay, so I have this problem here where I need to find the sum of the first 12 terms of a sequence. The sequence is defined by the general term a_n = n⁴ + 6n³ + 11n² + 6n. Alright, let's try to figure this out step by step.First, let me make sure I understand the problem. The sequence is given by a formula for each term, and I need to sum the first 12 terms. That means I need to calculate S₁₂ = a₁ + a₂ + a₃ + ... + a₁₂. Each term a_n is a polynomial in n of degree 4. So, the sum S₁₂ is going to be the sum of these polynomials from n=1 to n=12.Hmm, summing up polynomials term by term can sometimes be simplified using formulas for the sums of powers of integers. I remember that there are formulas for the sum of n, sum of n², sum of n³, and sum of n⁴. Maybe I can use those here. Let me recall those formulas:- Sum of the first m natural numbers: Σn from n=1 to m = m(m+1)/2- Sum of squares: Σn² from n=1 to m = m(m+1)(2m+1)/6- Sum of cubes: Σn³ from n=1 to m = [m(m+1)/2]²- Sum of fourth powers: Σn⁴ from n=1 to m = m(m+1)(2m+1)(3m² + 3m -1)/30So, since a_n is a combination of n⁴, n³, n², and n, the sum S₁₂ will be the sum of each of these components multiplied by their coefficients. Let me write that out:S₁₂ = Σ(n⁴ + 6n³ + 11n² + 6n) from n=1 to 12 = Σn⁴ + 6Σn³ + 11Σn² + 6Σn, each summed from n=1 to 12.So, if I can compute each of these four sums separately and then combine them with their coefficients, I should get the total sum. Let me calculate each one step by step.First, let's compute Σn from n=1 to 12. Using the formula: 12*13/2 = (156)/2 = 78.Next, Σn² from n=1 to 12: 12*13*25/6. Wait, hold on. Let me check the formula again. It's m(m+1)(2m+1)/6. So, substituting m=12: 12*13*(2*12 +1)/6 = 12*13*25/6. Let's compute this step by step. 12 divided by 6 is 2, so 2*13*25. 2*13 is 26, then 26*25. 25*26 is 650. So that's 650.Next, Σn³ from n=1 to 12: [12*13/2]². First, compute 12*13/2. That's 156/2 = 78. Then 78 squared. Let me calculate 78*78. 70*70=4900, 70*8=560, 8*70=560, 8*8=64. So, (70+8)*(70+8) = 70² + 2*70*8 +8² = 4900 + 1120 +64 = 4900+1120=6020, 6020+64=6084. So Σn³ = 6084.Now, Σn⁴ from n=1 to 12. Using the formula: m(m+1)(2m+1)(3m² + 3m -1)/30. Let me substitute m=12 here. So, 12*13*(2*12 +1)*(3*(12)^2 +3*12 -1)/30. Let's compute each part step by step.First, 12*13 = 156.Next, (2*12 +1) = 24 +1 =25.Then, 3*(12)^2 +3*12 -1. 12 squared is 144, so 3*144 = 432. 3*12 =36. So, 432 +36 -1 = 467.Therefore, the numerator is 156*25*467. Let me compute this. First, 156*25. 25*100=2500, 25*50=1250, 25*6=150. So 2500+1250=3750, +150=3900. So 156*25=3900. Then 3900*467. Hmm, that's a big number. Let me break it down.First, 3900*400 = 1,560,0003900*60 = 234,0003900*7 = 27,300Adding them together: 1,560,000 +234,000 = 1,794,0001,794,000 +27,300 = 1,821,300So the numerator is 1,821,300. Then divide by 30: 1,821,300 /30. Let's divide 1,821,300 by 10 first to get 182,130, then divide by 3: 182,130 /3 = 60,710. So Σn⁴ from 1 to12 is 60,710.Wait, let me verify that division. 3*60,000 = 180,000. 182,130 - 180,000 = 2,130. 3*700 =2,100. 2,130 -2,100=30. 3*10=30. So total is 60,000 +700 +10=60,710. Yes, that's correct. So Σn⁴ =60,710.So now, let's put it all together.S₁₂ = Σn⁴ +6Σn³ +11Σn² +6Σn = 60,710 +6*6,084 +11*650 +6*78.Compute each term:First term: 60,710Second term:6*6,084. Let's compute that. 6*6,000=36,000. 6*84=504. So total is 36,000+504=36,504.Third term:11*650. 10*650=6,500. 1*650=650. Total 6,500+650=7,150.Fourth term:6*78=468.Now, add them all together:60,710 +36,504 = 97,21497,214 +7,150 = 104,364104,364 +468 =104,832.Therefore, S₁₂=104,832.But wait, let me check if all the calculations are correct step by step because that's a lot of numbers and I might have made a mistake somewhere.First, Σn⁴: I calculated 60,710. Let me double-check the formula for Σn⁴. The formula is m(m+1)(2m+1)(3m² +3m -1)/30. For m=12:12*13=15625 (from 2*12 +1=25)3*(12)^2 +3*12 -1: 3*144=432, 3*12=36, 432+36=468-1=467. So 156*25=3,900. Then 3,900*467. Let's do this multiplication again.3,900*400=1,560,0003,900*60=234,0003,900*7=27,300Adding them: 1,560,000 +234,000=1,794,000 +27,300=1,821,300. Divide by 30: 1,821,300 /30=60,710. That seems correct.Σn³=6,084. 78 squared is 6,084. 78*78: 70*70=4,900, 70*8=560, 8*70=560, 8*8=64. So 4,900+560+560+64=6,084. Correct.Σn²=650. For m=12: 12*13*25/6. 12/6=2, 2*13=26, 26*25=650. Correct.Σn=78. 12*13/2=78. Correct.Now, the coefficients:6,084*6: Let's compute 6,000*6=36,000, 84*6=504, total 36,504. Correct.650*11: 650*10=6,500 +650=7,150. Correct.78*6=468. Correct.Adding all together:60,710 +36,504=97,214. Then +7,150=104,364. Then +468=104,832. That seems correct.But let me cross-validate this by calculating the sum another way. Maybe by actually computing each term from n=1 to 12 and adding them up. Although that would be tedious, perhaps for a few terms to check.Compute a_1:1⁴ +6*1³ +11*1² +6*1 =1 +6 +11 +6=24.a_2:16 +6*8 +11*4 +6*2=16+48+44+12=120.a_3:81 +6*27 +11*9 +6*3=81+162+99+18=360.Wait, let me check a_3:n=3: 3⁴=81, 6*3³=6*27=162, 11*3²=11*9=99, 6*3=18. 81+162=243, 243+99=342, 342+18=360. Correct.a_4:4⁴=256, 6*4³=6*64=384, 11*4²=11*16=176, 6*4=24. So 256+384=640, 640+176=816, 816+24=840.a_5:5⁴=625, 6*5³=6*125=750, 11*25=275, 6*5=30. 625+750=1375 +275=1650 +30=1680.a_6:6⁴=1296, 6*6³=6*216=1296, 11*36=396, 6*6=36. 1296+1296=2592 +396=2988 +36=3024.a_7:7⁴=2401, 6*343=2058, 11*49=539, 6*7=42. 2401+2058=4459 +539=5000-1 +42=5041? Wait, 4459 +539=5000-1=4999? Wait, no. Let's compute:2401 +2058: 2000 +2000=4000, 401 +58=459, so total 4459.4459 +539: 4400 +500=4900, 59 +39=98. So 4900 +98=4998.Then 4998 +42=5040.a_7=5040.a_8:8⁴=4096, 6*512=3072, 11*64=704, 6*8=48. 4096+3072=7168 +704=7872 +48=7920.a_9:9⁴=6561, 6*729=4374, 11*81=891, 6*9=54. 6561+4374=10935 +891=11826 +54=11880.a_10:10⁴=10000, 6*1000=6000, 11*100=1100, 6*10=60. 10000+6000=16000 +1100=17100 +60=17160.a_11:11⁴=14641, 6*1331=7986, 11*121=1331, 6*11=66. 14641+7986=22627 +1331=23958 +66=24024.a_12:12⁴=20736, 6*1728=10368, 11*144=1584, 6*12=72. 20736+10368=31104 +1584=32688 +72=32760.Now, let's sum up these terms:a1=24a2=120a3=360a4=840a5=1680a6=3024a7=5040a8=7920a9=11880a10=17160a11=24024a12=32760Let's add them step by step:Start with 24 (a1)24 +120 =144 (a1+a2)144 +360 =504 (sum up to a3)504 +840 =1344 (sum up to a4)1344 +1680 =3024 (sum up to a5)3024 +3024 =6048 (sum up to a6)6048 +5040 =11088 (sum up to a7)11088 +7920 =19008 (sum up to a8)19008 +11880 =30888 (sum up to a9)30888 +17160 =48048 (sum up to a10)48048 +24024 =72072 (sum up to a11)72072 +32760 =104832 (sum up to a12)So, adding all terms individually, I also get 104,832. That matches the previous result. Therefore, it's confirmed. The sum S₁₂ is 104,832.Alternatively, maybe the original expression can be factored to simplify the summation. Let me check if the polynomial n⁴ +6n³ +11n² +6n can be factored. Let's see.Factor out an n: n(n³ +6n² +11n +6). Now, let's try to factor the cubic polynomial. Let's look for rational roots using Rational Root Theorem. The possible roots are ±1, ±2, ±3, ±6.Testing n=-1: (-1)^3 +6*(-1)^2 +11*(-1) +6 = -1 +6 -11 +6 =0. So, n=-1 is a root. Therefore, (n+1) is a factor.Divide the cubic polynomial by (n+1). Let's perform polynomial division or use synthetic division.Using synthetic division for n³ +6n² +11n +6 divided by (n+1):Coefficients: 1 | 6 |11 |6Root: -1Bring down 1Multiply by -1: -1Add to next coefficient:6 + (-1)=5Multiply by -1: -5Add to next coefficient:11 + (-5)=6Multiply by -1: -6Add to last coefficient:6 + (-6)=0So, the cubic factors as (n+1)(n² +5n +6). Then, factor n² +5n +6: (n+2)(n+3). Therefore, the original polynomial factors as n(n+1)(n+2)(n+3).Wait, that's a nice factorization! So, a_n = n(n+1)(n+2)(n+3). Let me check this:Expand n(n+1)(n+2)(n+3). Let's group them as (n(n+3))((n+1)(n+2)) = (n² +3n)(n² +3n +2) = Let's multiply these two quadratics:(n² +3n)(n² +3n +2) = n²(n² +3n +2) +3n(n² +3n +2) = n⁴ +3n³ +2n² +3n³ +9n² +6n = n⁴ +6n³ +11n² +6n. Which matches the original a_n. Great!So, the general term is a_n = n(n+1)(n+2)(n+3). That's the product of four consecutive integers starting from n. Hmm, maybe this can help in summing the terms more easily. But how?Well, the product of four consecutive integers can sometimes be expressed in terms of combinations or through telescoping series. Let me think.Alternatively, note that n(n+1)(n+2)(n+3) is equal to (n+3)! / (n-1)! ) but that's only if n starts from 1, but n=1 would be 4! /0! which is 24, which matches a_1=24. But I'm not sure if factorial expressions help here for summation.Alternatively, maybe express this product as a difference of terms to create a telescoping series. For example, products of consecutive integers can sometimes be written as a difference of higher-order terms so that when summed, most terms cancel out.Let me recall that for telescoping sums, if we can write a term as f(n) - f(n-1), then summing over n will result in cancellation. So, perhaps we can find such a representation for n(n+1)(n+2)(n+3).Let me consider the fifth-degree polynomial. Let's suppose that n(n+1)(n+2)(n+3) can be written as the difference of two consecutive terms of a fifth-degree polynomial. Let's consider that:Suppose that n(n+1)(n+2)(n+3) = f(n) - f(n-1), where f(n) is some function to be determined. Then, summing from n=1 to m would give f(m) - f(0).So, let's try to find f(n) such that f(n) - f(n-1) = n(n+1)(n+2)(n+3). Let's consider f(n) as a fifth-degree polynomial. Let f(n) = An⁵ + Bn⁴ + Cn³ + Dn² + En + F.Then, f(n) - f(n-1) = A[n⁵ - (n-1)^5] + B[n⁴ - (n-1)^4] + C[n³ - (n-1)^3] + D[n² - (n-1)^2] + E[n - (n-1)] + F[1 -1].Compute each term:n⁵ - (n-1)^5 = n⁵ - (n⁵ -5n⁴ +10n³ -10n² +5n -1) =5n⁴ -10n³ +10n² -5n +1Similarly:n⁴ - (n-1)^4 = n⁴ - (n⁴ -4n³ +6n² -4n +1)=4n³ -6n² +4n -1n³ - (n-1)^3 =n³ - (n³ -3n² +3n -1)=3n² -3n +1n² - (n-1)^2 =n² - (n² -2n +1)=2n -1n - (n-1)=1Therefore, f(n) -f(n-1)=A(5n⁴ -10n³ +10n² -5n +1) + B(4n³ -6n² +4n -1) + C(3n² -3n +1) + D(2n -1) + E(1) +0.This should equal n(n+1)(n+2)(n+3)=n⁴ +6n³ +11n² +6n.Therefore, equate coefficients:For n⁴:5A =1 => A=1/5For n³: -10A +4B =6. Since A=1/5, -10*(1/5)= -2, so -2 +4B=6 =>4B=8 =>B=2.For n²:10A -6B +3C=11. Substituting A=1/5, B=2: 10*(1/5)=2; -6*2=-12; 2 -12 +3C=11 => -10 +3C=11 =>3C=21 =>C=7.For n terms: -5A +4B -3C +2D=6. Substituting A=1/5, B=2, C=7:-5*(1/5)= -1; 4*2=8; -3*7= -21; so -1 +8 -21 +2D=6 => (-14) +2D=6 =>2D=20 =>D=10.For constants: A -B +C -D +E=0. Wait, let me check the constants.From the expansion:A*(1) + B*(-1) + C*(1) + D*(-1) + E*(1) =0.Because:Original constants: A*1 (from the n⁵ term) + B*(-1) (from the n⁴ term) + C*1 (from the n³ term) + D*(-1) (from the n² term) + E*1 (from the n term) =0.So, A -B +C -D +E=0.Substituting A=1/5, B=2, C=7, D=10:1/5 -2 +7 -10 +E=0 =>1/5 -5 +E=0 => (-24/5) +E=0 =>E=24/5=4.8.But E should be an integer if f(n) is to have integer coefficients? Wait, but maybe f(n) can have fractional coefficients.Wait, let's check:E=24/5. Then, f(n)= (1/5)n⁵ +2n⁴ +7n³ +10n² + (24/5)n +F.But F cancels out in the telescoping sum since f(n) -f(n-1) doesn't involve F. Therefore, we can set F=0 for simplicity.But let's confirm. The constant term in f(n) -f(n-1) is A*(1) + B*(-1) + C*(1) + D*(-1) + E*(1) + F*(0). So, if we set this equal to zero (since the original polynomial n(n+1)(n+2)(n+3) has no constant term when expanded). Wait, actually when we expand n(n+1)(n+2)(n+3), it's a quartic polynomial, but when we set the constants equal, the sum of the constants from f(n)-f(n-1) must equal the constant term of the original polynomial. But n(n+1)(n+2)(n+3) when n=0 is 0, so the constant term is 0. Therefore, the constant terms from f(n)-f(n-1) must sum to zero. Therefore:A -B +C -D +E=0. Which we already used to find E=24/5.Therefore, f(n)= (1/5)n⁵ +2n⁴ +7n³ +10n² + (24/5)n +F. Since the telescoping sum S₁₂ = sum_{n=1}^12 [f(n)-f(n-1)] = f(12) -f(0).f(0) would be (1/5)(0)^5 +2(0)^4 +7(0)^3 +10(0)^2 +24/5(0) +F = F.But since the original equation for the constants A -B +C -D +E=0 holds, we don't need to worry about F because it cancels out. Wait, actually, let's check:When we compute the telescoping sum from n=1 to 12, it's [f(1)-f(0)] + [f(2)-f(1)] + ... + [f(12)-f(11)] = f(12) -f(0). So, S₁₂= f(12) -f(0). But f(0) is F. However, in the equation for the constants, we had A -B +C -D +E=0. Which was derived from setting the constants of f(n)-f(n-1) equal to zero, since the original polynomial has no constant term. Therefore, F is arbitrary? Wait, but if we set F=0, then f(0)=0. Let me check with n=0:If F=0, then f(0)=0. Let's see what f(n) is.f(n) = (1/5)n⁵ +2n⁴ +7n³ +10n² + (24/5)n.Therefore, S₁₂ = f(12) -f(0) = f(12) -0 =f(12).So, compute f(12):(1/5)(12)^5 +2*(12)^4 +7*(12)^3 +10*(12)^2 + (24/5)*12.Compute each term:First term: (1/5)(12^5). 12^5=12*12*12*12*12=12^2=144, 12^3=1728, 12^4=20736, 12^5=248832. So (1/5)(248832)=49766.4Second term:2*(12)^4=2*20736=41472Third term:7*(12)^3=7*1728=12096Fourth term:10*(12)^2=10*144=1440Fifth term:(24/5)*12= (24*12)/5=288/5=57.6Now, sum all these:49766.4 +41472 =91238.491238.4 +12096 =103,334.4103,334.4 +1440 =104,774.4104,774.4 +57.6 =104,832.0So, f(12)=104,832. Therefore, S₁₂=104,832. Which matches our previous result. So this method also gives the same answer, which is reassuring.Therefore, regardless of the method used—direct summation using power sum formulas or factoring the general term and using telescoping sums—the result is 104,832.I think that's thorough. Both methods lead to the same answer, so I'm confident that the sum of the first 12 terms is 104,832.Final AnswerThe sum of the first 12 terms ( S_{12} ) is boxed{104832}.</think>Given the sequence ({a_n}) with the general term (a_n = n^4 + 6n^3 + 11n^2 + 6n), we need to find the sum of the first 12 terms (S_{12}).First, we recognize that the general term can be factored as (a_n = n(n+1)(n+2)(n+3)). This product of four consecutive integers can be used to simplify the summation process using a telescoping series approach.We express (a_n) as a telescoping series. By finding a polynomial (f(n)) such that (a_n = f(n) - f(n-1)), the sum (S_{12}) will telescope to (f(12) - f(0)).After determining the polynomial (f(n)) through polynomial fitting, we find:[ f(n) = frac{1}{5}n^5 + 2n^4 + 7n^3 + 10n^2 + frac{24}{5}n ]Calculating (f(12)):[f(12) = frac{1}{5}(12^5) + 2(12^4) + 7(12^3) + 10(12^2) + frac{24}{5}(12)][= frac{1}{5}(248832) + 2(20736) + 7(1728) + 10(144) + frac{24}{5}(12)][= 49766.4 + 41472 + 12096 + 1440 + 57.6][= 104832]Since (f(0) = 0), the sum (S_{12} = f(12) - f(0) = 104832).Thus, the sum of the first 12 terms (S_{12}) is (boxed{104832}).]

🔑:7. 104832 .Notice that,begin{array}{l}a_{n}=n^{4}+6 n^{3}+11 n^{2}+6 n =n(n+1)(n+2)(n+3) . text { Let } f(n)=frac{1}{5} n(n+1)(n+2)(n+3)(n+4) .end{array}Then a_{n}=f(n)-f(n-1), S_{n}=f(n).Therefore, S_{12}=f(12)=104832.