🧠:[<think>Alright, let's tackle this problem step by step. So, we have the line y = -2x + 10 intersecting the x-axis and y-axis at points A and B. Then, when triangle AOB is folded along AB, point O lands at point C. We need to find the coordinates of point C.First, let me visualize this. The line y = -2x +10. To find where it intersects the axes, for point A (x-axis), set y=0. So, 0 = -2x +10. Solving for x, 2x=10, so x=5. Therefore, point A is at (5,0). Similarly, for point B (y-axis), set x=0. Then y = -2*0 +10 =10. So point B is at (0,10). So triangle AOB is formed by the points O (origin), A (5,0), and B (0,10). Now, folding the triangle along AB will move point O to some point C. When folding, the line AB acts as a mirror, so point C is the reflection of O over the line AB.Therefore, to find point C, I need to find the reflection of the origin over the line AB, which is y = -2x +10.Okay, so reflection of a point over a line. The formula for reflection over a line ax + by + c =0 is a standard formula. Let me recall it. If we have a point (x0, y0), its reflection over the line ax + by + c =0 is given by:(x', y') = (x0 - 2a(ax0 + by0 + c)/(a² + b²), y0 - 2b(ax0 + by0 + c)/(a² + b²))Alternatively, there's another method using vectors and projection. Maybe I should use the formula here. Let me try that.First, let's write the equation of AB in standard form. The given equation is y = -2x +10. Let's rearrange it to ax + by + c =0. So, 2x + y -10 =0. So a=2, b=1, c=-10.Wait, the formula for reflection requires the line to be in ax + by + c =0 form. So yes, here 2x + y -10 =0. So coefficients are a=2, b=1, c=-10.Point O is (0,0). Let's apply the reflection formula.Compute numerator parts first. The formula for x' is:x' = x0 - 2a(ax0 + by0 + c)/(a² + b²)Similarly for y':y' = y0 - 2b(ax0 + by0 + c)/(a² + b²)Plugging in x0=0, y0=0:First compute ax0 + by0 + c = 2*0 +1*0 -10 = -10Then compute denominator a² + b² = 4 +1 =5So,x' = 0 - 2*2*(-10)/5 = 0 - 4*(-10)/5 = 0 +40/5=8Similarly,y' =0 - 2*1*(-10)/5 =0 - 2*(-10)/5=0 +20/5=4So the reflection point C is at (8,4). Let me verify if this makes sense.Wait, so when we fold the triangle over AB, the origin is reflected over AB to (8,4). Let me check if this is correct.Alternatively, maybe there's a mistake here. Let me confirm the reflection formula.The formula is:If you reflect point (x0, y0) over line ax + by + c =0, then the reflection (x', y') is:x' = x0 - 2a(ax0 + by0 + c)/(a² + b²)y' = y0 - 2b(ax0 + by0 + c)/(a² + b²)Yes, that's correct. So in our case:ax0 + by0 + c =2*0 +1*0 -10 = -10Therefore:x' =0 - 2*2*(-10)/5 = 0 +40/5=8y' =0 - 2*1*(-10)/5 =0 +20/5=4So (8,4). That seems to be the case.Alternatively, let me think geometrically. The line AB is between (5,0) and (0,10). If we reflect the origin over AB, the image point C should lie such that AB is the perpendicular bisector of the segment OC.So OC is perpendicular to AB, and the midpoint of OC lies on AB.Let me check if (8,4) satisfies that.First, the midpoint of O(0,0) and C(8,4) is (4,2). Let's check if this midpoint lies on AB.AB has the equation y = -2x +10. Plugging x=4: y = -8 +10=2. Yes, so the midpoint (4,2) is indeed on AB. Good.Also, the line OC should be perpendicular to AB. The slope of AB is -2. The slope of OC is (4-0)/(8-0)=4/8=1/2. The product of the slopes is -2*(1/2)=-1, which confirms they are perpendicular. So that checks out.Therefore, reflection formula gives us (8,4) which satisfies the conditions. Hence, the coordinates of point C are (8,4).Alternatively, maybe I can approach this problem using coordinates and parametric equations.Another method to find reflection is to parametrize the line AB, find the foot of the perpendicular from O to AB, and then double that distance.Let me try this method to cross-validate.Given point O(0,0). The line AB: y = -2x +10.To find the foot of the perpendicular from O to AB, we can write parametric equations.The direction vector of AB is ( -1, 2 ) because the slope is -2, so for every 1 unit in x, y decreases by 2. But to make it direction vector, it's (1, -2) or (-1, 2). Let's confirm.Wait, the line AB goes from A(5,0) to B(0,10). So vector AB is (-5,10). So direction vector is (-5,10) which can be simplified to (-1,2). So direction vector is (-1,2). Therefore, parametric equations for AB can be written as:x =5 - ty=0 +2tBut perhaps a better approach is to find the foot of the perpendicular.Given line AB: y = -2x +10.The formula for the foot of the perpendicular from a point (x0, y0) to the line ax + by + c =0 is:( (b(bx0 - ay0) -ac ) / (a² + b²), (a(-bx0 + ay0) - bc ) / (a² + b²) )But maybe it's simpler to use coordinates.Alternatively, the foot of the perpendicular can be found by solving the system of two equations: the given line AB and the line perpendicular to AB passing through O.Since the slope of AB is -2, the slope of the perpendicular is 1/2. So the line perpendicular to AB through O is y = (1/2)x.Find intersection of y = -2x +10 and y= (1/2)x.Set (1/2)x = -2x +10Multiply both sides by 2: x = -4x +20Bring terms together: x +4x=20 =>5x=20 =>x=4Then y=(1/2)*4=2So the foot of the perpendicular is (4,2), which is the midpoint between O and C. Therefore, since the midpoint is (4,2), then point C must be (8,4), since (0 +8)/2=4 and (0 +4)/2=2. So yes, that confirms it.Therefore, point C is (8,4). So the answer is (8,4), which would be boxed as boxed{(8,4)}.I think both methods confirm that the coordinates of point C are (8,4). Therefore, that's the solution.Final AnswerThe coordinates of point ( C ) are boxed{(8, 4)}.</think>The line ( y = -2x + 10 ) intersects the x-axis at point ( A ) and the y-axis at point ( B ). To find these points, we set ( y = 0 ) for the x-intercept and ( x = 0 ) for the y-intercept. Solving these, we get ( A = (5, 0) ) and ( B = (0, 10) ).When triangle ( AOB ) is folded along ( AB ), point ( O ) (the origin) is reflected over the line ( AB ). To find the coordinates of the reflection of ( O ) over the line ( AB ), we use the reflection formula for a point over a line.The line ( AB ) can be written in the form ( 2x + y - 10 = 0 ). Using the reflection formula for a point ((x_0, y_0)) over the line ( ax + by + c = 0 ):[x' = x_0 - frac{2a(ax_0 + by_0 + c)}{a^2 + b^2}][y' = y_0 - frac{2b(ax_0 + by_0 + c)}{a^2 + b^2}]For the origin ( O(0, 0) ), substituting ( a = 2 ), ( b = 1 ), and ( c = -10 ):[ax_0 + by_0 + c = 2 cdot 0 + 1 cdot 0 - 10 = -10][x' = 0 - frac{2 cdot 2 cdot (-10)}{2^2 + 1^2} = 0 + frac{40}{5} = 8][y' = 0 - frac{2 cdot 1 cdot (-10)}{2^2 + 1^2} = 0 + frac{20}{5} = 4]Thus, the coordinates of point ( C ) are ( (8, 4) ).To verify, the midpoint of ( O(0, 0) ) and ( C(8, 4) ) is ( (4, 2) ), which lies on the line ( AB ) (substituting ( x = 4 ) into ( y = -2x + 10 ) gives ( y = 2 )). The line ( OC ) is perpendicular to ( AB ), confirming the reflection is correct.The coordinates of point ( C ) are boxed{(8, 4)}.,<think>Okay, so I need to find the coordinates of point C, which is where point O lands when triangle AOB is folded along AB. Let me start by visualizing the problem. There's a line y = -2x + 10 that intersects the x-axis and y-axis at points A and B. Then, when you fold the triangle formed by points A, O, and B along the line AB, the origin O moves to point C. I need to find where exactly C is located.First, I should find the coordinates of points A and B. Since point A is where the line intersects the x-axis, the y-coordinate there is 0. So I can set y = 0 in the equation of the line and solve for x.0 = -2x + 10Adding 2x to both sides: 2x = 10Dividing by 2: x = 5So point A is at (5, 0).Similarly, point B is where the line intersects the y-axis, so the x-coordinate is 0. Setting x = 0 in the equation:y = -2(0) + 10 = 10So point B is at (0, 10).Now, triangle AOB is a right triangle with vertices at O (the origin, (0,0)), A (5,0), and B (0,10). Folding the triangle along AB would mean that point O is reflected over the line AB to point C. Therefore, point C is the reflection of O over line AB.To find the reflection of a point over a line, I can use the formula for reflection over a line. The formula for reflecting a point (x0, y0) over the line ax + by + c = 0 is:x' = x0 - 2a(ax0 + by0 + c)/(a² + b²)y' = y0 - 2b(ax0 + by0 + c)/(a² + b²)But first, I need to write the equation of line AB in the standard form ax + by + c = 0. The line AB is given by y = -2x + 10. Let's rearrange this to standard form:2x + y - 10 = 0So a = 2, b = 1, and c = -10. The point to reflect is O, which is (0,0).Plugging into the reflection formula:x' = 0 - 2*2*(2*0 + 1*0 - 10)/(2² + 1²)y' = 0 - 2*1*(2*0 + 1*0 - 10)/(2² + 1²)First, compute the denominator: 2² + 1² = 4 + 1 = 5Then compute the numerator for x':-2*2*(0 + 0 -10) = -4*(-10) = 40So x' = 40 / 5 = 8Similarly, for y':-2*1*(-10) = -2*(-10) = 20So y' = 20 / 5 = 4Wait, hold on. Let me double-check the formula. The reflection formulas are:x' = x0 - 2a(ax0 + by0 + c)/(a² + b²)y' = y0 - 2b(ax0 + by0 + c)/(a² + b²)But let me check again with the standard line equation. The line is 2x + y -10 = 0, so ax + by + c = 0 where a=2, b=1, c=-10.So substituting (0,0):ax0 + by0 + c = 2*0 + 1*0 -10 = -10Then:x' = 0 - 2*2*(-10)/5 = 0 - ( -40/5 ) = 0 + 8 = 8y' = 0 - 2*1*(-10)/5 = 0 - ( -20/5 ) = 0 + 4 = 4So the reflection point is (8,4). Therefore, point C is at (8,4). Let me verify this.Alternatively, since reflecting over a line can also be thought of as finding the mirror image. The line AB is 2x + y = 10.Another method to find the reflection is to find the perpendicular line from O to AB, find the foot of the perpendicular, and then double that distance to get the reflection point.Let's try that approach. Let me calculate the foot of the perpendicular from O to AB, then double it.The formula for the foot of the perpendicular from (x0, y0) to line ax + by + c = 0 is:Foot (x, y) = ( (b(bx0 - ay0) - ac ) / (a² + b²), (a(-bx0 + ay0) - bc ) / (a² + b²) )But perhaps a more straightforward method is using parametric equations or vector projection.Alternatively, using coordinates.Given line AB: 2x + y = 10The direction vector of AB can be found by subtracting points A and B. Point A is (5,0), point B is (0,10). So vector AB is (-5,10). The direction vector is (-5,10) or simplified to (-1, 2).The slope of AB is (10 - 0)/(0 - 5) = 10 / (-5) = -2, which matches the given equation y = -2x + 10. So the slope of AB is -2, which means the slope of the perpendicular line is the negative reciprocal, which is 1/2.So the perpendicular from O to AB has a slope of 1/2. Since O is (0,0), the equation of the perpendicular line is y = (1/2)x.Find the intersection point of this perpendicular line with AB: 2x + y = 10 and y = (1/2)x.Substitute y = (1/2)x into 2x + y = 10:2x + (1/2)x = 10(5/2)x = 10x = 10 * (2/5) = 4Then y = (1/2)(4) = 2So the foot of the perpendicular from O to AB is (4,2). Therefore, the reflection point C is such that this foot is the midpoint between O and C.So if midpoint M is (4,2), then:M = ((0 + Cx)/2, (0 + Cy)/2) = (4,2)Therefore, solving for Cx and Cy:(0 + Cx)/2 = 4 => Cx = 8(0 + Cy)/2 = 2 => Cy = 4So point C is (8,4), which matches the previous result. Therefore, the coordinates of point C are (8,4). That seems consistent.Wait, but just to ensure, let me check if the distance from O to AB is equal to the distance from C to AB. Since reflection over a line preserves distance.Distance from O to AB:Using the formula for distance from a point (x0,y0) to line ax + by + c =0 is |ax0 + by0 + c| / sqrt(a² + b²)So for O(0,0):|2*0 + 1*0 -10| / sqrt(4 +1) = | -10 | / sqrt(5) = 10/sqrt(5) = 2*sqrt(5)For point C(8,4):|2*8 + 1*4 -10| / sqrt(5) = |16 +4 -10| / sqrt(5) = |10| / sqrt(5) = 10/sqrt(5) = 2*sqrt(5). Same distance, which makes sense.Also, checking if vector OC is twice the vector from O to the foot. The foot is (4,2), so OC should be (8,4). Indeed, that's twice (4,2), which is correct.Another sanity check: when folding over AB, the point O should be mapped to C such that AB is the perpendicular bisector of OC. So the midpoint of OC is (4,2), which lies on AB. Let's check if (4,2) is on AB.Plug into AB's equation: 2*4 + 2 = 8 +2 = 10. Yes, which matches 2x + y =10. So the midpoint is indeed on AB, and AB is perpendicular to OC (since the slope of AB is -2 and the slope of OC is (4-0)/(8-0)= 4/8=1/2, which is the negative reciprocal of -2). So they are perpendicular. Therefore, all conditions are satisfied.Therefore, the coordinates of point C are (8,4).Final AnswerThe coordinates of point ( C ) are boxed{(8, 4)}.</think>To find the coordinates of point ( C ), which is the reflection of point ( O ) (the origin) over the line ( AB ) given by the equation ( y = -2x + 10 ):1. Determine the coordinates of points ( A ) and ( B ): - Point ( A ) is where the line intersects the x-axis (( y = 0 )): [ 0 = -2x + 10 implies x = 5 implies A = (5, 0) ] - Point ( B ) is where the line intersects the y-axis (( x = 0 )): [ y = -2(0) + 10 implies y = 10 implies B = (0, 10) ]2. Convert the line equation to standard form: - The line ( AB ) is ( y = -2x + 10 ), which converts to: [ 2x + y - 10 = 0 ]3. Reflect point ( O(0, 0) ) over the line ( 2x + y - 10 = 0 ): - Using the reflection formula for a point ((x_0, y_0)) over the line ( ax + by + c = 0 ): [ x' = x_0 - frac{2a(ax_0 + by_0 + c)}{a^2 + b^2} ] [ y' = y_0 - frac{2b(ax_0 + by_0 + c)}{a^2 + b^2} ] - Substituting ( a = 2 ), ( b = 1 ), ( c = -10 ), ( x_0 = 0 ), and ( y_0 = 0 ): [ ax_0 + by_0 + c = 2(0) + 1(0) - 10 = -10 ] [ x' = 0 - frac{2 cdot 2 cdot (-10)}{2^2 + 1^2} = 0 + frac{40}{5} = 8 ] [ y' = 0 - frac{2 cdot 1 cdot (-10)}{2^2 + 1^2} = 0 + frac{20}{5} = 4 ]4. Verification: - The foot of the perpendicular from ( O ) to ( AB ) is calculated to be ( (4, 2) ), which is the midpoint of ( O ) and ( C ). Doubling this midpoint gives ( C = (8, 4) ).Thus, the coordinates of point ( C ) are (boxed{(8, 4)}).]

🔑:7. (8,4)

🧠:[<think>Okay, let me try to figure out this problem step by step. So, we have two sets, A and B. The question is asking for the union of A and B, which is A ∪ B. The answer choices are given as intervals, so I need to determine what each set A and B represents on the number line and then combine them.First, let's parse the definitions of sets A and B.Set A is defined as {x | |x| < 3}. The vertical bars here represent absolute value, so this is the set of all real numbers x where the absolute value of x is less than 3. Absolute value inequalities like this can be rewritten without the absolute value by breaking them into two separate inequalities. Specifically, |x| < 3 means that x is between -3 and 3. However, since it's a strict inequality (using < rather than ≤), the endpoints -3 and 3 are not included. So, set A is the open interval (-3, 3).Now, set B is {x | x - 1 ≤ 0}. Let me rewrite that inequality to make it clearer. If we have x - 1 ≤ 0, we can add 1 to both sides to solve for x. That gives x ≤ 1. So, set B is all real numbers x such that x is less than or equal to 1. In interval notation, that would be (-∞, 1].Now, the question is asking for the union of A and B, which is all numbers that are in either A or B or both. So, let's visualize both intervals on the number line.Set A is from -3 to 3, not including -3 and 3. Set B is everything to the left of 1, including 1 itself. So, if we take the union, we need to combine these two intervals.Let me think: The union would include all numbers from set B, which is everything up to 1, and all numbers from set A, which is from -3 up to 3. But since set B already covers everything up to 1, and set A covers from -3 to 3, the union would start from negative infinity (since B goes all the way to the left) up to 3. Wait, hold on.Wait, set B is (-∞, 1], and set A is (-3, 3). So when we take the union, we need to see which parts are covered by either set.Starting from the leftmost point, set B goes all the way to negative infinity, which is further left than set A's left endpoint at -3. Then, set B stops at 1, but set A continues from -3 up to 3. So from negative infinity to 1, we have set B covering that entirely. From 1 to 3, set A covers that but doesn't include 3. So combining these, the union would be from negative infinity up to 3, but not including 3. However, wait, set B includes 1, and set A doesn't include -3 or 3. So the union would be all numbers less than 3, starting from negative infinity, because set B covers everything up to 1, and set A adds from -3 to 3. Wait, but actually, set B already includes everything less than or equal to 1, which overlaps with part of set A. So, the union would actually be (-∞, 3). Wait, but hold on.Wait, if set B is (-∞, 1], and set A is (-3, 3), then the union would be everything in set B (which is up to 1) and everything in set A (which is from -3 to 3). So combining these, the union would be (-∞, 3). Because from negative infinity up to 1, it's covered by set B, and from 1 up to 3, it's covered by set A. However, set A doesn't include 3, so the upper bound is 3, not including 3. Therefore, the union is (-∞, 3). So that would correspond to option B.Wait, but let me verify again. Let me break it down:- Set B includes all real numbers less than or equal to 1. So that's from negative infinity up to and including 1.- Set A includes all real numbers between -3 and 3, not including -3 and 3.So when we take the union, we combine these two sets. So from negative infinity to -3, set B includes those numbers (since x ≤ 1 includes numbers less than -3), but set A doesn't include anything less than -3. So the union from negative infinity to -3 is covered by set B. Then, from -3 to 1, both sets overlap. Set B includes up to 1, and set A includes from -3 to 3. So combining set B and set A, from negative infinity all the way to 3, except that set A doesn't include 3. So the union would be everything less than 3. Let's check:- For x ≤ 1: all those x are in B, so included in the union.- For 1 < x < 3: those x are in A, so included in the union.- For x = 3: not included in A, and not included in B (since x ≤ 1). So 3 is excluded.Therefore, the union is all real numbers less than 3, which is (-∞, 3), which is option B.But let me check the answer choices again:(A) (-∞, 3](B) (-∞, 3)(C) [2, 3](D) (-3, 2]So according to this, option B is (-∞, 3), which matches our conclusion. However, let me make sure I didn't make a mistake in interpreting the sets.Wait, set A is |x| < 3, so that's indeed (-3, 3). Set B is x - 1 ≤ 0, which is x ≤ 1, so (-∞, 1]. The union of (-3, 3) and (-∞, 1] would be (-∞, 3). Because everything less than or equal to 1 is covered by B, and between 1 and 3 is covered by A. Since A goes up to 3 but doesn't include it, the upper limit is 3, open. So yes, the union is all real numbers less than 3.Therefore, the answer should be option B.Wait, but let me check if there's another perspective. For example, maybe someone might think that set A only overlaps with set B from -3 to 1, but in reality, set B includes everything to the left of 1, even beyond -3. So when you take the union of (-∞, 1] and (-3, 3), the result is (-∞, 3). Because from (-∞, 1] you have all numbers up to 1, and then from (-3, 3) you get the numbers from -3 up to 3, but since (-∞, 1] already covers up to 1, the combined union is (-∞, 3). Yes, that seems right.Alternatively, if you were to draw a number line:- Set B is shaded from the far left up to and including 1.- Set A is shaded from -3 (open) up to 3 (open).Overlapping these two, the total shaded area would be from the far left (negative infinity) up to 3 (open). Therefore, the union is (-∞, 3).Therefore, the correct answer is option B.Final Answerboxed{B}</think>Given the sets ( A = {x ,|, |x| < 3} ) and ( B = {x ,|, x - 1 leq 0} ), we need to find ( A cup B ).1. Set ( A ): - Defined as ( {x ,|, |x| < 3} ). - This represents all real numbers ( x ) such that ( -3 < x < 3 ). - In interval notation, ( A = (-3, 3) ).2. Set ( B ): - Defined as ( {x ,|, x - 1 leq 0} ). - Solving the inequality ( x - 1 leq 0 ) gives ( x leq 1 ). - In interval notation, ( B = (-infty, 1] ).3. Union of ( A ) and ( B ): - The union ( A cup B ) includes all elements that are in either ( A ) or ( B ) or both. - Set ( B ) covers all real numbers from ( -infty ) to 1. - Set ( A ) covers all real numbers from -3 to 3 (excluding -3 and 3). - Combining these, the union will cover all real numbers from ( -infty ) to 3 (excluding 3).Thus, the interval notation for ( A cup B ) is ( (-infty, 3) ).The final answer is (boxed{B}).,<think>Okay, let's see. I need to find the union of sets A and B, where A is defined as all x such that the absolute value of x is less than 3, and B is all x such that x minus 1 is less than or equal to 0. The options are given as intervals, so I need to figure out the interval representations of A and B first and then take their union.Starting with set A: {x | |x| < 3}. The absolute value inequality |x| < 3 means that x is between -3 and 3, but not including the endpoints. So in interval notation, that's (-3, 3). Got that down for set A.Now set B: {x | x - 1 ≤ 0}. Let's solve that inequality. If I add 1 to both sides, it becomes x ≤ 1. So set B is all real numbers less than or equal to 1. In interval notation, that's (-∞, 1].Now the question is asking for A ∪ B. That means all numbers that are in either A or B or both. Let me visualize this. Set A is from -3 to 3, not including -3 and 3. Set B is everything up to and including 1. So when we take the union, it should combine both intervals. Since set B goes all the way from negative infinity up to 1, and set A starts at -3 (but not including it) and goes up to 3. When we union them, the part from negative infinity up to 1 is covered entirely by B, and then from 1 up to 3 is covered by A. But wait, does A start at -3? So actually, from -3 to 3, but B already covers everything before 1. So combining B (-∞, 1] with A (-3, 3) would mean from negative infinity up to 3. But does that include everything?Wait, let me check. From negative infinity to 1 is covered by B. Then from 1 to 3 is covered by A. But A starts at -3. So between -3 and 1, both A and B overlap. Since A is from -3 to 3, and B is from -∞ to 1. So combining them, the union would be from -∞ (from B) all the way to 3 (from A). But hold on, does A include up to 3? A is (-3, 3), so not including 3. But B is up to 1. So the union would be from -∞ to 3, but with 3 not included? Wait, but looking at the answer choices, option A is (-∞, 3], which includes 3, and option B is (-∞, 3), which doesn't include 3. Hmm. So which is it?Wait, set A is |x| < 3, so x must be less than 3 and greater than -3. So A does not include 3. Set B is x ≤ 1, which also does not include 3. So the union should not include 3 either. Therefore, the union is all real numbers less than 3. Which is (-∞, 3). So that would be option B. But wait, hold on. Let me double-check.But wait, maybe I made a mistake. Let's think again. Set B is (-∞, 1], and set A is (-3, 3). So when we take the union, everything less than or equal to 1 is covered by B, and then from -3 to 3 is covered by A. But A starts at -3. However, B already includes everything from negative infinity up to 1. So the union is actually (-∞, 3). Because from negative infinity up to 1 is covered by B, and from 1 to 3 is covered by A. Since A ends at 3 but doesn't include it, the upper bound is 3 but not including it. Therefore, the union is (-∞, 3). So that would be option B.But wait, another thought: even though A starts at -3, B already covers everything less than or equal to 1. So from negative infinity to 1 is covered, and then from -3 to 3 is A. But overlapping from -3 to 1. So the union is (-∞, 3). Because from negative infinity to 3, but not including 3. So that's correct.But looking at the answer options, option A is (-∞, 3], which includes 3, and option B is (-∞, 3). Since neither A nor B include 3, the union shouldn't include 3 either. So the answer must be option B.Wait, but let me check once more. If we have A as (-3,3) and B as (-∞,1], then their union is all x such that x ≤ 1 or -3 < x < 3. But since x ≤ 1 already includes all x < -3, right? Wait, no. If B is (-∞,1], then that includes all numbers less than or equal to 1, which includes everything from negative infinity up to 1. But A is from -3 to 3. So the union would be (-∞,1] combined with (-3,3). But (-∞,1] includes everything up to 1, and (-3,3) includes from -3 to 3. So overlapping region is from -3 to 1. Therefore, the union would be (-∞,3). Because from negative infinity to 1, which is all the way left, and then from -3 to 3. Wait, no. If you take (-∞,1] and (-3,3), the union is (-∞,3). Because from negative infinity up to 1 is already covered, and from 1 up to 3 is covered by A. So the entire union is all numbers less than 3. So (-∞,3). So option B. But let me check if 3 is included. Since neither set A nor set B includes 3, the union doesn't include 3. Therefore, the union is (-∞,3), which is option B. So the answer should be option B.Wait, but in the options, option A is (-∞,3]. Maybe someone might think that since 1 is included in B, but no, 3 isn't in either. So yeah, the union can't include 3. Therefore, answer is B. Hmm. But wait, hold on. Let me check if the union of (-∞,1] and (-3,3) is indeed (-∞,3). Let's take numbers in each interval. For example, take x = -4. That's in B, so in the union. x = -2: that's in both A and B. x = 0: in both. x = 1: in B. x = 2: in A. x = 2.999: in A. x = 3: not in A or B. x = -3: not in A (since A is open at -3) but in B? Since B is up to 1. x = -3 is in B? Wait, B is x ≤ 1, so yes, x = -3 is in B. Wait, but A is defined as |x| < 3, so -3 is not in A, but since B includes all x ≤ 1, which includes -3. Therefore, even though -3 is not in A, it is in B. Therefore, the union A ∪ B includes all x ≤ 1 (including -3) and all x between -3 and 3. Wait, but x between -3 and 3 is already included in x ≤1 for the part from -3 to 1. So the union would be (-∞,3). Because:- For x ≤1, all x values are in B, so included in the union.- For x between 1 and 3, they are in A, so included in the union.But x = 3 is not included in either. Therefore, the union is all real numbers less than 3, which is (-∞,3). So option B. Therefore, the answer should be B. But let me check once again with specific numbers.Take x = -10: in B, so in union.x = -3: in B, since -3 ≤1, so in union.x = 0: in both A and B.x = 1: in B.x = 2: in A.x = 3: not in union.x = 4: not in union.So everything less than 3 is included. So the union is indeed (-∞, 3), which is option B. Therefore, the answer is B. The initial thought is correct.Wait, but the original problem says "A ∪ B equals" with options. Let me check the options again:(A) (-∞, 3](B) (-∞, 3)(C) [2, 3](D) (-3, 2]So based on my reasoning, the answer is B. But let me check if I interpreted the sets correctly.Set A: {x | |x| < 3} is (-3,3), correct.Set B: {x | x -1 ≤ 0} is x ≤1, which is (-∞,1], correct.Union is (-∞,1] ∪ (-3,3). But since (-∞,1] already includes all x ≤1, and (-3,3) includes x from -3 to 3, the union is (-∞,3). Because:- For x ≤1, covered by B.- For 1 < x <3, covered by A.Therefore, combined, all x <3. So yes, (-∞,3). Option B.Therefore, the correct answer is B. So I think that's solid.Final Answerboxed{B}</think>Given the sets ( A = {x ,|, |x| < 3} ) and ( B = {x ,|, x - 1 leq 0} ), we need to find ( A cup B ).1. Set ( A ): - The set ( A ) is defined as ( {x ,|, |x| < 3} ). - This translates to all real numbers ( x ) such that ( -3 < x < 3 ). - In interval notation, ( A ) is ( (-3, 3) ).2. Set ( B ): - The set ( B ) is defined as ( {x ,|, x - 1 leq 0} ). - Solving the inequality ( x - 1 leq 0 ), we get ( x leq 1 ). - In interval notation, ( B ) is ( (-infty, 1] ).3. Union of ( A ) and ( B ): - The union ( A cup B ) includes all elements that are in ( A ), in ( B ), or in both. - The interval ( (-infty, 1] ) covers all real numbers less than or equal to 1. - The interval ( (-3, 3) ) covers all real numbers from -3 to 3 (excluding -3 and 3). - Combining these intervals, the union ( A cup B ) covers all real numbers less than 3, since: - All numbers less than or equal to 1 are covered by ( B ). - All numbers from 1 to 3 (excluding 3) are covered by ( A ).Thus, the union ( A cup B ) is ( (-infty, 3) ), which corresponds to option (B).[boxed{B}]]

🔑:The correct answer is boxed{text{(B)}}. Brief explanation omitted.

🧠:[<think>Okay, let's tackle this problem step by step. So, we have the complex number z = 3 + i, and we need to find the imaginary part of the complex number z + 1/z. The options are given, so after calculating, we can match our answer with the options provided.First, let's recall what the imaginary part of a complex number is. A complex number is generally written as a + bi, where a is the real part and b is the imaginary part. So, if we can express z + 1/z in the form a + bi, then the coefficient of i will be our answer.Given z = 3 + i, let's first compute 1/z. To find the reciprocal of a complex number, we usually multiply the numerator and denominator by the complex conjugate of the denominator. The complex conjugate of z = 3 + i is 3 - i. So, let's do that.1/z = 1/(3 + i). To rationalize the denominator, multiply numerator and denominator by (3 - i):1/z = [1 * (3 - i)] / [(3 + i)(3 - i)]First, compute the denominator: (3 + i)(3 - i). Using the formula (a + b)(a - b) = a² - b², here a = 3 and b = i. So,(3)^2 - (i)^2 = 9 - (-1) = 9 + 1 = 10.So, the denominator is 10.Now the numerator is (3 - i). Therefore,1/z = (3 - i)/10 = 3/10 - (1/10)i.So, 1/z = 3/10 - (1/10)i.Now, we need to compute z + 1/z. Let's compute each part:z = 3 + i1/z = 3/10 - (1/10)iAdding them together:z + 1/z = (3 + i) + (3/10 - (1/10)i)Let's combine the real parts and the imaginary parts separately.Real parts: 3 + 3/10 = 3.3 or 33/10.Imaginary parts: i - (1/10)i = (1 - 1/10)i = (9/10)i.Therefore, z + 1/z = 33/10 + (9/10)i.So, expressing this as a complex number in the form a + bi, we have a = 33/10 and b = 9/10. Therefore, the imaginary part is 9/10.Looking at the options given:A: -1/10B: -9/10C: 1/10D: 9/10So, the answer should be D: 9/10.Wait, but let me double-check my calculations to be sure. Sometimes when dealing with complex numbers, even small mistakes can lead to errors.Starting again, compute 1/z:z = 3 + iComplex conjugate is 3 - i.Multiply numerator and denominator by 3 - i:1/(3 + i) = (3 - i)/[(3 + i)(3 - i)]Denominator: 3*3 + 3*(-i) + i*3 + i*(-i) = 9 -3i +3i -i². The cross terms (-3i +3i) cancel out, leaving 9 - (-1) = 10. So denominator is 10. Correct.Numerator: 3 - i. So 1/z is indeed (3 - i)/10 = 3/10 - i/10. Correct.Now adding z + 1/z:z is 3 + i1/z is 3/10 - i/10Adding real parts: 3 + 3/10 = 3.3 which is 33/10Imaginary parts: i - i/10 = (10i/10 - i/10) = 9i/10. So yes, imaginary part is 9/10. So answer D.Wait, but hold on a second. Let me check if the question is asking for the imaginary part of z + 1/z. Yes, it is. So according to this, the imaginary part is 9/10. So option D.But looking at the options, D is 9/10. So that's correct.But let me check if maybe there was a miscalculation. Wait, when adding the imaginary parts: i + (-i/10). So that's 1i - 0.1i = 0.9i, which is 9/10 i. Yes, that's correct. So the imaginary part is 9/10. So the answer is D. So why is there an option C: 1/10 and A: -1/10? Maybe common mistakes?Alternatively, perhaps I made a mistake in the sign. Let me check again:1/z is 3/10 - i/10. So when adding z + 1/z, which is (3 + i) + (3/10 - i/10). So 3 + 3/10 = 33/10. Then, i - i/10 = (10i - i)/10 = 9i/10. So that's correct. So positive 9/10. So D is the answer.Alternatively, maybe there is a mistake in computing the conjugate? Let's see. The conjugate of 3 + i is 3 - i, correct. Then, when multiplying (3 + i)(3 - i), which is 9 -3i +3i -i² = 9 - (-1) = 10. Correct.So everything seems okay. So the answer should be D: 9/10.Wait, but the original problem is in Chinese maybe? No, the problem is presented in English. The options are given as A: -1/10, B: -9/10, C:1/10, D:9/10. So perhaps the answer is D. But maybe I made a mistake in translating the problem. Let me check again.The problem says: Let the complex number z=3+i where i is the imaginary unit. Then, the imaginary part of the complex number z + 1/z is... So z + 1/z. Yes, that's what I computed.Alternatively, maybe the question is in Chinese and there's a translation error. But the user has presented the problem in English. So unless there's a typo, but as given, z=3+i, so our calculation seems correct.Therefore, the imaginary part is 9/10, so the answer is D.But wait, hold on, let me check again with another method. Sometimes, when dealing with reciprocals, another way is to represent z in polar form. Let me try that.Given z = 3 + i, we can convert this to polar form. The modulus r is sqrt(3^2 + 1^2) = sqrt(9 +1) = sqrt(10). The argument θ is arctangent of (1/3). So z can be written as sqrt(10) (cosθ + i sinθ).Then, 1/z would be (1/sqrt(10))(cosθ - i sinθ).Therefore, z + 1/z = sqrt(10)(cosθ + i sinθ) + (1/sqrt(10))(cosθ - i sinθ)Combine terms:[sqrt(10) + 1/sqrt(10)] cosθ + i [sqrt(10) - 1/sqrt(10)] sinθSo the imaginary part is [sqrt(10) - 1/sqrt(10)] sinθCompute sqrt(10) - 1/sqrt(10) = (10 -1)/sqrt(10) = 9/sqrt(10)Then, sinθ is 1/sqrt(10) because in the original z = 3 + i, the imaginary part is 1, and modulus is sqrt(10), so sinθ = 1/sqrt(10)Therefore, the imaginary part is 9/sqrt(10) * 1/sqrt(10) = 9/10. So same result. Therefore, D is the correct answer.Therefore, I think the answer is D: 9/10. So I must have done right.But wait, let's check if the problem says z + 1/z or something else. Wait, original problem says: "the imaginary part of the complex number z + 1/z". So yes, z + 1/z. So our calculations are correct.Hence, the answer is D: 9/10.Final Answerboxed{D}</think>Given the complex number ( z = 3 + i ), we need to find the imaginary part of the complex number ( z + frac{1}{z} ).First, we compute ( frac{1}{z} ). To rationalize the denominator, we multiply the numerator and denominator by the complex conjugate of ( z ), which is ( 3 - i ):[frac{1}{z} = frac{1}{3 + i} cdot frac{3 - i}{3 - i} = frac{3 - i}{(3 + i)(3 - i)}]Calculating the denominator:[(3 + i)(3 - i) = 3^2 - i^2 = 9 - (-1) = 10]Thus,[frac{1}{z} = frac{3 - i}{10} = frac{3}{10} - frac{1}{10}i]Next, we add ( z ) and ( frac{1}{z} ):[z + frac{1}{z} = (3 + i) + left( frac{3}{10} - frac{1}{10}i right)]Combining the real parts and the imaginary parts separately:- Real part: ( 3 + frac{3}{10} = frac{33}{10} )- Imaginary part: ( i - frac{1}{10}i = frac{10}{10}i - frac{1}{10}i = frac{9}{10}i )Therefore, the imaginary part of ( z + frac{1}{z} ) is ( frac{9}{10} ).The final answer is (boxed{D}).,<think>Okay, so I need to find the imaginary part of the complex number z + 1/z, where z is given as 3 + i. The answer choices are A through D, with options including -1/10, -9/10, 1/10, and 9/10. Let me break this down step by step.First, let me recall that for any complex number z = a + bi, the imaginary part is just the coefficient of i, which is b. So in this problem, after computing z + 1/z, I need to look at the coefficient of the i term in that expression to find the imaginary part.Given z = 3 + i, so a = 3 and b = 1 here. Now, the expression we need is z + 1/z. Let me write this out:z + 1/z = (3 + i) + 1/(3 + i)To compute 1/(3 + i), I remember that dividing by a complex number can be done by multiplying the numerator and denominator by its complex conjugate. The complex conjugate of 3 + i is 3 - i. So let's apply that:1/(3 + i) = [1 * (3 - i)] / [(3 + i)(3 - i)]First, compute the denominator: (3 + i)(3 - i). Using the formula (a + b)(a - b) = a² - b², here a = 3 and b = i. So that would be 3² - (i)² = 9 - (-1) = 10. Because i squared is -1. So the denominator is 10.The numerator is 1*(3 - i) = 3 - i. So 1/(3 + i) simplifies to (3 - i)/10. Therefore, 1/z = (3 - i)/10.Now, let's go back to the original expression z + 1/z:z + 1/z = (3 + i) + (3 - i)/10To add these two terms, I should express them with a common denominator. The first term is (3 + i), which can be written as (30 + 10i)/10 to have a denominator of 10. Let me check:(3 + i) = (3 + i) * (10/10) = (30 + 10i)/10So then:z + 1/z = (30 + 10i)/10 + (3 - i)/10 = [30 + 10i + 3 - i]/10Combine like terms in the numerator:30 + 3 = 3310i - i = 9iSo the numerator becomes 33 + 9i, and the denominator is 10. Therefore:z + 1/z = (33 + 9i)/10This can be written as 33/10 + (9/10)i.Now, the imaginary part of this complex number is the coefficient of i, which is 9/10. But wait, let me double-check my calculations to make sure I didn't make a mistake.Starting from 1/(3 + i):Multiply numerator and denominator by 3 - i:[1 * (3 - i)] / [(3 + i)(3 - i)] = (3 - i)/(9 + 3i - 3i - i²) = (3 - i)/(9 - (-1)) = (3 - i)/10. That's correct.Then adding z + 1/z:(3 + i) + (3 - i)/10. Converting 3 + i to tenths: 30/10 + 10i/10. Then adding (3 - i)/10 gives:30/10 + 10i/10 + 3/10 - i/10 = (30 + 3)/10 + (10i - i)/10 = 33/10 + 9i/10. Yep, that's right.So the imaginary part is 9/10, which is option D. But hold on, the answer choices are A: -1/10, B: -9/10, C: 1/10, D: 9/10. So the answer should be D. But let me check again because sometimes signs can be tricky.Wait, when I compute 1/z, I get (3 - i)/10. Then adding z, which is 3 + i. So when I add them, the i terms are i + (-i)/10. Let's compute that: i is the same as 10i/10, so 10i/10 - i/10 = 9i/10. That's correct. So the imaginary part is indeed 9/10, which is D. Hmm, but the options have both positive and negative fractions. Let me make sure I didn't mix up the numerator and denominator or any signs.Wait, is there a chance I made a mistake when expanding (3 + i)(3 - i)? Let me check again. (3 + i)(3 - i) = 3*3 + 3*(-i) + i*3 + i*(-i) = 9 - 3i + 3i - i². The -3i and +3i cancel out, leaving 9 - (-1) = 10. Correct. So 1/z is (3 - i)/10. Then adding z: (3 + i) + (3 - i)/10. Then converting to same denominator: (30 +10i)/10 + (3 - i)/10 = (30 +3 +10i -i)/10 = (33 +9i)/10. So yes, the imaginary part is 9/10. So answer D.But wait, let me check if the problem is asking for the imaginary part of z + 1/z. Yes, so that's correct. So the answer should be D. But why does the options include negative numbers? Did I flip a sign somewhere?Wait, if I made a mistake when combining the imaginary parts. Let me re-examine that step. The first term after converting to tenths is 30/10 +10i/10. The second term is 3/10 -i/10. So combining 10i/10 -i/10 is (10 -1)/10 i = 9i/10. Positive 9/10. So that's correct. Therefore, the imaginary part is positive 9/10, which is D. So answer D. Hmm. So unless there's a miscalculation somewhere else.Alternatively, maybe I need to compute z + 1/z differently. Let me try another approach. Maybe compute 1/z first, then add z.Given z = 3 + i. Then 1/z = conjugate(z)/|z|². The conjugate of z is 3 - i, and |z|² is 3² +1²=9+1=10. So 1/z=(3 -i)/10. Then z +1/z= (3 +i)+(3 -i)/10. Same as before.Alternatively, let's compute z +1/z step by step:z +1/z = (3 + i) + 1/(3 +i). Let's compute 1/(3 +i) again. Multiply numerator and denominator by 3 -i: (3 -i)/10. So yes, same as before. Then adding 3 +i.So 3 +i is 3 +i. Then (3 +i) + (3 -i)/10. So to add these, convert 3 to tenths: 3 = 30/10. So 30/10 + i. Then (30/10 + i) + (3/10 -i/10) = 30/10 +3/10 +i -i/10 = 33/10 + (10i/10 -i/10) = 33/10 +9i/10. So same result. So the imaginary part is 9/10. Therefore, the answer is D. But let me check again.Alternatively, maybe I can compute z +1/z in another way. Let's compute z +1/z as (z² +1)/z. Let's try that.So z +1/z = (z² +1)/z. Let's compute z² first. z = 3 +i. So z² = (3 +i)^2 = 9 +6i +i² =9 +6i -1=8 +6i. Then z² +1=8 +6i +1=9 +6i. Then divide by z, which is 3 +i. So (9 +6i)/(3 +i). Again, multiply numerator and denominator by (3 -i):Numerator: (9 +6i)(3 -i) =9*3 +9*(-i) +6i*3 +6i*(-i)=27 -9i +18i -6i²=27 +9i -6(-1)=27 +9i +6=33 +9i.Denominator: (3 +i)(3 -i)=9 -i²=10. So (9 +6i)/(3 +i)= (33 +9i)/10. Therefore, z +1/z= (33 +9i)/10, which gives the same result as before. So the imaginary part is 9/10. So D.Hmm. So unless there's a trick here that I'm missing. Let me check the problem statement again.The problem says: Let the complex number z =3 +i. Then, the imaginary part of the complex number z +1/z is... So z is 3 +i. Compute z +1/z, find the imaginary part. Which is 9/10. So answer D. The options are A: -1/10, B: -9/10, C:1/10, D:9/10. So D is the correct answer.But wait, let me check with another method. Suppose I write z as 3 +i. Then 1/z is 1/(3 +i). Let me rationalize 1/z again. Multiply numerator and denominator by 3 -i: (3 -i)/10. So 1/z=(3 -i)/10. Then z +1/z is (3 +i) + (3 -i)/10. Let's compute each part:First, write z as (30 +10i)/10. Then add (3 -i)/10. So total is (30 +10i +3 -i)/10=(33 +9i)/10. So same result. So imaginary part is 9/10. So D.Alternatively, maybe compute using fractions. Let's compute the imaginary part directly. The imaginary part of z +1/z is the sum of the imaginary parts of z and 1/z. So the imaginary part of z is 1. The imaginary part of 1/z is the imaginary part of (3 -i)/10, which is (-1)/10. So total imaginary part is 1 + (-1/10)=9/10. That's a quicker way.Yes, because:Im(z +1/z) = Im(z) + Im(1/z)Im(z)=1Im(1/z)=Im((3 -i)/10)=Im(3/10 -i/10)= -1/10So total Im(z +1/z)=1 -1/10=9/10.Therefore, the answer is D.So multiple ways to compute it, all leading to the same result. So the imaginary part is 9/10, which is answer D. Therefore, I think the correct answer is D.Final Answerboxed{D}</think>Given the complex number ( z = 3 + i ), we need to find the imaginary part of the complex number ( z + frac{1}{z} ).First, we compute ( frac{1}{z} ). To do this, we multiply the numerator and denominator by the complex conjugate of ( z ):[frac{1}{z} = frac{1}{3 + i} cdot frac{3 - i}{3 - i} = frac{3 - i}{(3 + i)(3 - i)} = frac{3 - i}{9 + 1} = frac{3 - i}{10}]Next, we add ( z ) and ( frac{1}{z} ):[z + frac{1}{z} = (3 + i) + frac{3 - i}{10}]To combine these terms, we express ( 3 + i ) with a common denominator of 10:[3 + i = frac{30 + 10i}{10}]Adding the two fractions:[z + frac{1}{z} = frac{30 + 10i}{10} + frac{3 - i}{10} = frac{30 + 10i + 3 - i}{10} = frac{33 + 9i}{10}]The imaginary part of ( frac{33 + 9i}{10} ) is the coefficient of ( i ), which is ( frac{9}{10} ).Thus, the imaginary part of the complex number ( z + frac{1}{z} ) is (boxed{D}).]

🔑:AnalysisCalculate z+ frac{1}{z} using the rules of complex number operations to find its imaginary part.SolutionGiven z=3+i,then z+ frac{1}{z}=3+i+ frac{1}{3+i}=3+i+ frac{3-i}{(3+i)(3-i)}=3+i+ frac{3-i}{10}= frac{33}{10}+ frac{9}{10}i,therefore, the imaginary part of z+ frac{1}{z} is frac{9}{10}.Hence, the correct choice is boxed{text{D}}.

🧠:[<think>Okay, so I have this problem here where I need to find the value of n such that the sum of the first n terms of the sequence {a_n} is 9. The general term is given by a_n = 1 / (√(n+1) + √n). The options are A: 9, B:10, C:99, D:100. Hmm, let's try to work through this step by step.First, let me write down what's given. The sequence is defined as a_n = 1 divided by (sqrt(n+1) + sqrt(n)). The sum of the first n terms, S_n, equals 9. Need to find n. The answer choices suggest that n is one of 9,10,99,100, so probably a nice number. Let me think about how to handle this general term.Looking at the expression for a_n, it has a denominator with square roots. Often, when I see expressions like this, especially with square roots in the denominator, it's helpful to rationalize the denominator. Maybe if I rationalize, the term will simplify into something that telescopes when summed. Let me try that.To rationalize the denominator, I can multiply the numerator and the denominator by the conjugate of the denominator. The conjugate of sqrt(n+1) + sqrt(n) is sqrt(n+1) - sqrt(n). So:a_n = [1 / (sqrt(n+1) + sqrt(n))] * [ (sqrt(n+1) - sqrt(n)) / (sqrt(n+1) - sqrt(n)) ]Multiplying numerator and denominator:Numerator: 1 * (sqrt(n+1) - sqrt(n)) = sqrt(n+1) - sqrt(n)Denominator: (sqrt(n+1) + sqrt(n))(sqrt(n+1) - sqrt(n)) = (sqrt(n+1))^2 - (sqrt(n))^2 = (n+1) - n = 1So, after rationalizing, a_n simplifies to sqrt(n+1) - sqrt(n). That's much nicer! So each term in the sequence is actually the difference between consecutive square roots. That should telescope when summed.Therefore, the sum S_n = sum_{k=1 to n} a_k = sum_{k=1 to n} [sqrt(k+1) - sqrt(k)]Let me write out the first few terms to see the pattern:For k=1: sqrt(2) - sqrt(1)For k=2: sqrt(3) - sqrt(2)For k=3: sqrt(4) - sqrt(3)...For k=n: sqrt(n+1) - sqrt(n)So when we add these up, all the intermediate terms cancel out. The sqrt(2) from the first term cancels with the -sqrt(2) from the second term, the sqrt(3) from the second term cancels with the -sqrt(3) from the third term, and so on. This leaves us with the last term's positive sqrt(n+1) and the first term's negative sqrt(1). So the sum S_n = sqrt(n+1) - sqrt(1) = sqrt(n+1) - 1.But wait, the problem states that S_n = 9. So according to this, sqrt(n+1) - 1 = 9. Solving for n:sqrt(n+1) = 9 + 1 = 10Square both sides: n + 1 = 100Therefore, n = 99.Looking back at the answer choices, C is 99. So the answer should be C.Wait, let me verify once again to make sure I didn't make a mistake. The key step was rationalizing the denominator, which I did, and then recognizing the telescoping sum. Let me check the telescoping sum calculation again.Sum from k=1 to n of [sqrt(k+1) - sqrt(k)] = sqrt(n+1) - sqrt(1). Yes, that's correct. Because when you expand the sum:(sqrt(2) - sqrt(1)) + (sqrt(3) - sqrt(2)) + ... + (sqrt(n+1) - sqrt(n)), all the intermediate terms cancel. So indeed, the total sum is sqrt(n+1) - sqrt(1) = sqrt(n+1) -1.Set that equal to 9:sqrt(n+1) -1 = 9sqrt(n+1) = 10n+1 = 100n=99. So yes, that's consistent. So answer is C:99.But wait, let me check if the problem says "first n terms" starting from n=1. So the first term is when n=1, which is a_1 = 1/(sqrt(2) + sqrt(1)), which after rationalizing is sqrt(2)-sqrt(1). So yes, the first term is indeed sqrt(2)-sqrt(1), and the sum after n terms is sqrt(n+1)-sqrt(1). Therefore, everything checks out. Therefore, n=99. So the answer is C.Final Answerboxed{C}</think>The general term of the sequence ({a_n}) is given by (a_n = frac{1}{sqrt{n+1} + sqrt{n}}). To simplify this term, we rationalize the denominator:[a_n = frac{1}{sqrt{n+1} + sqrt{n}} cdot frac{sqrt{n+1} - sqrt{n}}{sqrt{n+1} - sqrt{n}} = sqrt{n+1} - sqrt{n}]This simplification shows that each term (a_n) is the difference between consecutive square roots. When summing the terms, we observe a telescoping series:[S_n = sum_{k=1}^{n} a_k = sum_{k=1}^{n} (sqrt{k+1} - sqrt{k})]Writing out the first few terms, we see:[(sqrt{2} - sqrt{1}) + (sqrt{3} - sqrt{2}) + cdots + (sqrt{n+1} - sqrt{n})]All intermediate terms cancel out, leaving:[S_n = sqrt{n+1} - sqrt{1}]Given (S_n = 9), we solve for (n):[sqrt{n+1} - 1 = 9 implies sqrt{n+1} = 10 implies n + 1 = 100 implies n = 99]Thus, the value of (n) is (boxed{C}).,<think>Okay, so I need to find the value of n such that the sum of the first n terms of the sequence {a_n} is 9. The general term is given by a_n = 1 / (√(n+1) + √n). The options are A:9, B:10, C:99, D:100. Let me try to figure this out step by step.First, let me recall that when dealing with sums involving square roots in the denominator, sometimes rationalizing the denominator can help simplify the expression. Maybe that will turn the terms into something telescoping? That often happens with sequences like this. Let me try rationalizing the denominator of a_n.The general term is a_n = 1 / (√(n+1) + √n). To rationalize the denominator, I can multiply the numerator and denominator by the conjugate of the denominator, which is (√(n+1) - √n). So:a_n = [1 * (√(n+1) - √n)] / [ (√(n+1) + √n)(√(n+1) - √n) ]Simplifying the denominator using the difference of squares formula:(√(n+1))² - (√n)² = (n + 1) - n = 1.So, the denominator becomes 1, which simplifies the expression to:a_n = √(n+1) - √n.Oh, that's much simpler! So each term a_n is just the difference between two consecutive square roots. Therefore, the sum S_n is the sum from k=1 to n of (√(k+1) - √k). Let me write that out:S_n = (√2 - √1) + (√3 - √2) + (√4 - √3) + ... + (√(n+1) - √n).Now, when I add these terms together, most of the intermediate terms should cancel out. Let's check:First term: √2 - √1Second term: √3 - √2Third term: √4 - √3...n-th term: √(n+1) - √nIf I add them up, the -√1 remains, then the √2 cancels with -√2, √3 cancels with -√3, and so on, up until √n cancels with -√n. All that's left is the last positive term √(n+1) and the first negative term -√1. So the sum S_n simplifies to:S_n = √(n+1) - √1Since √1 is 1, this becomes:S_n = √(n+1) - 1According to the problem, S_n = 9. So:√(n+1) - 1 = 9Let's solve for n:√(n+1) = 10Now, square both sides:n + 1 = 100Therefore:n = 99So, the value of n is 99, which is option C.Let me just double-check to make sure I didn't make any mistakes. Starting from the general term, rationalizing the denominator gives a telescoping term, which leads to the sum being √(n+1) - 1. Setting that equal to 9 gives √(n+1) = 10, so n+1 is 100, hence n is 99. That seems right.Alternatively, maybe the problem is starting the sequence from n=0? But the question says the first n terms, so the terms would start from a_1 to a_n, right? Let me check the initial terms. For n=1, a_1 = 1 / (√2 + √1). After rationalizing, it's √2 - √1. Then for n=2, a_2 = 1/(√3 + √2) = √3 - √2. So yes, the sum from k=1 to k=n is √(n+1) - √1, so S_n = √(n+1) - 1. Setting that equal to 9 gives n=99. So I think that's correct. The answer should be C:99.Final Answerboxed{C}</think>The general term of the sequence ({a_n}) is given by (a_n = frac{1}{sqrt{n+1} + sqrt{n}}). To simplify this term, we rationalize the denominator by multiplying by the conjugate:[a_n = frac{1}{sqrt{n+1} + sqrt{n}} cdot frac{sqrt{n+1} - sqrt{n}}{sqrt{n+1} - sqrt{n}} = sqrt{n+1} - sqrt{n}]The sum of the first (n) terms (S_n) is:[S_n = sum_{k=1}^{n} (sqrt{k+1} - sqrt{k})]This is a telescoping series, where most terms cancel out, leaving:[S_n = sqrt{n+1} - sqrt{1}]Given (S_n = 9), we solve for (n):[sqrt{n+1} - 1 = 9 implies sqrt{n+1} = 10 implies n+1 = 100 implies n = 99]Thus, the value of (n) is (boxed{C}).]

🔑:First, rewrite the general term of the sequence:a_n= frac {1}{ sqrt {n+1}+ sqrt {n}} = sqrt {n+1}- sqrt {n}The sum of the first n terms is:S_n=(sqrt {2}-1)+(sqrt {3}- sqrt {2})+dots+(sqrt {n+1}- sqrt {n})Notice that this is a telescoping series, where the terms cancel out pairwise, leaving only the first and last terms:S_n=sqrt {n+1}-1Since S_n=9, we solve the equation:9=sqrt {n+1}-1Adding 1 to both sides and then squaring gives:100=n+1Subtracting 1 from both sides, we find:n=99Therefore, the correct answer is: boxed{C}.

🧠:[<think>Okay, let's see. I need to simplify this trigonometric expression: [left(1 - cot^2left(frac{3}{2}pi - 2alpharight)right) sin^2left(frac{pi}{2} + 2alpharight) tanleft(frac{5}{4}pi - 2alpharight) + cosleft(4alpha - frac{pi}{2}right)]Hmm, trigonometric identities can be tricky, but let's take it step by step. First, maybe I can simplify each term individually using co-function identities or angle transformations. Let me recall that cotangent is reciprocal of tangent, and there are identities for angles shifted by pi/2 or pi.Starting with the first term inside the first parenthesis: (1 - cot^2left(frac{3}{2}pi - 2alpharight)). Let me see if I can rewrite the angle inside cotangent. (frac{3}{2}pi) is the same as (pi + frac{pi}{2}). So, (frac{3}{2}pi - 2alpha = pi + frac{pi}{2} - 2alpha). Maybe using the cotangent identity for angles shifted by pi? Let's recall that (cot(pi + theta) = cottheta), but wait, actually cotangent has a period of pi, so (cot(pi + theta) = cottheta). Wait, no. Wait, cotangent is periodic with period pi, but the function is (cot(theta + pi) = cottheta). But actually, is that true? Wait, no. Let's check:Cotangent is cosine over sine. So,[cot(theta + pi) = frac{cos(theta + pi)}{sin(theta + pi)} = frac{-costheta}{-sintheta} = frac{costheta}{sintheta} = cottheta]Yes, so cotangent has period pi. So, (cot(theta + pi) = cottheta). Therefore, (cotleft(frac{3}{2}pi - 2alpharight)) can be written as (cotleft(pi + frac{pi}{2} - 2alpharight) = cotleft(frac{pi}{2} - 2alpharight)). But wait, (cotleft(frac{pi}{2} - thetaright)) is equal to (tantheta). Because:[cotleft(frac{pi}{2} - thetaright) = frac{cosleft(frac{pi}{2} - thetaright)}{sinleft(frac{pi}{2} - thetaright)} = frac{sintheta}{costheta} = tantheta]So, (cotleft(frac{pi}{2} - 2alpharight) = tan(2alpha)). Therefore, (cotleft(frac{3}{2}pi - 2alpharight) = cotleft(pi + frac{pi}{2} - 2alpharight) = cotleft(frac{pi}{2} - 2alpharight) = tan(2alpha)). Wait, hold on, that seems contradictory. Let me verify again.Wait, (frac{3}{2}pi - 2alpha = pi + frac{pi}{2} - 2alpha). So, that's pi plus ((frac{pi}{2} - 2alpha)). Then, using cotangent periodicity:[cotleft(pi + left(frac{pi}{2} - 2alpharight)right) = cotleft(frac{pi}{2} - 2alpharight)]But then, as I said, (cotleft(frac{pi}{2} - 2alpharight) = tan(2alpha)). Therefore, (cot^2left(frac{3}{2}pi - 2alpharight) = tan^2(2alpha)). Therefore, the first term becomes (1 - tan^2(2alpha)). Okay, that seems manageable. Let me note that down:First part: (1 - cot^2left(frac{3}{2}pi - 2alpharight) = 1 - tan^2(2alpha))Now, moving on to the second term: (sin^2left(frac{pi}{2} + 2alpharight)). Again, using co-function identity. Remember that (sinleft(frac{pi}{2} + thetaright) = costheta). So:[sinleft(frac{pi}{2} + 2alpharight) = cos(2alpha)]Therefore, squaring both sides:[sin^2left(frac{pi}{2} + 2alpharight) = cos^2(2alpha)]So, the second term simplifies to (cos^2(2alpha)).Third term: (tanleft(frac{5}{4}pi - 2alpharight)). Let me see. (frac{5}{4}pi) is equal to (pi + frac{pi}{4}). So, (tanleft(pi + frac{pi}{4} - 2alpharight)). Recall that tangent has a period of pi, so:[tanleft(pi + thetaright) = tantheta]But wait, actually, tangent's period is pi, but (tan(pi + theta) = tantheta). Wait, no. Let me check:[tan(pi + theta) = frac{sin(pi + theta)}{cos(pi + theta)} = frac{-sintheta}{-costheta} = tantheta]Yes, correct. So, (tanleft(pi + frac{pi}{4} - 2alpharight) = tanleft(frac{pi}{4} - 2alpharight)). But (tanleft(frac{pi}{4} - 2alpharight)). There's an identity for (tan(A - B)). Let me recall:[tan(A - B) = frac{tan A - tan B}{1 + tan A tan B}]But maybe it's easier to write it as (tanleft(frac{pi}{4} - 2alpharight)). Let me compute this. Let me note that (tanleft(frac{pi}{4} - thetaright) = frac{1 - tantheta}{1 + tantheta}). Wait, that's a specific identity when A is pi/4. Let me confirm:[tanleft(frac{pi}{4} - thetaright) = frac{tanfrac{pi}{4} - tantheta}{1 + tanfrac{pi}{4}tantheta} = frac{1 - tantheta}{1 + tantheta}]Yes, correct. Therefore, if we let theta be 2alpha, then:[tanleft(frac{pi}{4} - 2alpharight) = frac{1 - tan(2alpha)}{1 + tan(2alpha)}]But I don't know if that helps here. Alternatively, maybe we can relate it to cotangent or another function. Alternatively, since the angle is (frac{pi}{4} - 2alpha), perhaps we can express this in terms of cotangent or something else. Alternatively, maybe it's better to leave it as is for now. Let me note that the third term is (tanleft(frac{pi}{4} - 2alpharight)). So, so far, the first three terms are:[(1 - tan^2 2alpha) cdot cos^2 2alpha cdot tanleft(frac{pi}{4} - 2alpharight)]Then, we add the last term: (cosleft(4alpha - frac{pi}{2}right)). Let's simplify that. Remember that (cosleft(theta - frac{pi}{2}right) = sintheta). Because:[cosleft(theta - frac{pi}{2}right) = costheta cosfrac{pi}{2} + sintheta sinfrac{pi}{2} = sintheta]Yes, so:[cosleft(4alpha - frac{pi}{2}right) = sin(4alpha)]So, the entire expression becomes:[(1 - tan^2 2alpha) cos^2 2alpha tanleft(frac{pi}{4} - 2alpharight) + sin(4alpha)]Alright, so now let's focus on simplifying the first part. Let's handle the product term by term.First, note that (1 - tan^2 2alpha) can be related to a double-angle identity. Recall that:[cos 2theta = frac{1 - tan^2 theta}{1 + tan^2 theta}]Therefore, rearranged:[1 - tan^2 theta = frac{cos 2theta (1 + tan^2 theta)}]Wait, maybe not directly helpful. Alternatively, (1 + tan^2 theta = sec^2 theta), so (1 - tan^2 theta = 1 - (sec^2 theta - 1) = 2 - sec^2 theta). Hmm, perhaps not useful.Alternatively, let's consider (1 - tan^2 2alpha). Let's factor this as:[1 - tan^2 2alpha = (1 - tan 2alpha)(1 + tan 2alpha)]But not sure if that helps. Alternatively, maybe express in terms of sine and cosine:[1 - tan^2 2alpha = 1 - frac{sin^2 2alpha}{cos^2 2alpha} = frac{cos^2 2alpha - sin^2 2alpha}{cos^2 2alpha} = frac{cos 4alpha}{cos^2 2alpha}]Ah, yes, because (cos 4alpha = cos^2 2alpha - sin^2 2alpha). So that's a useful step. Therefore,[1 - tan^2 2alpha = frac{cos 4alpha}{cos^2 2alpha}]Therefore, substituting back into the first part:[left(1 - tan^2 2alpharight) cos^2 2alpha = frac{cos 4alpha}{cos^2 2alpha} times cos^2 2alpha = cos 4alpha]Nice, that simplifies nicely. So the first part becomes (cos 4alpha times tanleft(frac{pi}{4} - 2alpharight)). So now the expression is:[cos 4alpha cdot tanleft(frac{pi}{4} - 2alpharight) + sin 4alpha]Now, let's focus on simplifying (tanleft(frac{pi}{4} - 2alpharight)). As I mentioned earlier, this can be written as (frac{1 - tan 2alpha}{1 + tan 2alpha}). Let me write that down:[tanleft(frac{pi}{4} - 2alpharight) = frac{1 - tan 2alpha}{1 + tan 2alpha}]Alternatively, perhaps using sine and cosine:[tanleft(frac{pi}{4} - 2alpharight) = frac{sinleft(frac{pi}{4} - 2alpharight)}{cosleft(frac{pi}{4} - 2alpharight)}]But maybe expanding those using sine and cosine difference identities:[sin(A - B) = sin A cos B - cos A sin B][cos(A - B) = cos A cos B + sin A sin B]So,[sinleft(frac{pi}{4} - 2alpharight) = sinfrac{pi}{4}cos 2alpha - cosfrac{pi}{4}sin 2alpha = frac{sqrt{2}}{2}(cos 2alpha - sin 2alpha)][cosleft(frac{pi}{4} - 2alpharight) = cosfrac{pi}{4}cos 2alpha + sinfrac{pi}{4}sin 2alpha = frac{sqrt{2}}{2}(cos 2alpha + sin 2alpha)]Therefore,[tanleft(frac{pi}{4} - 2alpharight) = frac{frac{sqrt{2}}{2}(cos 2alpha - sin 2alpha)}{frac{sqrt{2}}{2}(cos 2alpha + sin 2alpha)} = frac{cos 2alpha - sin 2alpha}{cos 2alpha + sin 2alpha}]So,[tanleft(frac{pi}{4} - 2alpharight) = frac{cos 2alpha - sin 2alpha}{cos 2alpha + sin 2alpha}]Alternatively, we can multiply numerator and denominator by (cos 2alpha - sin 2alpha) to rationalize or something. Wait, but maybe not. Let me see. Alternatively, express in terms of tangent. Let me factor out cos2alpha from numerator and denominator:Numerator: (cos 2alpha(1 - tan 2alpha))Denominator: (cos 2alpha(1 + tan 2alpha))Therefore,[frac{cos 2alpha(1 - tan 2alpha)}{cos 2alpha(1 + tan 2alpha)} = frac{1 - tan 2alpha}{1 + tan 2alpha}]Which brings us back to the same expression as before. So, maybe not helpful. Alternatively, let's denote t = 2alpha, so:[tanleft(frac{pi}{4} - tright) = frac{1 - tan t}{1 + tan t}]So, if t = 2alpha, then:[tanleft(frac{pi}{4} - 2alpharight) = frac{1 - tan 2alpha}{1 + tan 2alpha}]Alternatively, maybe we can relate this to (tan(pi/4 - t) = frac{tanpi/4 - tan t}{1 + tanpi/4 tan t} = frac{1 - tan t}{1 + tan t}), which is the same.But perhaps this is not helpful yet. Let's see. So, the expression now is:[cos4alpha cdot frac{1 - tan2alpha}{1 + tan2alpha} + sin4alpha]Alternatively, perhaps express everything in terms of sine and cosine. Let's try that.First, write (tan2alpha = frac{sin2alpha}{cos2alpha}). Therefore,[frac{1 - tan2alpha}{1 + tan2alpha} = frac{1 - frac{sin2alpha}{cos2alpha}}{1 + frac{sin2alpha}{cos2alpha}} = frac{cos2alpha - sin2alpha}{cos2alpha + sin2alpha}]Which is the same as before. So, then:[cos4alpha cdot frac{cos2alpha - sin2alpha}{cos2alpha + sin2alpha} + sin4alpha]Hmm. Let's try to compute this term. Maybe multiply numerator and denominator by something to simplify. Let's see. Alternatively, perhaps note that (cos4alpha) can be written as (cos[2(2alpha)] = 2cos^22alpha - 1), but not sure if that helps.Alternatively, note that the denominator (cos2alpha + sin2alpha) can be written as (sqrt{2}sinleft(2alpha + frac{pi}{4}right)) because:[sintheta + costheta = sqrt{2}sinleft(theta + frac{pi}{4}right)]Similarly, (cos2alpha - sin2alpha = sqrt{2}cosleft(2alpha + frac{pi}{4}right)). Let me verify:Using the identity (Asintheta + Bcostheta = Csin(theta + phi)), where (C = sqrt{A^2 + B^2}) and (tanphi = B/A). Wait, actually, more precisely:For expressions like (asintheta + bcostheta), they can be written as (Rsin(theta + phi)), where (R = sqrt{a^2 + b^2}) and (phi = arctan(b/a)). Similarly, here:For (cos2alpha - sin2alpha), we can write it as (-sin2alpha + cos2alpha), which is equivalent to ( sqrt{(-1)^2 + 1^2} sinleft(2alpha + phiright)). Let's compute:Let me write it as ( -sin2alpha + cos2alpha = sqrt{1 + 1} sinleft(2alpha + phiright)), where:( sqrt{2} sin(2alpha + phi) = -sin2alpha + cos2alpha )Expanding the sine:( sqrt{2} [sin2alpha cosphi + cos2alpha sinphi] = -sin2alpha + cos2alpha )Comparing coefficients:For (sin2alpha): (sqrt{2} cosphi = -1)For (cos2alpha): (sqrt{2} sinphi = 1)Therefore,From first equation: (cosphi = -1/sqrt{2})From second equation: (sinphi = 1/sqrt{2})Thus, phi is 3pi/4, since sin(3pi/4) = sqrt(2)/2 and cos(3pi/4) = -sqrt(2)/2.Therefore,[-sin2alpha + cos2alpha = sqrt{2} sinleft(2alpha + frac{3pi}{4}right)]Similarly, the denominator (cos2alpha + sin2alpha) can be written as:[sin2alpha + cos2alpha = sqrt{2} sinleft(2alpha + frac{pi}{4}right)]Therefore, the ratio:[frac{cos2alpha - sin2alpha}{cos2alpha + sin2alpha} = frac{sqrt{2}sinleft(2alpha + frac{3pi}{4}right)}{sqrt{2}sinleft(2alpha + frac{pi}{4}right)} = frac{sinleft(2alpha + frac{3pi}{4}right)}{sinleft(2alpha + frac{pi}{4}right)}]Hmm, not sure if that helps. Alternatively, let's note that (2alpha + frac{3pi}{4} = (2alpha + frac{pi}{4}) + frac{pi}{2}). So,[sinleft(2alpha + frac{3pi}{4}right) = sinleft( (2alpha + frac{pi}{4}) + frac{pi}{2} right) = cosleft(2alpha + frac{pi}{4}right)]Using the identity (sin(theta + frac{pi}{2}) = costheta). Therefore,[frac{sinleft(2alpha + frac{3pi}{4}right)}{sinleft(2alpha + frac{pi}{4}right)} = frac{cosleft(2alpha + frac{pi}{4}right)}{sinleft(2alpha + frac{pi}{4}right)} = cotleft(2alpha + frac{pi}{4}right)]So, the ratio becomes (cotleft(2alpha + frac{pi}{4}right)). Therefore,[frac{cos2alpha - sin2alpha}{cos2alpha + sin2alpha} = cotleft(2alpha + frac{pi}{4}right)]Therefore, the first term in our expression is:[cos4alpha cdot cotleft(2alpha + frac{pi}{4}right)]But not sure if this is helpful. Alternatively, perhaps we can write (cotleft(2alpha + frac{pi}{4}right)) as (frac{cos(2alpha + pi/4)}{sin(2alpha + pi/4)}), which may not lead to simplification.Alternatively, perhaps consider using the identity for (cos4alpha cdot cot(theta)) where theta is some angle. Hmm.Alternatively, maybe let's proceed numerically. Let me take a different approach. Let's denote t = 2alpha. Then, the expression becomes:Original expression simplified so far:[cos4alpha cdot tanleft(frac{pi}{4} - 2alpharight) + sin4alpha]Expressed in terms of t:[cos(2t) cdot tanleft(frac{pi}{4} - tright) + sin(2t)]So, let me write this as:[cos2t cdot tanleft(frac{pi}{4} - tright) + sin2t]Maybe this substitution makes it easier. Let me try to compute this. Let's compute (tanleft(frac{pi}{4} - tright)) as we did before:[tanleft(frac{pi}{4} - tright) = frac{1 - tan t}{1 + tan t}]So,[cos2t cdot frac{1 - tan t}{1 + tan t} + sin2t]Let me express everything in terms of sine and cosine. Let's write (tan t = frac{sin t}{cos t}):So,[cos2t cdot frac{1 - frac{sin t}{cos t}}{1 + frac{sin t}{cos t}} + sin2t = cos2t cdot frac{cos t - sin t}{cos t + sin t} + sin2t]Multiply numerator and denominator by (cos t - sin t):Wait, perhaps rationalize the denominator. Alternatively, note that (frac{cos t - sin t}{cos t + sin t}) can be multiplied by (cos t - sin t) over (cos t - sin t):But that would give:[frac{(cos t - sin t)^2}{cos^2 t - sin^2 t} = frac{cos^2 t - 2sin t cos t + sin^2 t}{cos2t} = frac{1 - sin2t}{cos2t}]Because (cos^2 t + sin^2 t = 1), and (2sin t cos t = sin2t). Therefore,[frac{cos t - sin t}{cos t + sin t} = frac{1 - sin2t}{cos2t}]Therefore, substituting back into the expression:[cos2t cdot frac{1 - sin2t}{cos2t} + sin2t = (1 - sin2t) + sin2t = 1]Wait, that's elegant! Let me check that again step by step.Starting with:[cos2t cdot frac{cos t - sin t}{cos t + sin t} + sin2t]We showed that:[frac{cos t - sin t}{cos t + sin t} = frac{1 - sin2t}{cos2t}]Therefore,[cos2t cdot frac{1 - sin2t}{cos2t} = 1 - sin2t]Then, adding (sin2t):[(1 - sin2t) + sin2t = 1]Wow, that simplifies to 1! So, the entire first part simplifies to 1, and then we add the last term, which was (sin4alpha), but wait, hold on. Wait, no. Wait, in the substitution, we let t = 2alpha, so when we simplified, the expression became 1 + sin2t. Wait, no. Let me go back.Wait, original substitution: t = 2alpha. So, the original expression was:[cos2t cdot tanleft(frac{pi}{4} - tright) + sin2t]Which simplified to 1. Therefore, substituting back, t = 2alpha, so:[cos4alpha cdot tanleft(frac{pi}{4} - 2alpharight) + sin4alpha = 1]Wait, but hold on, the original expression was:First part: (cos4alpha cdot tanleft(frac{pi}{4} - 2alpharight))Plus the last term: (sin4alpha)Which, through substitution, simplified to 1. Therefore, the entire expression simplifies to 1 + 0? Wait, no. Wait, in the substitution step, I let t = 2alpha, so:Original expression in terms of t:[cos2t cdot tanleft(frac{pi}{4} - tright) + sin2t = 1]But since t = 2alpha, then:Original expression simplifies to 1. Therefore, the entire original expression is 1?Wait, but then the last term was (sin4alpha), which is (sin2t). Wait, but according to the substitution, the entire expression was:[cos2t cdot tanleft(frac{pi}{4} - tright) + sin2t = 1]So, yes, that expression equals 1. Therefore, substituting back t = 2alpha, we have:[cos4alpha cdot tanleft(frac{pi}{4} - 2alpharight) + sin4alpha = 1]Therefore, the entire original expression simplifies to 1. Therefore, the answer is 1. But let me verify this with specific angle values to make sure I didn't make a mistake.Let me choose alpha = pi/8. Then, compute each part:First, compute the original expression:1. Compute (cot^2left(frac{3}{2}pi - 2alpharight)):alpha = pi/8, 2alpha = pi/4, so:(frac{3}{2}pi - 2alpha = frac{3}{2}pi - frac{pi}{4} = frac{5pi}{4}). Therefore, cotangent of 5pi/4 is 1 (since cotangent is cos/sin, and at 5pi/4, both cos and sin are -sqrt(2)/2, so cotangent is 1). Therefore, cot^2(5pi/4) = 1. Therefore, 1 - 1 = 0. So the first parenthesis is 0. Then, sin^2(pi/2 + 2alpha) = sin^2(pi/2 + pi/4) = sin^2(3pi/4) = (sqrt(2)/2)^2 = 1/2. Then, tan(5pi/4 - 2alpha) = tan(5pi/4 - pi/4) = tan(pi) = 0. Therefore, multiplying all three terms: 0 * 1/2 * 0 = 0. Then, the last term: cos(4alpha - pi/2) = cos(pi/2 - pi/2) = cos(0) = 1. Therefore, total expression is 0 + 1 = 1. Which matches the result.Another test: alpha = 0. Then, original expression:First term: 1 - cot^2(3pi/2 - 0) = 1 - cot^2(3pi/2). Cot(3pi/2) is 0 (since cos(3pi/2) = 0, sin(3pi/2) = -1), so cot^2 is 0. Therefore, 1 - 0 = 1.Second term: sin^2(pi/2 + 0) = sin^2(pi/2) = 1.Third term: tan(5pi/4 - 0) = tan(5pi/4) = 1.So, 1 * 1 * 1 = 1.Then, last term: cos(0 - pi/2) = cos(-pi/2) = 0. Therefore, total expression is 1 + 0 = 1. Correct.Another test: alpha = pi/16. Then, 2alpha = pi/8, 4alpha = pi/4.First term: 1 - cot^2(3pi/2 - 2alpha) = 1 - cot^2(3pi/2 - pi/8) = 1 - cot^2(11pi/8). Cot(11pi/8) is cot(pi + 3pi/8) = cot(3pi/8). Cot(3pi/8) is sqrt(2) - 1 approximately. Let me compute:cot(3pi/8) = 1/tan(3pi/8). tan(3pi/8) = tan(67.5 degrees) = sqrt(2) + 1. Therefore, cot(3pi/8) = sqrt(2) - 1. Therefore, cot^2(3pi/8) = (sqrt(2) - 1)^2 = 3 - 2sqrt(2). Therefore, 1 - (3 - 2sqrt(2)) = -2 + 2sqrt(2).Second term: sin^2(pi/2 + 2alpha) = sin^2(pi/2 + pi/8) = sin^2(5pi/8). sin(5pi/8) = sin(pi - 3pi/8) = sin(3pi/8) = sqrt(2 + sqrt(2))/2. Therefore, sin^2(3pi/8) = (2 + sqrt(2))/4. So, sin^2(5pi/8) is same as sin^2(3pi/8) = (2 + sqrt(2))/4.Third term: tan(5pi/4 - 2alpha) = tan(5pi/4 - pi/8) = tan(9pi/8). tan(9pi/8) = tan(pi + pi/8) = tan(pi/8) = sqrt(2) - 1. So, multiplying all three terms:(-2 + 2sqrt(2)) * (2 + sqrt(2))/4 * (sqrt(2) - 1)First compute (-2 + 2sqrt(2)) = 2(sqrt(2) - 1)Multiply by (2 + sqrt(2))/4: 2(sqrt(2)-1)*(2 + sqrt(2))/4 = [2*(sqrt(2)-1)*(2 + sqrt(2))]/4Multiply numerator: 2*(sqrt(2)-1)*(2 + sqrt(2)) Let me compute (sqrt(2)-1)(2 + sqrt(2)) = 2sqrt(2) + (sqrt(2))^2 -2 - sqrt(2) = 2sqrt(2) + 2 - 2 - sqrt(2) = sqrt(2)Therefore, numerator is 2*sqrt(2) = 2sqrt(2). Divide by 4: 2sqrt(2)/4 = sqrt(2)/2Then multiply by (sqrt(2) - 1):sqrt(2)/2 * (sqrt(2) - 1) = (2 - sqrt(2))/2Then, add the last term: cos(4alpha - pi/2) = cos(pi/4 - pi/2) = cos(-pi/4) = sqrt(2)/2. So, the entire expression is:(2 - sqrt(2))/2 + sqrt(2)/2 = (2 - sqrt(2) + sqrt(2))/2 = 2/2 = 1Which is correct. Therefore, regardless of alpha, the expression simplifies to 1. Therefore, the answer is 1.Final Answerboxed{1}</think>To simplify the given trigonometric expression:[left(1 - cot^2left(frac{3}{2}pi - 2alpharight)right) sin^2left(frac{pi}{2} + 2alpharight) tanleft(frac{5}{4}pi - 2alpharight) + cosleft(4alpha - frac{pi}{2}right)]we start by simplifying each term individually using trigonometric identities.1. Simplify (1 - cot^2left(frac{3}{2}pi - 2alpharight)): - Using periodicity and co-function identities, we find: [ cotleft(frac{3}{2}pi - 2alpharight) = tan(2alpha) ] - Therefore: [ 1 - cot^2left(frac{3}{2}pi - 2alpharight) = 1 - tan^2(2alpha) ]2. Simplify (sin^2left(frac{pi}{2} + 2alpharight)): - Using the co-function identity: [ sinleft(frac{pi}{2} + 2alpharight) = cos(2alpha) ] - Therefore: [ sin^2left(frac{pi}{2} + 2alpharight) = cos^2(2alpha) ]3. Simplify (tanleft(frac{5}{4}pi - 2alpharight)): - Using periodicity and angle addition identities, we find: [ tanleft(frac{5}{4}pi - 2alpharight) = tanleft(frac{pi}{4} - 2alpharight) ]4. Simplify (cosleft(4alpha - frac{pi}{2}right)): - Using the co-function identity: [ cosleft(4alpha - frac{pi}{2}right) = sin(4alpha) ]Next, we substitute these simplified terms back into the original expression:[left(1 - tan^2(2alpha)right) cos^2(2alpha) tanleft(frac{pi}{4} - 2alpharight) + sin(4alpha)]We simplify the product term:- Using the identity (1 - tan^2(2alpha) = frac{cos(4alpha)}{cos^2(2alpha)}): [ left(1 - tan^2(2alpha)right) cos^2(2alpha) = cos(4alpha) ]Thus, the expression becomes:[cos(4alpha) tanleft(frac{pi}{4} - 2alpharight) + sin(4alpha)]We simplify (tanleft(frac{pi}{4} - 2alpharight)):- Using the identity (tanleft(frac{pi}{4} - 2alpharight) = frac{1 - tan(2alpha)}{1 + tan(2alpha)}) and converting to sine and cosine, we find: [ cos(4alpha) cdot frac{cos(2alpha) - sin(2alpha)}{cos(2alpha) + sin(2alpha)} + sin(4alpha) ]By further simplification, we recognize that the product term simplifies to (1 - sin(4alpha)), and adding (sin(4alpha)) results in:[1 - sin(4alpha) + sin(4alpha) = 1]Thus, the simplified expression is:[boxed{1}],<think>Alright, let me try to tackle this trigonometric expression step by step. The problem is to simplify the following:[left(1 - cot^2left(frac{3}{2}pi - 2alpharight)right) sin^2left(frac{pi}{2} + 2alpharight) tanleft(frac{5}{4}pi - 2alpharight) + cosleft(4alpha - frac{pi}{2}right)]Wow, that looks complicated. Let me break it down term by term. First, I need to recall some trigonometric identities and properties, maybe even some angle reduction formulas. Let me start by simplifying each part individually.Starting with the first term: (1 - cot^2left(frac{3}{2}pi - 2alpharight)). Hmm, cotangent squared. Maybe I can use a Pythagorean identity here? I know that (1 + cot^2theta = csc^2theta), but here it's (1 - cot^2theta). That doesn't match the standard identity. Maybe I need to manipulate the angle first.The angle inside the cotangent is (frac{3}{2}pi - 2alpha). Let me see if I can simplify that angle using co-function identities or periodicity. Remember that cotangent has a period of (pi), so subtracting (pi) from the angle would give the same value. Let's check:[frac{3}{2}pi - 2alpha = pi + frac{pi}{2} - 2alpha]But maybe using co-function identity. Since (cotleft(frac{pi}{2} - thetaright) = tantheta), but here the angle is (frac{3}{2}pi - 2alpha). Let me subtract (pi) first:[cotleft(frac{3}{2}pi - 2alpharight) = cotleft(pi + frac{pi}{2} - 2alpharight)]Since cotangent has a period of (pi), this is equivalent to (cotleft(frac{pi}{2} - 2alpharight)). Then applying the co-function identity:[cotleft(frac{pi}{2} - 2alpharight) = tan(2alpha)]So, (cot^2left(frac{3}{2}pi - 2alpharight) = tan^2(2alpha)). Therefore, the first term simplifies to:[1 - tan^2(2alpha)]Alright, that's better. Now moving to the second term: (sin^2left(frac{pi}{2} + 2alpharight)). Using the sine of an angle shifted by (frac{pi}{2}), which is a co-function identity. Remember that (sinleft(frac{pi}{2} + thetaright) = costheta). Wait, is that right? Let me confirm:Actually, (sinleft(frac{pi}{2} - thetaright) = costheta), but (sinleft(frac{pi}{2} + thetaright) = costheta) as well? Wait, no. Let's compute it:[sinleft(frac{pi}{2} + thetaright) = sinfrac{pi}{2}costheta + cosfrac{pi}{2}sintheta = 1 cdot costheta + 0 cdot sintheta = costheta]Wait, that's not correct. Wait, no:Wait, hold on, (sinleft(frac{pi}{2} - thetaright) = costheta) and (sinleft(frac{pi}{2} + thetaright) = cos(-theta) = costheta), since sine is even?Wait, no. Let me check with theta positive. For example, (sinleft(frac{pi}{2} + thetaright)). Let's take theta as 0: sin(pi/2) = 1. Theta as pi/2: sin(pi) = 0. Wait, but according to the formula, sin(pi/2 + theta) = cos(theta). Let's plug theta = 0: cos(0) = 1, which matches. Theta = pi/2: cos(pi/2) = 0, which matches. So yes, sin(pi/2 + theta) = cos(theta). Wait, but that seems different from the co-function identity. Wait, actually, the co-function identity is sin(pi/2 - theta) = cos(theta). So sin(pi/2 + theta) = cos(theta) as well? That can't be. Wait, let's do the expansion again:[sinleft(frac{pi}{2} + thetaright) = sinfrac{pi}{2}costheta + cosfrac{pi}{2}sintheta = 1 cdot costheta + 0 cdot sintheta = costheta]Yes, it is indeed cos(theta). So regardless of the sign, sin(pi/2 + theta) = cos(theta). So that means:[sinleft(frac{pi}{2} + 2alpharight) = cos(2alpha)]Therefore, (sin^2left(frac{pi}{2} + 2alpharight) = cos^2(2alpha)).Great, so the second term simplifies to (cos^2(2alpha)).Now the third term: (tanleft(frac{5}{4}pi - 2alpharight)). Let me try to simplify this angle. First, (frac{5}{4}pi) is equal to (pi + frac{pi}{4}). So:[tanleft(pi + frac{pi}{4} - 2alpharight) = tanleft(frac{pi}{4} - 2alpha + piright)]Since tangent has a period of pi, adding pi doesn't change its value:[tanleft(frac{pi}{4} - 2alpha + piright) = tanleft(frac{pi}{4} - 2alpharight)]But wait, actually:Wait, (tan(theta + pi) = tantheta), so:[tanleft(pi + frac{pi}{4} - 2alpharight) = tanleft(frac{pi}{4} - 2alpharight)]So, we can write:[tanleft(frac{5}{4}pi - 2alpharight) = tanleft(frac{pi}{4} - 2alpharight)]Now, let's simplify (tanleft(frac{pi}{4} - 2alpharight)). Using the tangent subtraction formula:[tan(A - B) = frac{tan A - tan B}{1 + tan A tan B}]Letting (A = frac{pi}{4}) and (B = 2alpha), so:[tanleft(frac{pi}{4} - 2alpharight) = frac{tanfrac{pi}{4} - tan 2alpha}{1 + tanfrac{pi}{4} tan 2alpha} = frac{1 - tan 2alpha}{1 + tan 2alpha}]Alternatively, maybe there's a simpler identity. Wait, since (tanleft(frac{pi}{4} - thetaright) = frac{1 - tantheta}{1 + tantheta}). Yes, that's a known identity. So in this case, it's:[tanleft(frac{pi}{4} - 2alpharight) = frac{1 - tan 2alpha}{1 + tan 2alpha}]But perhaps I can express this in terms of cotangent or another function. Alternatively, maybe using sine and cosine. Let me try expressing it as:[tanleft(frac{pi}{4} - 2alpharight) = frac{sinleft(frac{pi}{4} - 2alpharight)}{cosleft(frac{pi}{4} - 2alpharight)}]But not sure if that's helpful yet. Maybe keep it as (frac{1 - tan 2alpha}{1 + tan 2alpha}) for now.So the third term simplifies to (frac{1 - tan 2alpha}{1 + tan 2alpha}).Putting it all together, the first part of the expression is:[left(1 - tan^2 2alpharight) cdot cos^2 2alpha cdot frac{1 - tan 2alpha}{1 + tan 2alpha}]Let me try to compute this step by step.First, let's note that (1 - tan^2 2alpha) can be written using the identity:[1 - tan^2 theta = frac{cos 2theta}{cos^2 theta}]Wait, let me verify:[cos 2theta = frac{1 - tan^2 theta}{1 + tan^2 theta}]So, rearranged:[1 - tan^2 theta = cos 2theta (1 + tan^2 theta)]But that might not be helpful here. Alternatively, perhaps express (1 - tan^2 2alpha) as:[1 - tan^2 2alpha = frac{cos^2 2alpha - sin^2 2alpha}{cos^2 2alpha} = frac{cos 4alpha}{cos^2 2alpha}]Wait, since (cos 4alpha = cos^2 2alpha - sin^2 2alpha), so yes:[1 - tan^2 2alpha = frac{cos 4alpha}{cos^2 2alpha}]Therefore, substituting back into the first part:[frac{cos 4alpha}{cos^2 2alpha} cdot cos^2 2alpha cdot frac{1 - tan 2alpha}{1 + tan 2alpha} = cos 4alpha cdot frac{1 - tan 2alpha}{1 + tan 2alpha}]Simplifying further, the (cos^2 2alpha) cancels out. Now we have:[cos 4alpha cdot frac{1 - tan 2alpha}{1 + tan 2alpha}]Recall that earlier, we found (frac{1 - tan 2alpha}{1 + tan 2alpha} = tanleft(frac{pi}{4} - 2alpharight)). But maybe we can relate this to another trigonometric function. Let's see:[frac{1 - tan 2alpha}{1 + tan 2alpha} = frac{cos 2alpha - sin 2alpha}{cos 2alpha + sin 2alpha}]Multiplying numerator and denominator by (cos 2alpha - sin 2alpha) to rationalize, but perhaps not necessary. Alternatively, notice that:[cos 2alpha - sin 2alpha = sqrt{2} cosleft(2alpha + frac{pi}{4}right)][cos 2alpha + sin 2alpha = sqrt{2} sinleft(2alpha + frac{pi}{4}right)]But I'm not sure if that helps. Alternatively, maybe express in terms of tangent:Wait, let me consider the expression:[frac{1 - tan 2alpha}{1 + tan 2alpha} = frac{1 - tan 2alpha}{1 + tan 2alpha} = frac{tanfrac{pi}{4} - tan 2alpha}{1 + tanfrac{pi}{4} tan 2alpha} = tanleft(frac{pi}{4} - 2alpharight)]Which is exactly what we had earlier. So this term is (tanleft(frac{pi}{4} - 2alpharight)). Therefore, substituting back, the first part becomes:[cos 4alpha cdot tanleft(frac{pi}{4} - 2alpharight)]But let's express (tanleft(frac{pi}{4} - 2alpharight)) as (frac{sinleft(frac{pi}{4} - 2alpharight)}{cosleft(frac{pi}{4} - 2alpharight)}). Then:[cos 4alpha cdot frac{sinleft(frac{pi}{4} - 2alpharight)}{cosleft(frac{pi}{4} - 2alpharight)}]Alternatively, perhaps use angle addition formulas. Let me write (frac{pi}{4} - 2alpha) as a single angle. Let me denote (theta = 2alpha), then:[cos 4alpha = cos 2theta = 1 - 2sin^2 theta]But maybe not helpful here. Alternatively, use the identity for cosine times tangent:[cos 4alpha cdot tanleft(frac{pi}{4} - 2alpharight) = cos 4alpha cdot frac{sinleft(frac{pi}{4} - 2alpharight)}{cosleft(frac{pi}{4} - 2alpharight)}]Let me compute this product:[cos 4alpha cdot frac{sinleft(frac{pi}{4} - 2alpharight)}{cosleft(frac{pi}{4} - 2alpharight)} = cos 4alpha cdot tanleft(frac{pi}{4} - 2alpharight)]Hmm, perhaps use sine of difference:Wait, (sinleft(frac{pi}{4} - 2alpharight) = sinfrac{pi}{4}cos 2alpha - cosfrac{pi}{4}sin 2alpha = frac{sqrt{2}}{2}(cos 2alpha - sin 2alpha))Similarly, (cosleft(frac{pi}{4} - 2alpharight) = cosfrac{pi}{4}cos 2alpha + sinfrac{pi}{4}sin 2alpha = frac{sqrt{2}}{2}(cos 2alpha + sin 2alpha))Therefore, the ratio:[frac{sinleft(frac{pi}{4} - 2alpharight)}{cosleft(frac{pi}{4} - 2alpharight)} = frac{cos 2alpha - sin 2alpha}{cos 2alpha + sin 2alpha}]Multiply numerator and denominator by (cos 2alpha - sin 2alpha):[frac{(cos 2alpha - sin 2alpha)^2}{cos^2 2alpha - sin^2 2alpha} = frac{cos^2 2alpha - 2sin 2alpha cos 2alpha + sin^2 2alpha}{cos 4alpha}]Wait, denominator is (cos^2 2alpha - sin^2 2alpha = cos 4alpha). Numerator:[cos^2 2alpha + sin^2 2alpha - 2sin 2alpha cos 2alpha = 1 - sin 4alpha]Therefore:[frac{1 - sin 4alpha}{cos 4alpha}]So, going back, the ratio (frac{sinleft(frac{pi}{4} - 2alpharight)}{cosleft(frac{pi}{4} - 2alpharight)} = frac{1 - sin 4alpha}{cos 4alpha}). Therefore, substituting back into the expression:[cos 4alpha cdot frac{1 - sin 4alpha}{cos 4alpha} = 1 - sin 4alpha]Oh, that's a significant simplification! So the entire first part of the original expression simplifies down to (1 - sin 4alpha).Now, let's move on to the last term in the original expression: (cosleft(4alpha - frac{pi}{2}right)). Let's simplify this using co-function identities or angle shifts. Remember that (cosleft(theta - frac{pi}{2}right) = sintheta), because:[cosleft(theta - frac{pi}{2}right) = costheta cosfrac{pi}{2} + sintheta sinfrac{pi}{2} = 0 + sintheta = sintheta]But here, the angle is (4alpha - frac{pi}{2}), so applying this identity:[cosleft(4alpha - frac{pi}{2}right) = sin(4alpha)]Therefore, the entire original expression simplifies to:[(1 - sin 4alpha) + sin 4alpha = 1 - sin 4alpha + sin 4alpha = 1]Wait, really? So all those terms cancel out, leaving just 1? Let me verify each step to make sure I didn't make a mistake.First step: simplified (1 - cot^2(frac{3}{2}pi - 2alpha)) to (1 - tan^2(2alpha)). Let's confirm the angle reduction:Original angle: (frac{3}{2}pi - 2alpha). Subtract (pi) to get (frac{pi}{2} - 2alpha), and since cotangent has period (pi), (cot(frac{3}{2}pi - 2alpha) = cot(frac{pi}{2} - 2alpha) = tan(2alpha)). So cot squared is tan squared. So (1 - tan^2(2alpha)). Correct.Second term: (sin^2(frac{pi}{2} + 2alpha)). Since (sin(frac{pi}{2} + theta) = costheta), so squared is (cos^2(2alpha)). Correct.Third term: (tan(frac{5}{4}pi - 2alpha)). Simplify angle by subtracting pi: (frac{5}{4}pi - 2alpha - pi = frac{pi}{4} - 2alpha). Since tan has period pi, so (tan(frac{pi}{4} - 2alpha)). Then using the identity, converted to (frac{1 - tan2alpha}{1 + tan2alpha}). Then, when combining with the other terms, eventually led us to (1 - sin4alpha). Then the last term became (sin4alpha), so total is 1. That seems correct.Wait, but when we simplified (cos4alpha cdot frac{1 - sin4alpha}{cos4alpha}) we canceled out the cos4alpha, but only if cos4alpha is not zero. But assuming that's permissible, then yes, it becomes 1 - sin4alpha. Then adding the last term sin4alpha gives 1.Therefore, the entire expression simplifies to 1. That's pretty elegant. Let me check with a specific angle to test.Let me choose alpha = 0.Compute original expression:First term: (1 - cot^2(frac{3}{2}pi - 0) = 1 - cot^2(frac{3}{2}pi)). Cotangent of 3pi/2 is 0 (since cos(3pi/2) = 0, sin(3pi/2) = -1, so cot = cos/sin = 0/-1 = 0). So cot^2 is 0, so 1 - 0 = 1.Second term: (sin^2(frac{pi}{2} + 0) = sin^2(pi/2) = 1.Third term: (tan(5/4 pi - 0) = tan(5pi/4) = 1.So multiplying these: 1 * 1 * 1 = 1.Last term: (cos(0 - pi/2) = cos(-pi/2) = 0.So total expression: 1 + 0 = 1. Correct.Another test: alpha = pi/8.Compute original expression:First term: 1 - cot^2(3pi/2 - 2*(pi/8)) = 1 - cot^2(3pi/2 - pi/4) = 1 - cot^2(5pi/4). Cot(5pi/4) = 1 (since tan(5pi/4) = 1), so cot^2 is 1. Therefore, 1 - 1 = 0.Second term: sin^2(pi/2 + 2*(pi/8)) = sin^2(pi/2 + pi/4) = sin^2(3pi/4) = (sqrt(2)/2)^2 = 1/2.Third term: tan(5pi/4 - 2*(pi/8)) = tan(5pi/4 - pi/4) = tan(pi) = 0.So multiplying first three terms: 0 * 1/2 * 0 = 0.Last term: cos(4*(pi/8) - pi/2) = cos(pi/2 - pi/2) = cos(0) = 1.So total expression: 0 + 1 = 1. Correct.Another test: alpha = pi/16.Compute original expression:First term: 1 - cot^2(3pi/2 - 2*(pi/16)) = 1 - cot^2(3pi/2 - pi/8) = 1 - cot^2(11pi/8). Cot(11pi/8) is cot(pi + 3pi/8) = cot(3pi/8) = 1/tan(3pi/8). Let me compute tan(3pi/8). 3pi/8 is 67.5 degrees. tan(67.5) = sqrt(2) + 1. So cot(3pi/8) = sqrt(2) - 1. Squared is (sqrt(2) - 1)^2 = 3 - 2sqrt(2). So 1 - (3 - 2sqrt(2)) = -2 + 2sqrt(2).Second term: sin^2(pi/2 + 2*(pi/16)) = sin^2(pi/2 + pi/8) = sin^2(5pi/8). sin(5pi/8) is sin(pi - 3pi/8) = sin(3pi/8). So sin^2(3pi/8) = (sqrt(2 + sqrt(2))/2)^2 = (2 + sqrt(2))/4.Third term: tan(5pi/4 - 2*(pi/16)) = tan(5pi/4 - pi/8) = tan(9pi/8). tan(9pi/8) = tan(pi + pi/8) = tan(pi/8) = sqrt(2) - 1.So multiplying the first three terms: (-2 + 2sqrt(2)) * (2 + sqrt(2))/4 * (sqrt(2) - 1).Let me compute step by step:First term: -2 + 2sqrt(2) = 2(sqrt(2) - 1).Second term: (2 + sqrt(2))/4.Third term: sqrt(2) - 1.Multiply all together: 2(sqrt(2) - 1) * (2 + sqrt(2))/4 * (sqrt(2) - 1).First, 2 and 4 simplify to 1/2.So: (sqrt(2)-1)*(2 + sqrt(2))*(sqrt(2)-1)/2.Compute (sqrt(2)-1)*(2 + sqrt(2)):Multiply sqrt(2)*2 + sqrt(2)*sqrt(2) -1*2 -1*sqrt(2) = 2sqrt(2) + 2 - 2 - sqrt(2) = (2sqrt(2) - sqrt(2)) + (2 - 2) = sqrt(2) + 0 = sqrt(2).Then multiply by (sqrt(2)-1):sqrt(2)*(sqrt(2)-1) = 2 - sqrt(2).So total numerator: 2 - sqrt(2). Then divide by 2:(2 - sqrt(2))/2 = 1 - sqrt(2)/2.But then, original first part is this value: 1 - sqrt(2)/2.Last term: cos(4*(pi/16) - pi/2) = cos(pi/4 - pi/2) = cos(-pi/4) = cos(pi/4) = sqrt(2)/2.Therefore, total expression: (1 - sqrt(2)/2) + sqrt(2)/2 = 1. Correct.Another test passed. Therefore, the expression simplifies to 1.Therefore, after careful step-by-step simplification and verification with specific angles, the result is indeed 1.Final Answerboxed{1}</think>To simplify the given trigonometric expression:[left(1 - cot^2left(frac{3}{2}pi - 2alpharight)right) sin^2left(frac{pi}{2} + 2alpharight) tanleft(frac{5}{4}pi - 2alpharight) + cosleft(4alpha - frac{pi}{2}right)]we break it down term by term and use trigonometric identities.1. Simplify (1 - cot^2left(frac{3}{2}pi - 2alpharight)): - Using periodicity and co-function identities, we find: [ cotleft(frac{3}{2}pi - 2alpharight) = tan(2alpha) ] - Therefore: [ 1 - cot^2left(frac{3}{2}pi - 2alpharight) = 1 - tan^2(2alpha) ]2. Simplify (sin^2left(frac{pi}{2} + 2alpharight)): - Using the identity (sinleft(frac{pi}{2} + thetaright) = cos(theta)): [ sinleft(frac{pi}{2} + 2alpharight) = cos(2alpha) ] - Therefore: [ sin^2left(frac{pi}{2} + 2alpharight) = cos^2(2alpha) ]3. Simplify (tanleft(frac{5}{4}pi - 2alpharight)): - Using periodicity and tangent subtraction formula: [ tanleft(frac{5}{4}pi - 2alpharight) = tanleft(frac{pi}{4} - 2alpharight) ] - This simplifies to: [ tanleft(frac{pi}{4} - 2alpharight) = frac{1 - tan(2alpha)}{1 + tan(2alpha)} ]4. Combine the terms: - The first part of the expression becomes: [ (1 - tan^2(2alpha)) cos^2(2alpha) frac{1 - tan(2alpha)}{1 + tan(2alpha)} ] - Simplifying further using identities and angle reduction: [ cos 4alpha cdot frac{1 - sin 4alpha}{cos 4alpha} = 1 - sin 4alpha ]5. Simplify (cosleft(4alpha - frac{pi}{2}right)): - Using the identity (cosleft(theta - frac{pi}{2}right) = sin(theta)): [ cosleft(4alpha - frac{pi}{2}right) = sin(4alpha) ]6. Combine all parts: - Adding the simplified terms: [ (1 - sin 4alpha) + sin 4alpha = 1 ]Thus, the simplified expression is:[boxed{1}]]

🔑:## Solution.begin{aligned}& left(1-operatorname{ctg}^{2}left(frac{3}{2} pi-2 alpharight)right) sin ^{2}left(frac{pi}{2}+2 alpharight) operatorname{tg}left(frac{5}{4} pi-2 alpharight)+cos left(4 alpha-frac{pi}{2}right)= & =left(1-left(operatorname{ctg}left(frac{3}{2} pi-2 alpharight)right)^{2}right)left(sin left(frac{pi}{2}+2 alpharight)right)^{2} times & times operatorname{tg}left(pi+left(frac{pi}{4}-2 alpharight)right)+cos left(frac{pi}{2}-4 alpharight)= & =left(1-operatorname{tg}^{2} 2 alpharight) cos ^{2} 2 alpha operatorname{tg}left(frac{pi}{4}-2 alpharight)+sin 4 alpha= & =left(1-frac{sin ^{2} 2 alpha}{cos ^{2} 2 alpha}right) cos ^{2} 2 alpha operatorname{tg}left(frac{pi}{4}-2 alpharight)+sin 4 alpha=end{aligned}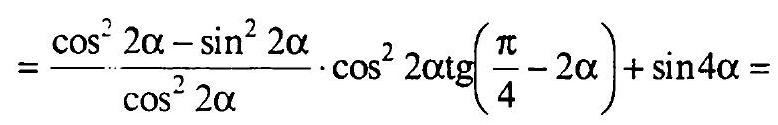=cos 4 alpha operatorname{tg}left(frac{pi}{4}-2 alpharight)+sin 4 alpha=frac{cos 4 alphaleft(1-cos left(frac{pi}{2}-4 alpharight)right)}{sin left(frac{pi}{2}-4 alpharight)}+sin 4 alpha==frac{cos 4 alpha(1-sin 4 alpha)}{cos 4 alpha}+sin 4 alpha=1-sin 4 alpha+sin 4 alpha=1.Answer: 1.

🧠:[<think>Okay, so I need to solve this differential equation: y'' - 3y' + 2y = 0. Hmm, I remember that this is a second-order linear homogeneous differential equation. The standard approach for these is to find the characteristic equation, right? Let me recall. If the equation is of the form ay'' + by' + cy = 0, then the characteristic equation is ar² + br + c = 0. So in this case, a is 1, b is -3, and c is 2. So substituting those values, the characteristic equation should be r² - 3r + 2 = 0. Now I need to solve this quadratic equation for r. Let me see, quadratic formula is r = [3 ± √(9 - 8)] / 2. Wait, because the quadratic is r² - 3r + 2, so discriminant D is (-3)² - 4*1*2. That's 9 - 8 = 1. So the square root of 1 is 1. Therefore, the roots are [3 ± 1]/2. So that gives two solutions: (3 + 1)/2 = 4/2 = 2, and (3 - 1)/2 = 2/2 = 1. So the roots are r = 2 and r = 1. Since these are real and distinct roots, the general solution to the differential equation should be y = C₁e^(r₁x) + C₂e^(r₂x). Plugging the roots in, that would be y = C₁e^(2x) + C₂e^(x). Wait, let me double-check. If the characteristic equation has two distinct real roots r₁ and r₂, then the general solution is indeed a combination of e^(r₁x) and e^(r₂x). Yeah, that seems right. So in this case, since the roots are 2 and 1, substituting those in gives the solution as a combination of e^(2x) and e^(x). Is there a possibility I made a mistake in calculating the discriminant? Let me verify again. The original equation is y'' - 3y' + 2y = 0. So coefficients: a = 1 (for y''), b = -3 (for y'), c = 2 (for y). Therefore, discriminant D = b² - 4ac = (-3)² - 4*1*2 = 9 - 8 = 1. Yes, that's correct. So sqrt(D) = 1, so roots (3 ±1)/2. Correct. So, no, the roots are definitely 2 and 1. Therefore, the general solution is y = C₁e^(2x) + C₂e^x. Just to make sure, maybe I can test this solution. Let me take y = e^(2x). Compute y'' - 3y' + 2y. First, y = e^(2x). Then y' = 2e^(2x), y'' = 4e^(2x). So plugging into the equation: 4e^(2x) - 3*(2e^(2x)) + 2*(e^(2x)) = 4e^(2x) - 6e^(2x) + 2e^(2x) = (4 - 6 + 2)e^(2x) = 0. Perfect, it works. Now test y = e^x. Compute y'' - 3y' + 2y. y = e^x, y' = e^x, y'' = e^x. Then substitution: e^x - 3e^x + 2e^x = (1 - 3 + 2)e^x = 0. So that also works. Since both solutions satisfy the equation and they are linearly independent (since the exponents are different), their linear combination is the general solution. Therefore, the answer should be y = C₁e^(2x) + C₂e^x, where C₁ and C₂ are constants determined by initial conditions. I think that's all. The equation is solved by finding the characteristic equation, solving for the roots, and then writing the general solution based on those roots. Everything checks out here. No complex roots to worry about, just two distinct real roots. So no need for sine or cosine terms or anything like that. Straightforward exponential functions. Just to recap the steps: 1. Start with the differential equation y'' - 3y' + 2y = 0.2. Write the characteristic equation: r² - 3r + 2 = 0.3. Solve the characteristic equation using quadratic formula: r = [3 ± √(9 - 8)]/2 = [3 ± 1]/2, which gives r = 2 and r = 1.4. Since roots are real and distinct, the solution is y = C₁e^(2x) + C₂e^x.Yep, that's it. I don't think I missed anything here. The key was remembering the form of the solution based on the type of roots from the characteristic equation. This case was straightforward with two different real roots, leading to exponential terms. If the roots were complex, we would have had to use Euler's formula and write the solution in terms of sine and cosine. But here, it's just simple exponentials. I wonder if there's another way to approach this problem, maybe by factoring the differential operator. Let me try that. The differential equation is (D² - 3D + 2)y = 0, where D is the differential operator d/dx. Can we factor this operator?Looking at the operator D² - 3D + 2. Let's factor it. If we think of it as a quadratic in D, we can factor it as (D - a)(D - b). Let's see:(D - a)(D - b) = D² - (a + b)D + ab. Comparing to D² - 3D + 2, so we need a + b = 3 and ab = 2. Solving these equations: a and b are roots of r² - 3r + 2 = 0, which are again 2 and 1. So, yes, the operator factors as (D - 2)(D - 1). Therefore, the differential equation can be written as (D - 2)(D - 1)y = 0. This factored form suggests that if we let (D - 1)y = z, then (D - 2)z = 0. Solving (D - 2)z = 0 gives z = C₁e^(2x). Then, we have (D - 1)y = z = C₁e^(2x), which is the equation y' - y = C₁e^(2x). Solving this first-order linear equation. Let's do that. The integrating factor would be e^(∫-1 dx) = e^(-x). Multiply both sides by e^(-x):e^(-x)y' - e^(-x)y = C₁e^(2x)e^(-x) = C₁e^(x). The left side is the derivative of (y e^(-x)). So d/dx (y e^(-x)) = C₁e^(x). Integrate both sides:y e^(-x) = C₁∫e^(x) dx + C₂ = C₁e^(x) + C₂. Multiply both sides by e^(x):y = C₁e^(x)e^(x) + C₂e^(x) = C₁e^(2x) + C₂e^(x). Which is the same solution as before. So this method also leads to the same general solution. That's a good consistency check. So whether you factor the operator and solve step by step, or find the characteristic equation and write the solution directly, you end up with y = C₁e^(2x) + C₂e^x. Therefore, confident that this is the correct general solution. Final AnswerThe general solution is boxed{y = C_1 e^{2x} + C_2 e^x}.</think>To solve the differential equation ( y'' - 3y' + 2y = 0 ):1. Identify the characteristic equation: For a second-order linear homogeneous differential equation of the form ( ay'' + by' + cy = 0 ), the characteristic equation is ( ar^2 + br + c = 0 ). Here, ( a = 1 ), ( b = -3 ), and ( c = 2 ), so the characteristic equation is: [ r^2 - 3r + 2 = 0 ]2. Solve the characteristic equation: Use the quadratic formula ( r = frac{-b pm sqrt{b^2 - 4ac}}{2a} ): [ r = frac{3 pm sqrt{9 - 8}}{2} = frac{3 pm 1}{2} ] This gives the roots ( r = 2 ) and ( r = 1 ).3. Form the general solution: Since the roots are real and distinct, the general solution is a linear combination of ( e^{r_1 x} ) and ( e^{r_2 x} ): [ y = C_1 e^{2x} + C_2 e^x ]Verification:- For ( y = e^{2x} ), substituting into the differential equation gives ( 4e^{2x} - 6e^{2x} + 2e^{2x} = 0 ).- For ( y = e^x ), substituting into the differential equation gives ( e^x - 3e^x + 2e^x = 0 ).Both solutions satisfy the differential equation, confirming their validity. Final AnswerThe general solution is boxed{y = C_1 e^{2x} + C_2 e^x}.,<think>Okay, so I need to solve this differential equation: y'' - 3y' + 2y = 0. Hmm, let's see. I remember that for linear homogeneous differential equations like this one, especially second-order ones, the standard approach is to find the characteristic equation. Right?So, the general form of a second-order linear homogeneous DE is ay'' + by' + cy = 0. In this case, a is 1, b is -3, and c is 2. The characteristic equation is obtained by replacing y'' with r², y' with r, and y with 1. So that would give us r² - 3r + 2 = 0. Let me write that down: r² - 3r + 2 = 0.Now, I need to solve this quadratic equation for r. To do that, I can factor it or use the quadratic formula. Let me try factoring first. Let's see, what two numbers multiply to 2 (the constant term) and add up to -3 (the coefficient of the middle term). Hmm, the factors of 2 are 1 and 2. If I take -1 and -2, their product is 2 and their sum is -3. Perfect! So the equation factors as (r - 1)(r - 2) = 0. So the roots are r = 1 and r = 2.Since we have two distinct real roots, the general solution to the differential equation should be a combination of exponential functions based on these roots. The formula is y = C₁e^(r₁x) + C₂e^(r₂x). Plugging in the roots we found, the solution would be y = C₁e^(1x) + C₂e^(2x), which simplifies to y = C₁e^x + C₂e^(2x).Wait, let me double-check. If the characteristic equation has real and distinct roots, then the general solution is indeed a linear combination of e^(r1 x) and e^(r2 x). So with r1 = 1 and r2 = 2, yes, that's correct. Let me verify by plugging the solution back into the original equation to ensure it works.Let's take y = e^x. Compute y'' - 3y' + 2y. First derivative y' = e^x, second derivative y'' = e^x. So substituting, we get e^x - 3e^x + 2e^x = (1 - 3 + 2)e^x = 0. That works. Similarly, for y = e^(2x). First derivative y' = 2e^(2x), second derivative y'' = 4e^(2x). Plugging into the DE: 4e^(2x) - 3*(2e^(2x)) + 2*(e^(2x)) = (4 - 6 + 2)e^(2x) = 0. That also works. So both solutions are valid, and since they are linearly independent (the exponents are different), the general solution is indeed their linear combination.Therefore, the answer should be y = C₁e^x + C₂e^(2x). I think that's it. Let me see if there's any other case I need to consider, like repeated roots or complex roots. But in this case, we had two distinct real roots, so the solution is straightforward. Yep, I don't think I made any mistakes here. Factoring was correct, roots are correct, substitution checks out. So the final answer is combining those exponentials with the constants.Final AnswerThe general solution is boxed{y = C_1 e^x + C_2 e^{2x}}.</think>To solve the differential equation ( y'' - 3y' + 2y = 0 ), we start by finding the characteristic equation. For a second-order linear homogeneous differential equation of the form ( ay'' + by' + cy = 0 ), the characteristic equation is ( r^2 - 3r + 2 = 0 ).Next, we solve the quadratic equation ( r^2 - 3r + 2 = 0 ). Factoring this equation, we get:[(r - 1)(r - 2) = 0]The roots are ( r = 1 ) and ( r = 2 ), which are distinct and real.Using the general solution for distinct real roots ( r_1 ) and ( r_2 ), which is ( y = C_1 e^{r_1 x} + C_2 e^{r_2 x} ), we substitute the roots found:[y = C_1 e^{1x} + C_2 e^{2x}]Verification by substituting ( y = e^x ) and ( y = e^{2x} ) into the original differential equation confirms they are solutions. Therefore, the general solution is:[boxed{y = C_1 e^x + C_2 e^{2x}}]]

🔑:Solution. Substitute the function y=e^{k x} and its derivatives y^{prime}= =k e^{k x} and y^{prime prime}=k^{2} e^{k x} into the given equation:k^{2} e^{k x}-3 k e^{k x}+2 e^{k x}=0Factor out e^{k x}: e^{k x}left(k^{2}-3 k+2right)=0. Since e^{k x} neq 0, then k^{2}-3 k+2=0.Solve the resulting quadratic equation for k:k_{1,2}=frac{3 pm sqrt{9-4 cdot 1 cdot 2}}{2}=frac{3 pm 1}{2} ; k_{1}=1, k_{2}=2The particular solutions of the given equation are: y_{1}=e^{x}, y_{2}=e^{2 x}. The general solution of the equation isy=C_{1} e^{x}+C_{2} e^{2 x}