🧠:[<think>Okay, so I need to solve this arithmetic sequence problem. Let me first parse the question again.We have an arithmetic sequence {a_n} with a non-zero common difference. That means each term is the previous term plus some constant d, right? So the general formula for the nth term of an arithmetic sequence is a_n = a₁ + (n-1)d, where a₁ is the first term and d is the common difference.The problem states that a₂, a₃, a₉ form a geometric sequence. Hmm, a geometric sequence is one where each term is multiplied by a constant ratio. So if these three terms form a geometric sequence, the ratio between a₃ and a₂ should be the same as the ratio between a₉ and a₃.Mathematically, that means (a₃ / a₂) = (a₉ / a₃). Which implies that (a₃)^2 = a₂ * a₉. That's the key equation I need to use here.Then, we are asked to find the value of (a₂ + a₃ + a₄) divided by (a₄ + a₅ + a₆). The answer choices are given, so after solving, I can check which one it matches.First, let me write down expressions for each of these terms in the arithmetic sequence.Since it's arithmetic, a₂ = a₁ + d, a₃ = a₁ + 2d, a₄ = a₁ + 3d, a₅ = a₁ + 4d, a₆ = a₁ + 5d, and a₉ = a₁ + 8d.Given that a₂, a₃, a₉ form a geometric sequence, so using the geometric sequence condition:(a₃)^2 = a₂ * a₉.Substituting the expressions in terms of a₁ and d:(a₁ + 2d)^2 = (a₁ + d) * (a₁ + 8d)Let me expand both sides:Left side: (a₁)^2 + 4a₁d + 4d²Right side: (a₁ + d)(a₁ + 8d) = a₁² + 8a₁d + a₁d + 8d² = a₁² + 9a₁d + 8d²Set them equal:a₁² + 4a₁d + 4d² = a₁² + 9a₁d + 8d²Subtract a₁² from both sides:4a₁d + 4d² = 9a₁d + 8d²Bring all terms to the left side:4a₁d + 4d² - 9a₁d - 8d² = 0Combine like terms:(4a₁d - 9a₁d) + (4d² - 8d²) = 0(-5a₁d) + (-4d²) = 0Factor out -d:-d(5a₁ + 4d) = 0Since the common difference d is non-zero (given in the problem), we can divide both sides by -d:5a₁ + 4d = 0So, 5a₁ = -4d => a₁ = (-4/5)dOkay, so now we have a relationship between a₁ and d. The first term is (-4/5)d.Now, the next part is to find the value of (a₂ + a₃ + a₄) / (a₄ + a₅ + a₆)Let's compute each term:First, express each term in terms of a₁ and d.a₂ = a₁ + da₃ = a₁ + 2da₄ = a₁ + 3dSimilarly, a₅ = a₁ + 4da₆ = a₁ + 5dSo, numerator: a₂ + a₃ + a₄ = (a₁ + d) + (a₁ + 2d) + (a₁ + 3d) = 3a₁ + 6dDenominator: a₄ + a₅ + a₆ = (a₁ + 3d) + (a₁ + 4d) + (a₁ + 5d) = 3a₁ + 12dSo the ratio is (3a₁ + 6d)/(3a₁ + 12d)We can factor out 3 in numerator and denominator:Numerator: 3(a₁ + 2d)Denominator: 3(a₁ + 4d)Cancel out the 3:(a₁ + 2d)/(a₁ + 4d)But we already found that a₁ = (-4/5)d, so substitute that into the expression:Numerator: (-4/5)d + 2dDenominator: (-4/5)d + 4dLet me compute each part:First, numerator:(-4/5)d + 2d = (-4/5 + 2)d = (-4/5 + 10/5)d = (6/5)dDenominator:(-4/5)d + 4d = (-4/5 + 20/5)d = (16/5)dTherefore, the ratio is (6/5 d) / (16/5 d)The d terms cancel (since d ≠ 0), and 5 cancels:6/16 = 3/8So the value is 3/8, which is option B.Wait, let me check the calculation again to make sure I didn't make a mistake.First, when substituting a₁ = (-4/5)d into numerator:a₁ + 2d = (-4/5)d + 2d = (-4/5 + 10/5)d = 6/5 d. Correct.Denominator: a₁ + 4d = (-4/5)d + 20/5 d = 16/5 d. Correct.Then 6/5 divided by 16/5 is (6/5)*(5/16) = 6/16 = 3/8. Yes, that's correct. So 3/8 is option B. Hmm, but wait the answer choices are A: 1/3, B: 3/8, C:3/7, D:3/5. So B is correct. Wait, but I thought in some similar problems the answer might be different. Let me check the steps again.Starting from the beginning: arithmetic sequence with a2, a3, a9 geometric. So we set up the equation (a3)^2 = a2 * a9. Which led us to 5a1 +4d=0, so a1= -4d/5. Then substituting into numerator and denominator.Wait, let's compute the numerator and denominator again:Numerator is a2 + a3 + a4. Each term:a2 = a1 + d = (-4d/5) + d = (1 - 4/5)d = (1/5)dWait, hold on, this is different. Wait, no, I think I made a mistake here. Wait, if a1 is (-4/5)d, then a2 = a1 + d = (-4/5)d + d = (1/5)d. Similarly, a3 = a1 + 2d = (-4/5)d + 2d = (6/5)d, a4 = a1 + 3d = (-4/5)d + 3d = (11/5)d. Wait, but then a2 + a3 + a4 would be (1/5 + 6/5 + 11/5)d = (18/5)d.Denominator: a4 + a5 + a6. a4 is (11/5)d, a5 = a1 +4d = (-4/5)d +4d = (16/5)d, a6 = a1 +5d = (-4/5)d +5d = (21/5)d. So sum is (11/5 +16/5 +21/5)d = (48/5)d. Then the ratio is (18/5)/(48/5) = 18/48 = 3/8. So same result. So that's correct.But maybe I confused with the initial substitution. Alternatively, perhaps there's a smarter way to do this by expressing everything in terms of a1 and d, then using the ratio. But seems like the steps are correct. Therefore, the answer should be B: 3/8.Final Answerboxed{B}</think>Given an arithmetic sequence ({a_n}) with a non-zero common difference (d), and the terms (a_2), (a_3), (a_9) form a geometric sequence, we need to find the value of (frac{a_2 + a_3 + a_4}{a_4 + a_5 + a_6}).First, we express the terms of the arithmetic sequence in terms of the first term (a_1) and the common difference (d):[a_2 = a_1 + d, quad a_3 = a_1 + 2d, quad a_9 = a_1 + 8d]Since (a_2), (a_3), (a_9) form a geometric sequence, we have:[(a_3)^2 = a_2 cdot a_9]Substituting the expressions for (a_2), (a_3), and (a_9):[(a_1 + 2d)^2 = (a_1 + d)(a_1 + 8d)]Expanding both sides:[a_1^2 + 4a_1d + 4d^2 = a_1^2 + 9a_1d + 8d^2]Simplifying:[4a_1d + 4d^2 = 9a_1d + 8d^2][-5a_1d - 4d^2 = 0][d(5a_1 + 4d) = 0]Since (d neq 0), we get:[5a_1 + 4d = 0 implies a_1 = -frac{4}{5}d]Next, we compute the required terms for the ratio:[a_2 = -frac{4}{5}d + d = frac{1}{5}d][a_3 = -frac{4}{5}d + 2d = frac{6}{5}d][a_4 = -frac{4}{5}d + 3d = frac{11}{5}d][a_5 = -frac{4}{5}d + 4d = frac{16}{5}d][a_6 = -frac{4}{5}d + 5d = frac{21}{5}d]Summing the terms in the numerator and denominator:[a_2 + a_3 + a_4 = frac{1}{5}d + frac{6}{5}d + frac{11}{5}d = frac{18}{5}d][a_4 + a_5 + a_6 = frac{11}{5}d + frac{16}{5}d + frac{21}{5}d = frac{48}{5}d]Thus, the ratio is:[frac{frac{18}{5}d}{frac{48}{5}d} = frac{18}{48} = frac{3}{8}]The final answer is (boxed{B}).,<think>Okay, let me see. The problem says that we have an arithmetic sequence {a_n} with a non-zero common difference. Then, the terms a2, a3, a9 form a geometric sequence. We need to find the value of (a2 + a3 + a4)/(a4 + a5 + a6). The answer choices are A: 1/3, B: 3/8, C: 3/7, D: 3/5. Hmm, alright.First, let's recall what an arithmetic sequence is. An arithmetic sequence has a common difference, let's call it d. So, each term is the previous term plus d. Therefore, the general term a_n can be written as a1 + (n-1)d, where a1 is the first term. Since the common difference is non-zero, d ≠ 0.Now, the problem states that a2, a3, a9 form a geometric sequence. A geometric sequence has a common ratio, so each term is multiplied by a constant ratio r to get the next term. So, in this case, a3 / a2 = a9 / a3. That's the key property of a geometric sequence: the square of the middle term is equal to the product of the first and third terms. So, (a3)^2 = a2 * a9.Let me write that equation down. Let's express each term in terms of a1 and d.First, a2 = a1 + d(2 - 1) = a1 + dSimilarly, a3 = a1 + d(3 - 1) = a1 + 2da9 = a1 + d(9 - 1) = a1 + 8dSo, substituting into the equation (a3)^2 = a2 * a9:(a1 + 2d)^2 = (a1 + d)(a1 + 8d)Let's expand both sides.Left side: (a1)^2 + 4a1d + 4d^2Right side: (a1 + d)(a1 + 8d) = (a1)^2 + 8a1d + a1d + 8d^2 = (a1)^2 + 9a1d + 8d^2So, set left equal to right:(a1)^2 + 4a1d + 4d^2 = (a1)^2 + 9a1d + 8d^2Subtract (a1)^2 from both sides:4a1d + 4d^2 = 9a1d + 8d^2Bring all terms to one side:4a1d + 4d^2 - 9a1d - 8d^2 = 0Combine like terms:(4a1d - 9a1d) + (4d^2 - 8d^2) = 0-5a1d - 4d^2 = 0Factor out -d:-d(5a1 + 4d) = 0Since d ≠ 0 (given that the common difference is non-zero), we can divide both sides by -d:5a1 + 4d = 0Therefore, 5a1 = -4dSo, a1 = (-4/5)dOkay, so now we have a1 in terms of d. That's useful. The problem asks for the ratio (a2 + a3 + a4)/(a4 + a5 + a6). Let's compute each term.First, let's find a2, a3, a4, a5, a6 in terms of a1 and d.But since we know a1 = (-4/5)d, we can express all terms in terms of d.Let me compute each term:a1 = (-4/5)da2 = a1 + d = (-4/5)d + d = (1/5)da3 = a1 + 2d = (-4/5)d + 2d = (6/5)da4 = a1 + 3d = (-4/5)d + 3d = (11/5)da5 = a1 + 4d = (-4/5)d + 4d = (16/5)da6 = a1 + 5d = (-4/5)d + 5d = (21/5)dWait, let me check these calculations step by step.a1 is (-4/5)d.a2 is a1 + d: (-4/5)d + d = (-4/5 + 5/5)d = (1/5)d. Correct.a3: a1 + 2d = (-4/5)d + 2d = (-4/5 + 10/5)d = (6/5)d. Right.a4: a1 + 3d = (-4/5)d + 3d = (-4/5 + 15/5)d = (11/5)d. Correct.a5: a1 + 4d = (-4/5)d + 4d = (-4/5 + 20/5)d = (16/5)d. Yes.a6: a1 + 5d = (-4/5)d + 5d = (-4/5 + 25/5)d = (21/5)d. Correct.So, now the numerator is a2 + a3 + a4 = (1/5)d + (6/5)d + (11/5)d.Adding those up: (1 + 6 + 11)/5 d = 18/5 d.Denominator is a4 + a5 + a6 = (11/5)d + (16/5)d + (21/5)d.Adding those: (11 + 16 + 21)/5 d = 48/5 d.Therefore, the ratio is (18/5 d) / (48/5 d) = (18/5)/(48/5) = 18/48 = 3/8. Hmm, 18 divided by 48 reduces to 3/8. So that's answer B: 3/8.Wait, but let me verify again. Maybe I made a mistake in arithmetic.Numerator: a2 + a3 + a4 = (1/5 + 6/5 + 11/5) d = (1 + 6 + 11)/5 d = 18/5 d. Correct.Denominator: a4 + a5 + a6 = (11/5 + 16/5 + 21/5) d = (11 + 16 +21)/5 d = 48/5 d. 11+16 is 27, 27+21 is 48. Correct.So the ratio is 18/5 d divided by 48/5 d. The d cancels, as does the 5: 18/48 = 3/8. So 3/8 is answer B.But wait, the answer choices include C: 3/7 and D: 3/5. Hmm. Let me check if I made a mistake in the initial setup.Wait, let's check if the geometric sequence condition was applied correctly. The terms a2, a3, a9. So, the geometric sequence is a2, a3, a9. So the ratio between a3 and a2 should be equal to the ratio between a9 and a3. Therefore, (a3)/(a2) = (a9)/(a3). Therefore, (a3)^2 = a2 * a9.Yes, that's correct. Then we substituted the terms in terms of a1 and d. Let's check those substitutions again.a2 = a1 + da3 = a1 + 2da9 = a1 + 8dYes, since a_n = a1 + (n-1)d. So, for n=2: a1 + d, n=3: a1 + 2d, n=9: a1 + 8d. Correct.Then expanding (a1 + 2d)^2 = (a1 + d)(a1 + 8d):Left: (a1)^2 + 4a1d + 4d^2Right: (a1)^2 + 9a1d + 8d^2Subtracting, we get -5a1d -4d^2 = 0. Then factoring gives -d(5a1 + 4d)=0. Since d ≠0, 5a1 +4d=0. So, a1 = -4d/5. Correct.So, substituting back, a1 = -4d/5, so each term can be expressed in terms of d. Then computing a2, a3, a4, a5, a6:a2 = -4d/5 + d = (1/5)da3 = -4d/5 + 2d = (6/5)da4 = -4d/5 + 3d = (11/5)da5 = (16/5)da6 = (21/5)dAdding numerator: 1/5 +6/5 +11/5 =18/5. Denominator:11/5 +16/5 +21/5=48/5. 18/48=3/8. So answer B. Therefore, the correct answer is B: 3/8.But let me check if there's another way this could be approached. Maybe by assuming a particular value for d? For example, let me set d=5, which might make the fractions integers. Let's see.If d=5, then a1 = -4/5 *5 = -4.So, a1 = -4, d=5.Then:a2 = -4 +5=1a3= -4 +10=6a9= -4 + 40=36So, check if a2, a3, a9 form a geometric sequence: 1,6,36. The ratio between 6 and1 is 6, and between 36 and6 is 6. So yes, that's a geometric sequence with ratio 6. So this example works.Then compute the required ratio:Numerator: a2 +a3 +a4 =1 +6 +11=18Wait, a4 is a1 +3d= -4 +15=11. Yes.Denominator: a4 +a5 +a6=11 +16 +21=4818/48=3/8. So 3/8. Therefore, answer B. So this example confirms the result. Therefore, 3/8 is correct. So the answer is B.But just to make sure, let me try another value for d. Let's take d=10.Then a1= -4/5 *10= -8So, a1= -8, d=10.a2= -8 +10=2a3= -8 +20=12a9= -8 +80=72Check geometric sequence: 2,12,72. The ratio is 12/2=6, 72/12=6. So yes, it works.Then numerator: a2 +a3 +a4=2 +12 +22=36. a4 is -8 +30=22.Denominator: a4 +a5 +a6=22 +32 +42=96Ratio 36/96=3/8. Same result.Therefore, the answer is B: 3/8.Final Answerboxed{B}</think>Given an arithmetic sequence ({a_n}) with a non-zero common difference (d), and the terms (a_2), (a_3), (a_9) form a geometric sequence, we need to find the value of (frac{a_2 + a_3 + a_4}{a_4 + a_5 + a_6}).First, we express the terms (a_2), (a_3), and (a_9) in terms of the first term (a_1) and the common difference (d):- (a_2 = a_1 + d)- (a_3 = a_1 + 2d)- (a_9 = a_1 + 8d)Since (a_2), (a_3), (a_9) form a geometric sequence, we have ((a_3)^2 = a_2 cdot a_9). Substituting the expressions, we get:[(a_1 + 2d)^2 = (a_1 + d)(a_1 + 8d)]Expanding both sides:[a_1^2 + 4a_1d + 4d^2 = a_1^2 + 9a_1d + 8d^2]Simplifying, we get:[4a_1d + 4d^2 = 9a_1d + 8d^2][-5a_1d - 4d^2 = 0][-d(5a_1 + 4d) = 0]Since (d neq 0), we have (5a_1 + 4d = 0), leading to (a_1 = -frac{4}{5}d).Next, we express the terms (a_2), (a_3), (a_4), (a_5), and (a_6) in terms of (d):- (a_2 = -frac{4}{5}d + d = frac{1}{5}d)- (a_3 = -frac{4}{5}d + 2d = frac{6}{5}d)- (a_4 = -frac{4}{5}d + 3d = frac{11}{5}d)- (a_5 = -frac{4}{5}d + 4d = frac{16}{5}d)- (a_6 = -frac{4}{5}d + 5d = frac{21}{5}d)Calculating the numerator and denominator:- Numerator: (a_2 + a_3 + a_4 = frac{1}{5}d + frac{6}{5}d + frac{11}{5}d = frac{18}{5}d)- Denominator: (a_4 + a_5 + a_6 = frac{11}{5}d + frac{16}{5}d + frac{21}{5}d = frac{48}{5}d)Thus, the ratio is:[frac{frac{18}{5}d}{frac{48}{5}d} = frac{18}{48} = frac{3}{8}]The value is (boxed{B}).]

🔑:Let the common difference of the arithmetic sequence {an} be d ≠ 0, and a2, a3, a9 form a geometric sequence.∴ a_{ 3 }^{ 2 } = a2 • a9,∴ (a_{1}+2d)^{2} = (a1 + d) (a1 + 8d),a1 = -frac {4}{5}d ≠ 0.Then, frac {a_{2}+a_{3}+a_{4}}{a_{4}+a_{5}+a_{6}} = frac {3a_{1}+6d}{3a_{1}+12d} = - frac {- frac {4}{5}d+2d}{- frac {4}{5}d+4d} = frac {3}{8}.So, the answer is: boxed{text{B}}.Given that the common difference of the arithmetic sequence {an} is d ≠ 0, and a2, a3, a9 form a geometric sequence, we can derive that a_{ 3 }^{ 2 } = a2 • a9, i.e., (a_{1}+2d)^{2} = (a1 + d) (a1 + 8d), which simplifies to a1 = -frac {4}{5}d ≠ 0. Substituting these values into frac {a_{2}+a_{3}+a_{4}}{a_{4}+a_{5}+a_{6}} will yield the answer.This problem tests your understanding of the general terms formula and properties of both arithmetic and geometric sequences, as well as your reasoning and computational skills. It is a moderately difficult problem.

🧠:[<think>Alright, so I have this trigonometry problem here. It says to simplify the expression (sin x + 2 cos x)² + (2 sin x - cos x)² and choose the correct answer from the options given. The options are (A) 0, (B) 3 sin x + cos x, (C) cos 2x, (D) 1, and (E) 5. Hmm, okay. Let me think about how to approach this.First, I remember that when you have an expression squared like (a + b)², you can expand it using the formula a² + 2ab + b². Similarly, (a - b)² would be a² - 2ab + b². So maybe I should start by expanding both of these squared terms and then combining like terms. Let me try that step by step.Starting with the first part: (sin x + 2 cos x)². Let's expand this. Using the formula (a + b)² = a² + 2ab + b², where a is sin x and b is 2 cos x. So, substituting in, we get:sin²x + 2*(sin x)*(2 cos x) + (2 cos x)².Calculating each term:First term: sin²x.Second term: 2*(sin x)*(2 cos x) = 4 sin x cos x.Third term: (2 cos x)² = 4 cos²x.So the expansion of the first part is sin²x + 4 sin x cos x + 4 cos²x.Now, moving on to the second part: (2 sin x - cos x)². Again, using the formula (a - b)² = a² - 2ab + b², where a is 2 sin x and b is cos x.So, expanding this:(2 sin x)² - 2*(2 sin x)*(cos x) + (cos x)².Calculating each term:First term: (2 sin x)² = 4 sin²x.Second term: -2*(2 sin x)*(cos x) = -4 sin x cos x.Third term: (cos x)² = cos²x.So the expansion of the second part is 4 sin²x - 4 sin x cos x + cos²x.Now, the original expression is the sum of these two expanded parts. So, let's add them together:First expansion: sin²x + 4 sin x cos x + 4 cos²xSecond expansion: 4 sin²x - 4 sin x cos x + cos²xAdding term by term:sin²x + 4 sin²x = 5 sin²x4 sin x cos x - 4 sin x cos x = 0 (they cancel out)4 cos²x + cos²x = 5 cos²xSo, putting it all together, we get 5 sin²x + 5 cos²x.Hmm, that simplifies to 5(sin²x + cos²x). Wait, since sin²x + cos²x = 1, right? That's one of the fundamental Pythagorean identities. So this simplifies to 5*1 = 5.Therefore, the entire expression simplifies to 5, which is option E. Let me double-check my steps to make sure I didn't make a mistake.First expansion:- (sin x + 2 cos x)²: sin²x + 4 sin x cos x + 4 cos²x. Correct.Second expansion:- (2 sin x - cos x)²: 4 sin²x - 4 sin x cos x + cos²x. Correct.Adding them:sin²x + 4 sin x cos x + 4 cos²x + 4 sin²x - 4 sin x cos x + cos²xCombining like terms:sin²x + 4 sin²x = 5 sin²x4 sin x cos x - 4 sin x cos x = 04 cos²x + cos²x = 5 cos²xTotal: 5 sin²x + 5 cos²x = 5(sin²x + cos²x) = 5*1 = 5. Yep, that seems right.Looking at the answer options, E is 5, so that's the correct answer. Let me just check the other options to make sure none of them could be equivalent, but 5 is a constant, and none of the other options (except maybe 1) are constants. Option D is 1, but we got 5, so D is incorrect. The others are functions of x or 0, so they don't apply here. Therefore, E is the answer.Final Answerboxed{E}</think>To simplify the expression ((sin x + 2 cos x)^2 + (2 sin x - cos x)^2), we start by expanding each term separately.First, expanding ((sin x + 2 cos x)^2):[(sin x + 2 cos x)^2 = sin^2 x + 2 cdot sin x cdot 2 cos x + (2 cos x)^2 = sin^2 x + 4 sin x cos x + 4 cos^2 x]Next, expanding ((2 sin x - cos x)^2):[(2 sin x - cos x)^2 = (2 sin x)^2 - 2 cdot 2 sin x cdot cos x + cos^2 x = 4 sin^2 x - 4 sin x cos x + cos^2 x]Adding the two expanded expressions together:[(sin^2 x + 4 sin x cos x + 4 cos^2 x) + (4 sin^2 x - 4 sin x cos x + cos^2 x)]Combining like terms:[sin^2 x + 4 sin^2 x + 4 cos^2 x + cos^2 x + 4 sin x cos x - 4 sin x cos x]Simplifying each term:[5 sin^2 x + 5 cos^2 x]Using the Pythagorean identity (sin^2 x + cos^2 x = 1):[5 (sin^2 x + cos^2 x) = 5 cdot 1 = 5]Thus, the simplified expression is (boxed{E}).,<think>Okay, let me try to figure out this problem. The question is asking to simplify the expression ((sin x + 2 cos x)^2 + (2 sin x - cos x)^2) and choose the correct answer from the given options. The options are A through E, with E being 5. Hmm, let's break it down step by step.First, I know that expanding squared terms in algebra usually involves using the formula ((a + b)^2 = a^2 + 2ab + b^2) or ((a - b)^2 = a^2 - 2ab + b^2). So maybe I can apply that here.Let me start with the first part: ((sin x + 2 cos x)^2). If I let (a = sin x) and (b = 2 cos x), then according to the formula, this should expand to (a^2 + 2ab + b^2). Let's compute each term:- (a^2 = (sin x)^2 = sin^2 x)- (2ab = 2 times sin x times 2 cos x = 4 sin x cos x)- (b^2 = (2 cos x)^2 = 4 cos^2 x)So, expanding the first part gives me (sin^2 x + 4 sin x cos x + 4 cos^2 x).Now, moving on to the second part: ((2 sin x - cos x)^2). Here, (a = 2 sin x) and (b = cos x). Since it's a subtraction, the formula becomes (a^2 - 2ab + b^2). Let's calculate each term:- (a^2 = (2 sin x)^2 = 4 sin^2 x)- (2ab = 2 times 2 sin x times cos x = 4 sin x cos x)- (b^2 = (cos x)^2 = cos^2 x)But wait, since it's minus, the middle term becomes negative. So, expanding this gives (4 sin^2 x - 4 sin x cos x + cos^2 x).Now, let's add the two expanded parts together:First part: (sin^2 x + 4 sin x cos x + 4 cos^2 x)Second part: (4 sin^2 x - 4 sin x cos x + cos^2 x)Adding them:- (sin^2 x + 4 sin x cos x + 4 cos^2 x + 4 sin^2 x - 4 sin x cos x + cos^2 x)Let me combine like terms:1. Terms with (sin^2 x): 1 (sin^2 x) + 4 (sin^2 x) = 5 (sin^2 x)2. Terms with (sin x cos x): 4 (sin x cos x) - 4 (sin x cos x) = 03. Terms with (cos^2 x): 4 (cos^2 x) + 1 (cos^2 x) = 5 (cos^2 x)So, after combining, the expression simplifies to (5 sin^2 x + 5 cos^2 x).Hmm, I notice both terms have a factor of 5. Let me factor that out:5((sin^2 x + cos^2 x))But wait, I remember that one of the fundamental trigonometric identities is (sin^2 x + cos^2 x = 1). So substituting that in:5(1) = 5Therefore, the entire expression simplifies to 5. Looking back at the options, E is 5. So the answer must be E.But let me double-check my steps to make sure I didn't make a mistake. It's easy to mess up signs or coefficients when expanding squares.First expansion: ((sin x + 2 cos x)^2)- (sin^2 x + 4 sin x cos x + 4 cos^2 x) → Correct.Second expansion: ((2 sin x - cos x)^2)- (4 sin^2 x - 4 sin x cos x + cos^2 x) → Correct.Adding them together:5 (sin^2 x) + 0 (sin x cos x) + 5 (cos^2 x) → Correct.Factor out 5: 5((sin^2 x + cos^2 x)) = 5*1 = 5. Yep, that checks out. So I think E is the correct answer.I wonder if there's a different approach, maybe using some other identities or recognizing the expression as the sum of squares which relates to the magnitude of a vector? Like if you consider ((sin x + 2 cos x)) and ((2 sin x - cos x)) as components of a vector, then the expression is the magnitude squared, which would be the sum of the squares. But maybe that's overcomplicating. Anyway, my initial approach worked, so I feel confident that E is correct.Final Answerboxed{E}</think>To simplify the expression ((sin x + 2 cos x)^2 + (2 sin x - cos x)^2), we start by expanding each term separately.First, expanding ((sin x + 2 cos x)^2):[(sin x + 2 cos x)^2 = sin^2 x + 4 sin x cos x + 4 cos^2 x]Next, expanding ((2 sin x - cos x)^2):[(2 sin x - cos x)^2 = 4 sin^2 x - 4 sin x cos x + cos^2 x]Adding these two expanded expressions together:[sin^2 x + 4 sin x cos x + 4 cos^2 x + 4 sin^2 x - 4 sin x cos x + cos^2 x]Combining like terms:- Terms with (sin^2 x): (1 sin^2 x + 4 sin^2 x = 5 sin^2 x)- Terms with (sin x cos x): (4 sin x cos x - 4 sin x cos x = 0)- Terms with (cos^2 x): (4 cos^2 x + 1 cos^2 x = 5 cos^2 x)This simplifies to:[5 sin^2 x + 5 cos^2 x]Factoring out the common factor of 5:[5 (sin^2 x + cos^2 x)]Using the Pythagorean identity (sin^2 x + cos^2 x = 1):[5 times 1 = 5]Thus, the simplified expression is (boxed{E}).]

🔑:A5. In the expression, we remove the parentheses and get 5 sin ^{2} x+5 cos ^{2} x=5left(sin ^{2} x+cos ^{2} xright)=5 cdot 1=5.

🧠:[<think>Okay, let's see. So the problem is about Xiaoxia and Xiaoming's savings. Initially, Xiaoxia has 52, and Xiaoming has 70. Then each month, Xiaoxia saves 15 and Xiaoming saves 12. We need to figure out after how many months, n, Xiaoxia's savings will be more than Xiaoming's. And the question is asking which inequality represents that situation. The options are A, B, C, D with different combinations.First, let me break it down. Let's think about what each person's savings will be after n months. For Xiaoxia, she starts with 52 and adds 15 each month. So after n months, her total savings would be the original 52 plus 15 times the number of months, which is 52 + 15n. Similarly, Xiaoming starts with 70 and adds 12 each month, so his total savings would be 70 + 12n.The problem states that we need to find when Xiaoxia's savings exceed Xiaoming's. That means we want the time when Xiaoxia's total is greater than Xiaoming's total. So we set up the inequality:Xiaoxia's savings > Xiaoming's savingsWhich translates to:52 + 15n > 70 + 12nLooking at the options, A is exactly that: 52 +15n >70 +12n. So option A should be the correct answer.Wait, let me double-check. Maybe I mixed up the amounts? Let me confirm again. Original savings: Xiaoxia has 52, saves 15 per month. Xiaoming has 70, saves 12 per month. So after n months, Xiaoxia has 52 +15n, Xiaoming has 70 +12n. The inequality when Xiaoxia's exceeds is 52 +15n >70 +12n. Yes, that's what option A says. So the answer is A.Alternatively, maybe someone could get confused and reverse the coefficients or the initial amounts, but according to the problem statement, it's clear. Let me check the options again.Option B is 52 +15n <70 +12n, which would be the opposite, so that's not right. Option C is 52 +12n >70 +15n, which swaps the monthly savings, so that's incorrect. Option D is 52 +12n <70 +15n, which also swaps the monthly rates. So definitely, A is correct.I think that's solid. So the answer is A.Final Answerboxed{A}</think>Xiaoxia originally has 52 in savings and saves 15 each month, while Xiaoming originally has 70 in savings and saves 12 each month. We need to determine the inequality that represents when Xiaoxia's savings exceed Xiaoming's after ( n ) months.Xiaoxia's savings after ( n ) months can be expressed as:[ 52 + 15n ]Xiaoming's savings after ( n ) months can be expressed as:[ 70 + 12n ]We need to find the inequality where Xiaoxia's savings exceed Xiaoming's:[ 52 + 15n > 70 + 12n ]This corresponds to option A. The other options either reverse the inequality sign or swap the monthly savings amounts, which is incorrect.Thus, the correct answer is:[boxed{A}],<think>Okay, let's see. The problem is about Xiaoxia and Xiaoming's savings. I need to figure out after how many months Xiaoxia's savings will exceed Xiaoming's. The question gives me their initial savings amounts and how much they save each month. Then it asks which inequality represents the situation where Xiaoxia's savings are greater than Xiaoming's after n months. The options are A to D.First, let's parse the information. Xiaoxia starts with 52, and each month she saves 15. So after n months, her total savings would be her original amount plus 15 times the number of months. That would be 52 + 15n. Similarly, Xiaoming starts with 70 and saves 12 each month, so his total after n months is 70 + 12n. The problem wants to know when Xiaoxia's savings exceed Xiaoming's, so we need to set up an inequality where her total is greater than his. That would be 52 + 15n > 70 + 12n. Let me check the options. Option A is exactly that: 52 +15n >70 +12n. So that's probably the answer. But wait, let me make sure I didn't mix up the people or the numbers.Let me double-check. The problem says Xiaoxia originally had 52 and saves 15 each month. So yes, 52 +15n. Xiaoming had 70 and saves 12, so 70 +12n. The question is when Xiaoxia's savings exceed Xiaoming's. So indeed, 52 +15n >70 +12n. That's option A. The other options: B is the reverse, so that would be Xiaoxia's savings being less, which isn't what we want. C and D have the savings per month swapped, 12n for Xiaoxia and 15n for Xiaoming, which isn't correct based on the problem statement. So the answer must be A.But let me think again just to be thorough. Maybe there's a trick here. The problem says "starting from this month," so the first month they add their pocket money. So if n is 0, Xiaoxia has 52, Xiaoming has 70. After 1 month, Xiaoxia would have 52 +15 =67, Xiaoming 70 +12=82. Still Xiaoming has more. After 2 months: 52 +30=82, Xiaoming 70 +24=94. Still Xiaoming. After 3 months: 52 +45=97, Xiaoming 70 +36=106. Still Xiaoming. Wait, maybe after 4 months? Let's see: 52 +60=112, Xiaoming 70 +48=118. Hmm, still Xiaoming. Wait, maybe after 5 months: Xiaoxia:52 +75=127, Xiaoming:70 +60=130. Still Xiaoming. Wait, when does Xiaoxia overtake? Let's compute.Set 52 +15n >70 +12n.Subtract 12n both sides: 52 +3n >70Subtract 52: 3n >18Divide by 3: n >6So after 6 months, n=6: Xiaoxia has 52 +90=142, Xiaoming has 70 +72=142. Equal. Then n=7: Xiaoxia 52 +105=157, Xiaoming 70 +84=154. So at n=7, Xiaoxia's savings exceed. So the inequality would hold when n >6. So the inequality is 52 +15n >70 +12n, which is option A. So that seems correct.The answer should be A. Let me check the options again to make sure I didn't transpose A and B. The options are:A: 52+15n >70+12nB: 52+15n <70+12nSo yes, A is correct. So I think the answer is A.Final Answerboxed{A}</think>Xiaoxia originally has 52 and saves 15 each month, while Xiaoming originally has 70 and saves 12 each month. We need to determine the inequality that represents when Xiaoxia's savings exceed Xiaoming's after ( n ) months.1. Savings Calculation: - Xiaoxia's savings after ( n ) months: ( 52 + 15n ) - Xiaoming's savings after ( n ) months: ( 70 + 12n )2. Setting up the Inequality: - We need to find when Xiaoxia's savings exceed Xiaoming's: ( 52 + 15n > 70 + 12n )3. Verification: - Subtract ( 12n ) from both sides: ( 52 + 3n > 70 ) - Subtract 52 from both sides: ( 3n > 18 ) - Divide by 3: ( n > 6 )This confirms that after 6 months, Xiaoxia's savings will exceed Xiaoming's. The correct inequality is ( 52 + 15n > 70 + 12n ), which corresponds to option A.[boxed{A}]]

🔑:To solve this problem, we start with the information given:- Xiaoxia originally has 52 and saves 15 each month.- Xiaoming originally has 70 and saves 12 each month.We are asked to find the inequality that represents the condition where Xiaoxia's savings exceed Xiaoming's after n months. Given that Xiaoxia starts with 52 and saves 15 each month, her savings after n months can be represented as 52 + 15n. Similarly, Xiaoming starts with 70 and saves 12 each month, so his savings after n months can be represented as 70 + 12n.To find when Xiaoxia's savings exceed Xiaoming's, we set up the inequality:[52 + 15n > 70 + 12n]This inequality correctly represents the condition where Xiaoxia's savings are greater than Xiaoming's after n months.Therefore, the correct answer is boxed{A}.

🧠:[<think>Alright, so the problem is asking how many four-digit numbers can be formed where the sum of their digits is 3. And also to list these numbers. Hmm, okay. Let's break this down step by step.First, a four-digit number. That means the number has to be between 1000 and 9999, right? So the first digit can't be zero. The other three digits can be from 0 to 9, but the sum of all four digits must be 3. So we need to find all combinations of four digits (with the first digit at least 1) that add up to 3. Then, for each combination, figure out how many different numbers can be formed by arranging the digits, considering that some digits might repeat.Wait, but actually, since the sum is 3, and digits are non-negative integers, we can model this as a stars and bars problem. The stars and bars theorem is used to find the number of ways to distribute indistinguishable objects (in this case, the "sum" of 3) into distinguishable bins (the four digits). However, there's a constraint here: the first digit (thousands place) must be at least 1, and the others can be zero or more. So we need to adjust for that.Let me recall the stars and bars formula. For the equation x1 + x2 + x3 + x4 = 3, where xi ≥ 0, the number of non-negative integer solutions is C(3 + 4 - 1, 4 - 1) = C(6,3) = 20. But since the first digit must be at least 1, we can adjust by setting x1' = x1 - 1, so that x1' ≥ 0. Then the equation becomes x1' + x2 + x3 + x4 = 2. The number of solutions here is C(2 + 4 - 1, 4 - 1) = C(5,3) = 10. So there are 10 four-digit numbers where the digits sum to 3? Wait, but hold on. That gives the number of solutions, but each solution corresponds to a different combination of digits. However, some combinations might have digits that are the same, which would affect the number of unique permutations. Wait, no. Wait, the problem is asking for four-digit numbers, so each solution is a unique combination, but different permutations of the same digits would count as different numbers. Except when there are leading zeros, but since we already fixed the first digit to be at least 1, all permutations would result in valid four-digit numbers. But some of these combinations might have repeated digits, so when we permute them, the number of unique numbers would be less than 4!.Wait, perhaps I need to clarify. The stars and bars count gives the number of ordered solutions where digits can repeat. But in reality, the numbers are formed by arranging the digits, so if there are duplicate digits, the number of unique permutations is less. Wait, no. Wait, stars and bars counts the number of solutions where order matters? Wait, no. Wait, the stars and bars formula counts the number of unordered solutions. So for example, if we have x1, x2, x3, x4 digits, each combination is a multiset. Then, when we convert that into four-digit numbers, we need to consider the number of distinct permutations of each multiset.Therefore, the correct approach is first to find all the possible combinations of four digits (with the first digit at least 1) that sum to 3, then for each combination, calculate the number of unique four-digit numbers that can be formed by permuting those digits. Then sum all those up.Okay, let's start by listing all possible digit combinations where the sum is 3 and the first digit is at least 1. Let's denote the digits as thousands, hundreds, tens, and units places: d1, d2, d3, d4, with d1 ≥ 1 and d1 + d2 + d3 + d4 = 3.Since d1 is at least 1, let's set d1 = 1, 2, or 3 (since the total sum is 3, and d1 can't exceed 3). Let's consider each case:Case 1: d1 = 1. Then the remaining digits sum to 2: d2 + d3 + d4 = 2. The number of non-negative integer solutions here is C(2 + 3 - 1, 3 - 1) = C(4,2) = 6. But each solution here is a combination of digits for d2, d3, d4. However, when considering permutations, if there are duplicate digits, the number of unique permutations decreases.But actually, in this case, the digits can be 0s and 1s and 2s. Let's list all possible combinations for d2, d3, d4:- 2,0,0: sum is 2- 1,1,0: sum is 2- 1,0,1: same as above- 0,2,0: same as first- 0,0,2: same as first- 0,1,1: same as second- etc. But in terms of unique multisets, there are two types:Either two 0s and one 2, or two 1s and one 0.So the unique combinations are [2,0,0] and [1,1,0].For each of these, the number of unique permutations is:For [2,0,0]: three digits where two are the same (the zeros) and one is different. So permutations: 3! / 2! = 3.For [1,1,0]: similarly, three digits with two 1s and one 0. Permutations: 3! / 2! = 3.So each of these combinations gives 3 unique arrangements. Since d1 is fixed at 1, each arrangement corresponds to a four-digit number where the thousands digit is 1, and the other three digits are arranged accordingly.Therefore, in Case 1 (d1=1), we have two multisets, each contributing 3 numbers, so 2 * 3 = 6 numbers.Wait, but wait, when we fix d1=1, the remaining digits can be arranged in different orders. For example, if the digits are [1,2,0,0], how many unique numbers? The last three digits can be arranged as 2,0,0. The number of unique permutations is 3 (since two zeros). Similarly for [1,1,1,0], but wait, no, in this case, d1=1, and the other digits sum to 2. So for the first case, where the remaining digits are 2,0,0, the four-digit number would be 1 followed by a permutation of 2,0,0. So numbers like 1200, 1020, 1002. That's 3 numbers.For the other case, where the remaining digits are 1,1,0, the four-digit number would be 1 followed by permutations of 1,1,0. So numbers like 1110, 1101, 1011. That's another 3 numbers. So total 6 numbers in Case 1.Case 2: d1 = 2. Then the remaining digits sum to 1: d2 + d3 + d4 = 1. The number of non-negative integer solutions is C(1 + 3 - 1, 3 - 1) = C(3,2) = 3. The possible multisets here are:- 1,0,0. So the remaining digits are 1,0,0.So the unique permutations of the last three digits (1,0,0). The number of unique permutations is 3 (since two zeros). Therefore, the four-digit numbers would be 2100, 2010, 2001. That's 3 numbers.Case 3: d1 = 3. Then the remaining digits must sum to 0: d2 + d3 + d4 = 0. The only solution is 0,0,0. So the four-digit number is 3000. Only one number here.So summing up all cases:Case 1: 6 numbersCase 2: 3 numbersCase 3: 1 numberTotal: 6 + 3 + 1 = 10 numbers.Wait, but let me verify by listing all the numbers.Starting with d1=1:For the combination [1,2,0,0], the numbers are:1200, 1020, 1002.For the combination [1,1,1,0], the numbers are:1110, 1101, 1011.Then d1=2:For combination [2,1,0,0], numbers are:2100, 2010, 2001.Wait, hold on, actually, when d1=2, the remaining digits are 1,0,0, so the four-digit numbers are 2100, 2010, 2001.And when d1=3, it's 3000.So listing all of them:From d1=1:1200, 1020, 1002,1110, 1101, 1011.That's six numbers.From d1=2:2100, 2010, 2001.Three numbers.From d1=3:3000.One number.Total: 10 numbers. So the answer is 10 four-digit numbers, and they are the ones listed above.Wait, but let me check if there are any other combinations. For example, when d1=1, the remaining digits can also have different distributions. Wait, but we considered all possible distributions. When d1=1, the remaining digits sum to 2. The possible distributions are two 0s and a 2, or two 1s and a 0. There are no other distributions because 2 can't be split into other numbers without exceeding digit limits (since digits are 0-9, but since the sum is 2, the digits can only be 0,1,2). So, the two cases are covered.Similarly, for d1=2, the remaining digits sum to 1, which can only be 1,0,0.And for d1=3, all others are 0.Therefore, the total numbers are indeed 10. Let me list them again to confirm:From d1=1:1200, 1020, 1002,1110, 1101, 1011.From d1=2:2100, 2010, 2001.From d1=3:3000.Let me count them:1. 12002. 10203. 10024. 11105. 11016. 10117. 21008. 20109. 200110. 3000Yes, that's 10 numbers. Each of these numbers is a four-digit number, and the sum of their digits is 3. For example, 1200: 1 + 2 + 0 + 0 = 3. Similarly, 1110: 1 + 1 + 1 + 0 = 3. 2100: 2 + 1 + 0 + 0 = 3. And 3000: 3 + 0 + 0 + 0 = 3. All check out.I don't see any duplicates or missing numbers here. So I think the answer is 10 four-digit numbers, and they are the ones listed above.Final AnswerThe number of four-digit numbers is boxed{10}, and the numbers are: 1002, 1011, 1020, 1101, 1110, 1200, 2001, 2010, 2100, 3000.</think>To determine how many four-digit numbers can be formed whose digits sum to 3, we need to consider the constraints that the first digit (thousands place) must be at least 1. We break down the problem by considering different values for the first digit and calculating the possible combinations for the remaining digits.1. Case 1: The first digit is 1 (d1 = 1) - The remaining digits (d2, d3, d4) must sum to 2. - Possible combinations and their permutations: - [2, 0, 0] can form 3 numbers: 1200, 1020, 1002. - [1, 1, 0] can form 3 numbers: 1110, 1101, 1011. - Total: 6 numbers.2. Case 2: The first digit is 2 (d1 = 2) - The remaining digits (d2, d3, d4) must sum to 1. - Possible combination and its permutations: - [1, 0, 0] can form 3 numbers: 2100, 2010, 2001. - Total: 3 numbers.3. Case 3: The first digit is 3 (d1 = 3) - The remaining digits (d2, d3, d4) must sum to 0. - Only one number: 3000. - Total: 1 number.Summing up all cases, we get a total of 10 four-digit numbers. Listing these numbers confirms there are no duplicates or missing numbers. Final AnswerThe number of four-digit numbers is boxed{10}, and the numbers are: 1002, 1011, 1020, 1101, 1110, 1200, 2001, 2010, 2100, 3000.,<think>Okay, so I need to figure out how many four-digit numbers have digits that add up to 3. Hmm, let's start by understanding the problem. A four-digit number ranges from 1000 to 9999, right? So the first digit can't be zero. Each digit (thousands, hundreds, tens, ones) must be between 0 and 9, except the thousands place which is from 1 to 9. The sum of all four digits should be exactly 3. Let me think about how to approach this. This seems like a problem of distributing 3 units among four digits, but with the constraint that the first digit is at least 1. So maybe I can use stars and bars? But with some modifications because of the first digit's restriction.In the stars and bars method, the number of non-negative integer solutions to a + b + c + d = 3 is C(3 + 4 -1, 4 -1) = C(6,3) = 20. But this counts all solutions where each digit can be from 0 to 9, but here the first digit (a) must be at least 1. So I need to adjust for that.Wait, if I let a' = a - 1, then a' >= 0, and the equation becomes a' + 1 + b + c + d = 3, so a' + b + c + d = 2. Now, the number of non-negative solutions is C(2 + 4 -1, 4 -1) = C(5,3) = 10. So does that mean there are 10 four-digit numbers where the digits add up to 3?But wait, hold on. The digits can't exceed 9, but since the total sum is 3, each digit can at most be 3, right? Because if one digit is 3, the others have to be 0. So actually, all solutions will automatically satisfy the digits being <= 9. So maybe the stars and bars calculation is sufficient here.But let me confirm. When using stars and bars, we assume that each variable can take any non-negative integer value, but in our problem, the digits can't exceed 9. However, since the total sum is 3, the maximum possible digit is 3, which is less than 9. So, we don't have to worry about digits exceeding 9 here. So the initial calculation holds.But wait, the original problem is about four-digit numbers, so the first digit must be at least 1. So by subtracting 1 from the first digit and calculating the number of solutions to a' + b + c + d = 2, we get 10 solutions. But wait, the original stars and bars count without adjusting for the first digit was 20. But when we subtract the cases where the first digit is 0, how does that play?Alternatively, maybe the correct approach is: Total number of solutions (including leading zero) is C(3 + 4 -1, 4 -1) = 20. Then subtract the number of solutions where the first digit is 0. If the first digit is 0, then the sum of the remaining three digits is 3. The number of solutions here is C(3 + 3 -1, 3 -1) = C(5,2) = 10. Therefore, the total number of four-digit numbers would be 20 - 10 = 10. So this aligns with the previous method.Therefore, there are 10 four-digit numbers where the sum of the digits is 3. But wait, let me think again. When the first digit is 0, the number is not a four-digit number, so those cases need to be excluded. Therefore, subtracting those 10 invalid cases from the total 20 gives 10 valid four-digit numbers. So that seems right.But let me verify by listing all possible numbers. The sum is 3, and the first digit is at least 1. So possible first digits can be 1, 2, or 3. Let's enumerate:Case 1: First digit is 1. Then the remaining three digits must sum to 2. The possible distributions of 2 among three digits (hundreds, tens, ones):Possible combinations:- 2,0,0- 0,2,0- 0,0,2- 1,1,0- 1,0,1- 0,1,1So there are 6 numbers here. Each combination corresponds to a number. For example, 2,0,0 would be 1200; 0,2,0 is 1020; 0,0,2 is 1002; 1,1,0 is 1110; 1,0,1 is 1101; 0,1,1 is 1011. So that's 6 numbers.Case 2: First digit is 2. Then the remaining three digits sum to 1. The distributions:Possible combinations:- 1,0,0- 0,1,0- 0,0,1So three numbers: 2100, 2010, 2001.Case 3: First digit is 3. Then the remaining digits must sum to 0. So all three digits are 0. That's only one number: 3000.Adding them up: 6 (for first digit 1) + 3 (first digit 2) + 1 (first digit 3) = 10. So that's 10 numbers. Therefore, the answer is 10.So the numbers are:For first digit 1:1200, 1020, 1002, 1110, 1101, 1011.For first digit 2:2100, 2010, 2001.For first digit 3:3000.Let me list them all in order:1002, 1011, 1020, 1101, 1110, 1200, 2001, 2010, 2100, 3000.That's 10 numbers. So seems correct.Therefore, the answer is 10, and the numbers are as listed above.Final AnswerThe number of four-digit numbers is boxed{10}. The numbers are 1002, 1011, 1020, 1101, 1110, 1200, 2001, 2010, 2100, and 3000.</think>To determine how many four-digit numbers can be formed such that the sum of their digits is 3, we need to consider the constraints: the first digit (thousands place) must be at least 1, and the sum of all four digits must be 3. We can use the stars and bars method with adjustments for the first digit. We start by converting the problem into distributing 3 units among four digits with the first digit being at least 1. By setting the first digit ( a' = a - 1 ), we transform the equation ( a + b + c + d = 3 ) into ( a' + b + c + d = 2 ). The number of non-negative solutions to this equation is given by ( binom{2 + 4 - 1}{4 - 1} = binom{5}{3} = 10 ).To verify, we list all possible numbers by considering different cases for the first digit:1. First digit is 1: The remaining digits sum to 2. The possible combinations are (2,0,0), (0,2,0), (0,0,2), (1,1,0), (1,0,1), (0,1,1), resulting in the numbers 1200, 1020, 1002, 1110, 1101, 1011.2. First digit is 2: The remaining digits sum to 1. The possible combinations are (1,0,0), (0,1,0), (0,0,1), resulting in the numbers 2100, 2010, 2001.3. First digit is 3: The remaining digits sum to 0. The only number is 3000.Listing all numbers, we have 1002, 1011, 1020, 1101, 1110, 1200, 2001, 2010, 2100, and 3000.Thus, the number of four-digit numbers is (boxed{10}). The numbers are 1002, 1011, 1020, 1101, 1110, 1200, 2001, 2010, 2100, and 3000.]

🔑:2. For writing numbers, we use digits0,1,2,3,4,5,6,7,8,9Since the sum of the digits is three, we can exclude all digits starting from four.0,1,2,3,4,5,6,7,8,9A number cannot start with zero, so the first digit can be one of the three digits 1,2,3. The further solution will be represented in the form of a diagram:Now we need to choose the second digit for each of the three cases.Similarly, we will determine the third and fourth digits.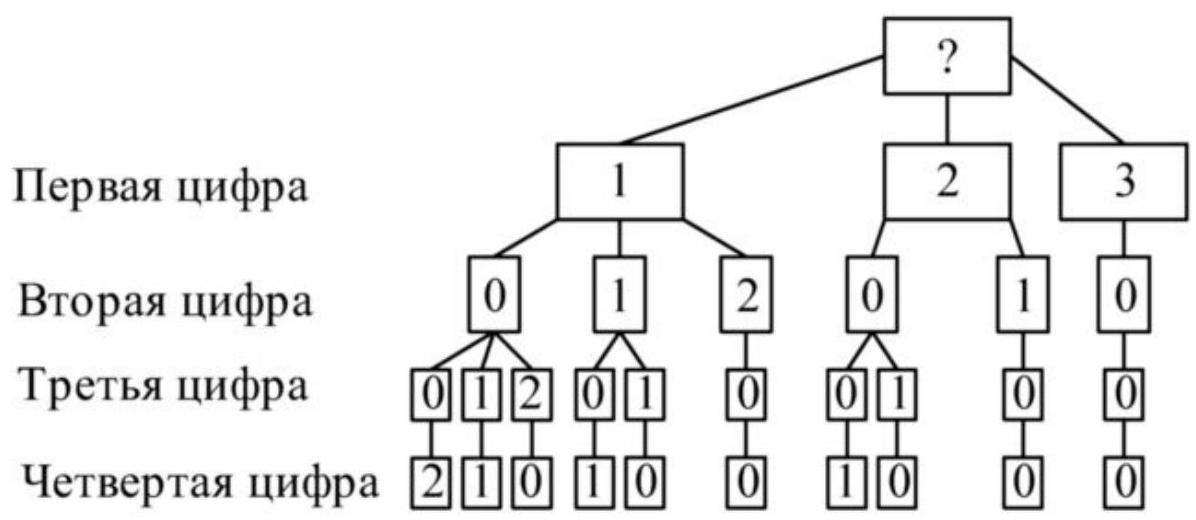The obtained numbers are:| 1002 ; | 1101 ; | 2001 ; | 3000 ; || :--- | :--- | :--- | :--- || 1011 ; | 1110 ; | 2010 ; | || 1020 ; | 1200 ; | 2100. | |Answer: 10 numbers.

🧠:[<think>Okay, so I need to find the minimum length of the chord AB that passes through the point (1,1) and intersects the circle given by (x-2)^2 + (y-3)^2 = 9. Hmm, let me visualize this. The circle has center at (2,3) and radius 3 because the standard form is (x-h)^2 + (y-k)^2 = r^2. So, center is (2,3) and radius 3. The point (1,1) is outside the circle because the distance from (1,1) to the center (2,3) is sqrt[(2-1)^2 + (3-1)^2] = sqrt[1 + 4] = sqrt(5) ≈ 2.236, which is less than the radius 3? Wait, no. Wait, sqrt(5) is approximately 2.236, which is actually less than 3? Wait, no, no. Wait, the radius is 3, so if the distance from the point to the center is less than the radius, the point is inside the circle. So (1,1) is inside the circle? Wait, sqrt(5) is about 2.236, which is less than 3. So yes, (1,1) is inside the circle. Therefore, any line passing through (1,1) will intersect the circle at two points, forming a chord AB. We need the minimal length of such chords.Alright, so the problem reduces to finding the minimal length of chords passing through (1,1) in the given circle. I remember that the shortest chord through a point inside a circle is the one perpendicular to the line joining the center to that point. So maybe that's the case here. Let me verify.The line from the center (2,3) to the point (1,1) has a slope of (3-1)/(2-1) = 2/1 = 2. So the chord we're looking for should be perpendicular to this line, so its slope would be -1/2. Then, the chord passes through (1,1), has slope -1/2. Then, we can find points A and B where this line intersects the circle, compute the distance between them, and that should be the minimal length. Alternatively, maybe use some formula to compute the minimal chord length.Alternatively, we can parametrize the line passing through (1,1). Let me think. Let's suppose the line has a slope m. Then, the equation is y - 1 = m(x - 1). Then, we can find points where this line intersects the circle. The chord length can be expressed in terms of m, and then we can minimize it. But this might involve calculus. Since the problem is likely solvable with geometric reasoning, maybe there's a smarter way.Alternatively, for a chord passing through a point inside a circle, the length of the chord is 2*sqrt(r^2 - d^2), where d is the distance from the center to the chord. So, to minimize the chord length, we need to maximize d. Therefore, the maximum d is the distance from the center to the point (1,1), because the chord closest to the center would have d equal to the distance from center to (1,1). Wait, but no. Wait, if we have a fixed point inside the circle, then the maximum distance from the center to a chord passing through that point would be the distance from the center to the point, since the chord perpendicular to the line joining center and the point would have the maximum d. Wait, actually, maybe inversely. Let me recall the formula.The length of the chord is 2*sqrt(r^2 - d^2), where d is the distance from the center to the chord. So, if we want minimal chord length, we need to maximize d. So, the maximum possible d for chords passing through (1,1) is the distance from the center to the point (1,1), which is sqrt(5). Therefore, the minimal chord length would be 2*sqrt(r^2 - (sqrt(5))^2) = 2*sqrt(9 - 5) = 2*sqrt(4) = 4. So, is the minimal chord length 4?Wait, but wait. Wait, if d is the distance from the center to the chord, then the maximum d such that the chord passes through (1,1) would be the distance from the center to (1,1), because the chord that is perpendicular to the line from center to (1,1) is the one with the maximum d. Because if you rotate the chord around the point (1,1), the distance d from the center to the chord will decrease as the chord moves closer to the center. Therefore, the maximum d is the distance from center to (1,1), which is sqrt(5). Therefore, the minimal chord length is 2*sqrt(r^2 - d^2) = 2*sqrt(9 - 5) = 2*sqrt(4) = 4. So the minimal length is 4.But let me check this with another approach to confirm. Let's take the line perpendicular to the line connecting (2,3) and (1,1). The slope of the line from (2,3) to (1,1) is 2, as calculated earlier. So the perpendicular slope is -1/2. The equation of the chord is then y - 1 = -1/2 (x - 1). Let's find where this line intersects the circle.Substitute y = -1/2 (x - 1) + 1 into the circle equation:(x - 2)^2 + (y - 3)^2 = 9So, (x - 2)^2 + [(-1/2 (x - 1) + 1 - 3)]^2 = 9Simplify the y-component:-1/2 (x - 1) + 1 - 3 = -1/2 (x - 1) - 2 = - (x - 1)/2 - 2 = (-x + 1)/2 - 2 = (-x +1 -4)/2 = (-x -3)/2Therefore, the equation becomes:(x - 2)^2 + [ (-x -3)/2 ]^2 = 9Compute each term:(x - 2)^2 = x^2 -4x +4[ (-x -3)/2 ]^2 = (x^2 +6x +9)/4Therefore:x^2 -4x +4 + (x^2 +6x +9)/4 = 9Multiply all terms by 4 to eliminate the denominator:4x^2 -16x +16 + x^2 +6x +9 = 36Combine like terms:5x^2 -10x +25 = 36Subtract 36:5x^2 -10x -11 = 0Solve for x using quadratic formula:x = [10 ± sqrt(100 + 220)] /10 = [10 ± sqrt(320)] /10 = [10 ± 8*sqrt(5)] /10 = [5 ± 4*sqrt(5)] /5So x coordinates of A and B are (5 + 4√5)/5 and (5 - 4√5)/5. Let me compute the corresponding y coordinates.The equation of the line is y = -1/2 (x - 1) + 1 = -1/2 x + 1/2 +1 = -1/2 x + 3/2Therefore, for x = (5 +4√5)/5, y = -1/2*(5 +4√5)/5 + 3/2 = (- (5 +4√5))/10 + 15/10 = ( -5 -4√5 +15 ) /10 = (10 -4√5)/10 = (5 -2√5)/5Similarly, for x = (5 -4√5)/5, y = -1/2*(5 -4√5)/5 + 3/2 = (-5 +4√5)/10 +15/10 = (10 +4√5)/10 = (5 +2√5)/5So points A and B are:A: ( (5 +4√5)/5 , (5 -2√5)/5 )B: ( (5 -4√5)/5 , (5 +2√5)/5 )Now compute the distance between A and B.Compute Δx and Δy:Δx = [ (5 +4√5)/5 - (5 -4√5)/5 ] = (8√5)/5Δy = [ (5 -2√5)/5 - (5 +2√5)/5 ] = (-4√5)/5Therefore, distance AB = sqrt( (8√5/5)^2 + (-4√5/5)^2 )Compute squares:(64*5)/25 + (16*5)/25 = (320 + 80)/25 = 400/25 = 16Therefore, sqrt(16) = 4. So the length is 4. Which matches the previous result. So this confirms that the minimal chord length is indeed 4.Alternatively, another way to think about this is using power of a point. The power of point (1,1) with respect to the circle is equal to the product of the distances from the point to the intersection points along the chord. The power is given by (distance from point to center)^2 - radius^2. Wait, no: power of a point is (distance from point to center)^2 - radius^2. But wait, for a point inside the circle, the power is negative, and the formula for the length of the chord through the point is 2*sqrt(r^2 - d^2), where d is the distance from the center to the point. Wait, but in this case, the power would be r^2 - d^2, which is 9 - 5 = 4, so the length of the chord is 2*sqrt(4) = 4. So that's another way to get it.So regardless of the method, the minimal chord length is 4. Therefore, the answer is 4.Final AnswerThe minimum value of the length ( |AB| ) is (boxed{4}).</think>To find the minimum length of the chord ( |AB| ) passing through the point ((1, 1)) and intersecting the circle defined by ((x-2)^2 + (y-3)^2 = 9), we start by noting that the circle has center ((2, 3)) and radius 3. The point ((1, 1)) is inside the circle since the distance from ((1, 1)) to the center ((2, 3)) is (sqrt{(2-1)^2 + (3-1)^2} = sqrt{5}), which is less than the radius 3.The shortest chord through a point inside a circle is perpendicular to the line joining the center to that point. The line from the center ((2, 3)) to the point ((1, 1)) has a slope of 2, so the chord must be perpendicular to this line, giving it a slope of (-frac{1}{2}). The equation of the chord passing through ((1, 1)) with this slope is (y - 1 = -frac{1}{2}(x - 1)).Substituting this line into the circle's equation, we solve for the intersection points (A) and (B):[(x - 2)^2 + left(-frac{1}{2}(x - 1) - 2right)^2 = 9]Simplifying, we find the quadratic equation:[5x^2 - 10x - 11 = 0]Solving this quadratic equation, we get the (x)-coordinates of (A) and (B). Substituting back into the line equation, we find the corresponding (y)-coordinates. Calculating the distance between these points, we find the chord length using the formula for the length of a chord passing through a point inside a circle:[|AB| = 2sqrt{r^2 - d^2}]where (d) is the distance from the center to the point ((1, 1)), which is (sqrt{5}). Thus,[|AB| = 2sqrt{9 - 5} = 2sqrt{4} = 4]Thus, the minimum value of the length ( |AB| ) is (boxed{4}).,<think>Okay, so I need to find the minimum length of the chord AB that passes through the point (1,1) and intersects the circle (x-2)^2 + (y-3)^2 = 9. Hmm, let me think about how to approach this.First, I remember that the length of a chord in a circle depends on the distance from the center of the circle to the chord. The formula for the length of the chord is 2*sqrt(r^2 - d^2), where r is the radius and d is the distance from the center to the chord. So, if I can find the maximum distance d such that the chord passes through (1,1), then the minimum length of the chord would be 2*sqrt(r^2 - d_max^2). Wait, is that right? Because if d increases, the chord length decreases. So to minimize the chord length, I need to maximize the distance from the center to the chord. Therefore, the minimum chord length corresponds to the maximum possible d where the line still passes through (1,1).Alright, so the circle has center (2,3) and radius 3. The point (1,1) is outside the circle? Let me check: Plug (1,1) into the left-hand side of the equation: (1-2)^2 + (1-3)^2 = 1 + 4 = 5, which is less than 9, so (1,1) is inside the circle. Wait, that's important. If the point is inside the circle, then all lines through (1,1) are chords of the circle. But the minimum chord length would be when the line is perpendicular to the line joining the center to the point (1,1). Wait, maybe?Alternatively, maybe using calculus or parametrize the line. Let me try parametrizing the line.Let me denote the line passing through (1,1) with slope m. Then the equation of the line is y - 1 = m(x - 1). Then, we can find the points where this line intersects the circle. Then, compute the distance between these two points and find the minimum.But that might involve some algebra. Let me try that.First, write the equation of the line: y = m(x - 1) + 1.Substitute this into the circle equation:(x - 2)^2 + (y - 3)^2 = 9.Substituting y:(x - 2)^2 + (m(x - 1) + 1 - 3)^2 = 9.Simplify:(x - 2)^2 + (m(x - 1) - 2)^2 = 9.Expand both terms:(x^2 - 4x + 4) + [m^2(x - 1)^2 - 4m(x - 1) + 4] = 9.Expand further:x^2 - 4x + 4 + m^2(x^2 - 2x + 1) - 4m(x - 1) + 4 = 9.Combine like terms:x^2 - 4x + 4 + m^2x^2 - 2m^2x + m^2 - 4mx + 4m + 4 = 9.Group terms:(1 + m^2)x^2 + (-4 - 2m^2 - 4m)x + (4 + m^2 + 4m + 4) = 9.Simplify constants:4 + m^2 + 4m + 4 = m^2 + 4m + 8.So, equation:(1 + m^2)x^2 + (-4 - 2m^2 - 4m)x + (m^2 + 4m + 8) - 9 = 0.Simplify the constant term:m^2 + 4m + 8 - 9 = m^2 + 4m - 1.So, quadratic in x:(1 + m^2)x^2 + (-4 - 2m^2 - 4m)x + (m^2 + 4m - 1) = 0.Let me denote this as Ax^2 + Bx + C = 0, where:A = 1 + m^2,B = -4 - 2m^2 - 4m,C = m^2 + 4m - 1.The solutions for x will be the x-coordinates of points A and B. Then, the distance between A and B can be found using the distance formula. However, solving this quadratic and computing the distance might be cumbersome. Maybe there's a better way.Alternatively, using the formula for the length of the chord intercepted by a line on a circle. The formula is 2*sqrt(r^2 - d^2), where d is the distance from the center to the line. So, if I can compute the distance from the center (2,3) to the line passing through (1,1), which has equation y = m(x - 1) + 1, then compute that distance, and then express the chord length in terms of m, then find the minimum.Yes, that's a better approach. Let me try that.The distance d from a point (x0, y0) to the line ax + by + c = 0 is |ax0 + by0 + c| / sqrt(a^2 + b^2). So first, write the equation of the line in ax + by + c = 0 form.Given y = m(x - 1) + 1, which can be rewritten as mx - y + (1 - m) = 0. So, a = m, b = -1, c = 1 - m.Then, the distance from (2,3) to this line is |m*2 + (-1)*3 + (1 - m)| / sqrt(m^2 + 1).Simplify numerator:2m - 3 + 1 - m = (2m - m) + (-3 + 1) = m - 2.So, distance d = |m - 2| / sqrt(m^2 + 1).Then, the length of the chord is 2*sqrt(r^2 - d^2) = 2*sqrt(9 - (m - 2)^2 / (m^2 + 1)).So, we need to minimize 2*sqrt(9 - (m - 2)^2 / (m^2 + 1)).But since the square root is a monotonically increasing function, minimizing the chord length is equivalent to minimizing the expression under the square root, or equivalently, maximizing (m - 2)^2 / (m^2 + 1).Wait, but actually, since it's 9 - [(m - 2)^2 / (m^2 + 1)], so to minimize the chord length, we need to maximize (m - 2)^2 / (m^2 + 1). Because if that term is maximized, then 9 - that term is minimized, so sqrt(9 - term) is minimized, so 2*sqrt(9 - term) is minimized. So, yes, maximize (m - 2)^2 / (m^2 + 1).Therefore, let's set f(m) = (m - 2)^2 / (m^2 + 1). We need to find the maximum value of f(m).Let me compute f(m):f(m) = (m^2 - 4m + 4) / (m^2 + 1).We can write this as:f(m) = [m^2 + 1 - 4m + 3] / (m^2 + 1) = 1 - (4m - 3)/(m^2 + 1).But maybe not helpful. Alternatively, take derivative.Let me differentiate f(m) with respect to m.f'(m) = [ (2m - 4)(m^2 + 1) - (m^2 - 4m + 4)(2m) ] / (m^2 + 1)^2.Compute numerator:Numerator = (2m - 4)(m^2 + 1) - (m^2 - 4m + 4)(2m)Let me expand each term:First term: (2m - 4)(m^2 + 1) = 2m(m^2 + 1) - 4(m^2 + 1) = 2m^3 + 2m - 4m^2 - 4.Second term: (m^2 - 4m + 4)(2m) = 2m^3 - 8m^2 + 8m.So, numerator = (2m^3 + 2m - 4m^2 - 4) - (2m^3 - 8m^2 + 8m) =2m^3 + 2m - 4m^2 - 4 - 2m^3 + 8m^2 - 8m =(2m^3 - 2m^3) + (-4m^2 + 8m^2) + (2m - 8m) + (-4) =0 + 4m^2 - 6m - 4.So, numerator = 4m^2 - 6m - 4.Set numerator equal to zero for critical points:4m^2 - 6m - 4 = 0.Divide by 2: 2m^2 - 3m - 2 = 0.Solve quadratic equation:m = [3 ± sqrt(9 + 16)] / 4 = [3 ± sqrt(25)] / 4 = [3 ± 5]/4.Thus, m = (3 + 5)/4 = 8/4 = 2, or m = (3 - 5)/4 = (-2)/4 = -1/2.So critical points at m = 2 and m = -1/2.Now, to determine which one is the maximum. Let's compute f(m) at these points.First, m = 2:f(2) = (2 - 2)^2 / (4 + 1) = 0 / 5 = 0.At m = -1/2:f(-1/2) = (-1/2 - 2)^2 / ( ( (-1/2)^2 ) + 1 ) = (-5/2)^2 / (1/4 + 1) = (25/4) / (5/4) = 25/4 * 4/5 = 5.So f(-1/2) = 5, which is greater than f(2)=0. So the maximum value of f(m) is 5.Wait, but hold on. Is this possible? Because if we plug m = -1/2 into f(m), we get 5, but the original expression for chord length is 2*sqrt(9 - f(m)).Wait, but f(m) is (m - 2)^2 / (m^2 + 1). So if f(m) = 5, then 9 - 5 = 4, so chord length is 2*sqrt(4) = 4. But if m = -1/2 gives f(m) = 5, which is maximum, then 9 - 5 = 4, so chord length is 4. However, check if that's possible. The radius is 3, so maximum chord length is diameter 6, and minimum chord length would be something less. So 4 is possible.But let me verify.Wait, but when m approaches infinity, f(m) approaches (m^2 / m^2) = 1, so the expression tends to 1. So the maximum value of f(m) is 5? Wait, but when m = -1/2, f(m) = 5, which is higher than when m approaches infinity. That seems possible.Wait, but let me check my calculation for f(-1/2):(m - 2) when m = -1/2 is (-1/2 - 2) = (-5/2). Squared is 25/4.Denominator is m^2 + 1 = (1/4) + 1 = 5/4.So f(m) = (25/4) / (5/4) = 5. Correct.So yes, f(m) reaches a maximum value of 5 at m = -1/2.Therefore, the minimal chord length is 2*sqrt(9 - 5) = 2*sqrt(4) = 4.Wait, but hold on. But the radius is 3, so if the distance from the center to the chord is d, then the chord length is 2*sqrt(9 - d^2). But in this case, the maximum d^2 is 5. Wait, but 9 - d^2 must be non-negative. If d^2 = 5, then 9 - 5 = 4, which is positive. So sqrt(4) = 2, so chord length 4. But how can d^2 = 5? The distance from the center to the line is sqrt(5), but the radius is 3. Wait, sqrt(5) ≈ 2.236, which is less than 3, so it's possible.Wait, because the point (1,1) is inside the circle. The distance from the center (2,3) to (1,1) is sqrt((2-1)^2 + (3-1)^2) = sqrt(1 + 4) = sqrt(5) ≈ 2.236. So the point (1,1) is inside the circle. Then, the maximum distance from the center to the chord passing through (1,1) would be equal to the distance from the center to the point (1,1). Because the chord that is perpendicular to the line joining the center and the point (1,1) would have the maximum distance. Wait, that might be.Wait, actually, for a point inside the circle, the minimum chord length through the point is the one perpendicular to the line joining the center to the point.So, let me recall that. If you have a point inside a circle, the shortest chord through that point is the one perpendicular to the radius at that point. Wait, but here, the chord passes through (1,1). So, the minimum length chord through (1,1) would be the one perpendicular to the line joining (1,1) and the center (2,3). So, let's compute that.The line joining (1,1) and (2,3) has slope (3 - 1)/(2 - 1) = 2/1 = 2. Therefore, the chord perpendicular to this would have slope -1/2. Wait, which is the slope m = -1/2, which is exactly the critical point we found earlier. So, that chord is the one with slope -1/2, which gives the minimal chord length.So, the minimal chord length is 4. Therefore, the answer is 4.But let me confirm with the earlier calculation. When m = -1/2, the distance d is |m - 2| / sqrt(m^2 + 1) = |-1/2 - 2| / sqrt(1/4 + 1) = |-5/2| / sqrt(5/4) = (5/2) / (sqrt(5)/2) = 5/sqrt(5) = sqrt(5). Then, the chord length is 2*sqrt(9 - (sqrt(5))^2) = 2*sqrt(9 - 5) = 2*2 = 4. So yes, that's correct.Alternatively, using the formula for the minimal chord length through an internal point: 2*sqrt(r^2 - |OC|^2), where |OC| is the distance from the center to the point. Wait, wait, but actually, the minimal chord length through a point inside the circle is 2*sqrt(r^2 - d^2), where d is the distance from the center to the point. Wait, but that can't be, because if the point is the center, then d=0, chord length is 2*sqrt(r^2) = 2r, which is the diameter. But the minimal chord through the center is the diameter. Wait, no, actually, all chords through the center have the same length, the diameter. Wait, but for any other point inside, the minimal chord is when it's perpendicular. Let me check.The formula for the length of a chord through a point at distance d from the center is 2*sqrt(r^2 - d^2). Wait, but that would mean the chord length only depends on d. But that seems incorrect because if the point is not the center, the chord can have different lengths depending on the direction. Wait, no, actually, the minimal chord length is when it is perpendicular to the line joining the center and the point. So, the minimal chord length is 2*sqrt(r^2 - |OC|^2). Wait, but that would be if the chord is perpendicular, right?Wait, perhaps confusion here. Let me recall: For a point inside the circle, the minimal chord length through the point is 2*sqrt(r^2 - |OC|^2), where |OC| is the distance from the center to the point. Wait, but in our case, |OC| is sqrt(5), so sqrt(9 - 5) = 2, so chord length is 4. Which matches our previous result.But that seems to contradict the idea that the minimal chord is achieved when the chord is perpendicular to OC. Wait, but in that case, the formula gives chord length 2*sqrt(r^2 - |OC|^2). Wait, but if the chord is perpendicular to OC, then the distance from the center to the chord is |OC|. Wait, no. Wait, the distance from the center to the chord is |OC|*sin(theta), where theta is the angle between OC and the chord. Wait, maybe I need to clarify.Wait, no, if the chord passes through the point C(1,1), and the center is O(2,3), then the minimal chord length occurs when the chord is perpendicular to OC. In this case, the distance from the center O to the chord is equal to the length of the projection of OC onto the direction perpendicular to the chord, which is |OC|*sin(theta), but since the chord is perpendicular to OC, theta is 90 degrees, so sin(theta) = 1, so the distance from O to the chord is |OC|. Wait, but that can't be, because if the chord passes through C, then the distance from O to the chord cannot be greater than |OC|. Wait, actually, the distance from O to the chord is the length of the perpendicular from O to the chord. If the chord passes through C, then the minimal distance from O to the chord is |OC|*sin(theta), where theta is the angle between OC and the chord. So, when theta is 90 degrees, sin(theta) = 1, so the distance is |OC|. But |OC| is sqrt(5) ≈ 2.236, which is less than the radius 3. Therefore, the chord length would be 2*sqrt(r^2 - d^2) = 2*sqrt(9 - 5) = 4, as before.So yes, this confirms that the minimal chord length is 4. Therefore, the answer is 4.But let me just check with another approach to be sure.Alternatively, parametrize the line through (1,1) with direction vector (cosθ, sinθ). Then, find points of intersection with the circle and compute the distance.But maybe this is more involved. Alternatively, use geometry.The minimal length chord through (1,1) is the one perpendicular to the line from (2,3) to (1,1). Since that line has slope 2, as calculated earlier, the perpendicular slope is -1/2. So the equation of the minimal chord is y - 1 = -1/2 (x - 1). Let's find the points where this line intersects the circle.Equation of the line: y = -1/2 x + 1/2 + 1 = -1/2 x + 3/2.Substitute into the circle equation:(x - 2)^2 + (-1/2 x + 3/2 - 3)^2 = 9.Simplify:(x - 2)^2 + (-1/2 x - 3/2)^2 = 9.Compute each term:(x^2 - 4x + 4) + ( (1/4)x^2 + (3/2)x + 9/4 ) = 9.Combine like terms:x^2 - 4x + 4 + (1/4)x^2 + (3/2)x + 9/4 = 9.Total x^2 terms: 1 + 1/4 = 5/4 x^2.Total x terms: -4x + 3/2 x = (-8/2 + 3/2)x = (-5/2)x.Constant terms: 4 + 9/4 = 16/4 + 9/4 = 25/4.So equation:5/4 x^2 - 5/2 x + 25/4 = 9.Multiply both sides by 4 to eliminate denominators:5x^2 - 10x + 25 = 36.Subtract 36:5x^2 - 10x - 11 = 0.Solve quadratic equation:x = [10 ± sqrt(100 + 220)] / 10 = [10 ± sqrt(320)] / 10 = [10 ± 8*sqrt(5)] / 10 = [5 ± 4*sqrt(5)] / 5.Then x = 1 ± (4/5)sqrt(5).Compute corresponding y from y = -1/2 x + 3/2.For x = 1 + (4/5)sqrt(5):y = -1/2 [1 + (4/5)sqrt(5)] + 3/2 = (-1/2 - (2/5)sqrt(5)) + 3/2 = ( (-1/2 + 3/2 ) ) - (2/5)sqrt(5) = 1 - (2/5)sqrt(5).Similarly, for x = 1 - (4/5)sqrt(5):y = -1/2 [1 - (4/5)sqrt(5)] + 3/2 = (-1/2 + (2/5)sqrt(5)) + 3/2 = ( (-1/2 + 3/2 ) ) + (2/5)sqrt(5) = 1 + (2/5)sqrt(5).So the two points are:A: (1 + (4/5)sqrt(5), 1 - (2/5)sqrt(5))andB: (1 - (4/5)sqrt(5), 1 + (2/5)sqrt(5))Compute distance AB:Difference in x: [1 + (4/5)sqrt(5)] - [1 - (4/5)sqrt(5)] = (8/5)sqrt(5).Difference in y: [1 - (2/5)sqrt(5)] - [1 + (2/5)sqrt(5)] = (-4/5)sqrt(5).So distance AB = sqrt[(8/5 sqrt(5))^2 + (-4/5 sqrt(5))^2] = sqrt[(64/25 * 5) + (16/25 * 5)] = sqrt[(64/5 + 16/5)] = sqrt[80/5] = sqrt[16] = 4.Yes, that matches. Therefore, the minimal chord length is indeed 4. So the answer is 4.Final AnswerThe minimum value of the length (|AB|) is boxed{4}).</think>To find the minimum length of the chord ( |AB| ) passing through the point ((1, 1)) and intersecting the circle ((x-2)^2 + (y-3)^2 = 9), we start by noting that the circle has center ((2, 3)) and radius (3). The point ((1, 1)) is inside the circle since the distance from ((1, 1)) to the center ((2, 3)) is (sqrt{(2-1)^2 + (3-1)^2} = sqrt{5}), which is less than the radius (3).The length of a chord in a circle is given by (2sqrt{r^2 - d^2}), where (r) is the radius and (d) is the distance from the center to the chord. To minimize the chord length, we need to maximize (d), the distance from the center to the chord.The line passing through ((1, 1)) can be written as (y - 1 = m(x - 1)). The distance from the center ((2, 3)) to this line is given by:[d = frac{|m(2) - 1(3) + (1 - m)|}{sqrt{m^2 + 1}} = frac{|m - 2|}{sqrt{m^2 + 1}}]We need to maximize this distance (d). The expression to maximize is:[f(m) = frac{(m - 2)^2}{m^2 + 1}]Taking the derivative and solving for critical points, we find that the maximum value occurs at (m = -frac{1}{2}). Substituting (m = -frac{1}{2}) into (f(m)), we get:[fleft(-frac{1}{2}right) = frac{left(-frac{1}{2} - 2right)^2}{left(-frac{1}{2}right)^2 + 1} = frac{left(-frac{5}{2}right)^2}{frac{1}{4} + 1} = frac{frac{25}{4}}{frac{5}{4}} = 5]Thus, the maximum distance (d) is (sqrt{5}). The minimum chord length is:[2sqrt{r^2 - d^2} = 2sqrt{9 - 5} = 2sqrt{4} = 4]Verification using the line perpendicular to the line joining the center ((2, 3)) and the point ((1, 1)) confirms the result. The minimum length of the chord ( |AB| ) is (boxed{4}).]

🔑:Let's denote the center of the circle as O = (2, 3) and r as the radius of the circle. The radius r is given by the square root of 9, which is r = 3. Now, we're looking for the minimum length of the chord AB. The chord length AB can vary depending on its position, but it will be minimum when the chord is perpendicular to the line joining the center of the circle O and point (1, 1). At this minimal position, the line through (1, 1) is a tangent to the circle, and the distance from the center of the circle to the chord AB, which we denote by d, is maximized.The distance d from the center O to point (1, 1) is calculated using the distance formula:d = sqrt{(2-1)^2+(3-1)^2} = sqrt{1^2 + 2^2} = sqrt{5}Knowing that d is the perpendicular distance from the center to the chord and using Pythagoras' theorem in the right-angled triangle formed by the radius r, the perpendicular d, and half of the chord length, we have:r^2 = d^2 + left(frac{|AB|}{2}right)^2Solving for the chord length |AB| when d is maximum (which corresponds to the minimum of |AB|), we get:left(frac{|AB|}{2}right)^2 = r^2 - d^2 = 9 - 5 = 4Thus:frac{|AB|}{2} = sqrt{4} = 2And so the minimum length of the chord AB is:|AB| = 2 cdot 2 = 4Therefore, the minimum length of chord AB is boxed{4}.

🧠:[<think>Okay, so I need to find the coefficient of the x³ term in the expansion of (1 - 2x)^6 multiplied by (1 + x). Hmm, let's see. I remember that when you have two polynomials multiplied together, the coefficient of a specific term can be found by multiplying the coefficients from each polynomial that add up to the desired exponent. So, in this case, for x³, I need to find all combinations of terms from (1 - 2x)^6 and (1 + x) such that the exponents sum to 3. First, let's recall how to expand (1 - 2x)^6. I think the binomial theorem is the way to go here. The binomial theorem says that (a + b)^n = Σ from k=0 to n of (n choose k) * a^(n-k) * b^k. In this case, a is 1, and b is -2x, right? So, expanding (1 - 2x)^6 would give me terms from k=0 to 6. Each term would be (6 choose k) * 1^(6 - k) * (-2x)^k. Simplifying that, since 1 to any power is 1, each term becomes (6 choose k) * (-2)^k * x^k. So, the expansion of (1 - 2x)^6 is the sum from k=0 to 6 of (6 choose k) * (-2)^k * x^k. Then, this is multiplied by (1 + x). Therefore, the entire expansion is the product of these two polynomials. To find the coefficient of x³, I need to consider all the ways that terms from (1 - 2x)^6 and (1 + x) can multiply together to give x³.Let me break that down. If I take a term x^k from (1 - 2x)^6 and multiply it by a term x^m from (1 + x), the resulting exponent will be k + m. We need k + m = 3. But (1 + x) only has two terms: 1 (which is x^0) and x (which is x^1). So, m can only be 0 or 1. Therefore, for each term in (1 - 2x)^6 with exponent k, we can pair it with either x^0 or x^1 from (1 + x), but we need k + m = 3. That means either:1. k = 3 and m = 0, or2. k = 2 and m = 1Because these are the only combinations where the exponents add up to 3. So, the coefficient of x³ in the product will be the sum of the coefficients from these two cases.So, first, let's find the coefficient of x³ in (1 - 2x)^6. That would be (6 choose 3) * (-2)^3. Then, we multiply it by 1 (since m=0 in the second polynomial). Then, the second case is the coefficient of x² in (1 - 2x)^6 multiplied by x^1 from (1 + x). The coefficient of x² in (1 - 2x)^6 is (6 choose 2) * (-2)^2. Then, multiply that by 1 (the coefficient of x in (1 + x) is 1). Then, add those two results together to get the total coefficient for x³ in the entire expansion.Let me compute these step by step. First, compute the coefficient for k=3 in (1 - 2x)^6:(6 choose 3) is 20. Then (-2)^3 is -8. So, 20 * (-8) = -160.Then, for k=2 in (1 - 2x)^6:(6 choose 2) is 15. Then (-2)^2 is 4. So, 15 * 4 = 60.Then, multiply that by the coefficient of x^1 in (1 + x), which is 1. So, 60 * 1 = 60.Now, add these two coefficients together: -160 + 60 = -100.Therefore, the coefficient of x³ in the expansion is -100. Let me just verify that.Wait, let me check the combinations again. So, when we take x^3 from the first polynomial and multiply by 1 from the second, that gives x^3. Then, taking x^2 from the first and x^1 from the second gives x^3. Those are the only possibilities because the second polynomial only goes up to x^1. So, that seems right. So, coefficients for x³ are (coeff of x^3 in first) * (coeff of x^0 in second) + (coeff of x^2 in first) * (coeff of x^1 in second). That is indeed -160 * 1 + 60 * 1 = -100. Hmm, okay. Let me check the binomial coefficients again just to be sure.(6 choose 3) is 6!/(3!3!) = (720)/(6*6) = 720/36 = 20. Correct. (-2)^3 is -8, so 20 * -8 is -160. Then (6 choose 2) is 15, which is 6!/(2!4!) = 720/(2*24) = 720/48 = 15. (-2)^2 is 4, so 15*4=60. Then 60*1=60. So, adding -160 and 60 gives -100. So, that seems correct.Alternatively, maybe I can expand (1 - 2x)^6 and multiply by (1 + x) term by term and see if the x³ term comes out to -100. But expanding the entire thing would be tedious, but maybe we can check a few terms.First, (1 - 2x)^6 can be expanded using binomial coefficients:k=0: (6 choose 0)*(-2)^0 x^0 = 1*1*1 = 1k=1: (6 choose 1)*(-2)^1 x^1 = 6*(-2)x = -12xk=2: (6 choose 2)*(-2)^2 x^2 = 15*4x² = 60x²k=3: (6 choose 3)*(-2)^3 x³ = 20*(-8)x³ = -160x³k=4: (6 choose 4)*(-2)^4 x^4 = 15*16x^4 = 240x^4But actually, we only need up to x³ for the term, but since we're multiplying by (1 + x), we need up to x³ and x². Wait, but in the expansion of (1 - 2x)^6, we need the terms up to x³, since when multiplied by (1 + x), the x³ term would come from x³*1 and x²*x.So, expanding (1 - 2x)^6:1 - 12x + 60x² - 160x³ + ... (higher terms)Then, multiplying by (1 + x):Multiply each term by 1 and by x, then combine like terms.So:(1)(1) = 1(1)(x) = x(-12x)(1) = -12x(-12x)(x) = -12x²(60x²)(1) = 60x²(60x²)(x) = 60x³(-160x³)(1) = -160x³(-160x³)(x) = -160x^4And then higher terms, but we can stop here for x³.Now, combining like terms:The constant term is 1.The x term: x -12x = -11xThe x² term: -12x² + 60x² = 48x²The x³ term: 60x³ -160x³ = -100x³So, yes, the coefficient of x³ is indeed -100. So, that confirms the previous result.Therefore, the answer should be -100, which in boxed form is boxed{-100}.Final AnswerThe coefficient of the term containing (x^3) is boxed{-100}.</think>To find the coefficient of the term containing (x^3) in the expansion of ((1 - 2x)^6(1 + x)), we use the binomial theorem and consider the contributions from each polynomial.First, we expand ((1 - 2x)^6) using the binomial theorem:[(1 - 2x)^6 = sum_{k=0}^{6} binom{6}{k} (-2x)^k]We need the coefficients of (x^3) and (x^2) from this expansion because when multiplied by (1) and (x) from ((1 + x)), respectively, they will contribute to the (x^3) term in the product.1. The coefficient of (x^3) in ((1 - 2x)^6) is:[binom{6}{3} (-2)^3 = 20 cdot (-8) = -160]2. The coefficient of (x^2) in ((1 - 2x)^6) is:[binom{6}{2} (-2)^2 = 15 cdot 4 = 60]Next, we multiply these coefficients by the corresponding terms from ((1 + x)):- The term (x^3) from ((1 - 2x)^6) is multiplied by (1) (the constant term from ((1 + x))).- The term (x^2) from ((1 - 2x)^6) is multiplied by (x) (the linear term from ((1 + x))).Adding these contributions together gives the coefficient of (x^3) in the product:[-160 cdot 1 + 60 cdot 1 = -160 + 60 = -100]Thus, the coefficient of the term containing (x^3) is (boxed{-100}).,<think>Okay, so I need to find the coefficient of the term containing ( x^3 ) in the expansion of ( (1 - 2x)^6(1 + x) ). Hmm, let me think how to approach this. First, I remember that when expanding the product of two polynomials, the coefficient of a specific term can be found by multiplying the corresponding coefficients from each polynomial that contribute to that term and then summing them up. So, in this case, since we have ( (1 - 2x)^6 ) multiplied by ( (1 + x) ), the term with ( x^3 ) will come from the products of terms in ( (1 - 2x)^6 ) and ( (1 + x) ) such that the exponents add up to 3. Let me break it down. Let's denote ( A = (1 - 2x)^6 ) and ( B = (1 + x) ). Then, the expansion of ( A times B ) will have terms where each term from ( A ) is multiplied by each term from ( B ). So, to get the ( x^3 ) term, we need combinations of exponents from ( A ) and ( B ) that sum to 3. Since ( B ) has only two terms, ( 1 ) and ( x ), the exponents from ( B ) can be either 0 or 1. Therefore, the exponents from ( A ) needed would be either 3 (when multiplied by 1) or 2 (when multiplied by ( x )). So, the coefficient of ( x^3 ) in the product will be the sum of the coefficient of ( x^3 ) in ( A ) multiplied by 1 (the coefficient of ( x^0 ) in ( B )) plus the coefficient of ( x^2 ) in ( A ) multiplied by the coefficient of ( x^1 ) in ( B ). Okay, so now I need to find the coefficients of ( x^3 ) and ( x^2 ) in the expansion of ( (1 - 2x)^6 ). To do this, I should use the binomial theorem. The binomial theorem states that ( (a + b)^n = sum_{k=0}^{n} binom{n}{k} a^{n - k} b^k ). In our case, ( a = 1 ), ( b = -2x ), and ( n = 6 ). Therefore, the general term in the expansion of ( (1 - 2x)^6 ) is ( binom{6}{k} (1)^{6 - k} (-2x)^k ), which simplifies to ( binom{6}{k} (-2)^k x^k ). So, the coefficient of ( x^k ) in ( A ) is ( binom{6}{k} (-2)^k ). Therefore, the coefficient of ( x^3 ) in ( A ) is ( binom{6}{3} (-2)^3 ). Let's compute that:First, ( binom{6}{3} = frac{6!}{3!3!} = 20 ). Then, ( (-2)^3 = -8 ). Multiplying these together gives ( 20 times (-8) = -160 ). So, the coefficient of ( x^3 ) in ( A ) is -160.Next, the coefficient of ( x^2 ) in ( A ). Following the same formula, it's ( binom{6}{2} (-2)^2 ). Calculating that:( binom{6}{2} = frac{6!}{2!4!} = 15 ), and ( (-2)^2 = 4 ). Multiplying these gives ( 15 times 4 = 60 ). So, the coefficient of ( x^2 ) in ( A ) is 60.Now, the coefficient of ( x^1 ) in ( B ) is 1, since ( B = 1 + x ). The coefficient of ( x^0 ) in ( B ) is also 1. Putting it all together, the coefficient of ( x^3 ) in the product ( A times B ) is:(coefficient of ( x^3 ) in A) * (coefficient of ( x^0 ) in B) + (coefficient of ( x^2 ) in A) * (coefficient of ( x^1 ) in B)Which is:(-160) * 1 + 60 * 1 = -160 + 60 = -100Wait, that gives -100. But let me double-check my steps to make sure I didn't make a mistake. First, verifying the coefficients in ( A ):For ( x^3 ):( binom{6}{3} = 20 ), correct. ( (-2)^3 = -8 ). 20 * (-8) = -160, that's right.For ( x^2 ):( binom{6}{2} = 15 ), correct. ( (-2)^2 = 4 ). 15 * 4 = 60, that's also right.Then, multiplying by the coefficients from ( B ):Since ( B ) is ( 1 + x ), the coefficients are 1 for ( x^0 ) and 1 for ( x^1 ).So, -160 * 1 (from ( x^3 ) term in A multiplied by constant term in B) and 60 * 1 (from ( x^2 ) term in A multiplied by x term in B). Adding them together gives -160 + 60 = -100. Hmm, seems correct.But wait, let me think again. Maybe I should expand ( (1 - 2x)^6 ) and multiply by ( (1 + x) ), then check the ( x^3 ) term. Maybe there's another way to verify.Alternatively, the expansion of ( (1 - 2x)^6 ) can be written as:( 1 - 12x + 60x^2 - 160x^3 + 240x^4 - 192x^5 + 64x^6 )Wait, let me compute that to verify. Using binomial coefficients:- The constant term (x^0): ( binom{6}{0}(-2)^0 = 1 )- x^1: ( binom{6}{1}(-2)^1 = 6*(-2) = -12 )- x^2: ( binom{6}{2}(-2)^2 = 15*4 = 60 )- x^3: ( binom{6}{3}(-2)^3 = 20*(-8) = -160 )- x^4: ( binom{6}{4}(-2)^4 = 15*16 = 240 )- x^5: ( binom{6}{5}(-2)^5 = 6*(-32) = -192 )- x^6: ( binom{6}{6}(-2)^6 = 1*64 = 64 )Yes, that's correct. So the expansion of ( (1 - 2x)^6 ) is:( 1 - 12x + 60x^2 - 160x^3 + 240x^4 - 192x^5 + 64x^6 )Now, when we multiply this by ( (1 + x) ), let's perform the multiplication step by step.Multiplying each term in ( (1 - 2x)^6 ) by 1 gives the same polynomial:( 1 - 12x + 60x^2 - 160x^3 + 240x^4 - 192x^5 + 64x^6 )Multiplying each term in ( (1 - 2x)^6 ) by x gives:( x - 12x^2 + 60x^3 - 160x^4 + 240x^5 - 192x^6 + 64x^7 )Now, adding these two results together:Constant term (x^0): 1x^1 term: -12x + x = -11xx^2 term: 60x^2 - 12x^2 = 48x^2x^3 term: -160x^3 + 60x^3 = -100x^3x^4 term: 240x^4 - 160x^4 = 80x^4x^5 term: -192x^5 + 240x^5 = 48x^5x^6 term: 64x^6 - 192x^6 = -128x^6x^7 term: 64x^7So, combining all these terms:( 1 - 11x + 48x^2 - 100x^3 + 80x^4 + 48x^5 - 128x^6 + 64x^7 )Therefore, the coefficient of ( x^3 ) is indeed -100. Wait a second, that matches the previous result. So, my initial calculation was correct. The coefficient is -100.But just to be thorough, let me check again. Maybe I made a mistake in adding the coefficients?Looking at the x^3 term:From the first polynomial (multiplied by 1), the x^3 term is -160x^3.From the second polynomial (multiplied by x), the x^3 term comes from multiplying x^2 by x, which is 60x^2 * x = 60x^3.Therefore, adding those: -160x^3 + 60x^3 = (-160 + 60)x^3 = -100x^3. Correct.So, yes, the coefficient is -100. I think that's solid. But let me think if there's another method. For example, using generating functions or combinations.Alternatively, the problem can be approached by considering that when multiplying two polynomials, the coefficient of x^3 is the sum over all k from 0 to 3 of (coefficient of x^k in (1 - 2x)^6) * (coefficient of x^(3 - k) in (1 + x)).But since (1 + x) only has two terms, x^0 and x^1, the possible k's are 3 - 0 = 3 and 3 - 1 = 2. So, that's exactly the same as before: coefficients from k=3 and k=2 in (1 - 2x)^6 multiplied by coefficients from (1 + x) at 0 and 1, respectively. So, same result.Therefore, regardless of the method, the coefficient is -100. I think that's the correct answer. Maybe the problem is trying to test understanding of combining coefficients in polynomial multiplication. Since both steps—calculating the binomial coefficients and then combining them correctly—are essential here.Another check: let's compute the entire expansion step by step, but that might take too long. Alternatively, use substitution. For example, if we let x = 1, the sum of all coefficients in the expansion would be (1 - 2*1)^6*(1 + 1) = (-1)^6*2 = 1*2 = 2. But that might not help directly here. Alternatively, if I compute the coefficient of x^3 using the binomial theorem for the product. Wait, but the product is of a binomial raised to the 6th power and a binomial. Alternatively, use generating functions. But in this case, the straight-forward method is the most efficient. I don't see any mistakes in my calculations, so I think the answer is -100.Final AnswerThe coefficient of the term containing ( x^3 ) is boxed{-100}.</think>To find the coefficient of the term containing ( x^3 ) in the expansion of ( (1 - 2x)^6(1 + x) ), we use the binomial theorem and polynomial multiplication.First, we expand ( (1 - 2x)^6 ) using the binomial theorem:[(1 - 2x)^6 = sum_{k=0}^{6} binom{6}{k} (-2x)^k]The coefficients of ( x^3 ) and ( x^2 ) in this expansion are:- Coefficient of ( x^3 ): (binom{6}{3} (-2)^3 = 20 times (-8) = -160)- Coefficient of ( x^2 ): (binom{6}{2} (-2)^2 = 15 times 4 = 60)Next, we consider the polynomial ( (1 + x) ). The coefficients of ( x^0 ) and ( x^1 ) are both 1.To find the coefficient of ( x^3 ) in the product ( (1 - 2x)^6(1 + x) ), we combine the coefficients from each polynomial:- The term ( x^3 ) is obtained by multiplying the coefficient of ( x^3 ) in ( (1 - 2x)^6 ) by the constant term in ( (1 + x) ): ( -160 times 1 = -160 )- The term ( x^3 ) is also obtained by multiplying the coefficient of ( x^2 ) in ( (1 - 2x)^6 ) by the ( x ) term in ( (1 + x) ): ( 60 times 1 = 60 )Adding these contributions together gives:[-160 + 60 = -100]Thus, the coefficient of the term containing ( x^3 ) is (boxed{-100}).]

🔑:The term containing x^3 can be obtained by selecting the x^3 term from the first expression and the constant term from the second expression, as well as selecting the x^2 term from the first expression and the x term from the second expression. The general term of the binomial expansion of the first expression is T_{r+1} = C_6^r(-2x)^r. Therefore, the coefficient of the term containing x^3 is C_6^3(-2)^3 + C_6^2(-2)^2 = -100. Hence, the answer is boxed{-100}.