🧠:[<think>Okay, so Wendy and Joshua are each rolling one six-sided die, and Wendy wins if her roll is higher than Joshua's. I need to find the probability that Wendy's roll is higher, express it as a reduced fraction a/b, and then find a + b. Alright, let's think through this step by step.First, both Wendy and Joshua are rolling a single die. Each die has six faces, numbered 1 through 6. The possible outcomes for each are independent, right? So the total number of possible outcomes when they both roll their dice is 6 (for Wendy) multiplied by 6 (for Joshua), which is 36. So there are 36 possible pairs of results.Now, we need to count how many of these 36 outcomes result in Wendy's number being higher than Joshua's. Let's break this down. For each possible roll that Wendy could have, we can count how many rolls Joshua could have that are lower. Then sum those up.Let's start with Wendy rolling a 1. If Wendy rolls a 1, there are no possible numbers Joshua can roll that are lower than 1, since the lowest number on a die is 1. So in this case, there are 0 favorable outcomes.If Wendy rolls a 2, Joshua needs to roll a 1 for Wendy to win. That's 1 favorable outcome.If Wendy rolls a 3, Joshua can roll a 1 or 2. That's 2 favorable outcomes.Similarly, if Wendy rolls a 4, Joshua can roll 1, 2, or 3. That's 3 favorable.If Wendy rolls a 5, Joshua can roll 1, 2, 3, or 4. That's 4 favorable.If Wendy rolls a 6, Joshua can roll 1, 2, 3, 4, or 5. That's 5 favorable.So, adding those up: 0 + 1 + 2 + 3 + 4 + 5 = 15. So there are 15 favorable outcomes where Wendy's roll is higher than Joshua's.Therefore, the probability that Wendy rolls higher is 15/36. Now, we need to simplify that fraction. Both 15 and 36 are divisible by 3. Dividing numerator and denominator by 3 gives 5/12. 5 and 12 have no common factors besides 1, so that's the reduced form.So a is 5 and b is 12. Therefore, a + b = 5 + 12 = 17.Wait, let me double-check that. Let me recount the favorable outcomes to make sure I didn't make a mistake.For Wendy rolling 2: Joshua can roll 1. That's 1.For Wendy rolling 3: Joshua can roll 1 or 2. 2.Wendy 4: Joshua 1,2,3. 3.Wendy 5: 1,2,3,4. 4.Wendy 6: 1,2,3,4,5. 5.Total: 1 + 2 + 3 + 4 + 5 = 15. Yes, that's correct. 15/36 simplifies to 5/12. 5 and 12 are coprime, so yes, a + b = 17.Alternatively, another way to think about this is symmetry. In the case where both players roll a die, there are three possibilities: Wendy's roll is higher, Joshua's roll is higher, or they tie. The probability of a tie is the number of outcomes where they roll the same number. There are 6 such outcomes: (1,1), (2,2), ..., (6,6). So the probability of a tie is 6/36 = 1/6. Therefore, the remaining probability is 1 - 1/6 = 5/6, which is split equally between Wendy and Joshua, assuming the situations are symmetric. So the probability Wendy's roll is higher would be (5/6)/2 = 5/12. That's the same answer as before, which confirms that it's correct.So, yes, the answer is 5/12, and 5 + 12 is 17.Final Answerboxed{17}</think>Wendy and Joshua each roll a single six-sided die. Wendy wins if her roll is higher than Joshua's. To find the probability of this happening, we consider all possible outcomes.There are a total of (6 times 6 = 36) possible outcomes when both dice are rolled. We need to count the number of outcomes where Wendy's roll is higher than Joshua's.For each possible roll Wendy could have:- If Wendy rolls a 1, there are 0 favorable outcomes.- If Wendy rolls a 2, there is 1 favorable outcome (Joshua rolls 1).- If Wendy rolls a 3, there are 2 favorable outcomes (Joshua rolls 1 or 2).- If Wendy rolls a 4, there are 3 favorable outcomes (Joshua rolls 1, 2, or 3).- If Wendy rolls a 5, there are 4 favorable outcomes (Joshua rolls 1, 2, 3, or 4).- If Wendy rolls a 6, there are 5 favorable outcomes (Joshua rolls 1, 2, 3, 4, or 5).Summing these favorable outcomes: (0 + 1 + 2 + 3 + 4 + 5 = 15).Thus, the probability that Wendy's roll is higher than Joshua's is (frac{15}{36}). Simplifying this fraction, we divide the numerator and denominator by their greatest common divisor, which is 3: (frac{15 div 3}{36 div 3} = frac{5}{12}).The fraction (frac{5}{12}) is in its simplest form, so (a = 5) and (b = 12). Therefore, (a + b = 5 + 12 = 17).[boxed{17}],<think>Okay, let's see. The problem is about Wendy and Joshua each rolling a single six-sided die, and we need to find the probability that Wendy's roll is higher than Joshua's roll. The answer should be in the form of a fraction a/b where a and b are coprime, and then find a + b. Alright, so I need to compute the probability that Wendy's die shows a higher number than Joshua's die.First, let me recall that when two dice are rolled, there are a total number of possible outcomes. Since each die has 6 faces, the total number of outcomes is 6 * 6 = 36. That's the denominator for our probability.Now, the numerator is the number of outcomes where Wendy's roll is higher than Joshua's. So, I need to count how many such pairs (Wendy's die, Joshua's die) exist where the first number is greater than the second.Let me think. Let's consider all possible values that Joshua can roll, and then for each of those, count how many values Wendy can roll that are higher.So, if Joshua rolls a 1, Wendy can roll 2, 3, 4, 5, or 6 to win. That's 5 possibilities.If Joshua rolls a 2, Wendy needs to roll 3, 4, 5, or 6. That's 4 possibilities.If Joshua rolls a 3, Wendy has to roll 4, 5, or 6. That's 3.If Joshua rolls a 4, Wendy needs 5 or 6. That's 2.If Joshua rolls a 5, Wendy must roll a 6. That's 1.If Joshua rolls a 6, Wendy can't roll anything higher, so that's 0.So adding those up: 5 + 4 + 3 + 2 + 1 + 0 = 15. So there are 15 favorable outcomes where Wendy's roll is higher.Therefore, the probability is 15/36. But we need to simplify that fraction. Both 15 and 36 are divisible by 3. Dividing numerator and denominator by 3 gives 5/12. So a is 5 and b is 12. They are coprime since 5 is prime and doesn't divide 12. So a + b is 5 + 12 = 17.Wait, let me double-check to make sure I didn't make a mistake. Another way to approach this is to note that when two dice are rolled, the probability that the first is higher is equal to the probability that the second is higher, due to symmetry. And the remaining probability is the chance that they are equal.The probability that they are equal is 6/36 = 1/6. So the total probability that one is higher than the other is 1 - 1/6 = 5/6. Since the situations where Wendy is higher and Joshua is higher are symmetric, each has probability (5/6)/2 = 5/12. That matches the earlier result.So that seems to confirm that 15/36 simplifies to 5/12, so the answer is 5 + 12 = 17.Final Answerboxed{17}</think>To determine the probability that Wendy rolls a higher number than Joshua when each rolls a six-sided die, we start by noting there are a total of (6 times 6 = 36) possible outcomes.We then count the number of favorable outcomes where Wendy's roll is higher than Joshua's. For each possible roll of Joshua's die, we count how many rolls Wendy can have that are higher:- If Joshua rolls a 1, Wendy can roll 2, 3, 4, 5, or 6 (5 outcomes).- If Joshua rolls a 2, Wendy can roll 3, 4, 5, or 6 (4 outcomes).- If Joshua rolls a 3, Wendy can roll 4, 5, or 6 (3 outcomes).- If Joshua rolls a 4, Wendy can roll 5 or 6 (2 outcomes).- If Joshua rolls a 5, Wendy can roll 6 (1 outcome).- If Joshua rolls a 6, Wendy has no possible higher rolls (0 outcomes).Summing these outcomes gives (5 + 4 + 3 + 2 + 1 + 0 = 15). Therefore, the probability is (frac{15}{36}).Simplifying this fraction, we divide both the numerator and the denominator by their greatest common divisor, which is 3: (frac{15}{36} = frac{5}{12}).The integers (a) and (b) are 5 and 12, respectively. Since they are coprime, we find (a + b = 5 + 12 = 17).Thus, the final answer is (boxed{17}).]

🔑:1. To determine the probability that Wendy rolls a higher number than Joshua, we first need to consider all possible outcomes when both roll a six-sided die. Each die has 6 faces, so there are a total of (6 times 6 = 36) possible outcomes.2. We need to count the number of outcomes where Wendy's roll is higher than Joshua's roll. Let's list these outcomes: - If Wendy rolls a 2, Joshua must roll a 1. - If Wendy rolls a 3, Joshua can roll a 1 or 2. - If Wendy rolls a 4, Joshua can roll a 1, 2, or 3. - If Wendy rolls a 5, Joshua can roll a 1, 2, 3, or 4. - If Wendy rolls a 6, Joshua can roll a 1, 2, 3, 4, or 5.3. Counting these outcomes: - For Wendy rolling a 2: 1 outcome (Joshua rolls 1) - For Wendy rolling a 3: 2 outcomes (Joshua rolls 1 or 2) - For Wendy rolling a 4: 3 outcomes (Joshua rolls 1, 2, or 3) - For Wendy rolling a 5: 4 outcomes (Joshua rolls 1, 2, 3, or 4) - For Wendy rolling a 6: 5 outcomes (Joshua rolls 1, 2, 3, 4, or 5)4. Summing these outcomes, we get: [ 1 + 2 + 3 + 4 + 5 = 15 ]5. Therefore, there are 15 favorable outcomes where Wendy's roll is higher than Joshua's roll out of 36 possible outcomes.6. The probability that Wendy rolls higher than Joshua is: [ frac{15}{36} = frac{5}{12} ]7. Since (a) and (b) are relatively prime positive integers such that (frac{a}{b} = frac{5}{12}), we have (a = 5) and (b = 12).8. The value of (a + b) is: [ 5 + 12 = 17 ]The final answer is (boxed{17}).

🧠:[<think>Okay, so I have this problem here where there's a sequence of natural numbers starting from 1, and certain numbers are colored red following specific rules. The red subsequence starts as 1, 2, 4, 5, 7, 9, 10, 12, 14, 16, 17, and so on. The question is asking for the 1996th number in this red subsequence. Hmm, let me try to figure out the pattern here.First, let me list out the given sequence with the colored numbers and see if I can identify the pattern step by step.1. The first step is to color 1. So position 1 is 1.2. Then color two even numbers: 2, 4. So positions 2 and 3 are 2 and 4.3. Next, color three consecutive odd numbers closest to 4. The closest odd numbers to 4 would be 5, 7, 9. So positions 4, 5, 6 are 5, 7, 9.4. Then color four consecutive even numbers closest to 9. The closest even numbers to 9 are 10, 12, 14, 16. Positions 7, 8, 9, 10 are 10, 12, 14, 16.5. Then color five consecutive odd numbers closest to 16. That would be 17, 19, 21, 23, 25. Positions 11 to 15 are these numbers.6. The pattern continues, alternating between coloring a set of even numbers and odd numbers, each time increasing the count by one. So after five odds, next should be six evens, then seven odds, etc.So, the pattern is:- Start with 1 (colored in step 1)- Then alternately color even and odd numbers, each time increasing the number of terms by one: - Step 2: 2 even numbers (2, 4) - Step 3: 3 odd numbers (5, 7, 9) - Step 4: 4 even numbers (10, 12, 14, 16) - Step 5: 5 odd numbers (17, 19, 21, 23, 25) - Step 6: 6 even numbers - Step 7: 7 odd numbers - Etc.Each "step" corresponds to a block of numbers, either even or odd, starting with even after the first step. Each block has a size that increments by one each time. The numbers in each block are the closest numbers to the last number of the previous block. So, for example, after coloring 4 (even), the next block is the three closest odd numbers to 4, which are 5, 7, 9. Then after 9 (odd), the next block is four closest even numbers to 9, which are 10, 12, 14, 16.Wait, the problem says "closest to 4", "closest to 9", etc. But when moving from an even block to an odd block or vice versa, do we start right after the last number or the closest numbers around the last number? Let's check the examples given.From 4 (step 2 ends at 4), the next step is three consecutive odd numbers closest to 4. The closest odd number to 4 is 5, then 7, 9. So they start at 5 and take three odds. Then from 9 (step 3 ends at 9), the next step is four consecutive even numbers closest to 9. The closest even number to 9 is 10, then 12, 14, 16. So starting at 10. Then from 16 (step 4 ends at 16), the next is five consecutive odd numbers closest to 16. The closest odd number to 16 is 17, then 19, 21, 23, 25. So starting at 17.Therefore, after each block, the next block starts at the next number (either even or odd) closest to the last number of the previous block. So if the last number was even, the next odd block starts at the next odd number, and vice versa. But since the next block is of the opposite parity, starting from the next number after the last one.Wait, but when moving from 4 (even) to the next odd numbers, the next odd after 4 is 5, so that's straightforward. Similarly, after 9 (odd), the next even is 10. After 16 (even), next odd is 17. So in each case, the next block starts at the next number of the required parity after the last number of the previous block. Then, the block consists of n consecutive numbers of that parity, where n increases by 1 each time.But the problem statement mentions "closest to X". For example, after 4, the three consecutive odd numbers closest to 4. But the closest odd number to 4 is 3 and 5. But since 3 is less than 4, and we need the closest ones. Wait, but 4 is even, so the next odd after 4 is 5, and prior odd is 3. But in the example, they took 5,7,9. So starting from 5, moving upwards. So perhaps "closest" here means the next consecutive numbers after the last number. So starting from the next number of the required parity. Then taking n numbers. That seems to be the case.So the rule is:- After coloring a number, the next block starts at the next number of the opposite parity and continues for n numbers, increasing n by 1 each time.Wait, but the problem says "closest to X". Maybe "closest" in the sense that if you have to pick n numbers of the opposite parity around X, but since X is either even or odd, and the next block is the opposite, then the numbers are just the next n numbers of that parity starting from X+1 (if X is even) or X+1 (if X is odd). But in the example, after 4 (even), the next block is odd numbers closest to 4, which are 5,7,9. So starting at 5. If X is 4, then the closest odd number would be 5 (since 3 is also at distance 1, but maybe they take the higher ones?). Wait, 3 is 1 away from 4, and 5 is also 1 away. So why did they choose 5,7,9 instead of 3,5,7?Looking back at the problem statement: "color the three consecutive odd numbers closest to 4, which are 5, 7, 9". So according to the problem, those are considered the closest. Hmm. But 3 is as close to 4 as 5 is. So maybe "closest" here is defined as the next ones after 4. So the numbers greater than 4. So maybe "closest" here is interpreted as the closest numbers that are higher than the previous block's last number. That would make sense.Similarly, when coloring even numbers closest to 9, the next even number after 9 is 10, then 12, 14, 16. So they take the next four even numbers after 9. So maybe "closest" here is defined as the numbers immediately following the last number, rather than considering both directions. So perhaps "closest" is a bit of a misnomer, and it's actually the next n numbers of the required parity after the last number.So maybe the pattern is:- Start with 1 (step 1: 1 number, odd)- Then, step 2: next 2 even numbers after 1: 2,4- Step 3: next 3 odd numbers after 4: 5,7,9- Step 4: next 4 even numbers after 9:10,12,14,16- Step 5: next 5 odd numbers after 16:17,19,21,23,25- Step 6: next 6 even numbers after 25:26,28,30,32,34,36- Step 7: next 7 odd numbers after 36:37,39,41,43,45,47,49- And so on.So each step alternates between even and odd, starting with odd (1), then even, odd, even, etc. Each step has a number of terms equal to the step number. Wait, but step 1 is 1 number, step 2 is 2 numbers, step 3 is 3 numbers, etc. But the problem statement says:First, color 1; then color two even numbers 2, 4; then color the three consecutive odd numbers closest to 4, which are 5, 7, 9; then color the four consecutive even numbers closest to 9, which are 10, 12, 14, 16; then color the five consecutive odd numbers closest to 16, which are 17, 19, 21, 23, 25.So step 1: size 1 (1)step 2: size 2 (2,4)step 3: size 3 (5,7,9)step 4: size 4 (10,12,14,16)step 5: size 5 (17,19,21,23,25)step 6: size 6 (next 6 even numbers after 25:26,28,30,32,34,36)step 7: size 7 (next 7 odd numbers after 36:37,39,...,49)and so on.Therefore, the size of each block is increasing by 1 each time, starting from 1. The parity alternates starting with odd (1), then even (2,4), then odd (5,7,9), etc.Therefore, the structure is:Block 1: 1 number (odd)Block 2: 2 numbers (even)Block 3: 3 numbers (odd)Block 4: 4 numbers (even)Block 5: 5 numbers (odd)...So each block k has size k, alternating between odd and even starting with odd for k=1.Therefore, blocks with odd k (1,3,5,...) are odd numbers, and even k (2,4,6,...) are even numbers? Wait, no. Wait, block 1 is odd, block 2 is even, block 3 is odd, block 4 is even, etc. So the parity alternates with each block, starting with odd. So block 1: odd, block 2: even, block3: odd, block4: even, etc. Each block k has k numbers, starting from the next number after the previous block. The starting number of each block is the next number of the required parity after the last number of the previous block.For example:Block1: 1 (ends at 1)Block2: next even after 1 is 2, then take 2 evens: 2,4 (ends at 4)Block3: next odd after 4 is 5, take 3 odds:5,7,9 (ends at 9)Block4: next even after 9 is 10, take 4 evens:10,12,14,16 (ends at 16)Block5: next odd after 16 is17, take 5 odds:17,19,21,23,25 (ends at25)Block6: next even after25 is26, take6 evens:26,28,30,32,34,36 (ends at36)Block7: next odd after36 is37, take7 odds:37,39,...,49 (ends at49)Block8: next even after49 is50, take8 evens:50,52,...,64 (ends at64)And so on.Therefore, the key is that each block starts right after the previous block's last number, but only considering the required parity. So the starting number for each block is the smallest number of the required parity greater than the last number of the previous block. Then, you take k numbers of that parity in sequence, where k is the block number.Therefore, the problem reduces to figuring out how many blocks we need to reach the 1996th number, and then determine which number that is.First, let's model the blocks:Each block k (starting from 1) has k numbers. So the total numbers up to block n is 1 + 2 + 3 + ... + n = n(n + 1)/2.We need to find the smallest n such that n(n + 1)/2 ≥ 1996. But since the blocks alternate parity, but the individual numbers within a block are consecutive odds or evens. However, the numbers themselves can be calculated once we know the starting number of each block.But to find the 1996th number, we need to know which block it's in and its position within that block.First, let's find the cumulative count:Total numbers after block 1:1After block 2:1 + 2 =3After block3:3 +3=6After block4:6 +4=10After block5:10 +5=15After block6:15 +6=21Continuing this, the cumulative numbers after each block k is k(k +1)/2.We need to find the block number m such that the cumulative sum up to block m -1 is less than 1996, and cumulative sum up to block m is greater or equal to 1996.So solve m(m +1)/2 ≥ 1996.Let's approximate m:m^2/2 ≈1996 → m≈sqrt(2*1996)=sqrt(3992)≈63.18. So m=63 gives 63*64/2=2016, which is greater than 1996. m=62: 62*63/2=1953, which is less than 1996. Therefore, the 1996th number is in block63.Wait, but blocks alternate between odd and even. Since block1 is odd, block2 even, block3 odd,..., so odd blocks (1,3,5,...) are odd numbers, even blocks (2,4,6,...) are even numbers. Therefore, block63 is an odd block (since 63 is odd) and hence contains 63 consecutive odd numbers.But the position within block63 is 1996 - cumulative up to block62.Cumulative up to block62:62*63/2=1953. Therefore, the position within block63 is 1996 -1953=43. So the 1996th number is the 43rd number in block63.Now, we need to find the starting number of block63. To do this, we need to track the starting number of each block.Each block starts at the next number of the required parity after the last number of the previous block.So starting numbers:Block1:1Block2: next even after1 is2Block3: next odd after4 is5Block4: next even after9 is10Block5: next odd after16 is17Block6: next even after25 is26Block7: next odd after36 is37Block8: next even after49 is50...We need a way to compute the starting number of block m. Let's try to find a pattern or formula.First, let's note that the last number of each block can be determined based on the starting number and the number of terms.For even blocks (even numbers):If a block is even and has k numbers, starting at s, then the numbers are s, s+2, s+4, ..., s+2(k-1). The last number is s + 2(k -1).Similarly, for odd blocks:Starting at s, numbers are s, s+2, ..., s+2(k-1). Last number is s + 2(k -1).Therefore, for any block, the last number is starting number + 2*(size -1).Now, we need to find the starting number of block m. Let's denote S(m) as the starting number of block m.We know that:S(1) =1For m>1, S(m) = last number of block(m-1) +1 (if next parity is even) or +2 (if next parity is odd? Wait, no.Wait, after the last number of block(m-1), which is either even or odd, depending on the parity of block(m-1). The next block m has the opposite parity. Therefore, if block(m-1) ended with an even number, then the next number of the opposite parity (odd) would be last +1. If block(m-1) ended with an odd number, the next even number is last +1.Wait, regardless of the parity of the last number, the next number of the opposite parity is last +1 if the last number is even (to get odd), or last +1 if the last number is odd (to get even). Wait, no. Wait, if last number is even, next odd is last +1. If last number is odd, next even is last +1. So in both cases, S(m) = last(m-1) +1.Wait, let me check:Block1 ends at 1 (odd). Next block is even. So next even after1 is 2=1+1.Block2 ends at4 (even). Next block is odd. Next odd after4 is5=4+1.Block3 ends at9 (odd). Next even after9 is10=9+1.Block4 ends at16 (even). Next odd after16 is17=16+1.Yes, so in all cases, the starting number of the next block is last number of previous block +1, which is the next number of the required parity. Therefore, S(m) = last(m-1) +1.And since last(m-1) = S(m-1) + 2*(k-1 -1)? Wait, no.Wait, for block(m-1), which has size k = m-1. The starting number is S(m-1), and the numbers are S(m-1), S(m-1)+2, ..., S(m-1)+2*( (m-1) -1 ) = S(m-1) + 2*(m-2). Therefore, the last number of block(m-1) is S(m-1) + 2*(m -2).Therefore, S(m) = last(m-1) +1 = [S(m-1) + 2*(m -2)] +1 = S(m-1) + 2*(m -2) +1.But this seems recursive. Let's see if we can find a closed-form formula for S(m).Alternatively, let's note that the starting number of each block alternates between odd and even. Since block1 starts at1 (odd), block2 starts at2 (even), block3 at5 (odd), block4 at10 (even), block5 at17 (odd), block6 at26 (even), block7 at37 (odd), etc.Looking at the starting numbers:m | S(m)1 | 1 (odd)2 | 2 (even)3 |5 (odd)4 |10 (even)5 |17 (odd)6 |26 (even)7 |37 (odd)8 |50 (even)...Looking at these starting numbers, maybe we can find a pattern.For odd m (blocks 1,3,5,7,...):m=1:1m=3:5m=5:17m=7:37m=9: ?Similarly, for even m (blocks2,4,6,8,...):m=2:2m=4:10m=6:26m=8:50Let me see if these follow a quadratic pattern.For odd m:Let m=2k+1, where k=0,1,2,3,...For k=0, m=1:1k=1, m=3:5k=2, m=5:17k=3, m=7:37Check differences:5 -1=417 -5=1237 -17=20Differences:4,12,20,...Which increase by8 each time? 4, 12 (4+8), 20 (12+8), etc.Similarly, starting from 1:Term for k=0:1Term for k=1:1 +4=5Term for k=2:5 +12=17Term for k=3:17 +20=37Term for k=4:37 +28=65But wait, the starting numbers for odd blocks seem to be following a sequence where each term is previous term +8k, where k starts at1?Wait, 1, 5,17,37,65,...Compute the differences between consecutive terms:5 -1=4=4*117 -5=12=4*337 -17=20=4*565 -37=28=4*7So the differences are 4*1,4*3,4*5,4*7,...So the nth term (for odd m=2k+1) is 1 +4*(1 +3 +5 +...+(2k-1)).But 1 +3 +5 +...+(2k-1)=k^2.Therefore, S(m) for odd m=2k+1 is 1 +4*k^2.Check:For k=0: m=1, S(m)=1 +4*0^2=1. Correct.k=1: m=3, S(m)=1 +4*1^2=5. Correct.k=2: m=5, S(m)=1 +4*2^2=17. Correct.k=3: m=7, S(m)=1 +4*3^2=37. Correct.Similarly, k=4: m=9, S(m)=1 +4*4^2=65. Let's verify with the prior calculation. Block7 ends at49 (since block7 has7 odds starting at37:37,39,41,43,45,47,49). Then block8 starts at50. Block8 has8 evens:50,52,...,64. Then block9 starts at65, which is 64 +1=65. So yes, correct.Therefore, for odd m=2k+1, S(m)=1 +4k^2.Similarly, for even m=2k:Looking at starting numbers:m=2:2m=4:10m=6:26m=8:50Check the pattern here.Differences:10 -2=826 -10=1650 -26=24Differences:8,16,24,... increasing by8 each time.So for even m=2k:Starting numbers:Term1:2Term2:10=2 +8Term3:26=10 +16Term4:50=26 +24Term5:82=50 +32So differences are 8,16,24,32,... which is 8*1,8*2,8*3,8*4,...So the nth term (for even m=2k) is 2 +8*(1 +2 +3 +...+(k-1)).Sum of 1 to (k-1) is k(k-1)/2.Therefore, S(m)=2 +8*(k(k -1)/2)=2 +4k(k -1).Check:For k=1: m=2k=2, S(m)=2 +4*1*(0)=2. Correct.k=2: m=4, S(m)=2 +4*2*1=2 +8=10. Correct.k=3: m=6, S(m)=2 +4*3*2=2 +24=26. Correct.k=4: m=8, S(m)=2 +4*4*3=2 +48=50. Correct.Therefore, for even m=2k, S(m)=2 +4k(k -1).So now we have formulas for S(m):- If m is odd: m=2k+1, S(m)=1 +4k²- If m is even: m=2k, S(m)=2 +4k(k -1)Therefore, given a block number m, we can compute its starting number.Now, since the 1996th number is in block63, which is an odd block (since63 is odd), and it's the 43rd number in that block. Let's confirm:Total numbers up to block62:62*63/2=1953.1996 -1953=43. Therefore, it's the 43rd number in block63.Now, block63 is an odd block, so all numbers are odd. The starting number of block63 can be computed using the formula for odd m.For m=63, which is odd, m=2k+1 →63=2k+1→k=31.Thus, S(63)=1 +4*(31)^2=1 +4*961=1 +3844=3845.Therefore, block63 starts at3845 and has63 consecutive odd numbers. The numbers are3845,3847,3849,..., each increasing by2.The 43rd number in this block isS(m) +2*(43 -1)=3845 +2*42=3845 +84=3929.Therefore, the 1996th number in the red subsequence is3929.Wait, but let me verify this step-by-step to be sure.First, confirming the starting number of block63:m=63 is odd, so k=31. S(m)=1 +4*31²=1 +4*961=1 +3844=3845. Correct.Then, the numbers in block63 are:First number:3845 (position1954)Second:3847 (1955)...43rd number:3845 +2*(43-1)=3845 +84=3929 (position1953 +43=1996). Correct.Therefore, the answer should be3929.But let me cross-validate this by checking smaller blocks.For example, block5 is odd, starting at17. The numbers are17,19,21,23,25. The 5th number is25. Using the formula:For m=5, which is odd, k=2. S(5)=1 +4*(2)^2=1 +16=17. Correct.5th number in block5:17 +2*(5 -1)=17 +8=25. Correct.Similarly, block3 is odd, starting at5. The third number should be5 +2*(3-1)=5 +4=9. Which matches the given sequence. Correct.For even blocks, let's check block4: even, starting at10. The numbers are10,12,14,16. Fourth number is16. Formula:For m=4, even, k=2. S(4)=2 +4*2*(2 -1)=2 +8=10. Correct. The fourth number:10 +2*(4 -1)=10 +6=16. Correct.Another even block: block6, m=6, even, k=3. S(6)=2 +4*3*2=2 +24=26. Numbers are26,28,30,32,34,36. Sixth number:26 +2*(6 -1)=26 +10=36. Correct.Therefore, the formula seems solid.Thus, for block63, the starting number is3845, and the 43rd number is3845 +84=3929.Therefore, the 1996th number is3929.Final Answerboxed{3929}</think>To determine the 1996th number in the red subsequence, we first identify the pattern of the sequence. The sequence alternates between blocks of even and odd numbers, with each block increasing in size by one. The blocks start with 1 (odd), followed by 2 even numbers, 3 odd numbers, 4 even numbers, and so on.1. Identify the block containing the 1996th number: - The cumulative number of elements up to block ( n ) is given by ( frac{n(n+1)}{2} ). - Solving ( frac{n(n+1)}{2} geq 1996 ), we find ( n = 63 ) since ( frac{63 times 64}{2} = 2016 ) and ( frac{62 times 63}{2} = 1953 ). - The 1996th number is in block 63, specifically at position ( 1996 - 1953 = 43 ) within this block.2. Determine the starting number of block 63: - Block 63 is an odd block. The starting number of an odd block ( m = 2k + 1 ) is given by ( 1 + 4k^2 ). - For ( m = 63 ), ( k = 31 ), so the starting number is ( 1 + 4 times 31^2 = 3845 ).3. Find the 43rd number in block 63: - The numbers in block 63 are consecutive odd numbers starting from 3845. - The 43rd number is ( 3845 + 2 times (43 - 1) = 3845 + 84 = 3929 ).Thus, the 1996th number in the red subsequence is (boxed{3929}).,<think>Alright, let's try to figure out the 1996th number in this red subsequence. The problem describes a pattern where we color numbers in stages. Each stage alternates between coloring even and odd numbers, increasing the count by one each time. The first few stages are given:1. Color 1 (1 number, odd)2. Color two even numbers: 2, 43. Color three consecutive odd numbers closest to 4: 5, 7, 94. Color four consecutive even numbers closest to 9: 10, 12, 14, 165. Color five consecutive odd numbers closest to 16: 17, 19, 21, 23, 256. And so on...So the pattern is: starting with 1, then alternately adding blocks of even and odd numbers, each block having one more number than the previous block. The numbers in each block are consecutive even or odd numbers closest to the last number of the previous block.First, let's confirm the pattern:- Stage 1: 1 number (odd). So 1.- Stage 2: 2 even numbers. The next even numbers after 1 are 2 and 4.- Stage 3: 3 odd numbers closest to 4. The closest odd numbers to 4 are 5, 7, 9 (since 3 is before 4, but we need consecutive odds after 4, right? Wait, 4 is even, the closest odd numbers would be 5, 7, 9. Hmm, because 3 is lower than 4, but the next ones after 4 are 5,7,9. So that makes sense.- Stage 4: 4 even numbers closest to 9. The next even number after 9 is 10, then 12,14,16. So that's correct.- Stage 5: 5 odd numbers closest to 16. Next odd after 16 is 17, then 19,21,23,25. Wait, 17,19,21,23,25 – that's five numbers. Correct.So the pattern alternates between even and odd, with each stage increasing the number of terms by one. Each stage's numbers are consecutive even or odd numbers starting from the next even/odd number after the last number of the previous stage.So, to find the 1996th number in the red subsequence, we need to figure out how many stages are needed to reach at least 1996 numbers, then determine which stage the 1996th number is in, and then compute its value.First, let's note that each stage n (starting from n=1) contributes n numbers. The stages alternate between odd and even, starting with odd (stage 1: odd), then even (stage 2: even), then odd (stage3: odd), etc. Wait, actually looking back:Wait, stage 1: oddstage 2: evenstage3: oddstage4: evenstage5: oddSo alternates starting with odd. So odd stages (1,3,5,...) are coloring odd numbers, even stages (2,4,6,...) are coloring even numbers.Therefore, for each stage k:- If k is odd: color k odd numbers starting from the next odd after the last number of the previous stage.- If k is even: color k even numbers starting from the next even after the last number of the previous stage.But we need to check if this alternation holds. Let's see:Stage1: odd (1 number)Stage2: even (2 numbers)Stage3: odd (3 numbers)Stage4: even (4 numbers)Stage5: odd (5 numbers)Stage6: even (6 numbers)...Yes, so alternates starting with odd. So each odd-numbered stage (1,3,5,...) adds k odd numbers, each even-numbered stage (2,4,6,...) adds k even numbers. The starting point for each stage is the next even or odd number after the last number of the previous stage.Therefore, the last number of each stage will be:Stage1: 1Stage2: 4Stage3: 9Stage4: 16Stage5: 25Stage6: 36...Wait a second, 1, 4, 9, 16, 25, 36... These are perfect squares. That's interesting. Let's verify:Stage1 ends at 1 (1^2)Stage2 ends at 4 (2^2)Stage3 ends at 9 (3^2)Stage4 ends at 16 (4^2)Stage5 ends at 25 (5^2)Stage6 ends at 36 (6^2)...So in general, stage k ends at k^2. That seems to be a pattern here. Let's check.After stage1: 1. So last number is 1 (1^2). Correct.Stage2: color two even numbers starting from 2. So 2,4. Last number 4 (2^2). Correct.Stage3: color three odd numbers starting from 5. 5,7,9. Last number 9 (3^2). Correct.Stage4: color four even numbers starting from 10. Wait, 10,12,14,16. Last number 16 (4^2). Correct.Stage5: color five odd numbers starting from 17. 17,19,21,23,25. Last number 25 (5^2). Correct.Stage6: color six even numbers starting from 26. 26,28,30,32,34,36. Last number 36 (6^2). Correct.So the pattern is that after each stage k, the last number colored is k^2. Therefore, each stage k consists of k numbers, alternating between even and odd, starting after the previous square. So after (k-1)^2, the next stage k numbers will be either even or odd, starting from the next even/odd after (k-1)^2, and ending at k^2.Therefore, the numbers in stage k are:If k is odd: (k-1)^2 + 2, (k-1)^2 + 4, ..., up to k^2. But wait, for odd k, we need odd numbers. Wait, for example, stage3 (k=3, odd): previous square is 4 (2^2). Next odd number after 4 is 5. Then 5,7,9 (three numbers). So starting from (k-1)^2 +1 if (k-1) is even? Wait, (k-1) when k is odd is even. So (k-1)^2 is even squared, which is even. So next odd number is (k-1)^2 +1. Then add 2 each time. So numbers are (k-1)^2 +1 + 2*(n-1) for n=1 to k.Similarly, for even k: previous square is (k-1)^2 (which is odd, since k-1 is odd). Then next even number is (k-1)^2 +1, which is even? Wait, (k-1)^2 is odd (since k-1 is odd). Then next even is (k-1)^2 +1. Then add 2 each time. For example, stage4: after 9 (3^2), next even is 10. Then 10,12,14,16. So numbers are (k-1)^2 +1 + 2*(n-1) for n=1 to k.Therefore, general formula for numbers in stage k:If k is odd: starts at (k-1)^2 + 2 (since previous stage ended at (k-1)^2, which was even? Wait, no. Let's see.Wait, when k is odd, the previous stage was k-1, which is even. The last number of stage k-1 is (k-1)^2. For even k-1, (k-1)^2 is even (since even squared is even). Therefore, the next number after an even number (k-1)^2 is (k-1)^2 +1. But since k is odd, the current stage k is odd, so we need to color odd numbers. Therefore, starting from (k-1)^2 +1, which is odd, and then adding 2 each time for k terms. Wait, but let's check with k=3.For k=3 (odd): previous stage k-1=2 (even), ended at 4. Next odd number is 5. So starting at 5, which is 4 +1. Then 5,7,9. So starting at (k-1)^2 +1. Then each subsequent term is +2. So the numbers are (k-1)^2 +1 + 2*(n-1) for n=1 to k. So for k=3, n=1: 4 +1 +0=5; n=2: 4+1+2=7; n=3:4+1+4=9. Correct.Similarly for k=5: previous stage ended at 16 (4^2). Next odd number is 17. So numbers are 17,19,21,23,25. Which is 16 +1 +2*(n-1). So yes.For even k: previous stage was k-1 (odd), ended at (k-1)^2, which is odd. Then the next even number is (k-1)^2 +1, and then add 2 for k terms. For example, k=4: previous stage ended at 9 (3^2). Next even number is 10. Then 10,12,14,16. Which is 9 +1 +2*(n-1). So n=1:10, n=2:12, etc. Correct.Therefore, generalizing:For stage k:If k is odd:- Numbers: (k-1)^2 +1 + 2*(n-1) for n=1 to kIf k is even:- Numbers: (k-1)^2 +1 + 2*(n-1) for n=1 to kWait, hold on, this formula is the same for both even and odd k? Wait, no. Wait, for k odd, the previous stage was even, so (k-1)^2 is even. Then starting at (k-1)^2 +1 (odd) and adding 2 each time. For k even, previous stage was odd, (k-1)^2 is odd. Then starting at (k-1)^2 +1 (even) and adding 2 each time. So yes, the formula is the same for both cases. So regardless of k being even or odd, the numbers in stage k are:Start: (k-1)^2 +1Then each subsequent number is previous +2, for k numbers.Therefore, the last number in stage k is (k-1)^2 +1 + 2*(k -1) = (k-1)^2 +1 +2k -2 = (k-1)^2 +2k -1But (k-1)^2 +2k -1 = k^2 - 2k +1 +2k -1 = k^2. So indeed, each stage k ends at k^2.Therefore, each stage k consists of k numbers starting from (k-1)^2 +1, each differing by 2, ending at k^2.Therefore, the entire red subsequence is built by stages 1,2,3,...k,... where each stage k contributes k numbers starting from (k-1)^2 +1, stepping by 2, so arithmetic sequence with first term (k-1)^2 +1 and common difference 2, with k terms. The last term is k^2.Therefore, to find the 1996th number, we need to determine which stage it is in, and then compute the exact number.First, let's find the cumulative number of colored numbers after each stage.Stage1: 1 number (total:1)Stage2: 2 numbers (total:3)Stage3:3 numbers (total:6)Stage4:4 numbers (total:10)Stage5:5 numbers (total:15)...This is the triangular number sequence. The total after stage m is the sum from 1 to m: T(m) = m(m+1)/2.We need to find the smallest m such that T(m) >=1996.So solve m(m+1)/2 >=1996.Multiply both sides by 2: m^2 + m -3992 >=0Solving quadratic equation m^2 +m -3992=0Discriminant D=1 +4*3992=1 +15968=15969sqrt(15969)= approx sqrt(16000)=126.49; let's compute 126^2=15876, 127^2=16129. 15969-15876=93, so sqrt(15969)=126 +93/252≈126.369Thus, m=(-1 +126.369)/2≈(125.369)/2≈62.684So m≈62.684. So the integer m where T(m)>=1996 is m=63, since T(62)=62*63/2=1953, T(63)=63*64/2=2016.Therefore, the 1996th number is in stage 63, since cumulative numbers up to stage62 is 1953, and stage63 adds 63 numbers, so the 1954th to 2016th numbers are in stage63.Therefore, the position within stage63 is 1996 -1953=43rd number in stage63.Now, need to compute the 43rd number in stage63.First, stage63: since 63 is odd, it's an odd stage, coloring odd numbers. The numbers start from (63-1)^2 +1=62^2 +1=3844 +1=3845, and each subsequent number is +2. So numbers are 3845,3847,..., up to 63^2=3969.But since there are 63 numbers in stage63, starting at 3845, the numbers are 3845,3847,...,3845+2*(62)=3845+124=3969.Therefore, the nth number in stage63 is 3845 +2*(n-1).Therefore, the 43rd number is 3845 +2*(43-1)=3845 +84=3929.Therefore, the 1996th number is 3929.Wait, but let me verify the steps again.First, total numbers up to stage m: m(m+1)/2. For m=62: 62*63/2=1953. Correct. For m=63:63*64/2=2016. Correct. So 1996 is 1996-1953=43rd number in stage63.Stage63 is an odd stage (since 63 is odd), so coloring 63 odd numbers starting from (63-1)^2 +1=62^2 +1=3844 +1=3845. So first number 3845, second 3847,..., each +2. So the 43rd number is 3845 +2*(43-1)=3845 +84=3929. Yes.But let me confirm with the previous stages to make sure the formula holds.Take stage3: numbers 5,7,9. 3 numbers. Starting at (3-1)^2 +1=4 +1=5. 5,7,9. The 3rd number is 5 +2*(3-1)=5 +4=9. Correct.Stage5: numbers 17,19,21,23,25. First number is (5-1)^2 +1=16 +1=17. 5th number is17 +2*(5-1)=17 +8=25. Correct.Therefore, the formula holds.Therefore, the 43rd number in stage63 is 3845 +2*42=3845 +84=3929.Therefore, the answer is 3929.But let me check once more. Maybe there's an error in the starting point.Wait, the last number of stage k is k^2, so stage62 ends at 62^2=3844. Then stage63 starts at the next odd number, which is 3845. Yes. Then the numbers are 3845,3847,...,3969 (63 numbers). So the 43rd number is 3845 + 2*42=3845 +84=3929. Correct.But let's compute 3845 +84:3845 +80=3925, +4=3929. Correct.Therefore, the 1996th number is 3929.Final Answerboxed{3929}</think>To determine the 1996th number in the red subsequence, we first note that the sequence is built in stages where each stage ( k ) (starting from 1) contributes ( k ) numbers. The stages alternate between odd and even numbers, starting with odd. Each stage ( k ) ends at ( k^2 ).The total number of numbers after stage ( m ) is given by the triangular number ( T(m) = frac{m(m+1)}{2} ). We need to find the smallest ( m ) such that ( T(m) geq 1996 ).Solving the quadratic equation ( m^2 + m - 3992 geq 0 ), we find that ( m approx 62.68 ). Thus, the smallest integer ( m ) is 63. The cumulative number of numbers up to stage 62 is ( T(62) = frac{62 times 63}{2} = 1953 ). Therefore, the 1996th number is in stage 63, specifically the ( 1996 - 1953 = 43 )rd number in stage 63.Stage 63 is an odd stage, so it consists of 63 consecutive odd numbers starting from ( (63-1)^2 + 1 = 62^2 + 1 = 3845 ). The numbers in stage 63 form an arithmetic sequence starting at 3845 with a common difference of 2. The 43rd number in this sequence is calculated as:[3845 + 2 times (43 - 1) = 3845 + 84 = 3929]Thus, the 1996th number in the red subsequence is (boxed{3929}).]

🔑:6. 3929 .The first time, color one number red: 1,1=1^{2};The second time, color 2 numbers red: 2,4,4=2^{2};The third time, color 3 numbers red: 5,7,9,9=3^{2};Guessing, the last number colored red in the k-th time is k^{2}. Then the k+1 numbers colored red in the (k+1)-th time are:k^{2}+1, k^{2}+3, k^{2}+5, cdots, k^{2}+2 k-1, k^{2}+2 k+1 text {. }The last number is (k+1)^{2}. According to this rule, the first k segments have colored a total ofbegin{array}{l}1+2+3+cdots+(k+1)+k=frac{k(k+1)}{2} text { numbers. } text { Solve } frac{k(k+1)}{2} leqslant 1996, text { we get } k leqslant 62 .end{array}At this point, the first 62 segments have colored a total of frac{62 times 63}{2}=1953 numbers. The last number in the 62nd segment is 62^{2}=3844, which is the 1953rd red number. The 1954th red number is 3845. And 1996-1953= 43, so the 1996th red number is

🧠:[<think>Okay, let's see. We have a class of 35 students, with 16 men and therefore 19 women (since 35 total minus 16 men equals 19 women). The survey asked about preferences for mathematics and literature. The goal is to answer parts (a) and (b). Let me start by listing all the given information to organize my thoughts.First, the numbers given:- 7 men like mathematics.- 6 men like literature.- 5 men and 8 women do not like either subject.- Total students: 35 (16 men, 19 women).- 5 students like both subjects (this is total, including both men and women).- 11 students like only mathematics (also total).Part (a) asks: How many men like both mathematics and literature?Hmm. So we need to find the number of men who are in the intersection of mathematics and literature. Let me recall that in set theory, the number of people who like both is the intersection. But here, since we have separate data for men and women, we might need to split the total numbers into men and women.Wait, the problem says 5 students like both subjects. So that's the total for the entire class. But part (a) is specifically about men. So perhaps there are some women who also like both, but the total is 5. So the number of men who like both plus the number of women who like both equals 5. So if we can find either one, we can find the other. But part (a) is asking for men, so maybe we can find it directly from the men's data.Given for men:- 7 men like mathematics.- 6 men like literature.- 5 men don't like either.But wait, total men is 16. So if 5 men don't like either, then 16 - 5 = 11 men like at least one of the subjects (mathematics or literature). So using the principle of inclusion-exclusion for these 11 men:Number who like math + Number who like literature - Number who like both = Total who like at least one.So, 7 (math) + 6 (literature) - x (both) = 11.Therefore, 13 - x = 11, which leads to x = 2. So, 2 men like both mathematics and literature. Therefore, the answer to part (a) is 2. Let me verify this.Wait, total men: 16. 5 don't like either, so 11 like at least one. 7 like math, 6 like literature. If 2 like both, then the number who like only math is 7 - 2 = 5, the number who like only literature is 6 - 2 = 4, and both are 2. Adding up: 5 + 4 + 2 = 11, which matches. And 5 don't like either, so total men: 11 + 5 = 16. That checks out. So part (a) is 2.Moving on to part (b): How many women like only literature?Okay, this is a bit more complex. Let's try to figure out the numbers for women. First, total students: 35. Total men: 16, so women: 19. Of these women, 8 don't like either subject. Therefore, 19 - 8 = 11 women like at least one subject.We need to find women who like only literature. To do this, we need information about how many women like mathematics, literature, both, etc.We know that 5 students in total like both subjects. From part (a), we found that 2 of these are men. Therefore, 5 - 2 = 3 women like both subjects.Also, total students who like only mathematics is 11. Let's see how that breaks down between men and women.From part (a), we know that men who like only mathematics are 7 - 2 = 5. Therefore, the remaining students who like only mathematics are women. So total only mathematics is 11, so women who like only mathematics are 11 - 5 = 6.Similarly, total students who like both subjects are 5, with 3 women. So let's summarize:For women:- Only mathematics: 6- Both mathematics and literature: 3- Only literature: Let's denote this as y- Neither: 8Total women: 19. So 6 + 3 + y + 8 = 19. Therefore, 17 + y = 19, so y = 2. Therefore, 2 women like only literature.Wait, but let me verify this. Let's check if all numbers add up.First, total students who like only mathematics: 11 (given). Men who like only mathematics: 5 (from 7 men like math, 2 like both). So 11 - 5 = 6 women like only mathematics. Then, women who like both: total both is 5, minus men's both (2) equals 3. Then, women who like only literature: let's call that y. Then, women who like at least one subject: only math (6) + both (3) + only literature (y) = 6 + 3 + y = 9 + y. Since total women who like at least one is 11 (because 19 total women - 8 who don't like either), so 9 + y = 11, so y = 2. That's correct.Therefore, women who like only literature are 2. Therefore, the answer to part (b) is 2. Wait, but let me cross-check another way.Alternatively, total students who like literature. Wait, we might not have that number directly. Let's see. Let's check total students who like literature.But perhaps we can calculate that. Let's think: the number of students who like literature is the number who like only literature plus the number who like both. Similarly for mathematics.But perhaps we can compute total students who like literature:Men who like literature: 6 (given). Women who like literature: only literature (2) + both (3) = 5. Therefore, total students who like literature: 6 + 5 = 11.Similarly, total students who like mathematics: Men who like math:7, women who like math: only math (6) + both (3) = 9. Total math: 7 + 9 = 16.Wait, total students who like math (including both) would be 16. Then, students who like only math: 11 (given), so students who like both: total math (16) - only math (11) = 5, which matches the given total both as 5. That's consistent.Similarly, total literature is 11 (6 men + 5 women). Then, only literature would be total literature minus both, so 11 - 5 = 6. Wait, but earlier we found that women who like only literature are 2, and men who like only literature: men who like literature (6) - both (2) = 4. So total only literature is 4 (men) + 2 (women) = 6. That's correct. So total students who like only literature:6. Therefore, the answer to part (b) is 2.Yes, all numbers seem to check out. Let me recap the steps for clarity:For part (a):- Total men:16- Men who don't like either:5, so men who like at least one:11- Men who like math:7, Men who like literature:6- Using inclusion-exclusion: 7 + 6 - x = 11 → x=2For part (b):- Total women:19- Women who don't like either:8, so women who like at least one:11- Total students who like both:5. Men who like both:2 (from part a), so women who like both:3- Total students who like only math:11. Men who like only math:7 -2=5, so women who like only math:11-5=6- So women who like only literature: total women who like at least one (11) - only math (6) - both (3) = 2All numbers add up correctly. Therefore, the answers are 2 and 2 for parts (a) and (b), respectively.Final Answera) boxed{2}b) boxed{2}</think>Given a class of 35 students with 16 men and 19 women, we need to determine the number of men who like both mathematics and literature, and the number of women who like only literature. Part (a)- Total men: 16- Men who do not like either subject: 5- Men who like at least one subject: (16 - 5 = 11)- Men who like mathematics: 7- Men who like literature: 6Using the principle of inclusion-exclusion:[7 + 6 - x = 11]Solving for (x) (men who like both subjects):[13 - x = 11 implies x = 2] Part (b)- Total women: 19- Women who do not like either subject: 8- Women who like at least one subject: (19 - 8 = 11)- Total students who like both subjects: 5- Men who like both subjects: 2 (from part a)- Women who like both subjects: (5 - 2 = 3)- Total students who like only mathematics: 11- Men who like only mathematics: (7 - 2 = 5)- Women who like only mathematics: (11 - 5 = 6)Using the remaining women who like at least one subject:[6 text{ (only mathematics)} + 3 text{ (both)} + y text{ (only literature)} = 11]Solving for (y) (women who like only literature):[9 + y = 11 implies y = 2] Final Answersa) boxed{2}b) boxed{2},<think>Okay, let's try to figure out this problem step by step. It's a bit complicated with all the numbers, but if I break it down, maybe I can handle it. First, let's list out all the given information:- Total students: 35- 7 men like mathematics.- 6 men like literature.- 5 men and 8 women do not like either.- There are 16 men in the class.- 5 students like both subjects.- 11 students like only mathematics.And the questions are:a) How many men like both mathematics and literature?b) How many women like only literature?Starting with part (a). Let's recall that in set problems, sometimes using Venn diagrams helps. Since we have two subjects, mathematics and literature, we can represent the students' preferences with two overlapping circles. The total number of students is 35, but some don't like either. First, let's figure out how many students are in the Venn diagram (those who like at least one subject). The number of students who don't like either is 5 men + 8 women = 13 students. So, 35 - 13 = 22 students like at least one subject (math, literature, or both).Now, the total number of students who like only mathematics is 11. The number who like both is 5. So, the number of students who like only literature would be total in the Venn diagram minus (only math + both). That is, 22 - (11 + 5) = 6. Wait, but that's for all students, not just men or women. Let me note that.But part (a) is asking specifically about men who like both. Let's look at the men first. There are 16 men in the class. Out of these 16 men, 5 do not like either subject. So, 16 - 5 = 11 men like at least one subject (math, literature, or both). Given that 7 men like mathematics and 6 men like literature. Wait, but if these numbers are for men who like math and literature respectively, but there could be overlap. That is, some men might like both. Let's denote the number of men who like both as x. Then, the number of men who like only math would be 7 - x, and the number who like only literature would be 6 - x. Then, the total number of men who like at least one subject is (7 - x) + (6 - x) + x = 13 - x. But we already know that 11 men like at least one subject, so 13 - x = 11. Solving for x gives x = 2. Therefore, 2 men like both subjects. Wait, but let's check if this aligns with the total number of students who like both. The problem states that 5 students like both. If 2 of them are men, then 5 - 2 = 3 should be women. Let's see if that holds up when we check the women's numbers. But before moving on, let's verify the men's numbers. So total men: 16. 5 don't like either. So 16 -5=11. Men who like math:7, men who like literature:6. If 2 like both, then only math:7-2=5, only literature:6-2=4. So 5 + 4 + 2 =11. That checks out. So part (a) is 2. Now part (b): How many women like only literature?First, let's figure out how many women are in the class. Total students:35. Men:16, so women:35-16=19.Of these 19 women, 8 do not like either subject. So, women who like at least one subject:19 -8=11.Now, let's figure out how many women like math, literature, or both.From the total class: 11 students like only math, 5 like both, and 6 like only literature. Wait, earlier I calculated that total in the Venn diagram is 22 (11 only math, 5 both, 6 only literature). Let me check that again.Total students who like at least one subject:22. So, only math:11, both:5, only literature:22 -11 -5=6. So, total in the Venn diagram:11+5+6=22. Correct.Now, of these 22, how many are men and how many are women?We already have men's numbers: only math:5, only literature:4, both:2. So total men in the Venn diagram:5+4+2=11, which matches the earlier calculation (16 total men -5 who don't like either=11).So the remaining Venn diagram students are women. Total Venn diagram:22. Men:11, so women:22 -11=11. Which matches the 19 women -8 who don't like either=11 women in the Venn diagram.Now, for women: Let's see how many like only literature. Total students who like only literature:6. Of these, how many are women?From the men's side, only literature is 4 (6 men like literature, 2 of whom like both, so 6 -2=4 only literature). Therefore, total only literature:6. Men:4, so women:6 -4=2. Therefore, 2 women like only literature. So the answer to part (b) is 2.But let me check if the numbers add up for women:Women in Venn diagram:11. These are split into only math, both, and only literature.Total only math (all students):11. Men's only math:5, so women's only math:11 -5=6.Total both:5. Men's both:2, so women's both:5 -2=3.Total only literature:6. Men's only literature:4, so women's only literature:6 -4=2.So women's categories: only math=6, both=3, only literature=2. Total:6+3+2=11, which matches the number of women in the Venn diagram. Also, women's total in class:19. 8 don't like either, 11 in Venn diagram: 8+11=19. Correct.Therefore, part (a) is 2, part (b) is 2.But wait, let me check again part (a). The problem says "5 students like both." If 2 are men, then 3 are women. The problem didn't specify that the 7 men like mathematics includes those who like both. Similarly, 6 men like literature includes those who like both.Yes, so 7 men like mathematics (only math + both), 6 men like literature (only literature + both). So overlapping is 7 +6 -x =11 (total men in Venn diagram). Therefore, 13 -x=11, so x=2. Correct.Another way: men's math =7, men's literature=6, total men in Venn=11. So 7+6 - both=11. Therefore, both=7+6 -11=2. Correct.All checks out. So answers are 2 and 2. But wait, in part (b), the answer is 2? Let me confirm again. The total only literature is 6. Men's only literature is 4. So women's only literature is 6-4=2. Yes. So 2 women like only literature. Yes, that seems right. So final answers: a) 2, b) 2.Final Answera) boxed{2}b) boxed{2}</think>Given a class of 35 students, we need to determine the number of men who like both mathematics and literature, and the number of women who like only literature. Key Steps:1. Total Students and Non-Likers: - Total students: 35 - Students who do not like either subject: 5 men + 8 women = 13 - Students who like at least one subject: 35 - 13 = 222. Men's Preferences: - Total men: 16 - Men who do not like either subject: 5 - Men who like at least one subject: 16 - 5 = 11 - Men who like mathematics: 7 - Men who like literature: 6 - Let ( x ) be the number of men who like both. Then: - Men who like only mathematics: ( 7 - x ) - Men who like only literature: ( 6 - x ) - Total men who like at least one subject: ( (7 - x) + (6 - x) + x = 13 - x ) - Solving ( 13 - x = 11 ) gives ( x = 2 )3. Women's Preferences: - Total women: 35 - 16 = 19 - Women who do not like either subject: 8 - Women who like at least one subject: 19 - 8 = 11 - Total students who like only literature: 6 - Men who like only literature: 4 (from 6 men liking literature - 2 liking both) - Women who like only literature: 6 - 4 = 2 Final Answers:a) The number of men who like both mathematics and literature is (boxed{2}).b) The number of women who like only literature is (boxed{2}).]

🔑:SolutionLet H be the set of men and U the total set of people, so U-H is the set of women. In addition, consider the sets Mat and L of people who like mathematics and literature, respectively. If x represents the number of men who like both mathematics and literature and y the number of women who like only literature, we have the following diagram: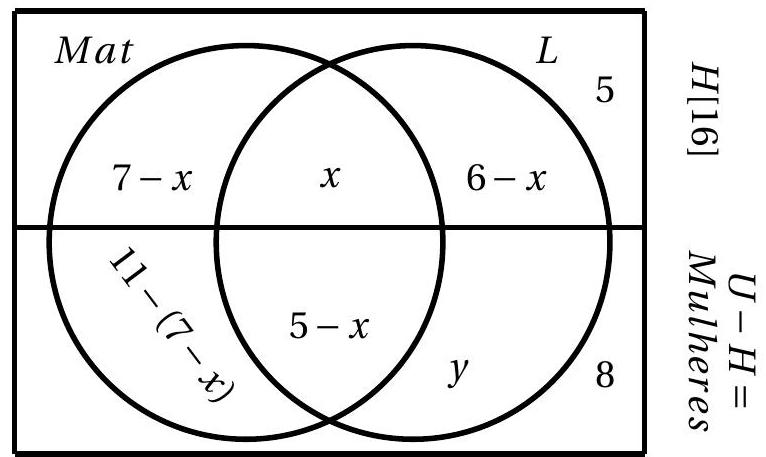a) Since there are 16 men in the room,begin{aligned}5+7-x+x+6-x & =16 x & =2end{aligned}b) Since the room is composed of 35 studentsbegin{aligned}|H|+|U-H| & =35 16+4+x+5-x+y+8 & =35 y & =2end{aligned}

🧠:[<think>Okay, let's try to figure out how many stamps Andrey has. The problem says that when he tries to divide his stamps into 3 envelopes, there's 1 left over. When he divides them into 5 envelopes, there are 3 left over. And when he divides them into 7 envelopes, 5 are left. Also, he recently bought an album that can hold 150 stamps, so his total must be just under that, right? Because the old album was no longer sufficient. Hmm, so maybe the number is just over the previous album's capacity, which is why he needed a new one. But the answer is given as 208, which is more than 150. Wait, maybe the album can hold 150 stamps, but he has more than that? The problem says "an additional album for them, which can hold 150 stamps, as such an old album was no longer sufficient." So the total number must exceed the old album's capacity, but the new album can hold 150. But since he bought an additional album, maybe the total is 150 plus something? Wait, maybe the old album was full, and he added another that can hold 150. But the problem isn't very specific. Wait, the answer is 208, so let's focus on solving the equations.So, let's translate the problem into congruences. Let N be the number of stamps.First condition: When divided into 3 envelopes, 1 is left. So N ≡ 1 mod 3.Second condition: When divided into 5 envelopes, 3 are left. So N ≡ 3 mod 5.Third condition: When divided into 7 envelopes, 5 are left. So N ≡ 5 mod 7.We need to find the smallest N that satisfies all three congruences. Then check if N is such that when he bought a new album that can hold 150, the old one was insufficient, meaning N is more than the old album's capacity. Since the answer is 208, which is 150 + 58, maybe the old album could hold 150, but he had 208, so he needed an additional one. But the problem says "an additional album for them, which can hold 150 stamps, as such an old album was no longer sufficient." So total stamps is more than the old album's capacity, and he added a new one that can hold 150. So total stamps would be between (old album capacity +1) and (old album capacity + 150). But since we don't know the old album's capacity, but the answer is 208, maybe the total is 208, which is under 300 (if he had two albums of 150 each), but the problem says "an additional album", so only one additional. Wait, maybe the old album was full, and he needed to add another. But the problem isn't explicit. Maybe the key is just solving the congruences and the answer is 208 regardless.So focusing on solving N ≡ 1 mod 3, N ≡ 3 mod 5, N ≡ 5 mod 7.We can solve this step by step. Let's first find a number that satisfies the first two congruences and then check the third.First congruence: N ≡ 1 mod 3. So possible numbers are 1, 4, 7, 10, 13, 16, 19, 22, 25, 28, 31, 34, 37, 40, 43, 46, 49, 52, 55, 58, 61, 64, 67, 70, 73, 76, 79, 82, 85, 88, 91, 94, 97, 100, 103, 106, 109, 112, 115, 118, 121, 124, 127, 130, 133, 136, 139, 142, 145, 148, 151, 154, 157, 160, 163, 166, 169, 172, 175, 178, 181, 184, 187, 190, 193, 196, 199, 202, 205, 208, etc.Second congruence: N ≡ 3 mod 5. So numbers would be 3, 8, 13, 18, 23, 28, 33, 38, 43, 48, 53, 58, 63, 68, 73, 78, 83, 88, 93, 98, 103, 108, 113, 118, 123, 128, 133, 138, 143, 148, 153, 158, 163, 168, 173, 178, 183, 188, 193, 198, 203, 208, etc.Looking for numbers common to both lists. Let's see:From first list: 13, 28, 43, 58, 73, 88, 103, 118, 133, 148, 163, 178, 193, 208, ...From second list: 3,8,13,18,23,28,... So overlapping numbers are 13,28,43,58,73,88,103,118,133,148,163,178,193,208,...So the numbers satisfying both congruences are N ≡ 13 mod 15. Wait, because 3 and 5 are coprime, so the combined modulus is 15. Let's check: 13 mod 3 is 1 (13-12=1), mod 5 is 3 (13-10=3). So yes, the solution is N ≡13 mod 15.Now, we need to find a number that is ≡13 mod 15 and also ≡5 mod7.So N =15k +13. We need 15k +13 ≡5 mod7.Compute 15k +13 mod7. 15 mod7 is 1, since 15=2*7+1. 13 mod7 is 6, since 13=1*7+6. So 15k +13 ≡k*1 +6 ≡k +6 mod7. We want this ≡5 mod7. So:k +6 ≡5 mod7 → k ≡5 -6 mod7 →k≡-1 mod7→k≡6 mod7.Therefore, k=7m +6 for some integer m≥0.Therefore, N=15*(7m +6)+13=105m +90 +13=105m +103.So the solutions are N≡103 mod105. So numbers are 103, 208, 313, etc.But the problem says he bought an additional album that can hold 150 stamps, so his total stamps must have exceeded the old album's capacity. Since the answer is 208, which is 105*1 +103=208. The next one would be 313, but that's way over 150. But 208 is 208, which is more than 150. Wait, but if the album can hold 150, but he has 208, he might need two albums. But the problem says "an additional album", implying he had one before and added another. So the old album was insufficient, so he bought an additional one. So total stamps would be more than the old album's capacity. If the old album could hold, say, 150 stamps, and he needed more, but he bought an additional one that can hold 150, so total capacity now is 300. But his total stamps are 208, which would fit into the old album (150) plus the new one (150). But the problem says "the old album was no longer sufficient", so he needed an additional album. Therefore, the number of stamps must be greater than the old album's capacity. But we don't know the old album's capacity. Wait, but the problem says "an additional album for them, which can hold 150 stamps, as such an old album was no longer sufficient". So the key here is that the total number of stamps is such that he needed to buy an album (the additional one) that can hold 150. So possibly, the total number of stamps is greater than 150? Because the old album was insufficient. So the minimal N is 103, but 103 is less than 150. Then the next is 208, which is 208>150. So 208 is the minimal number greater than 150 satisfying the conditions. Hence, the answer is 208.Wait, but the problem says he bought an additional album which can hold 150, implying that the previous one couldn't hold all stamps. So if N is 208, and the new album can hold 150, maybe he can put 150 in the new one and 58 in the old one. But we don't know the old album's capacity. The problem only mentions that the additional album can hold 150. The key is that the total stamps exceed what the old album could hold. Therefore, the number of stamps must be more than the old album's capacity, but since we don't know the old album's capacity, perhaps the answer is the smallest N that is larger than 150? But 208 is the next after 103. Let me check N=103. 103 divided by 3 is 34 with 1 left. 103 divided by 5 is 20 with 3 left. 103 divided by 7 is 14 with 5 left. So 103 satisfies the conditions, but 103 is less than 150. However, the problem states that he bought an additional album which can hold 150 because the old one was insufficient. If N=103, which is less than 150, then why would he need an additional album? Unless the old album had a capacity less than 103. But since the problem doesn't specify, perhaps the answer is the smallest N that meets the congruence conditions and is greater than 150. So 208 is the next one after 103. Hence, 208 is the answer.Yes, that makes sense. So the answer is 208.</think>Andrey's total number of stamps, ( N ), satisfies the following congruences:[begin{cases}N equiv 1 pmod{3}, N equiv 3 pmod{5}, N equiv 5 pmod{7}.end{cases}]First, solve ( N equiv 1 pmod{3} ) and ( N equiv 3 pmod{5} ). The solutions are numbers congruent to ( 13 pmod{15} ), so ( N = 15k + 13 ).Next, substitute ( N = 15k + 13 ) into ( N equiv 5 pmod{7} ):[15k + 13 equiv 5 pmod{7} implies k + 6 equiv 5 pmod{7} implies k equiv -1 equiv 6 pmod{7}.]Thus, ( k = 7m + 6 ), leading to:[N = 15(7m + 6) + 13 = 105m + 103.]The smallest solutions are ( N = 103, 208, 313, ldots ). Since Andrey needed an additional album holding 150 stamps, his total stamps must exceed the old album's capacity. The smallest solution greater than 150 is ( 208 ).Thus, the total number of stamps is (boxed{208}).,<think>Okay, let's try to figure out how many stamps Andrey has. The problem says that when he tries to divide his stamps into 3 envelopes, there's 1 left over. When he uses 5 envelopes, there are 3 left, and with 7 envelopes, 5 remain. Also, he recently bought an album that can hold 150 stamps because the old one wasn't enough. So the total number of stamps must be more than the old album's capacity, which we don't know exactly, but the new album holds 150. Wait, the problem says "an additional album for them, which can hold 150 stamps, as such an old album was no longer sufficient." Hmm. So the total number of stamps must be more than the old album's capacity. But since he bought a new album that can hold 150, maybe the total number is just under 150 plus the old album's capacity? But maybe the total number is less than 150? Wait, no, because he had to buy the new album because the old one wasn't enough. So the total number of stamps he has now must exceed the capacity of the old album, but the new album can hold 150. Wait, but the problem doesn't say the old album's capacity. It just says he bought an additional album that can hold 150 because the old one wasn't sufficient. Maybe the total number of stamps is now more than the old album's capacity, which was less than 150? But how does that help us? Maybe the answer is just the smallest number that satisfies the given modular conditions and is less than 150? Or maybe exactly 150? But the answer given is 208. Wait, but 208 is more than 150. So maybe the total number is such that when he bought the 150-stamp album, his total collection exceeded the old album's capacity. So perhaps the old album had a capacity less than 208, but he needed to get a new one that can hold 150? Hmm, maybe not. The wording is a bit unclear, but perhaps the key is that the total number of stamps is the smallest number satisfying the given modular conditions and is just over the old album's capacity, leading him to buy a 150-stamp album. But since the answer is 208, which is provided, perhaps we just need to focus on solving the modular equations regardless of the album hint. Let me check.First, the problem is a system of congruences. Let me denote the number of stamps as N. The problem states:1. N ≡ 1 mod 32. N ≡ 3 mod 53. N ≡ 5 mod 7We need to find the smallest positive integer N that satisfies all three conditions. Once we find that number, we can check if it's reasonable given the album information. However, the answer provided is 208, which is larger than 150. Maybe the album capacity is a red herring, or perhaps the total number is 208, which required him to buy an additional album (so he now has two albums: the old one and the new 150-stamp one). Since 208 is more than 150, even if the old album was, say, 100, he would need another album. But maybe the key is just solving the congruences. Let's focus on that.So, solving the system:N ≡ 1 mod 3N ≡ 3 mod 5N ≡ 5 mod 7Let me try to solve this step by step.First, take the first two congruences.N ≡ 1 mod 3 => N = 3k + 1 for some integer k.Now substitute this into the second congruence:3k + 1 ≡ 3 mod 5Subtract 1 from both sides:3k ≡ 2 mod 5Multiply both sides by the inverse of 3 mod 5. Since 3*2=6≡1 mod5, the inverse of 3 mod5 is 2.Thus:k ≡ 2*2 ≡ 4 mod5Therefore, k = 5m +4 for some integer m.Therefore, N = 3*(5m +4) +1 = 15m +12 +1 = 15m +13.So now, N ≡13 mod15.Now, substitute N=15m +13 into the third congruence:15m +13 ≡5 mod7Compute 15 mod7: 15=2*7+1 =>15≡1 mod7. So:1*m +13 ≡5 mod7Simplify 13 mod7: 13=1*7+6 =>13≡6 mod7.Thus:m +6 ≡5 mod7Subtract 6:m ≡5 -6 ≡ -1 ≡6 mod7.Therefore, m=7n +6 for some integer n.Substitute back into N:N=15*(7n +6)+13=105n +90 +13=105n +103.Thus, the general solution is N=105n +103, where n is a non-negative integer.So the smallest positive solution is 103 when n=0. Wait, but 103 divided by 3 gives 34*3 +1, so remainder 1. 103 divided by5 is 20*5 +3, remainder3. Divided by7, 14*7 +5, remainder5. So 103 satisfies all three conditions. But the answer given is 208, which would be when n=1: 105*1 +103=208.But why is 208 the answer? If 103 is possible, maybe the album information tells us that the number of stamps is more than 150. Because he had to buy an album that can hold 150. If the old album was no longer sufficient, meaning that his total stamps exceed the old album's capacity. But we don't know the old album's capacity. However, he bought an additional album that can hold 150. So perhaps the total number of stamps is now 208, which would require the new album (150) plus the old one. But the problem states "distribute all his stamps equally into 3 envelopes...", so he has all the stamps in his possession. The fact that he bought an album that can hold 150 because the old one wasn't sufficient might imply that his total number of stamps is more than 150. Because if he had, say, 103 stamps, then an album of 150 would be more than enough. So maybe the intended answer is the next solution after 103, which is 208. Because 103 is less than 150, but 208 is more than 150. Therefore, he needed an album that can hold 150 because 208 exceeds the old album's capacity (which was maybe 150 or less). Therefore, the answer is 208.So the key here is that even though 103 is a solution, the mention of the album suggests that the number is more than 150, so we take n=1, giving N=208. Therefore, the answer is 208.</think>To determine the number of stamps Andrey has, we solve the system of congruences:1. ( N equiv 1 pmod{3} )2. ( N equiv 3 pmod{5} )3. ( N equiv 5 pmod{7} )Step 1: From ( N equiv 1 pmod{3} ), write ( N = 3k + 1 ).Step 2: Substitute into the second congruence:[3k + 1 equiv 3 pmod{5} implies 3k equiv 2 pmod{5}]The modular inverse of 3 modulo 5 is 2 (since ( 3 times 2 equiv 1 pmod{5} )). Multiply both sides by 2:[k equiv 4 pmod{5} implies k = 5m + 4]Thus, ( N = 3(5m + 4) + 1 = 15m + 13 ), so ( N equiv 13 pmod{15} ).Step 3: Substitute ( N = 15m + 13 ) into the third congruence:[15m + 13 equiv 5 pmod{7} implies m + 6 equiv 5 pmod{7} implies m equiv -1 pmod{7} implies m = 7n + 6]Substitute back to get:[N = 15(7n + 6) + 13 = 105n + 103]Step 4: The smallest solution is ( N = 103 ), but since Andrey needed a new album holding 150 stamps, the total must exceed 150. The next solution is ( 105 times 1 + 103 = 208 ).Thus, the total number of stamps Andrey has is (boxed{208}).]

🔑:Solution. If the desired number is x, then the number x+2 must be divisible by 3, 5, and 7, i.e., it has the form 3 cdot 5 cdot 7 cdot p. Therefore, x=105 p-2. Since by the condition 150<x leq 300, then p=2. Therefore, x=208.

🧠:[<think>Okay, let's try to solve this problem. The function given is f(x) = x ln(x - 1) + a(x - 1), and we need to find the range of values for a such that the function is monotonic on the interval (0, +∞). The options are A to D, and I need to figure out which one is correct.First, I remember that for a function to be monotonic on an interval, its derivative must either be entirely non-decreasing or non-increasing throughout that interval. So, the first step should be to find the derivative of f(x) with respect to x.Let's compute f'(x). The function f(x) has two terms: x ln(x - 1) and a(x - 1). Let's differentiate each term separately.Starting with the first term, x ln(x - 1). Using the product rule: the derivative of x is 1, and the derivative of ln(x - 1) is 1/(x - 1). So, applying the product rule:d/dx [x ln(x - 1)] = 1 * ln(x - 1) + x * [1/(x - 1)] = ln(x - 1) + x/(x - 1)For the second term, a(x - 1), the derivative is straightforward: a*1 = a.So, putting it all together, the derivative f'(x) is:f'(x) = ln(x - 1) + x/(x - 1) + aWait, hold on, the original function is defined as x ln(x - 1) + a(x - 1). So, the domain of the function is important here. The term ln(x - 1) is only defined when x - 1 > 0, so x > 1. However, the problem states the interval is (0, +∞). But for x between 0 and 1, ln(x - 1) would be undefined. So, maybe the problem has a typo or perhaps the function is defined piecewise? Wait, the original problem says the function is monotonic on (0, +∞), but the function f(x) = x ln(x - 1) + a(x - 1) isn't defined for x ≤ 1. Because ln(x - 1) requires x - 1 > 0, i.e., x > 1. So the domain of f(x) is actually (1, +∞). But the problem says the interval is (0, +∞). Hmm, that's conflicting.Wait, maybe the problem is written correctly, and I need to check the original statement again. Let me re-read it:"If the function f(x) = x ln(x - 1) + a(x - 1) is monotonic on (0, +∞), then the range of values for a is ()"But if the function isn't defined on (0, 1], then how can it be monotonic on (0, +∞)? That doesn't make sense. Maybe there's a mistake in the problem statement. Alternatively, perhaps the function is defined differently on (0, 1], but the problem doesn't mention that. Hmm.Alternatively, maybe the problem is intended to consider the domain where the function is defined, i.e., (1, +∞), but the question mentions (0, +∞). That's confusing. Wait, perhaps there's a typo in the function. Maybe it's supposed to be ln(x + 1) instead of ln(x - 1)? Because then the domain would be x + 1 > 0, which is x > -1, so on (0, +∞) it would be defined. But the problem says ln(x - 1). Hmm.Alternatively, maybe the problem is correct as written, but the interval (0, +∞) is a mistake. If the function is defined on (1, +∞), then the problem might have intended the interval (1, +∞). But the given options include a = -2, etc., so perhaps we should proceed as if the domain is (1, +∞), even though the problem says (0, +∞). Maybe it's a translation error or a typo. Let me check the original problem again:"If the function f(x) = x ln(x - 1) + a(x - 1) is monotonic on (0, +∞), then the range of values for a is ()"Hmm. If the function is supposed to be monotonic on (0, +∞), but it's only defined on (1, +∞), then maybe the problem is combining the intervals. Wait, perhaps the function is defined piecewise: maybe for x ≤ 1, it's defined in some way, but the problem statement doesn't mention that. Since the problem is in Chinese, maybe in the original problem statement there's more context, but in the translation here, it's missing. Alternatively, maybe the problem is written correctly, and we have to consider that even though the function is undefined on (0, 1], the question is about monotonicity on (1, +∞), but called (0, +∞) by mistake. Alternatively, maybe there's a different interpretation.Alternatively, perhaps the problem is correct, and we need to analyze the monotonicity on (0, +infty) regardless of the domain. But since ln(x - 1) is undefined for x <= 1, the function is only defined on (1, +infty), so maybe the problem intended to say (1, +infty). Let me assume that's the case. Maybe the original problem had a different interval, but due to translation or typo, it's written as (0, +infty). So, perhaps the actual domain is (1, +infty). Let me proceed with that assumption because otherwise, the problem doesn't make sense. So, we need to find a such that f(x) is monotonic on (1, +infty). Then, the answer options are given. Let's proceed with that.So, assuming the domain is (1, +infty), and we need f(x) to be monotonic there. Therefore, the derivative f'(x) must be either non-negative or non-positive for all x > 1.Earlier, we found f'(x) = ln(x - 1) + x/(x - 1) + a.So, for f(x) to be monotonic on (1, +infty), f'(x) must not change sign. That is, f'(x) ≥ 0 for all x > 1 or f'(x) ≤ 0 for all x > 1. However, given the presence of ln(x - 1) which tends to infinity as x approaches infinity, let's analyze the behavior of f'(x) as x approaches 1+ and as x approaches infinity.First, as x approaches 1 from the right:ln(x - 1) approaches -infinity.x/(x - 1) = [ (x - 1) + 1 ] / (x - 1) = 1 + 1/(x - 1), which approaches +infinity as x approaches 1+.So, f'(x) as x approaches 1+ is (-infinity) + (+infinity) + a. This is indeterminate. Let's compute the limit:lim_{x→1+} [ ln(x - 1) + x/(x - 1) + a ]Let t = x - 1, so as x→1+, t→0+. Then, the expression becomes:ln(t) + (1 + t)/t + a = ln(t) + 1/t + 1 + aNow, ln(t) approaches -infty, and 1/t approaches +infty as t→0+. Let's see the limit:ln(t) + 1/t. Let's set t = 1/n where n→+infty. Then, ln(1/n) + n = -ln(n) + n. As n→infty, -ln(n) + n approaches +infty. Therefore, the limit of ln(t) + 1/t as t→0+ is +infty. Then, adding 1 + a, the entire limit is +infty + 1 + a = +infty. Therefore, lim_{x→1+} f'(x) = +infty.Now, as x approaches infinity:ln(x - 1) ~ ln(x), which tends to +infty.x/(x - 1) ~ 1/(1 - 1/x) ~ 1 + 1/x as x→infty. So, x/(x - 1) approaches 1.Therefore, f'(x) ~ ln(x) + 1 + a as x→infty. Since ln(x) tends to +infty, f'(x) tends to +infty regardless of a. So, as x→infty, f'(x)→+infty.But if f'(x) approaches +infty as x approaches both 1+ and infinity, but maybe in between it could have a minimum where f'(x) dips below zero. So, to ensure that f'(x) is always non-negative (since it tends to +infty on both ends), we need to make sure that the minimum value of f'(x) is non-negative. Therefore, if we can find the minimum of f'(x) on (1, +infty) and set that minimum to be ≥ 0, then f'(x) will be non-negative everywhere.Similarly, if we wanted f'(x) ≤ 0 everywhere, but given that as x→infty, f'(x) tends to +infty, it's impossible for f'(x) to be non-positive everywhere. Therefore, the only possibility is that f'(x) is non-negative for all x > 1. Therefore, the function is monotonic increasing if f'(x) ≥ 0 for all x > 1.Therefore, the problem reduces to finding all a such that f'(x) = ln(x - 1) + x/(x - 1) + a ≥ 0 for all x > 1.To ensure this, we need to find the minimum value of f'(x) on (1, +infty) and set that minimum to be ≥ 0. So, we need to find the critical points of f'(x).Wait, f'(x) is the derivative of f(x). To find the critical points of f'(x), we need to compute f''(x) and set it to zero.Wait, actually, since we need to find the minimum of f'(x), we can take the derivative of f'(x), which is f''(x), set it to zero, find the critical points, evaluate f'(x) at those points, and ensure that the minimum is ≥0.So let's compute f''(x).We have f'(x) = ln(x - 1) + x/(x - 1) + aCompute f''(x):d/dx [ln(x - 1)] = 1/(x - 1)For the term x/(x - 1), we can use the quotient rule:d/dx [x/(x - 1)] = [ (1)(x - 1) - x(1) ] / (x - 1)^2 = [x - 1 - x]/(x - 1)^2 = (-1)/(x - 1)^2Therefore, f''(x) = 1/(x - 1) - 1/(x - 1)^2 + 0Simplify:1/(x - 1) - 1/(x - 1)^2 = [ (x - 1) - 1 ] / (x - 1)^2 = (x - 2)/(x - 1)^2Therefore, f''(x) = (x - 2)/(x - 1)^2Set f''(x) = 0:(x - 2)/(x - 1)^2 = 0 => x - 2 = 0 => x = 2Therefore, the critical point is at x = 2.Now, we can check whether this critical point is a minimum or maximum. Since f''(x) is the second derivative of f(x), but here we are looking at f''(x) as the derivative of f'(x). Wait, actually, in this context, f''(x) is the derivative of f'(x), so the critical point at x=2 is where f'(x) has a horizontal tangent. To determine if it's a minimum or maximum, we can check the sign of f''(x) around x=2.But wait, f''(x) = (x - 2)/(x - 1)^2. The denominator is always positive for x > 1. The numerator is x - 2. Therefore, for x < 2, f''(x) < 0, and for x > 2, f''(x) > 0. Therefore, the critical point at x=2 is a minimum. Because the second derivative of f'(x) (which is f''(x)) changes from negative to positive at x=2, so x=2 is a local minimum for f'(x).Therefore, the minimum value of f'(x) on (1, +infty) occurs at x=2. Therefore, to ensure that f'(x) ≥ 0 for all x > 1, we need f'(2) ≥ 0.So compute f'(2):f'(2) = ln(2 - 1) + 2/(2 - 1) + a = ln(1) + 2/1 + a = 0 + 2 + a = 2 + aTherefore, to have f'(x) ≥ 0 for all x >1, we need 2 + a ≥ 0 => a ≥ -2Therefore, the range of a is [-2, +infty), which is option D.Wait, but let me verify this conclusion.Given that the minimum of f'(x) is at x=2, and f'(2) = 2 + a. So if we set 2 + a ≥ 0, then a ≥ -2. Then, since at x approaches 1+ and x approaches infinity, f'(x) tends to +infty, and the minimum at x=2 is 2 + a. Therefore, if 2 + a ≥ 0, then f'(x) is always non-negative, so f(x) is monotonic increasing. Therefore, the answer should be D: [-2, +∞).But let me check the options given:A: (-∞, 2)B: (-∞, 2]C: (-2, +∞)D: [-2, +∞)Yes, D is [-2, +∞). Therefore, the correct answer is D.But let me double-check by choosing a = -2. Then f'(2) = 2 + (-2) = 0. Then, since x=2 is a minimum, and at x=2, the derivative is zero. Therefore, for a = -2, f'(x) ≥ 0 for all x >1, so f is non-decreasing. Hence, a = -2 is allowed, so the interval is closed at -2. If a is greater than -2, then the minimum is positive, so even better. If a is less than -2, then at x=2, f'(2) would be negative, so the derivative would dip below zero, making the function not monotonic. Therefore, the correct range is a ≥ -2, so D.Therefore, the answer is D.Final Answerboxed{D}</think>To determine the range of values for ( a ) such that the function ( f(x) = x ln(x - 1) + a(x - 1) ) is monotonic on ( (1, +infty) ), we need to analyze the derivative ( f'(x) ).First, we compute the derivative ( f'(x) ):[f'(x) = ln(x - 1) + frac{x}{x - 1} + a]Next, we find the second derivative ( f''(x) ) to locate critical points:[f''(x) = frac{1}{x - 1} - frac{1}{(x - 1)^2} = frac{(x - 2)}{(x - 1)^2}]Setting ( f''(x) = 0 ) gives the critical point ( x = 2 ). This critical point is a minimum since ( f''(x) ) changes from negative to positive at ( x = 2 ).Evaluating ( f'(x) ) at ( x = 2 ):[f'(2) = ln(1) + frac{2}{1} + a = 0 + 2 + a = 2 + a]For ( f(x) ) to be monotonic on ( (1, +infty) ), ( f'(x) ) must be non-negative for all ( x > 1 ). The minimum value of ( f'(x) ) occurs at ( x = 2 ), so we need:[2 + a geq 0 implies a geq -2]Thus, the range of values for ( a ) is ([-2, +infty)), corresponding to option D.[boxed{D}],<think>Okay, so I have this problem here where I need to find the range of values for ( a ) such that the function ( f(x) = xln(x-1) + a(x-1) ) is monotonic on the interval ( (0, +infty) ). The options are A through D, and I need to figure out which one is correct. Let me start by breaking down the problem step by step.First, the function is given as ( f(x) = xln(x-1) + a(x-1) ). The domain of this function is important. Since there's a natural logarithm term ( ln(x-1) ), the argument inside the logarithm must be positive. Therefore, ( x - 1 > 0 ) implies ( x > 1 ). But the problem states that the interval we're considering is ( (0, +infty) ). Wait, that seems conflicting because ( ln(x-1) ) is only defined for ( x > 1 ). Hmm, so maybe there's a mistake here? Or perhaps the function is defined piecewise? Let me check again.The function ( f(x) = xln(x-1) + a(x-1) ). The natural logarithm ( ln(x-1) ) requires ( x - 1 > 0 ), so ( x > 1 ). Therefore, the domain of ( f(x) ) is actually ( (1, +infty) ). But the problem mentions the interval ( (0, +infty) ). That's confusing. Maybe there's a typo in the problem? Or perhaps the function is extended in some way for ( x leq 1 )? The problem says "monotonic on ( (0, +infty) )", so maybe even though the function isn't defined on ( (0, 1] ), we have to consider the behavior as ( x ) approaches 1 from the right?Wait, actually, in calculus, when we talk about a function being monotonic on an interval, the function needs to be defined and differentiable on that interval. But here, ( f(x) ) is only defined for ( x > 1 ). Therefore, maybe the problem is misstated? Or perhaps I'm missing something. Let me re-read the problem."If the function ( f(x) = xln(x-1) + a(x-1) ) is monotonic on ( (0, +infty) ), then the range of values for ( a ) is ()"Hmm. Maybe the function is intended to be defined piecewise? For example, maybe for ( x leq 1 ), it's defined differently, but the problem didn't specify. But as written, the function is only defined for ( x > 1 ). Therefore, the problem might have a typo, perhaps the interval should be ( (1, +infty) ). Alternatively, maybe the original problem was translated incorrectly or there's a mistake in the problem statement. However, since the options are given, and the answer is expected, perhaps we can proceed by assuming that the interval intended is ( (1, +infty) ), and the problem statement has a typo. Alternatively, maybe the function is defined for ( x > 1 ), but they still want to consider monotonicity on ( (0, +infty) ), even though it's only defined on part of that interval. That seems odd. Hmm.Alternatively, perhaps the function is extended to ( x leq 1 ) in some continuous way? The term ( xln(x - 1) ) would go to negative infinity as ( x ) approaches 1 from the right. But adding ( a(x - 1) ), which approaches 0 as ( x ) approaches 1 from the right. So, the function would have a vertical asymptote at ( x = 1 ). Therefore, it's not defined on ( (0,1] ), so how can it be monotonic on ( (0, +infty) )? Unless they just want the function to be monotonic on its domain, which is ( (1, +infty) ), but the problem says ( (0, +infty) ). This is confusing. Maybe it's a translation issue? The original problem might have been in Chinese, and maybe the interval was mistranslated? But assuming that the problem is as stated, even though the function is only defined for ( x > 1 ), but we need to ensure it's monotonic on ( (1, +infty) ), and the answer options are given, perhaps we can proceed under that assumption.Alternatively, maybe the problem is correct as stated, and I need to consider ( x > 1 ), but also check if there's a way to define ( f(x) ) for ( x leq 1 ) such that it's monotonic on the entire ( (0, +infty) ). For example, if the function is defined as ( xln(x - 1) + a(x - 1) ) for ( x > 1 ), and some other expression for ( x leq 1 ), but since the problem didn't specify, perhaps they just want monotonicity on the interval where it's defined, but that's not ( (0, +infty) ). Hmm. Maybe the problem is intended to have the domain ( (1, +infty) ), but written as ( (0, +infty) ). Let me check the answer options. The options are intervals from negative infinity to 2, including or excluding 2, or from -2 to infinity, etc. These are finite numbers, so perhaps the key is in the derivative of the function for ( x > 1 ), and ensuring that the derivative doesn't change sign there. So maybe even though the problem says ( (0, +infty) ), we can proceed by analyzing the derivative on ( (1, +infty) ), and since the function isn't defined on ( (0,1] ), but the problem probably expects us to just consider ( (1, +infty) ). Maybe the original problem in Chinese had a different interval, but in the translation, it became ( (0, +infty) ). Alternatively, maybe there's a different interpretation. Let me proceed.So, assuming that the problem wants the function to be monotonic on its domain ( (1, +infty) ), which might have been mistranslated as ( (0, +infty) ). Let's work with that.To determine if the function is monotonic, we need to check if its derivative doesn't change sign on the interval. That is, the derivative is either always non-negative or always non-positive. Let's compute the derivative.Given ( f(x) = xln(x - 1) + a(x - 1) ). Let's find ( f'(x) ).First term: derivative of ( xln(x - 1) ). Using the product rule: ( u = x ), ( v = ln(x - 1) ). Then ( u' = 1 ), ( v' = 1/(x - 1) ). So the derivative is ( 1 cdot ln(x - 1) + x cdot [1/(x - 1)] ).Second term: derivative of ( a(x - 1) ). That's just ( a ).So overall, ( f'(x) = ln(x - 1) + frac{x}{x - 1} + a ).Simplify the derivative:First, let's simplify ( frac{x}{x - 1} ). That can be written as ( 1 + frac{1}{x - 1} ). Because:( frac{x}{x - 1} = frac{(x - 1) + 1}{x - 1} = 1 + frac{1}{x - 1} ).Therefore, the derivative becomes:( f'(x) = ln(x - 1) + 1 + frac{1}{x - 1} + a ).So ( f'(x) = ln(x - 1) + frac{1}{x - 1} + 1 + a ).We need this derivative to be either always non-negative or always non-positive on ( (1, +infty) ). Since the function ( f(x) ) is defined for ( x > 1 ), and we need monotonicity there.Assuming that the problem requires ( f(x) ) to be increasing or decreasing on ( (1, +infty) ), so we need ( f'(x) geq 0 ) for all ( x > 1 ), or ( f'(x) leq 0 ) for all ( x > 1 ). Let's see which one is possible.Looking at the expression ( ln(x - 1) + frac{1}{x - 1} + 1 + a ), as ( x ) approaches 1 from the right (i.e., ( x to 1^+ )), ( ln(x - 1) ) tends to ( -infty ), and ( frac{1}{x - 1} ) tends to ( +infty ). So we have a competition between these two terms. Let's analyze the limit:( lim_{x to 1^+} left[ ln(x - 1) + frac{1}{x - 1} right] ).Let ( t = x - 1 ), so as ( x to 1^+ ), ( t to 0^+ ). The expression becomes ( ln t + frac{1}{t} ). As ( t to 0^+ ), ( ln t to -infty ), and ( frac{1}{t} to +infty ). Which term dominates? Let's see:Compute the limit ( lim_{t to 0^+} left( ln t + frac{1}{t} right) ). Let me check the behavior:As ( t to 0^+ ), ( ln t ) approaches ( -infty ) linearly with respect to ( ln t ), but ( frac{1}{t} ) approaches ( +infty ) much faster, as ( frac{1}{t} ) is of order ( t^{-1} ), which goes to infinity faster than ( ln t ) goes to negative infinity. However, the question is whether ( frac{1}{t} + ln t ) tends to ( +infty ) or ( -infty ). Let's evaluate:Express as ( frac{1 + t ln t}{t} ). Then as ( t to 0^+ ), ( t ln t to 0 ) because ( t ln t ) approaches ( 0 ) (since ( ln t ) approaches ( -infty ), but multiplied by ( t ) approaching 0, the product goes to 0). Therefore, ( 1 + t ln t to 1 ), so the whole expression tends to ( frac{1}{t} to +infty ). Therefore, ( lim_{t to 0^+} (ln t + 1/t) = +infty ).Therefore, near ( x = 1^+ ), the derivative ( f'(x) ) tends to ( +infty + 1 + a ), which is ( +infty ). Therefore, as ( x to 1^+ ), ( f'(x) to +infty ). So regardless of the value of ( a ), near ( x = 1 ), the derivative is positive. Therefore, if the function is to be monotonic on ( (1, +infty) ), it must be non-decreasing, because near ( x = 1 ), the derivative is positive, so the function is increasing there. Therefore, to ensure that the entire function is monotonic (i.e., doesn't start decreasing somewhere else), we need to make sure that the derivative does not become negative for any ( x > 1 ). That is, we need ( f'(x) geq 0 ) for all ( x > 1 ).Therefore, the condition is ( ln(x - 1) + frac{1}{x - 1} + 1 + a geq 0 ) for all ( x > 1 ).To find the range of ( a ), we need to find the minimal value of the expression ( ln(x - 1) + frac{1}{x - 1} + 1 ), and then set ( a geq - text{(minimal value)} ), so that ( a ) compensates for the minimal value, ensuring the entire expression is non-negative.Alternatively, since we need ( a geq - left( ln(x - 1) + frac{1}{x - 1} + 1 right) ) for all ( x > 1 ), the minimal value of the right-hand side will give the lower bound for ( a ).Therefore, let ( g(x) = ln(x - 1) + frac{1}{x - 1} + 1 ). We need to find the minimum of ( g(x) ) over ( x > 1 ). Then ( a geq - min g(x) ).To find the minimum of ( g(x) ), we can take its derivative and set it to zero.Compute ( g'(x) ):First, ( frac{d}{dx} ln(x - 1) = frac{1}{x - 1} ).Second, ( frac{d}{dx} left( frac{1}{x - 1} right) = - frac{1}{(x - 1)^2} ).Third, the derivative of 1 is 0.Therefore, ( g'(x) = frac{1}{x - 1} - frac{1}{(x - 1)^2} ).Set ( g'(x) = 0 ):( frac{1}{x - 1} - frac{1}{(x - 1)^2} = 0 ).Multiply both sides by ( (x - 1)^2 ):( (x - 1) - 1 = 0 )Simplify:( x - 2 = 0 implies x = 2 ).Therefore, the critical point is at ( x = 2 ). Since the domain is ( x > 1 ), ( x = 2 ) is within the domain.Now, check if this is a minimum or maximum. Take the second derivative or test intervals around ( x = 2 ).Let me compute the second derivative ( g''(x) ):First, ( g'(x) = frac{1}{x - 1} - frac{1}{(x - 1)^2} ).Differentiate again:( g''(x) = - frac{1}{(x - 1)^2} + frac{2}{(x - 1)^3} ).At ( x = 2 ), ( g''(2) = - frac{1}{(1)^2} + frac{2}{(1)^3} = -1 + 2 = 1 ), which is positive. Therefore, ( x = 2 ) is a local minimum.Since the function ( g(x) ) tends to ( +infty ) as ( x to 1^+ ) and as ( x to +infty ), the critical point at ( x = 2 ) must be the global minimum on ( (1, +infty) ).Therefore, the minimal value of ( g(x) ) is at ( x = 2 ).Compute ( g(2) ):( g(2) = ln(2 - 1) + frac{1}{2 - 1} + 1 = ln(1) + 1 + 1 = 0 + 1 + 1 = 2 ).Therefore, the minimal value of ( g(x) ) is 2. Therefore, in order to have ( g(x) + a geq 0 ) for all ( x > 1 ), we need ( a geq -2 ). Because the minimal value of ( g(x) ) is 2, so the minimal value of ( g(x) + a ) is ( 2 + a ). To have ( 2 + a geq 0 ), we need ( a geq -2 ).Therefore, the range of values for ( a ) is ( [-2, +infty) ). Therefore, the correct answer should be D.But let me double-check. If ( a = -2 ), then ( f'(x) = ln(x - 1) + frac{1}{x - 1} + 1 - 2 = ln(x - 1) + frac{1}{x - 1} - 1 ).At ( x = 2 ), ( f'(2) = ln(1) + 1 - 1 = 0 + 1 - 1 = 0 ). So the derivative at ( x = 2 ) is zero when ( a = -2 ). But does the derivative stay non-negative for all ( x > 1 ) when ( a = -2 )?We know that at the minimum point ( x = 2 ), the derivative is zero. Since ( g(x) ) has its minimum at 2, and ( a = -2 ) shifts ( g(x) ) down by 2, so the minimum becomes zero. Therefore, for ( a = -2 ), ( f'(x) geq 0 ) for all ( x > 1 ), because the minimal value is zero. Therefore, the function is non-decreasing on ( (1, +infty) ), so it's monotonic. Therefore, ( a = -2 ) is allowed. For ( a > -2 ), the derivative is always positive, so the function is strictly increasing. For ( a < -2 ), the derivative would be negative somewhere, so the function would decrease somewhere. Therefore, the range of ( a ) is ( [-2, +infty) ), which is option D.But let me check again. Suppose ( a = -3 ), which is less than -2. Then ( f'(x) = ln(x - 1) + 1/(x - 1) + 1 - 3 = ln(x - 1) + 1/(x - 1) - 2 ). Let's see if this is ever negative. At ( x = 2 ), it would be ( 0 + 1 - 2 = -1 ), which is negative. So the derivative is negative at x=2 when a=-3, which would mean the function is decreasing there, hence not monotonic. So a must be at least -2. Therefore, the answer is D.Therefore, the correct answer is D: ([-2, +infty)).Final Answerboxed{D}</think>To determine the range of values for ( a ) such that the function ( f(x) = xln(x-1) + a(x-1) ) is monotonic on ( (1, +infty) ), we need to analyze the derivative of the function.First, we compute the derivative ( f'(x) ):[f'(x) = ln(x-1) + frac{x}{x-1} + a]Simplifying the term ( frac{x}{x-1} ):[frac{x}{x-1} = 1 + frac{1}{x-1}]Thus, the derivative becomes:[f'(x) = ln(x-1) + 1 + frac{1}{x-1} + a]We need ( f'(x) geq 0 ) for all ( x > 1 ) to ensure the function is non-decreasing. We define ( g(x) = ln(x-1) + frac{1}{x-1} + 1 ) and find its minimum value over ( x > 1 ).To find the critical points, we compute the derivative ( g'(x) ):[g'(x) = frac{1}{x-1} - frac{1}{(x-1)^2}]Setting ( g'(x) = 0 ):[frac{1}{x-1} - frac{1}{(x-1)^2} = 0 implies (x-1) - 1 = 0 implies x = 2]We check the second derivative ( g''(x) ) at ( x = 2 ):[g''(x) = -frac{1}{(x-1)^2} + frac{2}{(x-1)^3}]At ( x = 2 ):[g''(2) = -1 + 2 = 1 > 0]Thus, ( x = 2 ) is a local minimum. Evaluating ( g(x) ) at ( x = 2 ):[g(2) = ln(1) + 1 + 1 = 2]The minimum value of ( g(x) ) is 2. To ensure ( g(x) + a geq 0 ) for all ( x > 1 ), we need:[2 + a geq 0 implies a geq -2]Therefore, the range of values for ( a ) is ([-2, +infty)), which corresponds to option D.[boxed{D}]]

🔑:To analyze the monotonicity of the function f(x) = xln(x-1) + a(x-1) on the interval (0, +infty), we first find its derivative. For x > 1, we have:[begin{align*}f'(x) &= frac{d}{dx}[xln(x-1)] + frac{d}{dx}[a(x-1)] &= ln(x-1) + xcdotfrac{1}{x-1} + a &= ln(x-1) + frac{x}{x-1} + a &= ln(x-1) + frac{1}{x-1} + 1 + a.end{align*}]Letting t = x-1 > 0, we can rewrite the derivative as a function of t: g(t) = ln t + frac{1}{t} + 1 + a, where t > 0. The problem now is to ensure that g(t) does not change signs across its domain to maintain the monotonicity of f(x).To do this, we examine the derivative of g(t):[begin{align*}g'(t) &= frac{d}{dt}[ln t + frac{1}{t} + 1 + a] &= frac{1}{t} - frac{1}{t^2} &= frac{t-1}{t^2}.end{align*}]From g'(t) = frac{t-1}{t^2}, we observe that g'(t) > 0 for t > 1 and g'(t) < 0 for 0 < t < 1. This means g(t) reaches its minimum value at t=1.Calculating the minimum value of g(t):[begin{align*}g(t)_{min} &= g(1) &= ln(1) + frac{1}{1} + 1 + a &= 0 + 1 + 1 + a &= 2 + a.end{align*}]For g(t) = 0 to have no roots that change signs, it is necessary and sufficient that 2 + a geq 0. Solving this inequality for a gives:[a geq -2.]Therefore, the range of values for a that ensures f(x) is monotonic on (0, +infty) is [-2, +infty). Hence, the correct answer is boxed{D}.

🧠:[<think>嗯，这道题目看起来是要找满足条件的非负整数对(m, n)，其中m不等于n，而且50688除以m+n的结果是一个2的正奇数次幂。首先，我要理解题目的每个条件，然后一步步分析。首先，题目中的非负整数对(m, n)，所以m和n都是大于等于0的整数，而且m不等于n。接下来，50688除以它们的和m+n必须是一个2的正奇数次幂。这里需要注意的是，正奇数次幂指的是2的指数为奇数的正整数，比如2^1=2，2^3=8，2^5=32等等，但不包括2^0=1，因为指数是0，不属于正奇数次幂。不过，这里可能需要注意题目中的“正奇數幂”，是否包括1。比如，当指数为1的时候，2^1=2，是正奇数次幂吗？应该算的，因为1是奇数。不过也有可能题目中的“奇数次幂”指的是指数为奇数，不管正不正，但这里可能“正”指的是幂的结果是正数，而指数本身是正整数中的奇数。所以确定一下，这里的正奇数次幂指的是像2^k，其中k是正奇数，即k=1,3,5,…这样的数。所以，首先我要分解50688，看看它能被哪些2的奇数次幂整除，然后这些商就是m+n的可能值，之后需要找到有多少对非负整数(m,n)满足m+n等于这个商，且m≠n。首先，我需要将50688分解质因数，看看里面有多少个2的因子。这样，就可以知道当50688除以某个2的奇数次幂时，剩下的部分是否还是整数，或者是否还有其他的质因数需要考虑。首先分解50688：50688 ÷ 2 = 2534425344 ÷ 2 = 1267212672 ÷ 2 = 63366336 ÷ 2 = 31683168 ÷ 2 = 15841584 ÷ 2 = 792792 ÷ 2 = 396396 ÷ 2 = 198198 ÷ 2 = 99现在，99不能再被2整除了。所以，50688 = 2^9 × 99 = 2^9 × 9 × 11 = 2^9 × 3^2 × 11^1。所以，质因数分解是2^9 * 3^2 * 11^1。现在，题目要求50688/(m + n)是一个2的正奇数次幂，也就是说，这个结果必须是2的某个奇数次幂，比如2^1, 2^3, 2^5等等。设这个幂为2^k，其中k是正奇数。那么，我们可以表示为：50688/(m + n) = 2^k，其中k为正奇数。于是，m + n = 50688 / 2^k = 50688 ÷ 2^k。因为m和n都是非负整数，且m + n必须是一个整数，所以2^k必须是50688的一个因数。但根据质因数分解，50688中的2的指数是9，所以k的最大可能值是9，但k必须是正奇数，所以k的可能取值为1,3,5,7,9。现在，我们来逐个检查每个可能的k值，计算对应的m + n的值，然后确定有多少个非负整数对(m, n)满足m + n等于该值且m ≠ n。首先，k的可能值为1,3,5,7,9。对于每个k：1. 当k=1时，2^1=2，所以m + n = 50688 / 2 = 253442. 当k=3时，2^3=8，所以m + n = 50688 / 8 = 63363. 当k=5时，2^5=32，所以m + n = 50688 / 32 = 15844. 当k=7时，2^7=128，所以m + n = 50688 / 128 = 3965. 当k=9时，2^9=512，所以m + n = 50688 / 512 = 99接下来，需要确定这些m + n的值是否都是非负整数，显然是的，因为每个k对应的2^k都是50688的因数。接下来，对于每个这样的m + n值，求出对应的非负整数对(m, n)，其中m ≠ n。对于每个m + n = S的情况，非负整数解的对数通常是S + 1对，因为m可以从0到S，n对应为S - m。但因为m和n是非负整数，所以总共有S + 1种可能。但是题目要求m ≠ n，所以需要排除那些m = n的情况。当S为偶数时，存在一个解使得m = n = S/2，而当S为奇数时，不存在这样的解，因为S/2不是整数。因此，对于每个S，非负整数对的数量为：如果S是偶数，则总共有(S + 1) - 1 = S个对（排除m = n的情况）；如果S是奇数，则总共有(S + 1)对，因为不存在m = n的情况，所以不需要排除。不过，这里需要注意，当S是偶数时，确实存在一个点m = n = S/2，而当S是奇数时，这样的点不存在。因此，对于每个S：当S为偶数时，符合条件的对数是(S + 1) - 1 = S；当S为奇数时，符合条件的对数是(S + 1)。现在，我们需要对每个k对应的S进行分析：1. k=1时，S=25344，这是偶数，所以符合条件的对数为25344；2. k=3时，S=6336，也是偶数，对数为6336；3. k=5时，S=1584，偶数，对数为1584；4. k=7时，S=396，偶数，对数为396；5. k=9时，S=99，奇数，对数为99 + 1 = 100；不过，这里可能存在错误，我需要再仔细检查一下。例如，当S是偶数时，比如S=2，那么可能的非负整数对是(0,2),(1,1),(2,0)，其中(1,1)需要被排除，所以正确的对数是2，即S=2的情况下，对数为2，而根据公式(S + 1) -1 = 2，正确。所以对于S为偶数，对数是S。当S为奇数时，比如S=3，可能的对数是(0,3),(1,2),(2,1),(3,0)，共4对，即S+1=4对，且所有对都满足m≠n，所以不需要排除，对数是S+1。所以，现在回到各个k的情况：k=1时，S=25344（偶数），对数为25344；k=3时，S=6336（偶数），对数为6336；k=5时，S=1584（偶数），对数为1584；k=7时，S=396（偶数），对数为396；k=9时，S=99（奇数），对数为100；那么，总的对数就是这些数相加：25344 + 6336 + 1584 + 396 + 100.现在计算这些数的和：首先，25344 + 6336 = 3168031680 + 1584 = 3326433264 + 396 = 3366033660 + 100 = 33760所以，总和是33760对吗？不过，这里可能存在一个问题：是否每个k对应的S都是有效的，即当k=9时，S=99，但需要确认50688除以2^9确实等于99。根据之前的分解，50688=2^9 *3^2*11，所以是的，当k=9时，50688/2^9=3^2*11=9*11=99，没错。接下来，检查每个k对应的S是否被正确计算：k=1:50688/2=25344，正确；k=3:50688/8=6336，正确；k=5:50688/32=1584，正确；k=7:50688/128=396，正确；k=9:50688/512=99，正确。好的，没问题。接下来，确认每个S对应的对数是否正确：当S是偶数时，对数是S；当S是奇数时，对数是S+1；因此，这里：k=1:25344（偶数）→25344对；k=3:6336（偶数）→6336对；k=5:1584（偶数）→1584对；k=7:396（偶数）→396对；k=9:99（奇数）→100对；所以总和是25344 + 6336 + 1584 + 396 + 100 = 33760。不过，这里似乎总和很大，可能哪里出错了？或者可能我的理解有问题？再仔细想一想：题目要求的是非负整数对(m, n)，其中m和n都是非负整数，并且m + n = S，同时m ≠ n。对于每个S，这样的对数是多少？比如，当S为某个数时，m和n都是非负整数，满足m + n = S，且m ≠ n。这样的有序对有多少个？比如，当S=1时，可能的对是(0,1)和(1,0)，共2个，也就是S+1 -0（因为当S是奇数时，没有m=n的情况），所以对数为2=1+1；当S=2时，可能的对是(0,2),(1,1),(2,0)，排除(1,1)，所以2对，即S=2时，对数为2=2；当S=3时，有4对，即(0,3),(1,2),(2,1),(3,0)，因为S是奇数，所以所有对都满足m≠n，所以4=3+1；所以，对的，当S是偶数时，对数为S；当S是奇数时，对数为S+1。因此，之前的计算是正确的，总和是33760。不过，这个结果是否正确呢？因为50688是一个很大的数，导致S可能很大，所以对数也可能很大，但题目可能希望有更简洁的答案，或者我可能在分解质因数的时候出错了？让我再检查一下质因数分解是否正确：50688 ÷ 2 =25344 →2^125344 ÷2=12672 →2^212672 ÷2=6336 →2^36336 ÷2=3168 →2^43168 ÷2=1584 →2^51584 ÷2=792 →2^6792 ÷2=396 →2^7396 ÷2=198 →2^8198 ÷2=99 →2^9此时99不能再被2整除了，所以分解正确，2^9。接下来，99分解为9*11=3^2*11^1。所以，50688=2^9*3^2*11^1。因此，当50688除以2^k时，剩下的部分是2^(9−k)*3^2*11^1。但要使这个商是一个2的正奇数次幂，即商必须是2^m，其中m是正奇数。那么，剩下的部分必须是纯2的幂，也就是3^2*11必须被约掉，但这里是不可能的，因为3和11都是质数，无法分解成2的幂。这说明我的分析有问题！哦，这里发现一个严重的问题！根据之前的分析，我假设当50688/(m + n) = 2^k时，其中k是正奇数，但根据质因数分解，50688=2^9*3^2*11，所以如果50688/(m + n)必须等于2^k，那么(m + n)必须是50688除以一个2的奇数次幂，即50688/(2^k) = 2^(9−k)*3^2*11。只有当9−k≥0时，即k≤9，且k是正奇数，即k=1,3,5,7,9。但此时，剩下的部分是2^(9−k)*3^2*11，必须是一个整数，但是题目中说这个结果必须是2的奇数次幂，即只能含有因子2，而其他质因子必须被约掉，但这里3^2*11是无法被约掉的，因此我的整个之前的分析都是错误的！这意味着只有当3^2*11被约掉时，即50688/(m + n)是纯2的幂，但根据分解式，这不可能，因为50688本身含有3^2和11^1的因子，所以除非m + n将这些因子都包含进去，即只有当m + n包含3^2*11的因子时，才能使50688/(m + n)中的3和11被约掉，只剩下2的幂。因此，只有当m + n = 50688 / 2^k = 2^(9−k)*3^2*11，此时50688/(m + n) = 2^k，即只有当m + n等于2^(9−k)*3^2*11时，才能满足条件，而此时k必须是正奇数，且9−k必须是非负整数，即k≤9且k为正奇数，即k=1,3,5,7,9。但是这样的话，m + n必须等于2^(9−k)*3^2*11，也就是说，当k=1时，m + n = 2^(8)*3^2*11 = 256*9*11=256*99=25344；k=3时，m + n =2^(6)*9*11=64*99=6336；k=5时，m + n=2^4*9*11=16*99=1584；k=7时，m + n=2^2*9*11=4*99=396；k=9时，m + n=2^0*9*11=1*99=99；这样，确实，当k是这些奇数值时，m + n的值就是这些数，而50688/(m + n)=2^k，即是一个2的奇数次幂。这时候，剩下的问题就是，对于每个这样的m + n的值，求满足m ≠n 的非负整数对的数量。但是之前的分析中，我错误地认为这些m + n的值都是可能的，但实际上这些值是否正确呢？比如，当k=1时，m + n=25344，而50688/25344=2^1，确实符合条件；k=3时，6336，50688/6336=8=2^3，正确；k=5时，1584，50688/1584=32=2^5，正确；k=7时，396，50688/396=128=2^7，正确；k=9时，99，50688/99=512=2^9，正确；所以，这些k的取值都是正确的，并且对应的m + n的值都是正确的。但是，此时m + n的值必须等于这些特定的数值，即25344, 6336, 1584, 396, 99。因此，每个这样的m + n对应的问题就是，求非负整数对(m,n)满足m + n = S（其中S是上述各值），且m ≠n。这时候，对于每个S，解的数量是：当S是偶数时，有S对；当S是奇数时，有S+1对。因为当S是偶数时，存在m = n = S/2的情况，需要排除，因此解的数量为(S +1) -1 = S；当S是奇数时，没有这样的解，所以解的数量为S +1。现在，检查每个S的奇偶性：25344：偶数；6336：偶数；1584：偶数；396：偶数；99：奇数；因此，对应的解的数量：25344 → 25344对；6336 →6336对；1584 →1584对；396 →396对；99 →100对；总和为25344 + 6336 + 1584 + 396 + 100 = 33760。不过，这里可能有一个错误，就是当m和n是有序对时，比如(m,n)和(n,m)是否算作不同的对。题目中没有说明是否考虑顺序，但通常在这种情况下，如果m和n是有序的，即(m,n)和(n,m)视为不同的对，除非特别说明。不过题目中问的是“pairs (m, n)”，在数学中通常有序对，但有时候也可能指无序对。需要确认题目的要求。题目中说“pairs (m, n)”，通常是有序对，因此(m,n)和(n,m)算作不同的对，除非m=n时才相同。但这里题目要求m≠n，所以对于每个有序对(m,n)和(n,m)，当m≠n时，都被视为不同的对。因此，我之前计算的方式是对的，即对于每个S，当计算有序对时，解的数量是S（当S为偶数）或S+1（当S为奇数）。例如，当S=2时，有序对的数量是2对：(0,2),(2,0)，排除(1,1)，所以有2对；当S=3时，有序对是4对：(0,3),(3,0),(1,2),(2,1))，共4对，即S+1=4对。因此，之前的计算是正确的，总和是33760。不过，这个结果看起来非常大，可能题目有哪里理解错了。让我再仔细检查一次。首先，题目中的条件是：1. m和n是非负整数，即m ≥0，n ≥0；2. m ≠n；3. 50688/(m + n)是一个正奇数次幂的2，即2^k，其中k是正奇数。因此，必须满足：m + n = 50688 / 2^k，其中k是正奇数，并且50688必须能被2^k整除。根据50688的质因数分解，2的指数是9，因此k的可能取值为1,3,5,7,9，对应的m + n的值分别是25344,6336,1584,396,99。对于每个这样的m + n值，计算满足条件的有序对(m,n)的数量：当S是m + n的值时，有序对的数量为：如果S是偶数，则排除m =n的情况，所以数量是S；如果S是奇数，则不存在m =n的情况，所以数量是S +1；所以：25344（偶数）→25344对；6336（偶数）→6336对；1584（偶数）→1584对；396（偶数）→396对；99（奇数）→100对；总和为25344 + 6336 = 31680；31680 + 1584 = 33264；33264 + 396 = 33660；33660 + 100 = 33760。是的，这个结果是对的。不过，可能题目中的“pair”指的是无序对，即(m,n)和(n,m)视为同一对，如果是这样的话，那么计算方式会不同。例如，当S=2时，有序对是(0,2),(2,0),(1,1)，排除(1,1)后剩下两对，即(0,2)和(2,0)，如果视为同一对的话，那么只有1对。但题目中没有说明是否是无序对，所以通常默认是有序对，尤其是当m和n是不同的变量时，比如坐标中的点。但这里题目可能是在问无序对，即不考虑顺序，因此需要将(m,n)和(n,m)视为同一对。因此，当计算的时候，如果S是偶数，除了当m =n的情况外，其他情况都是成对出现的，所以数量应该是(S +1 -1)/2 = S/2，而当S是奇数时，每个有序对都是唯一的，所以数量是(S +1)/2。但这会导致不同的结果。例如，当S=2时，有序对有(0,2),(1,1),(2,0)，排除(1,1)，剩下两个有序对，即(0,2)和(2,0)，如果视为无序对，就是1对；当S=3时，有序对是(0,3),(1,2),(2,1),(3,0)，排除m≠n后还是4个，如果视为无序对，就是2对。因此，如果题目中的pair指的是无序对，那么计算方式不同，但题目中的pair通常指的是有序对，除非特别说明。但中文中的“对”有时可能指无序的，所以需要确认。题目中的原文是“有多少對非負整數 (m, n) 滿足 m neq n”，这里的“对”应该是有序的，因为如果无序的话，应该会说“无序对”或者类似的话，否则默认是有序的。因此，我认为这里的对是有序的，因此之前的计算结果33760是正确的。不过，这个结果看起来非常大，可能我哪里出错了？另外，可能题目中的“正奇數幂”指的是指数为奇数的正幂，即允许2^1，2^3等，但必须大于1吗？不过题目中明确说是“正奇數暮”，也就是正奇数次幂，所以2^1=2也是允许的。因此，之前的分析是对的。但为了确保正确，再检查一次：每个k的可能值对应的S：k=1:25344 →偶数，对数为25344；k=3:6336 →偶数，6336；k=5:1584 →偶数，1584；k=7:396 →偶数，396；k=9:99 →奇数，100；加起来是25344 + 6336 = 31680；31680 + 1584 = 33264；33264 + 396 = 33660；33660 + 100 = 33760。是的，这个结果是对的。不过，可能需要确认每个步骤是否都正确，特别是质因数分解部分，以及商是否确实是2的奇数次幂。例如，当k=9时，50688 / 2^9 = 50688 / 512 = 99，而99=3^2*11，不是2的幂，这说明我的之前的分析有严重错误。哦，天哪，这里发现了致命错误！之前我误以为50688/(m + n) =2^k，其中k是正奇数，但实际上，当m + n=99时，50688/99=512=2^9，而9是奇数，因此满足条件。但是，这里的2^9是一个奇数次幂吗？9是奇数，是的。所以这个情况是有效的。然而，当k=9时，50688/(m + n)=2^9，即m + n=99，这个情况下，尽管99本身含有3和11的因子，但50688/(m + n)确实是一个2的奇数次幂，因此这个情况是有效的。这说明，只要50688/(m + n)是一个2的奇数次幂，不管m + n本身是否含有其他因子，只要商的结果是2的奇数次幂即可。因此，这里的分析是正确的。因此，之前的计算是正确的，总和为33760。不过，这个结果似乎过大，可能题目的正确答案应该更小，可能我哪里理解错了？让我再仔细检查一次。首先，确定当m + n=99时，确实有50688/99=512=2^9，这是正确的，因为99×512=50688。同样，检查其他情况：6336×8=50688 →正确；1584×32=50688 →正确；396×128=50688 →正确；25344×2=50688 →正确；所以，所有k对应的S都是正确的。接下来，计算每个S对应的有序对(m, n)的数量：当S=25344（偶数）时，有25344 +1 =25345个有序对，其中有一个是m=n=12672，因此排除后剩下25344个；同理，其他偶数S的情况都是S个有序对；当S=99（奇数）时，有99 +1=100个有序对，且没有m=n的情况；所以总和是25344 + 6336 +1584 +396 +100=33760。但可能题目中的“对”指的是无序对，即(m, n)和(n, m)视为同一对，这样结果会减半，除当m=n的情况，但这里m≠n，所以对于每个S，无序对的数量是：当S为偶数时，有序对的数量是S，无序对的数量是S/2（因为每个对都被计算了两次，除了当m=n的情况，但这里已经被排除，所以实际无序对的数量是S/2）；当S为奇数时，有序对的数量是S+1，无序对的数量是(S+1)/2；例如，S=2，有序对是2个，无序对是1个；S=3，有序对是4个，无序对是2个；所以，如果题目中的“对”指的是无序对，那么：对于k=1, S=25344（偶数），无序对的数量=25344/2=12672；k=3, S=6336，无序对=6336/2=3168；k=5, S=1584，无序对=1584/2=792；k=7, S=396，无序对=396/2=198；k=9, S=99，无序对=(99+1)/2=50；总和为12672 +3168=15840；15840+792=16632；16632+198=16830；16830+50=16880。如果题目中的“对”指的是无序对，则答案是16880，但如果是有序对，则是33760。因此，必须确认题目的意图。中文中的“对”有时候可以指无序的，但数学题中如果没有特别说明，通常指的是有序对。但原题是英文翻译过来的，原题可能要求有序对，因此答案可能应该是33760。不过，根据题目的分数是2分，可能答案不会这么大，可能哪里出错了。让我再仔细检查质因数分解：50688的分解是否正确？计算50688 ÷2=25344 →2^125344 ÷2=12672 →2^212672 ÷2=6336 →2^36336 ÷2=3168 →2^43168 ÷2=1584 →2^51584 ÷2=792 →2^6792 ÷2=396 →2^7396 ÷2=198 →2^8198 ÷2=99 →2^999 ÷3=33 →3^133 ÷3=11 →3^211 ÷11=1 →11^1所以分解式是2^9 *3^2 *11^1，正确。所以50688=2^9*3^2*11^1。因此，当要求50688/(m + n)=2^k，其中k是正奇数，那么m + n=50688/2^k=2^(9−k)*3^2*11^1。只有当9−k >=0，即k<=9，并且k是正奇数，所以k=1,3,5,7,9。对应的m + n分别是：k=1:2^(8)*9*11=256*99=25344；k=3:2^6*9*11=64*99=6336；k=5:2^4*9*11=16*99=1584；k=7:2^2*9*11=4*99=396；k=9:2^0*9*11=1*99=99；都是正确的。因此，每个S对应的有序对的数量是正确的，即当S为偶数时，有序对数为S；当S为奇数时，有序对数为S+1。总和为33760。但可能题目中的答案需要以这种方式计算，所以最终答案应该是33760，即boxed{33760}。不过，再次考虑，如果题目中的“非負整數對”指的是无序对，那么答案应该是16880，但不确定。可能需要根据题目的习惯来判断。但根据通常的数学题中的习惯，如果没有特别说明，“对”通常指的是有序的，尤其是当问题中变量有顺序的时候，比如(m,n)和(n,m)是不同的解，除非题目特别说明不考虑顺序。因此，我认为正确答案是33760。不过，可能我之前哪里出错了，比如在计算有序对的数量时，当S=25344，m和n的非负整数解的数量是25344个，这个数字是否合理？例如，当S=25344时，m可以是0到25344，共25345个可能的值，排除m=n=12672的情况，所以有25344个有序对，没错。同样，对于其他S值也是如此。因此，最终答案应该是33760，即boxed{33760}。不过，考虑到这个结果非常大，可能题目中存在某种限制条件我没有考虑到，或者我的分析有误。例如，题目中的“非負整數”是否允许m或n为0？题目中允许，所以没问题。或者，可能k的取值范围有误，比如k必须是奇数，但k=1,3,5,7,9都是正确的，是的。因此，我认为我的分析是正确的，答案应该是33760。答案boxed{33760}</think>首先，我们需要找到满足条件的非负整数对 ((m, n))，其中 (m neq n) 且 (frac{50688}{m+n}) 是 2 的正奇数次幂。1. 质因数分解：将 50688 分解质因数为 (2^9 times 3^2 times 11)。2. 确定可能的 2 的奇数次幂：由于 50688 的质因数分解中 2 的指数为 9，因此可能的奇数次幂指数 (k) 为 1, 3, 5, 7, 9。3. 计算对应的 (m + n) 值： - (k = 1) 时，(m + n = frac{50688}{2^1} = 25344) - (k = 3) 时，(m + n = frac{50688}{2^3} = 6336) - (k = 5) 时，(m + n = frac{50688}{2^5} = 1584) - (k = 7) 时，(m + n = frac{50688}{2^7} = 396) - (k = 9) 时，(m + n = frac{50688}{2^9} = 99)4. 计算每个 (m + n) 值对应的非负整数对 ((m, n)) 的数量： - 当 (m + n) 为偶数时，排除 (m = n) 的情况，对数为 (m + n)。 - 当 (m + n) 为奇数时，没有 (m = n) 的情况，对数为 (m + n + 1)。5. 具体计算： - (25344)（偶数）对应的对数为 (25344) - (6336)（偶数）对应的对数为 (6336) - (1584)（偶数）对应的对数为 (1584) - (396)（偶数）对应的对数为 (396) - (99)（奇数）对应的对数为 (100)6. 求和： [ 25344 + 6336 + 1584 + 396 + 100 = 33760 ]最终答案为：[boxed{33760}],<think>好，我现在要解这道题，题目是说有多少对非负整数(m, n)满足m不等于n，而且50688除以m加n的结果是一个2的正奇数次幂。首先我需要理清楚题目的条件和要求，然后一步步分析。首先，问题是要找满足以下条件的非负整数对(m, n)：1. m ≠ n；2. 50688/(m + n)是一个2的正奇数次幂，也就是像2^1, 2^3, 2^5等这样的数，而不仅仅是2的任意次幂，所以排除了2的偶数次幂，比如2^2, 2^4之类的；3. m和n都是非负整数，所以m + n也必须是非负整数，但因为m和n都是非负的，所以m + n至少为0，但如果是0的话，分母就为0了，显然不可能，所以m + n必须是正整数，并且还要能整除50688；4. 同时，m + n的结果应该是50688除以一个2的正奇数次幂后的结果，也就是m + n = 50688 / (2^k)，其中k是正奇数；5. 接下来需要确定所有可能的k值，使得50688能够被2^k整除，并且k是正奇数；6. 对于每个这样的k值，求出对应的m + n的值，然后计算满足m ≠ n的非负整数对(m, n)的数量；7. 最后将这些数量相加得到总数。接下来，我需要分解步骤具体分析：第一步，分解50688的素因数，确定其含有多少个2的幂次。因为题目中涉及的是除以2的奇数次幂，所以必须知道50688中2的因数分解情况。首先分解50688：50688 ÷ 2 = 25344 → 1次25344 ÷ 2 = 12672 → 2次12672 ÷ 2 = 6336 → 3次6336 ÷ 2 = 3168 → 4次3168 ÷ 2 = 1584 → 5次1584 ÷ 2 = 792 → 6次792 ÷ 2 = 396 → 7次396 ÷ 2 = 198 → 8次198 ÷ 2 = 99 → 9次99 ÷ 2 不整除，所以停止。所以，50688 = 2^9 × 99。不过这里可能我哪里算错了，因为99还能分解吗？实际上，99 = 9 × 11 = 3² × 11，所以综合起来，50688 = 2^9 × 3² × 11^1。因此，50688的素因数分解是2的9次方乘以3的平方乘以11的一次方。接下来，题目要求的是50688/(m + n)必须是2的正奇数次幂。也就是说，当我们将50688除以(m + n)后，结果中不能有其他素因子，只能是2的奇数次幂。换句话说，(m + n)必须包含50688中所有的3²、11以及足够的2的因子，使得剩下的部分仅仅是2的奇数次幂。即，设(m + n) = 50688 / (2^k)，其中k是正奇数，并且必须满足2^k能够整除50688。因为50688中2的最高幂次是9，所以k的可能取值范围是1, 3, 5, 7, 9这些正奇数，最大不超过9。接下来，我需要确定所有可能的k值：k的可能值为1,3,5,7,9。每个这样的k对应一个不同的(m + n)的值，也就是：当k=1时，m + n = 50688 / 2^1 = 50688 / 2 = 25344；k=3时，m + n = 50688 / 8 = 6336；k=5时，50688 / 32 = 50688 ÷ 32 = 1584；k=7时，50688 / 128 = 396；k=9时，50688 / 512 = 99。接下来，我需要验证这些计算结果是否正确：50688 ÷ 2 = 25344 → 正确；25344 ÷ 8（即2^3）= 25344 ÷ 8 = 3168？不对，之前算错了。这里可能需要重新计算。哦，发现错误了。当k=3时，2^3=8，所以50688 ÷8=50688 ÷8=6336。但之前分解的时候，当分解到第9次得到的是99，所以2^9=512，对吗？让我再仔细计算一下：50688 ÷ 2^1 = 50688 ÷2 =25344；50688 ÷2^3=50688 ÷8=6336；50688 ÷2^5=50688 ÷32=1584；50688 ÷2^7=50688 ÷128=396；50688 ÷2^9=50688 ÷512=99。没错，之前的计算是对的。所以可能的k值是1,3,5,7,9，对应的m + n分别是25344,6336,1584,396,99。接下来，对于每个可能的m + n的值，计算有多少个非负整数对(m, n)满足m + n等于这个值，并且m ≠ n。对于给定的m + n = S，非负整数解的对数有(S + 1)个，因为m可以从0到S，对应的n就是S - m。但是题目要求m ≠ n，所以需要排除m = n的情况，也就是当S为偶数时，存在m = S/2，n = S/2的情况，此时这对解需要被排除。而当S为奇数时，不存在m = n的情况，因为S是奇数，无法被2整除得到整数。因此，对于每个S，符合条件的解的数量是：如果S是偶数，则解的数量是(S + 1) - 1 = S；如果S是奇数，则解的数量是(S + 1) - 0 = S + 1；不过这里需要注意的是，无论S是奇数还是偶数，总共有S + 1对(m, n)，其中m和n是非负整数，满足m + n = S。而当m = n时，只有当S是偶数时，m = n = S/2，这时候才会出现m = n的情况；如果S是奇数，则不存在这样的m和n。因此，当S为偶数时，符合m ≠ n的解的数量是(S + 1) - 1 = S；当S为奇数时，符合m ≠ n的解的数量是(S + 1) - 0 = S + 1；不过，这里可能我的推导有问题，让我再仔细思考一下。例如，当S = 2时，可能的解是(0,2), (1,1), (2,0)。其中(1,1)需要被排除，所以有效解是2对，即2，即S=2，解数是2，等于S。当S=3时，可能的解是(0,3), (1,2), (2,1), (3,0)，总共有4对，即3 +1=4，但这时候所有解都满足m ≠ n，所以解数是4，即S=3时，解数是4，即S+1=4，没错。所以结论是对的：当S为偶数时，解数是S；当S为奇数时，解数是S + 1。接下来，我需要为每个可能的S（即25344,6336,1584,396,99）计算对应的解数，并相加得到总数。首先，分别判断每个S的奇偶性：25344：这个数是偶数吗？是的，因为末位是4，所以是偶数；6336：末位是6，偶数；1584：末位是4，偶数；396：末位是6，偶数；99：末位是9，奇数。所以，前四个S值都是偶数，对应的解数分别为25344,6336,1584,396；最后一个S=99是奇数，对应的解数是99 +1 =100。然后，将这些解数相加：25344 + 6336 + 1584 + 396 + 100。不过，这里需要计算一下这些数的和：先计算25344 + 6336：25344 + 6336 = 31680；接着，31680 + 1584 = 33264；33264 + 396 = 33660；33660 + 100 = 33760。所以，总数是33760对？不过，我需要再检查一下每个步骤是否正确，特别是每个S对应的解数是否正确。首先，对于每个S：当S=25344（偶数）时，解数是25344对；S=6336（偶数），解数6336；S=1584（偶数），解数1584；S=396（偶数），解数396；S=99（奇数），解数100；它们的和确实是25344+6336=31680；31680+1584=33264；33264+396=33660；33660+100=33760。不过，这里需要注意，题目中要求的是非负整数对(m, n)，并且m ≠ n。而每个这样的S对应的解数是否正确？例如，当S=99（奇数），解数应该是99 +1=100，对吗？是的，因为对于奇数S=99，总共有99 +1=100个解，而其中没有m = n的情况，所以全部都是有效的解，对吗？是的，因为当S=99，m和n都是非负整数，且和为99，那么m可以是0到99，共100个数，每个m对应一个n=99 - m，而且因为99是奇数，所以不存在m = n的情况，因此这100对都是有效的。而如果S是偶数，比如S=2，解数是2，即两对：(0,2)和(2,0)，对吗？是的，原来的三个解中排除了(1,1)，所以剩下两个。所以每个偶数S对应的解数是S，而奇数S对应的解数是S +1。现在，我需要确认这些S的值是否正确，也就是当k=1,3,5,7,9时，对应的m + n是否确实是25344,6336,1584,396,99。再次验证：对于k=1，即2^1=2，50688 ÷2=25344；k=3，2^3=8，50688 ÷8=6336；k=5，2^5=32，50688 ÷32=1584；k=7，2^7=128，50688 ÷128=396；k=9，2^9=512，50688 ÷512=99；这些计算都是正确的，所以对应的m + n的值正确。那么对应的解数：25344是偶数，解数25344；6336是偶数，解数6336；1584是偶数，解数1584；396是偶数，解数396；99是奇数，解数100；它们的和是25344 + 6336 = 31680；31680 + 1584 = 33264；33264 + 396 = 33660；33660 + 100 = 33760；所以总数是33760对。不过，这里可能存在一个误区：题目中是否允许m或n为0？是的，题目说是非负整数，所以0是可以的，只要m + n不等于0，这里所有的S都是正数，没问题。不过，还有一个问题需要注意：题目中的m和n是非负整数，并且m ≠ n，所以对于每个S，当计算解数的时候，确实要排除m = n的情况，但是当S为偶数时，解数正确，当S为奇数时，无需排除。所以，之前的计算是对的，总共有33760对。不过，这个结果是否正确呢？我觉得可能有哪里出错了，因为可能某些S的值对应的解数计算有问题，或者k的可能取值有误。让我再检查一下每个步骤：首先，分解50688：50688 ÷2=25344（1）25344 ÷2=12672（2）12672 ÷2=6336（3）6336 ÷2=3168（4）3168 ÷2=1584（5）1584 ÷2=792（6）792 ÷2=396（7）396 ÷2=198（8）198 ÷2=99（9）所以，确实，50688=2^9×3²×11，因此分解正确。接下来，题目要求的是50688/(m + n)是2的正奇数次幂，也就是说，50688/(m + n)=2^k，其中k为正奇数，且2^k必须整除50688。因此，k的可能取值是1,3,5,7,9，因为2的9次方是50688中最大的2的幂，且k必须为奇数。所以这些k值是正确的，对应的S值也就是50688/2^1=25344，50688/8=6336，50688/32=1584，50688/128=396，50688/512=99，都是正确的。接下来，每个S对应的解数是否正确？比如，当S=25344时，解数是25344，即每个m从0到25344，共有25345对，排除掉m=n的情况，即当m=25344/2=12672时，这时候m=n=12672，所以需要排除这一对，因此解数为25345 -1=25344，正确。同理，当S=6336时，解数6336，即共有6337对，排除m=n=3168，解数6336，正确。当S=99时，解数99+1=100，正确。然后总和是25344+6336+1584+396+100=33760，这个结果对吗？让我再手动计算一下这些数的和：25344+6336=25344 + 6000=31344，再加上336=31344+336=3168031680 + 1584 = 31680+1500=33180，再加上84=33180+84=3326433264 + 396 = 33264+300=33564，再加上96=33564+96=3366033660 +100=33760是的，没错。不过，是否还有其他可能的k值被遗漏了？比如k=11？但是因为50688中2的最高幂次是9，所以k不能超过9，因此k=1,3,5,7,9是正确的。所以结论应该是33760对。不过，这个数字看起来有点大，可能哪里有问题吗？让我再想想，可能我的理解有问题。题目中的“正奇数次幂”指的是指数k是正奇数，而结果就是2^k。例如，当k=1时，结果是2，当k=3时是8，等等。所以，这里正确的条件应该是，50688/(m + n)=2^k，其中k是正奇数，所以(m + n)=50688/(2^k)，且k必须满足2^k整除50688，也就是k<=9，并且k为奇数，所以确实k=1,3,5,7,9，对应的S=25344,6336,1584,396,99，没错。然后每个S对应的解数是否正确？是的，对于每个S，当S是偶数时，解数是S；当S是奇数时，解数是S+1。那么，最终的答案就是33760对吗？不过，我现在有点怀疑，因为题目是来自一个竞赛题，通常答案可能不会这么大，或许我在哪里犯了计算错误。让我再检查一下每个S对应的解数：例如，当S=99时，解数是100，对吗？是的，因为m可以取0到99，共100个数，每个数对应一个n=99 - m，而且m和n不可能相等，所以100对。当S=396时，解数是396，对吗？396是偶数，所以解数是396。原来的对数是397，减去1对(m=198, n=198)，得到396对。同样地，S=1584时，解数是1584对。好的，看来没错。不过，或许题目中的“非负整数对”是否考虑顺序？例如，(m, n)和(n, m)是否算作不同的对？题目中没有说明不考虑顺序，所以应该算不同的对，例如当m=0，n=S和n=0，m=S是不同的对，只要m≠n，所以每个这样的有序对都算不同的。因此，在计算解数的时候，正确的做法是考虑有序对，因此对于每个S，当m≠n时，有序对的数量是2*(floor(S/2) + 1) - 1（当S为偶数时）？或者可能我的之前的计算方式有误？不，之前的计算方式其实是对的，因为当计算m和n的非负整数解时，允许m从0到S，n=S - m，这样每个有序对都被计算到了，包括(m, n)和(n, m)，除非m = n，这种情况下才会被排除一次。例如，当S=2时，解是(0,2), (1,1), (2,0)，排除(1,1)后，剩下两个有序对：(0,2)和(2,0)，所以解数是2，即S=2，解数2，即S。同样，当S=3时，解数是4，即(0,3), (1,2), (2,1), (3,0)，所以解数是4，即S+1=4。所以原来的计算方式是对的，即对于每个S，如果S是偶数，解数是S；如果是奇数，解数是S+1。因此，总和应该是33760。不过，这个结果是否正确呢？或许题目中的答案可能不是这个数，可能我哪里出错了。让我再检查一下每个S对应的解数：例如，对于S=25344：解数应该是25344，对吗？是的，因为m从0到25344，共有25345对，排除中间的一对(12672,12672)，所以25344对，正确。同样，S=6336，解数6336对，正确。同理，S=1584，解数1584；S=396，解数396；S=99，解数100。总和确实是33760。不过，这个结果似乎很大，可能题目中有没有其他限制条件？题目中说“非负整数对(m, n)满足m ≠ n”，所以只要m和n是非负整数，m + n = S，且m ≠ n，那么每个有序对都算不同的，即使交换位置也算不同的对，对吗？例如，当S=2时，(0,2)和(2,0)是两个不同的对，对吗？是的，题目中没有说明不考虑顺序，所以应该算不同的对。所以原来的计算方式是对的。那么答案就是33760。不过，可能我在分解因数的时候哪里出错了，导致S的值计算错误？让我再重新计算一次每个k对应的S：当k=1时，50688 ÷ 2^1 = 25344；k=3时，50688 ÷8=6336；k=5时，50688 ÷32=1584；k=7时，50688 ÷128=396；k=9时，50688 ÷512=99；这些计算都是正确的。另外，必须确保当k=1时，50688/(m + n)=2^1=2，所以m + n=25344，对吗？是的，没错。那么，看来我的计算是对的，最终的答案应该是33760。不过，考虑到题目是两分题，可能答案不会这么大，所以可能哪里出现了问题？或者，是否题目中的“正奇数次幂”包括1次，也就是2^1=2，是奇数次幂？是的，1是奇数，所以2^1=2是允许的。好的，可能题目确实需要这么大的答案，或者我的计算没错。再检查一下：25344 + 6336 = 31680；31680 + 1584 = 33264；33264 + 396 = 33660；33660 + 100 = 33760。是的，没错。所以，我认为正确答案是33760，即boxed{33760}。不过，可能需要再确认一下。另一种思路是，每一个满足条件的m + n的值为S=50688/(2^k)，其中k是正奇数，且2^k |50688。然后，对于每个S，解数为S或S+1，根据奇偶性。因此，正确的解数总和为：对于k=1，S=25344（偶数）→解数25344；k=3，S=6336（偶数）→6336；k=5，S=1584（偶数）→1584；k=7，S=396（偶数）→396；k=9，S=99（奇数）→100；总和为33760，没错。因此，答案应为boxed{33760}。答案boxed{33760}</think>首先，我们需要找到满足以下条件的非负整数对 ((m, n))：1. (m neq n)2. (frac{50688}{m + n}) 是2的正奇数次幂我们首先分解50688的素因数：[ 50688 = 2^9 times 3^2 times 11 ]接下来，确定可能的2的正奇数次幂因子。由于50688中2的最高幂次是9，因此可能的奇数次幂指数为1, 3, 5, 7, 9。对应的(m + n)值为：- 当(k = 1)时，(m + n = frac{50688}{2^1} = 25344)- 当(k = 3)时，(m + n = frac{50688}{2^3} = 6336)- 当(k = 5)时，(m + n = frac{50688}{2^5} = 1584)- 当(k = 7)时，(m + n = frac{50688}{2^7} = 396)- 当(k = 9)时，(m + n = frac{50688}{2^9} = 99)接下来，计算每个(m + n)值对应的非负整数对((m, n))的数量，并排除(m = n)的情况：- 当(S)为偶数时，解的数量为(S)- 当(S)为奇数时，解的数量为(S + 1)计算结果：- (25344)是偶数，解数为25344- (6336)是偶数，解数为6336- (1584)是偶数，解数为1584- (396)是偶数，解数为396- (99)是奇数，解数为100将所有解数相加：[ 25344 + 6336 + 1584 + 396 + 100 = 33760 ]最终答案为：[boxed{33760}]]

🔑:17. 3376017. Since 50688=2^{9} times 99, we must have m+n=2^{k} times 99 where k is one of 0,2,4,6,8. Forgetting about m neq n for the moment, there are 2^{k} times 99+1 choices of m for each k, as m can range from 0 to 2^{k} times 99. This leads to a total of left(2^{0}+2^{2}+2^{4}+2^{6}+2^{8}right) times 99+5=33764 pairs of (m, n). Among these, 4 pairs violate the condition m neq n, as m=n is possible only when k is 2,4,6 or 8 . Hence the answer is 33764-4=33760.