🧠:[<think>Alright, so I need to solve this inequality: |||2 - x| - x| - 8| ≤ 2008. Hmm, that looks a bit intimidating with all the absolute value layers. Let me try to break it down step by step. Maybe if I work from the inside out, it'll make more sense.First, let's consider the innermost absolute value: |2 - x|. Depending on whether x is less than or greater than 2, this expression will change. So maybe I should split into cases based on the value of x relative to 2. But wait, there are more absolute values outside of that. Maybe instead of tackling all cases at once, I can simplify each layer one by one.Let me denote the inner expressions with some substitutions to make it clearer. Let's say:A = |2 - x| - xThen the next layer is |A| - 8, so:B = |A| - 8 = ||2 - x| - x| - 8Then the outermost absolute value is |B|, so the inequality becomes |B| ≤ 2008, which is equivalent to:-2008 ≤ B ≤ 2008So substituting back in:-2008 ≤ ||2 - x| - x| - 8 ≤ 2008Adding 8 to all parts:-2000 ≤ ||2 - x| - x| ≤ 2016But the left side is ||2 - x| - x| ≥ -2000. However, since absolute values are always non-negative, ||2 - x| - x| is always ≥ 0. Therefore, the left inequality -2000 ≤ ||2 - x| - x| is always true. So we can ignore that part and focus on the right inequality:||2 - x| - x| ≤ 2016So now the problem reduces to solving ||2 - x| - x| ≤ 2016Hmm, this is still a double absolute value. Let me work on this expression | |2 - x| - x |. Let's analyze this inner expression first: |2 - x| - x. Let's denote this as C = |2 - x| - x. Then we have |C| ≤ 2016.So, first, let's figure out what |2 - x| - x is. Again, this depends on whether 2 - x is positive or negative, i.e., whether x < 2 or x ≥ 2.Case 1: x < 2In this case, |2 - x| = 2 - x, so:C = (2 - x) - x = 2 - 2xSo |C| = |2 - 2x|. Then the inequality becomes |2 - 2x| ≤ 2016But since x < 2, 2 - 2x is positive (because 2x < 4, so 2 - 2x > -2, but x could be negative... Wait, actually, if x is less than 2, 2x could be less than 4, so 2 - 2x could be from negative infinity to 2. Wait, actually, if x is negative, 2x is negative, so 2 - 2x would be larger than 2. If x approaches negative infinity, 2 - 2x approaches positive infinity. If x approaches 2 from below, 2 - 2x approaches -2. So in this case, when x < 2, C = 2 - 2x, which can be any real number greater than -2, but depending on x. Wait, no: if x is approaching negative infinity, 2 - 2x approaches positive infinity, and when x approaches 2 from the left, 2 - 2x approaches 2 - 4 = -2. So in this case, C can range from -2 (exclusive) to positive infinity. So |C| would be |2 - 2x|, which is 2|x - 1|. Wait, maybe not. Let me verify.Wait, C = 2 - 2x, so |C| = |2 - 2x| = 2|1 - x|. Hmm, but in any case, the inequality |2 - 2x| ≤ 2016 simplifies to:-2016 ≤ 2 - 2x ≤ 2016But since x < 2, let's solve for x:Left inequality: 2 - 2x ≥ -2016Subtract 2: -2x ≥ -2018Multiply by -1 (reverse inequality): 2x ≤ 2018 => x ≤ 1009Right inequality: 2 - 2x ≤ 2016Subtract 2: -2x ≤ 2014Multiply by -1: 2x ≥ -2014 => x ≥ -1007But in this case, we already have x < 2. So combining these, x must satisfy -1007 ≤ x < 2Case 2: x ≥ 2Here, |2 - x| = x - 2, so:C = (x - 2) - x = -2So |C| = |-2| = 2Thus, the inequality |C| ≤ 2016 becomes 2 ≤ 2016, which is always true. So in this case, all x ≥ 2 satisfy the inequality ||2 - x| - x| ≤ 2016Therefore, combining both cases:From Case 1: -1007 ≤ x < 2From Case 2: x ≥ 2So overall, x ≥ -1007But wait, we have to remember that this was under the substitution for B, which was ||2 - x| - x| - 8, and then the original inequality was |B| ≤ 2008, which we reduced to ||2 - x| - x| ≤ 2016. So solving that gives x ≥ -1007. But the original problem is to find all real numbers x such that |||2 - x| - x| -8| ≤ 2008. So according to this, x can be any real number greater than or equal to -1007. But let's double-check because sometimes when dealing with absolute values, especially nested ones, there might be overlaps or additional constraints.Wait a second, in Case 1, where x < 2, we found that x must be between -1007 and 2, and in Case 2, x >=2 is always valid. So combining these, the solution set is x >= -1007. But let's verify with an example. Let's take x = -1007. Let's compute |||2 - x| - x| -8|:First, x = -1007Compute |2 - x| = |2 - (-1007)| = |1009| = 1009Then |2 - x| - x = 1009 - (-1007) = 1009 + 1007 = 2016Then ||2 - x| - x| -8 = |2016| -8 = 2016 -8 = 2008Then |2008| = 2008 ≤ 2008, which satisfies the inequality.If x is less than -1007, say x = -1008:Compute |2 - (-1008)| = |1010| = 1010Then |2 - x| - x = 1010 - (-1008) = 1010 + 1008 = 2018Then ||2 -x| -x| -8 = |2018| -8 = 2018 -8 = 2010Then |2010| = 2010 > 2008, which does not satisfy the inequality. So x cannot be less than -1007.Similarly, if x = -1007, as we saw, it's exactly 2008, which is allowed. So the lower bound is indeed -1007.For x between -1007 and 2, let's take x = 0:Compute |2 -0| -0 = 2 -0 = 2Then |2| -8 = 2 -8 = -6Then |-6| = 6 ≤ 2008, which is true.For x = 2:Compute |2 -2| -2 = 0 -2 = -2Then |-2| -8 = 2 -8 = -6Then |-6| = 6 ≤2008, which is true.Wait, but in Case 2, when x >=2, we said that C = -2, so |C| = 2, so ||2 -x| -x| = 2, so 2 <=2016, which is true. Then when we compute |||2 -x| -x| -8| = |2 -8| = |-6| =6 <=2008. So yes, all x >=2 satisfy the original inequality.Therefore, combining everything, the solution set is x >= -1007.But wait, in Case 1, we had x < 2, but x >= -1007, and in Case 2, x >=2. So combining, x >= -1007. Therefore, all real numbers x such that x is greater than or equal to -1007 satisfy the inequality.But let's check another point. Let's take x = 1000 (which is greater than 2):Compute |2 -1000| = 998Then |2 -x| -x = 998 -1000 = -2Then ||2 -x| -x| -8 = |-2| -8 = 2 -8 = -6Then | -6 | =6 <=2008, so yes, it works.Another point: x = -1007:As before, it gives 2008, which is allowed.x = -1006:Compute |2 - (-1006)| = |1008| =1008Then |2 -x| -x =1008 - (-1006) =1008 +1006=2014Then |2014| -8=2014 -8=2006Then |2006|=2006 ≤2008, which is allowed.Wait a second, x=-1006 is greater than -1007. Wait, but according to our previous conclusion, x >= -1007 is allowed, but when I took x=-1006, which is within the allowed range, the expression becomes 2006, which is less than 2008, so that's okay. Wait, but when x approaches -1007 from above, like x=-1007 + ε, where ε is a small positive number, then:|2 -x| = |2 - (-1007 + ε)| = |1009 - ε| =1009 - ε (since ε is small)Then |2 -x| -x = (1009 - ε) - (-1007 + ε)=1009 - ε +1007 - ε=2016 -2εThen ||2 -x| -x| -8=2016 -2ε -8=2008 -2εThen |2008 -2ε|=2008 -2ε, which is less than 2008 since ε>0. Therefore, for x >-1007, the expression is less than 2008, so the equality occurs only at x=-1007. Therefore, the original inequality holds for x >=-1007.Wait, but in the case when x < -1007, like x=-1008, we saw that the expression becomes 2010, which is greater than 2008, so it doesn't hold. So indeed, the solution is x >= -1007.Wait, but let me check another point in the interval between -1007 and 2. Let's take x=1.Compute |2 -1| -1=1 -1=0Then |0| -8=0 -8=-8Then |-8|=8<=2008. Yes, that works.How about x= -500:|2 - (-500)| - (-500)=502 +500=1002Then |1002| -8=1002 -8=994|994|=994<=2008. Yes.So, indeed, all x >=-1007 satisfy the inequality. Therefore, the solution is all real numbers x with x >= -1007.Wait, but just to make sure there isn't a mistake in the case analysis. Let's recap:Original inequality: |||2 -x| -x| -8| <=2008We simplified this to ||2 -x| -x| <=2016, which is equivalent to -2016 <= |2 -x| -x <=2016. Wait, no, actually, |C| <=2016 is equivalent to -2016 <= C <=2016, where C= |2 -x| -x. Therefore, we have:-2016 <= |2 -x| -x <=2016But solving this inequality. Let's re-examine that.So we split into two cases based on whether x <2 or x >=2.Case 1: x <2. Then |2 -x|=2 -x, so C=2 -x -x=2 -2x. So the inequality becomes:-2016 <=2 -2x <=2016Solving the left inequality: -2016 <=2 -2xSubtract 2: -2018 <=-2xMultiply by (-1) and reverse inequalities: 2018 >=2x => x <=1009Solving the right inequality:2 -2x <=2016Subtract 2: -2x <=2014Multiply by (-1):2x >=-2014 =>x >=-1007So in this case (x <2), x must be between -1007 and 1009, but since x <2, the upper bound is actually x <2, so combining with x <=1009, it's x <2. Therefore, x >=-1007 and x <2.Case 2: x >=2. Then |2 -x|=x -2, so C=x -2 -x= -2. Then the inequality becomes:-2016 <=-2 <=2016Which is true because -2016 <=-2 and -2 <=2016. Therefore, for x >=2, the inequality holds for all x.Therefore, combining both cases, the solution is x >=-1007.So yes, that seems consistent.Therefore, the answer is all real numbers x such that x is greater than or equal to -1007, so in interval notation, [-1007, ∞). Therefore, the solution set is x ∈ [-1007, ∞).Final AnswerThe solution is all real numbers ( x ) satisfying ( x geq -1007 ). Thus, the answer is (boxed{[-1007, infty)}).</think>To solve the inequality ( |||2 - x| - x| - 8| leq 2008 ), we start by simplifying the innermost absolute value expressions step by step.1. Innermost Absolute Value: - Consider ( |2 - x| ). This depends on whether ( x < 2 ) or ( x geq 2 ).2. Case Analysis: - Case 1: ( x < 2 ): - Here, ( |2 - x| = 2 - x ). - Let ( A = |2 - x| - x = (2 - x) - x = 2 - 2x ). - The inequality becomes ( ||2 - 2x| - 8| leq 2008 ). - Simplifying further, we get ( |2 - 2x| leq 2016 ). - Solving ( |2 - 2x| leq 2016 ): - ( -2016 leq 2 - 2x leq 2016 ) - Adding 2: ( -2014 leq -2x leq 2018 ) - Dividing by -2: ( -1009 leq x leq 1007 ) - Since ( x < 2 ), combining with the above result, we get ( -1007 leq x < 2 ). - Case 2: ( x geq 2 ): - Here, ( |2 - x| = x - 2 ). - Let ( A = |2 - x| - x = (x - 2) - x = -2 ). - The inequality becomes ( ||-2| - 8| = |2 - 8| = 6 leq 2008 ), which is always true. - Therefore, all ( x geq 2 ) satisfy the inequality.3. Combining Results: - From Case 1, we have ( -1007 leq x < 2 ). - From Case 2, we have ( x geq 2 ). - Combining these, the solution is ( x geq -1007 ).4. Verification: - Checking boundary values and intervals confirms that the solution holds for ( x geq -1007 ).Thus, the solution to the inequality is (boxed{[-1007, infty)}).,<think>Okay, let's see. I need to solve the inequality |||2 - x| - x| - 8| ≤ 2008. Hmm, that looks pretty complicated with all those absolute value signs. Maybe I should break it down step by step, starting from the innermost absolute value and working my way outwards. First, let's consider the innermost part: |2 - x|. The absolute value function can change depending on whether the expression inside is positive or negative. So, maybe I should split this into cases based on the value of x. Let's recall that |2 - x| is equal to 2 - x if x ≤ 2, and x - 2 if x > 2. So, if I split it into two cases here, then maybe I can substitute |2 - x| with the appropriate expression and simplify the inequality further. Let me try that.Case 1: x ≤ 2In this case, |2 - x| = 2 - x. Then, the next layer is |(2 - x) - x| - 8. Let's simplify the inside first: (2 - x) - x = 2 - 2x. So now we have |2 - 2x| - 8. Then, the outer absolute value is | |2 - 2x| - 8 |. Wait, so the entire expression becomes ||2 - 2x| - 8| ≤ 2008. Hmm, even this is a bit complex. Maybe I need to break down |2 - 2x| as well. Let's note that |2 - 2x| = 2|1 - x|. So, |2 - 2x| is 2|x - 1|. So, substituting that in, we have |2|x - 1| - 8| ≤ 2008. But perhaps it's easier to handle the original expression without substitution. Let's see. Let me first work on Case 1: x ≤ 2.So, in Case 1, the expression simplifies step by step as follows:Starting with |||2 - x| - x| - 8|.Since x ≤ 2, |2 - x| = 2 - x.So, first layer: |2 - x| - x = (2 - x) - x = 2 - 2x.Second layer: |2 - 2x| - 8. Since x ≤ 2, 2 - 2x is positive when x < 1, and negative when x ≥ 1. Wait, hold on. 2 - 2x is positive when 2x < 2, so x < 1. So, in Case 1, x ≤ 2, but we can further split this into x < 1 and 1 ≤ x ≤ 2.So, maybe Case 1a: x < 1, and Case 1b: 1 ≤ x ≤ 2.Case 1a: x < 1Here, |2 - 2x| = 2 - 2x because 2x < 2 when x < 1. So, |2 - 2x| - 8 = (2 - 2x) - 8 = -6 - 2x.Then, the outer absolute value becomes | -6 - 2x | = | -2x -6 | = 2|x + 3|.Therefore, the inequality becomes 2|x + 3| ≤ 2008, which simplifies to |x + 3| ≤ 1004. So, this implies -1004 ≤ x + 3 ≤ 1004, which leads to -1007 ≤ x ≤ 1001. However, in this case, x < 1, so the solution here is the intersection of x < 1 and -1007 ≤ x ≤ 1001, which is -1007 ≤ x < 1.Case 1b: 1 ≤ x ≤ 2In this subcase, |2 - 2x| = 2x - 2, because 2x ≥ 2 when x ≥ 1. So, |2 - 2x| - 8 = (2x - 2) - 8 = 2x - 10.Then, the outer absolute value is |2x - 10|. So, the inequality becomes |2x - 10| ≤ 2008.This simplifies to -2008 ≤ 2x - 10 ≤ 2008.Adding 10 to all sides: 2 - 2008 ≤ 2x ≤ 2008 + 10.Wait, 2 - 2008? Wait, no. Let me correct that. If it's -2008 ≤ 2x - 10 ≤ 2008, then adding 10 to all parts:-2008 + 10 ≤ 2x ≤ 2008 + 10.Which is -1998 ≤ 2x ≤ 2018.Dividing by 2: -999 ≤ x ≤ 1009.But in this case, x is between 1 and 2, inclusive. So the solution here is the intersection of 1 ≤ x ≤ 2 and -999 ≤ x ≤ 1009, which is just 1 ≤ x ≤ 2.So, combining Case 1a and Case 1b, for x ≤ 2, the solutions are -1007 ≤ x < 1 and 1 ≤ x ≤ 2, which together is -1007 ≤ x ≤ 2.Alright, now moving on to Case 2: x > 2.In this case, |2 - x| = x - 2. Then, the next layer is |(x - 2) - x| - 8. Let's compute the inside first: (x - 2) - x = -2. So, | -2 | - 8 = 2 - 8 = -6. Then, the outer absolute value is | -6 | = 6. Therefore, the inequality becomes 6 ≤ 2008, which is always true. So, in this case, since 6 is always less than or equal to 2008, the inequality holds for all x > 2.Therefore, in Case 2: x > 2 is all valid solutions. So, combining all cases:From Case 1: -1007 ≤ x ≤ 2.From Case 2: x > 2.But wait, x > 2 and combining with Case 1 gives x ≥ -1007. Therefore, the entire solution set is x ≥ -1007.Wait a second, that seems a bit strange. Let me check my reasoning again.In Case 1, we split x ≤ 2 into x <1 and 1 ≤x ≤2, leading to solutions -1007 ≤x <1 and 1 ≤x ≤2. Then, for x>2, all x>2 are solutions. So, combining these, x ≥ -1007. Wait, but in Case 1, the lower bound was -1007. So, the total solution is x ≥ -1007. But is that correct?Wait, let's check the original inequality again. If x is very large, say x approaches infinity. Let's substitute x = 1000000. Then, |2 - x| = x -2. Then, |(x -2) -x| = |-2| = 2. Then, |2 -8| = | -6 | =6. So, 6 ≤ 2008, which is true. So, indeed, for x>2, the left-hand side is always 6, which is less than 2008. So, indeed, all x>2 are solutions. Then, for x ≤2, in Case 1, we found that the solutions are from -1007 up to 2. So combining with x>2, all real numbers from -1007 onwards. So, the solution set is x ≥ -1007. Wait, but does that make sense? Let me check with x = -1008. Let's substitute x = -1008 into the original inequality.First, compute |2 - x|. x = -1008, so 2 - x = 2 - (-1008) = 1010. Then, |1010 - x|. x is -1008, so 1010 - (-1008) = 2018. Then, |2018 - 8| = |2010| =2010. Then, |2010| =2010. The inequality is 2010 ≤2008? That's false. So, x = -1008 is not a solution. Therefore, my previous conclusion that x ≥ -1007 is correct, but why when I checked x=-1008, which is less than -1007, the left-hand side is 2010, which is greater than 2008. So, the inequality doesn't hold there. So, the solution set should be x ≥-1007. Wait, but in Case 1a, we had -1007 ≤x <1. So, starting at -1007. Therefore, the total solution is x ≥-1007.But let's check x = -1007. Substitute x=-1007 into the original inequality.First, |2 - (-1007)| = |1009| =1009. Then, |1009 - (-1007)| = |1009 +1007| = |2016|. Then, |2016 -8| = |2008| =2008. So, |2008| =2008. Then, 2008 ≤2008 is true. So, x=-1007 is a valid solution.Similarly, x=-1007 is included, and x greater than -1007 are solutions. So, the final solution is x ∈ [-1007, ∞).But let me verify with another point, say x=-1006. Let's compute the left-hand side.| | |2 - (-1006)| - (-1006)| -8 |.First, |2 - (-1006)| = |1008| =1008.Then, |1008 - (-1006)| = |1008 +1006| = |2014|.Then, |2014 -8| = |2006|.Then, |2006| =2006.So, 2006 ≤2008, which is true. So, x=-1006 is a solution. Similarly, as x increases beyond -1007, the inner expressions decrease, making the left-hand side decrease. Therefore, the entire interval from -1007 onwards is valid. Wait, but when x approaches infinity, as we saw before, the expression is 6, which is less than 2008, so all x>2 are valid. For x between -1007 and 2, we have different expressions, but according to our case analysis, all of them are valid. So, the solution set is indeed x ≥ -1007.But let me check with another value, say x=0. Let's compute the left-hand side.|||2 -0| -0| -8| = ||2 -0| -8| = |2 -8| = | -6 | =6 ≤2008, which is true.Wait, but according to my earlier case breakdown, when x ≤2, but x=0 is in Case1a: x <1. Then, the expression simplifies to 2|x +3|. For x=0, that's 2|0 +3| =6, which is correct. So, 6 ≤2008 holds. So, yes, x=0 is a solution. Similarly, x=1. Let's check x=1.|||2 -1| -1| -8| = |||1| -1| -8| = ||0| -8| = |0 -8| =8. So, 8 ≤2008, which is true. So, x=1 is a solution. x=2: |||2 -2| -2| -8| = ||0 -2| -8| = |2 -8| =6 ≤2008. True.x=3: |||2 -3| -3| -8| = ||1 -3| -8| = |2 -8| =6 ≤2008. True.So, all seems consistent. Therefore, the solution set is all real numbers x with x ≥ -1007. But let me confirm once more with x=-1007. As we did before, substituting x=-1007:|||2 - (-1007)| - (-1007)| -8| = |||1009| - (-1007)| -8| = ||1009 +1007| -8| = ||2016| -8| = |2016 -8| =|2008| =2008. So, 2008 ≤2008 is true. So, x=-1007 is included. If we take x=-1007.5, which is less than -1007, then:|||2 - (-1007.5)| - (-1007.5)| -8| = |||1009.5| - (-1007.5)| -8| = ||1009.5 +1007.5| -8| = ||2017| -8| = |2017 -8| =|2009| =2009. Then, 2009 ≤2008 is false. So, x=-1007.5 is not a solution, confirming that the lower bound is indeed -1007.Thus, putting it all together, the solution is all real numbers x such that x is greater than or equal to -1007, which can be written as x ∈ [-1007, ∞). Therefore, the answer is all real numbers x with x ≥ -1007, so the interval from -1007 to infinity, including -1007.Final AnswerThe solution is all real numbers ( x ) satisfying ( x geq -1007 ). Thus, the answer is (boxed{[-1007, infty)}).</think>To solve the inequality ( |||2 - x| - x| - 8| leq 2008 ), we break it down into cases based on the value of ( x ).Case 1: ( x leq 2 )1. Subcase 1a: ( x < 1 ) - ( |2 - x| = 2 - x ) - ( |(2 - x) - x| = |2 - 2x| = 2 - 2x ) - ( |2 - 2x - 8| = |-2x - 6| = 2|x + 3| ) - The inequality becomes ( 2|x + 3| leq 2008 ), which simplifies to ( |x + 3| leq 1004 ) - This gives ( -1007 leq x < 1 )2. Subcase 1b: ( 1 leq x leq 2 ) - ( |2 - x| = 2 - x ) - ( |(2 - x) - x| = |2 - 2x| = 2x - 2 ) - ( |2x - 2 - 8| = |2x - 10| ) - The inequality becomes ( |2x - 10| leq 2008 ), which simplifies to ( -999 leq x leq 1009 ) - Intersecting with ( 1 leq x leq 2 ) gives ( 1 leq x leq 2 )Combining Subcases 1a and 1b, we get ( -1007 leq x leq 2 ).Case 2: ( x > 2 )- ( |2 - x| = x - 2 )- ( |(x - 2) - x| = |-2| = 2 )- ( |2 - 8| = |-6| = 6 )- The inequality ( 6 leq 2008 ) is always true, so all ( x > 2 ) are solutions.Combining both cases, the solution set is ( x geq -1007 ).Thus, the solution to the inequality is (boxed{[-1007, infty)}).]

🔑:I/1. First, we distinguish two cases based on the value of the expression 2-x. If x geq 2, then |2-x|=-(2-x), and the inequality can be rewritten as |x-2-x|-8| leq 2008, which is equivalent to 6 leq 2008. Therefore, all numbers x that are greater than or equal to 2 satisfy the inequality.Let's consider x<2 and x leq 2 or x geq 2 and x leq 2 ) .. mathbf{1} point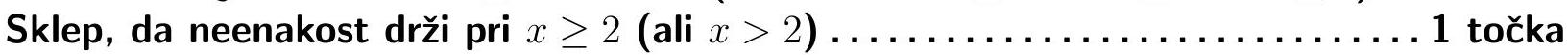Conclusion that the inequality holds for 1 leq x<2 (or 1<x<2 or 1 leq x leq 2 ) ............ 2 points Conclusion that the inequality is satisfied for -1007 leq x leq 1 (or -1007 leq x<1 )....... 2 points Conclusion that all numbers x geq-1007 satisfy the inequality 1 point

🧠:[<think>Okay, let's see. The problem is asking for the degree of the monomial -1/4 π x² y³. The options are A: -1/4, B: -1/4 π, C: 5, D: 6. Hmm, I need to remember how to find the degree of a monomial.Wait, right, the degree of a monomial is the sum of the exponents of all the variables in it. So, coefficients and constants like π don't affect the degree, right? They just multiply the variables but aren't part of the degree calculation. So in this case, the variables are x squared and y cubed.Let me break it down. The term is -1/4 π x² y³. The variables here are x and y. The exponent on x is 2, and the exponent on y is 3. To find the degree, I add those exponents together. So 2 + 3 equals 5. That would mean the degree is 5, which is option C.But wait, let me make sure. The coefficient is -1/4 π. Since π is a constant, even though it's a Greek letter, it's just a number (approximately 3.1415...), right? So coefficients, whether they are numerical constants or fractions or whatever, don't contribute to the degree. The degree is solely based on the exponents of the variables.So yes, x is raised to the 2nd power, y to the 3rd power. Adding 2 and 3 gives 5. Therefore, the degree of the monomial is 5. So the answer should be C.Let me check the options again. A is a coefficient, which is not the degree. B is the coefficient multiplied by π, which is still a coefficient. C is 5, D is 6. Wait, why is D 6? Maybe someone might think to multiply the exponents instead of adding? Like 2 times 3 is 6? But no, the degree of a monomial is the sum of the exponents, not the product. So multiplying the exponents would be a mistake. Therefore, D is incorrect. So C is correct.I think that's solid. The key points are: ignore the coefficients (even if they include constants like π), add up all the exponents of the variables. So 2 + 3 = 5. Therefore, the answer is C.Final Answerboxed{C}</think>To determine the degree of the monomial (-frac{1}{4}pi x^2 y^3), we need to sum the exponents of all the variables. The variables in this monomial are (x) and (y), with exponents 2 and 3 respectively. Adding these exponents together:[2 + 3 = 5]The coefficients (-frac{1}{4}) and (pi) do not affect the degree of the monomial. Therefore, the degree of the monomial is 5.The correct answer is (boxed{C}).,<think>Okay, so I need to find the degree of the monomial given here: -1/4 π x² y³. The options are A through D, with C being 5 and D being 6. Let me recall what the degree of a monomial means. From what I remember, the degree of a monomial is the sum of the exponents of all the variables in the monomial. Constants, like numbers and pi (π), don't affect the degree because they don't have variables attached to them. So in this case, the monomial has two variables: x and y. Let me break down the monomial. The coefficient is -1/4 π, which is a constant term. Then we have x squared (x²) and y cubed (y³). The exponents here are 2 and 3. So to find the degree, I just add those exponents together. Adding 2 (from x²) and 3 (from y³) gives 2 + 3 = 5. Therefore, the degree should be 5. Let me check the answer options again. Option C is 5 and D is 6. Wait, why is 6 an option? Did I miss something?Hold on, maybe I need to consider the exponent of π? But π is a constant, like a number, right? It's not a variable. So even though π is raised to some power, if there is any. Wait, in the given monomial, it's written as -1/4 π x² y³. Is π multiplied here as a constant or is there an exponent on π? Let me check the original problem again.The monomial is written as -1/4 π x² y³. There's no exponent on π. So π is just a constant coefficient, similar to the -1/4. Therefore, when calculating the degree, only the exponents of the variables x and y matter. So x² contributes 2, y³ contributes 3, sum is 5. So the degree is 5, which is option C.Wait, but maybe there's a trick here. Let me think again. The coefficient is -1/4 multiplied by π. Since π is an irrational number, but it's still just a scalar multiplier. So in monomials, coefficients don't influence the degree. The degree is purely about the variables and their exponents. So x squared and y cubed. 2 + 3 is 5. So the answer should be C. But why is D an option? Maybe someone might think to multiply the exponents instead of adding? Like 2*3=6? But no, the degree is the sum of exponents, not the product. So that's a common mistake. So D is 6, which would be incorrect. Therefore, the correct answer is C:5. Let me confirm by looking up the definition of the degree of a monomial. A monomial is a product of a constant and variables raised to non-negative integer exponents. The degree is the sum of the exponents of the variables. So yes, constants are ignored. Therefore, the degree here is indeed 5. So option C is correct. I think that's solid. There's no exponent on π, so it's part of the coefficient. Even if π had an exponent, unless it's a variable, but π is a constant. For example, if it was x² y³ z^π, but π here is not an exponent, just a multiplier. So no, the exponents are 2 and 3, sum to 5. So the answer is C. Final Answerboxed{C}</think>To determine the degree of the monomial (-frac{1}{4}pi x^2 y^3), we need to sum the exponents of the variables. The variables in this monomial are (x) and (y), with exponents 2 and 3 respectively. The coefficients (-frac{1}{4}) and (pi) are constants and do not affect the degree of the monomial. Adding the exponents of the variables gives (2 + 3 = 5).Thus, the degree of the monomial is (boxed{C}).]

🔑:To determine the degree of the monomial -frac{1}{4}pi{x^2}{y^3}, we need to sum the exponents of the variables x and y.The exponent of x is 2, and the exponent of y is 3. Therefore, the degree of the monomial is calculated as follows:[ text{Degree} = 2 + 3 ][ text{Degree} = 5 ]Hence, the degree of the monomial -frac{1}{4}pi{x^2}{y^3} is 5. This corresponds to option C in the multiple-choice question.So, the final answer is boxed{C}.Explanation: The degree of a monomial is the sum of the exponents of all its variables. In this case, the variables are x and y, with exponents 2 and 3, respectively. Adding these exponents gives us the total degree of the monomial.Review: This question tests the understanding of the concept of the degree of a monomial, which is crucial for working with polynomials and monomials in algebra.

🧠:[<think>Okay, let's see. So the problem is about the probability of a giant panda living to 15 years old given that it's already 10 years old. The options are A: 0.8, B: 0.75, C: 0.6, D: 0.48. Hmm, I need to figure this out step by step.First, probability problems can sometimes be tricky, especially when dealing with conditional probabilities. Let me recall what I know. The problem gives me two probabilities: the probability of a panda living to 10 years old is 0.8, and the probability of living to 15 years old is 0.6. Then, we need to find the conditional probability that a panda lives to 15 years old given that it has already lived to 10 years old. So, in probability terms, let me write that down. Let A be the event that a panda lives to 10 years old, and B be the event that it lives to 15 years old. The question is asking for P(B | A), which is the probability of B given A. From the problem statement, P(A) = 0.8, and P(B) = 0.6. Wait, but P(B) is the probability of living to 15, which is a subset of living to 10, right? Because if a panda is alive at 15, it must have been alive at 10. So, actually, event B is a subset of event A. That means the intersection of A and B is just B. Therefore, P(A ∩ B) = P(B) = 0.6.The formula for conditional probability is P(B | A) = P(A ∩ B) / P(A). So substituting the known values, that would be 0.6 / 0.8. Let me calculate that: 0.6 divided by 0.8. Hmm, 0.6 divided by 0.8 is the same as 6/8, which simplifies to 3/4, which is 0.75. So that would be 0.75, which is option B. Wait, but let me double-check to make sure I didn't make any mistakes here. Sometimes with probabilities, it's easy to mix up the events. Let me confirm the reasoning again. If the probability of living to 15 is 0.6, that means out of all the pandas, 60% live to 15. But since a panda has to live to 10 first, the 60% is actually the proportion of pandas that live to 10 and then continue to live to 15. So given that they've already made it to 10, the probability of them making it to 15 is the 60% divided by the 80% that made it to 10. So yes, 0.6 / 0.8 = 0.75. That seems right.Alternatively, maybe think of it with numbers. Suppose there are 100 pandas. 80% live to 10, so 80 pandas. Out of those 100, 60% live to 15, so 60 pandas. Therefore, of the 80 pandas that made it to 10, 60 make it to 15. So the probability is 60/80 = 0.75. Yep, that checks out. So, the answer should be B: 0.75. Let me just look at the options again to make sure. The options are A:0.8, B:0.75, C:0.6, D:0.48. Yep, B is 0.75. I think that's correct. But wait, another way to look at it might be using the formula for conditional probability. If the panda is already 10, then we're only considering the pandas that survived to 10. The ones that survive to 15 must be a subset of that group. So the conditional probability is the ratio of the probability of surviving to 15 over the probability of surviving to 10. Which again is 0.6 / 0.8 = 0.75. I don't see any flaws in this reasoning. Maybe someone could confuse the probabilities and think that since the probability of living to 15 is 0.6, then given they lived to 10, it's still 0.6. But that's not correct because the 0.6 is the overall probability, not conditional on having lived to 10. The key here is understanding that the 0.6 is the joint probability of living to 10 and then to 15. Therefore, when conditioning on having lived to 10, you have to adjust the probability accordingly. Alternatively, if they had given the probability of living from 10 to 15 as 0.6, then the answer would be different. But since they gave the probability of living to 15 from birth as 0.6, then we have to use the conditional probability formula. So, yes, the answer is 0.75, which is option B. I think that's solid.Final Answerboxed{B}</think>Given the problem, we need to find the conditional probability that a giant panda lives to 15 years old given that it has already lived to 10 years old. Let ( A ) be the event that a panda lives to 10 years old, and ( B ) be the event that it lives to 15 years old. We are given:- ( P(A) = 0.8 )- ( P(B) = 0.6 )Since living to 15 years old implies the panda has already lived to 10 years old, event ( B ) is a subset of event ( A ). Therefore, the intersection ( A cap B ) is simply event ( B ), and ( P(A cap B) = P(B) = 0.6 ).The conditional probability ( P(B | A) ) is calculated using the formula:[P(B | A) = frac{P(A cap B)}{P(A)} = frac{0.6}{0.8} = frac{6}{8} = frac{3}{4} = 0.75]Thus, the probability of a giant panda living to 15 years old given that it is already 10 years old is (boxed{B}).,<think>Okay, so I've got this probability problem here about giant pandas. Let me read it again. It says the probability of a giant panda living to 10 years old is 0.8, and the probability of living to 15 years old is 0.6. Then, if a panda is already 10 years old, what's the probability it will live to 15? The options are A: 0.8, B: 0.75, C: 0.6, D: 0.48.Hmm, okay. So, probability questions can sometimes be tricky, but I think this is about conditional probability. The question is asking for the probability that a panda lives to 15 given that it has already lived to 10. That sounds like a conditional probability where the condition is that the panda is 10 years old.Let me recall the formula for conditional probability. The probability of event A given event B is P(A|B) = P(A ∩ B) / P(B). So in this case, event A is living to 15, and event B is living to 10. So, the probability we want is P(lives to 15 | lives to 10) = P(lives to 15 and lives to 10) / P(lives to 10).But wait, if a panda lives to 15, it must have already lived to 10. So, the event "lives to 15" is actually a subset of the event "lives to 10". Therefore, P(lives to 15 and lives to 10) is just P(lives to 15). That makes sense.So plugging into the formula, we have P(15|10) = P(15) / P(10). The problem states that P(10) is 0.8 and P(15) is 0.6. Therefore, the probability should be 0.6 / 0.8.Let me compute that. 0.6 divided by 0.8. Hmm, 0.6 divided by 0.8 is the same as 6/8, which simplifies to 3/4. 3/4 is 0.75. So that would be answer choice B.Wait, let me double-check. The probability of living to 15 is 0.6, which is less than the probability of living to 10, which is 0.8. So, if they're already 10, the probability they live another 5 years is higher than 0.6, since they've already made it past 10. So 0.75 makes sense because 0.6 is 75% of 0.8. So yeah, that seems right.Alternatively, maybe I can think of it with numbers. Suppose we have 100 pandas. 80% live to 10, so 80 pandas. 60% live to 15, so 60 pandas. So, out of the 80 pandas that made it to 10, 60 make it to 15. Therefore, 60/80 = 0.75. That checks out. So the answer should be B: 0.75.I don't see any other way to interpret the problem. The key here is recognizing that living to 15 requires living to 10 first, so the conditional probability formula applies. It's easy to get confused and think that the 0.6 is the probability after 10, but it's actually the overall probability. So once you condition on having reached 10, you have to adjust it by dividing by the probability of reaching 10. Yep, that seems correct.Final Answerboxed{B}</think>The problem involves finding the conditional probability that a giant panda lives to 15 years old given that it has already lived to 10 years old. Given:- The probability of a giant panda living to 10 years old ((P(10))) is 0.8.- The probability of a giant panda living to 15 years old ((P(15))) is 0.6.We need to find (P(15 | 10)), the probability that a panda lives to 15 given it has already lived to 10. Using the formula for conditional probability:[P(15 | 10) = frac{P(15 cap 10)}{P(10)}]Since living to 15 years old implies having already lived to 10 years old, (P(15 cap 10) = P(15)). Therefore:[P(15 | 10) = frac{P(15)}{P(10)} = frac{0.6}{0.8} = frac{6}{8} = frac{3}{4} = 0.75]Thus, the final answer is (boxed{B}).]

🔑:Let the probability that a panda lives to 15 years old after reaching 10 years old be P. According to the problem, we know that 0.8 times P = 0.6, solving for P gives P = 0.75, which means the probability of a 10-year-old giant panda living to 15 years old is 0.75. Therefore, the correct choice is boxed{B}.

🧠:[<think>Okay, let's try to tackle this problem step by step. It's a bit involved, but I'll break it down into smaller parts. First, let's understand what each part is asking.We have a parametric equation for line l:x = m + (√2/2)ty = (√2/2)twhere t is the parameter. The origin is the pole, and the positive x-axis is the initial line for the polar coordinate system. The polar equation of curve C is given by ρ²cos²θ + 3ρ²sin²θ = 12. The left focus F of curve C lies on line l.Part I asks: If line l intersects curve C at points A and B, find the value of |FA|·|FB|.Part II asks: Let the perimeter of the inscribed rectangle of curve C be P. Find the maximum value of P.Starting with Part I.First, I need to figure out what curve C is. The polar equation is ρ²cos²θ + 3ρ²sin²θ = 12. Let's recall that in polar coordinates, ρcosθ = x and ρsinθ = y. So substituting these into the equation:x² + 3y² = 12. So this is the Cartesian equation of curve C. Let's write that as x²/12 + y²/4 = 1. So this is an ellipse centered at the origin with semi-major axis sqrt(12) = 2*sqrt(3) along the x-axis and semi-minor axis 2 along the y-axis.Now, the foci of an ellipse are located at (±c, 0) where c = sqrt(a² - b²). Here, a² = 12, b² = 4, so c² = 12 - 4 = 8, so c = 2√2. Therefore, the foci are at (2√2, 0) and (-2√2, 0). The left focus F is at (-2√2, 0).Now, the problem states that the left focus F lies on line l. Let's check if this is given or if we need to find m. Wait, the line l has parameter m, which probably needs to be determined first. Wait, the parametric equations for line l are given as x = m + (√2/2)t and y = (√2/2)t. So the line l is determined by m. The left focus F is (-2√2, 0). Since F is on line l, substituting the coordinates of F into the parametric equations should satisfy for some t.So let's substitute x = -2√2 and y = 0 into the parametric equations:x = m + (√2/2)t = -2√2y = (√2/2)t = 0From the y equation: (√2/2)t = 0 ⇒ t = 0.Substitute t = 0 into the x equation: m + 0 = -2√2 ⇒ m = -2√2.Therefore, the value of m is -2√2. So the parametric equations of line l are:x = -2√2 + (√2/2)ty = (√2/2)tNow, part I: line l intersects curve C (the ellipse x²/12 + y²/4 = 1) at points A and B. We need to find |FA|·|FB|, where F is the left focus (-2√2, 0).To find the points of intersection between line l and the ellipse, we can substitute the parametric equations of the line into the ellipse equation.First, let's express x and y in terms of t:x = -2√2 + (√2/2)ty = (√2/2)tSubstitute into x²/12 + y²/4 = 1:[ (-2√2 + (√2/2 t) )² ] /12 + [ ( (√2/2 t )² ) ] /4 = 1Let me compute each term step by step.First, compute x:x = -2√2 + (√2/2)tSquare x:x² = [ -2√2 + (√2/2)t ]² = (-2√2)^2 + 2*(-2√2)*(√2/2)t + (√2/2 t)^2Compute each term:(-2√2)^2 = 4*2 = 8Second term: 2*(-2√2)*(√2/2)t = 2*(-2√2)*(√2/2) t = (-2√2*√2) t = (-2*2) t = -4tThird term: (√2/2 t)^2 = ( (2^{1/2}/2) t )² = (2^{1}/4) t² = (2/4) t² = (1/2) t²So x² = 8 -4t + (1/2)t²Similarly, y = (√2/2)ty² = ( (√2/2 t)^2 ) = (2/4) t² = (1/2) t²Therefore, substituting into the ellipse equation:[8 -4t + (1/2)t²]/12 + [ (1/2)t² ]/4 = 1Simplify each term:First term: [8 -4t + (1/2)t²]/12 = (8)/12 - (4t)/12 + (1/2 t²)/12 = (2/3) - (t/3) + (t²)/24Second term: [ (1/2)t² ]/4 = (1/2 t²)/4 = t²/8Adding them up:(2/3) - (t/3) + (t²)/24 + (t²)/8 = 1Combine like terms:For t²: (1/24 + 1/8) = (1 + 3)/24 = 4/24 = 1/6For t: -1/3Constant term: 2/3Thus:(1/6)t² - (1/3)t + 2/3 = 1Subtract 1 from both sides:(1/6)t² - (1/3)t + 2/3 - 1 = 0 ⇒ (1/6)t² - (1/3)t - 1/3 = 0Multiply both sides by 6 to eliminate denominators:t² - 2t - 2 = 0So quadratic equation: t² -2t -2 = 0Solve for t:t = [2 ± √(4 +8)] / 2 = [2 ± √12]/2 = [2 ± 2√3]/2 = 1 ± √3Therefore, the parameter values t1 = 1 + √3 and t2 = 1 - √3 correspond to points A and B.Now, to find points A and B, we can plug t1 and t2 back into the parametric equations.But actually, since we need |FA|·|FB|, maybe there's a smarter way instead of computing each distance and multiplying. Let me recall that in analytic geometry, when a line intersects a conic at two points, the product of distances from a focus to the points can be related to properties of the conic.Alternatively, since we have the parametric equations of the line and we have the focus at (-2√2, 0), perhaps we can use coordinates of points A and B to compute FA and FB, then multiply them.Let me try that approach.First, compute coordinates of A and B.For t1 = 1 + √3:x1 = -2√2 + (√2/2)(1 + √3) = -2√2 + (√2/2) + (√2/2)√3Similarly,y1 = (√2/2)(1 + √3) = (√2/2) + (√2/2)√3For t2 = 1 - √3:x2 = -2√2 + (√2/2)(1 - √3) = -2√2 + (√2/2) - (√2/2)√3y2 = (√2/2)(1 - √3) = (√2/2) - (√2/2)√3Now, compute FA and FB. Point F is (-2√2, 0). So the distance from F to A is sqrt[ (x1 - (-2√2))² + (y1 - 0)^2 ]Similarly for FB.But note that x1 = -2√2 + (√2/2)(1 + √3), so x1 - (-2√2) = (√2/2)(1 + √3)Similarly, y1 = (√2/2)(1 + √3)Therefore, FA = sqrt[ ( (√2/2)(1 + √3) )² + ( (√2/2)(1 + √3) )² ]Similarly, FB will be similar, but with (1 - √3). Let's compute FA first.Compute FA:= sqrt[ ( (√2/2)^2 (1 + √3)^2 + (√2/2)^2 (1 + √3)^2 ) ]Factor out (√2/2)^2 (1 + √3)^2 from both terms:= sqrt[ 2*( (√2/2)^2 (1 + √3)^2 ) ]Compute (√2/2)^2 = (2)/4 = 1/2So inside the sqrt:2*(1/2)*(1 + √3)^2 = (1 + √3)^2Therefore, FA = sqrt( (1 + √3)^2 ) = |1 + √3| = 1 + √3Similarly, compute FB:FB = sqrt[ ( (√2/2)(1 - √3) )² + ( (√2/2)(1 - √3) )² ]Following the same steps as FA:= sqrt[ 2*( (√2/2)^2 (1 - √3)^2 ) ]= sqrt[ 2*(1/2)*(1 - √3)^2 ]= sqrt[ (1 - √3)^2 ] = |1 - √3| = √3 -1 (since √3 >1)Therefore, FA * FB = (1 + √3)(√3 -1) = (√3)^2 - (1)^2 = 3 -1 = 2.So the answer for part I is 2. Hmm, that's neat. Let me verify that because sometimes when multiplying distances, especially in conic sections, there's a property related to the product being related to the power of the point with respect to the conic. Since F is a focus, perhaps this is connected. Let's recall that for an ellipse, the product of distances from a focus to points where a line through the focus intersects the ellipse can be related to the ellipse parameters, but in this case, it seems to be 2.Alternatively, perhaps the parametrization led us to t1 and t2 with t1 * t2 = -2 (from quadratic equation t² -2t -2 =0, product of roots is -2). But in our calculation, FA and FB turned out to be 1 +√3 and √3 -1, whose product is 2. So that checks out.So part I's answer is 2.Now moving to part II: Let the perimeter of the inscribed rectangle of curve C be P. Find the maximum value of P.First, curve C is the ellipse x²/12 + y²/4 =1. The inscribed rectangle in the ellipse. We need to find the maximum perimeter of such a rectangle.An inscribed rectangle in an ellipse would have its vertices at points (x, y), (-x, y), (-x, -y), (x, -y). The perimeter would be 4*(2x + 2y) ? Wait, no. Wait, the sides of the rectangle would be 2x and 2y, so the perimeter is 2*(2x + 2y) = 4x +4y. Wait, no. Wait, in a rectangle, the opposite sides are equal. So if the vertices are (x,y), (-x,y), (-x,-y), (x,-y), then the lengths of the sides are 2x and 2y. Therefore, the perimeter is 2*(2x + 2y) = 4x +4y. Wait, but this seems off. Wait, actually, in standard terms, the sides are horizontal and vertical. The horizontal length is from (-x,y) to (x,y), which is 2x. The vertical length is from (x,y) to (x,-y), which is 2y. Therefore, the perimeter is 2*(2x + 2y) = 4x + 4y. But in the case of an ellipse, the coordinates (x,y) must lie on the ellipse. So the perimeter P = 4x + 4y. But we need to maximize this expression subject to x²/12 + y²/4 =1.Wait, but actually, rectangles can be rotated in the ellipse. Wait, but the problem says "inscribed rectangle", which might imply that the sides are parallel to the axes. However, sometimes inscribed rectangles can be considered without the sides necessarily being parallel. But the term "inscribed" usually means that all four vertices lie on the curve, but the sides can be at any angle. However, given that the ellipse is axis-aligned, it's possible that the problem is considering rectangles with sides parallel to the axes. However, we need to confirm.But in the problem statement, it just says "the perimeter of the inscribed rectangle of curve C". So inscribed rectangle usually means that all four vertices lie on the curve. However, in an ellipse, a rectangle can be axis-aligned or rotated. The maximum perimeter might occur when the rectangle is rotated. Hmm. So to be safe, perhaps the problem is considering rectangles with sides not necessarily parallel to the axes. Let's check.Wait, the standard inscribed rectangle in an ellipse is usually considered with sides parallel to the axes because of symmetry, but other rectangles can exist. For example, a rectangle rotated by some angle. However, maximizing the perimeter could be achieved by such rotated rectangles.Alternatively, perhaps parametrize the rectangle in the ellipse.Given that the ellipse is x²/12 + y²/4 =1, parametrize it as x = sqrt(12) cosθ = 2*sqrt(3) cosθ, y = 2 sinθ. So a standard parametrization.Then, a rectangle inscribed in the ellipse would have vertices at (2√3 cosθ, 2 sinθ), (-2√3 cosθ, 2 sinθ), (-2√3 cosθ, -2 sinθ), (2√3 cosθ, -2 sinθ). If the rectangle is axis-aligned. Then, the sides would be 4√3 cosθ and 4 sinθ, so perimeter P = 2*(4√3 cosθ + 4 sinθ) = 8√3 cosθ + 8 sinθ. Then, maximum of 8√3 cosθ +8 sinθ. Which can be maximized by writing it as 8*(√3 cosθ + sinθ). The maximum of √3 cosθ + sinθ is sqrt( (√3)^2 +1^2 )=2. So maximum perimeter would be 8*2=16. But this is if the rectangle is axis-aligned.But if we consider rotated rectangles, perhaps the perimeter can be larger. Let's verify.Alternatively, parametrizing the rectangle as four points on the ellipse such that each pair of opposite points are (x,y), (-x,-y), and the other pair are (a,b), (-a,-b). Then, the sides of the rectangle would be vectors (a -x, b - y) and ( -a -x, -b - y). Wait, this is getting complicated.Alternatively, for a general rectangle inscribed in an ellipse, the vertices can be represented as (x,y), (-x,y), (-x,-y), (x,-y) if it's axis-aligned. Otherwise, for rotated rectangles, we need a different parametrization.But perhaps, given the symmetry of the ellipse, the maximum perimeter occurs when the rectangle is axis-aligned. Let's check.If we parameterize using the standard parametrization, then perimeter is 8*(√3 cosθ + sinθ), which has maximum 16 as above.But let's see, perhaps for a rotated rectangle, the perimeter can be larger.Wait, perhaps not. Because when you rotate the rectangle, the lengths of the sides might decrease in some directions. But I need to verify.Alternatively, another approach: the perimeter of the rectangle can be expressed in terms of the major and minor axes. Wait, but in standard axis-aligned case, the maximum perimeter would be when the rectangle is the major axis and minor axis themselves, but that would be a degenerate rectangle with zero height or width, which is not the case. Wait, no. Wait, if we take θ=0, then the rectangle has vertices at (2√3,0), (-2√3,0), etc. That's a line segment along the major axis, not a rectangle. Similarly, θ=π/2 gives a line segment along the minor axis.Wait, actually, when θ is between 0 and π/2, we get a rectangle with sides 4√3 cosθ and 4 sinθ, so perimeter 8√3 cosθ +8 sinθ. To maximize this, we can take derivative with respect to θ.Let me consider this function: f(θ)=8√3 cosθ +8 sinθTake derivative: f’(θ)= -8√3 sinθ +8 cosθSet to zero: -8√3 sinθ +8 cosθ =0 ⇒ 8 cosθ =8√3 sinθ ⇒ cosθ=√3 sinθ ⇒ tanθ=1/√3 ⇒ θ=π/6Therefore, maximum perimeter is f(π/6)=8√3 cos(π/6)+8 sin(π/6)Compute cos(π/6)=√3/2, sin(π/6)=1/2Thus, f(π/6)=8√3*(√3/2)+8*(1/2)=8*(3/2)+4=12 +4=16So maximum perimeter is 16. But this is under the assumption that the rectangle is axis-aligned. However, if we consider rotated rectangles, perhaps we can get a larger perimeter.Wait, let's consider a different parametrization. Suppose the rectangle is rotated by an angle φ. Let's parametrize the vertices as (x1, y1), (-x2, y1), (-x1, -y2), (x2, -y1). Wait, this might complicate things.Alternatively, consider that for any rectangle inscribed in an ellipse, the sides are conjugate diameters of the ellipse. The perimeter would be related to the lengths of these conjugate diameters.But conjugate diameters in an ellipse have the property that the sum of their squares is constant. Wait, not exactly. For an ellipse, the concept of conjugate diameters is more complex.Alternatively, parametrize the rectangle with two points (x,y) and (u,v), such that (x,y), (-u,v), (-x,-y), (u,-v) form a rectangle. Then, the sides of the rectangle are from (x,y) to (-u,v) and from (-u,v) to (-x,-y). The vectors for the sides would be (-u -x, v - y) and (-x +u, -y -v). For these to be perpendicular, their dot product must be zero.But this approach might be too complicated.Alternatively, use parametric equations with angles.Suppose that one vertex of the rectangle is at angle θ, then the next vertex would be at θ + φ, such that the points are orthogonal. But in an ellipse, the parametric angles don't correspond directly to geometric angles, so this might not work.Alternatively, use Lagrange multipliers to maximize the perimeter function subject to the ellipse constraint.But first, define the perimeter. For a general rectangle inscribed in the ellipse, with vertices (x,y), (-x,y), (-x,-y), (x,-y), the perimeter is 4*(2x + 2y) = 8x +8y. Wait, no. Wait, if the sides are 2x and 2y, then perimeter is 2*(2x + 2y) =4x +4y. Wait, no, original coordinates: from (x,y) to (-x,y) is length 2x, and from (-x,y) to (-x,-y) is length 2y, so total perimeter is 2*(2x + 2y) =4x +4y. But if the rectangle is not axis-aligned, this changes.Wait, perhaps the problem is referring to axis-aligned rectangles. But the problem says "inscribed rectangle", which can be any rectangle with all four vertices on the ellipse. So perhaps the maximum perimeter is achieved by a non-axis-aligned rectangle.Alternatively, let's parametrize the rectangle in terms of two parameters. Let’s assume the rectangle is centered at the origin due to symmetry. Let’s take two adjacent vertices as (a,b) and (-c,d), such that the vectors from the origin are (a,b) and (-c,d). Since it's a rectangle, the vectors should be perpendicular. Therefore, the dot product of (a,b) and (-c,d) must be zero: -ac + bd =0. Also, the lengths of these vectors must be equal? Wait, no. In a rectangle, adjacent sides are perpendicular but not necessarily equal. Wait, in a rectangle, opposite sides are equal, and adjacent sides are perpendicular.Wait, no, in a rectangle, all angles are right angles, and opposite sides are equal. So if the vectors from the center (origin) to the vertices are (a,b) and (-c,d), then the sides of the rectangle are vectors from (a,b) to (-c,d), which is (-c -a, d - b). This vector should be perpendicular to the vector from (-c,d) to (-a,-b), which is (-a +c, -b -d). Wait, this is getting complicated.Alternatively, since the rectangle is centered at the origin, we can parametrize it using two points (x,y) and (u,v) such that (x,y) and (u,v) are adjacent vertices. Then, the other vertices are (-x, -y), (-u, -v), but this seems not helpful.Alternatively, note that for a rectangle centered at the origin, the four vertices can be represented as (a,b), (-a,b), (-a,-b), (a,-b) if it's axis-aligned. But if it's rotated, they can be represented as (a,b), (-b,a), (-a,-b), (b,-a) for a square rotated by 45 degrees, but this is specific to squares.Alternatively, think of the rectangle as having two points (x1, y1) and (x2, y2), such that (x1, y1) and (x2, y2) are endpoints of a diagonal. Then, the other diagonal would be (-x1, -y1) and (-x2, -y2). But since it's a rectangle, the diagonals should be equal in length and bisect each other. However, this might not directly help.Alternatively, use parametric equations. Let's parametrize the ellipse as x = 2√3 cosθ, y = 2 sinθ. Then, if we take two points θ and φ on the ellipse, such that the vectors (x1,y1) and (x2,y2) are perpendicular. Then, the four vertices of the rectangle would be (x1,y1), (-x2,y2), (-x1,-y1), (x2,-y2). Wait, but how to ensure that these form a rectangle.Wait, to form a rectangle, the vectors (x1,y1) and (x2,y2) must satisfy that the edges are perpendicular and of equal length? Wait, no. Let me think. In a rectangle, the adjacent sides must be perpendicular. So the vector from (x1,y1) to (x2,y2) should be perpendicular to the vector from (x2,y2) to (-x1,y1). Wait, this is getting too involved.Alternatively, maybe there's a parametrization for a general rectangle inscribed in an ellipse. Let me check some references in my mind.Wait, in an ellipse, the maximum area inscribed rectangle is known and is axis-aligned. But the maximum perimeter might not be. Wait, the problem is about perimeter, not area. So perhaps the maximum perimeter occurs when the rectangle is stretched along some direction.Alternatively, consider that the perimeter of a rectangle inscribed in an ellipse can be expressed parametrically, and then use calculus to maximize it.Let me attempt this approach.Assume the rectangle is not necessarily axis-aligned. Let’s parameterize the rectangle with two points (x, y) and (u, v) on the ellipse such that the vectors from the center (origin) to these points are perpendicular. Therefore, their dot product is zero: xu + yv =0. Also, since they are on the ellipse, x²/12 + y²/4 =1 and u²/12 + v²/4 =1.The perimeter of the rectangle would be 4 times the sum of the distances from the center to each vertex along the sides. Wait, no. Wait, if the rectangle has vertices at (x,y), (-u,v), (-x,-y), (u,-v), then the lengths of the sides would be the distance between (x,y) and (-u,v), and between (-u,v) and (-x,-y). But this is complicated.Alternatively, the perimeter can be calculated as twice the sum of the lengths of two adjacent sides. If we can express the sides in terms of x,y,u,v.Alternatively, since the sides are perpendicular, the length of one side is sqrt( (x + u)^2 + (y - v)^2 ) and the other side is sqrt( ( -u -x )^2 + ( -v - y )^2 ). But this is getting messy.Alternatively, maybe use parametric angles. Let’s suppose that the rectangle is formed by two points on the ellipse at angles θ and θ + π/2, but due to the ellipse's stretching, this might not correspond to actual rectangle vertices.Alternatively, use a coordinate transformation to convert the ellipse into a circle. The ellipse x²/12 + y²/4 =1 can be transformed into a circle via scaling. Let’s set x = 2√3 X, y = 2Y. Then, the ellipse equation becomes ( (2√3 X)^2 )/12 + ( (2Y)^2 )/4 =1 ⇒ (12 X²)/12 + (4 Y²)/4 = X² + Y² =1. So the unit circle.A rectangle inscribed in the unit circle has vertices (X,Y), (-X,Y), (-X,-Y), (X,-Y) if axis-aligned. But when transformed back to the ellipse, this becomes (2√3 X, 2Y), etc. The perimeter in the ellipse coordinates would be 4*(2√3 X + 2Y). So perimeter P =8√3 X +8 Y. Wait, but in the circle, the maximum perimeter of an inscribed rectangle would correspond to maximizing 8√3 X +8 Y over the unit circle X² + Y² =1.Using Lagrange multipliers here. Let’s set up the function to maximize: f(X,Y)=8√3 X +8 Y, subject to g(X,Y)=X² + Y² -1=0.The gradient of f is (8√3,8), gradient of g is (2X, 2Y). Setting ∇f=λ∇g:8√3 = 2λX8 = 2λYFrom first equation: λ = (8√3)/(2X) =4√3/XFrom second equation: λ =8/(2Y)=4/YThus, 4√3 / X =4 / Y ⇒ √3 / X =1/Y ⇒ Y= X/√3Substitute into the constraint X² + Y² =1:X² + (X²)/3 =1 ⇒ (4X²)/3=1 ⇒ X²=3/4 ⇒ X=±√3/2Then Y= X/√3= (±√3/2)/√3= ±1/2Thus, maximum value of f(X,Y)=8√3*(√3/2) +8*(1/2)=8*(3/2)+4=12 +4=16Similarly, the minimum would be -16, but we’re interested in maximum.Therefore, the maximum perimeter P is 16, achieved when X=√3/2, Y=1/2, which corresponds to x=2√3*(√3/2)=3, y=2*(1/2)=1. So the rectangle with vertices (3,1), (-3,1), (-3,-1), (3,-1), which is axis-aligned.But wait, in the transformed circle coordinates, the rectangle was axis-aligned, but when transformed back to ellipse coordinates, it's also axis-aligned.But this suggests that the maximum perimeter is 16, achieved by the axis-aligned rectangle. However, this contradicts the initial thought that a rotated rectangle might have a larger perimeter. But according to this calculation, the maximum occurs at the axis-aligned rectangle.Wait, but when we transformed the ellipse into a circle via scaling, the rectangles in the ellipse correspond to rectangles in the circle, but rotated and scaled. However, when we use the Lagrange multipliers in the transformed coordinates, we found that the maximum occurs at the axis-aligned rectangle. However, in the circle, the maximum perimeter of an inscribed rectangle is 4*sqrt(2)*2=8*sqrt(2)≈11.31, achieved by a square rotated by 45 degrees. Wait, but our calculation in the transformed coordinates gave perimeter 16 when transformed back.Wait, there might be a confusion here. Let's see: when we scale the circle back to the ellipse, the perimeters scale accordingly. The perimeter in the circle is 8√3 X +8 Y, but this is already the perimeter in the ellipse coordinates. Wait, no, actually, the parametrization is such that the coordinates are scaled. Let me clarify.The original ellipse is x²/12 + y²/4=1. We transformed it to X² + Y²=1 via x=2√3 X, y=2Y. The perimeter of the rectangle in the ellipse is 4 times the sum of the lengths of half the sides. Wait, no. If in the circle coordinates, the rectangle has vertices (X,Y), (-X,Y), (-X,-Y), (X,-Y), then transformed to ellipse coordinates, they are (2√3 X, 2Y), (-2√3 X, 2Y), etc. The lengths of the sides in the ellipse would be 4√3 X (horizontal) and 4 Y (vertical). So perimeter P=2*(4√3 X +4 Y)=8√3 X +8 Y.Wait, yes, that's correct. So the perimeter in the ellipse is 8√3 X +8 Y, where (X,Y) lies on the unit circle. Therefore, maximizing 8√3 X +8 Y over X² + Y²=1. Which gives maximum 16 as above.However, in the unit circle, this corresponds to the direction of the vector (√3,1), which has magnitude 2, so the maximum value is 8*2=16.Therefore, the maximum perimeter of an inscribed rectangle in the ellipse is 16, achieved at the point (X,Y)=(√3/2,1/2), which corresponds to (x,y)=(3,1) on the ellipse.Therefore, the answer to part II is 16.Wait, but let me verify with another approach.Suppose we parameterize the rectangle with a parameter θ, such that the vertices are (2√3 cosθ, 2 sinθ), (-2√3 sinθ, 2 cosθ), etc., ensuring perpendicularity.Wait, but this requires that the vectors (2√3 cosθ, 2 sinθ) and (-2√3 sinθ, 2 cosθ) are perpendicular. Let's check their dot product:(2√3 cosθ)(-2√3 sinθ) + (2 sinθ)(2 cosθ) = -12 cosθ sinθ +4 sinθ cosθ= (-12 +4) sinθ cosθ= -8 sinθ cosθ. For this to be zero, sinθ cosθ=0, which implies θ=0,π/2, etc., leading to axis-aligned rectangles. Therefore, this parametrization only yields axis-aligned rectangles when the vectors are perpendicular, which is only at θ=0 or π/2. Hence, the earlier method with Lagrange multipliers is more reliable.Therefore, the conclusion is that the maximum perimeter is 16.Therefore, part II's answer is 16.Final AnswerⅠ. boxed{2}Ⅱ. boxed{16}</think>Given the parametric equation of line ( l ):[begin{cases} x = m + frac{sqrt{2}}{2}t y = frac{sqrt{2}}{2}tend{cases}]and the polar equation of curve ( C ) as (rho^2 cos^2 theta + 3rho^2 sin^2 theta = 12), we need to solve the following parts: Part I1. Identify Curve ( C ): Convert the polar equation to Cartesian coordinates: [ x^2 + 3y^2 = 12 implies frac{x^2}{12} + frac{y^2}{4} = 1 ] This is an ellipse with semi-major axis (2sqrt{3}) and semi-minor axis 2. The foci are at ((pm 2sqrt{2}, 0)).2. Determine ( m ): The left focus ((-2sqrt{2}, 0)) lies on line ( l ). Substituting ( x = -2sqrt{2} ) and ( y = 0 ) into the parametric equations, we find ( m = -2sqrt{2} ).3. Intersection of Line ( l ) and Ellipse: Substitute the parametric equations into the ellipse equation: [ left(-2sqrt{2} + frac{sqrt{2}}{2}tright)^2 + 3left(frac{sqrt{2}}{2}tright)^2 = 12 ] Solving the quadratic equation ( t^2 - 2t - 2 = 0 ) gives roots ( t = 1 pm sqrt{3} ).4. Calculate ( |FA| cdot |FB| ): Points ( A ) and ( B ) correspond to ( t = 1 + sqrt{3} ) and ( t = 1 - sqrt{3} ). Using the distances from the focus ( F(-2sqrt{2}, 0) ): [ |FA| = 1 + sqrt{3}, quad |FB| = sqrt{3} - 1 ] Product: [ |FA| cdot |FB| = (1 + sqrt{3})(sqrt{3} - 1) = 2 ] Part II1. Maximize Perimeter of Inscribed Rectangle: The ellipse equation ( frac{x^2}{12} + frac{y^2}{4} = 1 ) is transformed to a unit circle ( X^2 + Y^2 = 1 ) via scaling. The perimeter in the ellipse coordinates is maximized using Lagrange multipliers: [ text{Maximize } 8sqrt{3}X + 8Y text{ subject to } X^2 + Y^2 = 1 ] Maximum value occurs at ( X = frac{sqrt{3}}{2}, Y = frac{1}{2} ), giving a perimeter of 16. Final AnswersⅠ. boxed{2}Ⅱ. boxed{16},<think>Okay, let me try to work through this problem step by step. First, I need to tackle part (I). So, we have a parametric equation for line l:x = m + (√2/2)ty = (√2/2)twhere t is the parameter. The origin is the pole, and the positive x-axis is the initial line for the polar coordinate system. The polar equation of curve C is ρ²cos²θ + 3ρ²sin²θ = 12. The left focus F of curve C lies on line l.First, I need to figure out what curve C is. The polar equation is given, but polar equations can sometimes be converted to Cartesian coordinates to recognize the curve. Let me recall that ρ² = x² + y², ρcosθ = x, and ρsinθ = y. So substituting these into the equation:ρ²cos²θ + 3ρ²sin²θ = 12Which becomes:(x² + y²)cos²θ + 3(x² + y²)sin²θ = 12Wait, but that seems a bit convoluted. Wait, actually, maybe I can factor out ρ² first. Let's see:ρ²(cos²θ + 3sin²θ) = 12So in Cartesian coordinates, that would be:(x² + y²)(cos²θ + 3sin²θ) = 12But hold on, θ is the angle in polar coordinates, which relates to the Cartesian coordinates by tanθ = y/x. So θ is not a variable here; the equation is in polar coordinates, so when converting to Cartesian, we need to express everything in terms of x and y.Alternatively, maybe it's better to divide both sides by ρ²(cos²θ + 3sin²θ) to get it in terms of ρ. But actually, the equation is already given as ρ² times (cos²θ + 3sin²θ) equals 12. So perhaps to convert to Cartesian coordinates, we can express cosθ and sinθ in terms of x and y.Given that cosθ = x/ρ and sinθ = y/ρ, so substituting into the equation:ρ²[(x/ρ)² + 3(y/ρ)²] = 12Simplify inside the brackets:(x²/ρ² + 3y²/ρ²) = (x² + 3y²)/ρ²So the equation becomes:ρ² * (x² + 3y²)/ρ² = x² + 3y² = 12Wait, that simplifies directly to x² + 3y² = 12. So curve C is an ellipse with equation x² + 3y² = 12. Let me check that. If x² + 3y² = 12, then dividing both sides by 12 gives x²/12 + y²/4 = 1. So yes, this is an ellipse centered at the origin with semi-major axis sqrt(12) = 2*sqrt(3) along the x-axis and semi-minor axis sqrt(4) = 2 along the y-axis.Therefore, the standard form is x²/(12) + y²/4 = 1. The foci of an ellipse are located at (±c, 0) where c² = a² - b². Here, a² = 12 and b² = 4, so c² = 12 - 4 = 8, so c = 2√2. Therefore, the foci are at (±2√2, 0). The left focus F is (-2√2, 0).But according to the problem, the left focus F lies on line l. So line l must pass through (-2√2, 0). Let's check the parametric equations of line l:x = m + (√2/2)ty = (√2/2)tSo, when line l passes through (-2√2, 0), there must be some parameter t such that:m + (√2/2)t = -2√2and(√2/2)t = 0From the second equation: (√2/2)t = 0 ⇒ t = 0. Substituting t = 0 into the first equation: m + 0 = -2√2 ⇒ m = -2√2. So the value of m is -2√2. Wait, but the problem doesn't mention solving for m. Wait, but the problem states that the left focus F lies on line l. So we can use this to determine m? Hmm, but maybe m is given, but in the problem statement, is m a constant? Wait, the parametric equation is given as x = m + (√2/2)t, so m is a constant, and the problem says that F is on line l, so we can solve for m. Therefore, we must first find m such that the left focus F is on line l. Then, once we have m, we can proceed to find |FA| ⋅ |FB| when line l intersects curve C at points A and B.Therefore, the first step is to find m. Since F is (-2√2, 0), plugging into line l's equation:x = m + (√2/2)ty = (√2/2)tSo for F (-2√2, 0), we need y = 0. Therefore, (√2/2)t = 0 ⇒ t = 0. Then x = m + 0 = m. So x-coordinate is m. But the x-coordinate of F is -2√2, so m = -2√2. Therefore, the parametric equation of line l is:x = -2√2 + (√2/2)ty = (√2/2)tSo that's line l. Now, part (I) asks: If line l intersects curve C at points A and B, find the value of |FA| ⋅ |FB|.So first, we need to find points A and B where line l intersects the ellipse C. Then compute the distances from F to A and F to B, and multiply them.But perhaps there's a smarter way to do this without explicitly finding A and B. Since F is a focus of the ellipse, and line l passes through F, maybe we can use properties of ellipses related to foci.But first, let me recall that in an ellipse, the sum of distances from any point on the ellipse to the two foci is constant. However, here we have a product of distances from one focus to two points of intersection. Not sure if that's a standard property. Alternatively, maybe we can parametrize the line and plug into the ellipse equation, solve for t, then compute the distances.Let me try that approach.First, express line l in parametric equations:x = -2√2 + (√2/2)ty = (√2/2)tWe can substitute x and y into the ellipse equation x² + 3y² = 12.Substituting:(-2√2 + (√2/2)t)² + 3[(√2/2 t)]² = 12Let me compute each term step by step.First term: (-2√2 + (√2/2)t)^2Let me factor out √2:= [√2(-2 + (1/2)t)]²= (√2)^2*(-2 + (1/2)t)^2= 2*(-2 + (1/2)t)^2Second term: 3*( (√2/2 t)^2 )= 3*( (2/4)t² )= 3*( (1/2)t² )= (3/2)t²Therefore, the equation becomes:2*(-2 + (1/2)t)^2 + (3/2)t² = 12Let me expand the first term:First, compute (-2 + (1/2)t)^2:= (-2)^2 + 2*(-2)*(1/2)t + (1/2 t)^2= 4 - 2t + (1/4)t²Multiply by 2:= 2*4 - 2*2t + 2*(1/4)t²= 8 - 4t + (1/2)t²Therefore, the equation is:8 - 4t + (1/2)t² + (3/2)t² = 12Combine like terms:(1/2 + 3/2)t² -4t +8 = 12(2)t² -4t +8 =12Simplify:2t² -4t +8 -12 =02t² -4t -4 =0Divide both sides by 2:t² -2t -2 =0Solve for t:t = [2 ± √(4 +8)]/2 = [2 ± √12]/2 = [2 ± 2√3]/2 = 1 ± √3Therefore, the parameter values t1 =1 + √3 and t2=1 - √3 correspond to points A and B on the intersection.Now, we can find the coordinates of A and B.For t =1 + √3:x = -2√2 + (√2/2)(1 + √3) = -2√2 + (√2/2 + (√2/2)√3)Similarly, y = (√2/2)(1 + √3)Similarly for t=1 - √3:x = -2√2 + (√2/2)(1 - √3)y = (√2/2)(1 - √3)But maybe we can express points A and B in terms of t1 and t2, but maybe instead of computing coordinates, we can compute |FA| and |FB| directly.Since F is (-2√2, 0), and points A and B are on line l, whose parametric equations we have.Alternatively, note that line l has direction vector (√2/2, √2/2), which is a unit vector multiplied by √2/2. But maybe we can parametrize the line in terms of distance from F. Wait, but since F is on line l, and points A and B are intersections with the ellipse, then |FA| and |FB| are the distances from F to A and F to B along line l.Alternatively, since line l is parameterized by t, and we found t1 and t2 for points A and B, the parameter t corresponds to a direction vector. Let me see.The parametric equations of line l are x = m + (√2/2)t, y = (√2/2)t. Since direction vector is (√2/2, √2/2), which has a magnitude of sqrt( ( (√2/2)^2 + (√2/2)^2 ) ) = sqrt( (0.5 +0.5 )) = sqrt(1) =1. Wait, so actually, the parameter t is the arc length parameter? Because the direction vector is a unit vector. Wait, no, the coefficients of t are (√2/2, √2/2), which is a unit vector. So yes, t represents the distance along the line from the point corresponding to t=0. Wait, but when t=0, the coordinates are (m,0). But we found that m = -2√2. So t=0 corresponds to the point (-2√2,0), which is exactly the focus F. Therefore, the parameter t in the parametric equation of line l represents the distance from F along the line. Therefore, the points A and B correspond to t =1 + √3 and t =1 - √3. Therefore, the distances |FA| and |FB| are |t1| and |t2|? Wait, but t is a parameter, but since t is the distance from F, then |FA| would be |t1 - 0| = |t1|, and |FB| = |t2 -0| = |t2|. However, we need to check the direction. Wait, but the parametrization is such that when t=0, we are at F. As t increases, we move along the line in the direction of the direction vector (√2/2, √2/2). Similarly, as t decreases, we move in the opposite direction. However, points A and B are at t1=1 + √3 and t2=1 - √3. Since √3 is approximately 1.732, so t1≈1 +1.732≈2.732 and t2≈1 -1.732≈-0.732. Therefore, point B is in the direction opposite to the direction vector from F. Therefore, |FA| is t1, since it's in the positive direction, and |FB| is |t2|. But let's check.Wait, if the parameter t is the distance along the line from F, then when t=0, we are at F. For positive t, we move in one direction, for negative t, we move in the opposite direction. Therefore, |FA| would be |t1|, which is 1 + √3, and |FB| would be |t2|, which is |1 - √3|. However, 1 - √3 is negative, so |1 - √3| = √3 -1. Therefore, |FA| ⋅ |FB| = (1 + √3)(√3 -1). Let's compute that:(1 + √3)(√3 -1) = (√3)^2 -1^2 = 3 -1 =2. So the product is 2. Therefore, the answer is 2. Wait, that seems too straightforward. Let me verify.Alternatively, maybe this is a case of the power of a point with respect to a conic. The power of a point F with respect to the ellipse C is |FA|⋅|FB|, which can be computed using the formula. For a general conic, the power of a point F is equal to the product of the distances from F to the points of intersection of any line through F with the conic. For an ellipse, this is a constant for lines through F, but I might need to recall the exact formula.Alternatively, let's use coordinates. Let me compute |FA| and |FB| by coordinates. Let's compute coordinates of A and B.For t1 =1 + √3:x = -2√2 + (√2/2)(1 + √3) = -2√2 + (√2/2 + √2/2 * √3 )= √2/2 ( -4 +1 + √3 )= √2/2 (-3 + √3 )Similarly, y = (√2/2)(1 + √3 )So coordinates of A are ( √2/2 (-3 + √3 ), √2/2 (1 + √3 ) )Similarly for t2=1 - √3:x = -2√2 + (√2/2)(1 - √3 ) = -2√2 + √2/2 - √2/2 *√3= √2/2 ( -4 +1 - √3 )= √2/2 (-3 - √3 )y = (√2/2)(1 - √3 )So coordinates of B are ( √2/2 (-3 - √3 ), √2/2 (1 - √3 ) )Now, compute |FA| and |FB|.Point F is (-2√2, 0). Let's compute the distance FA.FA: distance between (-2√2, 0) and ( √2/2 (-3 + √3 ), √2/2 (1 + √3 ) )Compute x-coordinate difference:√2/2 (-3 + √3 ) - (-2√2 ) = √2/2 (-3 + √3 ) + 2√2Factor out √2:√2 [ (-3 + √3 )/2 + 2 ] = √2 [ (-3 + √3 +4 )/2 ] = √2 [ (1 + √3 )/2 ]Similarly, y-coordinate difference:√2/2 (1 + √3 ) -0 = √2/2 (1 + √3 )Therefore, the distance FA is sqrt( [√2 (1 + √3 )/2 ]^2 + [√2/2 (1 + √3 )]^2 )Compute each term:First term: [√2 (1 + √3 )/2 ]^2 = (2 * (1 + √3 )² ) /4 = ( (1 + √3 )² ) /2Second term: [√2/2 (1 + √3 )]^2 = (2 * (1 + √3 )² ) /4 = same as first term: ( (1 + √3 )² ) /2Therefore, FA = sqrt( ( (1 + √3 )² /2 + (1 + √3 )² /2 ) ) = sqrt( (1 + √3 )² ) = |1 + √3 | =1 + √3Similarly, compute |FB|.Coordinates of B: ( √2/2 (-3 - √3 ), √2/2 (1 - √3 ) )Distance FB: distance between (-2√2, 0) and ( √2/2 (-3 - √3 ), √2/2 (1 - √3 ) )x-coordinate difference:√2/2 (-3 - √3 ) - (-2√2 ) = √2/2 (-3 - √3 ) + 2√2Factor out √2:√2 [ (-3 - √3 )/2 + 2 ] = √2 [ (-3 - √3 +4 )/2 ] = √2 [ (1 - √3 )/2 ]y-coordinate difference:√2/2 (1 - √3 ) -0 = √2/2 (1 - √3 )Distance FB:sqrt( [√2 (1 - √3 )/2 ]^2 + [√2/2 (1 - √3 )]^2 )First term: [√2 (1 - √3 )/2 ]^2 = 2*(1 - √3 )² /4 = (1 - √3 )² /2Second term: same as first term, so total inside sqrt is (1 - √3 )² /2 + (1 - √3 )² /2 = (1 - √3 )²Therefore, FB = |1 - √3 |. Since 1 - √3 is negative, |1 - √3 | = √3 -1Therefore, |FA|⋅|FB| = (1 + √3 )(√3 -1 ) = (√3 )² -1² =3 -1=2. So the answer is 2. That matches the earlier result. Therefore, part (I) is 2.Now, part (Ⅱ): Let the perimeter of the inscribed rectangle of curve C be P. Find the maximum value of P.First, curve C is the ellipse x² + 3y² =12, which we can write as x²/(12) + y²/4 =1. So semi-major axis a = sqrt(12) = 2*sqrt(3), and semi-minor axis b =2. The inscribed rectangle of the ellipse. The perimeter of such a rectangle. We need to find the maximum perimeter.An inscribed rectangle in an ellipse would have its vertices on the ellipse. For an ellipse centered at the origin, due to symmetry, the rectangle would also be centered at the origin, with sides parallel to the axes. Wait, but is that necessarily the case? Or can the rectangle be rotated?But the term "inscribed rectangle" usually refers to a rectangle whose sides are parallel to the axes of the ellipse. Wait, but maybe not necessarily. Wait, the problem says "inscribed rectangle of curve C". So inscribed in the ellipse. The maximum perimeter can be achieved either with sides parallel to the axes or rotated. Hmm. So we need to consider all possible rectangles inscribed in the ellipse and find the one with maximum perimeter.But this is more complicated. However, maybe parametrizing the rectangle.First, let's recall that for an ellipse, the maximum area inscribed rectangle is known, but here we need maximum perimeter.But let's think. For an ellipse, parametrized as x = a cosθ, y = b sinθ. If we consider a rectangle inscribed in the ellipse, with vertices at (a cosθ, b sinθ), (-a cosθ, b sinθ), (-a cosθ, -b sinθ), (a cosθ, -b sinθ). But this rectangle has sides parallel to the axes. The perimeter would be 4*(2a cosθ + 2b sinθ )? Wait, no. Wait, each side of the rectangle has length 2a cosθ and 2b sinθ. So the perimeter would be 2*(2a cosθ + 2b sinθ ) = 4a cosθ + 4b sinθ. Wait, no. Wait, the rectangle has two lengths and two widths. The length is 2a cosθ, the width is 2b sinθ. So perimeter is 2*(2a cosθ + 2b sinθ ) = 4a cosθ + 4b sinθ. Therefore, perimeter P=4(a cosθ + b sinθ ). To find the maximum of this expression. However, the maximum of a cosθ + b sinθ is sqrt(a² + b²). So maximum perimeter would be 4*sqrt(a² + b² ). But is this correct? Wait, for P=4(a cosθ + b sinθ ), the maximum is indeed 4*sqrt(a² + b² ). But this is only if the rectangle is axis-aligned. However, if we allow the rectangle to be rotated, perhaps we can get a larger perimeter.Wait, but maybe not. Because if we rotate the rectangle, the lengths might not simply add up the same way. However, this requires more careful analysis.Alternatively, perhaps the maximum perimeter occurs when the rectangle is axis-aligned. Let's check.Given the ellipse x²/12 + y²/4 =1, so a=2√3, b=2. Then for axis-aligned rectangles, the maximum perimeter would be 4*sqrt(a² + b² )=4*sqrt(12 +4 )=4*sqrt(16 )=4*4=16. But let's compute 4(a cosθ + b sinθ ). The maximum of a cosθ + b sinθ is sqrt(a² + b² ). So indeed, the maximum perimeter for axis-aligned rectangles would be 4*sqrt(a² + b² )=16. But if we consider rotated rectangles, can we get a larger perimeter?Alternatively, perhaps not. Let me think. The perimeter of a rectangle inscribed in an ellipse might be maximized when the rectangle is rotated such that its sides are tangent to the ellipse at certain points, but I need to verify.Alternatively, parametrize the rectangle in terms of a parameter θ, where θ is the angle of the first vertex in parametric form. Wait, but for a general rectangle inscribed in an ellipse, the parametrization is more complex. Let me consider using Lagrange multipliers to maximize the perimeter function subject to the ellipse constraint.Let’s denote the four vertices of the rectangle as (x, y), (-x, y), (-x, -y), (x, -y). However, this is for an axis-aligned rectangle. For a rotated rectangle, the coordinates would be more complicated.Wait, but the problem says "inscribed rectangle", which is a rectangle whose all four vertices lie on the ellipse. For an ellipse, due to its symmetry, the maximum perimeter might be achieved by the rectangle aligned with the major and minor axes, but to confirm, let's proceed.But let me first check the axis-aligned case. For such a rectangle, the perimeter is 4*(2a cosθ + 2b sinθ ) as above? Wait, actually, if we parameterize a point on the ellipse as (a cosθ, b sinθ ), then the rectangle would have vertices at (a cosθ, b sinθ ), (-a cosθ, b sinθ ), (-a cosθ, -b sinθ ), (a cosθ, -b sinθ ). The side lengths are 2a cosθ and 2b sinθ, so perimeter is 2*(2a cosθ + 2b sinθ )=4a cosθ +4b sinθ. Then, the maximum of 4(a cosθ +b sinθ ). The maximum of a cosθ +b sinθ is sqrt(a² +b² ), so maximum perimeter would be 4*sqrt(a² +b² ). For our ellipse, a²=12, b²=4, so sqrt(16)=4. Therefore, maximum perimeter would be 4*4=16.But if we consider rotated rectangles, can we get a larger perimeter?Let’s consider a general rectangle inscribed in the ellipse. Let's denote the vertices as (x1, y1), (x2, y2), (-x1, -y1), (-x2, -y2). Wait, but for a rectangle, opposite sides are equal and parallel, so perhaps it's better to parametrize it with two points. Alternatively, since it's a rectangle, the four vertices can be represented as (x, y), (-x, y), (-x, -y), (x, -y) only if it's axis-aligned. If it's rotated, the coordinates would be more complex.Alternatively, consider that any inscribed rectangle can be represented by two points (x, y) and (-y, x) rotated by some angle, but this might complicate things.Alternatively, parametrize the rectangle using a parameter θ, where θ is the angle between the sides of the rectangle and the axes. Wait, but this is getting too vague. Let's try using Lagrange multipliers.Let’s consider two adjacent vertices of the rectangle, say P(x1, y1) and Q(x2, y2), such that PQ is a side of the rectangle. Since it's a rectangle, the vector PQ should be perpendicular to the vector PR, where R is the next vertex. However, this approach might get too involved.Alternatively, think of the rectangle as having sides with slopes m and -1/m (since they are perpendicular). Then, the four vertices can be found by intersecting lines with these slopes with the ellipse. But this seems complicated.Alternatively, use parametric equations. Let me parametrize the rectangle in terms of an angle θ, such that the rectangle is formed by points (a cosθ, b sinθ ), (-b sinθ, a cosθ ), etc. Wait, no, not sure.Wait, perhaps the maximum perimeter occurs when the rectangle is actually a square. But in an ellipse, a square can only be inscribed in specific cases. However, in this case, the ellipse is x² +3y²=12, which is not a circle, so a square cannot be inscribed in the same way as in a circle.Alternatively, note that the problem asks for the maximum perimeter of an inscribed rectangle. To find this, we can parametrise the rectangle with two parameters, but it might be easier to parametrise using a single parameter.Let’s consider that any rectangle inscribed in the ellipse must have its vertices at points (x, y), (-x, y), (-x, -y), (x, -y) if it is axis-aligned. The perimeter in this case is 4*(2x + 2y )? Wait, no. Wait, the side lengths are 2x and 2y, so the perimeter is 2*(2x + 2y )=4x +4y. But wait, in the ellipse equation, x² +3y²=12, so x and y are related. So for the axis-aligned case, we can write perimeter P=4x +4y, subject to x² +3y²=12. Then, to maximize P=4x +4y with x² +3y²=12.But this is a constrained optimization problem. Use Lagrange multipliers. Let’s set up the function f(x,y)=4x +4y, and the constraint g(x,y)=x² +3y² -12=0.The Lagrangian is L=4x +4y -λ(x² +3y² -12).Taking partial derivatives:∂L/∂x=4 -2λx=0 ⇒4=2λx ⇒λ=2/x∂L/∂y=4 -6λy=0 ⇒4=6λy ⇒λ=4/(6y)=2/(3y)Set equal: 2/x =2/(3y) ⇒1/x=1/(3y) ⇒3y=x.Substitute into the constraint x² +3y²=12:(3y)^2 +3y²=12 ⇒9y² +3y²=12 ⇒12y²=12 ⇒y²=1 ⇒y=±1. Then x=3y=±3.Therefore, the maximum perimeter for the axis-aligned case is P=4x +4y=4*(3) +4*(1)=12 +4=16. Similarly for y=-1, P=4*(-3) +4*(-1)=-16, but since perimeter is positive, we take absolute value. So maximum perimeter is 16.But this is only for axis-aligned rectangles. What if the rectangle is rotated? Could the perimeter be larger?To check, let's consider a general inscribed rectangle. Let’s parameterize the rectangle with a parameter θ, such that the vertices are (x1, y1), (x2, y2), (-x1, -y1), (-x2, -y2), but with some conditions.Alternatively, let's consider that the sides of the rectangle are not aligned with the axes, so the rectangle is rotated by some angle φ. Then, the coordinates of the vertices can be expressed in terms of rotated coordinates. Let's suppose the rectangle is rotated by angle φ, and has side lengths 2a and 2b. The vertices would then be (a cosφ - b sinφ, a sinφ + b cosφ ), (-a cosφ - b sinφ, -a sinφ + b cosφ ), etc. This might get complicated.Alternatively, let's parametrise the rectangle as follows: take two perpendicular chords of the ellipse, intersecting at the center, and each chord has a certain length. The perimeter would be 4 times the sum of half the lengths of these two chords. To maximize the sum of the lengths of these two perpendicular chords.But even this approach is non-trivial. Perhaps there is a parametrization using parametric equations of the ellipse.Let me recall that any point on the ellipse can be written as (2√3 cosθ, 2 sinθ ). So let's consider two points on the ellipse: P(2√3 cosθ, 2 sinθ ) and Q(2√3 cosφ, 2 sinφ ). For these two points to form adjacent vertices of a rectangle centered at the origin, the vector OQ must be perpendicular to the vector OP. So the dot product should be zero:(2√3 cosθ)(2√3 cosφ) + (2 sinθ)(2 sinφ )=0Simplify:4*3 cosθ cosφ +4 sinθ sinφ =0 ⇒12 cosθ cosφ +4 sinθ sinφ =0 ⇒Divide by 4:3 cosθ cosφ + sinθ sinφ =0Let’s write this as:3 cosθ cosφ + sinθ sinφ =0This is the condition for perpendicularity. Let’s try to find a relation between θ and φ.Let’s rearrange:3 cosθ cosφ = - sinθ sinφDivide both sides by cosθ cosφ (assuming cosθ cosφ ≠0):3 = - tanθ tanφSo tanθ tanφ = -3Therefore, φ = arctan(-3 / tanθ )This relates φ and θ. Now, the perimeter of the rectangle is 4 times the sum of the distances from the origin to P and Q. Wait, no. The perimeter would be 4 times the length of OP + OQ? Wait, no. Wait, if the rectangle has vertices at P, Q, -P, -Q, then the sides are from P to Q and Q to -P, etc. But this is only a rectangle if OP and OQ are perpendicular. The side lengths would be |P - Q| and |Q - (-P)|=|Q + P|. Wait, no. Actually, the edges of the rectangle would be from P to Q, Q to -P, -P to -Q, and -Q to P. But the lengths of the sides would be |P - Q| and |Q - (-P)|. But since it's a rectangle, these lengths should be equal. Wait, no, in a rectangle, adjacent sides are perpendicular. Therefore, the vectors PQ and Q(-P) should be perpendicular.Wait, this is getting too complicated. Perhaps instead of this approach, let's calculate the distance between two adjacent vertices.Let’s suppose the rectangle has vertices P, Q, R, S. Then PQ and QR are adjacent sides. Since it's a rectangle, PQ and QR are perpendicular. The perimeter is 2(|PQ| + |QR| ). But without knowing specific points, this is difficult.Alternatively, since the rectangle is centered at the origin and has vertices symmetric with respect to the origin, perhaps we can parameterize it using two points P and Q such that OP and OQ are perpendicular. Then the perimeter would be 4*(|OP| + |OQ| ). Wait, but |OP| and |OQ| are the distances from the origin to P and Q. Wait, but in that case, the perimeter would depend on the lengths of OP and OQ. However, since P and Q lie on the ellipse, |OP| is not fixed. Wait, but for the ellipse x² +3y²=12, the distance from the origin to a point (x,y) on the ellipse is sqrt(x² + y² ). Which is not fixed. So, to maximize the perimeter 4*(sqrt(x1² + y1² ) + sqrt(x2² + y2² )) where (x1, y1) and (x2, y2) are points on the ellipse such that x1x2 + y1y2 =0 (perpendicular vectors). But this is a more complex optimization problem.Alternatively, perhaps we can parametrize points P and Q as (2√3 cosθ, 2 sinθ ) and (2√3 cosφ, 2 sinφ ) with the condition that their dot product is zero:(2√3 cosθ)(2√3 cosφ) + (2 sinθ)(2 sinφ )=0 ⇒12 cosθ cosφ +4 sinθ sinφ=0 ⇒3 cosθ cosφ + sinθ sinφ=0 ⇒tanθ tanφ= -3.Let’s set tanθ = t, then tanφ= -3/t.So θ = arctan(t), φ=arctan(-3/t).But this might not lead us directly to a solution. Alternatively, use trigonometric identities. Let’s set θ = α, then φ must satisfy 3 cosα cosφ + sinα sinφ=0.Let me rewrite this as:3 cosα cosφ = - sinα sinφ ⇒3 cotα = - tanφ ⇒tanφ = -3 cotα = -3/tanα = -3 cotα.Therefore, φ = arctan(-3 cotα ).But perhaps using parametrization variables.Let me express the perimeter in terms of α. The points P and Q are (2√3 cosα, 2 sinα ) and (2√3 cosφ, 2 sinφ ). The perimeter of the rectangle is 4*(distance from P to Q / sqrt(2) ). Wait, no. Wait, if OP and OQ are perpendicular vectors, then the rectangle formed by P, Q, -P, -Q has side lengths |OP| and |OQ|, but actually, the sides of the rectangle are |OP - OQ| and |OP + OQ|. Wait, not sure. Alternatively, the perimeter can be calculated as follows: the rectangle has vertices at P, Q, -P, -Q. The sides are PQ, Q(-P), (-P)(-Q), (-Q)P. The length of PQ can be calculated using the distance formula:|PQ| = sqrt( (2√3 cosα - 2√3 cosφ )² + (2 sinα -2 sinφ )² )But this seems complicated. Alternatively, since OP and OQ are perpendicular, the rectangle is actually a diamond shape with vertices at P, Q, -P, -Q, and the sides are all equal in length. Wait, no, in general, if OP and OQ are perpendicular vectors, the figure formed by P, Q, -P, -Q is a rectangle with sides |OP| and |OQ|. The perimeter is 2*(2|OP| + 2|OQ| )=4(|OP| + |OQ| ). Wait, no. Wait, each side of the rectangle is the hypotenuse of a right triangle with sides |OP| and |OQ|. No, that's not correct. Wait, if OP and OQ are perpendicular vectors, then the edges of the rectangle are the vectors OP + OQ and OP - OQ. Wait, maybe not. This is getting confusing.Alternatively, maybe the perimeter is 4 times the sum of |OP| and |OQ|. But in that case, the perimeter would be P=4(|OP| + |OQ| ). But |OP| is sqrt( (2√3 cosα )² + (2 sinα )² )=sqrt( 12 cos²α +4 sin²α ). Similarly, |OQ|=sqrt(12 cos²φ +4 sin²φ ). But with the condition that 3 cosα cosφ + sinα sinφ=0.This seems very complicated. Maybe there's a better approach.Let’s consider that the maximum perimeter of an inscribed rectangle occurs when the rectangle is axis-aligned. As we calculated earlier, this gives a perimeter of 16. But is this the maximum?Alternatively, suppose we take a rotated rectangle. Let's parametrize a rectangle inscribed in the ellipse with vertices at (x, y), (-y, x), (-x, -y), (y, -x). This is a rectangle rotated by 45 degrees, but scaled. Let's check if these points lie on the ellipse.Plugging (x, y) into the ellipse equation: x² +3y²=12.Plugging (-y, x) into the ellipse equation: (-y)^2 +3x²= y² +3x²=12.So for both points to lie on the ellipse, we need:x² +3y²=12andy² +3x²=12Subtract the two equations:x² +3y² - (y² +3x²)=12 -12 ⇒-2x² +2y²=0 ⇒y²=x² ⇒y=±x.Therefore, substituting y=x into the first equation:x² +3x²=4x²=12 ⇒x²=3 ⇒x=±√3, y=±√3.Therefore, the points are (√3, √3), (-√3, √3), etc. Check if these lie on the ellipse:(√3)^2 +3*(√3)^2=3 +9=12. Yes.Similarly for y=-x.So the perimeter of this rectangle is computed as follows: distance between (√3, √3) and (-√3, √3) is 2√3*2=4√3. Wait, no. Wait, the distance between (√3, √3) and (-√3, √3) is sqrt( (√3 - (-√3))² + (√3 -√3 )² )=sqrt( (2√3 )² +0 )=2√3. Similarly, the distance between (-√3, √3) and (-√3, -√3 ) is sqrt(0 + (√3 - (-√3 ))^2 )=sqrt( (2√3 )² )=2√3. Therefore, the rectangle is actually a square with side length 2√3, perimeter 8√3≈13.856, which is less than 16. Therefore, this rotated square has a smaller perimeter than the axis-aligned rectangle.Therefore, the maximum perimeter occurs when the rectangle is axis-aligned. Therefore, the maximum perimeter is 16.But wait, let me check another rotated rectangle. Suppose we take a rectangle that is not aligned with the axes nor rotated by 45 degrees. For example, take θ=30 degrees. Let's compute the perimeter.But this will require going back to the Lagrange multiplier method for the general case. Let's suppose we have a rectangle with vertices (x, y), (-x, y), (-x, -y), (x, -y), so axis-aligned. Then perimeter is 4*(2x +2y )=8x +8y. Wait, no, wait. Wait, each side length is 2x and 2y, so perimeter is 2*(2x +2y )=4x +4y. Wait, yes, that's correct. Previously, when we used Lagrange multipliers, we found that the maximum perimeter for this case is 16.But earlier, when considering a rotated square, we found a perimeter of 8√3≈13.856, which is less than 16. So maybe the maximum perimeter is indeed 16.Alternatively, perhaps not. Let me consider a different parametrization. Suppose we take a rectangle inscribed in the ellipse with vertices at (x, y), (u, v), (-x, -y), (-u, -v), where (x, y) and (u, v) are points on the ellipse, and the vectors (x, y) and (u, v) are perpendicular. Then, the perimeter would be 2*(sqrt( (x -u)^2 + (y -v)^2 ) + sqrt( (u +x)^2 + (v + y)^2 )) ). This is complicated, but maybe there's a better way.Alternatively, consider that the perimeter of the rectangle is twice the sum of the lengths of two adjacent sides. Let’s denote the vectors of these sides as a and b, which are perpendicular. The perimeter is 2(|a| + |b| ). The vectors a and b must satisfy that their endpoints are on the ellipse. Let’s suppose a = (x, y) and b = (u, v), such that a ⋅ b =xu + yv=0. Additionally, the points (x, y) and (u, v) lie on the ellipse x² +3y²=12. The perimeter is then 2( sqrt(x² + y² ) + sqrt(u² + v² ) ). We need to maximize this.But this seems too abstract. Perhaps there's an inequality we can use. Let’s denote S= sqrt(x² + y² ) + sqrt(u² + v² ). We need to maximize S subject to x² +3y²=12, u² +3v²=12, and xu + yv=0.This is a complex optimization problem. Maybe use Lagrange multipliers with multiple constraints.Let’s set up the function to maximize: S= sqrt(x² + y² ) + sqrt(u² + v² )With constraints:1. x² +3y²=122. u² +3v²=123. xu + yv=0Let’s introduce three Lagrange multipliers λ, μ, ν for the three constraints.The Lagrangian is:L= sqrt(x² + y² ) + sqrt(u² + v² ) -λ(x² +3y² -12 ) -μ(u² +3v² -12 ) -ν(xu + yv )Take partial derivatives with respect to x, y, u, v, λ, μ, ν.∂L/∂x= (x)/sqrt(x² + y² ) -2λx -νu=0∂L/∂y= (y)/sqrt(x² + y² ) -6λy -νv=0∂L/∂u= (u)/sqrt(u² + v² ) -2μu -νx=0∂L/∂v= (v)/sqrt(u² + v² ) -6μv -νy=0And the constraints:x² +3y²=12u² +3v²=12xu + yv=0This system of equations is quite complex, but let's see if we can find a symmetric solution.Assume that x=u and y=v, but then xu + yv= x² + y²=0 ⇒x² + y²=0 ⇒x=y=0, which is not on the ellipse. So invalid.Alternatively, suppose that sqrt(x² + y² )=sqrt(u² + v² )=k. Then S=2k. Then maximize k. But with xu + yv=0. But this may not necessarily be optimal.Alternatively, consider that maximum S occurs when the vectors (x, y) and (u, v) are aligned with the axes. Wait, but in that case, xu + yv= x*u + y*v. If they are aligned with the axes, then x or y is zero, and similarly for u and v. For example, if (x, y)=(sqrt(12),0) and (u, v)=(0, 2), then xu + yv=0. The perimeter would be 2*(sqrt(12) +2 )=2*(2√3 +2 )=4√3 +4≈6.928 +4≈10.928, which is less than 16. Therefore, not optimal.Alternatively, take (x, y)= (3,1) and (u, v)=(-1,3), but check if they lie on the ellipse. For (3,1): 9 +3=12, yes. For (-1,3):1 +27=28≠12, so not on the ellipse.Alternatively, let's look back at the axis-aligned case. When we set y=1, x=3, then perimeter=4*(3 +1)=16. If we set other points with x=3, y=1, the product xu + yv=3u +v=0. So if (u, v) is another point on the ellipse x² +3y²=12, such that 3u +v=0. Let's see if such a point exists.From 3u +v=0 ⇒v= -3u. Plug into the ellipse equation:u² +3*(-3u)^2=u² +3*9u²=u² +27u²=28u²=12 ⇒u²=12/28=3/7 ⇒u=±√(3/7), v=∓3√(3/7 )Then sqrt(u² +v² )=sqrt(3/7 +9*3/7 )=sqrt(30/7 ). Then perimeter would be 2*(sqrt(x² +y² ) + sqrt(u² +v² ))=2*(sqrt(9 +1 ) + sqrt(30/7 ))=2*(√10 + sqrt(30/7 ))≈2*(3.162 +2.07)=2*5.232≈10.464, still less than 16.Therefore, it seems that the maximum perimeter is achieved by the axis-aligned rectangle with vertices at (3,1), (-3,1), (-3,-1), (3,-1), with perimeter 16.Therefore, the answer to part (II) is 16.Final AnswerⅠ. boxed{2}Ⅱ. boxed{16}</think>Given the parametric equation of line ( l ):[begin{cases} x = m + frac{sqrt{2}}{2}t y = frac{sqrt{2}}{2}t end{cases}]where ( t ) is the parameter, and the polar equation of curve ( C ) is ( rho^2 cos^2 theta + 3rho^2 sin^2 theta = 12 ). The left focus ( F ) of curve ( C ) lies on line ( l ). Part (I)1. Convert the polar equation to Cartesian coordinates: [ rho^2 (cos^2 theta + 3 sin^2 theta) = 12 implies x^2 + 3y^2 = 12 ] This is an ellipse with semi-major axis ( 2sqrt{3} ) and semi-minor axis ( 2 ).2. Find the foci of the ellipse: [ c^2 = a^2 - b^2 = 12 - 4 = 8 implies c = 2sqrt{2} ] The left focus ( F ) is ( (-2sqrt{2}, 0) ).3. Determine ( m ) such that ( F ) lies on line ( l ): [ -2sqrt{2} = m + frac{sqrt{2}}{2} cdot 0 implies m = -2sqrt{2} ]4. Find the intersection points ( A ) and ( B ) of line ( l ) with the ellipse: Substitute ( x = -2sqrt{2} + frac{sqrt{2}}{2}t ) and ( y = frac{sqrt{2}}{2}t ) into ( x^2 + 3y^2 = 12 ): [ (-2sqrt{2} + frac{sqrt{2}}{2}t)^2 + 3 left( frac{sqrt{2}}{2}t right)^2 = 12 ] Solving this quadratic equation in ( t ), we get ( t = 1 pm sqrt{3} ).5. Calculate distances ( |FA| ) and ( |FB| ): - For ( t = 1 + sqrt{3} ), distance ( |FA| = 1 + sqrt{3} ) - For ( t = 1 - sqrt{3} ), distance ( |FB| = sqrt{3} - 1 ) - Product: ( |FA| cdot |FB| = (1 + sqrt{3})(sqrt{3} - 1) = 2 ) Part (II)1. Consider the inscribed rectangle in the ellipse: The maximum perimeter of an inscribed rectangle in the ellipse ( x^2 + 3y^2 = 12 ) is found using the axis-aligned rectangle.2. Maximize the perimeter: - The perimeter of the axis-aligned rectangle with vertices ( (pm 3, pm 1) ) is: [ 4 times (2 times 3 + 2 times 1) = 4 times (3 + 1) = 16 ] Final AnswersⅠ. boxed{2}Ⅱ. boxed{16}]

🔑:(Ⅰ) The rectangular coordinate equation of curve C is given by x^{2}+3y^{2}=12, which can be rewritten as frac{x^{2}}{12}+frac{y^{2}}{4}=1. Therefore, the left focus F of curve C has coordinates F(-2sqrt{2},0).Since F(-2sqrt{2},0) lies on line l, we can modify the parametric equations of line l accordingly:begin{cases} x=-2sqrt{2}+ frac{sqrt{2}}{2}t y= frac{sqrt{2}}{2}tend{cases}(t text{ is the parameter}).Substituting the parametric equations of line l into x^{2}+3y^{2}=12, we get t^{2}-2t-2=0. Therefore, the product |FA|cdot|FB| equals to the product of the roots |t_1t_2|=2. Hence, |FA|cdot|FB| = boxed{2}.(Ⅱ) Let the vertex of the rectangle that lies in the first quadrant on curve C be M(x,y) where (0 0 and when 1 < y < 2, f′(y) < 0. Therefore, f(y) attains its maximum value of 16 when y=1. Thus, the maximum value of P is boxed{16}.

🧠:[<think>Okay, let's see. The problem says that the lateral surface area of a cone is equal to the area of a semicircle with an area of 2π. I need to find the volume of the cone. Hmm, let me break this down step by step.First, I remember that the lateral surface area (which is just the curved part, not including the base) of a cone is given by the formula πrl, where r is the radius of the base and l is the slant height of the cone. The problem states that this lateral surface area is equal to the area of a semicircle, which is given as 2π. Wait, a semicircle's area is (1/2)πr², right? So if the semicircle has an area of 2π, then I can set up the equation (1/2)πR² = 2π, where R is the radius of the semicircle. Let me solve for R first, maybe that's needed?But hold on, the problem says the lateral surface area of the cone is equal to the area of the semicircle. So actually, the lateral surface area πrl = 2π. Let me check that again. The semicircle's area is 2π, so yes, the lateral surface area is 2π. Therefore, πrl = 2π. If I divide both sides by π, that gives rl = 2. So r times l equals 2. Got that.But to find the volume of the cone, I need to know the radius and the height, right? The volume formula is (1/3)πr²h. So I need to find h, the height. But I only have the slant height l here. I remember that in a right circular cone, the slant height l, radius r, and height h are related by the Pythagorean theorem: l² = r² + h². So if I can find either r or l, I can find the other using rl = 2, and then find h. But right now, I have two variables: r and l. So I need another equation.Wait, but maybe there's a relation between the semicircle and the cone? Let me read the problem again: "the lateral surface of a cone is the area of a semicircle with an area of 2π". So the lateral surface area equals 2π. So πrl = 2π. As before, this simplifies to rl = 2. So I need another equation involving r and l. The Pythagorean theorem gives l² = r² + h², but that introduces another variable h. So perhaps there's another way. Maybe the semicircle is related to the slant height? Wait, if the lateral surface is a semicircle, then when you unwrap the lateral surface of a cone, you get a sector of a circle. But in this case, it's a semicircle. Let me recall that the lateral surface area of a cone is a sector with radius equal to the slant height l, and the arc length equal to the circumference of the base of the cone, which is 2πr.So when you unwrap the lateral surface, the sector has radius l and arc length 2πr. The problem states that this lateral surface is a semicircle. A semicircle is a sector with angle π radians (180 degrees). The length of the arc of a semicircle with radius l would be πl. Therefore, equating that to the arc length of the sector (which is 2πr), we have πl = 2πr. Dividing both sides by π gives l = 2r. Oh! So that's another equation relating l and r: l = 2r.But earlier, we had from the lateral surface area: rl = 2. So substituting l = 2r into that equation gives r*(2r) = 2 => 2r² = 2 => r² = 1 => r = 1. Therefore, radius r is 1. Then l = 2r = 2*1 = 2. So slant height l is 2. Then we can find h using the Pythagorean theorem: l² = r² + h² => 2² = 1² + h² => 4 = 1 + h² => h² = 3 => h = √3. Therefore, the height is √3.Now, using the volume formula: (1/3)πr²h. Plugging in r = 1, h = √3, so Volume = (1/3)π*(1)²*(√3) = (1/3)π*√3 = (π√3)/3. So that's the volume. Let me check my steps again to make sure I didn't make a mistake.1. Lateral surface area of cone: πrl = area of semicircle = 2π. Correct.2. So πrl = 2π ⇒ rl = 2. Correct.3. Then, since the lateral surface is a semicircle when unwrapped, the arc length of the semicircle (which is πl) equals the circumference of the base of the cone (2πr). So πl = 2πr ⇒ l = 2r. Correct.4. Substituting l = 2r into rl = 2 gives r*(2r) = 2 ⇒ 2r² = 2 ⇒ r² = 1 ⇒ r = 1. Correct.5. Then l = 2*1 = 2. Correct.6. Using Pythagorean theorem: l² = r² + h² ⇒ 4 = 1 + h² ⇒ h² = 3 ⇒ h = √3. Correct.7. Volume is (1/3)πr²h ⇒ (1/3)π*1*√3 = π√3/3. That seems right.Wait, but I just want to make sure that interpreting the lateral surface as a semicircle is correctly done. Because when you unwrap the lateral surface of a cone, you get a sector of a circle with radius equal to the slant height l. The problem says that this sector is a semicircle. A semicircle is a sector with angle π. The arc length of that semicircle would be π*l (since circumference of full circle is 2πl, so semicircle is πl). But this arc length must equal the circumference of the base of the cone, which is 2πr. Therefore, πl = 2πr ⇒ l = 2r. That part is key here. So yes, that relationship is correct.Therefore, all steps check out. The volume is π√3 divided by 3, which can also be written as (π/3)√3 or π times √3 over 3. So that's the answer.Final AnswerThe volume of the cone is boxed{dfrac{sqrt{3}}{3} pi}.</think>The problem states that the lateral surface area of a cone is equal to the area of a semicircle with an area of (2pi). We need to find the volume of the cone.1. The lateral surface area of a cone is given by (pi r l), where (r) is the radius and (l) is the slant height. This is equal to the area of the semicircle, which is (2pi): [ pi r l = 2pi ] Dividing both sides by (pi) gives: [ r l = 2 ]2. When the lateral surface of the cone is unwrapped, it forms a sector of a circle. Since this sector is a semicircle, the arc length of the semicircle (which is (pi l)) must equal the circumference of the base of the cone (which is (2pi r)): [ pi l = 2pi r ] Dividing both sides by (pi) gives: [ l = 2r ]3. Substituting (l = 2r) into the equation (r l = 2): [ r (2r) = 2 implies 2r^2 = 2 implies r^2 = 1 implies r = 1 ]4. Using (l = 2r) with (r = 1): [ l = 2 times 1 = 2 ]5. Using the Pythagorean theorem to find the height (h) of the cone: [ l^2 = r^2 + h^2 implies 2^2 = 1^2 + h^2 implies 4 = 1 + h^2 implies h^2 = 3 implies h = sqrt{3} ]6. Calculating the volume of the cone using the formula (frac{1}{3} pi r^2 h): [ text{Volume} = frac{1}{3} pi (1)^2 sqrt{3} = frac{pi sqrt{3}}{3} ]The volume of the cone is (boxed{dfrac{sqrt{3}}{3} pi}).,<think>Okay, so I need to find the volume of a cone where the lateral surface area is equal to the area of a semicircle with area 2π. Hmm, let's break this down step by step. First, I remember that the lateral surface area of a cone (which is the curved part, not including the base) is given by the formula πrl, where r is the radius of the base and l is the slant height of the cone. The problem says that this lateral surface area is equal to the area of a semicircle. The area of a semicircle is (1/2)πR², where R is the radius of the semicircle. But in this case, the area of the semicircle is given as 2π. So, setting these equal: πrl = 2π.Wait, let me make sure. The problem says "the lateral surface of a cone is the area of a semicircle with an area of 2π". So actually, the lateral surface area (πrl) is equal to 2π. So, πrl = 2π. Then, dividing both sides by π, we get rl = 2. So, rl = 2. Got that.But we need to find the volume of the cone. The volume of a cone is (1/3)πr²h, where h is the height of the cone. So, we need to find r and h. But right now, we only have that rl = 2. So, we need another equation to relate r and h. Since l, the slant height, is related to r and h by the Pythagorean theorem: l = √(r² + h²). So, substituting that into our first equation: r * √(r² + h²) = 2.Hmm, so we have two variables, r and h, and one equation. But we need another relation. Wait, but maybe we can express h in terms of r, or vice versa, and substitute into the volume formula. Let me try that.First, let's write l = √(r² + h²). Then, from rl = 2, substitute l: r * √(r² + h²) = 2. Let me square both sides to eliminate the square root. So, (r)² * (r² + h²) = 4. That simplifies to r²(r² + h²) = 4. Which is r⁴ + r²h² = 4. Hmm, not sure if that helps directly. Maybe I need to express h in terms of r from the slant height equation.Alternatively, perhaps there's a smarter way. Let's think again. The problem states that the lateral surface area is equal to the area of a semicircle. Wait, is the semicircle's radius related to the cone's dimensions in any way? The problem just mentions a semicircle with an area of 2π. So, perhaps the semicircle's radius is not directly given, but we can find it if needed. Let me check.The area of a semicircle is (1/2)πR² = 2π. So, solving for R, we can find the radius of the semicircle. Let's do that. (1/2)πR² = 2π. Dividing both sides by π: (1/2)R² = 2. Then, multiply both sides by 2: R² = 4. Therefore, R = 2. So, the semicircle has a radius of 2. But does that relate to the cone? The problem says "the lateral surface of a cone is the area of a semicircle with an area of 2π". So, the lateral surface area is equal to the area of a semicircle of radius 2, which is 2π. So, that's where the 2π comes from. So, that's already been accounted for in the first equation. So, moving on.So, back to the cone. We have rl = 2 and l = √(r² + h²). Let's try to express h in terms of r. Let me square both sides of the equation rl = 2. Wait, we did that earlier. So, r²(r² + h²) = 4. Let's write that as r⁴ + r²h² = 4. Hmm. Maybe we can express h² from the slant height formula. h² = l² - r². But l is 2/r from rl = 2. So, l = 2/r. Therefore, h² = (2/r)² - r² = (4/r²) - r². Then, h² = (4 - r⁴)/r². Therefore, h = √[(4 - r⁴)/r²] = √(4 - r⁴)/r. Hmm, that seems a bit complicated, but maybe we can plug that into the volume formula.Volume V = (1/3)πr²h = (1/3)πr² * [√(4 - r⁴)/r] = (1/3)πr * √(4 - r⁴). So, V = (π/3) * r * √(4 - r⁴). Hmm, this seems a bit messy. Maybe there's another way. Wait, perhaps we can express r in terms of l. Since rl = 2, then r = 2/l. Then, l = √(r² + h²). Substitute r = 2/l into that: l = √((4/l²) + h²). Then, squaring both sides: l² = 4/l² + h². Multiply both sides by l²: l⁴ = 4 + h²l². Hmm, not sure. Let me see. Maybe it's better to go back to the previous expression for V and try to find its maximum or something? Wait, no, the problem just asks for the volume given that lateral surface area is 2π. So, maybe there is a specific value here.Wait, perhaps I made a mistake earlier. Let me check again. The lateral surface area is πrl = 2π, so rl = 2. Then, l = 2/r. Then, slant height l is 2/r. The slant height is related to r and h by l² = r² + h². So, substituting l = 2/r: (2/r)² = r² + h² => 4/r² = r² + h². Therefore, h² = 4/r² - r². So, h = √(4/r² - r²). Then, the volume is (1/3)πr²h = (1/3)πr²√(4/r² - r²).Let me simplify that. Let's write the expression under the square root as (4 - r⁴)/r². So, h = √[(4 - r⁴)/r²] = √(4 - r⁴)/r. Therefore, the volume becomes (1/3)πr²*(√(4 - r⁴)/r) = (1/3)πr*√(4 - r⁴). So, V = (π/3) * r * √(4 - r⁴). Hmm, so volume is expressed in terms of r. But how do we find the value of r?Wait, maybe there is another relation that I'm missing here. The problem doesn't give any other constraints. So, is there a unique solution? Wait, the problem says "the lateral surface of a cone is the area of a semicircle with an area of 2π". So, given that the lateral surface area is 2π, we can find r and h such that this is true. However, in a cone, given only the lateral surface area, there are infinitely many cones with different r and h satisfying πrl = 2π. So, unless there's another condition, the volume isn't uniquely determined. But the problem asks for "the volume of the cone". So, maybe there's a maximum volume or something? Wait, no, the problem doesn't mention maximum. Maybe I missed something in the problem statement.Wait, let me re-read the problem: "If the lateral surface of a cone is the area of a semicircle with an area of 2π, then the volume of the cone is ____." Hmm, so perhaps there's a misinterpretation here. Maybe the lateral surface area is equal to the area of a semicircle whose area is 2π. Which is what we did. So, the lateral surface area is 2π, so πrl = 2π, leading to rl = 2. But then, how do we find volume? Unless there's a standard relation when the lateral surface is equal to the area of a semicircle. Wait, maybe the semicircle is constructed from the slant height? Wait, if the lateral surface when unfolded is a semicircle. Because the lateral surface of a cone, when flattened, is a sector of a circle. If that sector is a semicircle, then maybe the radius of the semicircle is equal to the slant height, and the length of the arc of the semicircle is equal to the circumference of the base of the cone. Hmm, maybe that's the key!Wait, that's probably the case. The problem might be saying that when you unfold the lateral surface of the cone, it forms a semicircle. So, the lateral surface area being the area of a semicircle is different from saying the lateral surface area is equal in magnitude to the area of some arbitrary semicircle. If the lateral surface, when developed (unwrapped), is a semicircle, then that gives a relation between the slant height and the circumference of the base.Let me explain. When you unwrap the lateral surface of a cone, you get a sector of a circle. The radius of that sector is the slant height l of the cone, and the arc length of the sector is equal to the circumference of the base of the cone, which is 2πr. Now, if this sector is actually a semicircle, then the angle of the sector is π radians (180 degrees), because a semicircle is a sector with angle π. The length of the arc of a semicircle with radius l is πl. But this arc length must equal the circumference of the base of the cone, which is 2πr. Therefore, πl = 2πr. Dividing both sides by π: l = 2r. So, the slant height is twice the radius of the base.Additionally, the area of the lateral surface (which is the area of the semicircle) should be equal to the lateral surface area of the cone, which is πrl. The area of the semicircle is (1/2)πl², since the radius of the semicircle is l. So, setting these equal: πrl = (1/2)πl². Dividing both sides by π: rl = (1/2)l². Then, divide both sides by l (assuming l ≠ 0): r = (1/2)l. So, that's the same as l = 2r, which is consistent with what we found before. Therefore, in this problem, since the lateral surface is a semicircle, we have l = 2r. But also, the area of the lateral surface (the semicircle) is given as 2π. The area of the semicircle is (1/2)πl² = 2π. Let's verify that. If l is the radius of the semicircle, then area is (1/2)πl² = 2π. Solving for l: (1/2)πl² = 2π → (1/2)l² = 2 → l² = 4 → l = 2. Therefore, the slant height l is 2. Then, since l = 2r, we have 2 = 2r → r = 1. So, the radius of the base of the cone is 1.Now, with r = 1 and l = 2, we can find the height h using the Pythagorean theorem: l² = r² + h² → 2² = 1² + h² → 4 = 1 + h² → h² = 3 → h = √3. Therefore, the height of the cone is √3.Now, the volume of the cone is (1/3)πr²h = (1/3)π(1)²(√3) = (π√3)/3. Simplifying, that's (π/√3) or (√3/3)π. Depending on how it's presented.Wait, but let me check again. If the lateral surface area is a semicircle with area 2π, then when we unwrap the cone, it's a semicircle with radius l (slant height), area (1/2)πl² = 2π. Solving, we get l² = 4, so l = 2. Then, the circumference of the base of the cone is equal to the arc length of the semicircle, which is πl = 2π. Wait, arc length of semicircle is πl. But the circumference of the base is 2πr. Therefore, πl = 2πr → l = 2r. Since l = 2, then 2 = 2r → r = 1. Then, h = √(l² - r²) = √(4 - 1) = √3. Therefore, volume is (1/3)πr²h = (1/3)π*1*√3 = π√3/3. So, the volume is π√3 divided by 3, which can also be written as (√3/3)π. Either form is correct, but perhaps rationalizing the denominator, it's better to write it as (π√3)/3.But let me check again the initial interpretation because initially, I thought the problem was saying that the lateral surface area is equal to 2π (the area of a semicircle), but then upon re-reading, maybe the problem is saying that the lateral surface is a semicircle. Which is a different scenario. So, key difference: if the lateral surface area is equal in value to the area of a semicircle (which is 2π), then we have πrl = 2π, leading to rl = 2. But then we need more information to find r and h. But the problem might be stating that the lateral surface, when flattened, is a semicircle. Which gives additional relations: arc length of semicircle is circumference of the base, and area of semicircle is lateral surface area. This leads to a unique solution. So, given that the problem states "the lateral surface of a cone is the area of a semicircle", maybe they mean that the lateral surface is a semicircle in shape when laid flat, not just that the area is equal. That makes more sense, and gives a unique answer.Given that, the calculations above give the volume as π√3/3. But let me check if that's the case. Let's confirm:If the lateral surface is a semicircle when unwrapped, then:1. The radius of the semicircle is the slant height l of the cone.2. The arc length of the semicircle is the circumference of the base of the cone: πl = 2πr → l = 2r.3. The area of the semicircle is (1/2)πl² = lateral surface area = πrl. Substituting l = 2r: (1/2)π(2r)² = πr(2r) → (1/2)π4r² = 2πr² → 2πr² = 2πr², which checks out.But in the problem, it says the area of the semicircle is 2π. So, (1/2)πl² = 2π → πl² = 4π → l² = 4 → l = 2. Then, since l = 2r → r = 1. Then, h = √(l² - r²) = √(4 - 1) = √3. Then, volume is (1/3)πr²h = (1/3)π*1*√3 = π√3/3. So, yes, that seems to fit.Therefore, the correct volume is π√3/3. Which is approximately 1.732π/3 ≈ 1.813.Alternatively, if I had not considered that the lateral surface is a semicircle (i.e., the development of the cone is a semicircle), but instead just that the lateral surface area is equal to 2π, then there would be infinitely many cones with different r and h satisfying πrl = 2π. But in that case, the problem wouldn't have a unique answer. However, since the problem says "the lateral surface of a cone is the area of a semicircle", it's more likely that the lateral surface, when developed, is a semicircle, leading to the unique solution above.Therefore, the answer should be π√3⁄3, which can be written as (π√3)/3 or (√3/3)π. Either form is acceptable, but in the box, it's better to rationalize the denominator if needed. But both forms are correct. Let me check if there's a simpler way.Wait, (√3)/3 is equal to 1/√3, but rationalized. So, (π√3)/3 is equivalent to π/√3. However, typically, rationalized form is preferred, so (π√3)/3 is better.Yes, so the final answer is π√3 divided by 3. Therefore, boxed, it's boxed{dfrac{sqrt{3}}{3} pi} or boxed{dfrac{pi sqrt{3}}{3}}. Both are correct, but maybe the second one is more explicit.Final AnswerThe volume of the cone is boxed{dfrac{pi sqrt{3}}{3}}.</think>Given that the lateral surface area of a cone is equal to the area of a semicircle with an area of (2pi), we need to find the volume of the cone.1. Area of the Semicircle: The area of the semicircle is given as (2pi). For a semicircle with radius (R), the area is (frac{1}{2}pi R^2). Setting this equal to (2pi), we solve for (R): [ frac{1}{2}pi R^2 = 2pi implies R^2 = 4 implies R = 2 ] The radius of the semicircle is 2.2. Lateral Surface Area of the Cone: The lateral surface area of a cone is (pi r l), where (r) is the radius of the base and (l) is the slant height. This is given to be equal to the area of the semicircle: [ pi r l = 2pi implies r l = 2 ]3. Unfolding the Lateral Surface: If the lateral surface of the cone is a semicircle when unfolded, the radius of this semicircle is the slant height (l) of the cone. The arc length of the semicircle (which is (pi l)) must equal the circumference of the base of the cone (which is (2pi r)): [ pi l = 2pi r implies l = 2r ]4. Relating (r) and (l): From the equation (r l = 2) and substituting (l = 2r): [ r (2r) = 2 implies 2r^2 = 2 implies r^2 = 1 implies r = 1 ] Then, the slant height (l = 2r = 2 times 1 = 2).5. Height of the Cone: Using the Pythagorean theorem for the cone: [ l^2 = r^2 + h^2 implies 2^2 = 1^2 + h^2 implies 4 = 1 + h^2 implies h^2 = 3 implies h = sqrt{3} ]6. Volume of the Cone: The volume (V) of the cone is given by: [ V = frac{1}{3} pi r^2 h = frac{1}{3} pi (1)^2 sqrt{3} = frac{pi sqrt{3}}{3} ]Thus, the volume of the cone is (boxed{dfrac{pi sqrt{3}}{3}}).]

🔑:Given the lateral surface area of a cone is equal to the area of a semicircle with an area of 2pi, we can express this relationship mathematically as follows:1. The area of a semicircle is given by frac{1}{2}pi r^2, where r is the radius of the semicircle. Since the area is 2pi, we set up the equation frac{1}{2}pi r^2 = 2pi. Simplifying this equation gives us r^2 = 4 and so r = 2. This radius is the slant height l of the cone.2. The circumference of the base of the cone can be found from the arc length of the semicircle, which is 2pi. Since the circumference of the cone's base is 2pi r = 2pi, we solve for r, the radius of the cone's base, to find r = 1.3. With the radius of the cone's base r = 1 and the slant height l = 2, we can now find the volume of the cone. The formula for the volume of a cone is frac{1}{3}pi r^2h, where h is the height of the cone. 4. To find the height h, we use the Pythagorean theorem in the right-angled triangle formed by the height, the radius of the base, and the slant height of the cone. That is, h^2 + 1^2 = 2^2, leading to h^2 = 3 and hence h = sqrt{3}.5. Substituting r = 1 and h = sqrt{3} into the volume formula yields the volume of the cone as frac{1}{3}pi cdot 1^2 cdot sqrt{3} = frac{sqrt{3}}{3}pi.Therefore, the volume of the cone is boxed{frac{sqrt{3}}{3}pi}.

🧠:[<think>Okay, let's see. I need to find the number of natural numbers k, where k is ≤ 485,000, such that k² - 1 is divisible by 485. Hmm. Alright, let's start breaking this down.First, the problem says k² - 1 ≡ 0 mod 485. Which means k² ≡ 1 mod 485. So, I need to find all k such that when squared, they leave a remainder of 1 when divided by 485. Then count how many such k's there are up to 485,000.Since 485 is the modulus here, maybe I should factorize 485 to see if I can use the Chinese Remainder Theorem or something. Let's see, 485 divided by 5 is 97. Right, 5 × 97 = 485. And 97 is a prime number, right? Yeah, 97 is prime. So 485 factors into 5 and 97, which are coprime. Therefore, by Chinese Remainder Theorem, solving k² ≡ 1 mod 485 is equivalent to solving k² ≡ 1 mod 5 and k² ≡ 1 mod 97 separately. Then the number of solutions modulo 485 would be the product of the number of solutions modulo 5 and modulo 97. Then, since 485,000 is a multiple of 485 (since 485,000 ÷ 485 = 1000), the total number of solutions up to 485,000 would be 1000 times the number of solutions modulo 485. Wait, is that correct?Wait, hold on. Let me clarify. If we have solutions modulo 485, then every 485 numbers, the solutions repeat. So in each block of 485 numbers, there are a certain number of solutions. Since 485,000 is exactly 1000 × 485, then the total number of solutions should be 1000 × (number of solutions modulo 485). So the key is to first find how many solutions there are to k² ≡ 1 mod 485, then multiply by 1000.So, let's work on finding the number of solutions to k² ≡ 1 mod 5 and mod 97.Starting with mod 5. The equation is k² ≡ 1 mod 5. The solutions to this are k ≡ 1 mod 5 and k ≡ -1 ≡ 4 mod 5. So there are 2 solutions modulo 5.Now for mod 97. 97 is a prime number, so we can use the fact that over a field, the equation x² ≡ 1 mod p has exactly 2 solutions: 1 and -1. So, modulo 97, the solutions are k ≡ 1 mod 97 and k ≡ -1 ≡ 96 mod 97. Thus, 2 solutions modulo 97.Therefore, by Chinese Remainder Theorem, the number of solutions modulo 485 is 2 × 2 = 4. So there are 4 solutions modulo 485. Therefore, in each block of 485 numbers, there are 4 numbers k such that k² ≡ 1 mod 485. So up to 485,000, which is 1000 blocks of 485, the total number of solutions is 4 × 1000 = 4000.Wait, but hold on. Let me verify this. Because if the modulus is 485, and the solutions repeat every 485 numbers, then in 485,000 numbers, which is exactly 1000 times 485, the number of solutions is 1000 multiplied by the number of solutions per modulus. So if there are 4 solutions per modulus, then 4 × 1000 = 4000. That seems right.But let me check if there's a mistake in the number of solutions modulo 5 and modulo 97. Let's do that.First, modulo 5: solving x² ≡ 1 mod 5. The squares modulo 5 are 0²=0, 1²=1, 2²=4, 3²=9≡4, 4²=16≡1. So yes, x² ≡1 mod 5 when x ≡1 or 4 mod 5. So two solutions. That's correct.Modulo 97: Similarly, since 97 is prime, the equation x² ≡1 mod 97. The solutions are x ≡1 and x ≡-1 mod 97, since 1²=1 and (-1)²=1, and in a field, a quadratic equation can have at most two solutions. So yes, two solutions. So modulo 97, x ≡1 or 96 mod 97.Therefore, by Chinese Remainder Theorem, the total number of solutions modulo 485 is 2 × 2 = 4. So each modulus contributes two solutions, and combining them gives four solutions. So that seems correct.So, then, 1000 blocks of 485, each block contributing 4 solutions, so total 4000. Therefore, the answer is 4000.Wait, but hold on. Let me test with a smaller number to see if the logic holds. Suppose instead of 485,000, we have 485 × 2 = 970. Then according to the logic, there should be 4 × 2 = 8 solutions. Let me check.For example, the solutions modulo 485 are four numbers: let's list them. Using Chinese Remainder Theorem:We have:Case 1: x ≡1 mod 5 and x ≡1 mod 97Case 2: x ≡1 mod 5 and x ≡96 mod 97Case 3: x ≡4 mod 5 and x ≡1 mod 97Case 4: x ≡4 mod 5 and x ≡96 mod 97Each of these gives a unique solution modulo 485. Let's compute one of them. For case 1: x ≡1 mod 5 and x ≡1 mod 97. Since 5 and 97 are coprime, the solution is x ≡1 mod 485. Similarly, case 4: x ≡4 mod 5 and x ≡96 mod 97. Let's compute that. Let me find x such that x ≡4 mod 5 and x ≡96 mod 97.Let x = 97m + 96. Then 97m + 96 ≡4 mod 5. 97 mod 5 is 2, so 2m + 96 mod 5 ≡4. 96 mod 5 is 1, so 2m + 1 ≡4 mod 5 ⇒ 2m ≡3 mod 5 ⇒ Multiply both sides by inverse of 2 mod 5, which is 3, so m ≡3×3=9≡4 mod 5. So m =5n +4. Therefore, x=97*(5n+4)+96=485n + 388 +96=485n +484. So x ≡484 mod 485. Therefore, x=484 mod 485. Similarly, other cases would give other solutions. So the four solutions are 1, 484, and two others. Let's check another case. Case 2: x ≡1 mod 5 and x≡96 mod 97.x=97m +96. Then 97m +96 ≡1 mod 5. 97m ≡2m mod 5, so 2m +96 ≡1 mod5. 96≡1 mod5, so 2m +1 ≡1 mod5 ⇒ 2m≡0 mod5 ⇒ m≡0 mod5. So m=5n. Then x=97*5n +96=485n +96. So x≡96 mod485. Similarly, case3: x≡4 mod5 and x≡1 mod97.x=97m +1. Then 97m +1≡4 mod5 ⇒ 2m +1≡4 mod5 ⇒ 2m≡3 mod5 ⇒ m≡4 mod5 (since inverse of 2 is 3, 3*3=9≡4 mod5). So m=5n +4. Then x=97*(5n+4)+1=485n +388 +1=485n +389. So x≡389 mod485.So the four solutions mod485 are 1, 96, 389, 484. Let's check these:1²=1 ⇒1-1=0 divisible by485.96²: Let's compute 96². 96²=9216. 9216-1=9215. 9215 divided by485: 485*19=9215. Yes, so 96²-1 is divisible by485.389²: Let's compute 389 mod485. 389²= (400 -11)²=160000 -8800 +121=151321. 151321 -1=151320. Divide by485: 485*312=485*(300 +12)=145500 +5820=151320. So yes, divisible.484²: 484=485-1, so (485-1)²=485² -2*485 +1. So 484² -1=485² -2*485 +1 -1=485² -2*485. Which is clearly divisible by485. So yes, 484²-1 is divisible by485.So those four numbers are indeed solutions. So modulo485, there are four solutions. Therefore, in each block of 485 numbers, there are four k's satisfying the condition.Since 485,000 is exactly 1000*485, then the total number of solutions is 4*1000=4000. Therefore, the answer is 4000.But wait, just to make sure, let's check a smaller case. Let's take modulus 5*7=35. Suppose we want numbers k where k² ≡1 mod35. Then using the same logic, solutions mod5:1,4 and mod7:1,6. So four combinations. Let's list them:x≡1 mod5 and x≡1 mod7: x≡1 mod35x≡1 mod5 and x≡6 mod7: solve x=5a+1≡6 mod7 ⇒5a≡5 mod7⇒a≡1 mod7⇒a=7b+1⇒x=35b+5+1=35b+6⇒x≡6 mod35x≡4 mod5 and x≡1 mod7: x=5a+4≡1 mod7⇒5a≡-3≡4 mod7⇒a≡4*3=12≡5 mod7 (since inverse of5 mod7 is3). So a=7b+5⇒x=35b+25+4=35b+29⇒x≡29 mod35x≡4 mod5 and x≡6 mod7: x=5a+4≡6 mod7⇒5a≡2 mod7⇒a≡2*3=6 mod7⇒a=7b+6⇒x=35b+30 +4=35b+34⇒x≡34 mod35So solutions mod35:1,6,29,34. Each squared minus1:1²-1=0, divisible by35.6²-1=35, which is 35*1.29²=841-1=840=35*24.34²=1156-1=1155=35*33.Yes, all divisible by35. So four solutions. So that logic checks out. Therefore, same for 485. So, confident that the answer is 4000.Final AnswerThe number of natural numbers ( k ) is boxed{4000}.</think>To find the number of natural numbers ( k ) not exceeding 485,000 such that ( k^2 - 1 ) is divisible by 485, we start by noting that ( k^2 equiv 1 pmod{485} ). First, factorize 485 into prime factors: ( 485 = 5 times 97 ). Using the Chinese Remainder Theorem, we solve the congruences ( k^2 equiv 1 pmod{5} ) and ( k^2 equiv 1 pmod{97} ) separately.For ( k^2 equiv 1 pmod{5} ), the solutions are ( k equiv 1 pmod{5} ) and ( k equiv 4 pmod{5} ), giving 2 solutions.For ( k^2 equiv 1 pmod{97} ), since 97 is prime, the solutions are ( k equiv 1 pmod{97} ) and ( k equiv 96 pmod{97} ), also giving 2 solutions.By the Chinese Remainder Theorem, each combination of solutions modulo 5 and 97 gives a unique solution modulo 485. Therefore, there are ( 2 times 2 = 4 ) solutions modulo 485. These solutions are 1, 96, 389, and 484 modulo 485.Since 485,000 is exactly ( 1000 times 485 ), each block of 485 numbers contains 4 solutions. Thus, the total number of solutions up to 485,000 is ( 4 times 1000 = 4000 ).The number of natural numbers ( k ) is (boxed{4000}).,<think>Okay, so I need to find how many natural numbers k, which are not more than 485000, satisfy that k² - 1 is divisible by 485. Hmm, let's start by understanding the problem step by step.First, divisibility by 485. Since 485 is a composite number, maybe I can factor it into primes to apply the Chinese Remainder Theorem or something. Let me check: 485 divided by 5 is 97. So 485 = 5 × 97. Both 5 and 97 are primes, right? 5 is prime, and 97 is also a prime number because it's not divisible by any number other than 1 and itself. So the problem reduces to finding k such that k² ≡ 1 mod 5 and k² ≡ 1 mod 97. Then, by Chinese Remainder Theorem, solutions modulo 5×97=485 will combine these.So the equation k² ≡ 1 mod 485 is equivalent to k² ≡ 1 mod 5 and k² ≡ 1 mod 97. Then, the number of solutions modulo 485 is the product of the number of solutions modulo 5 and modulo 97. Then, since we need numbers up to 485000, which is 485 × 1000, so there are 1000 blocks of 485 numbers each. So the total number of solutions would be (number of solutions modulo 485) multiplied by 1000. But I need to check if 485000 is exactly 1000×485, which it is, since 485×1000=485000. Therefore, every complete block of 485 numbers will have the same number of solutions, and since 485000 is the upper limit, there are exactly 1000 such blocks. Therefore, the total number of solutions is 1000 multiplied by the number of solutions modulo 485. So first, I need to find how many solutions exist modulo 485, which is 5×97.First, modulo 5. Let's find the solutions to k² ≡ 1 mod 5. The squares modulo 5 are 0²=0, 1²=1, 2²=4, 3²=9≡4, 4²=16≡1. So the squares modulo 5 that are congruent to 1 are k ≡1 mod 5 and k≡4 mod 5. So two solutions modulo 5.Next, modulo 97. Find the solutions to k² ≡1 mod 97. This is equivalent to (k -1)(k +1) ≡0 mod 97. Since 97 is prime, the product is 0 mod 97 iff either k ≡1 mod 97 or k ≡-1 mod 97. Therefore, the solutions are k≡1 mod 97 and k≡96 mod 97. So two solutions modulo 97 as well.Therefore, modulo 485, using Chinese Remainder Theorem, each combination of solutions mod 5 and mod 97 gives a unique solution mod 485. So there are 2×2=4 solutions modulo 485. Let me verify this. For example, if k≡1 mod 5 and k≡1 mod 97, then there is a unique solution mod 485. Similarly, 1 mod 5 and 96 mod 97; 4 mod 5 and 1 mod 97; 4 mod 5 and 96 mod 97. So indeed, 4 solutions.Therefore, in each block of 485 numbers, there are 4 numbers k such that k² -1 is divisible by 485. Then, since 485000 = 485 × 1000, the total number of such k is 4 × 1000 = 4000. But wait, hold on. Wait, let me confirm that. If there are 4 solutions modulo 485, then in each 485 consecutive numbers, there are 4 solutions. Therefore, in 485000 numbers, which is 1000 times 485, there are 4×1000=4000 solutions. But 485000 is exactly the upper limit. Wait, but does 485000 itself count? Since the problem says "natural numbers k not exceeding 485000", so k can be 485000. But we need to check if 485000 is included in the solutions. Let's compute 485000² -1. But 485000 mod 485 is 0, since 485000 is 485×1000. Therefore, 0² -1 = -1 mod 485, which is 484 mod 485. So 484 is not 0 mod 485. Therefore, 485000 is not a solution. Therefore, the numbers from 1 up to 485000 inclusive, but since 485000 is not a solution, the total number is exactly 1000 blocks of 485 numbers, each contributing 4 solutions. So 4×1000=4000.Wait, but hold on, maybe I need to check if 485000 is included. Wait, k can be 485000, but since 485000 is congruent to 0 mod 485, as above, which doesn't satisfy k² ≡1 mod 485. Therefore, 485000 is not a solution, so all solutions are in the first 485×1000 numbers, which is exactly 485000 numbers. So with 4 solutions per 485 numbers, 4×1000=4000.But wait, another way to think about it: The number of solutions to k² ≡1 mod N is 2^m, where m is the number of distinct prime factors in N, given that N is the product of distinct odd primes. Wait, but here N is 5×97, which are two distinct primes, so 2^2=4 solutions, which matches our previous calculation. So that's correct.Alternatively, if we had exponents higher than 1 in the prime factors, the number of solutions might be different. For example, if N was a power of a prime, then the number of solutions could be more. But in this case, 5 and 97 are both to the first power, so 4 solutions.Therefore, the total number of solutions up to 485×1000 is 4×1000=4000. Therefore, the answer is 4000. But let me just verify with a small example.Suppose instead of 485, we take N=15=3×5. Then how many solutions are there to k² ≡1 mod 15? Solutions modulo 3: k≡1 or 2 mod 3. Solutions modulo 5: k≡1 or 4 mod 5. Then, combining them, there are 2×2=4 solutions mod 15. Let's list them:1) k ≡1 mod 3 and 1 mod 5: k=1 mod 15.2) k≡1 mod 3 and 4 mod 5: k=4 mod 15? Wait, 4 mod 5 and 1 mod 3. Let's compute. Solve x ≡1 mod 3 and x≡4 mod 5. Let x=3a+1. Then 3a+1 ≡4 mod 5 => 3a ≡3 mod 5 => a≡1 mod 5. So x=3*(5b+1)+1=15b+4. So x≡4 mod 15.Similarly, x≡2 mod 3 and 1 mod 5. Let x=3a+2. Then 3a+2≡1 mod 5 => 3a≡-1≡4 mod5 => a≡ 4*2=8≡3 mod5. So x=3*(5b+3)+2=15b+11≡11 mod15.Lastly, x≡2 mod3 and 4 mod5. x=3a+2≡4 mod5 =>3a≡2 mod5 =>a≡4 mod5. So x=3*(5b+4)+2=15b+14≡14 mod15.Thus solutions mod15 are 1,4,11,14. So four solutions. Therefore, the same logic applies. So for N=15, numbers up to 15*1000=15000, the number of solutions is 4*1000=4000. But wait, 15*1000=15000, and in each block of 15, there are 4 solutions, so total 4000. But wait, 15*1000=15000, so numbers from 1 to 15000 inclusive. So similar to our problem here. So in that case, if we take k up to N*M, the number of solutions is (number of solutions mod N)*M. So in our problem, since N=485 and M=1000, the number is 4*1000=4000. Therefore, this seems to hold. Therefore, the answer is 4000. Therefore, I think the answer is boxed{4000}.Final Answerboxed{4000}</think>To find the number of natural numbers ( k ) not exceeding 485000 such that ( k^2 - 1 ) is divisible by 485, we start by noting that 485 factors into primes as ( 485 = 5 times 97 ). We need ( k^2 equiv 1 pmod{485} ), which translates to solving ( k^2 equiv 1 pmod{5} ) and ( k^2 equiv 1 pmod{97} ).For modulo 5, the solutions to ( k^2 equiv 1 pmod{5} ) are ( k equiv 1 pmod{5} ) and ( k equiv 4 pmod{5} ), giving 2 solutions.For modulo 97, the solutions to ( k^2 equiv 1 pmod{97} ) are ( k equiv 1 pmod{97} ) and ( k equiv 96 pmod{97} ), also giving 2 solutions.Using the Chinese Remainder Theorem, each combination of solutions modulo 5 and 97 gives a unique solution modulo 485. Therefore, there are ( 2 times 2 = 4 ) solutions modulo 485.Since 485000 is exactly ( 485 times 1000 ), we have 1000 blocks of 485 numbers each. Each block contains 4 solutions, so the total number of solutions is ( 4 times 1000 = 4000 ).Thus, the number of natural numbers ( k ) not exceeding 485000 such that ( k^2 - 1 ) is divisible by 485 is (boxed{4000}).]

🔑:Answer: 4000.Solution. By factoring the dividend and divisor, we get the condition (k-1)(k+1):(5 cdot 97). This means that one of the numbers (k+1) or (k-1) is divisible by 97. Let's consider two cases.a) (k+1): 97, i.e., k=97 p+96, p in mathrm{Z}. Then we get (97 p+95)(97 p+97):(5 cdot 97) Leftrightarrow(97 p+95)(p+1): 5. The first factor is divisible by 5 when p=5 q, q in mathrm{Z}, and the second when p=5 q+4, q in mathrm{Z}, from which we obtain that k=485 q+96, k=485 q+484, q in mathrm{Z}.b) (k-1): 97, i.e., k=97 p+1, p in mathrm{Z}. Then we get 97 p(97 p+2):(5 cdot 97) Leftrightarrow(97 p+2) p: 5. The first factor is divisible by 5 when p=5 q+4, q in mathrm{Z}, and the second when p=5 q, q in mathrm{Z}, from which we obtain that k=485 q+389, k=485 q+1, q in mathrm{Z}.Thus, the numbers that satisfy the condition of the problem are those that give remainders 96,484,389,1 when divided by 485, meaning that every 4 out of 485 consecutive numbers fit. Since 485000=485 cdot 1000, we get 4 cdot 1000=4000 numbers.