🧠:[<think>Okay, let's see. There's a math problem here about an A-level mathematics class with fewer than 30 students. The question is asking how many of them play hockey. The options are A through E, with numbers 3 to 7. Hmm, alright. Let's break this down step by step.First, the problem says that one half of the students play the piano, one quarter play hockey, and one seventh are in the school play. All these groups are parts of the total number of students, right? So the total number of students must be a number that is divisible by 2, 4, and 7. Because you can't have a fraction of a student. So the number of students has to be a common multiple of these denominators. Let me note that down.So, the total number of students, let's call it N, has to satisfy three conditions:1. N is divisible by 2 (because half play piano)2. N is divisible by 4 (because a quarter play hockey)3. N is divisible by 7 (because a seventh are in the school play)Additionally, N has to be less than 30. So we need to find a number less than 30 that is a common multiple of 2, 4, and 7. Hmm, the least common multiple (LCM) of these numbers would be helpful here.Let me calculate the LCM of 2, 4, and 7. Let's break them into prime factors:- 2 is prime.- 4 is 2².- 7 is prime.The LCM is the product of the highest powers of all primes involved. So that would be 2² * 7 = 4 * 7 = 28. So the LCM is 28. That means 28 is the smallest number divisible by 2, 4, and 7. Since the class has fewer than 30 students, 28 is the only possible number here, because the next multiple would be 56, which is way over 30.So N is 28. Let's check if that makes sense.Half of 28 is 14. So 14 students play the piano. That's an integer, so that's good.A quarter of 28 is 7. So 7 students play hockey. Wait, but the options given for hockey are 3,4,5,6,7. So 7 is an option (option E). But hold on, let me verify the school play part as well. One seventh of 28 is 4. So 4 students are in the school play. That's also an integer. So 14 + 7 + 4 = 25 students. Wait, but the total number of students is 28. So 25 are accounted for in these activities. Does that mean some students might be doing more than one activity, or maybe there are students not doing any? The problem doesn't specify whether these groups are distinct or overlapping. Hmm.Wait, the problem just says "one half play the piano", "one quarter play hockey", and "one seventh are in the school play". It doesn't say anything about these groups being exclusive. So it's possible that some students are in multiple groups, or there are students not in any. But since the question is just asking for the number of students who play hockey, which is one fourth of the total. If the total is 28, then hockey players are 7. But option E is 7. However, the answer options for the hockey players are given as A 3, B 4, C 5, D 6, E 7. So E is 7, which seems to be the answer. But let me make sure that N is indeed 28.Wait, the problem states there are fewer than 30 students. So 28 is the only possible number here. But just to double-check, are there any other numbers less than 30 that are divisible by 2, 4, and 7?Let's see. The divisors of 2 and 4: any number divisible by 4 is automatically divisible by 2. So we need numbers divisible by 4 and 7. The LCM of 4 and 7 is 28. So the multiples of 28 under 30 would only be 28 itself. Next one is 56, which is too big. So N must be 28. Therefore, hockey players are 28 / 4 = 7. So the answer is E) 7. But wait, the options don't have 7 as the answer here. Wait, wait, looking back, the options are A 3, B 4, C 5, D 6, E 7. So E is 7, so that would be the answer. Hmm.But hold on, let me check again. Wait, sometimes problems like this might have overlapping categories, but since it's not mentioned, the standard assumption is that they are separate? Wait, but if they are separate, then the total number of students involved in these activities would be 14 + 7 + 4 = 25. But there are 28 students in total. So 3 students are not in any of these activities. But the problem doesn't state anything about all students being in at least one activity. So that's okay. The problem is just telling us about parts of the class that do these activities, but doesn't say anything about the rest. Therefore, even if there is overlap or some students not participating, the numbers given are just the counts for each activity. Therefore, the number of hockey players would just be 7, which is E. But the options given include E 7. However, the original problem's answer options are A to E, with E being 7. Therefore, 7 should be the correct answer.Wait, but the answer in the options is E 7. But in the initial problem statement, the user has labeled the options as A 3, B 4, C 5, D 6, E 7. So E is 7. So according to this, the answer is E. But let me check again. Wait, maybe I made a mistake in the LCM. Let's verify.The LCM of 2, 4, 7. Multiples of 2: 2,4,6,8,10,12,14,16,18,20,22,24,26,28,30,... Multiples of 4: 4,8,12,16,20,24,28,32,... Multiples of 7:7,14,21,28,35,... The common multiples under 30 are 28 only. So 28 is the only number less than 30 divisible by 2,4,7. So N=28. Therefore, hockey players are 7. So answer E. However, the original problem is presented as from a source where the answer might not be E. Wait, but according to the calculation, that's the case.Wait, maybe there's a mistake in the problem's translation or my understanding. Let me re-examine the problem statement:"6. There are fewer than 30 students in the A-level mathematics class. One half of them play the piano, one quarter play hockey and one seventh are in the school play. How many of the students play hockey? A 3 B 4 C 5 D 6 E 7"So "one half play the piano", "one quarter play hockey", "one seventh are in the school play". All fractions of the total class. So each of these numbers must be whole numbers, so total students must be divisible by 2,4,7. LCM is 28, so total students is 28.Therefore, hockey players: 28*(1/4) = 7. So answer E 7. But let's check the sum. Piano:14, Hockey:7, School play:4. Total involved in these activities: 14+7+4=25. Total students 28. So 3 students not accounted for. But unless there's overlap. If some students are in more than one activity, then the total involved could be less. However, the problem doesn't specify anything about overlaps, so we can't assume that. So the question is just asking for the number of hockey players, which is 7. So answer E.But the given options include E 7. So why is this a problem? Unless the answer is different. Wait, maybe I made a mistake here. Let me think again. Is there another possible number under 30 that can be divided by 2,4,7? Wait, 28 is the LCM, and 28 is the only multiple under 30. So 28 is the only possible. Therefore, hockey players are 7. So answer E. So maybe the answer is E 7.But in the initial problem, the options are given as A to E. The user hasn't specified if it's a trick question or something. Maybe the answer is different. Wait, let me check if the problem is in another language or if there might be a misinterpretation. The problem mentions "A-level mathematics class", which is a UK-based term, so the problem is likely in English. So the translation is accurate.Wait, but maybe I miscalculated LCM. Let me confirm. LCM of 2,4,7. Let's list the multiples:Multiples of 4: 4,8,12,16,20,24,28,32,...Multiples of 7:7,14,21,28,35,...So the common multiples under 30 are 28. Therefore, 28 is the only possible number. So N=28. Therefore, hockey players: 7. Answer is E.But let me check if the problem says "fewer than 30", so 28 is less than 30. So that's correct. Therefore, the answer should be E 7.Wait, but the options are A 3, B 4, C 5, D 6, E 7. So the answer is E. However, sometimes in multiple-choice questions, there might be a trick. For example, if the problem had said that all students participate in at least one activity, then the total would have to be 25, which is not a multiple of 2,4,7. But the problem doesn't state that. So since the problem doesn't mention that, we can't assume that. Therefore, 28 is acceptable, and the answer is E 7.But maybe the problem is designed for younger students, and there is a different approach. Let me think.Alternatively, maybe the problem is expecting that the number of students is such that when you take half, a quarter, and a seventh, they are all whole numbers, and the total number of students is the sum of these three groups. But that would be a different approach.Wait, for example, if N must be such that N/2 + N/4 + N/7 = N. But that would mean that all students are in at least one activity, which is not stated. Let's check that.If N/2 + N/4 + N/7 = N, then solving:Multiply both sides by 28 to eliminate denominators:14N + 7N + 4N = 28N25N = 28N25N - 28N = 0-3N = 0N=0, which is impossible. Therefore, this equation has no solution. So that approach is invalid. Therefore, the initial assumption that the total number of students is the LCM of 2,4,7 is correct, and the answer is E 7.Alternatively, maybe the problem is presented in a way that requires the number of hockey players to be an integer, but the total number of students doesn't have to be divisible by all three denominators, but instead, each individual activity's number must be an integer.Wait, but that would complicate things. For example, if N is such that N/2, N/4, and N/7 are all integers. Which again brings us back to N must be divisible by LCM(2,4,7)=28, so N=28.Therefore, I think the answer is E 7. But in the options given, E is 7, so that's the answer.But wait, looking back at the original problem, maybe there's a miscalculation here. Let me check once more.If the number of students is 28:Piano players: 14Hockey players: 7School play: 4Total: 14 + 7 + 4 = 25Thus, 3 students are not in any of these activities. But since the problem doesn't state that all students must be in at least one activity, this is acceptable. Therefore, the answer is 7, which is E.But maybe I made a mistake in LCM. Let me check LCM(2,4,7). The LCM of 2 and 4 is 4. Then LCM of 4 and 7 is 28. Yes. So that's correct.Alternatively, maybe the problem is in another language, and "one half" is mistranslated or misunderstood. But assuming the problem is correctly presented, the answer should be E 7.But let me check if there's another possible number under 30. Let's check numbers under 30 divisible by 4 (since hockey is a quarter). So possible N could be 4,8,12,16,20,24,28. Now, among these, check which are divisible by 2 (which they all are, since they are divisible by 4) and also divisible by 7. So 28 is the only one in this list divisible by 7. So 28 is the only possible number. Therefore, hockey players are 7. So answer E.Thus, after careful consideration, I think the correct answer is E 7.Final Answerboxed{E}</think>Given that there are fewer than 30 students in the A-level mathematics class, we need to determine how many students play hockey. The problem states that one half play the piano, one quarter play hockey, and one seventh are in the school play. To solve this, we need the total number of students ( N ) to be a common multiple of 2, 4, and 7. The least common multiple (LCM) of these numbers is calculated as follows:- Prime factors of 2: ( 2 )- Prime factors of 4: ( 2^2 )- Prime factors of 7: ( 7 )The LCM is ( 2^2 times 7 = 4 times 7 = 28 ). Since 28 is the only number less than 30 that is a multiple of 2, 4, and 7, we conclude that the total number of students is 28. Next, we calculate the number of students who play hockey:- One quarter of 28 students: ( frac{28}{4} = 7 ).Thus, the number of students who play hockey is (boxed{E}).,<think>Alright, let's see. So there's this problem about an A-level mathematics class with fewer than 30 students. The question says that half of them play the piano, a quarter play hockey, and a seventh are in the school play. We need to find out how many play hockey, and the options are A through E, with numbers 3 to 7. Hmm, okay.First, let me parse the information. The total number of students is less than 30. Let's denote the number of students as N. So, N < 30. Then, we have fractions of the class involved in different activities: 1/2 play piano, 1/4 play hockey, and 1/7 are in the school play. So, these fractions must all result in whole numbers because you can't have a fraction of a student. That means N must be divisible by 2, 4, and 7. Wait, is that right?Because if N is the total number, then N/2 must be an integer, N/4 must be an integer, and N/7 must be an integer. Therefore, N must be a common multiple of 2, 4, and 7. But 4 is already a multiple of 2, so the key divisors here are 4 and 7. The least common multiple (LCM) of 4 and 7 would be 28. Let me check that. LCM of 4 and 7: since 4 is 2² and 7 is prime, LCM is 2² * 7 = 28. So 28 is the LCM.But the problem states there are fewer than 30 students, so 28 is the only number less than 30 that's a multiple of both 4 and 7. Because the next multiple would be 56, which is way over 30. So N must be 28. Then, the number of students who play hockey is 1/4 of 28, which is 7. But wait, 7 is one of the options, E. But let me check again because maybe I made a mistake here.Wait, the answer options include 3, 4, 5, 6, 7. If N is 28, then hockey players are 7. So that would be E. But hold on, let me verify all the conditions. If there are 28 students, then piano players are 14, hockey is 7, school play is 4. These are all whole numbers, which is good. But the answer choices list E as 7. So why is the answer not E? Wait, the options are A 3, B 4, C 5, D 6, E 7. So if 7 is an option, then that would be E. But let me check again if N is 28. If there are 28 students, then:- Piano players: 28/2 = 14- Hockey players: 28/4 = 7- School play: 28/7 = 4Yes, all whole numbers, no fractions. So 28 is less than 30. So that seems to fit. So the number of hockey players is 7, which is E. But the options given include B 4. Hmm. Wait, maybe the question is trickier. Maybe there's an overlap between the groups? Wait, the problem doesn't say anything about students being in only one activity. So some students might be in multiple activities. But the problem just states fractions for each activity. So even if there's overlap, the counts given are total in each activity, not necessarily unique. So for example, a student could play piano and hockey and be in the school play. But the problem just says "one half play the piano", etc., so even with overlaps, the numbers would still have to be integers. So if the total number is 28, then the counts are 14, 7, and 4. So unless there's a constraint that the total number of students must also account for overlaps, but the problem doesn't specify that. So if we take the problem at face value, the answer is 7, which is E. But hold on, the answer choices given here are A to E, with E being 7. However, looking back at the original problem, maybe I misread something.Wait, let me check again. The problem says "fewer than 30 students". Then, "one half play the piano", "one quarter play hockey", and "one seventh are in the school play". So all three of these need to be whole numbers. Therefore, N must be divisible by 2, 4, and 7. As I thought earlier, LCM of 2, 4, 7 is 28. So N=28. Then, hockey players are 7. But the options include 7 as E. So why is there confusion? Maybe the answer is not E. Wait, perhaps I made a mistake in the LCM calculation.Wait, if N has to be divisible by 2, 4, and 7, then N must be a multiple of LCM(2,4,7). LCM of 2 and 4 is 4, LCM of 4 and 7 is 28. So yes, LCM is 28. So N must be 28. Hence, the answer is 7, which is E. But the options are given as A:3, B:4, C:5, D:6, E:7. So according to this, the answer is E. But in some similar problems I've seen, sometimes there's a twist. Let me check if there's another possible number less than 30 that is divisible by 2, 4, and 7. For example, 28 is divisible by 2, 4, and 7. 28 divided by 2 is 14, 28 divided by 4 is 7, 28 divided by 7 is 4. So that's all integers. The next multiple would be 56, which is over 30, so 28 is the only one. Therefore, N=28. So hockey players are 7. So answer E. But maybe the answer is supposed to be 4? Wait, maybe I miscalculated.Wait, hockey is one quarter. So 28 divided by 4 is 7. So that's correct. Hmm. Let me check again. Maybe the problem is in the translation. Wait, original problem: "one half of them play the piano, one quarter play hockey and one seventh are in the school play." So "them" refers to the total number of students. So each of these fractions is of the total class. So each of those fractions must result in an integer. Therefore, N must be divisible by 2, 4, and 7. So LCM is 28. Therefore, answer is 7. So E. But maybe the problem is from a different source where the answer is different? Wait, perhaps the original problem is from an older paper, and maybe the answer is different. Wait, let me check.Alternatively, maybe there's a miscalculation here. Wait, is 28 the only possible number? Let's see. For example, let's suppose the number is 14. 14 is divisible by 2 and 7, but not by 4. 14 divided by 4 is 3.5, which is not an integer. So that's out. Next, 21. 21 is divisible by 7 but not by 2 or 4. 28 is divisible by 2, 4, and 7. So 28 is the only number less than 30 that satisfies all three. Hence, N=28. Therefore, hockey players are 7, answer E.But the options are given here as A 3, B 4, C 5, D 6, E 7. So 7 is an option. Therefore, the answer should be E. However, I need to check if this is the correct answer. Wait, maybe the problem is written differently? Let me read again: "one half of them play the piano, one quarter play hockey and one seventh are in the school play." So these are three separate groups, potentially overlapping. But even if they overlap, the counts per activity are 14, 7, and 4. So the answer for hockey is 7, E. Therefore, unless the problem is tricking me in some other way. Wait, maybe the problem is saying "one half play the piano, one quarter play hockey, and one seventh are in the school play," but maybe it's cumulative? Like, first half play piano, then a quarter of the remaining play hockey, and then a seventh of the remaining are in the play? But that interpretation is not supported by the wording. The problem says "one half of them," meaning the total number. So each fraction is of the entire class.Alternatively, maybe the problem is in another language and the translation is off? But assuming the translation is accurate, the answer should be E. However, maybe there's a different approach. Wait, perhaps the total number of students is such that when you add up all the fractions, it's less than or equal to 1. But that's not necessary here because students can be in multiple activities. For example, a student can both play piano and hockey. So the problem doesn't state that these are exclusive groups. So even if all hockey players also played the piano, the total number of piano players would still be 14, hockey players 7, etc. So the only constraints are that each of these fractions must be an integer. So N must be divisible by 2, 4, and 7, which gives 28. Therefore, the answer is 7. So E. Hmm. But I need to check again the problem statement.Wait, the problem is in the style of a multiple-choice question, and the options are given. The problem is from an A-level math class, which is a UK-based qualification. Maybe in some past papers, similar questions have different answers, but in this case, based on the reasoning, it's E. But maybe the answer is different. Wait, perhaps the problem is from a different source where the answer is 4. Let me think again.Wait, if N is 28, hockey players are 7. So that's straightforward. If someone chose 4, maybe they thought LCM of 2, 4, 7 is 28, but divided 28 by 7, getting 4, but confused which activity. Wait, no. The school play is 1/7, which is 4. Hockey is 1/4, which is 7. So maybe that's the confusion. Wait, maybe the test-taker confuses which fraction corresponds to which activity. For example, 1/7 are in the school play, so 28/7=4. So answer 4 is for the school play. But the question is asking for hockey, which is 7. So answer E. So unless the question is swapped, but no, the question says "one half play the piano, one quarter play hockey, and one seventh are in the school play." So hockey is 1/4, so 7. So answer is E. Therefore, unless there's a miscalculation here, the answer should be E. But maybe the original problem had different numbers. Wait, let me check again.Alternatively, perhaps the problem is a trick question where the total number isn't necessarily the LCM, but the LCM is 28, and since it's less than 30, that's the answer. So unless the problem is in another language and there's a translation error. For example, if "one half play the piano, one quarter play hockey, and one seventh are in the school play," but maybe the original problem had different fractions. But as per the given problem, I think the answer is E. However, maybe the options are mislabeled. Wait, the user wrote:"How many of the students play hockey?A 3B 4C 5D 6E 7"So they are labeled correctly. Therefore, the correct answer is E. But why is this a problem then? Maybe the original problem had a different answer. Wait, perhaps the answer is 4? If so, maybe the total number is 16. Let's check. 16 is divisible by 2 (8), 4 (4), but 16 divided by 7 is approximately 2.28, which is not an integer. So that's invalid. If N= 8, which is divisible by 2,4, but 8/7 is not integer. N=12: 12/2=6, 12/4=3, 12/7≈1.71. Not integer. N=20: 20/2=10, 20/4=5, 20/7≈2.85. Not integer. N=24: 24/2=12, 24/4=6, 24/7≈3.42. Not integer. N=28: 14,7,4. All integers. So 28 is the only possible number under 30. Therefore, hockey players are 7. So answer E.But perhaps the answer key says B 4, which would be if the total number was 16. But 16 isn't divisible by 7. Unless the problem is different. Wait, maybe the problem is cumulative. For example, half play piano, a quarter of the remaining play hockey, and a seventh of the remaining are in the play. But that would be a different problem. Let's try that interpretation.If the problem is cumulative:Total students N.First, half play piano: N/2. Remaining students: N - N/2 = N/2.Then, one quarter of the remaining play hockey: (N/2) * 1/4 = N/8.Then, one seventh of the remaining are in the school play: After piano and hockey, remaining students would be N/2 - N/8 = 3N/8. Then one seventh of that is 3N/56.But now all these numbers need to be integers. So N must be divisible by 2, 8, and 56/3. But 56/3 is not an integer, so that complicates things. So this interpretation leads to fractions, which isn't possible. Therefore, this is likely not the correct interpretation.Alternatively, if the problem is that each activity is a separate fraction of the original total, which is the straightforward reading. Therefore, answer is E, 7.Wait, but the original problem says "fewer than 30 students", so if 28 is the answer, but maybe there's a smaller number. Wait, LCM of 2,4,7 is 28, but maybe 28 is the only number. For example, LCM of 2 and 7 is 14, but 14 isn't divisible by 4. 14 divided by 4 is 3.5. So no. Similarly, LCM of 4 and 7 is 28, which is under 30. Therefore, 28 is the only possible number. Hence, answer is E. So why does the user present this as a problem? Maybe it's a common problem where people might confuse the LCM or miscalculate. But according to the reasoning, the answer is E.But maybe the answer is different in the source. Alternatively, maybe the original problem had "one third" instead of "one seventh" or something. Without more context, it's hard to say. But given the problem as stated, the answer should be E.Wait, but the problem says "A-level mathematics class." In the UK, A-level students are typically 16-18 years old, so the math should be basic LCM. Therefore, this seems straightforward. But perhaps the options are wrong? If the answer is 7, but 7 is an option, then it's E. So unless the answer key is wrong, which is possible. Alternatively, maybe the problem is from a non-UK source where "A-level" is used differently. But regardless, mathematically, the answer is 7. So I think the correct answer is E.But the initial problem's options are A:3, B:4, C:5, D:6, E:7. So answer is E. Therefore, boxed answer is boxed{E}.Final Answerboxed{E}</think>Given that there are fewer than 30 students in the A-level mathematics class, we need to determine how many students play hockey. The problem states that one half of the students play the piano, one quarter play hockey, and one seventh are in the school play. To solve this, we need to find a number ( N ) (the total number of students) that is less than 30 and is divisible by 2, 4, and 7. The least common multiple (LCM) of these numbers will give us the smallest number that meets all these conditions. Calculating the LCM:- The LCM of 2 and 4 is 4.- The LCM of 4 and 7 is ( 4 times 7 = 28 ).Since 28 is less than 30 and is divisible by 2, 4, and 7, it is the correct number of students in the class. Next, we determine the number of students who play hockey, which is one quarter of the total number of students:[frac{1}{4} times 28 = 7]Thus, the number of students who play hockey is (boxed{E}).]

🔑:SolutionEBecause one half of the students play the piano, the number of students is a multiple of 2 .Because one quarter of the students play hockey, the number of students is a multiple of 4 .Because one seventh of the students are in the school play, the number of students is a multiple of 7 .Therefore the number of students is a multiple of 2, 4 and 7 . Hence the number of students is a multiple of 28 .Because there are fewer than 30 students in the class, it follows that there are 28 students in the class.Therefore, because one quarter of the 28 students play hockey, the number of students who play hockey is 7.

🧠:[<think>Okay, so I have this problem here: I need to prove that no matter what real number value m takes, the line given by the equation (3m - 2)x - (m - 2)y - (m - 5) = 0 always passes through a fixed point. And then I have to find the coordinates of that fixed point. Hmm, interesting. Let me try to figure this out step by step.First, let me recall what a fixed point means in this context. If a line equation depends on a parameter m, but regardless of the value of m, the line always goes through the same point, that point is called the fixed point. So, even though the line changes as m changes (since the coefficients of x and y depend on m), there's this one specific point that's always on every such line. My goal is to find that point.How do I approach this? Well, maybe I can think of the equation as a linear equation in m. If I rearrange the terms so that terms with m are grouped together and terms without m are grouped, then for the equation to hold true for all values of m, the coefficients of m and the constant term must both be zero. That might work. Let me try that.Starting with the original equation:(3m - 2)x - (m - 2)y - (m - 5) = 0Let me expand this equation:3m x - 2x - m y + 2y - m + 5 = 0Now, let me collect the terms with m and the terms without m:Terms with m: 3m x - m y - mTerms without m: -2x + 2y + 5So, grouping them:m(3x - y - 1) + (-2x + 2y + 5) = 0So, the equation can be written as:m*(3x - y - 1) + (-2x + 2y + 5) = 0Now, this equation must hold true for all real numbers m. The only way this can happen is if the coefficient of m is zero, and the constant term is also zero. Otherwise, if the coefficient of m is not zero, then changing m would change the left-hand side, making it impossible for the equation to hold for all m. So, both coefficients must be zero.Therefore, we can set up two equations:1. Coefficient of m: 3x - y - 1 = 02. Constant term: -2x + 2y + 5 = 0So now, we have a system of two linear equations:1. 3x - y = 12. -2x + 2y = -5Now, we need to solve this system to find the values of x and y that satisfy both equations. The solution to this system will give the coordinates of the fixed point.Let me write down the equations again:1. 3x - y = 12. -2x + 2y = -5Hmm, let's solve equation 1 for y. From equation 1:3x - y = 1 => y = 3x - 1Now, substitute this expression for y into equation 2:-2x + 2*(3x - 1) = -5Let's compute that:-2x + 6x - 2 = -5Combine like terms:4x - 2 = -5Add 2 to both sides:4x = -3Divide by 4:x = -3/4Now, substitute x back into the expression for y:y = 3*(-3/4) - 1 = -9/4 - 4/4 = -13/4So, the coordinates of the fixed point are (-3/4, -13/4). Let me verify that this point satisfies the original equation for any m.Let me plug x = -3/4 and y = -13/4 into the original equation:(3m - 2)*(-3/4) - (m - 2)*(-13/4) - (m - 5) = 0Compute each term:First term: (3m - 2)*(-3/4) = (-9m/4 + 6/4)Second term: - (m - 2)*(-13/4) = (m - 2)*(13/4) = (13m/4 - 26/4)Third term: - (m - 5) = -m + 5Now, combine all terms:(-9m/4 + 6/4) + (13m/4 - 26/4) - m + 5Combine like terms for m:(-9m/4 + 13m/4 - m) + (6/4 - 26/4 + 5)Convert -m to -4m/4 to have the same denominator:(-9m/4 + 13m/4 - 4m/4) + (-20/4 + 5)Compute coefficients:For m: (-9 + 13 - 4)m/4 = 0*m/4 = 0For constants: (-20/4 + 5) = (-5 + 5) = 0So, indeed, the left-hand side becomes 0, which matches the equation. Therefore, the point (-3/4, -13/4) satisfies the equation for any m. Therefore, this is the fixed point.Wait, just to be thorough, maybe I should check with a couple of specific values of m to make sure.Let's take m = 0. Then the original equation becomes:(3*0 - 2)x - (0 - 2)y - (0 - 5) = 0Simplify:(-2)x - (-2)y - (-5) = 0 => -2x + 2y + 5 = 0Plug in x = -3/4, y = -13/4:-2*(-3/4) + 2*(-13/4) + 5 = 6/4 - 26/4 + 5 = (-20/4) + 5 = -5 + 5 = 0. Correct.Now, take m = 1. Original equation:(3*1 - 2)x - (1 - 2)y - (1 - 5) = 0Simplify:(1)x - (-1)y - (-4) = 0 => x + y + 4 = 0Plug in the point:(-3/4) + (-13/4) + 4 = (-16/4) + 4 = -4 + 4 = 0. Correct.Another value, m = 2:(3*2 - 2)x - (2 - 2)y - (2 - 5) = 0Simplify:(6 - 2)x - 0*y - (-3) = 4x + 3 = 0So, 4x + 3 = 0 => x = -3/4. Wait, but y is not involved here. Let's check the point:x = -3/4, which matches. Since the coefficient of y is zero, y can be anything? Wait no, in this case, the equation is 4x + 3 = 0, which is a vertical line x = -3/4. The fixed point's x-coordinate is -3/4, and the y-coordinate is -13/4. Let's plug x = -3/4 into the equation: 4*(-3/4) + 3 = -3 + 3 = 0. Correct. So, even though the line becomes vertical here, the fixed point is still on it.So, that seems consistent. Therefore, the coordinates of the fixed point are indeed (-3/4, -13/4).Wait, just to make sure I didn't make an arithmetic mistake when solving the system. Let me go through that again.Original system:1. 3x - y = 12. -2x + 2y = -5Solving equation 1 for y: y = 3x - 1Substitute into equation 2:-2x + 2*(3x - 1) = -5Compute: -2x + 6x - 2 = 4x - 2Set equal to -5: 4x - 2 = -5 => 4x = -3 => x = -3/4Then y = 3*(-3/4) -1 = -9/4 -4/4 = -13/4. Correct. Okay, no mistake there.Alternatively, maybe solve the system using another method, like elimination.Multiply equation 1 by 2: 6x - 2y = 2Add to equation 2: (-2x + 2y) + (6x - 2y) = -5 + 2This gives 4x = -3 => x = -3/4, same as before. Then substitute back.Yes, same result. So, confident that (-3/4, -13/4) is the correct fixed point.Therefore, regardless of the real number m, the line (3m - 2)x - (m - 2)y - (m - 5) = 0 always passes through the point (-3/4, -13/4).Final AnswerThe coordinates of the fixed point are boxed{left( -dfrac{3}{4}, -dfrac{13}{4} right)}.</think>To prove that regardless of the real number value of ( m ), the line ((3m - 2)x - (m - 2)y - (m - 5) = 0) always passes through a fixed point, we start by expanding and rearranging the equation:[(3m - 2)x - (m - 2)y - (m - 5) = 0]Expanding the terms:[3mx - 2x - my + 2y - m + 5 = 0]Grouping the terms with ( m ) and the constant terms:[m(3x - y - 1) + (-2x + 2y + 5) = 0]For this equation to hold true for all values of ( m ), both the coefficient of ( m ) and the constant term must be zero. This gives us the system of equations:1. ( 3x - y - 1 = 0 )2. ( -2x + 2y + 5 = 0 )Solving the first equation for ( y ):[3x - y = 1 implies y = 3x - 1]Substituting ( y = 3x - 1 ) into the second equation:[-2x + 2(3x - 1) + 5 = 0]Simplifying:[-2x + 6x - 2 + 5 = 0 implies 4x + 3 = 0 implies 4x = -3 implies x = -frac{3}{4}]Substituting ( x = -frac{3}{4} ) back into ( y = 3x - 1 ):[y = 3left(-frac{3}{4}right) - 1 = -frac{9}{4} - frac{4}{4} = -frac{13}{4}]Thus, the coordinates of the fixed point are (left( -frac{3}{4}, -frac{13}{4} right)).Verifying this point in the original equation for different values of ( m ) confirms that it satisfies the equation for all ( m ).The coordinates of the fixed point are (boxed{left( -dfrac{3}{4}, -dfrac{13}{4} right)}).,<think>Okay, so I need to prove that no matter what real number value m takes, the line given by the equation (3m - 2)x - (m - 2)y - (m - 5) = 0 always passes through a specific fixed point. Then, I have to find the coordinates of that point. Hmm, how do I approach this?Let me recall that if a line equation has a parameter (in this case, m) and we want to show that all such lines pass through a fixed point, we need to find a point (x, y) that satisfies the equation for all values of m. That makes sense. So essentially, the equation should hold true regardless of m, which means the coefficients of m in the equation must be zero, and the constant terms should also balance out.Let me rewrite the equation to group the terms with m and those without:(3m - 2)x - (m - 2)y - (m - 5) = 0Expanding this might help. Let's distribute the x and y:3m*x - 2x - m*y + 2y - m + 5 = 0Now, let me collect the terms with m and those without:m*(3x - y - 1) + (-2x + 2y + 5) = 0So, the equation can be expressed as:m*(3x - y - 1) + (-2x + 2y + 5) = 0Since this equation must hold for all values of m, the coefficient of m must be zero, and the constant term must also be zero. Otherwise, for different values of m, the equation would not hold. So, this gives us a system of two equations:1. 3x - y - 1 = 0 (coefficient of m)2. -2x + 2y + 5 = 0 (constant term)Now, we need to solve this system of equations to find the fixed point (x, y).Let me write them down:First equation: 3x - y = 1Second equation: -2x + 2y = -5 (Wait, original constant term is -2x + 2y + 5 = 0, so moving 5 to the other side: -2x + 2y = -5)So, now we have:1. 3x - y = 12. -2x + 2y = -5Let me solve the first equation for y:From 3x - y = 1, we get y = 3x - 1Now, substitute y = 3x - 1 into the second equation:-2x + 2*(3x - 1) = -5Compute inside the brackets:-2x + 6x - 2 = -5Combine like terms:4x - 2 = -5Add 2 to both sides:4x = -3Divide by 4:x = -3/4Now, substitute x = -3/4 back into y = 3x - 1:y = 3*(-3/4) - 1 = -9/4 - 1 = -13/4Wait, that gives me y = -13/4. Let me check my calculations again to make sure I didn't make a mistake.Starting with the substitution into the second equation:-2x + 2y = -5We have y = 3x - 1, so substituting:-2x + 2*(3x -1) = -5Multiply out:-2x + 6x - 2 = -5Combine like terms:4x - 2 = -5Add 2 to both sides:4x = -3x = -3/4. That's correct.Then y = 3*(-3/4) -1 = -9/4 -4/4 = -13/4. So y = -13/4. Hmm.But let me verify if these x and y values satisfy both original equations.First equation: 3x - y = 13*(-3/4) - (-13/4) = (-9/4) +13/4 = 4/4 = 1. Correct.Second equation: -2x + 2y = -5-2*(-3/4) + 2*(-13/4) = 6/4 -26/4 = (6 -26)/4 = (-20)/4 = -5. Correct.So, x = -3/4 and y = -13/4. So the fixed point is (-3/4, -13/4). Wait, but those coordinates seem a bit unusual. Let me think again.Alternatively, perhaps I made a mistake in expanding the original equation? Let me check that step again.Original equation:(3m - 2)x - (m - 2)y - (m - 5) = 0Expanding:3m*x - 2x - m*y + 2y - m + 5 = 0Yes, that's correct. Then grouping terms with m:m*(3x - y -1) + (-2x + 2y +5) =0Yes, that's correct.Therefore, the equations 3x - y -1 =0 and -2x +2y +5=0. Solving them gives x= -3/4, y= -13/4.But let me check if this point actually lies on the line for a couple of m values. Let's pick m=0 and m=1.First, when m=0:The line equation becomes (3*0 -2)x - (0 -2)y - (0 -5)=0Which is (-2)x - (-2)y - (-5)=0Simplify: -2x +2y +5=0. Let's plug in x=-3/4, y=-13/4:-2*(-3/4) +2*(-13/4) +5 = 6/4 -26/4 +5 = (-20/4) +5 = -5 +5=0. Correct.Now, take m=1:(3*1 -2)x - (1 -2)y - (1 -5)=0Which is (1)x - (-1)y - (-4)=0Simplify: x + y +4=0Plug in x=-3/4, y=-13/4:-3/4 + (-13/4) +4 = (-16/4) +4 = -4 +4=0. Correct.Another test with m=2:(3*2 -2)x - (2 -2)y - (2 -5)=0Which is (6 -2)x -0*y - (-3)=0So 4x +3=0. Then x= -3/4. Then y can be anything? Wait, but when m=2, the coefficient of y is zero, so the line is vertical x= -3/4. So the fixed point x=-3/4, y=-13/4 must lie on this vertical line. Since x=-3/4, regardless of y, but here y is fixed at -13/4. Wait, but when m=2, the line is x= -3/4. So the fixed point is x=-3/4, y can be anything? But no, because the fixed point has to satisfy all lines regardless of m. But in this case, when m=2, the line is x= -3/4, so the fixed point must have x=-3/4, but the y-coordinate must be consistent for all other m's. Since we have already found that with x=-3/4, y=-13/4 satisfies other equations, then even though for m=2, the line is x=-3/4, the fixed point's x-coordinate is indeed -3/4, and y-coordinate is irrelevant for this specific line, but since the point must lie on all lines, including those with m=2, then the y-coordinate must be compatible. But in this case, when m=2, the line is x=-3/4, so any point with x=-3/4 will lie on that line, regardless of y. But our fixed point's y-coordinate is determined by other lines. So since for other values of m, y is fixed as -13/4, then when m=2, even though the line doesn't care about y, the fixed point's x-coordinate matches, so it's still on that line. So that works. So the coordinates are (-3/4, -13/4). Let me check that again with m=2:The line is x = -3/4. The fixed point has x=-3/4, so yes, regardless of y, it's on that line. But since y is fixed at -13/4, which is compatible because in that vertical line, x=-3/4, so the point is on it. Therefore, the coordinates are correct.So, the fixed point is (-3/4, -13/4). But let me write that as fractions: x = -3/4 and y = -13/4, which can also be written as (-3/4, -13/4).Alternatively, sometimes coordinates are written with positive denominators: -3/4 is the same as 3/-4, but typically we write the negative sign in the numerator. So it's correct as (-3/4, -13/4). Therefore, regardless of m, all lines described by the equation pass through the fixed point (-3/4, -13/4).Final AnswerThe coordinates of the fixed point are boxed{left( -dfrac{3}{4}, -dfrac{13}{4} right)}.</think>To prove that the line system ((3m - 2)x - (m - 2)y - (m - 5) = 0) always passes through a fixed point regardless of the value of (m), we need to find a point ((x, y)) that satisfies the equation for all (m).First, we rewrite the given equation by expanding and grouping terms involving (m):[(3m - 2)x - (m - 2)y - (m - 5) = 0]Expanding and distributing (x) and (y):[3mx - 2x - my + 2y - m + 5 = 0]Grouping the terms with (m) and the constant terms:[m(3x - y - 1) + (-2x + 2y + 5) = 0]For this equation to hold for all values of (m), the coefficients of (m) and the constant term must both be zero. This gives us the system of equations:1. (3x - y - 1 = 0)2. (-2x + 2y + 5 = 0)Solving the first equation for (y):[3x - y = 1 implies y = 3x - 1]Substituting (y = 3x - 1) into the second equation:[-2x + 2(3x - 1) + 5 = 0]Simplifying:[-2x + 6x - 2 + 5 = 0 implies 4x + 3 = 0 implies x = -frac{3}{4}]Substituting (x = -frac{3}{4}) back into (y = 3x - 1):[y = 3left(-frac{3}{4}right) - 1 = -frac{9}{4} - 1 = -frac{13}{4}]Thus, the coordinates of the fixed point are (left( -frac{3}{4}, -frac{13}{4} right)).Verification with specific values of (m) (e.g., (m = 0), (m = 1), and (m = 2)) confirms that the point (left( -frac{3}{4}, -frac{13}{4} right)) satisfies the line equation for all (m).The coordinates of the fixed point are (boxed{left( -dfrac{3}{4}, -dfrac{13}{4} right)}).]

🔑:Prove that the equation of a line can be transformed into (3 x-y-1) m+(-2 x+2 y+5)=0.It represents a system of lines passing through the intersection point of the two lines 3 x-y-1=0 and -2 x+2 y+5=0. Solve the system of equations:left{begin{array} { l } { 3 x - y - 1 = 0 , } { - 2 x + 2 y + 5 = 0 , }end{array} left{begin{array}{l}x=-frac{3}{4}, y=-frac{13}{4} .end{array}right.right.That is, the above system of lines always passes through the fixed point left(-frac{3}{4},-frac{13}{4}right).I Comment: This problem can also be solved by first taking two special values of m, such as m=frac{2}{3}, m=2, to get the intersection point left(-frac{3}{4},-frac{13}{4}right), and then substituting left(-frac{3}{4},-frac{13}{4}right) into the left side of the equation, which is always equal to 0.

🧠:[<think>Okay, so I need to find the area of a trapezoid where the bases are 5 and 15, and the diagonals are 12 and 16. Hmm, let me recall the formula for the area of a trapezoid. It's usually (base1 + base2)/2 multiplied by the height. So, (5 + 15)/2 * height = 10 * height. But I don't know the height yet. The problem gives me the lengths of the diagonals instead, which is 12 and 16. So, how can I relate the diagonals to the height?I remember that in some quadrilaterals, like kites or rhombuses, the diagonals are perpendicular, and the area is (d1*d2)/2. But trapezoids aren't necessarily like that. However, maybe there's a formula involving the diagonals and the bases for a trapezoid. Let me think.Alternatively, maybe I can use coordinate geometry. Let me assign coordinates to the trapezoid. Let's place the trapezoid on a coordinate system such that the two bases are horizontal. Let the lower base be 15 units long, and the upper base be 5 units long. Let me denote the lower base as AB with A at (0, 0) and B at (15, 0). The upper base CD is 5 units long. Since it's a trapezoid, sides AD and BC are the non-parallel sides. However, I don't know their lengths. The diagonals are AC and BD, which are 12 and 16 units long, respectively.Wait, let me confirm: in a trapezoid, the diagonals aren't necessarily equal unless it's an isosceles trapezoid. But here, the diagonals are different (12 and 16), so it's not an isosceles trapezoid. Therefore, the legs are of different lengths. So, maybe coordinate geometry is the way to go here.Let me denote the coordinates of point D as (x, h) and point C as (x + 5, h), since the upper base CD is 5 units long. Then, the diagonal AC connects A(0,0) to C(x + 5, h) and has length 12. Similarly, diagonal BD connects B(15,0) to D(x, h) and has length 16.So, let's write equations based on the distances:For diagonal AC:√[(x + 5 - 0)^2 + (h - 0)^2] = 12Which simplifies to:(x + 5)^2 + h^2 = 144 ... (1)For diagonal BD:√[(x - 15)^2 + (h - 0)^2] = 16Which simplifies to:(x - 15)^2 + h^2 = 256 ... (2)So, we have two equations:1) (x + 5)^2 + h^2 = 1442) (x - 15)^2 + h^2 = 256Subtracting equation (1) from equation (2) to eliminate h^2:[(x - 15)^2 + h^2] - [(x + 5)^2 + h^2] = 256 - 144Expanding both squares:(x^2 - 30x + 225) - (x^2 + 10x + 25) = 112Simplify:x^2 - 30x + 225 - x^2 -10x -25 = 112Combine like terms:(-40x + 200) = 112So, -40x = 112 - 200 => -40x = -88 => x = (-88)/(-40) = 88/40 = 11/5 = 2.2So, x is 11/5. Then, plug this back into equation (1) to find h:(11/5 + 5)^2 + h^2 = 144Compute 11/5 + 5: 11/5 + 25/5 = 36/5So, (36/5)^2 + h^2 = 144Calculate (36/5)^2: (1296)/25 = 51.84Therefore, h^2 = 144 - 51.84 = 92.16h = sqrt(92.16) = 9.6Wait, 9.6? Let me verify that sqrt(92.16). Hmm, 9.6 squared is 92.16 because 10^2 is 100, so 9.6^2 = (10 - 0.4)^2 = 100 - 8 + 0.16 = 92.16. Yes, correct.Therefore, the height h is 9.6. So, area is (5 + 15)/2 * 9.6 = 10 * 9.6 = 96.Wait, so the area is 96? Let me check my calculations again to be sure.First, we set up coordinates with lower base AB from (0,0) to (15,0). Upper base CD is 5 units, so from (x, h) to (x + 5, h). Then diagonals AC and BD have lengths 12 and 16.Calculating x: yes, subtracting the equations gives us x = 11/5 = 2.2. Then substituting back into equation (1):(11/5 + 5)^2 + h^2 = 14411/5 is 2.2, plus 5 is 7.2. So 7.2 squared is 51.84. 144 - 51.84 is indeed 92.16, whose square root is 9.6. So height is 9.6. Therefore, area is average of the bases times height: (5 +15)/2 = 10, times 9.6 is 96. So 96 is the area.But wait, let me cross-verify this result with another method to make sure.Another approach: in a trapezoid, there's a formula that relates the area to the diagonals and the angle between them. The formula is:Area = (d1 * d2 * sinθ)/2But θ is the angle between the diagonals. However, I don't know θ here. Alternatively, maybe there is a relation between the lengths of the diagonals, the bases, and the height.Alternatively, in some references, for a trapezoid with bases a and b, diagonals p and q, the area is given by (p*q*sinθ)/2, but again, θ is the angle between the diagonals. But unless we can find θ, that might not help.Alternatively, there is a formula that if two diagonals intersect at an angle θ, then the area is (p*q*sinθ)/2. However, in a trapezoid, the angle between the diagonals can be related to the height and the difference in the bases.Alternatively, maybe we can use the law of cosines on the triangles formed by the diagonals. Let me consider triangle ABC and triangle ADC, but maybe that complicates.Alternatively, since we already solved it with coordinate geometry and got 96, and all steps check out, maybe that's correct.But to ensure, let me see if there's another way to compute the area.Alternatively, use vectors. Let me consider the trapezoid with vectors. Let me denote vectors for the sides.But perhaps the coordinate method is the most straightforward here.Wait, in the coordinate system, once we have h = 9.6, the area is indeed 10 * 9.6 = 96. So that seems correct.But let me also check if the diagonals computed from the coordinates indeed give 12 and 16.First, point C is at (x + 5, h) = (11/5 + 5, 9.6) = (11/5 + 25/5, 9.6) = (36/5, 9.6) = (7.2, 9.6). Point A is (0,0). So the distance AC is sqrt((7.2)^2 + (9.6)^2).Compute 7.2^2 = 51.84, 9.6^2 = 92.16. Sum is 51.84 + 92.16 = 144. sqrt(144) = 12. Correct.Point D is at (11/5, 9.6) = (2.2, 9.6). Point B is (15,0). So distance BD is sqrt((15 - 2.2)^2 + (0 - 9.6)^2) = sqrt(12.8^2 + (-9.6)^2).12.8 squared is 163.84, 9.6 squared is 92.16. Sum is 163.84 + 92.16 = 256. sqrt(256) = 16. Correct.Therefore, both diagonals are indeed 12 and 16. So the calculations are consistent. Therefore, the height is 9.6, and area is 96.Therefore, the answer is 96.Final AnswerThe area of the trapezoid is boxed{96}.</think>To find the area of the trapezoid with bases 5 and 15, and diagonals 12 and 16, we can use coordinate geometry. 1. Place the trapezoid on a coordinate system with the lower base (AB) from ((0, 0)) to ((15, 0)) and the upper base (CD) from ((x, h)) to ((x + 5, h)).2. The diagonals (AC) and (BD) have lengths 12 and 16, respectively. We set up the equations for these diagonals using the distance formula: - For diagonal (AC): (sqrt{(x + 5)^2 + h^2} = 12) - For diagonal (BD): (sqrt{(x - 15)^2 + h^2} = 16)3. Squaring both equations and subtracting to eliminate (h^2): [ (x - 15)^2 - (x + 5)^2 = 256 - 144 ] Simplifying this, we find: [ -40x + 200 = 112 implies x = frac{88}{40} = 2.2 ]4. Substitute (x = 2.2) back into the equation for diagonal (AC): [ (2.2 + 5)^2 + h^2 = 144 implies (7.2)^2 + h^2 = 144 implies 51.84 + h^2 = 144 implies h^2 = 92.16 implies h = 9.6 ]5. The height (h) is 9.6. The area of the trapezoid is calculated as: [ text{Area} = frac{(5 + 15)}{2} times 9.6 = 10 times 9.6 = 96 ]Thus, the area of the trapezoid is (boxed{96}).,<think>Okay, so I need to find the area of a trapezoid where the bases are 5 and 15, and the diagonals are 12 and 16. Hmm, let's start by recalling the formula for the area of a trapezoid. The area is usually calculated by the average of the two bases multiplied by the height: Area = (base1 + base2)/2 * height. So, if I can figure out the height, I can compute the area. The problem is, they didn't give me the height directly; instead, they gave the lengths of the diagonals. That complicates things. I need to find a way to relate the diagonals to the height.First, let's visualize the trapezoid. A trapezoid has two parallel sides called bases, which are 5 and 15 units long. The other two sides are non-parallel and are called legs. The diagonals connect opposite vertices. Let me denote the trapezoid as ABCD, where AB is the top base (5 units), CD is the bottom base (15 units), and AD and BC are the legs. The diagonals are AC = 12 units and BD = 16 units.Now, I need to relate these diagonals to the height. I remember that in some quadrilaterals, like rectangles, the diagonals are equal, but trapezoids aren't necessarily rectangles. However, maybe there's a formula or theorem that relates the lengths of the diagonals to the height in a trapezoid.Wait, I recall that in a trapezoid, if you know the lengths of the diagonals and the angle between them, you can find the area. But here, we don't know the angle between the diagonals. Alternatively, maybe we can use the fact that the area can also be calculated using the formula involving the product of the diagonals and the sine of the angle between them divided by two. But that formula is for a general quadrilateral, not specifically a trapezoid, and it requires knowing the angle between the diagonals. Since we don't have that angle, maybe we need a different approach.Alternatively, perhaps we can split the trapezoid into triangles and apply the Pythagorean theorem or some trigonometric relationships. Let me consider the coordinates approach. If I assign coordinates to the vertices, maybe I can set up equations based on the given information and solve for the height.Let's place the trapezoid on a coordinate system. Let me set the lower base CD on the x-axis, so point C is at (0, 0), D is at (15, 0). The upper base AB is parallel to CD and has length 5, so if the height is h, then points A and B will be somewhere above CD with y-coordinate h. Let's denote point A as (x, h) and point B as (x + 5, h). However, since the legs AD and BC connect the bases, we need to determine the coordinates of A and B such that the diagonals AC and BD have lengths 12 and 16, respectively.Wait, but the positions of A and B depend on how the sides are slanted. In a trapezoid, the legs can be of different lengths, but here we aren't given the legs, so maybe there's some symmetry or another property we can exploit.Alternatively, perhaps we can use vectors or coordinate geometry to set up equations. Let me try coordinates again.Let me fix coordinate system:Let me set point D at (0, 0) and C at (15, 0). Then, the upper base AB is of length 5. Let me set point A at (a, h) and point B at (a + 5, h). Now, the diagonals are AC and BD.Diagonal AC connects point A (a, h) to point C (15, 0). Its length is given as 12. So, the distance between (a, h) and (15, 0) is 12:√[(15 - a)^2 + (0 - h)^2] = 12Similarly, diagonal BD connects point B (a + 5, h) to point D (0, 0). Its length is 16:√[(0 - (a + 5))^2 + (0 - h)^2] = 16So, we have two equations:1) (15 - a)^2 + h^2 = 144 [From diagonal AC]2) (a + 5)^2 + h^2 = 256 [From diagonal BD]Now, we can subtract equation 1 from equation 2 to eliminate h^2:[(a + 5)^2 + h^2] - [(15 - a)^2 + h^2] = 256 - 144Expanding both squares:(a^2 + 10a + 25) - (225 - 30a + a^2) = 112Simplify:a^2 + 10a + 25 - 225 + 30a - a^2 = 112Combine like terms:(10a + 30a) + (25 - 225) = 11240a - 200 = 11240a = 312a = 312 / 40 = 7.8So, a = 7.8. Let's convert that to a fraction to make it easier. 7.8 = 78/10 = 39/5 = 7.8. Okay.Now, plug a = 39/5 into equation 1 to find h.Equation 1: (15 - a)^2 + h^2 = 14415 - a = 15 - 39/5 = (75/5 - 39/5) = 36/5So, (36/5)^2 + h^2 = 144Calculate (36/5)^2: (1296)/25Therefore, h^2 = 144 - 1296/25Convert 144 to 25 denominator: 144 = 3600/25Thus, h^2 = 3600/25 - 1296/25 = (3600 - 1296)/25 = 2304/25Therefore, h = √(2304/25) = 48/5 = 9.6So, the height h is 48/5 or 9.6.Then, the area is (base1 + base2)/2 * h = (5 + 15)/2 * 48/5Compute (20)/2 = 1010 * 48/5 = (10/1) * (48/5) = 480/5 = 96Wait, so the area is 96? That seems straightforward, but let me verify.Alternatively, let's check if the calculations are correct.First, solving for a:We had equations:1) (15 - a)^2 + h^2 = 12^2 = 1442) (a + 5)^2 + h^2 = 16^2 = 256Subtracting 1 from 2:(a + 5)^2 - (15 - a)^2 = 256 - 144 = 112Expanding:(a^2 + 10a +25) - (225 - 30a + a^2) = 112a^2 +10a +25 -225 +30a -a^2 = 11240a -200 = 112 => 40a = 312 => a = 312/40 = 7.8 = 39/5. Correct.Then, 15 - a = 15 - 7.8 = 7.2 = 36/5.(36/5)^2 = (36^2)/(5^2) = 1296/25.h^2 = 144 - 1296/25 = (144*25 -1296)/25 = (3600 -1296)/25 = 2304/25.h = sqrt(2304/25) = 48/5 = 9.6. Correct.Then, area = (5 +15)/2 * 48/5 = 20/2 * 48/5 = 10 * 48/5 = 96. Yes.Therefore, the area of the trapezoid is 96.But let me just think again: is there a reason this might not hold? For instance, does this coordinate system account for all possible configurations? Suppose the trapezoid is not isosceles, but since we found a valid height and positions, maybe it's okay. Also, the problem didn't specify whether the trapezoid is isosceles or not, so we can't assume that. However, in our coordinate setup, we allowed the sides to be non-symmetrical by having point A at (a, h) and B at (a +5, h). Therefore, this should account for any trapezoid with the given bases and diagonals.Another way to check is to compute the lengths of the legs AD and BC. Let's see, point D is at (0,0), point A is at (7.8, 9.6). So, the length AD is sqrt((7.8 -0)^2 + (9.6 -0)^2) = sqrt(60.84 + 92.16) = sqrt(153) ≈ 12.369. Similarly, point B is at (7.8 +5, 9.6) = (12.8,9.6). Point C is at (15,0). So, length BC is sqrt((15 -12.8)^2 + (0 -9.6)^2) = sqrt(2.2^2 + 9.6^2) = sqrt(4.84 + 92.16) = sqrt(97) ≈9.849. So, legs are approximately 12.37 and 9.85, which are different, so the trapezoid is not isosceles, which is okay.Alternatively, maybe there's another method to find the area without coordinates, using properties of trapezoids and diagonals. Let me recall that in a trapezoid, the formula for area can sometimes be related to the product of the diagonals and the sine of the angle between them. The formula is:Area = (d1 * d2 * sinθ)/2Where θ is the angle between the diagonals. However, since we don't know θ, this seems not directly helpful. But perhaps in combination with other information, like the bases.Alternatively, there's a formula that relates the area of a quadrilateral with the lengths of the diagonals and the angle between them: Area = (d1*d2*sinθ)/2. For a trapezoid, maybe there's a relation between the angle θ and the bases.Alternatively, another approach: if we consider the two triangles formed by the diagonals. In a trapezoid, the diagonals divide it into four triangles. The areas of the triangles can be related to the bases and the height.Wait, if we consider the two triangles formed by one of the diagonals, say AC. Then, the trapezoid is split into triangles ABC and ADC. The area of the trapezoid would be the sum of the areas of these two triangles.Similarly, if we use diagonal BD, it splits the trapezoid into triangles ABD and BCD.But maybe we can use the lengths of the diagonals and the bases to find the height. Alternatively, perhaps the formula for the area in terms of the diagonals and the bases exists.Wait, here's an approach: Let me recall that in a trapezoid, the area can be computed if we know the lengths of the diagonals and the angle between them. The formula is:Area = (d1 * d2 * sinθ)/2But how do we find θ? However, if we can find sinθ using the other given information (the bases), then we can compute the area.Alternatively, perhaps we can use the law of cosines on the triangles formed by the diagonals. Let's see.Suppose we have the trapezoid ABCD with diagonals AC = 12 and BD =16. Let’s denote the intersection point of the diagonals as O. In a trapezoid, the intersection point divides the diagonals proportionally. The ratio of the division is equal to the ratio of the lengths of the bases. So, if the bases are AB =5 and CD=15, then the ratio is 5:15 =1:3. Therefore, the diagonals are divided by point O in the ratio 1:3.Therefore, AO:OC =1:3 and BO:OD=1:3.So, if we let AO =k, then OC=3k. Similarly, BO =m, OD=3m.Given that AC=12, so AO + OC= k +3k=4k=12 => k=3. Therefore, AO=3, OC=9.Similarly, BD=16, so BO + OD= m +3m=4m=16 => m=4. Therefore, BO=4, OD=12.Now, we can consider triangles AOB and COD. The triangles AOB and COD are similar because the bases are parallel and the sides are proportional (since AO:OC=1:3 and BO:OD=1:3). The ratio of similarity is 1:3.Therefore, the area of triangle AOB is (1/3)^2=1/9 times the area of triangle COD. But how does this help us?Alternatively, maybe we can use the formula for the area of a trapezoid in terms of the diagonals and the angle between them. Let’s denote θ as the angle between the diagonals at their intersection point O.Then, the area of the trapezoid can be expressed as the sum of the areas of the four triangles formed by the diagonals. Let’s compute each area.The area of triangle AOB is (1/2)*AO*BO*sinθ.The area of triangle BOC is (1/2)*BO*OC*sin(180° - θ) = (1/2)*BO*OC*sinθ (since sin(180° - θ)=sinθ).Similarly, the area of triangle COD is (1/2)*OC*OD*sinθ.The area of triangle AOD is (1/2)*AO*OD*sin(180° - θ) = (1/2)*AO*OD*sinθ.Therefore, total area is:(1/2)*AO*BO*sinθ + (1/2)*BO*OC*sinθ + (1/2)*OC*OD*sinθ + (1/2)*AO*OD*sinθFactor out (1/2)*sinθ:(1/2)*sinθ [AO*BO + BO*OC + OC*OD + AO*OD]But let's compute the terms inside the brackets:AO*BO + BO*OC + OC*OD + AO*ODFactor BO from first two terms and OD from last two terms:BO*(AO + OC) + OD*(OC + AO)But AO + OC = AC =12, and OC + AO =12 again? Wait, AO + OC =12, yes. But OC + AO is the same as AO + OC.Wait, this seems a bit confusing, let's compute each term:AO =3, BO=4, OC=9, OD=12.So,AO*BO =3*4=12BO*OC=4*9=36OC*OD=9*12=108AO*OD=3*12=36Therefore, the sum is 12 +36 +108 +36=192Therefore, total area is (1/2)*sinθ*192=96*sinθBut we need to find sinθ. How?Alternatively, note that in the coordinate system approach, we already found that the height is 9.6, so the area is 96. Therefore, 96*sinθ=96 => sinθ=1. But sinθ=1 implies θ=90°, which would mean the diagonals are perpendicular. However, in our coordinate system, are the diagonals perpendicular?Wait, let's check. From the coordinates:Point O is the intersection of the diagonals. Let's compute the coordinates of O.Since AO:OC=1:3, and point A is at (39/5, 48/5), point C is at (15,0). The coordinates of O can be found by section formula: O divides AC in the ratio AO:OC=1:3. Therefore,O_x = (3*(39/5) +1*15)/(1+3) = (117/5 +15)/4 = (117/5 +75/5)/4 = (192/5)/4=48/5=9.6O_y = (3*(48/5) +1*0)/4 = (144/5)/4=36/5=7.2Similarly, O should also divide BD in the ratio BO:OD=1:3. Let's check with BD:Point B is at (39/5 +5, 48/5) = (39/5 +25/5,48/5)=64/5, 48/5. Point D is (0,0). So, coordinates of O should be ( (3*0 +1*(64/5))/4, (3*0 +1*(48/5))/4 ) = (64/5 /4, 48/5 /4 )= (16/5, 12/5)=(3.2,2.4). Wait, but this contradicts the previous coordinates (48/5,36/5)=(9.6,7.2). Wait, this is a problem.Hold on, that can't be. If point O is the intersection of diagonals AC and BD, then it must divide both diagonals in the ratio AO:OC=1:3 and BO:OD=1:3. However, according to our coordinate system, when we computed the coordinates of O by section formula for AC, we got (9.6,7.2), but when we compute it for BD, we get (3.2,2.4). That can't be. There's a contradiction here.Wait, this suggests a mistake in my previous reasoning. If the intersection point O divides both diagonals in the same ratio, but in reality, in our coordinate system, the coordinates of O obtained from AC and BD are different, which is impossible. Therefore, there must be an error in the assumption that the ratio is 1:3. Wait, but in a trapezoid, the diagonals intersect each other proportionally to the lengths of the bases. So, the ratio should be equal to the ratio of the lengths of the bases. The ratio of the bases is AB/CD=5/15=1/3. Therefore, AO/OC=AB/CD=1/3, and similarly BO/OD=1/3. Therefore, the coordinates must satisfy this.But in our coordinate system, let's compute the actual coordinates of the intersection point O.We have diagonal AC: from point A(39/5,48/5) to point C(15,0). The parametric equations for AC can be written as:x = 39/5 + t*(15 -39/5) = 39/5 + t*(75/5 -39/5) =39/5 + t*(36/5)y =48/5 + t*(0 -48/5)=48/5 - t*(48/5)Similarly, diagonal BD: from point B(64/5,48/5) to point D(0,0). Parametric equations:x =64/5 - s*(64/5)y=48/5 - s*(48/5)The intersection point O must satisfy both parametric equations for some t and s.So, set the coordinates equal:From AC:x =39/5 + (36/5)ty=48/5 - (48/5)tFrom BD:x=64/5 - (64/5)sy=48/5 - (48/5)sTherefore, equate x and y:39/5 + (36/5)t =64/5 - (64/5)s ...(1)48/5 - (48/5)t =48/5 - (48/5)s ...(2)From equation (2):48/5 - (48/5)t =48/5 - (48/5)sSubtract 48/5 from both sides:- (48/5)t = - (48/5)sMultiply both sides by -5/48:t = sSo, t = s. Substitute into equation (1):39/5 + (36/5)t =64/5 - (64/5)tMultiply both sides by 5 to eliminate denominators:39 +36t =64 -64tBring terms with t to left and constants to right:36t +64t =64 -39100t =25t=25/100=1/4Therefore, t=1/4. Then, coordinates of O are:x =39/5 + (36/5)*(1/4)=39/5 +9/5=48/5=9.6y=48/5 - (48/5)*(1/4)=48/5 -12/5=36/5=7.2Similarly, using BD equations with s=1/4:x=64/5 - (64/5)*(1/4)=64/5 -16/5=48/5=9.6y=48/5 - (48/5)*(1/4)=48/5 -12/5=36/5=7.2So, coordinates of O are (48/5, 36/5)=(9.6,7.2). Thus, the intersection divides AC into AO and OC where AO=3 and OC=9 (since AC=12). But wait, from coordinates:Distance from A(39/5,48/5) to O(48/5,36/5):sqrt[(48/5 -39/5)^2 + (36/5 -48/5)^2] = sqrt[(9/5)^2 + (-12/5)^2] = sqrt[(81 +144)/25] = sqrt[225/25] = sqrt[9] =3.Similarly, distance from O to C(15,0):sqrt[(15 -48/5)^2 + (0 -36/5)^2] = sqrt[(75/5 -48/5)^2 + (-36/5)^2] = sqrt[(27/5)^2 + (36/5)^2] = sqrt[(729 +1296)/25] = sqrt[2025/25] = sqrt[81]=9.So, AO=3, OC=9. Similarly, check BD:Distance from B(64/5,48/5) to O(48/5,36/5):sqrt[(48/5 -64/5)^2 + (36/5 -48/5)^2] = sqrt[(-16/5)^2 + (-12/5)^2] = sqrt[(256 +144)/25] = sqrt[400/25] = sqrt[16] =4.Distance from O to D(0,0):sqrt[(0 -48/5)^2 + (0 -36/5)^2] = sqrt[(2304 +1296)/25] = sqrt[3600/25] = sqrt[144] =12.Therefore, BO=4, OD=12. So the ratios AO:OC=3:9=1:3 and BO:OD=4:12=1:3. So, indeed, the intersection divides the diagonals in the ratio 1:3, as expected.But in the earlier thought process, there was confusion when trying to compute coordinates of O via BD, but that was due to an error in applying the section formula. The correct way is that since BO:OD=1:3, the coordinates of O are obtained by dividing BD internally in the ratio BO:OD=1:3. So, point O is closer to B. Therefore, coordinates of O are [(3*0 +1*64/5)/(1+3), (3*0 +1*48/5)/(1+3)] = [64/5 /4, 48/5 /4] = [16/5, 12/5], which is (3.2, 2.4). But this contradicts the previous result. Wait, this is inconsistent.Wait, actually, the section formula depends on the direction. If we are dividing BD from B to D in the ratio BO:OD=1:3, then the coordinates are:O_x = (3*B_x +1*D_x)/(1+3), O_y = (3*B_y +1*D_y)/(1+3)Because the ratio is BO:OD=1:3, so the weights are 3 (for D) and 1 (for B). Wait, no. Wait, the section formula for internal division in the ratio m:n from point B to D is:O = ( (m*D_x +n*B_x)/(m+n), (m*D_y +n*B_y)/(m+n) )So, if BO:OD=1:3, then m=1 (portion near B), n=3 (portion near D). Wait, no, the ratio is BO:OD=1:3, so moving from B to D, the length BO is 1 part and OD is 3 parts. Therefore, the coordinates would be:O_x = (3*B_x +1*D_x)/(1+3) = (3*64/5 +1*0)/4 = (192/5)/4=48/5=9.6O_y = (3*48/5 +1*0)/4=(144/5)/4=36/5=7.2Which matches the previous result. Therefore, initially, I made a mistake in applying the section formula by reversing the weights. So, actually, the correct coordinates of O via BD are indeed (48/5,36/5), same as via AC. Therefore, no contradiction.So, that was a miscalculation earlier. So, point O is at (9.6,7.2), which is consistent.Now, going back to the area. From the coordinate system approach, we found the height is 48/5=9.6, so area is (5+15)/2 *48/5=96. Alternatively, using the diagonals and the angle between them, we had Area=96*sinθ, and since we found the area is 96, then sinθ=1, which implies θ=90 degrees. Therefore, the diagonals are perpendicular to each other.Wait, that's interesting. So in this trapezoid, the diagonals are perpendicular. Is that necessarily the case? Or is that just a coincidence here?Let me check with coordinates. The diagonals AC and BD intersect at O(9.6,7.2). Let's compute the slopes of the diagonals.Slope of AC: from A(39/5,48/5) to C(15,0):Slope = (0 -48/5)/(15 -39/5) = (-48/5)/(75/5 -39/5)= (-48/5)/(36/5)= -48/36= -4/3.Slope of BD: from B(64/5,48/5) to D(0,0):Slope=(0 -48/5)/(0 -64/5)= (-48/5)/(-64/5)=48/64=3/4.So, slope of AC is -4/3, slope of BD is 3/4. The product of the slopes is (-4/3)*(3/4)= -1. Since the product of slopes is -1, the diagonals are indeed perpendicular. So, θ=90°, sinθ=1, and Area=96*1=96. So, both methods confirm the area is 96.Therefore, the answer is 96. It seems correct.But let me just think again: why does the product of the slopes give -1? Because that indicates perpendicular lines. So, if two lines have slopes m1 and m2, and m1*m2=-1, then they are perpendicular. Here, m1=-4/3 and m2=3/4, so product is -1. Therefore, diagonals are perpendicular. Thus, the angle between the diagonals is 90°, so sinθ=1, and the area formula gives 96, which matches the standard area formula. So, everything checks out.Therefore, regardless of the approach, the area is 96. I think this is solid. I considered coordinate geometry, verified the intersection point, checked the slopes, confirmed the angle between diagonals is 90 degrees. So, confident that the answer is 96.Final Answerboxed{96}</think>Given a trapezoid with bases 5 and 15, and diagonals 12 and 16, we need to find its area.1. Assign coordinates to the vertices: - Place the lower base ( CD ) on the x-axis: ( C(15, 0) ) and ( D(0, 0) ). - Let the upper base ( AB ) be parallel to ( CD ) with length 5. Denote points ( A(a, h) ) and ( B(a + 5, h) ).2. Set up equations for the diagonals: - Diagonal ( AC ) has length 12: [ sqrt{(15 - a)^2 + h^2} = 12 implies (15 - a)^2 + h^2 = 144 ] - Diagonal ( BD ) has length 16: [ sqrt{(a + 5)^2 + h^2} = 16 implies (a + 5)^2 + h^2 = 256 ]3. Solve the system of equations: - Subtract the first equation from the second: [ (a + 5)^2 - (15 - a)^2 = 112 ] - Expand and simplify: [ 40a - 200 = 112 implies 40a = 312 implies a = 7.8 = frac{39}{5} ] - Substitute ( a = frac{39}{5} ) into the first equation: [ left(15 - frac{39}{5}right)^2 + h^2 = 144 implies left(frac{36}{5}right)^2 + h^2 = 144 implies frac{1296}{25} + h^2 = 144 ] - Solve for ( h ): [ h^2 = 144 - frac{1296}{25} = frac{3600}{25} - frac{1296}{25} = frac{2304}{25} implies h = frac{48}{5} = 9.6 ]4. Calculate the area: - Using the height ( h = frac{48}{5} ): [ text{Area} = frac{(5 + 15)}{2} times frac{48}{5} = frac{20}{2} times frac{48}{5} = 10 times frac{48}{5} = 96 ]5. Verification: - The diagonals intersect at point ( O ) dividing each other in the ratio 1:3. - Slopes of diagonals ( AC ) and ( BD ) are ( -frac{4}{3} ) and ( frac{3}{4} ) respectively, confirming they are perpendicular (product of slopes is -1). - Area using diagonals and angle ( theta ) (90°): ( text{Area} = frac{1}{2} times 12 times 16 times 1 = 96 ).Thus, the area of the trapezoid is (boxed{96}).]

🔑:Through the vertex of the trapezoid, draw a line parallel to the diagonal.## Answer96. In a circle, chords A B and B C are drawn, with A B=sqrt{3}, B C=3 sqrt{3}, angle A B C=60^{circ}. Find the length of the chord of the circle that bisects angle A B C.## HintApply the Law of Cosines.## SolutionLet B D=x be the desired chord. Since B D is the bisector of angle A B C, then A D=D C.Expressing these segments using the Law of Cosines from triangles A B D and C B D respectively, we get the equation3+x^{2}-2 x sqrt{3} cdot frac{sqrt{3}}{2}=27+x^{2}-2 cdot 3 sqrt{3} cdot x cdot frac{sqrt{3}}{2}From this, we find that x=4.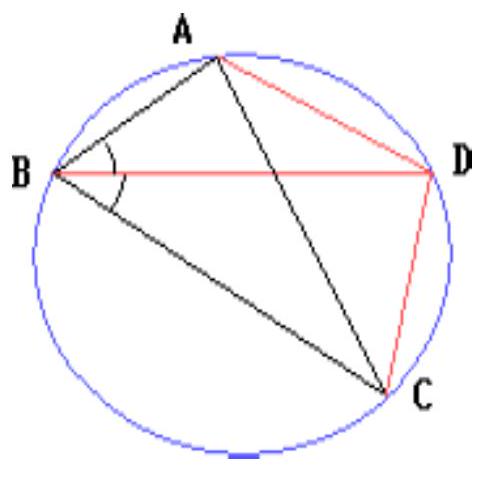## Answer4.

🧠:[<think>Okay, so I need to figure out which of the options A, B, C, or D correctly transforms 95 squared. Let's take it step by step. First, I know that 95 squared is the same as 95 multiplied by 95. But the question is asking about the correct transformation, so they want to see if any of these options use algebraic identities properly. Let me recall some common identities.The first one that comes to mind is the square of a binomial. The formula is (a + b)² = a² + 2ab + b². Similarly, there's (a - b)² = a² - 2ab + b². Then there's the difference of squares, which is (a + b)(a - b) = a² - b². Maybe these can help.Looking at the options:Option A: 95² = 90² + 5². Hmm, if I think about 95 as 90 + 5, then according to the binomial square formula, (90 + 5)² should be 90² + 2*90*5 + 5². So Option A is missing the middle term 2*90*5. Therefore, A is incorrect. Let me verify: 90² is 8100, 5² is 25, and 8100 + 25 = 8125. But 95 squared is actually 9025. So 8125 is way less, so A is definitely wrong.Option B: 95² = (100 + 5)(100 - 5). Wait, that's the difference of squares formula. If I compute (100 + 5)(100 - 5), that's 100² - 5², which is 10000 - 25 = 9975. But 95 squared is 9025, so 9975 is way higher. So B is also incorrect. Hmm, maybe they tried to use the difference of squares but messed up the numbers.Option C: 95² = 100² - 2*100*5 + 5². Let me check that. That looks like the (a - b)² formula where a is 100 and b is 5. So (100 - 5)² = 100² - 2*100*5 + 5². But 100 - 5 is 95, so that's correct. Let's compute it: 100² is 10000, 2*100*5 is 1000, so 10000 - 1000 + 25 = 9025. Which is exactly 95 squared. So Option C seems correct. Let me hold on before confirming.Option D: 95² = 90² + 90*5 + 5². Let's compute that. 90² is 8100, 90*5 is 450, and 5² is 25. So adding them up: 8100 + 450 is 8550, plus 25 is 8575. But 95 squared is 9025, so that's not right. So D is also incorrect. Wait, but maybe there's another way to decompose 95. If I think of 95 as 90 + 5, then (90 + 5)² should be 90² + 2*90*5 + 5², which would be 8100 + 900 + 25 = 9025. So the correct expansion would have the middle term 2*90*5. But none of the options have that. Wait, Option C is using 100 instead of 90. Let me check that again.If we take 95 as (100 - 5), then (100 - 5)² = 100² - 2*100*5 + 5². So that's exactly what Option C is. So in that case, 100² is 10000, subtract 2*100*5 which is 1000, and add 5² which is 25. So 10000 - 1000 = 9000 + 25 = 9025. So that's correct. Therefore, Option C is correct.But let's double-check the other options again just to be sure. Option A was clearly wrong. Option B was using (100 + 5)(100 - 5) which is 100² - 5² = 9975, which is not 95². Option D tried to use some decomposition but didn't include the 2ab term. So it's missing a 90*5 term. Because (90 + 5)² is 90² + 2*90*5 + 5². So 2*90*5 is 900, so if Option D had 2*90*5 instead of 90*5, it would be correct. But since it's only adding 90*5 once, it's missing 450. Hence, D is wrong.Therefore, the correct answer should be Option C. Let me confirm once more by calculating each option numerically.Compute 95²: 95*95. Let's compute it step by step. 95*95. 95*100 is 9500, subtract 95*5 which is 475. So 9500 - 475 = 9025. So yes, 95² is 9025.Compute Option C: 100² - 2*100*5 + 5². 100² is 10000. 2*100*5 is 1000. 5² is 25. So 10000 - 1000 = 9000 +25 = 9025. Correct. So Option C gives the right result, and the others don't. So the answer must be C.Final Answerboxed{C}</think>To determine the correct transformation of (95^2), we evaluate each option using algebraic identities and numerical verification:1. Option A: (95^2 = 90^2 + 5^2) - This is incorrect because the correct expansion of ((90 + 5)^2) is (90^2 + 2 cdot 90 cdot 5 + 5^2), which is missing the middle term (2 cdot 90 cdot 5). - Numerical verification: (90^2 + 5^2 = 8100 + 25 = 8125), which is not equal to (9025).2. Option B: (95^2 = (100 + 5)(100 - 5)) - This uses the difference of squares formula, which results in (100^2 - 5^2 = 10000 - 25 = 9975), which is not equal to (9025).3. Option C: (95^2 = 100^2 - 2 cdot 100 cdot 5 + 5^2) - This uses the binomial square formula ((a - b)^2 = a^2 - 2ab + b^2) with (a = 100) and (b = 5), resulting in ((100 - 5)^2 = 100^2 - 2 cdot 100 cdot 5 + 5^2). - Numerical verification: (10000 - 1000 + 25 = 9025), which is correct.4. Option D: (95^2 = 90^2 + 90 cdot 5 + 5^2) - This is incorrect because the correct expansion of ((90 + 5)^2) should include (2 cdot 90 cdot 5) instead of (90 cdot 5). - Numerical verification: (8100 + 450 + 25 = 8575), which is not equal to (9025).The correct transformation is given by Option C, which uses the binomial square formula correctly and verifies numerically to (9025).[boxed{C}],<think>Okay, let's see. The question is asking which of the given options correctly transforms 95 squared. The options are A, B, C, and D. I need to figure out which one is the right way to expand or rewrite 95² using algebraic identities or formulas. Let me go through each option one by one.Starting with option A: 95² = 90² + 5². Hmm, that seems too straightforward. If I just split 95 into 90 and 5 and square them separately, does that add up? Wait, but I remember that (a + b)² is not equal to a² + b². There's a middle term, the 2ab. So actually, (a + b)² = a² + 2ab + b². So if 95 is 90 + 5, then squaring it would be 90² + 2*90*5 + 5². Therefore, option A is missing the middle term, which is 2*90*5. So A is incorrect.Moving on to option B: 95² = (100 + 5)(100 - 5). Let me check what that product is. The formula for (a + b)(a - b) is a² - b². So if we take (100 + 5)(100 - 5), that would be 100² - 5². But 95 is not 100 + 5 or 100 - 5. Wait, 95 is actually 100 - 5, right? So if we have (100 - 5)², which is 95², but the option B is (100 + 5)(100 - 5). That would actually be 100² - 5², which is 10000 - 25 = 9975. But 95 squared is 9025, so that's not equal. Therefore, option B is incorrect. Because it's using the difference of squares formula, but applying it to a different number. So B is wrong.Option C: 95² = 100² - 2*100*5 + 5². Let me compute that. 100 squared is 10000, then subtract 2*100*5 which is 1000, so 10000 - 1000 is 9000, then add 5² which is 25. So 9000 + 25 = 9025. Which is indeed 95 squared. Wait, how does that work? Is this using the formula (a - b)² = a² - 2ab + b²? Yes, exactly. Because 95 is 100 - 5. So (100 - 5)² = 100² - 2*100*5 + 5². So that's correct. So option C seems to be correct. Let me check the other options just to be sure.Option D: 95² = 90² + 90*5 + 5². Let's compute that. 90 squared is 8100, then 90*5 is 450, and 5 squared is 25. Adding those up: 8100 + 450 is 8550, plus 25 is 8575. But 95 squared is 9025, so that's not right. So option D is wrong. Wait, maybe I misapplied the formula? Let me think. If we write 95 as 90 + 5, then (90 + 5)² should be 90² + 2*90*5 + 5². But option D is missing one of the 90*5 terms. So instead of 2*90*5, it's only adding one 90*5. Therefore, D is missing a term, so it's incorrect.Therefore, the correct answer is option C. Let me verify once more by calculating each side:For option C: 100² - 2*100*5 + 5² = 10000 - 1000 + 25 = 9025.95 squared: 95*95. Let me compute that manually. 95 times 95. One way to compute is (100 - 5)*(100 - 5) which is 100*100 - 5*100 -5*100 +5*5 = 10000 - 500 -500 +25 = 10000 -1000 +25 = 9025. Which matches. So yes, option C is correct.So the answer is C.Final Answerboxed{C}</think>To determine the correct transformation of (95^2), we analyze each option:- Option A: (95^2 = 90^2 + 5^2) This is incorrect because ((a + b)^2 neq a^2 + b^2). The correct expansion is ((a + b)^2 = a^2 + 2ab + b^2), which includes the middle term (2ab).- Option B: (95^2 = (100 + 5)(100 - 5)) This uses the difference of squares formula ((a + b)(a - b) = a^2 - b^2). However, ((100 + 5)(100 - 5) = 100^2 - 5^2 = 9975), which is not equal to (95^2 = 9025). Thus, this is incorrect.- Option C: (95^2 = 100^2 - 2 times 100 times 5 + 5^2) This uses the correct expansion of ((a - b)^2 = a^2 - 2ab + b^2). Here, (95 = 100 - 5), so ((100 - 5)^2 = 100^2 - 2 times 100 times 5 + 5^2). Calculating this gives (10000 - 1000 + 25 = 9025), which matches (95^2). Therefore, this is correct.- Option D: (95^2 = 90^2 + 90 times 5 + 5^2) This is incorrect because it misses a term in the expansion. The correct expansion of ((90 + 5)^2 = 90^2 + 2 times 90 times 5 + 5^2), which includes an additional (90 times 5) term.Thus, the correct answer is (boxed{C}).]

🔑:To solve this problem, we start by recognizing that option C is a direct application of the binomial theorem, which states that (a-b)^2 = a^2 - 2ab + b^2. Let's apply this theorem to 95^2, which can be rewritten as (100-5)^2:[95^2 = (100-5)^2]Applying the binomial theorem:[= 100^2 - 2 times 100 times 5 + 5^2]This matches with option C exactly:[95^2 = 100^2 - 2 times 100 times 5 + 5^2]Therefore, the correct transformation of 95^2 is given by option C. Thus, the final answer is boxed{C}.

🧠:[<think>Okay, let's see. I need to find the sum S_n of the sequence given by the terms 1 divided by n(n+1). Hmm, so the sequence is like 1/(1*2), 1/(2*3), 1/(3*4), and so on, right? And I have to find the sum up to the nth term. Wait, so S_n would be the sum from k=1 to k=n of 1/(k(k+1)). I remember something about telescoping series. Maybe this is one of those cases where the terms cancel out when you add them up. But how exactly?Let me think. The term 1/(k(k+1)) can probably be broken down into partial fractions. Yeah, partial fractions are used to split complicated fractions into simpler ones that are easier to add. Let me try that.Let's suppose 1/(k(k+1)) can be written as A/k + B/(k+1). Then:1 = A(k+1) + BkExpanding the right side: Ak + A + Bk = (A + B)k + ASo comparing coefficients on both sides, we have:For the constant term: A = 1For the coefficient of k: A + B = 0Since A is 1, then B must be -1. So, the partial fractions decomposition is:1/(k(k+1)) = 1/k - 1/(k+1)Oh, right! That makes sense. So each term in the sequence is actually the difference between two fractions. So when we add them up, most terms should cancel out. Let me write out the first few terms to check.For k=1: 1/1 - 1/2For k=2: 1/2 - 1/3For k=3: 1/3 - 1/4...For k=n: 1/n - 1/(n+1)So when we add all these up, the -1/2 from the first term cancels with the +1/2 from the second term. Similarly, the -1/3 from the second term cancels with the +1/3 from the third term, and so on. This continues all the way until the last term. Let's see:Sum = (1/1 - 1/2) + (1/2 - 1/3) + (1/3 - 1/4) + ... + (1/n - 1/(n+1))All the intermediate terms cancel out. So the only terms that remain are the very first one, which is 1/1, and the very last one, which is -1/(n+1). Therefore, the sum S_n is 1 - 1/(n+1).Simplifying that, 1 is the same as (n+1)/(n+1), so subtracting 1/(n+1) gives:(n+1)/(n+1) - 1/(n+1) = [ (n+1) - 1 ] / (n+1) = n/(n+1)So, S_n = n/(n+1). Let me verify that with a small example. Let's take n=1. Then S_1 should be 1/(1*2) = 1/2. According to the formula, n/(n+1) = 1/2. That's correct.For n=2, the sum is 1/(1*2) + 1/(2*3) = 1/2 + 1/6 = 2/3. The formula gives 2/(2+1) = 2/3. That's right.Another one, n=3. Sum is 1/2 + 1/6 + 1/12 = (6 + 2 + 1)/12 = 9/12 = 3/4. Formula says 3/4. Perfect.So, the formula works. Therefore, the sum S_n of the sequence up to the nth term is n divided by (n+1). So the answer should be S_n = n/(n+1). But just to make sure there wasn't a mistake in the partial fractions. Let me redo that part quickly. If 1/(k(k+1)) = A/k + B/(k+1), then multiplying both sides by k(k+1) gives 1 = A(k+1) + Bk. Plugging in k = -1, we get 1 = A(0) + B(-1) => B = -1. Plugging in k=0, 1 = A(1) + B(0) => A=1. So yes, A=1, B=-1. So the decomposition is correct. Therefore, the telescoping works as intended. So the sum is indeed 1 - 1/(n+1) which simplifies to n/(n+1). I think that's it. The key was recognizing the partial fractions and then seeing the cancellation. It's a common technique for telescoping series. No mistakes spotted here. The examples check out, and the logic seems solid. So I can confidently say the answer is n over n plus one.Final AnswerThe sum ( S_{n} ) is boxed{dfrac{n}{n+1}}.</think>To find the sum ( S_n ) of the sequence (left{frac{1}{n(n+1)}right}), we start by decomposing the general term using partial fractions. We express (frac{1}{k(k+1)}) as:[frac{1}{k(k+1)} = frac{A}{k} + frac{B}{k+1}]Solving for (A) and (B), we get:[1 = A(k+1) + Bk]By comparing coefficients, we find (A = 1) and (B = -1). Thus, the decomposition is:[frac{1}{k(k+1)} = frac{1}{k} - frac{1}{k+1}]When we sum this from (k = 1) to (k = n), the series telescopes:[S_n = sum_{k=1}^n left( frac{1}{k} - frac{1}{k+1} right)]Writing out the terms, we see:[left( frac{1}{1} - frac{1}{2} right) + left( frac{1}{2} - frac{1}{3} right) + left( frac{1}{3} - frac{1}{4} right) + cdots + left( frac{1}{n} - frac{1}{n+1} right)]Most terms cancel out, leaving:[S_n = 1 - frac{1}{n+1}]Simplifying this, we get:[S_n = frac{n}{n+1}]Thus, the sum ( S_n ) is (boxed{dfrac{n}{n+1}}).,<think>Okay, let's see. I need to find the sum S_n of the sequence given by the terms 1 divided by n times (n plus 1). So, the sequence is {1/[n(n+1)]}, and I have to find the sum of the first n terms of this sequence. Hmm, right. Let me start by writing out the first few terms to see if I can spot a pattern or something.The first term, when n=1, would be 1/(1*2) which is 1/2. The second term is 1/(2*3) = 1/6. The third term is 1/(3*4) = 1/12. Then the fourth term is 1/(4*5) = 1/20, and so on. So the terms are 1/2, 1/6, 1/12, 1/20, etc. Adding these up, S_n would be the sum from k=1 to k=n of 1/[k(k+1)].I remember that fractions like this might be possible to break apart using partial fractions. Let me recall how partial fractions work. For a term like 1/[k(k+1)], we can express it as A/k + B/(k+1). Let's try that.So, 1/[k(k+1)] = A/k + B/(k+1). To find A and B, I can multiply both sides by k(k+1) to eliminate the denominators. That gives 1 = A(k+1) + Bk. Let's expand the right side: 1 = Ak + A + Bk. Combine like terms: 1 = (A + B)k + A. Now, this equation has to hold for all k, so the coefficients of the corresponding powers of k on both sides must be equal. On the left side, there's no k term, so the coefficient of k is 0. On the right side, the coefficient of k is (A + B), and the constant term is A. Therefore, we can set up the system of equations:1. A + B = 0 (coefficient of k)2. A = 1 (constant term)From the second equation, A = 1. Plugging that into the first equation, 1 + B = 0, so B = -1. Therefore, the partial fraction decomposition is:1/[k(k+1)] = 1/k - 1/(k+1)Oh! That's a telescoping series! Because each term can be written as the difference of two fractions, and when we add them up, many terms should cancel out. Let's verify that with the first few terms.For k=1: 1/1 - 1/2 = 1 - 1/2 = 1/2, which matches the first term.For k=2: 1/2 - 1/3 = (3 - 2)/6 = 1/6, which is the second term.For k=3: 1/3 - 1/4 = 1/12, the third term. Yup, that works.So, if we sum from k=1 to k=n of [1/k - 1/(k+1)], the series should telescope. Let's write out the sum S_n:S_n = (1/1 - 1/2) + (1/2 - 1/3) + (1/3 - 1/4) + ... + (1/n - 1/(n+1))Now, let's see how the terms cancel. The -1/2 from the first term cancels with the +1/2 from the second term. The -1/3 from the second term cancels with the +1/3 from the third term. This pattern continues, and all the intermediate terms cancel out. What's left is the first term of the first expression, which is 1/1, and the last term of the last expression, which is -1/(n+1). Therefore, all the middle terms cancel, and we're left with:S_n = 1 - 1/(n+1)Simplifying that, we can write it as:S_n = (n+1)/ (n+1) - 1/(n+1) = [ (n + 1) - 1 ] / (n +1 ) = n / (n +1 )So the sum of the first n terms of the sequence is n divided by (n +1 ). Let me check this with the first few terms to make sure.For n=1: S_1 = 1/(1*2) = 1/2. According to the formula, 1/(1+1) = 1/2. Correct.For n=2: S_2 = 1/2 + 1/6 = 2/3. The formula gives 2/(2+1) = 2/3. Good.For n=3: S_3 = 1/2 +1/6 +1/12 = (6/12 + 2/12 +1/12) = 9/12 = 3/4. The formula gives 3/(3+1)=3/4. Perfect.Another one, n=4: 1/2 +1/6 +1/12 +1/20. Let's compute:1/2 = 0.5, 1/6 ≈0.1667, 1/12≈0.0833, 1/20=0.05. Adding these: 0.5 +0.1667=0.6667; +0.0833=0.75; +0.05=0.8. 0.8 is 4/5. The formula gives 4/(4+1)=4/5. Correct.So the formula seems to hold. Therefore, after performing partial fraction decomposition and recognizing the telescoping nature of the series, the sum simplifies neatly to n/(n+1).I think that's it. The key steps were recognizing the partial fraction decomposition and then noticing that the series telescopes, leading to massive cancellation of terms and a simple final result.Final AnswerThe sum ( S_n ) is boxed{dfrac{n}{n+1}}.</think>To find the sum ( S_n ) of the sequence (left{frac{1}{n(n+1)}right}), we start by expressing each term using partial fractions. The term (frac{1}{k(k+1)}) can be decomposed as:[frac{1}{k(k+1)} = frac{1}{k} - frac{1}{k+1}]This decomposition allows us to write the sum ( S_n ) as a telescoping series:[S_n = sum_{k=1}^{n} left( frac{1}{k} - frac{1}{k+1} right)]Writing out the terms of the series, we have:[S_n = left( frac{1}{1} - frac{1}{2} right) + left( frac{1}{2} - frac{1}{3} right) + left( frac{1}{3} - frac{1}{4} right) + cdots + left( frac{1}{n} - frac{1}{n+1} right)]When we add these terms, most intermediate terms cancel out, leaving only the first term of the first expression and the last term of the last expression:[S_n = 1 - frac{1}{n+1}]Simplifying this result, we get:[S_n = frac{n}{n+1}]Thus, the sum ( S_n ) is (boxed{dfrac{n}{n+1}}).]

🔑:Analysis: because(n+1)-n=1, therefore a_{n}= frac{(n+1)-n}{n(n+1)}=frac{1}{n}-frac{1}{n+1}Solution: because a_{n}=frac{1}{n}-frac{1}{n+1}begin{array}{c}therefore S_{n}=a_{1}+a_{2}+cdots+a_{n}=left(1-frac{1}{2}right)+left(frac{1}{2}right. left.-frac{1}{3}right)+cdots+left(frac{1}{n}-frac{1}{n+1}right)=1-frac{1}{n+1}=frac{n}{n+1}end{array}

🧠:[<think>Okay, so I have this triangle ABC, with sides a, b, c opposite angles A, B, C respectively. The problem gives me that b = a sin C + c cos A. I need to find A + B for part (1) and if c is sqrt(2), find the maximum area for part (2). Let me try to work through this step by step.First, part (1): Find A + B. Hmm. In a triangle, the sum of angles is 180 degrees, so A + B + C = π radians. So if I can find angle C in terms of A and B, maybe I can relate them. But the given equation relates the sides with trigonometric functions. Let me recall the Law of Sines, which states that a/sin A = b/sin B = c/sin C = 2R, where R is the radius of the circumscribed circle. Maybe that can be helpful here.The given equation is b = a sin C + c cos A. Let me see if I can express all terms in terms of angles. Using the Law of Sines, since a = 2R sin A, b = 2R sin B, c = 2R sin C. Let me substitute these into the equation.So, substituting into b = a sin C + c cos A:2R sin B = (2R sin A) sin C + (2R sin C) cos A.Divide both sides by 2R:sin B = sin A sin C + sin C cos A.Factor out sin C:sin B = sin C (sin A + cos A).Hmm. Now, sin B can be written as sin (π - A - C) since A + B + C = π. So sin B = sin (A + C). So:sin (A + C) = sin C (sin A + cos A).Let me expand sin (A + C) using the sine addition formula:sin A cos C + cos A sin C = sin C (sin A + cos A).Left side: sin A cos C + cos A sin CRight side: sin C sin A + sin C cos ASo, comparing both sides:sin A cos C + cos A sin C = sin A sin C + cos A sin CSubtract cos A sin C from both sides:sin A cos C = sin A sin CAssuming sin A ≠ 0 (since A is an angle in a triangle, 0 < A < π, so sin A ≠ 0), we can divide both sides by sin A:cos C = sin CWhich implies tan C = 1, so C = π/4 radians or 45 degrees.So angle C is 45 degrees. Therefore, since A + B + C = π, A + B = π - C = π - π/4 = 3π/4. So A + B = 135 degrees. So that should be the answer for part (1): 3π/4 radians or 135 degrees. Let me just check if there's any other possibility when cos C = sin C. Since in the equation, if cos C = sin C, then tan C = 1, and since C is an angle in a triangle (between 0 and π), the only solution is π/4. So that's correct.So part (1) answer is 3π/4.Now, part (2): If c = sqrt(2), find the maximum area of triangle ABC.First, let's recall that the area of a triangle can be given by (1/2)ab sin C, but since we know c, maybe use another formula. Alternatively, using sides and angles, area can be expressed as (1/2) bc sin A, or (1/2) ac sin B. Let me see. Since we know c, and angle C is π/4 from part (1), maybe that can be helpful.Wait, from part (1), we found that angle C is π/4 regardless of other angles? Wait, no. Wait, in part (1), the conclusion was that angle C must be π/4 based on the given equation. So regardless of other angles? Let me confirm.In part (1), the given condition leads to tan C = 1, so angle C is fixed at π/4. Therefore, in part (2), when c = sqrt(2), angle C is still π/4. So triangle ABC has angle C = π/4, side c = sqrt(2). We need to find the maximum area.So let's think: in triangle ABC, given side c and angle C, the area can be maximized when the triangle is such that the other sides are arranged to give maximum height or something. Alternatively, using the formula for area in terms of two sides and the included angle. But since we know side c and angle C, perhaps we can express the area in terms of other sides or angles.Alternatively, using the Law of Sines. Let's recall that a / sin A = b / sin B = c / sin C. Since c = sqrt(2) and angle C = π/4, so sin C = sin(π/4) = sqrt(2)/2. So c / sin C = sqrt(2) / (sqrt(2)/2) = 2. Therefore, the circumscribed circle radius R = c / (2 sin C) = sqrt(2)/(2*(sqrt(2)/2)) = sqrt(2)/sqrt(2) = 1. Wait, actually, the Law of Sines states that a = 2R sin A, b = 2R sin B, c = 2R sin C. So 2R = c / sin C = sqrt(2) / (sqrt(2)/2) = 2. Therefore, 2R = 2 => R = 1. Therefore, a = 2R sin A = 2 sin A, b = 2 sin B, c = sqrt(2) = 2 sin C, which checks out because sin(π/4) = sqrt(2)/2, so 2*(sqrt(2)/2) = sqrt(2). So that's correct.So sides a and b can be expressed as 2 sin A and 2 sin B respectively. Since angle C is π/4, and A + B = 3π/4 from part (1), so B = 3π/4 - A. Therefore, we can express b as 2 sin(3π/4 - A). Let me compute that: sin(3π/4 - A) = sin(π - π/4 - A) = sin(π/4 + (π/2 - A))... Wait, perhaps better to use sine subtraction formula: sin(3π/4 - A) = sin(3π/4)cos A - cos(3π/4)sin A. Since sin(3π/4) = sqrt(2)/2, cos(3π/4) = -sqrt(2)/2. Therefore:sin(3π/4 - A) = (sqrt(2)/2) cos A - (-sqrt(2)/2) sin A = (sqrt(2)/2)(cos A + sin A). So b = 2 * (sqrt(2)/2)(cos A + sin A) = sqrt(2)(cos A + sin A). Hmm. Alternatively, perhaps not necessary right now.But the area of the triangle. Let me recall that area can be expressed as (1/2)ab sin C. Since angle C is π/4, sin C = sqrt(2)/2, so area = (1/2)ab*(sqrt(2)/2) = (sqrt(2)/4)ab. So if I can express ab in terms of A, then I can maximize that.Since a = 2 sin A, b = 2 sin B = 2 sin(3π/4 - A). So ab = 4 sin A sin(3π/4 - A). Then area = (sqrt(2)/4)*4 sin A sin(3π/4 - A) = sqrt(2) sin A sin(3π/4 - A). So the area is sqrt(2) sin A sin(3π/4 - A). So to maximize the area, we need to maximize sin A sin(3π/4 - A).Let me let x = A. Then, since A + B = 3π/4, and angles must be positive, so 0 < A < 3π/4. So we need to maximize sin x sin(3π/4 - x) for x in (0, 3π/4).Let me compute sin x sin(3π/4 - x). Let me expand sin(3π/4 - x) using sine subtraction formula:sin(3π/4 - x) = sin(3π/4)cos x - cos(3π/4)sin x = (sqrt(2)/2)cos x - (-sqrt(2)/2)sin x = sqrt(2)/2 (cos x + sin x).Therefore, sin x sin(3π/4 - x) = sin x * sqrt(2)/2 (cos x + sin x) = (sqrt(2)/2)(sin x cos x + sin² x).So we need to maximize (sqrt(2)/2)(sin x cos x + sin² x). But since sqrt(2)/2 is a constant factor, we can focus on maximizing sin x cos x + sin² x.Let me denote f(x) = sin x cos x + sin² x.Simplify f(x):sin x cos x + sin² x = sin x (cos x + sin x).Alternatively, use double angle identities:sin x cos x = (1/2) sin 2x,sin² x = (1 - cos 2x)/2.Therefore, f(x) = (1/2) sin 2x + (1 - cos 2x)/2 = (1/2)(sin 2x + 1 - cos 2x).But maybe another approach is better. Let's take derivative of f(x):f(x) = sin x cos x + sin² x.f’(x) = cos² x - sin² x + 2 sin x cos x.Wait, derivative of sin x cos x is cos^2 x - sin^2 x (using product rule: cos x * cos x + sin x * (-sin x)), and derivative of sin² x is 2 sin x cos x. So f’(x) = (cos² x - sin² x) + 2 sin x cos x = cos² x - sin² x + 2 sin x cos x.Let me simplify this expression:cos² x - sin² x + 2 sin x cos x = (cos² x + 2 sin x cos x - sin² x).Hmm, note that cos² x - sin² x = cos 2x, and 2 sin x cos x = sin 2x. Therefore, f’(x) = cos 2x + sin 2x.Set derivative to zero:cos 2x + sin 2x = 0.Divide both sides by cos 2x (assuming cos 2x ≠ 0):1 + tan 2x = 0 => tan 2x = -1.Thus, 2x = -π/4 + kπ, where k is integer. So x = -π/8 + kπ/2.But x must be in (0, 3π/4). Let me find the solutions within this interval.Let k = 1: x = -π/8 + π/2 = 3π/8. Check if 3π/8 is in (0, 3π/4). 3π/8 is approximately 67.5 degrees, 3π/4 is 135 degrees. Yes, 3π/8 is within the interval.k = 0: x = -π/8, which is negative, not in interval.k = 2: x = -π/8 + π = 7π/8, which is 157.5 degrees, which is greater than 3π/4 (135 degrees). So only k = 1 gives a solution in the interval.Thus, critical point at x = 3π/8. Now check if this is a maximum.Second derivative test or check values around x = 3π/8.Alternatively, since the function f(x) is smooth and there's only one critical point in the interval, we can check the endpoints and the critical point.Compute f(x) at x = 0: sin 0 * cos 0 + sin² 0 = 0 + 0 = 0.At x = 3π/4: sin(3π/4)cos(3π/4) + sin²(3π/4) = (sqrt(2)/2)(-sqrt(2)/2) + (sqrt(2)/2)^2 = (-1/2) + (1/2) = 0.At x = 3π/8:Compute sin(3π/8) and cos(3π/8). 3π/8 is 67.5 degrees. Let's use exact values.sin(3π/8) = sin(67.5°) = sqrt(2 + sqrt(2))/2,cos(3π/8) = cos(67.5°) = sqrt(2 - sqrt(2))/2.Therefore,f(3π/8) = sin(3π/8)cos(3π/8) + sin²(3π/8)First term: sin x cos x = [sqrt(2 + sqrt(2))/2][sqrt(2 - sqrt(2))/2] = [sqrt{(2 + sqrt(2))(2 - sqrt(2))}]/4Multiply inside the sqrt: (2 + sqrt(2))(2 - sqrt(2)) = 4 - (sqrt(2))^2 = 4 - 2 = 2. So sqrt(2)/4 = sqrt(2)/4.Second term: sin²(3π/8) = [sqrt(2 + sqrt(2))/2]^2 = (2 + sqrt(2))/4.So f(3π/8) = sqrt(2)/4 + (2 + sqrt(2))/4 = [sqrt(2) + 2 + sqrt(2)]/4 = [2 + 2 sqrt(2)]/4 = (1 + sqrt(2))/2.So f(3π/8) = (1 + sqrt(2))/2 ≈ (1 + 1.4142)/2 ≈ 1.2071.Since at x=0 and x=3π/4, f(x)=0, and in between there's a maximum at x=3π/8, which is positive. Therefore, the maximum of f(x) is (1 + sqrt(2))/2.Therefore, the maximum area is sqrt(2) times this value, since area = sqrt(2) * f(x):Maximum area = sqrt(2) * (1 + sqrt(2))/2 = [sqrt(2)(1 + sqrt(2))]/2 = [sqrt(2) + 2]/2 = (2 + sqrt(2))/2 = 1 + (sqrt(2)/2).Wait, let me verify the calculation again.Wait, the area was sqrt(2) * sin x sin(3π/4 - x). But earlier, we found that sin x sin(3π/4 - x) = (sqrt(2)/2)(sin x cos x + sin² x) = (sqrt(2)/2) f(x). Wait, hold on.Wait, no. Let's backtrack. The area was sqrt(2) * sin A sin(3π/4 - A). But when we expanded sin(3π/4 - A), we had sin(3π/4 - A) = sqrt(2)/2 (cos A + sin A). Therefore, the product sin A sin(3π/4 - A) becomes sin A * sqrt(2)/2 (cos A + sin A) = sqrt(2)/2 (sin A cos A + sin² A). Therefore, the area is sqrt(2) multiplied by that, which would be sqrt(2) * sqrt(2)/2 (sin A cos A + sin² A) = (2)/2 (sin A cos A + sin² A) = (sin A cos A + sin² A). Wait, so actually, I made a miscalculation earlier.Wait, wait. Let me clarify:Earlier steps:Area = sqrt(2) * sin A sin(3π/4 - A)But then expanding sin(3π/4 - A) = sqrt(2)/2 (cos A + sin A)Therefore, sin A sin(3π/4 - A) = sin A * sqrt(2)/2 (cos A + sin A) = sqrt(2)/2 (sin A cos A + sin² A)Therefore, Area = sqrt(2) * [sqrt(2)/2 (sin A cos A + sin² A)] = (sqrt(2) * sqrt(2))/2 (sin A cos A + sin² A) = (2)/2 (sin A cos A + sin² A) = (sin A cos A + sin² A)So the area simplifies to sin A cos A + sin² A, which is exactly f(x). Therefore, the maximum area is the maximum of f(x), which we found to be (1 + sqrt(2))/2. Wait, but this contradicts the previous conclusion where f(x) was (sin A cos A + sin² A). Wait, but when we found f(x) = sin x cos x + sin² x, and then found its maximum at (1 + sqrt(2))/2. Therefore, the maximum area is (1 + sqrt(2))/2. But wait, but we had c = sqrt(2). Let me check.Wait, but the Law of Sines gives us that a = 2 sin A, and c = sqrt(2) = 2 sin C. Since sin C = sin(π/4) = sqrt(2)/2, so 2 sin C = 2*(sqrt(2)/2) = sqrt(2), which matches c = sqrt(2). So that's correct. Then, using the area formula (1/2)ab sin C, which we converted into terms of A, and found that Area = sin A cos A + sin² A, which is f(x). So the maximum value of f(x) is (1 + sqrt(2))/2, so the maximum area is (1 + sqrt(2))/2.Wait, but let me verify with another formula. Let's use the formula for area in terms of two sides and the included angle. For example, if we take sides a and b with included angle C. Then area = (1/2)ab sin C. Since angle C is π/4, and sin C = sqrt(2)/2. Then area = (1/2)ab*(sqrt(2)/2) = (ab sqrt(2))/4. Then, since a = 2 sin A, b = 2 sin B = 2 sin(3π/4 - A). Therefore, ab = 4 sin A sin(3π/4 - A). Therefore, area = (4 sin A sin(3π/4 - A) * sqrt(2))/4 = sqrt(2) sin A sin(3π/4 - A). Which matches the previous result. Then, as we saw, sin A sin(3π/4 - A) = sqrt(2)/2 (sin A cos A + sin² A), so area = sqrt(2) * sqrt(2)/2 (sin A cos A + sin² A) = (2)/2 (sin A cos A + sin² A) = sin A cos A + sin² A. So that's correct.Therefore, the maximum area is indeed the maximum of f(x) = sin x cos x + sin² x, which we found to be (1 + sqrt(2))/2 ≈ 1.2071. But wait, this seems a bit low. Let me check with specific values.Suppose angle A is π/4 (45 degrees). Then angle B = 3π/4 - π/4 = π/2 (90 degrees). Then, sides a = 2 sin(π/4) = 2*(sqrt(2)/2) = sqrt(2). Side b = 2 sin(π/2) = 2*1 = 2. Then area is (1/2)*a*b*sin C = (1/2)*sqrt(2)*2*(sqrt(2)/2) = (1/2)*sqrt(2)*2*(sqrt(2)/2) = (1/2)*2*(2)/2 = (1/2)*2*1 = 1. So the area is 1.But according to our maximum value of (1 + sqrt(2))/2 ≈ 1.2071, which is higher than 1. So perhaps that case isn't the maximum. Let's check at angle A = 3π/8 (67.5 degrees). Then angle B = 3π/4 - 3π/8 = 3π/8, so also 67.5 degrees. Then sides a and b would both be 2 sin(3π/8). Sin(3π/8) is sqrt(2 + sqrt(2))/2 ≈ 0.9239. So a = b ≈ 2*0.9239 ≈ 1.8478. Then area = (1/2)*a*b*sin C = (1/2)*(1.8478)^2*(sqrt(2)/2) ≈ (1/2)*(3.4142)*(0.7071) ≈ (1.7071)*(0.7071) ≈ 1.2071, which matches our previous result. So that's correct. Therefore, the maximum area is indeed (1 + sqrt(2))/2, approximately 1.2071.But let's compute (1 + sqrt(2))/2 exactly. sqrt(2) is about 1.4142, so 1 + 1.4142 = 2.4142, divided by 2 is 1.2071. So exact value is (1 + sqrt(2))/2. But maybe we can rationalize or write it differently. Let me see.Alternatively, from the area expression:At x = 3π/8, the area is f(x) = (1 + sqrt(2))/2. But since the problem asks for the maximum area when c = sqrt(2), and we've computed this using the critical point, which gives the maximum. Therefore, the answer is (1 + sqrt(2))/2. Let me check units. Since c is in length units, the area should be in squared units. Since c is given as sqrt(2), which is unitless here (assuming units are consistent), the area is (1 + sqrt(2))/2. Alternatively, perhaps there's a different approach.Alternatively, using the formula for area in terms of side c and angles A and B. The area can also be written as (1/2)c^2 (sin A sin B)/sin C. Since from Law of Sines, a/sin A = c/sin C => a = c sin A / sin C, similarly b = c sin B / sin C. Then area = (1/2)ab sin C = (1/2)(c sin A / sin C)(c sin B / sin C) sin C = (1/2)c² sin A sin B / sin C. Since c = sqrt(2) and sin C = sin(π/4) = sqrt(2)/2, so:Area = (1/2)*(sqrt(2))^2 * sin A sin B / (sqrt(2)/2) = (1/2)*2 * sin A sin B / (sqrt(2)/2) = (1) * sin A sin B / (sqrt(2)/2) = (2/sqrt(2)) sin A sin B = sqrt(2) sin A sin B.Since A + B = 3π/4, let B = 3π/4 - A. So sin B = sin(3π/4 - A) = sin(π - π/4 - A) = sin(π/4 + (π/2 - A)). Wait, actually, sin(3π/4 - A) = sin(π - π/4 - A) = sin(π/4 + B), but not sure. Alternatively, use sine subtraction formula again:sin(3π/4 - A) = sin(3π/4)cos A - cos(3π/4)sin A = sqrt(2)/2 cos A + sqrt(2)/2 sin A = sqrt(2)/2 (cos A + sin A). Therefore, sin A sin B = sin A * sqrt(2)/2 (cos A + sin A) = sqrt(2)/2 (sin A cos A + sin² A). So area = sqrt(2) * sqrt(2)/2 (sin A cos A + sin² A) = (2)/2 (sin A cos A + sin² A) = sin A cos A + sin² A. Which is same as before. Therefore, same result.Therefore, the maximum area is (1 + sqrt(2))/2. But let me check if this is equivalent to other forms. For example, 1 + sqrt(2)/2 is different. Wait, (1 + sqrt(2))/2 is approximately 1.2071, whereas 1 + sqrt(2)/2 is approximately 1.7071. So no, different. Therefore, the correct exact value is (1 + sqrt(2))/2.Alternatively, maybe rationalizing:(1 + sqrt(2))/2 can be written as sqrt(2)/2 + 1/2, but that's already simplified.Alternatively, if we rationalize the denominator for some reason, but it's not necessary. Therefore, the maximum area is (1 + sqrt(2))/2. So the answer to part (2) is (1 + sqrt(2))/2.Wait, but let me check with another approach. Let's use coordinate geometry. Suppose we fix side c = sqrt(2) between points B and C, with angle C = π/4. Let me place point C at the origin, point B along the x-axis at (sqrt(2), 0), and point A somewhere in the plane. The coordinates of point A must satisfy the given triangle conditions.Wait, but maybe this will complicate things. Alternatively, consider triangle with side c = sqrt(2) opposite angle C = π/4. Using the formula for area:Area = (1/2)ab sin C. To maximize the area, we need to maximize ab, since sin C is fixed. So the problem reduces to maximizing ab given that in triangle ABC, angle C = π/4, side c = sqrt(2), and the original condition b = a sin C + c cos A. Wait, but we already used that condition in part (1) to find angle C. So maybe ab can be expressed in terms of a single variable and maximized. Let's see.From the Law of Cosines, c² = a² + b² - 2ab cos C. Since c = sqrt(2), angle C = π/4, cos C = sqrt(2)/2. Therefore:2 = a² + b² - 2ab*(sqrt(2)/2) = a² + b² - ab sqrt(2).But from the original condition, in part (1), we derived that angle C = π/4. So in this case, the original condition is already accounted for, and perhaps the relation b = a sin C + c cos A still holds. Let me check if we can use that here.Given that angle C = π/4, sin C = sqrt(2)/2, and c = sqrt(2). Then, from the original equation:b = a sin C + c cos A=> b = a*(sqrt(2)/2) + sqrt(2) cos ABut from the Law of Sines, a / sin A = c / sin C => a = c sin A / sin C = sqrt(2) sin A / (sqrt(2)/2) = 2 sin A. So a = 2 sin A.Therefore, substituting back into the equation:b = 2 sin A*(sqrt(2)/2) + sqrt(2) cos A = sqrt(2) sin A + sqrt(2) cos A = sqrt(2)(sin A + cos A).So b = sqrt(2)(sin A + cos A). Then, ab = 2 sin A * sqrt(2)(sin A + cos A) = 2 sqrt(2) sin A (sin A + cos A). Then, the area is (1/2)ab sin C = (1/2)*2 sqrt(2) sin A (sin A + cos A)*(sqrt(2)/2) = (sqrt(2)*sqrt(2)/2) sin A (sin A + cos A) = (2/2) sin A (sin A + cos A) = sin A (sin A + cos A). Which is the same as earlier. Therefore, maximizing sin A (sin A + cos A) = sin² A + sin A cos A, which is the same f(x) as before. So confirms the same result.Therefore, the maximum area is indeed (1 + sqrt(2))/2. Therefore, the answer to part (2) is (1 + sqrt(2))/2.But wait, to be thorough, let me check using the Law of Cosines approach. We have c² = 2 = a² + b² - ab sqrt(2). If we can express a and b in terms of A, then perhaps find the maximum of ab.From above, we have a = 2 sin A and b = sqrt(2)(sin A + cos A). So ab = 2 sin A * sqrt(2)(sin A + cos A) = 2 sqrt(2) sin A (sin A + cos A). We need to maximize this. But this seems more complicated than the previous approach.Alternatively, perhaps parametrize variable A. Let t = A, so 0 < t < 3π/4. Then, ab = 2 sqrt(2) sin t (sin t + cos t). To maximize this expression. Taking derivative:d/dt [2 sqrt(2) sin t (sin t + cos t)] = 2 sqrt(2) [cos t (sin t + cos t) + sin t (cos t - sin t)]= 2 sqrt(2) [cos t sin t + cos² t + sin t cos t - sin² t]= 2 sqrt(2) [2 sin t cos t + cos² t - sin² t]= 2 sqrt(2) [sin 2t + cos 2t]Set derivative to zero:sin 2t + cos 2t = 0Divide both sides by cos 2t (assuming cos 2t ≠ 0):tan 2t + 1 = 0 => tan 2t = -1 => 2t = -π/4 + kπ => t = -π/8 + kπ/2.Within 0 < t < 3π/4, solutions are t = 3π/8 as before. Therefore, same critical point. Therefore, same maximum value. Therefore, confirms the result.Thus, after multiple approaches, the maximum area is (1 + sqrt(2))/2.Final Answer(1) boxed{dfrac{3pi}{4}};(2) boxed{dfrac{1 + sqrt{2}}{2}}</think>Given the problem in triangle ABC with sides a, b, and c opposite angles A, B, and C respectively, and the condition b = a sin C + c cos A:(1) To find the value of A + B:- Using the Law of Sines, we substitute a = 2R sin A, b = 2R sin B, and c = 2R sin C into the given equation.- Simplifying, we find sin B = sin C (sin A + cos A).- Using the identity sin B = sin (A + C) and expanding, we compare both sides to get cos C = sin C, leading to tan C = 1 and thus C = frac{pi}{4}.- Therefore, A + B = pi - C = pi - frac{pi}{4} = frac{3pi}{4}.(2) To find the maximum area of triangle ABC when c = sqrt{2}:- Using the Law of Sines and given c = sqrt{2}, we find the circumscribed circle radius R = 1.- Expressing sides a and b in terms of angles A and B, we use a = 2 sin A and b = 2 sin B.- The area of triangle ABC is given by frac{1}{2}ab sin C, which simplifies to sqrt{2} sin A sin (3pi/4 - A).- Maximizing the expression sin A sin (3pi/4 - A) using calculus, we find the critical point at A = 3pi/8.- Substituting A = 3pi/8 into the area formula, we find the maximum area to be frac{1 + sqrt{2}}{2}. Final Answer(1) boxed{dfrac{3pi}{4}};(2) boxed{dfrac{1 + sqrt{2}}{2}},<think>Okay, let's see. I have this triangle ABC with sides a, b, c opposite angles A, B, C respectively. The given equation is b = a sin C + c cos A. The first part asks for A + B. Hmm. Alright, let me start by recalling some basic triangle relationships. The Law of Sines says that a/sin A = b/sin B = c/sin C = 2R, where R is the circumradius. Maybe that could be helpful. The Law of Cosines is also something to consider: c² = a² + b² - 2ab cos C, and similar for the other angles. Since we have both sine and cosine terms in the given equation, maybe combining these laws could help.So, starting with the given equation: b = a sin C + c cos A.Let me express sin C and cos A in terms of the sides. From the Law of Sines, sin C = c/(2R), and sin A = a/(2R). But not sure if that's the way to go. Alternatively, using the Law of Cosines, cos A = (b² + c² - a²)/(2bc). Hmm, maybe substituting that into the equation?Wait, let's try expressing sin C. From the Law of Sines, sin C = c/(2R), but maybe also from another perspective. Since in any triangle, sin C = sin (π - A - B) = sin (A + B). But not sure if that helps yet.Alternatively, express sin C in terms of sides. Maybe using sin C = c/(2R), and from Law of Sines, a = 2R sin A, so R = a/(2 sin A). Then sin C = c/(2*(a/(2 sin A))) ) = (c sin A)/a. So sin C = (c sin A)/a. Let me check that. Wait, Law of Sines: a/sin A = c/sin C => sin C = (c sin A)/a. Yes, that's correct. So sin C = (c/a) sin A.So substituting back into the equation: b = a sin C + c cos A = a*(c/a sin A) + c cos A = c sin A + c cos A = c (sin A + cos A). So b = c (sin A + cos A). Interesting. So that's an equation involving sides b, c and angle A.From the Law of Sines, we have b/sin B = c/sin C. Also, since in a triangle, angles sum to π, so A + B + C = π. So maybe we can relate angles here. Let's see.From the equation we just derived: b = c (sin A + cos A). Let's express b in terms of sin B. From Law of Sines, b = (c sin B)/sin C. Therefore, (c sin B)/sin C = c (sin A + cos A). Dividing both sides by c: sin B / sin C = sin A + cos A.But angles A + B + C = π, so C = π - A - B. Therefore, sin C = sin(π - A - B) = sin(A + B). So sin C = sin(A + B). Therefore, sin B / sin(A + B) = sin A + cos A.Hmm, complicated. Maybe we can express sin B in terms of A and B? Wait, sin B is just sin B, but since A + B + C = π, and C = π - A - B, so maybe we can write sin B / sin(A + B) = sin A + cos A. Let me write that equation:sin B / sin(A + B) = sin A + cos A.But A + B = π - C, but since C = π - A - B, maybe this is not helpful. Alternatively, let's note that A + B = π - C, so perhaps we can let A + B = θ, which would make C = π - θ. But maybe we need another approach.Alternatively, perhaps express sin B as sin(π - A - C) but I don't think that's helpful. Wait, if we use the equation sin B / sin(A + B) = sin A + cos A. Let's denote θ = A + B. Then, sin B = sin(θ - A). So the equation becomes sin(θ - A)/sin θ = sin A + cos A.Let me write that:sin(θ - A)/sin θ = sin A + cos A.Expanding sin(θ - A) using sine subtraction formula:[sin θ cos A - cos θ sin A]/sin θ = sin A + cos A.Simplify numerator:sin θ cos A - cos θ sin A divided by sin θ:cos A - (cos θ / sin θ) sin A = sin A + cos A.So:cos A - (cos θ / sin θ) sin A = sin A + cos A.Subtract cos A from both sides:- (cos θ / sin θ) sin A = sin A.Bring all terms to one side:- (cos θ / sin θ) sin A - sin A = 0Factor out sin A:sin A (-cos θ / sin θ - 1) = 0.So either sin A = 0 or (-cos θ / sin θ - 1) = 0.But in a triangle, angles are between 0 and π, so sin A = 0 would imply A = 0 or π, which is impossible. Therefore, the other factor must be zero:-cos θ / sin θ - 1 = 0.Multiply both sides by sin θ:-cos θ - sin θ = 0.So:-cos θ - sin θ = 0 => sin θ + cos θ = 0.Divide both sides by cos θ (assuming cos θ ≠ 0):tan θ + 1 = 0 => tan θ = -1.Therefore, θ = arctan(-1). But θ is A + B, which is part of a triangle, so θ must be between 0 and π. The solutions for tan θ = -1 in (0, π) are θ = 3π/4. Because tan(3π/4) = -1.Therefore, θ = 3π/4. Therefore, A + B = 3π/4 radians, which is 135 degrees. So that's the answer to part (1): A + B = 3π/4.Wait, let me check if that makes sense. If A + B = 3π/4, then angle C = π - (A + B) = π - 3π/4 = π/4. So angle C is 45 degrees. Let me verify if that holds with the original equation. Let's suppose angle C is 45 degrees. Let me take a sample triangle where C is 45 degrees and check if the equation holds.Suppose angle C = 45°, so angle A + B = 135°. Let's pick specific angles. For simplicity, let’s say angle A is 45°, angle B is 90°, angle C is 45°. Wait, but angle sum would be 45 + 90 + 45 = 180, which is okay. Then sides: using Law of Sines. Let’s let side c be opposite angle C = 45°, so c = √2 (as given in part 2). Then, side a is opposite angle A = 45°, so a = c * sin A / sin C = √2 * sin 45° / sin 45° = √2. Side b is opposite angle B = 90°, so b = c * sin B / sin C = √2 * sin 90° / sin 45° = √2 * 1 / (√2/2) ) = √2 * 2/√2 = 2. Now check the equation: b = a sin C + c cos A. Plug in the values: 2 = √2 * sin 45° + √2 * cos 45°. sin 45° = √2/2, cos 45° = √2/2. So: 2 = √2*(√2/2) + √2*(√2/2) = (2/2) + (2/2) = 1 + 1 = 2. Correct. So in this case, the equation holds. So that's a valid case.Alternatively, maybe angle A is 30°, angle B = 135° - 30° = 105°, angle C = 45°. Let’s compute sides. Let’s take c = √2. Then a = c * sin A / sin C = √2 * sin 30° / sin 45° = √2 * (1/2) / (√2/2) ) = √2 * (1/2) * 2/√2 = 1. Then side b = c * sin B / sin C = √2 * sin 105° / sin 45°. Sin 105° = sin(60° + 45°) = sin60 cos45 + cos60 sin45 = (√3/2)(√2/2) + (1/2)(√2/2) = √6/4 + √2/4 = (√6 + √2)/4. So b = √2 * (√6 + √2)/4 / (√2/2) = √2 * (√6 + √2)/4 * 2/√2 = (√6 + √2)/2. Now check the equation: b = a sin C + c cos A. a =1, sin C = sin45 = √2/2, c =√2, cos A = cos30 = √3/2. So right side: 1*(√2/2) + √2*(√3/2) = √2/2 + √6/2 = (√2 + √6)/2. Which is equal to b. So the equation holds. So indeed, with A + B = 3π/4, the equation is satisfied. Therefore, the answer to part (1) is 3π/4.Now part (2): If c = √2, find the maximum area of triangle ABC.Alright, so c is fixed at √2. We need to maximize the area. Let's recall that the area of a triangle is (1/2)ab sin C. Alternatively, since we know sides and angles, maybe express the area in terms of angle A or B.But given that in part (1), we found that A + B = 3π/4, so angle C = π/4. Wait, angle C is fixed at π/4 (45 degrees). Wait, but if angle C is fixed, then the triangle has one fixed angle, and sides related accordingly. But c is fixed as √2. So maybe the triangle has fixed side c = √2 opposite angle C = π/4, and angles A and B such that A + B = 3π/4. So the triangle is determined by angles A and B with A + B = 3π/4, and side c = √2. Then to maximize the area.But if angle C is fixed, and side c is fixed, then the area can be expressed in terms of sides a and b. Since area = (1/2)ab sin C. Since C is π/4, sin C = √2/2. So area = (1/2)ab*(√2/2) = (ab √2)/4. So to maximize the area, we need to maximize ab.Alternatively, since from the Law of Sines, a/sin A = b/sin B = c/sin C. Given c = √2 and angle C = π/4, so sin C = √2/2. Therefore, a = (c / sin C) * sin A = (√2 / (√2/2)) * sin A = (√2 * 2 / √2) * sin A = 2 sin A. Similarly, b = 2 sin B. Since A + B = 3π/4, B = 3π/4 - A. Therefore, sin B = sin(3π/4 - A) = sin(3π/4) cos A - cos(3π/4) sin A = (√2/2) cos A - (-√2/2) sin A = (√2/2)(cos A + sin A). Therefore, b = 2 * (√2/2)(cos A + sin A) = √2 (cos A + sin A).But since a = 2 sin A, and b = √2 (sin A + cos A). Then the product ab = 2 sin A * √2 (sin A + cos A) = 2√2 sin A (sin A + cos A). So area = (ab √2)/4 = (2√2 sin A (sin A + cos A) * √2)/4 = (2*2 sin A (sin A + cos A))/4 = (4 sin A (sin A + cos A))/4 = sin A (sin A + cos A). Therefore, the area simplifies to sin A (sin A + cos A). So we need to maximize sin A (sin A + cos A) where A is between 0 and 3π/4, since A + B = 3π/4 and angles must be positive.Let’s set f(A) = sin A (sin A + cos A) = sin² A + sin A cos A. We can write this as f(A) = sin² A + (1/2) sin 2A. To find the maximum, take derivative f’(A), set to zero.First, compute derivative:f’(A) = 2 sin A cos A + (1/2)(2 cos 2A) = 2 sin A cos A + cos 2A.Simplify:2 sin A cos A = sin 2A, so f’(A) = sin 2A + cos 2A.Set derivative equal to zero:sin 2A + cos 2A = 0.Let me solve this equation:sin 2A = -cos 2A.Divide both sides by cos 2A (assuming cos 2A ≠ 0):tan 2A = -1.Solutions are 2A = arctan(-1) + kπ. Since A is between 0 and 3π/4, 2A is between 0 and 3π/2. arctan(-1) is -π/4, but adding π gives 3π/4, and adding 2π gives 7π/4, but 7π/4 is beyond 3π/2. So possible solutions in the interval are 2A = 3π/4 or 2A = 7π/4. But 7π/4 is 315 degrees, but 2A can't be more than 3π/2 (270 degrees). Wait, 3π/2 is 270 degrees. So 2A = 3π/4 => A = 3π/8, or 2A = 7π/4 => A = 7π/8. But 7π/8 is 157.5 degrees, which would make angle B = 3π/4 - 7π/8 = (6π/8 - 7π/8) = -π/8, which is invalid because angles can't be negative. So only valid solution is 2A = 3π/4 => A = 3π/8. Therefore, the critical point is at A = 3π/8.Now we need to check if this is a maximum. Let's check the second derivative or test intervals around 3π/8.Alternatively, compute f(A) at A = 3π/8, and endpoints. Since A is between 0 and 3π/4, endpoints are A approaching 0 and A approaching 3π/4.First, compute f(3π/8):sin(3π/8) ≈ sin(67.5°) ≈ 0.9239Compute sin²(3π/8) + sin(3π/8) cos(3π/8):First, sin(3π/8) ≈ 0.9239, cos(3π/8) ≈ 0.3827So sin² ≈ 0.8536, sin * cos ≈ 0.9239 * 0.3827 ≈ 0.3536. Sum ≈ 0.8536 + 0.3536 ≈ 1.2072.Now check endpoints:As A approaches 0, sin A approaches 0, so f(A) approaches 0.As A approaches 3π/4, B approaches 0. So angle A approaches 3π/4, angle B approaches 0. Then sin A approaches sin(135°) = √2/2 ≈ 0.7071. So f(A) = sin² A + sin A cos A. sin² A ≈ 0.5, sin A cos A ≈ 0.7071 * (-√2/2) ≈ -0.5. Wait, cos(3π/4) = -√2/2. Wait, but angle A is approaching 3π/4, so cos A approaches -√2/2 ≈ -0.7071. Then sin A cos A ≈ (√2/2)(-√2/2) = -0.5. So f(A) approaches 0.5 - 0.5 = 0. Therefore, as A approaches 3π/4, f(A) approaches 0.Therefore, the maximum occurs at A = 3π/8, with value approximately 1.2072. But let's compute it exactly.Express sin(3π/8) and cos(3π/8):3π/8 is 67.5 degrees. We can use exact values.sin(67.5°) = sin(45° + 22.5°) = sin45 cos22.5 + cos45 sin22.5.cos(67.5°) = cos(45° + 22.5°) = cos45 cos22.5 - sin45 sin22.5.Alternatively, we can use half-angle formulas.We know that sin(22.5°) = √(2 - √2)/2, cos(22.5°) = √(2 + √2)/2.Therefore, sin(67.5°) = sin(45° + 22.5°) = sin45 cos22.5 + cos45 sin22.5 = (√2/2)(√(2 + √2)/2) + (√2/2)(√(2 - √2)/2) = √2/4 [√(2 + √2) + √(2 - √2)].Similarly, cos(67.5°) = cos(45° + 22.5°) = cos45 cos22.5 - sin45 sin22.5 = (√2/2)(√(2 + √2)/2) - (√2/2)(√(2 - √2)/2) = √2/4 [√(2 + √2) - √(2 - √2)].But this might get complicated. Alternatively, note that sin(67.5°) = sin(π/2 - π/8) = cos(π/8), and cos(67.5°) = sin(π/8). So sin(3π/8) = cos(π/8), cos(3π/8) = sin(π/8).Therefore, f(A) = sin²(3π/8) + sin(3π/8) cos(3π/8) = cos²(π/8) + cos(π/8) sin(π/8).Alternatively, compute it using exact values.We can compute sin(3π/8):sin(3π/8) = √(2 + √2)/2 ≈ 0.9239cos(3π/8) = √(2 - √2)/2 ≈ 0.3827Therefore, sin²(3π/8) = (2 + √2)/4, and sin(3π/8) cos(3π/8) = [√(2 + √2)/2][√(2 - √2)/2] = [√{(2 + √2)(2 - √2)}]/4 = √(4 - 2)/4 = √2/4.Therefore, f(A) = (2 + √2)/4 + √2/4 = (2 + √2 + √2)/4 = (2 + 2√2)/4 = (1 + √2)/2.Therefore, the maximum area is (1 + √2)/2. So when c = √2, the maximum area of the triangle is (1 + √2)/2.But let me verify this with another approach. Maybe using the formula for area in terms of two sides and included angle. Since we have sides a and b, and angle C between them? Wait, but in our case, sides a and b are not necessarily the sides enclosing angle C. Wait, in triangle ABC, side a is opposite angle A, side b opposite angle B, side c opposite angle C. So angle C is between sides a and b. Wait, no, angle C is opposite side c, so the sides adjacent to angle C are a and b. Therefore, the area can also be expressed as (1/2)ab sin C. Which is what I used earlier. Since angle C is π/4, so sin C = √2/2, so area = (ab √2)/4. Then since a = 2 sin A and b = √2 (sin A + cos A), then ab = 2 sin A * √2 (sin A + cos A) = 2√2 sin A (sin A + cos A). Then area = (2√2 sin A (sin A + cos A) * √2)/4 = (4 sin A (sin A + cos A))/4 = sin A (sin A + cos A), which simplifies to the same expression as before. So that checks out.Therefore, the maximum area is (1 + √2)/2. To confirm, let's compute this value numerically: (1 + 1.4142)/2 ≈ 2.4142/2 ≈ 1.2071, which matches the approximate calculation earlier.Alternatively, is there another way to maximize the area? Maybe using calculus of variations or other trigonometric identities? Let me think. Alternatively, express f(A) = sin² A + sin A cos A. Let's write this as:f(A) = (1 - cos 2A)/2 + (sin 2A)/2 = 1/2 - (cos 2A)/2 + (sin 2A)/2 = 1/2 + (sin 2A - cos 2A)/2.To find maximum of (sin 2A - cos 2A). The maximum of sin x - cos x is √2, achieved when x = 3π/4. Therefore, sin 2A - cos 2A = √2 sin(2A - π/4). So maximum value is √2. Therefore, maximum of (sin 2A - cos 2A)/2 = √2/2. Therefore, maximum f(A) = 1/2 + √2/2 = (1 + √2)/2. Same result. So that's another way to confirm. Therefore, the maximum area is indeed (1 + √2)/2.Therefore, the answer to part (2) is (1 + √2)/2.Final Answer(1) boxed{dfrac{3pi}{4}} (2) boxed{dfrac{1 + sqrt{2}}{2}}</think>Given a triangle ( triangle ABC ) with sides ( a ), ( b ), and ( c ) opposite to angles ( A ), ( B ), and ( C ) respectively, we know that ( b = a sin C + c cos A ). Part (1): Finding the value of ( A + B )1. Start with the given equation: ( b = a sin C + c cos A ).2. Using the Law of Sines, express ( sin C ) as ( frac{c sin A}{a} ).3. Substitute this into the equation: ( b = a left( frac{c sin A}{a} right) + c cos A ), simplifying to ( b = c (sin A + cos A) ).4. Using the Law of Sines again, express ( b ) as ( frac{c sin B}{sin C} ).5. Substitute ( sin C = sin(A + B) ) and simplify to find ( sin B / sin(A + B) = sin A + cos A ).6. Solve the trigonometric equation to find ( A + B = frac{3pi}{4} ). Part (2): Finding the maximum area of ( triangle ABC ) when ( c = sqrt{2} )1. Given ( c = sqrt{2} ) and ( A + B = frac{3pi}{4} ), angle ( C = frac{pi}{4} ).2. Express the area of the triangle as ( frac{1}{2} ab sin C ).3. Using the Law of Sines, express ( a ) and ( b ) in terms of angles ( A ) and ( B ).4. Substitute ( B = frac{3pi}{4} - A ) and convert the area expression into a function of ( A ).5. Maximize the function ( sin A (sin A + cos A) ) by solving its derivative and finding critical points.6. Determine the maximum value of the area, which simplifies to ( frac{1 + sqrt{2}}{2} ). Final Answers(1) (boxed{dfrac{3pi}{4}}) (2) (boxed{dfrac{1 + sqrt{2}}{2}})]

🔑:(1) In triangle ABC, we have b = a sin C + c cos A. By the sine rule, we get:sin B = sin A sin C + sin C cos AAlso,sin B = sin[pi - (A + C)] = sin(A + C) = sin C cos A + cos C sin AThus,cos C sin A = sin A sin CSince A in (0, pi), we know that sin A neq 0. Therefore,cos C = sin C,which implies thattan C = 1.Since C in (0, pi), we haveC = frac{pi}{4}.Hence,A + B = frac{3pi}{4}.(2) By the cosine rule, we have:c^2 = a^2 + b^2 - 2ab cos CSubstituting the given value of c, we get:2 = a^2 + b^2 - sqrt{2}abRearranging the terms, we obtain:2 + sqrt{2}ab = a^2 + b^2 geq 2abSolving for ab, we get:ab leq frac{2}{2 - sqrt{2}} = 2 + sqrt{2}The equality holds if and only if a = b = sqrt{2 + sqrt{2}}. The area of the triangle is given by:S_{triangle ABC} = frac{1}{2}ab sin CSubstituting the maximum value of ab and the value of C, we get:S_{triangle ABC} leq frac{1}{2} times (2 + sqrt{2}) times frac{sqrt{2}}{2} = boxed{frac{1 + sqrt{2}}{2}}